南京工业大学期末高等数学A试卷A
高等数学a上期末考试试题和答案

高等数学a上期末考试试题和答案高等数学A上期末考试试题一、选择题(每题3分,共30分)1. 极限的定义是()。
A. 函数在某点的值B. 函数在某点的增量C. 函数在某点的导数D. 函数在某点的无穷小答案:D2. 函数f(x)=x^2在x=0处的导数是()。
A. 0B. 1C. 2D. 3答案:C3. 定积分∫₀¹x²dx的值是()。
A. 1/3B. 1/2C. 1D. 2答案:C4. 函数f(x)=sinx在x=π/2处的值是()。
A. 0B. 1C. -1D. π/2答案:B5. 函数f(x)=e^x的原函数是()。
A. e^xB. e^(-x)C. ln(x)D. x答案:A6. 函数f(x)=x^3-3x^2+2的极值点是()。
A. 0B. 1C. 2D. 3答案:B7. 函数f(x)=x^2+2x+1的最小值是()。
A. 0B. 1C. 2D. 3答案:B8. 函数f(x)=ln(x)的定义域是()。
A. (-∞, 0)B. (0, +∞)C. (-∞, +∞)D. [0, +∞)答案:B9. 函数f(x)=x^3-6x^2+11x-6的拐点是()。
A. 1B. 2C. 3D. 4答案:B10. 函数f(x)=x^4-4x^3+6x^2-4x+1的零点是()。
A. 0B. 1C. 2D. 3答案:B二、填空题(每题3分,共30分)11. 函数f(x)=x^3-3x^2+2的导数是______。
答案:3x^2-6x12. 函数f(x)=e^x的二阶导数是______。
答案:e^x13. 函数f(x)=ln(x)的不定积分是______。
答案:xln(x)-x+C14. 函数f(x)=x^2-4x+4的顶点坐标是______。
答案:(2, 0)15. 函数f(x)=sinx+cosx的周期是______。
答案:2π16. 函数f(x)=x^3-3x^2+2的单调增区间是______。
高等数学期末考试A(附答案)

-------------------------------------密-----------------------封-----------------------线---------------------------------系部___________ 班级___________ 考场_________ 姓名______________ 学号_________高等数学期末试卷(A )一、选择题(共25小题,每题2分,共计50分) 1.下列各对函数定义域相同的是( ).A.2)()(,)(x x g x x f ==B.x x g x x f ==)(,)(2C.x x g x x f lg 2)(,lg )(2== D.11)(,1)(2--=+=x x x g x x f2.下列函数在其定义域内不是奇函数的是( ). A.x y sin = B.x y cos = C.x y tan = D.x x y -=33.函数)(x f 在0x x =处有定义是0x x →时)(x f 有极限的( ). A 必要条件 B 充分条件 C 充要条件 D.无关条件 4.下列各式中正确的是( ). A.0sin lim0=→x x x B.1sin lim =∞→x x x C.e n n x =+∞→)11(lim D.e nx =+→)11(lim 05.=+→xx x 1)41(lim ( ).A.4-eB.4e C.41e D.41-e6.=→xxx 5tan 3tan lim( ). A .1 B.53 C.35D.07.设)2(x f y -=,则='y ( ).A.)2(x f 'B.)2(x f -'-C.)2(x f -'D.)2(2x f -'-8.设函数⎩⎨⎧≥+<=0,0,)(x x a x e x f x ,是),(+∞-∞上的连续函数,则)(=aA. 0B.1C.1-D.2 9.下列各式错误的是( ).A.1-)(μμμx x ='B.a a a x x ln )(⋅='C.x x cos )(sin ='D.x x sin )(cos =' 10.函数)(x f 在0x 处连续是)(x f 在0x 处可导的( ).A.必要条件B.充分条件C.充要条件D.无关条件 11.函数2)(-=x x f 在点2=x 处的导数为( ). A.1 B.0 C.1- D.不存在12.设x 为自变量,当,1=x 0=∆x .1时,=)(3x d ( ). A.3.0 B.0 C.01.0 D.03.013.设)(),(x v v x u u ==都是可微函数,则=)(uv d ( ). A.vdv udu + B.du v dv u '+' C.vdu udv + D.vdu udv -14.设曲线22++=x x y 在点M 处的切线斜率为3,则点M 的坐标为( ). A.)(4,1 B.)(1,4 C.)0,1( D.)1,0( 15.已知函数⎩⎨⎧>≤-=-,0,0,1)(x e x x x f x 则)(x f 在0=x 处( ).A.间断B.连续但不可导C.1)0(-='fD.1)0(='f 16.若)(x f 在点a x =的邻域内有定义,且除去点a x =外恒有0)()()(2>--a x a f x f ,则以下结论正确的是( ).A.)(x f 在点a 的邻域内单调增加B.)(x f 在点a 的邻域内单调减少C.)(a f 为函数)(x f 的极大值D.)(a f 为函数)(x f 的极小值 17.函数)(x f y =在点0x 处取极大值,则必有( ).A.0)(0='x fB.0)(0<''x fC.0)(0='x f ,0)(0<''x fD.0)(0='x f 或)(0x f '不存在 18.下列函数在其定义域内不是单调递增的是( ).A.x x x f 2)(3+=B.)1ln()(2x x x f +-=C.x x x f cos )(+=D.3)1)(1()(+-=x x x f 19.下列极限计算正确的是( ).A.626lim )2(223lim )2(42lim 222232==--=---→→→x x x x x x x x x B.6122lim 222lim )2()22)(2(lim )2(42lim 222222232=+=-++=-++-=---→→→→x x x x x x x x x x x x x x x C.∞=--=---→→)2(223lim )2(42lim 22232x x x x x x x D.不存在2232232)2(lim )42(lim )2(42lim---=---→→→x x x x x x x x x20.当0→x 时,1)1(212-+ax与x cos 1-为等价无穷小,则=a ( ).x2A.1 B.0 C.1- D.常数21.设)(x f 是可导函数,则))(('⎰dx x f 为( ). A.)(x f B.C x f +)( C.)(x f ' D.C x f +')( 22.下列等式中成立的是( ).A.⎰=)()(x f dx x f dB.⎰=dx x f dx x f dxd)()(C.⎰+=c x f dx x f dxd)()( D.dx x f dx x df )()(= 23.在区间),(b a 内,如果)()(x g x f '=',则下列各式中一定成立的是( ). A.)()(x g x f = B.1)()(+=x g x f C.))(())(('='⎰⎰dx x g dx x f D.⎰⎰'='dx x g dx x f )()( 24.)(x f 在区间[]b a ,上连续,则⎰⎰-babadt t f dx x f )()(( ).A. 小于零B.等于零C.大于零D.不确定25.用定积分表示右图x y 2=,2=x 和x 轴围成的面积,正确的是( A.⎰212xdx B.⎰22xdx C.⎰xtdt 02 D.⎰22xtdt二、填空题(共5小题,每题2分,共计10分) 26.(=dx ))32(x d - )()(xxe d dx e --=.27.设n n n n a x a x a x a x f ++++=--1110)( ,则[]=')0(f .28.若函数bx ax x f +=2)(在点1=x 处取极大值2,则=a ,=b .29.设⎰=xx e dt t f 02)(,则=)(x f .30.判断下列两个定积分的大小,⎰12dx x⎰13dx x . 三、判断题(共5小题,每题2分,共计10分) 31.驻点一定是极值点.( )32.可导一定连续,连续不一定可导.( )33.设函数)(x f 在0x 处具有二阶导数,且0)(,0)(00≠''='x f x f ,则当0)(0<''x f 时,)(x f 在点0x 处取极大值.( )34.若函数)(x f 在[]b a ,上连续,在),(b a 内可导,则在),(b a 内至少存在一点)(b a <<ξξ,使得0)(='ξf .( )35.1)21(211122222-=-+-=⎥⎦⎤⎢⎣⎡-=⎰--x dx x .( )四、求下列各式的极限(共2小题,每题4分,共计8分)36.xe e xx x 20lim-→- 37.xdt txa tx ⎰++∞→)11(lim )0(>a五、计算下列不定积分(共2小题,每题4分,共计8分) 38.⎰+dx x )23sin( 39.⎰xdx x cos六、计算下列定积分(共1小题,共计4分)40.⎰-17)12(dx x七、综合题(共1小题,共计10分)41.平面图形D 由抛物线2x y =,1=x 和x 轴组成,请 (1)画出D 的草图 (2)求D 的面积答案:一、选择题(共25小题,每题2分,共计50分)1.B 2.B 3.D 4.C 5.B 6.B 7.D 8.B 9.D 10.A. 11.D 12.A 13.C 14.A 15.C 16.D 17.D 18.D 19.C 20.A 21.A. 22.D 23.C 24.B 25.B二、填空题(共5小题,每题2分,共计10分)26.31- - 27.0 28.=a -2 =b 4 29.=)(x f x e 22 30.>三、判断题(共5小题,每题2分,共计10分) 31.× 32.√ 33.√ 34.× 5.× 四、求下列各式的极限(共2小题,共计8分)36.x e e xx x 20lim -→-=1)2(lim 20x e e x x x ---→————3分=1————————————1分37.x dt t xa t x ⎰++∞→)11(lim )0(>a =1)11(lim x x x ++∞→——3分 =e ————1分五、计算下列不定积分(共2小题,共计8分) 38.⎰+dx x )23sin(=⎰++)23()23sin(31x d x ——2分 =C x ++-)23cos(31————2分39.⎰xdx x cos =⎰x xd sin ——2分=⎰-xdx x x sin sin ————1分 =C x x x ++cos sin ————1分六、计算下列定积分(共1小题,共计4分)40.⎰-107)12(dx x =⎰--107)12()12(21x d x ——2分=108])12(81[21-⋅x ————1分 =0]11[161=-————1分七、综合题(共1小题,共计10分) 41.(1)略————5分(2)⎰=12dx x D ————3分=10331⎥⎦⎤⎢⎣⎡x ————1分 =31——————1分。
高等数学A-1试卷A(10.01)

南京工业大学高等数学A-1试卷(江浦A 卷、闭)2009-2010学年第一学期一、选择题(每小题3分, 共12分)1、设的是,则)(01arctan )(x f x xx x f =⋅=( ))(A 可去间断点 )(B 跳跃间断点 )(C 连续点 )(D 第二类间断点2、设,2sin )(,11)(32x x g x x x f =-++=则当0→x 时 ( ))(A )()(x g x f 是的高阶无穷小量 )(B )()(x g x f 是的低阶无穷小量 )(C )()(x g x f 是的是同阶但非等价无穷小量 )(D )()(x g x f 与是等价无穷小量3、设函数()f x 在(,)-∞+∞连续,在(,0)(0,)-∞+∞内具有二阶导数,其导函数()f x '的图像如图,则()f x ( ))(A 有两个极大值点和一个极小值点,曲线)(x f y =有一个拐点)(B 有一个极大值点和两个极小值点,曲线)(x f y =有一个拐点)(C 有一个极大值点和一个极小值点,曲线)(x f y =有两个拐点)(D 有两个极大值点和两个极小值点,曲线)(x f y =有一个拐点4、下列广义积分中收敛的是 ( ))(A dx xx eln 1⎰+∞ )(B dx xx e2ln 1⎰+∞ )(C dx x x e ln ⎰+∞ )(D dx x x e 2ln ⎰∞+二、填空题(每空3分, 共12分,把答案填在题中横线上) 1、设)0('f 存在,则=-→xx f f x )2()0(lim_____________________。
2、xoy 面内的曲线1:22=-y x C 绕x 轴旋转一周所生成的曲面方程为_______________________________。
3、已知⎰-⋅=Φx dt t x f t x 022)()(,则=Φ')(x ________________________。
南京工业大学期末考试(A)卷

南京工业大学期末考试(A)卷课程:«化工原理»(上册)每题1.(1) x01a05155如图所示,若敞口罐液面恒定,罐上方压强为Pa,忽略流动阻力损失,出水管管径为d,则出水管的出口速度u与有关。
(A)H(B)H、d(C)d(D)Pa(E)H、d、Pa水有一并联管路,两段管路的流量,流速、管径、管长及流动阻力损失分别为V1,u1,d1,l1,hf1及V2,u2,d2,l2,hf2。
若d1=2d2,l1=2l2,则:①hf1/hf2=()(A)2(B)4(C)1/2;(D)1/4(E)1②当两段管路中流体均作滞流流动时,V1/V2=()(A)2(B)4(C)8(D)1/2(E)1(3)x01b05043转子流量计的主要特点是()(A)恒截面、恒压差(B)变截面、变压差(C)恒流速、恒压差(D)变流速、恒压差2.X02a05106⑴已知流体经过泵后,压力增大∆P N/m2,则单位重量流体压能的增加为()(A)∆P (B)∆P/ρ (C)∆P/ρg (D)∆P/2g⑵离心泵的下列部分是用来将动能转变为压能()(A)泵壳和叶轮(B)叶轮(C)泵壳(D)叶轮和导轮3.x03a05095(1)过滤介质阻力忽略不计,滤饼不可压缩进行恒速过滤时,如滤液量增大一倍,则___ (A)操作压差增大至原来的√2倍(B)操作压差增大至原来的4倍(C)操作压差增大至原来的2倍(D)操作压差保持不变(2)恒压过滤时,如介质阻力不计,过滤压差增大一倍时同一过滤时刻所得滤液量___ (A)增大至原来的2倍(B)增大至原来的4倍(C)增大至原来的√2倍(D)增大至原来的1.5倍4.x04a05056比较下列对流给热系数的大小空气流速为6m/s的α1,空气流速为25m/s的α2,水流速为1.2m/s的α3,水流速为2.5m/s的α4,蒸汽膜状冷凝的α5,自大到小的顺序为:> > > >二、填空题:(每题5分,共20分)1.t01b05027①1atm=__________kN/m2。
2020-2021大学《高等数学》(下)期末课程考试试卷A2(含答案)

2020-2021《高等数学》(下)期末课程考试试卷A2适用专业: 考试日期:试卷类型:闭卷 考试时间:120分钟 试卷总分:100分一. 判断题(每小题2分,共10分)1.二元函数(),z f x y =在平面区域上的积分为二重积分。
( )2.二元函数(),z f x y =的极值点只能是使得0z zx y∂∂==∂∂的点。
( )3.二元函数z =在()0,0点连续但偏导数不存在。
( )4.闭区域上的二元连续函数一定存在最大最小值,且一定可积。
( )5.二元函数z =在()0,0点连续但偏导数不存在。
( )二.单项选择题(每小题2分,共20分)1.平面2y = ( ) A.垂直于xOz 平面 B.平行于xOy 平面 C.平行于xOz 平面 D. 平行于Oy 轴2. 二元函数(),z f x y =在某点()00,x y 连续,那么(),z f x y =在该点一定 ( )A .极限存在 B.两个偏导存在 C.可微 D.以上都不对3. 极限()(),0,0lim x y xyx y→+的结果为 ( )A.0B.∞C. 12D.不存在4.若区域D 是由1x y +≤与12x y +≥所围成,则积分()22ln Dx y d σ+⎰⎰的值( )A.大于零B. 小于零C.等于零D. 不存在 5.下列绝对收敛的级数是 ( )A.∑∞=--1n nn1n 23)1( B.∑∞=--1n 1n n )1(C.∑∞=--1n 51n n)1(D.∑∞=--1n n 21)1(6. 下列无穷级数中发散的无穷级数是 ( )A.∑∞=+1n 221n 3n B. ∑∞=+-1n n 1n )1(C. ∑∞=--3n 1n n ln )1(D. ∑∞=+1n 1n n32 7. 点(0,0,1)到平面z=1的距离为 ( ) A .0 B .1 C .2 D .38. 积分2011dx x +∞+⎰的结果为 ( )A.0B. 2πC. 2π-D.不存在9. 函数()arctan f x x =在 []0,1上,使拉格朗日中值定理成立的ξ是( )A.-10.设()f x 在(),a b 内满足()'0f x <,()''0f x >,则曲线()f x 在(),a b 内是( )A.单调上升且是凹的B. 单调下降且是凹的C.单调上升且是凸的D. 单调下降且是凸的三.填空题(每小题2分,共10分) 1. 设函数z x y =-,则xz∂∂=___________。
南京工业大学2012-2013高等数学期末试卷A及答案

南京工业大学2012-2013高等数学期末试卷A 及答案一、填空题(每小题3分,共36分)1.=⎪⎪⎭⎫⎝⎛+∞→∞→x y x xy 11lim ==⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+∞→∞→∞→∞→⋅∞→∞→01lim111lim 11lim e xy xy yxyy x yxy y x y x 1 .2.函数),(y x z z =由方程0sin =+x y e xz 确定,则=-=-=∂∂xz z y xe x y x F F y z cos 1xz ex x y 2cos - . 3.设函数222lnz y x u ++=,则它在点)1,1,1(0-M 处的方向导数的最大值为33. 4.设函数y xy ax x y x f 22),(22+++=在点)1,1(-处取得极值,则常数=a 5-.5.空间曲线x z x y -==1,222在点)22,1,21(处的切线方程为 212211121--=-=-z y x .6.改变积分次序:==⎰⎰-dy y x f dx I x x 22020),(dx y x f dy y y ⎰⎰-+--2211111),( .7.设平面曲线L 为下半圆周21x y --=,则=⋅=⋅=+⎰⎰π2221211)(LLds ds y x π . 8.设∑为曲面22y x z +=在10≤≤z 的部分,则⎰⎰∑=xdS 0 .9.设,0,10,)(⎩⎨⎧<≤<≤-=-ππx x e x f x 则其以π2为周期的傅里叶级数在π=x 处收敛于)1(21πe + . 10.设321,,y y y 是微分方程)()()(x f y x q y x p y =+'+''的三个不同的解,且≠--3221y y y y 常数,则微分方程的通解为 1322211)()(y y y C y y C +-+- .11.函数x x f -=21)(展开为x 的幂级数的形式为)2,2(2101-∈∑∞=+x x nn n .12.微分方程x xe y xy =-'1的通解为 x xe Cx + . 二、计算下列各题(每小题6分,共18分)1.设),(xye xy f z =,)(x y ϕ=,其中ϕ,f 均为一阶可微函数,求dxdz . 解:)(221y x y e f xy x y f dx dz xy'+⋅'+-'⋅'= ))()(()()(221x x x e f xx x x f xyϕϕϕϕ'+⋅'+-'⋅'= 2.求曲面)(21422y x z +-=与平面2=z 所围立体的体积.解:所围立体在xoy 面的投影域4:22≤+y x D ,所围立体的体积 dxdy y x dxdy dxdy y x V D DD ⎰⎰⎰⎰⎰⎰+-=⎭⎬⎫⎩⎨⎧-+-=)(2122)](214[2222 πππθππ4482122202202=-=-⨯=⎰⎰rdr r d3.在曲面6632222=++z y x 上第一卦限部分求一点,使该点的切平面与已知平面1=++z y x 平行.解:设曲面在第一卦限的切点的坐标为),,(z y x M ,令=),,(z y x F 6632222-++z y x ,则切平面的法向量)6,4,2(),,(z y x F F F n M z y x ==, 已知平面1=++z y x 的法向量)1,1,1(1=n依题意1//n n,即令t z y x ===161412 代入曲面方程中解的2,3,6===z y x ,即切点坐标为)2,3,6(M . 三、计算下列各题(每小题6分,共18分) 1.设Ω是由锥面22y x z +=与半球面221y x z --=围成的空间区域,∑是Ω的整个边界的外侧,求曲面积分⎰⎰∑++zdxdy ydzdx xdydz .解:已知x z y x P =),,(,y z y x Q =),,(,z z y x R =),,(,由高斯公式有dv zR y Q x P zdxdy ydzdx xdydz ⎰⎰⎰⎰⎰Ω∑∂∂+∂∂+∂∂=++)(dr r d d dv ϕϕθππsin 33122040⎰⎰⎰⎰⎰⎰==Ωππ)22(31)221(23-=⨯-⨯⨯= 2.写出级数++++43227252321的通项,判别该级数的敛散性.若级数收敛时,试求其和. 解:该数项级数的通项为nn n u 212-=;级数为正项级数,由于 21121221lim lim1=-+⋅=∞→+∞→n n u u n nn n ,由比值审敛法知该级数收敛.令)1,1()()(22)12()(211111-∈-=-=-=∑∑∑∞=∞=-∞=x x s x xs x xn x x n x s n n n n nn ,则xxx dt ntdt t s n xn n n x-===∑⎰∑⎰∞=∞=-1)(1111, 于是2011)1(1)()(x dtt s dx d x s x -=⎥⎦⎤⎢⎣⎡=⎰, 又xxx x s n n -==∑∞=1)(12, 所以)1,1()1(1)1(2)(222-∈-+=---=x x x x x x x x x s ,于是3)1(21)12()21(21221=⎥⎦⎤⎢⎣⎡-+=-==∞=∑x n n x x x n s .3.求微分方程x e y y y 223=+'-''的通解.解:微分方程对应的齐次线性微分方程的特征方程0232=+-r r 的特征根为2,121==r r ,x e x f 2)(=的1=λ为特征方程的单根,则原方程的特解为x Axe y =*,代入原方程中得2-=A ,齐次线性微分方程的通解为x x e C e C Y 221+=,所以原方程的通解为=+=*y Y y x x x xe e C e C 2221-+.四、计算下列各题(每小题6分,共18分) 1.求函数22)(4),(y x y x y x f ---=的极值.解:由于x y x f x 24),(-=,y y x f y 24),(--=,令,0),(0),(⎩⎨⎧==y x f y x f yx 得驻点,22⎩⎨⎧-==y x 又 2),(-==y x f A xx ,0),(==y x f B xy ,2),(-==y x f C yy ,及4)()2,2(2-=--AC B , 则点)2,2(-位极大值点,极大值为8)2(2)]2(2[4)2,2(22=-----=-f .2.求幂级数∑∞=-12)1(n nnn x 的收敛半径及收敛域. 解:令 1-=x t ,则 nn nn n n t n n x ∑∑∞=∞==-11212)1(,由于 212)1(2lim lim 11=+=+∞→+∞→n n n nn n n n a a , 则收敛半径2=R .又当2-=t 时,级数∑∞=-1)1(n nn 收敛,当2=t 时,级数∑∞=11n n 发散,所以)2,2[-∈t ,即级数的收敛域为)3,1[-.3.设),()sin(y x x xy z ϕ+=,其中),(v u ϕ具有二阶偏导数,求yx z∂∂∂2.解:),(1),()cos(21yxx y y x x xy y x z ϕϕ'+'+=∂∂,)(),(1),(1)(),()sin()cos(222222122yxy x x y y x x y y x y x x xy xy xy y x z -⋅''+'--⋅''+-=∂∂∂ϕϕϕ五、(本题5分)求函数2),(22+-=y x y x f 在椭圆域}14|),{(22≤+=y x y x D 上的最大值和最小值.解:由于x y x f x 2),(=,y y x f y 2),(-=,令,0),(0),(⎩⎨⎧==y x f y x f y x 在D 内求得驻点)0,0(.在D 的边界上,设)14(2),,(2222-+++-=y x y x y x F λλ,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+==+-==+=)3(014),,()2(0212),,()1(022),,(22y x y x F y y y x F x x y x F y x λλλλλλ当0≠x ,由(1)得1-=λ,代入(2)得0=y ,在代入(3)得⎩⎨⎧=±=01y x ;同理当0≠y 得⎩⎨⎧±==20y x ;由于2)0,0(=f , 3)0,1(=±f , 2)2,0(-=±f ,所以最大值为3,最小值为2-.六、(本题5分)设在上半平面}0|),{(>=y y x D 内,函数),(y x f 具有连续偏导数,且对任意的0>t 都有),(),(2y x f t ty tx f -=,证明对D 内的任意分段光滑的有向简单闭曲线L ,都有0),(),(=-⎰dy y x xf dx y x yf L.解:由格林公式,对D 内的任意分段光滑的有向简单闭曲线L ,⎰⎰⎰----±=-1)],(),(),(),([),(),(D y xLdxdyy x yfy x f y x xf y x f dyy x xf dx y x yf .dxdy y x yf y x xf y x f y D x )],(),(),(2[1---±=⎰⎰ (*)由于函数),(y x f 具有连续偏导数,且对任意的0>t 都有),(),(2y x f t ty tx f -=,即),(),(2ty tx f y x f t =上式两端对t 求导有),(),(),(221ty tx f y ty tx f x y x tf '+'= 特取1=t 得),(),(),(2y x yf y x xf y x f y x += 由(*)式既有0),(),(=-⎰dy y x xf dx y x yf L。
南京工业大学期末高等数学A试卷A

南京工业大学期末高等数学A试卷AYUKI was compiled on the morning of December 16, 2020南京工业大学 高等数学A-2 试卷(A )卷(闭)2010--2011学年 第 二 学期 使用班级 江浦10级 学院 __ 班级 __学号 __ 姓名 __ ___一、选择题(本题共4小题,每小题3分,满分12分,每小题给出四个选项,请将正确答案填在题后的括号内)1.若),(y x f 在),(00y x 处可微,则在),(00y x 点下列结论中不一定成立的是( C ))(A 连续 )(B 偏导数存在 )(C 偏导数连续 )(D 切平面存在2. 直线01152312325=--+-=-+=-z y x z y x 与平面的位置关系是( D ) )(A 平行但不在平面上 )(B 在平面上 )(C 垂直 )(D 斜交3. 若曲面∑:2222a z y x =++,则2()x y z dS ∑++⎰⎰=( C )4.设)11ln()1(nu n n +-=,则级数( B ))(A ∑∞=1n n u 与∑∞=12n n u 都收敛 )(B ∑∞=1n n u 收敛而∑∞=12n n u 发散)(C ∑∞=1n n u 与∑∞=12n n u 都发散 )(D ∑∞=1n n u 发散而∑∞=12n n u 收敛二、填空题(本题共4小题,每小题3分,满分12分,请将正确答案填在题后的横线上)1.已知矢量,a b 的模分别为()2||2,||2,6a b a b a b==⋅=⨯=及,则 2 __ 。
⒉ 已知=+=)1,1(),1ln(dz y xz 则 ()12dx dy - 。
3.幂级数1(1)2nn n x n∞=-⋅∑的收敛域是 [)1,3- ____ 。
4.设函数⎩⎨⎧≤<+≤<--=ππx x x x f 0,10,1)(2,则其以π2为周期的傅里叶级数在点π=x 处收敛于 _ 。
高数a大一期末考试题简单及答案

高数a大一期末考试题简单及答案一、选择题(每题4分,共40分)1. 极限的定义中,如果对于任意的正数ε,存在正数δ,使得当0<|x-a|<δ时,有|f(x)-L|<ε,则称函数f(x)当x趋近于a时的极限为L。
以下哪个选项不是极限的定义?A. 函数f(x)在某点a处的极限B. 函数f(x)在某点a的左极限C. 函数f(x)在某点a的右极限D. 函数f(x)在某点a处的连续性答案:D2. 以下哪个函数是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = |x|答案:B3. 以下哪个函数是偶函数?A. f(x) = x^3B. f(x) = x^2C. f(x) = x^4D. f(x) = |x|答案:B4. 以下哪个函数在x=0处不可导?A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = x^4答案:B5. 以下哪个选项是正确的不定积分?A. ∫x dx = x^2 + CB. ∫x^2 dx = x^3 + CC. ∫1/x dx = ln|x| + CD. ∫e^x dx = e^x + C答案:C6. 以下哪个选项是正确的定积分?A. ∫[0,1] x dx = 1/2B. ∫[0,1] x^2 dx = 1/3C. ∫[0,1] x^3 dx = 1/4D. ∫[0,1] x^4 dx = 1/5答案:B7. 以下哪个选项是正确的微分方程的通解?A. y' = 2y => y = Ce^(2x)B. y' = 3y => y = Ce^(3x)C. y' = 4y => y = Ce^(4x)D. y' = 5y => y = Ce^(5x)答案:A8. 以下哪个选项是正确的二阶导数?A. y = x^3, y'' = 6xB. y = x^2, y'' = 2C. y = x^4, y'' = 12x^2D. y = x^5, y'' = 20x^3答案:B9. 以下哪个选项是正确的洛必达法则的应用?A. ∫0/0 型不定式,分子分母同时乘以分母的导数B. ∫∞/∞ 型不定式,分子分母同时乘以分子的导数C. ∫0/0 型不定式,分子分母同时除以分子的导数D. ∫∞/∞ 型不定式,分子分母同时除以分母的导数答案:D10. 以下哪个选项是正确的泰勒级数展开?A. e^x = 1 + x + x^2/2! + x^3/3! + ...B. sin(x) = x - x^3/3! + x^5/5! - ...C. cos(x) = 1 - x^2/2! + x^4/4! - ...D. ln(1+x) = x - x^2/2 + x^3/3 - ...答案:A二、填空题(每题4分,共20分)11. 函数f(x) = x^2 + 3x + 2的导数是________。
南工大高数A—答案

南京工业大学高等数学A -2试题A 、闭卷解答2009--2010学年第 2 学期 使用班级 江浦09级 一、单项选择题本大题共5小题; 每小题3分; 总计15分 1、)(A 2 、)(C 3、)(D 4、)(C 5、)(B 二、填空题 本大题共5小题; 每小题3分;总计15分 1 、043=--+z y x 2、32π3、a 30-4、 10≤<p5、0'''=-'-''+y y y y三、解答下列各题本大题共4小题;每题7分;总计28分;每题要有必要的解题步骤1、设数量场586432),,(222+---++=z y x z y x z y x f 求:1函数f 在点(),1,22处的梯度..2函数f 在点(),1,22处方向导数的最大值.. 解:1{}86,64,42---=z y x gradf ;{}4,2,0)2,1,2(-=gradf………4分252)2,1,2(=gradf ;故f 在点(),1,22处方向导数的最大值为..………7分2、计算二次积分⎰⎰-ππππ2sin y dx x xdy .. 解:⎰⎰-ππππ2sin y dxx x dy =⎰⎰+πππsin x dy xxdx ………4分=⎰πsin xdx=2………7分3、求微分方程x e y y y 332-=-'+''的通解..特征方程3,1032212-==⇒=-+r r r r ;对应齐次方程的通解为 x x e C e C Y 321-+= 其中21,C C 为任意常数 ………4分因3-=λ是特征根;设特解为x Axe y 3*-=;其中A 为待定常数;代入原方程; 得x xe y A 3*4141--=⇒-= ………6分 从而得通解xx x xe e C e C y 332141---+=………7分4、计算积分⎰-+-+=-Lx dy y y x dx y y x e I )sin ()cos 3sin (42;其中L 是从点)0,(π-A 沿曲线x y sin =到点)0,(πB 的弧段..解:这里y y x e P x cos 3sin 2-+=-;4sin y y x Q -=.. 由于y xQ y y P sin ,sin 3=∂∂+=∂∂;可见xQy P ∂∂=∂∂不成立..………2分记y x eP xcos sin 21-=-;则)3(,32211⎰⎰⎰=+++=LLLydx I I I ydx Qdy dx P I 记.. 则曲线积分1I 满足与路径无关的条件;选择与L 起终点相同的直线段0=y ;有πππ2)1sin (21-=-=⎰--dx x eI x ;而0sin 332===⎰⎰-ππxdx ydx I L………6分 故所求积分π2-=I .. ………7分 四、解答下列各题本大题共4小题;每题7分;总计28分;每题要有必要的解题步骤1、设()xy y x f z ,22-=;其中函数f 具有二阶连续的偏导数;试求x z ∂∂;yx z ∂∂∂2.. 解:212f y f x xz'+'=∂∂………3分()'2221222112224f xyf f y x xyf yx z ++-+-=∂∂∂”“” ………7分2、计算曲面积分()()⎰⎰∑-+++=dxdy z dzdx z y dydz xz I 322912其中∑为曲面122++=y x z ()21≤≤z ;取下侧.. 解:取平面21=∑z :;取上侧.则∑与1∑构成封闭曲面;取外侧.令∑与1∑所围空间区域为Ω;由Gauss 公式;得⎰⎰⎰⎰∑∑+∑-=11I ………2分()⎰⎰⎰≤+---=13212229)1(y x dxdydz z π2π-=………7分3、求幂级数∑∞=---12112)1(n n n x n 的收敛域及和函数;并数项级数∑∞=---1112)1(n n n 的和..解:12)1(1--=-n a n n ;1lim 1==+∞→n n n a a R ;1±=x 时原级数为∑∞=---1112)1(n n n 收敛;故此幂级数的收敛域为[],11-..………2分设∑∞=---=12112)1()(n nn x n x s ;)11(≤≤-x ;则 )11(,arctan )))(())((12)1(12)1()(1211211121121≤≤-⋅=-⋅=-⋅=--⋅=--=-∞=-∞=∞=--∞=-∑⎰∑⎰∑∑x x x dx x x dx x x x n x x n x s n n xn n x n n n n n n………5分 故4)1(12)1(11π==--∑∞=-s n n n ………7分4、设)(x f 是周期为π2的周期函数;且x x f =)( ππ<≤-x ;试将)(x f 展开成傅立叶级数..解:所给函数满足收敛定理的条件;它在点x ))12((π+=k x 处不连续;因此;)(x f 的傅立叶级数收敛于02=-+)(ππ;在连续点x ))12((π+≠k x 收敛于)(x f .. ………2分若不计π)12(+=k x ;则)(x f 是周期为π2的奇函数...0=n a ),2,1,0( =n ………3分)1(0)1(2sin 2sin )(2+-===⎰⎰n n nnxdx x nxdx x f b ππππ),3,2,1( =n ………5分故 )sin )1(3sin 312sin 21(sin 2)()1( +-+-+-=+nx nx x x x f n ),3,,( ππ±±≠∈x R x 且………7分 五、解答题本题8分已知曲线过点(),11;曲线上任一点),(y x P 处的切线交y 轴于点Q ;以PQ为直径所作的圆均过点)0,1(F ;求此曲线的方程.. 解:过点),(y x P 的切线方程)('x X y y Y -=-;令'0xy y Y X -==得;即),0('xy y Q - ………2分由题意;222PQ QF PF =+得2'22'22)()(1)1(xy x xy y y x +=-+++-;化简xy x y dx dy -+=12;即111-⋅-=-y xx y x dx dy Bernoulli 方程 ………4分 令2y z =;得xx z x dx dz )1(22-=-;其通解为212cx x z +-= 故原方程通解为2212cx x y +-=;又1)1(=y ;得0=c ..所以该曲线的方程为122-=x y .. ………8分 六、证明题本题6分已知正项级数1n n a ∞=∑收敛;证明数列()()(){}12111n a a a ++⋅⋅+收敛..证明:记()()()12111n n x a a a =++⋅⋅+因正项级数1n n a ∞=∑收敛;故0lim =∞→n n a ;又1)1ln(lim=+∞→nn n a a ;由正项级数比较审敛法的极限形式知级数1ln(1)n n a ∞=+∑也收敛并记其和为s ………4分即s a nk k n =+∑=∞→1)1ln(lim ;于是s x n n =∞→ln lim ;s n n e x =∞→lim 故数列()()(){}12111n a a a ++⋅⋅+收敛.. ………6分。
《高等数学》期末考试A卷(附答案)

《高等数学》期末考试A卷(附答案)【编号】ZSWD2023B0089一、填空题(每小题2分,共20分)1.设 是正整数, 为非零实数,若20001lim ()x x x x,则 _________________,______________________。
【答案】120012001,2.设)(x f 的定义域是]1,0[,且102a ,则()()f x a f x a 的定义域是____________________________ .【答案】1[,]a a3.2211sin()lim x x x x ______________________。
【答案】04.设1111010,(),x x x x e e x f x e e x,0 x 是)(x f 的___________间断点. 【答案】跳跃5.设24cos y x ,则dy ________________________. 【答案】3448sin cos x x x dx6.203sin limxx t dt x _________________________________.【答案】137. 函数2412()()x f x x的渐近线有______________________________.【答案】20,x y8.函数()x f x x e 的单调递增区间为____________________________.【答案】(,0)9.若 C x dx xx f sin )(ln ',则 )(x f .【答案】C e x )sin( 10.[()()]aaf x f x dx ______________________________________.【答案】0二、单项选择题(每小题2分,共10分) 1.若下列极限存在,则成立的是( ) .A. 0()()lim '()x f a x f a f a x B. 0000()()lim '() x f x f x x f x xC. 0(12)(1)lim '(1)t f t f f tD. 4(8)(4)lim '(4)4x f x f f x【答案】B2.当0 x 时,与x 等价的无穷小量是( )A. x x 1sinsin B. xx sin C. x x 22 D. )1ln(x【答案】D3. 当0x x 时,0'()f x ,当0x x 时,0'()f x ,则0x 必定是函数()f x 的( )A. 驻点B. 最大值点C.极小值点D. 以上都不对 【答案】D4.设'()f x 存在且连续,则()'df x ( )A. ()f xB. '()f xC. '()f x cD. ()f x c 【答案】B 5.设4()2xx f t dt,则40 f dx ( )A. 16B. 8C. 4D. 2【答案】A三、计算下列各题(每小题5分,共35分)1. 求极限)sin 11(cot lim 0xx x x解: )sin 11(cot lim 0x x x x xx x xx x tan sin sin lim 030sin lim x xx x (0 x 时x sin ~x ,x tan ~x )2031cos lim x x x 616sin lim 0 x x x2. 设3sin 2,0()9arctan 2(1),0xx ae x f x x b x x ,确定,a b 的值,使函数在0 x 处可导。
高等数学A-1试卷A卷(11.01)

南京工业大学高等数学A-1试卷(江浦A 卷、闭)2010-2011学年第一学期一、选择题(每小题3分, 共15分)1、设的是,则)(0)1()(2x f x x x xx x f =-+=( ))(A 可去间断点 )(B 跳跃间断点 )(C 无穷间断点 )(D 振荡间断点2、设,arcsin )(,)1ln()(20110dt t x g dt t x f x x ⎰⎰=+=-+则当0→x 时 ( ))(A )()(x g x f 是的高阶无穷小 )(B )()(x g x f 是的低阶无穷小 )(C )()(x g x f 是的同阶但非等价无穷小 )(D )()(x g x f 与是等价无穷小3、若函数)(x f 在a x =处可导,则)(x f 在a x =处( ))(A 一定连续且可导 )(B 一定连续但不可导 )(C 一定连续但不一定可导 )(D 不一定连续且不一定可导4、设函数)(),(x g x f 在[]a a ,-上均具有连续导数,且)(x f 为奇函数,)(x g 为偶函数,则积分[]d x x g x fa a⎰-+)()(''=( ))(A )()(a g a f + )(B )()(a g a f - )(C )(2a g )(D )(2a f5、曲线xe y =与过原点的切线ex y =及y 轴所围成的平面图形的面积S 为( ))(A dx ex e x ⎰-10)( )(B dy y e y ⎰-10)ln ( )(C dx ex e e x⎰-1)( )(D dy y e y e ⎰-1)ln ( 二、填空题(每空3分, 共15分,把答案填在题中横线上)1、设k 是正整数,且极限kk n n n n )1(lim 2010--∞→的值是非零常数,则k = ____2、设⎪⎩⎪⎨⎧=≠+=0,0,1sin sin 1)(x a x xx x x x f ,在0=x 处连续,则 =a ____ 3、设nx y =在点)1,1(处的切线与x 轴交于点)0,(n ξ,则_________lim =∞→n n n ξ4、设函数)(x f 在点)0,1(处有)(x o x y ∆+∆=∆,则极限)1ln()(lim21x dtt f xe x +⎰→= ____5、曲线x y 23sin =(π≤≤x 0)与x 轴围成的平面图形绕x 轴旋转一周所得的旋转体的体为 ____1、求极限().11lim 22--+∞→n nnn 。
南京工业大学期末考试高等数学A 试卷A

南京工业大学 高等数学A-2 试题(A )卷(闭)2013---2014 学年 第2学期 使用班级 江浦大一学生 班级 学号 姓名一、单项选择题(本大题共5小题, 每小题3分, 总计15分)1、直线12:201x y z l --==与平面:2+60x y z π--=之间的夹角为( ) )(A 0 )(B 6π )(C 4π )(D 2π2、设函数(,)f x y 在点(,)a b 的偏导数存在,则0(,)(,)limx f a x b f a x b x→+--=( ) )(A 0 )(B (2,)x f a b )(C (,)x f a b )(D 2(,)x f a b3、二次积分40(,)xdx f x y dy ⎰⎰交换积分次序后为( ))(A 40(,)y dy f x y dx ⎰⎰)(B 2404(,)yy dy f x y dx ⎰⎰)(C 2440(,)yydy f x y dx ⎰⎰)(D 44(,)dy f x y dx ⎰⎰4、设椭圆L :13422=+y x 的周长为l ,则⎰=+L ds y x 2)23(( ) )(A l )(B l 3 )(C l 4 )(D l 125、极限lim 0n n u →∞=是级数1nn u∞=∑收敛的( ))(A 充要条件 )(B 充分条件 )(C 必要条件 )(D 既非充分也非必要条件二、填空题(本大题共5小题, 每小题3分,总计15分)1、已知曲面224z x y =--在点M 处的切平面与平面2210x y z ++-=平行,则点M 的坐标 为__________________。
2、设函数2x y xe =是某二阶常系数线性齐次微分方程的解,则该微分方程为_________________。
3、设∑为曲面2222x y z R ++=,则曲面积分2221dS x y z ∑++⎰⎰= _______ 。
4、函数1()f x x=展开成2x -的幂级数为____________________________。
高等数学A试卷A解答

南京工业大学 高等数学A-2试卷(A )解答2012--2013学年 第 二 学期 使用班级 江浦12级一、选择题(本大题共5小题, 每小题3分, 总计15分)1、)(C2、()A3、)(B4、()D5、)(B 二、填空题(本大题共5小题, 每小题3分,总计15分) 1、221x x y -+= ⒉、 1 3、2π 4、43-5、 2π 三、解答下列各题(本大题共4小题,每小题7分,总计28分,每题要有必要的解题步骤)1、设函数6),,(+---++=z y x yz zx xy z y x f ,问在点)0,4,3(P 处沿怎样的方向l ,f 的变化率最大?并求其最大的变化率。
解:)6,2,3()1,1,1()0,4,3(=-+-+-+=P y x z x z y gradff 沿方向(3,2,6)l =的变化率最大; ……4分其最大的变化率为(3,4,0)7Pf gradf l∂==∂。
……3分2、设22(,)y z f x y x =+,其中(,)f u v 具有二阶连续偏导数,求x z∂∂、yx z ∂∂∂2。
解:1222z yx f f x x∂''=⋅-⋅∂, ……3分2111222122221112(2)(2)z y x yf f f yf f x y x x x x∂'''''''''=+--+∂∂ 22111222223142(1)y yf xyf f f x x x'''''''=-++-- ……4分 3、计算二次积分11sinxxdx y dy y⎰⎰。
解:111000sinsin y xx xdx y dy dy y dx y y=⎰⎰⎰⎰(交换积分顺序) ……2分120(1cos1)y dy =-⎰……3分1(1cos1)3=- ……2分 4、计算Lxds ⎰,其中L 为由直线y x =及抛物线2y x =所围成的区域的整个边界。
高等数学(A)下期末试卷及答案

《高等数学 A 》( 下)期末试卷 A 答案及评分标准 得 一、选择题(本大题分 5 小题,每题 3 分,共 15 分分)e dxln x f ( x, y)dy 的积分序次为1、互换二次积分1(c )e ln xf ( x, y)dxe1 (A)dy(B)e ydyf ( x, y)dx11 eln xe(C)dy e y f ( x, y)dx(D)dy1f ( x, y)dx2、锥面zx2y 2在柱面 x2y22x 内的那部分面积为( D )d2 cos2d2 cos 2d(A)2d2(B)222cos 2d22 cosd(C)2 d(D)2 d2 023、若级数a n ( x 2) n在 x2 处收敛,则级数n 1na n ( x 2)n 1( B )在 x 5n 1(A)条件收敛 (B) 绝对收敛 (C) 发散 (D) 收敛性不确立4、以下级数中收敛的级数为( A )(A)( n ) n(B)n2 3n 1 n 1 n 1 n 1(C)sin1(D)n!n 1 3 n n 1 n 15、若函数f ( z)( x 2 y 2 2 xy) i( y 2 axy x2 ) 在复平面上到处分析,则实常数 a 的值为(c )(A) 0 (B) 1 (C) 2 (D) -2得 二、填空题(本大题分 5 小题,每题 4 分,共 20 分分)、曲面 z x2y21 在点 (2,1,4) 处的切平面1方程为 4x 2 y z62 、已知L : x2y2a 2(a 0) , 则L [ x 2y2sin( xy)]ds2 a33、 是由曲面zx2y 2及平面 zR(R0) 所围成的闭地区,在柱面坐标下化三重积分f ( x2y 2)dxdydz 为2 RR2)dz三次积分为ddf (4、函数 f (x) x (0 x) 睁开成以 2 为周期的正弦级 数 为x2 ( 1) n 1 sin nx,收敛区间为n 1n0 x5、Ln( 1 i)ln 2 i(32k ), k 0, 1, 24Re s[e z,0]12得 三、 (此题 8 分)设zf ( x2y 2) g( x, xy) ,分y此中函数 f (t) 二阶可导, g(u, v) 拥有二阶连续偏导数,求 z ,2zx x y解: z 2xf1g 1yg23 分xy2z4xyfg 2xyg 221 g 1 x g 11 5 分x yy 2 y 3得x 2y 2z 21内分四、(此题 8 分)在已知的椭球面43全部内接的长方体(各边分别平行坐标轴)中,求最大的内接长方体体积。
南京工业大学高等数学A-2期末考试试卷A解答(2014.06)
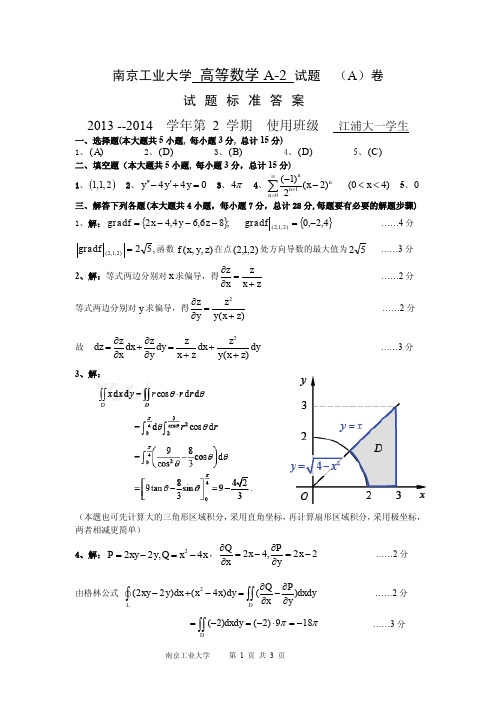
x
y
……2 分
由格林公式 (2xy 2 y)dx (x2 4x)dy (Q P )dxdy
L
D x y
(2)dxdy (2) 9 18
D
南京工业大学 第 1 页 共 3 页
……2 分 ……3 分
四、解答下列各题(本大题共 4 小题,每小题 7 分,总计 28 分,每题要有必要的解题步骤)
1、1,1, 2 2、 y 4y 4y 0 3、 4
4、
n0
(1)n 2n1
(x
2)n
(0 x 4) 5、 0
三、解答下列各题(本大题共 4 小题,每小题 7 分,总计 28 分,每题要有必要的解题步骤)
1、解: gradf 2x 4,4 y 6,6z 8; gradf (2,1,2) 0,2,4
1、解:由条件可知 dy 2x y ,且 y 0 0
dx
……2 分
其通解为
y
e
dx
2xedxdx c ex 2
xexdx c cex 2x 2
……4 分
将 y 0 0 代入通解中,得 c 2 ,故所求曲线方程为 y 2ex 2x 2
……3 分
比较得最大值: f (0, 2) f (0, 2) 25 ,最小值: f (0, 0) 9
……2 分
3、解:先考查
n1
(1)n
1 3n
n
n1
1 3n n
,记 un
1 ,则 3n n
lim un1 u n
n
lim
n
13~14(一)高数(工)1期末考试(A)试卷解答

上海应用技术学院2013—2014学年第一学期《高等数学(工)1》期(末)试卷A一、单项选择题(本大题共10小题,每小题2分,共20分) 1.B ; 2.A ; 3.B ; 4.C ; 5.C ; 6.C ; 7.D ; 8.B ; 9.D ; 10.A .二.填空题(本大题共6小题,每小题3分,共18分),请在每小题的空格中填上正确答案,错填、不填均无分. 11.a be; 12.2; 13.1111(1)e e y x y x e e e++-=-=-或;14.4e-; 15.43; 16.122(1)y x -=+.三.计算题(本大题共8小题,每小题6分,共48分). 17.求极限111lim 1ln x x x →⎛⎫-⎪-⎝⎭. 解:1111ln 1lim lim 1ln (1)ln x x x x x x x x →→-+⎛⎫-=⎪--⎝⎭................(1分) 111lim 1ln x xx x x →-=-+................................(2分) 2121lim 11x xx x →-=+................................(2分) 12=- ................................(1分)18.设arctan ln(y x x =+,求221x d ydx=.解:2211111y x x ⎛⎫'=+=++................(2分) 332222222221122121(3)(3)x xx y x x x x x --''=-=-++++()()................(3分)158x y =''=-................................................(1分)19.设函数)2arcsin(2)1(x x y +=,求dxdy. 解:2ln arcsin(2)ln(1)y x x =+.......................................(2分)2212)arcsin(2)1xy x x y x '=+++..............................(3分)2arcsin(2)222(1))arcsin(2)1x x y x x x x ⎛⎫'=+++⎪+⎭........(1分) 另解:2arcsin(2)ln(1)x x y e+=.......................................(2分)()2arcsin(2)ln(1)2arcsin(2)ln(1)x xy e x x +''=+............................(1分)2arcsin(2)222=(1))arcsin(2)1x x x x x x ⎛⎫+++⎪+⎭..............(3分)20.判定曲线2()(714)xf x e x x =-+的凹凸性与拐点.解:22()(714)(27)(57)x x x f x e x x e x e x x '=-++-=-+...................(1分)22()(57)(25)(32)(2)(1)x x x x f x e x x e x e x x e x x ''=-++-=-+=--.......(1分)令()0f x ''=,得到1,2x x ==..............................................(1分).....................................................................(2分)在(,1)-∞内,曲线2()(714)x f x e x x =-+是凹的;在(1,2)内,曲线2()(714)x f x e x x =-+是凸的;在(2,)+∞内,曲线2()(714)x f x e x x =-+是凹的;拐点2(1,8),(2,4)e e ..............................................(1分)21.计算不定积分()cos ln 2x x dx x+⎰.解:()()2cos ln 2cos ln ln (1)x x dx x d x x x+=++⎰⎰........(4分) (注:加号前后各2分)3222sin(ln )(1)3x x C =+++..............................................(2分)(注:前两个一个一分,但是两个都写对了C 漏写还是要扣一分)22.计算定积分2. 解: sec x t =令,sec tan dx t tdt =,23x t π=→=,4x t π=→=........(2分)22334344tan tan sec sec t t tdt dt t t ππππ==⎰⎰....................(1分) 234sin cos t tdt ππ=⎰.....................................(1分) 234sin sin td t ππ=⎰.....................................(1分) ()334sin 324t ππ==..........................(1分)23.计算定积分1320arctan()x x dx ⎰.解:1320arctan()x x dx ⎰1241arctan()4x dx =⎰..................................(1分)()142142001arctan()arctan()4x x x d x =-⎰.................(1分) 144012441x x dx x π⎛⎫=- ⎪+⎝⎭⎰...............................(1分) 14012441x x dx x π⎛⎫⎛⎫=-- ⎪ ⎪+⎝⎭⎝⎭⎰...........................(1分) 112400112441xdx dx x π⎛⎫=-+ ⎪+⎝⎭⎰⎰.........................(1分) 1122001arctan()44x x π⎛⎫=-+ ⎪⎝⎭1214448πππ-⎛⎫=-+=⎪⎝⎭ (注:或者11arctan124-).......(1分)24.求微分方程2223,xdy xy x e dx-=满足初始条件01==x y 的特解.解:(解法一)dyxy dx=.............................................................(1分) dy xdx y = dy xdx y⇒=⎰⎰ 2l n l n 2x y C ⇒=+ 22xy C e ⇒=..........(1分) 令原方程的通解为22()x y C x e =...........................................(1分)则2222()()x x y C x e C x e x ''=+,代入原方程得222222222()()()3x x x x C x e C x e x xC x e x e '+-=2()3C x x '⇒=.........................................................(1分) 23()3C x x dx x C ==+⎰通解为232()x y x C e =+...................................................(1分)由01==x y ,则1C =-232(1)x y x e =-....................................(1分) (解法二)令()P x x =-,222()3x Q x x e =............................(1分)通解()()(())P x dx P x dx y e Q x e dx C -⎰⎰=+⎰...................................(1分) 222(3)x xdxxdxe x e e dx C -⎰⎰=+⎰.....................................(1分)2222222(3)x x x e x e edx C -=+⎰...........................................(1分)222(3)x e x dx C =+⎰232()x e x C =+....................................(1分)由于01==x y ,则1C =-,所以特解为232(1)x y e x =-.................(1分)四.应用与证明题(本大题共2小题,每小题7分,共14分). 25.求由曲线xy 1=,直线x y +=1,1=x 及2=x 所围图形的面积,并求该图形绕x 轴旋转一周所得的旋转体的体积. 解:(1)22111(1)S x dx dx x=+-⎰⎰..........................................(2分) 22211(1)5ln ln 222x x +=-=-....................................(1分) (2) 2222111(1)x V x dx dx x ππ=+-⎰⎰..................................(2分) 22311(1)13x x ππ+=+...........................................(1分) 278135(1)326πππ-=+-=.....................................(1分) (注:如果公式全写错但图形画对了但可以给1分)26.设)(x f 在[0,1]上可导,且11(1)022f f ⎛⎫=≠ ⎪⎝⎭.又设 212()()x x F x f t dt +=⎰. (1)求()F x ';(2)证明:至少存在一点(0,1)ξ∈,使得()0F ξ'=;(3)证明:至少存在一点(0,1)η∈,使得()()0F F ηηη'''+=.证:(1)211()()2()22x F x f x x f +'=-;..................................(2分) (2)13(1)2(1)(1)(1)22F f f f '=-=且11(0)()22F f '=-,....................(1分)则()23(1)(0)(1)02F F f ''=-<,由于()F x '在[0,1]上连续,由零点存在定理,存在一点(0,1)ξ∈,使得()0F ξ'=。
高等数学A试卷A()

南京工业大学 高等数学A-2 试题(A 、闭)卷2011--2012 学年第 2 学期 使用班级 江浦2011级学院 班级 学号 姓名1)(A )xOz(B)yOz成(C )xOz(D )yOz成2、设z y y x= )(C)3、设区域是平面上以点)1,1(A 、)1,1(-B 、为顶点的三角形区域,区域1D 是D 在第一象限的部分,则:=+⎰⎰dxdy y x xy D)sin cos (( )(A)⎰⎰1)sin (cos 2D dxdy y x(B)⎰⎰12D xydxdy(C)⎰⎰+1)sin cos (4D dxdy y x xy(D) 04、设∑为曲面222()z x y =-+在xoy 平面上方的部分,则zdS∑=⎰⎰()(A )(222202r d r πθ--⎰⎰(B )(22202d r πθ-⎰⎰(C ))22002d r rdr πθ-⎰ (D )22002.d r πθ-⎰5、正项级数(1) ∑∞=1n n u 、(2) ∑∞=13n nu ,则下列说法正确的是( )(A )若(1)发散、则(2)必发散 (B )若(2)收敛、则(1)必收敛 (C )若(1)发散、则(2)不确定 (D )若(1)、(2)敛散性相同二、填空题(本大题共5小题, 每小题3分,总计15分)1、已知三个单位向量a 、b 、c 满足0a b c ++=,则a b b c c a ⋅+⋅+⋅=___________2、函数z xy x u 22+-=在点()1,2,1-处的方向导数的最小值为3、将10(,)y eedy f x y dx ⎰⎰交换积分次序得 __________________4、设∑是母线平行于oz 轴的柱面的部分,它的底是位于xoy 平面上的光滑曲线L ,它的高z 是,x y 的非负函数(,)z f x y =,用曲线积分表示柱面∑的面积A =___________5、设函数21,0(),0x f x x x ππ--<≤⎧=⎨<≤⎩,则其以π2为周期的傅里叶级数在点π=x 处收敛于 _____ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京工业大学 高等数学A-2 试卷(A )卷(闭)
2010--2011学年 第 二 学期 使用班级 江浦10级 学院 __ 班级 __学号 __ 姓名 __ ___
一、选择题(本题共4小
题,每小题3分,满分12分,每小题给出四个选项,请将正确答案填在题后的括号内) 1.若),(y x f 在),(00y x 处可微,则在),(00y x 点下列结论中不一定成立的是( C )
)(A 连续 )(B 偏导数存在 )(C 偏导数连续 )(D 切平面存在
2. 直线
011523
1
2325=--+-=-+=-z y x z y x 与平面的位置关系是( D ) )(A 平行但不在平面上 )(B 在平面上 )(C 垂直 )(D 斜交
3. 若曲面∑:2
2
2
2
a z y x =++,则2
()x y z dS ∑
++⎰⎰=( C ) 4.设)11ln()1(n
u n
n +
-=,则级数( B )
)(A ∑∞
=1n n u 与∑∞
=12n n u 都收敛 )(B
∑∞=1
n n u 收敛而∑∞
=1
2
n n u 发散
)(C ∑∞
=1
n n u 与∑∞
=1
2
n n u 都发散 )(D ∑∞
=1
n n u 发散而∑∞
=1
2
n n u 收敛
二、填空题(本题共4小题,每小题3分,满分12分,请将正确答案填在题后的横线上) 1.已知矢量,a b 的模分别为()
2
||2,||2,6a b a b a b
==⋅=⨯=及,则 2 __ 。
⒉ 已知=+
=)1,1(),1ln(dz y x
z 则 ()12
dx dy - 。
3.幂级数1
(1)2n
n n x n ∞
=-⋅∑的收敛域是 [)1,3- ____ 。
4.设函数⎩⎨⎧≤<+≤<--=π
πx x x x f 0,10,1)(2
,则其以π2为周期的傅里叶级数在点π=x 处收敛于 _ 。
三、计算题(本题共4小题,每小题7分,满分28分,写出必要的解题过程)
1.求过点)2,1,3(-且通过直线43:
521
x y z
L -+==的平面方程。
由已知点)0,3,4(),2,1,3(--B A 在平面上,直线L 的方向向量为)1,2,5(=s
则)2,4,1(-=AB ,所求平面的法向量为)22,9,8(-=⨯=s AB n
平面直线的方程为0)2(22)1(9)3(8=+----z y x 即为0592298=---z y x
2. 设
ln x z z y = ,求,z z x y ∂∂∂∂。
1,,ln ln 1x y z z
F F F y z y
==
=--; 3. 计算积分
y
x
D
e
dxdy ⎰⎰,其中2:,2D y x y x ==由所围成的区域。
4. 计算半径为R 、中心角为2α的圆弧L 对于它的对称轴的转动惯量I (设线密度1μ=)。
四、计算题(本题共4小题,每小题7分,满分28分,写出必要的解题过程)
1.设(,)z f x xy =,其中f 具有二阶连续偏导数,求2z
x y
∂∂∂。
2. 设22(,,)x y z
f x y z e
x y =++, (1) 求f 在点()1,1,1P
处的梯度; (2) 求f 在点()1,1,1P 处方向导数的最大值。
3.计算曲面积分()()
⎰⎰∑-+++=dxdy z dzdx z y dydz xz I
322912
其中∑为曲面12
2
++=y x z ()21≤≤z ,取下侧。
4. 将函数()2
1
32
f x x x =
-+展开成()3x -的幂级数,并求展开式成立的区间。
五、应用题题(本题满7分) 求质点(,)M x y )受作用力j x y i x y F
)2()3(-++=沿路径L 所作的功W ,其中L 是沿椭圆
2244x y +=顺时针方向的一周。
六、综合题(本题满7分)
某工厂生产两种型号的机床,其产量分别为x 台和
y 台,成本函数为
xy y x y x c -+=222),
( (万元)
若市场调查分析,共需两种机床8台,求如何安排生产,总成本最少?最小成本为多少? 七、证明题(本题满6分) 设40
tan d n
n
a x x π
=⎰,证明:级数∑∞
=++12)(1
n n n a a n
收敛于1。
