2014年中考复习提能训练课件_第四章 第1讲相交线和平行线
合集下载
浙江新中考2014届总复习课件(13)线段、角、相交线与平行线
A． 35° C． 110°
B． 70° D． 145°
【思路点拨】首先根据角平分线的定义可得 ∠ BOD ＝ 2∠ BOC ＝ 70° ， 再 根据 邻补 角的性 质可 得 ∠ AOD 的度数． 方法总结 在遇到相交线问题时，会产生对顶角和邻补角； 在遇到角平分线问题时，会产生相等的角或角的倍分 关系 .灵活运用这些性质，会给解题带来方便，在中考 命题中，通常和三角形的内角和定理或特殊三角形的 性质结合考查 .
【思路点拨】先判定 a∥b，再由平行线的性质得 ∠ 2＝ ∠1. 方法总结 1.平行线的判定是根据同位角、 内错角的“相等 ” 和同旁内角的 “互补 ”这种数量关系得到平行的位置 关系 . 2.平行线的性质是在 “平行 ”这种位置关系下， 得 到的两个角的 “数量关系 ”，即同位角相等、内错角 相等、同旁内角互补 .
要说明命题：“一组对边平行且对角 线相等的四边形是矩形”是假命题，可以举的反例是 ( A ) B．矩形 D．直角梯形 A．等腰梯形 C．菱形
(2013· 深 圳 ) 下 列 命题 是 真命 题 的有 ( C ) ①对顶角相等； ②两直线平行，内错角相等； ③两个锐角对应相等的两个直角三角形全等； ④有三个角是直角的四边形是矩形； ⑤平分弦的直径垂直于弦， 并且平分弦所对的弧． A． 1 个 B． 2 个 C． 3 个 D． 4 个
解析：三个角相等，不能说明这三个角是直角， ∴不一定是矩形，∴ A 是假命题；对角线互相垂直且 相等但并没有说明互相平分， ∴这个四边形不一定是 正方形， ∴B 是假命题； C 是真命题；正五边形是轴 对称图形但不是中心对称图形，∴D 是假命题．故选 C. 答案： C 方法总结 识别命题的真假，可采用排除法，通过举出反例 的方法将假命题排除 .
相交线与平行线复习课专题PPT教学课件(数学人教版七年级下册)
∴∠MCE=∠E ∠EAB=∠MNB
∵ AB∥CD
C
D
∴∠MCD=∠MNB
M
图(2)
请按下暂停键， 证明一下。
∴∠EAB=∠MCD ∵∠MCE=∠MCD+∠ECD ∴∠E=∠EAB+∠ECD
数学初中
添加辅助线
A
B
E
C
F
D
A
F
B
E
C
D
数学初中
（3）若将橡皮筋拉成图(3)的形状，则∠A、∠C、∠AEC之间
的三角板的一个顶点在纸条的另一边上，则∠1的度数是( C )
A．30° B．20° C．15° D．14°
请按下暂停键，动手算一下
数学初中
添加辅助线
类比
E
E
A
B
A
B
N
F
C
D
C
D
M
数学初中
（6）若将橡皮筋拉成图(6)的形状，则∠EAB、∠C之间有什么
关系？
E
A
B
C
图(6)
D
∠EAB=∠C
数学初中
（7）若将橡皮筋拉成图(7)的形状，则∠A、∠C、∠AEC之间
有什 么关系？
A
B
A
B
A
B
C
D
C
DC
D
E
E
图(7)
E
请按下暂停键，动手算一下
数学初中
添加辅助线
类比
A
E
B N
MC
D
图(4)
数学初中
（5）若将橡皮筋拉成图(5)的形状，则∠A、∠C、∠AEC之间
有什 么关系？
E
∵ AB∥CD
C
D
∴∠MCD=∠MNB
M
图(2)
请按下暂停键， 证明一下。
∴∠EAB=∠MCD ∵∠MCE=∠MCD+∠ECD ∴∠E=∠EAB+∠ECD
数学初中
添加辅助线
A
B
E
C
F
D
A
F
B
E
C
D
数学初中
（3）若将橡皮筋拉成图(3)的形状，则∠A、∠C、∠AEC之间
的三角板的一个顶点在纸条的另一边上，则∠1的度数是( C )
A．30° B．20° C．15° D．14°
请按下暂停键，动手算一下
数学初中
添加辅助线
类比
E
E
A
B
A
B
N
F
C
D
C
D
M
数学初中
（6）若将橡皮筋拉成图(6)的形状，则∠EAB、∠C之间有什么
关系？
E
A
B
C
图(6)
D
∠EAB=∠C
数学初中
（7）若将橡皮筋拉成图(7)的形状，则∠A、∠C、∠AEC之间
有什 么关系？
A
B
A
B
A
B
C
D
C
DC
D
E
E
图(7)
E
请按下暂停键，动手算一下
数学初中
添加辅助线
类比
A
E
B N
MC
D
图(4)
数学初中
（5）若将橡皮筋拉成图(5)的形状，则∠A、∠C、∠AEC之间
有什 么关系？
E
2014年中考一轮复习课件：图形的初步认识及相交线、平行线
如果两条直线都与第三条直线平行，那 平行 么这两条直线也互相________
同位角相等，两直线平行 平行线的 判定 内错角相等，两直线平行 同旁内角互补，两直线平行 两直线平行，同位角相等 平行线的 性质 两直线平行，内错角相等 两直线平行，同旁内角互补
考点7
垂直 直角 ，那么这两条直 如果两条直线相交成______ 定义 线互相垂直，其中一条叫做另一条的垂线， 互相垂直的两条直线的交点叫做垂足 ______
垂直
(1)两条直线垂直是两条直线相交的特殊情 特别 况，特殊在它们所交的角是直角；(3)线段 说明 与线段、射线与线段、射线与射线的垂直， 都是指它们所在直线垂直 在同一平面内，过一点有且只有______ 条直 一 线与已知直线垂直
垂直的性质
定义 垂线段
从直线外一点引一条直线的垂线，这点 垂线段 和垂足之间的线段叫做______
新人教新课标版中考一轮复习
图形的初步认识 及相交线、平行线
考点梳理
考点1 三种基本图形——直线、射线、线段
一 经过两点有且只有________ 条直线 线段 最短 两点之间，________ 长度 ，叫做 连接两点间的线段的________ 这两点间的距离
直线公理 线段公理 两点间的 距离
考点2 角
如果两个角在截线l的同侧，在被截直线 同旁 a、b之间(内)叫做同旁内角．∠5和∠2， 内角 ∠3和∠8是同旁内角
考点6
平行 不相交 的两条直线叫 在同一平面内，________ 做平行线 一 条直线 经过直线外一点，有且只有____ 平行 与这条直线______
平行线的 定义 平行 公理
平行公理 的推论
【解析】∵AB∥CD，∴∠BAC+
(初中)九年级数学《相交线、平行线》中考专题阶段复习讲解教学课件
4.(中考)如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的 度数为( )
A.55° C.45°
B.50° D.40°
【解析】选A.因为BD平分∠ABC, 所以∠ABD=∠CBD,所以∠ABC=2∠ABD. 因为CD∥AB,所以∠CBA+∠BCD=180°. 所以2∠ABD+∠BCD=180°. 所以2∠ABD=180°-∠BCD=180°-70°=110°, 所以∠ABD=55°.
A.30°
B.40°
C.50°
D.60°
【解析】选C.因为AB∥EF,∠2=50°,所以∠A=∠2=50°.又因为
AC∥DF,所以∠1=∠A=50°.
3.(中考)如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD 的度数为 ( )
A.40° C.50°
B.35° D.45°
【解析】选A.因为AD平分∠BAC,∠BAD=70°, 所以∠BAC=140°. 因为AB∥CD,所以∠ACD=180°-∠BAC=40°.
2
的距离是BC的长的2倍,所以AD=2BC,CE=BC,所以四边形ACED的
面积= 1(AD+CE)·h=1 (2BC+BC)·h=13× BC·h=3×5=15.
2
2
2
答案:15
4.(中考)如图,矩形ABCD中,AB=6.第1次平移矩形ABCD沿AB的方 向向右平移5个单位,得到矩形A1B1C1D1;第2次平移矩形A1B1C1D1 沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2;…;第n次平 移矩形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位,得到矩 形AnBnCnDn(n≥2).
九年级数学中考复习 第4章 第1节 相交线与平行线(共45张PPT)
A．50° C．70°
B．60° D．80°
当堂达标
5．如图，已知矩形纸片的一条边经过直角三角形纸片的直角顶点，若矩 形纸片的一组对边与直角三角形纸片的两条直角边相交成∠1，∠2，则 ∠2－∠1＝ 90°．
当堂达标
6．(2019·绵阳)如图，AB∥CD，∠ABD 的平分线与∠BDC 的平分线交于 点 E，则∠1＋∠2＝ 90° ．
A．180°＋α＋β－γ
B．180°－α－γ＋β
C．β＋γ－α
D．α＋β＋γ
②如图 5，AB∥CD，且∠AFE＝40°，∠FGH＝90°，∠HMN＝30°，∠CNP
＝50°，请你根据上述结论直接写出∠GHM 的度数是 30° ．
课后精练
解：(1)∠APC＝∠PAB＋∠PCD. 证明：如图 1，过点 P 作 OP∥AB. ∵AB∥CD，∴OP∥AB∥CD. ∴∠1＝∠PAB，∠2＝∠PCD. ∴∠APC＝∠1＋∠2＝∠PAB＋∠PCD.
＝110°，则∠AON 的度数为
度．
【答案】145
核心讲解
线段的有关概念及计算 例 2 已知点 C 在线段 AB 上，线段 AC＝7 cm，BC＝5 cm，点 M，N 分 别是 AC，BC 的中点，求 MN 的长度． 【思路分析】根据 M，N 分别为 AC，BC 的中点和 AC，BC 的长求出 MC 与 CN 的长，由 MC＋CN 求出 MN 的长即可．
B．45° D．75°
课后精练
5．(2017·内江)如图，直线 m∥n，直角三角板 ABC 的顶点 A 在直线 m 上， 则∠α 的余角等于( D )
A．19° C．42°
B．38° D．52°
课后精练
6．如图，将矩形纸片 ABCD 沿 BD 折叠，得到△BC′D，C′D 与 AB 交 于点 E.若∠1＝35°，则∠2 的度数为( A )
2014届中考数学总复习课件：第12节角、相交线与平行线
2、如图，AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF= 度．
3、若∠α=30°，则∠α的补角是（
）
变式：若∠A=67°，则∠A的余角是（
）
2014级中考复习三合初级中学 邓华
4、
5、如图，直线a⊥直线c，直线 b⊥直线c，若∠1=70°，则∠2 等于（ ）
2014级中考复习三合初级中学 邓华
2014级中考复习三合初级中学 邓华
知识框架
• 考点一：直线与线段（基础） • 考点二：角及角平分线（结合其它知识考查） • 考点三：相交线（垂线） • 考点四：平行线的判定及性质（必考点）
ቤተ መጻሕፍቲ ባይዱ
解决你们的困惑，所以请你仔 细听一听！
2014级中考复习三合初级中学 邓华
例题讲解
1、如图，已知a∥b，小亮把三角板的直角顶点放在直线b 上．若∠1=40°，则∠2的度数为 ．
变式1：如图，AB//CD， ∠A+∠E=75°，则 ∠C 为【 】 A． 60° B．65° C．75° D．80°
变式2：如图，已知AB∥CD， ∠EBA=45°，∠E+∠D的度 数为（ ）
2014级中考复习三合初级中学 邓华
2014预测
2014级中考复习三合初级中学 邓华
课堂小结
通过本节课的学习: 你学到了什么？ 你学会了什么？ 你没学会的是什么？ 我们大家一起来谈谈收获！
2014级中考复习三合初级中学 邓华
命题规律
从近几年来看，得用平行线性质求角度数为重庆中考必考内容，基本 上都出现在选择题第4题，分值4分，属于容易题，只有2008年出现在 填空题，2013年A卷考查了补角（第3题），第5题考查了利用平行线、 角平分线的性质求角度数，B卷出现在第2题，先判断平行，再利用性 质求角的度数。
3、若∠α=30°，则∠α的补角是（
）
变式：若∠A=67°，则∠A的余角是（
）
2014级中考复习三合初级中学 邓华
4、
5、如图，直线a⊥直线c，直线 b⊥直线c，若∠1=70°，则∠2 等于（ ）
2014级中考复习三合初级中学 邓华
2014级中考复习三合初级中学 邓华
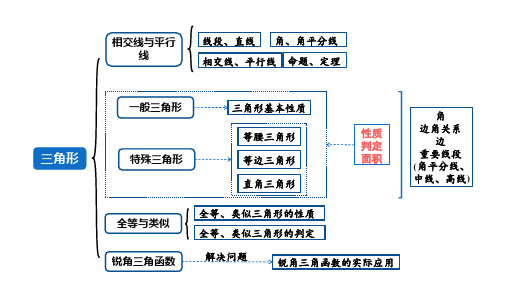
知识框架
• 考点一：直线与线段（基础） • 考点二：角及角平分线（结合其它知识考查） • 考点三：相交线（垂线） • 考点四：平行线的判定及性质（必考点）
ቤተ መጻሕፍቲ ባይዱ
解决你们的困惑，所以请你仔 细听一听！
2014级中考复习三合初级中学 邓华
例题讲解
1、如图，已知a∥b，小亮把三角板的直角顶点放在直线b 上．若∠1=40°，则∠2的度数为 ．
变式1：如图，AB//CD， ∠A+∠E=75°，则 ∠C 为【 】 A． 60° B．65° C．75° D．80°
变式2：如图，已知AB∥CD， ∠EBA=45°，∠E+∠D的度 数为（ ）
2014级中考复习三合初级中学 邓华
2014预测
2014级中考复习三合初级中学 邓华
课堂小结
通过本节课的学习: 你学到了什么？ 你学会了什么？ 你没学会的是什么？ 我们大家一起来谈谈收获！
2014级中考复习三合初级中学 邓华
命题规律
从近几年来看，得用平行线性质求角度数为重庆中考必考内容，基本 上都出现在选择题第4题，分值4分，属于容易题，只有2008年出现在 填空题，2013年A卷考查了补角（第3题），第5题考查了利用平行线、 角平分线的性质求角度数，B卷出现在第2题，先判断平行，再利用性 质求角的度数。
中考总复习---相交线与平行线复习PPT课件
1直角 ＝90° 1°＝60’ 1’=60”
⑶角平分线定义: 从角的顶点出发把角分成两个相等 的角的一条射线叫做角平分线。
OC是∠AOB
的平分线
<====>
AOC
BOC
1
AOB
2
⑷互为余角: 两个角的和是一个直角,这两 个角互为余角。
∠A 、∠B 互为余角 <====> A B 90
⑸互为补角: 两个角的和是一个平角,这两 个角互为补角。
角相等
a
(3)了解垂线、垂线段等概念
⑷了解垂线段最短
a
⑸体会点到直线距离的意义
a
⑹知道过一点有且仅有一条直线垂直已知直线 a
⑺会用三角尺或量角器过一点画一条直线的垂线b
⑻了解线段垂直平分线及其性质
a
中考考试目标
30.平行线
(1)知道两直线平行同位角相等
a
(2)探索平行线的性质
c
(3)知道过直线外一点有且仅有一条直线平行已知
生活中的数学
▪ 如图，l是一直线形的河流，一牧童在A处放 牧。 （1）若牧童要牵马到河边饮水，请在 图中画出最短的路线；
（2）若B为牧童的家，牧童牵马饮水后即刻回 家，要使牧童牵马饮水及时回家所路程最短， 则牧童应走怎样的路线?请在图中画出，并说 明理由。 B A
l
探究题；
（1）两条直线相交，有多少交点？ （2）三条直线两两相交，可能有多少交点？ （3）四条直线两两相交，可能有多少交点？ （4）多条直线两两相交，交点个数有什么规 律吗？你能用代数式表示吗？
4.如图,在三角形ABC中, ∠A=420,∠B与∠C
的三等分线交于点D、E,则
∠BDC=____8_8_0___, ∠BEC=___1_34_0__
⑶角平分线定义: 从角的顶点出发把角分成两个相等 的角的一条射线叫做角平分线。
OC是∠AOB
的平分线
<====>
AOC
BOC
1
AOB
2
⑷互为余角: 两个角的和是一个直角,这两 个角互为余角。
∠A 、∠B 互为余角 <====> A B 90
⑸互为补角: 两个角的和是一个平角,这两 个角互为补角。
角相等
a
(3)了解垂线、垂线段等概念
⑷了解垂线段最短
a
⑸体会点到直线距离的意义
a
⑹知道过一点有且仅有一条直线垂直已知直线 a
⑺会用三角尺或量角器过一点画一条直线的垂线b
⑻了解线段垂直平分线及其性质
a
中考考试目标
30.平行线
(1)知道两直线平行同位角相等
a
(2)探索平行线的性质
c
(3)知道过直线外一点有且仅有一条直线平行已知
生活中的数学
▪ 如图，l是一直线形的河流，一牧童在A处放 牧。 （1）若牧童要牵马到河边饮水，请在 图中画出最短的路线；
（2）若B为牧童的家，牧童牵马饮水后即刻回 家，要使牧童牵马饮水及时回家所路程最短， 则牧童应走怎样的路线?请在图中画出，并说 明理由。 B A
l
探究题；
（1）两条直线相交，有多少交点？ （2）三条直线两两相交，可能有多少交点？ （3）四条直线两两相交，可能有多少交点？ （4）多条直线两两相交，交点个数有什么规 律吗？你能用代数式表示吗？
4.如图,在三角形ABC中, ∠A=420,∠B与∠C
的三等分线交于点D、E,则
∠BDC=____8_8_0___, ∠BEC=___1_34_0__
第4章相交线与平行线小结与复习PPT课件
要点梳理
与垂线段有关的作图，一般是过一点作已知直线的垂线，作 图的根据是“垂线段最短”．
例题讲授
例3 （1）如图所示，∠1 = 72°，∠2 = 72°，∠3 = 60°，求∠4 的度数；
解：因为∠1 =∠2 = 72°， 所以 a∥b (内错角相等，两直线平行). 所以∠3 +∠4 = 180° (两直线平行，同旁内角互补). 因为∠3 = 60°，所以∠4 = 120°.
E A
所以 EF∥BC (平行于同一条直线的两条直线互相平行).
针对训练
3. 如图 (1)，已知 AB∥CD，∠1 = 30°，∠2 = 90°，则∠3 = __6_0_°.
A1
B
2
3
C
D
图 (1)
A
B E
F
C
D
图 (2)
4. 如图 (2)，若 AE∥CD，∠EBF = 135°，∠BFD = 60°，
同位角 “F ”型 内错角 “Z ”型 同旁内角 “U ”型
l3
21
34
l1
65
l2
78
要点梳理
四、平行线 1. 在同一平面内，没__有__公__共__点___的两条直线叫做平行线. 2. 经过直线外一点，有__且__只__有__一条直线与已知直线平行.
3. 平行于同一条直线的两条直线_平__行___.
AO
B
C
F
所以∠EOF =∠EOB +∠BOF = 90° + 40° = 130°.
所以∠COF =∠COD－∠DOF = 180°－80° = 100°.
例题讲授
例2 如图 AC⊥BC，CD⊥AB 于点 D，CD = 4.8 cm，AC = 6 cm， BC = 8 cm，则点 C 到 AB 的距离是 4.8 cm，点 A 到 BC 的距离是 6 cm，点 B 到 AC 的距离是 8 cm.
《相交线与平行线复习课》课件(16张ppt)
A 2 D 3
1 C
O
4
B
l3
2 1 3 4 6 5 7 8
l1
l2
截线 同位角 内错角 同旁内角
同旁 两旁 同旁
被截线
同侧 之间(交错 之间
)
结构特征
F (或倒置 Z
) (或反置)
U
3、垂线： 当两条直线相交所构成的四个角中有一个 角是直角时，就说这两条直线互相垂直， 其中的一条叫做另一条的垂线。 C 1 B D 垂线的性质： ①过一点有且只有一条直线与已知直线 互相垂直 ②连接直线外一点与直线上各点的所有 线段中，垂线段最短 点到直线的距离：直线外一点到这条直线的 垂线段的长度。
邻补角 两条 直线 相交
一般情况
邻补角互补
对顶角相等 存在性和唯一性
对顶角
相 交 线
特殊
垂直
垂线段最短
两条直线被 第三条所截
点到直线 的距离
同位角、内错角、同旁内角 平行线的判定 平行线的性质
平行公理及其推论
两条平行线的距离 命题
平 行 线
平移
平移的性质
一、相交线 如果一个角的两边是另一个角的两边的反向 １、对顶角：
B
例题精讲:
例2 : 如图，BD⊥AC，EF⊥AC，D、F分别为 垂足，∠1＝∠2，试说明∠ADG ＝∠C 。
A D F C
2 1
G B
E
探究创新:
已知：如图AB∥CD，试探究
∠BED与∠B，∠D的关系
A
A
B
1 E
B
1
F
C
2 D
E C
2
D
F
的两条直线 ②平行公理：过直线外 ②若a∥b，a ∥ c， 叫平行线 一点有且只有一条直线 则b ∥ c
1 C
O
4
B
l3
2 1 3 4 6 5 7 8
l1
l2
截线 同位角 内错角 同旁内角
同旁 两旁 同旁
被截线
同侧 之间(交错 之间
)
结构特征
F (或倒置 Z
) (或反置)
U
3、垂线： 当两条直线相交所构成的四个角中有一个 角是直角时，就说这两条直线互相垂直， 其中的一条叫做另一条的垂线。 C 1 B D 垂线的性质： ①过一点有且只有一条直线与已知直线 互相垂直 ②连接直线外一点与直线上各点的所有 线段中，垂线段最短 点到直线的距离：直线外一点到这条直线的 垂线段的长度。
邻补角 两条 直线 相交
一般情况
邻补角互补
对顶角相等 存在性和唯一性
对顶角
相 交 线
特殊
垂直
垂线段最短
两条直线被 第三条所截
点到直线 的距离
同位角、内错角、同旁内角 平行线的判定 平行线的性质
平行公理及其推论
两条平行线的距离 命题
平 行 线
平移
平移的性质
一、相交线 如果一个角的两边是另一个角的两边的反向 １、对顶角：
B
例题精讲:
例2 : 如图，BD⊥AC，EF⊥AC，D、F分别为 垂足，∠1＝∠2，试说明∠ADG ＝∠C 。
A D F C
2 1
G B
E
探究创新:
已知：如图AB∥CD，试探究
∠BED与∠B，∠D的关系
A
A
B
1 E
B
1
F
C
2 D
E C
2
D
F
的两条直线 ②平行公理：过直线外 ②若a∥b，a ∥ c， 叫平行线 一点有且只有一条直线 则b ∥ c
2014年中考一轮复习讲义：图形的初步认识及相交线、平行线
2014年中考一轮复习讲义：图形的初步认识及相交线、平行线【考纲要求】：1．了解直线、线段、射线的相关性质以及线段中点、线段的和、差和两点间距离的意义．2．理解角的有关概念，熟练进行角的运算．3．了解补角、余角、对顶角、垂线、垂线段等概念及性质．4．会识别同位角、内错角和同旁内角，掌握相交线与平行线的定义，熟练运用垂线的性质，平行线的性质和判定.【命题趋势】：中考中，对这部分内容命题的难度较小，主要以选择题、填空题的形式出现，重点考查互为余角、互为补角的角的性质、平行线的性质与判定的应用.【知识梳理】一、直线、射线、线段1．直线的基本性质(1)两条直线相交，只有一个交点．(2)经过两点有且只有一条直线，即：两点确定一条直线．2．线段的性质所有连接两点的线中，线段最短，即：两点之间线段最短．3．线段的中点把一条线段分成两条相等线段的点，叫做这条线段的中点．二、角的有关概念及性质1．角的有关概念角是由一条射线绕着它的端点旋转而成的图形．射线端点叫做角的顶点，两条射线是角的两边．从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线就叫做这个角的角平分线．2．角的单位与换算1°＝60′，1′＝60″，1周角＝2平角＝4直角．3．余角与补角如果两个角的和等于90°，就说这两个角互为余角；如果两个角的和等于180°，就说这两个角互为补角．同角(或等角)的余角相等；同角(或等角)的补角相等．4．对顶角与邻补角在两条相交直线形成的四个角中，如果两个角有公共顶点，一个角的两边分别是另一个角两边的反向延长线，这样的两个角称为对顶角．如果两个角有公共顶点，有一条公共边，它们的另一边互为反向延长线，这样的两个角为邻补角．对顶角相等，邻补角互补．三、垂线的性质与判定1．垂线及其性质垂线：两条直线相交所构成的四个角中有一个角是直角，则这两条直线互相垂直，其中一条直线叫做另一条直线的垂线．性质：(1)过一点有且只有一条直线与已知直线垂直；(2)直线外一点与直线上各点连接的所有线段中，垂线段最短．(简说成：垂线段最短)2．点到直线的距离直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．四、平行线的性质与判定1．概念：在同一平面内，不相交的两条直线，叫做平行线．2．平行公理经过直线外一点，有且只有一条直线与已知直线平行．3．性质如果两条直线平行，那么同位角相等，内错角相等，同旁内角互补．4．判定同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；在同一平面内垂直于同一直线的两直线平行，平行于同一直线的两直线平行．题型分类、深度剖析：考点一、直线、射线、线段【例1】在直线l上任取一点A，截取AB＝16 cm，再截取AC＝40 cm，求AB的中点D与AC 的中点E 的距离．解：(1)当C 在AB 的延长线上时，如图， ∵D 是AB 的中点，AB ＝16 cm ， ∴AD ＝12AB ＝12×16＝8(cm)．∵E 是AC 的中点，AC ＝40 cm ， ∴AE ＝12AC ＝12×40＝20(cm)．∴DE ＝AE －AD ＝20－8＝12(cm)．(2)当C 在BA 的延长线上时，如图，由(1)知AD ＝8 cm ，AE ＝20 cm.∴DE ＝AE ＋AD ＝20＋8＝28(cm)． 答：D 点与E 点的距离是12 cm 或28 cm.方法总结 对于线段的和、差关系以及线段的中点问题的计算，需结合图形，认真观察分析．若已知线段上给出的点未明确其位置，还需要分类讨论，千万不要漏解．触类旁通1 如图，点C 是线段AB 上的点，点D 是线段BC 的中点，若AB ＝12，AC ＝8，则CD ＝__________.考点二、角的计算【例2】如图，已知直线AB ，CD 相交于点O ，OA 平分∠EOC ，∠EOC ＝100°，则∠BOD 的度数是( )A ．20°B ．40°C ．50°D ．80°解析：∵OA 平分∠EOC ，∠EOC ＝100°， ∴∠AOC ＝12∠EOC ＝50°.又∵∠BOD 与∠AOC 是对顶角， ∴∠BOD ＝∠AOC ＝50°，故选C.答案：C方法总结解决有关图形中的角的计算问题时，首先要从图形中读出具有度量关系的角，如互余、互补、对顶角等，然后合理利用相关的定义、性质求解．触类旁通2 如图，直线EO⊥CD，垂足为点O，AB平分∠EOD，则∠BOD的度数为( )A．120° B．130°C．135° D．140°考点三、平行线的性质与判定【例3】如图，已知∠1＝∠2＝∠3＝55°，则∠4的度数是( )A．110° B．115° C．120° D．125°解析：∵∠2＝∠6，∠1＝∠2，∴∠1＝∠6，∴l1∥l2，∴∠3＋∠5＝180°.∵∠3＝55°，∴∠5＝125°.∵∠4与∠5是对顶角，∴∠4＝∠5＝125°，故选D.答案：D方法总结平行线的性质和判定常用来解决下列问题：(1)作图形的平移；(2)证明线段或角相等；(3)证明两直线平行；(4)证明两直线垂直．触类旁通3 如图，已知直线a∥b，∠1＝40°，∠2＝60°，则∠3等于( )A．100° B．60° C．40° D．20°。
2014年中考数学复习课件系列：第2部分-第4章-第1讲-线、角、相交线和平行线
5．知道过一点有且仅有一条直线垂直于已知直线，会用三 角尺或量角器过一点画一条直线的垂线．
6．了解线段垂直平分线及其性质． 7．知道两直线平行同位角相等，进一步探索平行线的性质． 8．知道过直线外一点有且仅有一条直线平行于已知直线， 会用三角尺或直尺过已知直线外一点画这条直线的平行线． 9．会度量两条平行线之间的距离． 10．了解定义、命题、逆命题、定理等相关概念，会识别 两个互逆命题．
(4)余角、补角和对顶角： ①∠1＋∠2＝90°⇔∠1 与∠2 互为余角；同角(或等角)的余 角___相__等___； ②∠1＋∠2＝180°⇔∠1 与∠2 互为__补__角____；同角(或等角) 的补角相等； ③一个角的两边是另一个角的两边的反向延长线，则称这 两个角是对顶角；对顶角_相__等___．
第二部分 空间与图形
第四章 三角形与四边形
第1讲 线、角、相交线和平行线
1．会比较角的大小，能估计一个角的大小，会计算角度的 和与差，认识度、分、秒，会进行简单换算．
2．了解角平分线及其性质． 3．了解补角、余角、对顶角，知道等角的余角相等、等角 的补角相等、对顶角相等． 4．了解垂直、垂线段等概念，了解垂线段最短的性质，体 会点到直线距离的意义．
5．有如下命题：①三角形的内角和等于 180°；②两直线平 行，同位角相等；③矩形的对角线相等；④相等的角是对顶角． 其中属于假命题的有_____④_____(填序号)．
考点 1
余角、补角、对顶角
1．(2011 年广东广州)已知∠α＝26°，则∠α 的补角是
___1_5_4___度．
2．(2011 年广东清远)已知∠α＝35°，则∠α 的余角是( B )
3．垂线 (1)过一点有且仅有__一__条____直线与已知直线垂直． (2)直线外一点与直线上各点连接的所有线段中，_垂__线__段___ 最短． (3)线段的垂直平分线及其性质： ①定义：垂直并且平分一条线段的直线叫做这条线段的 _垂__直__平__分__线___； ②性质及其推论：线段垂直平分线上的点到这条线段两端 点的距离__相__等____；到一条线段两端点的距离相等的点在这条 线段的__垂__直__平__分__线__上．
河南中考数学专题复习第四章第一节线段、角、相交线与平行线课件
性质
________
判定
互补
同旁内角
【温馨提示】
1.同一平面内，垂直于同一条直线的两条直线平行；
2.两条平行线之间的距离处处相等
比例线段
性质1：如果 a ＝ c ，那么ad＝___b_c____(abcd≠0)性质2(合比性
比例的 性质
质)：如果 质)：如果
bd a ＝ ，那么
b ＝ ＝…＝a
dc(bc＝＋_d_＋__…_a_＋b_m_bn(b≠d≠0)，0c)性则d 质d 3(等比性
第9题图
请完成精练本习题
定理：两条直线被一组平行线所截，所得的对应线段l5时，有 DE
AB BC
＝___DE__FE___，AACB
＝
___D_F____等
推论：平行于三角形一边的直线截其他两边(或两边的延长线)，
所得的对应线段成比例．如图⑧，当DE∥BC时，有 AE AD AE
AD DB
＝ac m a b d
n
bd n b
黄金分割比例：如图⑥，若
AC AB
BC ＝____A_C___，则线段AB被点C黄金分割，
点C叫做线段AB的黄金分割点，AC与AB的比叫黄金比，且 AC ＝ 5 1
≈0.618.简记为“ 长 ＝ 短 ＝ 5 1 ”
AB 2
全长
2
图⑥
比例线段
平行线 分线段 成比例
A. 45° C. 55°
B. 50° D. 60°
第7题图
8. [重视过程性考查]下面是投影屏上出示的抢答题，需要回答横线上符号
代表的内容，则下列回答正确的是( C ) 已知：如图，∠BEC＝∠B＋∠C.
求证：AB∥CD.
人教版初中数学中考复习精品课件第二部分 第四章 第1讲 相交线和平行线(24张)
分∠ABC，∠CDE＝150°，则∠C 的度数是( C )
图 4－1－8 A．100° B．110° C．120° D．150°
小结与反思：角平分线的运用可以得到两个角相等．
2019/4/15
22
命题与证明 例题：(2010 年四川巴中)下列命题是真命题的是( C )
A．若 a2＝b2，则 a＝b B．若 x＝y，则 2－3x>2－3y C．若 x2＝2，则 x＝± 2 D．若 x3＝8，则 x＝± 2
解析：A 项中 a2＝b2 可得 a＝± b；B 项中 x＝y 可得 2－3x ＝2－3y；D 项中 x3＝8 可得 x＝2.
2019/4/15
23
10．命题“圆的直径所对的圆周角是直角”是真 ____命题(填 “真”或“假”)． ★考点误区★
易错题：下列命题中正确的是( A．对顶角相等
C．内错角相等 正解：A
思路点拨：若两个角的和为90°，则这两个角互余，本题由 互余的定义确定各自的对数．
2019/4/15
15
3．(2010 年浙江宁波)如图 4－1－2，直线 AB 与直线 CD
相交于点 O，E 是∠AOD 内一点，已知 OE⊥AB，∠BOD＝45°， 则∠COE 的度数是( B )
图 4－1－2 A．125° B．135° C．145° D．155°
余角、补角、对顶角 1．(2011 年安徽芜湖)一个角的补角是 36°35′，这个角是
143°25′ ___________.
2019/4/15
14
2．如图 4－1－1，点 A、O、B 在同一直线上，∠AOC＝ ∠BOC，若∠1＝∠2，则图中互余的角共有( B )
图 4－1－1 A．5 对 B．4 对 C．3 对 D．2 对
中考总复习相交线与平行线复习课PPT精选文档共31页文档
55、 为 中 华 之 崛起而 读书。 ——周 恩来
中考总复习相交线与平行线复习课 PPT精选文档
51、没有哪个社会可以制订一部——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现，法律就是这样 一种的 网，触 犯法律 的人， 小的可 以穿网 而过， 大的可 以破网 而出， 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏，庇 护着我 们大家 ；它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
谢谢！
51、 天 下 之 事 常成 于困约 ，而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸，生 命是活 动。——卢 梭
53、 伟 大 的 事 业，需 要决心 ，能力 ，组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
中考总复习相交线与平行线复习课 PPT精选文档
51、没有哪个社会可以制订一部——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现，法律就是这样 一种的 网，触 犯法律 的人， 小的可 以穿网 而过， 大的可 以破网 而出， 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏，庇 护着我 们大家 ；它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
谢谢！
51、 天 下 之 事 常成 于困约 ，而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸，生 命是活 动。——卢 梭
53、 伟 大 的 事 业，需 要决心 ，能力 ，组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
角)的补角相等．
相等 ． (3)对顶角________
考点2
相交线
1．垂线的性质．
一条 性质 1：过一点有且只有__________ 直线与已知直线垂直． 性质 2 ：直线外一点与直线上各点连接的所有线段中，
垂线段 最短． __________
2．点到直线的距离． 长度 ，叫做点到直线 直线外一点到这条直线的垂线段的_______ 的距离．
A．1 个
B．2 个
C．3 个
D．4 个
3．线段 AB＝4 cm，在线段 AB 上截取 BC＝1 cm，则 AC 3 ＝__________cm.
4．有如下命题：①三角形的三个内角和等于180°；②两直
线平行，同位角相等；③矩形的对角线相等；④相等的角是对 ④ 顶角．其中属于假命题的有__________ ． 5．如图4-1-3，在△ABC 中，∠A＝90°，点 D在AC 边上，
会点到直线距离的意义． 5．知道过一点有且仅有一条直线垂直于已知直线，会用三 角尺或量角器过一点画一条直线的垂线． 6．了解线段垂直平分线及其性质． 7．知道两直线平行，同位角相等，进一步探索平行线的性 质．
8．知道过直线外一点有且仅有一条直线平行于已知直线， 会用三角尺或直尺过已知直线外一点画这条直线的平行线． 9．会度量两条平行线之间的距离． 10．通过具体例子，了解定义、命题、逆命题、定理等相
4.补充平行线的判定方法． 平行 ． (1)平行于同一条直线的两直线_________ 平行 ． (2)在同一平面内，垂直于同一条直线的两直线________ (3)平行线的定义．
考点4
角平分线和线段的垂直平分线的性质与判定
1．线段的垂直平分线． 两端点 (1)性质：线段的垂直平分线上的点到这条线段的________
关概念，会识别两个互逆命题． 11．通过实例，理解反例的作用，体会反证法的含义，掌
握用综合法证明的格式，体会证明的过程要步步有据．
考点1
线与角
一条 直线． 1．直线公理：经过两点有且只有__________ ．余角、补角与对项角．
(1)∠1＋∠2＝90°⇔∠1 与∠2 互为余角；同角(或等角)的 相等 ． 余角________ 补角 ；同角(或等 (2)∠1＋∠2＝180°⇔∠1 与∠2 互为________
65°． DE∥BC，若∠1＝155°，则∠B 的度数为_____
图 4-1-3
与线(直线、射线、线段)、 角(互余、互补、垂直)有 关的计算
例题：(2013 年江苏南通)如图 4-1-4，直线 AB，CD 相交于
点 O，OE⊥AB，∠BOD＝20°，则∠COE＝__________.
解析：由垂直关系构建互余计算．
第四章
三角形与四边形
第1讲
相交线和平行线
1．会比较角的大小，能估计一个角的大小，会计算角度的 和与差，认识度、分、秒，会进行简单换算． 2．了解角平分线及其性质． 3．了解补角、余角、对顶角，知道等角的余角相等、等角
的补角相等、对顶角相等．
4．了解垂线、垂线段等概念，了解垂线段最短的性质，体
考点3
平行线的性质与判定
1．在同一平面内，不重合的两条直线的位置关系只有两种： 相交 平行 __________ 或 __________.
一条 直线 2．平行线公理：经过直线外一点，有且只有________
与这条直线平行．
3．平行线的判定与性质. 直线平行的判定 相等 ，两直线平行 同位角________ 相等 ，两直线平行 内错角________ 互补 ，两直线平行 同旁内角_______ 由“数量关系”确定图形的 “位置关系” 直线平行的性质 相等 两直线平行，同位角________ 相等 两直线平行，内错角________ 互补 两直线平行，同旁内角_____ 由图形的“位置关系”确定 “数量关系”
图 4-1-5
图 4-1-6
2．(2013 年云南曲靖)如图 4-1-6，直线 AB，CD 相交于点 40° O，若∠BOD＝40°，OA 平分∠COE，则∠AOE＝________.
名师点评：在有关线、角、三角板等的背景图中，应着眼 于一些比较特殊的平角、角平分线、互余、互补的角、垂直等 概念，立足于基本性质，构建相关量之间的位置及数量大小关 系进行分析与解题．
直平分线，常向两端把线连．
1．如图 4-1-1，梯子的各条横档互相平行，若∠1＝80°， 则∠2 的度数是( B ) A.80° B．100° C．120° D．150°
图 4-1-1
2．将一直角三角板与两边平行的纸条按图 4-1-2 所示放置， 下列结论：
图 4-1-2 ①∠1＝∠2；②∠3＝∠4；③∠2＋∠4＝90°；④∠4＋∠5 ＝180°. 其中正确的个数是( D )
题设 和______ 结论 两部分组成． 1．每个命题都是由______ 真命题 2．真命题和假命题：正确的命题叫做____________ ，错误 的命题叫做____________ ． 假命题
定理 3．用推理的方法判断为正确的命题叫做__________ ．
【学有奇招】 1．以几何学具、实物为背景的角度计算题，注意运用学具 或实物中的平行关系、垂直关系，构造图形，然后计算相关角 度，关键是灵活处理与转化图形的位置关系和数量关系． 2．作辅助线．图中有角平分线，可向两边作垂线，线段垂
∵OE⊥AB，∴∠EOA＝90°. ∵∠AOC＝∠BOD＝20°， ∴∠COE＝90°－20°＝70°. 答案：70° 图4-1-4
【试题精选】 1．(2013 年湖南长沙)如图 4-1-5，BD 是∠ABC 的平分线，
P 是 BD 上的一点，PE⊥BA 于点 E，PE＝4 cm，则点 P 到边 4 BC 的距离为__________cm.
距离相等．
两端点 距离相等的______ 点 ，在 (2)其逆定理：到一条线段________
这条线段的垂直平分线上．
2．角平分线． 相等 ． (1)性质：角平分线上的点到角的两边的距离_______ 相等 的点在角 (2)逆定理：角的内部到角的两边的距离________ 的角平分线上．
考点5
命题、定理、证明