圆周角定理(试题复习)
圆周角复习讲义(知识总结+例题+练习题)
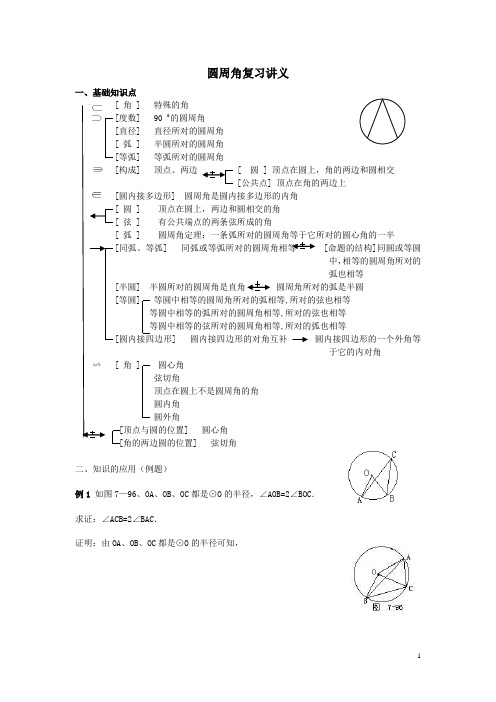
圆周角复习讲义一、基础知识点角 ] 特殊的角[] 90 0的圆周角[] 直径所对的圆周角弧 ] 半圆所对的圆周角] 等弧所对的圆周角[] 顶点、两边圆 ] 顶点在圆上,角的两边和圆相交[公共点] 顶点在角的两边上[] 圆周角是圆内接多边形的内角[ 圆 ] 顶点在圆上,两边和圆相交的角弦 ] 有公共端点的两条弦所成的角弧 ] 圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半] 命题的结构]同圆或等圆中,相等的圆周角所对的弧也相等] 圆周角所对的弧是半圆] 等圆中相等的圆周角所对的弧相等,所对的弦也相等等圆中相等的弧所对的圆周角相等,所对的弦也相等等圆中相等的弦所对的圆周角相等,所对的弧也相等] 圆内接四边形的对角互补圆内接四边形的一个外角等于它的内对角角 ] 圆心角弦切角顶点在圆上不是圆周角的角圆内角圆外角顶点与圆的位置] 圆心角角的两边圆的位置] 弦切角二、知识的应用(例题)例1 如图7—96、OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.证明:由OA、OB、OC都是⊙O的半径可知,例2 如图7—97,已知:⊙O是△ABC的外接圆,∠BAC=50°,∠ABC=47°,求∠AOB.解:∵⊙O是△ABC的外接圆∴∠A、∠B、∠C是圆周角,∠AOB是圆心角.又∵∠BAC=50°,∠ABC=47°,∴∠ACB=180°-(∠A+∠B)=180°-(50°+47°)=83°.∠AOB=2∠ACB=2×83°=166°.例3、如下右图,BC为⊙O的直径,AD⊥BC于D,P是弧AC上一动点,连结PB分别交AD、AC于点E、F.(1)当弧PA=弧AB时,求证:AE=EB;(2)当点P在什么位置时,AF=EF,证明你的结论.[过程](1)连结AB.证AE=EB.需证∠ABE=∠BAE.(2)执果索因寻条件:要AF=EF,即要∠A=∠AEF,而∠AEF=∠BED,而要∠A=∠BED,只需∠B=∠C,从而转化为弧PC=弧AB.[结果](1)证明:延长AD交⊙O于点M,连结AB、BM.∵BC为⊙O的直径,AD⊥BC于D.∴弧AB=弧BM.∴∠BAD=∠BMD.又∵弧AB=弧AP,∴∠ABP=∠BMD.∴∠BAD=∠ABP.∴AE=BE.(2)当弧PC=弧AB时,AF=EF.证明:∵弧PC=弧AB,∴∠PBC=∠ACB.而∠AEF=∠BED=90°-∠PBC,∠EAF=90°-∠ACB.∴∠AEF=∠EAF.∴AF=EF.三、课堂练习:1.若⊙O是△ABC的外接圆,OD⊥BC于D,且∠BOD=48°.则∠BAC=_____2.△ABC是半径为2 cm的圆内接三角形,若BC=23 cm,则∠A的度数为 .3.在⊙O中,直径AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于D,则BC= cm,AD= cm,BD= cm.参考答案:1.48°或132° 2.60°或120°3.8 52 52。
圆周角定理经典训练卷(含答案)

圆周角定理经典训练卷一.选择题1.如图,AB、CD都是⊙O的弦,且AB⊥CD.若∠CDB=62°,则∠ACD的大小为()(1)(2)(3)A.28°B.31°C.38°D.62°2.如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为()A.40°B.30°C.45°D.50°3.如图,AB是⊙O的弦,点C在圆上,已知∠OBA=40°,则∠C=()A.40°B.50°C.60°D.80°4.如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是()(4)(5)(6)(7)A.30°B.40°C.50°D.60°5.如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是()A.50°B.55°C.60°D.65°6.如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为()A.2B.4C.D.27.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为()A.80°B.75°C.70°D.65°8.如图,在⊙O中,AB平分∠CAO,∠BAO=25°,则∠BOC的大小为()A.25°B.50°C.65°D.80°(8)(9)(10)9.如图,⊙O中,劣弧AB所对的圆心角∠AOB=120°,点C在劣弧AB上,则圆周角∠ACB=()A.60°B.120°C.135°D.150°10.如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是()A.60°B.120°C.60°或120°D.30°或150°11.如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知和所对的圆心角分别为90°和50°,则∠P=()A.45°B.40°C.25°D.20°12.已知△ABC中,AB=AC,∠A=50°,⊙O是△ABC的外接圆,D是优弧BC上任一点(不与A、B、C重合),则∠ADB的度数是()A.50°B.65°C.65°或50°D.115°或65°13.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是()(13)(14)(15)A.75°B.60°C.45°D.30°14.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为()A.30°B.45°C.60°D.75°15.如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是()A.25°B.30°C.40°D.50°16.如图,AB是⊙O的直径,CD是⊙O的弦.若∠BAC=23°,则∠ADC的大小为()A.23°B.57°C.67°D.77°17.如图,AB为⊙O的直径,CD为⊙O的弦,∠ABD=53°,则∠BCD为()(16)A.37°B.47°C.45°D.53°(17)(18)(19)18.如图,若AB为⊙O的直径,CD是⊙O的弦,∠ABD=65°,则∠BCD的度数为()A.25°B.45°C.55°D.75°19.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=()A.20°B.30°C.40°D.70°20.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42°B.84°C.42°或138°D.84°或96°二.填空题21.如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=.(21)(22)(23)22.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=.23.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于.24.如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是°.25.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠B=20°,则∠ADC的度数为.26.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为.27.如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为.(25)(26)(27)28.如图,在⊙O中,AB为直径,C、D为⊙O上两点,若∠C=25°,则∠ABD=.29.如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC=.(28)(29)(30)30.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为cm.三.解答题31.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.32、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.33.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.34.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.35.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;.36.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC 于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.37.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.8.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析AC、AF、AB的关系,并说明理由.39.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,(1)判断△DBC的形状,并说明理由.(2)若∠BAC=60°,判断AD、AB、AC有怎样的关系?并说明理由.40.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?一.选择题(共20小题)1.D;2.C;3.A;4.C;5.A;6.D;7.A;8.B;9.C;10.A;11.D;12.C;13.C;14.B;15.B;16.A;17.C;18.D;19.A;20.D;二.填空题(共10小题)21.;22.80°;23.70°;24.60°;25.5;26.40°;27.60;28.65°;29.;30.4;三解答题28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.【解答】解:如图,∵AB是⊙O的直径,∴∠ACB=90°,∠ADB=90°.∴AB===10(cm).∵AC=6cm,BC=8cm,∵CD是∠ACB的平分线,∴∠ACD=∠BCD,则=,∴AD=BD,∴BD=AB=5cm.综上所述,AB和BD的长分别是10cm,5cm.29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.【解答】解:作直径CD,连结BD,如图,∵CD为直径,∴∠CBD=90°,∵∠D=∠A=30°,∴CD=2BC=2×3=6,∴⊙O的半径为3cm.30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;(2)已知AG=10,ED:AD=3:4,求AC的长.【解答】(1)证明:∵点C是弧AF的中点,∴∠B=∠CAE,∵AB是⊙O的直径,∴∠ACB=90°,即∠ACE+∠BCD=90°,∵CD⊥AB,∴∠B+∠BCD=90°,∴∠B=∠CAE=∠ACE,∴AE=CE …(6分)(2)解:∵∠ACB=90°,∴∠CAE+∠CGA=90°,又∵∠ACE+∠BCD=90°,∴∠CGA=∠BCD,∵AG=10,∴CE=EG=AE=5,∵ED:AD=3:4,∴AD=4,DE=3,∴AC=…(10分).31.(2015秋•扬中市期中)如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.【解答】证明:(1)连接BD,DC,∵AD平分∠BAC,∴∠BAD=∠CAD,∴弧BD=弧CD,∴BD=CD,∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,∵∠M=∠DEB=90°,DE=DM,在Rt△DEB和Rt△DMC中,,∴Rt△DEB≌Rt△DMC(HL),∴BE=CM.(2)∵DE⊥AB,DM⊥AC,∵∠M=∠DEA=90°,在Rt△DEA和Rt△DMA中∴Rt△DEA≌Rt△DMA(HL),∴AE=AM,∴AB﹣AC,=AE+BE﹣AC,=AM+BE﹣AC,=AC+CM+BE﹣AC,=BE+CM,=2BE.34.(2009秋•哈尔滨校级期中)如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.【解答】解:连接AE,∵CE为直径,∴∠EAC=90°,∴∠ACE=90°﹣∠AEC,∵CD是高,D是垂足,∴∠BCD=90°﹣∠B,∵∠B=∠AEC(同弧所对的圆周角相等),∴∠ACE=∠BCD,∴∠ACE+∠ECD=∠BCD+∠ECD,∴∠ACD=∠BCE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE 的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.【解答】解:延长CE交⊙O于M,∵AD是⊙O的直径,作CE⊥AD,∴弧AC=弧AM,∴∠ACF=∠ABC(在同圆中,等弧所对的圆周角相等).40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.【解答】解:△DBC为等腰三角形.理由如下:∵AD为△ABC的外角平分线,∴∠EAD=∠DAC,∵∠EAD=∠DCB,∠DBC=∠DAC,∴∠DBC=∠DCB,∴△DBC为等腰三角形.1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?【解答】解:∠FGC与∠AGD相等.理由如下:连接AD,如图,∵CD⊥AB,∴=,∴∠AGD=∠ADC,∵∠FGC=∠ADC,∴∠FGC=∠AGD11。
人教版九年级上期末考前复习:《圆之圆周角定理》含答案

人教版九年级上期末考前复习:《圆之圆周角定理》1.已知AB是⊙O的直径.(Ⅰ)如图①,==,∠MON=35°,求∠AON的大小;(Ⅱ)如图②,E,F是⊙O上的两个点,AD⊥EF于点D,若∠DAE=20°,求∠BAF的大小.2.如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F.(1)求证:CB平分∠ABD;(2)若AB=8,AD=6,求CF的长.3.如图,在⊙O中,点P为弧AB的中点,弦AD,PC互相垂直,垂足为M.BC分别与AD,PD相交于点E,N.(Ⅰ)求∠DNE的大小;(Ⅱ)求证EN=BN.4.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上的点,AG,DC延长线交于点F.(1)求证:∠FGC=∠AGD.(2)若BE=2,CD=8,求AD的长.5.半圆O的直径AB=8,C为半圆上一点.(1)若AC=6,则BC的长是;(2)①如图①,若D是的中点,且AD=2,求BC的长;②如图②,若D、E是的三等分点,且AD=2,直接写出BC的长.6.已知,AB为⊙O的直径,AB=10,C为⊙O上一点,D为的中点,连接AD.(Ⅰ)如图①,若∠CAB=60°,求AD的长;(Ⅱ)如图②,若AC=6,OD与CB相交于点P,求PB、PD的长.7.已知AB是⊙O的直径,弦CD与AB相交,D为的中点.(1)求∠ABD的大小;(2)若AC=6,BD=5,求BC的长.8.如图①,在⊙O中,AB为直径,C为⊙O上一点,∠A=30°,过点C作⊙O的切线,与AB的延长线相交于点P.(Ⅰ)求∠P的大小;(Ⅱ)如图②,过点B作CP的垂线,垂足为点E,与AC的延长线交于点F,①求∠F的大小;②若⊙O的半径为2,求AF的长.9.如图,在Rt △ABC 中,∠ABC =90°,AB =CB ,以AB 为直径的⊙O 交AC 于点D ,连接BD ,点E 是AB 边上一点(点E 不与点A ,B 重合),DE 的延长线交⊙O 于点G ,DF ⊥DG ,且交BC 于点F .(1)求证:AE =BF ;(2)连接GB ,EF ,求证:GB ∥EF ;(3)若AE =3cm ,EB =6cm ,求DG 的长.10.已知OA 是⊙O 的半径,OA =1,点P 是OA 上一动点,过P 作弦BC ⊥OA ,连接AB 、AC .(1)如图1,若P 为OA 中点,则AC = ,∠ACB = °;(2)如图2,若移动点P ,使AB 、CO 的延长线交于点D .记△AOC 的面积为S 1,△BOD 的面积为S 2.△AOD 的面积为S 3,且满足,求的值.参考答案1.解:(I)∵==,∠MON=35°,∴∠MON=∠MOC=∠BOC=35°,∴∠AON=180°﹣∠MON﹣∠MOC﹣∠BOC=180°﹣35°﹣35°﹣35°=75°;(II)连接BF,∵AD⊥直线l,∴∠ADE=90°,∵∠DAE=20°,∴∠AEF=∠ADE+∠DAE=110°,∵A、E、F、B四点共圆,∴∠ABF+∠AEF=180°,∴∠ABF=70°,∵AB是⊙O的直径,∴∠AFB=90°,∴∠BAF=180°﹣∠AFB﹣∠ABF=20°.2.(1)证明:∵OC∥BD,∴∠OCB=∠DBC,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC=∠DBC,∴CB平分∠ABD;(2)解:∵AB是⊙O的直径,∴∠ADB=90°,由勾股定理得:DB===2,∵OC∥BD,AO=BO,∴AF=DF,∴OF=BD==,∵直径AB=8,∴OC=OB=4,∴CF=OC﹣OF=4﹣.3.(I)解:∵点P为弧AB的中点,∴=,∴∠C=∠NDE,∵AD⊥CP,∴∠EMC=90°,∵∠CEM=∠DEN,∴∠DNE=180°﹣∠NDE﹣∠DEN=180°﹣∠C﹣∠CEM=∠EMC=90°;(II)证明:∵∠DNE=90°,∴∠DNE=∠DNB=90°,∵=,∴∠EDN=∠BDN,在△EDN和△BDN中,,∴△EDN≌△BDN(ASA),∴EN=BN.4.(1)证明:∵弦CD⊥AB,∴∠AGD=∠ADC,∵四边形ABCG是圆内接四边形,∴∠FGC=∠ADC,∴∠FGC=∠AGD;(2)解:连接OD,如图,∵CD⊥AB,CD=8∴DE=CE=4,在Rt△DOE中,∵DO2=OE2+ED2,∴DO2=(OD﹣2)2+42,解得OD=5,∴AE=10﹣2=8,∴AD=.5.解:(1)如图1中,连接AC.∵AB是直径,∴∠ACB=90°,∴BC===2.故答案为2.(2)如图1中,连接OD交AC于H,连接OC,则OA=OC=OD=4.∵D是的中点,∴CD=AD=2,OD垂直平分线段AC,设DH=x,则OH=4﹣x,∵AC⊥OD,∴∠CHD=∠CHO=90°,∴CD2﹣DH2=CO2﹣OH2,∴22﹣x2=42﹣(4﹣x)2,解得x=,∴CH===,∵OD垂直平分AC,∴AC=2CH=,∵AB是直径,∴∠ACB=90°,∴BC===7.②连接AE,AC,过点A作AH⊥ED交ED的延长线于H,过的C作CI⊥DE交DE的延长线于I.∵D,E,C是的三等分点,∴==,∴EC=DE=AD=2,∠DEA=∠EAC,∴DE∥AC,∵∠H=∠I=90°,∴∠HAC=180°﹣90°=90°,∴四边形AHIC是矩形,∴AH=CI,AC=HI,∵AD=CE,∠H=∠I=90°,∴Rt△AHD≌Rt△CIE(HL),∴EI=DH,设DH=x,则HE=x+2,∵∠H=90°,∴AE2﹣EH2=AH2=AD2﹣DH2,∴()2﹣(x+2)2=22﹣x2,解得x=,∵EI=DH=,∴HI=DH+DE+EI=+2+=,∴AC=HI=,∵AB是直径,∴∠ACB=90°,∴BC===.6.解:(Ⅰ)如图①中,连接DB.∵AB是⊙O的直径,∴∠ADB=90°,∵=,∠CAB=60°,∴∠CAD=∠DAB=30°,∴BD=AB=5,∴AD===5.(Ⅱ)如图②中,∵AB是⊙O的直径,∴∠ACB=90°,∴CB===8,∵=,∴∠BAD=∠CAD,∵OA=OD,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AC,∴∠OPB=∠ACB=90°,∴OD⊥BC,∴PB=BC=4,又O为AB的中点,∴OP=AC=3,∴PD=OD﹣OP=2.7.解:(1)∵D为的中点,∴=,∴DA=DB,∵AB是直径,∴∠ADB=90°,∴∠ABD=∠DAB=45°.(2)∵AD=BD=5,∠ADB=90°,∴AB=AD=10,∵AB是直径,∴∠ACB=90°,∴BC===8.8.解:(Ⅰ)如图①中,连接OC.∵⊙O与PC相切于点C,∴OC⊥PC,即∠OCP=90°,∵∠A=30°,∴∠BOC=2∠A=60°,在Rt△OPC中,∠POC+∠P=90°,∴∠P=90°﹣60°=30°.(Ⅱ)如图②中,①由(Ⅰ)∠OCP=90°,又∵BF⊥PC,即∠PEB=90°,∴OC∥BF,∴∠F=∠ACO=∠A=30°,②由①∠F=∠A,∴AB=BF,连接BC,则∠BCA=90°,即BC⊥AF,∴AC=CF,∵∠BOC=60°,OC=OB,∴△OBC是正三角形,∴BC=OC=2,∴,∴AF=.9.(1)证明:连接BD.如图,在Rt△ABC中,∠ABC=90°,AB=BC,∴∠A=∠C=45°.∵AB是⊙O的直径,∴∠ADB=90°,即BD⊥AC,∴BD=AD=CD,∠CBD=∠C=45°,∵DF⊥DG,∠FDG=90°,∴∠FDB+∠BDG=90°,又∵∠EDA+∠BDG=90°,∴∠EDA=∠FDB,在△AED和△BFD中,,∴△AED≌△BFD(ASA),∴AE=BF;(2)证明:如图,由(1)知△AED≌△BFD,∴DE=DF.∵∠EDF=90°.∴△EDF是等腰直角三角形,∴∠DEF=45°,∵∠G=∠A=45°.∴∠G=∠DEF,∴GB∥EF;(3)解:∵AE=BF,AE=3,∴BF=3.在Rt△EBF中,EF===3,∵△DED为等腰直角三角形,∠EDF=90°,∴DE=EF=×3=,∵∠G=∠A,∠GEB=∠AED,∴△GEB∽△AED,∴,即GE•DE=AE•BE,∴GE==,∴DG=GE+ED==.10.解:(1)∵P为OA的中点,OA⊥BC,∴AC=OA,∵OC=OA,∴OC=OA=AC,∴△AOC为等边三角形,∴AC=1,∠ACO=60°,∵PC⊥OA,∴∠ACB=∠BCO=∠AOC=30°,故答案为:1;30.(2)若DC与圆O相交于点E,连接BE,∵BC⊥OA,∴PB=PC,∴AB=AC,∵OB=CO,OA=OA,∴△ABO≌△ACO(SSS),∴S△ABO =S△ACO=S1,∴S1+S2=S3,∵,∴,∴S12+S1S2﹣S22=0,∴﹣1=0.解得:,∴,∴,∴,∵CE为直径,∴∠CBE=90°,∴AO∥BE,∴△AOD∽△BED,∴,∵OE=OC,∴OP=BE,∴,∴+1,∴,∴.。
中考数学复习《圆周角定理的应用》专题训练题含答案

圆周角定理综合训练一.选择题(共14小题)1.如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于()A.OM的长B.2OM的长C.CD的长 D.2CD的长2.如图,已知AB是⊙O的直径,C是⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D.E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,AC=2,则AG•AF是()A.10 B.12 C.8 D.163.如图,半圆O的直径AB=7,两弦AC、BD相交于点E,弦CD=,且BD=5,则DE等于()A.B.C.D.4.如图,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接正方形的面积为()A.2 B.4 C.8 D.165.如图,四边形ABCD内接于⊙O,它的对角线把四个内角分成八个角,其中相等的角有()A.2对 B.4对 C.6对 D.8对6.已知,如图弧BC与弧AD的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB等于()A.50°B.45°C.40°D.35°7.如图,B是线段AC的中点,过点C的直线l与AC成60°的角,在直线L上取一点P,使∠APB=30°,则满足条件的点P的个数是()A.3个 B.2个 C.1个 D.不存在8.如图,已知∠DEC=80°,弧CD的度数与弧AB的度数的差为20°,则∠DAC的度数为()A.35°B.45°C.25°D.50°9.如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是()A.72°B.60°C.54°D.36°10.如图,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为()A.1 B.2 C.1+D.2﹣11.如图,已知△ABC为等腰直角三角形,D为斜边BC的中点,经过点A、D 的⊙O与边AB、AC、BC分别相交于点E、F、M.对于如下五个结论:①∠FMC=45°;②AE+AF=AB;③;④2BM2=BE•BA;⑤四边形AEMF为矩形.其中正确结论的个数是()A.2个 B.3个 C.4个 D.5个12.已知:圆内接四边形ABCD中,对角线AC⊥BD,AB>CD.若CD=4,则AB 的弦心距为()A.B.2 C.D.13.如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于()A.20°B.30°C.40°D.50°14.如图,在△ABC中,AD是高,△ABC的外接圆直径AE交BC边于点G,有下列四个结论:①AD2=BD•CD;②BE2=EG•AE;③AE•AD=AB•AC;④AG•EG=BG•CG.其中正确结论的个数是()A.1个 B.2个 C.3个 D.4个二.填空题(共5小题)15.如图,⊙O是正△ABC的外接圆,点D是弧AC上一点,则∠BDC的度数是度.16.如图,点A、B、C是⊙O上的三点,若∠BOC=56°,则∠A=度.17.如图,圆内接四边形ABCD的两条对角线交于点P.已知AB=BC,CD=BD=1,设AD=x,用关于x的代数式表示PA与PC的积:PA•PC=.18.如图所示,在圆O中,弧AB=弧AC=弧CD,AB=3,AE•ED=5,则EC的长为.19.如图,△ABC内接于⊙O,AE是⊙O的直径,AE与BC交于点D,且D是OE 的中点,则tan∠ABC•tan∠ACB=.三.解答题(共7小题)20.如图,AB是⊙O的直径,AC切⊙O于点A,AD是⊙O的弦,OC⊥AD于F 交⊙O于E,连接DE,BE,BD.AE.(1)求证:∠C=∠BED;(2)如果AB=10,tan∠BAD=,求AC的长;(3)如果DE∥AB,AB=10,求四边形AEDB的面积.21.如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD与⊙O交于点D,与BC交于点E,延长BD,与AC的延长线交于点F,连接CD,G是C D的中点,连接OG.(1)判断OG与CD的位置关系,写出你的结论并证明;(2)求证:AE=BF;(3)若OG⋅DE=3(2﹣),求⊙O的面积.22.如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE 于点F.(1)求证:CF=BF;(2)若AD=2,⊙O的半径为3,求BC的长.23.如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.(1)求证:△CBE∽△AFB;(2)当时,求的值.24.如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF,与直线CD交于点G.求证:BC2=BG•BF.25.如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E.(1)求证:ID=BD;(2)设△ABC的外接圆的半径为5,ID=6,AD=x,DE=y,当点A在优弧上运动时,求y与x的函数关系式,并指出自变量x的取值范围.26.已知:如图,等边△ABC内接于⊙O,点P是劣弧上的一点(端点除外),延长BP至D,使BD=AP,连接CD.(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?参考答案与试题解析一.选择题(共14小题)1.如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于()A.OM的长B.2OM的长C.CD的长 D.2CD的长【解答】解:连接AO并延长交圆于点E,连接BE.则∠C=∠E,由AE为直径,且BD⊥AC,得到∠BDC=∠ABE=90°,所以△ABE和△BCD都是直角三角形,所以∠CBD=∠EAB.又△OAM是直角三角形,∵AO=1,∴sin∠CBD=sin∠EAB==OM,即sin∠CBD的值等于OM的长.故选:A.2.如图,已知AB是⊙O的直径,C是⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D.E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,AC=2,则AG•AF是()A.10 B.12 C.8 D.16【解答】解:连接BC,则∠B=∠F,∵CD⊥AB,∴∠ACD+∠CAD=90°,∵AB是直径,∴∠ACB=90°,∠CAB+∠B=90°,∴∠ACG=∠F.又∵∠CAF=∠FAC,∴△ACG∽△AFC,∴AC:AF=AG:AC,即AG•AF=AC2=(2)2=8.故选:C.3.如图,半圆O的直径AB=7,两弦AC、BD相交于点E,弦CD=,且BD=5,则DE等于()A.B.C.D.【解答】解法一:∵∠D=∠A,∠DCA=∠ABD,∴△AEB∽△DEC;∴=;设BE=2x,则DE=5﹣2x,EC=x,AE=2(5﹣2x);连接BC,则∠ACB=90°;Rt△BCE中,BE=2x,EC=x,则BC=x;在Rt△ABC中,AC=AE+EC=10﹣3x,BC=x;由勾股定理,得:AB2=AC2+BC2,即:72=(10﹣3x)2+(x)2,整理,得4x2﹣20x+17=0,解得x1=+,x2=﹣;由于x<,故x=﹣;则DE=5﹣2x=2.解法二:连接OD,OC,AD,∵OD=CD=OC则∠DOC=60°,∠DAC=30°又AB=7,BD=5,∴AD=2,在Rt△ADE中,∠DAC=30°,所以DE=2.故选:A.4.如图,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接正方形的面积为()A.2 B.4 C.8 D.16【解答】解:如图,连接BO并延长交圆于点E,连接AE,则∠E=∠C=30°,∠EAB=90°;∴直径BE==2,∵直径是圆内接正方形的对角线长,∴圆内接正方形的边长等于∴⊙O的内接正方形的面积为2.故选:A.5.如图,四边形ABCD内接于⊙O,它的对角线把四个内角分成八个角,其中相等的角有()A.2对 B.4对 C.6对 D.8对【解答】解:由圆周角定理知:∠ADB=∠ACB;∠CBD=∠CAD;∠BDC=∠BAC;∠ABD=∠ACD;由对顶角相等知:∠1=∠3;∠2=∠4;共有6对相等的角.故选:C.6.已知,如图弧BC与弧AD的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB等于()A.50°B.45°C.40°D.35°【解答】解:由题意,弧BC与弧AD的度数之差为20°,∴两弧所对圆心角相差20°,∴2∠A﹣2∠C=20°,∴∠A﹣∠C=10°…①;∵∠CEB是△AEC的外角,∴∠A+∠C=∠CEB=60°…②;①+②,得:2∠A=70°,即∠A=35°.故选:D.7.如图,B是线段AC的中点,过点C的直线l与AC成60°的角,在直线L上取一点P,使∠APB=30°,则满足条件的点P的个数是()A.3个 B.2个 C.1个 D.不存在【解答】解:如图,分别以AC,BC为边,作等边△APC,等边△BP′C,连接BP,依题意,结合等边三角形的性质可知∠APB=∠AP′B=30°,所以满足条件的点P的个数为2个.故选:B.8.如图,已知∠DEC=80°,弧CD的度数与弧AB的度数的差为20°,则∠DAC的度数为()A.35°B.45°C.25°D.50°【解答】解:∵弧CD的度数与弧AB的度数的差为20°,∴2(∠A﹣∠D)=20°即∠A﹣∠D=10°∵∠DEC=80°∴∠DEC=∠D+∠A=80°∴∠A=45°,∠D=35°.故选:B.9.如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是()A.72°B.60°C.54°D.36°【解答】解:∵⊙O是正五边形ABCDE的外接圆,∴∠AOB=360°÷5=72°.故选:A.10.如图,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为()A.1 B.2 C.1+D.2﹣【解答】解:连接AD,OD∵∠BAC=90°,AB=AC=2∴△ABC是等腰直角三角形∵AB是圆的直径∴∠ADB=90°∴AD⊥BC∴点D是BC的中点∴OD是△ABC的中位线∴∠DOA=90°∴△ODA,△ADC都是等腰直角三角形∴两个弓形的面积相等=AD2=1.∴阴影部分的面积=S△ADC故选:A.11.如图,已知△ABC为等腰直角三角形,D为斜边BC的中点,经过点A、D 的⊙O与边AB、AC、BC分别相交于点E、F、M.对于如下五个结论:①∠FMC=45°;②AE+AF=AB;③;④2BM2=BE•BA;⑤四边形AEMF为矩形.其中正确结论的个数是()A.2个 B.3个 C.4个 D.5个【解答】解:连接AM,根据等腰三角形的三线合一,得AD⊥BC,再根据90°的圆周角所对的弦是直径,得EF、AM是直径,根据对角线相等且互相平分的四边形是矩形,得四边形AEMF是矩形,∴①根据等腰直角三角形ABC的底角是45°,易得∠FMC=45°,正确;②根据矩形和等腰直角三角形的性质,得AE+AF=AB,正确;③连接FD,可以证明△EDF是等腰直角三角形,则③中左右两边的比都是等腰直角三角形的直角边和斜边的比,正确;④根据BM=BE,得左边=4BE2,故需证明AB=4BE,根据已知条件它们之间不一定有这种关系,错误;⑤正确.所以①②③⑤共4个正确.故选C.12.已知:圆内接四边形ABCD中,对角线AC⊥BD,AB>CD.若CD=4,则AB 的弦心距为()A.B.2 C.D.【解答】解:如图,设AC与BD的交点为O,过点O作GH⊥CD于G,交AB于H;作MN⊥AB于M,交CD于点N.在Rt△COD中,∠COD=90°,OG⊥CD;∴∠DOG=∠DCO;∵∠GOD=∠BOH,∠DCO=∠ABO,∴∠ABO=∠BOH,即BH=OH,同理可证,AH=OH;即H是Rt△AOB斜边AB上的中点.同理可证得,M是Rt△COD斜边CD上的中点.设圆心为O′,连接O′M,O′H;则O′M⊥CD,O′H⊥AB;∵MN⊥AB,GH⊥CD;∴O′H∥MN,OM∥GH;即四边形O′HOM是平行四边形;因此OM=O′H.由于OM是Rt△OCD斜边CD上的中线,所以OM=O′H=CD=2.故选:B.13.如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于()A.20°B.30°C.40°D.50°【解答】解:连接OD,∵AO=OC=OD,DA=DC,∴△ADO≌△CDO.∴∠COD=∠AOD=∠AOC=80°.∴∠ODC=∠OCD=∠ODA=∠OAD=50°.∴∠CDA=100°.∵AD∥BC,∴∠DCB=180°﹣∠CDA=180°﹣100°=80°.∴∠BCO=∠BCD﹣∠OCD=80°﹣50°=30°.故选:B.14.如图,在△ABC中,AD是高,△ABC的外接圆直径AE交BC边于点G,有下列四个结论:①AD2=BD•CD;②BE2=EG•AE;③AE•AD=AB•AC;④AG•EG=BG•CG.其中正确结论的个数是()A.1个 B.2个 C.3个 D.4个【解答】解:①若△ABD∽△CAD,则一定有AD:BD=CD:AD,即AD2=BD•CD,而两三角形只有一对角对应相等,不会得到另外的对应角相等,故①不正确;②若△BEG∽△AEB,则一定有BE:EG=AE:BE,即BE2=EG•AE,而两三角形只有一对公共角相等,不会得到另外的对应角相等,故②不正确;③∵∠ABD=∠AEC,∠ADB=∠ACE=90°,∴△ABD∽△AEC,∴AE:AC=AB:AD,即AE•AD=AC•AB,故③正确;∵根据相交弦定理,可直接得出AG•EG=BG•CG,故④正确.故选:B.二.填空题(共5小题)15.如图,⊙O是正△ABC的外接圆,点D是弧AC上一点,则∠BDC的度数是60度.【解答】解:∵△ABC是正三角形,∴∠BAC=60°;由圆周角定理,得:∠BDC=∠A=60°.16.如图,点A、B、C是⊙O上的三点,若∠BOC=56°,则∠A=28度.【解答】解:∵∠BOC=56°∴∠A=∠BOC=28°.17.如图,圆内接四边形ABCD的两条对角线交于点P.已知AB=BC,CD=BD=1,设AD=x,用关于x的代数式表示PA与PC的积:PA•PC=﹣x2+x.【解答】解:根据相交弦定理,可知PA•PC=BP•PD,∵CD=1,BD=2而AB=BC∴∴∠ADB=∠BDC∵∠ABD=∠ACD∴△ADB∽△PDC∴CD:BD=PD:AD而BD=2CD∴PD=x∴BP=BD﹣PD=2﹣x∴PA•PC=BP•PD=(2﹣x)×x=﹣x2+x.18.如图所示,在圆O中,弧AB=弧AC=弧CD,AB=3,AE•ED=5,则EC的长为2.【解答】解:∵弧AB=弧AC=弧CD,∴∠1=∠2=∠3=∠4;∴△AEC∽△BAC;∴CE:AC=AC:BC;∵AC=AB=3,因此CE•BC=3×3=9;∵BC=BE+CE,∴CE(BE+CE)=9,整理得:CE•BE+CE2=9 ①;由根据相交弦定理得,BE•CE=A E•ED=5 ②;②代入①得:5+CE2=9,解得:CE=2(负值舍去).19.如图,△ABC内接于⊙O,AE是⊙O的直径,AE与BC交于点D,且D是OE 的中点,则tan∠ABC•tan∠ACB=3.【解答】解:连接BE、CE,则∠ABE=∠ACE=90°.∵∠EAC=∠CBE,∠BED=∠ACB,∴△ADC∽△BDE,∴.①同理可由△ADB∽△CDE,得.②①×②,得==3.Rt△AEC中,tan∠AEC=.同理得tan∠AEB=.故tan∠AEC•tan∠AEB==3.∵∠EAC=∠CBE,∠BED=∠ACB,∴tan∠ABC•tan∠ACB=3.三.解答题(共7小题)20.如图,AB是⊙O的直径,AC切⊙O于点A,AD是⊙O的弦,OC⊥AD于F 交⊙O于E,连接DE,BE,BD.AE.(1)求证:∠C=∠BED;(2)如果AB=10,tan∠BAD=,求AC的长;(3)如果DE∥AB,AB=10,求四边形AEDB的面积.【解答】(1)证明:∵AB是⊙O的直径,CA切⊙O于A,∴∠C+∠AOC=90°;又∵0C⊥AD,∴∠OFA=90°,∴∠AOC+∠BAD=90°,∴∠C=∠BAD.又∵∠BED=∠BAD,∴∠C=∠BED.(2)解:由(1)知∠C=∠BAD,tan∠BAD=,∴tan∠C=.在Rt△OAC中,tan∠C=,且OA=AB=5,∴,解得.(3)解:∵OC⊥AD,∴,∴AE=ED,又∵DE∥AB,∴∠BAD=∠EDA,∴,∴AE=BD,∴AE=BD=DE,∴,∴∠BAD=30°,又∵AB是直径,∴∠ADB=90°,∴BD=AB=5,DE=5,在Rt△ABD中,由勾股定理得:AD=,过点D作DH⊥AB于H,∵∠HAD=30°,∴DH=AD=,∴四边形AEDB的面积=.21.如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD与⊙O交于点D,与BC交于点E,延长BD,与AC的延长线交于点F,连接CD,G是CD的中点,连接OG.(1)判断OG与CD的位置关系,写出你的结论并证明;(2)求证:AE=BF;(3)若OG⋅DE=3(2﹣),求⊙O的面积.【解答】(1)解:猜想OG⊥CD.证明:如图,连接OC、OD,∵OC=OD,G是CD的中点,∴由等腰三角形的性质,有OG⊥CD.(2)证明:∵AB是⊙O的直径,∴∠ACB=90°,而∠CAE=∠CBF(同弧所对的圆周角相等),在Rt△ACE和Rt△BCF中,∵∠ACE=∠BCF=90°,AC=BC,∠CAE=∠CBF,∴Rt△ACE≌Rt△BCF(ASA).∴AE=BF.(3)解:如图,过点O作BD的垂线,垂足为H,则H为BD的中点.∴OH=AD,即AD=2OH,又∠CAD=∠BAD⇒CD=BD,∴OH=OG.在Rt△BDE和Rt△ADB中,∵∠DBE=∠DAC=∠BAD,∴Rt△BDE∽Rt△ADB,∴,即BD2=AD•DE.∴.又BD=FD,∴BF=2BD,∴①,设AC=x,则BC=x,AB=,∵AD是∠BAC的平分线,∴∠FAD=∠BAD.在Rt△ABD和Rt△AFD中,∵∠ADB=∠ADF=90°,AD=AD,∠FAD=∠BAD,∴Rt△ABD≌Rt△AFD(ASA).∴AF=AB=,BD=FD.∴CF=AF﹣AC=.在Rt△BCF中,由勾股定理,得②,由①、②,得,∴x2=12,解得或(舍去),∴,∴⊙O的半径长为.=π•()2=6π.∴S⊙O22.如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE 于点F.(1)求证:CF=BF;(2)若AD=2,⊙O的半径为3,求BC的长.【解答】(1)证明:连接AC,如图∵C是弧BD的中点∴∠BDC=∠DBC(1分)又∵∠BDC=∠BAC在△ABC中,∠ACB=90°,CE⊥AB∴∠BCE=∠BAC∠BCE=∠DBC(3分)∴CF=BF;(4分)(2)解:解法一:作CG⊥AD于点G,∵C是弧BD的中点∴∠CAG=∠BAC,即AC是∠BAD的角平分线.(5分)∴CE=CG,AE=AG(6分)在Rt△BCE与Rt△DCG中,CE=CG,CB=CD∴Rt△BCE≌Rt△DCG(HL)∴BE=DG(7分)∴AE=AB﹣BE=AG=AD+DG即6﹣BE=2+DG∴2BE=4,即BE=2(8分)又∵△BCE∽△BAC∴BC2=BE•AB=12(9分)BC=±2(舍去负值)∴BC=2.(10分)解法二:∵AB是⊙O的直径,CE⊥AB ∴∠BEF=∠ADB=90°,(5分在Rt△ADB与Rt△FEB中,∵∠ABD=∠FBE∴△ADB∽△FEB,则,即,∴BF=3EF(6分)又∵BF=CF,∴CF=3EF利用勾股定理得:(7分)又∵△EBC∽△ECA则,则CE2=AE•BE(8分)∴(CF+EF)2=(6﹣BE)•BE即(3EF+EF)2=(6﹣2EF)•2EF ∴EF=(9分)∴BC=.(10分)23.如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.(1)求证:△CBE∽△AFB;(2)当时,求的值.【解答】(1)证明:∵AE=EB,AD=DF,∴ED是△ABF的中位线,∴ED∥BF,∴∠CEB=∠ABF,又∵∠C=∠A,∴△CBE∽△AFB.(2)解:由(1)知,△CBE∽△AFB,∴,又AF=2AD,∴.24.如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF,与直线CD交于点G.求证:BC2=BG•BF.【解答】证明:∵AB是⊙O的直径,∠ACB=90°,又CD⊥AB于D,∴∠BCD=∠A,又∠A=∠F.∴∠F=∠BCD.在△BCG和△BFC中,,∴△BCG∽△BFC.∴.即BC2=BG•BF.25.如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E.(1)求证:ID=BD;(2)设△ABC的外接圆的半径为5,ID=6,AD=x,DE=y,当点A在优弧上运动时,求y与x的函数关系式,并指出自变量x的取值范围.【解答】(1)证明:∵点I是△ABC的内心∴∠BAD=∠CAD,∠ABI=∠CBI(2分)∵∠CBD=∠CAD∴∠BAD=∠CBD(3分)∴∠BID=∠ABI+∠BAD,∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,∵∠IBD=∠CBI+∠CBD,∴∠BID=∠IBD∴ID=BD;(5分)(2)解:∵∠BAD=∠CBD=∠EBD,∠D=∠D∴△ABD∽△BED(7分)∴∴AD×DE=BD2=ID2(8分)∵ID=6,AD=x,DE=y∴xy=36(9分)又∵x=AD>ID=6,AD不大于圆的直径10∴6<x≤10∴y与x的函数关系式是(6<x≤10).(10分)说明:只要求对xy=36与6<x≤10,不写最后一步,不扣分.26.已知:如图,等边△ABC内接于⊙O,点P是劣弧上的一点(端点除外),延长BP至D,使BD=AP,连接CD.(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?【解答】解:(1)如图①,△PDC为等边三角形.(2分)理由如下:∵△ABC为等边三角形∴AC=BC∵在⊙O中,∠PAC=∠PBC又∵AP=BD∴△APC≌△BDC∴PC=DC∵AP过圆心O,AB=AC,∠BAC=60°∴∠BAP=∠PAC=∠BAC=30°∴∠PBC=∠PAC=30°,∠BCP=∠BAP=30°∴∠CPD=∠PBC+∠BCP=30°+30°=60°∴△PDC为等边三角形;(6分)(2)如图②,△PDC仍为等边三角形.(8分)理由如下:∵△ABC为等边三角形∴AC=BC∵在⊙O中,∠PAC=∠PBC又∵AP=BD∴△APC≌△BDC∴PC=DC∵∠BAP=∠BCP,∠PBC=∠PAC∴∠CPD=∠PBC+∠BCP=∠PAC+∠BAP=60°∴△PDC为等边三角形.(12分)31 / 31。
中考数学专题复习:圆周角定理

36.已知:在△ABC 中,以 AC 边为直径的⊙O 交 BC 于点 D,在劣弧 上取一 点 E 使∠EBC=∠DEC,延长 BE 依次交 AC 于点 G,交⊙O 于 H.
A.32°
B.38°
C.52°
D.66°
12.如图,⊙O 中,弦 BC 与半径 OA 相交于点 D,连接 AB,OC.若∠A=60°,
∠ADC=85°,则∠C 的度数是( )
A.25°
B.27.5°
C.30°
D.35°
第 12 题
第 13 题
13.如图,点 D 在半圆 O 上,半径 OB= ,AD=10,点 C 在弧 BD 上移动,
8.解:连接 OA, ∵OA=OC, ∴∠OAC=∠C=28°, ∴∠OAB=64°, ∵OA=OB, ∴∠B=∠OAB=64°, 故选:C.
9.解:连接 OC, ∵AO∥DC,
∴∠ODC=∠AOD=70°, ∵OD=OC, ∴∠ODC=∠OCD=70°, ∴∠COD=40°, ∴∠AOC=110°, ∴∠B= ∠AOC=55°. 故选:D. 10.解:圆上取一点 A,连接 AB,AD,如图所示,
∵DH⊥AC,
∴∠AHD=90°,
∴点 H 在以 M 为圆心,MD 为半径的⊙M 上,
∴当 M、H、B 共线时,BH 的值最小,
∵AB 是直径,
∴∠ADB=90°,
∴BD=
=12,
BM=
=
=13,
∴BH 的最小值为 BM﹣MH=13﹣5=8. 故选:D. 14.解:∵PA 是圆的切线. ∴∠OAP=90°, 同理∠OBP=90°, 根据四边形内角和定理可得: ∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,
初中数学专题复习(圆周角定理)

初中数学专题复习(圆周角定理)1.(2020•陕西)如图,点A、B、C在⊙O上,BC∥OA,连接BO并延长,交⊙O于点D,连接AC,DC.若∠A=25°,则∠D的大小为()A.25°B.30°C.40°D.50°解:∵BC∥OA,∴∠ACB=∠A=25°,∠B=∠AOB=2∠ACB=50°,∵BD是⊙O的直径,∴∠BCD=90°,∴∠D=90°﹣∠B=90°﹣50°=40°,故选:C.2.(2020•兰州)如图,AB是⊙O的直径,若∠BAC=20°,则∠ADC=()A.40°B.60°C.70°D.80°解:∵AB是直径,∴∠ACB=90°,∵∠BAC=20°,∴∠ABC=90°﹣20°=70°,∴∠ADC=∠ABC=70°,故选:C.3.(2020•阜新)如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为()A.57°B.52°C.38°D.26°解:连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∵∠ABC=38°,∴∠BAC=90°﹣∠ABC=52°,∴∠BDC=∠BAC=52°.故选:B.4.(2020•眉山)如图,四边形ABCD的外接圆为⊙O,BC=CD,∠DAC=35°,∠ACD=45°,则∠ADB的度数为()A.55°B.60°C.65°D.70°解:∵BC=CD,∴=,∵∠ABD和∠ACD所对的弧都是,∴∠BAC=∠DAC=35°,∵∠ABD=∠ACD=45°,∴∠ADB=180°﹣∠BAD﹣∠ABD=180°﹣70°﹣45°=65°.故选:C.5.(2020•十堰)如图,点A,B,C,D在⊙O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=()A.2B.4C.D.2解:连接OC,如图,∵∠ADC=30°,∴∠AOC=60°,∵OA⊥BC,∴CE=BE,在Rt△COE中,OE=OC,CE=OE,∵OE=OA﹣AE=OC﹣1,∴OC﹣1=OC,∴OC=2,∴OE=1,∴CE=,∴BC=2CE=2.故选:D.6.(2020•黄石)如图,点A、B、C在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D、E,若∠DCE=40°,则∠ACB的度数为()A.140°B.70°C.110°D.80°解:如图,在优弧AB上取一点P,连接AP,BP,∵CD⊥OA,CE⊥OB,∴∠ODC=∠OEC=90°,∵∠DCE=40°,∴∠AOB=360°﹣90°﹣90°﹣40°=140°,∴∠P=∠AOB=70°,∵A、C、B、P四点共圆,∴∠P+∠ACB=180°,∴∠ACB=180°﹣70°=110°,故选:C.7.(2020•荆门)如图,⊙O中,OC⊥AB,∠APC=28°,则∠BOC的度数为()A.14°B.28°C.42°D.56°解:∵在⊙O中,OC⊥AB,∴=,∵∠APC=28°,∴∠BOC=2∠APC=56°,故选:D.8.(2020•营口)如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是()A.110°B.130°C.140°D.160°解:如图,连接BC,∵AB为⊙O的直径,∴∠ACB=90°,∴∠B=90°﹣∠CAB=90°﹣40°=50°,∵∠B+∠ADC=180°,∴∠ADC=180°﹣50°=130°.故选:B.9.(2020•河池)如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=55°,则∠2=35°.解:如图,连接AD.∵AB是直径,∴∠ADB=90°,∵∠1=∠ADE,∴∠1+∠2=90°,∵∠1=55°,∴∠2=35°,故答案为35.10.(2020•聊城)如图,在⊙O中,四边形OABC为菱形,点D在上,则∠ADC的度数是60°.解:∵四边形ABCD内接于⊙O,∴∠B+∠D=180°,∵四边形OABC为菱形,∴∠B=∠AOC,∴∠D+∠AOC=180°,∵∠AOC=2∠D,∴3∠D=180°,∴∠ADC=60°,故答案为60°.11.(2020•宜宾)如图,A、B、C是⊙O上的三点,若△OBC是等边三角形,则cos∠A=.解:∵△OBC是等边三角形,∴∠BOC=60°,∴∠A=30°,∴cos∠A=cos30°=.故答案为:.12.(2020•随州)如图,点A,B,C在⊙O上,AD是∠BAC的角平分线,若∠BOC=120°,则∠CAD的度数为30°.21教育网解:∵∠BAC=∠BOC=×120°=60°,而AD是∠BAC的角平分线,∴∠CAD=∠BAC=30°.故答案为:30°.13.(2020•宿迁)如图,在△ABC中,D是边BC上一点,以BD为直径的⊙O经过点A,且∠CAD=∠ABC.(1)请判断直线AC是否是⊙O的切线,并说明理由;(2)若CD=2,CA=4,求弦AB的长.解:(1)直线AC是⊙O的切线,理由如下:如图,连接OA,∵BD为⊙O的直径,∴∠BAD=90°=∠OAB+∠OAD,∵OA=OB,∴∠OAB=∠ABC,又∵∠CAD=∠ABC,∴∠OAB=∠CAD=∠ABC,∴∠OAD+∠CAD=90°=∠OAC,∴AC⊥OA,又∵OA是半径,∴直线AC是⊙O的切线;(2)方法一、过点A作AE⊥BD于E,∵OC2=AC2+AO2,∴(OA+2)2=16+OA2,∴OA=3,∴OC=5,BC=8,=×OA×AC=×OC×AE,∵S△OAC∴AE==,∴OE===,∴BE=BO+OE=,∴AB===.方法二、∵∠CAD=∠ABC,∠C=∠C,∴△ACD∽△BCA,∴=,∴,∴BC=8,AB=2AD,∴BD=6,∵AB2+AD2=BD2,∴5AD2=36,∴AD=,∴AB=2AD=.14.(2020•南京)如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D 作DF∥BC,交⊙O于点F.求证:(1)四边形DBCF是平行四边形;(2)AF=EF.证明:(1)∵AC=BC,∴∠BAC=∠B,∵DF∥BC,∴∠ADF=∠B,∵∠BAC=∠CFD,∴∠ADF=∠CFD,∴BD∥CF,∵DF∥BC,∴四边形DBCF是平行四边形;(2)连接AE,∵∠ADF=∠B,∠ADF=∠AEF,∴∠AEF=∠B,∵四边形AECF是⊙O的内接四边形,∴∠ECF+∠EAF=180°,∵BD∥CF,∴∠ECF+∠B=180°,∴∠EAF=∠B,∴∠AEF=∠EAF,∴AF=EF.15.(2020•温州)如图,C,D为⊙O上两点,且在直径AB两侧,连接CD交AB于点E,G是上一点,∠ADC =∠G.(1)求证:∠1=∠2.(2)点C关于DG的对称点为F,连接CF.当点F落在直径AB上时,CF=10,tan∠1=,求⊙O的半径.解:(1)∵∠ADC=∠G,∴=,∵AB为⊙O的直径,∴=,∴∠1=∠2;(2)如图,连接DF,∵=,AB是⊙O的直径,∴AB⊥CD,CE=DE,∴FD=FC=10,∵点C,F关于DG对称,∴DC=DF=10,∴DE=5,∵tan∠1=,∴EB=DE•tan∠1=2,∵∠1=∠2,∴tan∠2=,∴AE==,∴AB=AE+EB=,∴⊙O的半径为.16.(2020•泰州)如图,在⊙O中,点P为的中点,弦AD、PC互相垂直,垂足为M,BC分别与AD、PD相交于点E、N,连接BD、MN.(1)求证:N为BE的中点.(2)若⊙O的半径为8,的度数为90°,求线段MN的长.(1)证明:∵AD⊥PC,∴∠EMC=90°,∵点P为的中点,∴,∴∠ADP=∠BCP,∵∠CEM=∠DEN,∴∠DNE=∠EMC=90°=∠DNB,∵,∴∠BDP=∠ADP,∴∠DEN=∠DBN,∴DE=DB,∴EN=BN,∴N为BE的中点;(2)解:连接OA,OB,AB,AC,∵的度数为90°,∴∠AOB=90°,∵OA=OB=8,∴AB=8,由(1)同理得:AM=EM,∵EN=BN,∴MN是△AEB的中位线,∴MN=AB=4.。
2021年中考数学专题复习:圆周角定理

2021年中考数学专题复习:圆周角定理一.选择题(共10小题)1.如图,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是()A.22.5°B.30°C.45°D.60°2.如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为()A.60°B.50°C.40°D.20°3.如图:已知AB是⊙O的直径,点C在⊙O上,点D在半径OA上(不与点O,A重合).若∠COA=60°,∠CDO=70°,∠ACD的度数是()A.60°B.50°C.30°D.10°4.如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D,连接AC,CD.则下列结论中错误的是()A.AC=CD B.+=C.OD⊥AB D.CD平分∠ACB 5.如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=30°,OD=2,那么DC的长等于()A.2 B.4 C.D.26.如图,AB是的直径,C、D是圆上两点,连接AC,AD,CD.若∠CAB=35°,则∠ADC的度数为()A.55°B.45 C.35°D.25°7.如图,在⊙O中,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB和∠COD互补,且AB=2,CD=4,则⊙O的半径是()A.B.2 C.D.48.如图,AD是⊙O的直径,=,若∠AOB=40°,则圆周角∠BPC的度数是()A.40°B.50°C.60°D.70°9.如图,AB是⊙O的弦,点C在上,点D是AB的中点.将在沿AC折叠后恰好经过点D,若⊙O的半径为2,AB=8.则AC的长是()A.6B.C.2D.410.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为()A.B.2C.D.二.填空题(共6小题)11.如图,AB是半圆的直径,O为圆心,C是半圆上的点,AB=10,BC=5,D是上的点,则∠D的度数为.12.如图,已知,在⊙O中,∠AOB=150°,E是优弧AB上一点,C、D是劣弧AB上不同的两点(不与A、B两点重合),则∠C+∠D的度数为°.13.如图,点A,B,C在⊙O上,∠A=50°,∠C=10°,则∠B=°.14.如图,AD为⊙O的直径,A,B,C三点在⊙O上,AB=BC,BD交AC于点E,∠ABC=110°,则∠CAD为°.15.如图,A(2,0)、B(6,0),以AB为直径作⊙M,射线OF交⊙M于E、F两点,C为弧AB的中点,D为EF的中点.当射线OF绕O点旋转时,CD的最小值为.16.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM的最小值为.三.解答题(共4小题)17.如图,圆内接四边形ABCD,AB是⊙O的直径,OD∥AC交BC于点E.(1)求证:△BCD为等腰三角形;(2)若BE=4,AC=6,求DE.18.如图,以平行四边形ABCD的顶点A为圆心,AB为半径作圆A,分别交BC,AD于E,F 两点,交BA的延长线于点G.(1)求证:=;(2)若为140°,求∠EGB的度数.19.如图,AB是⊙O的直径,CD⊥AB于E,BF∥OC,连接BC,CF,AC.(1)求证:∠OCF=∠ECB;(2)若∠BAC=30°,AC=6cm,求⊙O的半径.20.已知点C在⊙O上.AC=AB,点P与点C位于直径AB的异侧(点P不与A.B两点重合),连接BP.过点C作直线PB的垂线CD,交直线PB于点D.连接CP.(1)如图①,求∠CPD的度数;(2)如图②,当CP⊥AB,AC=2时,求△BPC的周长.参考答案一.选择题1.解:设圆心为O,连接OA、OB,如图,∵弦AB的长度等于圆半径的倍,即AB=OA,∴OA2+OB2=AB2,∴△OAB为等腰直角三角形,∠AOB=90°,∴∠ASB=∠AOB=45°.故选:C.2.解:连接AD,∵AB为⊙O的直径,∴∠ADB=90°.∵∠BCD=40°,∴∠A=∠BCD=40°,∴∠ABD=90°﹣40°=50°.故选:B.3.解:∵OA=OC,∠COA=60°,∴△ACO为等边三角形,∴∠CAD=60°,又∵∠CDO=70°,∴∠ACD=∠CDO﹣∠CAD=10°.故选:D.4.解:A、过D作DD'⊥BC,交⊙O于D',连接CD'、BD',由折叠得:CD=CD',∠ABC=∠CBD',∴AC=CD'=CD,故①正确;B、∵AC=CD',∴,由折叠得:,∴=,故②正确;C、∵D为AB的中点,∴OD⊥AB,故③正确;D、延长OD交⊙O于E,连接CE,∵OD⊥AB,∴∠ACE=∠BCE,∴CD不平分∠ACB,故④错误;故选:D.5.解:如图,连接OC,设AB交CD于E.∵AB⊥CD,AB是直径,∵OA=OC,∠OAC=∠OCA=30°,∴∠COE=60°,∴EC=OC•sin60°=,∴CD=2DE=2,故选:D.6.解:连接BD,∵,∴∠CDB=∠CAB=35°,∵AB为直径,∴∠ADB=90°,∴∠ADC=∠ADB﹣∠CDB=55°,故选:A.7.解:作直径DE,连接CE,如图,∵∠AOB+∠COD=180°,∠COD+∠COE=180°,∴∠AOB=∠COE,∴=,∴CE=AB=2,∵DE为直径,∴∠DCE=90°,∴DE==2,∴OD=,即⊙O的半径是.8.解:∵=,∠AOB=40°,∴∠COD=∠AOB=40°,∵∠AOB+∠BOC+∠COD=180°,∴∠BOC=100°,∴∠BPC=∠BOC=50°,故选:B.9.解:如图,延长BO交⊙O于E,连接AE,OA,OD,OC,BC,作CH⊥AB于H.∵AD=DB,∴OD⊥AB,∴∠ADO=90°,∵OA=2,AD=DB=4,∴OD==2,∵BE是直径,∴∠BAE=90°,∵AD=DB,EO=OB,∴OD∥AE,AE=2OD=4,∴AE=AD,∴=,∴=,∴∠CAE=∠CAH=45°,∴∠BOC=2∠CAB=90°,∴BC=OC=2,∵CH⊥AB,∴∠CAH=∠ACH=45°,∴AH=CH,设AH=CH=x,则BH=8﹣x,在Rt△BCH中,∵CH2+BH2=BC2,∴x2+(8﹣x)2=(2)2,∴x=6或2(舍弃),在Rt△ACH中,∵AC=,∴AC=6.故选:A.10.解:作直径CD,在Rt△OCD中,CD=6,OC=2,则OD==4,tan∠CDO==,由圆周角定理得,∠OBC=∠CDO,则tan∠OBC=,故选:D.二.填空题(共6小题)11.解;如图,连接BD,∵AB是半圆的直径,AB=10,BC=5,∴OC=OB=BC=5,∠ADB=90°.∴△OBC是等边三角形.∴∠BOC=60°.∵∠BDC=∠BOC=30°,∴∠ADC=∠ADB+∠CDB=90°+30°=120°.故答案是:120°.12.解:连接OE,∵在⊙O中,∠AOB=150°,∴∠AOE+∠BOE=360°﹣∠AOB=210°,∵∠D=∠BOE,∠C=∠AOE,∴∠C+∠D=∠AOE+∠BOE=(∠AOE+∠BOE)=105°.故答案为:105.13.解:∵∠A=50°,∴∠BOC=2∠A=100°,∵∠B+∠A=∠BOC+∠C,∴∠B=100°+10°﹣50°=60°.故答案为60.14.解:∵AD为⊙O的直径,∴∠ABD=90°,∵∠ABC=110°,∴∠DBC=110°﹣90°=20°.∴∠CAD=∠DBC=20°.故答案为20.15.解:连接MD,如图,∵D为EF的中点,∴MD⊥EF,∴∠ODM=90°,∴点D在以A点为圆心,2为半径的圆上,当D点为CA与⊙A的交点时,CD的值最小,此时CD=AC﹣2=2﹣2,即CD的最小值为2﹣2.故答案为:2﹣2.16.解:如图,连接OM,CM,过点A作AT⊥CM交CM的延长线于T.∵=,∴OM⊥PD,∴∠MOD=90°,∴∠MCD=∠MOD=45°,∵∠ACB=90°,∴∠ACT=45°,∵AT⊥CT,∴∠ATC=90°,∵AC=10,∴AT=AC•sin45°=5,∵AM≥AT,∴AM≥5,∴AM的最小值为5,故答案为5.三.解答题(共4小题)17.解:(1)∵OD⊥BC于E,∴=,∴BD=CD,∴△BDC是等腰三角形.(2)∵AB是⊙O的直径,∴∠ACB=90°,∵OD⊥BC于E,∴OD∥AC,∵点O是AB的中点,∴OE是△ABC的中位线,∴OE=AC=×6=3,在Rt△OBE中,∵BE=4,OE=3,∴OB===5,即OD=OB=5,∴DE=OD﹣OE=5﹣3=2.18.(1)证明:连接AE.∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EAF=∠AEB,∠GAF=∠B,∵AE=AB,∴∠B=∠AEB,∴∠EAF=∠GAF,∴=;(2)∵GB为⊙A的直径,∴为180°,∵为140°,∴为40°,∴∠BAE=40°∵∠EGB=∠BAE,∴∠EGB=20°.19.(1)证明:∵OC∥BF,∴∠OCF=∠BFC,∵AB⊥CD,∴,∴∠BFC=∠BCD,∴∠OCF=∠ECB;(2)解:∵AB是⊙O的直径,∴∠ACB=90°,在Rt△ACB中,∵∠BAC=30°,∴BC=AC=×6=2,∴AB=2BC=4,∴⊙O的半径为.20.解:(1)∵AB是⊙O的直径,∴∠ACB=90°,∵AC=AB,∴∠ABC=30°,∴∠A=60°,∴∠CPD=∠A=60°;(2)由(1)知,∠A=60°,∴∠P=∠A=60°,∵CP⊥AB,∴∠ACP=30°,∴∠BCP=60°,∴△PBC是等边三角形,∵AC=2,∴BC=AC=2,∴△BPC的周长=6.。
九年级数学圆周角定理(基础)(含答案)

圆周角定理(基础)一、单选题(共11道,每道8分)1.如图,点A,B,C都在⊙O上,若∠ACB=48°,则∠AOB的度数为( )A.96°B.48°C.42°D.24°答案:A解题思路:圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半∵∠ACB与∠AOB对着同一条弧AB,∠ACB=48°∴∠AOB=2∠ACB=96°试题难度:三颗星知识点:略2.如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是( )A.∠BB.∠CC.∠DEBD.∠D答案:D解题思路:同弧或等弧所对的圆周角相等∵∠A与∠D都是弧BC所对的圆周角∴∠D=∠A试题难度:三颗星知识点:略3.如图,⊙O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是( )A.25°B.27.5°C.30°D.35°答案:D解题思路:∵∠A=60°,∠ADC=85°∴∠B=∠ADC-∠A=25°∵∠B与∠AOC对着同一条弧AC∴∠AOC=2∠B=50°∴∠C=∠ADC-∠AOC=35°试题难度:三颗星知识点:略4.如图,AB是⊙O的直径,C,D为圆上两点,若∠AOC=130°,则∠D等于( )A.20°B.25°C.35°D.50°答案:B解题思路:∵AB是⊙O的直径,∠AOC=130°∴∠BOC=180°-∠AOC=50°∵∠D与∠BOC对着同一条弧BC∴∠D=∠BOC=25°试题难度:三颗星知识点:略5.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的度数分别为88°,30°,则∠ACB的大小为( )A.15°B.28°C.29°D.34°答案:C解题思路:如图,点A,B的度数分别为88°,30°∴∠AOB=88°-30°=58°∵∠ACB与∠AOB对着同一条弧AB∴∠ACB=∠AOB=29°试题难度:三颗星知识点:略6.如图,已知圆心角∠AOB=110°,则圆周角∠ACB=( )A.55°B.110°C.120°D.125°答案:D解题思路:如图,设点E是优弧AB上的一点,连接EA,EB∵∠E与∠AOB对着同一条弧AB,∠AOB=110°∴∠E=∠AOB=55°又∠ACB+∠E=180°∴∠ACB=180°-55°=125°试题难度:三颗星知识点:略7.如图,在⊙O中,AD是直径,∠ABC=40°,则∠CAD等于( )A.40°B.50°C.60°D.70°答案:B解题思路:∵∠ADC与∠ABC对着同一条弧AC,∠ABC=40°∴∠ADC=∠ABC=40°∵AD是⊙O的直径∴∠DCA=90°∴∠CAD=90°-∠ADC=50°试题难度:三颗星知识点:略8.如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=30°,则∠BOC 的度数为( )A.30°B.40°C.50°D.60°答案:D解题思路:∵∠AOC与∠ADC对着同一条弧AC,∠ADC=30°∴∠AOC=2∠ADC=60°∵AB是⊙O的弦,OC⊥AB交⊙O于点C∴弧AC=弧BC∴∠BOC=∠AOC=60°试题难度:三颗星知识点:略9.如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )A.110°B.120°C.135°D.140°答案:D解题思路:∵四边形ABCD内接于⊙O∴∠A+∠C=180°又∠A=40°∴∠C=180°-40°=140°试题难度:三颗星知识点:略10.如图,圆内接四边形ABCD中,边BA的延长线上有一点E,且∠EAD=50°,则∠C的度数为( )A.50°B.40°C.130°D.140°答案:A解题思路:∵点E在BA的延长线上,∠EAD=50°∴∠BAD=180°-∠EAD=130°∵四边形ABCD内接于圆∴∠C+∠BAD=180°∴∠C=180°-∠BAD=50°试题难度:三颗星知识点:略11.如图,四边形ABCD是半圆的内接四边形,AB是直径,弧CB=弧CD.若∠C=110°,则∠ABC 的度数等于( )A.55°B.60°C.65°D.70°答案:A解题思路:如图,连接AC∵四边形ABCD是半圆的内接四边形,∠C=110°∴∠DAB=180°-∠C=70°又弧CB=弧CD∴∠BAC=∠DAC=∠DAB=35°∵AB是直径∴∠ACB=90°∴∠ABC=90°-∠BAC=55°试题难度:三颗星知识点:略。
圆周角定理中考题含解析图文稿

圆周角定理中考题含解析集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY-圆周角定理中考题(含解析)一.解答题(共4小题)1.已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.(1)求证:AB=AC;(2)若AB=4,BC=2,求CD的长.2.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状:;(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.3.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;(Ⅱ)如图②,若∠CAB=60°,求BD的长.4.如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C,(1)求证:CB∥PD;(2)若BC=3,sin∠P=,求⊙O的直径.圆周角定理中考题(含解析)参考答案与试题解析一.解答题(共4小题)1.(2016?宁夏)已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.(1)求证:AB=AC;(2)若AB=4,BC=2,求CD的长.【解答】(1)证明:∵ED=EC,∴∠EDC=∠C,∵∠EDC=∠B,∴∠B=∠C,∴AB=AC;(2)方法一:解:连接AE,∵AB为直径,∴AE⊥BC,由(1)知AB=AC,∴BE=CE=BC=,∵△CDE∽△CBA,∴,∴CECB=CDCA,AC=AB=4,∴2=4CD,∴CD=.方法二:解:连接BD,∵AB为直径,∴BD⊥AC,设CD=a,由(1)知AC=AB=4,则AD=4﹣a,在Rt△ABD中,由勾股定理可得:BD2=AB2﹣AD2=42﹣(4﹣a)2在Rt△CBD中,由勾股定理可得:BD2=BC2﹣CD2=(2)2﹣a2∴42﹣(4﹣a)2=(2)2﹣a2整理得:a=,即:CD=.2.(2015?德州)如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状:等边三角形;(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.【解答】证明:(1)△ABC是等边三角形.证明如下:在⊙O中∵∠BAC与∠CPB是所对的圆周角,∠ABC与∠APC是所对的圆周角,∴∠BAC=∠CPB,∠ABC=∠APC,又∵∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC为等边三角形;(2)在PC上截取PD=AP,如图1,又∵∠APC=60°,∴△APD是等边三角形,∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.又∵∠APB=∠APC+∠BPC=120°,∴∠ADC=∠APB,在△APB和△ADC中,,∴△APB≌△ADC(AAS),∴BP=CD,又∵PD=AP,∴CP=BP+AP;(3)当点P为的中点时,四边形APBC的面积最大.理由如下,如图2,过点P作PE⊥AB,垂足为E.过点C作CF⊥AB,垂足为F.∵S△APB =AB?PE,S△ABC=AB?CF,∴S四边形APBC=AB(PE+CF),当点P为的中点时,PE+CF=PC,PC为⊙O的直径,∴此时四边形APBC的面积最大.又∵⊙O的半径为1,∴其内接正三角形的边长AB=,∴S四边形APBC=×2×=.3.(2014?天津)已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;(Ⅱ)如图②,若∠CAB=60°,求BD的长.【解答】解:(Ⅰ)如图①,∵BC是⊙O的直径,∴∠CAB=∠BDC=90°.∵在直角△CAB中,BC=10,AB=6,∴由勾股定理得到:AC===8.∵AD平分∠CAB,∴=,∴CD=BD.在直角△BDC中,BC=10,CD2+BD2=BC2,∴易求BD=CD=5;(Ⅱ)如图②,连接OB,OD.∵AD平分∠CAB,且∠CAB=60°,∴∠DAB=∠CAB=30°,∴∠DOB=2∠DAB=60°.又∵OB=OD,∴△OBD是等边三角形,∴BD=OB=OD.∵⊙O的直径为10,则OB=5,∴BD=5.4.(2013?黔西南州)如图,AB是⊙O的直径,弦CD⊥AB与点E,点P 在⊙O上,∠1=∠C,(1)求证:CB∥PD;(2)若BC=3,sin∠P=,求⊙O的直径.【解答】(1)证明:∵∠C=∠P又∵∠1=∠C∴∠1=∠P∴CB∥PD;(2)解:连接AC∵AB为⊙O的直径,∴∠ACB=90°又∵CD⊥AB,∴=,∴∠P=∠CAB,又∵sin∠P=,∴sin∠CAB=,即=,又知,BC=3,∴AB=5,∴直径为5.。
圆周角定理练习题(A)
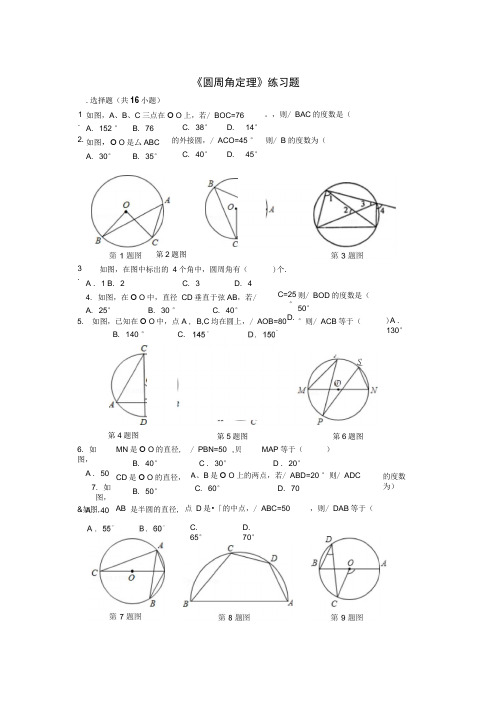
1. 2. 《圆周角定理》练习题.选择题(共16小题) 如图,A 、B 、C 三点在O O 上,若/ BOC=76A . 152 °B . 76 如图,O O 是厶ABC A . 30° B . 35° C . 38°D . 14° 的外接圆,/ ACO=45 ° C . 40° D . 45° 。
,则/ BAC 的度数是( 则/ B 的度数为( 第2题图 如图,在图中标出的 4个角中,圆周角有( A . 1 B . 2C . 3D . 4 4. 如图,在O O 中,直径 CD 垂直于弦AB ,若/ A . 25°B . 30 °C . 40° 3.)个. C=25 °D . 5. 如图,已知在O O 中,点A , B,C 均在圆上,/ AOB=80 B . 140 ° C .则/ BOD 的度数是( 50° °则/ ACB 等于( )A . 130°OS 06.如图,A . 507. 如图, A . 40 第4题图 MN 是O O 的直径, B . 40°CD 是O O 的直径, B . 50° &如图, 是半圆的直径, AB 第5题图/ PBN=50 °,贝 C . 30°第6题图 MAP 等于( )D . 20°A 、B 是O O 上的两点,若/ ABD=20 °则/ ADC C . 60°D . 70 点 D 是•「的中点,/ ABC=50C .65°D . 70° ,则/ DAB 等于( 的度数为)9. 如图,AB 是O O 的直径,C , D 为圆上两点,/ AOC=130 °则/ D 等于( A . 25°B . 30°C . 3510. 如图,/ 1、/ 2、/ 3、/ 4的大小关系是A . / 4</ 1 </ 2</ 3 C ./4</ 1 </3/211 .如图,AB 是半圆O 的直径, A . 30° B . 45°12 . 如图,在O O 中, OA 丄 BC , / AOC=50 ° 贝9/ ADB 的度数为( )A . 15°B . 20°C . 25 °D . 50° 13 . 在O O 中, 点A 、 B 在O O 上,且/ AOB=84 ° 则弦 AB 所对的圆周角是( )A . 42°B . 84°C . 42°或 138°D . 84 °或 96°14 .如图所示, 在O O 中,AB 是O O 的直径,/ ACB 的角平分线 CD 交O O 于 D ,则/ ABD的度数等于( )A . 90°B .60°C . 45°D .30°15 . 已知如图, AB 是O O 的直径, CD 是O O 的弦, / CDB=40 °, 则/ CBA 的度数为(4<Z 1 = / 3<Z 2 4<Z 1<Z 3= /2)B . / D . / / BAC=60 ° D 是半圆上任意一点,那么/ D 的度数是()16.如图,AB A . 30°是圆的直径, B .AB 丄 CD ,/ BAD=30C . 60°贝AEC D . B第12题图的度数等于( 70°8小题)二.填空题(共 17.如图,O O 的直径CD 经过弦EF 的中点G ,/DCF=20 °,则/ EOD 等于DBo第11题图第12题图DB50°C. 40°D. 30 °A . 60° B.21. 如图,等腰△ ABC 的底边BC 的长为4cm ,以腰AB 为直径的O O 交BC 于点D ,交 AC 于点E ,贝U DE 的长为 _____ cm . 22.如图,在 世界杯”足球比赛中,甲带球向对方球门PQ 进攻,当他带球冲到 A 点时,同 样乙已经助攻冲到 B 点,丙助攻到C 点•有三种射门方式:第一种是甲直接射门;第二 种是甲将球传给乙,由乙射门•第三种是甲将球传给丙,由丙射门•仅从射门角度考虑, 应选择 ____ 种射门方式. 三•解答题(共16小题)25. 28.如图,AB 是O O 的直径,C 是O O 上的点,AC=6cm , BC=8cm ,/ ACB 的平分 线交O O 于点D ,求AB 和BD 的长.26. 如图,已知 CD 是O O 的直径,弦 AB 丄CD ,垂足为点 M ,点P 是八上一点,且/ BPC=60 °试判断△ ABC 的形状,并说明你的理由.第19题图18. 占 八、第17题图 第18题图如图,点 A 、B 在O O 上,/ AOB=100 °点C 是劣弧 AB 上不与A 、B 重合的任意 则/ C=在O O 中,弦AB=2cm ,/ ACB=30 °则O O 的直径为_ 如图,O O 中弦AB 等于半径R ,则这条弦所对的圆心角是cm .—,圆周角是C第21题图Q3第20题图pB第22题图BB27、如图,△ ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG . 求证:HD=GD .28. 已知:如图,AB为O O的直径,AB=AC , BC交O O于点D , AC交O O于点E./BAC=40 °(1) 求/ EBC的度数;(2) 求证:BD=CD .29. 如图,△ ABC是O O的内接三角形,/ A=30 °, BC=3cm .求O O的半径.B 30. 如图,AB是O O的直径,过圆上一点C作CD丄AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE ;.31. 如图,△ ABC中,AB > AC,/ BAC的平分线交外接圆于于M .(1)求证:BE=CM .(2)求证:AB - AC=2BE .32. 如图,0A是O 0的半径,以OA为直径的O C与O 0的弦AB相交于点 D .求证:AD=BD .33. 如图,已知: AB 是O O 的弦,D 为O O 上一点, 证:M 是弧AB 的中点.35.已知:如图, AE 是O O 的直径,AF 丄BC 于D ,证明:BE=CF .34.如图,△ ABC 的三个顶点都在O O 上,CD 是高, D 是垂足,CE 是直径,求证:/ ACD=BDC 丄AB 于C , DM 平分/ CDO .求BCD5三ODBE36.已知AB 为O O 的直径,弦 BE=DE , AD , BE 的延长线交于点 C ,求证:AC=ABC37.如图,AB 是圆O 的直径,OC 丄AB ,交O O 于点C , D 是弧AC 上一点,E 是AB 上 一点,EC 丄CD ,交BD 于点F .问:AD 与BF 相等吗?为什么?38. 如图,AB是O O的直径,AC、DE是O O的两条弦,且于点DE丄AB,延长AC、DE相交F,求证:/ FCD= / ACE .39. 如图,已知O O是厶ABC的外接圆,AD是O O的直径,作CE丄AD,垂足为E,CE 的延长线与AB交于F.试分析/ ACF与/ ABC是否相等,并说明理由.40. 如图,△ ABC内接于O O, AD ABC的外角平分线,交O O于点D,连接BD , CD , 判断△ DBC的形状,并说明理由.EDB<?41.如图,AB是O O的直径,弦CD丄AB,垂足为点E, G是「'上的任意一点,AG、DC 的延长线相交于点F,/ FGC与/ AGD的大小有什么关系?为什么?42.如图,AB是圆0的直径,C是圆0上一点,D是弧AC中点,DE丄AB垂足为E, AC 分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?43. 如图,0A是O 0的半径,以0A为直径的O C与O 0的弦AB交于点D,求证:D是AB的中点.44. 如图,在△ ABC中,/ ACB=90 ° D是AB的中点,以边于DC为直径的O O交厶ABC的G , F, E点.求证:(1) F是BC的中点;(2)/ A= / GEF.45. 如图,圆内接四边形ABCD的外角/ DCH= / DCA , DP I AC垂足为P, DH丄BH垂足为H,求证:CH=CP, AP=BH .《圆周角定理》2222222222参考答案与试题解析一•选择题(共16小题)1. (2012?呼伦贝尔)如图,A、B、C三点在O O上,若/ BOC=76 °则/ BAC的度数是()A. 152°B. 76°C. 38°D. 14°【解答】解:•••;'所对的圆心角是/ BOC,圆周角是/ BAC ,又•••/ BOC=76 °•••/ A=76 °X—=38 ° 故选C.2. (2015?眉山)如图,O O是厶ABC的外接圆,/ ACO=45 °则/ B的度数为()CA. 30°B. 35°C. 40 °D. 45°【解答】解:I OA=OC,/ ACO=45 °•••/ OAC=45 °•••/ AOC=180 °- 45 °- 45°90 °•••/ B= - / AOC=45 °故选D .3. (2010秋?海淀区校级期末)如图,在图中标出的4个角中,圆周角有()个.D . 4【解答】解: /1和/3符合圆周角的定义,/ 2顶点不在圆周上,/ 4的一边不和圆相交,故图中圆周角有/ 1和/ 3两个.故选B .4. ( 2015?珠海)如图,在O O 中,直径CD 垂直于弦 AB ,若/ C=25 °则/ BOD 的度数是 ( )40 ° D . 50°【解答】解:•••在O O 中,直径CD 垂直于弦AB , •••二匸 11,•••/ DOB=2 / C=50 ° 故选:D .5. ( 1997?陕西)如图,已知在O O 中,点 A , B , C 均在圆上,/ AOB=80 °则/ ACB 等•••/ AOB=80 ° •••/ E= 1 / AOB=40 ° 2•••/ ACB=180 °-Z E=140°故选:B .C . 145D . 150 °【解答】解:设点E 是优弧AB 上的一点,连接EA , EBA . 130°B . 140A . 40°B . 50°C . 60°D . 70【解答】解:vZ ABD=20 °• Z C=Z ABD=20 °v CD 是O O 的直径• Z CAD=90 ° 6.如图,MN 是O O 的直径,/ PBN=50 °则/ MAP 等于() 可得/ MAP= 1 / MOP ,/ NBP=— / NOP ,2 2 •/ MN 为直径,•••/ MOP + Z NBP=180 °•••/ MAP+Z NBP=90 °vZ PBN=50 °• Z MAP=90 °-Z PBN=40 ° 故选B .7. (2007?太原)如图,CD 是O O 的直径,A 、B 是O O 上的两点, 若Z ABD=20 ° 贝UZ ADCA . 50°B . 40°C . 30°D . 20°【解答】解:连接OP ,•••/ ADC=90 ° - 20 °70 ° 故选D .& ( 2013?苏州)如图,AB 是半圆的直径,点 D 是AC 的中点,/ ABC=50 °则/ DAB 等于•••点D 是;的中点,即弧 CD=弧AD , •••/ ABD= / CBD , 而/ ABC=50 °•••/ ABD= X 50°25 ° 2•/ AB 是半圆的直径,•••/ ADB=90 °•••/ DAB=90 ° - 25 °65 ° 故选C .【解答】 解:•••/ AOC=130° •••/ BOC=50 ° •••/。
圆周角定理测试题汇编

1.求出下列圆中角X 的值2.如图,在⊙O 中,∠AOB 的度数为m ,C 是弧ACB 上一动点,D 、E 是弧AB3.°,则∠DAB 等于4.(2013•遵义)如图,OC 是⊙O 的半径,AB 是弦,且OC ⊥AB ,点P 在⊙O 上,∠APC=26°, 则∠BOC= 度.5.(2013•黔西南州)如图所示⊙O 中,已知∠BAC=∠CDA=20°,则∠ABO 的度数为 .6.写出y 与x 的函数关系式为3题 4题 5题 6题7、(2013•自贡)如图,边长为1的小正方形网格中,⊙O 的圆心在格点上,则∠AED 的余弦值是 .8.(2013•巴中)如图,已知⊙O 是△ABD 的外接圆,AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD=58°,则∠BCD 等于 9、(2013•包头)如图,点A 、B 、C 、D 在⊙O 上,OB ⊥AC ,若∠BOC=56°,则∠ADB= 度.10(2013•嘉兴)如图,⊙O 的半径OD ⊥弦AB 于点C ,连结AO 并延长交⊙O 于点E ,连结EC .若AB=8, CD=2,则EC 的长为7题 8题 9题 10题综合练习1.已知:如图,⊙O是△ABC的外接圆,AD⊥BC于D,AE平分∠BAC交⊙O于E.求证:AE平分∠OA D.2.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,M为上一点,AM的延长线交DC于F.求证:∠AMD=∠FM C.3如图,AB是⊙O的弦,P是AB所对优弧上一点,直径CD⊥AB,PB交CD于E,延长AP交CD 的延长线于F.求证:△EPF∽△EO A.4. 如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.(1)求证:DB平分∠ADC;(2)若BE=3,ED=6,求AB的长.图①图②5.如图所示,已知AB 为⊙O 的直径,CD 是弦,且AB ⊥CD 于点E .连接AC 、OC 、BC . (1)求证:∠ACO =∠BCD .(2)若E B =8cm ,CD =24cm ,求⊙O 的直径.6已知:如图等边ABC △内接于⊙O ,点P 是劣弧BC ⋂上的一点(端点除外),延长BP 至D ,使BD AP =,连结CD .(1)若AP 过圆心O ,如图①,请你判断PDC △是什么三角形?并说明理由. (2)若AP 不过圆心O ,如图②,PDC △又是什么三角形?为什么?7(2013•苏州)如图,在Rt △ABC 中,∠ACB=90°,点D 是AB 边上一点,以BD 为直径的⊙O 与边AC 相切于点E ,连接DE 并延长DE 交BC 的延长线于点F .(1)求证:BD=BF ;(2)若CF=1,cosB=,求⊙O 的半径.8、(2013•黔西南州)如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C,(1)求证:CB∥PD;(2)若BC=3,sin∠P=35,求⊙O的直径.9、(2013哈尔滨))如图,在△ABC中,以BC为直径作半圆0,交AB于点D,交AC于点E.AD=AE(1)求证:AB=AC; (2)若BD=4,BO=AD的长.10(2013•资阳)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.。
圆周角定理复习1

圆周角定理复习1.如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是________.2.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是________.3.如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的度数是________.4.如图,四边形内接于,是直径,,,则为________.5.半径等于的圆内有长为的弦,则此弦所对的圆周角的度数为________.6.如图,是的直径,,点在上,,是的中点,是直径上的一动点,若,则周长的最小值为________.7.如图,四边形ABCD内接于,若四边形ABCO是平行四边形,则的大小为________.8.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为____ .9.如图,在⊙O中,∠BOC=50°,OC∥AB,则∠BDC= 度;10.圆外一点到圆的最大距离是14cm,到圆的最小距离是6cm,则圆的半径是________.11.如图,在⊙O中,弦AB=1.8cm,圆周角∠ACB=30°,则⊙O的直径等于12.如图,经过原点O 的⊙P 与x 、y 轴分别交于A 、B 两点,点C 是劣弧上一点,则∠ACB=________.13.如图,四边形内接于,为的直径,点为的中点.若,求B 的度数.14.如图,AB 是半圆的直径,点O 为圆心,OA=5,弦AC=8,OD ⊥AC ,垂足为E ,交⊙O 于D ,连接BE .设∠BEC=α,求sin α的值.15.如图在⊙O 中,直径AB 为10cm ,弦AC 为6cm ,∠ACB 的平分线交⊙O 于D ,(1)求BC 的长(2)求∠ABD 的度数. O D CB A16.如图,已知过D 、A 、C 三点的圆的圆心为E ,过B 、E 、F 三点的圆的圆心为D ,如果∠A =63 º,求∠B 的度数.。
专题03 圆周角定理(原卷版)

15.如图,在⊙O中, 所对的∠AOB的度数为m,C是 上一点,D、E是 上不同的两点(不与A、B两点重合),则∠D+∠E的度数为.
16.如右图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则sin∠APB等于.
17.如图,在Rt△ABC中,∠BAC=90°,且AB=2AC,以AB为直径作⊙O,交于BC点D,点E为⊙O上的另外一点,那么tan∠AED=.
三.解答题
18.如图,AB是⊙O的直径, = ,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
19.已知:如图.△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
A.1个B.2个C.3个D.4个
8.如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是( )
A.2.4B.2C.2.5D.
9.如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
A.12.5°B.25°C.37.5°D.50°
4.如图,△ABC内接于圆,AD是高,AE为圆的直径,AB=4,AC=3,AD=2,则直径AE的长为( )
A.5B.6C.7D.8
5.如图所示,已知四边形ABCD的四个顶点都在⊙O上,∠BCD=120°,则∠B0D=( )
A.100°B.120°C.130°D.150°
(1)求证:∠DAC=∠DBA;
中考数学复习----《圆周角定理》知识点总结与专项练习题(含答案)

中考数学复习----《圆周角定理》知识点总结与专项练习题(含答案)知识点总结1.圆心角、弦以及弧之间的关系:①定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
②推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧。
2.圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
3.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
4.圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
5.圆的内接四边形:①定义:四个顶点都在圆上的四边形叫做圆的内接四边形。
②性质:I:圆内接四边形的对角互补。
II:圆内接四边形的任意一个外角等于它的内对角。
练习题1、(2022•襄阳)已知⊙O的直径AB长为2,弦AC长为2,那么弦AC所对的圆周角的度数等于.【分析】首先利用勾股定理逆定理得∠AOC=90°,再根据一条弦对着两种圆周角可得答案.【解答】解:如图,∵OA=OC=1,AC=,∴OA2+OC2=AC2,∴∠AOC=90°,∴∠ADC=45°,∴∠AD'C=135°,故答案为:45°或135°.2、(2022•日照)一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为.【分析】连接AC,根据∠ABC=90°得出AC是圆形镜面的直径,再根据勾股定理求出AC 即可.【解答】解:连接AC,∵∠ABC=90°,且∠ABC是圆周角,∴AC是圆形镜面的直径,由勾股定理得:AC===13(cm),所以圆形镜面的半径为cm,故答案为:cm.3、(2022•永州)如图,AB是⊙O的直径,点C、D在⊙O上,∠ADC=30°,则∠BOC=度.【分析】根据在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半求出∠AOC的度数,根据平角的定义即可得到∠BOC=180°﹣∠AOC的度数.【解答】解:∵∠ADC是所对的圆周角,∴∠AOC=2∠ADC=2×30°=60°,∴∠BOC=180°﹣∠AOC=180°﹣60°=120°.故答案为:120.4、(2022•苏州)如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D=°.【分析】如图,连接BC,证明∠ACB=90°,求出∠ABC,可得结论.【解答】解:如图,连接BC.∵AB是直径,∴∠ACB=90°,∴∠ABC=90°﹣∠CAB=62°,∴∠D=∠ABC=62°,故答案为:62.5、(2022•湖州)如图,已知AB 是⊙O 的弦,∠AOB =120°,OC ⊥AB ,垂足为C ,OC 的延长线交⊙O 于点D .若∠APD 是AB ⌒所对的圆周角,则∠APD 的度数是 .【分析】由垂径定理得出,由圆心角、弧、弦的关系定理得出∠AOD =∠BOD ,进而得出∠AOD =60°,由圆周角定理得出∠APD =∠AOD =30°,得出答案.【解答】解:∵OC ⊥AB ,∴,∴∠AOD =∠BOD ,∵∠AOB =120°,∴∠AOD =∠BOD =∠AOB =60°,∴∠APD =∠AOD =×60°=30°,故答案为:30°.6、(2022•徐州)如图,A 、B 、C 点在圆O 上,若∠ACB =36°,则∠AOB = .【分析】利用一条弧所对的圆周角等于它所对的圆心角的一半即可得出结论.【解答】解:∵∠ACB =∠AOB ,∠ACB =36°,∴∠AOB =2×∠ACB =72°.故答案为:72°.7、(2022•锦州)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,连接AC,则∠BAC的度数为.【分析】利用圆内接四边形的性质和∠ADC的度数求得∠B的度数,利用直径所对的圆周角是直角得到∠ACB=90°,然后利用直角三角形的两个锐角互余计算即可.【解答】解:∵四边形ABCD内接于⊙O,∠ADC=130°,∴∠B=180°﹣∠ADC=180°﹣130°=50°,∵AB为⊙O的直径,∴∠ACB=90°,∴∠CAB=90°﹣∠B=90°﹣50°=40°,故答案为:40°.8、(2022•雅安)如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=72°,那么∠BOD的度数为.【分析】根据邻补角的概念求出∠BCD,根据圆内接四边形的性质求出∠A,根据圆周角定理解答即可.【解答】解:∵∠DCE=72°,∴∠BCD=180°﹣∠DCE=108°,∵四边形ABCD内接于⊙O,∴∠A=180°﹣∠BCD=72°,由圆周角定理,得∠BOD=2∠A=144°,故答案为:144°.9、(2022•甘肃)如图,⊙O是四边形ABCD的外接圆,若∠ABC=110°,则∠ADC=°.【分析】根据圆内接四边形的对角互补即可得到结论.【解答】解:∵四边形ABCD内接于⊙O,∠ABC=110°,∴∠ADC=180°﹣∠ABC=180°﹣110°=70°,故答案为:70.。
圆周角定理经典训练卷(含答案)

圆角定理经典训练卷一.选择题1.如图,AB、CD都是⊙O的弦,且AB⊥CD.假设∠CDB=62°,那么∠ACD的大小为〔〕〔1〕〔2〕〔3〕A.28°B.31°C.38°D.62°2.如图,⊙O是△ABC的外接圆,∠ABO=40°,那么∠ACB的大小为〔〕A.40°B.30°C.45°D.50°3.如图,AB是⊙O的弦,点C在圆上,∠OBA=40°,那么∠C=〔〕A.40°B.50°C.60°D.80°4.如图,AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,那么∠BAD的度数是〔〕〔4〕〔5〕〔6〕〔7〕A.30°B.40°C.50°D.60°5.如图,圆心角∠BOC=100°,那么圆角∠BAC的大小是〔〕A.50°B.55°C.60°D.65°6.如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,那么弦AB的长为〔〕A.2 B.4 C.D.27.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,那么∠OAB的度数为〔〕A.80°B.75°C.70°D.65°8.如图,在⊙O中,AB平分∠CAO,∠BAO=25°,那么∠BOC的大小为〔〕A.25°B.50°C.65°D.80°〔8〕〔9〕〔10〕9.如图,⊙O中,劣弧AB所对的圆心角∠AOB=120°,点C在劣弧AB上,那么圆角∠ACB=〔〕A.60°B.120°C.°D.150°10.如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,那么弦AB所对的圆角的度数是〔〕A.60°B.120°C.60°或120°D.30°或150°11.如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,和所对的圆心角分别为90°和50°,那么∠P=〔〕A.45°B.40°C.25°D.20°12.△ABC中,AB=AC,∠A=50°,⊙O是△ABC的外接圆,D是优弧BC上任一点〔不与A、B、C重合〕,那么∠ADB的度数是〔〕A.50°B.65°C.65°或50°D.115°或65°13.如图,AB是⊙O的直径,BC是⊙O的弦.假设∠OBC=60°,那么∠BAC的度数是〔〕〔13〕〔14〕〔15〕A.75°B.60°C.45°D.30°14.如图,BD是⊙O的直径,∠CBD=30°,那么∠A的度数为〔〕A.30°B.45°C.60°D.75°15.如图,CD是⊙O的直径,过点D的弦DE平行于半径OA,假设∠D的度数是50°,那么∠C的度数是〔〕A.25°B.30°C.40°D.50°16.如图,AB是⊙O的直径,CD是⊙O的弦.假设∠BAC=23°,那么∠ADC的大小为〔〕A.23°B.57°C.67°D.77°17.如图,AB为⊙O的直径,CD为⊙O的弦,∠ABD=53°,那么∠BCD为〔〕〔16〕A.37°B.47°C.45°D.53°〔17〕〔18〕〔19〕18.如图,假设AB为⊙O的直径,CD是⊙O的弦,∠ABD=65°,那么∠BCD的度数为〔〕A.25°B.45°C.55°D.75°19.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.假设∠DOB=140°,那么∠ACD=〔〕A.20°B.30°C.40°D.70°20.在⊙O中,点A、B在⊙O上,且∠AOB=84°,那么弦AB所对的圆角是〔〕A.42°B.84°C.42°或138°D.84°或96°二.填空题21.如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,那么⊙O的半径R=.〔21〕〔22〕〔23〕22.如图,在⊙O中,弦AB∥CD,假设∠ABC=40°,那么∠BOD=.23.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,那么∠EOD等于.24.如图,在⊙O中,∠CBO=45°,∠CAO=15°,那么∠AOB的度数是°.25.如图,CD是⊙O的直径,A、B是⊙O上的两点,假设∠B=20°,那么∠ADC的度数为.26.如图,BD是⊙O的直径,∠CBD=30°,那么∠A的度数为.27.如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,B〔8,0〕,C〔0,6〕,那么⊙A的半径为.〔25〕〔26〕〔27〕28.如图,在⊙O中,AB为直径,C、D为⊙O上两点,假设∠C=25°,那么∠ABD=.29.如图,△ABC接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,假设AD=6,那么AC=.〔28〕〔29〕〔30〕30.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于D,假设AC:BC=4:3,AB=10cm,那么OD的长为cm.三.解答题31.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O 于点D,求AB和BD的长.32、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.33.:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°〔1〕求∠EBC的度数;〔2〕求证:BD=CD.34.如图,△ABC是⊙O的接三角形,∠A=30°,BC=3cm.求⊙O的半径.35.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.〔1〕求证:AE=CE;.36.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.〔1〕求证:BE=CM.〔2〕求证:AB﹣AC=2BE.37.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.8.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析AC、AF、AB的关系,并说明理由.39.如图,△ABC接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,〔1〕判断△DBC的形状,并说明理由.〔2〕假设∠BAC=60°,判断AD、AB、AC有怎样的关系?并说明理由.40.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?一.选择题〔共20小题〕1.D;2.C;3.A;4.C;5.A;6.D;7.A;8.B;9.C;10.A;11.D;12.C;13.C;14.B;15.B;16.A;17.C;18.D;19.A;20.D;二.填空题〔共10小题〕21.;22.80°;23.70°;24.60°;25.5;26.40°;27.60;28.65°;29.;30.4;三解答题28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O 于点D,求AB和BD的长.【解答】解:如图,∵AB是⊙O的直径,∴∠ACB=90°,∠ADB=90°.∴AB===10〔cm〕.∵AC=6cm,BC=8cm,∵CD是∠ACB的平分线,∴∠ACD=∠BCD,那么=,∴AD=BD,∴BD=AB=5cm.综上所述,AB和BD的长分别是10cm,5cm.29.如图,△ABC是⊙O的接三角形,∠A=30°,BC=3cm.求⊙O的半径.【解答】解:作直径CD,连结BD,如图,∵CD为直径,∴∠CBD=90°,∵∠D=∠A=30°,∴CD=2BC=2×3=6,∴⊙O的半径为3cm.30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.〔1〕求证:AE=CE;〔2〕AG=10,ED:AD=3:4,求AC的长.【解答】〔1〕证明:∵点C是弧AF的中点,∴∠B=∠CAE,∵AB是⊙O的直径,∴∠ACB=90°,即∠ACE+∠BCD=90°,∵CD⊥AB,∴∠B+∠BCD=90°,∴∠B=∠CAE=∠ACE,∴AE=CE …〔6分〕〔2〕解:∵∠ACB=90°,∴∠CAE+∠CGA=90°,又∵∠ACE+∠BCD=90°,∴∠CGA=∠BCD,∵AG=10,∴CE=EG=AE=5,∵ED:AD=3:4,∴AD=4,DE=3,∴AC=…〔10分〕.31.〔2021 秋•扬中市期中〕如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE ⊥AB于E,DM⊥AC于M.〔1〕求证:BE=CM.〔2〕求证:AB﹣AC=2BE.【解答】证明:〔1〕连接BD,DC,∵AD平分∠BAC,∴∠BAD=∠CAD,∴弧BD=弧CD,∴BD=CD,∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,∵∠M=∠DEB=90°,DE=DM,在Rt△DEB和Rt△DMC中,,∴Rt△DEB≌Rt△DMC〔HL〕,∴BE=CM.〔2〕∵DE⊥AB,DM⊥AC,∵∠M=∠DEA=90°,在Rt△DEA和Rt△DMA中∴Rt△DEA≌Rt△DMA〔HL〕,∴AE=AM,∴AB﹣AC,=AE+BE﹣AC,=AM+BE﹣AC,=AC+CM+BE﹣AC,=BE+CM,=2BE.34.〔2021秋•校级期中〕如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.【解答】解:连接AE,∵CE为直径,∴∠EAC=90°,∴∠ACE=90°﹣∠AEC,∵CD是高,D是垂足,∴∠BCD=90°﹣∠B,∵∠B=∠AEC〔同弧所对的圆角相等〕,∴∠ACE=∠BCD,∴∠ACE+∠ECD=∠BCD+∠ECD,∴∠ACD=∠BCE.39.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.【解答】解:延长CE交⊙O于M,∵AD是⊙O的直径,作CE⊥AD,∴弧AC=弧AM,∴∠ACF=∠ABC〔在同圆中,等弧所对的圆角相等〕.40.如图,△ABC接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.【解答】解:△DBC为等腰三角形.理由如下:∵AD为△ABC的外角平分线,∴∠EAD=∠DAC,∵∠EAD=∠DCB,∠DBC=∠DAC,∴∠DBC=∠DCB,∴△DBC为等腰三角形.1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?【解答】解:∠FGC与∠AGD相等.理由如下:连接AD,如图,∵CD⊥AB,∴=,- .. - -可修编. ∴∠AGD=∠ADC ,∵∠FGC=∠ADC ,∴∠FGC=∠AGD。
圆周角定理练习题(A)

《圆周角定理》练习题一.选择题(共16小题)1.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是()A.152°B.76°C.38°D.14°2.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°第1题图第2题图第3题图3.如图,在图中标出的4个角中,圆周角有()个.A.1 B.2 C.3 D.44.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25°B.30°C.40°D.50°5.如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于()A.130°B.140°C.145°D.150°第4题图第5题图第6题图6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于()A.50°B.40°C.30°D.20°7.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为)A.40°B.50°C.60°D.70°8.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°第7题图第8题图第9题图9.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于()A.25°B.30°C.35°D.50°10.如图,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠211.如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是()A.30°B.45°C.60°D.90°第10题图第11题图第12题图12.如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为()A.15°B.20°C.25°D.50°13.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42°B.84°C.42°或138°D.84°或96°14.如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD 的度数等于()A.90°B.60°C.45°D.30°15.已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为()A.60°B.50°C.40°D.30°第10题图第11题图第12题图16.如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于()A.30°B.50°C.60°D.70°二.填空题(共8小题)17.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于.第17题图第18题图第19题图18.如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C=°.19.在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为cm.20.如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是,圆周角是.第20题图第21题图第22题图21.如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为cm.22.如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择种射门方式.三.解答题(共16小题)25.28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.26.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.27、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.28.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;.31.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC 于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.32.如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.33.如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.34.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.36.已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE 的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.41.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?42.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC 分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?43.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.44.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)F是BC的中点;(2)∠A=∠GEF.45.如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.《圆周角定理》2222222222参考答案与试题解析一.选择题(共16小题)1.(2012•呼伦贝尔)如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是()A.152°B.76°C.38°D.14°【解答】解:∵所对的圆心角是∠BOC,圆周角是∠BAC,又∵∠BOC=76°,∴∠A=76°×=38°.故选C.2.(2015•眉山)如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°【解答】解:∵OA=OC,∠ACO=45°,∴∠OAC=45°,∴∠AOC=180°﹣45°﹣45°=90°,∴∠B=∠AOC=45°.故选D.3.(2010秋•海淀区校级期末)如图,在图中标出的4个角中,圆周角有()个.A.1 B.2 C.3 D.4【解答】解:∠1和∠3符合圆周角的定义,∠2顶点不在圆周上,∠4的一边不和圆相交,故图中圆周角有∠1和∠3两个.故选B.4.(2015•珠海)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25°B.30°C.40°D.50°【解答】解:∵在⊙O中,直径CD垂直于弦AB,∴=,∴∠DOB=2∠C=50°.故选:D.5.(1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于()A.130°B.140°C.145°D.150°【解答】解:设点E是优弧AB上的一点,连接EA,EB∵∠AOB=80°∴∠E=∠AOB=40°∴∠ACB=180°﹣∠E=140°.故选:B.6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于()A.50°B.40°C.30°D.20°【解答】解:连接OP,可得∠MAP=∠MOP,∠NBP=∠NOP,∵MN为直径,∴∠MOP+∠NBP=180°,∴∠MAP+∠NBP=90°,∵∠PBN=50°,∴∠MAP=90°﹣∠PBN=40°.故选B.7.(2007•太原)如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC 的度数为()A.40°B.50°C.60°D.70°【解答】解:∵∠ABD=20°∴∠C=∠ABD=20°∵CD是⊙O的直径∴∠CAD=90°∴∠ADC=90°﹣20°=70°.故选D.8.(2013•苏州)如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°【解答】解:连结BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故选C.9.(2009•枣庄)如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于()A.25°B.30°C.35°D.50°【解答】解:∵∠AOC=130°,∴∠BOC=50°,∴∠D=∠BOC=25°.故选A.10.(2013秋•沙洋县校级月考)如图,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2 C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2【解答】解:如图,利用圆周角定理可得:∠1=∠3=∠5=∠6,根据三角形的外角的性质得:∠5>∠4,∠2>∠6,∴∠4<∠1=∠3<∠2,故选B.11.(2012秋•天津期末)如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是()A.30°B.45°C.60°D.90°【解答】解:连接BC,∵AB是半圆的直径∴∠ACB=90°∵∠BAC=60°,∴∠ABC=90°﹣∠BAC=30°,∴∠D=∠ABC=30°.故选A.12.(2009•塘沽区二模)如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为()A.15°B.20°C.25°D.50°【解答】解:∵OA⊥BC,∠AOC=50°,∴,∴∠ADB=∠AOC=25°.故选C.13.(2012秋•宜兴市校级期中)在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42°B.84°C.42°或138°D.84°或96°【解答】解:如图,∵∠AOB=84°,∴∠ACB=∠AOB=×84°=42°,∴∠ADB=180°﹣∠ACB=138°.∴弦AB所对的圆周角是:42°或138°.故选C.14.(2011•南岸区一模)如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD 交⊙O于D,则∠ABD的度数等于()A.90°B.60°C.45°D.30°【解答】解:连接AD,∵在⊙O中,AB是⊙O的直径,∴∠ADB=90°,∵CD是∠ACB的角平分线,∴=,∴AD=BD,∴△ABD是等腰直角三角形,∴∠ABD=45°.故选C.15.(2015秋•合肥校级期末)已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为()A.60°B.50°C.40°D.30°【解答】解:连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∵∠A=∠CDB=40°,∴∠CBA=90°﹣∠A=50°.故选B.16.(2013•万州区校级模拟)如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于()A.30°B.50°C.60°D.70°【解答】解:∵∠BAD=30°,∴=60°,∵AB是圆的直径,AB⊥CD,∴==60°,∴=180°﹣60°=120°,∴∠AEC==×120°=60°.故选C.二.填空题(共8小题)17.(2016•大冶市模拟)如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD 等于40°.【解答】解:∵⊙O的直径CD过弦EF的中点G,∠DCF=20°,∴弧DF=弧DE,且弧的度数是40°,∴∠DOE=40°,答案为40°.18.(2015•历城区二模)如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是65°.【解答】解:连结BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故答案为65°.19.(2013秋•滨湖区校级期末)如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB 上不与A、B重合的任意一点,则∠C=130°.【解答】解:在优弧AB上取点D,连结AD、BD,如图,∴∠D=∠AOB=×100°=50°,∵∠D+∠C=180°,∴∠C=180°﹣50°=130°.故答案为130.20.(2008秋•苏州校级期中)球员甲带球冲到A点时,同伴乙已经助攻冲到B点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择第二种种射门方式较为合理.【解答】解:连接OC.根据圆周角定理,得∠PCQ=∠B,根据三角形的外角的性质,得∠PCQ>∠A,则∠B>∠A.故答案为第二种.21.(2015•黄岛区校级模拟)在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为4cm.【解答】解:连接OA,OB,∵∠ACB=30°,∴∠AOB=60°,∴△AOB是等边三角形,∴OA=OB=AB=2cm,∴⊙O的直径=4cm.故答案为:4.22.(2014春•海盐县校级期末)如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是60°,圆周角是30°或150°.【解答】解:连结OA、OB,∠APB和∠AP′B为弦AB所对的圆周角,如图,∵弦AB等于半径R,∴△OAB为等边三角形,∴∠AOB=60°,∴∠APB=∠AOB=30°,∴∠AP′B=180°﹣∠APB=150°,即这条弦所对的圆心角是60°,圆周角是30°或150°.故答案为60°;是30°或150°.23.(2012•义乌市模拟)如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O 交BC于点D,交AC于点E,则DE的长为2cm.【解答】解:连接AD,∵∠DEC为圆内接四边形ABDE的外角,∴∠DEC=∠B,又等腰△ABC,BC为底边,∴AB=AC,∴∠B=∠C,∴∠DEC=∠C,∴DE=DC,∵AB为圆O的直径,∴∠ADB=90°,即AD⊥BC,∴BD=CD=BC,又BC=4cm,∴DE=2cm.故答案为:224.(2012秋•哈密地区校级月考)如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第二种射门方式.【解答】解:设AP与圆的交点是C,连接CQ;则∠PCQ>∠A;由圆周角定理知:∠PCQ=∠B;所以∠B>∠A;因此选择第二种射门方式更好.故答案为:第二.三.解答题(共16小题)25.(2009•沈阳模拟)如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.【解答】证明:∵∠C=∠G,△ABC的高AD、BE,∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,∴∠C=∠AHE,∵∠AHE=∠BHG=∠C,∴∠G=∠BHG,∴BH=BG,又∵AD⊥BC,∴HD=DG.26.(2013秋•虞城县校级期末)如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.【解答】解:△ABC为等边三角形.理由如下:∵AB⊥CD,CD为⊙O的直径,∴弧AC=弧BC,∴AC=BC,又∵∠BPC=∠A=60°,∴△ABC为等边三角形.27.(2013秋•耒阳市校级期末)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.【解答】(1)解:∵AB=AC,∴∠ABC=∠C,∵∠BAC=40°,∴∠C=(180°﹣40°)=70°,∵AB为⊙O的直径,∴∠AEB=90°,∴∠EBC=90°﹣∠C=20°;证明:连结AD,如图,∵AB为⊙O的直径,∴∠ADB=90°,∴AD⊥BC,而AB=AC,∴BD=DC.28.(2014秋•高密市期中)如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.【解答】解:如图,∵AB是⊙O的直径,∴∠ACB=90°,∠ADB=90°.∴AB===10(cm).∵AC=6cm,BC=8cm,∵CD是∠ACB的平分线,∴∠ACD=∠BCD,则=,∴AD=BD,∴BD=AB=5cm.综上所述,AB和BD的长分别是10cm,5cm.29.(2013秋•宜兴市校级期中)如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.【解答】解:作直径CD,连结BD,如图,∵CD为直径,∴∠CBD=90°,∵∠D=∠A=30°,∴CD=2BC=2×3=6,∴⊙O的半径为3cm.30.(2010秋•瑞安市校级月考)如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;(2)已知AG=10,ED:AD=3:4,求AC的长.【解答】(1)证明:∵点C是弧AF的中点,∴∠B=∠CAE,∵AB是⊙O的直径,∴∠ACB=90°,即∠ACE+∠BCD=90°,∵CD⊥AB,∴∠B+∠BCD=90°,∴∠B=∠CAE=∠ACE,∴AE=CE …(6分)(2)解:∵∠ACB=90°,∴∠CAE+∠CGA=90°,又∵∠ACE+∠BCD=90°,∴∠CGA=∠BCD,∵AG=10,∴CE=EG=AE=5,∵ED:AD=3:4,∴AD=4,DE=3,∴AC=…(10分).31.(2015秋•扬中市期中)如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.【解答】证明:(1)连接BD,DC,∵AD平分∠BAC,∴∠BAD=∠CAD,∴弧BD=弧CD,∴BD=CD,∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,∵∠M=∠DEB=90°,DE=DM,在Rt△DEB和Rt△DMC中,,∴Rt△DEB≌Rt△DMC(HL),∴BE=CM.(2)∵DE⊥AB,DM⊥AC,∵∠M=∠DEA=90°,在Rt△DEA和Rt△DMA中∴Rt△DEA≌Rt△DMA(HL),∴AE=AM,∴AB﹣AC,=AE+BE﹣AC,=AM+BE﹣AC,=AC+CM+BE﹣AC,=BE+CM,=2BE.32.(2013•宁夏模拟)如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.【解答】证明:连结OD,如图,∵OA为⊙C的直径,∴∠ADO=90°,∴OD⊥AB,∴AD=BD.33.(2011秋•宁波期中)如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.【解答】解:连接OM∵OD=OM,∴∠ODM=∠OMD,∵DM平分∠ODC,∴∠ODM=∠CDM,∴∠CDM=∠OMD,∴CD∥OM,∵CD⊥AB,∴OM⊥AB,∴弧AM=弧BM,即点M为劣弧AB的中点.34.(2009秋•哈尔滨校级期中)如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.【解答】解:连接AE,∵CE为直径,∴∠EAC=90°,∴∠ACE=90°﹣∠AEC,∵CD是高,D是垂足,∴∠BCD=90°﹣∠B,∵∠B=∠AEC(同弧所对的圆周角相等),∴∠ACE=∠BCD,∴∠ACE+∠ECD=∠BCD+∠ECD,∴∠ACD=∠BCE.35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.【解答】证明:∵AE是⊙O的直径,∴∠ABE=90°,∴∠E+∠BAE=90°,∵AF⊥BC于D,∴∠FAC+∠ACB=90°,∵∠E=∠ACB,∴∠BAE=∠FAC,∴弧BE=弧CF,∴BE=CF.36.(2015秋•哈尔滨校级期中)已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.【解答】证明:连接AE,∵AB为⊙O的直径,∴∠AEB=90°,∴∠AEB=∠AEC=90°,∵弦BE=DE,∴=,∴∠DAE=∠BAE,∵∠C=90°﹣∠DAE,∠B=90°﹣∠BAE,∴∠B=∠C,∴AC=AB.37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?【解答】解:AD和BF相等.理由:如图,连接AC、BC,∵OC⊥AB,∴∠BOC=90°∴∠BDC=∠BAC=45°∵EC⊥CD,∴∠DCE=∠ACB=90°,∴△DCF和△ACB都是等腰直角三角形,∴DC=FC,AC=BC,∵∠DCA+∠ACF=∠BCF+∠ACF=90°,∴∠DCA=∠FCB在△ACD和△BCF中,{,∴△ACD≌△BCF∴DA=BF.38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.【解答】证明:连接AD,AE,∵AB是直径.AB⊥DE,∴AB平分DE,弧ACE=弧AD,∴∠ACD=∠ADE,∵A、C、E、D四点共圆,∴∠FCE=∠ADE,∴∠FCE=∠ACD,∴∠FCE+∠DCE=∠DAC+∠ECD,∴∠FCD=∠ACE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE 的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.【解答】解:延长CE交⊙O于M,∵AD是⊙O的直径,作CE⊥AD,∴弧AC=弧AM,∴∠ACF=∠ABC(在同圆中,等弧所对的圆周角相等).40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.【解答】解:△DBC为等腰三角形.理由如下:∵AD为△ABC的外角平分线,∴∠EAD=∠DAC,∵∠EAD=∠DCB,∠DBC=∠DAC,∴∠DBC=∠DCB,∴△DBC为等腰三角形.一.解答题(共6小题)1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?【解答】解:∠FGC与∠AGD相等.理由如下:连接AD,如图,∵CD⊥AB,∴=,∴∠AGD=∠ADC,∵∠FGC=∠ADC,∴∠FGC=∠AGD2.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC 分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?【解答】解:AF=FG,理由是:连接AD,∵AB是直径,DE⊥AB,∴∠ADB=∠DEB=90°,∴∠ADE=∠ABD,∵D为弧AC中点,∴∠DAC=∠ABD,∴∠ADE=∠DAC,∴AF=DF,∠FAE=∠DAC,∴DF=FG,∴AF=FG.3.如图,AB为⊙O的直径,以OA为直径作⊙C,AD为⊙O的弦,交⊙C于E,试问,当D点在⊙O上运动时(不与A重合),AE与ED的长度有何关系?证明你的结论.【解答】解:AE=ED.理由:连接OE,∵AO是⊙C的直径,∴∠OEA=90°,∴OE⊥AD,∵OE过圆O的圆心O,∴AE=ED.4.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.【解答】证明:连接OD,∵OA为⊙C的直径,∴∠ODA=90°,即OD⊥AB,∴D是AB的中点.5.(2007•鄂尔多斯)如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)F是BC的中点;(2)∠A=∠GEF.【解答】证明一:(1)连接DF,∵∠ACB=90°,D是AB的中点,∴BD=DC=AB,(2分)∵DC是⊙O的直径,∴DF⊥BC,(4分)∴BF=FC,即F是BC的中点;(5分)(2)∵D,F分别是AB,BC的中点,∴DF∥AC,(6分)∴∠A=∠BDF,(7分)∵∠BDF=∠GEF(圆周角定理),(8分)∴∠A=∠GEF.(9分)证明二:(1)连接DF,DE,∵DC是⊙O直径,∴∠DEC=∠DFC=90°.(1分)∵∠ECF=90°,∴四边形DECF是矩形.∴EF=CD,DF=EC.(2分)∵D是AB的中点,∠ACB=90°,∴EF=CD=BD=AB.(3分)∴△DBF≌△EFC.(4分)∴BF=FC,即F是BC的中点.(5分)(2)∵△DBF≌△EFC,∴∠BDF=∠FEC,∠B=∠EFC.(6分)∵∠ACB=90°(也可证AB∥EF,得∠A=∠FEC),∴∠A=∠FEC.(7分)∵∠FEG=∠BDF(同弧所对的圆周角相等),(8分)∴∠A=∠GEF.(9分)(此题证法较多,大纲卷参考答案中,又给出了两种不同的证法,可供参考.)6.(2000•兰州)如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.【解答】证明:(1)在△DHC与△DPC中,∵∠DCH=∠DCA,DP⊥AC,DH⊥BH,DC为公共边,∴△DHC≌△DPC,∴CH=CP.(2)连接DB,由圆周角定理得,∠DAC=∠DBH,∵△DHC≌△DPC,∴DH=DP,∵DP⊥AC,DH⊥BH,∴∠DHB=∠DPC=90°,∴△DAP≌△DBH,∴AP=BH.。
初中数学精品试题:圆周角定理

3.5.1圆周角定理班级姓名评价_________1.如图,点A、B、C在⊙O上,若∠BAC=20°.则∠BOC的度数为_________2.如图,在以AB为直径的半圆O中,C是它的中点,若AC=2,则△ABC的面积是_________3.如图,∠AOB=100°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为_________4.如图,点A、B、C是⊙0上的三点,若∠OBC=50°,则∠A的度数是_________ 5.如图,在⊙O中,∠ABC=50°,则∠AOC等于_________6.如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于_________7.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为_________8.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为_________9.如图,△ABC的外接圆上,AB,BC,CA三弧的度数比为12:13:11.自劣弧BC上取一点D,过D分别作直线AC,直线AB的平行线,且交于E,F两点,则∠EDF的度数为_________10.如图,AB是半⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为_________11.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=_________12.已知AB、CD是⊙O的两条直径,∠ABC=30°,那么∠BAD=_________13.如图,▱ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为_________14.如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB=_________°.15.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB=______度.16.如图,=1:2:3:4,那么∠BDC是_________度.17.如图,A,B,C是⊙O上的三点,∠BAC=30°,则∠BOC=_________度.18.如图,在平面直角坐标系xOy中,△OCB的外接圆与y轴交于点A(0,),∠OCB=60°,∠COB=45°,OC的长为_________.19.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.(1)求证:△ABC为等边三角形;(2)求DE的长;(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.20.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.(1)求∠B的大小;(2)已知圆心0到BD的距离为3,求AD的长.21.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.(1)求证:∠B=∠D;(2)若AB=4,BC﹣AC=2,求CE的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十四章圆
24.1.4圆周角
阜康市二中鲁斌
一、教材内容:人教版九年级上册第二十四章圆第四课时垂直于圆周角教学设计
二、教材分析:
《圆周角》是人教版九年级上册数学教材《圆》这一章中的重要一节,它是引入圆心角之后又学习的另一个与圆有关的重要的角,圆周角及圆周角定理是这一章的基本概念和定理,学生掌握的熟练程度直接影响着学生后续知识的学习。
因此让学生多角度、多层次地理解并三、教学目标:
1. 理解圆周角的概念.探索并证明圆周角定理并能应用圆周角定理,解决简单问题。
2. 在探索圆周角的过程中,培养动手操作、自主探索与合作交流的能力,体会分情况逐一证明的必要性。
3. 在互相交流的过程中,培养解决数学问题的能力,激发学习数学的兴趣.
四、教学重点难点
重点:探索同弧所对的圆周角与圆心角度数的关系.
难点:应用圆周角定理解决简单问题
五、学情分析:
在此之前,学生已经掌握了圆心角的定义,对圆心角、弧、弦的关系有了认识,因此在学习圆周角的定义时,学生会对圆内的又一类角很有兴致,同时圆周角的定义是类比圆心角得到的,让学生体会类比思想的重要性,而圆周角定理的证明用到了完全归纳法,分为三种情况证明,对于学生有些难度。
六、教学过程:
(一)、创设情境引入新知出示多媒体课件:
足球训练场上教练在球门前划了一个圆圈进行
无人防守的射门训练,甲、乙两名运动员分别在C、
D两处,他们都说在自己所在位置对球门AB的张
角大,你认为他们谁说的对?
(甲对球门AB的张角为∠C乙对球门AB的张角为∠D)
问题∠C、∠D两个角还是我们学过的圆心角吗?(像∠C、∠D这样的角我们叫它圆周角。
) 他们有什么共同特点?
(①角的顶点在圆上②角的两边都与圆相交).
设计意图:联系生活中的实际创设具有一定挑战性的问题情境,导入新课.激发学生的探索激情和求知欲望,把学生的注意力尽快地集中到本节课的学习中
问题你能类比圆心角的定义给圆周角下个定义吗?
圆周角定义: 顶点在圆上,两边都和圆相交的角叫圆周角
特征:①角的顶点在圆上.②角的两边都与圆相交
设计意图:让学生给圆周角下定义,提高学生的概括能力.
练习1:如图,判断下列各图形中所画出的角是否为圆周角并说明理由。
小结:
判断要点:①角的顶点在圆上.②角的两边都与圆相交
问题如图,任取一段,那么它所对的圆心角有几个?那弧AB
所对的圆周角有多少个呢?
一条弧所对的圆心角只有一个,一条弧所对的圆周角有无数个。
(任取优弧上一点,连接的两个端点即为所对的一个圆周角)
(二)那么今天我们就来研究一下,所对的圆周角与它所对的圆心角
之间的关系.。
