n次方根和n次算术根
笔算开n次方的方法

笔算开n次方笔算开n次方的方法:1、把被开方的整数部分从个位起向左每隔n位为一段,把开方的小数部分从小数点第一位起向右每隔n位为一段,用撇号分开;2、根据左边第一段里的数,求得开n次算术根的最高位上的数,假设这个数为a;3、从第一段的数减去求得的最高位上数的n次方,在它们的差的右边写上第二段数作为第一个余数;4、把n(10a)^(n-1)去除第一个余数,所得的整数部分试商(如果这个最大整数大于或等于10,就用9做试商);5、设试商为b。
如果(10a+b)^n-(10a)^n小于或等于余数,这个试商就是n次算术根的第二位;如果(10a+b)^n-(10a)^n大于余数,就把试商逐次减1再试,直到(10a+b)^n-(10a)^n小于或等于余数为止。
6、用同样的方法,继续求n次算术跟的其它各位上的数(如果已经算了k位数数字,则a要取为全部k位数字)。
例如计算987654321987654321的五次算术根,就算到小数点后四位。
3 9 7 1. 1 9 2 95√987'65432'19876'54321.00000'00000'00000'00000243________________________________________________744 65432......................................74465432/(5×30^4)整数部分是18,用9作试商 659 24199......................................39^5-30^5_____________________________________________85 41233 19876................................854123319876/(5×390^4)的整数部分是7,用7作试商83 92970 61757................................397^5-390^5____________________________________________1 48262 58119 54321..........................1482625811954321/(5×3970^4)的整数部分是1,用1作试商1 24265 57094 08851..........................3971^5-3970^5___________________________________________23997 01025 45470 00000....................23997010254547000000/(5×39710^4)的整数部分是1,用1作试商12433 44352 06091 99551....................39711^5-39710^5_________________________________________11563 56673 39378 00449 00000..............1156356673393780044900000/(5×397110^4)的整数部分是9,用9作试商11191 17001 57043 20516 21599..............397119^5-397110^5_________________________________________372 39671 82334 79932 78401 00000........3723967182334799327840100000/(5×3971190^4)的整数部分是2,用2作试商248 70419 01386 56554 83574 43232........3971192^5-3971190^5_______________________________________123 69252 80948 23377 94826 56768 00000..123692528094823377948265676800000/(5×39711920^4)的整数部分是9,用9作试商111 91704 90192 14028 71518 74119 30649..39711929^5-39711920^5_______________________________________11 77547 90756 09349 23307 82648 69351这样就得到987654321987654321的五次算术根精确到小数点前四位为3971.1929。
【附2套中考卷】2020中考数学:代数式的定义及分类

2020中考数学:代数式的定义及分类一个大于1的整数,如果除了它本身和1以外不能被其它正整数所整除,那么这个数称为质数。
一个大于1的数,如果除了它本身和1以外还能被其它正整数所整除,那么这个数知名人士为合数,1既不是质数又不是合数……表示物体个数的1、2、3、4···等都称为自然数【质数与合数】一个大于1的整数,如果除了它本身和1以外不能被其它正整数所整除,那么这个数称为质数。
一个大于1的数,如果除了它本身和1以外还能被其它正整数所整除,那么这个数知名人士为合数,1既不是质数又不是合数。
【相反数】只有符号不同的两个实数,其中一个叫做另一个的相反数。
零的相反数是零。
【绝对值】一个正数的绝对值是它本身,一个负数绝对值是它的相反数,零的绝对值为零。
从数轴上看,一个实数的绝对值是表示这个数的点离开原点距离。
【倒数】1除以一个非零实数的商叫这个实数的倒数。
零没有倒数。
【完全平方数】如果一个有理数a的平方等于有理数b,那么这个有理数b叫做完全平方数。
【方根】如果一个数的n次方(n是大于1的整数)等于a,这个数叫做a的n次方根。
【开方】求一数的方根的运算叫做开方。
【算术根】正数a的正的n次方根叫做a的n次算术根,零的算术根是零,负数没有算术根。
【代数式】用有限次运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连结所得的式子,叫做代数式。
【代数式的值】用数值代替代数式里的字母,计算后所得的结果,叫做当这个字母取这个数值时的代数式的值。
代数式的分类【有理式】只含有加、减、乘、除和乘方运算的代数式叫有理式。
【无理式】根号下含有字母的代数式叫做无理式。
【整式】没有除法运算或者虽有除法运算而除式中不含字母的有理式叫整式。
【分式】除式中含字母的有理式叫分式。
2019-2020学年数学中考模拟试卷一、选择题1.下列图形都是由同样大小的黑色菱形纸片组成,其中第①个图中有3个黑色菱形纸片,第②个图中有5个黑色菱形纸片,第③个图中有7个黑色菱形纸片,…按此规律排列下去,第20个图中黑色菱形纸片的张数为( )A.38 B.39 C.40 D.412.如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,△ABC的周长为14,则BC的长为( )A.3B.4C.5D.63.若一次函数y=kx+b的图象如图所示,则下列结论中,正确的有( )①二次函数y=x2+kx+b的图象一定经过点(0,2);②二次函数y=x2+kx+b的图象开口向上;③二次函数y=x2+kx+b的图象对称轴在y轴左侧;④二次函数y=x2+kx+b的图象不经过第二象限.A.1个B.2个C.3个D.4个4.如图是将一多边形剪去一个角,则新多边形的内角和()A.比原多边形少180°B.与原多边形一样C.比原多边形多360°D.比原多边形多180°5.若函数,则当函数值y=8时,自变量x的值是()A.±B.4C.±或4D.4或-6.由个大小相同的正方形搭成的几何体,被小颖拿掉两个后,得到如图所示的几何体,如图是原几何体的三视图,请你判断小颖拿掉的两个正方体原来放在()A.4号的左右B.3号的前后C.1号的前后D.2号的前后7.下列事件中,属于必然事件的是()A.“世界杯新秀”姆巴佩发点球 100%进球B.任意购买一张车票,座位刚好挨着窗口C.三角形内角和为180°D.叙利亚不会发生战争8.二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数y=ax与一次函数y=bx﹣c在同一坐标系内的图象大致是( )A. B.C.D.9.如图,ΔAOB绕点O顺时针旋转40︒后得到的图形,若点C恰好落在AB上,且AOD∠的度数为90,则B∠的度数为( )A.30︒B.40︒C.50︒D.60︒10.二元一次方程组225x y x y -=-⎧⎨+=⎩的解为( ) A .16x y =-⎧⎨=⎩ B .7383x y ⎧=⎪⎪⎨⎪=⎪⎩ C .32x y =⎧⎨=⎩ D .14x y =⎧⎨=⎩11.一次函数1y kx b =+与2y x a =+的图象如图所示,给出下列结论:①k 0<;②0a >;③当3x <时,12y y <.其中正确的有( )A.0个B.1个C.2个D.3个12.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,对称轴为12x =-.下列结论:①0abc >②0a b +=③20b c +>④42a c b +<.其中正确的有( )A .1个B .2个C .3个D .4个二、填空题 13.在矩形ABCD 中,8AD =,14AB =,E 为DC 上一个点,把ADE ∆沿AE 折叠,使点D 落在点'D 处,若以点C 、B 、'D 为等腰三角形时,则DE 的长为_____________ .14.如图,将边长为3的正方形纸片ABCD 对折,使AB 与DC 重合,折痕为EF ,展平后,再将点B 折到边CD 上,使边AB 经过点E ,折痕为GH ,点B 的对应点为M ,点A 的对应点为N ,那么折痕GH 的长为_____.15.在实数范围内分解因式:24x-=______________________.16.一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳的平均距离,即149600000千米,用科学记数法表示1个天文单位是_____千米.17.方程3223x x+=--的解是_____.18.二次函数y=12(x-2)2+3的顶点坐标是_____.三、解答题19.计算31(3)|12|2π-⎛⎫-+-+-⎪⎝⎭+tan45°﹣2sin30°.20.《杨辉算法》中有这么一道题:“直田积八百六十四步,只云长阔共六十步,问长多几何?”意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多了多少步?21.已知直线l:y=kx+b(k,b为常数,k≠0)与函数y=2x的图象交于点A(-1,m)(1)求m;(2)当k=______时,则直线l经过第一、三、四象限(任写一个符合题意的值即可);(3)求(2)中的直线l的解析式和它与两坐标轴围成的三角形面积.22.有甲、乙两个圆柱体形蓄水池,将甲池中的水以一定的速度注入乙池.甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,其中,甲蓄水池中水的深度y(米)与注水时间x(时)之间的函数关系式为y=﹣23x+2.结合图象回答下列问题:(1)求出乙蓄水池中水的深度y与注水时间x之间的函数关系式;(2)图中交点A的坐标是;表示的实际意义是.(3)当甲、乙两个蓄水池的水的体积相等时,求甲池中水的深度.23.某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类(记为A)、音禾类(记为B)、球类(记为C)、其他类(记为D).根据调査结果发现该班每个学生都进行了登记且每人只登记了一种自己最喜欢的课外活动.班主任根据调査情况把学生进行了归类,并制作了如下两幅统计图.请你结合图中所给信息解答下列同题:(1)七年级(1)班学生总人数为______人,扇形统计图中D类所对应扇形的圆心角为______度,请补全条形统计图;(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名学生擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.(3)如果全市有5万名初中生,那么全市初中生中,喜欢球类的学生有多少人?24.如图,在平面直角坐标系中,抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A、B两点与y轴相交于点C,顶点为D,直线DC与x轴相交于点E.(1)当a=﹣1时,抛物线顶点D的坐标为,OE=;(2)OE的长是否与a值有关,说明你的理由;(3)设∠DEO=β,当β从30°增加到60°的过程中,点D运动的路径长;(4)以DE为斜边,在直线DE的右上方作等腰Rt△PDE.设P(m,n),请直接写出n关于m的函数解析式及自变量m的取值范围.25.如图,在下列9×9的网格中,横纵坐标均为整数的点叫做格点,例如:A(1,1)、B(8,3)都是格点,E、F为小正方形边的中点,C为AE、BF的延长线的交点.(1)AE的长等于;(2)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图示所示的网格中,用无刻度的直尺,画出线段PQ,并直接写出P、Q两点的坐标.【参考答案】***一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12答案 D C B D D D C C D DB A 二、填空题13.648157-或83314.1015.()()22x x +-16.496×10817.135x = 18.(2,3)三、解答题19.28-【解析】【分析】原式前两项分别利用负整数指数幂和零指数幂法则计算,第三项利用绝对值的性质计算,第四项和第五项利用特殊角的三角函数值化简,即可得到结果.【详解】原式=﹣8+1+2﹣1+1﹣1=2﹣8.【点睛】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.20.12【解析】【分析】设矩形的长为x步,则宽为(60﹣x)步,根据题意列出方程,求出方程的解即可得到结果.【详解】解:设矩形的长为x步,则宽为(60﹣x)步,依题意得:x(60﹣x)=864,整理得:x2﹣60x+864=0,解得:x=36或x=24(不合题意,舍去),∴60﹣x=60﹣36=24(步),∴36﹣24=12(步),则该矩形的长比宽多12步.【点睛】此题考查了一元二次方程的应用,找出题中的等量关系是解本题的关键.21.(1)m=-2;(2)1;(3)y=x-1,12.【解析】【分析】(1)把A(-1,m)代入y=2x中,便可求得m的值;(2)先把A点的坐标代入y=kx+b中,用k的代数式表示b,再根据直线直线l经过第一、三、四象限,必须满足k>0,b<0,列出k的不等式组,求得k的取值范围,便可在此取值范围中任写一个k值;(3)求出直线l与坐标轴的交点坐标,再根据三角形的面积公式便可求得结果.【详解】解:(1)把A(-1,m)代入y=2x中,得m=-2;(2)由(1)知,m=-2,∴A(-1,-2),把A(-1,-2)代入y=kx+b中,得-2=-k+b,∴b=k-2,∵直线l经过第一、三、四象限,∴0 kb⎧⎨⎩><,∴20 kk>⎧⎨-<⎩,解得,0<k<2,∴k可以取1,故答案为:1;(3)由(2)知,k=1,b=k-2=-1,∴直线l的解析式为:y=x-1,∴直线l与坐标轴的交点坐标为B(0,-1),A(1,0),如图所示,∴OA=1,OB=1,∴111122 OABS∆=⨯⨯=.【点睛】本题是一次函数与反比例函数图象的交点问题,考查了待定系数法,一次函数的图象与性质,关键是熟记性质,数形结合.22.(1)y=x+1(2)(35,85),当注水时间为35小时,甲乙两水池的水面高度相同,为85米(3)43【解析】【分析】(1)如图,根据甲蓄水池的函数关系式求出放完水的时间,即函数图象与x轴的交点B,从而得到乙图象上的点C的坐标,然后利用待定系数法求一次函数解析式解答;(2)联立两函数解析式,解方程组即可得到交点A的坐标,根据交点的纵坐标相等可知,两水池的水面高度相等;(3)设甲、乙两蓄水池的底面积分别为a、b,根据开始时两水池的水量等于结束时的乙水池的水量列式求出a、b的关系,然后用两水池水量的一半除以甲水池的底面积,计算即可得解.【详解】解:(1)如图,当y=0时,﹣23x+2=0,解得x=3,所以,点C的坐标为(3,4),设乙蓄水池中水的深度y与注水时间x之间的函数关系式为y=kx+b,则134bk b=⎧⎨+=⎩,解得11 kb=⎧⎨=⎩,所以,函数关系式为y=x+1;(2)联立2231y xy x⎧=-+⎪⎨⎪=+⎩,解得3585 xy⎧=⎪⎪⎨⎪=⎪⎩,所以,交点A的坐标为(35,85),表示的实际意义是:当注水时间为35小时,甲乙两水池的水面高度相同,为85米,故答案为:(35,85),当注水时间为35小时,甲乙两水池的水面高度相同,为85米;(3)设甲、乙两个蓄水池的底面积分别为a、b,根据甲乙两水池的蓄水总量可得,2a+b=4b,整理得,a=32b,所以,当甲、乙两个蓄水池的水的体积相等时,甲池中水的深度为1424233b2b ba⨯==米.【点睛】本题考查了一次函数的应用,主要利用了一次函数图象与坐标轴的交点的求法,待定系数法求一次函数解析式,以及函数图象的交点的求解,(3)题要注意先求出两蓄水池的底面积的关系是解题的关键.23.(1)48人,105°,见解析;(2)23;(3)18750.【解析】【分析】(1)由条形统计图与扇形统计图可得七年级(1)班学生总人数为:12÷25%=48(人),继而可得扇形统计图中D类所对应扇形的圆心角为为:360°×1448=105°;然后求得C类的人数,则可补全统计图;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的情况,再利用概率公式即可求得答案.(3)利用样本估计总体思想求解可得.【详解】解:(1)七年级(1)班学生总人数为:12÷25%=48(人),扇形统计图中D类所对应扇形的圆心角为360°×1448=105°,;C类人数:48-4-12-14=18(人),如图:故答案为:48,105;(2)分别用A,B表示两名擅长书法的学生,用C,D表示两名擅长绘画的学生,画树状图得:∵共有12种等可能的结果,抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的有8种情况,∴抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率为:23.(3)全市初中生中,喜欢球类的学生有500001848=18750(人).【点睛】此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图.用到的知识点为:概率=所求情况数与总情况数之比.24.(1)(﹣1,4),3(2)OE的长与a值无关(3)833(4)n=m+1(m>﹣1)【解析】【分析】(1)求出直线CD的解析式即可解决问题;(2)利用参数a,求出直线CD的解析式求出点E坐标即可判断;(3)求出落在特殊情形下的a的值即可点D运动的路径长;(4)如图,作PM⊥对称轴于M,PN⊥AB于N.两条全等三角形的性质即可解决问题.【详解】(1)当a=﹣1时,抛物线的解析式为y=﹣x2﹣2x+3,∴顶点D(﹣1,4),C(0,3),∴直线CD的解析式为y=﹣x+3,∴E(3,0),∴OE=3,故答案为:(﹣1,4),3;(2)结论:OE的长与a值无关.理由:∵y=ax2+2ax﹣3a,∴C(0,﹣3a),D(﹣1,﹣4a),∴直线CD的解析式为y=ax﹣3a,当y=0时,x=3,∴E(3,0),∴OE=3,∴OE的长与a值无关.(3)如图,当β=30°时,OC=33OE=3,∴﹣3a=3,∴a=﹣33,此时点D′的坐标是(﹣1,433).当β=60°时,在Rt△OCE中,OC=3OE=33,∴﹣3a=33,∴a=﹣3,此时点D的坐标是(﹣1,43).∴点D运动的路径长为:43﹣433=833;(4)如图,作PM⊥对称轴于M,PN⊥x轴于N.∵PD=PE,∠PMD=∠PNE=90°,∠DPE=∠MPN=90°,∴∠DPM=∠EPN,∴△DPM≌△EPN(AAS),∴PM=PN,DM=EN,∵D(﹣1,﹣4a),E(3,0),∴由PM=PN得到:n=m+1.由DM=EN得到:m﹣3=﹣4a﹣n.当顶点D在x轴上时,P(1,2),此时m的值1,∵抛物线的顶点在第二象限,∴m>﹣1.∴n=m+1(m>﹣1).【点睛】本题考查二次函数综合题、一次函数的应用、等腰直角三角形的性质、全等三角形的判定和性质、解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.25.(1)AE=132;(2)如图,线段PQ即为所求.见解析;P(3,4),Q(6,6).【解析】【分析】(1)根据勾股定理即可得到结论;(2)取格点M,连接AM,并延长与BC交于Q,连接PQ,则线段PQ即为所求.【详解】(1)AE=22131 1.52+=;故答案为:132;(2)如图,AC与网格线相交,得到P,取格点M,连接AM,并延长与BC交于Q,连接PQ,则线段PQ即为所求.故答案为:AC与网格线相交,得到P,取格点M,连接AM,并延长与BC交于Q,连接PQ,则线段PQ即为所求.∴P(3,4),Q(6,6).【点睛】本题考查了作图﹣应用与设计作图,勾股定理,正确的作出图形是解题的关键.2019-2020学年数学中考模拟试卷一、选择题1.如图,数轴上A 、B 两点分别对应数a 、b ,则下列各式正确的是( )A.ab >0B.a+b >0C.|a|﹣|b|>0D.a ﹣b >0 2.若式子22(1)m m +-有意义,则实数m 的取值范围是( ) A .m >﹣2B .m >﹣2且m≠1C .m≥﹣2D .m≥﹣2且m≠1 3.小刚家2017年和2018年的家庭支出情况如图所示,则小刚家2018年教育方面支出的金额比2017年增加了( )A .0.216万元B .0.108万元C .0.09万元D .0.36万元4.一个塑料袋丢弃在地上的面积约占0.023m 2,如果100万个旅客每人丢一个塑料袋,那么会污染的最大面积用科学记数法表示是( )A .2.3×104m 2B .2.3×106m 2C .2.3×103m 2D .2.3×10﹣2m 25.下列图形中,是轴对称图形,不是中心对称图形的是( )A .正方形B .正三角形C .正六边形D .禁止标志6.如图,四边形ABCD 内接于圆O ,AD ∥BC ,∠DAB =48°,则∠AOC 的度数是( )A .48°B .96°C .114°D .132°7.如图,正方形ABCD .AB =4,点E 为BC 边上点,连接AE 延长至点F 连接BF ,若tan ∠FAB =tan ∠EBF =13,则AF 的长度是( )A .552102-B .810355-C .5106D .31028.如图,CD 是⊙O 的弦,∠ADC=35°,则∠CBA 的度数为( )A .35B .45C .55D .659.下列计算正确的是( )A.224·x x x -=B.()224x x -=C.234·x x x =D.()222m n m n -=-10.下列命题中,真命题是( )A .四边都相等的四边形是矩形B .对角线相等的四边形是矩形C .对角线互相垂直的平行四边形是正方形D .对角线互相垂直的平行四边形是菱形11.如图,已知⊙O 为四边形ABCD 的外接圆,O 为圆心,若∠BCD =120°,AB =AD =6,则⊙O 的半径长为( )A.23B.2C.233D.312.如图,在矩形ABCD 中,AD=4AB -+4AB -+8,点M 在边AD 上,连接BM ,BD 平分∠MBC ,则AM MD的值为( )A.12B.2C.53D.35二、填空题13.如图,△ABC 内接于⊙O ,若∠OAB=32°,则∠C=_____°.14.计算12273-=_____. 15.若关于x 的一元二次方程x 2+2(k ﹣1)x+k 2﹣1=0有两个不相等的实数根,则k 的取值范围是_____.16.方程22111x x =-- 的解为_____. 17.某时刻在南京中华门监测点监测到PM 2.5的含量为55微克/米3,即0.000055克/米3,将0.000055用科学记数法表示为_____.18.如图,△ABC 中,D 、E 分别是BC 、AC 的中点,BF 平分∠ABC ,交DE 于点F ,若AB =12,BC =9,则EF 的长是_____.三、解答题19.计算:214sin 4518222-⎛⎫︒----- ⎪⎝⎭. 20.(1)计算:()10012cos3020192π-⎛⎫---- ⎪⎝⎭ (2)解方程:4501x x -=- 21.如图,安徽江淮集团某部门研制了绘图智能机器人,该机器人由机座、手臂和末端操作器三部分组成,底座AE ⊥直线L 且25AE cm =,手臂60AB BC cm ==,末端操作器35CD cm =,AF 直线L .当机器人运作时,45,75,60BAF ABC BCD ∠=︒∠=︒∠=︒,求末端操作器节点D 到地面直线L 的距离.(结果保留根号)22.小张前往某精密仪器厂应聘,公司承诺工资待遇如下.工资待遇:每月工资至少3000元,每天工作8小时,每月工作25天,加工1件A 型零件计酬16元,加工1件B 型零件计酬12元,月工资=底薪(800元)+计件工资 .进厂后小张发现:加工1件A 型零件和3件B 型零件需要5小时;加工2件A 型零件和5件B 型零件需9小时.(1)小张加工1件A 型零件和1件B 型零件各需要多少小时?(2)若公司规定:小张每月必须加工A B 、两种型号的零件,且加工B 型的数量不大于A 型零件数量的2倍,设小张每月加工A 零件a 件,工资总额为W 元,请你运用所学知识判断该公司颁布执行此规定后是否违背了工资待遇承诺?23.如图,将BOA ∠放在每个小正方形的边长为1的网格中,点O 、A 均落在格点上,角的一边OA 与水平方向的网格线重合,另一边OB 经过格点B .(Ⅰ)tan BOA ∠等于__________;(Ⅱ)如果BOC ∠为BOA ∠内部的一个锐角,且2tan 3BOC ∠=,请在如图所示的网格中,借助无刻度的直尺画出COA ∠,使得COA BOA BOC ∠=∠-∠,并简要说明COA ∠是如何找到的(不要求证明)__________________________________________________________________________________________________________________________________________________.24.食品安全是老百姓关注的话题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输。
高中数学人教B版必修14.1.1实数指数幂及其运算课件

N+ ,且
m 为既约分数) n
m
a n ( n a )m n am
注(用-1意)语1/:3和言底(-数1叙)2a/6述>应0这当:个具正条有数件同不的样可的少mn意. 义次若,无幂但此(由m条分件,n数会∈指引N数起*幂,混且的乱n意,>义例1)可如, 得等出于1不这同的个结正果数: 的2 m次幂的n次算术根.
偶次方根 奇次方根
实 a0
数
n a
n a 0
a a 0 不存在 n a 0
n a 根式 n 根指数 a 被开方数
正数a的正次方根叫做a的n次算术方根
2、练习填空: (1)25的平方根等于_______;(2) 16的四次方根等于_______ (3)-32的五次方根等于_____;(4) 27的立方根等于________
练习:计算下列各式:
(1)(3 25 125) 4 5 (2) a2 (a 0)
a 3 a2
1.根式的概念.
2.根式的运算性质.
(1)(n a )n a(n>1,n∈N+)
a
当n为奇数时
(2)n a n | a | 当n为偶数时
(3)np a mp n a m , (a 0)
3.有理数指数幂的运算性质.
若x3 a,则x叫a的立方根(或三次方根)
a只有一个立方根
自主探究: 1、视察各式
思考1:若类比平方根、立方根的概念,你能给出n次方 根的定义吗?能举例说明定义吗?
若存在实数x,使xn a(a R, n 1, n N )则x叫a的n次方根.
求a的n次方根,叫做把a开n次方,称作开方运算
例1:求下列各式的值
(1) 3 (8)3 ;
初一初二数学知识汇总

初一初二数学知识汇总一、数与代数1.数与式2.实数及他的分类(补充)实数的性质:【质数与合数】一个大于1的整数,如果除了它本身和1以外不能被其它正整数所整除,那么这个数称为质数。
一个大于1的数,如果除了它本身和1以外还能被其它正整数所整除,那么这个数知名人士为合数,1既不是质数又不是合数。
【倒数】1除以一个非零实数的商叫这个实数的倒数。
零没有倒数。
实数a的倒数是(a≠0);【完全平方数】如果一个有理数a的平方等于有理数b,那么这个有理数b叫做完全平方数。
【方根】如果一个数的n次方(n是大于1的整数)等于a,这个数叫做a的n次方根。
【开方】求一数的方根的运算叫做开方。
【算术根】正数a的正的n次方根叫做a的n次算术根,零的算术根是零,负数没有算术根。
①实数a的相反数是-a,只有符号不同的两个实数,其中一个叫做另一个的相反数。
零的相反数是零。
②实数a的绝对值:一个正数的绝对值是它本身,一个负数绝对值是它的相反数,零的绝对值为零。
从数轴上看,一个实数的绝对值是表示这个数的点离开原点距离。
③正数大于0,负数小于0,两个负实数,绝对值大的反而小。
【代数式】用有限次运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连结所得的式子,叫做代数式。
【代数式的值】用数值代替代数式里的字母,计算后所得的结果,叫做当这个字母取这个数值时的代数式的值。
(2)【代数式的分类】【有理式】只含有加、减、乘、除和乘方运算的代数式叫有理式【无理式】根号下含有字母的代数式叫做无理式【整式】没有除法运算或者虽有除法运算而除式中不含字母的有理式叫整式 【分式】除式中含字母的有理式叫分式 整式与分式 ①同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,即(m、n为正整数); ②同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即(a≠0,m、n为正整数,m>n); ③幂的乘方法则:幂的乘方,底数不变,指数相乘,即(n为正整数); ④零指数:(a≠0); ⑤负整数指数:(a≠0,n为正整数); 公式包括整式乘法与因式分解分解是互逆的过程. ⑥平方差公式:两个数的和与这两个数的差的积等于这两个数的平方,即;⑦完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍,即; 分式①分式的基本性质:分式的分子和分母都乘以(或除以)同一个不等于零的整式,分式的值不变,即;,其中m是不等于零的代数式; ②分式的乘法法则:; ③分式的除法法则:; ④分式的乘方法则:(n为正整数); ⑤同分母分式加减法则:; ⑥异分母分式加减法则:;等式的基本性质:①等式两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式。
高中数学实数指数幂及其运算1理解n次方根的概念及性质课件人教版必修一
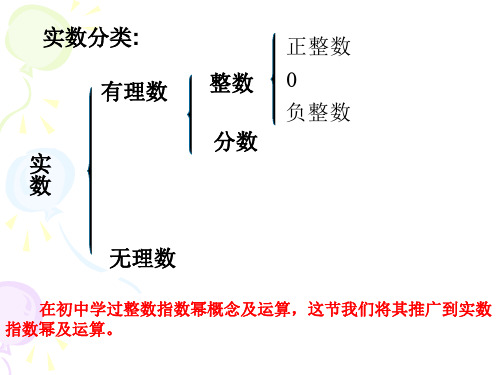
a
m n
(2)(a ) a am mn (3) n a (m n,a 0) a
m n
nm
(4)(ab)
m
a b
m m
由
am an
=
a
mn
(m n,a 0)
a0
a a 3 3 a3
3
3
a
0
1
a 35 1 2 a a a2 5 a
将正整数指数幂推广到整数指数幂
an
和
1.5 , , ,( 2的过剩近似值); 1.42 1.415 .....
来近似地计算无理指数幂 3 2的不足或过剩近似值。如果 2 的任何一个有理数 不足近似值记为 a ,其相应的有理数过剩近似值为 b , 那么当 n 无限增大
3 , , 3 3
1.5 1.42
n
1.415
时,
数
an , bn 就逼近于一个实数
a a 2b 2c 1 2 bc
2
2 分数指数
若x a,则x叫a的平方根(或二次方根)
2
a 0时,两个平方根: , a a a 0时,有一个平方根: 0 a 0时,无实根
若x a,则x叫a的立方根(或三次方根)
3
a只有一个立方根
方根
若存在实数x,使x n = a a ? R ,n ( 则x叫a的n 次方根。 1,n N + ),
求a 的 n 次方根,叫做把 a 开 n 次方 ,称作开方运算
偶次方根 奇次方根
n
实 a0 n a 数 a a 0 不存在
n
a 0 a 0
a 根式
n 根指数
n
立方根知识梳理

2.3立方根一、知识梳理1、立方根的概念(1)定义:一般地,如果一个数x 的立方等于a ,即a x =3,那么这个数x 就叫做a 的立方根(也叫做三次方根)(2)开立方:求一个数的立方根的运算叫做开立方。
开立方与立方根互为逆运算,因此在运算结果中可以相互检验其正确性。
2、立方根的性质。
(1)正数有一个正的立方根;(2)负数有一个负的立方根;(3)0有一个立方根,就是0本身.3、立方根的表示方法数a 的立方根用符号“3a ”表示,读作“三次根号a ”,其中a 是被开方数,3是根指数,注意,“3”不能省略。
4、开立方求一个数的立方根的运算,叫做开立方。
5、两个互为相反数的立方根之间的关系。
我们知道:8)2(,8233-=-=,∴8和-8的立方根分别是2和-2;又∵33=27,27)3(3-=-,∴27和-27的立方根分别是3和-3,其中8与-8,2与-2,27与-27,3与-3分别互为相反数。
设则,3a x =a x x -=-=-33)( 根据立方根的定义,可知:3a x =,3a x -=- ∴333a a a -=-=-这就是说,求一个负数的立方根时,只要先求出这个负数的绝对值的立方根,然后再取它的相反数即可,也就是说,三次根号内的负号可以移到根号外面。
6、n 次方根一般地,如果一个数的n 次方根(n 是大于1的整数)等于a ,那么这个数就叫做a 的n 次方根,即a x n =,那么x 就是a 的n 次方根。
例如:2-24164162-2,162-1625322,322445和次方根是的次方根,或者说的都是和,),(次方根,的是==∴=7、开n 次方求a 的n 次方根的运算,叫做把a 开n 次方,其中a 叫做被开方数,n 叫做根指数。
8、n 次算术根(1)定义:正数a 的正的n 次方根叫做a 的n 次算术根,零的n 次方根也叫做零的n 次算术根。
(2)表示方法:当0≥a 时,n a 就表示a 的n 次算术根。
初一数学《代数式》知识点精讲

初一数学《代数式》知识点精讲知识点总结一、代数式的定义:用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
单独的一个数或字母也是代数式。
注意:(1)单个数字与字母也是代数式;(2)代数式与公式、等式的区别是代数式中不含等号,而公式和等式中都含有等号;(3)代数式可按运算关系和运算结果两种情况理解。
三、整式:单项式与多项式统称为整式。
1.单项式:数与字母的积所表示的代数式叫做单项式,单项式中的数字因数叫做单项式的系数;单项式中所有字母的指数的和叫做单项式的次数。
特别地,单独一个数或者一个字母也是单项式。
2.多项式:几个单项式的和叫做多项式,在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项;在多项式里,次数最高项的次数就是这个多项式的次数。
四、升(降)幂排列:把一个多项式按某一个字母的指数从小到大(或从大到小)的顺序排列起来,叫做把多项式按这个字母升(降)幂排列。
五、代数式书写要求:1.代数式中出现的乘号通常用“·”表示或者省略不写;数与字母相乘时,数应写在字母前面;数与数相乘时,仍用“×”号;2.数字与字母相乘、单项式与多项式相乘时,一般按照先写数字,再写单项式,最后写多项式的书写顺序.如式子(a+b)·2·a应写成2a(a+b);3.带分数与字母相乘时,应先把带分数化成假分数后再与字母相乘;4.在代数式中出现除法运算时,按分数的写法来写;5.在一些实际问题中,有时表示数量的代数式有单位名称,如果代数式是积或商的形式,则单位直接写在式子后面;如果代数式是和或差的形式,则必须先把代数式用括号括起来,再将单位名称写在式子的后面,如2a 米,(2a-b)kg。
六、系数与次数单项式的系数和次数,多项式的项数和次数。
1.单项式的系数:单项式中的数字因数叫做单项式的系数。
注意:(1)单项式的系数包括它前面的符号;(2)若单项式的系数是"1”或-1“时,"1"通常省略不写,但“-”号不能省略。
2020高中数学 2.1.1N次方根的概念及性质教案 新人教A版必修1

n次方根的概念和性质一、教学分析分数指数幂是必修一第二章第一节的内容,是研究基本初等函数之一的指数函数的基础。
分数指数幂不同于整数指数幂,要理解分数指数幂,首先要深入理解n次方根的概念和性质.根式的概念教学是一个难点,但它是后续学习所必需的。
教学中可考虑以具体的例子为载体,类比平方根、立方根的定义,给出n次方根的定义,可以在给出定义前,让学生类比平方根、立方根举些例子。
将平方根和立方根的性质推广到n次方根时,多给学生提供一些实例,经过比较让学生自己归纳出结论。
教学时,要让学生充分体会当n是偶数时,正数的n次方根有两个,这两个数互为相反数。
对于结论0的n次方根都是0,要启发学生用n次方根的定义去理解。
根式的概念源于方根的概念,根据n次方根的意义就能得到n次方根的性质1。
但性质2是不能由n次方根的意义直接得出的,因此,教学中可让学生从具体实例中自己探究归纳得出结论。
二、学情分析学生在义务阶段的学习中已经知道了平方根和立方根的概念,掌握了平方根和立方根的相关性质。
然而知识需在运用中得到巩固,学生较长时间不接触平方根和立方根的知识,所以在教学中以正方形的面积和正方体的体积为例,帮助学生回顾平方根和立方根的概念。
教学中要充分利用学生已有的知识,着眼于学生的最近发展区,为学生提供学生感兴趣的的内容,调动学生的积极性,发挥其潜能。
由此,学生将很容易类比平方根和立方根的知识,得出n次方根的概念及其表示方法。
然而,让学生直接抽象地得出n次方根的相关性质,难度很大,学生的抽象概论能力还需进一步培养,所以,教学中应用大量丰富的实例,让学生从实例中观察,归纳得出结论。
通过本节课的学习,不仅要求学生掌握n次方根的相关知识,同时要培让学生感受基本数学思想,数学方法。
三、教学目标:(1)知识与技能:n次方根的概念,根式的性质(2)过程与方法:类比平方根和立方根,得出n次方根的概念;根据n次方根的概念,结合具体实例,总结n次方根性质;(3)情感态度价值观:类比思想,分类讨论思想;四、教学重难点重点:n次方根的概念和性质,难点:n次方根的性质五、教学过程1.触景生情问题1 据国务院发展研究中心2000年发表的《未来20年我国发展前景分析》判断,未来20年,我国GDP (国内生产总值)年平均增长率可望达到7.3%。
实数—专题二、立方根

实 数专题二、 立方根 【知识回顾】1.立方根:如果一个数x 的立方等于a ,即x 的三次方等于a(a x =3),即3个x 连续相乘等于a,那么这个数x 就叫做a 的立方根,也叫做三次方根。
2.开立方:求一个数的立方根的运算叫做开立方。
开立方与立方互为逆运算。
开立方的小数点移动规律:被开方数的小数点向右或向左每移动三位,则立方根的小数点就向右或向左移动一位。
3.常见立方数:113=; 823=; 2733=; 6443=; 12553=21663=; 34373=; 51283=; 72993=; 1000103=4、常用公式:a a =33,a a =33)( 5. 平方根与立方根的比较平 方 根立 方 根定 义如果一个数x 的平方等于a ,那么,这个数x 就叫做a 的平方根。
即:若)0(2≥=a a x 时,则x 称为a 的平方根,记作)0(≥±=a a x ,其中a 是被开方数,根指数是2如果一个数x 的立方等于a ,那么这个数x 就叫做a 的立方根(也称作a 的三次方根)。
即:若3x a =,则x 称为a 的立方根,记作x=3a ,其中a 是被开方数,根指数是3 性 质 1. 一个正数有两个平方根,它们互为相反数1. 正数有一个正的立方根2. 0的平方根是0 2. 0的立方根是03. 负数没有平方根 3. 负数有一个负的立方根 开平方与平方互为逆运算开立方与立方互为逆运算n 次根偶数次方根与平方根性质相同 奇数次方根与立方根性质相同6.n 次方根的定义:如果一个数的n 次方等于a ,这个数叫做a 的n 次方根。
n 次方根的性质:(1)正数的偶次方根有两个,它们互为相反数;负数没有偶次方根; (2)任何数a 的奇次方根只有一个,且与a 同正负; (3)0的任何次方根为0。
【典型例题】【例1】求下列各式的值:(1)3125; (2)3271-- ; (3)38-; (4)338【变式练习】 1、填空2549的平方根是 ; -512的立方根是 ; 2(9)-的平方根是 ; -27的立方根是 ;64的平方根是 ; 343的立方根是 。
实数

第六章 实数6.1 平方根知识点1 算术平方根一般地,如果一个正数x 的平方等于a ,即a x =2,那么这个正数x 叫做a 的算术平方根记为a ,读作“根号a ”,a 叫做被开方数.拓展: ①. 一个正数的算术平方根是正数,规定0的算术平方根为0.因此,对于任何一个非负数a ,它的算术平方根一定为非负数。
②.求一个非负数的算术平方根与求一个非负数的平方恰好是互逆的过程,只不过只有正数和0才有算术平方根,负数没有算数平方根。
例1: (2014 ∙厦门中考)4的算术平方根是 ( )A 16B 2C -2D 2±知识点2 平方根(1)定义:一般地,如果一个数的平方等于a ,那么这个数叫做a 的平方根或二次根式。
这就是说,如果a x =2,那么x 叫做a 的平方根。
求一个数a 的平方根的运算,叫做开平方。
(2)性质:正数的平方根有两个,它们互为相反数;0的平方根只有一个,就是它本身;负数没有平方根。
拓展: 如区别 联系平方根 算术平方根平方根包含算术平方根,算术平方根是平方根的一种,平方根与算术平方根都是相对于非负数而言的,只有0的平方根和算数正数a 的平方根为a ±,有两个正数a 的算术平方根为a ,只有一个正数的平方根有两个,两者互为相反数 正数的算术平方根一定是正数例2、下列各数有没有平方根?如果有,求出它的平方根与算术平方根;如果没有,请说明理由。
(1)25 (2)0.0081 (3)()27- (4)36.0- .小试牛刀:已知()的值求x x ,0121122=-+。
【基础达标】1、25的平方根是2、9=3、2)2(-的算术平方根是4、251的算术平方根的相反数是 ,平方根的倒数是 5、求下列各数的算术平方根(1) 2243+; (2) .)8()2(-⨯-6,解下列方程 (1)251962=x ; (2)()81242=-x6.2立方根知识点1 立方根1. 定义:如果一个数的立方等于a ,那么这个数叫做a 的立方根或三次方根。
4.1.1.1高教版-中职数学-n次根式
4.1.1分数指数幂---n次根式一、教材分析本节课是新课标职业高中数学基础模块上册第四章实数指数幂第一课时,也是指数运算的入门。
n次是初中平方根与立方根概念的拓展与延伸,同时也是学习分数指数幂的基础。
教材通过二次方根、三次方根扩充到n次方根以及根式的性质,本节内容是分数指数幂的基础和前提,便于我们将整数指数幂推广到分数指数幂,为研究后期的运算法则做好准备。
同时,通过对n次根式的学习,进一步培养和提升了学生的数学运算、直观想象、逻辑推理等核心素养。
二、学情分析我所教授的班级是商务专业,该专业的人才培养方向对数学的运算能力要求较高,而本章的指数与对数函数模型与该专业很多专业知识也联系紧密。
本班学生活泼好动,个性鲜明,头脑聪明灵活,但学习起点低,学习基础弱,部分学生有厌学现象,基础薄弱的学生“望数生畏”,游离于数学学习之外。
上课注意力不易集中,对数学的兴趣不易做到持之以恒,对枯燥持久的讲授方式容易厌倦。
基于这样的学情,在教学设计的过程中,我尽力做到思路清晰,简洁明了,通熟易懂,通过师生互动,生生互动,小组内优带差,优比优,打破课堂的沉闷,慢慢让学生体会到学习数学的快乐以及学习数学的价值。
三、教学设计基于本节课的内容和学生实际,作如下教学设计。
章前设疑回顾旧知得出概念最近呢,老师碰到一个问题想请同学们解决一下。
经过几年的努力,终于有了一笔存款,但银行有两种储蓄方法:1、存期一年,到期后连本带息自动转存,三年后取出;2、存三年期,到期取出;(一年期年利率2.50%,三年期年利率3.25%)三年后,哪种方式获利更多?你能帮我解决这个问题吗?解决过程中我们又是根据什么数学模型来计算的呢?从今天开始,我们便将进入第四章《对数函数与指数函数》的神奇世界。
章前设疑,激发兴趣.将问题发送至钉钉家校本,让同学们课后解决并提交方案。
学生利用原有的知识基础以及专业知识解决问题。
经过第三章《函数》的学习,学生已经对函数的概念、基本性质、以及研究函数的基本方法等函数的“共性”有了一定的了解,那么第四章的三类函数又有什么“个性”呢?结合学生专业特色和生活实际,在章前设疑,激发学生的求知欲望.初中我们学习过:,.x a a a=±一个正数的平方根有两个,它们互为相反数,即其中叫做的算术平方根例如:若23x=,则x= ;3±叫做3的;3叫做3的;332,=x a x a a=、若则叫做的立方根(三次方根).3338,2x x x==例如:则;=0,则x=0;x=-8,x=-2.一个正数的立方根是一个正数,一个负数的立方根是一个负数,0的立方根是0.(实数a的立方根只有一个.)引导学生回顾二次方根,立方根的概念及运算。
根号式的计算方法

根号式的计算方法(原创实用版3篇)篇1 目录1.引言:介绍根号式的计算方法的重要性和必要性2.根号式的基本概念:定义和符号3.根号式的计算方法:平方根、立方根和 n 次方根的计算4.根号式的性质:根号内的数值、正负性、乘法和除法规则5.实际应用:根号式在数学、物理和工程等领域的应用案例6.结论:总结根号式的计算方法和性质的重要性和应用价值篇1正文根号式的计算方法是数学中一个重要的领域,它在解决许多实际问题中都发挥着重要的作用。
了解和掌握根号式的计算方法,对于提高我们的数学素养和解决实际问题都具有重要的意义。
首先,让我们来了解一下根号式的基本概念。
根号式是用来表示一个数的平方、立方或其他高次幂的符号,通常用根号符号“√”表示。
例如,如果我们说一个数的平方根,就是指这个数的二次方根,用数学符号表示就是√x。
同样,一个数的立方根就是指这个数的三次方根,用数学符号表示就是√x。
在了解了根号式的基本概念后,我们来看一下根号式的计算方法。
平方根的计算方法是通过开平方,即将一个数不断平方直到得到所需的数值。
例如,9 的平方根就是 3,因为 3等于 9。
立方根的计算方法是通过开立方,即将一个数不断立方直到得到所需的数值。
例如,27 的立方根就是 3,因为 3等于 27。
对于 n 次方根,我们可以使用类似的方法,即将一个数不断 n 次方直到得到所需的数值。
除了计算方法外,根号式还有一些重要的性质。
首先,根号内的数值必须是非负的,因为任何数的平方都是非负的。
其次,根号式的正负性由根号内的数值决定。
例如,√9 和√(-9) 分别表示正 3 和负 3。
此外,根号式还满足乘法和除法规则,即√a ×√b = √(ab) 和√a ÷√b = √(a/b)。
最后,让我们来看一下根号式在实际应用中的案例。
在数学领域,根号式被广泛应用于代数、几何、微积分等学科。
在物理和工程领域,根号式也被广泛应用于计算物体的速度、加速度、位移等物理量。
1.2.1《n次方根 》-根式的概念-高职数学

当 n 为偶数时, n an = | a | =
a (a≥0)
-a (a<0)
P11-13 习题 1-2
则 -5 是 -125 的三次方根(立方根); (3) 6 4 = 1 296,
则 6 是 1 296 的 4 次方根.
结论:
(1) 当 n 为奇数时: 正数的 n 次方根为正数,负数的 n 次方根为负数.
记作 x = n a
(2) 当 n 为偶数时: 正数的 n 次方根有两个(互为相反数).
记作 x = ± n a
练习:求值
(2)x2 144 解:因为(12)2 144,所以x 12
(1))4 54
(4)(5)2
1.方根:x n = a( n > 1,n N ),
则 x 叫做 a 的 n 次方根.
2.根式
n a 叫做根式,n 叫根指数,a叫做被开方数.
根式的性质:
(1) ( n a ) n = a.
1.2.1 根式的概念
一、根式 1.n次方根
一般地,若 x n = a( n > 1,n R ),
则 x 叫做 a 的 n 次方根.
例如: (1) 3 2 = 9 ,
则 3 是 9 的二次方根(平方根); (-3) 2 = 9,
则 -3 也是 9 的二次方根(平方根); (2) (-5) 3 = -125,
根式的性质:
(2) 当 n 为奇数时, n an = a; 当 n 为偶数时, n an = | a | =
例如
a (a≥0)
-a (a<0)
3 (2)3 = -2; 4 34 = 3;
5 25 = 2; (3)2 = 3.
(完整)n次方根和n次算术根

(完整)n次方根和n次算术根
读一读 n次方根和n次算术根
这一章里,我们研究了数的平方根和立方根。
实际上,数的方根的概念可以推广。
一般地,如果一个数的n(n是大于1的整数)次方等于a,这个数就叫做a的n次方根。
换句话说,如果xn=a,那么x叫做a的n 次方根。
求a的n次方根的运算,叫做把a开n次方,a叫做被开方数,n叫做根指数.
例如,由于24=16和(-2)4=16,我们把2或-2叫做16的4次方根,这个运算叫做把16开4次方,16叫做被开方数,4叫做根指数.
如果a6=-64,a=?请你求一下。
一般地,正数的偶次方根有两个,它们互为相反数。
-表示,也可以把两个当n是偶数时,正数a的正的n次方根用符号n a表示,负的n次方根用符号n a
±例如416=2,—416=-2,合起来写作±416=±2.
方根合起来写作n a
想一想,负数有偶次方根吗?
我们已经知道,任何数都有一个立方根。
下面来进一步看一看:32的5次方根是多少?-128的7次方根呢?
因为25=32,所以2是32的5次方根;
因为(-2)7=-128,所以-2是-128的7次方根。
一般地,正数的奇次方根是一个正数,负数的奇次方根是一个负数。
一般地,如果a>0,n是正的奇数,那么,
正数a的正的n次方根叫做a的n次算术根.0的n次方根也叫做0的n次算术根。
求一个数的方根的运算,叫做开方.很明显,开n次方与n次方互为逆运算.。
有理指数幂及其运算

叫做根式,n叫做根指数。
(2)
说明:
3.根式性质:
01
02
ቤተ መጻሕፍቲ ባይዱ
03
分数指数幂(有理指数幂):
负分数指数幂:
正分数指数幂:
(3)0的任何次方根是0,对吗?
思考:
5.有理指数幂运算法则:
规定:0的正分数次幂是0,0的负分数次幂没有意义.
注意:(1)对于既含有分数指数幂,又含有根式的式子, 一般把根式 统一化成分数指数幂的形式,以便于计算。 如果根式中的根指数不同,也应化成分数指数幂的形式。 对于计算的结果,不强求统一用什么形式来表示, 但结果不能同时含有根号和分数指数,也不能既含有分 母又含有负指数。
4
小结:
, 则x叫做a的n次方根
如果存在实数x,使得
2.拓展:
(1)正数a的偶次方根有两个,它们互为相反数,记为
(2)负数的偶次方根在实数范围内不存在。
问题:a的n次方根一定存在吗? 如果存在,有几个?
(3)正数的奇次方根是一个正数,负数的奇次方根是一个负数。都记为 。
(1)正数a的正n次方根,叫做a的 n次算术根。
注意:一般地,进行指数幂运算时,化负指数为正指数, 化根式为分数指数幂,化小数为分数进行运算,便于进 行乘除、乘方、开方运算,以达到化繁为简的目的。
三、无理指数:
实数指数幂:
运算法则
根式和根式的性质:
1
指数幂的拓展:
2
实数指数幂的运算律:
3
实数指数幂的运算律的应用。
实数指数幂及运算
PLEASE ENTER YOUR TITLE HERE
汇报人姓名
掌握实数指数幂的拓展过程中的不变性质。 掌握根式和有理数指数幂的意义 注意指数幂的拓展过程中的底数的约束条件
开根号 公式

开根号公式
开根号基础公式是√a,如果一个非负数x的平方等于a,即x²=a,(a≥0),那么这个非负数x叫做a的算术平方根。
负数方根不能行,零取方根仍为零。
正数方根有两个,符号相反值相同。
2作根指可省略,其它务必要写明。
负数只有奇次根,算术方根零或正。
在数学中,若一个数b为数a的n次方根,则bn=a。
如果n是偶数,那么负数将没有主n次方根。
习惯上,将2次方根叫做平方根,将3次方根叫做立方根。
最早的根号“√”源于字母“L”的变形(出自拉丁语latus的首字母,表示“边长”),没有线括号(即被开方数上的横线),后来数学家笛卡尔给其加上线括号,但与前面的方根符号是分开的,因此在复杂的式子显得很乱。
笔算开n次方的方法

笔算开n次方的方法:1、把被开方的整数部分从个位起向左每隔n位为一段,把开方的小数部分从小数点第一位起向由每隔n位为一段,用撇号分开;2、根据左边第一段里的数,求得开n次算术根的最高位上的数,假设这个数为a;3、从第一段的数减去求得的最高位上数的n次方,在它们的差的右边写上第二段数作为第一个余数;4、把n(10a)^(n-1)去除第一个余数,所得的整数部分试商(如果这个最大整数大于或等于10,就用9做试商);5、设试商为b。
如果(10a+b)^n-(10a)^n小于或等于余数,这个试商就是n次算术根的第二位;如果(10a+b)^n-(10a)^n大于余数,就把试商逐次减1再试,直到(10a+b)^n-(10a)^n小于或等于余数为止。
6、用同样的方法,继续求n次算术跟的其它各位上的数(如果已经算了k位数数字,则a要取为全部k位数字)。
例如计算987654321987654321的五次算术根,就算到小数点后四位。
3 9 7 1. 1 9 2 95√987'65432'19876'54321.00000'00000'00000'00000243________________________________________________744 65432......................................74465432/(5×30^4)整数部分是18,用9作试商659 24199......................................39^5-30^5_____________________________________________85 41233 19876................................854123319876/(5×390^4)的整数部分是7,用7作试商83 92970 61757................................397^5-390^5____________________________________________1 48262 58119 54321..........................1482625811954321/(5×3970^4)的整数部分是1,用1作试商1 24265 57094 08851..........................3971^5-3970^5___________________________________________23997 01025 45470 00000....................23997010254547000000/(5×39710^4)的整数部分是1,用1作试商12433 44352 06091 99551....................39711^5-39710^5_________________________________________11563 56673 39378 00449 00000..............1156356673393780044900000/(5×397110^4)的整数部分是9,用9作试商11191 17001 57043 20516 21599..............397119^5-397110^5_________________________________________372 39671 82334 79932 78401 00000........3723967182334799327840100000/(5×3971190^4)的整数部分是2,用2作试商248 70419 01386 56554 83574 43232........3971192^5-3971190^5_______________________________________123 69252 80948 23377 94826 56768 00000..123692528094823377948265676800000/(5×39711920^4)的整数部分是9,用9作试商 111 91704 90192 14028 71518 74119 30649..39711929^5-39711920^5_______________________________________11 77547 90756 09349 23307 82648 69351这样就得到987654321987654321的五次算术根精确到小数点前四位为3971.1929。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
读一读 n次方根和n次算术根
这一章里,我们研究了数的平方根和立方根。
实际上,数的方根的概念可以推广。
一般地,如果一个数的n(n是大于1的整数)次方等于a,这个数就叫做a的n次方根。
换句话说,如果xn=a,那么x叫做a的n次方根。
求a的n次方根的运算,叫做把a开n次方,a叫做被开方数,n叫做根指数。
例如,由于24=16和(-2)4=16,我们把2或-2叫做16的4次方根,这个运算叫做把16开4次方,16叫做被开方数,4叫做根指数。
如果a6=-64,a=?请你求一下。
一般地,正数的偶次方根有两个,它们互为相反数。
当n是偶数时,正数a的正的n表示,负的n次方根用符号
作,,合起来写作±±2。
想一想,负数有偶次方根吗?
我们已经知道,任何数都有一个立方根。
下面来进一步看一看:32的5次方根是多少?-128的7次方根呢?
因为25=32,所以2是32的5次方根;
因为(-2)7=-128,所以-2是-128的7次方根。
一般地,正数的奇次方根是一个正数,负数的奇次方根是一个负数。
一般地,如果a>0,n是正的奇数,那么,
正数a的正的n次方根叫做a的n次算术根.0的n次方根也叫做0的n次算术根。
求一个数的方根的运算,叫做开方.很明显,开n次方与n次方互为逆运算。
