§1.1.1变化率问题1[1]
高中数学导数之变化率问题

课题:§1.1.1变化率及导数的概念三维目标: 1、 知识与技能⑴理解平均变化率的概念;⑵了解瞬时速度、瞬时变化率的概念;⑶理解导数的概念,知道瞬时变化率就是导数,体会导数的思想及其内涵; ⑷会求函数在某点的导数或瞬时变化率; ⑸理解导数的几何意义。
2、过程与方法⑴通过大量的实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,知道瞬时变化率就是导数;⑵通过动手计算培养学生观察、分析、比较和归纳能力;⑶通过问题的探究体会逼近、类比、以已知探求未知、从特殊到一般的数学思想方法。
3、情态与价值观⑴通过学生的积极参与、学习变化率与导数的知识,培养学生思维的科学性、严密性,不断认识数形结合和等价转化的数学思想;⑵通过运动的观点体会导数的内涵,使学生掌握导数的概念,从而激发学生学习数学的兴趣; ⑶通过对变化率与导数的学习,不断培养自主学习、合作交流、善于反思、勤于总结的科学态度和锲而不舍的钻研精神,提高参与意识和合作精神教学重点:瞬时速度、瞬时变化率的概念及导数概念的形成,导数及几何意义的理解。
教学难点:在平均变化率的基础上去探求瞬时变化率,导数及几何意义的理解。
教学过程:一、引入课题:为了描述现实世界中运动、过程等变化的现象,在数学中引入了函数,随着对函数的研究,产生了微积分,微积分的创立以自然科学中四类问题的处理直接相关:一、已知物体运动的路程作为时间的函数,求物体在任意时刻的速度与加速度等; 二、求曲线的切线;三、求已知函数的最大值与最小值; 四、求长度、面积、体积和重心等。
导数是微积分的核心概念之一它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具。
导数研究的问题即变化率问题:研究某个变量相对于另一个变量变化的快慢程度。
二、讲解新课:【探究1】气球膨胀率同学们,相信大家都玩过气球吧,我们回忆一下吹气球的过程,可以发现,随着气球内气体的容量的增加,气球的半径增加的越来越慢, 从数学角度,如何描述这种现象呢?气球的体积V (单位:L )与半径r (单位:dm )之间的函数关系是34()3V r r π=,如果将半径r 表示为体积V 的函数,那么()r V 。
课件1:5.1.1 变化率问题

∴ΔΔyx=-ΔΔxx++242,
∴k= lim Δx→0
ΔΔyx=Δlixm→0
-ΔxΔ+x-242=-44=-1.
又 x=2 时 y=242=1,
∴切线方程为 y-1=-1×(x-2),即 x+y-3=0.
【课堂小结】
1.函数 y=f (x)在 x=x0 处的切线斜率反映了函数在该点处的
瞬时变化率,它揭示了事物在某时刻的变化情况.即:
【学以致用】
1.一物体的运动方程是 s=3+2t,则在[2,2.1]这段时间
内的平均速度是( )
A.0.4
B.2
C.0.3
D.0.2
B [ v =s22.1.1--s22=4.02-.1 4=2.]
2.物体自由落体的运动方程为 s(t)=12gt2,g=9.8 m/s2,若 v
=lim Δt→0
率及瞬时速度的概念.(易混点) 及数学运算的核心素养.
1.平均变化率
【新知初探】
对于函数 y=f (x),从 x1 到 x2 的平均变化率:
(1)自变量的改变量:Δx=__x_2-__x_1_. (2)函数值的改变量:Δy=__f_(_x_2_)-__f_(_x_1)__.
(3)平均变化率ΔΔyx=
【例 2】 某物体的运动路程 s(单位:m)与时间 t(单位:s)的关
系可用函数 s(t)=t2+t+1 表示,求物体在 t=1 s 时的瞬时速度.
[解] ∵ΔΔst=s1+ΔΔtt-s1
=1+Δt2+1+ΔΔtt+1-12+1+1=3+Δt,
∴lim Δt→0
ΔΔst =Δlitm→0
(3+Δt)=3.
5.1.1 变化率问题
学习目标
核心素养
用一元二次方程解决增长率问题含答案

用一元二次方程解决增长率问题含答案1.解决增长率问题的一元二次方程1.1 平均变化率问题安徽中考题目:一种药品原价每盒25元,经过两次降价后每盒16元。
设两次降价的百分率都为x,则x满足(D)16(1+2x)=25.阳泉市平定县月考题目:共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆。
设该公司第二、三两个月投放单车数量的月平均增长率为x,则所列方程正确的为(A)1000(1+x)2=1000+440.巴中中考题目:巴中市某楼盘准备以每平方米5000元的均价对外销售,由于有关部门关于房地产的新政策出台后,部分购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4050元的均价开盘销售。
若两次下调的百分率相同,求平均每次下调的百分率。
解:设平均每次下调的百分率为x,根据题意,得5000(1-x)2=4050.解得x=10%。
广东中考题目:某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元。
求3月份到5月份营业额的月平均增长率。
解:设3月份到5月份营业额的月平均增长率为x,根据题意,得400×(1+10%)(1+x)2=633.6.解得x=20%。
1.2 市场经济问题泰安中考题目:某种花卉每盆的盈利与每盆的株数有一定的关系。
每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元。
要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是(A)(3+x)(4-0.5x)=15.达州中考题目:新世纪百货大楼“宝乐”牌童装平均每天可售出20件,每售出1件,价格就下降0.5元。
若该童装原价为10元/件,则在售完全部存货后,该童装的平均售价为(A) 9.5元/件。
为了迎接“六一”儿童节,商场决定采取适当的降价措施,每件童装盈利40元。
变化率问题举例

三、进行边际分析
【例3】
某厂生产某种产品,总成本c是产量x的函数 c(x)=200+4x+0.05x2,
求产量x=200时的边际成本. 解 因为c′(x)=(200+4x+0.05x2)′
=4+0.1x, 所以,当产量x=200时的边际成本为
c′(x)|x=200=4+0.1×200=24.
三、进行边际分析
变化率问题 举例
一、求非恒定电流的电流强度
由电学知识可知,恒定电流的电流强度是单位时间内通过 导体横截面的电量Q,即i=Q/t,而非恒定电流的电流强度就不 能按上述公式计算.
设非恒定电流通过导体横截面积的电量Q是时间t的函数, 即Q=Q(t),当时间由t0变到t0+Δt时,通过导体的电量由Q(t0) 变到Q(t0+Δt),此时的平均电流强度为
四、进行弹性分析
【例5】
设某商品的需求函数为Q=eห้องสมุดไป่ตู้p5(其中P是商品的价格 ,Q是商品的需求量),求: (1)需求弹性函数; (2)当P=3,P=5,P=6时的需求弹性,并说明其经济意义
.
四、进行弹性分析
第六节
函数的微分
引例1
一、引例
求自由落体运动中,物 体由时刻t到t+Δt所经过路程 的近似值.
设总成本函数c=c(q)是可导的,其中q表示产量,c表示总 成本,则产量为q的边际成本为
设定某种产品的单位售价为P(P不变),则总收入函数R(q)=P·q, 总利润函数 L(q)为
L(q)=R(q)-c(q)=P·q-c(q), 上式两边对q求导,有
L′(q)=R′(q)-c(q)=P-c′(q).
三、进行边际分析
变化的快慢与变化率

已知函数 f(x)=x2+x,计算 f(x)在区间[x0,x0+Δx]上的平均变化率, 并求当 x0=2,Δx=0.1 时平均变化率的值.
求函数 f(x)=-x2+3x 在 x=2 处的瞬时变化率.
当堂检测
1.求函数 y=-2x2+5 在区间[2,2+Δx]内的平均变化率. 2.一辆汽车按规律 s=3t2+1 做直线运动,估计汽车在 t=3 s 时,s 的 瞬时变化率.(时间单位:s;位移单位:m)
____t_2-__t1_____.
2.在刹车这一变化过程中,汽车行驶的速度 v 关于刹车时
间
t
的函数 v=v(t),从刹车开始 vt2-vt1
t=t1
到汽车停止
t=t2,汽车平
均减速_____t2_-__t1____.
3.已知函数 y=f(x),令 Δx=x2-x1,Δy=f(x2)-f(x1),则 当 Δx≠0 时,比值___f_x_x2_2--__fx_1x_1__=ΔΔxy,为函数 f(x)从 x1 到 x2 的 平均变化率,即函数 f(x)图像上两点 A(x1,f(x1))、B(x2,f(x2)) 连线的_斜__率__.
已知函数 f(x)=2x2+3x-5. (1)求当 x1=4,且 Δx=1 时,函数增量 Δy 和平均变化率ΔΔyx; (2)求当 x1=4,且 Δx=0.1 时,函数增量 Δy 和平均变化率ΔΔyx; (3)若设 x2=x1+Δx.分析(1)(2)题中的平均变化率的几何意义.
瞬时变化率
求函数y=f(x)=3x2+x在点x=1处的瞬时变化率.
瞬时变化率
对一般的函数 y=f(x),在自变量 x 从 x0 变化到 x1 的过程中, 若设fx1Δ-x=fxx10- x0,Δy=ffx(x0+1)-Δxf(-x0)f,x则0 函数的平均变化率为ΔΔyx= ____x_1_-__x_0______=_______Δ__x______.当 Δx 趋于 0 时,平均变 化率就趋于函数在 x0 点的瞬时变化率.
变化率问题举例

变化率问题举例前面我们从实际问题中抽象出了导数的概念,并利用导数的定义求一些函数的导数,这当然是很重要的一方面, 但另一方面,我们还应使抽象的概念回到具体的问题中去,在科学技术中常把导数称为变化率. 因为, 对于一个未赋予具体含义的一般函数)(x f y =来说x x f x x f x y ∆-∆+=∆∆)()(00是表示自变量x 在以0x 与x x ∆+0为端点的区间中每改变一个单位时,函数y 的平均变化量. 所以把x y∆∆称为函数)(x f y =在该区间中的平均变化率;把平均变化率当0→∆x 时的极限)('0x f 或0x x dx dy=称为函数0x 处的变化率. 变化率反映了函数y 随着自变量x 在0x 处的变化而变化的快慢程度. 显然,当函数有不同实际含义时,变化率的含义也不同. 如曲线上某一点处切线的斜率是曲线的纵坐标y 对横坐标x 的变化率;瞬时速度是物体位移s 对时间t 的变化率.下面我们通过实例来说明变化率在实际问题中的应用.一、变化率在工程技术上的几种常见类型例1 (电流模型)设在[0,t]这段时间内通过导线横截面的电荷为)(t Q Q =,求0t 时刻的电流.解 如果是恒定电流, 在t ∆时间段内通过导线横截面的电荷为Q ∆,那么它的电流为 t Q i ∆∆==时间电荷电流如果电流是非恒定电流,就不能直接用上面的公式求0t 时刻的电流,此时 t t Q t t Q t Q i ∆-∆+=∆∆=)()(00称为在t ∆这段时间内的平均电流.当t ∆很小时,平均电流i 的极限(如果极限存在),就称为时刻0t 的电流)(0t i ,即 )(')()(lim lim )(0000000t Q dt dQ t t Q t t Q t Q t i t t t t ==∆-∆+=∆∆==→∆→∆例2 (细杆的线密度模型)设一根质量非均匀分布的细杆放在x 轴上,在[0,x]上的质量m 是x 的函数m=m(x),求杆上0x 处的线密度.解 如果细杆质量分布是均匀的, 长度为x ∆的一段的质量为m ∆,那么它的线密度为x m ∆∆==长度质量ρ O如果细杆是非均匀的,就不能直接用上 面的公式求0x 处的线密度(如图2—3). 图2—3 设细杆[0,0x ]的质量m=m(x 0),在[0,x x ∆+0]的质量)(0x x m m ∆+=,于是在x ∆这段长度内,细杆的质量为)()(00x m x x m m -∆+=∆平均线密度为x x m x x m x m ∆-∆+=∆∆=)()(00ρ 当x ∆很小时,平均线密度ρ可作为细杆在0x 处的线密度的近似值,x ∆越小近似的程度越好.我们令0→∆x ,细杆的平均线ρ线的极限(如果极限存在),就称为细杆在0x 处的线密度,即)(')()(lim)(000000x m dx dm x x m x x m x x x x ==∆-∆+==→∆ρ例3 例3 (化学反应速度模型)在化学反应中某种物质的浓度N 和时间t 的关系为N=N(t)求在t 时刻该物质的瞬时反应速度.解 当时间从t 变到t t ∆+时,浓度的改变量为)()(t N t t N N -∆+=∆此时,浓度函数的平均变化率为t t N t t N t N ∆-∆+=∆∆)()(令0→∆t ,则该物质在t 时刻时瞬时反应速度为t t N t t N t N t N t t ∆-∆+=∆∆=→∆→∆)()(lim lim )('00二、变化率在经济分析中的应用(一)边际分析边际概念是经济学中的一个重要概念,一般指经济函数的变化率. 利用导数研究经济变量的边际变化的方法,称为边际分析法.边际分析法是经济理论中的一个重要方法.1.1.边际成本 在经济学中,边际成本定义为产量增加一个单位时所增加的成本. 设某产品产量为x 单位时所需的总成本为C=C(x),称C(x)为总成本函数,简称成本函数. 当产量由x 变为x x ∆+时,总成本函数的改变量为)()(x C x x C C -∆+=∆这时,总成本函数的平均变化率为x x C x x C x C ∆-∆+=∆∆)()(它表示产量由x 变到x x ∆+时,在平均意义下的边际成本.当总成本函数C (x )可导时,其变化率x x C x x C x C x C x x ∆-∆+=∆∆=→∆→∆)()(l i m l i m )('00表示该产品量为x 时的边际成本,即边际成本,即边际成本为成本函数关于产量的导数.2.2.边际收入 在经济学中,边际收入定义为多销售一个单位产品所增加的销售收入.设某产品的销售量为q 时的收入函数为)(q R R =.则收入函数关于销售量q 的导数就是该产品的边际收入)('q R .3.边际利润 设某产品的销售量为q 时的利润函数为)(q L L =,当)(q L 可导时,称)('q L 为销售量为q 时边际利润,它近似等于销售量为q 时再多销售一个单位产品所增加(或减小)的利润.由于利润函数为收入函数与总成本函数之差,即),()()(q C q R q L -=由导数运算法则可知).(')(')('q C q R q L -=即边际利润为边际收入与边际成本之差.例4 设某产品产量为q (单位:吨)时的总成本函数(单位:元)为.5071000)(q q q C ++=求:(1) 产量为100吨时的总成本;(2) 产量为100吨时的平均成本;(3) 产量从100吨增加到225吨时,总成本的平均变化率;(4) 产量为100吨时,总成本的变化率(边际成本).解(1)产量为100吨时的总成本为22001005010071000)100(=+⨯+=C (元).(2)产量为100吨时的平均成本为22100)100()100(==C C (元/吨).(3)产量从100吨增加到225吨时,总成本的平均变化率为912522003325100225)100()225(=-=--=∆∆C C q C (元/吨).(4)产量为100吨时,总成本的变化率即边际成本为|100)'5071000()100('=++=q q q C= 5.9257|100=⎪⎪⎭⎫ ⎝⎛+=q q (元).这个结论的经济含义是:当产量为100吨时,再多生产一吨所增加的成本为9.5元. 例5 设某产品的需求函数为p q 5100-=,求边际收入函数以及20=q 、50和70时的边际收入.解 收入函数为pq q R =)(,式中的销售价格p 需要从需求函数中反解出来,即)100(51q p -=,于是收入函数为,)100(51)(q q q R -=边际收入函数为 ),2100(51)('q q R -=.8)70(',0)50(',12)20('-===R R R由所得结果可知,当销售量即需求量为20个单位时,再增加销售可使总收入增加,再多销售一个单位产品,总收入约增加12个单位;当销售量为50个单位时,在增加销售总收入不会再增加;当销售量为70个单位时,再多销售一个单位产品,反而使总收入大约减少8个单位.(二)弹性分析弹性概念是经济学中的另一个重要概念, 用来定量地描述一个经济变量对另一个经济变量变化的反应程度, 或者说一个经济变量变动百分之一时会使另一个经济变量变动百分之几.弹性分析也是经济分析中常用的一种方法,主要用于对生产、供给、需求等问题的研究.给定变量,它在某处的改变量称作绝对改变量.给定改变量与变量在该处的值之比称作相对改变量.定义 对于函数)(x f y =,如果极限x x y y x //l i m 0∆∆→∆存在,则)('lim //lim00x f y x dx dy y x y x x y x x y y x x =⋅=⋅∆∆=∆∆→∆→∆ 称作函数)(x f 在点x 处的弹性,记作E ,即.dx dy y x E =从定义可以看出, 函数)(x f 的弹性是函数相对改变量与自变量相对改变量比值的极限,它是函数的相对变化率,或解释成当自变量变化百分之一时函数变化的百分数.由需求函数)(p Q Q =可得需求弹性为.dp dQ Q p E Q =需求弹性Q E 表示某商品需求量Q 对价格p 的变动的反应程度. 根据经济理论,需求函数是单调减少函数,所以需求弹性一般为负值.利用供给函数)(p S S =,同样定义供给弹性.dp dS S p E S =例6 例6 设某商品的需求函数为,300002.0p e Q -= 求价格为100时的需求弹性, 并解释其经济含义.解 )'3000(300002.002.0p p Q e e p dp dQ Q p E --⋅==)02.0()3000(300002.002.0-⋅⋅=--p p e e p p 02.0-= 所以 .2)100(-=Q E它的经济意义是:当价格为100时,若价格增加1%,则需求减少2%.。
1.1.1变化率问题与导数概念

法国《队报》网站的文章称刘翔以不可思议的速度 统治了赛场。这名21岁的中国人跑的几乎比炮弹还 快,赛道上显示的12.94秒的成绩已经打破了12.95 奥运会记录,但经过验证他是以12.91秒平了世界纪 录,他的平均速度达到8.52m/s。
1.1.1 变化率问题
问题1
吹气球
的值为-13.1 .
探1.运动员在某一时刻t0的瞬时速度 究 怎样表示? ?
瞬时速度,即是时间增量趋近于0时某一时刻的速度, 由极限的观点可知:当t 0, 时,
h t0Байду номын сангаас t h t0 瞬时速度为: lim t 0 t
2.函数f(x)在x=x0处的瞬时变化率怎样表示?
观 察 ?
当△t趋近于0时,平均 速度有什么样的变化趋 势?
我们发现:当△t趋近于0时,即无论t从 小于2的一边,还是从大于2的一边趋近 v 于2时,平均速度 都趋近于一个确定 的值-13.1。
从物理的角度看: 时间间隔| △t |无限变小时,平均速度 v 就无限趋近于t=2时的瞬时速度。 所以:运动员在t=2时的瞬时速度是-13.1m/s 为了表述方便,我们用:
令△x = x2 – x1 , △ y = f (x2) – f (x1) ,则
y f (x 2 ) f (x1 ) f (x 1 x) f (x 1 ) x x x 2 x1
问题: 平均变化率的几何意义是什么?
y f (x 2 ) f (x 1 ) x x 2 x1
y 及临近一点B(-1+Δx,-2+Δy), 则 =( x
)
A、3
B、3Δx-(Δx)2 D、3-Δx
C 、 3-(Δx)2
变化率 问题

(x1, f(x1)) A
x O x1 x2
问题2
这是某市2007年3月18日至4月20日每天最高气温 的变化图,
T (℃ )
C (34, 33.4) 30
20
10
B (32, 18.6)
A (1, 3.5) 10 20 30 34 t(d)
2 0 2
t=1到t=32与t=32到t=34这两段时间,哪段气温变化大?
例题讲解
小远从出生到第12个月的体重变化如图所示, 试分别计算小远从出生到第3个月与第6个月到 第12个月体重的平均变化率。 比较这两个时间段小远体重变化的快慢情况。
W(kg)
11 8(月)
例2 在高台跳水运动中,运动
员相对于水面的高度h(单位:
m)与起跳后的时间t(单位:s)
“形” 曲线“陡峭”程度
2.平均变化率的几何意义. 曲线上A、B两点连线的斜率。
“数” 平均变化率
已知函数 f ( x) x 2 ,分别计算 f ( x) 在下列区 间上的平均变化率:
(1)[1,3];
(2)[1,2]; (3)[1,1.1]; (4)[1,1.001]。
4
3 2.1
2.001
34 t(天)
(1)t=32到t=34这两天的温差达到了多少?
(2)t=1到t=32与t=32到t=34这两段时间,哪段气温变化大?
定义:
f ( x2 ) - f ( x1 ) 平均变化率: 式子 x2 - x1
称为函数 f (x)从x1到 x2的平均变化率.
令△x = x2 – x1 , △ y = f (x2) – f (x1) ,则
存在函数关系 h(t)=-4.9t2+6.5t+10. 分别计算运动员在0到0.5秒时 间段,1秒到2秒时间段,以及 65 时间段内的平均 0到 秒 49 速度. (1)运动员在这段时间里是静止的吗?
变化率问题
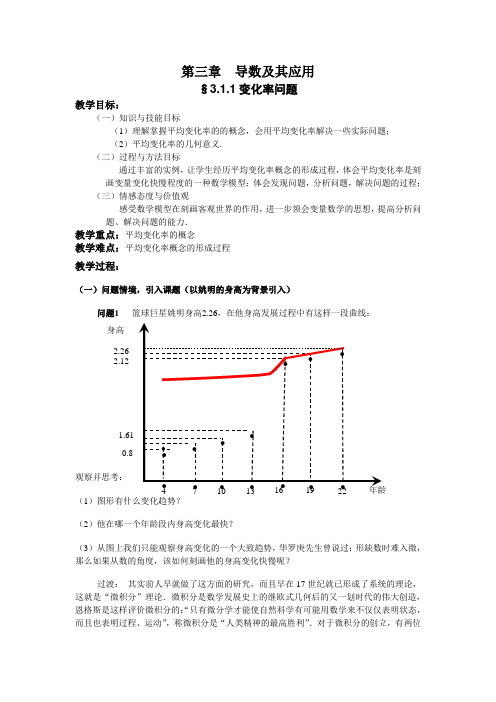
第三章 导数及其应用§3.1.1变化率问题教学目标:(一)知识与技能目标(1)理解掌握平均变化率的的概念,会用平均变化率解决一些实际问题;(2)平均变化率的几何意义.(二)过程与方法目标通过丰富的实例,让学生经历平均变化率概念的形成过程,体会平均变化率是刻 画变量变化快慢程度的一种数学模型;体会发现问题,分析问题,解决问题的过程;(三)情感态度与价值观感受数学模型在刻画客观世界的作用,进一步领会变量数学的思想,提高分析问 题、解决问题的能力.教学重点:平均变化率的概念教学难点:平均变化率概念的形成过程 教学过程:(一)问题情境,引入课题(以姚明的身高为背景引入)问题1 篮球巨星姚明身高2.26,在他身高发展过程中有这样一段曲线:观察并思考: (1)图形有什么变化趋势? (2)他在哪一个年龄段内身高变化最快?(3)从图上我们只能观察身高变化的一个大致趋势,华罗庚先生曾说过:形缺数时难入微,那么如果从数的角度,该如何刻画他的身高变化快慢呢?过渡: 其实前人早就做了这方面的研究,而且早在17世纪就已形成了系统的理论,这就是“微积分”理论.微积分是数学发展史上的继欧式几何后的又一划时代的伟大创造,恩格斯是这样评价微积分的:“只有微分学才能使自然科学有可能用数学来不仅仅表明状态,而且也表明过程、运动”,称微积分是“人类精神的最高胜利”.对于微积分的创立,有两位2.26 2.12 ● ● ● ● ● ● 年龄身高 4 710 13 16 ● 19 22 0.8 1.61 ● ● ●● ● ● ●科学家做出了重大的贡献:牛顿和莱布尼兹。
今天我们一起来学习微积分的基础:导数的概念第一课——变化率问题.(板书课题) 变化率问题主要是研究变量变化快慢程度(二)实例分析,探究概念 1、身高变化率我们先来看看有没有什么办法解决问题1中的最后一个问题:如何从数的角度刻画他身高 变化快慢,也就是身高的变化率?刚才通过我们对图形的观察发现,在[13,16]里曲线最陡,其他两段比较平缓如果我们将这段曲线近似的看成直线段,我们是如何刻画直线的倾斜程度的?——直线的斜率,那么我们是否可以用同样的方法来刻画一下身高的变化率呢?计算:在[13,16]这个年龄段里,身高的变化率:17.0131661.112.2=--=年龄的差值身高的差值(米/年) 那么这个年龄段的最陡,比值算出来是0.17(米/年),其他两端稍微平缓一些,也请同学们计算一下[4,13]这个年龄段里,比值是09.04-138.0-61.1=(米/年) [16,22]这个年龄段里,比值是023.061-22.122-.262≈(米/年) 从三个比值可以看出,13—16岁这个年龄段比值最大,从图形上看这个是最陡的,所以我们从形和数两个方面都予以了刻画,形上,这个年龄段最陡;数上,这个年龄段比值最大。
高中数学第一章导数及其应用1.1.1变化率问题1.1.2导数的概念课件新人教A版选修22072113

1.1.1 变化率问题(wèntí) 1.1.2 导数的概念
第一页,Байду номын сангаас32页。
学习目标
1.了解(liǎojiě)导数概念的实际背景. 2.会求函数在某一点附近的平均变化率. 3.会利用导数的定义求函数在某点处的导数.
问题(wèntí) 导学
题型探究 (tànjiū)
解析(jiě xī)
1 2345
2.物体自由落体的运动方程为 s(t)=12gt2,g=9.8 m/s2,若 v=
s1+Δt-s1
lim
Δx→0
Δt
=9.8 m/s,那么下列说法中正确的是( C )
A.9.8 m/s是物体(wùtǐ)从0 s到1 s这段时间内的速率
B.9.8 m/s是1 s到(1+Δt)s这段时间内的速率
简记(jiǎn jì)为一差,二比,三极限.
特别提醒 ①取极限前,要注意化简 ,Δy保证使Δx→0时分母不为0. Δx
②函数在x0处的导数f′(x0)只与x0有关,与Δx无关.
③导数可以描述任何事物的瞬时变化率,应用非常广泛.
第三十二页,共32页。
返回
x4]这几个(jǐ ɡè)区间内,平均变化率最大的一个区
间是________. [x3,x4]
解析 由平均变化率的定义可知,函数y=f(x)在区间[x1,x2],[x2,x3],[x3,
x4]上平均变化率分别为
fxx22--fx1x1,fxx33--fx2x2,fx结x44- -合(fxj3ixé3h,é)图象可
解 割线PQ的斜率(xiélǜ)即为函数f(x)从1到1+Δx的平均变化ΔΔ率yx . ∵Δy=f(1+Δx)-f(1)=(1+Δx)2-(1+Δx)-(12-1)=Δx+(Δx)2, ∴割线PQ的斜率k= Δ=y 1+Δx.
1.1.1和1.1.2变化率问题、导数的概念课件人教新课标1

【解析】(1)自变量x从1变到2时,函数f(x)=2x+1的函数值的
增量为Δy=5-3=2,故增量之比是2.
答案:2
(2)函数f(x)=x2在x=1处的瞬时变化率是 lim f (1 x) f (1)
x0
x
lim (1 x)2 12 lim (2 x) 2.
x0
x
x0
答案:2
(3)函数y=f(x)= 1 在x=-1处的导数可表示为f′(-1)或
【微思考】
(1)函数f(x)在区间[x1,x2]上的平均变化率的大小与曲线 y=f(x)在区间[x1,x2]上的“峻峭”程度有什么关系? 提示:平均变化率的绝对值越大,曲线y=f(x)在区间[x1,x2]
上越“峻峭”,反之亦然. (2)平均变化率可以是零吗? 举例说明. 提示:可以是零,如函数f(x)=a(a为常数).
Δx趋于0的距离要多近有多近,即|Δx-0|可以小于给定的任
意小的正数,且始终Δx≠0.
3.对导数概念的两点说明
(若1)当xy 的Δ极x≠限0不时存,在比,值则xyf的 (x极)在限点存x在0处,不则可f导(x或)在无点导x数0处.可导;
(2)在点x=x0处的导数的定义可变形为f′(x0)=
lim f (x0 x) f (x0 )
取定值,x1取不同的数值时,函数的平均变化率也是不同的.
特别地,当函数f(x)为常数函数时,Δy=0,则 y =0.
x
2.对平均变化率的三点说明 (1)y=f(x)在区间[x1,x2]上的平均变化率是曲线y=f(x)在 区间[x1,x2]上峻峭程度的“数量化”,曲线峻峭程度是平 均变化率的“视觉化”. (2)平均变化率的几何意义就是函数y=f(x)图象上两点P1(x1,
sect;1.1.1—2变化率问题、导数的概念

§1.1.1—2变化率问题、导数的概念※ 典型例题[解析]0000000()()[()]()lim lim ()()x x f x x f x f x x f x f x x x ∆→∆→-∆-+-∆-'=-=-∆-∆.故选B1. 解:B 计算0lim x ∆→(1)(1)s s t s tt∆+∆-=∆∆即可2. 【解题思路】计算连续函数()y f x =在点0x x =处的瞬时变化率实际上就是()y f x =在点0x x =处的导数.:解析:加速度v =tt ts t s t t ∆-∆+=∆-∆+→∆→∆225)5(lim )5()5(limlim →∆=t (10+Δt )=10 m /s.※ 当堂检测:1. B2. B3. C4. 18 ;5. 1 ;6..3 ;一、选择题 1.[答案] C[解析] 由定义,f ′(x 0)是当Δx 无限趋近于0时,Δy Δx 无限趋近的常数,故应选C.2.[答案] B[解析] ∵f (x )=x 2,x =1, ∴Δy =f (1+Δx )2-f (1)=(1+Δx )2-1=2·Δx +(Δx )2 ∴Δy Δx =2+Δx 当Δx →0时,ΔyΔx →2 ∴f ′(1)=2,故应选B. 3.[答案] D[解析] ∵Δs Δt =4(5+Δt )2-3-4×52+3Δt=40+4Δt ,∴s ′(5)=li m Δt →0 ΔsΔt =li m Δt →0 (40+4Δt )=40.故应选D.4.[答案] C[解析] 由导数的定义可知C 错误.故应选C. 5.[答案] D[解析] 当f (x )=b 时,f ′(x )=0,所以f (x )的图象为一条直线,故应选D.6.[答案]C [解析] li m x →a f (x )-f (a )x -a=li m x →a 1x -1ax -a=li m x →aa -x (x -a )·xa =-li m x →a 1ax =-1a2二、填空题7.[答案] -11,-112[解析] li m Δx →0f (x 0-Δx )-f (x 0)Δx=-li m Δx →0f (x 0-Δx )-f (x 0)-Δx=-f ′(x 0)=-11;li m x →x 0f (x )-f (x 0)2(x 0-x )=-12m Δx →0 f (x 0+Δx )-f (x 0)Δx=-12f ′(x 0)=-112.8. [答案] 0[解析] ∵Δy =⎝⎛⎭⎫1+Δx +11+Δx -⎝⎛⎭⎫1+11=Δx -1+1Δx +1=(Δx )2Δx +1,∴Δy Δx =Δx Δx +1.∴y ′|x =1=li m Δx →0 ΔxΔx +1=0.三、解答题9.[解析] 由导数定义有f ′(x 0)=li m Δx →0 f (x 0+Δx )-f (x 0)Δx =li m Δx →0(x 0+Δx )2-x 20Δx =li m Δx →0Δx (2x 0+Δx )Δx=2x 0,10.解析] 位移公式为s =12at 2∵Δs =12a (t 0+Δt )2-1220=at 0Δt +12(Δt )2∴Δs Δt =at 0+12Δt , ∴li m Δt →0Δs Δt =li m Δt →0 ⎝⎛⎭⎫at 0+12a Δt =at 0,已知a =5.0×105m/s 2,t 0=1.6×10-3s , ∴at 0=800m/s.所以枪弹射出枪口时的瞬时速度为800m/s.11.[解析] (1)Δy Δx =f (1+Δx )-f (1)Δx=(1+Δx )2+3-12-3Δx=2+Δx .(2)f ′(1)=lim Δx →0f (1+Δx )-f (1)Δx=lim Δx →0(2+Δx )=2.§1.1.3导数的几何意义※ 典型例题【解题思路】:点P 在函数的曲线上,因此过点P 的切线的斜率就是y '在1=x 处的函数值; 点Q 不在函数曲线上,因此不能够直接用导数求值,要通过设切点的方法求切线.切忌直接将P ,Q 看作曲线上的点用导数求解。
(名师整理)最新北师大版数学9年级上册第2章第6节《应用一元二次方程求解增长率、市场营销问题》精品课件

表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百
分率的 3 倍.设王老师第二次锻炼时平均步长减少的百分率为 x(0<x<0.5).
项目 步数(步) 平均步长(米/步) 距离(米) (1)根据题意完成表格填空;
第一次锻炼 10 000 0.6 6000
第二次锻炼 ① ②
7020
• 3.为了解决老百姓看病难的问题,卫生部门 决定下调药品的价格.某种药品经过连续两 次降价后,由每盒100元下调至64元,这种 药品平均每次降价的百分率是_______.
7
• 4.【广东广州中考】随着粤港澳大湾区建设的加速推进, 广东省正加速布局以5G等为代表的战略性新兴产业.据统 计,目前广东5G基站的数量约1.5万座,计划到2020年底, 全省5G基站数是目前的4倍,到2022年底,全省5G基站数 量将达到17.34万座.
的平均增长率是( )
• A.8%
B.9%
• C.10% D.11%
6
• 2.某商场将进货价为30元的台灯以40元售 出,平均每月能售出600个.这种台灯的售 价每上涨1元,其销售量(40就+x将-3减0)(6少00-1100x)个=1.0 00为0 了实现平均每月10 000元的销售利润,若设 每个台灯涨价为x元,则可列方程 _20_%______________________________.
. • (2)设该农场在第三、第四季度产值的平均下降的百分率为x.
根据题意,得该农场第四季度的产值为60-11.4=48.6(万 元).列方程,得60(1-x)2=48.6.解得x1=0.1,x2=1.9(不 符题意,舍去).即该农场在第三、第四季度产值的平均下 降的百分率为10%.
12
课件3:1.1.1 函数的平均变化率

C.0.43
D.0.44
解析:Δy=f(2+0.1)-f(2)=2.12+1-(22+1)=0.41.
答案:B
2.物体按照s(t)=3t2+t+4的规律作直线运动,求在 4到4+Δt之间的平均速度v. 解:Δs=s(4+Δt)-s(4) =3(4+Δt)2+(4+Δt)+4-(3×42+4+4) =25Δt+3(Δt)2. ∴v=ΔΔst=25+3Δt. 即物体在 4 到 4+Δt 之间的平均速度为 25+3Δt.
提示:从20 min到30 min变化快. 问题2:如何刻画体温变化的快慢? 提示:用平均变化率. 问题3:平均变化率一定为正值吗? 提示:不一定.可正,可负,可为零.
知识点解读
平均变化率
(1)定义:对一般的函数 y=f(x)来说,当自变f量(x2x)-从f(xx21)变为 x2 时,函数值从 f(x1)变为 f(x2),它的平均变化率为. x2-x1
其中自变量的变化 x2-x1 称作自变量的改变量,记作Δx ,
函数值的变化 f(x2)-f(x1) 称作函数值的改变量,记作Δy .这样,
函数的平均变化率就可以表示为函数值的改变量与自变量的改变
f(x2)-f(x1)
量之比,即ΔΔxy=
x2-x1 .
(2)作用:刻画函数值在 区间[x1,x2] 上变化的快慢.
瞬时变化率
(1)定义:对于一般的函数 y=f(x),在自变量 x 从 x0 变到 x1
的过程中,设 Δx=x1-x0,Δy=f(x1)-f(x0),则函数的平均变化
率是ΔΔxy=
fx1-fx0 = x1-x0
fx0+Δx-fx0 Δx
.而当 Δx趋于0
时,平
均变化率就趋于函数在 x0 点的瞬时变化率.
1.1变化率问题2

9
1.1变化率与导数
2013-1-26
用平均变化率逼近瞬时变化率(导数)
若y f ( x), 则函数y f ( x)在x x0时的 瞬时变化率该如何表示?
f ( x0 ) y
'
'
f ( x0 x) f ( x0 ) y lim lim |x x0 x0 x0 x x
y f ( x)
f ( x2 ) f ( x1 )
y f ( x)
f ( x2 ) f ( x1 ) x2 x1 x1 x 2
O
x1
x2
x
O
x
13
1.1变化率与导数
2013-1-26
'
切点处导数,切线斜率
k y |x x0 f ' ( x0 )
例1 : 求曲线f ( x) x 2 1在点P(1,)处的切线方程. 2
16
'
1.1变化率与导数
'
2013-1-26
f ( x x) f ( x) 导(函)数 f ( x) y lim x 0 x
从求函数f ( x)在x x0处求导数的过程可以看 到f ( x)是一个确定的数,那么当x变化时,f ( x)
' '
便是x的一个函数,我们称它为f ( x)的导函数, 记作f ( x)或y .
f ' (2) 3 说明原油温度大约以30C/h的速度下降;
f (6) 5
'
说明原油温度大约以50C/h的速度上升。
12
1.1变化率与导数
2013-1-26
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( x从 ) x1到x2的平均变化率.
,则平均变化率为
x2 x1 , y f ( x2 ) f ( x1 )
y f ( x2 ) f ( x1 ) f ( x1 x) f ( x1 ) x x2 x1 x
△x看作是对于x1的一个“增量”可用x1+Δx代替x2
2 01
10
20 主页
30
34
t(d)
§1.1.1 变化率问题
T (℃ ) 30
C (34,33.4)
B(32,18.6)
10
(3月18日 为第一天)
A(1,3.5)
2 01
10
20
30
34
t(d)
【问题1】分别计算AB, BC段温差 15.10C, 14.80C 结论: 气温差不能反映气温变化的快慢程度. 【问题2】如何“量化”(数学化)曲线上升的陡峭程度? 曲线AB、BC段几乎成了“直线” , 由此联想如何量化直线的倾斜程度?
导数是微积分的核心概念之一它是研究函 数增减、变化快慢、最大(小)值等问题 最一般、最有效的工具。
主页
§1.1.1 变化率问题
第一课时 函数的平均变化率
研究某个变量相对于另一个变量变化在一个范围内的快 慢程度.
主页
§1.1.1 变化率问题
一、研究课本问题1及问 题2,体会平均变化率及 其意义,思考怎样抽象到 一般函数?
主页
§1.1.1 变化率问题 若设 则平均变化率为 x x2 x1 , y , f ( x2 ) f ( x1 )
y f ( x2 ) f ( x1 ) f ( x1 x) f ( x1 ) x x2 x1 x
它的几何意义是什么呢? 观察函数 y f ( x) 图象
主页
§1.1.1 变化率问题
回答P73之探究
主页
§1.1.1 变化率问题
将两个具体问题抽 象到一般函数的平 均变化率。
主页
§1.1.1 变化率问题
平均变化率定义:
当自变量
对于函数
时,函数值就从 y1 变化到 y , x从x1变化到x2 2
y f ( x)
则
称为函数 f 若设 x
f ( x2 ) f ( x1 ) x2 x1
§1.1.1 变化率问题
第三章 导数及其应用
沿河民族中学:阚 辉
主页
§1.1.1 变化率问题
微积分主要与四类问题的处理相关:
• 一、已知物体运动的路程作为时间的函数, 求物体在任意时刻的速度与加速度等; • 二、求曲线的切线; • 三、求已知函数的最大值与最小值; • 四、求长度、面积、体积和重心等。
主页
§1.1.1 变化率问题
T (℃ ) 30
B(32,18.6)
C (34,33.4)
yC yB 比值 xC xB
近似地量化BC这一段曲 线的陡峭程度,并称该比 值为气温在 [32,34] 上的 平均变化率.
10
A(1,3.5)
2 01
10
20
30
34
t(d)
【问题3】分别计算气温在区间[1,32] ,[32, 34]的平 均变化率. 0.5, 7.4
1、平均变化率
一般的,函数 f ( x)在区间上
[ x1,x 2 ]的平均变化率为
f ( x1 ) f ( x2 ) x1 x2
2、平均变化率是曲线陡峭程度的“数量化”,是一种粗 略
的刻画
主页
§1.1.1 变化率问题
主页
人教A版选修2-2《导数及其应用》变化率与导数
1.1.1 平 均 变 化 率
y f(x2) B f(x2)-f(x1)=△y
直线AB的斜率
f(x1) O
A x2-x1=△x x x1 x2
主页
§1.1.1 变化率问题
平均变化率的 计算与应用
主页
§1.1.1 变化率问题
例1 : 求函数 y sin x在0到 和 到 之间的平均变化率 6 3 2
主页
§1.1.1 变化率问题
V
V
气球平均膨胀率=
r (V2 ) r (V1 ) V2 V1
3
3V2 3 3V1 4 4 V2 V1
主页
§1.1.1 变化率问题
问:平均膨胀率能否精确描述膨 胀情况?
主页
§1.1.1 变化率问题 问题2 高台跳水 在高台跳水运动中,运动员相对于水面 的高度h(单位:米)与起跳后的时间t(单位 :秒)存在函数关系h(t)=-4.9t2+6.5t+10.
4 3 V (r ) r 3
3 V r (V ) 3 4
气球平均膨胀率=
半径的增量
体积的增加量
主页
§1.1.1 变化率问题
当V从0增加到1时,气球半径增加了
r (1) r (0) 0.62(dm)
气球的平均膨胀率为
r (1) r (0) 0.62(dm / L) 1 0
主页
§1.1.1 变化率问题 问题1 气球膨胀率 我们都吹过气球. 思考:这一过程中,哪些量在改 变?
从吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半 径增加越来越慢.
从数学角度,如何描述这种现象呢?
主页
§1.1.1 变化率问题
体会实际问题数学化
主页
§1.1.1 变化率问题 气球体积:
§1.1.1 变化率问题
某市2008年4月20日最高气温为33.4℃,而4月19日和 4月18日的最高气温分别为24.4℃, 和18.6℃,短短两天 时间,气温陡增14.8℃,闷热中的人们无不感叹:“天 气热得太快了!”
T (℃ )
C (34,33.4)
30
B(32,18.6)
10
A(1,3.5)
丰富多彩的变化率问题随处可见,让我们从其 中的两个问题,开始变化率与导数的学习吧!
显然 0.62>0.16
当V从1增加到2时,气球半径增加了 r (2) r (1) 0.16(dm) 气球的平均膨胀率为
r (2) r (1) 0.16(dm / L) 2 1
随着气球体积逐渐变大,它的平均膨胀率逐渐变小
主页
Байду номын сангаас
§1.1.1 变化率问题 思考 当空气容量从 1 增加到 2时,气球的平均膨胀率是多少?
14
h
12
10
8
6
4
如何用运动员在某些时 间段内的平均速度粗略地描 述其运动状态?
-20 -15 -10 -5
2
o t
5
平均速度:物体的运动位移与所用时间的比称为平均速度。 -2
-4
主页
§1.1.1 变化率问题 h(t)=-4.9t2+6.5t+10
请计算 0 t 0.5和1 t 2时的平均速度v :
