相似专题三一线三等角相似模型
相似专题:一线三等角模型

由于角顶点位置的改变,或角绕顶点旋转会产生各 种各样的变式,但万变不离其宗: 都是构造相似三角形列比例式解决问题.
常见类型
考题赏析:
考题赏析
应用举例
应用举例.
2、当等角所对的边相等时的两个三角形全等. 如图,当CE=ED时,易得△AEC≌△BDE.
3、“中点型一线三等角”的特殊性质
如图,当∠1=∠2=∠3且D是BC中点时, △BDE∽△CFD∽△DFE.
四、一线三等角的常见构图(以等腰三角形为例)
A与E重合时如图所示
也可以在射线上
点D也可以在线段 BC外面
练习中的问题:
相似专题复习 :
合肥实验学校 孙红涛
引例
已知相邻两条平行线间距离相等,若等腰直角三角形顶 点分别在三条平行线上,则sinα =
C
a
B
起源
二、“一线三等角”的两种基本类型
1.三等角都在直线的同侧
2.三等角分居直线的两侧
三、“一线三等角”的性质
1.一般情况下,由∠1=∠2=∠3易得△AEC∽△BDE.
一线三等角中点相似模型证明

一线三等角中点相似模型证明在初中数学学习中,一线三等角中点相似模型是一个重要的知识点。
它不仅是数学学科中的基础概念,也是日常生活中的实用知识型模型。
一线三等角中点相似模型包含了三个关键要素,即一线、三等角和中点相似。
其中,一线指在一个三角形中连接两个角的线段,三等角指三角形中三个角的度数相等,中点相似则是指两个图形中对应线段的长度相等。
理解这个模型需要我们首先了解一些基础概念。
在三角形中,连接一个角的两边的线段称为这个角的平分线,平分线的中点称为这个角的顶点角平分线中点。
而三角形中线则是一条连接两个角的中点的线段。
在一个三角形中,三个顶点连成一条线段即为三角形的一条边。
有了这些基础概念之后,我们可以开始理解一线三等角中点相似模型的证明过程。
在证明这个模型时,我们需要使用到的基本公式是:在一个三角形中,连接一个角的两边的长度的比等于另外一个角的两边的长度的比,那么这个角的平分线上任意一点到两边的距离之比等于这两边的长度之比。
首先,证明一线三等角中点相似模型的前提是三角形ABC和DEF中,∠A=∠D,∠B=∠E,∠C=∠F。
我们需要构造中线DG与CB、EH与AC的交点K,LK为EF的平行线,并证明LK=AB/BG=AC/CH。
我们先考虑LK=AB/BG的证明。
因为LK∥EF,我们可以通过小学奥数中的对应角相等的定理,得出∠LBL~∠ABC,∠LKF~∠ACB。
由于LK是EF的平行线,所以LK=EF×BL/AC=AB/BG,得证。
接下来,我们需要证明LK=AC/CH。
由于AC是三角形ABC的中线,所以AC=2CH。
而LK=EF×BL/AC,因为∠LBL~∠ABC,所以BL=AC/AB。
代入LK中得LK=EF/AB×AC/CH=AC/CH,得证。
综上可知,LK=AB/BG=AC/CH,所以三角形ABC与DEF是相似的。
由于ABC与DEF相似,因此它们的相应线段比例相等。
因为CB与EF平行且有相同比例,在DG与EH交于K的情况下,由于ABC与DEF相似,所以三角形ABE与CDG也相似。
专题 相似三角形一线三等角模型(老师版)

专题04相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.例1.(2023·浙江·九年级专题练习)如图①,在等边三角形ABC中,点D是边BC上一动点(不与点B,C重合),以AD为边向右作等边△ADE,边DE与AC相交于点F,设BD=x,CF=y,若y与x的函数关系的大致图象如图②所示,则等边三角形ABC的面积为()A.3B.5C.2【答案】C,设90DFN DNF ∠+∠=︒MFH ∠90D MHD ∠=∠=︒在MFH MF MH FH 【答案】(1)见解析;(2)成立;理由见解析;(3)5【分析】(1)由90DPC A B ∠=∠=∠=︒可得ADP BPC ∠=∠,即可证到ADP BPC ∽即可解决问题;(2)由DPC A B α∠=∠=∠=可得ADP BPC ∠=∠,即可证到ADP 性质即可解决问题;(3)证明ABD DFE ∽△△,求出4DF =,再证EFC DEC ∽△△(1)如图2,在53⨯个方格的纸上,小正方形的顶点为格点、边长均为1,AB 为端点在格点的已知线段.请用三种不同连接格点.....的方法,作出以线段AB 为等联线、某格点P 为等联点的等联角,并标出等联角,保留作图痕迹;图3,在Rt APC △中,90A ∠=,AC AP >,延长AP 至点B ,使AB AC =,作A ∠的等联角,⊥(2)①PCF是等腰直角三角形.理由为:如图,过点C作CN BE由折叠得AC CM =,90CMP CME A ︒∠==∠=,12∠=∠AC AB =,A PBD N ∠︒=∠=∠,∴四边形ABNC 为正方形CN AC CM∴=又CE CE =,()Rt HL CME CNE ∴≌△34∴∠=∠,而12390∠+∠+∠+︒,90CPF ∠=︒例5.(2022·浙江·嘉兴一中一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①:在△ABC 中,∠ACB =90°,AC =BC ,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:△ADC ≌△CEB .(1)探究问题:如果AC ≠BC ,其他条件不变,如图②,可得到结论;△ADC ∽△CEB .请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线y =12x 与直线CD 交于点M (2,1),且两直线夹角为α,且tanα=32,请你求出直线CD 的解析式.(3)拓展应用:如图④,在矩形ABCD 中,AB =4,BC =5,点E 为BC 边上一个动点,连接AE ,将线段AE 绕点E 顺时针旋转90°,点A 落在点P 处,当点P 在矩形ABCD 外部时,连接PC ,PD .若△DPC 为直角三角形时,请你探究并直接写出BE 的长.【答案】(1)见解析(2)41577y x =-+(3)4或372+【分析】(1)由同角的余角相等可得∠BCE =∠DAC ,且∠ADC =∠BEC =90°,可得结论;(2)过点O 作ON ⊥OM 交直线CD 于点N ,分别过M 、N 作ME ⊥x 轴NF ⊥x 轴,由(1)的结论可得:△NFO ∽△OEM ,可得NF OF NO OE ME MO==,可求点N 坐标,利用待定系数法可求解析式;(3)分两种情况讨论,由全等三角形的性质和相似三角形的性质可求解.(1)解:理由如下,∵∠ACB =90°,∴∠ACD +∠BCE =90°,又∵∠ADC =90°,∴∠ACD +∠DAC =90°,∴∠BCE =∠DAC ,且∠ADC =∠BEC =90°,∴△ADC ∽△CEB ;(2)解:如图,过点O 作ON ⊥OM 交直线CD 于点N ,分别过M 、N 作ME ⊥x 轴,NF ⊥x 轴,由(1)可得:△NFO ∽△OEM ,∴NF OF NO OE ME MO==,∵点M (2,1),∴OE =2,ME =1,∵tanα=ON OM =32,∴3212NF OF ==,∴NF =3,OF =32,∴点N (32-,3),∵设直线CD 表达式:y =kx +b ,∴12332k b k b =+⎧⎪⎨=-+⎪⎩∴47157k b ⎧=-⎪⎪⎨⎪=⎪⎩∴直线CD 的解析式为:y =-47x +157;(3)若点D在BC的反向延长线上运动,是否存在点D,使∵D 和B 不重合,∴45AED ∠<︒,又45ADE ∠=︒,90DAE ∠>︒,∴AD AE ≠≠DE .FE ;(2)若3,4AB AD ==16∵3,4AB AD ==,∴BD AB =∵DF AE ⊥,∴12ABD S AB =△∴341255AB AD AF BD ⋅⨯===,∴1695BF BD DF =-=-=,∵A .()9,3B .(9,2【答案】D 【分析】过C 作CE ⊥x 轴于E ,根据矩形的性质得到而得出△BCE ∽△ABO ,根据相似三角形的性质得到结论.【详解】解:过C 作CE ⊥x 轴于∵四边形ABCD 是矩形,∴CD=AB ∴∠ABO+∠CBE=∠CBE+∠BCE=90°∵90AOB BEC ∠=∠=︒,∴△∴CE CB BE BO AB AO==,∵4OB =∵AB=2BC ,∴BC=1AB=4,∵=4.(2021·浙江台州·中考真题)如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=_____.【答案】54【分析】先证明ABF GAE ∽,得到AB BF GA AE =,进而即可求解.【详解】∵在正方形ABCD 中,AF ⊥EG ,∴∠AGE +∠GAM =90°,∠FAB +∠GAM =90°,∴∠FAB =∠AGE ,又∵∠ABF =∠GAE =90°,∴ABF GAE ∽,∴AB BF GA AE =,即:5511BF =-,∴BF =54.故答案是:54.【点睛】本题主要考查正方形的性质,相似三角形的判定和性质,证明ABF GAE ∽,是解题的关键.5.(2023·浙江九年级专题练习)如图,ABC 为等边三角形,点D ,E 分别在边AB ,AC 上,3BD =,将ADE V 沿直线DE 翻折得到FDE V ,当点F 落在边BC 上,且4BF CF =时,DE AF ⋅的值为.【答案】9833【分析】根据△ABC 为等边三角形,△ADE 与△FDE 关于DE 成轴对称,可证△BDF ∽△CFE ,根据BF =4CF ,可得CF =4,根据AF 为轴对称图形对应点的连线,DE 为对称轴,可得DE ⊥AF ,根据S 四边形ADFE =12DE AF ⋅=S △CEF =-S △ABC -S △CEF ,进而可求9833DE AF ⋅=.【详解】解:如图,作△ABC 的高AL ,作△BDF 的高DH ,DAE的函数关系式△∽△(1)求证:ABF FCE【答案】(1)见解析(2)CE长为【分析】(1)根据矩形的性质得到用角之间的互余关系推出(1)求证:BEG CDE△∽△;(2)求AFG 【答案】(1)证明见解析(2)9【分析】(1)先根据正方形的性质可得证;90 NAF CAD∠+∠= ANE DCE∠=∠,D D∠=∠,EDC∴∴343DE=,DE∴【解决问题]若点D是BC边上任意一点时,上述结论是否成立,请说明理由.(3)【拓展探究】在整个运动过程中,请直接写出N点运动的路径长,及CN的最小值.,(1)若正方形ABCD的边长为2,E是AD的中点.①如图1,当FEC∠=②如图2,当2tan3FCE∠=时,求AF的长;(2)如图3,延长CF,DA交于点证:AE AF=.【答案】(1)①详见解析;②6AF=(2)详见解析①90ADC BAD FEC∠=∠=︒,∴AEF CED∠+∠AEF ECD∴∠=∠,AEF DCE∽△,②如图,延长DA交于点G,作GH CE⊥,垂足为且CED GEH∠=∠,CED∴△2,1CD DE==,5CE∴=,5290EDC EHG ∠=∠=︒设,AD CD a GE DE ===x y t t a n ∴==,2,t x n ∴=在Rt CHG △中,sin FCE ∠①请按要求画图:将ABC 绕点A 顺时针方向旋转90︒,点B 的对应点为点B ',点C 的对应点为点②在①中所画图形中,AB B '∠=______︒.【问题解决】如图2,在Rt ABC △中,190BC C =∠=︒,,延长CA 到D ,使1CD =,将斜边90︒到AE ,连接DE ,求ADE ∠的度数.②由作图可知,AB AB '=,90BAB '∠=︒∴'ABB 是等腰直角三角形,∴45AB B '∠=︒,故答案为:45;【问题解决】如图2中,过点E 作EH CD ⊥交CD 的延长线于H .∵90C BAE H ∠=∠=∠=︒,∴90B CAB ∠+∠=︒,90CAB EAH ∠+∠=︒,∴B EAH ∠=∠,∵AB AE =,∴()AAS ABC EAH ≌,∴BC AH EH AC ==,,∵BC CD =,∴CD AH =,∴DH AC EH ==,∴45EDH ∠=︒,∴135ADE ∠=︒.【拓展延伸】如图3中,连接AC ,∵AE BC BE EC ⊥=,,即AE 垂直平分BC ,∴AB AC =,将ABD △绕点A 逆时针旋转得到ACG ,连接DG .则BD CG =,∵BAD CAG ∠=∠,∴BAC DAG ∠=∠,∵AB AC AD AG ==,,∴ABC ACB ADG ∠∠∠===∴ABC ADG ∽△△,∵2=AD AB ,∴24DG BC ==,(1)如图1,求直线AB 的解析式.(2)如图2,线段OA 上有一点C ,直线BC 为2(0)y kx k k =-<,AD y ⊥轴,将BC 绕点B 顺时针旋转∵DA y ⊥轴,∴90DAO AOB DHO ∠=∠=∠=∴四边形DAOH 为矩形,∴2DH AO OB ===,由题可得,90CBD ∠=︒,∴90CBO DBH ∠+∠=︒,又∵90DBH BDH ∠+∠=︒,∴CBO BDH ∠=∠,在CBO 与BDH △中,90COB BHD OB HD CBO BDH ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,∴(ASA)CBO BDH ≌,∴CO BH =,令0x =,则22y kx k k =-=-,∴(0,2)C k -,∴2BH CO k ==-,∴22OH OB BH k =+=-,∴(22,2)D k -;(3)如图2,连接CD ,取CD 中点N ,连接AN ,BN ,则在Rt ACD △中,AN CN DN ==,同理,BN CN DN ==,∴AN CN DN BN ===,∴A ,C ,B ,D 四点共圆,∴,ABC ADC CDB OAB ∠=∠∠=∠,∵,90OA OB AOB =∠=︒,∴45OAB OBA ∠=∠=︒,∵345ABC BDO ∠-∠=︒,∴()345ADC BDC CDO ∠-∠-∠=︒,∴2AOD ADC ∠=∠,在AD 上取一点M ,使MD MC =则MCD ADC ∠=∠,∴2AMC ADC AOD ∠=∠=∠,∴tan tan AMC AOD ∠=∠,∴AC AD AM AO=,AM x =,22,MC MD k x AC ==--∵222MC AM AC =+,∴222(22)(22)k x x k --=++,∴41k x k =-,∴2222421k k k +-=-,解得,13k =-,∴直线BC 解析式为:13y x =-+设直线OD 解析式为:y mx =,把8(,2)3D 代入得823m =,∴34m =,则直线OD 解析式为:34y x =,第一步,以点A为圆心,任意长为半径画弧,分别交BA的延长线和AC于点E,F,如图21EF的长为半径画弧,两弧相交于点D,作射线AD 第二步,分别以点E,F为圆心,大于GAD ∠=∠=∠由(1)(2)可得NAM CAM B18.(2022·湖南郴州·中考真题)如图1,在矩形ABCD 中,4AB =,6BC =.点E 是线段AD 上的动点(点E 不与点A ,D 重合),连接CE ,过点E 作EF CE ⊥,交AB 于点F .(1)求证:AEF DCE ∽;(2)如图2,连接CF ,过点B 作BG CF ⊥,垂足为G ,连接AG .点M 是线段BC 的中点,连接GM .①求AG GM +的最小值;②当AG GM +取最小值时,求线段DE 的长.【答案】(1)见解析(2)①5;②3DE =或3DE =【分析】(1)证明出DCE AEF ∠=∠即可求解;(2)①连接AM .先证明132BM CM GM BC ====.确定出点G 在以点M 为圆心,3为半径的圆上.当A ,G ,M 三点共线时,AG GM AM +=.此时,AG GM +取最小值.在Rt ABM 中利用勾股定理即可求出AM ,则问题得解.②先求出AF ,求AF 的第一种方法:过点M 作∥MN AB 交FC 于点N ,即有CMN CBF ∽△△,进而有12MN CM BF CB ==.设AF x =,则4BF x =-,()142MN x =-.再根据∥MN AB ,得到AFG MNG ∽△△,得到AF AG MN GM =,则有()21342x x =-,解方程即可求出AF ;求AF 的第二种方法:过点G 作GH AB ∥交BC 于点H .即有MHG MBA ∽△△.则有GM GH MH AM AB MB ==,根据5AM =,可得3543GH MH ==,进而求出125GH =,95MH =.由GH AB ∥得CHG CBF ∽△△,即可求出AF .求出AF 之后,由(1)的结论可得AF AE DE DC =.设DE y =,则6AE y =-,即有164y y -=,解得解方程即可求出DE .(1)证明:如图1,∵四边形ABCD 是矩形,∴90A D ∠=∠=︒,∴90CED DCE ∠+∠=︒.∵EF CE ⊥,∴90CED AEF ∠+∠=︒,∴DCE AEF ∠=∠,∴AEF DCE ∽;(2)①解:如图2-1,连接AM .∵BG CF ⊥,∴BGC 是直角二角形.∴132BM CM GM BC ====.∴点G 在以点M 为圆心,3为半径的圆上.当A ,G ,M 三点不共线时,由三角形两边之和大于箒三边得:AG GM AM +>,当A ,G ,M 三点共线时,AG GM AM +=.此时,AG GM +取最小值.在Rt ABM 中,5AM ==.∴AG GM +的最小值为5.②(求AF 的方法一)如图2-2,过点M 作∥MN AB 交FC 于点N ,∴CMN CBF ∽△△.∴12MN CM BF CB ==.设AF x =,则4BF x =-,∴()11422MN BF x ==-.∵∥MN AB ,∴AFG MNG ∽△△,∴AF AG MN GM =,由①知AG GM +的最小值为5、即5AM =,又∵3GM =,∴2AG =.∴()21342x x =-,解得1x =,即1AF =.(求AF 的方法二)如图2-3,过点G 作GH AB ∥交BC 于点H .∴MHG MBA ∽△△.∴GM GH MH AM AB MB==,由①知AG GM +的最小值为5,即5AM =,又∵3GM =,∴3543GH MH ==.∴125GH =,95MH =.由GH AB ∥得CHG CBF ∽△△,∴GH CH FB CB =,即1293556FB +=,解得3FB =.∴1AF AB FB =-=.由(1)的结论可得AF AE DE DC =.设DE y =,则6AE y =-,∴164y y -=,解得3y =或3∵036<+<,036<-<,∴3DE =或3DE =.【点睛】本题主要考查了相似三角形的判定与性质、平行的性质、勾股定理以及一元二次方程的应用等知识,掌握相似三角形的判定与性质是解答本题的关键.。
几何模型:一线三等角模型 (最终版)

初中几何模型之“一线三等角模型”一.【一线三等角概念】“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.【一线三等角的分类】2.1 全等篇_同侧A PA P锐角直角钝角2.2 全等篇_异侧PDPP锐角直角钝角2.3 相似篇_同侧DCA BPP锐角直角钝角2.4 相似篇_异侧PDPP锐角直角钝角三、【性质】1.相似,如图 3-1,由∠1=∠2=∠3,或者α=α2=α3易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如下图,若 CE=ED,则△AEC≌△BDE.异侧结果同样。
3.中点型“一线三等角”——相似中多了一位兄弟如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE. 4.“中点型一线三等角“的变式(了解)如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明)图 3-5四、【“一线三等角”的应用】1.应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,构造“一等角”模型解题;c.图形中只有直线上一个角,构造“二等角”模型解题.注意:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.适应场景:在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造步骤:找角、定线、构相似【引例】例 1如图,l1、l2、l3是同一平面内的三条平行线,l1、l2之间的距离是21/5,l2、l3之间的距离是21/10,等边△ABC 的三个顶点分别在l1、l2、l3上,求△ABC 的边长.思路引导:【脑洞大开-三角构造】例 1 如图,四边形 ABCD 中,∠ABC=∠BAD=90°,∠ACD=45°,AB=3,AD=5.求 BC 的长.横向构造纵向构造斜向构造斜A相似构造:例 2 如图,△ABC 中,∠BAC=45°,AD⊥BC,BD=2,CD=3,求 AD 的长.纵向横向斜向一线三垂直的补形:角含半角补形练一练:1.如图,在△ABC 中,∠BAC=135°, AC= 2AB, AD⊥AC 交 BC 于点 D,若 AD = 2,求△ABC的面积思路提示:【中点型一线三等角】例1、如图,在Rt⊿ABC 中,AB = AC =2,∠A = 90°,现取一块等腰直角三角板,将45° 角的顶点放在BC 中点O 处,三角板的直角边与线段AB、AC 分别交于点E、F,设BE =x,CF = y,∠BOE = α( 45° ≤ α ≤ 90°) .( 1) 试求y 与x 的函数关系式,并写出x 的取值范围;( 2) 试判断∠BEO 与∠OEF 的大小关系?并说明理由;( 3) 在三角板绕O 点旋转的过程中,⊿OEF 能否成为等腰三角形? 若能,求出对应x 的值; 若不能,请说明理由.例2.如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90∘,△DEF的顶点E与△ABC的斜边BC的中点重合。
2024年中考数学总复习考点梳理第四章专项3一线三等角模型

∴∠AEB=∠CFA=90°,
∴∠ABE+∠BAE=90°,
∵∠BAC=90°,
第5题图
专项3 一线三等角模型
∴∠CAF+∠BAE=90°, ∴∠ABE=∠CAF, 又∵AB=AC, ∴△ABE≌△CAF(AAS), ∴AE=CF=1,AF=BE=4, ∴EF=AF-AE=4-1=3.
第5题图
专项3 一线三等角模型
J
∵∠BED=∠BAC,∴∠ABE=∠CAJ,
专项3 一线三等角模型
AB CA
在△ABE和△CAJ中,ABE CAJ ,
BE AJ
∴△ABE≌△CAJ(SAS),
∴AE=CJ,∠AEB=∠CJA,
∵BE∥CF,∴∠BED=∠CFA,
∵∠AEB+∠BED=∠CFA+∠CFJ=180°,
第6题图
6. 如图,在△ABC中,AB=AC,D为BC边上一点,连接AD,E
为线段AD上一点,且∠BED=∠BAC,过点C作CF∥BE交AD
的延长线于点F.求证:AE=CF. 证明:如图,延长AF至点J,使得AJ=
BE,连接CJ,
由题意得∠BED=∠ABE+∠BAE, ∠BAC=∠BAE+∠CAJ,
第6题图
E
BD
C
第1题图
专项3 一线三等角模型
∴∠CDE+∠ADB=120°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴ AB DC ,即 AB AB 4,
BD CE
4
3
∴AB=16.
Hale Waihona Puke AEBDC
第1题图
专项3 一线三等角模型
【变式题】 2. 如图,在等边△ABC中,D,E,F分别是边BC,AC,AB上 的点,连接DF,DE,且∠FDE=60°,若BC=6,CE=BD=2, 求BF的长. 解:∵△ABC为等边三角形, ∴∠B=∠C=60°,∴∠BFD+∠FDB=120°, ∵∠FDE=60°, ∴∠CDE+∠FDB=120°,∴∠BFD=∠CDE. 第2题图
相似专题:一线三等角模型

相似专题复习---“一线三等角模型”
一、教学目标
1.学生会运用两组对应角分别相等的两个三角形为相似三角形的判定方法证明两个三角形相似。
2.学生经历观察、比较、归纳的学习过程,归纳出“一线三等角”图形的基本特征,并且能够在不同的背景中认识和把握基本图形。
3.学生在学习过程中感受几何直观图形对几何学习的重要性。
二、教学重点、难点
1、重点:运用判定方法解决“一线三等角”的相关计算与证明
2、难点:在不同背景中识别基本图形
三、教学方法:教师主导与学生合作探究相结合。
四、教学过程
二一线三等角的性质。
小专题一线三等角相似专题课完整版课件

连结BP,作∠BPQ=60°,交直线BC于点N.
(1)当P在线段AC上时,证明PA·PC=AB ·CN
(2)若P在AC的延长线上,上述关系是否成立?
(3)若P在CA的延长线上, CN=1.5,BC=2,求AP、BP
的长
60°
A
A
A
60° P
P
P
N
B
CB
Q
C
60°
Q
NB
N
C Q
如图,L1,L2,L3是同一平面内的 三条平行直线,L1与L2间的距离是1 ,L2与L3间的距离是2,正三角形 ABC的三顶点分别在L1,L2,L3上, 求△ABC的边长
反比例函数y=
(1 x>0)
x 的图像上,∠AOB=90°则
的
值为AO ________ x
BO
分析:
(1)根据一线三等角方法证明△AMO∽△ONB
(2)由反比例函数图像性质可知
S△AAMO 6 S△BNO 1
AO 6 BO 1
(相似三角形的面积之比等于相似比的平方
)
问题1:
如图,在正方形ABCD中,E为BC上任意一点(与B 、C不重合)∠AEF=90°.观察图形:
((1)2)△若ABEE为与B△CE的CF中是点否,相连似结?AF并,图证中明有你哪的些结相论似。三
角形?
△ABE∽ △ECF
∽ △AEF
A
D
A
D
F
B
E
C
F
B
E
C
问题2:
D
(12)延长BA、CB于C运的用中类点比,、若
α
∠B=∠C迁=移α,的∠数AE学F方= ∠法C,连当结
中考数学几何专项练习:相似模型-一线三等角及“K”模型(解析版)

中考数学几何专项练习:相似模型--一线三等角及“K”模型A.1.8B.【答案】C△△【分析】证明ADC∽为等边三角形,【详解】解:∵ABC∴60,B CA.1B.3【答案】D【分析】结合矩形的性质,证明A.2B.73【答案】D 【分析】证明CAD CBA ∽△△,得出【详解】解:∵EA ED ,∴1EAD ,∵1B ,∴EAD B ,∵C C ,∴CAD CBA ∽△△,∴CA CD CB CA =,∴686CD ,∴9CD =,A.3【答案】A 【分析】依据矩形的性质以及折叠,即可得到成比例即可得CF 的长.【详解】解:∵矩形ABCD 6CD ,又E ∵是CD 的中点,3DE CE ,Rt ADE △中,6AD 由题可得,D C 90AED CEF AED EFC ,ADE EFC ∽,CF CE DE DA ,即3CF 解得3CF ,故选:A.【点睛】本题主要考查了折叠问题、矩形的性质、相似三角形的判定与性质以及勾股定理的运用,翻折变换(折叠问题)实质上就是轴对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.5.如图,在等边ABCA.1B.4 3【答案】D【分析】利用等边三角形的性质和相似三角形的判定与性质解答即可得出结论.【详解】解:ABC∵ 为等边三角形,60B C∴.【答案】2132/2【分析】根据菱形的性质,折叠的性质,以及角和和平角的意义,得出BEG DGF例式列出方程,再根据AE AB,解出【答案】1或2【分析】设BP=x,则PC=3-x,根据平行线的性质可得∠B=90°,根据同角的余角相等可得∠CDP=∠APB,即可证明△CDP∽△BPA,根据相似三角形的性质列方程求出【详解】设BP=x,则PC=3-x,【答案】2.4【分析】根据折叠的性质可得∠CDF=∠BDE+∠BED=120°,从而得到∠到23CF BDDF DE,即6CF【答案】31:【分析】(1)由等边三角形的性质得到再由FD BC 推出BED (2),用k 表示DC 和似比,即可求出BE ,然后用【详解】解:(1)∵三角形∴60A B ,由折叠的性质可得AE ∵FD BC ,∴90FDB ,∴30EDB ,∴90BED ,∴3AE DE BE ,∴:31AE EB :,设,2CD k BD k ,∴3AB AC k ,∵ABC 为等边三角形,∴60A B ,由折叠的性质可得EDF ∴BED C BE DE BD △∴EDB FDC BED ∴BED FDC∵60B C ,∴BED CDF ∽,BED CDFC BE DC C ,∴54BE k k k,∴5,34BE k AE k∴:7:5AE BE ;【答案】32145【分析】根据DE同时平分BDE FDE△△,由三角形全等性质据BDE FDE△△和ABC是等边三角形,证明【答案】15 8【分析】过C作CF C D∥交B C 于CF和C D 的长,再由CFE DC E∽【详解】解:如图,过C作CF C D∥AB C D 是菱形,则AB C D ∥,∴CF AB ∥,∴B FC AB F B CF AB B ,∵AB C B ⅱÐ=Ð,∴B FC B ,【答案】8【分析】根据等边三角形的性质得相似,再根据相似三角形的性质即可得.PCD∵【详解】解:ABC,AB BC AC【答案】215【分析】证明BPE ADP ∽,由相似三角形的性质得出23CD x ,得出22633PB x x x 【详解】解:ABC ∵是等边三角形,【答案】30114【分析】延长BC 至M 使CD CM ,连接MD 【详解】∵EF DE ,60EFD∵在ABCD Y 中,3460AB BC B ,,,∴3460AB CD CM BC B DCM ,,∴DCM △是等边三角形∴3DM ,60B M EFD ,【答案】5:7【分析】如图,作EJ 等边三角形的性质得到相应的线段,再根据相似三角形的性质即可求解.【详解】解:连接BE 交设AE a ,3EC a ,【点睛】此题主要考查了翻折变换、等边三角形的性质、勾股定理、含似三角形的判定与性质,通过三角形相似求出相关线段是关键.16.如图,矩形ABCD中,角线AC与EF交于点G,则7【点睛】本题主要考查了矩形的性质,相似三角形的判定和性质,勾股定理,解题的关键是掌握相似三角形的判定方法,以及相似三角形对应边成比例.17.如图,在△ABC中,AB交AC于点E,且cos∠α=∵AB=AC=10,∠ADE=∠B=α,cosα=∴BG=ABcosB,【答案】21 2【分析】设AF x,由等边三角形的性质得出由折叠的性质得:AE证明BDE CFD△∽△识;熟练掌握折叠变换和等边三角形的性质,证明三角形相似是解题的关键.(1)如图1,在四边形ABCD 中,点P 为AB 上一点,90DPC A B ,求证:AD 【思考探究】(2)如图2,在四边形ABCD 中,点P 为AB 上一点,当DPC A B 时,上述结论是否依然成立?说明理由.【拓展延伸】△∽△(1)求证:ABF FCEAD,求(2)若23AB ,4(3)当点F是线段BC的中点时,求证:【答案】(1)证明见解析(1)求证:ABP PCM ∽△△;(2)设BP x ,CM y ,求y (3)当APM △为等腰三角形时,求∵PM PC PA AB,∴5PC AB ,∵APM B C ,∴PAM BAC 即点P 与点∵P 不与点B 、C 重合,舍去.∴MAP MPA ,∴MAP ABC △∽,∴5MP AC .(1)证明:BDA CED ∽;(2)若45B ,6BC ,当点D 在BC 上运动时(点D 不与B 、C BD 的长.【答案】(1)详见解析∴ADE∽ACD∴DA DE AC DC∴AC DC;(1)求证:AB CM BP PC△为直角三角形时,求线段PB (2)当PCM【答案】(1)见解析∵,AB AC,B C∵,APM B180180BAP B APB△△,BAP CPM∽由(1)知,90APB PMCAB AC ∵,点P 为BC 中点,8cm BC Q ,14cm BP CP BC ,由(1)知,90BAP CPM ∠∠作AD BC 于点D ,则14cm 2BD CD BC ,BDA 90BAP BDA(1)当ADEV是等腰三角形时,求(2)当22BD 时,求DE【答案】(1)422或2或35(2)解:取BC 的中点M ,连接AM ,ABC ∵ 是等腰直角三角形,122AM BM BC ,90AMB ,22BD ∵,【点睛】本题考查了等腰直角三角形的判定和性质,勾股定理,全等三角形的判定和性质,相似三角形的判定和性质,利用分类讨论的思想,熟练掌握全等三角形和相似三角形的判定和性质是解题关键.27.已知等边三角形ABC的边长为(1)如图,在边BC上有一个动点(2)如图,若点P在射线(3)在(2)的条件下,将点D【答案】(1)见详解(2)7(3)532∴90AEP ,∵ABC 是等边三角形,边长为∴4AC ,60ACB ,∴60PCE ACB ,在Rt CPE △中,2PC ,CPE ∴11CE PC ,根据勾股定理得,由(2)知,7AD ,∵4AC ,∴743CD AD AC ,由旋转知,120DCD ,CD ∵60DCP ,∴D CP DCD DCP(1)若55AP 时,求BE 的值.(2)求y 关于x 的函数解析式,并写出它的定义域.(3)当DEC 与APD △相似时,求AP 的长度.【答案】(1)94(2)215(025)2y x x x (3)259或22535195210BH PH PB ,90BHE C ∵,B B BEH BAC ∽,BE BH AB BC, 9510425BE ,9BE ;11522BH PB x ∵,cos BH BC B BE AB,5524x BE ,35424x CE BE ,当DEC 与APD △相似时,有A CDE ,90ACB DCE Q ,ABC DEC ∽,CD AC CE BC, 52123524x x,AE (1)当点D为BC的中点时,EB∵点D 为BC 的中点,ABC 为等边三角形,∴AD BC ,DAB DAC ∵将等边ABC 折叠,使点A 与点∴30ADE DAB ,∴903060EDB B ,。
2019年中考数学相似模型:一线三等角模型(经典,详细总结!!)

2019年中考数学相似模型:一线三等角模型(经典,详细总结!!)一.一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.一线三等角的分类全等篇三、“一线三等角”的性质1.一般情况下,如图 3-1,由∠1=∠2=∠3,易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如图3-1,若CE=ED,则△AEC≌△BDE.3.中点型“一线三等角”如图3-2,当∠1=∠2=∠3,且 D 是BC 中点时,△BDE∽△CFD∽△DFE.4.“中点型一线三等角“的变式(了解)如图 3-3,当∠1=∠2 且时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.如图3-4“中点型一线三等角”通常与三角形的内心或旁心相关,Ð这是内心的性质,反之未必是内心.在图 3-4(右图)中,如果延长 BE 与 CF,交于点 P,则点 D 是△PEF 的旁心.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明)其实这个第 4 图,延长 DC 反而好理解.相当于两侧型的,不延长理解,以为是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c.图形中只有直线上一个角,不上“二等角”构造模型解题.体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特殊性如图 3-6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过 C、D 两点作直线 l 的垂线是必不可少的。
部编数学九年级下册专项33相似三角形一线三等角模型综合应用(解析版)含答案
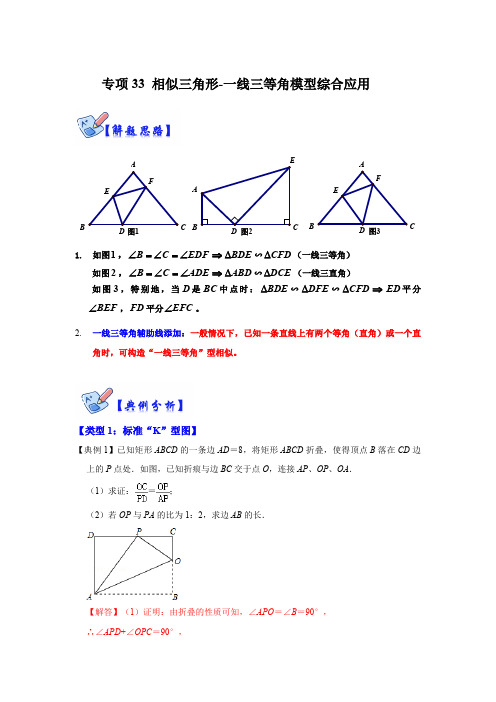
专项33 相似三角形-一线三等角模型综合应用1.如图1,BDE EDF C B ∆⇒∠=∠=∠∽CFD ∆(一线三等角)如图2,ABD ADE C B ∆⇒∠=∠=∠∽DCE ∆(一线三直角)如图3,特别地,当D 是BC 中点时:BDE ∆∽DFE ∆∽CFD ∆⇒ED 平分BEF ∠,FD 平分EFC ∠。
2.一线三等角辅助线添加:一般情况下,已知一条直线上有两个等角(直角)或一个直角时,可构造“一线三等角”型相似。
【类型1:标准“K ”型图】【典例1】已知矩形ABCD 的一条边AD =8,将矩形ABCD 折叠,使得顶点B 落在CD 边上的P 点处.如图,已知折痕与边BC 交于点O ,连接AP 、OP 、OA .(1)求证:=;(2)若OP 与PA 的比为1:2,求边AB 的长.【解答】(1)证明:由折叠的性质可知,∠APO =∠B =90°,∴∠APD +∠OPC =90°,CB BC A A∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠POC+∠OPC=90°,∴∠APD=∠POC,∴△OCP∽△PDA,∴=;(2)解:∵△OCP∽△PDA,∴,∵OP与PA的比为1:2,AD=8,∴,∴PC=4,设AB=x,则DC=x,AP=x,DP=x﹣4,在Rt△APD中,AP2=AD2+PD2,∴x2=82+(x﹣4)2,解得:x=10,∴AB=10.【变式1-1】如图,正方形ABCD中,点E在BC边上,且AE⊥EF,若BE=2,CF=,求正方形ABCD的边长.【解答】解:∵∠AEB+∠CEF=90°,∠BAE+∠AEB=90°,∴∠BAE=∠CEF,又∵∠B=∠C=90°,∴△BAE∽△CEF,∴=,∵AB=BC,∴,∴,∴CE=4,∴BC=CE+BE=4+2=6,∴正方形ABCD的边长为6.【变式1-2】如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于F,交AD的延长线于点E.(1)求证:△ABM∽△MCF;(2)若AB=4,BM=2,求△DEF的面积.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=BC=CD,∠B=∠C=90°,BC∥AD,∴∠BAM+∠AMB=90°,∵ME⊥AM,∴∠AME=90°,∴∠AMB+∠FMC=90°,∴∠BAM=∠FMC,∴△ABM∽△MCF;(2)解:∵AB=4,∴AB=BC=CD=4,∵BM=2,∴MC=BC﹣BM=4﹣2=2,由(1)得:△ABM∽△MCF,∴=,∴=,∴CF=1,∴DF=CD﹣CF=4﹣1=3,∵BC∥AD,∴∠EDF=∠MCF,∠E=∠EMC,∴△DEF∽△CMF,∴=,∴=,∴DE=6,∴△DEF的面积=DE•DF=×6×3=9,答:△DEF的面积为9【类型2:做辅助线构造“K”型图】【典例2】已知:在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上.(1)如图1,填空:当点G在CD上,且DG=1,AE=2,则EG= ;(2)如图2,若F是AD的中点,FG与CD相交于点N,连接EN,求证:∠AEF=∠FEN;(3)如图3,若AE=AD,EG,FG分别交CD于点M,N,求证:MG2=MN•MD.【解答】(1)解:∵∠EFG=90°,∴∠AFE+∠DFG=90°,∵∠AEF+∠AFE=90°,∴∠AEF=∠DFG,又∵∠A=∠D=90°,EF=FG,∴△AEF≌△DFG(AAS),∴AE=FD=2,∴FG=,∴EG=FG=,故答案为:;(2)证明:延长EA、NF交于点M,∵点F为AD的中点,∴AF=DF,∵AM∥CD,∴∠M=∠DNF,∠MAD=∠D,∴△MAF≌△NDF(AAS),∴MF=FN,∵EF⊥MG,∴ME=GE,∴∠MEF=∠FEN;(3)证明:如图,过点G作GP⊥AD交AD的延长线于P,∴∠P=90°,同(1)同理得,△AEF≌△PFG(AAS),∴AF=PG,PF=AE,∵AE=AD,∴PF=AD,∴AF=PD,∴PG=PD,∵∠P=90°,∴∠PDG=45°,∴∠MDG=45°,在Rt△EFG中,EF=FG,∴∠FGE=45°,∴∠FGE=∠GDM,∵∠GMN=∠DMG,∴△MGN∽△MDG,∴,∴MG2=MN•MD.【变式2-1】(2021春•永川区期末)如图,在边长为6的正方形ABCD中,E为BC上一点,CE=2BE,将△ABE沿AE折叠得到△AFE,连接DF,则线段DF的长为 .【解答】解:过点F作FN⊥BC,垂足为N,延长NF交AD于点M,∵四边形ABCD是正方形,∴AB=BC=AD=6,∠B=90°,AD∥BC,∴FM⊥AD,∴∠AMF=∠FNE=∠DMF=90°,∴四边形ABNM是矩形,∴AM=BN,∵CE=2BE,∴BE=BC=2,由折叠得:BE=FE=2,AB=AF=6,∠B=∠AFE=90°,∴∠AFM+∠EFN=90°,∵∠FEN+∠EFN=90°,∴∠FEN=∠AFM,∴△ENF∽△FMA,∴===,设EN=x,则FM=3x,∴AM=BN=BE+EN=2+x,在Rt△AFM中,AM2+FM2=AF2,∴(2+x)2+(3x)2=36,∴x=或x=﹣2(舍去),∴AM=2+x=,FM=3x=,∴DM=AD﹣AM=,在Rt△DMF中,DF===,故答案为:.【变式2-2】(2022秋•皇姑区校级月考)已知,如图,矩形ABCD中,AB=5,AD=3,点E是射线BC上一动点,将矩形ABCD沿直线AE翻折,点B落在点F处.(1)若点F恰好落在CD边上,如图1,求线段BE的长;(2)若BE=1,如图2,直接写出点F到BC边的距离;(3)若△CEF为直角三角形,直接写出CE所有值.【解答】解:(1)∵四边形ABCD是矩形,∴CD=AB=5,BC=AD=3,∠B=∠C=∠D=90°,由折叠的性质得:BE=FE,AF=AB=5,∴DF===4,∴CF=CD﹣DF=5﹣4=1,设BE=FE=x,则CE=BC﹣BE=3﹣x,在Rt△CEF中,由勾股定理得:CF2+CE2=FE2,即12+(3﹣x)2=x2,解得:x=,即线段BE的长为;(2)如图2,过F作FG⊥BC于G,延长GF交AD于H,则∠FGE=90°,四边形ABGH是矩形,∴HG=AB=5,BG=AH,∠AHF=90°=∠FGE,由折叠的性质得:AF=AB=5,∠AFE=∠B=90°,FE=BE=1,∴∠AFH+∠EFG=90°,∵∠AFH+∠FAH=90°,∴∠EFG=∠FAH,∴△EFG∽△FAH,∴==,∴AH=5FG,设FG=x,则BG=AH=5x,∴EG=BG﹣BE=5x﹣1,在Rt△EFG中,由勾股定理得:x2+(5x﹣1)2=12,解得:x=或x=0(不符合题意舍去),∴FG=,即点F到BC边的距离为;(3)分三种情况:①∠CFE=90°时,如图3,∵∠AFE=90°,∴∠AFE+∠CFE=180°,∴A、F、C三点共线,∵四边形ABCD是矩形,∴CD=AB=5,∠B=∠D=90°,AD∥BC,∴∠ECF=∠CAD,AC===,由折叠的性质得:AF=AB=5,FE=BE,∠AFE=∠B=90°,∴∠CFE=90°=∠D,CF=AC﹣AF=﹣5,∴△CEF∽△ACD,∴=,即=,解得:CE=;②点F在CD上,∠ECF=90°时,如图4,由(1)可知,BE=,∴CE=BC﹣BE=3﹣=;③∠CEF=90°时,如图5,由折叠的性质得:∠AEB=∠AEF=45°,∴△ABE是等腰直角三角形,∴BE=AB=5,∴CE=BE﹣BC=5﹣3=2;④点F在CD延长线上,∠ECF=90°时,如图6,由折叠的性质得:AF=AB=5,∠AFE=∠B=90°,∵∠ADF=180°﹣∠ADC=90°,∴DF===4,∴CF=CD+DF=5+4=9,∵∠CFE+∠CEF=90°,∠CFE+∠DFA=90°,∴∠CEF=∠DFA,∵∠ECF=∠ADF=90°,∴△CEF∽△DFA,∴===3,∴CE=3DF=12;综上所述,若△CEF为直角三角形,则CE的值为或或2或12.【类型2:特殊“K”型图】【典例3】(2021秋•通许县期中)感知:(1)数学课上,老师给出了一个模型:如图1,∠BAD=∠ACB=∠AED=90°,由∠1+∠2+∠BAD=180°,∠2+∠D+∠AED=180°,可得∠1=∠D;又因为∠ACB=∠AED =90°,可得△ABC∽△DAE,进而得到= .我们把这个数学模型称为“一线三等角”模型.应用:(2)实战组受此模型的启发,将三等角变为非直角,如图2,在△ABC中,点D在边BC上,并且DA=DE,∠B=∠ADE=∠C.若BC=a,AB=b,求CE的长度(用含a,b的代数式表示).拓展:(3)创新组突发奇想,将此模型迁移到平行四边形中,如图3,在▱ABCD中,E为边BC上的一点,F为边AB上的一点.若∠DEF=∠B.求证:AB•FE=BE•DE.【解答】(1)解:∵△ABC∽△DAE,∴,故答案为:;(2)解:∵∠B=∠ADE=∠C,∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,∴∠EDC=∠BAD,∵DA=DE,在△ADB与△DEC中,,∴△ADB≌△DEC(AAS),∴EC=BD,AB=DC=b,∴BD=BC﹣DC=a﹣b,即CE=a﹣b;(3)解:∵∠DEF=∠B,∴∠BFE+∠BEF=∠BEF+∠DEC,∴∠BFE=∠DEC,作CG∥FE交DE于点G,如图:∴∠DEF=∠EGC,∴∠B=∠EGC,∴△FBE∽△EGC,∴,∵四边形ABCD是平行四边形,∴∠B+∠BCD=180°,∵∠EGC+∠DGC=180°,∵∠B=∠EGC,∴∠DGC=∠BCD,∵∠EDC=∠CDG,∴△DGC∽△DCE,∴,∴,∴DC•FE=BE•DE,∵四边形ABCD是平行四边形,∴AB=DC,∴AB•FE=•BE•DE.解法二:延长BC到M,使得DC=DM.∵DC=DM,∵DC∥AB,∴∠DCM=∠B,∴∠B=∠M,∵∠BFE=∠DEM,∴△BFE∽△MED.∴=,∵AB=CD=DM,∴AB•FE=•BE•DE.【变式3-1】如图,AB=9,AC=8,P为AB上一点,∠A=∠CPD=∠B,连接CD.(1)若AP=3,求BD的长;(2)若CP平分∠ACD,求证:PD2=CD•BD.【解答】(1)解:∵AB=9,AC=3,∴BP=AB﹣AP=9﹣3=6,∵∠A=∠CPD,∠ACP+∠APC=180°﹣∠A,∠APC+∠BPD=180°﹣∠CPD,∴∠ACP=∠BPD,∵∠A=∠B,∴△ACP∽△BPD,∴=,∴=,∴BD=,∴BD的长为;(2)证明:∵CP平分∠ACD,∴∠PCD=∠ACP,∴∠PCD=∠DPB,∵∠CPD=∠B,∴△CPD∽△PBD,∴=,∴PD2=CD•BD.【变式3-2】(2022春•定海区校级月考)【基础巩固】(1)如图1,在△ABC中,∠ACB=90°,直线l过点C,分别过A、B两点作AE⊥l,BD⊥l,垂足分别为E、D.求证:△BDC∽△CEA.【尝试应用】(2)如图2,在△ABC中,∠ACB=90°,D是BC上一点,过D作AD的垂线交AB 于点E.若BE=DE,,AC=20,求BD的长.【拓展提高】(3)如图3,在平行四边形ABCD中,在BC上取点E,使得∠AED=90°,若AE=AB,,CD=,求平行四边形ABCD的面积.【解答】(1)证明:∵∠ACB=90°,∴∠BCD+∠ACE=90°,∵AE⊥CE,∴∠AEC=90°,∴ACE+∠CAE=90°.∴∠BCD=∠CAE.∵BD⊥DE,∴∠BDC=90°,∴∠BDC=∠AEC.∴△BDC∽△CEA.(2)解:过点E作EF⊥BC于点F.由(1)得△EDF∽△DAC.∴.∵AD⊥DE,,AC=20,∴,∴DF=16.∵BE=DE,∴BF=DF.∴BD=2DF=32.(3)解:过点A作AM⊥BC于点M,过点D作DN⊥BC的延长线于点N.∴∠AMB=∠DNC=90°.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠B=∠DCN.∴△ABM≌△DCN(AAS).∴BM=CN,AM=DN.∵AB=AE,AM⊥BC,∴BM=ME,∵,设AM=b,BE=4a,EC=3a.∴BM=ME=CN=2a,EN=5a.∵∠AED=90°,由(1)得△AEM∽△EDN.∴,∴,∴,∵,∴(2a)2+b2=14,∴a=1,.∴平行四边形ABCD的面积=.1.(2021秋•南京期末)如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE ⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )A.4B.C.D.5【答案】B【解答】解:∵EF⊥FG,∴∠EFB+∠GFC=90°,∵四边形ABCD为矩形,∴∠A=∠B=∠C=90°,AB=CD,∴∠GFC+∠FGC=90°,∴∠EFB=∠FGC,∴△EFB∽△FGC,∴,∵BE=3,BF=2,FC=6,∴,∴CG=4,同理可得△DAE∽△EBF,∴,∴,∴AE=,∴BA=AE+BE=+3=,∴DG=CD﹣CG=﹣4=.故选:B.2.(2022秋•二道区月考)如图,在△ABC中,AB=AC=9,BC=12,D,E分别是BC,AB上的动点(点D与B,C不重合),且2∠ADE+∠BAC=180°,若BE=4,则CD 的长为 .【答案】6【解答】解:∵AB=AC,∴∠C=∠B,∴∠C+∠B+∠BAC=2∠C+∠BAC=180°,又∵2∠ADE+∠BAC=180°,∴∠C=∠ADE,又∵∠BDE+∠ADC=180°﹣∠ADE,∠CAD+∠ADC=180°﹣∠C,∴∠BDE=∠CAD,∴△BDE∽△CAD,∴=,即=,解得CD=6.故答案为:6.3.(2022•杭州模拟)如图,点E是矩形ABCD边BC上一点,沿AE折叠,点B恰好落在CD边上的点F处.设=x(x>1),(1)若点F恰为CD边的中点,则x= .(2)设=y,则y关于x的函数表达式是 .【解答】解:(1)∵点F为CD边的中点,∴DC=2DF,∵四边形ABCD是矩形,∴AB=DC,∠B=∠C=∠D=90°,∴∠FEC+∠EFC=90°,由折叠得:BE=EF,AB=AF,∠B=∠AFE=90°,∴AB=AF=DC=2DF,∵∠EFC+∠AFD=90°,∴∠AFD=∠FEC,∴△AFD∽△FEC,∴==2,∴=2,∴x=2,故答案为:2;(2)由(1)可得AB=AF=DC=DF+CF,∵△AFD∽△FEC,∴=,∴=,∴x=,∴x=1+,∴x=1+,∴y=,故答案为:y=.4.(2021•海州区校级二模)如图,△DEF的三个顶点分别在等边△ABC的三条边上,BC =4,∠EDF=90°,=,则DF长度的最小值是 .【答案】【解答】解:过点F作FH⊥BC,垂足为H,∵∠EDF=90°,tan∠EFD==,∴∠EFD=60°,∴∠AFE+∠DFC=120°,∵△ABC是等边三角形,∴∠C=∠A=60°,AC=BC=4,∴∠AFE+∠AEF=120°,∴∠AEF=∠DFC,∴△AEF∽△CFD,∴=,∵∠EDF=90°,∠EFD=60°,∴cos∠EFD==,∴=2,∴设CD=a,则AF=2a,∴CF=AC﹣AF=4﹣2a,在Rt△CFH中,∠C=60°,∴CH=CF=2﹣a,∴FH=CH=2﹣a,∴DH=CD﹣CH=a﹣(2﹣a)=2a﹣2,在Rt△DFH中,DF2=DH2+FH2=(2a﹣2)2+(2﹣a)2=7a2﹣20a+16=7(a﹣)2+,∴DF2的最小值为,∴DF的最小值为:.5.如图,在等边三角形ABC中,点E,D分别在BC,AB上,且∠AED=60°,求证:△AEC∽△EDB.【解答】证明:∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠EDB+∠BED=120°,∠CAE+∠AEC=120°∵∠AED=60°,∴∠BED+∠AEC=180°﹣60°=120°,∴∠BED=∠CAE,∴△AEC∽△EDB.6.如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,点D、E分别在边BC、AC上,连接AD、DE,有∠ADE=45°.(1)证明:△BDA∽△CED.(2)若BC=6,当AE=ED时,求BD的长.【解答】(1)证明:∵∠AED=∠C+∠EDC=45°+∠EDC,而∠ADC=∠ADE+∠EDC.∵∠ADE=45°,∴∠ADC=45°+∠EDC,∴∠AED=∠ADC.∴∠DEC=∠ADB(等角的补角相等).而∠B=∠C=45°,∴△ABD∽△DCE.故△ABD∽△DCE得证.(2)解:当AE=DE时,∴∠ADE=∠DAE,∵∠ADE=45°,∴∠ADE=∠DAE=45°,∵∠BAC=90°,∠BAD=∠EAD=45°,∴AD平分BAC,∴AD垂直平分BC,∴BD=3.7.(2022•安徽三模)如图,在四边形ABCD中,∠A=∠D=90°,AD=AB,以BC为直径的半⊙O与边AD相切于点E.(1)求证:∠BCE=∠DCE;(2)若,求DE的长.【解答】(1)证明:连接OE,∵半⊙O与边AD相切于点E,∴∠OEA=90°,∵∠D=90°,∴∠D=∠OEA=90°,∴OE∥CD,∴∠ECD=∠OEC,∵OE=OC,∴∠OEC=∠OCE,∴∠BCE=∠DCE;(2)解:连接BE,∵BA⊥AD,OE⊥AD,CD⊥AD,∴AB∥CD∥OE,∵OB=OC,∴AE=DE,设DE=AE=x,则AD=AB=2x,∵BC为⊙O的直径,∴∠BEC=90°,∴∠DEC+∠AEB=180°﹣∠BEC=90°,∵∠A=∠D=90°,∴∠ABE+∠AEB=90°,∴∠ABE=∠DEC,∴△ABE∽△DEC,∴,∴,解得:,∴DE的长为.8.(2022•钦州一模)已知下列各图中,△ABC是直角三角形,∠ABC=90°.【基本模型感知】如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M、N.求证:△ABM∽△BCN;【基本模型应用】如图2,点P是边BC上一点,∠BAP=∠C,,求tan C的值;【灵活运用】如图3,点D是边CA延长线上一点,AE=AB,∠DEB=90°,,,请直接写出tan∠BEC的值.【解答】(1)证明:∵AM⊥MN,CN⊥MN,∴∠AMB=∠BNC=90°.∴∠BAM+∠ABM=90°.∵∠ABC=90°,∴∠ABM+∠CBN=90°.∴∠BAM=∠CBN.又∵∠AMB=∠CNB,∴△ABM∽△BCN.(2)解:如图2,过点P作PF⊥AP交AC于点F,过点F作FQ⊥BC交BC于点Q,在Rt△AFP中,tan∠PAC===,与(1)同理得,△ABP∽△PQF.∴===.设AB=a,PQ=2a(a>0),∵∠BAP=∠C=∠FPQ,∴PF=CF,且FQ⊥BC.∴PQ=CQ=2a.∴BC=BP+PQ+CQ=BP+2a+2a=4a+BP.∵∠BAP=∠C,∠B=∠B=90°,∴△ABP∽△CBA.∴=.∴BP⋅BC=AB2,即BP⋅(4a+BP)=.∴BP=a,BC=5a,在Rt△ABC中,tan C==.(3)解:在Rt△ABC中,sin∠BAC==,如图3,过点A作AG⊥BE于点G,过点C作CH⊥BE交EB的延长线于点H,∵∠DEB =90°,∴CH ∥AG ∥DE .∴==.与(1)同理得,△ABG ∽△BCH∴===.设BG =4m ,CH =3m ,AG =4n ,BH =3n ,∵AB =AE ,AG ⊥BE ,∴EG =BG =4m .∴GH =BG +BH =4m +3n .∴=.∴n =2m .∴EH =EG +GH =4m +4m +3n =8m +3n =8m +6m =14m .在Rt △CEH 中,tan ∠BEC ==.9.(2021•坪山区一模)如图,抛物线y =x 2+bx +c 与x 轴交于点A (﹣3,0)、B ,与y 轴交于点C (0,﹣3).(1)求抛物线的解析式;(2)在抛物线上求点P ,使S △BCP =2S △BCO ,求点P 的坐标;(3)如图2,直线y =x +3交抛物线于第一象限的点M ,若N 是抛物线y =x 2+bx +c 上一点,且∠MAN =∠OCB ,求点N 的坐标.【解答】解:(1)将C (0,﹣3)代入到抛物线解析式中得,c =﹣3,将B (﹣3,0)代入到抛物线解析式中得,9﹣3b ﹣3=0,∴b =2,∴抛物线解析式为:y =x 2+2x ﹣3;(2)令y =0,则x 2+2x ﹣3=0,解得x 1=﹣3,x 2=1,∴B (1,0),∴,∵S △BCP =2S △BCO ,∴S △BCP =3,如图1,过P 作PM ∥BC 交x 轴于M ,连接MC ,则S △MBC =S △BCP =3,∴,∴MB =2,∴M (﹣1,0),设直线BC 为y =k 1x ﹣3,代入点B (1,0)得,k 1=3,∴直线BC 为:y =3x ﹣3,则直线PM 设为:y =3x +b ,代入点M (﹣1,0)得,b =3,∴直线PM 为:y =3x +3,联立,解得,,∴P(3,12)或(﹣2,﹣3);(3)∵直线y=x+3交抛物线于第一象限的点M,∴联立,解得,,∴A(﹣3,0),M(2,5),在Rt△OBC中,tan∠OCB=,∴,①如图2,当N在AM下方时,过A作y轴平行线,过M作x轴平行线,两线交于点G过M作MQ⊥AM交AN于Q,过Q作y轴平行线交GM于H,∴∠AGM=∠MHQ=90°,∴∠AMG+∠GAM=90°,又AM⊥MQ,∴∠AMQ=90°,∴∠AMG+∠HMQ=90°,∴∠GAM=∠HMQ,又∠AGM=∠MHQ=90°,∴△AGM∽△MHQ,∴=,∵A(﹣3,0),M(2,5),∴AG=5,GM=5,∴MH=HQ=,∴Q(),设直线AQ为:y=k2(x+3),代入点Q,得,∴直线AQ为,联立,化简得,2x2+3x﹣9=0,解得x=或﹣3,当x=时,y=,∴N(),②当N在AM上方时,同理可得,N(3,12),∴N()或(3,12).。
专题“一线三等角”的相似模型教学设计

相关图表素材
几何图形解析
精心设计的图表,详细展示不同类型的几何图形及其相似性关系。
建筑模型对比
对比不同尺度的建筑物模型,形象说明相似模型的长度比、面积比等特征。
机械部件分析
利用工程图纸和细节截图,深入分析机械设备内部相似零件的设计。
教学评价
为了全面评估学生的学习效果,我们将采取多元化的教学评价方式,既包括学习过程中的观察和诊断,也涵盖期末的综合考核。通过这样的评价体系,我们可以及时发现学生的掌握程度,并针对性地提供帮助与反馈。
展示交流
1
小组展示
各小组将自己设计的相似模型进行展示,详细介绍模型的特点和设计思路。
2
师生点评
师生对小组展示的相似模型进行点评,提出建设性意见和建议。
3
交流讨论
师生就相似模型的应用、设计方法等进行讨论交流,互相学习。
小结反思
总结相似模型的重要性
通过本节课的学习,我们深入了解了相似模型的概念及其在生活中的广泛应用,极大地拓宽了视野。
动手制作自己的相似模型
为了巩固学习成果,我们将安排一系列的练习活动。首先,让学生在生活中寻找并识别各种相似模型,观察它们的共同特点。接下来,通过分析相似模型的长度比、面积比等指标,深化对相似模型概念的理解。最后,鼓励学生动手设计并制作自己独特的相似模型,运用所学知识将创意付诸实践。这些练习将帮助学生更好地掌握相似模型的本质内涵。
未来展望
1
融合创新
将相似模型概念与新兴技术如虚拟仿真、3D打印等深入融合,开拓更广阔的应用前景。
2
跨学科协作
与数学、物理、艺术等相关学科联手,探索跨界整合的教学模式,提升学生的综合素养。
3
持续优化
基于教学实践和反馈,不断优化教学内容、方法和资源,持续提高相似模型教学的质量和效果。
一线三等角相似模型

在物理学中,可以利用一线三等角 相似模型来研究物理现象和规律, 如光的反射和折射、波的传播等。
04 一线三等角相似模型的证 明方法
直接证明法
定义
直接证明法是通过直接使用已知条件和定理来证明结论的 方法。
步骤
首先,根据已知条件,明确一线三等角的定义和性质;然后, 通过比较两个三角形中的角度和边长,利用相似三角形的性质
03
注意事项
反证法需要熟练掌握反证法的原理和 推理技巧,以及能够灵活运用已知条 件。
综合法与分析法
定义
综合法是从已知条件出发,逐步推导出结论的方法;分析法是从结论出发,逐步推导出已知条件的方法。
步骤
在综合法中,首先明确已知条件和目标结论;然后,根据已知条件逐步推导所需结论;最后,总结推导过程。在分析 法中,首先明确目标结论和已知条件;然后,根据结论逐步推导所需条件;最后,总结推导过程。
,逐步推导出所需的结论。
注意事项
直接证明法需要熟练掌握相似三角形的性质和定理,以及 灵活运用已知条件。
反证法
01
定义
反证法是通过假设结论不成立,然后 推导出矛盾,从而证明结论成立的方 法。
02
步骤
首先,假设结论不成立;然后,根据 已知条件和反证法的原理,推导出与 已知条件相矛盾的结论;最后,根据 矛盾的结论,得出结论成立。
相似变换的性质
相似变换具有一些重要的性质,如保持角度不变、线 段长度比例不变等。
相似变换的应用
相似变换在几何学、物理学、工程学等领域有着广泛 的应用,如建筑设计、机械制造、航天技术等。
相似多边形的性质与应用
1 2
相似多边形的定义
相似多边形是指各对应角相等、各对应边成比例 的多边形。
相似三角形中的 “一线三等角”模型-2023年新九年级数学核心知识点与常见题型(沪教版)(解析版)

重难点专项突破:相似三角形中的“一线三等角”模型【知识梳理】一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
或叫“K字模型”。
三直角相似可以看着是“一线三等角”中当角为直角时的特例,三直角型相似通常是以矩形或者正方形形为背景,或者在一条直线上有一个顶点在该直线上移动或者旋转的直角,几种常见的基本图形如下:当题目的条件中只有一个或者两个直角时,就要考虑通过添加辅助线构造完整的三直角型相似,这往往是很多压轴题的突破口,进而将三角型的条件进行转化。
一般类型:基本类型:同侧“一线三等角”异侧“一线三等角”【考点剖析】例1.如图,直角梯形ABCD 中,AB // CD ,90ABC ∠=︒,点E 在边BC 上,且34AB BE EC CD ==, AD = 10,求AED ∆的面积.【答案】24.【解析】90ABC ∠=,//AB CD , ∴90DCB ABC ∠=∠=.又34AB BE EC CD ==, ABE ECD ∴∆∆∽.∴AEB EDC ∠=∠. ∴34AE AB ED EC ==.90EDC DEC ∠+∠=,∴90AEB DEC ∠+∠=. ∴90AED ∠=.在Rt AED ∆中,10AD =,68AE ED ∴==,. 24AED S ∆∴=.【总结】本题考查一线三等角模型的相似问题,还有外角知识、平行的判定等.例2.已知:如图,△ABC 是等边三角形,点D 、E 分别在边BC 、AC 上,∠ADE =60°.(1)求证:△ABD ∽△DCE ;(2)如果AB =3,EC =,求DC 的长.【分析】(1)△ABC 是等边三角形,得到∠B =∠C =60°,AB =AC ,推出∠BAD =∠CDE ,得到△ABD∽△A B C DEDCE ;(2)由△ABD ∽△DCE ,得到=,然后代入数值求得结果.【解答】(1)证明:∵△ABC 是等边三角形,∴∠B =∠C =60°,AB =AC ,∵∠B+∠BAD =∠ADE+∠CDE ,∠B =∠ADE =60°,∴∠BAD =∠CDE∴△ABD ∽△DCE ;(2)解:由(1)证得△ABD ∽△DCE ,∴=,设CD =x ,则BD =3﹣x ,∴=,∴x =1或x =2,∴DC =1或DC =2.【点评】本题考查了等边三角形的性质,相似三角形的判定和性质,注意数形结合和方程思想的应用. 例3.已知,在等腰ABC ∆中,AB = AC = 10,以BC 的中点D 为顶点作EDF B ∠=∠, 分别交AB 、AC 于点E 、F ,AE = 6,AF = 4,求底边BC 的长.【答案】46.【解析】EDC B BED ∠=∠+∠,而EDC EDF FDC ∠=∠+∠,∴B BED EDF FDC ∠+∠=∠+∠. 又EDF B ∠=∠,∴BED FDC ∠=∠.AB C D EFAB AC=,∴B C∠=∠.EDB DCF∴∆∆∽.BE BDDC CF∴=.106104BDDC−∴=−,24DC BD∴=.又12CD DB BC==,BC∴=【总结】本题是对“一线三等角”模型的考查.例4.已知:如图,AB⊥BC,AD // BC, AB = 3,AD = 2.点P在线段AB上,联结PD,过点D作PD的垂线,与BC相交于点C.设线段AP的长为x.(1)当AP = AD时,求线段PC的长;(2)设△PDC的面积为y,求y关于x的函数解析式,并写出函数的定义域;(3)当△APD∽△DPC时,求线段BC的长.满分解答:(1)过点C作CE⊥AD,交AD的延长线于点E.∵AB⊥BC,CE⊥AD,PD⊥CD,AD // BC,∴∠ABC =∠AEC =∠PDC = 90°,CE = AB = 3.∵AD // BC,∴∠A +∠ABC = 180°.即得∠A = 90°.又∵∠ADC =∠DCE +∠DEC,∠ADC =∠ADP +∠PDC,∴∠ADP =∠DCE.又由∠A =∠DEC = 90°,得△APD∽△DCE.∴AD APCE DE=.于是,由AP = AD = 2,得DE = CE = 3.…………………………(2分)在Rt△APD和Rt△DCE中,得PD=,CD=1分)AB CDPAB CD(备用图)于是,在Rt △PDC 中,得 PC = (1分)(2)在Rt △APD 中,由 AD = 2,AP = x ,得 PD 1分)∵ △APD ∽△DCE ,∴AD PD CE CD =.∴ 32CD PD ==1分)在Rt △PCD 中,22113332224PCD S PD CD x ∆=⋅⋅=⨯=+.∴ 所求函数解析式为2334y x =+.…………………………………(2分) 函数的定义域为 0 < x ≤ 3.…………………………………………(1分)(3)当△APD ∽△DPC 时,即得 △APD ∽△DPC ∽△DCE .…………(1分)根据题意,当△APD ∽△DPC 时,有下列两种情况:(ⅰ)当点P 与点B 不重合时,可知 ∠APD =∠DPC .由 △APD ∽△DCE ,得 AP PD DE DC =.即得AP DE PD CD =. 由 △APD ∽△DPC ,得AP AD PD DC =. ∴AD DE CD CD =.即得 DE = AD = 2. ∴ AE = 4.易证得四边形ABCE 是矩形,∴ BC = AE = 4.…………………(2分)(ⅱ)当点P 与点B 重合时,可知 ∠ABD =∠DBC .在Rt △ABD 中,由 AD = 2,AB = 3,得 BD =.由 △ABD ∽△DBC ,得AD BD BD BC =.即得 =. 解得 132BC =.………………………………………………………(2分)∴ △APD ∽△DPC 时,线段BC 的长分别为4或132.方法总结本题重点在于:过点C 作CE ⊥AD ,交AD 的延长线于点E .(构造一线三角,出现相似三角形,进行求解) 例5.在梯形ABCD 中,AD ∥BC ,︒=∠===90,2,1A BC AB AD .(如图1)(1)试求C ∠的度数;(2)若E 、F 分别为边AD 、CD 上的两个动点(不与端点A 、D 、C 重合),且始终保持︒=∠45EBF ,BD 与EF交于点P .(如图2)①求证:BDE ∆∽BCF ∆;②试判断BEF ∆的形状(从边、角两个方面考虑),并加以说明;③设y DP x AE ==,,试求y 关于x 的函数解析式,并写出定义域.答案:(1)作BC DH ⊥,垂足为H ,在四边形ABHD 中,AD ∥BC ,︒=∠==90,1A AB AD ,则四边形ABHD 为正方形又在CDH ∆中,1,1,90=−====∠︒BH BC CH AB DH DHC , ∴︒︒=∠−=∠452180DHC C .(2)①∵四边形ABHD 为正方形,∴︒=∠45CBD ,︒=∠45ADB ,又∵︒=∠45EBF ,∴CBF DBE ∠=∠又∵︒=∠=∠45C BDE ,∴BDE ∆∽BCF ∆.②BEF ∆是等腰直角三角形,∵BDE ∆∽BCF ∆, ∴CB FB BD BE =,又∵︒=∠=∠45DBC EBF ,∴EBF ∆∽DBC ∆,又在DBC ∆中,︒=∠=∠45C DBC ,为等腰直角三角形,∴BEF ∆是等腰直角三角形. ③x x x x x x y +−=+−⨯=1221222,(0<x <1).方法总结 第三问方法提示:过点P 作AD 的垂线于点H ,构造一线三直角相似,进行求解,很简单。
相似专题:一线三等角相似模型(用)解析

基本 8型 图形
K型
?
问题1: 如图,在正方形ABCD中,E为BC上任意一点(与 B、C不重合)∠AEF=90°.观察图形:
△ABE 与△ECF 是否相似?并证明你的结论。
A
D
△ABE∽ △ECF
F
B
E
C
A
△ABE∽ △ECF((21))点点EE为为BBCC上上任任意意一一点点,
若若∠∠BB==∠∠CC==α6,0∠°A,E∠FA=E∠F= F C∠,则C△,则A△BEAB与E△与△ECEFC的F关的
A
E B
P
N F
Q C
D
注意运用转 化的数学思
想
A
D
B
E
C
AD
α
αα
B
E
C
A
D
B
E
C
A
D
B
E
C
A
α
B
F D
α
E
α
C
C
B
D
αα
α
OP
A
从复杂图形中分离出基本图形,对解决问题有
化繁为简的效果。一线三等角模型在解题中,可 以帮助我们快速找到解决问题的突破口。希望这 个模型能起到抛砖引玉的作用,让我们平时多总 结多归纳,出现更多的好方法!
D
C
A
x
O
B
已知:如图,AB⊥BC,AD∥BC,AB=3,AD=2,点P 在线段AB上,连接PD,过点D作PD的垂线,与BC 相交于点C;设线段AP的长为x, (1)当AP=AD时,求线段PC的长; (2)设△PDC的面积为y,求y关于x的函数关系;
构造一线三直角可以解决所有问题
2024年中考数学压轴题重难点知识剖析及训练—一线三等角相似、三垂直模型压轴题专题(含解析)

2024年中考数学压轴题重难点知识剖析及训练—一线三等角相似、三垂直模型压轴题专题(含解析)一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
“一线三等角”的两种基本类型1.三等角都在直线的同侧2.三等角分居直线的两侧3.在初三各学校的考试和中考试题中,一线三等角的相似属于压轴题的热点题型之一,本专题从中考试题和初三各名校的试题中,精选一线三等角相似模型的经典好体,并根据角度区别把一线三等角模型细分为三类题型:三垂直模型、一线三锐角、一线三钝角,适合于初三学生进行压轴题专项突破时使用。
类型一:三垂直模型1.(雅礼)如图,点A 是双曲线()80y x x=<上一动点,连接OA ,作OB OA ⊥,使2OA OB =,当点A 在双曲线()80y x x =<上运动时,点B 在双曲线ky x=上移动,则k 的值为.【解答】解:过A 作AC ⊥y 轴于点C ,过B 作BD ⊥y 轴于点D ,∵点A 是反比例函数y =(x <0)上的一个动点,点B 在双曲线y =上移动,∴S △AOC =×|﹣8|=4,S △BOD =|k |,∵OB ⊥OA ,∴∠BOD +∠AOC =∠AOC +∠OAC =90°,∴∠BOD =∠OAC ,且∠BDO =∠ACO ,∴△AOC ∽△OBD ,∵OA =2OB ,∴=()2=,∴=,∴|k |=2.∴k <0,∴k =﹣2,故答案为:﹣2.2.(青竹湖)如图,︒=∠90AOB ,反比例函数()04<-=x xy 的图象过点()a A ,1-,反比例函数xky =()0,0>>x k 的图象过点B ,且x AB //轴,过点B 作OA MN //,交x 轴于点M ,交y 轴于点N ,交双曲线x ky =于另一点,则OBC ∆的面积为.【解答】解:∵反比例函数的图象过点A (﹣1,a ),∴a =﹣=4,∴A(﹣1,4),过A作AE⊥x轴于E,BF⊥x轴于F,∴AE=4,OE=1,∵AB∥x轴,∴BF=4,∵∠AOB=90°,∴∠EAO+∠AOE=∠AOE+∠BOF=90°,∴∠EAO=∠BOF,∴△AEO∽△OFB,∴=,∴OF=16,∴B(16,4),∴k=16×4=64,∵直线OA过A(﹣1,4),∴直线AO的解析式为y=﹣4x,∵MN∥OA,∴设直线MN的解析式为y=﹣4x+b,∴4=﹣4×16+b,∴b=68,∴直线MN的解析式为y=﹣4x+68,∵直线MN交x轴于点M,交y轴于点N,∴M(17,0),N(0,68),解得,或,∴C(1,64),﹣S△OCN﹣S△OBM=﹣﹣=510,∴△OBC的面积=S△OMN故答案为510.3.(广益)如图,点A,B在反比例函数y=(k>0)的图象上,点A的横坐标为2,点B的纵坐标为1,OA⊥AB,则k的值为.【解答】解:过点A作AM⊥x轴于点M,过点B作BN⊥AM于N,∵∠OAB=90°,∴∠OAM+∠BAN =90°,∵∠AOM+∠OAM=90°,∴∠BAN=∠AOM,∴△AOM∽△BAN,∴=,∵点A,B在反比例函数y=(k>0)的图象上,点A的横坐标为2,点B的纵坐标为1,∴A(2,),B(k,1),∴OM=2,AM=,AN=﹣1,BN=k﹣2,∴=,解得k1=2(舍去),k2=8,∴k的值为8,故答案为:8.4.(长沙中考2020)在矩形ABCD 中,E 为DC 上的一点,把ADE ∆沿AE 翻折,使点D 恰好落在BC 边上的点F .(1)求证:ABF FCE∆∆:(2)若23,4AB AD ==,求EC 的长;(3)若2AE DE EC -=,记,BAF FAE αβ∠=∠=,求tan tan αβ+的值.【详解】(1)证明:∵四边形ABCD 是矩形,∴∠B=∠C=∠D=90°,∴∠AFB+∠BAF=90°,∵△AFE 是△ADE 翻折得到的,∴∠AFE=∠D=90°,∴∠AFB+∠CFE=90°,∴∠BAF=∠CFE ,∴△ABF ∽△FCE .(2)解:∵△AFE 是△ADE 翻折得到的,∴AF=AD=4,∴()22224232AF AB --,∴CF=BC-BF=AD-BF=2,由(1)得△ABF ∽△FCE ,∴CE CF BF AB =,∴2223CE =,∴EC=233(3)解:由(1)得△ABF ∽△FCE ,∴∠CEF=∠BAF=α,∴tan α+tan β=BF EF CE EFAB AF CF AF+=+,设CE=1,DE=x ,∵2AE DE EC -=,∴AE=DE+2EC=x+2,AB=CD=x+1,2244AE DE x -=+∵△ABF ∽△FCE ,∴AB CF AF EF =2144x x x x -=+(211121x x x xx ++-+ ,∴112x x +=,∴1x x =-x 2-4x+4=0,解得x=2,∴CE=1,213x -=,EF=x=2,AF=2244AE DE x -=+=23tan α+tan β=CE EF CF AF +33323.5.(广益)矩形ABCD中,8AB=,12AD=,将矩形折叠,使点A落在点P处,折痕为DE.(1)如图1,若点P恰好在边BC上.①求证:△EBP∽△PCD;②求AE的长;(2)如图2,若E是AB的中点,EP的延长线交BC于点F,求BF的长.图1图2【解答】解:(1)①∵四边形ABCD是矩形,∴∠B=∠C=∠BAD=90°,∴∠BPE+∠BEP=90°,由折叠知,∠DPE=∠BAD=90°,∴∠BPE+∠CPD=90°,∴∠BEP=∠CPD,∵∠B=∠C=90°,∴△EBP∽△PCD;②∵四边形ABCD是矩形,∴∠B=∠C=90°,CD=AB=8,BC=AD=12,由折叠知,PE=AE,DP=AD=12,在Rt△DPC中,CP==4,∴BP=BC﹣CP=12﹣4,在Rt△PBE中,PE2﹣BE2=BP2,∴AE2﹣(8﹣AE)2=(12﹣4)2,∴AE=18﹣6;(2)如图,过点P作GH∥BC交AB于G,交CD于H.则四边形AGHD是矩形,设EG=x,则BG=4﹣x,∵∠A=∠EPD=90°,∠EGP=∠DHP=90°,∴∠EPG+∠DPH=90°,∠DPH+∠PDH=90°,∴∠EPG=∠PDH,∴△EGP∽△PHD,∴====,∴PH=3EG=3x,DH=AG=4+x,在Rt△PHD中,PH2+DH2=PD2,∴(3x)2+(4+x)2=122,解得x=(负值已经舍弃),∴BG=4﹣=,在Rt△EGP中,GP==,∵GH∥BC,∴△EGP∽△EBF,∴=,∴=,∴BF=3.6.(长郡)如图,在平面直角坐标系中,O 为原点,已知点Q 是射线OC 上一点,182OQ =,点P 是x 轴正半轴上一点,tan 1POC ∠=,连接PQ ,A 经过点O 且与QP 相切于点P ,与边OC 相交于另一点D .(1)若圆心A 在x 轴上,求A 的半径;(2)若圆心A 在x 轴的上方,且圆心A 到x 轴的距离为2,求A 的半径;(3)在(2)的条件下,若10OP <,点M 是经过点O ,D ,P 的抛物线上的一个动点,点F 为x 轴上的一个动点,若满足1tan 2OFM ∠=的点M 共有4个,求点F 的横坐标的取值范围.【解答】解:(1)∵圆心A 在x 轴上,⊙A 经过点O 且与QP 相切于点P ,∴PQ ⊥x 轴,OP 为直径,∵tan ∠POC =1,,∴PQ =OP ,∵在Rt △OPQ 中,.∴OP =18.∴⊙A 的半径为9;(2)如图所示,过点A 作AM ⊥x 轴于点M ,过点Q 作QB ⊥x 轴于B ,连接AP ,∵PQ是⊙A的切线,∴AP⊥PQ,则∠APQ=90°,∵AM⊥x轴,QB⊥x轴,∴∠AMP=∠PBC=90°,∴∠PAM=90°﹣∠APM=∠QPB,∴△APM∽△PBQ,∴,∵tan∠POC=1,QB=18,∴OB=QB=18,∵AM=2,设MP=MO=x,∴PB=18﹣2x,∴,解得x=3或x=6,∴MO=3或MO=x,∴A(3,2)或A(6,2),∴AP==或AP==2.∴半径为或2.(3)∵OP<10,∴BO=3,P(6,0),∴A(3,2),∵tan∠POC=1,设D(a,a),∵,∴(3﹣a)2+(2﹣a)2=13,解得:a=0或a=5,∴D(5,5),设抛物线解析式为y=ax2+bx,将点P(6,0),D(5,5)代入得,,解得:,∴y=﹣x2+6x,∵点F可能在点O的左边或点P的右边,,则|K FM|=,设直线MF:或,联立,,得或,当或,解得:或,∴直线MF:或,令y=0,解得:或,∴或.7.(麓山国际)有一边是另一边的倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的夹角叫做智慧角.(1)已知Rt△ABC为智慧三角形,且Rt△ABC的一边长为,则该智慧三角形的面积为;(2)如图①,在△ABC中,∠C=105°,∠B=30°,求证:△ABC是智慧三角形;(3)如图②,△ABC是智慧三角形,BC为智慧边,∠B为智慧角,A(3,0),点B,C在函数y=上(x>0)的图象上,点C在点B的上方,且点B的纵坐标为.当△ABC是直角三角形时,求k的值.=AC•AB,【解答】解:(1)如图1,设∠A=90°,AC≤AB,S△ABC①若AC=,i)AB=AC=2,∴S=,ii)BC=AC=2,则AB=,∴S=,②若AB=,i)AB=AC,即AC=,∴S=,ii)BC=AB=2,则AC=∴S=,③若BC=,若AB=AC==1,∴S=,若AB=AC,AB=,,S=××=,故答案为:或1或或或.(2)证明:如图2,过点C作CD⊥AB于点D,∴∠ADC=∠BDC=90°,在Rt△BCD中,∠B=30°,∴BC=2CD,∠BCD=90°﹣∠B=60°,∵∠ACB=105°,∴∠ACD=∠ACB﹣∠BCD=45°,∴Rt△ACD中,AD=CD,∴AC=,∴,∴△ABC是智慧三角形.(3)∵△ABC是智慧三角形,BC为智慧边,∠B为智慧角,∴BC=AB,∵△ABC是直角三角形,∴AB不可能为斜边,即∠ACB≠90°∴∠ABC=90°或∠BAC=90°①当∠ABC=90°时,过B作BE⊥x轴于E,过C作CF⊥EB于F,过C作CG⊥x轴于G,如图3,∴∠AEB=∠F=∠ABC=90°,∴∠BCF+∠CBF=∠ABE+∠CBF=90°,∴∠BCF=∠ABE,∴△BCF∽△ABE,∴,设AE=a,则BF=AE=a,∵A(3,0),∴OE=OA+AE=3+a,∵B的纵坐标为,即BE=,∴CF=BE=2,CG=EF=BE+BF=,B(3+a,),∴OG=OE﹣GE=OE﹣CF=3+a﹣2=1+a,∴C(1+a,),∵点B、C在在函数y=上(x>0)的图象上,∴(3+a)=(1+a)(+a)=k解得:a1=﹣2(舍去),a2=1,∴k=,②当∠BAC=90°时,过C作CM⊥x轴于M,过B作BN⊥x轴于N,如图4,∴∠CMA=∠ANB=∠BAC=90°,∴∠MCA+∠MAC=∠MAC+∠NAB=90°,∴∠MCA=∠NAB,∴△MCA∽△NAB,∵BC=,∴2AB2=BC2=AB2+AC2,∴AC=AB,∴△MCA≌△NAB(AAS),∴AM=BN=,∴OM=OA﹣AM=3﹣,设CM =AN =b ,则ON =OA +AN =3+b ,∴C (3﹣,b ),B (3+b ,),∵点B 、C 在在函数y =上(x >0)的图象上,∴(3﹣)b =(3+b )=k解得:b =,∴k =18+15,综上所述,k 的值为或。
相似三角形基本模型一线三等角PPT课件

Unit 7 Cultural relicsUnit 7 ultural relis• 重点词汇解析•1 inlude vt 包括;包含1)inluding为介词,后接名词、代词作宾语。
2)inluded为过去分词充当的形容词,无比较级和最高级,其前常用名词或代词。
3)比较inlude,ntaininlude作“包含”解时,其后的宾语只是整体的一部分。
ntain作此意解时,其后的宾语指的是整体的全部。
2 restre vt1)归还t restre stlen prpert 归还赃物2)恢复;复兴t restre la and rder 恢复法律和秩序3)恢复健康;复原restred after ne’s hlida 假期之后健康恢复了3 rebuild v 再建;重建rebuild a huse after the fire火灾后重建房子。
注意:re-前缀,加在动词或名词前。
“重新”。
如:rerite, repen, revisit, reae, reprint, reread4 burn vi, vt burnt 或burned, burning1) 燃烧The huse is burning 房子烧起了。
2) 发光;照亮a light burning 灯光亮着3) 发热;炙热the burning sand 炙热的沙子4) 热衷She is burning t tell u the nes 她急于要告诉你这消息。
Everbd is burning t n the gd nes大家都急于想知道这则好消息。
) 烧伤;烧坏;烧毁He burnt all his papers 他烧毁了(他)所有的。
n 烧伤burns n her hand 手部的烧伤burn up (因热度过高)烧坏; 快速旅行;赶路t burn up the rad 赶路beaut n1) 美,美貌a fler f great beaut 一朵非常美丽的花2) 美人;美的事物ur daughter is quite a beaut 你的女儿很漂亮。
“一线三等角”相似模型专题学习

§专题学习:“一线三等角”相似模型安海中学 谢伟良【教学目标】1、认识“一线三等角”的基本图形并会用模型解决相似中的相关问题2、通过抽象模型,图形变换,变式类比等方法提高综合解题能力 【教学重点】运用“一线三等角”相似模型解题。
【教学难点】“一线三等角”的基本图形的提炼、变式和构造运用 【教学方法】 合作探究、小组讨论 【教具准备】 三角尺,多媒体. 【教学过程】一.类比探究,问题导入:(1)如图,已知∠A=∠BCD=∠E=90°,图中有没有相似三角形?并说明理由。
如图,已知∠A=∠BCD=∠E=60°,图中有没有相似三角形?并说明理由。
(3)如图,已知∠A=∠BCD=∠E=120°,图中有没有相似三角形?并说明理由。
思考:解:△ABC ∽△ECD,理由如下: ∵∠ACD 是△CDE 的一个外角 ∴∠ACD=∠D+∠E=∠D+90°又∵∠ACD=∠ACB+∠BCD=∠ACB+90° ∴∠ACB=∠D ∵∠A=∠E=90° ∴△ABC ∽△ECDEEDCBA观察以上三个图形,同学们能否说说这三个图形的共同特点?1、点A 、C 、E 在同一条直线上2、∠A=∠BCD=∠E= α3、△ABC ∽△ECD我们简单的把这样的图形叫做“一线三等角”BB二、抽象模型,揭示实质如图,已知∠A=∠BCD=∠E=α°,图中有没有相似三角形,并写出证明过程。
特别注意:在写相似三角形时,要找好对应点。
三.运用新知,看图作答四、典例解析综合运用归纳:“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形。
这个等角可以是直角,也可以是锐角或者钝角。
解:△ABC∽△ECD,理由如下:∵∠ACD是△CDE的一个外角∴∠ACD=∠D+∠E=∠D+α°又∵∠ACD=∠ACB+∠BCD=∠ACB+α°∴∠ACB=∠D∵∠A=∠E=α°∴△ABC∽△ECD总结规律:顺口溜:“一线三等角,两头对应好,外角导等角,相似轻易找”E例1:下列每个图形中,∠1=∠2=∠3,请你快速找出“一线三等角”的基本图形所形成的相似三角形(对应顶点写在对应位置)。
几何模型一线三等角模型

一线三等角模型一.一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.一线三等角的分类全等篇同侧锐角直角钝角P异侧相似篇A同侧锐角直角钝角P异侧三、“一线三等角”的性质1.一般情况下,如图 3-1,由∠1=∠2=∠3,易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如图 3-1,若 CE=ED,则△AEC≌△BDE.3.中点型“一线三等角”如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE ∽△CFD ∽△DFE.4.“中点型一线三等角“的变式(了解) 如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.如图 3-4“中点型一线三等角”通常与三角形的内心或旁心相关,1902BOC BAC ∠=︒+∠这是内心的性质,反之未必是内心.在图 3-4(右图)中,如果延长 BE 与 CF ,交于点 P ,则点 D 是△PEF 的旁心.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明 )图 3-5其实这个第 4 图,延长 DC 反而好理解.相当于两侧型的,不延长理解,以为是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题 四、“一线三等角”的应用1.“一线三等角”应用的三种情况. a.图形中已经存在“一线三等角”,直接应用模型解题; b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c.图形中只有直线上一个角,不上“二等角”构造模型解题.体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特殊性如图 3-6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过 C、D 两点作直线 l 的垂线是必不可少的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相 似
A型
基本 8型 图形
K型
一线三等角是一个常见的相似模型,指的是有三 个等角的顶点在同一条直线上构成的相似图形, 这个角可以是直角,也可以是锐角或钝∠。不同 地区对此有不同的称呼,义乌通常称为“ K形图 ”,哈尔滨通常称为“ M形图”,以下统称为“ 一线三等角”。
K字型的一般形式
且∠ BEF=110°,若AE=3,
DF长为__1_.5_____.
? 4如图,在矩形ABCD中,AB=7,BC=3,E在 AD上,且AE=2,在边AB上是否存在点P,使 得以P,A,E为顶点的三角形与以P,B,C为 顶点的三角形相似?若不存在,请说明理由
;若存在,这样的点有几个?并计算出AP的 长.
? 如图,正方形ABCD边长为8,M、N分别是BC、CD上的两个动点, 当M点在BC上运动时,保持AM和MN垂直.
? (1)证明:Rt△ABM∽Rt△MCN;
? (2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式; 当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大 面积;
你能证明吗?
证明:? 在? ABC中 ? 1? ? A? ? ACB ? 180? 又? ? 2 ? ? DCE ? ? ACB ? 180? ? ? 1? ? 2? ? 3 ?? A ? ? DCE ? △ABC∽△CDE
三角形基架
K型 矩形基架
梯形基架
1、如图,等边△ABC的边长为3
,点D是BC上一点,且BD=1,在
? (3)当M点运动到什么位置时,Rt△ABM∽Rt△AMN?求此时x的 值.
AC上取点E,使∠ ADE=60度,AE
长为( c )A. 3 B. 2 Nhomakorabea2
3
C. 73D.
3 4
2. 在矩形ABCD中,AB=4,BC=5,AF平 分∠ DAE,EF ⊥AE,
则CF= 3/2 。
3、如图,梯形ABCD中,AD∥BC ,AB=DC=AD=,6 ∠ ABC=70°, 点E,F分别在线段AD,DC上,
