少片簧优化设计
少片簧改进设计与整车匹配之理论解析

板簧承载过 ab 、 点以后 , 橡胶副簧起作用 , 板簧 刚度 的非线性特性随 即表现 了出来 。在实际设计 中, 我们把半载时的板簧受力控制在 ab 、 两点附近 ,
而对于客车板簧来说 : 1 a ) 点之前 ,主簧起主要 的承载作用 ,由图 可 以看 出曲线呈直线 ,即反 映的板簧 刚度是不变 的; 2 ab , ) _ 段 板簧反映为主副簧的复合刚度 , 由
由图 5可 知 :
图中可知此段刚度非线性变化 ,也就是说此段板簧 反映出的刚度是不断变化的;
维普资讯
2 0 ( 总 2 0 轻 型汽 车技 术 0 7 2) 1
技 术纵横
1 9
少片簧改进设计与整车匹配之理论解析
魏 大 军
( 南京依维柯汽车有限公司产 品研究发展部 )
摘
要
本文介绍 了南京依维柯- 4现有产品后悬架板簧的结构状态和性能 ,解析 了板簧与 - 整车设 计 的 匹配 以及 少 片簧 材料 的 改进设 计 。 关键词 : 板簧 设计 整车匹配 分析
要标 准 。
厂 —— 悬架垂直变形 ( 绕度 ) 卜 悬 架 簧载 质量
C= / — — 悬架 刚度 ( f Mg) 由公 式 ( ) 见 : 1可 1 在悬 架所 受 垂直 载荷 一定 时 , 架 刚度 C ) 悬
越小 , 则汽车 自然振动频率 n 越低 ; 2 当悬架刚度 C一定时 , ) 簧载 质量 越大 , 则 悬架垂直变形. 厂 越大 , 自然振动频率 n 而 越低。 因此 , 了使簧载质量从汽车空载到满载的范 为 围内变化 时, 车身 自 然振动频率保持不变或变化很
两 片副簧
圈 2
钢板弹簧优化设计及CAE研究

少片式钢板弹簧的设计与计算_易双贵

悬架对汽车行驶平顺性有重要影响 。 少片式钢板弹簧是非独立悬架常用的弹性元件 , 较多片簧而言 , 因减少片间摩擦而改善了汽车的行驶平顺性 , 并且可以节省材料 , 减轻重量 , 更重要的是可以降低总成高 度 。 在保证同样寿命的前提下 , 重量大约比多片弹簧减少 40% 左右 , 因此得到广泛采用 。
k = 1 k =1 n n n 2 [ 3] E I k A k1 1 。 2 R R k 0 +ΔR k
1 1 u d U≈ E ∑ I 根据总变形能最小的条件 , 将 d 近似表示为 : 。 kA k 2 k= 1 d R d R R R 0 0 R k 0 +ΔR k 0 并令 d U = 0 , 同时将式 ( 4) 代入 , 便可解得 : d R 0 1 ( M ) 0k E ∑ k = 1 α =1 - n I A k k ∑ R k = 1 R 0 +Δ k 带入参数计算如下 : h 1 β′ = 1 -0. 52 = 0. 48 1 =1 h 2 W 1 = b h 21 6
k 2 3
∑M
i =1
0k
=0, 处理 ( 见表 1) 。 表 1 预弯矩计算公式
总片数 n=3 主片预弯矩 N ·m m M01 = ( 300 -σA) W1 W1 主片均值断面系数 /m m3 说 W1 =
少片变截面钢板弹簧优化设计_郑银环

3
x2 ⋅ x 1
(7)考虑弹簧的应力分布和其在 l1 段内的强度,最大 应力应小于允许应力[σ]1,约束方程为:
g 7 ( X ) = [σ ]1 −
6 Px3 ≥0 2 nbx1
(8)按弹簧强度要求,弹簧在载荷的作用下,其计算 应力应小于材料的许用应力[σ]2。 根据最大应力的位置不 同,得 当 x3 > ( x4 − l3 )(2
片数 n 3 4 x1=h1 (mm)
表 1 优化设计结果
x2=h2 (mm) x3=l1 (mm) x4=l (mm) F(X) (kg) K (N/mm)
8.1903 14.9547 100.0000 658.4834 31.2419 176.88 8.0000 12.2608 100.0000 597.8023 33.2925 176.88
g 5 ( X ) = L / 2 − x4 ≥ 0
(6)为了保证汽车具有良好的行驶平顺性, 弹簧刚度 K 对于设计要求的刚度 Kc 的误差应小于某个精度值 Ke,因 此得约束方程:
・48・ 机械 2004 年第 31 卷增刊 理系统已经应用于西华大学, 如何保证原有系统在校园一 卡通系统中的联接与应用,是本方案介绍的重点。 为了解决上述问题, 可采用了多种模式, 核心就是提 出的“信息高速公路”的概念。 模式之一: 由一卡通系统公共接口标准, 部分早期子 系统按照此接口标准进行修改,完成与一卡通系统的对 接; 模式之二: 部分早期子系统提供接口,然后由一卡通 系统与之对接; 模式之三:针对部分早期子系统开发中间接口子系 统,该接口子系统用于协议和数据格式的转换。 模式一适用于可以修改数据接口的子系统,模式二 为适用于可以提供数据接口的子系统, 模式三适用于既不 能修改数据接口, 又不能提供数据接口供其他系统调用的 子系统。简而言之,由校园一卡通工程构建“校园信息高 速公路” , 各个子系统按一定的接口标准接入一卡通系统, 其角色类似于高速公路出入口。 (上接第 45 页) [σ]2=500MPa。 给定端部等厚最小允许厚度 H1=8mm ,最大允许淬 透厚度 H2=15mm,允许刚度误差 Ke=0.005,改变弹簧的 片数来进行优化,结果如表 1 所示。 原设计中弹簧质量为 40.9kg,经过优化计算,弹簧质量下降许多,对应两种设 计结果,质量分别下降了 23.6%和 18.6%。 参考文献: [1] 徐 为 民 , 徐 兵 , 朱 显 灵 , 吴 文 喜 . 校 园 一 卡 通 和 数 字 化 校
浅析变截面少片簧计算
浅析变截面少片簧计算汤玉平李细平江照亮(三一重工股份有限公司邮编410010)摘要:少片簧具备很多优点,质量轻,摩擦小噪音低,同时还能改善车轮和路面的附着性能等。
所以在汽车领域少片簧的应用已经越来越广泛。
但是少片簧如果设计不当,也很容易出现致命的故障。
所以少片簧的设计计算尤为重要。
关键词:汽车少片簧优点计算引言:要想变截面少片簧在各截面处的应力相等,断面形式从理论上来讲,板簧各点厚度沿长度方向必须做成抛物线型式。
这种抛物线型式板簧是理想的等强度梁,板簧各点应力分布最合理。
材料利用率很高。
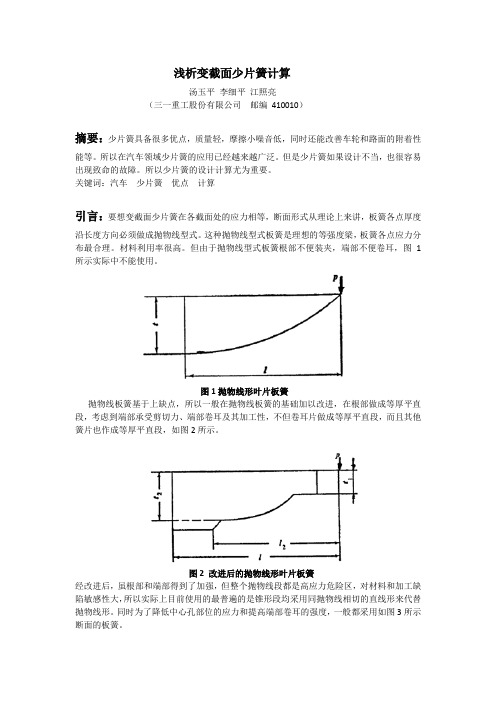
但由于抛物线型式板簧根部不便装夹,端部不便卷耳,图1所示实际中不能使用。
图1抛物线形叶片板簧抛物线板簧基于上缺点,所以一般在抛物线板簧的基础加以改进,在根部做成等厚平直段,考虑到端部承受剪切力、端部卷耳及其加工性,不但卷耳片做成等厚平直段,而且其他簧片也作成等厚平直段,如图2所示。
图2 改进后的抛物线形叶片板簧经改进后,虽根部和端部得到了加强,但整个抛物线段都是高应力危险区,对材料和加工缺陷敏感性大,所以实际上目前使用的最普遍的是锥形段均采用同抛物线相切的直线形来代替抛物线形。
同时为了降低中心孔部位的应力和提高端部卷耳的强度,一般都采用如图3所示断面的板簧。
图3 根部和端部同时加强的变截面板簧为了适合长跨度产品的需要,可采用图4所示断面的板簧图4 长跨度加强型变截面板簧1、 少片簧的计算1.1 已经条件在进行钢板弹簧计算之前,应当知道下列初始条件,轴(桥)负荷G 1、簧下部分荷重G 2、U 型螺栓距、板簧宽度、板簧跨度、板簧材料等。
1.2 少片簧厚度的计算本文将从等应力梁的角度,对少片簧的计算做初步的探讨。
图4所示 变截面簧,根部满足安装应做成等厚平直段,同时满足U 形螺栓夹紧处的工作应力cσ(cσ<[σ])。
则其厚度为h 22h = (1)式中: Pi ——板簧端部载荷 l ——板簧伸直长度之半 B ——板簧宽度 S ——U 形螺栓中心距板簧端部为了主片承载也需要做成等厚平直段,板簧连接处应做成圆角过渡。
某皮卡车少片变截面钢板弹簧后悬架设计讲解

目录1方案论证 (1)1.1悬架结构形式分析 (3)1.1.1 非独立悬架和独立悬架 (3)1.1.2前悬架方案的选择 (4)1.1.3 比较选型 (4)1.2少片变截面钢板板簧结构分析 (5)1.2.1抛物线形叶片弹簧 (5)1.2.2梯形变厚断面弹簧 (8)1.3钢板弹簧的布置方案 (9)2悬架主要部件 (11)2.1钢板弹簧的形式 (11)2.1.1叶片断面形状 (11)2.1.2叶片端部形状 (12)2.2 板簧两端与车架的连接 (12)2.2.1连接的结构形式 (12)2.2.2板簧卷耳与衬套 (13)2.3减震器 (14)2.3.1减振器的作用 (14)2.3.2减振器的结构: (15)2.3.3 减振器工作原理: (15)2.3.4减震器的选择 (15)3 悬架的设计计算 (17)3.1弹性元件的计算 (17)3.2优化设计 (20)3.3变截面钢板弹簧校核 (25)3.3.1校核刚度 (25)3.3.2 弹簧的最大应力点及最大应力 (26)3.4 钢板弹簧总成在自由状态下的弧高及曲率半径 (27)3.5 钢板弹簧各片自由状态下曲率半径的确定 (28)3.6钢板弹簧总成弧高的核算 (29)3.7钢板弹簧强度验算 (29)3.7.1驱动时计算应力 (29)3.7.2.汽车通过不平路面时钢板弹簧的强度 (30)3.8钢板弹簧卷耳和弹簧销的强度核算 (30)3.8.1卷耳应力的验算 (30)3.8.2钢板弹簧销的验算 (31)3.8.3 U形螺栓强度验算 (32)3.9减振器性能参数的选择 (33)3.9.1 相对阻尼系数ψ (33)3.9.2 减振器阻尼系数 的确定 (34)F的确定 (35)3.9.3 最大卸荷力3.9.4计算结果以及减震器的选择 (35)4 CATIA实体建模 (37)4.1CATIA简介 (37)4.2实体建模 (38)4.2.1钢板弹簧的绘制 (38)4.2.2盖板的实体图 (39)4.3主要零件实体图 (39)4.4装配 (42)5 结束语 ................................................................................................ 错误!未定义书签。
少片变厚断面钢板弹簧的设计

公司网址: 电子邮箱:4612757@1为减轻整车重量,使车辆轻量化,改善汽车的平顺性,作为汽车钢板弹簧易损件来说,是实现车辆轻量化的一个不可忽视的零件。
因此,目前国内许多汽车越来越多地开始采用由一片或几片纵向变厚断面弹簧组成的少片弹簧。
(见图一)图一现就宽度不变的抛物线叶片弹簧和梯形变厚叶片弹簧的刚度及其有关应力的计算介绍如下:一、抛物线叶片弹簧(见图二)1、等应力梁实际上抛物线叶片弹簧是一种等应力梁少片变厚断面钢板弹簧的设计公司网址: 电子邮箱:4612757@2设弹簧端部的载荷为P ,弹簧宽度为B ,那么弹簧中央部位A —A 处的应力бA 则为:бA=6P e /Bh 〈1〉弹簧在任一截面ex 处的应力бx 则为:бx=6Pe x /Bh x 〈2〉因弹簧是等应力梁,所以弹簧在任一截面处的应力均相等,由公式:〈1〉和公式〈2〉相等条件得到:hx=h (ex/e ) 〈3〉由上式可看出,欲使弹簧在各截面处的应力相等。
叶片弹簧各点厚度必须沿长度×方向做成抛物线形状。
实际上,理想的抛物线弹簧是无法使用的,这种弹簧在端部不能承受剪应力,卷耳端部强度差,加工难。
所以考虑卷耳端部的强度和弹簧中部实际装车夹紧状况,抛物线叶片弹簧应制成如下:见图三2221公司网址: 电子邮箱:4612757@3图三图中:A 、B 、C 、D 部份弹簧厚度不变,而B 、C 、O 部份弹簧厚度按抛物线变化。
2、抛物线叶片弹簧的刚度: 弹簧在任一截面处的惯性矩分别是 在(O —e 1)范围内J 1为常数 J 1= 式中:n 弹簧片数在(e 1e 2)范围内,断面惯性矩J 2为X 的函数。
J 2= 由公式〈3〉得:J 2= ×( )×n 在(e 2 e 1)范围内,J 3为常数。
J 3= 由于在不同长度范围内惯性矩J 值不同,经整理后刚度值为: C= · ·a式中a 断面修正系数,通常取0.9结论:事实上,抛物线叶片弹簧,在现实的汽车钢板弹簧3 3 3 231 12 ×n ×nBh 1╳nxBh 12 32Bh 12e xe 3 2Bh6E J 3 e (1+( )·K ) e 2 e 3公司网址: 电子邮箱:4612757@4加工中,不能付诸实现,因此较多地采用的是梯形变厚断面代替抛物线变化的梁。
梯形变截面板簧片简易设计方法_整理材料

梯形变截面板簧片的简易设计方法在少片簧设计中,为了节约材料,减轻自重,各板簧片尽可能做成等应力梁,使材料得到充分利用。
抛物线形板簧片属于等应力梁,但制作工艺要求较高,不易控制。
传统的少片簧板簧片采用梯形变截面结构,如果要少片簧设计的最轻,板簧材料得到充分利用,梯形变截面板簧片要设计的尽可能接近等应力梁。
目前梯形变截面板簧片的设计通常有两种方法,一种为试凑法,即根据经验初步选取尺寸参数,然后代入公式验算,经过反复计算,直到选择到最优的参数,这种设计方法不容易获得最佳设计方案,且费工时;另一种为最优化数学方法,将梯形弹簧的各设计参数做为变量,建立一系列函数方程,以理论质量最小作为目标函数,根据各约束要求,求解各参数,该方法虽然能得到最佳方案,但需要进行大量的计算,费工费时。
半 l ,线段NA 等于板簧片厚度h ;若将该梯形变截面板簧片设计的质量最轻,使之接近等应力梁,则线段BC 愈接近曲线OB ,此时梯形NABCO 的面积最小。
建立如下数学建模:由于OA 曲线为抛物线规律变化,则有:5.0⎪⎭⎫⎝⎛=l x h y (1)假设E 点坐标为(x 1,y 1)对(1)式E 点(x 1,y 1)求导可得,E 点的斜率k 为: ⋅=lx h k 12 (2)假设线段OC 长度为OC 则线段BC 的方程为:OC kx y += (3)又线段BC 过E 点(x 1,y 1),111kx y OC -=将(1)式、(2)式带入可得:115.01112x lx hl x h kx y OC -⎪⎭⎫ ⎝⎛=-= =lx h 12 (4) 线段CF 长度:lx h h OC h CF 21-=⋅-= (5)线段l 2长度:1122x l x kCFl -=⋅=(6) 三角形CBF 的面积S 为221l CF S = (7)将(5)式、(6) 式带入(7) 式整理得:()1112221x l x lx hh S -⎪⎪⎭⎫⎝⎛-==lx hx hx l x h 11114+- 若三角形S 面积最大,则梯形NABCO 面积最小,线段ABC 就愈接近抛物线,此时以截面为梯形NABCO 的板簧片就愈接近等应力梁。
基于Matlab的少片簧非线性优化及其用户界面设计

0.008
改变弹簧的片数来进行优化。优化结果如表 2: 表 2 优化设计结果
x1=h1 (mm) 8.0000 7.5279 x2=h2 (mm) x3=l1 (mm) x4=l (mm) F(X) (kg) σmax K (MPa) (N/mm) 71.087 70.968 71.076
14.2787 114.1692 723.7327 18.4302 449.086 13.2233 150.4721 740.4721 26.0125 347.31
DOI:10.15989/ki.hbnjzzs.20141119.001
《唐山市资源节约型企业现状、 困境与出路— ——以开滦集团为 基金项目: 唐山市社科联 例》 (TSSKL2014-026 )
汽车少片弹簧的优化设计方法研究

汽车少片弹簧的优化设计方法研究汽车的悬挂系统起到了支撑车身和缓解路面震动的作用,而汽车悬挂系统中的弹簧则是起到支撑车身重量和传递路面震动的作用。
然而,在现代汽车设计中,汽车生产厂商非常注重车身的轻量化,所以早期汽车的传统螺旋弹簧已经逐渐被少片弹簧所替代。
这是一项非常艰巨的工程任务,需要汽车制造商深入研究,设法钻研如何在保证汽车性能和安全的前提下,减少汽车弹簧的材料和数量,以此减轻车身重量,降低油耗和污染。
因此,这篇文章会讨论少片弹簧的优化设计方法的研究。
首先,我们需要了解什么是少片弹簧。
少片弹簧是由几个钢板片层叠而成,过去传统的螺旋弹簧使用钢丝在支撑车身重量。
由于少片弹簧采用层叠薄钢板组装,相对于传统的螺旋弹簧,它在弹性、安全性、减震性等方面有着更高的性能,同时也具有较低的重量和体积,近年来成为了汽车行业的首选。
目前,少片弹簧已经广泛应用于汽车悬挂系统中,但是由于车身结构和台架轮廓的限制,少片弹簧的结构并不总是理想的选择。
因此,研究人员提出了一种新的优化设计方法,以实现少片弹簧系统的完美结构。
1.少片弹簧层数的优化在设计少片弹簧的过程中,要控制的主要参数是弹簧的刚度和压缩程度。
由于少片弹簧的主体是由若干层薄钢板组成的,因此层数的多少会对弹簧的刚度产生较大的影响。
在考虑少片弹簧的层数时,需要平衡弹簧的稳定性和弹性,使其既能承受车身的重量,又能够缓解路面震动。
在通过实验和仿真等方式确定少片弹簧的理想层数后,还需要进行材料和生产工艺的进一步优化。
在钢板的选择上,需要优先考虑其材料性能和重量比,以保证弹簧具有足够的弹性并减轻车身重量。
同样,生产过程的优化也是至关重要的,因为良好的生产工艺不仅可以有效地减少零件成本,而且还能够提高产品的可靠性和安全性。
2.软轴的优化设计在少片弹簧的研究中,软轴的设计是一个重要的环节。
在传统悬挂系统中,弹簧的刚度直接影响车辆的悬挂性能和汽车的稳定性。
软轴是一种弹性元件,能够减缓弹簧的突然压缩,使汽车在行驶过程中更加稳定。
汽车少片弹簧的优化设计

汽车少片弹簧的优化设计1概述近几年来,许多国家从节能角度出发,力求使车辆轻量化,而汽车钢板弹簧则是实现汽车量化的一个不可忽视的部件。
为减轻钢板弹簧的重量和改善平顺性,在汽车上越来越多地使用由一片或几片纵向变厚端面弹簧组成的钢板弹簧。
这种弹簧不仅在轿车上用,而且在火车上应用也较多。
现在汽车上采用的变厚截面的弹簧主要有两种型式:叶片宽度不变和宽度向两端渐变的弹簧。
这里指讨论叶片宽度不变的少片弹簧。
2等应力梁及其几何形状等应力梁是指任一截面处最大应力都相等的梁。
如下图所示,假设等应力梁的上面为一平面,下面为一个曲面,作用在弹簧端部的载荷为P ,弹簧宽度为b ,那么弹簧中央部位A —A‘处的最大应力A σ为26A Pl bh σ=弹簧任一截面x 处的最大应力x σ为 26x x Px bh σ= 根据等应力梁的定义,二者影响等,故联立得12()x x h h l= 由此可见,等应力梁的厚度沿长度方向按抛物线规律变化。
图13 抛物线形叶片弹簧3.1理想的抛物线形弹簧和抛物线弹簧从理论上讲,讲叶片弹簧制造成等应力梁的形式,使各处最大应力相等时最合理的,材料作用也充分。
一般把上图所示的抛物线形状制造的叶片弹簧成为理想的抛物线形弹簧。
由于这种弹簧端部不能承受切向力,因此实际上是不能使用的。
要想使其端部能承受切应力,则需要加强卷耳末端的强度。
下图为加强了的抛物线形叶片弹簧,称之为抛物线形弹簧。
考虑到弹簧的装夹情况,将弹簧的中央和两端,将图中AB 段和CD 段两部分分别制成相等的厚度,将BC 部分制成按抛物线规律变化的厚度。
图23. 2抛物线形弹簧的刚度根据马莫发(虚载荷法)可以求出在载荷作用点处的变形0l p l xdx f M M EJ =∫ 算式中 p M l M 分别为由载荷P 和单位力所引起的力矩;x J 为叶片弹簧在任一截面处x 处的惯性矩。
弹簧在不同长度范围内x J 值各不相同,分别为10x l ≤≤时,311/12x J J bh n ==12l x l ≤≤时,333222/12()/12x xx J bh n b h n l == 2l x l ≤≤时,322/12x J J bh n ==p M l M 可分别表示为,p l M xP M x ==将上诉各个公示带入几分算式中,求得3322[1()]3Pl l f k EJ l=+ 332212/12,1,/J bh n k h h ββ==-=式中n 为弹簧的片数。
基于内点罚函数法的非对称钢板弹簧优化设计

基于内点罚函数法的非对称钢板弹簧优化设计潘俊斌;韦建平;肖光育;何煜【摘要】以某微客开发过程中的非对称少片变截面钢板弹簧为主要研究对象,进行钢板弹簧的优化设计及计算,建立该钢板弹簧的优化设计数学模型,并以内点罚函数法的优化设计理论为基础对钢板弹簧进行优化设计,在满足强度条件和刚度条件等约束的要求下,使钢板弹簧的质量减少,达到轻量化优化设计的目的.并将优化结果和ABAQUS计算结果进行比较,结果显示:优化结果不仅保持了钢板弹簧的计算精度,还可以提高钢板弹簧的计算效率.【期刊名称】《汽车零部件》【年(卷),期】2016(000)004【总页数】5页(P10-14)【关键词】非对称少片变截面钢板弹簧;内点罚函数法;优化设计【作者】潘俊斌;韦建平;肖光育;何煜【作者单位】上汽通用五菱汽车股份有限公司,广西柳州545006;柳州孔辉汽车科技有限公司,广西柳州545006;上汽通用五菱汽车股份有限公司,广西柳州545006;上汽通用五菱汽车股份有限公司,广西柳州545006【正文语种】中文【中图分类】U465.2传统多片钢板弹簧由于体积和质量较大,不利于人们对汽车驾乘性能的不断提高以及对能源、材料利用的认知,各大汽车厂家在进行钢板弹簧设计开发时不仅要求轻量化,还要求弹簧在各常用载荷状态下的偏频基本相同,这就使得钢板弹簧逐渐向少片变截面变刚度的方向发展。
与此同时,为了减小片间的摩擦,在满足汽车设计要求以及性能匹配要求的前提下,尽量使得悬架弹簧的片数越少越好,片数越少、质量越轻,这样才更有利于实现车辆的轻量化、提高车辆行驶的平顺性和乘坐舒适性等。
为了能够提高使用钢板弹簧悬架的汽车转向稳定性,可通过改变汽车前后轴质量分布,调整汽车轴距,并减少钢板弹簧纵向弯曲变形。
针对这一要求,有专家提出了采用非对称设计的钢板弹簧作为悬架支撑元件。
非对称钢板弹簧计算的主要任务是刚度的匹配设计及结构应力的校核。
其设计模式与对称板簧是一致的,都是基于工程图纸的物理样件制造及试验,并使这一过程反复进行,过程比较缓慢,周期比较漫长。
少片簧优化设计

少片簧优化设计张办;罗志龙【摘要】通过举例和理论计算分析少片簧的片数、长度和应力状态对少片簧质量的影响,指出在少片簧设计中其产品质量与应力状态成反比关系,与其片数和长度无关系,进而得出在少片簧设计中提高设计应力和选择较少片数和较短长度是生产成本最低、质量最轻的优化设计方法.【期刊名称】《汽车科技》【年(卷),期】2010(000)004【总页数】4页(P38-41)【关键词】少片簧;片数;长度;应力状态【作者】张办;罗志龙【作者单位】东风汽车悬架弹簧有限公司,十堰,442046;东风汽车悬架弹簧有限公司,十堰,442046【正文语种】中文【中图分类】U463.33资源短缺及环境污染已成为制约我国汽车产业可持续发展的突出问题,无论是从社会效益还是经济效益来考虑,降低汽车零部件的生产成本和生产满足使用要求的最轻化汽车零部件都是节约型社会发展的需要。
本文通过分析影响少片簧产品生产成本和质量的几个参数,得出少片簧设计最优化的设计方法。
1 根据不同片数和长度对比分析少片簧各参数之间的关系在悬架设计中钢板弹簧最主要的性能参数是承载能力和刚度,在满足主要性能要求时,少片簧的片数、长度和应力状态有很多组合,现分别按片数相同和长度相同分析各参数之间的关系。
1.1 分析长度对少片簧质量的影响按片数相同的情况,设计不同长度的少片簧,使其满足承载能力和刚度的要求,然后分析长度对少片簧的重量的影响。
假设簧载质量为2.5吨,为了满足舒适性要求刚度取3050N/cm设计少片簧,具体数据见表1、图1和表2、图2。
表1 2片方案对比方案号 2-1 2-2 2-3 2-4片数 2 2 2 2长度/mm 1 400 1 600 1 720 1 800刚度/N·cm-1 3 063 3 098 3 056 3 052质量/kg 31.2 40.6 46.5 50.9承载/质量(kN/kg) 0.801 0.616 0.538 0.491图1 各方案(2片)应力曲线图表2 3片方案对比方案号 3-1 3-2 3-3 3-4片数 3 3 3 3长度/mm 1 400 1 600 1 720 1 800刚度/N·cm-1 3 033 3 065 3 046 3 041质量/kg 40.5 53.1 61.7 67.1承载/质量(kN/kg) 0.617 0.471 0.405 0.373图2 各方案(3片)应力曲线图通过对表1、图1和表2、图2的对比分析可知片数相同时,其长度越短,少片簧的质量越轻,同时我们也可以看到其长度越短时,其应力和储能比越高。
少片不等长变截面钢板弹簧的优化设计_林小瑛

文章编号:1000-2243(2001)01-0056-04少片不等长变截面钢板弹簧的优化设计林小瑛(福州大学机械工程系,福建福州 350002)摘要:在保证钢板弹簧可靠使用的条件下,按钢板弹簧质量最小建立钢板弹簧优化设计的数学模型,并利用FORT RA N 77高级语言开发了优化计算程序T L SO DP.实例设计计算表明,用该数学模型和优化计算程序设计,钢板弹簧质量比原设计减少了29.6%.关键词:变截面钢板弹簧;优化;设计中图分类号:U 463.334.1文献标识码:A为了减轻汽车钢板弹簧的质量和改善平顺性,在汽车上越来越多地使用纵向变截面的少片弹簧(如图1).这种弹簧不仅在货车上广泛应用,而且在小客车上也有使用.当前,汽车上采用的变截面弹簧主要有两种形式:抛物线型和直线型(如图2).抛物线型弹簧应力分布合理,但制造工艺相对直线型难些;直线型弹簧虽不是完全的等应力分布,但制造工艺简单.本文设计中采用直线型模式.图1变截面弹簧结构示意图 图2变截面弹簧的形式 图3 第k 片受力分析简图1 数学模型的建立1.1 设计变量的确定由于钢板弹簧左右对称,故可取其一半进行分析(如图3).变截面钢板弹簧设计参数有h k ,h k ',l k ,s ,b,n.U 型螺栓装夹长度之半s 取决于弹簧在汽车上的装夹情况,叶片宽度b 取决于总布置和弹簧钢带尺寸规格,一般总片数n [4,且只取整数.为此,可认为s 、b 、n 为常数.于是,对于某一固定的n ,变截面钢板弹簧优化设计变量只有3n 个,即:X ={h 1,h '1,l 1,,,h k ,h 'k ,l k ,,,h n ,h 'n ,l n }T={x 1,x 2,x 3,,,x 3k-2,x k-1,x 3k ,,,x 3n-2,x 3n-1,x 3n }T1.2 目标函数的确定实现汽车轻量化,降低弹簧总质量是变截面钢板弹簧设计所追求的目标.为此,钢板弹簧的优化设计应以总质量最小作为目标函数,即:F(X )=m =Q bE nK =1M k直线型:M k =2[h k s +(h k +h k ')(l k -s)/2]=2[x 3k-2s +(x 3k-2+x 3k -1)(x 3k -s)/2]式中:M k 为第k 片质量因式;Q 为材料密度,对于钢,Q =7.8@10-6kg/mm 3;b 为弹簧宽度,mm .1.3 约束条件的确定1.3.1 刚度限制为保证汽车具有良好的行驶平顺性,弹簧的计算刚度C 0与汽车平顺性要求的刚度C (即设计刚度)收稿日期:2000-09-08作者简介:林小瑛(1956-),女,讲师.第29卷第1期福州大学学报(自然科学版)Vol.29No.12001年2月Jour nal of Fuzhou U niversity (N atural Science)F eb.2001之间的误差应小于E 0[1],即有约束条件:G 1(x )=(C 0-C )/C -E 0[0因为主片端部的变形就是弹簧总成一端的变形,所以计算主片端部变形,进而求得总成刚度C 0.如图3所示,主片(即k =1)分别在l 1和l 2处受到P 1和P 2的作用力,其端部变形f (1)B=P 1G (1)BB -P 2G (1)BA于是整付簧的刚度C 0为:C 0=2N (G (1)BB -G (1)BA P 2/P 1)-1式中:N 为修正系数,经验取N =0.9~0.92;G (k )ij 为变形系数,mm/N ,表示第k 片由于j 处单位作用力所产生的i 处的挠度;P k 为片端力,N .由梁弯曲理论,可推得变形系数G (k )ij 为:G (k )BB =l 3k /(3EI k )1-D3k 1+3#B -1k 0.5+B -1k1+l n (1-B k )#B -1k [2]G (k )BA =G (k )AB =l 3k /(3EI k )(Gc +Gd )G (k )A A =l 3k +1/(3EI k )1-D c 3k 1+3Bc -1k (0.5+B c -1k (1+l n (1-B c k )#B c -1k ))式中:G c =3D 3k #B -3k0.5((1+B k )C 3k -2C k )#(1-C k )-1-l n (1-C k ),G d =1-D 3k -1.5(1-l k +1#l -1k )(1-D 2k ),D k =1-s #l -1k ,B k =1-h c k #h -1k ;C k =B k (l k+1-s)(l k -s)-1,I k =1/12bh 3k ,E 为材料的弹性模量,E =2.1@105,N/mm 2.B c k =1-(h c k +(h k -h c k )#(l k -l k+1)#(l k -s )-1)#h -1k ,D c k =1-s #l -1k+1按照集中载荷假设,相邻两片在接触点具有相同挠度,即f(k )A=f (k+1)B,于是有[4]:P k G (k)AB -P k+1G (K )AA =P k+1G (k+1)BA按k =1,2,,,n -1展开此式可得n -1阶三对角型方程组,利用追赶法解方程组可得P k 表达式:P k =-Q k P k-1 (k =2,3,,,n )式中:Q k =G (k-1)A B (-G (k-1)A A -G (k )BB -G (k )BA Q k+1)-1,k =n,n -1,,,2,其中:Q n+1=0.1.3.2 强度限制由弹簧的强度要求,弹簧在载荷作用下,其计算的总成应力R c 和单片最大应力R k m ax 应分别不大于许用应力[R c ]和[R ][1],即有约束条件:G 2(x )=R c -[R c ][0G 3(x )=R k max -[R ][0 (k =1,2,,,n)对于各片不等长变截面钢板弹簧,一般用各片根部应力的平均值作为弹簧总成应力R c [2]:R c =1/nEnk=1W -1k (P k l k -P k+1l k +1)式中:W k 为叶片根部断面系数,W k =bh 2k /6,mm 3.单片最大应力R k m ax 一般分为三段考虑:1)0[l x [s :R k 1=(P k (l k -s )-P k +1(l k+1-s))/w k 2)s [l x [l k+1:R k 2=0.25B -1k W -1k (1-B k )-1(l k -s -D k )-1#(P k -P k +1)(l k -s)23)l k+1[l x [l k :R k 3=0.25B -1k W -1k (1-B k )-1#P k (l k -s)则R k max =max {R k 1,R k 2,R k 3},式中:D k =(1-B k )-1(P k -P k +1)-1#B k P k+1(l k -l k+1).1.3.3 极限工况强度限制汽车行驶时,钢板弹簧除受垂直载荷外,还受其它方向的力和力矩以及冲击载荷等作用,因此必须对这些受力工况的极限状态进行强度限制,以保证弹簧能可靠地工作[3].1)最大纵向力.紧急制动时,前钢板弹簧承受的载荷最大,其后半段出现最大应力;驱动时,后钢板弹簧承受的载荷最大,其前半段出现最大应力(图4)[3].P max =max {P 1,P 2}=m '#(G /2)#(l +U C c )/(2l )则R t m ax =P m a x l /W 0=0.25W -10m cG (1+U C c )#57#第1期林小瑛:少片不等长变截面钢板弹簧的优化设计图4 汽车作用在钢板弹簧上的力式中:m '为轴荷再分配系数,制动时m '=(G a /L a )(U h g +L 2)/G ,驱动时m '=L a /(L a -U h g );G a 为汽车总载荷,N ;h g 为汽车重心高度,mm ;L a 为轴距,mm ;L 2为汽车后轴中心线至重心的距离,mm ;G 为轴荷,N ;l 为弹簧的主片半长l =l 1,m m;C c 为弹簧固定点至路面的距离,m m ;U 为路面附着系数,取U =0.8;W 0为弹簧的总截面系数,W 0=EnK =1bh 2k /6.2)最大垂直力.汽车通过不平路面时,受到冲击载荷,产生最大垂直力[3]:Z k m a x =K G /2式中:K 为动载系数,K =f -1c (f c +fd );f c 为悬架的静挠度,mm ;f d 为悬架的动挠度,mm .则R k max =0.25W -10K Gl.为保证弹簧在极限工况下能可靠地工作,其工作应力不能超过材料的许用极限应力[R d ][3],即有约束条件:G 4(x )=0.25W -10#m c G (l +U C c )-[R d ][0G 5(x )=0.25W -10#K Gl -[R d ][01.3.4 根部厚度限制1)为保证弹簧钢材料的渗透性,弹簧根部厚度h k 应限制在某允许厚度h 0之内[1],即有约束条件:G 6(x )=x 3k-2-h 0[0 (k =1,2,,,n )2)由各叶片间厚度合理分配条件,第k +1片根部厚度h k +1应小于第k 片根部厚度h k ,即约束条件:G 7(x )=x 3k+1-x 3k-2[0 (k =1,2,,,n)1.3.5 端部厚度限制1)为满足变截面条件,叶片端部厚度h 'k 应不大于其根部厚度h k ,即有约束条件:G 8(x )=x 3k-1-x 3k-2[0 (k =1,2,,,n)2)为保证弹簧卷耳具有足够强度,主片端部厚度h '1应不小于某允许厚度h '0[1],即有约束条件:G 9(x )=h '0-x 2[0h c 0可通过验算卷耳处所受到的应力得到,即:R =3F X (D +h m )/(bh 2m )+F X /(bh m )[3]图5 卷耳受力简图式中:F X 为沿弹簧纵向作用在卷耳中心线上的力(如图5),F X =0.5m c G U ;D 为卷耳内径,m m ;h m 为钢板弹簧主片端部厚度,用h '0代替,mm .鉴于叶片在制动时F X 可能很大,故需要较大的安全系数,其许用应力较低,仅取[R ]=350N/mm 2,即:3F X (D +h c 0)/(b h c 20)+F X /(bh c 20)[350为此,约束条件G 9(x )可转为化为:G 9(x )=3F X (D +x 2)/(bx c 22)+F X /(bx c 22)-350[01.3.6 长度限制1)弹簧最大伸直长度受总布置限制,所以主片长度之半l 1应不大于某允许长度l 0,即有约束条件:G 10(x )=x 3-l 0[0 2)由各叶片长度分配合理条件,k +1片长度之半l k+1应不大于第k 片长度之半l k ,即有约束条件:G 11(x )=x 3k -x 3k-3[0 (k =2,3,,,n ) 3)为保证U 形螺栓装夹要求,最未片长度之半l n 应不小于某允许长度l 'o ,即有约束条件:#58#福州大学学报(自然科学版)第29卷G 12(x )=l 'o -x 3n [0综合上述各式,可以得到少片不等长变截面钢板弹簧优化设计的数学模型:min F (X )=mX ={x 1,x 2,x 3,,,x 3k -2,x 3k-1,x 3k ,,,x 3n-2,x 3n-1,x 3n }T ={h 1,h '1,l 1,,h k ,h 'k ,l k ,,,h n ,h 'n ,l n }T s #t G j (x )[0 (j =1,2,,,12)2 优化设计计算方法根据所建立的优化设计数学模型,已知该问题是一个维数较高、约束条件较多的非线性的最优化问题,而且约束条件均为不等式约束,所以可利用复合型法[4]来解决该问题.为此,利用FORTRAN 77高级语言开发了TLSODP(T aper Leaf Spring Optimum Design Program)程序.3 优化设计实例实例:BM2022A 型越野汽车的后钢板弹簧.已知:轴荷G =12103N,叶片宽b =70m m,U 形螺栓装夹长度之半s =55mm,总成许用应力[R c ]=500N/m m 2,材料许用应力[R ]=550N/mm 2,材料许用极限应力[R d ]=1000N/mm 2(弹簧材料为55SiM nVB),设计刚度C =130N/mm,允许误差E 0=0.03,静挠度f c =70mm,动挠度f d =70m m,根部允许厚度h o =16mm,主片最大允许长度之半l o =600mm,末片最小允许长度之半l c o =60mm,双向复合型法迭代收敛精度E c 0=0.01,汽车总载荷G a =20825N,汽车重心高度h g =900mm ,轴距L a =2500mm,汽车重心至后轴中心线的距离L 2=1050m m,弹簧固定点至路面高度C c =430m m.利用TLSODP 程序计算得到的结果和该越野车原始数据如表1所示.优化后的不等长变截面钢板弹簧的质量m =14.78kg,原设计的钢板弹簧质量m o =21kg ,比原设计减少29.6%.表1 优化结果和原始数据对照表优化项目n b/mm s/mm l 1/mm h 1/mm h 1'/mm m /kg 优化结果3705546216.99.814.78原始数据763606006.56.521参考文献:[1] 蒋立盛,方坚.少片弹簧的计算及其尺寸参数的选择[J].汽车技术,1984,6:25.[2] 彭莫,高军.变断面钢板弹簧的设计计算[J].汽车工程,1992,3:156.[3] 张洪欣.汽车设计[M ].北京:机械工业出版社,1989.[4] 刘惟信.机械最优化设计[M ].北京:清华大学出版社,1994.An optimu m design of the few different lengths of taper leaf springLIN Xiao-ying(Department of M echanical Eng ineering,Fuzhou U niv ersity,Fuzhou,Fujian 350002,China)Abstract:In order to improve the performances of the automobile stabilization and steering as well as to ensure the reliability of the leaf springs,a mathem atical model of optimum design for the leaf spring s is established on the basis of the smallest weig ht of the leaf springs and a calculation program T LSODP(Taper Leaf Spring Opt-i mum Desig n Program)is derived from FORTRAN 77.Finally,a practical example of design calculation is tak -en to show that the w eight of the improved leaf springs decreases 29.6%compared w ith the orig inal desig n by using the m athematical model and optimum calculation program.Keywords:taper leaf spring;optimum;design#59#第1期林小瑛:少片不等长变截面钢板弹簧的优化设计。
本文通过对某平衡悬架少片变截面钢板弹簧的CAE分析研究-有关汽车毕业论文

本文通过对某平衡悬架少片变截面钢板弹簧的CAE分析研究-有关汽车毕业论文摘要钢板弹簧是重型载重汽车平衡悬架系统中重要的弹性元件,关乎重型载重汽车的平顺性和节能性。
少片变截面钢板弹簧相比于传统多片等截面钢板弹簧质量更轻、平顺性更好,逐渐得到越来越多的重型车辆使用。
少片变截面钢板弹簧精益设计和疲劳寿命预测,是体现悬架性能和安全的两个重要方面,CAE技术的发展为解决这些问题提供了有力的工具。
本文通过对某平衡悬架少片变截面钢板弹簧的CAE分析研究,提供了从优化设计、精确建模到有限元分析以及一体化疲劳寿命仿真的整套流程,较好的完成了精益设计和数字化寿命预测,为平衡悬架少片变截面钢板弹簧的设计和性能研究提供一定的借鉴。
具体所做工作如下:研究了两种结构形式的少片变截面钢板弹簧,并利用MATLAB 软件对本次所设计板簧进行了参数优化。
对于少片变截面钢板弹簧三维模型的建立,提出了更加简捷精确的Pro/E骨架折弯建模方法,并进行了分析验证。
根据现代接触动力学相关理论,考虑大变形、片间接触和摩擦等多种非线性因素,在ANSYS Workbench 15.0中建立了少片变截面钢板弹簧的有限元模型,完成了板簧强度和刚度校核,探究了过渡段圆弧半径大小对板簧特性的影响,并对不同摩擦系数下的板簧应力分布、变形量、刚度和偏频进行了分析研究。
研究了疲劳寿命分析的基本理论,确定了少片变截面钢板弹簧疲劳寿命分析方法。
在综合考虑粗糙度、热处理和喷丸处理对板簧疲劳寿命影响的基础上,联合ANSYS Workbench与Designlife按照实际试验条件,对板簧进行了精确的一体化疲劳寿命仿真。
按照相关标准,对本次设计的少片变截面钢板弹簧进行了台架刚度试验和疲劳试验,验证了有限元分析与疲劳寿命仿真的正确与否。
关键词: 少片变截面钢板弹簧,优化设计,疲劳寿命仿真,有限元分析ABSTRACTLeaf spring is a important elastic element for heavy truck suspension balance system , which is a significant factor to the comfort and energy saving of heavy truck.Taper leaf spring is more lighter and better comfort compared to traditional leaf spring, which was widely used in heavy vehicles. The suspension performance and safety of Taper leaf spring can be reflected by lean design and fatigue life prediction, the development of CAE technology can provide a powerful tool to solve these problems.According to the CAE investigation of a taper leaf spring in a balanced suspension system. This paper presents a complete process for it, which include optimization design, precise modeling and finite element analysis, and the fatigue life simulation of the integration. Then lean design and digital life prediction of a balanced suspension taper leaf spring is conducted. It provides a certain reference to design and performance study. The detail process as follows: Studied two kinds of structure forms of taper leaf spring, and the parameter optimization of the plate spring is utilized by the MATLAB software.For taper leaf spring 3d model establishment, the more precise and simple modeling method of Pro/E frame bending is presented, and is validated.According to modern contact dynamics related theory, some nonlinear factors is considered, such as large deformation, contact and friction. The finite element model of taper leaf spring is established in the ANSYS Workbench 15.0, checking strength and rigidity of leaf spring, exploring the effect of transition arc radius on the characteristic of leaf spring, stress distribution and deformation, stiffness and frequency of the leaf spring are analyzed under different friction coefficient.To determine the analysis method of leaf spring fatigue life, the basic theory of fatigue life analysis is studied. The influence of roughness, heat treatment and shot peening treatment on leaf spring fatigue life is analysis. By combined ANSYS Workbench withDesignlife under the actual test condition, the precise integration fatigue life simulation of leaf spring is carried out.In accordance with the relevant standards, stiffness test and fatigue test of taper leaf spring is conducted. Then the finite element analysis and the fatigue life simulation is verified.Keywords: Taper leaf spring,Optimization design,fatigue life simulation, finite element analysis第一章绪论1.1 概述悬架系统是汽车上重要组成部分之一,它弹性地将车架(或承载式车身)与车轴(或车轮)连接起来[1]。
钢板弹簧的优化设计

第3章钢板弹簧的优化设计3.1钢板弹簧设计与分析概述钢板弹簧在汽车上工作承受着一定的负荷,作为安全部件其结构设计较为简单,但是相对于其结构钢板弹簧的计算方法确实有些复杂。
近些年来国内外对于汽车钢板弹簧的设计与分析也有很多研究,之所以引起众多国内外工程师的关注,是因为钢板弹簧在汽车悬架系统中得到了广泛的使用,同时悬架系统对于汽车的性能有着重要的影响,如行驶平顺性、操作稳定性、汽车燃油经济性、通过性等等。
在钢板弹簧的传统设计与分析中,一般是采用解析的方法。
它主要包括两种方法即是共同曲率法和集中载荷法,这两者应用的理论是在材料力学中提到的线性梁理论来解决在钢板弹簧中碰到的问题。
然而传统的分析方法过于简单,不符合实际中钢板弹簧各片的接触情况与其自身的以及同一模型中其它叶片的自由曲率、弧高、厚度、长度等几何形状有关,另外同其所受的载荷以及簧片装配力等因素相关,从本质上说是一个非线性问题即是工作载荷施加到簧片装配体上后形成的。
这样以来就不可能满足先前的设想,那么应用以往传统的方法就不可能很好地解释在汽车钢板弹簧中存在的一些问题。
传统中采用的解析法包含以下凡种方法;共同曲率法、集中载荷法、集中载荷法和共同曲率法相结合的方法、悬臂梁法[。
表3-1钢板弹簧的设计与分析方法解析法悬臂梁法、共同曲率法、集中载荷法、集中载荷和共同曲率结合法数值法有限元法悬臂梁法的应用是最早被采用的,设计者能够将板簧视为一个整体的变截面梁,以便对其应力和刚度进行估算,悬臂梁的最大应力在根部可通过材料力学中的相关原理来得到,进而采用公式即可求得,但是这种方法极为不精确。
共同曲率法是由前苏林工程设计专家帕尔希洛夫斯基在1954年提出来的,其基本的理论思想是设想在任何载荷下,能够将其简化为梯形单片来进行计算,即是簧片在同一接触面上曲率相等且各簧片在长度方向彼此无缝隙地接触。
这种方法比较典型用于刚度计算和应力分析,存在的不足是当片端无应力边界时不能应用,同时会使簧片的端点弯矩发生突变,以及造成后几个簧片的应力误差很大。
轻型卡车前钢板弹簧的设计

递力,必须使他们有一定的宽度。 因此,应该用中部
为矩形的双梯形钢板弹簧(见图 1)替代三角形钢板
弹簧才有真正的实用意义。 这种钢板弹簧各片具有
相同的宽度,但长度不同。 钢板弹簧各片长度就是基
于实际钢板各片展开图接近梯形梁的形状这一原则
来做图的,如图 2 所示。
b
B
L
图 1 双梯形钢板弹簧
L/2
△2 ∑h
本方案中选取 δ1=1.42
将所确定的数据带入(5)式,可求得:
h1=8.6 mm,圆整为 9 mm,即前钢板弹簧的厚度
为 9 mm。
1.7 钢板弹簧片宽的计算
有了 h 以后,再选取钢板弹簧的片宽 b 。 增大片
宽b,能 增 大 卷 耳 强 度 , 但 当 车 身 受 侧 向 力 作 用 倾 斜
时,弹簧的扭曲应力增大。 前悬架用宽的弹簧片,会
关键词:钢板弹簧;设计;校核
中 图 分 类 号 :TH123+.4
文 献 标 识 码 :A
文 章 编 号 :1673-3142(2009)11-0033-05
Design of Front Leaf Spring in Light-duty Truck
SUN Yun-zhu (Road Engineering Department of Dongying Road Bureau, Dongying 257041, China) Abstract: Design calculation for front leaf spring of light -duty truck is carried out, the parameters of number, width, thickness, length, arc height, curvature radius, inspection rigidity and assembling rigidity are determined and calibrated. The selected parameters have basicly met the requirement for smoothness, comfort and security of the trucks unloaded or fully loaded. Keywords: leaf spring; design; calibration
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O p i i a i n De i n o r b lc Sp i g tm z to sg f r Pa a o i r n s
ZH ANG Ban, LUO hi l n Z -o g
( n fn trS s e s n S r gC .t .S ia 4 0 6, hn ) Do ge gMoo u p n i p n oLd ,hy n4 2 4 C ia o i
c n i o n t e i a to e w ih fa p r b c s rn s p i t g o tt a a a  ̄i s r g d sg ft er p o u t i o d t n o h mp c ft e g to a a di p g , on i u h t r b c p n e i n o i r d cs s i h i n p i h
浚 潞 勰 究
d i 03 6 /i n1 0 - 5 02 1 .40 0 o: .9 9 .s .0 5 2 5 . O0 .1 1 js 0
汽车科 技第4 00 月 期21年7
少席薰
张 办 , 志 龙 罗
蘧谛
东 风 汽 车悬 架 弹 簧 有 限 公 司 。 堰 4 2 4 十 4 0 6)
摘要 : 通过 举例 和 理 论计 算 分 析 少 片簧 的 片 数 、 度 和 应 力 状 态 对 少 片簧 质 量 的 影 响 , 出 在 少 片 簧 设 计 中其 产 品 长 指 质 量 与 应 力状 态成 反 比关 系 , 其 片 数 和 长度 无 关 系 , 而 得 出 在 少 片 簧 设计 中 提 高 设计 应 力和 选 择较 少 片数 和 较 与 进 短 长 度 是 生产 成 本 最 低 、 量 最 轻 的优 化 设计 方法 。 质 关 键 词 : 片簧 : 少 片数 ; 度 ; 力状 态 长 应 中图 分 类 号 : 4 3 3 U 6. 3 文献 标 志 码 : A 文 章 编 号 :0 5 2 5 (0 0 0 — 0 8 0 1 0 — 5 论
参考 文献 : 本 文根据 电动 汽车动 力 系统 数学模 型 建立 的动 力 系统 Sm l k模 型 可 以有 效 仿 真 动 力 系 统 的运 i ui n
『 ] 列 铭 .中国 新 能 源汽 车 的 理 想 与 现 实 [ ] 生 态 经 济 , 1 顾 J.
Ke r s p rb l p i g ; u e fs rn e f l n t sr s o d t n y wo d : a a oi s rn s n mb r p g l a ; gh;t sc n i o c o i e e i
资 源短缺 及环境 污 染 已成 为制 约我 国汽 车产业 可持续 发展 的突 出 问题 ,无 论是 从社会 效 益还 是 经 济效益 来考虑 ,降低汽 车零 部件 的生产成 本 和生产 满足使 用要 求的最 轻化 汽车零 部 件都是 节约 型社 会 发展 的需要 。本 文通过 分析 影响 少片簧 产 品生产成 本和质 量 的几个参 数 ,得 出少片 簧设计最 优 化 的设
p o o t n l o t e r lt n h p b t e n w i h n t s o d t n,ah r ta h u e n e gh o p n e f h n r p ri a h ea i s i ew e e g t d s e sc n i o r te h n t e n mb ra d l n t f r g la . e o t o a r i si T o ti e n p r b l p i g d sg mp o e t e sr s o dto fp r b l p i g ,ee t n l l u e f p n e f b an d i a a o i s r e inI r v h te s c n i n o a a o i s r s s lc i i e n mb r o r g la c n i i c n o U si a d s o trln t st r d c h o e tl h e tw ih p i z d d sg . n h r e gh i o p o u e t el w s , g ts e g t t e i o mie e in
收 稿 日期 :0 0 0 — 5 2 1— 2 0
计 方法。
1 根 据 不 同 片 数 和 长 度 对 比分 析 少 片 簧 各
参 数 之 间 的 关 系
在悬 架设计 中钢 板弹 簧最 主要 的性 能参数是 承
载能 力和 刚度 , 满足 主要 性能 要求 时 , 片簧 的片 在 少
通 过 增 加 燃 料 电池 系 统 或 者 蓄 电 池 系 统 的 Smuik模块 ,本 文 的动力 系统 模型 就 可 以用来 进 i l n
行整 车能量 管理 策 略的研 究。
的主 要 限制 因素 是 实际部件 的工 作 负载 限制 ,而 不 是选 择较 大 后可 能出现 的不 稳定脉 冲 波动。
Ab t a t I h s p p r t i e a x mp e a d t e r t a ac lt n n lz u e f s r g l a ,e gh a d sr s sr c :n t i a e ,o g v n e a l n h o e i lc lu a i s a ay e n mb r o p n e f l n t n t s c o i e
