结构力学习题集结构的动力计算习题及复习资料
《结构力学习题集》(含答案)
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M 17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l ll/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/2219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
结构的动力计算习题

《结构的动力计算》习题一、判断题1、图示等效体系的关系是:3211111k k k k ++=。
( )2、结构的动力反应只与初始条件及动荷载有关。
( )3、任何动力荷载作用下均可以采用公式:1221-⎪⎪⎭⎫⎝⎛-=ωθβ计算动力系数。
( ) 4、外界感干扰力只影响振幅、不影响体系的自振频率。
( )5、体系的动力自由度数与质点的个数无关、也与结构静定或超静定无关。
( )6、图示体系各杆自重不计、EA =∞,则该体系在初始时刻的干扰力作用下将做竖向振动。
( )二、选择题1、增加单自由度体系的阻尼、但仍保持为低阻尼体系,其结果是( )。
A 、周期变长 B 、周期不变 C 、周期变短 D 、 周期视具体体系而定2、图示两个等效结构,正确的刚度关系是( )。
A 、k=k 1+k 2 B 、21111k k k += C 、21211k k k k k += D 、2112k kk k k +=3、图示体系不计阻尼,平稳阶段最大动位移y max =4Pl 3/7EI ,其最大动力弯矩为( )。
A 、3Pl /7 B 、4Pl /7 C 、12Pl /7 D 、4Pl /21 4、下列哪句话有错误或不够准确()。
第3题图A、在多自由度体系自由振动问题中,主要问题是确定体系的全部自振频率和相应的主振型; B 、多自由度体系的自振频率不止一个,其个数与自由度个数相等;C 、每个自振频率都有自己相应的主振型,主振型就是多自由度体系振动时各质点的位移变化形式;D 、与单自由度体系相同,多自由度体系的自振频率和相应的主振型也是体系本身的固有性质。
5、图示单自由度体系自振周期的关系为( )。
A 、(a)=(c)B 、(a)=(b)C 、(b)=(c)D 、都不相等6、单自由度振动体系中,若质点在杆的中点,各杆EI 、l 相同,其自振周期的大小排列顺序为(A 、(c)>(a)>(b)B 、(c)>(b)>(a) C 、(a)>(b)>(c) D 、(b)>(c)>(a)三、分析计算题1、梁的抗弯刚度为EI2m3、柱的自重不计,求图示刚架的自振频率。
(整理)《结构力学2》习题集同济版.

南华大学《结构力学II》习题集(适合于大土木工程各专业方向)组编:刘华良班级:姓名:学号:建筑工程与资源环境学院道路桥梁工程教研室衡阳2005年前言本习题集取材于第九章位移法9-l 确定下列各结构的位移法未知数目,并绘出基本结构。
9-2~9-3 用位移法计算下列结构内力.并绘出其弯矩图、剪力图和轴力图。
题9-2图题9-3图9-4~9-11 用位移法绘制下列结构弯矩图。
题9-4图题9-5图题9-6图题9-7图题9-8图题9-9图题9-10图题9-11图9-12~9-15 用位移法绘制下列具有斜杆的刚架的弯矩图。
题9-12图题9-13图题9-14图题9-15图9-16~9-17 列出下列结构的位移法典型方程式,并求出所有系数和自由项。
题9-16图题9-17图9-18~9-23 用位移法绘制下列具有无限刚性杆结构的M图。
题9-18图题9-19图题9-20图题9-21图题9-22图题9-23图9-24~9-26 用位移法绘制下列刚架M图。
题9-24图题9-25图题9-26图9-27 用位移法绘制图9-27所示结构弯矩图,并求桁架杆的轴向力。
题9-27图9-28 用位移法求图9-28所示桁架各杆轴向力。
题9-28图9-29 图9-29所示为一个三角形刚架,考虑杆件的轴向变形,试写出位移法的典型方程,并求出所有系数和自由项。
题9-29图9-30~9-31 用位移法计算图示有剪力静定杆组成的刚架的M图。
题9-30图题9-31图9-32~9-41 利用对称性,用位移法求作下列结构的M图。
题9-32图题9-33图题9-34图题9-35图题9-36图题9-37图题9-38图题9-39图题9-40图题9-41图9-42~9-48 试直接按平衡条件建立位移法方程计算题9-2、9-5、9-8、9-11、9-12、9-24、9-35,并绘出M图。
题9-42图题9-43图题9-44图题9-46图题9-47图题9-48图9-49~9-52 试用位移法求作下列结构由于支座位移产生的M图。
结构动力学复习资料

结构动力学复习资料一、概念题1.1 结构动力计算与静力计算的主要区别是什么?答:主要区别表现在:(1) 在动力分析中要计入惯性力,静力分析中无惯性力;(2) 在动力分析中,结构的内力、位移等是时间的函数,静力分析中则是不随时间变化的量;(3) 动力分析方法常与荷载类型有关,而静力分析方法一般与荷载类型无关。
1.2 什么是动力自由度,确定体系动力自由度的目的是什么?答:确定体系在振动过程中任一时刻体系全部质量位置或变形形态所需要的独立参数的个数,称为体系的动力自由度(质点处的基本位移未知量)。
确定动力自由度的目的是:(1) 根据自由度的数目确定所需建立的方程个数(运动方程数=自由度数),自由度不同所用的分析方法也不同;(2) 因为结构的动力响应(动力内力和动位移)与结构的动力特性有密切关系,而动力特性又与质量的可能位置有关。
1.3 结构动力自由度与体系几何分析中的自由度有何区别?答:二者的区别是:几何组成分析中的自由度是确定刚体系位置所需独立参数的数目,分析的目的是要确定体系能否发生刚体运动。
结构动力分析自由度是确定结构上各质量位置所需的独立参数数目,分析的目的是要确定结构振动形状。
1.4 结构的动力特性一般指什么?答:结构的动力特性是指:频率(周期)、振型和阻尼。
动力特性是结构固有的,这是因为它们是由体系的基本参数(质量、刚度)所确定的、表征结构动力响应特性的量。
动力特性不同,在振动中的响应特点亦不同。
1.5 什么是阻尼、阻尼力,产生阻尼的原因一般有哪些?什么是等效粘滞阻尼?答:振动过程的能量耗散称为阻尼。
产生阻尼的原因主要有:材料的内摩擦、构件间接触面的摩擦、介质的阻力等等。
当然,也包括结构中安装的各种阻尼器、耗能器。
阻尼力是根据所假设的阻尼理论作用于质量上用于代替能量耗散的一种假想力。
粘滞阻尼理论假定阻尼力与质量的速度成比例。
粘滞阻尼理论的优点是便于求解,但其缺点是往往与实际不符,为扬长避短,按能量等效原则将实际的阻尼耗能换算成粘滞阻尼理论的相关参数,这种阻尼假设称为等效粘滞阻尼。
结构动力计算课后习题答案

结构动力计算课后习题答案结构动力计算课后习题答案在学习结构动力学这门课程时,我们经常会遇到各种各样的习题。
这些习题旨在帮助我们巩固所学的知识,并提供实践的机会。
在这篇文章中,我将为大家提供一些结构动力计算课后习题的答案,希望能对大家的学习有所帮助。
1. 计算一个简支梁的固有频率。
答案:简支梁的固有频率可以通过以下公式计算:f = (1/2π) * √(k/m)其中,f为固有频率,k为刚度,m为质量。
在简支梁的情况下,刚度k等于弹性模量E乘以截面面积A除以长度L。
质量m等于密度ρ乘以截面面积A除以长度L。
2. 计算一个悬臂梁的固有频率。
答案:悬臂梁的固有频率可以通过以下公式计算:f = (1/2π) * √(3k/m)在悬臂梁的情况下,刚度k等于弹性模量E乘以截面面积A的三次方除以长度L的四次方。
质量m等于密度ρ乘以截面面积A除以长度L。
3. 计算一个简支梁的振动模态。
答案:简支梁的振动模态可以通过以下公式计算:f_n = (n^2 * v) / (2L)其中,f_n为第n个振动模态的频率,v为波速,L为长度。
n为振动模态的序号,从1开始。
4. 计算一个悬臂梁的振动模态。
答案:悬臂梁的振动模态可以通过以下公式计算:f_n = (2n-1) * (v/4L)其中,f_n为第n个振动模态的频率,v为波速,L为长度。
n为振动模态的序号,从1开始。
5. 计算一个简支梁的最大挠度。
答案:简支梁的最大挠度可以通过以下公式计算:δ_max = (5qL^4) / (384EI)其中,δ_max为最大挠度,q为均布载荷,L为长度,E为弹性模量,I为截面惯性矩。
6. 计算一个悬臂梁的最大挠度。
答案:悬臂梁的最大挠度可以通过以下公式计算:δ_max = (qL^4) / (8EI)其中,δ_max为最大挠度,q为均布载荷,L为长度,E为弹性模量,I为截面惯性矩。
以上是一些常见的结构动力计算课后习题的答案。
通过解答这些习题,我们可以更好地理解结构动力学的概念和原理,提高我们的计算能力和问题解决能力。
结构动力计算课后习题答案

结构动力计算课后习题答案结构动力计算是土木工程和机械工程领域中的一个重要分支,它涉及到结构在动力作用下的响应分析。
这门课程的课后习题通常要求学生运用所学的理论,解决实际工程问题。
以下是一些可能的习题答案示例,请注意,这些答案是基于假设的习题内容,实际的习题答案应根据具体的题目来确定。
习题1:单自由度系统的动力响应假设有一个单自由度系统,其质量为m,阻尼系数为c,刚度系数为k。
系统受到一个简谐激励F(t) = F0 * sin(ωt),其中F0是激励力的幅值,ω是激励频率。
求系统的稳态响应。
答案:对于单自由度系统,其运动方程可以表示为:\[ m\ddot{x}(t) + c\dot{x}(t) + kx(t) = F_0 \sin(\omega t) \]稳态响应可以通过求解上述方程的特解来获得。
特解的形式为:\[ x(t) = X \sin(\omega t + \phi) \]其中,振幅X和相位角φ可以通过以下公式计算:\[ X = \frac{F_0}{\sqrt{(\omega^2 m - \omega^2)^2 +(c\omega)^2}} \]\[ \phi = \arctan\left(\frac{c\omega}{\omega^2 m -\omega^2}\right) \]习题2:多自由度系统的模态分析考虑一个两自由度系统,其质量矩阵、刚度矩阵和阻尼矩阵分别为:\[ M = \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix},\quad K = \begin{bmatrix} k_1 & k_c \\ k_c & k_2\end{bmatrix}, \quad C = \begin{bmatrix} c_1 & 0 \\ 0 & c_2\end{bmatrix} \]求系统的自然频率和模态形状。
《结构力学习题集》9-结构动力计算

第九章 结构的动力计算一、是非题1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、忽略直杆的轴向变形,图示结构的动力自由度为4个。
3、仅在恢复力作用下的振动称为自由振动。
4、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
5、图 a 体 系 的 自 振 频 率 比 图 b 的 小 。
l /2l /2l /2l /2(a)(b)6、单 自 由 度 体 系 如 图 ,W =98.kN ,欲 使 顶 端 产 生 水 平位 移 ∆=001.m ,需 加 水 平 力 P =16kN ,则 体 系 的 自振 频 率 ω=-40s 1。
∆7、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、桁 架 ABC 在 C 结 点 处 有 重 物 W ,杆 重 不 计 ,EA 为 常 数 ,在 C 点 的 竖 向 初 位 移 干 扰 下 ,W 将 作 竖 向 自 由 振 动 。
AC10、不 计 阻 尼 时 ,图 示 体 系 的 运 动 方 程 为 :m m XX h EI EI EI EI X X P t 00148242424012312⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭+--⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭=⎧⎨⎩⎫⎬⎭()二、选择题1、图 示 体 系 ,质 点 的 运 动 方 程 为 : A .()()()y l Ps i n m y EI =-77683θ t /; B .()()m y EIy l Ps i n /+=19273θ t ; C .()()m y EIy l Ps i n /+=38473θ t ; D .()()()y l Ps i n m yEI =-7963θ t / 。
ll0.50.5 2、在 图 示 结 构 中 ,若 要 使 其 自 振 频 率 ω增 大 ,可 以A .增 大 P ;B .增 大 m ;C .增 大 E I ; D .增 大 l 。
结构力学习题集讲解
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;;B.D.C.=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M kM p21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
aa9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A两侧截面的相对转角ϕA,EI = 常数。
ql l l/211、求图示静定梁D端的竖向位移∆DV。
EI = 常数,a = 2m 。
10kN/ma a a14、求图示刚架B端的竖向位移。
q15、求图示刚架结点C的转角和水平位移,EI = 常数。
q17、求图示刚架横梁中D点的竖向位移。
EI=常数。
21、求图示结构B点的竖向位移,EI = 常数。
l l23、求图示刚架C点的水平位移 CH,各杆EI = 常数。
4m4m3m2kN/m27、求图示桁架中D点的水平位移,各杆EA 相同。
a30、求图示结构D点的竖向位移,杆AD的截面抗弯刚度为EI,杆BC的截面抗拉(压)刚度为EA。
a331、求图示结构D点的竖向位移,杆ACD的截面抗弯刚度为EI,杆BC抗拉刚度为EA 。
39、图示刚架杆件截面为矩形,截面厚度为h , h/l = 1/ 20 ,材料线膨胀系数为 α,求C 点的竖向位移。
CA-3-3+t+t ttl40、求图示结构B 点的水平位移。
15结构的动力计算--习题

P h 2.5 6
M st
2
2
4
3.75kN m
Mmax Mst 3.751.375 5.156kN m
Ph/4 Ph/4
P Ph/4
Ph/4
Ph/4
Ph/4
动荷幅值弯矩图
Ph/4
动弯矩幅值图
Ph/4
结构力学电子教程
15 结构的动力计算
15.12 图示一个重物W=500N,悬挂在刚度k=4N/mm的弹簧
15.3 求图示体系的自振频率。
解:
1 1 l h h 2 lh2
EI 2
3 3EI
1
m
3EI Mlh2
M
I1=∞ EI
l
h
1
h h M1
结构力学电子教程
15 结构的动力计算
15.5 求图示刚架水平振动的圆频率。
解: k 12EI 3 36EI
h3
h3
k m
36EI 2mh3
18EI mh3
st
Wh3
A
3 2 104
106 16 104 20 103 33
108
9.8
41.74s1
y y0 cost, A y0 0.1cm. v y0 sin t, vmax y0 0.1 41.74 4.174cm / s. a y02 cost, amax y02 0.1 41.742 174.2cm / s2.
0.05534
9.8
1 1 9.035
2 2 0.05534
k mW
g
Psin t
A y(t) max
yst
P k
=9.035
50 =0.11294m=112.94mm 4000
结构动力学复习题全解

-------------------------------------(7)
C cr 2m
,Cc r= 2mω(此式为确定临界阻尼的公式)
当为一般情况时,n =
C C C cr = ⋅ = ξω 2 m C cr 2 m
式中,ξ=
C 称为阻尼比。 C cr
对钢筋混凝土结构ξ< 5% ,一般取 3% 对钢结构ξ= 1% — 2% 3)当 n <ω时(弱阻尼) 此时,记 ω d = ω − n
例题2试建立图示结构的振动方程质点的质量都是m动力自由度为1即质点两个的水平位移忽略转动惯量及杆件的轴向变形侧移刚度k的求法用位移法计算质点有侧移为1无阻尼的自由振动振动方程acostbsint有阻尼的自由振动振动方程时强阻尼方程5的解为
结构动力学
*本章讨论结构在动力荷载作用下的反应。 **学习本章注重动力学的特征------惯性力。 *结构动力计算的目的在于确定结构在动力荷载作用下的位移、内力等量值随时间变化 的规律,从而找出其最大值作为设计的依据。 *动力学研究的问题:动态作用下结构或构件的强度、刚度及稳定性分析。 一、 本章重点 1.振动方程的建立 2.振动频率和振型的计算 3.振型分解法求解多自由度体系 4.最大动位移及最大动应力 二、 基础知识 1.高等数学 2.线性代数 3.结构力学 三、 动力荷载的特征 1.大小和方向是时间 t 的函数 例如:地震作用,波浪对船体的作用,风荷载,机械振动等 2.具有加速度,因而产生惯性力 四、 动力荷载的分类 1.周期性动力荷载 例如:①机械运转产生的动力荷载,②打桩时的锤击荷载。 P(t) P(t)
&(t ) , & &(t ) 为质点运动加速度,惯性力与运动方向相反。 y y FI= − m&
结构动力学复习题1 (优选.)

A
取横梁为研究对象,ΣX=0,得:K= 24EI L3
4)振动方程
- 2 m &y&(t) - K y(t) + Psinθt = 0 即,
2 m &y&(t)
+
24EI L3
y(t)
= Psinθt
一、 无阻尼的自由振动
振动方程 m&y&(t) +K y(t) = 0 , 写作:
&y&(t) + K y(t) = 0 m
---------------------------------------(10)
考虑 P(t)在(0,t)时间内作用于系统,
P(t)
认为是由无数个瞬时冲击荷载的叠加,如图。
考虑由时刻τ开始,在 dτ时间内的位移反应,
由(10)式可得:
0
ττ+dτ t
d y(t) = p(τ )dτ sinω(t-τ) mω
S&&(t) + (ω2 – n2 )S (t) = 0 --------------------------------------------(5)
1.当 n >ω时(强阻尼) 方程(5)的解为:
S (t) = A1sh n2 − ω 2 t +A2ch n 2 − ω 2 t
从而,方程(4)的解为:
2.振动频率和振型的计算
3.振型分解法求解多自由度体系
4.最大动位移及最大动应力
二、基础知识
1.高等数学
2.线性代数
3.结构力学
三、动力荷载的特征
1.大小和方向是时间 t 的函数
例如:地震作用,波浪对船体的作用,风荷载,机械振动等
工程力学结构动力学复习题集

工程力学结构动力学复习题一、简答题1、结构的动力特性主要指什么?对结构做动力分析可分为哪几个阶段?2、何谓结构的振动自由度?它与机动分析中的自由度有何异同?3、何谓动力系数?简谐荷载下动力系数与哪些因素有关?4、动力荷载与静力荷载有什么区别?动力计算与静力计算的主要差别是什么?5、为什么说结构的自振频率和周期是结构的固有性质?怎样改变他们?6、简述振型分解法是如何将耦联的运动方程解耦的.7、时域法求解与频域法求解振动问题各有何特点?&什么叫动力系数,动力系数大小与哪些因素有关?单自由度体系位移动力系数与内力动力系数是否一样?答:动力放大系数是指动荷载引起的响应幅值与动荷载幅值作为静荷载所引起的结构静响应之比值。
简谐荷载下的动力放大系数与频率比、阻尼比有关。
当惯性力与动荷载作用线重合时,位移动力系数与内力动力系数相等;否则不相等。
原因是:当把动荷载换成作用于质量的等效荷载时,引起的质量位移相等,但内力并不等效,根据动力系数的概念可知不会相等。
9、振型正交性的物理意义是什么?振型正交性有何应用?答:由振型关于质量、刚度正交性公式可知,i振型上的惯性力在j振型上作的虚功为0。
由此可知,既然每一主振型相应的惯性力在其他主振型上不做功,那么它的振动能量就不会转移到别的主振型上去。
换句话说,当一个体系只按某一主振型振动时,不会激起其他主振型的振动。
这说明各个主振型都能单独出现,彼此线性无关。
这就是振型正交的物理意义。
一是可用于校核振型的正确性;二是在已知振型的条件下,可以通过折算质量与折算刚度计算对应的频率。
而更主要的是任一同阶向量均可用振型的线性组合来表示,在受迫振动分析中,利用振型的正交性,在阻尼矩阵正交的假设下可使运动方程解藕。
10、什么是阻尼、阻尼力,产生阻尼的原因一般有哪些?什么是等效粘滞阻尼?答:振动过程的能量耗散称为阻尼。
产生阻尼的原因主要有:材料的内摩擦、构件间接触面的摩擦、介质的阻力等等。
结构动力学例题复习题含答案-2021年推荐必备
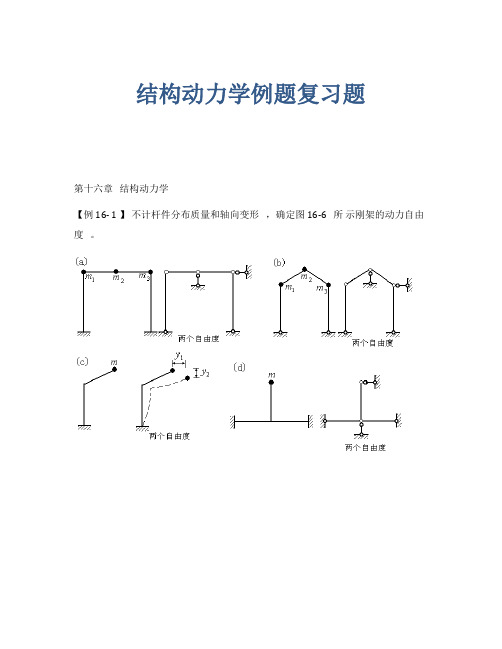
结构动力学例题复习题第十六章结构动力学【例 16- 1 】不计杆件分布质量和轴向变形,确定图 16-6 所示刚架的动力自由度。
图 16-6【解】各刚架的自由度确定如图中所示。
这里要注意以下两点:1.在确定刚架的自由度时,引用受弯直杆上任意两点之间的距离保持不变的假定。
根据这个假定并加入最少数量的链杆以限制刚架上所有质量的位置,则刚架的自由度数目即等于所加链杆数目。
2.集中质量的质点数并不一定等于体系的自由度数,而根据自由度的定义及问题的具体情形确定。
【例 16- 2 】试用柔度法建立图 16-7a 所示单自由度体系,受均布动荷载作用的运动方程。
【解】本题特点是,动荷载不是作用在质量上的集中荷载。
对于非质量处的集中动荷载的情况,在建立运动方程时,一般采用柔度法较为方便。
设图 a 质量任一时刻沿自由度方向的位移为 y (向下为正)。
把惯性力、阻尼力及动荷载,均看作是一个静荷载,则在其作用下体系在质量处的位移y ,由叠加原理(见图 b 、 c 、 d 及 e ),则式中,,。
将它们代入上式,并注意到,,得图 16-7经整理后可得式中,,称为等效动荷载或等效干扰力。
其含义为:直接作用于质量上所产生的位移和实际动荷载引起的位移相等。
图 a 的相当体系如图 f 所示。
【例 16- 3 】图 16-8 a 为刚性外伸梁, C 处为弹性支座 , 其刚度系数为,梁端点 A 、 D 处分别有和质量,端点 D 处装有阻尼器 c ,同时梁 BD 段受有均布动荷载作用,试建立刚性梁的运动方程。
【解】因为梁是刚性的,这个体系仅有一个自由度,故它的动力响应可由一个运动方程来表达,方程可以用直接平衡法来建立。
这个单自由度体系可能产生的位移形式如图 b 所示,可以用铰 B 的运动作为基本量,而其它一切位移均可利用它来表示。
图 16-8以顺时针向为正。
则 A 点有位移和加速度; D 点有位移和加速度及速度; C 点约束反力为。
由,有将惯性力、阻尼力及约束反力代入上式,得经整理,运动方程为小结:例 16- 2 及例 16- 3 讨论的是单自由度的一般情况下的运动方程的建立。
结构动力学习题+讲解

结构动力学*本章讨论结构在动力荷载作用下的反应。
**学习本章注重动力学的特征------惯性力。
*结构动力计算的目的在于确定结构在动力荷载作用下的位移、内力等量值随时间变化的规律,从而找出其最大值作为设计的依据。
*动力学研究的问题:动态作用下结构或构件的强度、刚度及稳定性分析。
一、本章重点1.振动方程的建立2.振动频率和振型的计算3.振型分解法求解多自由度体系4.最大动位移及最大动应力二、基础知识1.高等数学2.线性代数3.结构力学三、动力荷载的特征1.大小和方向是时间t的函数例如:地震作用,波浪对船体的作用,风荷载,机械振动等2.具有加速度,因而产生惯性力四、动力荷载的分类1.周期性动力荷载例如:①机械运转产生的动力荷载,②打桩时的锤击荷载。
P(t) Pt t(机械运转荷载)(打桩荷载)2.冲击荷载例如:①爆炸力产生的动力荷载,②车轮对轨道连接处的冲击。
P(t)P(t)P(t)t t t(爆炸力动力荷载)(吊车起吊钢索的受力)(随机动力荷载)3.突加常量荷载例如:吊车起吊重物时钢索的受力。
4.随机动力荷载前3类荷在是时间t的确定函数,称为确定性动力荷载;而地震作用,波浪对船体的作用,风荷载等其作用大小只能用统计的方法获得。
五、动力荷载的计算方法1.原理:达朗贝尔原理,动静法建立方程2.计算工具:微分方程,线性代数,结构力学六、体系振动的自由度---------动力自由度结构具有质量,有质量在运动时就有惯性力。
在进行动力计算时,一般把结构的质量简化为若干质点的质量,整个结构的惯性力就成为各质点的惯性力问题。
1.质点简化的一般要求①简单,②能反映主要的振动特性例如:楼房;质量集中在各层楼板平面内水塔:质量集中在水箱部分梁:无限自由度集中质量(楼房质量集中)(水塔质量集中)(梁的质量集中)2.位移y(t)即指质点的位移y(t),其加速度为y&&)(t3.动力自由度的确定即质点位移数量的确定。
结构动力计算结构力学学习资料

P(t )
P
t
t
简谐荷载(harmonic load) 一般周期荷载(periodic load)
2)冲击荷载:短时内剧增或剧减。θt
P
P(t )
P(t )
P
P
偏心质量m,偏心距e,匀角速度θ
t
tr (Suddenly
a突pp加lie荷d c载otn惯水sta性平nt力 分lo:量aPd=均)爆m为炸θ简tr荷2e谐,载其荷竖t载向. 分量随(和ra即nd荷o载m
1)集中质量法(method of lumped mess)把连续分布的质
量集中为几个质点,将一个无限自由度的问题简化成有限自由度 问题。
演示
m m>>m梁
m+αm柱
m+αm梁
I 厂房排架水平振动 I 2I
时的计算简图
三个自由度体系
单自由度体系
(single degree-of-freedom system)
1
k
EI
k11 k l 3
l
k11 3EI l3 k
m
m
•对于静定结构一般计算柔度系数方便。
•如果让振动体系沿振动方向发生单位位移时,所有刚节点
都不能发生转动(如横梁刚度为无穷大的刚架)计算刚度系数方
便。 两端刚结的杆的侧移刚度为:
12EI l3
3EI 一端铰结的杆的侧移刚度为: l 3
§15-3 单自由度体系的强迫振动
y ky m
my..
二、自由振动微分方程的解
my..+ky =0
( a) Þ y..+w 2 y =0
(w =
k )
m
y( t ) =C1 sinwt +C 2 coswt
(完整版)结构动力学-习题解答

解
11
5 48
l3 EI
;
3.098
EI ml 3
;
l/2
ml 3 T 2.027 ;
EI
m
EI y1(t)
l
l/2 l/2
l/4
7-1(b)试求图示体系的自振频率与周期。
解: 求柔度系数: 用位移法或力矩分配法 求单位力作用引起的弯矩图(图a); 将其与图b图乘,得
48EI 2k
T 2 ( 1 l3 1 )m
48 EI 2k
m
k EI
k
l/2
l/2
7-3 试求图示体系质点的位移幅值和最大弯矩值。
已知 0.6
l
解:
yst
FPl 3 EI
m
y1(t)
1
1
2
/
2
1.5625
位移幅值
A
yst
1.5625
FPl 3 EI
2l
yst
11
5 3
l3 EI
1 11
l
X11 0.4612 ; X12 4.336
X 21
X 22
12 7.965 EI / ml 3
2 2
65.53EI
/
ml 3
1 2.822 EI / ml3
8-6.试求图示刚架的自振频率和振型。设楼面质量分别为m1=120t和m2=100t,
柱的质量已集中于楼面, 柱的线刚度分别为i1=20MN.m和i2=14MN.m,横梁
m 2 A 0.3375 FP
l/2
EI=常数
FP sin t
2l
FP
FPl
结构动力学结构动力学试卷(练习题库)(2023版)

结构动力学结构动力学试卷(练习题库)1、结构动力计算与静力计算的主要区别是什么?2、什么是动力自由度,确定体系动力自由度的目的是什么?3、结构动力自由度与体系几何分析中的自由度有何区别?4、结构的动力特性一般指什么?5、什么是阻尼、阻尼力,产生阻尼的原因一般有哪些?什么是等效粘滞阻尼?6、采用集中质量法、广义位移法(坐标法)和有限元法都可使无限自由度体系简化为有限自由度体系,它们采用的手7、建立运动微分方程有哪几种基本方法?各种方法的适用条件是什么?8、直接动力平衡法中常用的有哪些具体方法?它们所建立的方程各代表什么条件?9、刚度法与柔度法所建立的体系运动方程间有何联系?各在什么情况下使用方便?10、计重力与不计重力所得到的运动方程是一样的吗?11、自由振动的振幅与哪些量有关?12、什么叫动力系数,动力系数大小与哪些因素有关?单自由度体系位移动力系数与内力动力系数是否一样?13、若要避开共振应采取何种措施?14、增加体系的刚度一定能减小受迫振动的振幅吗?15、突加荷载与矩形脉冲荷载有何差别。
16、平断面假定17、弯曲要素18、梁的边界条件19、叠加原理20、三弯矩方程21、平断面假定22、梁的边界条件23、叠加原理24、三弯矩方程25、虚位移原理26、虚力原理27、位能驻值原理28、板条梁29、开口和闭口薄壁杆件。
30、应力的重新分布。
31、几何不变体32、自由度33、多余约束34、超静定结构35、形常数和载常数36、试简述影响线与内力图的区别?37、力法和位移法的解题思路?38、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
39、有多余约束的体系一定是几何不变体系。
40、计算自由度W小于等于零是体系几何不变的充要条件。
41、两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必须满足的条件。
42、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
l l /411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
a aa22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。
3m 3m24、忽略质点m 的水平位移,求图示桁架竖向振动时的自振频率ω。
各杆EA = 常数。
m 4m4m25、图示体系E P W I =⨯====-2102052048004kN /cm s kN, kN, cm 214,,θ。
求质点处最大动位移和最大动弯矩。
W4mm2t26、图示体系EI k =⨯⋅==2102035kN m s 2-1,,θ×1055N /m, P =×N 103。
kN W 10=。
求质点处最大动位移和最大动弯矩。
m2m2sin P27、求图示体系在初位移等于l/1000,初速度等于零时的解答。
θωω=020.( 为自振频率),不计阻尼。
l28、图示体系受动力荷载作用,不考虑阻尼,杆重不计,求发生共振时干扰力的频率θ。
/3P tsin( )29、已知:m P ==38t, kN ,干扰力转速为150r/min ,不计杆件的质量,EI =⨯⋅6103kN m 2。
求质点的最大动力位移。
2m2m30、图示体系中,电机重kN 10=W 置于刚性横梁上,电机转速n r =500/min ,水平方向干扰力为) sin(kN 2)(t t P θ⋅=,已知柱顶侧移刚度kN/m 1002.14⨯=k ,自振频率ω=-100s 1。
求稳态振动的振幅及最大动力弯矩图。
m31、图示体系中,kN 10=W ,质点所在点竖向柔度917.1=δ,马达动荷载P t t ()sin()=4kN θ,马达转速n r =600/min 。
求质点振幅与最大位移。
32、图示体系中,W =8kN ,自振频率ω=-100s 1,电机荷载P (t ) = 5kN ·sin(θt ),电机转速n = 550r/min 。
求梁的最大与最小弯矩图。
2m2mP t ()33、求图示体系支座弯矩M A 的最大值。
荷载P t P t (),.==004sin θθω。
/2/234、求图示体系的运动方程。
llm0.50.535、求图示体系稳态阶段动力弯矩幅值图。
θωω=05.( 为自振频率),EI = 常数,不计阻尼。
lll36、图示体系分布质量不计,EI = 常数。
求自振频率。
aa37、图示简支梁EI = 常数,梁重不计,m m m m 122==,,已求出柔度系数()δ123718=a EI /。
求自振频率及主振型。
aaa38、求图示梁的自振频率及主振型,并画主振型图。
杆件分布质量不计。
a aa39、图示刚架杆自重不计,各杆EI = 常数。
求自振频率。
2m2m40、求图示体系的自振频率和主振型。
EI = 常数。
l ll /3/3/341、求图示体系的自振频率及主振型。
EI = 常数。
l /2l /2l /2l /242、求图示体系的自振频率及相应主振型。
EI = 常数。
/2l l/2l /2l /2l43、求图示结构的自振频率和主振型。
不计自重。
l /2l /244、求图示体系的自振频率和主振型。
不计自重,EI = 常数。
m aaa45、求图示体系的第一自振频率。
l /2l /2l /2l /246、求图示体系的自振频率。
已知:m m m 12==。
EI = 常数。
m1.51m1.5m1m1m47、求图示体系的自振频率和主振型,并作出主振型图。
已知:m m m 12==,EI = 常数。
2m24m 4m48、求图示对称体系的自振频率。
EI = 常数。
l l l l /2/2/2/249、图示对称刚架质量集中于刚性横粱上,已知:m 1=m ,m 2=2m 。
各横梁的层间侧移刚度均为k 。
求自振频率及主振型。
m 1m 22150、求图示体系的自振频率并画出主振型图。
m51、求图示体系的自振频率和主振型。
EI = 常数。
l l52、用最简单方法求图示结构的自振频率和主振型。
l l53、求图示体系的频率方程。
l54、求图示体系的自振频率和主振型。
EI =常数。
2aaa55、求图示体系的自振频率和主振型。
不计自重,EI = 常数。
a /2a /2a /2a /256、求图示体系的自振频率。
设EI = 常数。
l57、图示体系,设质量分别集中于各层横梁上,数值均为m 。
求第一与第二自振频率之比ωω12:。
258、求图示体系的自振频率和主振型。
lm m 2EI =∞EI =∞ EI 1EI 12EI 12EI 159、求图示体系的自振频率和主振型。
m m m m 122==,。
60、求图示桁架的自振频率。
杆件自重不计。
m 3m3m61、求图示桁架的自振频率。
不计杆件自重,EA = 常数。
m mm3362、作出图示体系的动力弯矩图,已知:θ=0825673.EIml 。
0.5l0.5l263、作图示体系的动力弯矩图。
柱高均为h ,柱刚度EI =常数。
l lθ=13257.EImh30.50.5P64、绘出图示体系的最大动力弯矩图。
已知:动荷载幅值P =10kN ,θ=-209441.s ,质量m =500kg ,a =2m ,EI =⨯⋅481062.N m 。
()Pt sin θ65、已知图示体系的第一振型如下,求体系的第一频率。
EI =常数。
振型101618054011 ..⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪/2第九章 结构的动力计算(参考答案)1、(X)2、(X)3、(X)4、(X)5、(O)6、(O)7、(O)8、(X)9、(X)10、ω=19253EIg Wl / 11、()ω=4kg /W12、)/(16,48/332311ml EI EI l ==ωδ13、)5/(48,48/5323ml EI EI l ==ωδ14、33477.11124ml EIml EI ==ω15、)5/(3,3/5323ml EI EI l ==ωδ16、323119,/9mlEIl EI k ==ω 17、()06424 , 5.123213231=--=A l m A l m EI mlEI ωωω, 0)248(3 , 28.423213232=-+=A EI l m A l m mlEIωωω 振 型 1振 型 218、1s 2.54-=ω19、()T Wh EIg =263π/ 20、()T WhEIg =2483π/21、)/(889.23ma EI =ω22、2:1:=b a ωω23、)/(56.16EAg W T =24、m EA m 5.10//1==δω25、cmYstp Y M ml EI 3029.1,,127.3)/1/(1,s 25.24)2/8/(Max Mstp Dmax 22-1====-===μμωθμω26、ωδ==+=-1143143416//(//).m m EI k s 1μθω=-=11152222/(/). m,006.0stp max ==y Y D μ,m, kN 61.7Dmax ==stp M M μ27、),sin(04167.1)sin(20833.0)cos(001.0,1000/ ,),cos()cos()sin(,04067.1 ,/st st st 22st t Y t Y t l Y l B Y A t m Pt B t A Y m P Y DD D θωωωθμθμωωωμω+-===++===28、)/(273ml EI =θ29、-1s 92.38=ω,-1s 71.15=θ,19.1=μ,m 10/09.23max =y 30、,378.1 ,s 36.52-1==βθ,mm 27.0 m,9610.1st 4st ===-y A y βMM F M D 756.2==β31、,s 83.62 ,s 50.71-1-1==θω;β=4389.;A F ==βδ337.mm ;m m 28.5)(max =+=δβF w y32、θβ==575961496.,.s -1,M F M M D ==β748.,{}M M M M TD 52.0 48.15st max =+=33、333 , 3l EIk ml EI ==ω,运动方程: mPy y k ky y m P 165, 21=+∆⋅=+ω&&&& 特征解y *:y P m t P mt *sin .sin =-=51600595222ωθωθθ11()l P M t l P t l P l P Pll y m M A A 0max 000*56.0, sin 56.0 sin )20595.0(2==+=+=θθ&& 34、 16)sin(533t P y l EI y m θ=+&&35、))(sit (3,3/4,4/3st t EIPlY EI Pl Y θμ-===36、{}EIma /1211.02123.3/1T32==ωλ)/(874.2,)/(558.03231ma EI ma EI ==ωω37、{}EI ma /07350.0125984.0/1T32==ωλ)/(|6886.3,)/(8909.03231ma EI ma EI ==ωω954.0/1/2111=Y Y ,()097.2/1/2212-=Y Y38、EIa EI a 6/,3/231232211===δδδ,)/(414.1,)/(0954.13231ma EI ma EI ==ωω{}λω==1561223////ma EI T,Y Y Y Y 112112221111//,//()==-M1M21第二主振型第一主振型图图111139、EIEIEI2834122211-===δδδ,,,⎭⎬⎫⎩⎨⎧==779.0554.812EImωλmEImEI1328.1,3419.021==ωω40、对称:,162/53EIl=δ,)/(69.52/131mlEI=ω反对称:,/00198.03EIl=δ,)/(46.222/132mlEI=ω41、EIlEIlEIl96/5,24/,48/532112322311====δδδδ3231/054.9,/736.2mlEImlEI==ωω{}[]Φ1105653=.,()T分{}[]Φ2117663=-.()T分42、对称:,)/(191.2,24/52/132311mlEIEIl==ωδ反对称:δδδ1132112348===l EI l EI/,/,δ22348=l EI/,,)/(69.7,)/(5.02/1322/131mlEImlEI==ωω{}[]Y 1=1 0.03 -0.03T ,{}[]Y 2=0 1 1T ,,{}[]Y 3=1 -31.86 31.86T43、ωω13231282==.,.,EI ml EIml 1.01,4.101,16,382,482212211132112322311-======Y Y Y Y EI l EI l EI l δδδδ 44、321321/2.397.0;/0975.007.1ma EI EI ma ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=ωωλλ61.3/;28.0/)2(2)2(1)1(2)1(1+=-=A A A A45、3/48ml EI =ω46、),/(7708.1,/)(4393.0),/(3189.0),/(1818.5),/(6875.1),/(1),/(5.4212121122211m EI m EI EI m EI m EI EI EI ====-====ωωλλδδδδ 47、)/(6664.2),/(6645.12)3/(32),/(4),3/(142122211211EI m EI m EI EI EI ===-===λλδδδδ5.0:1:,2:1:)/(6124.0,)/(281.022********=ΦΦ-=ΦΦ==m EI m EI ωω 48、31/47.10ml EI =ω,,/86.1332ml EI =ω49、k k k k k k k 112212212====-,,ωωω21222808021920468215102=⎧⎨⎩⎫⎬⎭==k m k m km..,.,. Y Y Y Y 112112221178110281==-.,. 50、k i l k k i l k i l 112211222226630===-=/,/,/,ω11/20146=.(/)EI m ,2/12)/(381.0ml EI =ω,{}[]{}[]T T 4.24- 1,0.236 121=Φ=Φ51、k EI l k EI l k EI l 1131232231812998==-=/,/,/,ωω132316925245==.,.EI m l EIm l52、利用对称性: 反对称:δω11313366245===l EIEI m l EIm l ,. , 对称:δω1132339696737===l EIEI m l EIm l ,.53、列幅值方程:δωδωδωδω1121222122222222m x m y x m x m y y +=+=⎫⎬⎭,21210211122221112m m m m ωδδωωδδω--=, δδδδ113122132233243====l EI l EI l EI,,22xδ112254、对称:δω223230183333032==.,.a EI EIma反对称:δω11313407071==a EI EI ma ,. 55、对称:11δ11324=a EI /(),ω1324=EI ma /()反对称:11δ1137768=a EI /(),ω137687=EI ma /()56、ωω132********==./,./EI ml EI ml57、设k EI l =243/ 频率方程:()()()22,024,0322242222±==+-=---mkk km m km k m k ωωωωω 828.5:11:1716.0:21==ωω58、ωω14241248==EIml EIml ,,ΦΦΦΦ11211222051==-., 59、k EI l k EI l k EIl1131232233351==-=,, []M m EI ml EI ml =⎡⎣⎢⎤⎦⎥==100216735071323,.,. ωω,[]Φ=-⎡⎣⎢⎤⎦⎥1114020132.. 60、W EAg W EAg /506.0,/379.021==ωω61、ωω12034048==././EA m EA m , 62、EIPl A A EI l EIl EI l 3213223123111397.00531.0348524⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧===,,,δδδ0.Pl 0047612.Pl63、EIPh A A h EI k h EI k h EI k 3213123223110500.00538.0242448⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧-===,,,0.0252Ph0.3220Ph0.347Ph64、反对称结构:δ=8EI,ω=-346411.s ,μ=15762. 两竖杆下端动弯矩为31524.kN m ⋅,左侧受拉。
