求双曲线标准方程的技巧(20210226102409)
双曲线标准方程的推导过程

双曲线标准方程的推导过程双曲线是一种二次曲线,与椭圆和抛物线类似,具有一些特殊的性质和形态。
双曲线的标准方程是一个关于x和y的方程,其推导过程较为复杂,需要从基本定义开始逐步推导。
首先介绍一下双曲线的定义:设点F_1(-c,0)和F_2(c,0)是平面上固定的两个点,点P(x,y)是平面上动态的点。
双曲线是满足PF_1 - PF_2 = 2a (a>0)的动点P所构成的图形。
根据定义推导双曲线的标准方程:1.根据两点之间的距离公式,可以得到PF_1和PF_2的距离公式:PF_1² = (x + c)² + y²PF_2² = (x - c)² + y²2.根据定义中的等式PF_1 - PF_2 = 2a,可以得到:(x + c)² + y² - (x - c)² - y² = 4a²化简后可得:4cx = 4a²化简后可得:x = a²/c3.将x = a²/c代入PF_1² = (x + c)² + y²中,得到:(a²/c + c)² + y² = PF_1²化简后可得:(a² + c²) / c² + y² = PF_1² / c²4.根据双曲线的性质PF_1² - PF_2² = 4a²,可以得到:PF_1² - PF_2² = 4a²(a² + c²) / c² - [(a² - c²) / c² + y²] = 4a² / c²化简后可得:2c² / c² - y² / c² = 4a² / c²化简后可得:2 - y² / c² = 4a² / c²化简后可得:y² / c² - 2 = 4a² / c²化简后可得:y² / c² - 4a² / c² = 2通过上述推导过程,我们得到了双曲线的标准方程:y² / c² - x² / a² = 1其中,c是双曲线的焦点到中心的距离,a是双曲线的半轴长度。
双曲线标准方程的推导
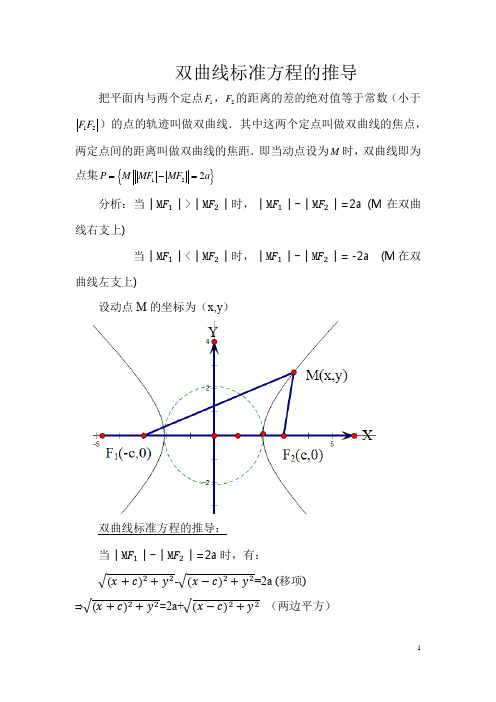
双曲线标准方程的推导把平面内与两个定点1F ,2F 的距离的差的绝对值等于常数(小于12F F )的点的轨迹叫做双曲线.其中这两个定点叫做双曲线的焦点,两定点间的距离叫做双曲线的焦距.即当动点设为M 时,双曲线即为点集P ={}122M MF MF a -=分析:当│M F 1│>│M F 2│时,│M F 1│-│M F 2│=2a (M 在双曲线右支上)当│M F 1│<│M F 2│时,│M F 1│-│M F 2│= -2a (M 在双曲线左支上)设动点M 的坐标为(x,y )双曲线标准方程的推导:当│M F 1│-│M F 2│=2a 时,有:√(x +c)2+y 2-√(x −c)2+y 2=2a (移项)⇒√(x +c)2+y 2=2a+√(x −c)2+y 2 (两边平方)⇒(x+c)2+y2=4a2+4a√(x−c)2+y2+(x−c)2+y2(展开)⇒x2+2cx+c2+y2=4a2+4a√(x−c)2+y2+x2-2cx+c2+y2(移项) ⇒x2−x2+2cx+2cx +c2−c2+y2-y2=4a2+4a√(x−c)2+y2(合并同类项)⇒4cx=4a2+4a√(x−c)2+y2(两边除以4)⇒cx=a2+a√(x−c)2+y2(移项)⇒cx-a2=a√(x−c)2+y2(两边平方)⇒c2x2-2a2cx+a4=a2[(x−c)2+y2](展开)⇒c2x2-2a2cx+a4=a2[x2-2 cx+c2+y2](展开)⇒c2x2-2a2cx+a4=a2x2-2a2 cx+a2c2+a2y2(移项)⇒-2a2cx+2a2cx+c2x2-a2x2-a2y2=a2c2-a4(合并同类项)⇒c2x2-a2x2-a2y2=a2c2-a4(按x,y顺序提取公因式)⇒(c2-a2)x2-a2y2=a2(c2-a2)(c2=a2+b2,等量代替)⇒b2x2-a2y2=a2b2(两边除以a2b2)⇒x 2a2-y2b2=1(a>0,b>0)当│M F1│-│M F2│=-2a时,有:√(x+c)2+y2-√(x−c)2+y2=-2a (移项)⇒√(x+c)2+y2=-2a+√(x−c)2+y2(两边平方)⇒(x+c)2+y2=4a2-4a√(x−c)2+y2+(x−c)2+y2(展开)⇒x2+2cx+c2+y2=4a2-4a√(x−c)2+y2+x2-2cx+c2+y2(移项)⇒x2−x2+2cx+2cx +c2−c2+y2-y2=4a2-4a√(x−c)2+y2(合并同类项)⇒4cx=4a2-4a√(x−c)2+y2(两边除以4)⇒cx=a2-a√(x−c)2+y2(移项)⇒cx-a2=−a√(x−c)2+y2(两边平方)⇒c2x2-2a2cx+a4=a2[(x−c)2+y2](展开)⇒c2x2-2a2cx+a4=a2[x2-2 cx+c2+y2](展开)⇒c2x2-2a2cx+a4=a2x2-2a2 cx+a2c2+a2y2(移项)⇒-2a2cx+2a2cx+c2x2-a2x2-a2y2=a2c2-a4(合并同类项)⇒c2x2-a2x2-a2y2=a2c2-a4(按x,y顺序提取公因式)⇒(c2-a2)x2-a2y2=a2(c2-a2)(c2=a2+b2,等量代替)⇒b2x2-a2y2=a2b2(两边除以a2b2)⇒x 2a2-y2b2=1(a>0,b>0)通过以上推导可知,一个方程x2a2-y2b2=1(a>0,b>0)涵盖了动点M左右两支运动轨迹,而不是一支运动轨迹。
双曲线方程的“巧设”

双曲线方程的“巧设”利用待定系数法是求双曲线的标准方程的常见方法,就是根据题设条件设出所求的双曲线方程,然后建立方程或方程组求得待定参数.在求解过程中,若能根据题目的特点,巧妙设出相应的双曲线方程,则可达到避繁就简的目的.本文将探讨求的双曲线方程的“巧设”.一、过两个已知点的双曲线方程的“巧设”例1求经过点P(-3,27),(-62,-7)的双曲线的标准方程.解析:设双曲线的方程为nx 2-my 2=1(mn ≠0),则有⎩⎨⎧ 9n -28m =172n -49m =1,解得⎩⎨⎧ n =-175m =-125, 所以双曲线方程为y 225-x 275=1. 点评:根据双曲线过两个已经点求双曲线的标准方程,一般采用待定系数法进行求解.由于双曲线的标准方程有x 2a 2-y 2b 2=1和y 2a 2-x 2b 2=1两种形式,因此在用待定系数法时,如果不知焦点在在x 轴还是在y 轴上,则常常需要先判断出焦点在哪条轴上,或者分别设出这两种标准形式进行求解,这无疑是麻烦的.实质上这类题目可以事先不加以判断,而直接设双曲线方程为nx 2-my 2=1(mn ≠0),这个方程实际上包括了上面两种情况.二、已知渐近线方程的双曲线方程的“巧设”例2已知双曲线的一条渐近线方程x -2y =0且过点P (4,3),求双曲线的标准方程。
解析:∵双曲线的一条渐近线方程为x -2y =0,∴可设双曲线方程为x 2-4y 2=k (k ∈R 且k ≠0).∵P (4,3)在双曲线上,∴42-4×32=k ,即k =-20.即y 25-x 220=1为所求的双曲线方程. 点评:本题若按照常规解法,需要根据双曲线上的已知点和渐近线的位置关系定双曲线焦点的位置.而上面解法则是根据双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程是y =±b ax ,进行逆向思维,即以y =±b ax 为渐近线的双曲线方程设为x 2a 2-y 2b 2=λ(λ≠0),避免了研究双曲线方程类型,简化了解题过程.此类题型还可以拓展:与双曲线x 2a 2-y 2b 2=1(a >0,b >0)有共同渐近线的双曲线系方程可设为x 2a 2-y 2b 2=λ(λ≠0). 三、与椭圆共焦点的双曲线方程的“巧设”例3已知双曲线与椭圆x 227+y 236=1有共同的焦点,且与椭圆相交,一个交点的纵坐标为4,求双曲线的方程.解析:设双曲线C 的方程为x 227-λ+y 236-λ=1,将点A(15,4)代入所设方程得(15)227-λ+4236-λ=1,解得λ1=32,λ1=0(舍去). ∴双曲线的方程y 24-x 25=1. 点评:与椭圆x 2a 2+y 2b 2=1有共同焦点的双曲线方程可设为x 2a 2-λ+y 2b 2-λ=1(b 2<λ<a 2).此结论还可以进一步拓展:与双曲线x 2a 2-y 2b2=1(a >0,b >0)有公共焦点的双曲线系方程可设为x 2a 2-λ-y 2b 2+λ=1(-b 2<λ<a 2). 四、等轴双曲线方程的“巧设”例4已经中心在原点、坐标轴为对称轴的双曲线两准线间的距离为42,且离心率为2,求此双曲线方程.解析:由于双曲线的离心率为2,由此易知所差双曲线为等轴双曲线.设所求双曲线的方程为x 2-y 2=k(k ≠0),∵2·a 2c =42,∴2·|k|2|k|⇒|k|(|k|-16)=0,∵k ≠0,∴k =±16,故所求双曲线方程为x 2-y 2=±16.点评:如果已知双曲线为等轴双曲线或经过分析可以判断出双曲线为等轴双曲线,则可以将所求双曲线的标准方程设为x 2-y 2=k(k≠0).。
求双曲线标准方程的方法

求双曲线标准方程的方法
随着互联网技术的不断发展,双曲线标准方程在计算机编程和机器视觉方面发挥着越来越重要的作用。
在这里,我们来介绍求双曲线标准方程的方法。
求双曲线标准方程的基本步骤:
一、找出双曲线的端点坐标和焦点坐标。
根据双曲线的可视特征,可以确定双曲线的端点坐标和焦点坐标,这样就可以计算出双曲线的离心率e。
二、求取双曲线的标准方程。
根据离心率e和双曲线的焦点坐标来计算双曲线的标准方程。
最后,结合上述步骤,我们可以得出双曲线标准方程。
双曲线标准方程的式子为:(x-x1)^2/a^2 - (y-y1)^2/b^2 = 1 ,其中(x1,y1)为焦点,a和b分别为半长轴和半短轴。
若双曲线在原点(0,0)上,则标准方程为:x^2/a^2 - y^2/b^2 = 1。
总之,求双曲线标准方程并不困难,要做的关键是要先分析出双曲线的图形特征,然后依据离心率及其他信息推导出该双曲线的标准方程,使用该标准方程可以帮助计算机或机器视觉更好地完成一些高级任务。
双曲线标准方程的详细推导过程

双曲线标准方程的详细推导过程嘿,朋友!咱今天来聊聊双曲线的标准方程是咋推导出来的。
先说说啥是双曲线。
你就想象有两个固定的点,咱叫它们焦点,然后一个动点到这两个焦点的距离之差是个定值,那这个动点的轨迹就是双曲线啦。
那怎么推导这标准方程呢?咱设这两个焦点在 x 轴上,坐标分别是(-c, 0) 和 (c, 0) ,动点的坐标是 (x, y) 。
根据双曲线的定义,动点到两个焦点的距离之差的绝对值是个定值2a 。
那距离咋算呢?这就得用到两点间的距离公式啦,这你总熟悉吧?咱先算动点到焦点 (-c, 0) 的距离,那就是√[(x + c)² + y²] 。
再算动点到焦点 (c, 0) 的距离,就是√[(x - c)² + y²] 。
因为距离之差的绝对值是 2a ,所以| √[(x + c)² + y²] - √[(x - c)² + y²] | = 2a 。
这式子看着是不是有点头疼?别急,咱两边平方来化简一下。
平方之后得到:( √[(x + c)² + y²] - √[(x - c)² + y²] )² = (2a)²。
展开之后,再经过一番整理和化简,你猜怎么着?就能得到双曲线的标准方程啦!你说这过程像不像解谜?一步一步,抽丝剥茧,最后找到答案。
这双曲线的标准方程推导,是不是还挺有趣的?其实数学里好多东西都这样,看着复杂,只要咱耐心点儿,一步步来,就能弄明白。
朋友,你是不是也觉得数学挺有意思的,只要肯钻研,就能发现其中的奥秘!这双曲线标准方程的推导,就是个很好的例子,不是吗?。
双曲线的标准方程公式

双曲线的标准方程公式
双曲线标准公式:x^2/a^2+y^2/b^2=1。
一般的,双曲线(希腊语“ὑπερβολή”,字面意思是“超过”或“超出”)是定义为平面交截直角圆锥面的两半的一类圆锥曲线。
它还可以定义为与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。
曲线,是微分几何学研究的主要对象之一。
直观上,曲线可看成空间质点运动的轨迹。
微分几何就是利用微积分来研究几何的学科。
为了能够应用微积分的知识,我们不能考虑一切曲线,甚至不能考虑连续曲线,因为连续不一定可微。
这就要我们考虑可微曲线。
但是可微曲线也是不太好的,因为可能存在某些曲线,在某点切线的方向不是确定的,这就使得我们无法从切线开始入手,这就需要我们来研究导数处处不为零的这一类曲线,我们称它们为正则曲线。
正则曲线才是经典曲线论的主要研究对象。
双曲线解题方法技巧

双曲线解题方法技巧
1. 嘿,双曲线解题可不能瞎碰运气呀!就像找宝藏要有地图一样。
比如给你个双曲线方程,那你是不是得先找出它的中心呀!这可太关键啦!就好比去一个陌生地方先得找到它的中心位置一样。
2. 哇塞,在解双曲线问题时,渐近线可是个大宝贝啊!你不利用它那可太亏啦!比如说,通过渐近线能迅速判断曲线的大致走向,这难道不神奇嘛!就像通过蛛丝马迹就能知道事情的发展方向。
3. 嘿哟,计算双曲线的离心率可别马虎呀!这可是反映双曲线“胖瘦”的关键。
举个例子,离心率大的双曲线那可就“瘦瘦”的,反之就“胖胖”的,是不是很形象呀!
4. 哎呀呀,遇到双曲线的焦点问题可别发怵!把焦点当成指引方向的灯塔呀!比如说根据焦点就能确定很多关键信息,就像有了灯塔船就不会迷失方向一样。
5. 哇哦,双曲线的定义可别小瞧呀!它能帮你解决大问题呢!举个例子,根据定义能很快判断某些点是否在双曲线上,多省事呀!
6. 嘿嘿,求解双曲线的最值问题的时候要动动脑筋呀!这就像是打游戏冲关一样刺激呢!比如说可以通过巧妙转化来求出最值,多有意思呀!
我的观点结论:双曲线解题方法技巧真的很有趣也很实用呀,掌握了这些,面对双曲线问题就不会头疼啦!。
高中数学双曲线解题技巧

高中数学双曲线解题技巧双曲线是高中数学中的一个重要内容,它在解析几何中有着广泛的应用。
在考试中,经常会出现与双曲线相关的各种题目,因此掌握双曲线的解题技巧对于高中学生来说至关重要。
本文将介绍一些常见的双曲线解题技巧,并通过具体的题目来说明。
一、双曲线的基本性质在解题之前,我们首先需要了解双曲线的基本性质。
双曲线的标准方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,其中$a$和$b$分别代表双曲线的横轴和纵轴的半轴长。
双曲线的中心位于原点$(0,0)$,横轴和纵轴分别为$x=a$和$y=b$。
二、双曲线的图像与方程通过观察双曲线的方程,我们可以得到以下结论:1. 当$a=b$时,双曲线变为一对直线,方程为$x=\pm y$;2. 当$a>b$时,双曲线开口朝向$x$轴,称为右开双曲线;3. 当$a<b$时,双曲线开口朝向$y$轴,称为上开双曲线。
三、双曲线的焦点和准线双曲线有两个焦点和两条准线,它们与双曲线的性质密切相关。
1. 焦点:双曲线的焦点位于横轴上,坐标为$(\pm c,0)$,其中$c=\sqrt{a^2+b^2}$;2. 准线:双曲线的准线位于横轴上,坐标为$(\pm a,0)$。
四、双曲线的渐近线双曲线有两条渐近线,它们与双曲线的方程有关。
1. 横渐近线:当$x\to\infty$或$x\to-\infty$时,双曲线趋于横渐近线$y=0$;2. 纵渐近线:当$y\to\infty$或$y\to-\infty$时,双曲线趋于纵渐近线$x=0$。
五、双曲线的对称性双曲线具有许多对称性,这些对称性可以帮助我们解题。
1. 关于$x$轴对称:当$(x,y)$在双曲线上时,$(-x,-y)$也在双曲线上;2. 关于$y$轴对称:当$(x,y)$在双曲线上时,$(-x,y)$也在双曲线上;3. 关于原点对称:当$(x,y)$在双曲线上时,$(-x,-y)$也在双曲线上。
双曲线方程推导步骤

双曲线方程推导步骤宝子,今天咱来唠唠双曲线方程的推导哈。
咱先从双曲线的定义说起,双曲线就是平面内到两个定点F1、F2的距离之差的绝对值是常数(这个常数要小于F1F2哦)的点的轨迹。
那咱就设这两个定点F1、F2在x轴上,坐标分别是(-c,0)和(c,0),然后设双曲线上任意一点P的坐标是(x,y)。
根据定义,PF1 - PF2 = 2a(a是个正数呢)。
那PF1的长度就是根号下[(x + c)² + y²],PF2的长度就是根号下[(x - c)²+ y²]。
这时候就有两种情况啦。
当PF1 - PF2 = 2a的时候,也就是根号下[(x + c)² + y²] - 根号下[(x - c)² + y²]=2a。
这个式子看起来有点复杂,咱得想办法把根号去掉。
那就把后面那个带根号的式子移到右边,然后两边同时平方。
这样就得到(x + c)² + y² = 4a²+ (x - c)² + y²+4a根号下[(x - c)² + y²]。
展开式子,x²+2cx + c²+y² = 4a²+x² - 2cx + c²+y²+4a根号下[(x - c)² + y²]。
一些项可以消掉啦,就剩下4cx - 4a² = 4a根号下[(x - c)² + y²]。
再化简一下,cx - a² = a根号下[(x - c)² + y²]。
再平方一次,(cx - a²)² = a²[(x - c)² + y²]。
展开又能得到好多项,c²x² - 2a²cx + a⁴ = a²(x² - 2cx + c²+ y²)。
高二必修一数学知识点求双曲线的标准方程

高二必修一数学知识点求双曲线的标准方程
大家把实际知识温习好的同时,也应该要多做题,从题中找到自己的缺乏,及时学懂,下面是查字典数学网小编为大家整理的14高二必修一数学知识点,希望对大家有协助。
求双曲线的规范方程
(1)焦点在X轴上,虚轴长为12,离心率为5/4?
(2)顶点间的距离为6,渐近线方程为y=+3/2x或-3/2x? 解:
(1)设双曲线方程为x^2/a^2 - y^2/b^2 = 1(a0)
依据题意2b=12,b=6 b^2=36
∵e^2 = c^2/a^2
=(a^2 + b^2 )/ a^2
=(a^2 + 36)/ a^2
= 25 / 16
a^2 = 64 双曲线方程为x^2/64 - y^2/36 = 1
(2)设双曲线方程为x^2/a^2 - y^2/b^2 = 1(a0)
或y^2/a^2 - x^2/b^2 = 1(a0)
∵顶点间的距离为6 2a=6 a=3 a^2 = 9
∵渐近线方程为y=(3/2)x
y=(b/a)x=(3/2)x 或 y=(a/b)x=(3/2)x
b=9/2 b^2 = 81/4 或 b=2 b^2=4
双曲线方程为x^2/9 - 4y^2/81 = 1 或 y^2/9 - x^2/4 = 1 要多练习,知道自己的缺乏,对大家的学习有所协助,以下是查字典数学网为大家总结的14高二必修一数学知识点,希望大家喜欢。
双曲线怎么求标准方程

双曲线怎么求标准方程双曲线是解析几何中的一个重要概念,它在数学和物理学中有着广泛的应用。
在学习双曲线的过程中,求其标准方程是一个基础且必须掌握的内容。
本文将详细介绍双曲线的标准方程求解方法,希望能够帮助大家更好地理解和掌握这一知识点。
1. 双曲线的定义。
在直角坐标系中,双曲线是一类特殊的曲线,其定义可以通过几何、代数或者参数方程进行描述。
在本文中,我们主要讨论双曲线的代数定义,即通过方程的形式来描述双曲线。
双曲线的代数定义为,设a、b为正实数,且a≠b,点F1(-c,0)和F2(c,0)为平面上两定点,且2c=2a。
点P(x,y)到F1、F2的距离之差的绝对值等于常数2a,即|PF1-PF2|=2a,则点P(x,y)的轨迹方程为x^2/a^2-y^2/b^2=1。
2. 求解双曲线的标准方程。
双曲线的标准方程是指将双曲线的方程化为一种特定的标准形式,便于对其性质进行分析和研究。
双曲线的标准方程通常采用以下形式,(x-h)^2/a^2-(y-k)^2/b^2=1或者(x-h)^2/a^2-(y-k)^2/b^2=-1。
求解双曲线的标准方程的一般步骤如下:步骤一,将双曲线的方程化为标准形式。
首先,我们需要将给定的双曲线方程化为标准形式。
具体的方法是利用平移变换和坐标轴旋转等技巧,将双曲线的方程化为上述所述的标准形式。
步骤二,确定标准方程中的参数。
在将双曲线的方程化为标准形式后,我们需要确定标准方程中的参数。
其中,参数(h,k)表示双曲线的中心坐标,参数a表示双曲线在x轴上的半轴长度,参数b 表示双曲线在y轴上的半轴长度。
步骤三,写出标准方程。
最后,根据确定的参数,我们可以将双曲线的标准方程写出来。
在写出标准方程时,需要保证等式两边的平方项系数分别为1,且一项为正一项为负。
3. 求解实例。
接下来,我们通过一个具体的实例来演示如何求解双曲线的标准方程。
例,求双曲线x^2/16-y^2/9=1的标准方程。
解,首先,我们将给定的双曲线方程化为标准形式,得到(x-0)^2/16-(y-0)^2/9=1。
双曲线标准方程的推导
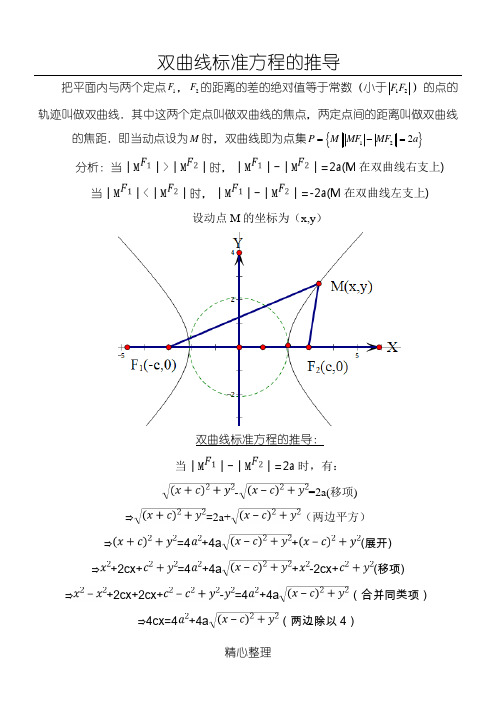
双曲线标准方程的推导
把平面内与两个定点1F ,2F 的距离的差的绝对值等于常数(小于12F F )的点的轨迹叫做双曲线.其中这两个定点叫做双曲线的焦点,两定点间的距离叫做双曲线
的焦距.即当动点设为M 时,双曲线即为点集P ={}122M MF MF a -= 分析:当│M │>│M
│时,│M
│-│M
│=2a(M 在双曲线右支上)
│M │-=2a(⇒=2a+(两边平方)
⇒=4+4a +(展开) ⇒+2cx+=4+4a
+-2cx+(移项) ⇒
+2cx+2cx+
-=4+4a
(合并同类项)
⇒4cx=4+4a
(两边除以4)
⇒cx=+a (移项) ⇒cx-(两边平方)
⇒-2+=[(展开)
⇒-2
+=[-2++(展开) ⇒-2
+=-2++(移项)
⇒
----
--)(+-(两边除以
)⇒-=1(a>0,b>0)
当│M
│-│M │=-2a 时,有:
-=-2a(移项) ⇒=-2a+(两边平方)
⇒
=4-4a
+
(展开)
⇒+2cx+=4-4a+-2cx+(移项)
⇒+2cx+2cx+-=4-4a(合并同类项)⇒4cx=4-4a(两边除以4)
⇒cx=-a(移项)
⇒cx-(两边平方)
⇒-2+=[-2+(
⇒+=-2++(移项)
+---(合并同类项)⇒---(按x,y顺序提取公因式)
---)(=+,等量代替)
-(两边除以)
⇒-=1(a>0,b>0)
一个方程-=1(a>0,b>0)
而不是一支运动轨迹。
故称其为“双曲线标准方程”。
双曲线方程的设法

双曲线方程的设法双曲线的一般方程为$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ 或$\frac{y^2}{b^2} - \frac{x^2}{a^2} = 1$,其中$a$ 和$b$ 是常数。
双曲线方程的设法的具体步骤如下:1. 根据题目的条件,确定双曲线的焦点位置。
如果焦点在$x$ 轴上,则一般选择$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ 作为方程;如果焦点在$y$ 轴上,则选择$\frac{y^2}{b^2} - \frac{x^2}{a^2} = 1$ 作为方程。
2. 根据题目给出的条件,确定$a$ 和$b$ 的值。
这些值通常由双曲线的半轴长、离心率等参数决定。
3. 将确定的$a$ 和$b$ 值代入相应的双曲线方程中,得到最终的双曲线方程。
例如,如果一个双曲线的焦点在$x$ 轴上,并且半轴长为$2a = 6$,离心率为$e = \frac{c}{a} = \frac{5}{3}$,则可以按照以下步骤设置方程:1. 由于焦点在$x$ 轴上,选择方程$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$。
2. 根据离心率的定义,有$c = ae = \frac{5}{3} \times 6 = 10$。
3. 由双曲线的性质,有$c^2 = a^2 + b^2$,代入$c = 10$ 和$a = 3$,解得$b^2 = c^2 - a^2 = 100 - 9 = 91$,即$b = \sqrt{91}$。
4. 将$a = 3$ 和$b = \sqrt{91}$ 代入方程$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$,得到最终的双曲线方程为$\frac{x^2}{9} - \frac{y^2}{91} = 1$。
高二数学必修知识:求双曲线的标准方程

依据题意2b=12,b=6 b^2=36
∵e^2 = c^2/a^2
=(a^2 + b^2 )/ a^2
=(a^2 + 36)/ a^2
= 2/36 = 1
(2)设双曲线方程为x^2/a^2 - y^2/b^2 = 1(a0)
或y^2/a^2 - x^2/b^2 = 1(a0)
高二数学必修知识:求双曲线的标准方程
要多练习,知道自己的缺乏,对大家的学习有所协助,详细内容请看下文2021高二数学必修知识。
求双曲线的规范方程
(1)焦点在X轴上,虚轴长为12,离心率为5/4?
(2)顶点间的距离为6,渐近线方程为y=+3/2x或-3/2x?
解:
(1)设双曲线方程为x^2/a^2 - y^2/b^2 = 1(a0)
∵顶点间的距离为6 2a=6 a=3 a^2 = 9
∵渐近线方程为y=(3/2)x
y=(b/a)x=(3/2)x 或 y=(a/b)x=(3/2)x
b=9/2 b^2 = 81/4 或 b=2 b^2=4
双曲线方程为x^2/9 - 4y^2/81 = 1 或 y^2/9 - x^2/4 = 1
我国现代的读书人,从上学之日起,就日诵不辍,普通在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为才疏学浅的文人。为什么在现代化教学的明天,我们念了十几年书的高中毕业生甚至大先生,竟提起作文就头疼,写不出像样的文章呢?吕叔湘先生早在1978年就尖利地提出:〝中小学语文教学效果差,中学语文毕业生语文水平低,……十几年上课总时数是9160课时,语文是2749课时,恰恰是30%,十年的时间,二千七百多课时,用来学本国语文,却是大少数不过关,岂非咄咄怪事!〞追本溯源,其主要缘由就是腹中无物。特别是写议论文,初中水平以上的先生都知道议论文的〝三要素〞是论点、论据、论证,也知晓议论文的基本结构:提出效果――剖析效果――处置效果,但真正动起笔来就犯难了。知道〝是这样〞,就是讲不出〝为什么〞。基本缘由还是无〝米〞下〝锅〞。于是便翻开作文集锦之类的书大段抄起来,抄人家的名言警句,抄人家的事例,不参考作文书就很难写出像样的文章。所以,词汇贫乏、内容空泛、千篇一概便成了中先生作文的通病。要处置这个效果,不能单在规划谋篇等写作技方面下功夫,必需看法到〝融会贯串〞的重要性,让先生积聚足够的〝米〞。
双曲线标准方程的推导

精心整理
双曲线标准方程的推导
把平面内与两个定点1F ,2F 的距离的差的绝对值等于常数(小于12F F )的点的
轨迹叫做双曲线.其中这两个定点叫做双曲线的焦点,两定点间的距离叫做双曲线的焦距.即当动点设为
M 时,双曲线即为点集P ={}122M MF MF a -=
│M ││M ││M
│-
=2a(?=2a+(两边平方)
?
=4+4a +(
?+2cx+=4+4a +-2cx+
?+2cx+2cx+-+4a
?4cx=4+4a (两边除以?cx=+a (移项)?cx-(两边平方)
?-2+=[(展开)
?-2
+=[-2++(展开)
?-2+=
-2++(移项) ?-2
+---(合并同类项)
?---(按x,y顺序提取公因式)
?(---)(=+,等量代替)
-(两边除以)
?-=1(a>0,b>0)
当│M│-│M│=-2a时,有:
?2a+
?=4-4a+
?+2cx+-4a+-2cx+(
?+2cx+2cx+--4a(合并同类项)
?4cx=4-4a(两边除以
?cx=(移项)
?cx-(两边平方)
?-2+=[(
?-2+=[-2++(
?-2+=-2++(移项)
?-2+---(合并同类项)
?--
?(---)(=+,等量代替)
-(两边除以)
?-=1(a>0,b>0)
通过以上推导可知,一个方程-=1(a>0,b>0)涵盖了动点M左右两支运动轨迹,
而不是一支运动轨迹。
故称其为“双曲线标准方程”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知过点(3x/2,2),且与双曲线 汙宁F 有共同焦点的双曲线的标准方程。
求双曲线标准方程的技巧
在求双曲线标准方程时,如果能根据已知条件设岀方程的合理形式,可以简化运算,优化 解题过程。
下而结合例题介绍求双曲线标准方程的方法。
—双曲线的一般方程
例1求经过点P (3,2j7).Q (-6Q7)的双曲线标准方程。
分析 双曲线的标准方程有两种形式:二-二=1 («>0.b>0 )或^-4=1(">
cr ir
x b ・
0, /9>0),可以讨论解决。
也可以应用下而的方法解决。
解 设双曲线方程为Ax 2 + By 2
=1 ( AZ? < 0 ) o 因为所求双曲线经过点
说明 求双曲线标准方程一般用待立系数法,当双曲线的焦点位置不确立时,为了避免 讨论焦点的位竄一般设双曲线方程为+
= 这样可以简化运算。
二等轴双曲线
例2等轴双曲线的中心在原点,焦点在x 轴上,与直线x-2y=0交于两点A 、B, 且|AB| = 2>/T5O 求此等轴双曲线的方程。
分析 根据等轴双曲线的特点,可以设含有一个参数的方程x 2-y 2=tr (6/>0 ) 岀
〃即可。
解 设等轴双曲线方程为X 2-V 2=«2
(4>0)。
由[x
'-y~=a
^解得交点A 、3的 [x-2y = 0・
说明 等轴双曲线是一类特殊的双曲线,它有一些特殊的性质,比如:离心率e = >/2,渐 近线方程为y=±x 且互相垂直等等。
三共焦点双曲线
/>(3,2育),0(-6血7),所以<
5 + 283 = 1,
72A+49B = 1・
解得A —严諾。
故所求双曲线
方程为針
2
—=1。
75
所以“=3。
故所求双曲线方程为X 2-F=9O
X 分析 根据双曲线焦点与庆的关系,有共同焦点的双曲线方程可设为
—一 =1 (-4 <k<\ 6),求出& 即可。
4 + R
求双曲线方程为計汁I °
说明 与双曲线^-4=1共焦点的双曲线方程可设为
——
=i(-b 2<
cT
X _k 次 +k
o 根据椭圆与双曲线的关系,与椭圆丹升I 共焦点的双曲线方程可设为 冲-尹厂心显-2),请注意
它们的区别。
四共渐近线双曲线
分析 因为双曲线罕一—二1的两条渐近线方程为双曲线罕一—=0,因此与它
9 16 9 16
共渐近线的双曲线方程可表示为双曲线—-^-=2(2^0 )。
9 16
2 2
解 设双曲线方程为才-^=2(2^0),因为双曲线经过点(一 3,20),所以 兄=凹_一匕里_ =丄。
故所求双曲线方程为£.£.=丄,即叮一吊=1。
9 16 4 9 16 4
9 4
4
说明求共渐近线的双曲线方程也可以讨论焦点分别在两条坐标轴上的情况,以上解 法避免了讨论过程,使解题更合理。
另外,以已知双曲线的实轴为虚轴、虚轴为实轴的双曲线 叫做原双曲线的共辄双曲线。
显然共轨双曲线有相同的渐近线,因此求共轨双曲线方程时可 以采用这个方法。
五同离心率的双曲线
16 —
k f v*
解设双曲线方程为贾2 6),
将(3施2)代入,得k=4.故所
例4求经过点(-3,2石),且与双曲线十-
計有共同渐近线的双曲线方程。
例5求经过点(2,0),且与双曲线—=1的离心率相同的双曲线的标准方程。
64 16
可能在x 轴上,也可能在y 轴上。
若焦点在x 轴上,它的方程可设为二-4=2(6/ >0# >
/ 少
0,2>0 ):若焦点在y 轴上,它的方程可设为帚寻=入(“>0">0, A>0)o
解(1)当所求双曲线的焦点在天轴上时,它的方程可设为—=2(2> 0 ),将
64 16
j 「
(2,0)代入,得;1 = —°此时所求双曲线的标准方程为〒■于=1。
16 4
2 2
(2)当所求双曲线的焦点在y 轴上时,它的方程可设为7-- —= 2 (2>0 ),将
64 16 (2,0)代入,得2 = -i<0(舍去)。
2
故所求双曲线的标准方程为—-F=l o
4
说明已知同离心率与相同渐近线求双曲线方程的方法类似,请你比较它们的区别。
六 已知双曲线渐近线的双曲线
例6求一条渐近线方程为3x + 4y = 0, 一个焦点是(4,0)的双曲线方程。
分析 由3x + 4y = 0,得- + -=0,因此借助与共渐近线方程问题的方法,设所求双曲
4 3
2 2
线方程为匚一 —=2(2H0),求出>1即可。
16 9
解 根据题意,可设所求双曲线方程为—一匚=2(2^0).又因为焦点在x 轴上, 16 9 所以几>0。
因为所以16几+ 9心6,解得花者故所求双曲线方程为着-茜
=lo
说明渐近线方程为护铲。
或g 严双曲线方程可设岭<2
X 分析因为-条双曲线和双曲线产沪
y =1(«>0j7>0)离心率相同,那么它的焦点
H0),然后确泄几的值。
因为求双曲线标准方程的条件是多种多样的,因此在解题时,一泄要认真审题,弄淸题意,根据条件选择适当的“方程形式S解决问题*。
