2018---2019学年度第一学期沪教版八年级数学单元测试题第十八章正比例函数与反比例函数

合集下载

沪教版(上海市)八年级(上)学第18章正比例函数与反比例函数单元测试卷 (解析版)

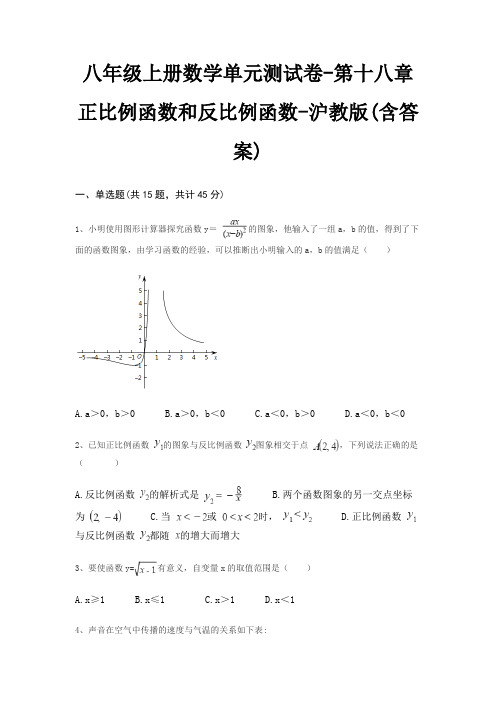
第18章正比例函数与反比例函数单元测试卷一．选择题（共6小题）1．圆周长公式2C R π=中，下列说法正确的是( ) A ．π、R 是变量，2为常量 B ．C 、R 为变量，2、π为常量 C ．R 为变量，2、π、C 为常量 D ．C 为变量，2、π、R 为常量2．函数13y x =+-x 的取值范围是( ) A ．2x ，且3x ≠ B ．2x C ．3x ≠ D ．2x >，且3x ≠3．已知反比例函数的图象经过点(2,4)-，那么这个反比例函数的解析式是( ) A ．2y x=B ．2y x=-C ．8y x=D ．8y x=-4．在下列函数中，当x 增大时，y 的值减小的函数是( ) A ．2y x=B ．5y x =C ．3y x=-D ．4x y =-5．关于函数2y x=-，下列说法中错误的是( ) A ．函数的图象在第二、四象限 B ．y 的值随x 的值增大而增大C ．函数的图象与坐标轴没有交点D ．函数的图象关于原点对称6．若1(3B -，1)y 、2(2,)A y -、3(1,)C y 三点都在函数(0)ky k x=>的图象上，则1y 、2y 、3y 的大小关系是( ) A ．312y y y >>B ．213y y y >>C ．231y y y >>D ．321y y y >>二．填空题（共12小题） 7．函数123y x =+的定义域是． 8．圆的面积计算公式2S R π=中是自变量． 9．已知33y x m =++是正比例函数，则m = ． 10．已知2()1f x x =-，那么f （3）的值是． 11．已知变量s 与t 的关系式是2132s t t =-，则当2t =-时，s = ．12．若y 与x 成正比例，且当1x =时，4y =-，则y 与x 的函数表达式为．13．已知反比例函数31m y x-=的图象有一分支在第二象限，那么常数m 的取值范围是． 14．已知正比例函数(y kx k =是常数，0)k ≠的图象经过第二、四象限，那么y 的值随着x 的值增大而．（填“增大”或“减小” ) 15．设函数4y x =-与3y x =的图象的交点坐标为(,)m n ，则11m n -的值为． 16．如图，过反比例函数(0)ky x x=<的图象上一点A 作AB x ⊥轴于点B ，连接AO ，若3AOB S ∆=，则反比例函数的表达式为．17．我们把[a ，]b 称为一次函数y ax b =+的“特征数”．如果“特征数”是[2，1]n +的一次函数为正比例函数，则n 的值为．18．从A 市到B 市汽车行驶的高速公路里程固定．假设汽车匀速行驶，汽车行驶的速度v （千米/时）与速度t （小时）的函数图象如图所示．若高速公路的速度限定不超过每小时120千米，则汽车从A 市到B 市行驶的最短时间为小时．三．解答题（共7小题）19．已知反比例函数的图象经过点(3,2)A -和(1,1)B m -，求m 的值和反比例函数的解析式．20．函数m y x =与函数(xy m k=、k 为不等于零的常数）的图象有一个公共点(3,2)A k -，其中正比例函数y 的值随x 的值增大而减小，求这两个函数的解析式．21．已知y 与x 成正比例，且当3x =时，4y =．（1）求y 与x 之间的函数解析式；（2）当1x =-时，求y 的值．22．已知正比例函数11(0)y k x k =≠的图象经过(2,4)A -、(,2)B m 两点．（1）求m 的值；（2）如果点B 在反比例函数22(0)k y k x=≠的图象上，求反比例函数的解析式．23．反比例函数ky x=的图象经过点(2,3)A 、(,3)B m -．（1）求这个函数的解析式及m 的值；（2）请判断点(1,6)C 是否在这个反比例函数的图象上，并说明理由．24．如图，直线(0)y ax a =>与双曲线(0)ky k x=>交于A 、B 两点，且点A 的坐标为(4,2)，点B 的坐标为(,2)n -．（1）求a ，n 的值；（2）若双曲线(0)ky y k x==>的上点C 的纵坐标为8，求AOC ∆的面积．25．如图所示是某一蓄水池每小时的排水量3(/)V m h 与排完水池中的水所用的时间()t h 之间的函数关系图象．（1）请你根据图象提供的信息求出此蓄水池的蓄水量；（2）求出此函数的解析式；（3）若要6h 排完水池中的水，那么每小时的排水量应该是多少？（4）如果每小时排水量不超过5 3000m ，那么水池中的水至少要多少小时排完？第18章正比例函数与反比例函数参考答案与试题解析一．选择题（共6小题）1．圆周长公式2C R π=中，下列说法正确的是( ) A ．π、R 是变量，2为常量 B ．C 、R 为变量，2、π为常量 C ．R 为变量，2、π、C 为常量D ．C 为变量，2、π、R 为常量解：在圆周长公式2C R π=中，2、π是常量，C ，R 是变量．故选：B ．2．函数13y x =+-x 的取值范围是( ) A ．2x ，且3x ≠ B ．2x C ．3x ≠ D ．2x >，且3x ≠解：根据题意得：20x -，且30x -≠，解得2x ，且3x ≠．故选：A ．3．已知反比例函数的图象经过点(2,4)-，那么这个反比例函数的解析式是( ) A ．2y x=B ．2y x=-C ．8y x=D ．8y x=-解：设反比例函数解析式为k y x=，将(2,4)-代入，得：42k -=，解得8k =-，所以这个反比例函数解析式为8y x=-，故选：D ．4．在下列函数中，当x 增大时，y 的值减小的函数是( ) A ．2y x= B ．5y x = C ．3y x=-D ．4x y =-解：2y x=的图象是双曲线，双曲线的两个分支分别位于一三象限，在每个象限内，y 随x 的增大而减小，因此①不符合题意；5y x =的图象是过原点，且图象位于一三象限的一条直线，y 随x 的增大而增大，因此②不符合题意；3y x=-的图象是双曲线，双曲线的两个分支分别位于二四象限，在每个象限内，y 随x 的增大而增大，因此③不符合题意； 4x y =-，即14y x =-，的图象是过原点，且图象位于二四象限的一条直线，y 随x 的增大而减小，因此④符合题意；故选：D ． 5．关于函数2y x=-，下列说法中错误的是( ) A ．函数的图象在第二、四象限 B ．y 的值随x 的值增大而增大C ．函数的图象与坐标轴没有交点D ．函数的图象关于原点对称解：函数2y x=-， ∴该函数的图象在第二、四象限，故选项A 正确；在每个象限内，y 随x 的增大而增大，故选项B 错误；函数的图象与坐标轴没有交点，故选项C 正确；函数的图象关于原点对称，故选项D 正确；故选：B ．6．若1(3B -，1)y 、2(2,)A y -、3(1,)C y 三点都在函数(0)ky k x=>的图象上，则1y 、2y 、3y 的大小关系是( ) A ．312y y y >> B ．213y y y >> C ．231y y y >> D ．321y y y >>解：0k >，∴反比例函数图象在一、三象限内，且在每个象限内y 随x 的增大而减小121(,),(2,)3B y A y --在第三象限，123->-，210y y ∴>> 3(1,)C y 在一象限， 30y ∴>， 321y y y ∴>>，故选：D ．二．填空题（共12小题） 7．函数123y x =+的定义域是 2x ≠ ．解：函数123y x =+， 230x ∴+≠，解得，32x ≠-，故答案为：32-．8．圆的面积计算公式2S R π=中 R 是自变量．解：圆的面积计算公式2S R π=中R 是自变量．故答案为：R ．9．已知33y x m =++是正比例函数，则m = 3- ．解：由题意得30m +=，解得3m =-．故答案为：3-． 10．已知2()1f x x =-，那么f （3）的值是 1 ．解：2()1f x x =-， f ∴（3）2131==-，故答案为：1．11．已知变量s 与t 的关系式是2132s t t =-，则当2t =-时，s = 8- ．解：把2t =-代入2132s t t =-，13(2)46282s =⨯--⨯=--=-，故答案为：8-．12．若y 与x 成正比例，且当1x =时，4y =-，则y 与x 的函数表达式为 4y x =- ．解：设y kx =，把1x =，4y =-代入y kx =，可得：4k -=，解得：4k =-，所以y 与x 的函数表达式为：4y x =-，故答案为：4y x =-． 13．已知反比例函数31m y x-=的图象有一分支在第二象限，那么常数m 的取值范围是 13m < ．解：反比例函数31m y x-=的图象有一分支在第二象限， 310m ∴-<，解得13m <，故答案是：13m <．14．已知正比例函数(y kx k =是常数，0)k ≠的图象经过第二、四象限，那么y 的值随着x 的值增大而减小．（填“增大”或“减小” )解：函数(0)y kx k =≠的图象经过第二、四象限，那么y 的值随x 的值增大而减小，故答案为：减小． 15．设函数4y x =-与3y x =的图象的交点坐标为(,)m n ，则11m n -的值为 43- ．解：函数4y x =-与3y x=的图象的交点坐标为(,)m n ， 4n m ∴-=-，3mn =， ∴114433n m m n mn ---===-，故答案为：43-．16．如图，过反比例函数(0)ky x x=<的图象上一点A 作AB x ⊥轴于点B ，连接AO ，若3AOB S ∆=，则反比例函数的表达式为 6y x=-．解：因为11||322AOB S OB BA x y ∆===又因为x y k = 即1||32k =所以6k =-故答案是：6y x=-． 17．我们把[a ，]b 称为一次函数y ax b =+的“特征数”．如果“特征数”是[2，1]n +的一次函数为正比例函数，则n 的值为 1- ．解：由题意得：10n +=，解得：1n =-，故答案为：1-．18．从A 市到B 市汽车行驶的高速公路里程固定．假设汽车匀速行驶，汽车行驶的速度v （千米/时）与速度t （小时）的函数图象如图所示．若高速公路的速度限定不超过每小时120千米，则汽车从A 市到B 市行驶的最短时间为 1 小时．解：根据题意可知从A 市到B 市汽车行驶的高速公路的里程为：80 1.5120⨯=（千米），高速公路的速度限定不超过每小时120千米， ∴从A 市到B 市行驶的最短时间为1小时．故答案为：1．三．解答题（共7小题）19．已知反比例函数的图象经过点(3,2)A -和(1,1)B m -，求m 的值和反比例函数的解析式．解：反比例函数的图象经过点(3,2)A -， ∴把(3,2)A -代入ky x=，得3(2)6k =⨯-=-， ∴反比例函数的解析式为6y x=-．把(1,1)B m -代入6y x=-得，16m -=-， 5m ∴=-．20．函数m y x =与函数(xy m k=、k 为不等于零的常数）的图象有一个公共点(3,2)A k -，其中正比例函数y 的值随x 的值增大而减小，求这两个函数的解析式．解：根据题意可得32k k=-，整理得2230k k -+=，解得11k =-，23k =，正比例函数y 的值随x 的值增大而减小， 1k ∴=-，∴点A 的坐标为(3,3)-， ∴反比例函数是解析式为：9y x=-；正比例函数的解析式为：y x =-．21．已知y 与x 成正比例，且当3x =时，4y =．（1）求y 与x 之间的函数解析式；（2）当1x =-时，求y 的值．解：（1）y 与x 成正比例，∴设y kx =，当3x =时，4y =， 43k ∴=，解得43k =， y ∴与x 之间的函数关系式为43y x =；（2）把1x =-代入43y x =得43y =-； 22．已知正比例函数11(0)y k x k =≠的图象经过(2,4)A -、(,2)B m 两点．（1）求m 的值；（2）如果点B 在反比例函数22(0)k y k x=≠的图象上，求反比例函数的解析式．解：（1）因为函数图象经过点(2,4)A -，所以124k =-，得12k =-．（2分）所以，正比例函数解析式：2y x =-．（1分）（2）根据题意，当2y =时，22m -=，得1m =-．（1分）于是，由点B 在反比例函数2k y x =的图象上，得221k=-，解得22k =-．所以，反比例函数的解析式是2y x =-．（2分） 23．反比例函数k y x=的图象经过点(2,3)A 、(,3)B m -．（1）求这个函数的解析式及m 的值；（2）请判断点(1,6)C 是否在这个反比例函数的图象上，并说明理由．解：（1）把(2,3)A 代入(2,3)A ，得：236k =⨯=，所以函数的解析式为6y x =，把(,3)B m -代入6y x =，得：63m-=，解得2m =-；（2）(1,6)C 在这个反比例函数的图象上；理由如下：把1x =代入6y x =，得：6y =，所以点(1,6)C 在这个反比例函数的图象上．24．如图，直线(0)y ax a =>与双曲线(0)k y k x=>交于A 、B 两点，且点A 的坐标为(4,2)，点B 的坐标为(,2)n -．（1）求a ，n 的值；（2）若双曲线(0)k y y k x ==>的上点C 的纵坐标为8，求AOC ∆的面积．解：（1）直线(0)y ax a =>与双曲线(0)k y k x=>交于A 、B 两点， ∴422a an =⎧⎨=-⎩，解得12a =，4n =-；（2）双曲线(0)k y k x=>经过A 点，双曲线(0)k y y k x==>的上点C 的纵坐标为8， C ∴点的坐标为(1,8)，如图，作AE x ⊥轴于E ，CD x ⊥轴于D ，()()18241152AOC COD AOE ACDE ACDE S S S S S ∆∆∆∴=+-==+-=梯形梯形．25．如图所示是某一蓄水池每小时的排水量3(/)V m h 与排完水池中的水所用的时间()t h 之间的函数关系图象．（1）请你根据图象提供的信息求出此蓄水池的蓄水量；（2）求出此函数的解析式；（3）若要6h 排完水池中的水，那么每小时的排水量应该是多少？（4）如果每小时排水量不超过5 3000m ，那么水池中的水至少要多少小时排完？解：（1）设k V t=．点(12,4000)在此函数图象上，∴蓄水量为312400048000m ⨯=；（2）点(12,4000)在此函数图象上，400012k ∴=，∴此函数的解析式48000V t =；（3）当6t =时，34800080006V m ==； ∴每小时的排水量应该是38000m ；（4）5000V ， ∴480005000t ，9.6t ∴．∴水池中的水至少要9.6小时排完．。

沪教版(上海市)八年级第一学期第18章正比例函数与反比例函数单元测试卷 (解析版)

第18章正比例函数与反比例函数单元测试卷一．选择题（共6小题）1．圆周长公式中，下列说法正确的是A．、是变量，2为常量B．、为变量，2、为常量C．为变量，2、、为常量D．为变量，2、、为常量2．函数的自变量的取值范围是A．，且B．C．D．，且3．已知反比例函数的图象经过点，那么这个反比例函数的解析式是A．B．C．D．4．在下列函数中，当增大时，的值减小的函数是A．B．C．D．5．关于函数，下列说法中错误的是A．函数的图象在第二、四象限B．的值随的值增大而增大C．函数的图象与坐标轴没有交点D．函数的图象关于原点对称6．若，、、三点都在函数的图象上，则、、的大小关系是A．B．C．D．二．填空题（共12小题）7．函数的定义域是．8．圆的面积计算公式中是自变量．9．已知是正比例函数，则．10．已知，那么（3）的值是．11．已知变量与的关系式是，则当时，．12．若与成正比例，且当时，，则与的函数表达式为．13．已知反比例函数的图象有一分支在第二象限，那么常数的取值范围是．14．已知正比例函数是常数，的图象经过第二、四象限，那么的值随着的值增大而．（填“增大”或“减小”15．设函数与的图象的交点坐标为，则的值为．16．如图，过反比例函数的图象上一点作轴于点，连接，若，则反比例函数的表达式为．17．我们把，称为一次函数的“特征数”．如果“特征数”是，的一次函数为正比例函数，则的值为．18．从市到市汽车行驶的高速公路里程固定．假设汽车匀速行驶，汽车行驶的速度（千米时）与速度（小时）的函数图象如图所示．若高速公路的速度限定不超过每小时120千米，则汽车从市到市行驶的最短时间为小时．三．解答题（共7小题）19．已知反比例函数的图象经过点和，求的值和反比例函数的解析式．20．函数与函数、为不等于零的常数）的图象有一个公共点，其中正比例函数的值随的值增大而减小，求这两个函数的解析式．21．已知与成正比例，且当时，．（1）求与之间的函数解析式；（2）当时，求的值．22．已知正比例函数的图象经过、两点．（1）求的值；（2）如果点在反比例函数的图象上，求反比例函数的解析式．23．反比例函数的图象经过点、．（1）求这个函数的解析式及的值；（2）请判断点是否在这个反比例函数的图象上，并说明理由．24．如图，直线与双曲线交于、两点，且点的坐标为，点的坐标为．（1）求，的值；（2）若双曲线的上点的纵坐标为8，求的面积．25．如图所示是某一蓄水池每小时的排水量与排完水池中的水所用的时间之间的函数关系图象．（1）请你根据图象提供的信息求出此蓄水池的蓄水量；（2）求出此函数的解析式；（3）若要排完水池中的水，那么每小时的排水量应该是多少？（4）如果每小时排水量不超过5 ，那么水池中的水至少要多少小时排完？第18章正比例函数与反比例函数参考答案与试题解析一．选择题（共6小题）1．圆周长公式中，下列说法正确的是A．、是变量，2为常量B．、为变量，2、为常量C．为变量，2、、为常量D．为变量，2、、为常量解：在圆周长公式中，2、是常量，，是变量．故选：．2．函数的自变量的取值范围是A．，且B．C．D．，且解：根据题意得：，且，解得，且．故选：．3．已知反比例函数的图象经过点，那么这个反比例函数的解析式是A．B．C．D．解：设反比例函数解析式为，将代入，得：，解得，所以这个反比例函数解析式为，故选：．4．在下列函数中，当增大时，的值减小的函数是A．B．C．D．解：的图象是双曲线，双曲线的两个分支分别位于一三象限，在每个象限内，随的增大而减小，因此①不符合题意；的图象是过原点，且图象位于一三象限的一条直线，随的增大而增大，因此②不符合题意；的图象是双曲线，双曲线的两个分支分别位于二四象限，在每个象限内，随的增大而增大，因此③不符合题意；，即，的图象是过原点，且图象位于二四象限的一条直线，随的增大而减小，因此④符合题意；故选：．5．关于函数，下列说法中错误的是A．函数的图象在第二、四象限B．的值随的值增大而增大C．函数的图象与坐标轴没有交点D．函数的图象关于原点对称解：函数，该函数的图象在第二、四象限，故选项正确；在每个象限内，随的增大而增大，故选项错误；函数的图象与坐标轴没有交点，故选项正确；函数的图象关于原点对称，故选项正确；故选：．6．若，、、三点都在函数的图象上，则、、的大小关系是A．B．C．D．解：，反比例函数图象在一、三象限内，且在每个象限内随的增大而减小在第三象限，，在一象限，，，故选：．二．填空题（共12小题）7．函数的定义域是．解：函数，，解得，，故答案为：．8．圆的面积计算公式中是自变量．解：圆的面积计算公式中是自变量．故答案为：．9．已知是正比例函数，则．解：由题意得，解得．故答案为：．10．已知，那么（3）的值是1．解：，（3），故答案为：1．11．已知变量与的关系式是，则当时，．解：把代入，，故答案为：．12．若与成正比例，且当时，，则与的函数表达式为．解：设，把，代入，可得：，解得：，所以与的函数表达式为：，故答案为：．13．已知反比例函数的图象有一分支在第二象限，那么常数的取值范围是．解：反比例函数的图象有一分支在第二象限，，解得，故答案是：．14．已知正比例函数是常数，的图象经过第二、四象限，那么的值随着的值增大而减小．（填“增大”或“减小”解：函数的图象经过第二、四象限，那么的值随的值增大而减小，故答案为：减小．15．设函数与的图象的交点坐标为，则的值为．解：函数与的图象的交点坐标为，，，，故答案为：．16．如图，过反比例函数的图象上一点作轴于点，连接，若，则反比例函数的表达式为．解：因为又因为即所以故答案是：．17．我们把，称为一次函数的“特征数”．如果“特征数”是，的一次函数为正比例函数，则的值为．解：由题意得：，解得：，故答案为：．18．从市到市汽车行驶的高速公路里程固定．假设汽车匀速行驶，汽车行驶的速度（千米时）与速度（小时）的函数图象如图所示．若高速公路的速度限定不超过每小时120千米，则汽车从市到市行驶的最短时间为1小时．解：根据题意可知从市到市汽车行驶的高速公路的里程为：（千米），高速公路的速度限定不超过每小时120千米，从市到市行驶的最短时间为1小时．故答案为：1．三．解答题（共7小题）19．已知反比例函数的图象经过点和，求的值和反比例函数的解析式．解：反比例函数的图象经过点，把代入，得，反比例函数的解析式为．把代入得，，．20．函数与函数、为不等于零的常数）的图象有一个公共点，其中正比例函数的值随的值增大而减小，求这两个函数的解析式．解：根据题意可得，整理得，解得，，正比例函数的值随的值增大而减小，，点的坐标为，反比例函数是解析式为：；正比例函数的解析式为：．21．已知与成正比例，且当时，．（1）求与之间的函数解析式；（2）当时，求的值．解：（1）与成正比例，设，当时，，，解得，与之间的函数关系式为；（2）把代入得；22．已知正比例函数的图象经过、两点．（1）求的值；（2）如果点在反比例函数的图象上，求反比例函数的解析式．解：（1）因为函数图象经过点，所以，得．（2分）所以，正比例函数解析式：．（1分）（2）根据题意，当时，，得．（1分）于是，由点在反比例函数的图象上，得，解得．所以，反比例函数的解析式是．（2分）23．反比例函数的图象经过点、．（1）求这个函数的解析式及的值；（2）请判断点是否在这个反比例函数的图象上，并说明理由．解：（1）把代入，得：，所以函数的解析式为，把代入，得：，解得；（2）在这个反比例函数的图象上；理由如下：把代入，得：，所以点在这个反比例函数的图象上．24．如图，直线与双曲线交于、两点，且点的坐标为，点的坐标为．（1）求，的值；（2）若双曲线的上点的纵坐标为8，求的面积．解：（1）直线与双曲线交于、两点，，解得，；（2）双曲线经过点，双曲线的上点的纵坐标为8，点的坐标为，如图，作轴于，轴于，．25．如图所示是某一蓄水池每小时的排水量与排完水池中的水所用的时间之间的函数关系图象．（1）请你根据图象提供的信息求出此蓄水池的蓄水量；（2）求出此函数的解析式；（3）若要排完水池中的水，那么每小时的排水量应该是多少？（4）如果每小时排水量不超过5 ，那么水池中的水至少要多少小时排完？解：（1）设．点在此函数图象上，蓄水量为；（2）点在此函数图象上，，此函数的解析式；（3）当时，；每小时的排水量应该是；（4），，．水池中的水至少要9.6小时排完．。

沪教版8年级上册数学第18章正比例函数与反比例函数单元检测卷

沪教版8年级上册数学第18章正比例函数与反比例函数单元检测卷一、选择题（共12小题；每小题3分，共36分）1.下列函数中，反比例函数是（）A. y=x﹣1B. y=C. y=+3x+1D. y=2.关于正比例函数y=﹣2x，下列说法错误的是（）A. 图象经过原点B. 图象经过第二，四象限C. y随x增大而增大D. 点（2，﹣4）在函数的图象上3.关于函数y=﹣x，下列结论正确的是（）A. 函数图象必过点（﹣2，﹣1）B. 函数图象经过第1、3象限C. y随x的增大而减小D. y随x的增大而增大4.如果反比例函数的图像经过点（－3，－4），那么函数的图像应在（）A. 第一、三象限B. 第一、二象限C. 第二、四象限D. 第三、四象限5.已知抛物线y=x2﹣2x+m+1与x轴有两个不同的交点，则函数y=的大致图象是（）A. B.C. D.6.双曲线与在第一象限内的图象如图所示，作一条平行于y轴的直线分别交双曲线于A、B 两点，连接OA、OB，则△AOB的面积为（）A. 1B. 2C. 3D. 47.函数y=﹣x+1与函数y=-在同一坐标系中的大致图象是（）A. B.C. D.8.函数y=中自变量x的取值范围是（）A. x≥﹣1B. x≤﹣1C. x＞﹣1D. x＜﹣19.如图，点A在双曲线y=上，点B在双曲线y=上，且AB∥x轴，C、D在x轴上，若四边形ABCD为矩形，则它的面积为（）A. 1B. 2C. 3D. 410.关于变量x，y有如下关系：①x﹣y=5；②y2=2x；③y=|x|；④y= ．其中y是x函数的是（）A. ①②③B. ①②③④C. ①③D. ①③④11.如图，反比例函数y＝（x＞0）的图象与一次函数y=ax+b的图象交于点A（1，6）和点B（3，2）．当ax+b＜时，则x的取值范围是（）A. 1＜x＜3B. x＜1或x＞3C. 0＜x＜1D. 0＜x＜1或x＞312.甲、乙二人沿相同的路线由A到B匀速行进，A，B两地间的路程为20km．他们行进的路程s（km）与甲出发后的时间t（h）之间的函数图像如图所示．根据图像信息，下列说法正确的是（）A. 甲的速度是4km/ hB. 乙的速度是10 km/ hC. 乙比甲晚出发1 hD. 甲比乙晚到B地3 h二、填空题（共10题；共30分）13.圆周长C与圆的半径r之间的关系为C=2πr，其中变量是________ ，常量是________ ．14.一块长方形花圃，长为x米，宽为y米，周长为18米，那么y与x的函数关系式为________．15.等腰△ABC的周长为10厘米，底边BC长为y厘米，腰AB长为x厘米，则y与x的关系式为：________．当x=2厘米时，y=________厘米；当y=4厘米时，x=________厘米．16.定义：数x、y、z中较大的数称为max{x，y，z}．例如max{﹣3，1，﹣2}=1，函数y=max{﹣t+4，t，}表示对于给定的t的值，代数式﹣t+4，t，中值最大的数，如当t=1时y=3，当t=0.5时，y=6．则当t=________ 时函数y的值最小．17.“早穿皮袄，午穿纱，围着火炉吃西瓜．”这句谚语反映了我国新疆地区一天中，________ 随________ 变化而变化，其中自变量是________ ，因变量是________ ．18.函数中，自变量x的取值范围是________．19.夏天高山上的气温从山脚起每升高l00m降低0.7℃，已知山脚下的气温是23℃，则气温y（℃）与上升的高度x（m）之间的关系式为________；当x=500时，y=________；当y=16时，x=________．20.一个反比例函数的图象位于第二、四象限．请你写出一个符合条件的解析式是________ ．21.圆的面积计算公式S=πR2中________ 是变量，________ 是常量．22.在△ABC中，AH⊥BC于点H，点P从B点开始出发向C点运动，在运动过程中，设线段AP的长为y，线段BP的长为x（如图1），而y关于x的函数图象如图2所示．Q （1，）是函数图象上的最低点．小明仔细观察图1，图2两图，作出如下结论：①AB=2；②AH=；③AC=2；④x=2时，△ABP是等腰三角形；⑤若△ABP为钝角三角形，则0＜x＜1；其中正确的是________ （填写序号）．三、解答题（共4题；共34分）23.已知某易拉罐厂设计一种易拉罐，在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系：（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）当易拉罐底面半径为2.4cm时，易拉罐需要的用铝量是多少？（3）根据表格中的数据，你认为易拉罐的底面半径为多少时比较适宜？说说你的理由．（4）粗略说一说易拉罐底面半径对所需铝质量的影响．24.如图，一次函数y=x+1的图象与反比例函数y=（k为常数，且k≠0）的图象都经过点A（m，2）．（1）求点A的坐标及反比例函数的表达式；（2）设一次函数y=x+1的图象与x轴交于点B，若点P是x轴上一点，且满足△ABP的面积是2，直接写出点P的坐标．25.如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=（m≠0）的图象交于A、B两点，与x轴交于C点，点A的坐标为（n，12），点C的坐标为（﹣4，0），且tan∠ACO=2．（1）求该反比例函数和一次函数的解析式；（2）求点B的坐标；（3）在x轴上求点E，使△ACE为直角三角形．（直接写出点E的坐标）26.如图，一次函数的图象与反比例函数的图象交于A（﹣3，1）、B（m，3）两点，（1）求反比例函数和一次函数的解析式；（2）写出使一次函数的值大于反比例函数的x的取值范围；（3）连接AO、BO，求△ABO的面积．参考答案一、选择题D C C A A B A A B D D C二、填空题13.C，r；2π14.y=9﹣x15.y=10﹣2x（0＜x＜5）；6；316.217.温度；时间；时间；温度18.x≥319.y=23﹣0.007x；19.5；100020.y=﹣，答案不唯一21.S和R；π22.①②③④三、解答题23.解：（1）易拉罐底面半径和用铝量的关系，易拉罐底面半径为自变量，用铝量为因变量；（2）当底面半径为2.4cm时，易拉罐的用铝量为5.6cm3（3）易拉罐底面半径为2.8cm时比较合适，因为此时用铝较少，成本低（4）当易拉罐底面半径在1.6～2.8cm变化时，用铝量随半径的增大而减小，当易拉罐底面半径在2.8～4.0cm 间变化时，用铝量随半径的增大而增大．24.解：（1）∵一次函数图象过A点，∴2=m+1，解得m=1，∴A点坐标为（1，2），又反比例函数图象过A点，∴k=1×2=2，∴反比例函数解析式为y=．（2）∵S△ABP=×PB×y A=2，A（1，2），∴2PB=4，∴PB=2，由y=x+1可知B（﹣1，0），∴点P的坐标为（1，0）或（﹣3，0）．25.解：（1）过点A作AD⊥x轴于D，∵C的坐标为（﹣4，0），A的坐标为（n，12），∴AD=12，CD=n+4，∵tan∠ACO=2，∴==2，解得：n=2，∴A（2，12），把A（2，12）代入y=，得m=2×12=24，∴反比例函数表达式为：y=，又∵点A（2，12），C（﹣4，0）在直线y=kx+b上，∴2k+b=12，﹣4k+b=0，解得：k=2，b=8，∴一次函数的表达式为：y=2x+8；（2）由方程组，解得：，，∵A（2，12），∴B（﹣6，﹣4）；（3）分两种情况：①当AE⊥x轴时，即点E与点D重合，此时E1（2，0）；②当EA⊥AC时，此时△ADE∽△CDA，则=，DE==24，又∵D的坐标为（2，0），∴E2（26，0）．综上所述，所求点E的坐标为E1（2，0），E2（26，0）．26.（1）解：设一次函数的解析式为y=kx+b（k≠0），反比例函数的解析式为y= （a≠0），把A（﹣3，1）代入y= 得：a=﹣3，即反比例函数的解析式为y=﹣，把B（m，3）代入y=﹣得：3=﹣，解得：m=﹣1，即B的坐标为（﹣1，3），把A、B的坐标代入y=kx+b得：，解得：k=1，b=4，即一次函数的解析式为y=x+4（2）解：∵函数y=﹣和y=x+4的交点为A（﹣3，1）、B（﹣1，3），∴使一次函数的值大于反比例函数的x的取值范围是﹣3＜x＜﹣1或x＞0（3）解：设一次函数y=x+4和x轴的交点为N，和y轴的交点为M，当x=0时，y=4，当y=0时，x=﹣4，即OM=4，ON=4，∵A（﹣3，1）、B（﹣1，3），∴△ABO的面积为S△MON﹣S△BOM﹣S△AON= ×4×4﹣×4×1﹣×4×1=4。

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题，共计45分)1、甲、乙两人以相同路线前往距离单位10km的培训中心参加学习．图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S（km）随时间t（分）变化的函数图象．以下说法：①乙比甲提前12分钟到达；②甲的平均速度为15千米/小时；③乙走了8km后遇到甲；④乙出发6分钟后追上甲．其中正确的有（）A.4个B.3个C.2个D.1个2、一列火车由甲市驶往相距600km的乙市，火车的速度是200km/时，火车离乙市的距离s(单位:km)随行驶时间t(单位:小时)变化的关系用图象表示正确的是( )A. B. C. D.3、圆周长公式C=2πR中，下列说法正确的是（）A.π、R是变量，2为常数B.C、R为变量，2、π为常数C.R为变量，2、π、C为常数D.C为变量，2、π、R为常数4、张老师带育才艺术团去北京参加文艺汇演，他们乘坐校车从南开大校门口出发到机场赶飞机．车开了一段时间后，张老师发现有一包演出服落在了校门口门卫处，于是马上打出租车返回去取，拿到服装后，他立即乘同一辆出租车追赶校车（下车取服装的时间忽略不计），结果，张老师在机场附近追上校车．设张老师与校车之间的距离为S，校车出发的时间为t，则下面能反映S与t的函数关系的大致图象是（）A. B. C. D.5、如图，点A是反比例函数图象上的一点，过点A作轴，垂足为点C，D为AC的中点，若的面积为1，则k的值为（）A. B. C.3 D.46、P1（x1， y1），P2（x2， y2）是正比例函数图象上的两点，下列判断中，正确的是A.y1＞y2B.y1＜y2C.当x1＜x2时，y1＜y2D.当x1＜x2时，y1＞y27、如图，已知三角形的面积一定，则其底边a和该底边上的高h之间的函数关系图象大致是（）A. B. C. D.8、小明从家到学校，先匀速步行到车站，等了几分钟后坐上了公交车，公交车沿着公路匀速行驶一段时间后到达学校，小明从家到学校行驶路程s（m）与时间t（min）的大致图象是（）A. B. C. D.9、已知 k1＜0＜k2，则函数 y=k1x 和的图象大致是（）A. B. C. D.10、已知二次函数y＝2x2＋9x+34，当自变量x取两个不同的值x1、x2时，函数值相等，则当自变量x取x1＋x2时的函数值与（）A. x＝1时的函数值相等B. x＝0时的函数值相等C. x＝时的函数值相等D. x＝－时的函数值相等11、如图，在平面直角坐标系中，点O为坐标原点，平行四边形的顶点A在反比例函数上，顶点B在反比例函数上，点C在x轴的正半轴上，则平行四边形的面积是（）A.2B.3C.4D.512、一次函数y＝kx＋b和反比例函数的图象如图所示，则有（）A.k＞0，b＞0，a＞0B.k＜0，b＞0，a＜0C.k＜0，b＞0，a＞0 D.k＜0，b＜0，a＞013、若点，，在反比例函数的图像上，则的大小关系是（）A. B. C. D.14、如图，正比例函数的图象和反比例函数的图象交于两点，分别过点作轴的垂线，垂足为，则与的面积之和为（）A. B. C.1 D.15、若是反比例函数，则a的取值为（）A.1B.-1C.±1D.任意实数二、填空题(共10题，共计30分)16、若点A(-3，y1)、B(0，y2)是二次函数y=-2(x-1)2+3图像上的点，那么y1与y2的大小关系是：y1 ________y2(填“>”，“<”或“=”)17、正比例函数y=kx（k≠0）的图象经过点A（﹣1，5），则k=________．18、如图，反比例函数的图象与直线交于，两点（点在点右侧），过点作轴的垂线，垂足为点，连接，，图中阴影部分的面积为12，则的值为________.19、已知点A为双曲线y= 图象上的点，点O为坐标原点，过点A作AB⊥x轴于点B，连接OA．若△AOB的面积为5，则k的值为________．20、已知一个函数，当x＞0时，函数值y随着x的增大而减小，请写出这个函数关系式________ （写出一个即可）21、反比例函数y1= （a＞0，a为常数）和y2= 在第一象限内的图象如图所示，点M 在y2= 的图象上，MC⊥x轴于点C，交y1= 的图象于点A；MD⊥y轴于点D，交y1=的图象于点B，当点M在y2= 的图象上运动时，以下结论：①S△ODB=S△OCA；②四边形OAMB的面积为2﹣a；③当a=1时，点A是MC的中点；④若S四边形OAMB=S△ODB+S△OCA，则四边形OCMD为正方形．其中正确的是________．（把所有正确结论的序号都填在横线上）22、在平面直角坐标系xOy中，已知A(2t,0)，B(0,-2t)，C(2t,4t)三点，其中t>0，函数的图象分别与线段BC，AC交于点P，Q．若S△PAB-S△PQB=t，则t的值为 ________．23、如图，点A在双曲线y=第三象限的分支上，连结AO并延长交第一象限的图象于点B，画BC∥x轴交反比例函数y=的图象于点C，若△ABC的面积为6，则k的值是________24、在△ABC中，AH⊥BC于点H，点P从B点开始出发向C点运动，在运动过程中，设线段AP的长为y，线段BP的长为x（如图1），而y关于x的函数图象如图2所示．Q （1，）是函数图象上的最低点．小明仔细观察图1，图2两图，作出如下结论：①AB=2；②AH=；③AC=2；④x=2时，△ABP是等腰三角形；⑤若△ABP为钝角三角形，则0＜x＜1；其中正确的是________ （填写序号）．25、在函数y= 中，自变量x的取值范围是________．三、解答题(共5题，共计25分)26、函数y＝（k﹣1）x2|k|﹣3是正比例函数，且y随x增大而减小，求（k+3）2018的值．27、如图，已知点A（1，a）是反比例函数y1= 的图象上一点，直线y2=﹣与反比例函数y1= 的图象的交点为点B、D，且B（3，﹣1），求：（Ⅰ）求反比例函数的解析式；（Ⅱ）求点D坐标，并直接写出y1＞y2时x的取值范围；（Ⅲ）动点P（x， 0）在x轴的正半轴上运动，当线段PA与线段PB之差达到最大时，求点P的坐标．28、已知正比例函数y=（3k﹣1）x，若y随x的增大而增大，求k的取值范围．29、如图，直线y=x+2与y轴交于点A，与反比例函数的图象交于点C，过点C作CB⊥x轴于点B，AO=2BO，求反比例函数的解析式．30、已知直线y=k1x+b与双曲线y=相交于点A（2，4），且与x轴、y轴分别交于B、C 两点，AD垂直平分OB，垂足为D，求直线和双曲线的解析式参考答案一、单选题(共15题，共计45分)1、B2、A3、B4、B5、D6、D7、D9、D10、B11、C12、B13、C14、C15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题，共计25分)26、29、30、。

沪教版(上海市)八年级(上)学第18章正比例函数与反比例函数单元测试卷 (含解析)

第18章正比例函数与反比例函数单元测试卷一．选择题（共6小题）1．一辆汽车以50/km h 的速度行驶，行驶的路程()s km 与行驶的时间()t h 之间的关系式为50s t =，其中变量是( )A ．速度与路程B ．速度与时间C ．路程与时间D ．三者均为变量2．八年级（6）班一同学感冒发烧住院洽疗，护士为了较直观地了解这位同学这一天24h 的体温和时间的关系，可选择的比较好的方法是( ) A ．列表法 B ．图象法C ．解析式法D ．以上三种方法均可3．在函数5x y x+=中，自变量x 的取值范围是( ) A ．0x >B ．5x -C ．5x -且0x ≠D ．0x 且0x ≠4．已知反比例函数的图象经过点(1,3)，则这个反比例函数的表达式为( ) A ．3y x=-B ．3y x=C ．13y x=D ．13y x=-5．在2(1)1y k x k =-+-中，若y 是x 的正比例函数，则k 值为( ) A ．1-B ．1C ．1±D ．无法确定6．已知蓄电池的电压为定值，使用蓄电池时，电流I （单位：)A 与电阻R （单位：)Ω是反比例函数关系，它的图象如图所示，则这个反比例函数的解析式为( )A ．24I R=B ．36I R=C ．48I R=D ．64I R=二．填空题（共12小题） 7．如果1()1f x x =-，那么(2)f = ． 8．已知变量s 与t 的关系式是232s t t =+，则当2t =-时，s = ． 9．若函数21my mx -=是正比例函数，且图象在二、四象限，则m = ．10．若正比例函数y kx =的图象经过点(2,4)，则该函数的解析式是． 11．已知反比例函数8k y x-=的图象位于第一、第三象限，则k 的取值范围是． 12．若点(,)A a b 在双曲线3y x=上，则代数式4ab -的值为． 13．如果函数(0)y kx k =≠的图象经过第二、四象限，那么y 的值随x 的值增大而．（填“增大”或“减小” )14．如图所示，为一个沙漏在计时过程中所剩沙子质量（克)与时间（小时）之间关系的图象，则从开始计时到沙子漏光所需的时间为小时．15．已知1(2,)A y ，2(3,)y 是反比列函数(0)ky k x=<的两点，则1y 2y ． 16．小玲家购买了一张面值600元的天燃气使用卡，这些天燃气所够使用的天数t 与小玲家平均每天使用天燃气的钱数m （元)之间的函数关系式为． 17．如图，已知点A 在反比例函数(0)ky k x=≠的图象上，过点A 作AB y ⊥轴于点B ，OAB ∆的面积是2．则k 的值是．18．如图，在双曲线16y x=的一支上有点1A ，2A ，3A ，⋯，正好构成图中多个正方形，点2A 的坐标为．三．解答题（共7小题）19．已知一个正比例函数的图象与反比例函数6y x=的图象都经过点(,3)A m -．求这个正比例函数的解析式．20．正比例函数y hx =和反比例函数ky x=的图象相交于A ，B 两点，已知点A 的坐标(1,3)．写出这两个函数的表达式．21．已知12y y y =-，1y 与x 成反比例，2y 与2x 成正比例．并且，当2x =时，6y =-；当1x =时，2y =．求y 与x 之间的函数解析式．22．已知x 与y 成反比例，且当34x =-时，43y =（1）求y 关于x 的函数表达式；（2）当23x =-时，y 的值是多少？23．已知正比例函数的图象过点P (3,3)-．（1）求这个正比例函数的表达式；（2）已知点2(A a ，4)-在这个正比例函数的图象上，求a 的值．24．已知近视眼镜片的度数y（度)是镜片焦距()(0)x cm x>的反比例函数，调查数据如表：（1）求y与x的函数表达式；（2）若近视眼镜镜片的度数为500度，求该镜片的焦距．25．某公交车每天的支出费用为600元，每天的乘车人数x（人)与每天利润（利润=票款收入-支出费用）y（元)的变化关系如下表所示（每位乘客的乘车票价固定不变）:根据表格中的数据，回答下列问题：（1）在这个变化关系中，自变量是什么？因变量是什么？（2）若要不亏本，该公交车每天乘客人数至少达到多少？（3）请你判断一天乘客人数为500人时，利润是多少？（4）试写出该公交车每天利润y（元)与每天乘车人数x（人)的关系式．第18章正比例函数与反比例函数单元测试卷参考答案与试题解析一．选择题（共6小题）1．一辆汽车以50/km h 的速度行驶，行驶的路程()s km 与行驶的时间()t h 之间的关系式为50s t =，其中变量是( )A ．速度与路程B ．速度与时间C ．路程与时间D ．三者均为变量解：由题意的：50s t =，路程随时间的变化而变化，则行驶时间是自变量，行驶路程是因变量；故选：C ．2．八年级（6）班一同学感冒发烧住院洽疗，护士为了较直观地了解这位同学这一天24h 的体温和时间的关系，可选择的比较好的方法是( ) A ．列表法 B ．图象法C ．解析式法D ．以上三种方法均可解：护士为了较直观地了解这位同学这一天24h 的体温和时间的关系，可选择的比较好的方法是图象法，有利于判断体温的变化情况，故选：B ．3．在函数y =中，自变量x 的取值范围是( ) A ．0x >B ．5x -C ．5x -且0x ≠D ．0x 且0x ≠解：根据题意得：500x x +⎧⎨≠⎩，解得：5x -且0x ≠．故选：C ．4．已知反比例函数的图象经过点(1,3)，则这个反比例函数的表达式为( ) A ．3y x=-B ．3y x=C ．13y x=D ．13y x=-解：设该反比例函数的解析式为：(0)ky k x=≠．把(1,3)代入，得 31k =，解得3k =．则该函数解析式为：3y x=．故选：B ．5．在2(1)1y k x k =-+-中，若y 是x 的正比例函数，则k 值为( ) A ．1- B ．1C ．1±D ．无法确定解：2(1)1y k x k =-+-，y 是x 的正比例函数，210k ∴-=，且10k -≠，解得：1k =-．故选：A ．6．已知蓄电池的电压为定值，使用蓄电池时，电流I （单位：)A 与电阻R （单位：)Ω是反比例函数关系，它的图象如图所示，则这个反比例函数的解析式为( )A ．24I R= B ．36I R=C ．48I R=D ．64I R=解：设KI R=，把(8,6)代入得： 8648K =⨯=，故这个反比例函数的解析式为：48I R=．故选：C ．二．填空题（共12小题） 7．如果1()1f x x =-，那么(2)f = 21+ ．解：1()1f x x =-， (2)2121f ∴==-；21+．8．已知变量s 与t 的关系式是232s t t =+，则当2t =-时，s = 2 ．解：当2t =-时，23(2)2(2)682s =⨯-+⨯-=-+=，故答案为：2．9．若函数21my mx -=是正比例函数，且图象在二、四象限，则m =解：由题意得：211m -=，解得：m =，图象在二、四象限， 0m ∴<，m ∴=，故答案为：10．若正比例函数y kx =的图象经过点(2,4)，则该函数的解析式是 2y x = ．解：正比例函数y kx =的图象经过点(2,4)， 42k ∴=，解得2k =，∴这个正比例函数的解析式为2y x =，故答案为：2y x =． 11．已知反比例函数8k y x-=的图象位于第一、第三象限，则k 的取值范围是 8k > ．解：反比例函数8k y x-=的图象位于第一、第三象限， 80k ∴->，解得8k >，故答案为8k >．12．若点(,)A a b 在双曲线3y x =上，则代数式4ab -的值为 1- ．解：点(,)A a b 在双曲线3y x=上， 3ab ∴=，4341ab ∴-=-=-．故答案为：1-．13．如果函数(0)y kx k =≠的图象经过第二、四象限，那么y 的值随x 的值增大而减小．（填“增大”或“减小” )解：函数(0)y kx k =≠的图象经过第二、四象限，那么y 的值随x 的值增大而减小，故答案为：减小．14．如图所示，为一个沙漏在计时过程中所剩沙子质量（克)与时间（小时）之间关系的图象，则从开始计时到沙子漏光所需的时间为 213小时．解：沙漏漏沙的速度为：1569-=（克/小时），∴从开始计时到沙子漏光所需的时间为：215913÷=（小时）．故答案为：21315．已知1(2,)A y ，2(3,)y 是反比列函数(0)ky k x=<的两点，则1y < 2y ．解：反比列函数ky x=的0k <， 0x ∴>时，y 随着x 的增大而增大，23<，12y y ∴<，故答案为：<．16．小玲家购买了一张面值600元的天燃气使用卡，这些天燃气所够使用的天数t 与小玲家平均每天使用天燃气的钱数m （元)之间的函数关系式为 t m= ．解：600tm =， 600t m∴=．故答案为：600t m=． 17．如图，已知点A 在反比例函数(0)ky k x=≠的图象上，过点A 作AB y ⊥轴于点B ，OAB ∆的面积是2．则k 的值是 4 ．解：设点A 的坐标为(A x ，)A y ，AB y ⊥，由题意可知：11222OAB A A S OB AB y x ∆===，4A A y x ∴=，又点A 在反比例函数图象上，故有4A A k x y ==．故答案为：4． 18．如图，在双曲线16y x=的一支上有点1A ，2A ，3A ，⋯，正好构成图中多个正方形，点2A 的坐标为 (225+，225)-+ ．解：双曲线16y x=的一支上有点1A ，正好构成正方形， ∴点1A 的坐标为(4,4)，双曲线16y x=的一支上有点2A ，正好构成正方形， ∴设构成的正方形边长为m ，则点2A 的坐标为(4,)m m +，164m m∴=+，解得：1225m =-+2225m =--（不合题意舍去）， ∴点2A 的坐标为(25+，225)-+；故答案为；(225+，225)-+．三．解答题（共7小题）19．已知一个正比例函数的图象与反比例函数6y x=的图象都经过点(,3)A m -．求这个正比例函数的解析式．解：把点(,3)A m -的坐标代入6y x=得2m =- ∴点A 的坐标为(2,3)--（2分）设正比例函数的解析式为(0)y kx k =≠（1分）把(2,3)--代入上式，得32k =（2分）所以这个正比例函数的解析式为32y x =（1分） 20．正比例函数y hx =和反比例函数ky x=的图象相交于A ，B 两点，已知点A 的坐标(1,3)．写出这两个函数的表达式．解：把(1,3)A 代入y hx =中，得31h =⨯， 3h ∴=，∴正比例函数的解析式为：3y x =；把(1,3)A 代入ky x=中，得133k =⨯=， ∴反比例函数的解析式为：3y x=． 21．已知12y y y =-，1y 与x 成反比例，2y 与2x 成正比例．并且，当2x =时，6y =-；当1x =时，2y =．求y 与x 之间的函数解析式．解：设出反比例函数与正比例函数的解析式分别为11k y x=，222y k x =，又知12y y y =-，则212k y k x x=-，根据题意当2x =时，6y =-；当1x =时，2y =，可得：12124622k k k k ⎧-=-⎪⎨⎪-=⎩，解得1242k k =⎧⎨=⎩．242y x x∴=-． 22．已知x 与y 成反比例，且当34x =-时，43y =（1）求y 关于x 的函数表达式；（2）当23x =-时，y 的值是多少？解：（1）x 与y 成反比例，∴可设(xy k k =为常数，0)k ≠，当34x =-时，43y =，∴解得1k =-，所以y 关于x 的表达式1y x=-；（2）当23x =-时，32y =．23．已知正比例函数的图象过点P (3,3)-．（1）求这个正比例函数的表达式；（2）已知点2(A a ，4)-在这个正比例函数的图象上，求a 的值．解：（1）把(3,3)P -代入正比例函数y kx =，得33k =-， 1k =-，所以正比例函数的解析式为y x =-；（2）把点2(A a ，4)-代入y x =-得， 24a -=-，解得2a =±．24．已知近视眼镜片的度数y （度)是镜片焦距()(0)x cm x >的反比例函数，调查数据如表：（1）求y 与x 的函数表达式；（2）若近视眼镜镜片的度数为500度，求该镜片的焦距．解：（1）根据题意得：y与x之积恒为10000，则函数的解析式是10000yx =；（2）令500y=，则10000 500x=，解得：20x=．即该镜片的焦距是20cm．25．某公交车每天的支出费用为600元，每天的乘车人数x（人)与每天利润（利润=票款收入-支出费用）y（元)的变化关系如下表所示（每位乘客的乘车票价固定不变）:根据表格中的数据，回答下列问题：（1）在这个变化关系中，自变量是什么？因变量是什么？（2）若要不亏本，该公交车每天乘客人数至少达到多少？（3）请你判断一天乘客人数为500人时，利润是多少？（4）试写出该公交车每天利润y（元)与每天乘车人数x（人)的关系式．解：（1）在这个变化关系中，自变量是每天的乘车人数x（人)；变量是每天利润y（元)；（2）当0y=时，300x=因此要不亏本，该公交车每天乘客人数至少达到300人；（3）500400 20010040050-+⨯=元，因此当一天乘客人数为500人时，利润是400元；（4）300100260050xy x-=⨯=-。

上海教育版数学八上第18章《正比例函数和反比例函数》单元测试

5x(B)y = 2.若反比例函数 y = k(D)函数 y = - 3 x ；5.点（3、4）是反比例函数 y = k()()） 9.已知 f （x ）= 1x 的图像上，则 k =______________.上海教育版数学八上第 18 章《正比例函数和反比例函数》单元测试一、选择题（2 分×6=12 分）1.下列函数中的正比例函数是（）.(A) y = 13 x x (C) y = 3 (D) y = 6 x - 1 .x 的图像在每个象限内，y 随 x 的增大而减小，则 k （(A) k ≥0；(B)k ＞0 ；(C)k ≤0 ； (D)k ＜0.3.下列说法中，错误的是（）.(A) 函数 y=kx(k ＜0）的图像经过第二、四象限；(B)正方形的周长与它的边长成正比例；(C)2x+1 是 x 的函数；x y随 x 的增大而减小.4.下列函数图像过一三象限的是（）.）.(A) y = 3(B)y=x 2 ； (C)y=-2x ； (D)y = - 7x .x 图像上一点，则此函数图像经过点（(A)（2，-6）；(B)（2，6）；(C)（4，-3； (D)（3，-4）.6.下列函数中，y 随 x 的增大而增大的是（）.(A) y = k 2 + 1 x ；(B) y = - k 2 + 1 x ；）.(C) y = k 2 + 1 x； (D) y = - k 2 + 1x .二、填空题（3 分×12=36 分）7.已知 y=(k -1)x 是正比例函数，则 k 满足条件_______________.8.函数 y =x - 3 的定义域是____________.x ，则 f （ 2 ）=________________.10.如果点 A （2，3）在反比例 y = k11.已知一正比例函数图像上有一点（1，3），则其解析式为____________.1 / 419.若 y 与 2x +1 成反比例，当 x =1 时， y = 4x 交于 M 、N 点，点 M 的横坐标是 2.80012.点 A （3，-1）B （n ，3）都在同一个正比例函数的图像上，则 n = ___________.13.函数 y=(2a -3)x 的图像过二四象限，则 a 的取值范围是______________.14.如果函数 y=2x 自变量 x 的取值范围是 -3＜x ＜0，那么 y 的取值范围是___________.15.写出一个图像过一三象限的反比例函数解析式___________.16.如果 y=(m-2)x +m 2-4 是正比例函数，那么 m= ____________.17.如图，△OPQ 是边长为 2 的等边三角形，O 为坐标原点，点 Q 在 x 轴上，若反比例函数的图像过点 P ,则它的解析式是______________.18.已知 A 、B 两地相距 20 千米，某人从 A 地步行前往 B 地，步行速度是 8 千米/小时，步行 t 小时后离 B 地 S 千米，写出 S 与 t 的函数解析式及定义域______________.三、简答题（5 分×2+6 分×2=22 分）3 ，求 y 与 x 的函数解析式.yPO Q x17题图20.若函数 y = (m - 3) x m 2-8 是正比例函数，求 m 的值并写出的解析式.21.已知直线 y=kx 与双曲线 y = 4(1)求 M 点的坐标;(2)写出正比例的函数解析式.22.某水库有水 Q （m 3）与排水时间 t （时）的Q(m3)函数图像如图所示，根据图像回答问题.6004002 / 4 200O10 20 30 40 t(时) 22题图(1)排水前，水池内有多少立方米水？(2)排水10小时后，水池还剩多少水？(3)剩水400m3时，已排水几小时？(4)写出Q与t的解析式及定义域.四、解答题（7分×2+8分×2=30分）23.已知y=y1+y2，y1与x+1成反比例，y2与x-1成正比例，且当x=0时，y=-1，当x=2时，y=3.(1)求y与x之间函数解析式；(2)判断A(2，-1)是否在这个图像上.24.如图，长方形ABCD的边AB=4，BC=5，点P、Q分别从A、C出发向D、B以相同的速度运动，设AP的长为x，四边形BPDQ的面积为y.(1)写出y关于x的函数解析式;(2)写出函数的定义域.A P DB Q C24题图25.正比例函数的图像经过点（-3，5），过图像上另一点A作y轴的垂线，垂足B点的坐标是（0，4），求点A的坐标与△AOB的面积.3/4y =- 3 1.26. 点 C 的坐标分别为 ,0 ⎪, ,0 ⎪, - ,0 ⎪, - ,0 ⎪26.已知 Rt ⊿ABC ,∠A =90°,∠B=60°,AB =1,将它放在直角坐标系中，使斜边 BC 在 x轴上，直角顶点 A 在反比例函数 y = 3 x的图像上，求点 C 的坐标.yO x正比例函数与反比例函数单元测试1.C2.B3.D4.A5.B6.A7.k ≠ 18. x ≥ 39.2 226题图10.6 11.y=3 x12.-9 13. a < 3 1 314.-6<y <0 15. y = 等 16.-2 17. y = 18.S=20-8 t2 x x（ 0 ≤ t ≤ 5 4） 19. y = . 20. m =-3, y=-6x . 21. M (2，2). y=x .2 2 x + 122.(1)800m 3; (2)600m 3;(3)20 小时 ;(4)q =800-20t （ 0 ≤ t ≤ 40 ） .23.(1)12- ( x - 1) . (2)点 A 在图像上.24. y=20-4x 0≤x ≤5. 25. A(- ,4)2( x + 1) 2 5S⎛ 1 ⎫ ⎛7 ⎫⎛ 1 ⎫⎛ 7 ⎫ 5 ⎝ 2 ⎭ ⎝ 2 ⎭⎝ 2 ⎭⎝ 2 ⎭4 / 4。

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题，共计45分)1、下列函数中,是关于的反比例函数的是( ).A. B. C. D.2、下列函数中，y与x成反比例的是（）A.y=B.y=C.y=3x 2D.y= +13、如图，等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动．如果MN=2AC=4cm，那么△ABC和正方形XYMN重叠部分的面积S（cm2）与匀速运动所用时间t （min）之间的函数的大致图像是（）A. B. C. D.4、如图，P（m，m）是反比例函数y= 在第一象限内的图象上一点，以P为顶点作等边△PAB，使AB落在x轴上，则△POB的面积为（）A. B.3 C. D.5、已知点A（﹣1，m），B（1，m），C（2，m+1）在同一个函数图象上，这个函数图象可以是（）A. B. C. D.6、二次函数()的图像如图所示，反比列函数与正比列函数在同一坐标系内的大致图像是（）A. B. C. D.7、函数y= 的自变量x的取值范围是（）A.x≥1且x≠2B.x≥2且x≠1C.x＞2且x≠1D.x＞28、函数的自变量的取值范围是（）A. B. C. D. 且9、函数y=ax2+1与y= （a≠0）在同一平面直角坐标系中的图象可能是（）A. B. C. D.10、如图，函数与的图象相交于点两点，则不等式的解集为（）A. B. 或 C. D. 或11、一次函数y=ax+b（a≠0）、二次函数y=ax2+bx和反比例函数y=（k≠0）在同一直角坐标系中的图象如图所示，A点的坐标为（-2，0），则下列结论中，正确的是（）A.b=2a+kB.a=b+kC.a＞b＞0D.a＞k＞012、反比例函数y= 图象上的两个点为( )、( ),且,则下列式子一定成立的是( )A. B. C. D.不能确定13、若定义f（x）＝3x﹣2，如f（﹣2）＝3×（﹣2）﹣2＝﹣8，下列说法中：①当f （x）＝1时，x＝1；②对于正数x，f（x）＞f（﹣x）均成立；③f（x﹣1）+f（1﹣x）＝0；④当a＝2时，f（a﹣x）＝a﹣f（x）．其中正确的是（）A.①②B.①③C.①②④D.①③④14、下列函数中，既是一次函数，又是正比例函数的是（）.A.y=15x 2B.y=x（ x-5）-x 2C.y=D.y=5x-115、在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强，如下表：则可以反映y与x之间的关系的式子是（）体积 x(mL) 100 80 60 40 20压强 y(kPa) 60 75 100 150 300A. 000xB. 000xC.D.二、填空题(共10题，共计30分)16、如图，在平面直角坐标系xOy中，点B在y轴上，AB=AO，反比例函数的图象经过点A，若△ABO的面积为2，则k的值为________．17、如图，函数y= (x>0)的图象与矩形OABC的边BC交于点D，分别过点A，D作AF ∥DE，交直线y=k2x(k2<0)于点F，E.若OE=OF，BD=2CD，四边形ADEF的面积为12，则k1的值为________。

沪教版(上海) 八年级数学(上)学期第18章正比例函数与反比例函数单元测试卷 (含解析)

八年级（上）数学第18章正比例函数与反比例函数单元测试卷一．选择题（共6小题）1．已知与成反比例，与成正比例，则与的关系是A．成正比例B．成反比例C．既成正比例也成反比例D．以上都不是2．下列函数中，随着的增大而减小的是A．B．C．D．3．关于函数，下列说法中错误的是A．函数的图象在第二、四象限B．的值随的值增大而增大C．函数的图象与坐标轴没有交点D．函数的图象关于原点对称4．已知反比例函数的图象经过点，则这个反比例函数的表达式为A．B．C．D．5．已知点，和点，在反比例函数的图象上，若，则A．B．C．D．6．小李家距学校3千米，中午12点他从家出发到学校，途中路过文具店买了些学习用品，12点50分到校．下列图象中能大致表示他离家的距离（千米）与离家的时间（分钟）之间的函数关系的是A．B．C．D．二．填空题（共12小题）7．在函数中，自变量的取值范围是．8．若函数是正比例函数，则常数的值是．9．请写出一个过第二、四象限的正比例函数的解析式．10．假期即将开始，李伟制定了一张“假期每天时间分配表”，其中课外阅读时间为1.5小时，这里的“1.5小时”为（填“常量”或“变量”．11．若正比例函数为常数，且的函数值随着的增大而减小，则的值可以是．（写出一个即可）12．函数中自变量的取值范围是．13．某款宝马汽车的油箱一次加满汽油50升，可行驶千米，设该汽车行驶百公里耗油升，假设汽车能行驶至油用完，则关于的函数解析式为．14．反比例函数的图象如图所示，则的取值范围为．15．已知正比例函数与反比例函数图象的一个交点坐标是，则另一个交点坐标是．16．一天，小明从家里骑自行车到图书馆还书，小明离家的路程（米关于时间（分的函数图象如图所示．若去图书馆时的平均车速为180米分，则从图书馆返回时的平均车速为米分．17．如图，正比例函数，，在同一平面直角坐标系中的图象如图所示．则比例系数，，的大小关系是．（按从大到小的顺序用“”连接）18．如图，在平面坐标系中，点是函数图象上的点，过点作轴的垂线交轴于点，点在轴上，则的面积为．三．解答题（共7小题）19．已知正比例函数的图象经过第一、三象限，且过点，求这个正比例函数的解析式．20．已知，与成反比例，与成正比例，且当时，，．求关于的函数解析式．21．已知反比例函数，当时，．（1）求关于的函数表达式．（2）当时，求自变量的值．22．已知正比例函数的图象过点．（1）求这个正比例函数的表达式；（2）已知点，在这个正比例函数的图象上，求的值．23．老李想利用一段5米长的墙（图中，建一个面积为32平方米的矩形养猪圈，另外三面（图中，，需要自己建筑．老李准备了可以修建20米墙的材料（可以不用完）．（1）设，，求关于的函数关系式．（2）对于（1）中的函数的值能否取到8.5？请说明理由．24．已知正反比例函数的图象交于、两点，过第二象限的点作轴，点的横坐标为，且，点在第四象限．（1）求这两个函数的解析式；（2）求这两个函数的图象的交点坐标；（3）若点在坐标轴上，联结、，写出当时的点坐标．25．如图，直线与双曲线交于、两点，且点的坐标为，点的坐标为．（1）求，的值；（2）若双曲线的上点的纵坐标为8，求的面积．参考答案一．选择题（共6小题）1．已知与成反比例，与成正比例，则与的关系是A．成正比例B．成反比例C．既成正比例也成反比例D．以上都不是解：与成反比例，与成正比例，设，，故，则，故（常数），则与的关系是：成反比例．故选：．2．下列函数中，随着的增大而减小的是A．B．C．D．解：、中，随着的增大而增大，不符合题意；、中，在每个象限内随着的增大而减小，不符合题意；、中，随着的增大而减小，符合题意；、中，在每个象限内随着的增大而增大，不符合题意；故选：．3．关于函数，下列说法中错误的是A．函数的图象在第二、四象限B．的值随的值增大而增大C．函数的图象与坐标轴没有交点D．函数的图象关于原点对称解：函数，该函数的图象在第二、四象限，故选项正确；在每个象限内，随的增大而增大，故选项错误；函数的图象与坐标轴没有交点，故选项正确；函数的图象关于原点对称，故选项正确；故选：．4．已知反比例函数的图象经过点，则这个反比例函数的表达式为A．B．C．D．解：设该反比例函数的解析式为：．把代入，得，解得．则该函数解析式为：．故选：．5．已知点，和点，在反比例函数的图象上，若，则A．B．C．D．解：反比例函数的图象分别在第一、三象限，在每一象限，随的增大而减小，而，点，和点，在第一象限，．故选：．6．小李家距学校3千米，中午12点他从家出发到学校，途中路过文具店买了些学习用品，12点50分到校．下列图象中能大致表示他离家的距离（千米）与离家的时间（分钟）之间的函数关系的是A．B．C．D．解：小李距家3千米，离家的距离随着时间的增大而增大，途中在文具店买了一些学习用品，中间有一段离家的距离不再增加，综合以上符合，故选：．二．填空题（共12小题）7．在函数中，自变量的取值范围是．解：由题意得，，解得．故答案为：．8．若函数是正比例函数，则常数的值是．解：依题意得：，解得：．9．请写出一个过第二、四象限的正比例函数的解析式（答案不唯一）．解：正比例函数的图象经过第二、四象限．故答案为：（答案不唯一）．10．假期即将开始，李伟制定了一张“假期每天时间分配表”，其中课外阅读时间为1.5小时，这里的“1.5小时”为常量（填“常量”或“变量”．解：假期即将开始，李伟制定了一张“假期每天时间分配表”，其中课外阅读时间为1.5小时，这里的“1.5小时”为常量，故答案为：常量．11．若正比例函数为常数，且的函数值随着的增大而减小，则的值可以是．（写出一个即可）解：正比例函数为常数，且的函数值随着的增大而减小，，则．故答案为：．12．函数中自变量的取值范围是且．解：由题意得，且，解得且．故答案为：且．13．某款宝马汽车的油箱一次加满汽油50升，可行驶千米，设该汽车行驶百公里耗油升，假设汽车能行驶至油用完，则关于的函数解析式为．解：汽车行驶每100千米耗油升，升汽油可走千米，．故答案为：14．反比例函数的图象如图所示，则的取值范围为．解：反比例函数的图象在第二象限，，．故答案为：．15．已知正比例函数与反比例函数图象的一个交点坐标是，则另一个交点坐标是．解：正比例函数与反比例函数图象都是关于原点对称的，另一个交点与一个交点也关于原点对称，另一个交点坐标为，故答案为：16．一天，小明从家里骑自行车到图书馆还书，小明离家的路程（米关于时间（分的函数图象如图所示．若去图书馆时的平均车速为180米分，则从图书馆返回时的平均车速为200米分．解：根据去图书馆时的平均车速为180米分，可得：从家里到图书馆的距离为米；所以从图书馆返回时的平均车速为米分，故答案为：20017．如图，正比例函数，，在同一平面直角坐标系中的图象如图所示．则比例系数，，的大小关系是．（按从大到小的顺序用“”连接）解：正比例函数，的图象在一、三象限，，，的图象比的图象上升得快，，的图象在二、四象限，，，故答案为：．18．如图，在平面坐标系中，点是函数图象上的点，过点作轴的垂线交轴于点，点在轴上，则的面积为．解：设点的坐标为、，点是函数图象上，，则的面积，故答案为：．三．解答题（共7小题）19．已知正比例函数的图象经过第一、三象限，且过点，求这个正比例函数的解析式．解：正比例函数的图象经过第一、三象限，把代入得，整理得，解得，，，这个正比例函数的解析式为．20．已知，与成反比例，与成正比例，且当时，，．求关于的函数解析式．解：根据题意，设，、．，，当时，，，．，．．21．已知反比例函数，当时，．（1）求关于的函数表达式．（2）当时，求自变量的值．解：（1）根据题意，得，解得，；该反比例函数的解析式是；（2）由（1）知，该反比例函数的解析式是，当时，，即．22．已知正比例函数的图象过点．（1）求这个正比例函数的表达式；（2）已知点，在这个正比例函数的图象上，求的值．解：（1）把代入正比例函数，得，，所以正比例函数的解析式为；（2）把点，代入得，，解得．23．老李想利用一段5米长的墙（图中，建一个面积为32平方米的矩形养猪圈，另外三面（图中，，需要自己建筑．老李准备了可以修建20米墙的材料（可以不用完）．（1）设，，求关于的函数关系式．（2）对于（1）中的函数的值能否取到8.5？请说明理由．解：（1）依题意，得：，．（2）当时，，解得：，．又，对于（1）中的函数的值不能取到8.5．24．已知正反比例函数的图象交于、两点，过第二象限的点作轴，点的横坐标为，且，点在第四象限．（1）求这两个函数的解析式；（2）求这两个函数的图象的交点坐标；（3）若点在坐标轴上，联结、，写出当时的点坐标．解：（1）如图，点的横坐标为，且轴，，，，则点，将点代入得：，则正比例函数解析式为；将点代入得：，则反比例函数解析式为；（2）由得：或，所以点坐标为．（3）若点在轴上，设，由可得，解得：或，此时点坐标为或；若点在轴上，设，由可得，解得：或，此时点坐标为或；综上，点的坐标为或或或．25．如图，直线与双曲线交于、两点，且点的坐标为，点的坐标为．（1）求，的值；（2）若双曲线的上点的纵坐标为8，求的面积．解：（1）直线与双曲线交于、两点，，解得，；（2）双曲线经过点，，双曲线的上点的纵坐标为8，点的坐标为，如图，作轴于，轴于，．。

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题，共计45分)1、下列图像中，不是的函数的是（）A. B. C. D.2、如图，菱形OABC的顶点C的坐标为（3，4）．顶点A在x轴的正半轴上，反比例函数y= （x＞0）的图象经过顶点B，则k的值为（）A.12B.20C.24D.323、下列语句不正确的是( )A.所有的正比例函数都是一次函数B.一次函数的一般形式是y=kx+b C.正比例函数和一次函数的图象都是直线 D.正比例函数的图象是一条过原点的直线4、柿子熟了，从树上落下来．下面的（）图可以大致刻画出柿子下落过程中（即落地前）的速度变化情况．A. B. C. D.5、如图，O是边长为4cm的正方形ABCD的中心，M是BC的中点，动点P由A开始沿折线A﹣B﹣M方向匀速运动，到M时停止运动，速度为1cm/s．设P点的运动时间为t（s），点P的运动路径与OA、OP所围成的图形面积为S（cm2），则描述面积S（cm2）与时间t （s）的关系的图象可以是（）A. B. C. D.6、如图1，一个电子蜘蛛从点A出发匀速爬行，它先沿线段AB爬到点B，再沿半圆经过点M爬到点C．如果准备在M、N、P、Q四点中选定一点安装一台记录仪，记录电子蜘蛛爬行的全过程．设电子蜘蛛爬行的时间为x，电子蜘蛛与记录仪之间的距离为y，表示y与x函数关系的图象如图2所示，那么记录仪可能位于图1中的（）A.点MB.点NC.点PD.点Q7、对于反比例函数，下列说法不正确的是A.图象分布在第二、四象限B.当时，随的增大而增大C.图象经过点（1,-2）D.若点，都在图象上，且，则8、如图，直线l的解析式为y=﹣x+4，它与x轴和y轴分别相交于A，B两点．平行于直线l的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动．它与x轴和y轴分别相交于C，D两点，运动时间为t秒（0≤t≤4），以CD为斜边作等腰直角三角形CDE（E，O两点分别在CD两侧）．若△CDE和△OAB的重合部分的面积为S，则S与t之间的函数关系的图象大致是（）A. B. C. D.9、如图，已知点A在反比例函数y= 的图象上，点B在反比例函数y= 的图象上，四边形ABCD是长方形，则长方形ABCD的面积是（）A.4B.6C.8D.1210、甲、乙两车沿同一平直公路由A地匀速行驶（中途不停留），前往终点B地，甲、乙两车之间的距离S（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．下列说法：①甲、乙两地相距210千米；②甲速度为60千米/小时；③乙速度为120千米/小时；④乙车共行驶3 小时，其中正确的个数为（）A.1个B.2个C.3个D.4个11、根据图中①所示的程序，得到了y与x的函数图象图中②，若点M是y轴正半轴上任意一点，过点M作PQ∥x轴交图象于点P、Q.连结OP、OQ，则下列结论正确的是（）A.△OPQ的面积为4.5B.x<0时，y=C.x>0时，y随x的增大而增大D.∠POQ不能等于90°12、若点A(–2，)、B( –1，)、C(1，)都在反比例函数( 为常数)的图像上，则、、的大小关系为（）A. B. C. D.13、已知反比例函数(a≠0)的图象，在每一象限内，的值随值的增大而减小，则一次函数y－ax＋a的图象不经过（）A.第一象限B.第二象限C.第三象限D.第四象限14、已知梯形的面积一定，它的高为h，中位线的长为x，则h与x的函数关系大致是A. B. C. D.15、已知点A（x1，y1），B（x2，y2）在反比例函数的图象上，若y1＜y2＜0，则下列结论正确的是（）A. x1＜x2＜0B. x2＜x1＜0C.0＜x1＜x2D.0＜x2＜x1二、填空题(共10题，共计30分)16、已知正比例函数y＝－4x与反比例函数y＝的图像交于A，B两点，若点A的坐标为(x，4)，则点B的坐标为________．17、下列各函数①y=；②y=；③y=；④y=；⑤y=x；⑥y=﹣3；⑦y=和⑧y=3x﹣1中，是y关于x的反比例函数的有：________（填序号）．18、在函数中，自变量x的取值范围是________.19、如果用s表示路程（单位：千米），t表示时间（单位：小时），v表示速度（单位：千米/时），那么t＝________时（用s和v表示）.20、汽车以60千米/时的速度匀速行驶，随着时间t（时）的变化，汽车行驶的路程s（千米）也在变化，则s与t的关系式为________．当t从2时变化到3.5时，汽车行驶路程s从________变化到________．21、函数y= 中自变量x的取值范围是________．22、如图，已知等边三角形OAB与反比例函数y= （k＞0，x＞0）的图象交于A、B两点，将△OAB沿直线OB翻折，得到△OCB，点A的对应点为点C，线段CB交x轴于点D，则的值为________．（已知sin15°= ）23、已知点A（1，m），B（2，n）在反比例函数图象上，则m与n的大小关系为________.24、如图，反比例函数y= 的图象与直线y=kx（k＞0）相交于A、B两点，AC∥y轴，BC ∥x轴，则△ABC的面积等于________个面积单位．25、已知双曲线与直线交于A、B两点(点A在点B的左侧).如图所示，点P是第一象限内双曲线上一动点，BC⊥AP于C，交x轴于F，PA交y轴于E，则下列结论：①；②AE=EF；③；④.其中正确的是：________.（填序号）三、解答题(共5题，共计25分)26、函数y＝（k﹣1）x2|k|﹣3是正比例函数，且y随x增大而减小，求（k+3）2018的值．27、如图，已知矩形OABC的两边OA，OC分别在x轴，y轴的正半轴上，且点B（4，3），反比例函数y=图象与BC交于点D，与AB交于点E，其中D（1，3）．（1）求反比例函数的解析式及E点的坐标；（2）求直线DE的解析式；（3）若矩形OABC对角线的交点为F (2,)，作FG⊥x轴交直线DE于点G．①请判断点F是否在此反比例函数y=的图象上，并说明理由；②求FG的长度．28、如图所示，在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5…，过A1、A2、A3、A4、A5…分别作x轴的垂线与反比例函数的图象交于点P1、P2、P3、P4、P5…，并设△OA1P1、△A1A2P2、△A2A3P3…面积分别为S1、S2、S3…，按此作法进行下去，则S n的值为（n为正整数）．29、一次越野跑中，当李明跑了1600米时，小刚跑了1450米，此后两人匀速跑的路程s （米）与时间t（秒）的关系如图，结合结合图象，求图中S1和S0的位置.30、求出下列函数中自变量x的取值范围．y=．参考答案一、单选题(共15题，共计45分)2、D3、B4、A5、A6、C</div>7、D8、C9、A10、C11、A12、C13、C14、D15、C二、填空题(共10题，共计30分)16、17、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、27、28、29、30、。

八年级上册数学单元测试卷-第十八章正比例函数和反比例函数-沪教版(含答案)

八年级上册数学单元测试卷-第十八章正比例函数和反比例函数-沪教版(含答案)一、单选题(共15题，共计45分)1、如图，直线y=x﹣b与y轴交于点C，与x轴交于点B，与反比例函数y=的图象在第一象限交于点A（3，1），连接OA，则△AOB的面积为（）A.1B.C.2D.32、甲、乙两人进行慢跑练习，慢跑路程y（米）与所用时间t（分钟）之间的关系如图所示，下列说法错误的是（）A.甲乙两人8分钟各跑了800米B.前2分钟，乙的平均速度比甲快 C.5分钟时两人都跑了500米 D.甲跑完800米的平均速度为100米∕分3、如图，点A的反比例函数y＝（x＞0）的图象上，点B在反比例函数y＝（x＞0）的图象上，AB∥x轴，BC⊥x轴，垂足为C，连接AC，若△ABC的面积是6，则k的值为（）A.10B.12C.14D.164、函数y=（2﹣a）x+b﹣1是正比例函数的条件是（）A.a≠2B.b=1C.a≠2且b=1D.a，b可取任意实数5、如图直线y1＝x+1与双曲线y2＝交于A （2，m）、B（﹣3，n）两点.则当y1＞y2时，x的取值范围是（）A.x＞﹣3或0＜x＜2B.﹣3＜x＜0或x＞2C.x＜﹣3或0＜x＜2 D.﹣3＜x＜26、已知函数y＝(k＜0)，又x1，x2对应的函数值分别是y1，y2，若x2＞x1＞0对，则有（）A. y1＞y2＞0B. y2＞y1＞0C. y1＜y2＜0D. y2＜y＜017、如图，在△ABC中，AC=BC=25，AB=30，D是AB上的一点（不与A、B重合），DE⊥BC，垂足是点E，设BD=x，四边形ACED的周长为y，则下列图象能大致反映y与x之间的函数关系的是（）A. B. C.D.8、函数y= 的自变量x的取值范围是（）A.x≥﹣2B.x≥﹣2且x≠0C.x≠0D.x＞0且x≠﹣29、如图直线与双曲线相交于两点，则不等式的解集是( )A. 或B. 或C. 或D. 或10、已知力F所作的功是15焦，则力F与物体在力的方向上通过的距离S的图象大致是如图中的（）A. B. C. D.11、已知正比例函数y＝kx的图象经过第二、四象限，则一次函数y＝kx﹣k的图象可能是图中的（）A. B. C. D.12、已知点（x1，y1），（x2，y2）是反比例函数y＝图象上的两点，且0＜x1＜x2，则y1，y2的大小关系是（）A.0＜y1＜y2B.0＜y2＜y1 C. y1＜y2＜0D. y ＜y1＜0213、点，点，在反比例函数的图象上，且，则（）A. B. C. D.不能确定14、如果一个正比例函数的图象经过不同象限的两点A（2，m），B（n,3），那么一定有（）A.m>0，n>0B.m>0，n<0C.m<0，n>0D.m<0，n<015、已知k1＜0＜k2，则函数y=k1x和y=的图象大致是（）A. B. C.D.二、填空题(共10题，共计30分)16、函数的自变量x的取值范围是________.17、在函数y= 中，自变量x的取值范围是________．18、直线与双曲线有两个交点，其中一交点坐标为(2,4)，则它们的另一交点坐标为________.19、将正比例函数y＝2x的图象向上平移3个单位，所得的直线不经过第________象限．20、函数关系常用的三种表示方法是________ ，________ ，________21、如图，在平面直角坐标系中，函数y=2x和y=﹣x的图象分别为直线l1， l2，过点（1，0）作x轴的垂线交l2于点A1，过点A1作y轴的垂线交l2于点A2，过点A2作x轴的垂线交l2于点A3，过点A3作y轴的垂线交l2于点A4，…依次进行下去，则点A2017的坐标为________．22、一次函数y=kx+k﹣1（k≠0）与反比例函数y= 的图象交点的个数为________．23、如图，在平面直角坐标系xOy中，直线y= x与双曲线y= 相交于A，B两点，C是第一象限内双曲线上一点，连接CA并延长交y轴于点P，连接BP，BC．若△PBC的面积是20，则点C的坐标为________．24、已知反比例函数的图象在其每一分支上，随的增大而增大，则此反比例函数的解析式可以是________．（注：只需写出一个正确答案即可）25、京沈高速公路全长658km，汽车沿京沈高速公路从沈阳驶往北京，则汽车行完全程所需时间 t（h）与行驶的平均速度 v（km/h）之间的函数关系式为 ________．三、解答题(共5题，共计25分)26、函数y=（m﹣2）x 是反比例函数，则m的值是多少？27、已知函数解析式y=1+．（1）在下表的两个空格中分别填入适当的数：（2）观察上表可知，当x的值越来越大时，对应的y值越来越接近于一个常数，这个常数是什么？x 5 500 5000 50000 …y=1+ 1.2 1.02 1.002 1.0002 …28、希望中学学生从12月份开始每周喝营养牛奶，单价为2元/盒，总价y元随营养牛奶盒数x变化．指出其中的常量与变量，自变量与函数，并写出表示函数与自变量关系的式子．29、如图，一次函数y=kx+1（k≠0）与反比例函数y=（m≠0）的图象有公共点A（1，2）．直线l⊥x轴于点N（3，0），与一次函数和反比例函数的图象分别交于点B，C．（1）求一次函数与反比例函数的解析式；（2）求△ABC的面积？30、一次越野跑中，当李明跑了1600米时，小刚跑了1450米，此后两人匀速跑的路程s （米）与时间t（秒）的关系如图，结合图象解答下列问题：Ⅰ.请你根据图象写出二条信息；Ⅱ.求图中S1和S0的位置.参考答案一、单选题(共15题，共计45分)1、A2、A3、D4、C5、B6、C7、A8、B9、B10、B12、B13、B14、D15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题，共计25分)26、27、28、29、30、。

八年级上册数学单元测试卷-第十八章正比例函数和反比例函数-沪教版(含答案)

八年级上册数学单元测试卷-第十八章正比例函数和反比例函数-沪教版(含答案)一、单选题(共15题，共计45分)1、小明使用图形计算器探究函数y＝的图象，他输入了一组a，b的值，得到了下面的函数图象，由学习函数的经验，可以推断出小明输入的a，b的值满足（）A.a＞0，b＞0B.a＞0，b＜0C.a＜0，b＞0D.a＜0，b＜02、已知正比例函数的图象与反比例函数图象相交于点，下列说法正确的是（）A.反比例函数的解析式是B.两个函数图象的另一交点坐标为C.当或时，D.正比例函数与反比例函数都随的增大而增大3、要使函数y=有意义，自变量x的取值范围是（）A.x≥1B.x≤1C.x＞1D.x＜14、声音在空气中传播的速度与气温的关系如下表:气温T/℃-20 -10 0 10 20 30声速v/(m/s) 318 324 330 336 342 348根据表格下列分析错误的是（）A.在这个变化过程中，气温和声速都是变量B.声速随气温的升高而增大 C.声速v与气温T的关系式为v=T+330 D.气温每升高10℃，声速增加6 m/s5、小高从家门口骑车去单位上班，先走平路到达点A，再走上坡路到达点B，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示．下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口需要的时间是（）A.12分钟B.15分钟C.25分钟D.27分钟6、若m＜-1，则下列函数：①y=（x＞0），②y=-mx+1，③y=mx，④y=（m+1）x中，y 的值随x的值增大而增大的函数共有（）A.1个B.2个C.3个D.4个7、函数y=kx的图象经过点P（3，﹣1），则k的值为（）A.3B.﹣3C.D.﹣8、函数y= 中，自变量x的取值范围是（）A.x＞1B.x≥1C.x＜1D.x≤19、如图，次哈尔滨至幸福镇的动车需要匀速通过一条隧道（隧道长大于火车长），火车在隧道内的长度与火车进入隧道的时间之间的关系用图象描述大致是（）A. B. C. D.10、反比例函数的图象上有两点，若则（）A. B. C. D.无法确定11、函数与在同一坐标系中的大致图象是（）A. B. C. D.12、若点，，在反比例函数（为常数）的图象上，则，，的大小关系为（）A. B. C. D.13、已知一次函数y=kx+b的图象经过第一、二、四象限，则函数y= 的图象在（）A.第一、三象限B.第二、四象限C.第三、四象限D.第一、二象限14、在圆的面积公式S=πr2中，是常量的是（）A.SB.πC.rD.S和r15、下列函数中是反比例函数的是（）A. B. C. D.二、填空题(共10题，共计30分)16、已知函数y= -1，给出一下结论：①y的值随x的增大而减小②此函数的图形与x轴的交点为（1，0）③当x>0时，y的值随x的增大而越来越接近-1④当x≤时，y的取值范围是y≥1以上结论正确的是________（填序号）17、设函数y= 与y=﹣2x﹣6的图象的交点坐标为（a，b），则+ 的值是________．18、已知点A为双曲线y= 图象上的点，点O为坐标原点，过点A作AB⊥x轴于点B，连接OA．若△AOB的面积为5，则k的值为________．19、在反比例函数y=﹣中，比例系数等于________．20、在函数中，自变量x的取值范围是________．21、函数中，自变量x的取值范围是________．22、如图，菱形OABC的顶点A的坐标是(-5，0)，点B，C在x轴上方，反比例函数y=(k>0，x>0)的图象分别与边OC、BC交于点D、点E，射线BD交y轴子点H，交反比例函数图象于点F，交x轴于点G，BD：DF：FG=2：3：1，若记△ODH的面积为S1，△CDE 的面积为S2，则的值是________23、如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为4，2，反比例函数y＝(x＞0)的图象经过A，B两点，若菱形ABCD的面积为2 ，则k的值为________.24、如图，点为矩形的边的中点，反比例函数的图象经过点，交边于点.若的面积为1，则________。

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题，共计45分)1、下列命题错误的是（）.A.如果 y是 x的反比例函数，那么 x也是 y的反比例函数．B.如果 y 是 z的反比例函数， z是 x的正比例函数，且 x≠0，那么 y是 x的反比例函数C.如果 y是 z的正比例函数， z是 x的反比例函数，且 x≠0，那么 y是 x的反比例函数D.如果 y是 z的反比例函数， z是 x的反比例函数，那么 y是 x的反比例函数2、反比例函数的图象如图所示，以下结论错误的是（）A. B.若点在图象上，则 C.在每个象限内，的值随值的增大而减小 D.若点，在图象上，则3、已知腰围的长度“cm”与裤子的尺码“英寸”之间存在一种换算关系如下：腰围cm 67.5 77．5 82．5尺码/英寸25 29 31小聪量了一下自己所穿裤子的腰围长是70cm，那么他的裤子尺码是（）A.30英寸B.28英寸C.27英寸D.26英寸4、如图，在平面直角坐标系中，第一象限内的点在反比例函数的图象上，第二象限内的点在反比例函数的图象上，且.若，则的值为（）A.1B.-1C.D.5、要使函数y=有意义，自变量x的取值范围是（）A.x≥1B.x≤1C.x＞1D.x＜16、已知正比例函数和反比例函数，在同一直角坐标系下的图象如图所示，其中符合的是（）A.①②B.①④C.②③D.③④7、对于函数y=2x，下列说法错误的是（）A.该函数是正比例函数B.该函数图象过点（1，2）C.该函数图象经过二、四象限D. y随着x的增大而增大8、若函数是反比例函数，且它的图象在第一、三象限，则m的值为( )A.2B.﹣2C.D.9、如图，两个反比例函数y1＝（其中k1＞0）和y2＝在第一象限内的图象依次是C1和C2，点P在C1上.矩形PCOD交C2于A、B两点，OA的延长线交C1于点E，EF⊥x轴于F 点，且图中四边形BOAP的面积为6，则EF：AC为（）A. ：1B.2：C.2：1D.29：1410、如图，函数和函数的图象相交于两点，则不等式的解集为（）A. B. C. 或 D. 或11、反比例函数的图像在第二、四象限内，则点在（）A.第一象限B.第二象限C.第三象限D.第四象限12、点在第一象限，且，点A的坐标为，设的面积为S，则下列图像中，能反映S与x之间的函数关系式的是（）A. B. C. D.13、一条直线与双曲线y=的交点是A（a，4），B（﹣1，b），则这条直线的关系式为（）A.y=4x﹣3B.C.y=4x+3D.y=﹣4x﹣314、反比例函数y=的图象如图所示，点M是该函数图象上一点，MN⊥x轴，垂足是点N，如果S△MON＝2，则k的值为（ )A.2B.－2C.4D.－415、如图，Rt△APC的顶点A，P在反比例函数y＝的图象上，已知P的坐标为（1，1），tanA=（n≥2的自然数）；当n=2，3，4…2010时，A的横坐标相应为a2， a3，a4，…，a2010，则+++…+=（)A. B.2021054 C.2022060 D.二、填空题(共10题，共计30分)16、如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y= 在第一象限的图象经过点B，若OA2-AB2=12，则k=________。

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题，共计45分)1、如图所示，一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．下列说法中正确的是（）A.B点表示此时快车到达乙地B.B﹣C﹣D段表示慢车先加速后减速最后到达甲地C.快车的速度为166 km/hD.慢车的速度为125km/h2、如图，在正方形ABCD中，AB=3cm，动点M自A点出发沿AB方向以每秒1cm的速度运动，同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动，到达B点时运动同时停止．设△AMN的面积为y（cm2）．运动时间为x（秒），则下列图象中能大致反映y与x之间函数关系的是（）A. B. C.D.3、自行车以10千米/小时的速度行驶，它所行走的路程S（千米）与所用的时间t（时）之间的关系为（）A.S=10+tB.C.S=D.S=10t4、汽车离开甲站10千米后，以60千米/时的速度匀速前进了t小时，则汽车离开甲站所走的路程s（千米）与时间t（小时）之间的关系式是（）A. s=10+60 tB. s=60 tC. s=60 t﹣10D. s=10﹣60 t5、已知反比例函数 y=，在下列结论中，错误的是（）A.图象位于第一、三象限B.图象必经过点（﹣2，﹣3）C.y随x 的增大而增小D.若x＞2，则0＜y＜36、如图，在平面直角坐标系中，函数的图象和ABC都在第一象限，，BC∥x轴，且BC =4，点A的坐标为(3，5)．若将ABC向下平移m(m>0)个单位，A、C两点的对应点同时落在函数的图象上，则k的值为（）A. B. C. D.7、在函数y= 中，自变量x取值范围是（）A.x＞1B.x＜﹣1C.x≠﹣1D.x≠18、对于反比例函数，下列说法正确的是（）A.图象经过点（1，－1）B.图象位于第二、四象限C.图象是中心对称图形D.当时，随的增大而增大9、函数y= 中，自变量x的取值范围是（）A.x＞﹣3B.x≥﹣3C.x≠﹣3D.x≤﹣310、已知正比例函数的图象过二、四象限，则一次函数的图象大致是（）A. B. C. D.11、如图，A、C是函数的图象上任意两点，过点A作y轴的垂线，垂足为B，过点C作y轴的垂线，垂足为D．记的面积为，的面积为，则和的大小关系是（）A. B. C. D.由A、C两点的位置确定12、已知反比例函数的图象过一、三象限，则一次函数y=kx+k的图象经过（）A.一、二、三象限B.二、三、四象限C.一、二、四象限D.一、三、四象限13、在函数中，自变量的取值范围是（）A. B. C. D.14、P1（x1， y1），P2（x2， y2）是正比例函数y=﹣x图象上的两点，下列判断中，正确的是（）A.y1＞y2B.y1＜y2C.当x1＜x2时，y1＜y2D.当x1＜x2时，y1＞y215、如图，在同一直角坐标系中，函数y= 与y=kx+k2的大致图象是（）A. B. C. D.二、填空题(共10题，共计30分)16、已知函数y＝中，自变量x的取值范围是________.17、一个圆柱的高为8cm，则圆柱体的体积Vcm3与底面直径Rcm的关系式为________，当R为5cm时，V=________cm3．18、某校阶梯教室礼堂共有25排座位，第一排有20个座位，后面每一排都比前一排多1个座位，则第二排有________个座位，第三排有________个座位，每排的座位数m与这排的排数n的函数关系式是m=________，自变量n的取值范围是________．（n取整数）19、如图所示，点A在双曲线y= 上，点A的坐标是（，2），点B在双曲线y= 上，且AB∥x轴，C、D在x轴上，若四边形ABCD为矩形，则它的面积为________．20、如图表示某地的气温变化情况．（1）在________ 时气温最高，为________ ℃；（2）在________ 时到________ 时这段时间气温是逐渐上升的．21、在函数y=中，自变量x的取值范围是________22、已知一次函数y＝ax+b，反比例函数y＝，（a，b，k是常数，且ak≠0），若其中一部分x，y的对应值如下表所示；则不等式ax+b＜的解集是________.x ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4y＝ax+b ﹣3 ﹣2 ﹣1 0 2 3 4 5y＝﹣﹣2 ﹣3 ﹣6 6 3 223、函数y= 中，自变量x的取值范围是________．24、如图，点A(m，6)，B(n，1)在反比例函数的图象上，AD⊥x轴于点D，BC⊥x 轴于点C，点E在CD上，CD=5，△ABE的面积为10，则点E的坐标是________．25、在温度不变的条件下，一定质量的气体的压强P与它的体积V成反比例，当V=200时，P=50，则当P=25时，V=________三、解答题(共5题，共计25分)26、已知, 与成正比例, 与成反比例，且当时, ;时, .试求当时, 的值.27、如图，在平面直角坐标系中，一次函数y=ax+b的图象与反比例函数y=的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为（2，m），点B的坐标为（n，﹣2），tan∠BOC=．（1）求该反比例函数和一次函数的解析式．（2）求△BOC的面积．（3）P是x轴上的点，且△PAC的面积与△BOC的面积相等，求P点的坐标．28、已知函数，与x成正比例，与x成反比例，且当时，；当时，．求y与x的函数表达式．29、当m，n为何值时，y=（5m﹣3）x2﹣n+（m+n）是关于x的一次函数？当m，n为何值时，y是关于x的正比例函数？30、一次函数的图像经过（1，2），求反比例函数的解析式。

2018---2019学年度第一学期沪教版八年级数学单元测试题第十八章正比例函数与反比例函数

2018--2019学年度第一学期沪教版八年级数学单元测试题第十八章正比例函数和反比例函数做卷时间100分满分120分班级姓名一、选择题（每小题3分计30分） 1、若点（3，6）在反比例函数xky =(k ≠0)的图象上，那么下列各点在此图象上的是（）（A ）（3-，6）（B ）（2，9）（C ）（2，9-）（D ）（3，6-）2. 已知反比例函数的图象过（2，－2）和（－1，n ），则n 等于（）（A ）3 （B ）4（C ）6（D ）123、点A 为反比例函数图象上一点，它到原点的距离为5，到x 轴的距离为3，若点A 在第二象限内.则这个反比例函数的解析式为（）（A ） 12y x =（B ） 12y x =- （C ） 112y x = （D ） 112y x=- 4、已知点(11,y x )和(22,y x )是直线y =－3x 上的两点，且21x x >，则1y 与2y 的大小关系是（）A ．1y >2y ;B ．1y <2y ;C ．1y ≥2y ;D ．1y ≤2y . 5、下列四组点中，可以在同一个正比例函数图象上的一组点是（）A ．（2．－3），（－4，6）B ．（－2，3），（4，6）C ．（－2，－3），（4，－6）D ．（2，3），（－4，6）6、若函数2(26)(1)y m x m x =++-是正比例函数，则m 的值是( )A 、m = -3B 、m =1C 、m = 3 C 、m > -3 7、已知11(,)x y 和22(,)x y 是直线3y x =-上的两点，且12x x >，则1y 与2y 的大小关系是( )A 、1y >2yB 、1y <2yC 、1y =2yD 、以上都不可能8. 已知12y y y =+，其中1y 与1x成反比例且比例系数为1k ，2y 与2x 成正比例且比例系数为2k ，若1-=x 时，0=y ，则1k 与2k 的关系为（）（A ）12k k =- （B ） 12k k ≠ （C ） 121k k =-（D ） 1k =2k 9．函数kx y =与xky -=在同一坐标系内的大致图像是…（）（1）（2）（3）（4）（A ）（1）和（2）；（B ）（1）和（3）；（C ）（2）和（3）；（D ）（2）和（4） 10．如图，是一台自动测温记录仪的图像，它反映了某市冬季某天气温T 随时间t 变化而变化的关系，观察图像得到下列信息，其中错误的是…（） A ．凌晨4时气温最低为3-℃B ．14时气温最高为8℃C ．从0时至14时，气温随时间增长而上升D ．从14时至24时，气温随时间增长而下降二、填空题（每小题4分，计32分）1、已知y 与x 成反比例，当1=y 时，4=x ，则当2=x 时，_____=y ；2. 反比例函数和正比例函数的图象都经过点A(1-，2-)，则这两个函数的解析式分别是_________和_________；3. 某厂有煤1500吨，求这些煤能用的天数y 与每天用煤的吨数x 之间的函数关系式为_________；4、函数1y x =-中自变量x 的取值范围是 . 5、如果函数23y mx m =+-是正比例函数，则m =6、如果正比例函数x k y )3-=（的图像经过第一、三象限，那么k 的取值范围是．7、已知1122(,),(,)P x y Q x y 在反比例函数(0)ky k x=的图像上，若120x x ，则1y 2y 。

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题，共计45分)1、一司机驾驶汽车从甲地去乙地，他以平均80千米/小时的速度用了4个小时到达乙地，当他按原路匀速返回时．汽车的速度v千米/小时与时间t小时的函数关系是（）A.v=320tB.v=C.v=20tD.v=2、反比例函数y=，当x≤3时，y的取值范围是（）A.y≤B.y≥C.y≥或y＜0D.0＜y≤3、函数中，自变量的取值范围是( )A. B. C.x≠—2 D.4、如图，在平面直角坐标系中，△ABC的顶点A、B均在y轴上，点C在x轴上，将△ABC 绕着顶点B旋转后，点C的对应点C′落在y轴上，点A的对应点A′落在反比例函数y＝在第一象限的图象上．如果点B、C的坐标分别是（0，﹣4）、（﹣2，0），那么点A′的坐标是（）A.（3，2）B.（，4）C.（2，3）D.（4，）5、已知函数y=的图象如图，当x≥﹣1时，y的取值范围是（）A.y＜﹣1B.y≤﹣1C.y≤﹣1或y＞0D.y＜﹣1或y≥06、教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热到100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系．直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温y（℃）和时间（min）的关系如图，为了在上午第一节下课时（8：45）能喝到不超过50℃的水，则接通电源的时间可以是当天上午的（ )A.7：20B.7：30C.7：45D.7：507、如图，点A是反比例函数y= （x＜0）的图象上的一点，过点A作平行四边形ABCD，使点B、C在x轴上，点D在y轴上．已知平行四边形ABCD的面积为6，则k的值为（）A.6B.﹣6C.3D.﹣38、如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A 出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止（不含点A和点B），则△ABP的面积S随着时间t变化的函数图象大致是（）A. B. C. D.9、如图，反比例函数y= （k＜0）与一次函数y=x+4的图象交于A、B两点的横坐标分别为﹣3，﹣1．则关于x的不等式＜x+4（x＜0）的解集为（）A.x＜﹣3B.﹣3＜x＜﹣1C.﹣1＜x＜0D.x＜﹣3或﹣1＜x＜10、函数的自变量x满足≤x≤2时，函数值y满足≤y≤1，则下列函数①y= x，②y= ，③y= ，④y=﹣x+ ，⑤y=（x﹣1）2，符合条件的函数有（）A.2个B.3个C.4个D.5个11、二次函数y＝ax2+bx+c的图象如图所示，反比例函数y＝与正比例函数y＝（2a+c）x在同一坐标系内的大致图象是（）A. B.C. D.12、已知常数k＜0，b＞0，则函数y=kx+b，的图象大致是下图中的（）A. B. C. D.13、如图，一次函数的图象与x轴，y轴交于A，B两点，与反比例函数的图象相交于C，D两点，分别过C，D两点作y轴，x轴的垂线，垂足为E，F，连接．有下列四个结论：①与的面积相等；②；③；④．其中正确的结论是（）A.1个B.2个C.3个D.4个14、在同一直角坐标系中，函数和的大致图象可能是( )．A. B. C. D.15、反比例函数y= (k>0)在第一象限内的图象如图，点M是图象上一点，MP垂直x轴于点P，如果△MOP的面积为1，那么k的值是（）A.1B.2C.4D.二、填空题(共10题，共计30分)16、使函数有意义的自变量x的取值范围是________．17、如图，直线与双曲线相交于A、B两点，以AB为边作正方形ABCD，则正方形ABCD面积的最小值为________．18、函数y＝2x+ 的自变量x的取值范围是________．19、在同一平面直角坐标系中，若函数与的图象有两个交点，则的取值范围是________．20、如图，点A、B在函数( ，且是常数)的图象上，且点A在点B 的左侧过点A作轴，垂足为M，过点B作轴，垂足为N，与的交点为C，连结、.若和的面积分别为1和4，则k的值为________.21、如图，点A在双曲线y＝（x＞0）上，过点A作AB⊥x轴于点B，点C在线段AB上且BC：CA＝1：2，双曲线y＝（x＞0）经过点C，则k＝________.22、一次函数的图象如图所示，当y＜0时，x的取值范围是________．23、在函数中，自变量x的取值范围是________．24、已知某工厂有煤1500吨，则这些煤能用的天数y与每天用煤的吨数x之间的函数关系式为________ ．25、某农户种植一种经济作物，总用水量y（米3）与种植时间x（天）之间的函数关系如图所示，当总用水量为2500米3时，该经济作物种植时间是________天．三、解答题(共5题，共计25分)26、函数y=（m﹣2）x 是反比例函数，则m的值是多少？27、某乡镇要在生活垃圾存放区建一个老年活动中心，这样必须把1200立方米的生活垃圾运走：（1）假如每天能运x立方米，所需时间为y天，写出y与x之间的函数表达式；（2）若每辆拖拉机一天能运12立方米，则5辆这样的拖拉机要用多少天才能运完？（3）在（2）的情况下，运了8天后，剩下的任务要在不超过6天的时间内完成，那么至少需要增加多少辆这样的拖拉机才能按时完成任务？28、已知二次函数y=ax2+bx+c中自变量x和函数值y的部分对应值如下表：x …﹣1 0 1 2 3 …y …10 5 2 1 2 …（1）求该二次函数的函数关系式；（2）在所给的直角坐标系中画出此函数的图象；（3）写出y≤5时自变量x的取值范围（可以结合图象说明）．29、已知x无论取何正值，y1=-3x+7都比y2=kx+5大，求k的取值范围.30、如图，点A是反比例函数y=﹣在第二象限内图象上一点，点B是反比例函数y= 在第一象限内图象上一点，直线AB与y轴交于点C，且AC=BC，连接OA、OB，求△AOB的面积．参考答案一、单选题(共15题，共计45分)1、B3、B4、A5、C6、A7、B8、B9、B10、B11、B12、D13、D14、A15、B二、填空题(共10题，共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、27、28、29、30、。

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题，共计45分)1、已知反比例函数的图象如图，则一元二次方程根的情况是（）A.有两个不等实根B.有两个相等实根C.没有实根D.无法确定.2、若点(1，2)同时在函数y=ax+b和y=的图象上，则点(a，b)为（）A.(－3，－1)B.(－3，1)C.(1，3)D.(－1，3)3、已知正比例函数y=（k+5）x，且y随x的增大而减小，则k的取值范围是（）A.k＞5B.k＜5C.k＞﹣5D.k＜﹣54、函数中自变量x的取值范围是（）A.x≤2B.x=3C.x＜2且x≠3D.x≤2且x≠35、如图，A，B分别为反比例函数y=﹣（x＜0），y= （x＞0）图象上的点，且OA⊥OB，则sin∠ABO的值为（）A. B. C. D.6、反比例函数y＝(m＋1)x－1中m的取值范围是( )A.m≠1B.m≠－1C.m≠±1D.全体实数7、下列选项中，能写成反比例函数的是（）A.人的体重和身高B.正三角形的边长和面积C.速度一定，路程和时间的关系D.销售总价不变，销售单价与销售数量的关系8、若反比例函数的图象在第一、第三象限，则m可能取的一个值为（）A.0B.1C.2D.39、函数y= 中，自变量x的取值范围是（）A.x＞2B.x≥﹣3C.x＞﹣3D.x≥210、下列函数关系中，属于正比例函数关系的是（）A.圆的面积与它的半径B.面积为常数S时矩形的长 y 与宽 xC.路程是常数时，行驶的速度v与时间 tD.三角形的底边是常数 a时它的面积S与这条边上的高 h11、如图分别给出了变量x与y之间的对应关系，其中y不是x的函数是（）A. B. C. D.12、函数的自变量x的取值范围是（）A.x＜8B.x＞8C.x≤8D.x≥813、如图，点P在直线AB上方，且∠APB=90°，PC⊥AB于C，若线段AB=6，AC=x，S△PAB=y，则y与x的函数关系图象大致是（）A. B. C. D.14、已知正比例函数y=kx（k＜0）的图象上两点A（x1， y1）、B（x2， y2），且x1＜x2，下列说法正确的是（）A.y1＜y2B.y1＞y2C.y1=y2D.不能确定15、下列函数中，是反比例函数的是（）A.y=2x+1B.y=5xC.x：y=8D.xy=﹣1二、填空题(共10题，共计30分)16、某农户种植一种经济作物，总用水量y（米3）与种植时间x（天）之间的函数关系如图所示，当总用水量为2500米3时，该经济作物种植时间是________天．17、如图，点A，B是反比例函数y= （x＞0）图象上的两点，过点A，B分别作AC⊥x 轴于点C，BD⊥x轴于点D，连接OA，BC，已知点C（2，0），BD=2，S△BCD=3，则S△AOC=________．18、已知反比例函数y=﹣，若y≤1，则自变量x的取值范围是________．19、已知A，B两地相距10千米，上午9：00甲骑电动车从A地出发到B地，9：10乙开车从B地出发到A地，甲、乙两人距A地的距离y（千米）与甲所用的时间x（分）之间的关系如图所示，则乙到达A地的时间为________．20、如图所示，一次函数与反比例函数的图象相交于点，两点．请根据图象写出一次函数值大于反比例函数值时的取值范围________．21、如图，在直角坐标系中，已知菱形ABCD的面积为5，顶点A在双曲线上，CD与y轴重合，则k的值是________.22、如图，正方形ABOC的边长为3，反比例函数y=的图象过点A，则k的值是________ ．23、已知点(－1，y1)、(2，y2)、( ，y3)在反比例函数的图像上，则y1、y2、y3的大小关系是________(用“>”连接)24、如图，点A是反比例函数（x＞0）图象上一点，过点A作x轴的平行线，交反比例函数（x＞0）的图象于点B，连接OA、OB，若△O AB的面积为2，则k的值为________．25、已知y与x成正比，且当x=-1时，y=-6，则y与x之间的函数关系式为________。

上海教育版数学八上第18章《正比例函数和反比例函数》单元测试

上海教育版数学八上第18章《正比例函数和反比例函数》单元测试一、选择题（2分×6=12分）1.下列函数中的正比例函数是（）.(A)x y 51=(B)x y 3= (C) 3x y = (D)16-=x y . 2.若反比例函数xky = 的图像在每个象限内，y 随x 的增大而减小，则k （）.(A) k ≥0； (B)k ＞0 ； (C)k ≤0 ； (D)k ＜0. 3.下列说法中，错误的是（）.(A) 函数y=kx (k ＜0）的图像经过第二、四象限； (B)正方形的周长与它的边长成正比例； (C)2x+1是x 的函数； (D)函数xy 3-=y 随x 的增大而减小. 4.下列函数图像过一三象限的是（）.(A)x y 3=； (B)y=x 2 ； (C)y=-2x ； (D)xy 7-=. 5.点（3、4）是反比例函数xky =图像上一点，则此函数图像经过点（）.(A)（2，-6）； (B)（2，6）； (C)（4，-3）； (D)（3，-4）. 6.下列函数中，y 随x 的增大而增大的是（）. (A)()x k y 12+= ； (B) ()x k y 12+-=；(C) x k y 12+= ； (D) xk y 12+-=. 二、填空题（3分×12=36分）7.已知y=(k -1)x 是正比例函数，则k 满足条件_______________. 8.函数3-=x y 的定义域是____________.9.已知f （x ）=x1，则f （2）=________________. 10.如果点A （2，3）在反比例xky = 的图像上，则k =______________.11.已知一正比例函数图像上有一点（1，3），则其解析式为____________.12.点A （3，-1）B （n ，3）都在同一个正比例函数的图像上，则n = ___________. 13.函数y=(2a -3)x 的图像过二四象限，则a 的取值范围是______________.14.如果函数y=2x 自变量x 的取值范围是 -3＜x ＜0，那么y 的取值范围是___________. 15.写出一个图像过一三象限的反比例函数解析式___________. 16.如果y=(m-2)x +m 2-4是正比例函数，那么m= ____________.17.如图，△OPQ 是边长为2的等边三角形，O 为坐标原点，点Q 在x 轴上，若反比例函数的图像过点P ,则它的解析式是______________.18.已知A 、B 两地相距20千米，某人从A 地步行前往B 地，步行速度是8千米/小时，步行t 小时后离B 地S 千米，写出S 与t 的函数解析式及定义域______________. 三、简答题（5分×2+6分×2=22分）19.若y 与2x +1成反比例，当x =1时，34=y ，求y 与x 的函数解析式.20.若函数82)3(--=m x m y 是正比例函数，求m 的值并写出的解析式.21.已知直线y=kx 与双曲线xy 4=交于M 、N 点，点M 的横坐标是2. (1)求M 点的坐标;(2)写出正比例的函数解析式.22.某水库有水Q （m 3）与排水时间t （时）的函数图像如图所示，根据图像回答问题.17题图400800(1)排水前，水池内有多少立方米水？ (2)排水10小时后，水池还剩多少水？ (3)剩水400m 3时，已排水几小时？ (4)写出Q 与t 的解析式及定义域.四、解答题（7分×2+8分×2=30分）23.已知y=y 1+y 2，y 1与x+1成反比例，y 2与x -1成正比例，且当x =0时，y =-1，当x =2时，y=3.(1)求y 与x 之间函数解析式； (2)判断A (2，-1)是否在这个图像上.24.如图，长方形ABCD 的边AB =4，BC =5，点P 、Q 分别从A 、C 出发向D 、B 以相同的速度运动，设AP 的长为x ，四边形BPDQ 的面积为y . (1)写出y 关于x 的函数解析式; (2)写出函数的定义域.25.正比例函数的图像经过点（-3，5），过图像上另一点A 作y 轴的垂线，垂足B 点的坐标是（0，4），求点A 的坐标与△AOB 的面积.ABCDP Q 24题图26.已知Rt ⊿ABC ,∠A =90°,∠B=60°,AB =1,将它放在直角坐标系中，使斜边BC 在x 轴上，直角顶点A 在反比例函数xy 3=的图像上，求点C 的坐标.正比例函数与反比例函数单元测试1.C2.B3.D4.A5.B6.A7.k ≠18.x ≥39.2210.6 11.y=3x 12.-9 13.23<a 14.-6<y <0 15.xy 1=等 16.-2 17.x y 3= 18.S=20-8t（250≤≤t ） 19. 124+=x y . 20. m =-3, y=-6x . 21. M (2，2). y=x . 22.(1)800m 3; (2)600m 3;(3)20小时;(4)q =800-20t （0≤t ≤40）. 23.(1))1(21)1(23--+-=x x y . (2)点A 在图像上. 24. y=20-4x 0≤x ≤5. 25. )4,512(-A524=∆AOB S .26. 点C 的坐标分别为⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛0,27,0,21,0,27,0,2126题图。

上海教育版数学八上第18章《正比例函数及反比例函数》单元测试

上海教育版数学八上第18 章《正比率函数和反比率函数》单元测试一、选择题（ 2 分× 6=12 分）1.以下函数中的正比率函数是（） .1(B)y 3(C) yx(D) y 6 x 1.(A) yx35xk2.若反比率函数y y 随 x 的增大而减小，则k（） .的图像在每个象限内，x(A) k≥0；(B)k＞ 0；(C) k≤；(D) k＜ 0.3.以下说法中，错误的选项是（）.(A)函数 y=kx (k＜0）的图像经过第二、四象限；(B)正方形的周长与它的边长成正比率；(C)2x+ 1 是 x 的函数；3(D)函数 yxy 随 x 的增大而减小 .4. 以下函数图像过一三象限的是（） .(A) y 3 ；(B) y=x 2；(C) y= - 2x ；(D) y7.xk x5. 点（ 3、 4）是反比率函数y）.图像上一点，则此函数图像经过点（x(A) （ 2， - 6）； (B) （2， 6）；；(D)（3， - 4）.(C) （ 4，- 3）6. 以下函数中， y 随 x 的增大而增大的是（） .(A) y k 2 1 x ；(B)y k 2 1 x ；(C) y k 2 1 ；(D)y k21.x x二、填空题（ 3 分× 12=36 分）7.已知 y= (k- 1)x 是正比率函数，则 k 满足条件 _______________.8.函数 y x 3 的定义域是____________.9.已知 f （x）= 1，则 f（2） =________________. x10.若是点 A（2， 3）在反比率y kk=______________.的图像上，则x11.已知一正比率函数图像上有一点（1， 3），则其剖析式为 ____________.1 / 412.点 A（ 3， -1 ） B（n， 3）都在同一个正比率函数的图像上，则n = ___________.13.函数 y=(2 a-3) x 的图像过二四象限，则 a 的取值范围是 ______________.14.若是函数 y=2x 自变量 x 的取值范围是 -3＜ x＜ 0，那么 y 的取值范围是 ___________.15.写出一个图像过一三象限的反比率函数剖析式___________.16.若是 y= (m-2) x+m2-4 是正比率函数，那么m= ____________.17.如图，△ OPQ 是边长为 2 的等边三角形， O 为坐标原点，点Q 在 x 轴上，若y反比率函数的图像过点P, 则它的剖析式是 ______________.P18.已知 A、B 两地相距 20 千米，某人从 A 地步行前往 B 地，步行速度是 8 千米/ 小时，步行 t 小时后离 B 地 S千米，写出 S与 t 的函数剖析式及定义域______________.Q xO 三、简答题（ 5 分× 2+6 分× 2=22 分）19. 若 y 与 2x+1 成反比率，当417题图x=1 时，y，求 y 与 x 的函数剖析式 .320. 若函数y(m 3) x m28是正比率函数，求m 的值并写出的剖析式.421. 已知直线y=kx 与双曲线y交于M、N点，点M的横坐标是 2.x(1)求M点的坐标;(2)写出正比率的函数剖析式 .22. 某水库有水 Q（m3）与排水时间t（时）的Q(m3 ) 800函数图像以下列图，依照图像回答以下问题.6004002 / 4200O10 20 30 40t( 时)22题图(1)排水前，水池内有多少立方米水？(2)排水 10 小时后，水池还剩多少水？(3)剩水 400m3时，已排水几小时？(4)写出 Q 与t的剖析式及定义域 .四、解答题（ 7 分× 2+8 分× 2=30 分）23. 已知 y=y 1+y 2，y1与 x+ 1 成反比率， y2与 x-1 成正比率，且当x=0 时， y=-1 ，当 x=2时， y=3.(1)求 y 与 x 之间函数剖析式；(2)判断 A(2，-1)可否在这个图像上.24.如图，长方形 ABCD 的边 AB=4，BC=5，点 P、Q 分别从 A、C 出发向 D、B 以相同的速度运动，设 AP 的长为 x，四边形 BPDQ 的面积为 y. (1) 写出 y 关于 x 的函数剖析式 ; (2)写出函数的定义域.A P DBQ C24题图25. 正比率函数的图像经过点（-3 ，5），过图像上另一点 A 作 y 轴的垂线，垂足 B 点的坐标是（ 0， 4），求点 A 的坐标与△ AOB 的面积 .3 / 426. 已知 Rt ⊿ ABC, ∠ A=90° , ∠ B= 60°, AB=1, 将它放在直角坐标系中，使斜边BC在x轴上，直角极点 A 在反比率函数y3C的坐标 .的图像上，求点xyO x26题图正比率函数与反比率函数单元测试7.k ≠ 1 8. x ≥ 3 9.210.6 11.y=3x 212.-9 13.314.-6 <y<0 15. y1y3a等 16.-2 17.18.S=20-8t 2x x（05）19.420.m=-3,y=-6x.21.M(2 ， 2).y=x .t y.2 2 x122.(1)800 m3;(2)600 m3;(3)20小时 ;(4)q=800-20 t （ 0≤ t ≤ 40 ） .23.(1)y31)1(x1) . (2)点 A 在图像上 . 24. y=20-4x 0≤x≤ 5. 25. A(12,4)2( x25SAOB 24.26.点 C 的坐标分别为171,75,0 ,,0 ,,0,022224 / 4。

八年级上册数学单元测试卷-第十八章正比例函数和反比例函数-沪教版(含答案)

八年级上册数学单元测试卷-第十八章正比例函数和反比例函数-沪教版(含答案)一、单选题(共15题，共计45分)1、给出的六个关系式：①x（y+1）②③④⑤⑥；其中y是x的反比例函数是（）A.①②③④⑥B.③⑤⑥C.①②④D.④⑥2、已知函数y＝，当x≥－1时，y的取值范围是（）A.y＜－1B.y≤－1C.y≤－1或y＞0D.y＜－1或y≥03、下列函数中，y随x增大而增大的是（）A. B.y=﹣x+5 C.y=- x D.4、如果z与y成反比例，y与x成反比例，那么z与x的关系为（）A.正比例B.反比例C.不成比例D.无法判断5、如图，Rt△APC的顶点A，P在反比例函数y＝的图象上，已知P的坐标为（1，1），tanA=（n≥2的自然数）；当n=2，3，4…2010时，A的横坐标相应为a2， a3， a4，…，a2010，则=（）A. B.2021054 C.2022060 D.6、已知反比例函数y=- ,则（）A.y随x的增大而增大B.当x>-3且x≠0时，y>4C.图象位于一、三象限D.当y<-3时，0<x<47、二次函数（a图象如图所示，则反比例函数与一次函数y=bx+c在同一平面直角坐标系的图象大致是（）．A. B. C. D.8、若反比例函数的图像在第一、第三象限，则可能取的一个值为（）A.0B.1C.2D.39、如图，若点P在反比例函数y=(≠0）的图象上，过点P作PM⊥x轴于点M，PN⊥y轴于点N，若矩形PMON的面积为6，则k的值是( )A.-3B.3C.-6D.610、如图，点A，B是双曲线y= 上的点，分别经过A，B两点向x轴、y轴作垂线段，若S阴影=1，则S1+S2=（）A.2B.3C.4D.511、位于第二象限的点E在反比例函数y= 的图象上，点F在x轴的负半轴上，O是坐标原点，若FO⊥EF，△EOF的面积等于2，则k的值是（）A.4B.﹣4C.2D.﹣212、如图，一次函数y＝k1x+b的图象与反比例函数y＝的图象相交于A（2，3），B （6，1）两点，当k1x+b＜时，x的取值范围为（）A. x＜2B.2＜x＜6C. x＞6D.0＜x＜2或x＞613、已知k1＜0＜k2，则函数y=k1x和y=的图象大致是（）A. B. C.D.14、在同一直角坐标系中，函数y=kx﹣k与y= （k≠0）的图象大致是（）A. B. C. D.15、下列变量之间的关系中，一个变量是另一个变量的正比例函数的是（）A.正方形面积S随边长a的变化而变化B.用10米长的绳子围一个矩形，则所围成的矩形的长y（米）随宽x（米）的变化而变化C.一场电影票价（元/张）一定时，则该场电影票房收入m（元）随出售票数n（张）的变化而变化 D.菱形的面积一定时，则一条对角线长度y随另一条对角线长度x 的变化而变化二、填空题(共10题，共计30分)16、如图，点P是反比例函数y＝图象上一点，过点P分别作x轴、y轴的垂线，如果构成的矩形面积是3，那么反比例函数的解析式是________．17、在函数y= +(x-2)0中，自变量x的取值范围是________18、已知P1（x1， y1），P2（x2， y2）两点都在反比例函数y= 的图象上，且x1＜x2＜0，则y1________y2（填“＞”或“＜”）．19、如图，在平面直角坐标系中直线y=x-2与y轴相交于点A，与反比例函数在第一象限内的图象相交于点B（m，2）．将直线y=x-2向上平移后与反比例函数图象在第一象限内交于点C，且△ABC的面积为18，求平移后的直线的函数关系式是________ ．20、小华要看一部300页的小说所需的天数y与平均每天看的页数x成________比例函数，表达式为________．21、从﹣1，0，1，3，4，这五个数中任选一个数记为a，则使双曲线y= 在第一、三象限且不等式组无解的概率是________．22、圆周长C与圆的半径r之间的关系为C=2πr，其中变量是________,________ ，常量是________ ．23、函数中自变量x的取值范围是________．24、如图，一次函数y=x﹣2的图象与反比例函数y= （k＞0）的图象相交于A．B两点，与x轴交于点C，若tan∠AOC= ，则k的值为________．25、直线y=kx+b与双曲线y=﹣交于A（﹣3，m），B（n，﹣6）两点，将直线y=kx+b 向上平移8个单位长度后，与双曲线交于D，E两点，则S△ADE=________．三、解答题(共5题，共计25分)26、已知, 与成正比例, 与成反比例，且当时, ;时, .试求当时, 的值.27、已知y=y1+y2，若y1与x﹣1成正比例，y2与x+1成反比例，当x=0时，y=﹣5；当x=2时，y=1．（1）求y与x的函数关系式；（2）求当x=﹣2时，y的值．28、科学家研究发现，声音在空气中传播的速度y（米/秒）与气温x（℃）有关，当气温是0℃时，音速是331米/秒；当气温是5℃时，音速是334米/秒；当气温是10℃时，音速是337米/秒；气温是15℃时，音速是340米/秒；气温是20℃时，音速是343米/秒；气温是25℃时，音速是346米/秒；气温是30℃时，音速是349米/秒．（1）请你用表格表示气温与音速之间的关系；（2）表格反映了哪两个变量之间的关系？哪个是自变量？哪一个是因变量？（3）当气温是35℃时，估计音速y可能是多少？（4）能否用一个式子来表示两个变量之间的关系？29、当m取什么值时，y=（m2﹣m）是反比例函数？它的图象在第几象限内？在每一个象限内，y随x的增大是增大，还是减小？30、如图，一次函数y1=x﹣2的图象与反比例函数y2= 的图象相交于A，B两点，与x轴相交于点C．已知tan∠BOC= ，点B的坐标为（m，n），求反比例函数的解析式．参考答案一、单选题(共15题，共计45分)1、D2、C3、A4、A5、B7、A8、A9、C10、A11、B12、D13、A14、B15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、23、24、25、三、解答题(共5题，共计25分)26、27、28、30、。

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题，共计45分)1、一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系，当x ＝2时，y＝20，则y与x的函数图象大致是( )A. B. C. D.2、下列函数不是反比例函数的是（）A.y=B.y=C.y=x ﹣1D.y=3、下列函数中，自变量的取值范围为的是（）A. B. C. D.4、已知点P（﹣3，2），点Q（2，a）都在反比例函数y= （k≠0）的图象上，过点Q 分别作两坐标轴的垂线，两垂线与两坐标轴围成的矩形面积为（）A.3B.6C.9D.125、已知点M(-2，4)在双曲线y= 上，则下列各点一定在该双曲线上的是（）A.(-2，-4)B.(4，-2)C.(2，4)D.(4，2)6、已知反比例函数y= ，当1＜x＜2时，y的取值范围是（）A.y＞10B.5＜y＜10C.1＜y＜2D.0＜y＜57、当前，雾霾严重，治理雾霾方法之一是将已生产的PM2.5吸纳降解，研究表明：雾霾的程度随城市中心区立体绿化面积的增大而减小，在这个问题中，自变量是（）A.雾霾程度B.PM2.5C.雾霾D.城市中心区立体绿化面积8、如图，直线分别于双曲线、交于、两点，且.则的值（）A.2B.4C.6D.89、函数 y=1﹣的自变量 x 的取值范围是（）A.x≤1B.x≥0C.x＞0D.x≤0．10、如图，射线l是下列哪个函数的图象A. B. C. D.11、已知抛物线与x轴没有交点，则函数的大致图象是（）A. B. C. D.12、n边形的内角和s=（n-2）•180°，其中自变量n的取值范围是（）A.全体实数B.全体整数C.n≥3D.大于或等于3的整数13、若反比例函数y= 的图象分布在第二、四象限，则k的取值范围是（）A.k<B.k>C.k>2D.k<214、若正比例函数的图象经过点（﹣1，2），则这个图象必经过点（）A.（1，2）B.（﹣1，﹣2）C.（2，﹣1）D.（1，﹣2）15、下列函数中，图象经过点（1，﹣1）的反比例函数关系式是（）A. B. C. D.二、填空题(共10题，共计30分)16、函数与图像的交点坐标为,则的值为________.17、反比例函数的图象，当时，随的增大而增大，则的取值范围是________．18、在反比例函数的图象上有两点，，，则________．（填“”或“”19、如果函数y=kx k﹣2是反比例函数，那么k=________ ，此函数的解析式是________ ．20、老师给出了一个函数，甲、乙、丙三位学生分别指出了这个函数的一个性质，甲：第一象限内有它的图象；乙：第三象限内有它的图象；丙：在每个象限内，随的增大而减小. 请你写一个满足上述性质的函数解析式________21、如图，过y轴上的一点p作x轴的平行线，与反比例函数的图象交于点A，与反比例函数的图象交于点B，若的面积为3，则的值为________.22、设函数与的图象的交点坐标为，则的值为________.23、某个函数具有性质：当x<0时，y随x的增大而减小，这个函数的表达式可以是________（只要写出一个符合题意的答案即可）.24、某住宅小区要种植面积为500m2的矩形草坪，草坪长y（m）与宽x（m）之间的函数关系为________ ．25、若函数y=（m﹣1）是反比例函数，则m的值等于________三、解答题(共5题，共计25分)26、已知 , 与成正比例, 与成反比例，且当时, ; 时,.试求当时, 的值.27、已知函数y=（m+1）x+（m2-1）当m取什么值时，y是x的一次函数？当m取什么值时，y是x的正比例函数.28、已知函数 y=（5m﹣3）x2﹣n+（n+m），（1）当m，n为何值时是一次函数？（2）当m，n为何值时，为正比例函数？（3）当m，n为何值时，为反比例函数？29、如图所示，已知一次函数y=kx+b（k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=（m≠0）的图象在第一象限交于C点，CD垂直于x轴，垂足为D．若OA=OB=OD=1．（1）求点A、B、D的坐标；（2）求一次函数和反比例函数的解析式．30、美美用300元钱全部用来买营养品送给她妈妈，写出她所能购买营养品的数量y （kg）与单价x（元/kg）之间的关系式．问y是x的函数吗？y是x的反比例函数吗？参考答案一、单选题(共15题，共计45分)1、C2、D3、D4、B5、B6、B7、D8、A10、B11、C12、D13、B14、D15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题，共计25分)26、27、28、30、。

2018---2019学年度第一学期沪教版八年级数学单元测试题第十八章正比例函数与反比例函数

沪教版(上海市)八年级(上)学 第18章 正比例函数与反比例函数 单元测试卷 (解析版)

沪教版(上海市)八年级第一学期 第18章 正比例函数与反比例函数 单元测试卷 (解析版)

沪教版8年级上册数学第18章正比例函数与反比例函数单元检测卷

第十八章 正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

沪教版(上海市)八年级(上)学 第18章 正比例函数与反比例函数 单元测试卷 (含解析)

上海教育版数学八上第18章《正比例函数和反比例函数》单元测试

第十八章 正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

沪教版(上海) 八年级数学(上)学期 第18章 正比例函数与反比例函数 单元测试卷 (含解析)

第十八章 正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

八年级上册数学单元测试卷-第十八章 正比例函数和反比例函数-沪教版(含答案)

八年级上册数学单元测试卷-第十八章 正比例函数和反比例函数-沪教版(含答案)

第十八章 正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章 正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

2018---2019学年度第一学期沪教版八年级数学单元测试题第十八章正比例函数与反比例函数

第十八章 正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章 正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

上海教育版数学八上第18章《正比例函数和反比例函数》单元测试

上海教育版数学八上第18章《正比例函数及反比例函数》单元测试

八年级上册数学单元测试卷-第十八章 正比例函数和反比例函数-沪教版(含答案)

第十八章 正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

沪教版(上海市)八年级(上)学第18章正比例函数与反比例函数单元测试卷 (解析版)

沪教版(上海市)八年级第一学期第18章正比例函数与反比例函数单元测试卷 (解析版)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

沪教版(上海市)八年级(上)学第18章正比例函数与反比例函数单元测试卷 (含解析)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

沪教版(上海) 八年级数学(上)学期第18章正比例函数与反比例函数单元测试卷 (含解析)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

八年级上册数学单元测试卷-第十八章正比例函数和反比例函数-沪教版(含答案)

八年级上册数学单元测试卷-第十八章正比例函数和反比例函数-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)

八年级上册数学单元测试卷-第十八章正比例函数和反比例函数-沪教版(含答案)

第十八章正比例函数和反比例函数数学八年级上册-单元测试卷-沪教版(含答案)