2010年温州中学提前招生数学模拟
2010年浙江省温州市中考试题及扫描答案

2010年浙江省温州市中考数学试卷卷 Ⅰ一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)(10浙江温州)1.给出四个数0,2,一21,0.3其中最小的是(▲)A .0B .2C .一21 D .0.3(10浙江温州)2.把不等式x+2>4的解表示在数轴上,正确的是(▲)(10浙江温州)3.计算a 2·a 4的结果是(▲)A .a 2B .a 6C .a 8D .a 16(10浙江温州)4.某班学生参加课外兴趣小组情况的统计图如图所示,则参加人数最多的课外兴趣 小组是(▲)A .书法B .象棋C .体育D .美术(10浙江温州)5.直线y=x+3与y 轴的交点坐标是(▲)A .(0,3)B .(0,1)C .(3,O)D .(1,0)(10浙江温州)6.如图,已知一商场自动扶梯的长z 为10米,该自动扶梯到达的高度h 为6米,自动扶梯与地面所成的角为θ,则tan θ的值等于(▲)(10浙江温州)7.下列命题中,属于假命题的是(▲)A .三角形三个内角的和等于l80°B .两直线平行,同位角相等C .矩形的对角线相等D .相等的角是对顶角.(10浙江温州)8.如图,AC ;BD 是矩形ABCD 的对角线,过点D 作DE //AC 交BC 的延长线于E ,则图中-与AABC 全等的 三角形共有(.▲)A .1个B .2个C .3个D .4个(10浙江温州)9.如图,在AABC 中,AB=BC=2,以AB 为直径的⊙0与BC 相切于点B ,则AC 等于(▲) A .2 B .3 c .22 D .23(10浙江温州)10.用若干根相同的火柴棒首尾顺次相接围成一个梯形(提供的火柴棒全部用完),下列根数的火柴棒不能围成梯形的是(▲) .A .5B .6C .7D .8卷 Ⅱ二、填空题(本题有6小题。
每小题5分,共30分)(10浙江温州)11.分解因式:m 2—2m= .(10浙江温州)12.在“情系玉树献爱心”捐款活动中,某校九(1)班同学人人拿出自己的零花钱,现将同学们的捐款数整理成统计表,则该班同学平均每人捐款 元.(10浙江温州)13.当x= 时,分式13-+x x 的值等于2.(10浙江温州)14.若一个反比例函数的图象位于二、四象限,则它的解析式可能是▲.(写出一个即可) (10浙江温州)15.某班级从文化用品市场购买了签字笔和圆珠笔共l5支,所付金额大于26元,但小于27元.已知签字笔每支2元,圆珠笔每支1.5元,则其中签字笔购买了 支.(10浙江温州)16.勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR 使得∠R=90°,点H 在边QR 上,点D ,E 在边PR 上,点G ,F 在边_PQ 上,那么APQR 的周长等于 .三、解答题(本题有8小题,共80分)(10浙江温州)17.(本题l0分)(1)计算:()121320108-⎪⎭⎫ ⎝⎛--+.(2)先化简,再求值:(n+6)(a-b)+a(2b-a),其中n=1.5,b=-2.(10浙江温州)18.(本题6分)由3个相同的小立方块搭成的几何体如图所示,请画出它的主视图和俯视图.(10浙江温州)19.(本题8分)2010年上海世博会某展览馆展厅东面有两个入口A ,B ,南面j 西面、北面各有一个出口,示意图如图所示.小华任选一个入口进入展览大厅,参观结束后任选一个出口离开. (1)她从进入到离开共有多少种可能的结果?(要求画出树状图) (2)她从入口A 进入展厅并从北出口或西出口离开的概率是多少?(10浙江温州)20.(本题8分)如图,在正方形ABCD 中,AB=4,0为对角线BD 的中点,分别以OB ,OD 为直径作⊙O 1,⊙02. 。
温州中学自主招生数学模拟试题
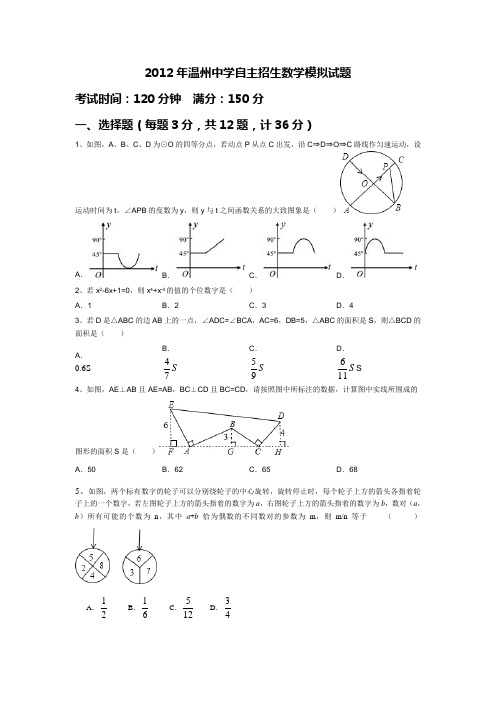
2012年温州中学自主招生数学模拟试题考试时间:120分钟 满分:150分一、选择题(每题3分,共12题,计36分)1、如图,A 、B 、C 、D 为⊙O 的四等分点,若动点P 从点C 出发,沿C ⇒D ⇒O ⇒C 路线作匀速运动,设运动时间为t ,∠APB 的度数为y ,则y 与t 之间函数关系的大致图象是( )A .B .C .D .2、若x 2-6x+1=0,则x 4+x -4的值的个位数字是( ) A .1B .2C .3D .43、若D 是△ABC 的边AB 上的一点,∠ADC=∠BCA ,AC=6,DB=5,△ABC 的面积是S ,则△BCD 的面积是( ) A .0.6SB .S 74 C .S 95 D .S 116S 4、如图,AE ⊥AB 且AE=AB ,BC ⊥CD 且BC=CD ,请按照图中所标注的数据,计算图中实线所围成的图形的面积S 是( )A .50B .62C .65D .685、如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字为a ,右图轮子上方的箭头指着的数字为b ,数对(a ,b )所有可能的个数为n ,其中a +b 恰为偶数的不同数对的参数为m ,则m/n 等于 ( )A .21 B .61 C .125 D .436、某一天的不同时刻老板把信交给秘书打字,每次都将信放在秘书信堆的最上面,秘书有时间就将信堆最上面的那封信取来打.假定共有5封信,且老板以1、2、3、4、5的顺序交来,在下列各顺序中,哪一顺序不可能是秘书打字的顺序?()A.12345 B.54321 C.23541 D.235147、如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连接EF交AB于H,则下列结论错误的是()A.AE⊥AFB.EF:AF=1:2C.AF2=FH•FE D.FB:FC=HB:EC8、在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为10,△BCF 的面积为20,△CEF的面积为16,则四边形区域ADFE的面积等于()A.22 B.24 C.36 D.449、如图,点A、D、G、M在半⊙O上,四边形ABOC、DEOF、HMNO均为矩形.设BC=a,EF=b,NH=c,则下列各式中正确的是()A.a>b>c B.b>c>a C.c>a>b D.a=b=c10、如图在梯形ABCD中,AD∥BC,AD⊥CD,BC=CD=2AD,E是CD上一点,∠ABE=45°,则tan ∠AEB的值等于()A.3 B.2 C.2.5D.1.511、两个不相等的正数满足a+b=2,ab=t-1,设S=(a-b)2,则S关于t的函数图象是()A.射线(不含端点)B.线段(不含端点)C.直线D.抛物线的一部分A .60°B .75°C .60°或45°D .15°或75°二、填空题(每空4分,共9空,计36分)13、若关于x 的方程(x-2)(x 2-4x+m )=0有三个根,且这三个根恰好可以作为一个三角形的三条边的长,则m 的取值范围是____________.14、如图,AB 是⊙O 的直径,AB=10cm ,M 是半圆AB 的一个三等分点,N 是半圆AB 的一个六等分点,P 是直径AB 上一动点,连接MP 、NP ,则MP+NP 的最小值是________cm.15、双曲线y=x1(x >0)与直线y=x 在坐标系中的图象如图所示,点A 、B 在直线上AC 、BD 分别平行y 轴,交曲线于C 、D 两点,若BD=2AC 则4OC 2-OD 2的值为_________.16、如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A ,B ,C 三点的拋物线对应的函数关系式是____________________________.17、设C 1,C 2,C 3,…为一群圆,其作法如下:C 1是半径为a 的圆,在C 1的圆内作四个相等的圆C 2(如图),每个圆C 2和圆C 1都内切,且相邻的两个圆C 2均外切,再在每一个圆C 2中,用同样的方法作四个相等的圆C 3,依此类推作出C 4,C 5,C 6,…,则(1)圆C 2的半径长等于________(用a 表示);(2)圆C k的半径为_________(k为正整数,用a表示,不必证明)18、已知正数a、b、c满足a2+c2=16,b2+c2=25,则k=a2+b2的取值范围为__________.19、已知x、y均为实数,且满足xy+x+y=17,x2y+xy2=66,则x4+x3y+x2y2+xy3+y4=___________.20、不论m取任何实数,抛物线y=x2+2mx+m2+m-1的顶点都在一条直线上,则这条直线的函数解析式是___________________________.三、简答题(共78分)21、如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明;(2)求m与n的函数关系式,直接写出自变量n的取值范围;(3)以△ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD2+CE2=DE2;(4)在旋转过程中,(3)中的等量关系BD2+CE2=DE2是否始终成立?若成立,请证明;若不成立,请说明理由.,∠BCM=.23、如图,BC是半圆⊙O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E.(1)求证:AC•BC=2BD•CD,(2)若AE=3,CD=25,求弦AB和直径BC的长.24、已知二次函数y=x2+bx-c的图象经过两点P(1,a),Q(2,10a).(1)如果a,b,c都是整数,且c<b<8a,求a,b,c的值.(2)设二次函数y=x2+bx-c的图象与x轴的交点为A、B,与y轴的交点为C.如果关于x的方程x2+bx-c=0的两个根都是整数,求△ABC的面积.的坐标;。
温州实验中学中考第一次模拟考试数学试题目共5页

温州实验中学2010年中考数学第一次模拟考题一、选择题:(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)1. 的相反数是( )A . B. C. 2- D. 22.计算y 8÷y 4 结果正确的是( )A .2 B. 4 C.y 2 D. y 43.如图,箭头表示投影的方向,则图中圆柱体的投影是( )A B C D4.五边形的内角和是( )A. 180°B. 360°C. 540°D. 720°5.下列能够说明“任何数的立方都是非负数”是假命题的反例是( )D.3.56.下图一定能说明∠1>∠2的是( )A B C D7.双曲线k y x=的每个分支上,y 都随x 的增大而减小,则k 的值可以是( )A .1 B. 0 C. -1 D. -28.为响应团中央“号召全国每位团员,少先队员捐一瓶水”的倡议,我校师生积极开展了“情系西南灾区”的捐款活动.某班6名同学捐款的数额分别是(单位:元):5,5,5,10,10,20.则这组数据的中位数和众数分别是( )元.E O D CB A 5, 7.59.如图,共有12个大不相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分.现从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的概率是( )10.如图,三个半径为1的等圆两两外切,若固定⊙O 1和⊙O ⊙O 3沿⊙O 1的边缘逆时针旋转到⊙O 3′的位置(即⊙O 1、⊙O 2 、⊙O 3′两两外切),圆心O 3所经过的路程为( )A. 2πB. 43πC. 83π D. 4π二、填空题(本题有6小题,每小题5分,共30分)11.分解因式: m 2-2m = ________.12.已知一组数据的頻率为0.35,数据总数为500个,则这组数据的頻数为____.13.如图平行四边形ABCD 的对角线AC 与BD 交于点O ,点E 是BC 的中点,OE=2,则AB 的长是___。
温州中学数学提前招模拟卷

2017年温州中学数学提前招模拟卷题号一二三总分1-8 9-14 15 16 17 18得分评卷人复查人答题时注意;1.用圆珠笔或钢笔作答2.解答书写时不要超过装订线3.可以用计算器一、选择题(共8小题,每小题5分,满分40分).1.已知|a+b|+|a-b|-2b=0,在数轴上给出了如图所示的关于a,b的四种位置关系,则可能成立的有( )A.1种B.2种C.3种D.4种2.已知a是方程3310x x+-=的一个实数根,则直线1y ax a=+-不经过()A.第一象限 B.第二象限 C.第三象限 D.第四象限3.2612111012111010(2)x x a x a x a x x a--=++++…+a,则12108642a a a a a a+++++=()(A)64 (B)32 (C)-32 (D)-644.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是()A. B. C. D.23-π332-π2332-π3-π第4题5. A 、B 、C 三个足球队举行单循环赛,下表给出了部分比赛信息:则A 、B 两队比赛时,A 队与B 队进球数之比为( ) ∶0 ∶0 ∶1 ∶16.定义新运算: a ⊕b=,则函数y=3⊕x 的图象大致是( )7..如图,∠XOY =90°,OW 平分∠XOY ,PA ⊥OY ,PB ⊥OX ,PC ⊥OW . 若OC =2-1,则OA +OB +OC =( )A .3B . 2C .1D .218.我们用()f x 代替函数中的变量y ,如:3y x =+可以记作()3f x x =+,“当x =1,y =4”可以记作“(1)4f =”.现有函数1()2f x x =,22()f x x=,3()6(1)(2)f x x x =---,记k I =100(1)99k k f f ⎛⎫-+ ⎪⎝⎭1001019999k k f f ⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭197(2)99L k k f f ⎛⎫+- ⎪⎝⎭, 其中k =1,2,3,则下列结论正确的是( )A .123I I I <<B .213I I I <<C .231I I I <<D .321I I I << 二、填空题(共6小题,每小题5分,满分30分)9.有一组数满足, ,2 ,0 ,2 ,0,2,14635241321Λ=-=-=-=-==a a a a a a a a a a按此规律进行下去,则=++++100321a a a a Λ___________.球队 比赛场次 胜 负 平 进球数 失球数 A 2 2场 1 B 2 1场 2 4 C 2 3 7BCOyxP W 第7题图A ABCDO10.如图,菱形ABCD 的边长为a ,点O 是对角线A C 上的一点, 且OA =a ,O B =OC =OD =1,则a 的值等于__________.11.直线k x y +=21与x 、y 轴的交点分别为A 、B ,如果S △AOB ≤1, 那么k 的取值范围是 。
温州中学提前招生数学模拟卷

2017年温州中学提前招生数学模拟卷(二)时量:90分钟满分:100分题号一二三总分合分人复查人13 14 15 16 17得分一.选择题(6×4=42分)1.若α、β是方程x2﹣x﹣2006=0的两个实数根,则α+β2的值是()A.1 B.2007 C.﹣1 D.20062.把一枚六个面编号分别为1,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m,n,则二次函数y=x2+mx+n的图象与x轴有两个不同交点的概率是()A.B.C.D.3.观察下列等式:=1﹣,=﹣,=﹣,…=﹣将以上等式相加得到+++…+=1﹣.用上述方法计算:+++…+其结果为()A. B. C. D.4.如图,在Rt△ABC中,∠P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为Q,连接AP.若AC=3,BC=4,则△AQP的面积的最大值是()A. B. C. D.5.已知a3±b3=(a±b)(a2±ab+b2),如果一列数a1,a2,…满足对任意的正整数n都有,则的值为()A.B. C. D.6.已知,实数x,y,z满足,则x4+y4+z4=()A.4 B. C. D.以上都不对二.填空题(6×4=24分)7.点A(x1,y1),B(x2,y2),C(x3,y3),D(﹣2,4)是双曲线上的四个点,若x3<x2<0<x1,则y1,y2,y3的大小关系是.8.若x、y、z满足3x+7y+z=1和4x+10y+z=2001,则分式的值为.9.如图,△ABC中,AD与B已知S△AFB=12cm2,S△BFD=9cm2,S△AFE=6cm2,那么四边形CDFE的面积为cm2.10.一枚商标示,点A1,A2,A3,A4和C1,C2,C3,C4分别是?ABCD边AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知?ABCD的面积5,则阴影四边形A4B2C4D2的面积是.11.如图,一个粒子在第一第一分钟内它从原点运动到(1,0),而后它接着按图所示在与x 轴、y轴平行的方向或在x轴、y轴上来回运动,且每分钟移动1个单位长度,那么在2071分钟后这个粒子所处位置为.12.已知一次函数f(b经过点(10,13),它在x轴上的截距是一个质数,在y轴上的截距是一个正整数,则函数的个数有个.三.解答题(共5小题,共58分)13.(10分)如图,D中,AB=3cm,BC=4cm.设P,Q分别为BD,BC上的动点,在点P自点D 沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P,Q移动的时间为t(0<t≤4).(1)当t为何值时,△PBQ为等腰三角形?(2)△PBQ能否成为等边三角形?若能,求t的值;若不能,说明理由.14.(10分)如图,△ABC是边三角形,P是AB边上的一个动点(P与B不重合),以线段CP 为边作等边△CPD(D、A在BC的同侧),连接AD.(1)判断四边形ABCD的形状,并给予证明;(2)设BP=x,△PAD的面积为y,求出y关于x的函数关系式,并求出△PAD面积的最大值及取得最大值时x的值.15.(12分)若直线l:y=x+3交x轴于点A,交y轴于点B.坐标原点O关于直线l的对称点O′在反比例函数y=的图象上.(1)求反比例函数y=的解析式;(2)将直线l绕点A逆时针旋转角θ(0°<θ<45°),得到直线l′,l′交y轴于点P,过点P作x轴的平行线,与上述反比例函数y=的图象交于点Q,当四边形APQO′的面积为9﹣时,求θ的值.16.(13分)已知在关于x的分式方程①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.(1)求k的取值范围;(2)当方程②有两个整数根x1、x2,k为整数,且k=m+2,n=1时,求方程②的整数根;(3)当方程②x1、x2,满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.17.(13分)如图,已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE 的中点,连接CF,DF.(1)如图①,当点D在AB上,点E在AC上时,请判断线段CF,DF有怎样的数量关系和位置关系?为什么?(2)如图②,将图①中的△ADE绕点A旋转到图②位置时,请判断(1)中的结论是否仍然成立?并证明你的判断.参考答案一.选择题(共6小题)1.【分析】定义,可知β2﹣β﹣2006=0,即β2=β+2006①,再由一元二次方程根与系数的关系,可得α+β=1②,然后把①②分别代入所求式子α+β2,即可求出其值.解:∵β是方程x2﹣x﹣2006=0的根,∴β2﹣β﹣2006=0,即β2=β+2006,又∵α、β是方程x2﹣x﹣2006=0的两个实数根,∴α+β=1.∴α+β2=α+(β+2006)=1+2006=2007.故选B.2.【分析】本题可先列出出况,因为二次图象开口向上,要使图象与x轴有两个不同的交点,则最低点要小于0,即4n﹣m2<0,再把m、n的值一一代入检验,看是否满足.最后把满足的个数除以掷骰子可能出现的点数的总个数即可.解:掷骰子有6×6=36种情况.根据题意有:4n﹣m2<0,因此满足的点有:n=1,m=3,4,5,6,n=2,m=3,4,5,6,n=3,m=4,5,6,n=4,m=5,6,n=5,m=5,6,n=6,m=5,6,共有17种,故概率为:17÷36=.故选C.3.【分析】本题是规律性题型,基本方法是,将一个分数分为两个分数的差,因为所求式子,每一个分母的两个因数相差2,一个分数分为两个分数时,需要乘以.解:由上式可知+++…+=(1﹣)=.故选A.4.【分析】先利用“两角法PBQ与△ABC相似,再设BP=x(0<x<4).由勾股定理、相似三角形的对应边成比例以及三角形的面积公式,列出S与x的函数关系式,利用配方法求得二次函数的最值.解:设BP=x(0<x<4),由勾股定理得 AB=5,∵∠PQB=∠C=90°,∠B=∠B,∴△PBQ∽△ABC,∴==,即==∴PQ=x,QB=xS△APQ=PQ×AQ=+x=∴当x=时,△APQ的面积最大,最大值是.故选(C)5.【分析】令n=1、2、3…,求出a1,a2,…的值,在表示出a2﹣1,a3﹣1,…从而得出规律,再提取后利用拆项法解答.解:根据题意,当n=1时,a1=13=1,当n=2时,a1+a2=23,a2=23﹣1=7,所以a2﹣1=7﹣1=6=3×(1×2),当n=3时,a1+a2+a3=33,a3=33﹣23=19,所以a3﹣1=19﹣1=18=3×(2×3),当n=4时,a1+a2+a3+a4=43,a4=43﹣33=37,所以a4﹣1=37﹣1=36=3×(3×4),…a100=1003﹣993=(100﹣99)×(1002+100×99+992)=1002+100×(100﹣1)+(100﹣1)2=1002+1002﹣100+1002﹣200+1=3×1002﹣300+1,所以a100﹣1=3×1002﹣300+1﹣1=100×(300﹣3)=100×297=3×(99×100),++…+=+++…+=(﹣+﹣+﹣+…+﹣)=×(1﹣)=×=.故选A.6.【分析】根据已知条件先求出xy+xz+yz=,再求出xyz=,根据完全平方公式即可求解.解:∵,∴由(1)代入上式得:xy+xz+yz=(4),而x3+y3+z3﹣3xyz=(x+y+z)(x2+y2+z2﹣xy﹣xz﹣yz),把(3)(4)代入上式得:xyz=(5),由(4)平方得:;把(5)代入上式得:,∴.故选C.二.填空题(共6小题)7.【分析】先根据点D(﹣2,4)在反比例函数y=的图象上求出k的值,再判断出函数图象所在的象限,根据函数图象在每一象限内的增减性即可得出结论.解:∵D(﹣2,4)是双曲线上的点,∴k=(﹣2)×4=﹣8<0,∴双曲线的两个分支分别位于二四象限,且在每一象限内y随x的增大而增大,∵x3<x2<0<x1,∴B(x2,y2),C(x3,y3)在第二象限,A(x1,y1)在第四象限,∴y2>y3>0,y1<0,∴y2>y3>y1.故答案为:y2>y3>y1.8.【分析】分式=,视x+3y与x+y+z为两个整体,对方程组进行整体改造后即可得出答案.解:由x、y、z满足3x+7y+z=1和4x+10y+z=2001,得出:,解得:,∴=,==﹣3999.故答案为:﹣3999.9.【分析】连接CF,设S△CEF=x,S△CDF=y,根据三角形的面积与三角形底边成比例,进而求出四边形CDFE的面积.解:连接CF,设S△CEF=x,S△CDF=y,则==,==,解得x=,y=,故四边形CDFE的面积=x+y=.故答案为:.10.【分析】可以设平CD的面积是S,根据等分点的定义利用平行四边形ABCD的面积减去四个角上的三角形的面积,就可表示出四边形A4B2C4D2的面积,从而得到两个四边形面积的关系,即可求解.解:设平行四边形ABCD的面积是S,设AB=5a,BC=3b.AB边上的高是3x,BC边上的高是5y.则S=5a?3x=3b?5y.即ax=by=.△AA4D2与△B2CC4全等,B2C=BC=b,B2C边上的高是?5y=4y.则△AA4D2和△B2CC4的面积是2by=.同理△D2C4D与△A4BB2的面积是.则四边形A4B2C4D2的面积是S﹣﹣=,又∵S=9,∴四边形A4B2C4D2的面积=×5=3.故答案为:3.11.【分析】要弄清粒子的运动规律,先观察横坐标和纵坐标的相同点:(0,0),粒子运动了0分钟.(1,1)就是运动了2=1×2分钟,将向左运动!(2,2)粒子运动了6=2×3分钟,将向下运动!(3,3),粒子运动了12=3×4分钟.将向左运动…(45,45)点处粒子运动了45×46=2070分钟!此时粒子会将左移动.解:要弄清粒子的运动规律,先观察横坐标和纵坐标的相同点:(0,0),粒子运动了0分钟.(1,1)就是运动了2=1×2分钟,将向左运动!(2,2)粒子运动了6=2×3分钟,将向下运动!(3,3),粒子运动了12=3×4分钟.将向左运动…于是会出现:(45,45)点处粒子运动了45×46=2070分钟,此时粒子会将左移动.从而在运动了2071分钟以后,粒子所在位置为(44,45)故答案填:(44,45).12.【分析】设与x轴交点为(p,0),与y轴交点为(0,q),把点(10,13)代入y=ax+b,得10a+b=13;把(p,0),(0,q)也代入y=ax+b,得b=q,a=﹣.所以13p=﹣10q+pq,则q=,p是质数,q是正整数,再利用整除的性质讨论即可.解:设于x轴交点为(p,0),与y轴交点为(0,q),把点(10,13)代入y=ax+b,得10a+b=13;把(p,0),(0,q)也代入y=ax+b,得b=q,a=﹣.所以13p=﹣10q+pq,则q=,p是质数,q是正整数,当p﹣10=1时,p=11,q=143,符合题意;当p﹣10=13时,p=23,q=23,符合题意;当p﹣10=p时,无解.所以满足条件的所有一次函数的个数为2个.故答案为2.三.解答题(共5小题)13.【分析】(1)此题由3种情况,①从假设△BPQ是等腰三角形入手.求证△BMP∽△BCD,利用对应边成比例即可求得t的值.在Rt△BMP中,利用cos∠DBC=,解得t.③如图,当BQ=PQ时,自点Q向BD引垂线,垂足为N.利用Rt△BNQ∽Rt△BCD其对应边成比例即可求得t.(2)若△PBQ为等边三角形,则BQ=BP=PQ.由②,知当BQ=BP时,.由①,知当BP=PQ 时,.而BQ=BP与BP=PQ不能同时成解:(1)若△BPQ是等腰三角形.①如图,当PB=PQ时,自点P向BC引垂线,垂足为M,则有BM=MQ.方法一:由△BMP∽△BCD,得,∴.∴,解得.方法二:在Rt△BMP中,.∴,解得.②当BQ=BP时,有t=5﹣t,解得.③如图,当BQ=PQ时,自点Q向BD引垂线,垂足为N.由Rt△BNQ∽Rt△BCD,得.∴,解得.(2)不能.若△PBQ为等边三角形,则BQ=BP=PQ.由(2)②,知当BQ=BP时,.由(2)①,知当BP=PQ时,.∴BQ=BP与BP=PQ不能同时成立,∴△PBQ不可能为等边三角形.14.【分析】(1)①当点P不与点A重合时,②当点P与点A重合时,分别证明即可;(2)由(1)知∠BAD=1=BP=x,过P作DA延长线的垂线PM,M为垂足,则∠PAM=60°,∠APM=30°,表示出△PAD面积然后根据配方法即可得出答案.解:(1)四边形ABCD是梯形或菱形,证明如下:①当点P不与点A重合时,∵△ABC与△CPD都是等边三角形,∴∠ACB=∠DCP=60°,∴∠1=∠2,∴△ADC≌△BPC,∴∠DAC=∠B=∠BCA=60°,∴AD∥BC.又∵∠1=∠2<60°,∴∠DCB<120°,即∠B+∠DCB<180°,∴DC与AB不平行,∴四边形ABCD是梯形;②当点P与点A重合时,PC与AC重合,此时AB=BC=CA=AD=DC,四边形ABCD是菱形,综上所述,四边形ABCD是梯形或菱形;(2)由(1)知∠BAD=120°,AD=BP=x,过P作DA延长线的垂线PM,M为垂足,则∠PAM=60°,∠APM=30°,又BP=x,AB=1,∴AP=1﹣x,∴AM=,PM=∴(0<x<1).当时,y取最大值为,即当时△PAD面积取得最大面积为.15.【分析】(1)求出点A、B的坐标,然后根据坐标原点O与O′关于直线l对称求出点O′,再利用待定系数法即可求解;(2)根据题意作出草图,设点P的坐标为(0,a),先求出点Q的坐标,然后分别求出梯形O′BPQ的面积与正方形AOBO′的面积,再根据S四边形APQO′=S梯形O′BPQ的面积+S正方形AOBO′﹣S△AOP,列式计算即可求出a的值为3,根据三角函数求出∠PAO=60°,∠BAO=45°,两角相减即可解:(1)当x=0时,y=0+3=3,当y=0时,x+3=0,解得x=﹣3,∴点A、B的坐标分别为A(﹣3,0),B(0,3),∵坐标原点O与O′关于直线l对称,∴O′(﹣3,3),∴3=,解得k=﹣9,∴反比例函数y=的解析式为:y=﹣;(2)设点P的坐标为(0,a),∵PQ∥x轴,∴a=﹣,解得x=﹣,∴点Q的坐标为(﹣,a);S四边形APQO′=S梯形O′BPQ的面积+S正方形AOBO′﹣S△AOP=×(+3)(a﹣3)+3×3﹣×3×a,=﹣+9,∵四边形APQO′的面积为9﹣,∴﹣+9=9﹣,解得a=3,∴tan∠PAO===,tan∠BAO===1,∴∠PAO=60°,∠BAO=45°,θ=∠PAO﹣∠BAO=60°﹣45°=15°.故答案为:15°.16.【分析】(1)先解出分式方程①的解,根据分式的意义和方程①的根为非负数得出k(2)先把k=m+2,n=1代入方程②化简,由方程②有两个整数实根得△是完全平方数,列等式得出关于m的等式,由根与系数的关系和两个整数根x1、x2得出m=1和﹣1,再根据方程有两个整数根得△>0,得出m>0或m<﹣,符合题意,分别把m=1和﹣1代入方程后解出即可.(3)根据(1)中k的取数得出k=﹣1,化简已知所给的等式,并将两根和与积代入计算得出m的等式,并由根的判别式组成两式可做出判断.解:(1)∵关于x的分式方程的根为非负数,∴x≥0且x≠1,又∵x=≥0,且≠1,∴解得k≥﹣1且k≠1,又∵一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0中2﹣k≠0,∴k≠2,综上可得:k≥﹣1且k≠1且k≠2;(2)∵一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0有两个整数根x1、x2,且k=m+2,n=1时,∴把k=m+2,n=1代入原方程得:﹣mx2+3mx+(1﹣m)=0,即:mx2﹣3mx+m﹣1=0,∴△>0,即△=(﹣3m)2﹣4m(m﹣1),且m≠0,∴△=9m2﹣4m(m﹣1)=m(5m+4)>0,则m>0或m<﹣;∵x1、x2是整数,k、m都是整数,∵x1+x2=3,x1?x2==1﹣,∴1﹣为整数,∴m=1或﹣1,由(1)知k≠1,则m+2≠1,m≠﹣1∴把m=1代入方程mx2﹣3mx+m﹣1=0得:x2﹣3x+1﹣1=0,x2﹣3x=0,x(x﹣3)=0,(3)|m|≤2成立,理由是:由(1)知:k≥﹣1且k≠1且k≠2,∵k是负整数,∴k=﹣1,(2﹣k)x2+3mx+(3﹣k)n=0且方程有两个实数根x1、x2,∴x1+x2=﹣==﹣m,x1x2==n,x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),x12﹣x1k+x22﹣x2k=x1x2﹣x1k﹣x2k+k2,x12+x22═x1x2+k2,(x1+x2)2﹣2x1x2﹣x1x2=k2,(x1+x2)2﹣3x1x2=k2,(﹣m)2﹣3×n=(﹣1)2,m2﹣4n=1,n=①,△=(3m)2﹣4(2﹣k)(3﹣k)n=9m2﹣48n≥0②,把①代入②得:9m2﹣48×≥0,m2≤4,则|m|≤2,∴|m|≤2成立.17.【分析】(1)根据“边上的中线等于斜边的一半”可知DF=BF=CF,根据∠DFE=2∠DCF,∠BFE=2∠BCF,得到∠EFD+∠EFB=2∠ABC=90°,进而得出DF⊥BF;(2)延长DF至G,连接BG,CG,DC,先判定△BFG≌△EFD(SAS),得到∠FBG=∠FED,BG=ED,结合△ADE和△ACB都是等腰直角三角形,得出∠CBG=∠DAC,再判定△BCG≌△ACD(SAS),进而得到GC=DC,∠BCG=∠ACD,根据△DCG是等腰直角三角形,以及F是DG的中点,即可得到CF⊥DF且CF=DF.解:(1)CF=DF且CF⊥DF.理由如下:∴∠BDE=90°,又∵∠BCE=90°,点F是BE的中点,∴CF=DF=BE=BF,∴∠1=∠3,∠2=∠4,∴∠5=∠1+∠3=2∠1,∠6=∠2+∠4=2∠2,∴∠CFD=∠5+∠6=2(∠1+∠2)=2∠ABC,又∵△ABC是等腰直角三角形,且∠ACB=90°,∴∠ABC=45°,∴∠CFD=90°,∴CF=DF且CF⊥DF.(2)(1)中的结论仍然成立.理由如下:如图,延长DF至G使FG=DF,连接BG,CG,DC,∵F是BE的中点,∴BF=EF,又∵∠BFG=∠EFD,GF=DF,∴△BFG≌△EFD(SAS),∴∠FBG=∠FED,BG=ED,∴BG∥DE,∵△ADE和△ACB都是等腰直角三角形,∴DE=DA,∠DAE=∠DEA=45°,AC=BC,∠CAB=∠CBA=45°,又∵∠CBG=∠EBG﹣∠EBA﹣∠ABC=∠DEF﹣(180°﹣∠AEB﹣∠EAB)﹣45°=∠DEF﹣180°+∠AEB+∠EAB﹣45°=(∠DEF+∠AEB)+∠EAB﹣225°=360°﹣∠DEA+∠EAB﹣225°=360°﹣45°+∠EAB﹣225°而∠DAC=∠DAE+∠EAB+∠CAB=45°+∠EAB+45°=90°+∠EAB,∴∠CBG=∠DAC,又∵BG=ED,DE=DA,∴BG=AD,又∵BC=AC,∴△BCG≌△ACD(SAS),∴GC=DC,∠BCG=∠ACD,∴∠DCG=∠DCB+∠BCG=∠DCB+∠ACD=∠ACB=90°,∴△DCG是等腰直角三角形,又∵F是DG的中点,∴CF⊥DF且CF=DF.。
2010普高提前招生数学试题

2010年普通高中提前招生试卷理科综合(数学)一、 选择题(本题共25分,每小题5分,请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)1. 已知n m ,是方程0122=--x x 的两根,且8)763)(147(22=--+-n n a m m ,则a 的值等于 ( )A .-5 B.5 C.-9 D.92. 如图,点B 是线段AC 的中点,过点C 的直线l 与AC 成60°的角,在直线l 上取一点p ,使∠APB=30°,则满足条件的点有几个( )A.3个B.2个C.1个D.不存在 3.如图,直线),(),,221y x B y 两点,则22183y x y x -A.-5 C.5 D.10 4.已知二次函数c bx ax y ++=2的图象如图所示,记b a c b a q b a c b a p -+++=+++-=2,2,则p 与q 的大小关系为( )A.q p >B.q P =C.q p <D.p 、q (第大小关系不能确定5.(09年全国初中数学竞赛题)将一枚六个面编号3,4,5,6的质地均匀的正方体骰子记第一次掷出的点数为a,第二次掷b yx,的方程组只有正数解的概率为()A.121 B.92 C.185 D.3613二、填空题(本题共20分,每小4分)6.如图,7根圆柱形木棒的横截面圆的半径均为1,则捆扎这7根木棒一周的绳子长度为。
7.如图,在平面直角坐标系中,O为原点,四边形OABC 是矩形,A(10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP 是腰长为5的等腰三角形时,点P的坐标是。
8.如图,射线AM,BN都垂直于线段AB,点E为AM 上一点,过点A作BE的垂线AC分别交BE,BN于点F,C,过点C作AM的垂线CD,垂足为D,若CD=CF,则ADAE。
(第(第7(第9.如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….则“17”在射线上;“2007”在射线上。
2010年温州市中考数学试题卷

数¥试题卷(WZ 〉第1页(共4页)2010年浙江省初屮毕业生学业考试(温州市卷)数学试题卷亲溢的同学:欢逹参加考试!请你认真审题■积极思考•如心答题•发挥聂隹木平・答题时•请注总以: 几点:1•全算共4頁,有三大题.24小处•全卷满分150分•考试时间120分钟・2. 答案必'须爲在答题纸柯应的位JK •上,写在试题卷、苹稿紙上均无效.3. 答题箭,认具阅读答题城上的《注意审项》•按规定答題・ 祝你成功I参考公式:一元一次方程aE+6z+c=0的两根是工=~"土%f 一他(y-4ac»0);二次函数y~ax :+dx+c 的图象的顶点坐标是(一石■兀•选择題(本题有10小题■每小题4分■共40分•每小题只有一个选项是正确的•不选、多选、 错选,均不给分)1•给出四个数0,血•一*・0・3,其中最小的是(▲〉A.0B.V2C.p 2•把不等式x+2>4的解表示在数轴上•正确的是(▲)二次函数 B.V2D. 0.3D.a l<5.直线y = x + 3与y 轴的交点坐标是(▲〉A. (0,3)B ・(0.1)C ・(3,0) 某贸学生呑加课外兴趣小俎情况统计田D. (ItO) (第4题)数学试题卷(WZ ) 第2页(共4页)&如KhAGBD 是矩形ABCD 的对角线•过点D 作DE//AC 交BC 的延长线于E •则图中与 9•如图•在△ABC 中,AB = BC=2・以AB 为宜径的€)0与BC 相切于点“则AC 芳丁( ▲)A.#B.V3C. 2V2D. 2^310 •用若干根相同的火柴棒首尾顺次相接丽成一个梯形(提供的火柴棒全部用完人下列根数的火柴棒不能围成梯形的是(▲) • •A.5C.7 二、填空题(本题有6小题■每小题5分•共30分)12•在“情系玉树献爱心”捐款活动中,某校九(1)班同学人人拿出白己的零花钱,现将同学们的捐款数整理成统计表,则该班同学平均塚人捐款亠_元・13. 当厂 ▲时,分武吿的值等于2. 14. 若_个反比例函数的图象位于二、巴象限•则它的解析式可能是_A_・(写出一个即可)15. 某班级从文化用品市场购买了签字笔和圆珠笔共15支,所付金额大于26元,但小于27 元.已知签字笔每支2元•圆珠笔每支1. 5元•则其中签字笔购买了—亠支・ 眉款数(元) 5 10 20 50人数 4 15 6 5 6•如图•已知-商场自动扶梯的氏Z 为10米,该自动扶梯到达的高度人为6米,自动扶梯与地面所成的角为比则tan 0的值零于(▲〉7•下列命题中•属于假密夢的是(▲〉A.三角形三个内角的和等于180° C •炬形的对角线相等 D.相等的角址对顶角 AABC 全尊的三角形共有(▲)A.1个B.2个 C ・3个 B.6 D.8卷 n11.分解因式:B.两直线平行,同位金相等 (第6题)(第10题)题〉16 •勾股定理有着悠久的历史■它曾引起很多人的兴趣• 1955年希蹄发行了一枚以勾股图为背景的邮票.所谓勾股图是指以宜角三角形的三边为边向外作正方形构成,它可以验证勾股定理•在右图的勾股图中,巳知ZACB = 90・,ZBAC= 30\AB = 4.作2QR使得ZR=90°・点H在边QR上,点D,E在边PR上,点G.F在边PQ上•那么的周长等于▲•三、解答题(本题有8小題,共80分)17.(本題10 分)⑴计算:78+<2010-73 r-Cy)-11(2)先化简,再求值:(a+A)(a-6)+a(2d-a),其中 a = l・ 5,6=2.1& (本题6分)由3个相同的小立方块搭成的几何体如图所示,请画岀它的主视图和俯视图.19.(本题8分)2010年上海世博会某展览馆展厅东面冇两个人口A.B■南面、西面、北面各有一个出口,示意图如图所示•小华任选一个入口进入展览大厅,参观结束后任选一个出口离开.(1)她从进入到离开共冇多少种可能的结果?(耍求画出树状图)(2)她从入U A进入展厅并从北出口或西出口离开的概率足多少?主视方向(第18题)(第19題)(第20題〉数学试题卷(WZ)第3页(共4页)20.(本题8分〉如图•在正方形ABCD中,AB = 4,0为对角线BD的中点,分別以OB,OD为直径作(1)求oa的半径■(2)求图中阴形部分的面积.21•〈本题10分)如图,在口A BCD中.EF//BD,分别交BCP,Q,交AB,AD的延长线于点E,F.巳知BE=BP.求证,(l)ZF=ZFi(2)CJABCD是菱形•(第21题)数学试题卷(WZ)第4页(共4页)50 1 2 34 5 0 7 8 9 10 11 12 (第23题〉根据图中提供的借息,回答下列问题,① 2009年小芳家月用电罐最小的是月■四个季度中用电量最大的是第季度:② 求2009年5月至6月用电员的月堆长率'(2)今年小芳家添盖了新电器•已知今年5月份的用电总足120千瓦时■根据2009年5月 至7月用电量的増长趋势,预计今年7月份的用电量将达到240千瓦吋.假设今年5月 至6月用电敖月增长率是6月至7月用电量月增长率的1. 5倍,预计小芳家今年6月 份的用电员是多少千瓦时?24. (本题 14 分)如图,在 RtZkABC 中,ZACB=90SACu3,BC=4,过点 B 作射线 BB : //AC.动点D 从点A 出发沿射线AC 方向以每秒5个单 位的速度运动,同时动点E 从点C 岀发沿射线 AC 方向以每秒3个单位的速皮运动.过点D 作 DH1.AB于H,过点E 作EF 丄AC 交射线BB. 于F,G 是EF 中点,连结DG.设点D 运动的时间 为t 秒.(1) 当/为何值时,AD=71B,并求出此时DE 的 长度;(2) 当HDEG 与AACB 相似时,求t 的值,(3) 以DH 所在直线为对称轴,线段AC 经轴对称变换后的图形为A'C : ① 当*>¥时,连结C'C,设四边形ACCA'的面积为S,衣S 关于/的函数关系式;② 当线段/VC 与射线BB\有公共点时■求r 的取值范围(写出答案即可).数学试题卷(WZ) 第4页(共4页)22. 〈本题12分)如图,抛物线y^a^+bx 经过点A(4,0),E(2・2八连结OB.AB.(1) 求该抛物线的解析式;(2) 求证:AOAB 是等腰直角三角形;(3) 将△»£绕点O 按顺时针方向旋转135°得到△ OA%',写 出A'B'的中点P 的坐标,试判断点P 足否在此抛物线上, 并说明理由.23. (木题12分)在日常生活中,我们经常有目的地收集数据,分析数嶠,作出预测.(1)下图是小芳家2009年全年月用电址的条形统计图.Mmt(TJUf).192 * 198 -J0埼 ITM ....... =• .... 盅廨他 ne o| | | m I I | £ I200 150 (第24题)。
温州市直十校联盟2010学年第二学期九年级一模数学试题

(第5题)温州市直十校联盟2010学年第二学期三模试卷卷Ⅰ一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)1.绝对值为3的实数是()A.±3B.3C.-3D.132.下列运算正确的是()A.523aaa=+B.632aaa=⋅C.22))((bababa-=-+D.222)(baba+=+3.以下列三个数为边长的三角形能.组成直角三角形的是()A.1, 1 ,2 B.3 ,4 ,5 C.5, 8 10 D.6 ,7 ,84.为测量如图所示上山坡道的倾斜度,小明测得图中所示的数据,则该坡道倾斜角α的正切值是()A.34B.43C.35D.455.如图,将小王某月手机费中各项费用的情况制成扇形统计图,则表示短信费的扇形圆心角的度数为( )A.60° B.72° C.75° D. 80°.6.已知⊙O1与⊙O2的半径分别为3和4,若圆心距O1O2=1,则两圆的位置关系是()A.相交B.内切C.相离D.外切7. 抛物线442+-=xxy与坐标轴...的交点个数()A.0个B.1个C.2个D.3个8.下列命题,正确的是( )A.如果|a|=|b|,那么a=bB.C.顺次连结四边形各边中点所D.相等的圆周角所对的弧相等9.如图,已知121=AA,9021=∠AOA,3021=∠OAA,以斜边2OA为直角边作直角三角形,使得3032=∠OAA,依次以前一个直角三角形的斜边为直角边一直作含o30角的直角三角形,则20112010OAARt∆的最小边长为A.20092 B.20102 C.2009)32( D.2010)32(34(第4题)α34m(单位:米)1A2A3A4A5A6A7A8A12AOE2D2E1D1EDCAB(第13题图)第10题图10.直角梯形OABC 中,BC ∥OA ,∠OAB=90°,OA=4,腰AB 上 有一点D ,AD=2,四边形ODBC 的面积为6,建立如图所示的直角坐标系,反比例函数x my =(x >0)的图象恰好经过点C 和点D ,则CB 与BD 的比值是 A .1 B .34 C .56 D .78卷Ⅱ二、填空题(本题有6小题。
浙江省温州市六校2010年九年级数学中考第三次联考试题浙教版

a ac 丙︒72︒50 乙︒50甲a ︒507250︒︒︒58c ba C B A 2010年初中学业考试数学模拟试题(2010-5)请仔细审题,相信你一定会有出色的表现! 参考公式:二次函数y=ax 2+bx+c (a ≠0)的图象的顶点坐标是24,24b ac b a a ⎛⎫-- ⎪⎝⎭试卷Ⅰ (选择题,共40分)一、选择题 (本大题有10小题,每小题4分,共40分。
请选出每个小题中一个符合题意的正确选项,不选、多选、错选,均不给分) 1. 5的倒数是A .51 B .51- C .-5 D .5 2.在函数12y x =-+中,自变量x 的取值X 围是( )A .2x -≥B .2x -≤C .2x ≠-D .2x ≠3.解集在数轴上表示为如图1所示的不等式组是( ) A .32x x >-⎧⎨⎩≥B .32x x <-⎧⎨⎩≤C .32x x <-⎧⎨⎩≥D .32x x >-⎧⎨⎩≤4.桌面上放着1个长方体和1个圆柱体,按下图所示的方式摆放在一起,其左视图是( )5.下列运算中,结果正确的是( )A .444a a a +=B .325()a a a = C.824a a a ÷=D .236(2)6a a -=-6.把抛物线22y x =-向左平移1个单位,得到的抛物线是( ) A .22(1)y x =-+B .22(1)y x =--C .221y x =-+D .221y x =--7.如图,已知△ABC 的六个元素,则下列甲、乙、丙三个三角形中和△ABC 全等的图形是( )A 、甲乙B 、甲丙C 、乙丙D 乙3-图112 8.为建设生态某某,我市某中学在植树节那天,组织初三年级八个班的学生到西城新区植下列说法错误的是( )C.这组数据的平均数是20D.这组数据的极差是139.如图1-1所示,将长为20cm ,宽为2cm 的长方形白纸条,折成图1-2所示的图形并在其一面着色,则着色部分的面积为( )图1-1A .234cmB .236cmC .238cmD .240cm10.把2010个边长为1的正方形排成如右图所示的图形,则这个图形的周长是 ( ). A .4020 B. 4022 C. 4024 D4026试卷Ⅱ (非选择题,共110分)二、填空题 (本题有6小题,每小题5分,共30分)11.如图,A B C ,,是⊙O 上三点,40ACB =∠,则∠AOB第12题12.如图,将一等边三角形剪去一个角后,12+∠∠=. 13.如图3,在距旗杆4米的A 处,用测角仪测得旗杆顶端C 的仰角为60,已知测角仪AB 的高为,则旗杆CE 的高等于米.(保留三个有效数字)14.如图,正方形ABCD 的边长为4cm ,正方形AEFG 的边长为1cm . 如果正方形AEFG 绕点A 旋转,那么C 、F 两点之间的最小距离 为cm .15.小明和小莉出生于1998年12月份,他们的出生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期之和是22,那么 小莉的出生日期是1998年12月________日第13题11题C EABCDGF(第14题)(第10题图)…16..如图15,△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3……△P n A n -1A n 都是等腰直角三角形,点P 1、P 2、P 3……P n 都在函数xy 4=(x > 0)的图象上,斜边OA 1、A 1A 2、A 2A 3……A n -1A n 都在x 轴上。
温州中学九年级提前招生数学模拟卷

68CEABD九年级实验班数学期中考试测试题一、选择题(每小题4分,共40分) 1.若0< x <1,则x 2,x ,x,x1这四个数中( )A .x1最大,x 2最小 B .x 最大,x1最小C .x 2最大,x最小 D .x 最大,x 2最小2. 将量角器按如图所示的方式放置在三角形纸板上,使点C 在半圆上.点A 、B 的读数分别为86°、30°,则∠ACB 的大小为( )A .15︒B .28︒C .29︒D .34︒3.直角三角形纸片的两直角边长分别为6,8,现将A B C △如右图那样折叠,使点A 与点B 重合,则折痕D E 的长是( )A .254 B .154 C .252D .1524.已知x 为整数,且分式2364x x +-的值为整数,则x 可取的值有( )A .4个B .3个C .2个D .1个5.若一次函数y kx b =+,当x 得值减小1,y 的值就减小2,则当x 的值增加2时,y 的值是( )A .增加4B .减小4C .增加2D .减小26.已知f (x )=1-(x -a )(x -b ),并且m ,n 是方程f (x )=0的两根,则实数a ,b ,m ,n 的大小关系可能是( ).A .m <a <b <nB .a <m <n <bC .a <m <b <nD .m <a <n <b 7、在不等腰A B C △中,90C ∠= ,设sinB n =,当B ∠是最小的内角时,n 的取值范围是( )A.02n <<B .102n <<C.03n <<D.02n <<8.无论m 为何值时,二次函数y=x 2+(2-m)x+m 的图象总过的点是( )9、如图,一次函数122y x =-+的图像上有两点A 、B ,A 点的横坐标为2,B 点的横坐标为(042)a a a <<≠且,过点A 、B 分别作x 的垂线,垂足为C 、D ,AO C BO D ∆∆、的面积分别为12S S 、,则12S S 、的大小关系是( ) A. 12S S > B. 12S S = C. 12S S < D. 无法确定10、.已知函数f (x )=x 2+λx ,p 、q 、r 为△ABC 的三边,且p < q <r ,若对所有的正整数p 、q 、r 都满足f (p )<f (q )<f (r ),则λ的取值范围是( ).A .λ >-2B .λ >-3C .λ >-4D .λ >-5 二、填空题(每小题5分,共30分)11、已知a =5-1,则2a 3+7a 2-2a -12 的值等于 .12、y x ,为实数,且0360tan 0=++-y x ,则=2011)(yx ________________.13、如图1,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC =6,BC =5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是_______________;14.设()11,A x y ,()22,B x y 为函数21k y x-=图象上的两点,且120x x <<,12y y >,则实数k 的取值范围是15.二次函数a ax x y ++=22在21≤≤-x 上有最小值4-,则a 的值为___________. 图2ABC图1ABC16.如图,CD 是直角三角形ABC 的斜边AD 上的高,I 1、I 2分别是△ADC、△BDC 的内心,若AC =3,BC =4, 则I1I 2=__________.三、解答题17. (满分10分)乐清某家俱市场现有大批如图所示的边角余料 (单位:cm)乐清中学数学兴趣小组决定将其加工成等腰三角形, 且方案如下:(1)三角形中至少有一边长为(218. (满分8分)将一个以自由转动的转盘可分成三等分,每一份内标上数字如图所示,第一次转动转盘,当转盘停止后,指针所在的区域的数字记为a ,第二次转动转盘,当转盘停止后,指针所在的区域的数字记为c ,(注意:如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止)用画树状图的方法,求抛物线cx x ay ++=212顶点在第一象限的概率.A BC DI 1I 219、(满分8分)定义{},,a b c 为函数2y ax bx c =++的 “特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x 的“特征数”是{0,-1,0}。
浙江省温州地区2010年九年级数学第三次中考模拟考试浙教版

2010年九年级中考第三次模拟考试数学试卷考生须知:1. 全卷共三大题,24小题,满分为150分.考试时间为120分钟,本次考试采用闭卷形式. 2.全卷分为卷Ⅰ(选择题)和卷ⅡⅠ的答案必须用2B 铅笔填涂;卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在答题纸相应位置上.3.参考公式:二次函数2y ax bx c =++图像的顶点坐标是24,24b ac b a a ⎛⎫-- ⎪⎝⎭卷 Ⅰ一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)1.下列各数中,是正分数的是( ▲ )A.12B. 2 0.32.某某世博会场地位于南浦大桥和卢浦大桥之间,沿着某某城区黄浦江两岸进行布局。
世博园区规划用地X 围为5280000m 2,用科学计数法表示为(▲ )×105 m 2×106 m 2C ×107 m 2×10-6m 23.如图,a ∥b,若∠1=55°,则∠2的度数为(▲ ) A .35° B .55° C .125° D .135°4.下列图案中是中心对称图形的是(▲ )(第3题图)A .B .C .D .5.四边形的内角和为( ▲ )°°°°6.下列四幅图形中,表示两棵小树在同一时刻阳光下影子的图形可能是( ▲)A .B .C .D .7.平面直角坐标系中点A (-3,1)关于y 轴的对称点A '的坐标为( ▲) A .(3,1)B .(-3,-1) C .(3,-1) D .(1,-3)8.关于抛物线y=(x-1)2+3的描叙错误..的是(▲ ) A .开口向上B .对称轴为直线x=1C .顶点坐标为(1,3) D .与y 轴交点为(0,3) 9日期一二三四五方差平均气温 最低气温1℃ -1℃ 2℃ 0℃ ■℃ ■℃21℃A .3,2B .3,65C .2,2D .2,8510.如图,等腰直角△ABC ,BC=9,从中裁剪正方形DEFG ,其中边 DE 落在斜边BC 上,点F 、G 分别在直角边AC 、AB 上。
温州实验中学中考第一次模拟考试数学试题目

温州实验中学中考第一次模拟考试数学试题目温州实验中学2010年中考数学第一次模拟考题一、选择题:(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)1. 2的相反数是()A.2 B. 2- C. 22- D. 22.计算y8÷y4 结果正确的是()A.2 B. 4 C.y2D. y43.如图,箭头表示投影的方向,则图中圆柱体的投影是()A B C D4.五边形的内角和是()A. 180°B. 360°C. 540°1 212 12 12D. 720°5.下列能够说明“任何数的立方都是非负数”是假命题的反例是()A.-3B.0C.7D.3.56.下图一定能说明∠1>∠2的是()A B CD7.双曲线kyx的每个分支上,y都随x的增大而减小,则k的值可以是()A.1 B. 0 C. -1D. -28.为响应团中央“号召全国每位团员,少先队员捐一瓶水”的倡议,我校师生积极开展了“情系西南灾区”的捐款活动.某班6名同学捐款的数额分别是(单位:元):5,5,5,10,10,20.则这组数据的中位数和众数分别是()元.A. 5, 5B. 10, 5C.10, 7.5 D. 5, 7.5O3'O2O1O3E ODCB A9.如图,共有12个大不相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分.现从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的概率是()10.如图,三个半径为1的等圆两两外切,若固定⊙O1和⊙O2,将⊙O3沿⊙O1的边缘逆时针旋转到⊙O3′的位置(即⊙O1、⊙O2、⊙O3′两两外切),圆心O3所经过的路程为()A. 2πB. 43πC. 83π D.4π二、填空题(本题有6小题,每小题5分,共30分)11.分解因式:m2-2m =________.12.已知一组数据的頻率为0.35,数据总数为500个,则这组数据的頻数为____.13.如图平行四边形ABCD的对角线AC与BD交于点O,点E是BC的中点,OE=2,则AB的长是___。
温州中学提前招生仿真考试试卷

1K2K温州市民办初中九年级学科综合测试科学试卷物理部分(100分)一、选择题(每题3分,共36分)1. 如图所示,水平传送带长为s,以速度v始终匀速运动,把质量为m的货物放到A点,货物与皮带间的动摩擦因数为μ.当货物从A点运动到B点的过程中,摩擦力对货物做的功不可能是()A.等于12m v2B.小于12m v2C.大于μmgs D.小于μmgs2.地球半径为R,地球自转周期为24小时,某地球同步卫星位于赤道上空且离地面的高度约为5.6R,卫星正下方地面上有一观察者,用天文望远镜观察被太阳光照射的此卫星。
若不考虑大气对光的折射,春分(即太阳光直射赤道)那天在日落的时间内,此人观察不到卫星的时间约为()A.40分钟B.70分钟C.100分钟D.140分钟3.面积很大的水池,水深为H,水面上浮着一正方体木块,木块边长为a,密度为水的1/2,质量为m.开始时,木块静止,有一半没入水中,如图所示.现用力将木块缓慢地压到池底.在这一过程中( ) A.木块的机械能增加了mg(H-a2)B.水池中水的机械能不变C.水池中水的机械能增加了2mg(H-a2)D水池中水的机械能增加了2mg(H-5a8)4.将50g0℃的雪(可看成冰水混合物)投入到装有450g40℃水的绝热容器中,发现水的温度下降了6℃。
那么在刚才已降温的容器中再投入100g上述同样的雪,容器中水的温度又要下降()A.7℃ B.8℃ C.9℃ D.10℃5.已知导体的电阻R可以用下式计算,SlRρ=,式中ρ为导体的电阻率(电阻率相同),l为导体的长度,S为导体的横截面积。
现已知直径为0.3mm的熔丝的熔断电流是1.8A,材料相同的直径为0.6mm的熔丝的熔断电流是5.0A,若将长度相同、材料也相同的20根直径为0.3mm的熔丝和一根直径为0.6mm的熔丝并联接入电路,当通入电流逐渐增大,达到下列哪个电流值时,电路将完全断开( ) A.5.0A B.30A C.36A D.55A6.如图6所示,两等长的弹簧,其劲度系数分别为1K、2K。
2010年温州中考试卷

2010年浙江省温州市中考数学试卷卷 Ⅰ一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)1.给出四个数0,2,一21,0.3其中最小的是( ) A .0 B .2 C .一21 D .0.3 2.把不等式x+2>4的解表示在数轴上,正确的是( )3.计算42a a 的结果是( )A .a 2B .a 6C .a 8D .a 164.某班学生参加课外兴趣小组情况的统计图如图所示,则参加人数最多的课外兴趣小组是( )A .书法B .象棋C .体育D .美术5.直线y=x+3与y 轴的交点坐标是( )A .(0,3)B .(0,1)C .(3,O)D .(1,0)6.如图,已知一商场自动扶梯的长z 为10米,该自动扶梯到达的高度h 为6米,自动扶梯与地面所成的角为θ,则tan θ的值等于( ) A.43 B.34 C.53 D.547.下列命题中,属于假命题的是( )A.三角形三个内角的和等于l80° B.两直线平行,同位角相等C.矩形的对角线相等 D.相等的角是对顶角.8.如图,AC;BD是矩形ABCD的对角线,过点D作DE//AC交BC的延长线于E,则图中与△ABC全等的三角形共有( )A.1个 B.2个 C.3个 D.4个9.如图,在△ABC中,AB=BC=2,以AB为直径的⊙0与BC相切于点B,则AC等于( )A.2 B.3 c.22 D.2310.用若干根相同的火柴棒首尾顺次相接围成一个梯形(提供的火柴棒全部用完),下列根数的火柴棒不能围成梯形的是( ) .A.5 B.6 C.7 D.8卷Ⅱ二、填空题(本题有6小题。
每小题5分,共30分)11.分解因式:m2—2m= .12.在“情系玉树献爱心”捐款活动中,某校九(1)班同学人人拿出自己的零花钱,现将同学们的捐款数整理成统计表,则该班同学平均每人捐款 元.13.当x= 时,分式13-+x x 的值等于2.14.若一个反比例函数的图象位于二、四象限,则它的解析式可能是 .(写出一个即可)15.某班级从文化用品市场购买了签字笔和圆珠笔共l5支,所付金额大于26元,但小于27元.已知签字笔每支2元,圆珠笔每支1.5元,则其中签字笔购买了 支.16.勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR 使得∠R=90°,点H 在边QR 上,点D ,E 在边PR 上,点G ,F 在边_PQ 上,那么△PQR 的周长等于 .三、解答题(本题有8小题,共80分)17.(本题l0分)(1)计算:()1021320108-⎪⎭⎫ ⎝⎛--+.(2)先化简,再求值:(a+6)(a-b)+a(2b-a),其中n=1.5,b=-2.18.(本题6分)由3个相同的小立方块搭成的几何体如图所示,请画出它的主视图和俯视图.19.(本题8分)2010年上海世博会某展览馆展厅东面有两个入口A ,B ,南面j 西面、北面各有一个出口,示意图如图所示.小华任选一个入口进入展览大厅,参观结束后任选一个出口离开.(1)她从进入到离开共有多少种可能的结果?(要求画出树状图)(2)她从入口A 进入展厅并从北出口或西出口离开的概率是多少?20.(本题8分)如图,在正方形ABCD 中,AB=4,0为对角线BD 的中点,分别以OB ,OD 为直径作⊙1O ,⊙2O 。
浙江省温州市啸秋中学2010学年高三数学第一学期会考模拟试卷新人教A版

温州市啸秋中学2010学年第一学期会考模拟考高三数学试卷一、选择题(1-20每小题2分,计40分;21-26每小题3分,计18分。
) 1.已知集合{01}A =, ,22{|1}B y x y x A =+=∈,,则A 与B 的关系是A .AB =B .A ⊂≠B C .A ⊃≠B D .A B ⊆2.已知0≠x , 那么函数221x x y +=有A .最小值2B .最大值2C . 最小值4D .最大值43.如右图所示,一个空间几何体的主视图和左视图都是边长为1的 正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为 A .π3 B .π2 C .π23D .π4 4. 下列函数中,周期为π的奇函数是A .sin y x =B .sin 2y x =C .x y 2tan =D .cos 2y x =5.一条直线的倾斜角的正弦值为23,则此直线的斜率为A .3B .±3C .33D .±33 6.下列命题正确的是A .ac >bc ⇒a >bB .2a >2b ⇒a >b C .a 1>b1⇒a <b D .a <b ⇒a <b 7.样本4,2,1,0,-2的标准差是A .1B .2C .4D .528.函数y =log 31(1-3x)的定义域是A .⎪⎭⎫⎢⎣⎡31,0 B .⎪⎭⎫ ⎝⎛+∞,31 C .(]0,∞- D .⎪⎭⎫ ⎝⎛∞-31, 9.已知抛物线px y 22=的焦点坐标为(2,0),则p 的值等于A .2B . 1C .4D .8 10.圆016622=--+y y x 的半径等于A .16B .5C .4D .2511.若{a n }为等差数列,且a 2+a 5+a 8=39,则a 1+a 2+…+a 9的值为主视图俯视图左视图A .117B .114C .111D .10812.下列函数中,在区间),0(+∞上为减函数的是A .xy 4-= B .x y 4= C .x y 31log = D .322+-=x x y13.抛掷两个骰子,则两个骰子点数之和大于4的概率为A .1318B .89C .712D .5614.若222x y x y ⎧⎪⎨⎪+⎩≤,≤,≥,则目标函数2z x y =+的取值范围是A .[26],B .[25],C .[36],D .[35],15.函数()sin cos f x x x =⋅的最小值是A .1-B .12-C .12D .1 16.已知两条直线m 、n 与两个平面α、β,下列命题正确的是A .若m //α,n //α,则m //nB . 若m //α,m //β,则α//βC .若m ⊥α,m ⊥β,则α//βD . 若m ⊥n ,m ⊥β,则n //β 17.在△ABC 中,B=135︒,C=15︒,a =5,则此三角形的最大边长为A . 35B .34 C. D .2418.已知数列{a n }的前n 项和S n =312n a n +=+,则A .201B .241 C .281 D .32119.已知向量a =(1,2),向量b =(,2)x -,且a ⊥(a -b ),则实数x 等于A. 4-B. 4C. 0D. 920.若点A (42+λ,4-μ,1+2γ)关于y 轴的对称点是B (-4λ,9,7-γ),则λ,μ,γ的值依次为A .1,-4,9B .2,-5,-8C .-3,-5,8D .2,5,821.方程x x 28lg -=的根)1,(+∈k k x ,k ∈Z ,则k =A .2B .3C .4D .5.22.已知函数)(x f y =是R 上的偶函数,且在(-∞,]0上是减函数,若)2()(f a f ≥,则实数a 的取值范围是A .a ≤2B .a ≤-2或a ≥2C .a ≥-2D .-2≤a ≤2 23.若执行下面的程序图的算法,则输出的k 的值为A .8B .9C .10D .1124.数列{}n a 满足⎪⎪⎩⎪⎪⎨⎧<≤-<≤=+)121(12)210(21n n n n n a a a a a若761=a ,则=8aA .76 B .75 C .73 D .71 25.如图,E 、F 分别是三棱锥P -ABC 的棱AP 、BC 的中点,PC =10, AB =6,EF =7,则异面直线AB 与PC 所成的角为A .60°B .45°C .0°D .120°26.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数)]6(6cos[-+=x A a y π(x =1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为 18℃,则10月份的平均气温值为A .20℃B .20.5℃C .21℃D .21.5℃. 二、选择题 (A .,.B .两组题...,任选其中一组完成........,每组各4小题,每小题3分,共12分.) A 组27.复数i Z +=31,i Z -=12,则21Z Z Z ⋅=的复平面内的对应点位于A .第一象限B .第二象限C .第三象限D .第四象限28.若曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=aA .1B .12C .- 12D .1-29.“21=m ”是“直线013)2(=+++my x m 与直线03)2()2(=-++-y m x m 垂直”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要 30.给出下列结论,其中正确的是A .渐近线方程为(0,0)by x a b a=±>>的双曲线的标准方程一定是12222=-b y a xB .抛物线221x y -=的准线方程是21=x C .等轴双曲线的离心率是2D .椭圆22221(0,0)x y m n m n+=>>的焦点坐标是221(,0)F m n --,222,0)F m n -开始K=2P=0P<20P=p+kK=k+2输出k结束是 否B 组31.从10种不同的作物种子中选出6种放入6个不同的瓶子中展出,如果甲、乙两种种子不能放入第1号瓶内,那么不同的放法共有( ) A .48210A C 种 B .5919A C 种 C .5918A C 种 D .5818A C 种32.已知9)222(-x展开式的第7项为421,则实数x 的值是( ) A .31- B .-3 C .41D .433.已知椭圆1532222=+n y m x 和双曲线1322222=-n y m x 有公共的焦点,那么双曲线的渐近线方程是A .y x 215±= B .x y 215±= C .y x 43±= D .x y 43±= 34.某人射击一次击中的概率为35,经过3次射击,此人至少有两次击中目标的概率为A .81125B .54125C .36125D .27125三、填空题(本题有5小题,每小题2分,共10分)35.命题 “对任意R x ∈,都有12+x ≥x 2”的否定是 。
数学文卷·2010届浙江省温州市高三第一次适用性测试(温州一模)(2010.02)

三、解答题(本大题共5小题,共72分)
18.(本小题满分14分)
解:(I)由题意得 ………………………………………3分
即 ,
故 ,所以 …………………………………………………………………6分
(II) ,…………………………………………………………………8分
期间等候时间累计共8分钟,则调价前后差▲元.
16.若某几何体的三视图如图所示,均是直角边长为1的等腰
直角三角形,则此几何体的体积是▲
17.甲、乙两人从4门课程中各选修2门,则甲、乙所选
的课程中恰有1门相同的概率为▲.
三、解答题:本大题共5小题,共72分,解答应写出文字说明、
证明过程或演算步骤.
18.(本题满分14分)在 中,角 、 、 所对应的
(II)设直线AP的斜率为 ,AQ的斜率为 ,
则直线AP的方程为
联立方程:
消去y,得: …………………………………………9分
同理,得 ………………………………………………12分
是一个与k无关的定值。………………………………………15分
22.(本小题满分15分)
解:(I)
…………………………………………………………………………………3分
边分别为 、 、 ,且满足
(I)求角C的值;
(II)若c=2,求 面积的最大值.
19.(本题满分14分)已知数列 ,数列 的前n项和为 ,满足
(I)求 的通项公式;
(II)试写出一个m,使得 是 中的项.
20.(本题满分14分)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC, , 、F分别为DB、CB的中点,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年新星学校温州中学提前招生模拟考试数 学 试 卷一、选择题:(每小题6分,共36分)1、若实数a 、b 、c 满足0a b c ++=,2abc =,0c >,则下列正确的是( ) A 、0ab < B 、||||2a b +≥ C 、||||4a b +> D 、0||||1a b <+≤2、一枚普通骰子被掷3次,若前两次所掷点数之和等于第3次的点数,则掷得点数至少有一次是2的概率是( )A 、61B 、158C 、21D 、1273、已知m 是质数,x 、y 均为整数,则方程||x y m +=的解的个数是( )A 、2B 、4C 、5D 、无数个4、已知一次函数y kx b =+的图像为直线l ,直线l 过点(2,1)P 且与,x y 轴的正半轴分别交于,A B 两点,若直线l 与x 、y 轴围成的三角形的面积为5,则这样的直线l 共有( )A 、1条B 、2条C 、3条D 、4条5、若干个棱长为2、3、5的长方体,依相同方向拼成棱长为90的正方体,则正方体的一条对角线贯穿的小长方体的个数是( ) A 、64 B 、66 C 、68 D 、706、已知实数,a b ,若a b >,22a b a b+=-ab 的最大值是( ) A 、1 B 、2 C 、2 D 、22 二、填空题:(每小题6分,共36分)7、已知=,且0x y <<,则满足上式的整数对(x ,y )有组。
8、在Rt △ABC 中,∠C=90O ,∠A >∠B ,12a b c +=,则sin 2A = 。
9、若抛物线222y x ax b =++-(其中a 、b 为实数)与x 轴交于相异的两点,其中一点的横坐标在0与1之间,另一点的横坐标在1与2之间,则41b a --的取值范围是 。
CQPD CBA10、如图,半圆O 的直径在梯形ABCD 的底边AB 上,且与其余三边BC ,CD ,DA 相切,若BC =3, DA =5,则AB 的长为 。
11、若关于x 的方程20ax +=与|1||2|20x x ---+=有三个相异的实数根,则常数a的取值范围是 。
12、如图,延长梯形ABCD 两腰DA 和CB 交于点P ,两对角线AC 和BD 交于点Q ,△PAB 和△QBC 的面积分别是20和6, 则△PCD 的面积是 。
三、解答题:(本题共有5个小题,共78分)13、(本题满分15分)把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数)。
设ij a (i 、j ∈N+)是位于这个三角形数表中从上往下数第i 行、从左往右数的第j 个数(如a 42=8)。
(1) 若a ij =2010,求i 、j 的值.(2) 记三角形数表从上往下数第n 行各数的和为b n ,令⎪⎩⎪⎨⎧≥-==2 ,1,1n nb n nc nn 。
若数列{}n c 的前n 项和为n T ,求n T 。
E FPDCBA14、(本题满分15分)如果对于正整数n ,n7的个位数用n a 表示,那么(1)求2010a 的值;(2)当n 为什么数时,n na n 22+-取得最大值,并求出这个最大值。
15、(本题满分15分)如图,过圆外一点P 作圆的两条切线PA 、PB ,A 、B 为切点,再过点P 作圆的一条割线分别交圆于点C 、D ,过点B 作PA 的平行线分别交直线AC 、AD 于点E 、F 。
求证:BE=BF 。
16、(本题满分15分)已知函数22(21)1y x m x m =+++-,其中m 为实数。
(1)当m 是什么数值时,y 有最小值为0?(2)求证:不论m 是什么数值时,抛物线的顶点都在同一直线l 上;(3)求证:任何一条平行于l 而与抛物线相交的直线被各抛物线截出的线段都相等。
17、(本题满分18分)将编号为1,2,…,18的18名乒乓球运动员分配在9张球台上进行单打比赛,规定每张球台上两选手编号之和均为大于4的平方数。
请问这一规定能否实现?若规定不能实现,请给出证明;若规定能够实现,请说明实现方案是否唯一。
2010年新星学校温州中学提前招生数学模拟试卷参考答案一、选择题:(每小题6分,共36分)1、B ∵0a b c ++= ∴a b c +=- ∵2abc =,0c > ∴0a <,0b < 考虑特殊值法,当1a b ==-,2c =时,有||||||2a b a b +≥+=,故选B 。
2、B 采用列表法或画树状图,前两次所掷点数之和等于第3次的点数共有15种可能,掷得点数至少有一次是2的有8种,概率为815,故选B 。
3、C ∵x y +与x y -2m = 于是有04x y x y +=⎧⎨-=⎩,11x y x y +=⎧⎨-=⎩,20x y x y +=⎧⎨-=⎩,11x y x y +=-⎧⎨-=⎩,2x y x y +=-⎧⎨-=⎩以上5个方程组均有整数解,故选C 。
4、B 由题意知,0k <,又直线l 过点(2,1)P ,代入y kx b =+得: 21k b +=,又∵(,),(,0)bA o bB k-,所以211()5221AOBb b S OA OB b k b ∆=⋅=-==- ∴2550b b -+=,b 有两个不等实根,∴直线l 共有2条,选B.5、B 由2,3,5的最小公倍数为30,由2,3,5组成的棱长为30的正方体的一条对角线穿过的长方体为整数个,所以由2,3,5组成棱长为90的正方体的一条对角线穿过的小长方体的个数应为3的倍数,选B 。
6、A 记a b x -=,ab t =,222()2a b a b ab a b a b +-+=--22x tx+==∴220x t -+=,24880b ac t ∆=-=-≥ ∴1t ≤仅当a b ==2,1a b ab -==成立,故选A. 二、填空题:(每小题6分,共36分)7、3 =∵0x y <<且x 、y 均为整数 ==∴7a b +=,且a b < ∴16a b =⎧⎨=⎩,25a b =⎧⎨=⎩,34a b =⎧⎨=⎩∴所求的整数对为(41,1476),(164,1025),(369,656)共3组。
8、12由已知得a b +=①,222a b c+=②,由①得b a =-③,代入②得2221)0a ca -=,∴a=,12a c =,∵A >B ∴a b > ∴2a =2a c =∴sin 2A = ∵0O <A <90O ∴A=60O ∴sin2A =sin 30O =129、143212b a -<-< 根据题意,设两个相异的实根为12,x x ,且12012x x <<<<, 则1213x x a <+=-<,120222x x b <=-<。
于是有 31,12a b -<<-<<,也即有111, 342214b a <<--<-<---。
故有143212b a -<-<。
10、8 连结OC 、OD ,∵AOD COD BOC ABCD S S S S ∆∆∆++梯形=∴1111()2222r AB CD r AD r CD r BC +=⨯+⨯+⨯ ∴AB AD BC =+ ∵BC =3,DA =5, ∴8AB = 11、102a <<不妨设12y ax =+,2|1||2|2y x x =---+ ∵21(1)21(12)3(2)x y x x x <⎧⎪=-≤<⎨⎪≥⎩∵直线12y ax =+过点A (0,2),∴分析得出满足题意的两种极端情况如下:当直线过图中点B (2,3)时,223a +=得12a =当直线平行于x 轴时,由2y =可知0a =。
要使方程20ax +=与|1||2|20x x ---+=有三个相异的实数根。
即使直线12y ax =+与函数2|1||2|2y x x =---+的图像交于三个不同的点,·DCOBAQPD CBA则102a <<。
12、45 ∵AB ∥CD ,△QBC 的面积为6, ∴△QAD 的面积也为6 设△ABQ 的面积为x ,△CDQ 的面积为y ∵66y AQx CQ==∴36xy = ∵ABP ABC S PB S BC ∆∆=,DBP DBC S PB S BC∆∆=∴2020666x x y ++=++ ∴220206206(6)66(6)366x x x x xx y x y x x x++-++====++-+--- ∴2261200x x +-= ∴14x =,230x =-(不合题意,舍去) ∴△PCD 的面积为206645x y ++++=。
三、解答题:(本题共有5个小题,共78分) 13、(本题满分15分)(1)三角形数表中前n 行共有1+2+…+n=(1)2n n +个,即第i 行的最后一个数是(1)2i i +。
因此,使a ij = 2010的i 是不等式(1)2i i +≥2010的最小正整数解。
因为62632⨯=1953,而63642⨯=2016,所以i=63。
于是,第63行的第一个数是62632⨯+1=1954。
故j=(2010-1 954)+1=57。
(2)前n 行的所有自然数的和为Sn=]12)1([2)1(21+++⨯n n n n =82)n 1)(n n(n 2+++。
则21(1)2n n n n n b S S -+=-=,所以当n ≥2时,c n =1111+--=-n n n b n n , ∴n T =11125+--n n 。
14(本题满分15分)解:(1)∵17a =,29a =,33a =,41a =,并且4n n a a +=,∴201029a a ==. (2)∵2222()n n n n na a n a -+=--当42n k ≠+时,n na n 22+-22780n a ≤≤<;当42n k =+时,22281(9)81180n n na n -+=--≤-=,仅当10n =时等号成立.∴当10n =时,n na n 22+-取得最大值80。
15、(本题满分15分)证明:如图,联结BC 、BA 、BD 。
所以∠ABC=∠PAC=∠E ,则△ABC ∽△AEB 。
从而,BE AB BC AC =,即AB BCBE AC⋅= ① 又∠ABF=∠PAB=∠ADB , ∴△ABF ∽△ADB ,从而BF AB BD AD =,即AB BDBF AD⋅= ②另一方面,又因△PBC ∽△PDB ,△PCA ∽△PAD ,∴BC PC BD PB =,AC PCAD PA=。
