第五讲-立体几何测试题
立体几何测试题

立体几何测试题一、选择题(每题3分,共15分)1. 在正方体ABCD-EFGH中,点M是棱AB的中点,点N是棱AD的中点,点P是棱CD上的点,且DP:PC=1:2。
求线段MN与MP所成角的余弦值。
A. 1/3B. √2/3C. √3/3D. 2/32. 已知圆锥的底面半径为r,高为h,求圆锥的侧面展开图的扇形半径。
A. rB. hC. √(r² + h²)D. 2πr3. 一个球的体积为V,求该球的表面积。
A. 3VB. 4πVC. 6VD. 4π(3V/π)^(2/3)4. 已知三棱锥P-ABC的四个顶点均在同一个球面上,且PA=PB=PC=4,AB=6,AC=BC=2√3,求球的半径。
A. 2B. 4C. 2√3D. 35. 一个正四面体的顶点都在一个球面上,且正四面体的边长为a,求球的半径。
A. a/√2B. a/2C. √3a/4D. a/√3二、填空题(每题4分,共20分)6. 若一个长方体的长、宽、高分别为l、w、h,则其对角线的长度为_________。
7. 已知一个圆柱的底面半径为r,高为h,求圆柱的体积,其体积为_________。
8. 若一个圆锥的底面半径为r,高为h,求圆锥的体积,其体积为_________。
9. 已知一个球的直径为d,求球的表面积,其表面积为_________。
10. 若一个正三棱柱的底面边长为a,高为h,求其体积,其体积为_________。
三、简答题(每题10分,共30分)11. 描述如何使用向量法证明两个平面的垂直性。
12. 给出一个球面上四点构成的四面体的体积公式。
13. 解释何为“内接球”和“外接球”,并给出一个几何体的内接球和外接球的半径计算方法。
四、计算题(每题15分,共30分)14. 已知一个正十二面体的边长为a,求其体积。
15. 已知一个圆锥的底面半径为r,高为h,求圆锥的内接球的半径。
五、证明题(15分)16. 证明:在一个正四面体中,从一个顶点出发的三条棱的中点,这四个点构成一个正四面体。
立体几何练习题含答案

立几测001试一、选择题:1.a 、b 是两条异面直线,以下结论正确的选项是〔 〕A .过不在a 、b 上的任一点,可作一个平面与a 、b 都平行B .过不在a 、b 上的任一点,可作一条直线与a 、b 都相交C .过不在a 、b 上的任一点,可作一条直线与a 、b 都平行D .过a 可以且只可以作一个平面与b 平行2.空间不共线的四点,可以确定平面的个数为 ( )A.0 B.1 C.1或4 D.无法确定3.在正方体1111ABCD A B C D -中,M 、N 分别为棱1AA 、1BB 的中点,则异面直线CM 和1D N 所成角的正弦值为 ( ) A.19 B.23C.459 D.2594.平面α⊥平面β,m 是α的一直线,n 是β的一直线,且m n ⊥,则:①m β⊥;②n α⊥;③m β⊥或n α⊥;④m β⊥且n α⊥。
这四个结论中,不正确...的三个是 ( )A.①②③B.①②④C.①③④D.②③④5.一个简单多面体的各个面都是三角形,它有6个顶点,则这个简单多面体的面数是( ) A. 4 B.5 C. 6 D. 86. 在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地最短距离为〔设地球半径为R 〕( )A.R π42B.R 3πC.R 2πD.3R7. 直线l ⊥平面α,直线m ⊂平面β,有以下四个命题(1)m l ⊥⇒βα//(2)m l //⇒⊥βα(3)βα⊥⇒m l //(4)βα//⇒⊥m l 其中正确的命题是( )A. (1)与(2)B. (2)与(4)C. (1)与(3)D. (3)与(4)8. 正三棱锥的侧面均为直角三角形,侧面与底面所成角为α,则以下不等式成立的是( ) A.60πα<< B.46παπ<< C.34παπ<< D.23παπ<<9.ABC ∆中,9AB =,15AC =,120BAC ∠=︒,ABC ∆所在平面α外一点P 到点A 、B 、C 的距离都是14,则P 到平面α的距离为( )A.7 B.9 C.11 D.1310.在一个45︒的二面角的一个平面有一条直线与二面角的棱成角45︒,则此直线与二面角的另一个平面所成角的大小为 ( )A.30︒ B.45︒ C.60︒ D.90︒11. 如图,E, F 分别是正方形SD 1DD 2的边D 1D,DD 2的中点, 沿SE,SF,EF 将其折成一个几何体,使D 1,D,D 2重合,记作 D.给出以下位置关系:①SD ⊥面DEF; ②SE ⊥面DEF; ③DF ⊥SE; ④EF ⊥面SED,其中成立的有: ( )A. ①与② B. ①与③ C. ②与③ D. ③与④12. *地球仪的北纬60度圈的周长为6πcm,则地球仪的外表积为( )A. 24πcm 2B. 48πcm 2C.144πcm 2D. 288πcm 2二、填空题〔本大题共4小题,每题4分,共16分〕13. 直二面角α—MN —β中,等腰直角三角形ABC 的斜边BC ⊂α,一直角边AC ⊂β,BC 与β所成角的正弦值是46,则AB 与β所成角大小为__________。
立体测试题及答案

立体测试题及答案一、单项选择题(每题2分,共10题)1. 下列哪个选项是立体几何中的基本元素?A. 点B. 线C. 面D. 体答案:D2. 空间中两条直线的位置关系有几种?A. 1种B. 2种C. 3种D. 4种答案:C3. 一个立方体有多少个顶点?A. 6B. 8C. 12D. 14答案:B4. 一个正四面体有多少条棱?A. 6B. 8C. 12D. 16答案:A5. 空间直角坐标系中,点(1,2,3)到原点的距离是多少?A. 1B. 2C. 3D. √14答案:D6. 一个球体的表面积公式是?A. 4πr²B. 2πr²C. πr²D. 4πr³答案:A7. 空间中两个平面的位置关系有哪些?A. 平行B. 相交C. 重合D. 以上都是答案:D8. 一个圆柱体的体积公式是?A. πr²hB. 2πrhC. πr²D. πr³答案:A9. 空间中一个点到一个平面的距离公式是?A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |Ax + By + Cz + D| / √(A² + B²)D. |Ax + By + Cz - D| / √(A² + B²)答案:B10. 空间中一个点到一条直线的距离公式是?A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |(Ax + By + Cz + D) / (A² + B² + C²)| * √(A² + B²)D. |(Ax + By + Cz - D) / (A² + B² + C²)| * √(A² + B²)答案:D二、多项选择题(每题3分,共5题)1. 空间中两个平面相交,它们的交线是?A. 直线B. 曲线C. 点D. 面答案:A2. 空间中一个点到一个平面的距离公式中,A、B、C、D分别代表什么?A. 平面方程的系数B. 平面方程的常数项C. 点的坐标D. 点到平面的距离答案:A, B3. 空间直角坐标系中,点(1,2,3)到点(4,5,6)的距离公式是?A. √((4-1)² + (5-2)² + (6-3)²)B. √((1-4)² + (2-5)² + (3-6)²)C. √((4-1)² + (5-2)² + (6-3)²)D. √((1-4)² + (2-5)² + (3-6)²)答案:A, B4. 空间中一个点到一条直线的距离公式中,A、B、C、D分别代表什么?A. 直线方程的系数B. 直线方程的常数项C. 点的坐标D. 点到直线的距离答案:A, C5. 空间中一个平面的方程可以表示为?A. Ax + By + Cz + D = 0B. Ax + By + Cz = DC. Ax + By + Cz + D = ED. Ax + By + Cz = 0答案:A, D结束语:以上是立体测试题及答案的全部内容,希望对你有所帮助。
立体几何考察试题答案

立体几何考察试题答案一、选择题1. 若一个正方体的棱长为2cm,则其对角线的长度为?A. 2√2 cmB. 2√3 cmC. 4 cmD. √8 cm答案:B2. 一个圆锥的底面半径为5cm,高为12cm,其侧面展开图的圆心角为?A. 144°B. 216°C. 288°D. 360°答案:B3. 一个球的表面积为4πR²,其中R为球的半径。
若球的半径为3cm,则球的体积为?A. 9π cm³B. 12π cm³C. 18π cm³D. 27π cm³答案:D4. 在直角坐标系中,点A(2,3)和点B(5,8)之间的距离为?A. √10 cmB. √26 cmC. √58 cmD. 10 cm答案:B5. 一个圆柱的底面半径为r,高为h,若将其沿高剖开,得到的长方形的面积为?A. 2πrhB. πr² + h²C. 2πr²D. πr²h答案:A二、填空题1. 一个正四面体的体积V与其边长a的关系为V=________。
答案:(a³/6√2)2. 一个圆台的上底半径为r,下底半径为R,高为h,其体积V为________。
答案:(1/3πh(R³ + R²r + r³))3. 一个球的半径为R,其表面积S为________。
答案:(4πR²)4. 在三维空间中,两点间的距离公式为________。
答案:(√((x2-x1)² + (y2-y1)² + (z2-z1)²))5. 一个锥体的体积V与其底面积A和高h的关系为V=________。
答案:(1/3Ah)三、解答题1. 请证明:在直角坐标系中,一个点P(x,y,z)到平面Ax + By + Cz+ D = 0的距离为|Ax + By + Cz + D|/√(A² + B² + C²)。
培优提升立体几何3

第五讲立体几何【例 1】(05年武汉明心杯数学挑战赛)如图所示,一个555⨯⨯的立方体,在一个方向上开有115⨯⨯的孔,在另一个方向上开有215⨯⨯的孔,在第三个方向上开有315⨯⨯的孔,剩余部分的体积是多少?表面积为多少?【解析】求体积:开了315⨯⨯的孔,挖去31515⨯⨯=,开了115⨯⨯的孔,挖去11514⨯⨯-=;开了215⨯⨯的孔,挖去215(22)6⨯⨯-+=,剩余部分的体积是:555(1546)100⨯⨯-++=.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:22412100⨯+=.求表面积:表面积能够看成外部和内部两部分.外部的表面积为55612138⨯⨯-=,内部的面积能够分为前后、左右、上下三个方向,面积分别为()22515121320⨯⨯+⨯-⨯-⨯=、()2153513132⨯⨯+⨯-⨯-=、()2151511214⨯⨯+⨯-⨯-=,所以总的表面积为138203214204+++=.(另解)使用类似于三视图的方法,记录每一方向上的不同位置上的裸露正方形个数:前后方向:32上下方向:30左右方向:40总表面积为()2323040204⨯++=.【总结】“切片法”:全面打洞(例如本题,五层一样),挖块成线(例如本题,在前一层的基础上,一条线一条线地挖),这里体现的思想方法是:化整为零,有序思考!【巩固】(2008年香港保良局第12届小学数学世界邀请赛)如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?【解析】对于这个类从立体图形中间挖掉一部分后再求体积(或小正方体数目)的题目一般第8题能够采用“切片法”来做,所谓“切片法”,就是把整个立体图形切成一片一片的(或一层一层的),然后分别计算每一片或每一层的体积或小正方体数目,最后再把它们相加.采用切片法,俯视第一层到第五层的图形依次如下,其中黑色部分表示挖除掉的部分.第1层第2层第3层第4层第5层从图中能够看出,第1、2、3、4、5层剩下的小正方体分别有22个、11个、11个、6个、22个,所以总共还剩下22111162272++++=(个)小正方体.【巩固】一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方体中相对的两面打通,右图就是抽空的状态.右图中剩下的小正方体有多少个?【解析】解法一:(用“容斥原理”5525⨯=个,由侧面图形抽出的小正方体有5525⨯=个,⨯=个,由底面图形抽出的小正方体有4520正面图形和侧面图形重合抽出的小正方体有1221228⨯+⨯+⨯=个,正面图形和底面图形重合抽出的小正方体有13227⨯+⨯=个,底面图形和侧面图形重合抽出的小正方体有1211227⨯+⨯+⨯=个,三个面的图形共同重合抽出的小正方体有4个.根据容斥原理,252520877452++---+=,所以共抽出了52个小正方体.1255273-=,所以右图中剩下的小正方体有73个.注意这里的三者共同抽出的小正方体是4个,必须知道是哪4块,这是最让人头疼的事.但你能够先构造空的两个方向上共同部分的模型,再由第三个方向来穿过“花墙”.这里,化虚为实的思想方法很重要.解法二:(用“切片法”来解)能够从上到下切五层,得:⑴从上到下五层,如图:⑵或者,从右到左五片,如图:请注意这里的挖空的技巧是:先认一种方向.比如:从上到下的每一层,首先都应该有第一层的空四块的情况,即——如果挖第二层:第(1)步,把中间这些位置的四块挖走如图:第(2)步,把从右向左的两块成线地挖走.(请注意挖通的效果就是成线挖去),如图:第(3)步,把从前向后的一块(请注意跟第二层相关的仅仅一块!)挖成线!如图:【例 2】(2009年迎春杯高年级组复赛)右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的倍.⑷⑶⑵⑴⑾⑽⑼⑻⑺⑹⑸【解析】本题中的两个图都是立体图形的平面展开图,将它们还原成立体图形,可得到如下两图:其中左图是以⑴⑵⑶⑷为平面展开图的立体图形,是一个四个面都是正三角形的正四面体,右图以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形,是一个不规则图形,底面是⑾,四个侧面是⑺⑻⑼⑽,两个斜面是⑸⑹. 对于这两个立体图形的体积,能够采用套模法来求,也就是对于这种我们不熟悉的立体图形,用一些我们熟悉的基本立体图形来套,看看它们与基本立体图形相比,缺少了哪些部分.因为左图四个面都是正三角形,右图底面是正方形,侧面是等腰直角三角形,想到都用正方体来套.对于左图来说,相当于由一个正方体切去4个角后得到(如下左图,切去1ABDA 、1CBDC 、111D AC D 、111B AC B );而对于右图来说,相当于由一个正方体切去2个角后得到(如下右图,切去1BACB 、1DACD ).D 1C 1B 1A 1D CBAABCDA 1B 1C 1D 1假设左图中的立方体的棱长为a ,右图中的立方体的棱长为b ,则以⑴⑵⑶⑷为平面展开图的立体图形的体积为:3231114233a a a a -⨯⨯⨯=,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积为3231122233b b b b -⨯⨯⨯=.因为右图中的立方体的棱长即是题中正方形⑾的边长,而左图中的立方体的每一个面的对角线恰好是正三角形⑴的边长,通过将等腰直角三角形⑺分成4个相同的小等腰直角三角形能够得到右图中的立方体的棱长是左图中的立方体的棱长的2倍,即2b a =.那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积的比为:()33331212::21:163333a b a a =⨯=,也就是说以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16倍.【例 3】 图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?图⑴图⑵【解析】首先,我们把展开图折成立体图形,见下列示意图:图⑴图⑵对于这类题目,一般采用“套模法”,即用一个我们熟悉的基本立体图形来套,这样做基于两点考虑,一是如果有类似的模型,可以直接应用其计算公式;二是如果可以补上一块或者放到某个模型里面,那么可以从这个模型入手.我们把图⑴中的立体图形切成两半,再转一转,正好放进去!我们看到图⑴与图⑶的图形位置的微妙关系:1和图3一致!60°图⑶图⑷由图⑷可见,图⑴这个立体的体积与图⑶这个被切去了8个角后的立体图形的体积相等.假设立方体的1条边的长度是1,那么一个角的体积是1111112222348⨯⨯⨯⨯=,所以切掉8个角后的体积是1518486-⨯=.再看图⑵中的正四面体,这个正四面体的棱长与图⑶中的每一条实线线段相等,所以应该用边长为12的立方体来套.如果把图⑵的立体图形放入边长为12的立方体里的话是可以放进去的.12这是切去了四个角后的图形,从上面的分析可知一个角的体积为148,所以图⑵的体积是:1111142224824⨯⨯-⨯=,那么前者的体积是后者的5120624÷=倍.【例 4】。
小学奥数-立体几何-题库学生版

第五讲 几何——立体部分教学目标:对于小学几何而言,立体图形的表面积和体积计算,既可以很好地考查学生的空间想象能力,又可以具体考查学生在公式应用中处理相关数据的能力,所以,很多重要考试都很重视对立体图形的考查.知识点拨:一、长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED CBA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥例题精讲:【例 1】 如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?【例 2】 右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l 厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)【巩固】在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【例 3】 下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 4】 一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?【巩固】(2008年走美六年级初赛)一个表面积为256cm 的长方体如图切成27个小长方体,这27个小长方体表面积的和是 2cm .【例 5】 如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?25块积木【例 6】 要把12件同样的长a 、宽b 、高h 的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?⑴当b=2h时,如何打包?⑵当b<2h时,如何打包?⑶当b>2h时,如何打包?【巩固】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?【例 7】如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.【例 8】(2008年“希望杯”五年级第2试)如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.【例 9】把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?【例 10】有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.【例 11】棱长是m厘米(m为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为13:12,此时m的最小值是多少?【例 12】有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个444⨯⨯的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?【例 13】三个完全一样的长方体,棱长总和是288厘米,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,给这三个长方体涂色,一个涂一面,一个涂两面,一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体,只有一个面涂色的小正方体最少有多少个?【例 14】把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?【例 15】把正方体的六个表面都划分成9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?【例 16】一个长、宽、高分别为21厘米、15厘米、12厘米的长方形.现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?【例 17】有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标A的为黑色,图中共有黑色积木多少块?A【巩固】这个图形,是否能够由112⨯⨯的长方体搭构而成?【巩固】有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少?33223323322323111111【例 18】 (05年武汉明心杯数学挑战赛)如图所示,一个555⨯⨯的立方体,在一个方向上开有115⨯⨯的孔,在另一个方向上开有215⨯⨯的孔,在第三个方向上开有315⨯⨯的孔,剩余部分的体积是多少?表面积为多少?【巩固】(2008年香港保良局第12届小学数学世界邀请赛)如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?第8题【巩固】一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方【例 19】 (2009年迎春杯高年级组复赛)右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的 倍.⑷⑶⑵⑴ ⑾⑽⑼⑻⑺⑹⑸【例 20】 图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?图⑴ 图⑵【例 21】 如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.5【例 22】 有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【例 23】 (第四届希望杯2试试题)圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是________立方厘米.(结果用π表示)【例 24】 如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.(π 3.14=)【巩固】如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?(π 3.14=)【例 25】 把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米.原来的圆柱体的体积是多少立方厘米?【例 26】 一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? (π 3.14=)【例 27】 (2008年”希望杯”五年级第2试)一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是_______ 立方厘米.(π取3.14)(单位:厘米)【巩固】一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米;瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?【巩固】一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(如下图所示),请你根据图中标明的数据,计算瓶子的容积是______.7cm4cm5cm【例 28】一个盛有水的圆柱形容器,底面内半径为5厘米,深20厘米,水深15厘米.今将一个底面半径为2厘米,高为17厘米的铁圆柱垂直放入容器中.求这时容器的水深是多少厘米?【例 29】有甲、乙两只圆柱形玻璃杯,其内直径依次是10厘米、20厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?【例 30】如图,甲、乙两容器相同,甲容器中水的高度是锥高的13,乙容器中水的高度是锥高的23,比较甲、乙两容器,哪一只容器中盛的水多?多的是少的的几倍?甲乙【例 31】(2008年仁华考题)如图,有一卷紧紧缠绕在一起的塑料薄膜,薄膜的直径为20厘米,中间有一直径为8厘米的卷轴,已知薄膜的厚度为0.04厘米,则薄膜展开后的面积是平方米.20cm8cm100cm【巩固】图为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多长?【例 32】如图,ABC是直角三角形,AB、AC的长分别是3和4.将ABC∆绕AC旋转一周,求ABC∆扫出的立体图形的体积.(π 3.14=)CBA43【例 33】 已知直角三角形的三条边长分别为3cm ,4cm ,5cm ,分别以这三边轴,旋转一周,所形成的立体图形中,体积最小的是多少立方厘米?(π取3.14)【巩固】如图,直角三角形如果以BC 边为轴旋转一周,那么所形成的圆锥的体积为16π,以AC 边为轴旋转一周,那么所形成的圆锥的体积为12π,那么如果以AB 为轴旋转一周,那么所形成的几何体的体积是多少?ABC【例 34】 如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD 相交O .E 、F 分别是AD 与BC的中点,图中的阴影部分以EF 为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米?(π取3)ABAB【巩固】(2006年第十一届华杯赛决赛试题)如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD相交O .图中的阴影部分以CD 为轴旋转一周,则阴影部分扫出的立体的体积是多少立方厘米?B A【例 35】 (人大附中分班考试题目)如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下底面的洞口是直径为4厘米的圆,求此立体图形的表面积和体积.课后练习练习1.(《小学生数学报》邀请赛)从一个棱长为10厘米的正方形木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少?(写出符合要求的全部答案)练习2.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm.把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm.酒瓶的容积是多少?(π取3)302515练习3.如右图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是多少平方米?练习4.(2008年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)一个圆柱体形状的木棒,沿着底面直径竖直切成两部分.已知这两部分的表面积之和比圆柱体的表面积大22008cm,则这个圆柱体木棒的侧面积是________2cm.(π取3.14)第2题练习5.如图,厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是180厘米,内直径是50厘米.这卷铜版纸的总长是多少米?月测备选【备选1】如右图,一个正方体形状的木块,棱长l米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大大小小的长方体60块.那么,这60块长方体表面积的和是多少平方米?【备选2】一个透明的封闭盛水容器,由一个圆柱体和一个圆锥体组成,圆柱体的底面直径和高都是12厘米.其内有一些水,正放时水面离容器顶11厘米,倒放时水面离顶部5厘米,那么这个容器的容积是多少立方厘米?(π3)5cm11cm【备选3】如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?【备选4】一个圆柱体底面周长和高相等.如果高缩短4厘米,表面积就减少50.24平方厘米.求这个圆柱体的表面积是多少?4cm【备选5】(2009年”希望杯”一试六年级)如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水升.。
立体几何测试题带答案解析
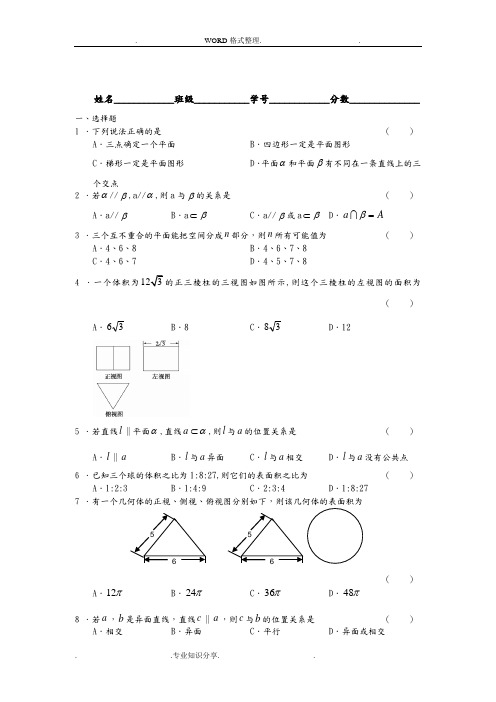
姓名____________班级___________学号____________分数______________一、选择题1 .下列说法正确的是( )A .三点确定一个平面B .四边形一定是平面图形C .梯形一定是平面图形D .平面α和平面β有不同在一条直线上的三个交点2 .若α//β,a//α,则a 与β的关系是( )A .a//βB .a β⊂C .a//β或a β⊂D .A a =β3 .三个互不重合的平面能把空间分成n 部分,则n 所有可能值为( )A .4、6、8B .4、6、7、8C .4、6、7D .4、5、7、84 .一个体积为123的正三棱柱的三视图如图所示,则这个三棱柱的左视图的面积为( )A .36B .8C .38D .125 .若直线l ∥平面α,直线a α⊂,则l 与a 的位置关系是( )A .l ∥aB .l 与a 异面C .l 与a 相交D .l 与a 没有公共点6 .已知三个球的体积之比为1:8:27,则它们的表面积之比为( )A .1:2:3B .1:4:9C .2:3:4D .1:8:27 7 .有一个几何体的正视、侧视、俯视图分别如下,则该几何体的表面积为( )A .π12B .π24C .π36D .π488 .若a ,b 是异面直线,直线c ∥a ,则c 与b 的位置关系是( )A .相交B .异面C .平行D .异面或相交65659 .设正方体的棱长为233,则它的外接球的表面积为 ( )A .π38B .2πC .4πD .π3410.已知一个全面积为44的长方体,且它的长、宽、高的比为3: 2:1,则此长方体的外接球的表面积为A .π7B .π14C .π21D .π2811.1l ,2l ,3l 是空间三条不同的直线,则下列命题正确的是( )A .12l l ⊥,23l l ⊥13//l l ⇒B .12l l ⊥,23//l l ⇒13l l ⊥C .233////l l l ⇒ 1l ,2l ,3l 共面D .1l ,2l ,3l 共点⇒1l ,2l ,3l 共面12.如图,正方体1111ABCDA B C D 中,E ,F分别为棱AB ,1CC 的中点,在平面11ADD A 内且与平面1D EF 平行的直线 ( ) A .有无数条 B .有2条C .有1条 D .不存在二、填空题13.已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸,计算这个几何体的表面积是______.14.如图,在正方体1111ABCD A B C D -中,点P 是上底面1111A B C D 内ABCD A 1 B 1C 1D 1EF一动点,则三棱锥P ABC -的主视图与左视图的面积的比值 为_________.15.如图,正方体1111ABCD A B C D -中,2AB =,点E 为AD 的1AB C ,中点,点F 在CD 上,若//EF 平面则EF =________.16.一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:(1)三角形;(2)矩形;(3)正方形;(4)正六边形.其中正确的结论是____________.(把你认为正确的序号都填上)三、解答题17.如图1,空间四边形ABCD 中,E ,H 分别是边AB ,AD 的中点,F ,G 分别是边BC ,CD 上的点,且32==CD CG CB CF ,求证:直线EF ,GH ,AC 交于一点.18.如果一个几何体的主视图与左视图都是全等的长方形,边长分别是4cm 与2cm 如图所示,俯视图是一个边长为4cm 的正方形. (1)求该几何体的全面积.(2)求该几何体的外接球的体积.PDC B A 1A 1D 1B 1C 左视主视AB C D EF 1A 1B 1C 1D 图119.空间四边形ABCD 的对角线AC=8,BD=6,M 、N 分别为AB 、CD 的中点,MN=5,求异面直线AC 与BD 所成的角20.已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形. (1)求该几何体的体积V ; (2)求该几何体的侧面积S .21.如图,四棱柱1111ABCD A B C D -中,底面ABCD 是正方形,侧棱1A A ⊥底面ABCD ,E为1A A 的中点.求证:1AC ∥平面EBD .ABCDNM 俯视图主视图左视图4224422.如图是一个长方体截去一个角所得的多面体的直观图及它的正(主)视图和侧(左)视图(单位:cm).(I)画出该多面体的俯视图;(Ⅱ)按照给出的尺寸,求该多面体的体积;(Ⅲ)在所给直观图中连结'BC ,证明:'BC ∥平面EFG .直观图E正视图AB B 1A 1 CC 1ED 1 D全国卷设置参考答案一、选择题 1. C 2. C 3. B 4. A 5. D 6. B 7. B 8. D 9. D 10. D 11.答案:B解析:A 答案还有异面或者相交,C 、D 不一定 12. A二、填空题 13. 11π 14. 116. (2),(3),(4) 三、解答题17.提示:FG EH //且FG EH≠,四边形EFGH 为梯形.设EF 与GH 交于点P ,证∈P (平面 ABC 平面DAC ). 18.解:(1)由题意可知,该几何体是长方体,底面是正方形,边长是4,高是2,因此该 几何体的全面积是:2×4×4+4×4×2=64cm2几何体的全面积是64cm 2..6(2)由长方体与球的性质可得,长方体的对角线是球的直径,记长方体的对角线为d,球的半径是r,d=63641616==++所以球的半径r=3因此球的体积v=3336273434cm r πππ=⨯=, 所以外接球的体积是336cm π 1219.解:取AD 的中点Q,连接MQ 、NQ又∵M、N 分别是AB 、CD 的中点 ∴MQ∥BD,NQ∥AC 且AC NQ BD MQ 21,21==∴∠MQ N 为异面直线AC 与BD 所成角或补角又AC=8,BD=6,MN=5∴△MQN 中,MQ=3,NQ=4,MN=5即△MQN 为直角三角形且∠MQN=90° ∴异面直线AC 与BD 所成的角为90°20.参考答案:由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为1h 的等腰三角形,左、右侧面均为底边长为6,高为2h 的等腰三角形. (1)几何体的体积为为116846433V S h ==⨯⨯⨯=矩形. (2)正侧面及相对侧面底边上的高为:15h ==,左、右侧面的底边上的高为:2h ==故几何体的侧面面积为:S = 2×(12×8×5+12)40=+考查内容:简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,三视图所表示的立体模型,球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式) 认知层次:b 难易程度:中21.参考答案:连接AC ,设ACBD F =,连接EF ,因为底面ABCD 是正方形, 所以F 为AC 的中点. 又E 为1A A 的中点,所以EF 是△1A AC 的中位线. 所以EF ∥1A C .因为EF ⊂平面EBD ,1A C ⊄平面EBD , 所以1A C ∥平面EBD .考查内容:直线与平面平行的判定定理,空间图形的位置关系的简单命题 认知层次:c 难易程度:中ABB 1A 1 C C 1 ED 1 D F22.解:(Ⅰ)如图俯视图(Ⅱ)所求多面体体积V V V =-长方体正三棱锥1144622232⎛⎫=⨯⨯-⨯⨯⨯⨯ ⎪⎝⎭3284(cm )3=(Ⅲ)证明:在长方体ABCD A B C D ''''-中, 连结AD ',则AD BC ''∥.因为E G ,分别为AA ',A D ''中点, 所以AD EG '∥,从而EG BC '∥.又BC '⊄平面EFG , 所以BC '∥平面EFGABC DE FGA 'B 'C 'D '。
立体几何练习题及解析

立体几何练习题及解析一、选择题1. 下列哪个是正方体?A. 圆柱体B. 球体C. 锥体D. 正四面体解析:正确答案为D。
正四面体是一个具有四个等边三角形面的多面体,也是一种立体几何体。
2. 以下哪个是圆锥体?A. 立方体B. 正方形C. 圆柱体D. 球体解析:正确答案为C。
圆柱体的两个底面都是同心圆,且高度与底面的半径相等。
3. 以下哪个不是球体的属性?A. 没有棱B. 没有边C. 没有顶点D. 没有底面解析:正确答案为D。
球体没有底面,它是由无数个相同半径的小球面组成的。
二、填空题1. 立方体有多少个面?解析:立方体有6个面。
2. 锥体有多少个顶点?解析:锥体有1个顶点。
3. 正四面体有多少个边?解析:正四面体有6个边。
三、计算题1. 一个圆柱体的底面半径为5 cm,高度为8 cm,计算其体积和表面积。
解析:圆柱体的体积公式为V = πr²h,表面积公式为S = 2πrh + 2πr²。
将底面半径r = 5 cm,高度h = 8 cm代入公式计算得:V = π(5)²(8) = 200π cm³S = 2π(5)(8) + 2π(5)² = 80π + 50π = 130π cm²2. 一个球体的半径为10 cm,计算其体积和表面积。
解析:球体的体积公式为V = (4/3)πr³,表面积公式为S = 4πr²。
将半径r = 10 cm代入公式计算得:V = (4/3)π(10)³ = 4000π/3 cm³S = 4π(10)² = 400π cm²3. 一个正方体的边长为6 cm,计算其体积和表面积。
解析:正方体的体积公式为V = a³,表面积公式为S = 6a²。
将边长a = 6 cm代入公式计算得:V = 6³ = 216 cm³S = 6(6)² = 216 cm²四、解答题1. 画出一个平行六面体,其中底面是边长为4 cm的正方形,高度为6 cm。
2022届高考数学一轮复习第8章立体几何第5讲空间角与距离空间向量及应用作业试题2含解析新人教版

第五讲空间角与距离、空间向量及应用1.[2020湖北部分重点中学高三测试]如图8-5-1,E,F分别是三棱锥P-ABC的棱AP,BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )图8-5-1A.30°B.60°C.120°D.150°2.[2020湖南长沙市长郡中学模拟]图8-5-2中的三个正方体ABCD-A1B1C1D1中,E,F,G均为所在棱的中点,过E,F,G 作正方体的截面.下列各选项中,关于直线BD1与平面EFG的位置关系描述正确的是( )图8-5-2∥平面EFG的有且只有①,BD1⊥平面EFG的有且只有②③1∥平面EFG的有且只有②,BD1⊥平面EFG的有且只有①1∥平面EFG的有且只有①,BD1⊥平面EFG的有且只有②1∥平面EFG的有且只有②,BD1⊥平面EFG的有且只有③13.[多选题]如图8-5-3,正方体ABCD-A1B1C1D1的棱长为1,则以下说法正确的是( )图8-5-31D1所成的角等于π4B.点C到平面ABC1D1的距离为√221C和BC1所成的角为π41D1-BB1C1的外接球的半径为√324.[2019吉林长春质量监测][双空题]已知正方体ABCD-A1B1C1D1的棱长为2,M,N,E,F分别是A1B1,AD,B1C1,C1D1的中点,则过EF且与MN平行的平面截正方体所得截面的面积为,CE 和该截面所成角的正弦值为.5.[2021广州市阶段模拟]如图8-5-4,在四棱锥E-ABCD中,底面ABCD为菱形,BE⊥平面ABCD,G为AC与BD的交点.(1)证明:平面AEC⊥平面BED.(2)若∠BAD=60°,AE⊥EC,求直线EG与平面EDC所成角的正弦值.图8-5-46.[2021晋南高中联考]如图8-5-5,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD,PA⊥PD,∠PAD=60°,Q为PD的中点.(1)证明:CQ∥平面PAB.(2)求二面角P-AQ-C的余弦值.图8-5-57.[2021湖南六校联考]如图8-5-6,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=2a,AD=√2a,点E是SD 上的点,且DE=λa(0<λ≤2).(1)求证:对任意的λ∈(0,2],都有AC⊥BE.(2)设二面角C-AE-D的大小为θ,直线BE与平面ABCD所成的角为φ,若sin φ=cos θ,求λ的值.图8-5-68.[2020福建五校联考]图8-5-7是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,⏜上的动点(不与B1,A1重合).且AC⊥BC,P为B1A1(1)证明:PA1⊥平面PBB1.,求二面角P-A1B1-C的余弦值.(2)若四边形ABB1A1为正方形,且AC=BC,∠PB1A1=π4图8-5-79.[2020全国卷Ⅱ,12分]如图8-5-8,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F.(2)设O为△A1B1C1的中心.若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.图8-5-810.[2021黑龙江省六校联考]如图8-5-9,正方形ABCD和ABEF所在的平面互相垂直,且边长都是1,M,N,G分别为线段AC,BF,AB上的动点,且CM=BN,AF∥平面MNG,记BG=a(0<a<1).(1)证明:MG⊥平面ABEF.(2)当MN的长度最小时,求二面角A-MN-B的余弦值.图8-5-911.[2021蓉城名校联考]如图8-5-10(1),AD是△BCD中BC边上的高,且AB=2AD=2AC,将△BCD沿AD翻折,使得平面ACD⊥平面ABD,如图8-5-10(2)所示.(1)求证:AB⊥CD.时,求直线AE与平面BCE (2)在图8-5-10(2)中,E是BD上一点,连接AE,CE,当AE与底面ABC所成角的正切值为12所成角的正弦值.图8-5-1012.[2020洛阳市联考]如图8-5-11,底面ABCD是边长为3的正方形,平面ADEF⊥平面ABCD,AF∥DE,AD⊥DE,AF=2√6,DE=3√6.(1)求证:平面ACE⊥平面BED.(2)求直线CA与平面BEF所成角的正弦值.的值;若不存在,请说明理由. (3)在线段AF上是否存在点M,使得二面角M-BE-D的大小为60°?若存在,求出AMAF图8-5-1113.如图8-5-12,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,平面α经过棱PC的中点E,与棱PB,AC分别交于点F,D,且BC∥平面α,PA∥平面α.(1)证明:AB⊥平面α.(2)若AB=BC=PA=2,点M在直线EF上,求平面MAC与平面PBC所成锐二面角的余弦值的最大值.图8-5-1214.[2021安徽江淮十校第一次联考]如图8-5-13(1),已知圆O的直径AB的长为2,上半圆弧上有一点C,∠COB=60°,点P是弧AC上的动点,点D是下半圆弧的中点.现以AB为折痕,使下半圆所在的平面垂直于上半圆所在的平面,连接PO,PD,PC,CD,如图8-5-13(2)所示.(1)当AB∥平面PCD时,求PC的长;(2)当三棱锥P-COD体积最大时,求二面角D-PC-O的余弦值.图8-5-13答案第四讲直线、平面垂直的判定及性质1.B 如图D 8-5-8,取AC的中点D,连接DE,DF,因为D,E,F分别为AC,PA,BC的中点,所以DF∥AB,DF=12AB,DE∥PC,DE=12PC,所以∠EDF或其补角为异面直线PC与AB所成的角.因为PC=10,AB=6,所以在△DEF中,DE=5,DF=3,EF=7,由余弦定理得cos∠EDF=DE2+DF2-EF22DE×DF =25+9−492×5×3=-12,所以∠EDF=120°,所以异面直线PC与AB所成的角为60°.故选B.图D 8-5-82.A 对于题图①,连接BD,因为E,F,G均为所在棱的中点,所以BD∥GE,DD1∥EF,又BD⊄平面EFG,DD1⊄平面EFG,从而可得BD∥平面EFG,DD1∥平面EFG,又BD∩DD1=D,所以平面BDD1∥平面EFG,所以BD1∥平面EFG.对于题图②,连接DB,DA 1,设正方体的棱长为1,因为E,F,G 均为所在棱的中点,所以BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·GE ⃗⃗⃗⃗⃗ =(DD 1⃗⃗⃗⃗⃗⃗⃗⃗ -DB ⃗⃗⃗⃗⃗⃗ )·(12DA 1⃗⃗⃗⃗⃗⃗⃗⃗ )=12(DD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·DA 1⃗⃗⃗⃗⃗⃗⃗⃗ -DB ⃗⃗⃗⃗⃗⃗ ·DA 1⃗⃗⃗⃗⃗⃗⃗⃗ )=12(1×√2×cos 45°-√2×√2×cos 60°)=0, 即BD 1⊥EG.连接DC 1,则BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·EF ⃗⃗⃗⃗⃗ =(DD 1⃗⃗⃗⃗⃗⃗⃗⃗ -DB ⃗⃗⃗⃗⃗⃗ )·(12DC 1⃗⃗⃗⃗⃗⃗⃗ )=12(DD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·DC 1⃗⃗⃗⃗⃗⃗⃗ -DB ⃗⃗⃗⃗⃗⃗ ·DC 1⃗⃗⃗⃗⃗⃗⃗ )=12(1×√2×cos 45°-√2×√2×cos 60°)=0,即BD 1⊥EF. 又EG ∩EF=E,所以BD 1⊥平面EFG.对于题图③,设正方体的棱长为1,连接DB,DG,因为E,F,G 均为所在棱的中点,所以BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·EG ⃗⃗⃗⃗⃗ =(DD 1⃗⃗⃗⃗⃗⃗⃗⃗ -DB ⃗⃗⃗⃗⃗⃗ )·(DG ⃗⃗⃗⃗⃗ -DE ⃗⃗⃗⃗⃗ )=(DD 1⃗⃗⃗⃗⃗⃗⃗⃗ -DB ⃗⃗⃗⃗⃗⃗ )·(DC ⃗⃗⃗⃗⃗ +12DD 1⃗⃗⃗⃗⃗⃗⃗⃗ -12DA ⃗⃗⃗⃗⃗ )=12DD 1⃗⃗⃗⃗⃗⃗⃗⃗ 2-DB ⃗⃗⃗⃗⃗⃗ ·DC ⃗⃗⃗⃗⃗ +12DB ⃗⃗⃗⃗⃗⃗ ·DA ⃗⃗⃗⃗⃗ =12-√2×1×√22+12×√2×1×√22=0, 即BD 1⊥EG.连接AF,则BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·EF ⃗⃗⃗⃗⃗ =(DD 1⃗⃗⃗⃗⃗⃗⃗⃗ -DB ⃗⃗⃗⃗⃗⃗ )·(AF ⃗⃗⃗⃗⃗ -AE ⃗⃗⃗⃗⃗ )=(DD 1⃗⃗⃗⃗⃗⃗⃗⃗ -DB ⃗⃗⃗⃗⃗⃗ )·(DD 1⃗⃗⃗⃗⃗⃗⃗⃗ +12DC ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ )=DD 1⃗⃗⃗⃗⃗⃗⃗⃗ 2-12DB ⃗⃗⃗⃗⃗⃗ ·DC ⃗⃗⃗⃗⃗ -12DB ⃗⃗⃗⃗⃗⃗ ·DA ⃗⃗⃗⃗⃗ =1-12×√2×1×√22-12×√2×1×√22=0, 即BD 1⊥EF.又EG ∩EF=E,所以BD 1⊥平面EFG.故选A.3.ABD 正方体ABCD-A 1B 1C 1D 1的棱长为1,对于A,直线BC 与平面ABC 1D 1所成的角为∠CBC 1=π4,故A 正确;对于B,点C 到平面ABC 1D 1的距离为B 1C 长度的一半,即距离为√22,故B 正确;对于C,连接AC,因为BC 1∥AD 1,所以异面直线D 1C 和BC 1所成的角即直线D 1C 和AD 1所成的角,又△ACD 1是等边三角形,所以异面直线D 1C 和BC 1所成的角为π3,故C 错误;对于D,三棱柱AA 1D 1-BB 1C 1的外接球就是正方体ABCD-A 1B 1C 1D 1的外接球,正方体ABCD-A 1B 1C 1D 1的外接球半径r=√12+12+122=√32,故D 正确.故选ABD.√2√1010如图D 8-5-9,正方体ABCD-A 1B 1C 1D 1中,设CD,BC 的中点分别为H,G,连接HE,HG,GE,HF,ME,NH.图D 8-5-9易知ME ∥NH,ME=NH,所以四边形MEHN 是平行四边形,所以MN ∥HE.因为MN ⊄平面EFHG,HE ⊂平面EFHG,所以MN ∥平面EFHG,所以过EF 且与MN 平行的平面为平面EFHG,易知平面EFHG 截正方体所得截面为矩形EFHG,EF=√2,FH=2,所以截面EFHG 的面积为2×√2=2√2.连接AC,交HG 于点I,易知CI ⊥HG,平面EFHG ⊥平面ABCD,平面EFHG ∩平面ABCD=HG,所以CI ⊥平面EFHG,连接EI,因为EI ⊂平面EFHG,所以CI ⊥EI,所以∠CEI 为直线CE 和截面EFHG 所成的角.在Rt △CIE 中,易知CE=√1+22=√5,CI=14AC=2√24=√22,所以sin ∠CEI=CICE=√1010. 5.(1)因为四边形ABCD 为菱形,所以AC ⊥BD.因为BE ⊥平面ABCD,AC ⊂平面ABCD,所以AC ⊥BE.又BE ∩BD=B,所以AC ⊥平面BED.又AC ⊂平面AEC,所以平面AEC ⊥平面BED.(2)解法一 设AB=1,在菱形ABCD 中,由∠BAD=60°,可得AG=GC=√32,BG=GD=12.因为AE ⊥EC,所以在Rt △AEC 中可得EG=AG=√32.由BE ⊥平面ABCD,得△EBG 为直角三角形,则EG 2=BE 2+BG 2,得BE=√22.如图D 8-5-10,过点G 作直线Gz ∥BE,因为BE ⊥平面ABCD, 所以Gz ⊥平面ABCD,又AC ⊥BD,所以建立空间直角坐标系 G-xyz.G(0,0,0),C(0,√32,0),D(-12,0,0),E(12,0,√22),图D 8-5-10所以GE ⃗⃗⃗⃗⃗ =(12,0,√22),DE ⃗⃗⃗⃗⃗ =(1,0,√22),CE ⃗⃗⃗⃗⃗ =(12,-√32,√22). 设平面EDC 的法向量为n=(x,y,z),由{DE ⃗⃗⃗⃗⃗ ·n =0,CE ⃗⃗⃗⃗⃗ ·n =0,得{x +√22z =0,12x -√32y +√22z =0,取x=1,则z=-√2,y=-√33,所以平面EDC 的一个法向量为n=(1,-√33,-√2).设直线EG 与平面EDC 所成的角为θ,则sin θ=|cos<GE⃗⃗⃗⃗⃗ ,n>|=|12+0−1√14+12×√1+13+2|=|-12√32×√103|=√1010. 所以直线EG 与平面EDC 所成角的正弦值为√1010. 解法二 设BG=1,则GD=1,AB=2,AG=√3.设点G 到平面EDC 的距离为h,EG 与平面EDC 所成角的大小为θ.因为AC ⊥平面EBD,EG ⊂平面EBD,所以AC ⊥EG.因为AE ⊥EC,所以△AEC 为等腰直角三角形.因为AC=2AG=2√3,所以AE=EC=√6,EG=AG=√3.因为AB=BD=2,所以Rt △EAB ≌Rt △EDB,所以EA=ED=√6.在△EDC 中,ED=EC=√6,DC=2,则S △EDC =√5.在Rt △EAB 中,BE=√EA 2-AB 2=√(√6)2-22=√2.V E-GDC =13BE ·12S △CBD =16×√2×S △ABD =16×√2×12×2×√3=√66.由V G-EDC =13h ·√5=V E-GDC =√66,得h=√62√5=√3010.所以sin θ=ℎEG =√1010.所以直线EG 与平面EDC 所成角的正弦值为√1010.解法三 如图D 8-5-11,以点B 为坐标原点,建立空间直角坐标系B-xyz.图D 8-5-11不妨设AB=2,在菱形ABCD 中,由∠BAD=60°,可得AG=GC=√3,BG=GD=1.因为AE ⊥EC,所以在Rt △AEC 中可得EG=AG=√3.由BE ⊥平面ABCD,得△EBG 为直角三角形,则EG 2=BE 2+BG 2,得BE=√2.则C(2,0,0),E(0,0,√2),D(1,√3,0),G(12,√32,0), 所以EG ⃗⃗⃗⃗⃗ =(12,√32,-√2),ED ⃗⃗⃗⃗⃗ =(1,√3,-√2),EC ⃗⃗⃗⃗⃗ =(2,0,-√2). 设平面EDC 的法向量为n=(x,y,z), 则{n ·ED ⃗⃗⃗⃗⃗ =0,n ·EC ⃗⃗⃗⃗⃗ =0,得{x +√3y -√2z =0,2x -√2z =0,令x=√3,则z=√6,y=1.所以平面EDC 的一个法向量为n=(√3,1,√6).设EG 与平面EDC 所成的角为θ,则sin θ=|cos<EG⃗⃗⃗⃗⃗ ,n>|=|√32+√32-2√3|√1+2×√3+1+6=√1010. 所以直线EG 与平面EDC 所成角的正弦值为√1010. 6.(1)如图D 8-5-12,取PA 的中点N,连接QN,BN.图D 8-5-12∵Q,N 分别是PD,PA 的中点,∴QN ∥AD,且QN=12AD. ∵PA ⊥PD,∠PAD=60°,∴PA=12AD, 又PA=BC,∴BC=12AD,∴QN=BC,又AD ∥BC,∴QN ∥BC,∴四边形BCQN 为平行四边形,∴BN ∥CQ.又BN ⊂平面PAB,CQ ⊄平面PAB,∴CQ ∥平面PAB.(2)在图D 8-5-12的基础上,取AD 的中点M,连接BM,PM,取AM 的中点O,连接BO,PO,如图D 8-5-13.图D 8-5-13设PA=2,由(1)得PA=AM=PM=2,∴△APM 为等边三角形,∴PO ⊥AM,同理BO ⊥AM.∵平面PAD ⊥平面ABCD,平面PAD ∩平面ABCD=AD,PO ⊂平面PAD,∴PO ⊥平面ABCD.以O 为坐标原点,分别以OB ⃗⃗⃗⃗⃗ ,OD⃗⃗⃗⃗⃗⃗ ,OP ⃗⃗⃗⃗⃗ 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系O-xyz, 则A(0,-1,0),C(√3,2,0),P(0,0,√3),Q(0,32,√32), ∴AC⃗⃗⃗⃗⃗ =(√3,3,0),AQ ⃗⃗⃗⃗⃗ =(0,52,√32), 设平面ACQ 的法向量为m=(x,y,z),则{m ·AC⃗⃗⃗⃗⃗ =0,m ·AQ ⃗⃗⃗⃗⃗ =0,∴{√3x +3y =0,52y +√32z =0,取y=-√3,得m=(3,-√3,5)是平面ACQ 的一个法向量,又平面PAQ 的一个法向量为n=(1,0,0),∴cos<m,n>=m ·n|m|·|n|=3√3737, 由图得二面角P-AQ-C 的平面角为钝角,∴二面角P-AQ-C 的余弦值为-3√3737. 7.(1)由题意SD ⊥平面ABCD,AD ⊥DC,以D 为原点,DA ⃗⃗⃗⃗⃗ ,DC ⃗⃗⃗⃗⃗ ,DS ⃗⃗⃗⃗⃗ 的方向分别作为x,y,z 轴的正方向建立如图D 8-5-14所示的空间直角坐标系,图D 8-5-14则D(0,0,0),A(√2a,0,0),B(√2a,√2a,0),C(0,√2a,0),E(0,0,λa), ∴AC ⃗⃗⃗⃗⃗ =(-√2a,√2a,0),BE ⃗⃗⃗⃗⃗ =(-√2a,-√2a,λa), ∴AC ⃗⃗⃗⃗⃗ ·BE⃗⃗⃗⃗⃗ =2a 2-2a 2+0×λa=0, 即AC ⊥BE.(2)解法一 由(1)得EA ⃗⃗⃗⃗⃗ =(√2a,0,-λa),EC ⃗⃗⃗⃗⃗ =(0,√2a,-λa),BE ⃗⃗⃗⃗⃗ =(-√2a,-√2a,λa). 设平面ACE 的法向量为n=(x,y,z),则由n ⊥EA ⃗⃗⃗⃗⃗ ,n ⊥EC ⃗⃗⃗⃗⃗ 得 {n ·EA ⃗⃗⃗⃗⃗ =0,n ·EC ⃗⃗⃗⃗⃗ =0,得{√2x -λz =0,√2y -λz =0,取z=√2,得n=(λ,λ,√2)为平面ACE 的一个法向量,易知平面ABCD 与平面ADE 的一个法向量分别为DS⃗⃗⃗⃗⃗ =(0,0,2a)与DC ⃗⃗⃗⃗⃗ =(0,√2a,0), ∴sin φ=|DS ⃗⃗⃗⃗⃗ ·BE ⃗⃗⃗⃗⃗ ||DS⃗⃗⃗⃗⃗ |·|BE ⃗⃗⃗⃗⃗ |=√λ2+4,易知二面角C-AE-D 为锐二面角,∴cos θ=|DC⃗⃗⃗⃗⃗ ·n||DC⃗⃗⃗⃗⃗ |·|n|=√2λ2+2,由sin φ=cos θ得√λ2+4=√2λ2+2,解得λ2=2,又λ∈(0,2],∴λ=√2.解法二 如图D 8-5-15,连接BD,由SD ⊥平面ABCD 知,∠DBE=φ.图D 8-5-15由(1)易知CD ⊥平面SAD.过点D 作DF ⊥AE 于点F,连接CF,则∠CFD 是二面角C-AE-D 的平面角,即∠CFD=θ.在Rt △BDE 中,BD=2a,DE=λa,∴BE=√4a 2+λ2a 2,sin φ=DEBE =√λ2+4,在Rt △ADE 中,AD=√2a,DE=λa,∴AE=a √λ2+2,∴DF=AD ·DE AE=√2λa√λ2+2, 在Rt △CDF 中,CF=√DF 2+CD 2=2√λ2+1√λ2+2a,∴cos θ=DFCF =√2λ2+2,由sin φ=cos θ得√λ2+4=√2λ2+2,解得λ2=2,又λ∈(0,2],∴λ=√2.8.(1)在半圆柱中,BB 1⊥平面PA 1B 1,PA 1⊂平面PA 1B 1,所以BB 1⊥PA 1.因为A 1B 1是上底面对应圆的直径,所以PA 1⊥PB 1.因为PB 1∩BB 1=B 1,PB 1⊂平面PBB 1,BB 1⊂平面PBB 1,所以PA 1⊥平面PBB 1.(2)根据题意,以C 为坐标原点建立空间直角坐标系C-xyz,如图D 8-5-16所示.图D 8-5-16设CB=1,则C(0,0,0),A 1(0,1,√2),B 1(1,0,√2), 所以CA 1⃗⃗⃗⃗⃗⃗⃗ =(0,1,√2),CB 1⃗⃗⃗⃗⃗⃗⃗ =(1,0,√2).易知n 1=(0,0,1)为平面PA 1B 1的一个法向量. 设平面CA 1B 1的法向量为n 2=(x,y,z),则{n 2·CA 1⃗⃗⃗⃗⃗⃗⃗ =0,n 2·CB 1⃗⃗⃗⃗⃗⃗⃗ =0,即{y +√2z =0,x +√2z =0,令z=1,则x=-√2,y=-√2,所以n 2=(-√2,-√2,1)为平面CA 1B 1的一个法向量.所以cos<n 1,n 2>=1×√5=√55.由图可知二面角P-A 1B 1-C 为钝角,所以所求二面角的余弦值为-√55.9.(1)因为M,N 分别为BC,B 1C 1的中点,所以MN ∥CC 1.又由已知得AA 1∥CC 1,故AA 1∥MN.因为△A 1B 1C 1是正三角形,所以B 1C 1⊥A 11C 1⊥MN,故B 1C 1⊥平面A 1AMN.所以平面A 1AMN ⊥平面EB 1C 1F.(2)由已知得AM ⊥BC.以M 为坐标原点,MA ⃗⃗⃗⃗⃗⃗ 的方向为x 轴正方向,|MB ⃗⃗⃗⃗⃗⃗ |为单位长度,建立如图D 8-5-17所示的空间直角坐标系M-xyz,则AB=2,AM=√3.图D 8-5-17连接NP,则四边形AONP 为平行四边形,故PM=2√33,E(2√33,13,0).由(1)知平面A 1AMN ⊥平面ABC.作NQ ⊥AM,垂足为Q,则NQ ⊥平面ABC.设Q(a,0,0),则NQ=(2√331(a,1,(2√33故B 1E ⃗⃗⃗⃗⃗⃗⃗ =(2√33-a,-23,-√4−(2√33-a)2),|B 1E ⃗⃗⃗⃗⃗⃗⃗ |=2√103. 又n=(0,-1,0)是平面A 1AMN 的一个法向量,故 sin(π2- n,B 1E ⃗⃗⃗⃗⃗⃗⃗ )=cos n,B 1E ⃗⃗⃗⃗⃗⃗⃗ =n ·B 1E⃗⃗⃗⃗⃗⃗⃗⃗ |n|·|B 1E ⃗⃗⃗⃗⃗⃗⃗⃗ |=√1010.所以直线B 1E 与平面A 1AMN 所成角的正弦值为√1010. 10.(1)因为AF ∥平面MNG,且AF ⊂平面ABEF,平面ABEF ∩平面MNG=NG,所以AF ∥NG,所以CM=BN=√2a,所以AM=√2(1-a),所以AMCM =AGBG =1−a a,所以MG ∥BC,所以MG ⊥AB.又平面ABCD ⊥平面ABEF,且MG ⊂平面ABCD,平面ABCD ∩平面ABEF=AB,所以MG ⊥平面ABEF.(2)由(1)知,MG ⊥NG,MG=1-a,NG=a,所以MN=√a 2+(1−a)2=√2a 2-2a +1=√2(a -12)2+12≥√22,当且仅当a=12时等号成立,即当a=12时,MN 的长度最小.以B 为坐标原点,分别以BA,BE,BC 所在的直线为x 轴、y 轴、z 轴建立如图D 8-5-18所示的空间直角坐标系B-xyz,则A(1,0,0),B(0,0,0),M(12,0,12),N(12,12,0),图D 8-5-18设平面AMN 的法向量为m=(x 1,y 1,z 1),因为AM ⃗⃗⃗⃗⃗⃗ =(-12,0,12),MN⃗⃗⃗⃗⃗⃗⃗ =(0,12,-12), 所以{m ·AM ⃗⃗⃗⃗⃗⃗ =−x12+z12=0,m ·MN⃗⃗⃗⃗⃗⃗⃗ =y 12-z 12=0,取z 1=1,得m=(1,1,1)为平面AMN 的一个法向量.设平面BMN 的法向量为n=(x 2,y 2,z 2),因为BM ⃗⃗⃗⃗⃗⃗ =(12,0,12),MN ⃗⃗⃗⃗⃗⃗⃗ =(0,12,-12), 所以{n ·BM ⃗⃗⃗⃗⃗⃗ =x22+z22=0,n ·MN ⃗⃗⃗⃗⃗⃗⃗ =y 22-z 22=0,取z 2=1,得n=(-1,1,1)为平面BMN 的一个法向量.所以cos<m,n>=m ·n|m||n|=13, 又二面角A-MN-B 为钝二面角,所以二面角A-MN-B 的余弦值为-13.11.(1)由题图(1)知,在题图(2)中,AC ⊥AD,AB ⊥AD.∵平面ACD ⊥平面ABD,平面ACD ∩平面ABD=AD,AB ⊂平面ABD,∴AB ⊥平面ACD,又CD ⊂平面ACD,∴AB ⊥CD.(2)以A 为坐标原点,AC,AB,AD 所在的直线分别为x,y,z 轴建立如图D 8-5-19所示的空间直角坐标系,不妨设AC=1,则A(0,0,0),B(0,2,0),C(1,0,0),D(0,0,1),AD ⃗⃗⃗⃗⃗ =(0,0,1),BC ⃗⃗⃗⃗⃗ =(1,-2,0),DB⃗⃗⃗⃗⃗⃗ =(0,2,-1).图D 8-5-19设E(x,y,z),由DE ⃗⃗⃗⃗⃗ =λDB ⃗⃗⃗⃗⃗⃗ (0<λ<1),得(x,y,z-1)=(0,2λ,-λ), 得E(0,2λ,1-λ),∴AE⃗⃗⃗⃗⃗ =(0,2λ,1-λ),又平面ABC 的一个法向量为AD ⃗⃗⃗⃗⃗ =(0,0,1),AE 与底面ABC 所成角的正切值为12, 所以|tan AD ⃗⃗⃗⃗⃗ ,AE ⃗⃗⃗⃗⃗ |=2,于是|cos AD ⃗⃗⃗⃗⃗ ,AE⃗⃗⃗⃗⃗ |=√5=√55, 即|√(2λ)2+(1−λ)2|=√55,解得λ=12,则E(0,1,12),AE ⃗⃗⃗⃗⃗ =(0,1,12),BE⃗⃗⃗⃗⃗ =(0,-1,12). 设平面BCE 的法向量为n=(x,y,z),则{n ·BC⃗⃗⃗⃗⃗ =0,n ·BE ⃗⃗⃗⃗⃗ =0,即{x -2y =0,-y +12z =0, 令y=1,得x=2,z=2,则n=(2,1,2)是平面BCE 的一个法向量,设直线AE 与平面BCE 所成的角是θ,则sin θ=|cos AE ⃗⃗⃗⃗⃗ ,n |=|AE⃗⃗⃗⃗⃗ ·n||AE ⃗⃗⃗⃗⃗ ||n|=√52×3=4√515, 故直线AE 与平面BCE 所成角的正弦值为4√515.12.(1)因为平面ADEF ⊥平面ABCD,平面ADEF ∩平面ABCD=AD,DE ⊂平面ADEF,DE ⊥AD,所以DE ⊥平面ABCD.因为AC ⊂平面ABCD,所以DE ⊥AC.又四边形ABCD 是正方形,所以AC ⊥BD.因为DE ∩BD=D,DE ⊂平面BED,BD ⊂平面BED,所以AC ⊥平面BED.又AC ⊂平面ACE,所以平面ACE ⊥平面BED.(2)因为DA,DC,DE 两两垂直,所以以D 为坐标原点,建立如图D 8-5-20所示的空间直角坐标系D-xyz. 则A(3,0,0),F(3,0,2√6),E(0,0,3√6),B(3,3,0),C(0,3,0),所以CA⃗⃗⃗⃗⃗ =(3,-3,0),BE ⃗⃗⃗⃗⃗ =(-3,-3,3√6),EF ⃗⃗⃗⃗⃗ =(3,0,-√6).图D 8-5-20设平面BEF 的法向量为n=(x,y,z), 则{n ·BE ⃗⃗⃗⃗⃗ =−3x -3y +3√6z =0,n ·EF ⃗⃗⃗⃗⃗ =3x -√6z =0,取x=√6,得n=(√6,2√6,3)为平面BEF 的一个法向量.所以cos<CA ⃗⃗⃗⃗⃗ ,n>=CA⃗⃗⃗⃗⃗ ·n |CA⃗⃗⃗⃗⃗ ||n|=√63√2×√39=-√1313. 所以直线CA 与平面BEF 所成角的正弦值为√1313.(3)假设在线段AF 上存在符合条件的点M,由(2)可设M(3,0,t),0≤t ≤2√6,则BM ⃗⃗⃗⃗⃗⃗ =(0,-3,t).设平面MBE 的法向量为m=(x 1,y 1,z 1), 则{m ·BM ⃗⃗⃗⃗⃗⃗ =−3y 1+tz 1=0,m ·BE⃗⃗⃗⃗⃗ =−3x 1-3y 1+3√6z 1=0,令y 1=t,得m=(3√6-t,t,3)为平面MBE 的一个法向量.由(1)知CA ⊥平面BED,所以CA ⃗⃗⃗⃗⃗ 是平面BED 的一个法向量,|cos<m,CA ⃗⃗⃗⃗⃗ >|=|m ·CA⃗⃗⃗⃗⃗ ||m||CA⃗⃗⃗⃗⃗ |=√6-3√2×√(3√6-t)2+t 2+9=cos 60°=12,整理得2t 2-6√6t+15=0,解得t=√62,故在线段AF 上存在点M,使得二面角M-BE-D 的大小为60°,此时AMAF =14. 13.(1)因为BC ∥平面α,BC ⊂平面PBC,平面α∩平面PBC=EF,所以BC ∥EF,且F 为棱PB 的中点,因为BC ⊥AB,所以EF ⊥AB.因为PA ∥平面α,PA ⊂平面PAC,平面α∩平面PAC=DE,所以PA ∥DE.因为PA ⊥平面ABC,所以PA ⊥AB, 所以DE ⊥AB.又DE ∩EF=E,DE ⊂平面DEF,EF ⊂平面DEF,所以AB ⊥平面DEF,即AB ⊥平面α.(2)如图D 8-5-21,以点B 为坐标原点,分别以BA,BC 所在直线为x,y 轴,过点B 且与AP 平行的直线为z 轴建立空间直角坐标系,则B(0,0,0),A(2,0,0),C(0,2,0),P(2,0,2),E(1,1,1),F(1,0,1),AC⃗⃗⃗⃗⃗ =(-2,2,0),BC ⃗⃗⃗⃗⃗ =(0,2,0), BP⃗⃗⃗⃗⃗ =(2,0,2).图D 8-5-21设M(1,t,1),平面MAC 的法向量为m=(x 1,y 1,z 1),则AM ⃗⃗⃗⃗⃗⃗ =(-1,t,1),则{m ·AC⃗⃗⃗⃗⃗ =−2x 1+2y 1=0,m ·AM ⃗⃗⃗⃗⃗⃗ =−x 1+ty 1+z 1=0,令x 1=1,则y 1=1,z 1=1-t,所以m=(1,1,1-t)为平面MAC 的一个法向量.设平面PBC 的法向量为n=(x 2,y 2,z 2),则{n ·BC ⃗⃗⃗⃗⃗ =2y 2=0,n ·BP ⃗⃗⃗⃗⃗ =2x 2+2z 2=0,得y 2=0,令x 2=1,则z 2=-1,所以n=(1,0,-1)为平面PBC 的一个法向量.设平面MAC 与平面PBC 所成的锐二面角为θ,则cos θ=|cos<m,n>|=|m ·n||m|×|n|=√12+12+(1-t)2×√2=√t 2-2t+3×√2.当t=0时,cos θ=0; 当t ≠0时, cos θ=√3t 2-2t+1×√2=√3(1t -13)+23×√2,当且仅当1t =13,即t=3时,3(1t -13)2+23取得最小值23,cos θ取得最大值,最大值为√23×√2=√32.所以平面MAC 与平面PBC 所成锐二面角的余弦值的最大值为√32.14.(1)因为AB ∥平面PCD,AB ⊂平面OCP,平面OCP ∩平面PCD=PC,所以AB ∥PC.又∠COB=60°,所以∠OCP=60°.又OC=OP,所以△OCP 为正三角形,所以PC=1.(2)由题意知DO ⊥平面COP,而V P-COD =V D-COP ,S △COP =12·OC ·OP ·sin ∠COP, 所以当OC ⊥OP 时,三棱锥P-COD 的体积最大.解法一 易知OP,OD,OC 两两垂直,以O 为坐标原点,OP⃗⃗⃗⃗⃗ ,OD ⃗⃗⃗⃗⃗⃗ ,OC ⃗⃗⃗⃗⃗ 的方向分别为x 轴、y 轴、z 轴的正方向,建立如图D 8-5-22所示的空间直角坐标系O-xyz,则P(1,0,0),D(0,1,0),C(0,0,1),PC ⃗⃗⃗⃗⃗ =(-1,0,1),DP ⃗⃗⃗⃗⃗ =(1,-1,0).图D 8-5-22设平面DPC 的法向量为n 1=(x,y,z),则{PC⃗⃗⃗⃗⃗ ·n 1=0,DP ⃗⃗⃗⃗⃗ ·n 1=0,即{-x +z =0,x -y =0,取x=1,得平面DPC 的一个法向量为n 1=(1,1,1).易知平面PCO 的一个法向量为n 2=(0,1,0),设二面角D-PC-O 的平面角为α,由题图知,二面角D-PC-O 的平面角为锐角,则cos α=|n 1·n 2||n 1||n 2|=√33, 所以二面角D-PC-O 的余弦值为√33.解法二如图D 8-5-23所示,取PC的中点H,连接OH,DH.图D 8-5-23 因为OC=OP,DC=DP,所以OH,DH都与PC垂直,即∠OHD为所求二面角的平面角.在Rt△OPC中,可得OH=√22,在Rt△OHD中,DH=(√22=√62,所以cos∠OHD=√22√62=√33,所以二面角D-PC-O的余弦值为√33.。
数学立体几何测试题

数学立体几何测试题测试题一:立体图形的表示1. 画出一个正方体,并标注出各个面、边和顶点。
测试题二:计算立体图形的性质2. 一个立方体的棱长为10cm,求它的表面积和体积。
3. 一个正方体的对角线长为12cm,求它的棱长。
4. 一个正方体的棱长为8cm,求它的对角线长。
测试题三:计算截面图形的面积5. 一个圆柱体的底面半径为6cm,高为10cm,求它的体积。
6. 一个球的半径为5cm,求它的表面积。
7. 一个锥体的高为12cm,底面半径为8cm,求它的体积。
测试题四:判断立体图形的性质8. 判断以下说法是否正确:a) 一个正方体的每个面都是正方形。
b) 一个棱柱的底面和顶面都是正多边形。
9. 判断以下说法是否正确:a) 一个正方体的对角线长度等于它的体对角线的两倍。
b) 一个圆柱的高等于它的侧面积除以底面积。
10. 判断以下说法是否正确:a) 一个棱锥的底面是一个正多边形。
b) 一个正球的体积等于它的表面积乘以π倍。
测试题五:运用立体几何解决实际问题11. 一张纸片的形状是一个以边长为6cm的正方形,若将这张纸片折叠成一个正立方体,则每个小正方体的体积是多少?12. 一个长方体箱子的长、宽、高分别为8cm、6cm、10cm,请问这个箱子的体积是多少立方厘米?13. 一个蜡烛用圆柱体塑料包装,如果塑料包装的高度是12cm,底面直径为4cm,蜡烛的高度为10cm,并且蜡烛剩余部分的直径与底面直径相等,求蜡烛的剩余部分的高度。
测试题六:解答题14. 已知一个棱长为a的正方体,将它的每个面都截去边长为b的正方形,最后剩下的多面体的体积是多少?15. 一个高度为h的圆锥的底面半径为r,切一个与底面平行的截面得到一个半径为R的圆,若R>r,则这个圆锥的高度能使得截面圆的面积最大吗?为什么?答案测试题一:立体图形的表示1. 略。
测试题二:计算立体图形的性质2. 表面积 = 6 * 边长² = 6 * 10² = 600 cm²体积 = 边长³ = 10³ = 1000 cm³3. 对角线长 = 边长* √3 = 10 * √3 cm4. 对角线长 = 边长* √3 = 8 * √3 cm测试题三:计算截面图形的面积5. 体积= π * 半径² * 高度= π * 6² * 10 = 360π cm³6. 表面积= 4π * 半径² = 4π * 5² = 100π cm²7. 体积= (1/3) * π * 半径² * 高度= (1/3) * π * 8² * 12 = 256π cm³测试题四:判断立体图形的性质8. a) 正确b) 正确9. a) 错误,它们相等。
立体几何教材试题答案

立体几何教材试题答案一、选择题1. 若一个正方体的棱长为2cm,则其对角线的长度为?A. 2√2 cmB. 2√3 cmC. 4 cmD. √8 cm答案:B2. 一个锥体的底面半径为3cm,高为4cm,其侧面展开图的周长为?A. 6π cmB. 8π cmC. 12π cmD. 16π cm答案:C3. 一个球的表面积为12π cm²,那么其半径为?A. 1 cmB. 2 cmC. 3 cmD. 4 cm答案:C4. 若一个圆柱的底面直径为6cm,高为10cm,求其体积。
A. 15π cm³B. 30π cm³C. 60π cm³D. 90π cm³答案:B5. 一个棱锥的底面是一个边长为5cm的正方形,高为7cm,求其体积。
A. 85 cm³B. 100 cm³C. 125 cm³D. 175 cm³答案:C二、填空题1. 一个球的半径为r,其体积公式为__________。
答案:V = (4/3)πr³2. 一个锥体的底面半径为r,高为h,其体积公式为__________。
答案:V = (1/3)πr²h3. 一个正方体的棱长为a,其表面积公式为__________。
答案:S = 6a²4. 一个圆柱的底面半径为r,高为h,其侧面积公式为__________。
答案:A = 2πrh5. 一个圆锥的底面半径为r,高为h,其底面积公式为__________。
答案:A = πr²三、计算题1. 一个正四面体的边长为3cm,求其体积。
解:正四面体的体积公式为V = (边长³ * √2) / 12,代入边长a = 3cm,得V = (3³ * √2) / 12 = (27 * √2) / 12 = (9 * √2) / 4 cm³。
2. 一个球的直径为10cm,求其表面积。
立体几何测试题(8套)

(B)若a与b相交,b与c相交,则a与c也相交
(C)若a//b,b//c,则a//c
(D)若a与b异面,b与c异面,则a与c也是异面直线
4.已知异面直线a、b分别在平面α、β内,且α∩β=c,那么直线c( )
(A)一定与a、b交于同一点
(B)至少与a、b中的一条相交
(C)至多与a、b中的一条相交
4.若a,b是两条平行直线,且都不垂直与平面 ,那么a,b在平面 内的射影为()。
(A)两条平行线 (B)相交的两直线
(C)两条平行线或同一直线 (D)相交的两直线或同一直线
5.相交的两直线都是平面 的斜线,那么这两斜线在平面 的设影是()。
(A)同一直线 (B)相交的两直线
(C)两条平行直线 (D)一直线或两相交直线
三、解答题
12、已知正方体ABCD-A`B`C`D`中,E,F分别是A`B`,B`C`的中点。
求证:EF∥面AD`C。
13、已知PA⊥正方形ABCD,PA=AB=2,M,N为BC,CD中点,
⑴求C到面PAM的距离,⑵求BD到面PMN的距离。
立体几何测试1
参考答案
一、选择题ADBCDCDC
二、填空题(每小题5分,共15分)
6.和两条异面直线都相交的两条直线是( )
(A)平行直线(B)异面直线(C)相交直线(D)异面直线或相交直线
7.在正方体ABCD-A1B1C1D1中,12条棱互成异面直线的对数有( )
(A) 48对(B) 36对(C) 24对(D) 12对
8.分别平行于两条异面直线的两条直线的位置关系是( )
(A)异面直线(B)平行直线
21.夹在直二面角 -MN- 内的线段PQ(P,Q MN)与 , 所成的角分别为 ,则 应满足的条件是。
立体几何测试题(共10篇)

立体几何测试题(共10篇)立体几何测试题(一): 立体几何问题立体几何试题已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D、B、F、E四点共面;(2)若A1C交平面DBFE于R点,则P、Q、R三点共线.1.EF平行于B1D1,B1D1平行于BD,所以EF平行于BD,EFBD四点共面2.F,D,A,C1属于平面A1ACC1,且AC1与PQ不平行,所以AC1与PQ相交A1C交平面DBFE于R点,又因为PQ属于平面DBFE,所以AC1与PQ相交于R 所以R属于PQ,PQR共线立体几何测试题(二): 几个书后练习题立体几何1.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.是否正确2.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.为什么不对谢不对,因为a有可能在经过b的面上,不是平行关系立体几何测试题(三): 一道数学基本的立体几何的题目~在正方形ABCD-A"B"C"D"中,P、Q分别为A"B"、BB"的中点.(1)求直线AP与CQ所成的角的大小(2)求直线AP与BD所成的角的大小我还没学过空间向量,1.取DC中点E,连EC,证明EC平行AP,用余弦定理算2.取AB中点F,连接FB,用余弦定理算【立体几何测试题】立体几何测试题(四): 求大量立体几何难题!立体几何综合试题(自己画图)1、已知正三棱柱ABC—A1B1C1中,各棱长都相等,D、E分别为AC1,BB1的中点.(1)求证:DE‖平面A1B1C1;(2)求二面角A1—DE—B1的大小.2、已知直三棱柱ABC—A1B1C1,AB=AC,F为棱BB1上一点,BF∶FB1=2∶1,BF =BC=2a.(I)若D为BC的中点,E为AD上不同于A、D的任意一点,证明EF⊥FC1;(II)试问:若AB=2a,在线段AD上的E点能否使EF与平面BB1C1C成60°角,为什么证明你的结论3、在底面是直角梯形的四棱锥中,AD‖BC,∠ABC=90°,且 ,又PA⊥平面ABCD,AD=3AB=3PA=3a.(I)求二面角P—CD—A的正切值;(II)求点A到平面PBC的距离.4、在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.(Ⅰ)确定点G的位置;(Ⅱ)求直线AC1与平面EFG所成角θ的大小.5、已知四棱锥P—ABCD,底面ABCD是菱形,平面ABCD,PD=AD,点E为AB中点,点F为PD中点.(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值6.在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P 在棱CC1上,且CC1=4CP.(Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);(Ⅱ)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;(Ⅲ)求点P到平面ABD1的距离.7、在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.(I)证明平面;(II)证明平面EFD;(III)求二面角的大小.8、已知在棱长为1的正方体ABCD—A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.(I)试确定点F的位置,使得D1E⊥平面AB1F;(II)当D 1E⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).9、直四棱柱ABCD-A1B1C1D1的底面是梯形,AB‖CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别是CC1、C1D1的中点.点P到直线AD1的距离为⑴求证:AC‖平面BPQ⑵求二面角B-PQ-D的大小10、已知长方体ABCD—A1B1C1D1中,AB=BC=4,AA1=8,E、F分别为AD和CC1的中点,O1为下底面正方形的中心.(Ⅰ)证明:AF⊥平面FD1B1;(Ⅱ)求异面直线EB与O1F所成角的余弦值;这些题应该还可以!你来试试吧!题不要求多就精就可以了!不懂的或不会做的,我来帮你解答!立体几何测试题(五): 立体几何初步练习题已知正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱B1C1,C1D1,A1B1,D1A1的中点,求证(1)MN平行于DEF,(2)平面AMN平行于平面CEF(1)连接B1D1因为MN、EF为三角形A1B1D1、B1C1D1的中位线,所以MN平行于EF因为MN不属于面DEF,EF属于面DEF所以MN平行于面DEF(2)这题题目错了吧,应该是DEF吧立体几何测试题(六): 解析几何基础知识练习题靠!一楼的那么多废话那么多选择题:集合,函数(图像),立体几何,圆锥一、数学命题原则 1.普通高等学校招生数学科的考试,按照“考查基础知识的【立体几何测试题】立体几何测试题(七): 高一必修二立体几何习题1-7的题仓库的房顶呈正四棱锥形,量的地面的边长为2.6m,侧棱长2.1m,先要在房顶上铺一层油毡纸,问:需要油毡纸的面积多少运用海伦公式房顶为4个相同的三角形海伦公式a=2.6 b=2.1 c=2.1 p=a+b+c/2=3.4S=根号下p*(p-a)*(p-b)*(p-c)=2.1444S=2.144*4=8.576平方米立体几何测试题(八): 怎么根据题目画数学的立体几何图形搞懂了题目的要求,就照那意思去画,立体几何记住透视很重要.立体几何测试题(九): 求立体几何判断题的解题方法.①过平面外一点有且仅有一个平面与已知平面垂直②过直线外一点有且仅有一个平面与已知直线平行③过直线外一点有且仅有一条直线与已知直线垂直④过平面外一点有且仅有一条直线与已知平面垂直⑤……等等,诸如此类.见到很多这样的题目,但是却总找不到解题的方法,概念定理也经常记混.本人感激不尽!记一些模型,例如墙角模型什么的这个很重要.遇见不熟悉的题,用书本和笔(手指也可以)比划一下.这种题目主要是找反例!想象力也很重要啦……立体几何测试题(十): 一道高中立体几何的题目.已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,O1是底面A1B1C1D1的中心.E 是CO1上的点,设CE等于X,四棱锥E-ABCD的体积为y,求y关于X的函数关系式..图只有自己画一下了,做EF垂直于平面ABCD 垂足为F易得出CEF相似于O1CC1因为C1O1=根号2 CC1=4 得CO1=3根号2CE/CO1=EF/CC1 得出EF=4X/3根号2Y=底面积*EF/3=4*4X/9根号2Y=8根号2*X/9职高立体几何测试题空间立体几何测试题。
立体几何测试卷含详解

距离为: 2 3
32
3 2
2
3 ;所以外接球的半径为:
(
3)2
3 2 2
21 . 2
所以外接球的表面积为: 4
21 2 2
21
.
故选:C
【点睛】
本题是基础题,考查正三棱柱的外接球的表面积的求法,找出球的球心是解题的关键,考查
空间想象能力,计算能力.
6.B 【分析】
依题意直接利用台体体积的计算公式即得结果.
接球即为三棱锥的外接球求解. 【详解】
因为 AB 平面 BCD, 所以 AB BC , AB BD , ∴ BC BD 42 (2 3)2 2 , 在△BCD 中, CD 2 2 , ∴ CD2 BC 2 BD2 , ∴ BC BD .
如图所示:
三棱锥 A BCD 的外接球即为长方体 AGFH-BCED 的外接球, 设球 O 的半径为 R,则 2R BA2 BC2 BD2 (2 3)2 22 22 2 5 , 解得 R 5 , 所以球 O 的表面积为 20π ,
三、解答题(共 70 分)
试卷第 3页,总 6页
1
17(本题满分 10 分).圆台的上底周长是下底周长的 ,轴截面面积等于 392,母线与
3
底面的夹角为 45°,求此圆台的高、母线长及两底面的半径.
18(本题满分 12 分).已知梯形 ABCD ,按照斜二测画法画出它的直观图 A ' B 'C ' D ' , 如图所示,其中 A ' D ' 2 , B 'C ' 4 , A ' B ' 1, 求:(1)梯形 ABCD 的面积; (2)梯形 ABCD 以 BC 为旋转轴旋转一周形成的几何体的表面积和体积.
立体几何测试题

立体几何测试题一、选择题1. 已知正方体ABCDA1B1C1D1的棱长为a,点E、F分别为AA1、BB1的中点,那么四面体EFBC1的体积是多少?A. 1/12a³B. 1/6a³C. 1/4a³D. 1/2a³2. 一个圆锥的底面半径为r,高为h,那么它的侧面积是多少?A. πr²B. 2πrhC. πrℎD. πr²+2πrh3. 一个球的半径为r,那么它的表面积是多少?A. 4πr²B. 2πr²C. πr²D. 8πr²4. 一个棱长为a的正方体,它的对角线长是多少?A. √2aB. √3aC. 2aD. 3a5. 一个圆柱的底面半径为r,高为h,那么它的体积是多少?A. πr²hB. 2πr²hC. πrhD. 2πr²h二、填空题6. 一个正四面体的体积为V,如果它的边长加倍,则体积变为__________。
7. 一个球的直径为d,那么它的体积是__________。
8. 一个圆锥的底面直径为D,高为h,那么它的体积是__________。
9. 一个圆柱的底面直径为d,高为h,那么它的侧面积是__________。
10. 一个正方体的表面积为S,如果它的边长减半,则表面积变为__________。
三、解答题11. 一个正方体的棱长为a,求它的所有棱长之和。
12. 一个球的半径为r,求它的所有内接正方体的棱长之和。
13. 一个圆柱的底面半径为r,高为h,求它的所有内接正方体的棱长之和。
14. 一个圆锥的底面半径为r,高为h,求它的所有内接正方体的棱长之和。
15. 一个球的半径为r,求它的所有内接正四面体的棱长之和。
四、证明题16. 证明:在一个正方体中,任意一个顶点出发的三个对面的顶点构成的三角形的面积之和等于正方体一个面的面积。
17. 证明:在一个球内,任意一个直径所分割的两个半圆的面积之和等于球的大圆面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013立体几何数学试卷
一. 选择题
1.四条直线相交于一点,它们能确定的平面的个数是( ) A.1 B.4 C.6 D.1或4或6
2.l 1,l 2,l 3是空间三条不同的直线,则下列命题正确的是( ) A .l 1⊥l 2,l 2⊥l 3⇒l 1∥l 3 B .l 1⊥l 2,l 2∥l 3⇒l 1⊥l 3
C .l 1∥l 2∥l 3⇒l 1,l 2,l 3共面
D .l 1,l 2,l 3共点⇒l 1,l 2,l 3共面 3.下列命题中错误..的是 A .如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β. B .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β. C .如果平面α⊥平面γ,平面β⊥平面γ,l αβ⋂=,那么l ⊥平面γ. D .如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β.
4.若二面角α-l -β为120°,直线m ⊥α,则β所在平面内的直线与m 所成角的取值范围是
A.0,2⎛π⎤ ⎥⎦
⎝ B.,63ππ⎡⎤⎢⎥⎣⎦ C.,32
ππ⎛⎫
⎪⎝⎭
D.,62ππ⎡⎤
⎢⎥⎣⎦
5.已知α,β表示两个不同的平面,m 为平面α内的一条直线,则“αβ⊥”是“m β⊥”的( ) A.必要不充分条件 B.充分不必要条件
C.充要条件
D.既不充分也不必要条件
6.若正四棱柱1111ABCD A B C D -的底面边长为1,1AB 与底面ABCD 成60°角,则11AC 到底面ABCD 的距离为 ( ) A .
3
3
B .1
C .2
D .3 7.设长方体的长、宽、高分别为2a 、a 、a,其顶点都在一个球面上,则该球的表面积为
A.3πa 2
B.6πa 2
C.12πa 2
D. 24πa 2
8.若地球半径为R ,在北纬300
圈上有A 、B 两地,它们的球面距离为2πR/3,则A 、B 两地的经度差是( )
A. 300
B.600
C.1500
D.1800
9. 已知正四棱柱1111ABCD A B C D -中,1AA =2AB ,E 为1AA 中点,则异面直线BE 与1CD 所形成角的余弦值为( ) A .
10
10 B. 15 C. 31010
D. 35
10. 已知正方体的八个顶点中,有四个点恰好为正四面体的顶点,则该正四面体的体积与正方体的体积之
比为( ) A.1:3
B.1:2
C.2:3
D.1:3
11.Rt △ABC 的两直角边AB=6,AC=8,在△ABC 所在平面外有一点P 和A 、B 、C 的距离都是13,那么点P
到△ABC 所在平面的距离为 ( ) A.13 B.12 C.10 D.9
12.已知棱长都相等的正三棱锥内接于一球,某人画出四个过球心的平面截球与正三棱锥所得的图形如图所示,则下列说法正确的是( )
A .以上四个图形都正确 B.只有②④正确 C .只有④错误 D.只有①②正确 二、填空题 13.已知两异面直线a,b 所成角为40°,则过空间一点O 能作____________条直线与a,b 所成角都是40°. 14.已知正三棱柱111ABC A
B
C -的各条棱长都相等,M 是侧棱1CC 的中点,则异面直线1AB BM 和所成
的角的大小是 。
15.正方体1111D C B A ABCD -中,棱长为a ,E 是1AA 的中点,
在对角面D D BB 11上取一点M ,使AM+ME 最小,其最小值为 .
16. 一个锐角为30
,斜边为2的直角三角形纸片,以斜边上的中线为折痕折成直二面角,折后斜边两
端点的距离等于_______.
三、解答题
17.如图,已知三棱锥的底面是边长为1的正三角形,两条侧棱DA=DC=
2
13, 试求第三条侧棱长DB 的取值范围.
18.如图,四边形ABCD 为正方形,PD ⊥平面AC,PD=DC, E 是PC 的中点,作EF ⊥PB 交PB 于点F.
A
C
B
D
B
D
C
A
A B
C
D
(1)证明:PA ∥平面EDB; (2)证明:PB ⊥平面EFD.
19、在正四棱柱ABCD-A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点E 是CC 1的中点. (1)求二面角E-BD-C 的大小; (2)求点D 1到平面BDE 的距离.
=a,2a,
1;(2)ABCD PD ABCD PD DC AD M N PB MNC ⊥==⊥20.如图,已知四边形是矩形,平面,、分别是AD ,PB 的中点()求证:平面求点A 到平面MNC 的距离。
21.如图,在三棱锥P ABC -中,PA ⊥底面,,60,90ABC PA AB ABC BCA ︒︒
=∠=∠=, 点D ,E 分别是棱,PB PC 的中点,
N D C
A
B
P
M
(Ⅰ)求证:BC ⊥平面PAC ;
(Ⅱ)求AD 与平面PAC 所成的角的大小;
22. 如图所示的几何体中,已知ABCD 是边长为3的正方形,SD ⊥底面ABCD ,SB 33=,点E 、G 分
别在AB 、SC 上,且1AE AB 3=
,1
CG SC 3
=. (1)证明:BG ∥平面SDE ;
(2)求面SAD 与面SBC 所成二面角的大小.。
