(完整word版)北师大版九年级下册数学第三章圆单元测试(含答案)
北师大版九年级数学下册《第三章圆》单元测试题(有答案)

北师大版九年级数学下册单元测试题第三章圆一、选择题(本大题共8小题,每小题4分,共32分;在每小题列出的四个选项中,只有一项符合题意)1.在下列四个命题中:①直径是最长的弦;②每个三角形都有一个内切圆;③三角形的外心到三角形各边的距离都相等;④如果两条弦相等,那么这两条弦所对的弧也相等.其中正确的有( ) A.1个 B.2个 C.3个 D.4个2.如图3-Z-1,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,若∠C =40°,则∠ABD的度数是( )A.30° B.25° C.20° D.15°图3-Z-13.如图3-Z-2,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )图3-Z-2A.45° B.50° C.60° D.75°4.如图3-Z-3,AB为⊙O的直径,弦DC⊥AB于点E,∠DCB=30°,EB=3,则弦AC的长为( ) A.3 3 B.4 3 C.5 3 D.6 3图3-Z-35.如图3-Z-4,四边形ABCD的边AB,BC,CD,DA和⊙O分别相切于点L,M,N,P.若四边形ABCD的周长为20,则AB+CD等于()图3-Z-4A.5 B.8 C.10 D.126.在圆柱形油槽内装有一些油,截面如图3-Z -5,油面宽AB 为6分米,如果再注入一些油后,油面AB 上升1分米,油面宽变为8分米,则圆柱形油槽的直径MN 为( )A .6分米B .8分米C .10分米D .12分米图3-Z -57.如图3-Z -6,某厂生产横截面直径为7 cm 的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳的视觉效果,字样在罐头侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()图3-Z -6A.π4 cmB.7π4 cmC.7π2cm D .7π cm 8.如图3-Z -7,四边形ABCD 是菱形,∠A =60°,AB =2,扇形BEF 的半径为2,圆心角为60°,则图中阴影部分的面积是( )图3-Z -7A.2π3-32B.2π3- 3 C .π-32D .π- 3 二、填空题(本大题共5小题,每小题4分,共20分)9.已知⊙O 的半径为5,点A 在⊙O 外,那么线段OA 的长度的取值范围是________.10.如图3-Z -8,已知经过原点的⊙P 与x 轴、y 轴分别交于A ,B 两点,C 是劣弧OB 上一点,则∠ACB 的度数为________.图3-Z -811.如图3-Z -9,在⊙O 中,弦DA ∥BC ,DA =DC ,∠AOC =160°,则∠BCO =________度.图3-Z -912.如图3-Z -10,正方形ABCD 内接于⊙O ,其边长为4,则⊙O 的内接正三角形EFG 的边长为________.图3-Z -1013.如图3-Z -11,在Rt △AOB 中,OA =OB =3 2,⊙O 的半径为1,P 是AB 边上的动点,过点P 作⊙O 的一条切线PQ (Q 为切点),则切线PQ 长的最小值为________.图3-Z -11三、解答题(本大题共4小题,共48分) 14.(10分)如图3-Z -12,已知四边形ABCD 内接于⊙O ,连接BD ,∠BAD =105°,∠DBC =75°. (1)求证:BD =CD ;(2)若⊙O 的半径为3,求BC ︵的长.图3-Z -1215.(12分)如图3-Z -13,BE 是⊙O 的直径,半径OA ⊥弦BC ,D 为垂足,连接AE ,EC . (1)若∠AEC =28°,求∠AOB 的度数;(2)若∠BEA=∠B,BC=6,求⊙O的半径.图3-Z-1316.(12分)如图3-Z-14,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.(1)连接AD,求证:AD平分∠BAC;(2)求AC的长.图3-Z-1417.(14分)如图3-Z-15①,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.(1)如图②,当PD∥AB时,求PD的长.(2)如图③,当DC ︵=AC ︵时,延长AB 至点E ,使BE =12AB ,连接DE .①求证:DE 是⊙O 的切线; ②求PC 的长.图3-Z -15详解详析1.[答案] B 2.[解析] B ∵AC 是⊙O 的切线,∴∠BAC =90°.又∠C =40°,∴∠AOC =90°-40°=50°,∴∠ABD =12∠AOC =12×50°=25°.故选B.3.[解析] C 连接OD ,∵OA =OD ,OD =OC ,∴∠DAO =∠ODA ,∠DCO =∠ODC ,∴∠DAO +∠DCO =∠ADC .∵四边形ABCO 是平行四边形,∴∠B =∠AOC .∵四边形ABCD 是圆内接四边形, ∴∠ADC +∠B =180°.∵∠ADC =12∠AOC ,∴∠ADC =12∠B ,即3∠ADC =180°,∴∠ADC =60°,即∠DAO +∠DCO =60°.故选C.4.[解析] D 如图,连接OC ,∵弦DC ⊥AB 于点E ,∠DCB =30°,∴∠ABC =60°,∴△BOC是等边三角形.∵EB =3,∴OB =6,∴AB =12.∵AB 为⊙O 的直径,∴∠ACB =90°.在Rt △ACB 中,AC =12×32=6 3.故选D. 5.[答案] C 6.[答案] C7.[解析] B ∵字样在罐头侧面所形成的弧的度数为90°,∴此弧所对的圆心角为90°,由题意可得R =72 cm ,则“蘑菇罐头”字样的长为90π×72180=7π4(cm).8.[解析] B 如图,连接BD .∵四边形ABCD 是菱形,∠A =60°,∴∠ADC =120°,∴∠1=∠2=60°,∴△DAB 是等边三角形,∴AB =BD ,∠3+∠5=60°.∵AB =2,∴△ABD 的高为 3.∵扇形BEF 的圆心角为60°,∴∠4+∠5=60°,∴∠3=∠4.设AD ,BE 相交于点G ,BF ,DC 相交于点H ,在△ABG 和△DBH 中,∠A =∠2,AB =BD ,∠3=∠4,∴△ABG ≌△DBH (ASA),∴S 四边形GBHD =S △ABD ,∴S 阴影=S 扇形EBF -S △ABD =60π×22360-12×2×3=2π3- 3.故选B. 9.[答案] OA >5[解析] ∵⊙O 的半径为5,点A 在⊙O 外,∴线段OA 的长度的取值范围是OA >5.故答案为OA >5.10.[答案] 90°[解析] ∵∠AOB =90°,∴∠ACB =∠AOB =90°.11.[答案] 30 [解析] 连接AC , ∵∠B =12∠AOC =80°,∴∠D =180°-∠B =100°. ∵DA =DC ,OA =OC ,∴∠DAC =∠ACD =40°,∠OCA =∠OAC =10°. ∵DA ∥BC ,∴∠ACB =∠DAC =40°, ∴∠BCO =30°.12.[答案] 2 6[解析] 连接AC ,OE ,OF ,过点O 作OM ⊥EF 于点M .∵四边形ABCD 是正方形,∴AB =BC =4,∠ABC =90°, ∴AC 是直径,AC =4 2, ∴OE =OF =2 2. ∵OM ⊥EF ,∴EM =MF .∵△EFG 是等边三角形,∴∠GEF =60°.在Rt △OME 中,∵OE =2 2,∠OEM =12∠GEF =30°,∴OM =2,EM =3OM =6,∴EF =2 6.13.[答案] 2 2[解析] 如图,连接OP ,OQ .∵PQ 是⊙O 的切线,∴OQ ⊥PQ ,∴PQ 2=OP 2-OQ 2,∴当OP ⊥AB 时,OP 最短,则此时线段PQ 最短.∵在Rt △AOB 中,OA =OB =3 2,∴AB =2OA =6,∴OP =OA ·OB AB=3,∴PQ =OP 2-OQ 2=32-12=2 2.14.解:(1)证明:∵四边形ABCD 内接于⊙O ,∴∠DCB +∠BAD =180°. ∵∠BAD =105°,∴∠DCB =180°-105°=75°, ∴∠DCB =∠DBC ,∴BD =CD .(2)由(1)可知∠DBC =∠DCB =75°,∴∠BDC =30°.由圆周角定理得BC ︵的度数为60°,故BC ︵的长为60π×3180=π.15.[解析] (1)根据垂径定理得到AC ︵=AB ︵,根据圆周角定理解答;(2)根据圆周角定理的推论得到∠C =90°,进而得到∠B =30°,根据余弦的定义求出BE 的长即可.解:(1)∵OA ⊥BC ,∴AC ︵=AB ︵,∴∠BEA =∠AEC =28°,由圆周角定理,得∠AOB =2∠AEB =56°. (2)∵BE 是⊙O 的直径,∴∠C =90°, ∴∠CEB +∠B =90°.又∵∠BEA =∠B ,∠BEA =∠AEC , ∴∠B =30°,∴BE =BCcos B =4 3,∴⊙O 的半径为2 3.16.解:(1)证明:连接OD . ∵BD 是⊙O 的切线,∴OD ⊥BD . 又∵AC ⊥BD ,∴OD ∥AC , ∴∠CAD =∠ODA .∵OA =OD ,∴∠OAD =∠ODA ,∴∠OAD =∠CAD ,即AD 平分∠BAC . (2)∵OD ∥AC ,∴△BOD ∽△BAC ,∴OD AC =BO BA ,即4AC =610, 解得AC =203,即AC 的长为203.17.解:(1)连接OD .∵OP ⊥PD ,PD ∥AB ,∴∠POB =90°.∵⊙O 的直径AB =12,∴OB =OD =6.在Rt △POB 中,∵∠ABC =30°,∴OP =OB ·tan30°=6×33=2 3. 在Rt △POD 中,PD =OD 2-OP 2=62-(2 3)2=2 6. (2)①证明:连接OD ,交CB 于点F ,连接BD . ∵DC ︵=AC ︵,∴∠DBC =∠ABC =30°,∴∠ABD =60°.又∵OB =OD ,∴△OBD 是等边三角形, ∴∠DOB =60°,则∠OFB =180°-60°-30°=90°, ∴OD ⊥FB ,∴OF =DF . 又∵BE =12AB ,OB =12AB ,∴OB =BE ,∴BF ∥DE ,∴∠ODE =∠OFB =90°, ∴DE 是⊙O 的切线.②由①知OD ⊥BC ,∴CF =BF =OB ·cos30°=6×32=3 3. 在Rt △POD 中,∵OF =DF ,∴PF =错误!OD =3,∴PC =CF -PF =3 错误!-3.。
北师大版九年级下数学《第三章圆》单元检测卷含答案

第三章圆单元检测卷姓名:__________ 班级:__________一、选择题(共12小题;共36分)1.如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为()A. 3B. 3C.D.2.如图,△ABC是⊙O的内接三角形,若∠C=60°,则∠AOB的度数是()A. 30°B. 60°C. 90°D. 120°3.如图,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为点E,若CE=2,则AB的长是( )A. 4B. 6C. 8D. 104.下列语句中正确的是()A. 相等的圆心角所对的弧相等B. 平分弦的直径垂直于弦C. 长度相等的两条弧是等弧D. 经过圆心的每一条直线都是圆的对称轴5.如图,⊙O的圆心O到直线l的距离为4cm,⊙O的半径为1cm,将直线l向右(垂直于l的方向)平移,使l与⊙O相切,则平移的距离为()A. 1cmB. 3cmC. 5cmD. 3cm或5cm6.如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于()A. B. C. D.7.下列说法中正确的是()①圆心角是顶点在圆心的角;②两个圆心角相等,它们所对的弦相等;③两条弦相等,圆心到这两弦的距离相等;④在等圆中,圆心角不变,所对的弦也不变.A. ①③B. ②④C. ①④D. ②③8.如图,A,B,C三点在已知的圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是的中点,连接DB,DC,则∠DBC的度数为()A. 30°B. 45°C. 50°D. 70°9.如图,PA、PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于()A. 60°B. 90°C. 120°D. 150°10.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为()A. B. C. 3 D. 211.如图,AB是⊙O的直径,AC为⊙O的弦,点D是直径AB上的一点,若OA=5cm,AC=8cm,则CD的长度不可能是()A. 4cmB. 5cmC. 6cmD. 8cm12.如图,A、B、C三点在⊙O上,∠BAC=60°,若⊙O的半径OC为12,则劣弧BC的长为()A. 8πB. 6πC. 4πD. 2π二、填空题(共9题;共27分)13.如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为________.14.如图,∠ACB=60°,⊙O的圆心O在边BC上,⊙O的半径为3,在圆心O向点C运动的过程中,当CO= ________时,⊙O与直线CA相切.15.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B=________度.16.直角三角形两直角边为3,4,则其外接圆和内切圆半径之和为________.17.矩形ABCD中,AB=4,AD=3,以AB为直径在矩形内作半圆.DE切⊙O于点E(如图),则tan∠CDF 的值为________ .18. 如图,已知A、B、C、D、E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C=________度.19.已知⊙O的半径是5,圆心O到直线AB的距离为2,则⊙O上有且只有________个点到直线AB的距离为3.20.如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于________.21.已知扇形的半径为3cm,此扇形的弧长是2πcm,则此扇形的圆心角等于________度,扇形的面积是________.(结果保留π)三、解答题(共4题;共37分)22.如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O 在AB上,⊙O与AB交于点E.(1)求证:直线BD与⊙O相切;(2)若AD:AE=4:5,BC=6,求⊙O的直径.23.如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,,C△ABC=10cm且∠C=60°.求:(1)⊙O的半径r;(2)扇形OEF的面积(结果保留π);(3)扇形OEF的周长(结果保留π)24.如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,S△ABC=10cm2,C△ABC=10cm,且∠C=60°求:(1)⊙O的半径r;(2)扇形OEF的面积(结果保留π);(3)扇形OEF的周长(结果保留π)。
北师大版九年级数学下册《第三章圆》单元检测卷带答案

北师大版九年级数学下册《第三章圆》单元检测卷带答案学校:___________班级:___________姓名:___________考号:___________【基础达标】1.已知点A在直径为8 cm的☉O内,则OA的长可能是()A.8 cmB.6 cmC.4 cmD.2 cm2.如图,在圆内接四边形ABCD中,若∠C=80°,则∠A等于()A.120°B.100°C.80°D.90°3.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上,点A,B的读数分别为85°,31°,则∠ACB的度数是()A.27°B.31°C.30°D.54°4.如图,点A,B,C对应的刻度分别为1,3,5,将线段CA绕点C按顺时针方向旋转,当点A首次落在矩形BCDE的边BE上时,记为点A',则此时线段CA扫过的图形的面积为()A.4√3B.6C.43πD.83π5.PA,PB是☉O的切线,其切点分别为A,B,AC是☉O的直径,已知∠BAC=35°,∠P的度数为.6.如图,AB ⏜的半径OA=2,OC ⊥AB 于点C ,∠AOC=60°. (1)求弦AB 的长. (2)求扇形OAB 的周长.【能力巩固】7.如图,在☉O 中,OA=AB ,OC ⊥AB ,交☉O 于点C ,那么下列结论错误的是( )A .∠BAC=30°B .弧AC 等于弧BCC .线段OB 的长等于圆内接正六边形的半径D .弦AC 的长等于圆内接正十二边形的边长8.考虑下面五个命题:(1)任意三点确定一个圆;(2)平分弦的直径垂直于弦,且平分这条弦所对的弧;(3)90°的圆周角所对的弦是直径;(4)同弧或等弧所对的圆周角相等;(5)相等的圆周角所对的弧相等.其中正确的命题有( ) A.2个B.3个C.4个D.5个9.如图,☉O 的半径为3,直径AB 与弦CD 相交于点E ,连接AC ,BD ,若AC=2,则tan D 的值是( )A .2√2B .2√23C .√24D .13 10.如图,已知AB 为☉O 的直径,直线BC 与☉O 相切于点B ,过A 作AD ∥OC 交☉O 于点D ,连接CD.(1)求证:CD 是☉O 的切线.(2)若AD=2,直径AB=6,求线段BC 的长.【素养拓展】11.如图,在☉O 上位于直径AB 的异侧有定点C 和动点P ,AC=12AB ,点P 在半圆弧AB⏜上运动(不与A ,B 两点重合),过点C 作直线PB 的垂线CD ,交PB 于点D. (1)如图1,求证:△PCD ∽△ABC.(2)当点P 运动到什么位置时,△PCD ≌△ABC ?请在图2中画出△PCD ,并说明理由. (3)如图3,当CP ⊥AB 时,求∠BCD 的度数.参考答案【基础达标】1.D2.B3.A4.D5.70°6.解:(1)∵AB ⏜的半径OA=2,OC ⊥AB 于点C ,∠AOC=60°,∴AC=OA ·sin 60°=2×√32=√3,∴AB=2AC=2√3.(2)∵OC ⊥AB ,∠AOC=60°,∴∠AOB=120°. ∵OA=2,∴AB⏜的长是120π×2180=4π3∴扇形OAB 的周长=AB⏜+AO+BO=4π3+4. 【能力巩固】 7.A 8.A 9.A10.解:(1)证明:如图,连接OD.∵AD∥OC∴∠COB=∠DAO,∠COD=∠ADO.∵AO=DO∴∠DAO=∠ADO.∴∠COD=∠COB.又∵DO=BO,CO=CO∴△CDO≌△CBO.∵直线BC与☉O相切于点B,∴∠CBO=90°.∴∠CDO=90°,即CD⊥OD ∴CD是☉O的切线.(2)如图,连接BD,∵AB是直径∴∠ADB=90°.在直角△ADB中BD=√AB2-AD2=√62-22=4√2∵∠ADB=∠OBC=90°,且∠COB=∠BAD∴△ADB∽△OBC.∴ADOB =DBBC,即23=4√2BC.∴BC=6√2.【素养拓展】11.解:(1)证明:∵AB是☉O的直径∴∠ACB=90°∵PD⊥CD,∴∠D=90°∴∠D=∠ACB∵∠A与∠P是BC⏜所对的圆周角∴∠A=∠P,∴△PCD∽△ABC.(2)在图2中画图略.当PC是☉O的直径时,△PCD≌△ABC.理由:∵AB,PC是☉O的直径,∴AB=PC∵△PCD∽△ABC,∴△PCD≌△ABC.AB(3)∵∠ACB=90°,AC=12∴∠ABC=30°∵△PCD∽△ABC,∴∠PCD=∠ABC=30°∵CP⊥AB,AB是☉O的直径⏜=AP⏜∴AC∴∠ACP=∠ABC=30°∴∠BCD=∠ACB-∠ACP-∠PCD=90°-30°-30°=30°.。
(完整)北师大版九年级下册数学第三章圆单元测试(含答案),推荐文档

一、选择题第三章圆1. 已知⊙O 的直径为 10,点 P 到点 O 的距离大于 8,那么点 P 的位置( )A. 一定在⊙O 的内部B. 一定在⊙O 的外部C. 一定在⊙O 上D. 不能确定2. 乌镇是著名的水乡,如图,圆拱桥的拱顶到水面的距离 CD 为 8m ,水面宽 AB 为 8m ,则桥拱半径 OC 为( )A. 4mB. 5mC. 6mD. 8m3. 给出下列说法:①直径是弦;②优弧是半圆;③半径是圆的组成部分;④两个半径不相等的圆中,大的半圆的弧长小于小的半圆的周长.其中正确的有( )A. 1 个B. 2 个C. 3 个D. 4 个4. 一个扇形的圆心角是 120°,面积为 3πcm 2, 那么这个扇形的半径是() A. cm B. 3cmC. 6cmD. 9cm5. 如图,点 A,B,C 均在坐标轴上,AO=BO=CO=1,过 A,O,C 作⊙D ,E 是⊙D 上任意一点,连结 CE, BE ,则的最大值是( )A. 4B. 5C. 6D.6. 如图,在⊙O 中,弦 AC与半径OB 平行,若∠BOC=50°,则∠B 的大小为()A. 25°B. 30°C. 50°D. 60°7.在研究圆的有关性质时,我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合”.由此说明()A.圆的直径互相平分B.垂直弦的直径平分弦及弦所对的弧C.圆是中心对称图形,圆心是它的对称中心D.圆是轴对称图形,任意一条直径所在的直线都是它的对称轴8.如图,AB 为⊙O 的直径,点E、C 都在圆上,连接AE,CE,BC,过点A 作⊙O 的切线交BC 的延长线于点D,若∠AEC=25°,则∠D 的度数为()A. 75°B. 65°C. 55°D. 74°9.如图,四边形ABCD 内接于圆O,E 为CD 延长线上一点,若∠B=110°,则∠ADE 的度数为()A. 115°B. 110°C. 90°D. 80°10.已知:⊙O 是△ABC 的外接圆,∠OAB=40°,则∠ACB 的大小为()A. 20°B. 50°C. 20°或160°D. 50°或130°11.如图,⊙O 内切于四边形ABCD,AB=10,BC=7,CD=8,则AD 的长度为()A. 8B. 9C. 10D. 1112.如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D 在半径OA 上,点F 在半径OB 上,点E 在上,则扇形与正方形的面积比是()A. π:8B. 5π:8C. π:4D. π:4二、填空题13.PA,PB 分别切⊙O 于A,B 两点,点C 为⊙O 上不同于AB 的任意一点,已知∠P=40°,则∠ACB 的度数是.14.如图,AB 为⊙O 的直径,直线l 与⊙O 相切于点C,AD⊥l,垂足为D,AD 交⊙O 于点E,连接OC、BE.若AE=6,OA=5,则线段DC 的长为.15.如图,AB 是⊙O 的直径,点C 在⊙O 上,∠AOC=40°,D 是BC 弧的中点,则∠ACD= .16.如图所示,⊙I 是Rt△ABC 的内切圆,点D、E、F 分别是且点,若∠ACB=90°,AB=5cm,BC=4cm,则⊙I 的周长为cm.17.如图,PA,PB 是⊙O 的切线,CD 切⊙O 于E,PA=6,则△PDC 的周长为.18.如图,⊙O 的半径为6cm,B 为⊙O 外一点,OB 交⊙O 于点A,AB=OA,动点P 从点A 出发,以πcm/s 的速度在⊙O 上按逆时针方向运动一周回到点A 立即停止.当点P 运动的时间为时,BP 与⊙O 相切.19.如图,在⊙O 的内接四边形ABCD 中,点E 在DC 的延长线上.若∠A=50°,则∠BCE= .20.如图,△ABC 中,∠BAC=90°,点G 是△ABC 的重心,如果AG=4,那么BC 的长为.21.如图,在△ABC 中,AB=AC=3,∠BAC=120°,以点A 为圆心,1 为半径作圆弧,分别交AB,AC 于点D,E,以点C 为圆心,3 为半径作圆弧,分别交AC,BC 于点A,F.若图中阴影部分的面积分别为S1,S2,则S1﹣S2的值为.22.如图所示,在半圆O 中,AB 为直径,P 为弧AB 的中点,分别在弧AP 和弧PB 上取中点A1和B1,再在弧PA1和弧PB1上分别取中点A2和B2,若一直这样取中点,求∠A n PB n= .三、解答题23.如图,AB 为⊙O 的直径,C 是⊙O 上一点,D 在AB 的延长线上,且∠DCB=∠A.求证:CD 是⊙O 的切线.24.如图,已知AB 是半圆O 的直径,∠BAC=32°,D 是弧AC 的中点,求∠DAC 的度数.25.如图,ABCD 是⊙O 的内接四边形,DP∥AC,交BA 的延长线于P,求证:AD•DC=PA•BC.26.(2017•通辽)如图,AB 为⊙O 的直径,D 为的中点,连接OD 交弦AC 于点F,过点D 作DE∥AC,交BA 的延长线于点E.(1)求证:DE 是⊙O 的切线;(2)连接CD,若OA=AE=4,求四边形ACDE 的面积.参考答案一、选择题B B A BC AD B B D D B二、填空题13. 70°或110°14. 4 15.125°16. 2π17. 1218. 2 秒或5 秒19. 50°20. 1221. - π22. 180°﹣×180°三、解答题23.解:证明:连接OC,∵AB 是⊙O 的直径,∴∠ACB=90°,∴∠A+∠ABC=90°,又∵OB=OC,∴∠OBC=∠OCB,又∵∠DCB=∠A,∴∠A+∠ABC=∠DCB+∠OCB=90°,∴OC⊥DC,∴CD 是⊙O 的切线.24.解:连接BC,∵AB 是半圆O 的直径,∠BAC=32°,∴∠ACB=90°,∠B=90°﹣32°=58°,∴∠D=180°﹣∠B=122°(圆内接四边形对角互补),∵D 是弧的中点,∴∠DAC=∠DCA=(180°﹣∠D)÷2=29°,即∠DAC 的度数是29°.25.证明:如图,连接AC,连接BD.∵DP∥AC,∴∠PDA=∠DAC.∵∠DAC=∠DBC,∴∠PDA=∠DBC.∵四边形ABCD 是圆内接四边形,∴∠DAP=∠DCB.∴△PAD∽△DCB.得PA:DC=AD:BC,即AD•DC=PA•BC.26.(1)证明:∵D 为的中点,∴OD⊥AC,∵AC∥DE,∴OD⊥DE,∴DE 是⊙O 的切线(2)解:连接DC,∵D 为的中点,∴OD⊥AC,AF=CF,∵AC∥DE,且OA=AE,∴F 为OD 的中点,即OF=FD,在△AFO 和△CFD 中,∴△AFO➴△CFD(SAS),∴S△AFO=S△CFD ,∴S 四边形ACDE=S△ODE在Rt△ODE 中,OD=OA=AE=4,∴OE=8,∴DE= =4 ,∴S 四边形ACDE=S△ODE= ×OD×DE= ×4×4 =8 .“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
北师大版九年级数学下册第三章-圆 单元测试题(含答案)

九年级数学圆单元测试题一、选择题1.若⊙O 所在平面内一点 P 到⊙O 上的点的最大距离为 a ,最小距离为 b (a>b ),则此圆的 半径为( )A .2a b + B .2a b- C .2a b +或2a b - D . a + b 或a - b 2.如图 24—A —1,⊙O 的直径为 10,圆心 O 到弦 AB 的距离 OM 的长为 3,则弦 AB 的 长是( ) A .4 B .6 C .7 D .8 3.已知点 O 为△ABC 的外心,若∠A=80°,则∠BOC 的度数为( ) A .40° B .80° C .160° D .120° 4.如图 24—A —2,△ABC 内接于⊙O ,若∠A=40°,则∠OBC 的度数为( ) A .20° B .40° C .50° D .70°图 24—A —2图 24—A —3 图 24—A —4 图 24—A —55.如图 24—A —3,小明同学设计了一个测量圆直径的工具,标有刻度的尺子 OA 、OB 在 O 点钉在一起,并使它们保持垂直,在测直径时,把 O 点靠在圆周上,读得刻度 OE=8 个 单位,OF=6 个单位,则圆的直径为( ) A .12 个单位 B .10 个单位 C .1 个单位 D .15 个单位 6.如图 24—A —4,AB 为⊙O 的直径,点 C 在⊙O 上,若∠B=60°,则∠A 等于( ) A .80° B .50° C .40° D .30° 7.如图 24—A —5,P 为⊙O 外一点,PA 、PB 分别切⊙O 于 A 、B ,CD 切⊙O 于点 E ,分 别交 PA 、PB 于点 C 、D ,若 PA=5,则△PCD 的周长为( ) A .5 B .7 C .8 D .10 8.若粮仓顶部是圆锥形,且这个圆锥的底面直径为 4m ,母线长为 3m ,为防雨需在粮仓顶 部铺上油毡,则这块油毡的面积是( )A .6m 2B . 6πm 2C .12m 2D .12πm 29.如图 24—A —6,两个同心圆,大圆的弦 AB 与小圆相切于点 P ,大圆的弦 CD 经过点 P ,且 CD=13,PC=4,则两圆组成的圆环的面积是( ) A .16π B .36π C .52π D .81π10.已知在△ABC 中,AB=AC=13,BC=10,那么△ABC 的内切圆的半径为( ) A .103 B .125C .2D .311.如图 24—A —7,两个半径都是 4cm 的圆外切于点 C ,一只蚂蚁由点 A 开 始依 A 、B 、C 、D 、E 、F 、C 、G 、A 的顺序沿着圆周上的 8 段长度相等的路径 绕行,蚂蚁在这 8 段路径上不断爬行,直到行走 2006π cm 后才停下来,则蚂蚁 停的那一个点为( )A .D 点B .E 点C .F 点D .G 点二、填空题12.如图 24—A —8,在⊙O 中,弦 AB 等于⊙O 的半径,OC ⊥AB 交⊙O 于点 C ,则∠ AOC= 。
北师大版九年级下册数学 第三章 圆 单元测试卷(含答案解析)

北师大版九年级下册数学第三章圆单元测试卷(满分120分;时间:120分钟)一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 下列说法正确的个数是()①直径是圆的对称轴;②半径相等的两个半圆是等弧;③长度相等的两条弧是等弧;④和圆有一个公共点的直线是圆的切线.A.1B.2C.3D.42. 圆内接四边形MNPQ中,∠M、∠N、∠P的度数比是3:4:6,则∠Q的度数为()A.60∘B.80∘C.100∘D.120∘3. 某公园计划砌一个形状如图(1)的喷水池,后来有人建议改为图(2)的形状,且外圆的直径不变,若两种方案砌各圆形水池的周边需用的材料费分别为W1和W2,则()A.W1<W2B.W1>W2C.W1=W2D.无法确定4. 如图,AB、CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F.如果AB=CD,那么下列判断中错误的是()̂=CD̂ B.∠AOB=∠CODA.ABC.OE=OFD.∠AOC=∠BOD̂的中点,连接OC,点E,F分别是OA,OC上的点,5. 如图,AB是⊙O的直径,C是AB若EF // AC,则∠EFC的度数为()A.45∘B.60∘C.135∘D.160∘6. 下列说法中,正确的是()A.90∘的圆周角所对的弦是直径B.平分弦的直径垂直于弦,并且平分弦所对的两条弧C.经过半径的端点并且垂直于这条半径的直线是这个圆的切线D.长度相等的弧是等弧7. 如图,⊙O阴影部分为残缺部分,现要在剩下部分裁去一个最大的正方形,若OP=2,⊙O半径为5,则裁去的最大正方形边长为多少?()A.7B.6C.5D.48. 如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是()。
北师大版九年级数学下册《第三章圆》单元测试题(有答案)
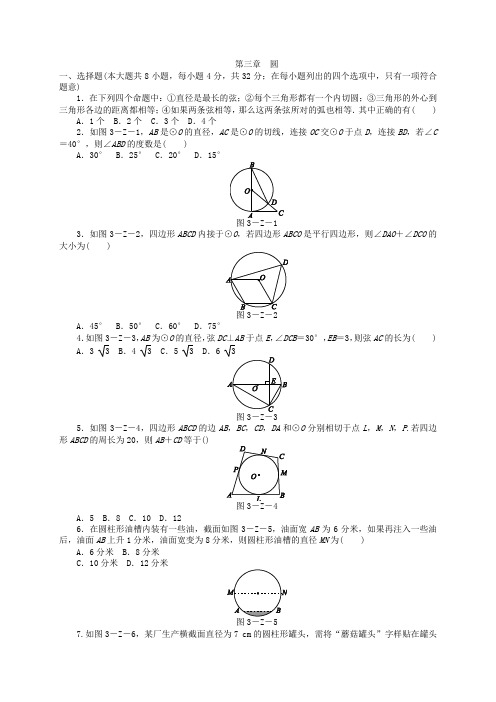
第三章圆一、选择题(本大题共8小题,每小题4分,共32分;在每小题列出的四个选项中,只有一项符合题意)1.在下列四个命题中:①直径是最长的弦;②每个三角形都有一个内切圆;③三角形的外心到三角形各边的距离都相等;④如果两条弦相等,那么这两条弦所对的弧也相等.其中正确的有( ) A.1个 B.2个 C.3个 D.4个2.如图3-Z-1,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,若∠C =40°,则∠ABD的度数是( )A.30° B.25° C.20° D.15°3.如图3-Z-2,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )A.45° B.50° C.60° D.75°4.如图3-Z-3,AB为⊙O的直径,弦DC⊥AB于点E,∠DCB=30°,EB=3,则弦AC的长为( )A.3 3 B.4 3 C.5 3 D.5.如图3-Z-4,四边形ABCD的边AB,BC,CD,DA和⊙O分别相切于点L,M,N,P.若四边形ABCD的周长为20,则AB+CD等于()A.5 B.8 C.10 D.126.在圆柱形油槽内装有一些油,截面如图3-Z-5,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,则圆柱形油槽的直径MN为( ) A.6分米 B.8分米C.10分米 D.12分米图3-Z-57.如图3-Z-6,某厂生产横截面直径为7 cm的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳的视觉效果,字样在罐头侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()图3-Z -6A.π4 cmB.7π4 cmC.7π2cm D .7π cm 8.如图3-Z -7,四边形ABCD 是菱形,∠A =60°,AB =2,扇形BEF 的半径为2,圆心角为60°,则图中阴影部分的面积是( )A.2π3-32B.2π3- 3 C .π-32D .π- 3 二、填空题(本大题共5小题,每小题4分,共20分)9.已知⊙O 的半径为5,点A 在⊙O 外,那么线段OA 的长度的取值范围是________.10.如图3-Z -8,已知经过原点的⊙P 与x 轴、y 轴分别交于A ,B 两点,C 是劣弧OB 上一点,则∠ACB 的度数为________.11.如图3-Z -9,在⊙O 中,弦DA ∥BC ,DA =DC ,∠AOC =160°,则∠BCO =________度.图3-Z -912.如图3-Z -10,正方形ABCD 内接于⊙O ,其边长为4,则⊙O 的内接正三角形EFG 的边长为________.13.如图3-Z -11,在Rt △AOB 中,OA =OB =3 2,⊙O 的半径为1,P 是AB 边上的动点,过点P 作⊙O 的一条切线PQ (Q 为切点),则切线PQ 长的最小值为________.图3-Z -11三、解答题(本大题共4小题,共48分) 14.(10分)如图3-Z -12,已知四边形ABCD 内接于⊙O ,连接BD ,∠BAD =105°,∠DBC =75°. (1)求证:BD =CD ;(2)若⊙O 的半径为3,求BC ︵的长.15.(12分)如图3-Z -13,BE 是⊙O 的直径,半径OA ⊥弦BC ,D 为垂足,连接AE ,EC . (1)若∠AEC =28°,求∠AOB 的度数; (2)若∠BEA =∠B ,BC =6,求⊙O图3-Z -1316.(12分)如图3-Z -14,⊙O 的半径为4,B 是⊙O 外一点,连接OB ,且OB =6,过点B 作⊙O 的切线BD ,切点为D ,延长BO 交⊙O 于点A ,过点A 作切线BD 的垂线,垂足为C .(1)连接AD ,求证:AD 平分∠BAC ; (2)求AC 的长.图3-Z -1417.(14分)如图3-Z -15①,⊙O 的直径AB =12,P 是弦BC 上一动点(与点B ,C 不重合),∠ABC =30°,过点P 作PD ⊥OP 交⊙O 于点D .(1)如图②,当PD ∥AB 时,求PD 的长.(2)如图③,当DC ︵=AC ︵时,延长AB 至点E ,使BE =12AB ,连接DE .①求证:DE 是⊙O 的切线; ②求PC 的长.图Z -15详解详析1.[答案] B 2.[解析] B ∵AC 是⊙O 的切线,∴∠BAC =90°.又∠C =40°,∴∠AOC =90°-40°=50°,∴∠ABD =12∠AOC =12×50°=25°.故选B.3.[解析] C 连接OD ,∵OA =OD ,OD =OC ,∴∠DAO =∠ODA ,∠DCO =∠ODC ,∴∠DAO +∠DCO =∠ADC .∵四边形ABCO 是平行四边形,∴∠B =∠AOC .∵四边形ABCD 是圆内接四边形, ∴∠ADC +∠B =180°.∵∠ADC =12∠AOC ,∴∠ADC =12∠B ,即3∠ADC =180°,∴∠ADC =60°,即∠DAO +∠DCO =60°.故选C.4.[解析] D 如图,连接OC ,∵弦DCB =30°,∴∠ABC =60°,∴△BOC 是等边三角形.∵EB =3,∴OB =6,∴AB =12.∵AB 为⊙O 的直径,∴∠ACB =90°.在Rt △ACB 中,AC =12×32=6 3.故选D.5.[答案] C 6.[答案] C7.[解析] B ∵字样在罐头侧面所形成的弧的度数为90°,∴此弧所对的圆心角为90°,由题意可得R =72 cm ,则“蘑菇罐头”字样的长为90π×72180=7π4(cm).8.[解析] B 如图,连接BD .A =60°,∴∠ADC =120°,∴∠1=∠2=60°,∴△DAB 是等边三角形,∴AB =BD ,∠3+∠5=60°.∵AB =2,∴△ABD 的高为 3.∵扇形BEF 的圆心角为60°,∴∠4+∠5=60°,∴∠3=∠4.设AD ,BE 相交于点G ,BF ,DC 相交于点H ,在△ABG 和△DBH 中,∠A =∠2,AB =BD ,∠3=∠4,∴△ABG ≌△DBH (ASA),∴S 四边形GBHD =S △ABD ,∴S 阴影=S 扇形EBF -S △ABD =60π×22360-12×2×3=2π3- 3.故选B. 9.[答案] OA >5[解析] ∵⊙O 的半径为5,点A 在⊙O 外,∴线段OA 的长度的取值范围是OA >5.故答案为OA >5.10.[答案] 90°[解析] ∵∠AOB =90°,∴∠ACB =∠11.[答案] 30 [解析] 连接AC ,∵∠B =12∠AOC =80°,∴∠D =180°-∠B =100°. ∵DA =DC ,OA =OC ,∴∠DAC =∠ACD =40°,∠OCA =∠OAC =10°. ∵DA ∥BC ,∴∠ACB =∠DAC =40°, ∴∠BCO =30°. 12.[答案] 2 6[解析] 连接AC ,OE ,OF ,过点O 作OM ⊥EF 于点M .∵四边形ABCD 是正方形,∴AB =BC =4 ∴AC 是直径,AC =4 2, ∴OE =OF =2 2. ∵OM ⊥EF ,∴EM =MF .∵△EFG 是等边三角形,∴∠GEF =60°.在Rt △OME 中,∵OE =2 2,∠OEM =12∠GEF =30°,∴OM =2,EM =3OM =6,∴EF =13.[答案] 2 2[解析] 如图,连接OP ,OQ .∵PQ 是⊙O 的切线,∴OQ ⊥PQ ,∴PQ 2=OP 2-OQ 2,∴当OP ⊥AB 时,OP 最短,则此时线段PQ 最短.∵在Rt △AOB 中,OA =OB =3 2,∴AB =2OA =6,∴OP =OA ·OB AB=3,∴PQ =OP 2-OQ 2=32-12=2 2.14.解:(1)证明:∵四边形ABCD 内接于⊙O ,∴∠DCB +∠BAD =180°. ∵∠BAD =105°,∴∠DCB =180°-105°=75°, ∴∠DCB =∠DBC ,∴BD =CD .(2)由(1)可知∠DBC =∠DCB =75°,∴∠BDC =30°.由圆周角定理得BC ︵的度数为60°,故BC ︵的长为60π×3180=π.15.[解析] (1)根据垂径定理得到AC ︵=AB ︵,根据圆周角定理解答;(2)根据圆周角定理的推论得到∠C =90°,进而得到∠B =30°,根据余弦的定义求出BE 的长即可.解:(1)∵OA ⊥BC ,∴AC ︵=AB ︵, ∴∠BEA =∠AEC =28°,由圆周角定理,得∠AOB =2∠AEB =56°. (2)∵BE 是⊙O 的直径,∴∠C =90°, ∴∠CEB +∠B =90°.又∵∠BEA =∠B ,∠BEA =∠AEC , ∴∠B =30°,∴BE =BCcos B=4 3,∴⊙O 的半径为2 3.16.解:(1)证明:连接OD . ∵BD 是⊙O 的切线,∴OD ⊥BD . 又∵AC ⊥BD ,∴OD ∥AC , ∴∠CAD =∠ODA .∵OA =OD ,∴∠OAD =∠ODA ,∴∠OAD =∠CAD ,即AD 平分∠BAC . (2)∵OD ∥AC ,∴△BOD ∽△BAC , ∴OD AC =BO BA ,即4AC =610, 解得AC =203,即AC 的长为203.17.解:(1)连接OD .∵OP ⊥PD ,PD ∥AB ,∴∠POB =90°. ∵⊙O 的直径AB =12,∴OB =OD =6.在Rt △POB 中,∵∠ABC =30°,∴OP =OB ·tan30°=6×33=2 3. 在Rt △POD 中,PD =OD 2-OP 2=62-(2 3)2=2 6. (2)①证明:连接OD ,交CB 于点F ,连接BD . ∵DC ︵=AC ︵,∴∠DBC =∠ABC =30°,∴∠ABD =60°. 又∵OB =OD ,∴△OBD 是等边三角形, ∴∠DOB =60°,则∠OFB =180°-60°-30°=90°, ∴OD ⊥FB ,∴OF =DF .又∵BE =12AB ,OB =12AB ,∴OB =BE ,∴BF ∥DE , ∴∠ODE =∠OFB =90°, ∴DE 是⊙O 的切线.②由①知OD ⊥BC ,∴CF =BF =OB ·cos30°=6×32=3 3.在Rt △POD 中,∵OF =DF ,∴PF =错误!OD =3,∴PC =CF -PF =3 错误!-3.。
北师版初中数学九年级下册第3章圆单元测试一及答案.doc

单元测试(一)一.选择题1.如图,四边形 ABCD内接⊙ O,AC 均分∠ BAD,则以下结论正确的选项是()A.AB=AD B.BC=CD C. D.∠ BCA=∠DCA2.如图,CD 为⊙ O 的直径,弦 AB⊥CD,垂足为 M,若 AB=12,OM:MD=5:8,则⊙ O 的周长为()A.26πB.13πC.D.3.如图, AB 是⊙ O 的直径,弦 CD 交 AB 于点 P,AP=2,BP=6,∠ APC=30°,则CD的长为()A.B.2C.2D.84.如图,△ ABC内接于⊙ O,若∠ A=α,则∠ OBC等于()A.180°﹣2αB.2α C.90°+αD.90°﹣α5.如图,四边形 ABCD为⊙ O 的内接四边形.延伸AB 与 DC订交于点 G, AO⊥CD,垂足为 E,连结 BD,∠ GBC=50°,则∠ DBC的度数为()A.50°B. 60°C.80°D.90°6.在平面直角坐标系中,点 O 为坐标原点,点 A、B、C 的坐标分别为 A(, 0)、B(3,0)、C(0,5),点 D 在第一象限内,且∠ ADB=60°,则线段 CD的长的最小值是()A.2﹣2B.2C.2D.27.以下说法中,正确的选项是()A.三点确立一个圆B.三角形有且只有一个外接圆C.四边形都有一个外接圆D.圆有且只有一个内接三角形8.如图,在平面直角坐标系中,点A,B,C 的坐标为( 1,4),(5,4),( 1,﹣ 2),则△ ABC外接圆的圆心坐标是()A.(2,3) B.(3,2) C.(1,3) D.(3,1)9.在平面直角坐标系xOy 中,经过点( sin45 ,°cos30 °)的直线,与以原点为圆心, 2 为半径的圆的地点关系是()A.订交B.相切C.相离D.以上三者都有可能10.如图,菱形 ABCD的边 AB=20,面积为 320,∠BAD<90°,⊙O 与边 AB,AD 都相切, AO=10,则⊙ O 的半径长等于()A.5B.6C.2D.3E,分11.如图, P 为⊙ O 外一点, PA、 PB分别切⊙ O 于 A、 B, CD 切⊙ O 于点别交 PA、PB于点 C、 D,若 PA=5,则△ PCD的周长为()A.5B.7C.8D.1012.如图, AB是⊙ O 的直径,点 E 为 BC的中点, AB=4,∠ BED=120°,则图中阴影部分的面积之和为()A.B.2C.D.1二、填空题13.如图, CD是⊙ O 的直径,弦 AB⊥CD 于点 H,若∠ D=30°,CH=1cm,则 AB= cm.14.在△ AOB 中, AB=OB=2,△ COD中, CD=OC=3,∠ ABO=∠DCO.连结 AD、BC,点 M 、N、P 分别为 OA、OD、BC的中点.①若 A、O、C 三点在同向来线上,且∠ABO=2α,则 =(用含有α的式子表示);②固定△AOB,将△ COD绕点O 旋转, PM 最大值为.15.如图,给定一个半径长为 2 的圆,圆心 O 到水平直线 l 的距离为 d,即OM=d.我们把圆上到直线 l 的距离等于 1 的点的个数记为 m.如 d=0 时, l 为经过圆心 O的一条直线,此时圆上有四个到直线l 的距离等于 1 的点,即m=4,由此可知:(1)当 d=3 时, m=;(2)当 m=2 时, d 的取值范围是.16.)如图,⊙ O 的半径为 6cm,B 为⊙ O 外一点, OB 交⊙ O 于点 A, AB=OA,动点 P 从点 A 出发,以π cm/s 的速度在⊙ O 上按逆时针方向运动一周回到点 A立刻停止.当点P 运动的时间为时,BP与⊙ O相切.17.芸豆17(2017?岳阳)我国魏晋期间的数学家刘徽创办了“割圆术”,以为圆内接正多边形边数无穷增添时,周长就越靠近圆周长,由此求得了圆周率π的近似值,设半径为 r 的圆内接正 n 边形的周长为 L,圆的直径为 d,如下图,当n=6 时,π≈==3,那么当 n=12 时,π≈=.(结果精准到0.01,参照数据:sin15 =cos75° ≈°0.259)三、解答题18.如图,在 Rt△AOB中,∠ B=40°,以 OA 为半径, O 为圆心作⊙ O,交 AB 于点 C,交 OB于点 D.求的度数.19.如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽 CD=米.(1)求此圆形门洞的半径;(2)求要打掉墙体的面积.20.如图,有两条公路 OM,ON 订交成 30°,沿公路 OM 方向离两条公路的交错处 O 点 80 米的 A 处有一所希望小学,当拖沓机沿 ON 方向行驶时,路两旁 50米内会遇到噪音影响,已知有两台相距 30 米的拖沓机正沿 ON 方向行驶,它们的速度均为 5 米 / 秒,问这两台拖沓机沿 ON 方向行驶时给小学带来噪音影响的时间是多少?21.如图, AN 是⊙M 的直径, NB∥x 轴, AB 交⊙ M 于点 C.(1)若点 A( 0, 6),N(0, 2),∠ ABN=30°,求点 B 的坐标;(2)若 D 为线段 NB 的中点,求证:直线CD是⊙ M 的切线.22.如图,直线 AB、BC、CD分别与⊙ O 相切于 E、F、G,且 AB∥ CD,OB=6cm,OC=8cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O 的半径.23.如图,在⊙ O 中,弦 AB=弦 CD,AB⊥CD于点 E,且 AE<EB,CE<ED,连结AO,DO,BD.(1)求证: EB=ED.(2)若 AO=6,求的长.24.中国扇文化有着深沉的文化底蕴,是民族文化的一个构成部分,它与竹文化、佛教文化有着亲密关系.向来中国被誉为制扇王国.扇子主要资料是:竹、木、纸、象牙、玳瑁、翡翠、飞禽翎毛、其他棕榈叶、槟榔叶、麦杆、蒲草等也能编制成各样千姿百态的日用工艺扇,造型优美,结构精制,经能工巧匠精心镂、雕、烫、钻或名人挥毫题诗作画,使扇子艺术身价倍增.折扇,古称“聚头扇“,或称为撒扇,或折叠扇,以其收拢时能够二头归并归一而得名.如图,折扇的骨柄OA 的长为 5a,扇面的宽 CA的长为 3a,折扇张开的角度为n°,求出扇面的面积(用代数式表示).答案与分析1.如图,四边形 ABCD内接⊙ O,AC 均分∠ BAD,则以下结论正确的选项是()A.AB=AD B.BC=CD C. D.∠ BCA=∠DCA【考点】 M4:圆心角、弧、弦的关系.【专题】选择题【剖析】依据圆心角、弧、弦的关系对各选项进行逐个判断即可.【解答】解:A、∵∠ ACB与∠ ACD的大小关系不确立,∴ AB 与 AD 不必定相等,故本选项错误;B、∵ AC均分∠ BAD,∴∠ BAC=∠ DAC,∴ BC=CD,故本选项正确;C、∵∠ ACB与∠ ACD的大小关系不确立,∴与不必定相等,故本选项错误;D、∠ BCA与∠ DCA的大小关系不确立,故本选项错误.应选 B.【评论】本题考察的是圆心角、弧、弦的关系,在同圆或等圆中,假如两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其他各组量都分别相等.2.如图,CD 为⊙ O 的直径,弦 AB⊥CD,垂足为 M,若 AB=12,OM:MD=5:8,则⊙ O 的周长为()A.26πB.13πC. D.【考点】 M2:垂径定理.【专题】选择题【剖析】连结OA,依据垂径定理获得AM=AB=6,设OM=5x, DM=8x,获得OA=OD=13x,依据勾股定理获得OA=×13,于是获得结论.【解答】解:连结 OA,∵CD为⊙ O 的直径,弦 AB⊥CD,∴ AM=AB=6,∵OM:MD=5: 8,∴设 OM=5x,DM=8x,∴AM=12x=6,∴x=,∴OA=×13,∴⊙ O 的周长 =2OA?π=13π,应选 B.【评论】本题考察的是垂径定理,依据题意作出协助线,结构出直角三角形,利用勾股定理求解是解答本题的重点.3.如图, AB 是⊙ O 的直径,弦 CD 交 AB 于点 P,AP=2,BP=6,∠ APC=30°,则CD的长为()A. B.2 C.2D.8【考点】 M2:垂径定理; KO:含 30 度角的直角三角形; KQ:勾股定理.【专题】选择题【剖析】作 OH⊥ CD于 H,连结 OC,如图,依据垂径定原因 OH⊥CD获得HC=HD,再利用 AP=2, BP=6可计算出半径 OA=4,则 OP=OA﹣AP=2,接着在Rt△ OPH中依据含 30 度的直角三角形的性质计算出 OH=OP=1,而后在 Rt△OHC 中利用勾股定理计算出 CH=,因此 CD=2CH=2.【解答】解:作 OH⊥ CD于 H,连结 OC,如图,∵OH⊥ CD,∴ HC=HD,∵AP=2, BP=6,∴ AB=8,∴ OA=4,∴ OP=OA﹣ AP=2,在 Rt△OPH中,∵∠OPH=30°,∴∠ POH=30°,在Rt△OHC中,∵OC=4,OH=1,∴ CH==,∴ CD=2CH=2.应选 C.【评论】本题考察了垂径定理:垂直于弦的直径均分这条弦,而且均分弦所对的两条弧.也考察了勾股定理以及含 30 度的直角三角形的性质.4.如图,△ ABC内接于⊙ O,若∠ A=α,则∠ OBC等于()A.180°﹣2αB.2α C.90°+αD.90°﹣α【考点】 M5:圆周角定理.【专题】选择题【剖析】第一连结 OC,由圆周角定理,可求得∠BOC的度数,又由等腰三角形的性质,即可求得∠ OBC的度数.【解答】解:∵连结 OC,∵△ ABC内接于⊙ O,∠ A=α,∴∠ BOC=2∠ A=2α,∵OB=OC,∴∠ OBC=∠OCB==90°﹣α.应选 D.【评论】本题考察了圆周角定理与等腰三角形的性质.本题比较简单,注意掌握协助线的作法,注意数形联合思想的应用.5.如图,四边形 ABCD为⊙ O 的内接四边形.延伸AB 与 DC订交于点 G, AO⊥CD,垂足为 E,连结 BD,∠ GBC=50°,则∠ DBC的度数为()A.50°B.60°C.80°D.90°【考点】 M6:圆内接四边形的性质.【专题】选择题【剖析】依据四点共圆的性质得:∠GBC=∠ ADC=50°,由垂径定理得:,则∠ DBC=2∠EAD=80°.【解答】解:如图,∵ A、B、 D、 C 四点共圆,∴∠ GBC=∠ADC=50°,∵AE⊥CD,∴∠ AED=90°,∴∠ EAD=90°﹣50°=40°,延伸 AE交⊙ O 于点 M,∵AO⊥ CD,∴,∴∠ DBC=2∠EAD=80°.应选 C.【评论】本题考察了四点共圆的性质:圆内接四边形的随意一个外角等于它的内对角,还考察了垂径定理的应用,属于基础题.6.在平面直角坐标系中,点 O 为坐标原点,点 A、B、C 的坐标分别为 A(, 0)、B(3,0)、C(0,5),点 D 在第一象限内,且∠ ADB=60°,则线段 CD的长的最小值是()A.2﹣2B.2C.2D.2【考点】 M8:点与圆的地点关系; D5:坐标与图形性质; M5:圆周角定理.【专题】选择题【剖析】作圆,求出半径和 PC的长度,判出点 D 只有在 CP上时 CD最短,CD=CP ﹣ DP求解.【解答】解:作圆,使∠ ADB=60°,设圆心为 P,连结 PA、PB、PC,PE⊥AB 于 E,如下图:∵A(,0)、B(3,0),∴E(2,0)又∠ ADB=60°,∴∠ APB=120°,∴ PE=1, PA=2PE=2,∴P(2,1),∵C(0,5),∴PC==2,又∵ PD=PA=2,∴只有点 D 在线段 PC上时, CD最短(点 D 在其他地点时构成△ CDP)∴CD最小值为: 2﹣2.应选: C.【评论】本题主要考察坐标与图形的性质,圆周角定理及勾股定理,解决本题的重点是判出点 D 只有在 CP上时 CD最短.7.以下说法中,正确的选项是()A.三点确立一个圆B.三角形有且只有一个外接圆C.四边形都有一个外接圆D.圆有且只有一个内接三角形【考点】 M9:确立圆的条件.【专题】选择题【剖析】依据确立圆的条件逐个判断后即可获得答案.【解答】解: A、不在同向来线上的三点确立一个圆,故原命题错误;B、三角形有且只有一个外切圆,原命题正确;C、其实不是全部的四边形都有一个外接圆,原命题错误;D、圆有无数个内接三角形.应选 B.【评论】本题考察了确立圆的条件,不在同向来线上的三点确立一个圆.8.如图,在平面直角坐标系中,点A,B,C 的坐标为( 1,4),(5,4),( 1,﹣ 2),则△ ABC外接圆的圆心坐标是()A.(2,3) B.(3,2) C.(1,3) D.(3,1)【考点】 MA:三角形的外接圆与外心;D5:坐标与图形性质.【专题】选择题【剖析】由已知点的坐标得出△ ABC为直角三角形,∠ BAC=90°,得出△ ABC的外接圆的圆心是斜边 BC的中点,即可得出结果.【解答】解:如下图:∵点 A,B,C 的坐标为( 1,4),(5,4),(1,﹣ 2),∴△ ABC为直角三角形,∠ BAC=90°,∴△ ABC的外接圆的圆心是斜边BC的中点,∴△ ABC外接圆的圆心坐标是(,),即( 3,1).应选: D.【评论】本题考察了三角形的外接圆与外心、坐标与图形性质、直角三角形的外心特点;熟记直角三角形的外心特点,依据题意得出三角形是直角三角形是解决问题的重点.9.在平面直角坐标系xOy 中,经过点( sin45 ,°cos30 °)的直线,与以原点为圆心, 2 为半径的圆的地点关系是()A.订交B.相切C.相离D.以上三者都有可能【考点】 MB:直线与圆的地点关系;D5:坐标与图形性质; T5:特别角的三角函数值.【专题】选择题【剖析】设直线经过的点为A,若点 A 在圆内则直线和圆必定订交;若点在圆上或圆外则直线和圆有可能订交或相切或相离,因此先要计算OA的长和半径 2 比较大小再做选择.【解答】解:设直线经过的点为A,∵点 A 的坐标为( sin45 °,cos30°),∴OA==,∵圆的半径为 2,∴OA< 2,∴点 A 在圆内,∴直线和圆必定订交,应选 A.【评论】本题考察了直线和圆的地点关系,用到的知识点有特别角的锐角三角函数值、勾股定理的运用,判断点 A 和圆的地点关系是解题重点.10.如图,菱形 ABCD的边 AB=20,面积为 320,∠BAD<90°,⊙O 与边 AB,AD 都相切, AO=10,则⊙ O 的半径长等于()A.5B.6C.2D.3【考点】 MC:切线的性质; L8:菱形的性质.【专题】选择题【剖析】如图作 DH⊥ AB 于 H,连结 BD,延伸 AO 交 BD 于 E.利用菱形的面积公式求出 DH,再利用勾股定理求出 AH,BD,由△ AOF∽△ DBH,可得 =,即可解决问题.【解答】解:如图作 DH⊥AB 于 H,连结 BD,延伸 AO 交 BD 于 E.∵菱形 ABCD的边 AB=20,面积为 320,∴AB?DH=32O,∴DH=16,在 Rt△ADH 中, AH==12,∴ HB=AB﹣ AH=8,在 Rt△BDH中, BD==8,设⊙ O 与 AB 相切于 F,连结 AF.∵AD=AB, OA 均分∠ DAB,∴ AE⊥BD,∵∠ OAF+∠ABE=90°,∠ ABE+∠BDH=90°,∴∠ OAF=∠BDH,∵∠ AFO=∠ DHB=90°,∴△ AOF∽△ DBH,∴=,∴=,∴OF=2.应选 C.【评论】本题考察切线的性质、菱形的性质、勾股定理、相像三角形的判断和性质等知识,解题的重点是学会增添常用协助线,结构直角三角形解决问题,属于中考常考题型.11.如图, P 为⊙ O 外一点, PA、 PB分别切⊙ O 于 A、 B, CD 切⊙ O 于点 E,分别交 PA、PB于点 C、 D,若 PA=5,则△ PCD的周长为()A.5B.7C.8D.10【考点】 MG:切线长定理.【专题】选择题【剖析】由切线长定理可得 PA=PB, CA=CE, DE=DB,由于△ PCD 的周长=PC+CE+ED+PD,因此△PCD的周=PC+CA+BD+PD=PA+PB=2PA,故可求得三角形的周长.【解答】解:∵ PA、PB 为圆的两条订交切线,∴PA=PB,同理可得: CA=CE, DE=DB.∵△ PCD的周长 =PC+CE+ED+PD,∴△ PCD的周长 =PC+CA+BD+PD=PA+PB=2PA,∴△ PCD的周长 =10,应选 D.【评论】本题考察了切线的性质以及切线长定理的运用.12.如图, AB是⊙ O 的直径,点 E 为 BC的中点, AB=4,∠ BED=120°,则图中阴影部分的面积之和为()A. B.2C. D.1【考点】 MO:扇形面积的计算.【专题】选择题【剖析】第一证明△ ABC是等边三角形.则△ EDC是等边三角形,边长是 2.而和弦 BE围成的部分的面积 =和弦 DE围成的部分的面积.据此即可求解.【解答】解:连结 AE, OD、 OE.∵AB是直径,∴∠AEB=90°,又∵∠BED=120°,∴∠ AED=30°,∴∠ AOD=2∠AED=60°.∵OA=OD∴△ AOD是等边三角形,∴∠ OAD=60°,∵点 E 为 BC的中点,∠ AEB=90°,∴AB=AC,∴△ ABC是等边三角形,边长是4.△ EDC是等边三角形,边长是2.∴∠ BOE=∠EOD=60°,∴和弦 BE围成的部分的面积 =和弦 DE围成的部分的面积.∴暗影部分的面积 =S△EDC=×22=.应选: A.【评论】本题考察了等边三角形的面积的计算,证明△EDC是等边三角形,边长是 4.理解和弦 BE围成的部分的面积 =和弦 DE 围成的部分的面积是重点.13.如图, CD是⊙ O 的直径,弦 AB⊥CD 于点 H,若∠ D=30°,CH=1cm,则 AB= 2cm.【考点】 M2:垂径定理.【专题】选择题【剖析】连结 AC、BC.利用圆周角定理知∠ D=∠B,而后依据已知条件“CD是⊙ O 的直径,弦 AB⊥CD 于点 H”,利用垂径定理知 BH=AB;最后再由直角三角形CHB的正切函数求得 BH 的长度,从而求得 AB 的长度.【解答】解:连结 AC、BC.∵∠ D=∠ B(同弧所对的圆周角相等),∠ D=30°,∴∠ B=30°;又∵ CD是⊙ O 的直径,弦 AB⊥CD于点 H,∴BH=AB;在 Rt△CHB中,∠ B=30°,CH=1cm,∴ BH=,即 BH=;∴ AB=2cm.故答案是: 2.【评论】本题考察了垂径定理和直角三角形的性质,解此类题目要注意将圆的问题转变成三角形的问题再进行计算.14.在△ AOB 中, AB=OB=2,△ COD中, CD=OC=3,∠ ABO=∠DCO.连结AD、BC,点 M 、N、P 分别为 OA、OD、BC的中点.①若 A、O、 C 三点在同向来线上,且∠ABO=2α,则 = 2sin α(用含有α的式子表示);②固定△ AOB,将△ COD绕点 O 旋转, PM 最大值为.【考点】 M9:确立圆的条件; KH:等腰三角形的性质;LL:梯形中位线定理;S9:相像三角形的判断与性质.【专题】填空题【剖析】 (1)连结 BM、CN,则 BM⊥OA,CN⊥OD,由四点共圆的判断知点B、C、M、N 在以 BC为直径的圆,且有 MP=PN=BC÷ 2,而 MN 是△ AOD的中位线,有MN 等于 AD 的一半,故 AD:BC=MN: PM,而可求得△ PMN∽△ BAO,有 MN:PN=AO:AB=2sin α,从而求得 AD:BC的值;(2)当 DC∥AB 时,即四边形 ABCO是梯形时, PM 有最大值,由梯形的中位线的公式可求解.【解答】解: (1)连结 BM、 CN,由题意知 BM⊥OA,CN⊥OD,∠ AOB=∠COD=90°﹣α,∵A、 O、C 三点在同向来线上,∴ B、 O、 D 三点也在同向来线上,∴∠ BMC=∠CNB=90°,∵P为 BC中点,∴在 Rt△ BMC 中, PM=BC,在 Rt△BNC中, PN=BC,∴PM=PN,∴B、 C、 N、 M 四点都在以点 P 为圆心, BC为半径的圆上,∴∠ MPN=2∠MBN,又∵∠ MBN=∠ABO=α,∴∠ MPN=∠ ABO,∴△PMN∽△ BAO,∴,由题意知 MN=AD,PM=BC,∴,∴,在 Rt△BMA 中, =sin α,∵ AO=2AM,∴ =2sin α,∴=2sin α;(2)取 BO 中点 G,连结 PG,MG,则 PG=OC=, GM=AB=1,因此当 M ,P,G 共线的时候 PM 最大 =1+1.5=2.5【评论】本题利用了相像三角形的性质和等腰三角形的性质:三线合一、四点共圆的判断、正弦的观点、梯形的中位线的性质求解15.如图,给定一个半径长为 2 的圆,圆心O 到水平直线l 的距离为d,即OM=d.我们把圆上到直线 l 的距离等于 1 的点的个数记为 m.如 d=0 时, l 为经过圆心 O 的一条直线,此时圆上有四个到直线 l 的距离等于 1 的点,即 m=4,由此可知:(1)当 d=3 时, m= 1;(2)当 m=2 时, d 的取值范围是1<d<3.【考点】 MB:直线与圆的地点关系.【专题】填空题【剖析】依据直线与圆的地点关系和直线与圆的交点个数以及命题中的数据剖析即可获得答案.【解答】解: (1)当 d=3 时,∵3> 2,即 d>r,∴直线与圆相离,则m=1,故答案为:1;(2)当 d=3 时, m=1;当 d=1 时, m=3;∴当 1<d<3 时, m=2,故答案为: 1<d<3.【评论】本题考察了直线与圆的地点关系,解题的重点是认识直线与圆的地点关系与 d 与 r 的数目关系.16.如图,⊙ O 的半径为 6cm,B 为⊙ O 外一点, OB交⊙ O 于点 A, AB=OA,动A 立点 P 从点 A 出发,以π cm/s 的速度在⊙ O 上按逆时针方向运动一周回到点即停止.当点 P 运动的时间为 2 秒或 10 秒时,BP与⊙ O相切.【考点】 MD:切线的判断.【专题】填空题【剖析】依据切线的判断与性质进行剖析即可.若BP与⊙ O相切,则∠ OPB=90°,又因为 OB=2OP,可得∠ B=30°,则∠ BOP=60°;依据弧长公式求得弧AP 长,除以速度,即可求得时间.【解答】解:连结 OP∵当 OP⊥PB 时, BP与⊙ O 相切,∵AB=OA, OA=OP,∴OB=2OP,∠OPB=90°;∴∠ B=30°;∴∠ O=60°;∵OA=6cm,弧AP==2π,∵圆的周长为: 12π,∴点P 运动的距离为2π或12π﹣2π=10π;∴当t=2 秒或10 秒时,有BP 与⊙O 相切.故答案为: 2 秒或 5 秒.【评论】本题考察的是切线的性质及弧长公式,解答本题时要注意过圆外一点有两条直线与圆相切,不要漏解.17.我国魏晋期间的数学家刘徽创办了“割圆术”,以为圆内接正多边形边数无穷增添时,周长就越靠近圆周长,由此求得了圆周率π的近似值,设半径为r 的圆内接正 n 边形的周长为 L,圆的直径为 d,如下图,当 n=6 时,π≈ ==3,那么当n=12 时,π≈= 3.11 .(结果精准到 0.01,参照数据: sin15 °=cos75°≈0.259)【考点】 MM :正多边形和圆; T7:解直角三角形.【专题】填空题【剖析】圆的内接正十二边形被半径分红顶角为30°的十二个等腰三角形,作辅助线结构直角三角形,依据中心角的度数以及半径的大小,求得L=24r?sin15 ,°d=2r,从而获得π≈≈ 3.11.【解答】解:如图,圆的内接正十二边形被半径分红12 个如下图的等腰三角形,其顶角为 30°,即∠ AOB=30°,作 OH⊥AB 于点 H,则∠ AOH=15°,∵ AO=BO=r,∵ Rt△AOH 中, sin∠AOH=,即 sin15 °=,∴ AH=r× sin15 °,AB=2AH=2r× sin15 °,∴ L=12×2r ×sin15 =24r°×sin15 ,°又∵ d=2r,∴π≈ =≈ 3.11,故答案为: 3.11【评论】本题主要考察了正多边形和圆以及解直角三角形的运用,把一个圆分红n (n 是大于 2 的自然数)等份,挨次连结各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆.18.如图,在 Rt△AOB中,∠ B=40°,以 OA 为半径, O 为圆心作⊙ O,交 AB 于点 C,交 OB于点 D.求的度数.【考点】 M4:圆心角、弧、弦的关系.【专题】解答题【剖析】连结 OC,求出∠ A 度数,依据等腰三角形性质求出∠ ACO,依据三角形外角性质求出即可.【解答】解:连结 OC,∵∠ O=90°,∠ B=40°,∴∠ A=180°﹣90°﹣40°=50°,∵OA=OC,∴∠ ACO=∠A=50°,∴∠ COD=∠ACO﹣∠ B=10°,∴的度数是 10°..【评论】本题考察了圆心角、弧、弦之间的关系,等腰三角形性质,三角形内角和定理,三角形外角性质的应用,重点是求出∠ COD的度数.19.如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高 AC=2米,宽 CD=米.(1)求此圆形门洞的半径;(2)求要打掉墙体的面积.【考点】 M3:垂径定理的应用; KQ:勾股定理.【专题】解答题【剖析】 (1)先证得 BC 是直径,在直角三角形BCD中,由 BD 与 CD 的长,利用勾股定理求出 BC的长,即可求得半径;(2)打掉墙体的面积 =2(S 扇形OAC﹣ S△AOC)+S扇形OAB﹣ S△AOB,依据扇形的面积和三角形的面积求出即可.【解答】解: (1)连结 AD、BC,∵∠ BDC=90°,∴BC是直径,∴BC==∴圆形门洞的半径为.(2)取圆心 O,连结 OA.由上题可知, OA=OB=AB=,∴△ AOB是正三角形,∴∠ AOB=60°,∠ AOC=120°,∴S△AOB=,S△AOC=∴S=2(S 扇形OAC﹣S△AOC)+S 扇形OAB﹣S△AOB=2(﹣) +(﹣)=π﹣∴打掉墙风光积为π﹣平方米.【评论】本题考察了圆周角定理和垂径定理,扇形和三角形的面积,矩形的性质,重点是理解暗影部分的面积是由哪几部分图形构成的,而后利用公式求值.20.如图,有两条公路 OM,ON 订交成 30°,沿公路 OM 方向离两条公路的交错处 O 点 80 米的 A 处有一所希望小学,当拖沓机沿 ON 方向行驶时,路两旁 50米内会遇到噪音影响,已知有两台相距 30 米的拖沓机正沿 ON 方向行驶,它们的速度均为 5 米 / 秒,问这两台拖沓机沿 ON 方向行驶时给小学带来噪音影响的时间是多少?【考点】 M8:点与圆的地点关系; N4:作图—应用与设计作图.【专题】解答题【剖析】过点 A 作 AC⊥ON,求出 AC 的长,第一台到 B 点时开始对学校有噪音影响,第一台到 C 点时,第二台到 B 点也开始有影响,第一台到 D 点,第二台到 C 点,直到第二台到 D 点噪音才消逝.【解答】解:如图,过点 A 作 AC⊥ ON,∵∠ MON=30°, OA=80米,∴AC=40米,当第一台拖沓机到 B 点时对学校产生噪音影响,此时 AB=50,由勾股定理得: BC=30,第一台拖沓机到 D 点时噪音消逝,因此 CD=30.因为两台拖沓机相距 30 米,则第一台到 D 点时第二台在 C 点,还须前行 30 米后才对学校没有噪音影响.因此影响时间应是: 90÷ 5=18 秒.答:这两台拖沓机沿ON 方向行驶给小学带来噪音影响的时间是18 秒.【评论】本题考察的是点与圆的地点关系,依据拖沓机行驶的方向,速度,以及它在以 A 为圆心,50 米为半径的圆行家驶的 BD 的弦长,求出对小学产生噪音的时间.21.如图, AN 是⊙M 的直径, NB∥x 轴, AB 交⊙ M 于点 C.(1)若点 A( 0, 6),N(0, 2),∠ ABN=30°,求点 B 的坐标;(2)若 D 为线段 NB 的中点,求证:直线CD是⊙ M 的切线.【考点】 MD:切线的判断; D5:坐标与图形性质.【专题】解答题【剖析】 (1)在 Rt△ABN 中,求出 AN、AB 即可解决问题;(2)连结 MC,NC.只需证明∠ MCD=90°即可;【解答】解: (1)∵A 的坐标为( 0, 6),N(0,2),∴AN=4,∵∠ ABN=30°,∠ ANB=90°,∴AB=2AN=8,∴由勾股定理可知: NB==,∴B(, 2).(2)连结 MC,NC∵AN 是⊙M 的直径,∴∠ ACN=90°,∴∠ NCB=90°,在 Rt△NCB中, D 为 NB 的中点,∴ CD=NB=ND,∴∠ CND=∠NCD,∵MC=MN,∴∠ MCN=∠ MNC,∵∠ MNC+∠ CND=90°,∴∠ MCN+∠ NCD=90°,即 MC⊥CD.∴直线 CD是⊙ M 的切线.【评论】本题考察圆的切线的判断、坐标与图形的性质、勾股定理等知识,解题的重点是灵巧运用所学知识解决问题,属于中考常考题型.22.如图,直线 AB、BC、CD分别与⊙ O 相切于 E、F、G,且 AB∥ CD,OB=6cm,OC=8cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O 的半径.【考点】 MG:切线长定理.【专题】解答题【剖析】 (1)依据切线的性质获得OB 均分∠ EBF,OC均分∠ GCF, OF⊥BC,再根据平行线的性质得∠ GCF+∠EBF=180°,则有∠ OBC+∠ OCB=90°,即∠ BOC=90°;(2)由勾股定理可求得BC的长,从而由切线长定理即可获得BE+CG的长;(3)最后由三角形面积公式即可求得OF 的长.【解答】解: (1)连结 OF;依据切线长定理得: BE=BF,CF=CG,∠ OBF=∠OBE,∠OCF=∠ OCG;∵ AB∥CD,∴∠ ABC+∠BCD=180°,∴∠ OBE+∠OCF=90°,∴∠ BOC=90°;(2)由(1)知,∠ BOC=90°.∵OB=6cm,OC=8cm,∴由勾股定理获得: BC==10cm,∴ BE+CG=BC=10cm.(3)∵OF⊥BC,∴OF==4.8cm.【评论】本题主假如综合运用了切线长定理和切线的性质定理.注意:求直角三角形斜边上的高时,能够借助直角三角形的面积进行计算.23.如图,在⊙ O 中,弦 AB=弦 CD,AB⊥CD于点 E,且 AE<EB,CE<ED,连结AO,DO,BD.(1)求证: EB=ED.(2)若 AO=6,求的长.【考点】 MN:弧长的计算; M5:圆周角定理.【专题】解答题【剖析】 (1)由 AB=CD,依据圆心角、弧、弦的关系定理得出=,即 +=+,那么 =,依据圆周角定理获得∠ CDB=∠ ABD,利用等角平等边得出EB=ED;(2)先求出∠ CDB=∠ABD=45°,再依据圆周角定理得出∠A OB=90°.又 AO=6,代入弧长公式计算即可求解.【解答】 (1)证明:∵ AB=CD,∴=,即 +=+,∴=,∵、所对的圆周角分别为∠CDB,∠ ABD,∴∠ CDB=∠ABD,∴EB=ED;(2)解:∵ AB⊥CD,∴∠ CDB=∠ABD=45°,∴∠ AOD=90°.∵AO=6,∴的长 ==3π.【评论】本题考察了弧长的计算,圆心角、弧、弦的关系定理,圆周角定理,等腰三角形的判断,证明出∠ CDB=∠ABD 是解题的重点.24.中国扇文化有着深沉的文化底蕴,是民族文化的一个构成部分,它与竹文化、佛教文化有着亲密关系.向来中国被誉为制扇王国.扇子主要资料是:竹、木、纸、象牙、玳瑁、翡翠、飞禽翎毛、其他棕榈叶、槟榔叶、麦杆、蒲草等也能编制成各样千姿百态的日用工艺扇,造型优美,结构精制,经能工巧匠精心镂、雕、烫、钻或名人挥毫题诗作画,使扇子艺术身价倍增.折扇,古称“聚头扇“,或称为撒扇,或折叠扇,以其收拢时能够二头归并归一而得名.如图,折扇的骨柄OA 的长为 5a,扇面的宽 CA的长为 3a,折扇张开的角度为n°,求出扇面的面积(用代数式表示).【考点】 MO:扇形面积的计算.【专题】解答题【剖析】由 OA=5a、AC=3a得 OC=2a,依据扇面的面积S=﹣列式化简即可得.【解答】解:∵ OA=5a,AC=3a,∴OC=2a,∴扇面的面积 S=﹣=﹣===.【评论】本题主要考察扇形的面积计算,掌握扇形面积的计算公式和扇面面积=大扇形面积﹣小扇形面积是解题的重点.。
第三章 圆数学九年级下册-单元测试卷-北师大版(含答案)

第三章圆数学九年级下册-单元测试卷-北师大版(含答案)一、单选题(共15题,共计45分)1、如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为()A.5B.C.5D.52、点到的圆心距离为,的半径为,点与的位置关系是( )A. 点在圆外B.点在圆上C.点在圆内D.无法确定3、如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是()A.15°B.30°C.45°D.60°4、如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为()5、如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为()A.30°B.50°C.60°D.70°6、已知⊙O与直线AB相交,且圆心O到直线AB的距离是方程2x-1=4的根,则⊙O的半径可为().A.1B.2C.2.5D.37、如图,点A,B,C在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,若∠DCE=40°则∠ACB的度数为A.140°B.110°C.80°D.70°8、若☉O的直径为5,直线l与☉O相交,圆心O到直线l的距离是d,则d的取值范围是( )A.4<d<5B.d>5C.2.5<d<5D.0≤d<2.59、如图,在正六边形ABCDEF中,四边形BCEF的面积为30,则正六边形ABCDEF的面积为()10、如图,⊙O的半径为6,四边形内接于⊙O,连结OA,OC,若∠AOC=∠ABC,则劣弧AC 的长为()A. B.2π C.4π D.6π11、在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于,则这个多边形的边数必为()A.7B.6C.5D.412、点P为⊙O内一点,且OP=4,若⊙O的半径为6,则过点P的弦长不可能为()A.8B.10.5C.D.1213、如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是()A.3πB.6πC.5πD.4π14、下列语句中,正确的有()A.圆是轴对称图形,任何一条直径都是它的对称轴B.平分弦的直径垂直于弦C.在同圆或等圆中,相等的圆心角所对的弧相等D.长度相等的两条弧相等15、如图,点A,B,C均在坐标轴上,AO=BO=CO=1,过A,O,C作⊙D,E是⊙D上任意一点,连结CE, BE,则的最大值是()A.4B.5C.6D.二、填空题(共10题,共计30分)16、如图等腰三角形△ABC的底角∠C为70°,以腰AB为直径作半圆,交BC于点D,交AC于点E,则的度数为________17、如图,在ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为________.18、在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为________cm.19、如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=________度.20、如图,AB是半圆O的直径,点P在AB的延长线上,PC切半圆O于点C,连接AC.若∠CPA=20°,则∠A的度数为________°.21、若正六边形的边长为3,则其面积为________.22、如图,在中,,,,把绕边上的点顺时针旋转得到,交于点,若,则阴影部分的面积是________.23、已知△ABC的外接圆半径为,且BC=2,则∠A=________.24、一个扇形的半径是12cm,面积是,则此扇形的圆心角的度数是________.25、如图,在矩形中,,,以点为圆心,的长为半径作交于点;以点为圆心,的长为半径作交于点,则图中阴影部分的面积为________.三、解答题(共5题,共计25分)26、如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B 关于⊙O的反演点,求A′B′的长.27、如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.28、如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠APB的度数.29、如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.(1)求∠D的度数;(2)求证:以点C,O,B,E为顶点的四边形是菱形.30、如图,AB是⊙O直径,弦CD与AB相交与点E,∠ADC=26°,求∠CAB的度数.参考答案一、单选题(共15题,共计45分)1、D2、A3、B4、B6、D7、B8、D9、D10、C11、C12、A13、B14、C15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、23、24、25、三、解答题(共5题,共计25分)27、28、29、30、。
北师版九年级数学下册 第三章 圆 单元测试卷及答案

北师版九年级数学下册 第三章 圆 单元测试卷及答案满分:120分 时间:100分钟一、选择题(本大题共10小题,每小题3分,共30分) 1.下列说法错误的是( )A .直径是弦B .相等的圆心角所对的弧相等C .弦的垂直平分线一定经过圆心D .平分弧的半径垂直于弧所对的弦2.⊙O 与点P 在同一平面内,⊙O 的半径为5,PO =4,则点P 与⊙O 的位置关系是( )A .点P 在⊙O 内B .点P 在⊙O 上C .点P 在⊙O 外D .无法确定3.已知AB 是半径为6的圆的一条弦,则AB 的长不可能是( )A .8B .10C .12D .144.如图,AB 是⊙O 的直径,∠ABC =60°,则tan ∠BAC 的值是( )A. 3B .1C.32D.33(第4题) (第5题) (第7题)5.如图是一圆柱形输水管的横截面,若水面AB 宽为8 cm ,水的最大深度为2 cm ,则该输水管的半径为( ) A .3 cmB .4 cmC .5 cmD .6 cm6.在⊙O 中,AB ︵=2CD ︵,则AB 和2CD 的大小关系是( )A .AB >2CD B .AB =2CDC .AB <2CDD .不能确定7.如图,P A ,PB 分别切⊙O 于点A ,B ,MN 切⊙O 于点C ,且分别交P A ,PB于点M ,N ,若P A =7.5 cm ,则△PMN 的周长是( )A .7.5 cmB .10 cmC .12.5 cmD .15 cm8.如图,⊙O 是△ABC 的内切圆,若∠A =70°,则∠BOC =( )A .125°B .115°C .110°D .130°(第8题) (第9题) (第10题)9.如图,在平面直角坐标系中,⊙M 与x 轴相切于点A (8,0),与y 轴交于点B (0,4)和点C (0,16),则圆心M 到坐标原点O 的距离是( ) A .10 B .8 2 C .4 13D .2 4110.如图,正方形ABCD 的边长为1,BD ︵和AC ︵都是以1为半径的圆弧,图中两个阴影部分的面积分别记为S 1和S 2,则S 1-S 2等于( ) A.π2-1 B .1-π4 C.π3-1D .1-π6二、填空题(本大题共5小题,每小题3分,共15分)11.已知△ABC 的三边长分别是6,8,10,则△ABC 外接圆的直径是________. 12.已知某扇形的圆心角为150°,弧长为20π cm ,则该扇形的面积为________cm 2. 13.如图,⊙O 是四边形ABCD 的内切圆,若AB =10,CD =12,则四边形ABCD的周长为________.(第13题) (第14题) (第15题)14.如图,△ABC 是⊙O 的内接三角形,∠C =45°,AB =6,则⊙O 的半径为________.15.如图,在平面直角坐标系中,C (0,4),A (3,0),⊙A 的半径为2,P 为⊙A上任意一点,E 是PC 的中点,则OE 的最小值是________. 三、解答题(一)(本大题共3小题,每小题8分,共24分)16.如图,四边形ABCD 内接于⊙O ,E 为AB 延长线上一点,若∠AOC =150°,求∠EBC 的度数.(第16题)17.如图,AB 、CD 是⊙O 的两条直径,CE ∥AB ,求证:BC ︵=AE ︵.(第17题)18.如图,在平面直角坐标系中,A (0,4)、B (4,4)、C (6,2). (1)经过A 、B 、C 三点的圆弧所在圆的圆心M 的坐标为__________; (2)⊙M 的半径为________;(3)判断点D(5,-2)与⊙M的位置关系.(第18题)四、解答题(二)(本大题共3小题,每小题9分,共27分)19.如图,AB是⊙O的直径,弦CD⊥AB于点M,连接CO,CB.(1)若AM=2,BM=8,求CD的长度;(2)若CO平分∠DCB,求证:CB=CD.(第19题)20.如图,直线AB、BC、CD分别与⊙O相切于点E、F、G,且AB∥CD,OB =6 cm,OC=8 cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.(第20题)21.如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.(1)求证:BC是⊙O的切线;(2)连接BF,求∠ABF的度数.(第21题)五、解答题(三)(本大题共2小题,每小题12分,共24分)22.如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F.(1)求证:AC 平分∠DAB ; (2)求证:△PCF 是等腰三角形;(3)若AF =6,EF =2 5,求⊙O 的半径.(第22题)23.(1)如图①,△ABC 是⊙O 的内接正三角形,点P 为BC ︵上一动点,求证:P A=PB +PC ;(2)如图②,四边形ABCD 是⊙O 的内接正四边形,点P 为BC ︵上一动点,求证:P A =PC +2PB ;(3)如图③,六边形ABCDEF 是⊙O 的内接正六边形,点P 为BC ︵上一动点,请直接写出P A 、PB 、PC 三者之间的数量关系.(第23题)答案一、1.B 2.A 3.D4.D5.C6.C7.D 8.A9.D10.A二、11.1012.240π13.4414.3215.1.5三、16.解:由圆周角定理得∠ADC =12∠AOC =12×150°=75°.∵四边形ABCD 内接于⊙O ,∴∠ADC +∠ABC =180°.又∵∠ABC +∠EBC =180°,∴∠EBC =∠ADC =75°.(第17题)17.证明:连接OE ,如图,∵CE ∥AB ,∴∠BOC =∠C ,∠AOE =∠E ,∵OC =OE ,∴∠C =∠E ,∴∠BOC =∠AOE ,∴BC ︵=AE ︵.18.解:(1)(2,0)(2)25(3)点D (5,-2)在⊙M 内.四、19.(1)解:∵AB 是⊙O 的直径,弦CD ⊥AB ,∴CM =DM ,∵AM =2,BM =8,∴AB =10,∴OA =OC =5.∴OM =5-2=3.∴CM =OC 2-OM 2=52-32=4,∴CD =8.(2)证明:过点O 作ON ⊥BC ,垂足为N ,如图.(第19题)∵CO 平分∠DCB ,ON ⊥BC ,CD ⊥AB ,∴OM =ON ,∴易得CB =CD .20.解:(1)∵直线AB 、BC 、CD 分别与⊙O 相切于点E 、F 、G ,∴易得∠OBF =∠OBE ,∠OCF =∠OCG .∵AB ∥CD ,∴∠ABC +∠BCD =180°,∴∠OBF +∠OCF =90°,∴∠BOC =90°.(2)∵OB =6cm ,OC =8cm ,∠BOC =90°,∴BC =OB 2+OC 2=10cm ,∵直线AB 、BC 、CD 分别与⊙O 相切于点E 、F 、G ,∴BE =BF ,CF =CG .∴BE +CG =BF +CF =BC =10cm.(3)连接OF ,则OF ⊥BC ,∴S △OBC =12OF ×BC =12OB ×OC ,即12OF ×10=12×6×8.∴OF =4.8cm.即⊙O 的半径为4.8cm.21.(1)证明:连接OB ,如图.(第21题)∵OB =OA ,CE =CB ,∴∠OAB =∠OBA ,∠CEB =∠ABC .∵CD ⊥OA ,∴∠OAB +∠AED =90°,∴∠OAB +∠CEB =90°.∴∠OBA +∠ABC =90°,即∠OBC =90°.∴OB⊥BC,∴BC是⊙O的切线.(2)解:连接OF,AF,∵DA=DO,CD⊥OA,∴AF=OF,又∵OA=OF,∴△OAF是等边三角形,∴∠AOF=60°,∴∠ABF=12∠AOF=30°.五、22.(1)证明:如图,连接OC.∵PD为⊙O的切线,∴OC⊥DP,又∵AD⊥DP,∴OC∥AD,∴∠DAC=∠OCA,∵OA=OC,∴∠OAC=∠OCA,∴∠OAC=∠DAC,∴AC平分∠DAB.(2)证明:如图,连接OE.∵AB为⊙O的直径,∴∠ACB=90°,∵CE平分∠ACB,∴∠BCE=45°.(第22题)∴∠BOE=2∠BCE=90°,∴∠OFE+∠OEF=90°,又∵∠OFE=∠CFP,∴∠CFP+∠OEF=90°,∵OC⊥PD,∴∠OCP=90°,即∠OCF+∠PCF=90°,∵OC=OE,∴∠OCF=∠OEF,∴∠PCF=∠CFP,∴CP=FP,∴△PCF是等腰三角形.(3)解:设⊙O的半径为r,则OE=r,OF=6-r,在Rt△EOF中,∵OE2+OF2=EF2,∴r2+(6-r)2=(25)2,解得r1=4,r2=2.当r=4时,OF=6-r=2,符合题意;当r=2时,OF=6-r=4,不合题意,舍去.∴⊙O的半径为4.23.(1)证明:延长BP至E,使PE=PC,连接CE.∵四边形ABPC是⊙O的内接四边形,∴∠BAC+∠BPC=180°,又∵∠BPC+∠EPC=180°,∴∠BAC=∠CPE.∵△ABC是正三角形,∴AC=BC,∠BAC=∠ACB=60°,∴∠CPE=60°.又∵PE=PC,∴△PCE是正三角形,∴CE=PC,∠E=∠PCE=60°.∴易得∠BCE=∠ACP.在△BEC和△APC中,=PC,BCE=∠ACP,=AC,∴△BEC≌△APC,∴PA=BE=PB+PE=PB+PC.(2)证明:连接OA,OB,过点B作BE⊥PB交PA于E,如图.∵四边形ABCD是⊙O的内接正四边形,∴∠AOB=90°,∠ABC=90°,AB=BC.∴∠1+∠2=90°,∠APB=45°,又∵∠2+∠3=90°,∴∠1=∠3.又∵∠BAP=∠BCP,∴△ABE≌△CBP.∴AE=CP.∵∠EBP=90°,∠APB=45°,∴PE=2PB.∴PA=AE+PE=PC+2PB.(3)解:PA=PC+3PB.(第23题)11。
北师大版九年级下册数学第三章 圆 单元测试卷(含答案)

一、精心选一选(每小题 3 分,共 30 分)1、下列命题为真命题的是 A 、点确定一个 圆 ( )B 、度数相等的弧相等C 、圆周角是直角的所对弦是直径D 、相等的圆心角所对的弧相等,所对的弦也相等2、若一个三角形的外心在这个三角形的斜边上,那么这个三角形是 ( )A 、锐角三角形 C 、钝角三角形B 、直角三角形D 、不能确定3、圆内接四边形 A B C D ,∠A ,∠B ,∠C 的度数之比为 3:4:6,则∠D 的度数为( )A 、60B 、80C 、100D 、1204、如图,正方形 A B C D 内接于圆 O 点 P 在弧 A D 上,∠BPC = ( )( A 、50 5、如图,圆周角∠A =30,弦 BC =3,则圆 O 的直径是A 、3B 、3 3C 、6B 、45C 、40D 、35) D 、6 3 6、如图,C D 是圆 O 的弦,A B 是圆 O 的直径,C D =8,A B =10,则点 A 、B 到直线 C D 的距离的和是 ( )A 、6B 、8C 、10D 、12A PA DB O B O A O OB ACD CE C D FB C 4 题 5 题 6 题 7 题7、如图,在以O 为圆心的两个同心圆中,大圆的弦A B 交小圆于C 和D 两点,AB=10c m,CD =6c m, 则 A C 长为 ( )A 0.5cmB 1cmC 1.5cmD 2cm8、C D 是⊙O 的一条弦,作直径 AB ,使 AB ⊥C D ,垂足为 E ,若 AB=10,C D=6,则 BE 的 长是( )A .1 或 9B .9C .1D .49、两圆的半径分别为R 和 r ,圆心距d=3,且R ,r 是方程 x 2 7x 10 0的两个根,则这 两个圆的位置关系是( A .内切 B .外切 10、手工课上,小明用长为 10π,宽为 5π 的绿色矩形卡纸,卷成以宽为高的圆柱,这个圆柱的底面圆半径是( A .5π B .5 )C .相交D .外离)C .10πD .10二、细心填一填(每小题 3 分,共 30 分)11.已知⊙O 的半径为 8, 圆心 O 到直线 l 的距离是 6, 则直线 l 与⊙O 的 位置关系是_________。
北师大版九年级数学下册《第三章圆》单元测试卷-带答案

北师大版九年级数学下册《第三章圆》单元测试卷-带答案学校:___________班级:___________姓名:___________考号:___________一、单选题(共10小题,满分40分)1.如图,已知⊙O 上三点A 、B 、C ,连接AB 、AC 、OB 、OC ,切线BD 交OC 的延长线于点D ,⊙A =25°,则⊙D 的度数为( )A .20°B .30°C .40°D .50° 2.如图,已知Rt ABC 中90C ∠=︒和3tan 4A =.D 、E 分别是边BC 、AB 上的点∥DE AC ,且2BD CD =.如果E 经过点A ,且与D 外切,那么D 与直线AC 的位置关系是( )A .相离B .相切C .相交D .不能确定3.如图,AB 是O 的直径35D ∠=︒,则BOC ∠=( )A .35°B .55°C .70°D .75°4.如图,AB 是O 的直径,过点A 作O 的切线AC ,连接BC ,与O 交于点D ,E 是O 上一点,连接AE DE ,.若48C ∠=︒,则AED ∠的度数为( )A .42︒B .48︒C .32︒D .38︒5.如图是一个半径为5cm 的圆柱形输油管的横截面,若油面宽AB=8cm ,则油面的深度为( )A .2cmB .2.5cmC .3cmD .3.5cm6.如图,PA PB 、是O 的切线,A 、B 为切点,若50P ∠=︒,则ABO ∠的度数是( )A .25︒B .35︒C .45︒D .50︒7.下列事件中,必然事件是( )A .明天是晴天B .购买福利彩票,中一等奖C .不在同一直线上的三个点确定一个圆D .掷一次骰子,向上一面的点数是6 8.如图,已知点A 为⊙O 内一点,点B 、C 均在圆上,⊙C=30°,⊙A=⊙B=45°,线段﹣1,则阴影部分的周长为( )A .43π3B .23π3C .43π3D .23π39.已知Rt⊙ABC 的一条直角边AB=8cm ,另一条直角边BC=6cm ,以AB 为轴将Rt⊙ABC 旋转一周,所得到的圆锥的侧面积是( )A .120πcm 2B .60πcm 2C .160πcm 2D .80πcm 210.如图,AB 是半圆O 的直径,C 是半圆O 上一点,OQ ⊙BC 于点Q ,过点B 作半圆O 的切线,交OQ 的延长线于点P ,P A 交半圆O 于R ,则下列等式中正确的是( )A .AQ AC AP AB = B .AC OQ OR AB = C .AQ BP AB BC =D .AC OR AP OP=二、填空题(共8小题,满分32分)11.时钟的分针长6厘米,从上午8:10到上午8:30,分针扫过的面积是 平方厘米.12.如图,在扇形AOB 中120AOB ∠=︒,半径OC 交弦AB 于点D ,且OC AO ⊥,若6OA =,则图中阴影部分的周长为 (结果保留π).13.如图,AB 是⊙O 的直径,弦CD 交AB 于点P ,AP =4,BP =12,⊙APC =30°,则CD 的长为 .14.已知如图所示,正方形ABCD 的边长为1,以AB 为直径作半圆,以点A 为圆心,AD为半径画弧.那么图中阴影部分的面积为 .15.如图,矩形ABCD 中4AB =,BC=3,E 为CD 上一点,且1DE =,在矩形ABCD 内部存在一点P ,并且满足BPC BEC ∠=∠,PB PC =则点Р到边BC 的距离为 .16.如图,AB 为O 的直径,AC 是O 的切线,点A 是切点,连接BC 交O 于点D ,连接OD ,若40C ∠=︒,则AOD ∠= 度.17.如图,在正方形ABCD 内有一点P ,AD =2,点M 是AB 的中点,且⊙PMA =2⊙P AD .连接PD ,则PD 的最小值为 .18.如图,边长为4的正三角形ABC ,点M ,N 分别是边AB ,AC 上的动点,连接BN ,CM 交于点P .若BN =CM ,当点M 由点B 运动到点A 时,点P 所经过的路径长为 .三、解答题(共6小题,每题8分,满分48分)19.圆心角都是90°的扇形OAB与扇形OCD如图所示那样叠放在一起,连接AC、BD.(1)求证:⊙AOC⊙⊙BOD;(2)若OA=3cm,OC=1cm,求阴影部分的面积.BC=,钢环所20.如图,一个圆形钢环靠在台阶直角处90(),已知台阶高20cm∠=︒ACBAC=求钢环的半径.在的O与地面相切于点A,60cm21.如图,已知点E在⊙ABC的边AB上,⊙C=90°,⊙BAC的平分线交BC于点D,且D 在以AE为直径的⊙O上.(1)求证:BC是⊙O的切线;(2)已知⊙B=30°,CD=4,求线段AB的长.22.如图,以AB边为直径的O经过点P,C是O上一点,连接PC交AB于点E,且=.∠=和PA PDACP︒60(1)证明:PD是O的切线.(2)若点C是弧AB的中点,已知2⋅的值.AB=,求CE CP23.在平面直角坐标系xOy中,点P坐标为(2,3),点Q为图形M上一点.我们将线段PQ长度的最大值与最小值之间的差定义为点P视角下图形M的“宽度”.(1)如图,⊙O半径为2,与x轴分别交于点A,B.⊙在点P视角下,⊙O的“宽度”为,线段AB的“宽度”为.⊙点G(m,0)为x轴上一点,若在点P视角下,线段AG的“宽度”为2,求m的取值范围.(2)⊙C的圆心在x轴上,且半径为r(r>1),一次函数y=x+1的图象与x轴,y轴分别交于点D,E.若线段DE上存在点K,使得在点K视角下,⊙C的“宽度”可以为2,求圆心C 的横坐标xC 的取值范围.24.已知抛物线2y ax bx c =++经过()30A -,、()10B ,和()0,3C -三点,直线l 是抛物线的对称轴.(1)求抛物线的解析式;(2)设点P 是直线l 上的一个动点,当PBC 的周长最小时,求点P 的坐标;(3)在直线l 上是否存在点M ,使以M 、B 、C 为顶点的三角形为直角三形.若存在,求出点M 的坐标;若不存在,请说明理由.参考答案:1.C2.B3.C4.A5.A6.A7.C8.A9.B10.A11.12π12.6π+/6π+13.1514..15 16.100171/1-18.19.(1)略;(2)22cm π20.钢环的半径为100cm .21.(1)11;(2)AB = 22.(1)略(2)223.(1)⊙4;2;⊙m 的范围为2≤m ≤6或m =2-;(2)-2≤x C 1.24.(1)223y x x =+-(2)()12--,(3)()12--,或()1,1--。
第三章 圆数学九年级下册-单元测试卷-北师大版(含答案)

第三章圆数学九年级下册-单元测试卷-北师大版(含答案)一、单选题(共15题,共计45分)1、在平面直角坐标系中,以点(3,2)为圆心、2为半径的圆,一定()A.与x轴相切,与y轴相切B.与x轴相切,与y轴相离C.与x轴相离,与y轴相切D.与x轴相离,与y轴相离2、下列说法中正确的个数有()①直径不是弦;②三点确定一个圆;③圆是轴对称图形,任何一条直径所在直线都是它的对称轴;④相等的圆心角所对的弧相等,所对的弦也相等A.1个B.2个C.3个D.4个3、如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于()A.28°B.54°C.18°D.36°4、若一个正六边形的半径为2,则它的边心距等于()A.2B.1C.D.25、如图,在Rt△ABC中,∠C=90°,AB=6,AD是∠BAC的平分线,经过A,D两点的圆的圆心O恰好落在AB上,⊙O分别与A、B、AC相交于点E、F.若圆半径为2.则阴影部分面积()A. B. C. D.6、Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A ,那么斜边中点D与⊙A的位置关系是( )A.点D在⊙A外B.点D在⊙A上C.点D在⊙A内D.无法确定7、如图,以BC为直径的⊙O与△ABC的另两边分别相交于D.E. 若∠A=60°,BC=6,则图中阴影部分的面积为( )A. πB.3πC.2πD. π8、九个相同的等边三角形如图所示,已知点O是一个三角形的外心,则这个三角形是()A. ABCB. ABEC. ABDD. ACE9、如图,已知⊙O的半径为 6,弦 AB,CD所对的圆心角分别是∠AOB,∠COD若∠AOB 与∠COD 互补,弦CD=6 ,则弦AB 的长为()A.6B.8C.3D.610、下列说法中,正确的个数为:①在等圆中,等弦对等弧;②直径是圆的对称轴;③平分弦的直径垂直于这条弦.()A.0B.1C.2D.311、如图,AB是⊙O的直径,,∠COD=34°,则∠AEO的度数是()A.51°B.56°C.68°D.78°12、有一个内角为120°的菱形的内切圆半径为,则该菱形的边长是()A. B. C.4 D.613、如图所示,AB是⊙O的直径,AB=4,AC是弦,AC=,则∠AOC为()A.120°B.130°C.140°D.150°14、下列命题:①有理数和数轴上的点一一对应;②带根号的数不一定是无理数;③在数据1,3,3,0,2中,众数是3,中位数是3;④若圆心到直线上一点的距离恰好等于圆的半径,则该直线是圆的切线;其中真命题的个数是()A.0个B.1个C.2个D.3个15、如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是()A.②④⑤⑥B.①③⑤⑥C.②③④⑥D.①③④⑤二、填空题(共10题,共计30分)16、已知正六边形的半径是2,则这个正六边形的边长是________17、如图,P为反比例函数y= (x>0)在第一象限内图象上的一点,过点P分别作x 轴、y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若AO、BO分别平分∠BAP、∠ABP,则k的值为 ________.18、如图,锐角△ABC内接于⊙O,于点,于点,且OM=3,CD=4,BD=12, 则的半径为 ________.19、如图,在△ABC中,∠B=90°,AB=3,BC=2,点O在AC边上,⊙O与AB、BC分别切于点D、E,则⊙O的半径长为________.20、⊙O直径为8cm,有M、N、P三点,OM=4cm,ON=8cm,OP=2cm,则M点在________,N 点在圆________,P点在圆________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、选择题
1. 已知O O的直径为10,点P到点0的距离大于8,那么点P的位置()
A. —定在O 0的内部
B. —定在O 0的外部
C. 一定在O 0上
D. 不能确定
2. 乌镇是著名的水乡,如图,圆拱桥的拱顶到水面的距离CD为8m,水面宽AB为8m ,则桥拱半径0C为
()
A. 4m
B. 5m
C. 6m
D. 8m
3. 给出下列说法:① 直径是弦;②优弧是半圆;③ 半径是圆的组成部分;④ 两个半径不相等的圆中,大
的半圆的弧长小于小的半圆的周长.其中正确的有()
5. 如图,点A,B,C均在坐标轴上,A0=B0=C0=1,过A,0,C作O D, E是O D上任意一点,连结CE, BE则
6. 如图,在O0中,弦AC与半径0B平行,若/ B0C=5O°则/ B的大小为()
第三章圆
A. 1个
B. 个
C.个
D. 个
4. 一个扇形的圆心角是120 °面积为3 Mm2那么这个扇形的半径是(
A. cm
B. 3cm
C. 6cm
D. 9cm
B. 5
C. 6
D.
A. 4
A. 25 °
B. 30
C. 50 °
D. 60 °
7. 在研究圆的有关性质时, 我们曾做过这样的一个操作 将一
张圆形纸片沿着它的任意一条直径翻折, 可以 看到直径两侧的两个半圆互相重合 ”.由此说明(
)
A. 圆的直径互相平分
B. 垂直弦的直径平分弦及弦所对的弧
C. 圆是中心对称图形,圆心是它的对称中心
D. 圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
8. 如图,AB 为O O 的直径,点E 、C 都在圆上,连接 AE , CE BC ,过点A 作O O 的切线交BC 的延长线于 点D ,若/ AEC=25,则/ D 的度数为(
)
9.
如图,四边形 ABCD 内接于圆O , E 为CD 延长线上一点,若 / B=110:则/ADE 的度数为(
)
10.
已知:O O 是厶ABC 的外接圆,/ OAB=40°,则/ ACB 的大小为(
)
A. 75
B. 65
C. 55
D. 74
B. 110
C. 90
D. 80
A. 115
A. 20
B. 50 °"C 20 或160 M D. 50 或130
11•如图,O O 内切于四边形 ABCD, AB=10, BC=7, CD=8,贝U AD 的长度为(
)
12. 如图,在圆心角为 45的扇形内有一正方形 CDEF 其中点C 、D 在半径0A 上,点F 在半径0B 上,点E 在匚-上,则扇形与正方形的面积比是(
、填空题
13. P A , PB 分别切O O 于A , B 两点,点C 为O O 上不同于AB 的任意一点,已知 / P=40°则/ ACB 的度数
14. 如图,AB 为O O 的直径,直线I 与O O 相切于点C, AD 丄I ,垂足为D , AD 交O O 于点E ,连接OC BE 若
B. 9
C. 10
D. 11
A. n 8
" B. 5 n :
8
A. 8
5
15. ________________________________________________________________________________ 如图,AB 是O O 的直径,点 C 在O O 上,/ AOC=40, D 是BC 弧的中点,贝U / ACD= ___________________
16. ___________ 如图所示,O I 是Rt A ABC 的内切圆,点 D 、E 、F 分别是且点,若 / ACB=90°, AB=5cm , BC=4cm,则O I 的周长为 __ cm .
17•如图,PA, PB 是O O 的切线,CD 切O O 于E , PA=6,则△ PDC 的周长为
18.如图,O O 的半径为6cm , B 为O O 外一点,OB 交O O 于点A , AB=OA,动点P 从点A 出发,以n cm/s
的速度在O O 上按逆时针方向运动一周回到点
A 立即停止.当点P 运动的时间为
________ 时,BP 与O O 相
ABCD 中,点E 在DC 的延长线上.若 / A=50 °则/
BCE= ___________
21.如图,在△ ABC 中,AB=AC=3, / BAC=120:以点A 为圆心,1为半径作圆弧,分别交 AB , AC 于点D , E, 以点C 为圆心,3为半径作圆弧,分别交AC , BC 于点A , F .若图中阴影部分的面积分别为
在弧PA i 和弧PB 1上分别取中点 A 2和B 2 ,若一直这样取中点,求 / A n PBn=
三、解答题
23. 如图,AB 为O O 的直径,C 是O O 上一点,D 在AB 的延长线上,且 / DCB=Z A .求证:CD 是O O 的切
P 为弧AB 的中点,分别在弧 AP 和弧PB 上取中点
A i 和
B i ,再
则S i - S 2的值为
/ BAC=32°
, D 是弧AC 的中点,求/ DAC 的度数. DP// AC ,交BA 的延长线于 P,求证:AD?DC=PA?BC
26. (2017?通辽)如图,AB 为O O 的直径,D 为 的中点,连接 OD 交弦AC 于点F ,过点D 作DE// AC ,
交BA 的延长线于点E.
(1) 求证:DE 是O O 的切线;
(2) 连接CD,若OA=AE=4,求四边形 ACDE 的面积.
参考答案
一、 选择题 BBABCADBBDDB 二、 填空题 13. 70 或 110 ° 14.
4
O 的直径,
15. 125 °
16. 2 n
17. 12
18. 2秒或5秒
19. 50 °
20. 12
21. - n
1
22. 180 °—X 180 °
三、解答题
••• / ACB=90 ,°
••• / A+Z ABC=90 °又•/ OB=OC, • Z OBC=Z OCB, 又•/ Z DCB=Z A°
••• / A+Z ABC=/ DCB+/ OCB=90 ,
••• OC X DC,
• CD是O O的切线.
24. 解:连接BC,
••• AB是半圆O的直径,Z BAC=32 ,°
•Z ACB=90 ,°Z B=90 - 32 =58 ,
•Z D=180 - Z B=122。
(圆内接四边形对角互补),•••D是弧的中点,
•Z DAC=Z DCA= (180 - Z D) - 2=29 °
即Z DAC的度数是29°.
A O B
25. 证明:如图,连接AC,连接BD.
••• DP// AC,
•Z PDA=Z DAC.
•/ Z DAC=Z DBC,
•Z PDA=Z DBC.
•••四边形ABCD是圆内接四边形,
•Z DAP=Z DCB
•△PA"A DCB.
得PA: DC=AD: BC,
即AD?DC=PA?BC
26. (1)证明:•/ D 为二〔的中点,• OD X AC,•/ AC/ DE,
• OD X DE,
••• DE是O O的切线
(2)解:连接DC,
••• D为二]的中点,
• 0D丄AC, AF=CF,
•/ AC// DE,且OA=AE
• F为OD的中点,即OF=FD
在厶AFO和厶CFD中,
r AF^CF
• ZAEO = ZCFD
1 OF二FD
•△ AFO^^ CFD (SAS ,
•S A AFO=S A CFD ,
• S 四边形ACDE=S A ODE
在Rt A ODE 中,OD=OA=AE=4
• OE=8,
• DE=—二-=4 丿,
X 4 X 4 =8 J .• • S 四边形ACDE=S A
=。
