Y第09章-3--电磁相互作用和稳恒磁场
大学物理 第九章_稳恒磁场
MRI
二、磁场和磁感应强度矢量
1. 磁场: 产生磁力的场
磁力:运动电荷对运动电荷的作用力。与电荷运动速度有关的力。
任一运动电荷或电流都在空间激发磁场。
磁场的对外表现:对处于其中的运动电荷有力的作用
运动 电荷1
磁场
运动 电荷2
2. 磁感应强度矢量 B (Magnetic Field)
数值反应该点磁场的强弱,方向为该点磁场的方向。
dB// dB sin
sin R
r
B
l
0 4
IRdl r3
0 4
IR r3
2R
0
2
IR 2 r3
B
0
2
IR 2 (R2 x2)32
方向: + x
dB
dB
Idl
方向:右手定则
x = 0 圆心处 B 0I
2R
x >> R
B
0
2
IR 2 x3
x
dB//
dB
θ
xθ
rdB
OR
Idl
静止电荷
dE
1
4 0
dq rˆ r2
电场 F qE
稳恒电流
B
0 4
q
v
rˆ
r2
dB
0 4
Idl rˆ r2
磁场
F
qv
B
F Idl B
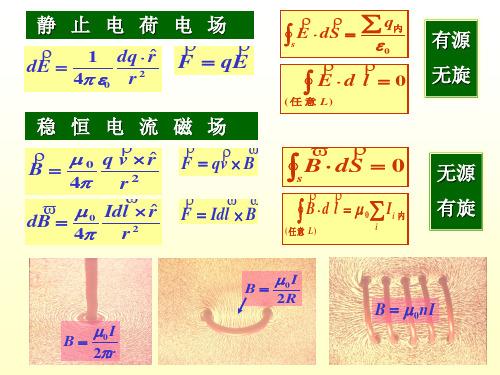
E dS
q内
s
0
Ed l 0
(任 意 L)
sB dS 0
B d l 0 Ii 内
(任意 L)
i
有源 无旋
无源 有旋
电流元不在自身方向上激发磁场.
普通物理学课件:9稳恒磁场(安培环路定理)

(1) r R2 , B 0
R2
R1
(2)
R1
r
R2 ,
B
0I 2r
I
rI
(3) r R1, B 0
电场、磁场中典型结论的比较
长直线
长 直
内
圆
柱外
面
长 直
内
圆
柱 体
外
电荷均匀分布
E
2 0r
E0
E
2 0r r
E 2 0 R2
E
2 0r
电流均匀分布
B 0I 2r
B0
B 0I 2r
B
0 Ir 2R 2
rd
0I 2
2
B • dl 0I
3、回路不环绕电流
.
B • dl 0
B
rd
dl
4
安培环路定理
B • dl
0 Ii
(
B ) • dl i
i
( Bi内 Bi外 ) • dl
I4
i
i
0Ii内 0 i
I内
说明:电流与环路成右旋时取正
例 B • dl 0 Ii
0(I2 I3)
d
c
Bdl cos 0
da Bdl
cos
2
B ab B cd
2B ab
利用安培环路定理求
B
B • dl 0n ab I
ba .........
cd
B 0 nI 2
例5:如图,两块无限大载流导体薄板平行放置。 通有相反方向的电流。求磁场分布。
已知:导线中电流强度 I、单位长度导线匝数n
保守场,或有势场
E • dS
1
s
稳恒磁场

μI B 0 (cosα1 cosα2 ) 4 a π
无限长载流直导线的磁场: (因为 α1 0 α2 π ) 半无限长载流直导线的磁场: (因为 α1
μI B 0 2 a π
μI B 0 4 a π
π
2
α2 π )
直导线延长线上一点的磁场: B 0
μ0 Idl sinα (因为在 dB 中α 0 ) 2 4 π r
的运动电荷 无关。 ②磁感应强度是矢量,方向为
Fm ×v
的方向。
(其中v 为正电荷运动方向) ③磁感应强度的单位:T (特斯拉)(SI) 工程上单位常用高斯(G) 1T 10 G
4
三、磁通量
1、磁力线
磁场中的高斯定理
在磁场中画一组曲线,曲线上每一点的切线方向 与该点的磁场方向一致,这一组曲线称为磁力线。 *磁力线描述磁场的方法 ①方向:
y
I
dl
α2
α
μ0 Idl sinα 大小 dB α1 r 2 4 π r l 方向 Idl r dB μ Idl sinα 0 o B dB r2 a P x 4 L π μI 统一积分变量求得: B 0 (cosα cosα2 ) 1 4 a π
一段载流直导线的磁场:
I J S
由于电荷是在一个体积中运动,称J为体电 流的面密度
S
I Jd S
S
I
l
若电荷在导体的表面流动,称为面电流 从而引入面电流的线密度
I 数值: J l
'
I
l
垂直通过单位横截线的电流强度 方向:该点正电荷运动方向
练习:求与无限长载流平面共面且距平面一边 为
普通物理学课件:9稳恒磁场(安培力2007)

c
B
I R
a b
二、洛仑兹力
dF Idl B
fm qv B
(运动电荷在磁场中所受的磁场力)
fm qv B
大小 fm qvB sin
方向
fm
q
B v
力与速度方向垂直。 不能改变速度大小, 只能改变速度方向。
粒子在同时存在电场和磁场的空间运动时,其受的合力:
F q(E v B) ——洛仑兹关系式
电场力 磁场力
三、 磁力的功
A Fx BIlx
Im
I.....
.. . . B. I.
.. ....F .... l
x
本章小结
方向
定义
大小 毕-沙定律
dB
0
4
Idl r
r3
求解
稳恒
安培环路定律 B • dl 0 Ii
有旋性
磁场 本质
电流元 I1dl1 所受作用力
dF1
0 4
I1dl1 I 2dl 2 r2
r
I1dl1
I 2dl2
电流元 I2dl2 所受作用力
dF2 0
? dF1 dF2
结论:牛顿第三定律对电流元不适用
例1 均匀磁场中载流直导线所受安培力
取电流元 Idl
受力大小
Idl ×
B
dF BIdl sin
dF
方向
§5 磁场对载流导线的作用 一、 安培定律
1 安培力 电流元在磁场中受到的磁力
2 安培定律
(1)微分形式 dF Idl B
大小 dF IdlBsin arcsin( Idl ,B )
方向 右手螺旋
(2)积分形式 F dF Idl B L
稳恒磁场与电磁场的相对性解读
第9章稳恒磁场与电磁场的相对性教研室:物理教师__第9章 稳恒磁场与电磁场的相对性9.1 磁场 磁感应强度基本磁现象1. 两个永久磁铁的磁极间的相互作用2. 电流和电流间的相互作用磁现象的本质都是由运动的带电粒子所产生的,例如,根据安培的分子电流假设,磁铁的磁现象来源于分子电流。
磁场磁的相互作用是通过场来实现的: 磁铁↔磁场↔磁铁 电流↔磁场↔电流磁场的物质性:磁场对磁场中的其它运动电荷或载流导体有磁力的作用,说明磁场具有动量; 磁场对磁场中的其它运动电荷或载流导体能做做功,说明磁场具有能量。
9.1.3 磁感应强度矢量 1.B的引入磁场的存在是通过对运动电荷或电流的作用显示的。
为了定量地描述磁场,如同电场,类似地引入磁感应强度作为磁场的描述参量,它可以通过磁场对作探测用的运动正点电荷0q (试验电荷)或载流小线圈(试验线圈)的力作用来确定。
磁感应强度常用字母B 表示,不难理解,它是一个矢量,是位置坐标的函数。
2.通过磁场对试验电荷的作用来定义磁感应强度B实验表明:以速度v 相对磁场运动的试验电荷0q (0q >0),在磁场中某位置处的受力不仅与电荷的电量0q 有关,还与它在该处相对磁场运动的方向和大小有关。
若仅改变0q 在此处的运动方向,发现存在两个特定方向,在其中一个方向上受力最大,记为m F ;在另一个方向上不受力,且这两个特定方向相互垂直。
洛伦兹力的一般表达式:B v q F ⨯=qvB F m =⇒ 因此定义磁场中该位置处的磁感应强度B 的大小为qvF B m=在实验室中,常采用磁场对试验线圈产生的力矩作用来测定磁场,相应也可以用类似方法来定义磁感应强度。
3.在国际单位制(SI)中,磁感应强度的单位称为特斯拉,用字母T 表示。
有时也用高斯(G)作单位,G T 4101=毕—萨定律运动电荷激发磁场,最通常和有实际意义的是稳恒电流所激发的磁场,叫做稳恒电流的磁场,简称稳恒磁场。
稳恒电流总是闭合的,又是多种多样的。
大学物理课件 第9章 稳恒磁场

向里
0 I 0 I B2 (sin 2 sin 1 ) (sin 1) 4b 4a cos 向外
则: B p
0 I
4a cos
(sin 1 cos )
向外
2)圆形电流轴线上的磁场
电流元产生的磁感应强度大小:
0 Idl sin 0 Idl dB 2 4 4 r 2 r
6
3a b
2
q 2
a 2 IS
例7:求旋转的带电圆盘的圆心处及轴线上的B。设圆盘的电荷 面密度为σ,半径为R,旋转的角速度为ω。 等效电流: 圆心:
max
磁感应强度的大小:
M max B Pm
Bb Ba a Bc
三、磁通量
1)磁力线(Magnetic force line) 为了形象的描述磁场,引入磁力线。
大小:通过垂直于磁力线单位面积的磁 力线数等于这一点磁感应强度的大小; 方向:曲线上任一点的切线方向。
b
c
B
磁力线特性: (1)磁力线是环绕电流的无头无尾的闭合曲线,每条磁力线与 电流相互套合,磁场是涡旋场、无源场; (2)任何两条磁力线在空间不相交; (3)磁力线的环绕方向与电流方向之间遵守右螺旋法则。
则电流:
由毕-萨定律:
I qnvS
0 qnvSdlsin(v , r ) dB 4 r2
dN nSdl
则一个粒子产生的磁场大小为:
0 qv r dB 0 qv sin(v , r ) B B 2 dN 4 4 r 3 r
由于同方向运动的正负电荷产生的电流方 向相反,故产生的磁感应强度相反。
(2)线元磁矩:
电磁学_09_稳恒磁场的高斯定理与安培环路定理

第九讲 稳恒磁场的高斯定理与安培环路定理01 磁感应线为描述空间磁场的分布,人为引入一系列假想的曲线(1831年法拉第首次引入)。
曲线的疏密反映磁感应强度的大小,曲线每一点切线方向表示磁感应强度的方向。
这些假想的曲线称为磁感应线。
如图XCH003_106所示,在磁场分布的空间一点选取一面积元dS ,面积元法线方向用单位矢量n表示,该面积元在磁感应强度方向上的投影大小dS ⊥。
磁感应强度大小: m d B dS ⊥Φ= —— 通过垂直B 方向上单位面积的磁感应线条数,也称为磁感应线密度 磁感应强度方向沿该点磁感应线的切线方向,即小磁针放在该点静止时,N 所指的方向。
02 磁通量如图XCH003_106所示,通过dS 的磁通量:m d B dS Φ=⋅02πθ≤< —— m d Φ为正;2πθπ<≤ —— m d Φ为负穿过曲面S 的磁通量:m S B dS Φ=⋅⎰ —— 如图XCH003_097所示规定面元法线方向由里向外为正,如图XCH003_107所示,通过一个闭合曲面S 的磁通量:Sm B dS Φ=⋅⎰ —— 穿过闭合曲面S 的磁通量为净穿过闭合曲面磁感应线的总条数 03 磁场的高斯定理0SB dS ⋅≡⎰ —— 无源场 由于磁感应线是闭合线,因此,对于一个闭合曲面S ,穿入的磁感应线的总数必然等于穿出的磁感应线总数,即通过任一闭合曲面的磁通量总是零。
稳恒磁场的高斯定理是电磁场理论的基本方程之一。
04 安培环路定理1安培环路定理在恒定电流产生的磁场中,磁感应强度沿任一闭合回路L 的线积分,等于闭合回路包围的所有电流代数和的0μ倍。
0int L LB dr I μ⋅=∑⎰ —— 安培环路定理的数学表达式 安培环路定理的证明1) 无限长载流直导线 —— 平面闭合回路L 垂直于导线,回路绕行方向和电流满足右手螺旋关系 导线周围的磁感应强度:02I B rμπ=,如图XCH003_126所示。
第9章稳恒电流的磁场精品

大学物理学A
第三篇 电磁学
第9章 稳恒电流的磁场
电流强度(I):单位时间内通过导体任一横
截面的电量 。
I dq dt
单位:安培 1A 1C s1
1A 103 mA 106 μ A
恒定电流(直流电):
导体中通过任一截面的电流强度不随时间变化(I =
恒量)。
电流强度的方向:导体中正电荷的流向。
磁感应强度 B
00,0,0,,,000, ,,vvvv////vv/v//BvB//B/v//B/BB/BF0/FF,BFFFF00000F 000 0v // B F 0 22222 222 vvvvvvBvBBBBBBFBFFmF2FmamFxamaxmaFxxmxmaxa amxxqqaqvqxvqqvvqvvqv方v方q方方方 v向向方向向 方 B向:v: 向 向v:v方: 向 : vv:vB: FvBB向: vBBmB: avBxBBq 00,0,0,,,,,0000,,,2,,,,2,,222,,2 222 FFFF0F,Fqq,qFvqvqvsqvvss2iqvinqsnsvisvinisnnqi sniv方 n方方si方向方n向方 向方: 向v向:v方向 F向 :v::vvB向 B方 :v: vBBB: 向 vBqBv: vBsi 对对对一对一 对一对 对 对 定一 一 对定实定一 一一 点 定 一定 点验点 定定点定 定点 证点点点点 明qq:qvqvvvsFqqFsi对 sFvsFqnviiinvsFnqnsFsFii一 snFvininnsFi定 常n常常常常 常 点 数数常常 数数数 ,数F数常 数 qmvax数 常 数
大学物理学A
第三篇 电磁学
第9章 稳恒电流的磁场
稳恒磁场: 磁场中各点的磁感应强度不随时间变化的磁场.
2013 电磁相互作用和稳恒磁场
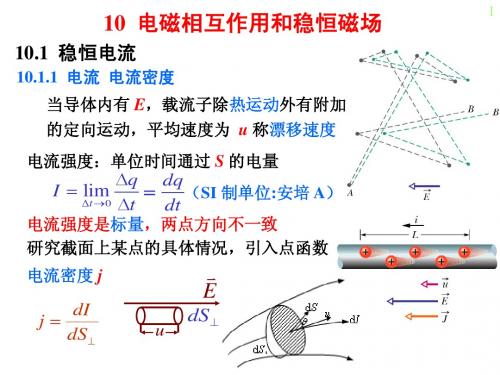
S S 那里有 j 那里有旋涡 B 0 j B 称为磁感应强度的旋度 积分形式
旋度 rot B
B dl 0 j ds
S
缩小
s
j
n j
s
B dl
) ( B) dS l (S rot x B 0 jx rot n B 0 jn
ds
一点附近单位时间单位体积产生的热量:
U U dU 点对应关系,适 用于非稳恒条件
ds
dI
Q p j 2 E 2 -- 热功率密度 dsdlt
p E
2
10.2 电磁相互作用
10.2.1 基本磁现象
6
《吕氏春秋》
7
安培:分子电流假说
8
相互作用通过磁场传递
运动电荷(即电流)在它周围的空间激发磁场,磁场对场 中的其他运动电荷施以作用力。
4
n 6Li 4He T
510 K
9
D T He n
4
1108 K
D 3He 4He p 6 D 2 4He 2 p 2n 43.1MeV
D 6Li 2 4He 22.4Mev
(可用来装高温等离子体)
范艾仑带
21
霍耳效应
22
续上
23
29
30
31
32
33
34
35
36
I
0
R
B0 ?
B0
0 I
4R
B0 ?
R 0
0 I cos 1 cos 2 B 4a
I
高二物理竞赛稳恒磁场及其基本规律课件

dB
(4)讨论:B
0I 4 r0
(cos1
cos2 )
若导线为无限长,
2
11
I
0 , 180 , B 匀强磁场对载流线圈的作用 1
2
2 r 求几种典型稳恒电流分布的磁场分布。
解:带电园盘旋转形成电流,园盘可看成许多环电流组成。
若导线为半无限长, 在计算时一般用其分量式。
0 0
与带电直线成 角
力矩 方向沿 nˆ B
M IS B
l1
d F
a
l2
B cn
F
b
例 半径为 R 的圆盘,带有正电荷,其电荷面密
3
度 kr, k是常数,r为圆盘上一点到圆心的距
离,圆盘放在一均匀磁场B中,B与盘面平行。
当圆盘以角速度绕过圆心 O点,且垂直与圆盘
平面的轴作逆时针旋转时,求圆盘所受磁力距的
大小和方向。
当圆盘以角速度 绕过圆心 O点,且垂直与圆盘平面的轴作逆时针旋转时,求圆盘所受磁力距的大小和方向。
2 半无限长载流直线:
解 取一对对称的电流源,
I 在计算时一般用其分量式。
线段 ad和bc受安培力等大、反向,可抵消;线段ab, dc 受力
I
I
I
Idl
r l
o r0
1
dB
• P (1) (2)• P
2
4 r 在计算时一般用其分量式。
方向: 右手螺旋法则。 如果是无限长带电直线:
3 载流直线的延长线上: 磁场分布。
磁场对载流线圈的作用(磁力矩)
例 求半径为R电流为I的载流园线圈轴线上的
三、 B-S 定律的应用-求磁场
与带电直线成 角 二、任意形状载流导线的 磁场
稳恒磁场(2)PPT课件

F2
F3
bc 边受力为:F3 Il2B ; da 边受 力为:F 4 I l2B.
这两个力是一对力偶. 故:F F 1 F 2 F 3 F 4 0
即作用在闭合线圈上的磁场力合力为零。
这一关系适用于匀强磁场中的任意形状线圈.
2021/4/8
上一张 下一张 返9回
作用在闭合线圈上的磁 场力合力为零,并不是说磁 场力对线圈不产生影响. 实 际上,由于F3 与F4 是一对力 偶,其作用是产生转动,磁 力矩为:
1,N 型半导体(电子型半导体): 载流子为带负电的电子.
2,P 型半导体(空穴型半导体): 载流子为带正电的空穴.
2021/4/8
上一张 下一张 返31回
f
v
B
f
B
v
2021/4/8
P 型半导体
I
正电空穴向右运动, 洛仑兹力 f qvB
向上,故:
(上正下负)
N 型半导体
I
负电电子向左运动, 洛仑兹力 f qvB
第九章 稳恒磁场
§9-1 磁感应强度 B
§9-2 毕奥—萨伐尔定律 §9-3 磁通量 磁场的高斯定理 §9-4 安培环路定理 §9-5 磁场对电流的作用 §9-6 带电粒子在电场和磁场中的运动
2021/4/8
1
有关磁场的一些典型结论:
1,无限长直电流 : B = 0I / (2 r)
半无限长端垂面上: B 1 0I 2 2r
2021/4/8
上一张 下一张 返14回
例3. 平行无限长载流直导线间的相互作用。
解: 导线1在导线2处产生的
磁感应强度为:
I1
B1
0I1 2a
I2
导线2的一段 d受l 2到的安
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v v v v v v v v v v ∫ M ⋅ dl = ∫ M ⋅ dl + ∫ M ⋅ dl + ∫ M ⋅ dl + ∫ M ⋅ dl
= js ab+ 0 + 0 + 0 = js ab = I s v r ∴ ∫ M ⋅ dl = I s I s 是 l 回路包围的总的分子电流
l
ab __
µ0
r 定义: 定义: H =
r B
v v ∫ H ⋅ dl = ∑Ii传
l i
µ0
r − M , --- 磁场强度,单位:安/米 磁场强度,单位:
-- 传导电流代数和
v v H ⋅ dl = ∑Ii传 (L包围) ∫
l
r H=
r B
讨论: 讨论:
µ = µ0 µr . µr = 1+ χm , v v v v H 如何计算介质中的 B ∑ ∫v ⋅ dl =vi Ii传 v H l 三、有介质的高斯定理 B = µH B
µr < 1 .
r 顺磁质 M与 r 抗磁质 M与
r B0同向; 同向; r B0反向。 反向。
5 . 磁化电流 以长直螺线管为例
4
管内充顺磁质,磁化 管内充顺磁质,磁化,
v mmi = IS S ∑
= jS lS= jS ∆V v v ∑mmi M= = jS ∆V jS -- 磁化电流密度
如图 9 — 33 有:
1
9-5
一、介质的磁化
磁介质
1 . 磁化机理和磁化强度 介质分类: 介质分类: 顺磁质, 顺磁质, µr ≥ 1 , µ ≥ µ0 . 抗磁质, 抗磁质, µr ≤ 1 , µ ≤ µ0 . 铁磁质, 铁磁质, 分子电流、 分子电流、分子磁矩 :
µr ≥ 1 , 几百、几千倍 几百、
r 电子绕核的轨道运动产生磁矢 B 1 r 电子自旋运动产生自旋磁矢 B2
等效于一个圆电流
都产生磁效应, 都产生磁效应,
→ 分子电流
r r r r r → 分子磁矩 P = IS 和角动量 l v 当 B0 ≠ 0 , M = me × B0 , 时 r r r r dL ∴ dL = Mdt M= dt r r r 时间内, ∴在 dt 时间内, L → L + dL, r v →Δ e与B0 反向 m 。
r r ∴ B = µH
i r r 1) M = χm H , χ m 是磁化率 ) r r r r r 2) B = µ0 H + µ0 Mr= µ0 (H + M ) r ) r = µ0 (H + χm H) = µ0 (1+ χm )H r r = µ0 µr H = µH
µ0
r −M
6
?{
2 . 铁磁质的磁化机理 —— 磁畴理论
9
r 当 B0 = 0 时,
相邻原子间的电子存在很强的交 换作用, 换作用,形成一个小小的自发磁 化区域 --- 磁畴
r 当 B0 ≠ 0 时,
磁畴转向外场方向排列 —— 铁磁质磁化
居里点
bc
cd __
da
5
二、有介质时的安培环路定理
r r 真空: 真空: ∫ B ⋅ dl = µ0 ∑I
v v 介质: 介质: B ⋅ dl = µ0 ∑(I传 + Is ) ∫
l
∑(I
传
+ Is ) 为穿过回路的总电流
v v 1 v v ∫ µ0 B⋅ dl = ∑(I传 + Is ) = ∑I传 + ∫ M ⋅ dl l v v v B ∴ ∫( − M ) ⋅ dl = ∑I传
r r r B = B0 + B′ r r r r r ∫∫ B ⋅ dS = ∫∫ (B + B′) ⋅ dS = 0
四、铁磁质
1 . 铁磁质的磁化特性
7
NI H= 2πr 测B, 改变I, 测出H ~ B曲线 。
2) µr — H曲线 )
1)起始磁化曲线 )
→ µ 随 H 变化
8
3) 磁滞回线 ) Br --- 剩磁 Hc --- 矫顽力 铁磁质中 B 的变化总 是落后于外加磁场 H 的变化 ---- 磁滞现象
2. 顺磁质磁化
2
r v B0 = 0 热运动分子磁矩无规则排列,不显磁性 ∑mmi = 0 , 热运动分子磁矩无规则排列, r r v B0 ≠ 0 ∑mmi ≠ 0 , 产生附加磁场 B′
r B0
r v m 进动产生的 Δ e → B′ 小,略去
r r r ∴ 合场B = B0 + B′ ,
r r r B = B0 + B′
同方向。 同方向。
µr > 1 .
3 . 抗磁质
3
r B0 = 0时, r B0 ≠ 0时,
v mmi = 0 . ∑
r v 反向, 由进动产生 ∆me 与 B0 反向, r r ∴ B′与B0 反向 。
r r r ∴ 合场B = B0 − B′ ,
r 4 . 磁化强度 M = v mmi ∑ ∆V
