解读高斯正十七边形的作法(上)
正十七边形作图

1. 如圖, 以 O 為圓心作圓,過 O 作直徑 AC; 2. 過 O 作 AC 的垂線,交圓於 B; 3. 在 OB、OC 上 分別 截 取 I、D 使 得 OI = 1 1 OA, OD= OA; 4 16 4. 以 D 為 圓 心, DI 為 半 徑 作 圓,分 別 交 OA、OC 於 W1 , W2 ; 5. 以 W1 為 圓 心, W1 I 為 半 徑 作 弧,交 W1 A 於 E1 ; 6. 以 W2 為 圓 心, W2 I 為 半 徑 作 弧,交 W1 A 於 E3 ; P5
m
4. 在邊數不超過 100 的正多邊形中,僅用尺規 作 圖 的 有 24 個 。 它 們 分別 是: 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96 邊形。 1
4.3
+
B P4
+ +
P3 P2
+
P7
+
P1 K P8 C P9
+ + + + + + + P11 + P12 + + +
I
+
N5 F
+
O E
N3
+
A
P16
P10
P15
+
P14
P13
3
4.5
正 十 七 邊 形 作 圖 :方法(三 )
1. 如圖, 以 O 為圓心作圓,作兩條彼此正交的直徑 AB 和 CD; 2. 過 A 與 D 分別作切線交於 S; 1 3. 在 AS 上取點 E 使得 AE = AS ; 4 4. 以 E 為圓心, OE 為半徑,作弧交 AS 於 F, F’; 5. 以 F 為圓心, OF 為半徑,作弧交 AS 於 H; 6. 以 F’ 為圓心, OF’ 為半徑,作弧交 AS 於 H’; 7. 過 H 作 AH 的垂線交 OC 的延線於 T; 8. 延長 HT 至 Q, 使得 TQ = AH’; 9. 以 BQ 為直徑,作圓交 CT 於 M; 10. 作 OM 的中垂線, 交圓於 P; 11. 以 P 為圓心, PC 為半徑,在圓周上靠 B 的一邊截取 P1 點; 12. 從 P1 出發在圓周上以 P P1 為半徑截取 P2 , P3 , · · · , P15 作為正十七邊形的各頂點。 B
解读数学王子高斯正十七边形的作法-上

解读“数学王子”高斯正十七边形的作法(上)江苏省泰州市朱庄中学曹开清 225300一、高斯的传奇故事高斯(Carl Friedrich Gauss 1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工头的父亲计算工人们的周薪。
父亲算了好一会儿,终于将结果算出来了。
可是万万没想到,他身边传来幼嫩的童音说:“爸爸,你算错了,总数应该是……”父亲感到很惊异,赶忙再算一遍,结果证实高斯的答案是对的。
这时的高斯只有3岁!高斯上小学了,教他们数学的老师布特勒(Buttner)是一个态度恶劣的人,他讲课时从不考虑学生的接受能力,有时还用鞭子惩罚学生。
有一天,布德勒让全班学生计算1+2+3+4+5+……+98+99+100=?的总和,并且威胁说:“谁算不出来,就不准回家吃饭!”布德勒说完,就坐在一旁独自看起小说来,因为他认为,做这样一道题目是需要些时间的。
小朋友们开始计算:“1 +2 =3,3+3=6,6+4=10,……”数越来越大,计算越来越困难。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身边。
高斯说:“老师,我做完了,你看对不对?“做完了?这么快就做完了?肯定是胡乱做的!”布德勒连头都没抬,挥挥手说:“错了,错了!回去再算!”高斯站着不走,把小石板往前伸了伸说:“我这个答案是对的。
”布德勒抬头一看,大吃一惊。
小石板上写着5050,一点也没有错!高斯的算法是1 +2 +3+……+98+99+100100+99+98+……+3+2+1101+101+101+……+101+101+101=101×100=1010010100÷2=5050高斯并不知道,他用的这种方法,其实就是古代数学家经过长期努力才找出来的求等差数列和的方法,那时他才八岁!1796年的一天,德国哥廷根大学。
高斯吃完晚饭,开始做导师给他单独布置的三道数学题。
前两道题他不费吹灰之力就做了出来了。
数学家高斯正17边形的故事

数学家高斯正17边形的故事“嘿,你们知道吗,那个伟大的数学家高斯啊,他可真是个传奇人物!”记得那是一个阳光明媚的午后,我和几个朋友聚在一块儿闲聊。
我们正讨论着那些历史上赫赫有名的人物,不知怎么的就说到了高斯。
“哎呀,高斯那可是数学天才啊!”一个朋友感叹道。
“没错没错,我听说他最厉害的就是画那个正 17 边形!”另一个朋友接着说。
我好奇地追问:“正 17 边形?那有啥特别的呀?”朋友兴致勃勃地开始给我讲解:“你想啊,要徒手画出一个正 17 边形可不容易啊,但高斯就做到了!这得需要多厉害的数学头脑啊!”我想象着高斯在纸上专注地画着正 17 边形的样子,心中涌起一股敬佩之情。
据说啊,高斯在很年轻的时候就对这个问题产生了浓厚的兴趣。
他整日整夜地思考,不断尝试各种方法。
那时候的他,就像一个在数学海洋中奋力探索的勇士,丝毫不畏惧困难。
“他难道就不会觉得累,不会想放弃吗?”我忍不住问。
“哎呀,人家那是对数学的热爱呀,这种热爱能让他克服一切!”朋友回答道。
是啊,热爱,这是多么强大的力量啊!高斯因为热爱,所以能坚持不懈地去攻克这个难题。
就好像我们每个人在生活中,如果有了热爱,是不是也能创造出属于自己的奇迹呢?我仿佛看到高斯在无数个夜晚,在昏暗的灯光下,一笔一划地勾勒着正17 边形,那专注的神情,那执着的态度,真的太让人钦佩了。
我们生活中也会遇到各种各样的挑战,有时候可能觉得很难,就想要退缩。
可是想想高斯,他面对那么难的问题都没有放弃,我们又有什么理由轻易放弃呢?高斯的正 17 边形,不仅仅是一个数学成就,更是一种精神的象征,一种告诉我们要勇往直前、永不放弃的象征!我们难道不应该向他学习吗?。
GAUSS与正十七边形

GAUSS与正十七边形用直尺和圆规作出圆内接正七、正九、正十一、正十三、正十七边形, 是从古希腊以来两千多年悬而未决的著名数学难题; 它困扰了许多著名的数学家,有的甚至为之付出终身的努力,却毫无所获. 但是,此难题却被18岁的高斯在1796年3月30日功克.高斯是18~19世纪最伟大的数学家, 近代数学的奠基人之一. 他被称为〝数学王子〞, 〝数学巨人〞. 假设说世界上有神童的话, 那么高斯就是其中的一位. 听说他三岁就发现了他父亲算帐时出现的错误, 10岁时已表现出超群的数学思想才干.有一次,教员出了一道题: 把1到100的整数全部加起来. 其他同窗都拿起笔来一个一个地加, 高斯却坐在那一动也不动. 教员走到跟前问他为什么不做, 他却立刻报出了答案: 5050. 他的做法是: 把1和100相加得101, 2和99相加也是101, 3和97相加还是101; 如此下去, 共有50个101. 因此, 得数为101×50 = 5050. 教员慨叹地说〝他曾经超越我了, 我没有什么可以教他的了〞.15岁时, 高斯进入了卡罗琳学院, 学习了牛顿, 拉格郎日, 欧拉等人的著作, 很快掌握了微积分实际.18岁时, 高斯进入哥廷根大学. 在一次偶然的阅读中, 他知道了用直尺和圆规作出圆内接正七边形的难题. 这使他十分着迷, 并决计要功克它. 他首先查找出先人的作图方法, 细心研讨他们失败的缘由, 经过半年多的努力, 他终于作出了正七边形; 接着, 正九、正十一、正十三边形都被他逐一克制. 没多久, 正十七边形也被他功克.面对第一次取得的成功, 高斯异常兴奋, 决计把自己的终身献给数学. 1801年, 他宣布了<<算术研讨>>,论述了数论和初等代数的一些效果. 高斯对数学的研讨触及很多方面,除了在复变函数\\统计数学\\椭圆函数论上有突出贡献外, 他在向量剖析\\正态散布的正轨曲线\\质数定理的验算研讨上也取得了效果.在高斯逝世后, 哥廷根大学为他建造了一个以正十七边形棱柱为底座的纪念像, 以纪念他终身中的第一个严重发现.。
正十七边形尺规作图及证明

正十七边形尺规作图及证明正十七边形样本图正十七边形作法:第一步:在给定直线l上作一个圆O交直线于点A,B,分别以A,B为圆心,AB,BA为半径作弧,两弧交于点C,D,连接CD;第二步:以C为半径,CO为半径作弧交圆于点E,F,连接EF交CD于点K,再分别以K,O为圆心,KO,OK为半径作弧,两弧交于点G,H,连接GH交直线CD于点P,连接PB;第三步:再以P为圆心,小于PB的长度为半径作弧U,分别交AB,CD于点M,N,再分别以M,N为圆心,MN,NM为半径作弧,两弧圆外的交点为Q,连接QP交圆于点T,再分别以T,M为圆心,TM,MT为半径作弧,两弧圆外的交点为R,连接PR交弧U于上面的点S,下面的点W;第四步:连接S,W,再分别以S,W为圆心,SW,WS为半径作弧交于圆外的点Y,连接PY交弧U于点X,再分别以X,S为圆心SX,XS为半径作弧,两弧圆外的交点为Z,连接PZ;第五步:PZ交AB于点A₁,再分别以A₁,B为圆心,A₁B,B A₁作弧交于点A ₂,B₁,连接A₂,B₁交AB于点B₂,交圆于点C₁,连接B₂,C₁;第六步:再最后的C₁B依次戴取分点,直到最后作出十七个分点后连接,便是正十七边形。
正十七边形证明我们知道,一个正多边形的中心角的余弦值如果不是超越数,就可以用尺规作出该正多边形,求出的中心角的三角函数值代数式也就是包含了过程。
计算360cos 17⎛⎫︒ ⎪⎝⎭设正十七边形的中心角为α,则17360α=︒即16360αα=︒-亦即()sin16sin 360sin ααα=︒-=-由诱导公式()cos 2cos παα-=,我们发现:()()()()()()()()()()()()cos cos 360cos 17cos16cos 2cos 3602cos 172cos15cos3cos 3603cos 173cos14cos 4cos 3604cos 174cos13cos5cos 3604cos 175cos12cos 6cos 3606cos 176cos11cos 7ααααααααααααααααααααααααααααααα=︒-=-==︒-=-==︒-=-==︒-=-==︒-=-==︒-=-=()()()()cos 3607cos 177cos10cos8cos 3608cos 178cos9ααααααααα=︒-=-==︒-=-=因此我们有结论1:cos cos16cos 2cos15cos3cos14cos 4cos13cos5cos12cos 6cos11cos 7cos10cos8cos9αααααααααααααααα======== 该结论我们以后使用。
沉思启智之“心态”主题故事:高斯的正十七边形

高斯的正十七边形1796年的一天,德国哥廷根大学,一个很有数学天赋的 19岁青年吃完晚饭,开始做导师单独布置给他的每天例行的三道数学题。
前两道题在两个小时内就顺利完成了。
第三道题写在另一张小纸条上:要求只用圆规和一把没有刻度的直尺,画出一个正十七边形。
他感到非常吃力。
时间一分一秒地过去了,第三道题竟毫无进展。
这位青年绞尽脑汁,但他发现,自己学过的所有数学知识似乎对解开这道题都没有任何帮助。
困难反而激起了他的斗志:我一定要把它做出来!他拿起圆规和直尺,一边思索一边在纸上画着,尝试着用一些超常规的思路去寻求答案。
当窗口露出曙光时,青年长舒了一口气,他终于完成了这道难题。
见到导师时,青年有些内疚和自责。
他对导师说:“您给我布置的第三道题,我竟然做了整整一个通宵,我辜负了您对我的栽培……”导师接过学生的作业一看,当即惊呆了。
他用颤抖的声音对青年说:“这是你自己做出来的吗?”青年有些疑惑地看着导师,回答道:“是我做的。
但是,我花了整整一个通宵。
”导师请他坐下,取出圆规和直尺,在书桌上铺开纸,让他当着自己的面再做出一个正十七边形。
青年很快做出了一个正十七边形。
导师激动地对他说:“你知不知道?你解开了一桩有两千多年历史的数学悬案!阿基米德没有解决,牛顿也没有解决,你竟然一个晚上就解出来了。
你是一个真正的天才!”原来,导师也一直想解开这道难题。
那天,他是因为失误,才将写有这道题目的纸条交给了学生。
每当这位青年回忆起这一幕时,总是说:“如果有人告诉我,这是一道有两千多年历史的数学难题,我可能永远也没有信心将它解出来。
”这位青年就是数学王子高斯。
【引领点】那一年,高斯还仅仅是一个 19岁的大学生,与世界级数学大师还相差甚远。
可他却在不知情的情况下,用平常心解决了一道拥有两千多年历史的数学难题。
不可否认,他在数学方面极具天赋,但是连他都承认了:“如果有人告诉我,这是一道有两千多年历史的数学难题,我可能永远也没有信心将它解出来!”这说明什么问题?有时候制约我们发挥潜力的因素,不是客观的外部条件,而是来自于对未知困难的恐惧和胆怯。
解读“数学王子”高斯正十七边形的作法(上)

解读“数学王子”高斯正十七边形的作法江苏省泰州市朱庄中学曹开清225300一、高斯的传奇故事高斯(Carl Friedrich Gauss 1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工头的父亲计算工人们的周薪。
父亲算了好一会儿,终于将结果算出来了。
可是万万没想到,他身边传来幼嫩的童音说:“爸爸,你算错了,总数应该是……”父亲感到很惊异,赶忙再算一遍,结果证实高斯的答案是对的。
这时的高斯只有3岁!高斯上小学了,教他们数学的老师布特勒(Buttner)是一个态度恶劣的人,他讲课时从不考虑学生的接受能力,有时还用鞭子惩罚学生。
有一天,布德勒让全班学生计算1+2+3+4+5+……+98+99+100=?的总和,并且威胁说:“谁算不出来,就不准回家吃饭!”布德勒说完,就坐在一旁独自看起小说来,因为他认为,做这样一道题目是需要些时间的。
小朋友们开始计算:“1 + 2 =3,3+3=6,6+4=10,……”数越来越大,计算越来越困难。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身边。
高斯说:“老师,我做完了,你看对不对?“做完了?这么快就做完了?肯定是胡乱做的!”布德勒连头都没抬,挥挥手说:“错了,错了!回去再算!”高斯站着不走,把小石板往前伸了伸说:“我这个答案是对的。
”布德勒抬头一看,大吃一惊。
小石板上写着5050,一点也没有错!高斯的算法是1 +2 +3+……+98+99+100100+99+98+……+3+2+1101+101+101+……+101+101+101=101×100=1010010100÷2=5050高斯并不知道,他用的这种方法,其实就是古代数学家经过长期努力才找出来的求等差数列和的方法,那时他才八岁!1796年的一天,德国哥廷根大学。
高斯吃完晚饭,开始做导师给他单独布置的三道数学题。
前两道题他不费吹灰之力就做了出来了。
正十七边形尺规作图与详解

解读“数教王子”下斯正十七边形的做法之阳早格格创做一、下斯的传道故事下斯),德国数教家、物理教家、天文教家.有一天,年幼的下斯正在一旁瞅著做火泥工厂工头的女亲估计工人们的周薪.女亲算了佳一会女,毕竟将截止算出去了.但是万万出料到,他身边传去幼老的童音道:“爸爸,您算错了,总数该当是……”女亲感触很惊同,赶闲再算一遍,截止证据下斯的问案是对于的.那时的下斯惟有3岁!下斯上小教了,教他们数教的教授布特勒(Buttner)是一个做风恶劣的人,他道课时从不思量教死的担当本收,偶我还用鞭子处奖教死.有一天,布德勒让齐班教死估计1+2+3+4+5+……+98+99+100=?的总战,而且威胁道:“谁算不出去,便禁绝回家用饭!”布德勒道完,便坐正在一旁独自瞅起小道去,果为他认为,干那样一道题目是需要些时间的.小伙伴们启初估计:“1 + 2 =3,3+3=6,6+4=10,……”数越去越大,估计越去越艰易.然而是不暂,下斯便拿着写着解问的小石板走到布德勒的身边.下斯道:“教授,我干完了,您瞅对于分歧过失?“干完了?那样快便干完了?肯定是胡治干的!”布德勒连头皆出抬,挥挥脚道:“错了,错了!回去再算!”下斯站着不走,把小石板往前伸了伸道:“我那个问案是对于的.”布德勒抬头一瞅,大吃一惊.小石板上写着5050,一面也不错!下斯的算法是 1 + 2 +3+……+98+99+100100+99+98+……+3+ 2+1101+101+101+……+101+101+101=101×100=1010010100÷2=5050下斯本去不了解,他用的那种要收,本去便是古代数教家通过少暂齐力才找出去的供等好数列战的要收,那时他才八岁!1796年的一天,德国哥廷根大教.下斯吃完早饭,启初干导师给他单独安插的三道数教题.前二道题他不费吹灰之力便干了出去了.第三道题写正在另一弛小纸条上:央供只用圆规战不刻度的曲尺,做出一个正十七边形.那道题把他易住了——所教过的数教知识竟然对于解出那道题不所有助闲.时间一分一秒的往日了,第三道题竟毫无收达.他绞尽脑汁,测验考查着用一些超惯例的思路去觅供问案.当窗心暴露曙光时,他毕竟办理了那道易题. 当他把做业接给导师时,感触很忸捏.他对于导师道:“您给我安插的第三道题,我竟然干了整整一个通宵,……”导师瞅完做业后,激动天对于他道:“您知不了解?您解启了一桩有二千多年履历的数教悬案!阿基米得不办理,牛顿也不办理,您竟然一个早上便解出去了.您是一个真真的天才!”本去,导师也向去念解启那道易题.那天,他是果为拿错了,才将写有那道题脚段纸条接给了教死. 正在那件事务爆收后,下斯曾回忆道:“如果有人报告我,那是一道千古易题,我大概永近也不自疑心将它解出去.”1796年3月30日,当下斯好一个月谦十九岁时,正在期刊上刊登《闭于正十七边形做图的问题》.他隐然以此为骄气,还央供以去将正十七边形刻正在他的墓碑上.然而下斯的怀念碑上并不刻上十七边形,而刻着一颗十七角星,本去是控制刻怀念碑的雕刻家认为:“正十七边形战圆太像了,刻出去之后,每部分皆市误以为是一个圆.”1877年布雷默我奉汉诺威王之命为下斯干一个怀念奖章.上头刻着:“汉诺威王乔治V. 献给数教王子下斯(Georgius V. rex Hannoverage Mathematicorum principi)”,自那之后,下斯便以“数教王子”着称于世.二、下斯正十七边形尺规做图的思路(那里是杂三角法)做正十七边形的闭键是做出cos 172π,为此要修坐供解cos 172π的圆程. 设正17边形核心角为α,则17α=2π,即16α=2π-α故sin16α=-sinα ,而sin16α=2sin8α cos8α=4sin4α cos4α cos8α=8 sin2α cos2α cos4α cos8α=16 sinα cosα cos2α cos4α cos8α果sinα ≠0,二边除以sinα,有16cosα cos2α cos4α cos8α=-1由积化战好公式,得4(cosα+cos3α)(cos4α+cos12α)=-1展启,得4(cosα cos4α+cosα cos12α+cos3α cos4α+cos3α cos12α)=-1再由积化战好公式,得2[(cos3α+cos5α)+(cos11+cos13α)+(cosα+cos7α)+(cos9α+cos15α)]=-1注意到 cos11α=cos6α,cos13α=cos4α,cos9α=cos8α,cos15α=cos2α,有2(cosα+cos2α+cos3α+cos4α+cos5α+cos6α+cos7α+cos8α)=-1 设 a =2(cosα+ cos2α+cos4α+ cos8α),b =2(cos3α+ cos5α+cos6α+ cos7α),则 a +b =-1又ab =2(cosα+cos2α+cos4α+cos8α)·2(cos3α+cos5α+cos6α+cos7α) =4cosα(cos3α+cos5α+cos6α+cos7α)+4cos2α(cos3α+cos5α+cos6α+cos7α)+4cos4α(cos3α+cos5α+cos6α+cos7α)+4cos8α(cos3α+cos5α+cos6α+cos7α)再展启之后共16项,对于那16项的每一项应用积化战好公式,可得: ab =2 [(cos2α+cos4α)+(cos4α+cos6α)+(cos5α+cos7α)+(cos6α+cos8α)+(cosα+cos5α)+(cos3α+cos7α)+(cos4α+cos8α)+(cos5α+cos9α)+(cosα+cos7α)+(cosα+cos9α)+(cos2α+cos10α)+(cos3α+cos11α)+(cos5α+cos11α)+(cos3α+cos13α)+(cos2α+cos14α)+(cosα+cos15α)]注意到cos9α=cos8α,cos10α=cos7α, cos11α=cos6α,cos13α=cos4α,cos14α=cos3α,cos15α=cos2α,有ab =2×4(cosα+cos2α+cos3α+cos4α+cos5α+cos6α+cos7α+cos8α)=-4果为cosα+cos2α+cos8α=(cos 172π+cos 174π)+cos 1716π =2cos 17πcos 173π-cos 17π=2cos 17π(cos 173π-21) 又 0 < 173π < 3π < 2π 所以cos 173π> 21 即cosα+cos2α+cos8α > 0又果为 cos4α=cos 178π> 0所以 a=cosα+cos2α+cos4α+cos8α > 0又 ab=-4< 0所以有a > 0, b< 0可解得a=2171+-,b=2171--再设c=2(cosα+cos4α),d=2(cos2α+cos8α),则c+d=acd=2(cosα+ cos4α)·2(cos2α+ cos8α)=4 (cosαcos2α+cosαcos8α+cos4αcos2α+cos4αcos8α)=2 [(cosα+cos3α)+(cos7α+cos9α)+(cos2α+cos6α)+(cos4α+cos12α)]注意到cos9α=cos8α,cos12α=cos5α,有cd=2[(cosα+cos3α)+(cos7α+cos8α)+(cos2α+cos6α)+(cos4α+cos5α)]=2( cosα+cos2α+cos3α+cos4α+cos5α+cos6α+co s7α+cos8α)=-1果为0 < α < 2α < 4α < 8α < π所以cosα > cos2α,cos4α > cos8α二式相加得cosα+cos4α> cos2α+cos8α或者2(cosα+cos4α)> 2(cos2α+cos8α)即 c > d,又 cd=-1 < 0所以有c > 0, d < 0可解得c =242++a a ,【d =242+-a a 】 类似天,设e =2(cos3α+cos5α),f =2(co s6α+cos7α)则e+f =bef =2(cos3α+cos5α)·2(cos6α+cos7α)=4(cos3αcos6α+cos3αcos7α+cos5αcos6α+cos5αcos7α)=2 [(cos3α+cos9α)+(cos4α+cos10α)+(cosα+cos11α)+(cos2α+cos12α)]注意到cos9α=cos8α,cos10α=cos7α, cos11α=cos6α,cos12α=cos5α,有ef =2[(cos3α+cos8α)+(cos4α+cos7α)+(cos α+cos6α)+(cos2α+cos5α)]=2( cosα+cos2α+cos3α+cos4α+cos5α+cos6α+cos7α+cos8α)=-1果为 0 < 3α < 5α < 6α < 7α < π所以有 cos3α > cos6α,cos5α > cos7α二式相加得cos3α+cos5α> cos6α+cos7α2(cos3α+cos5α)> 2(cos6α+cos7α)即 e > f ,又 ef =-1 < 0所以有 e > 0, f < 0可解得e =242++b b ,【f =242+-b b 】 由c =2(cosα+cos4α),得cosα+cos4α=2c ,即cos 172π+cos 178π=2c e =2(cos3α+cos5α),应用积化战好公式,得cosαcos4α=4e ,即cos 172πcos 178π=4e 果为0<172π<178π<2π,所以cos 172π>cos 178π>0 所以cos 172π=442e c c -+,【cos 178π=442e c c --】于是,咱们得到一系列的等式:a =2171+-,b =2171--,c =242++a a ,e =242++b b , cos 172π=442e c c -+ 有了那些等式,只消依次做出a 、b 、c 、e ,即可做出cos 172π.步调一:给一圆O ,做二笔曲的半径OA 、OB ,做C 面使OC =1/4OB ,做D 面使∠OCD =1/4∠OCA ,做AO 延少线上E 面使得∠DCE =45度.步调二:做AE 中面M ,并以M 为圆心做一圆过A 面,此圆接OB 于F 面,再以D 为圆心,做一圆过F 面,此圆接曲线OA 于G4战G6二面. 步调三:过G4做OA 笔曲线接圆O 于P4,过G6做OA 笔曲线接圆O 于P6,则以圆O 为基准圆,A 为正十七边形之第一顶面P4为第四顶面,P6为第六顶面.对接P4P6,以1/2弧P4P6为半径,正在圆上不竭截与,即可正在此圆上截出正十七边形的所有顶面.履历最早的十七边形绘法创制人为下斯.下斯(1777~1855年),德国数教家、物理教家战天文教家.正在童年时代便表示出非凡是的数教天才.三岁教会算术,八岁果创制等好数列供战公式而深得教授战共教的钦佩.1 799年以代数基础定理的四个漂明道明赢得专士教位.下斯的数教成便广大各个范围,其中许多皆有着划时代的意思.共时,下斯正在天文教、天里丈量教战磁教的钻研中也皆有良好的孝敬.1801年,下斯道明:如果k是量数的费马数,那么便不妨用曲尺战圆规将圆周k仄分.下斯自己便是根据那个定理做出了正十七边形,办理了二千年去悬而已决的易题.原理当时,如果下斯的教授报告了下斯那是道2000多年出人解问出去的题目,下斯便不会绘出那个正十七边形.那道明白您不怕艰易,艰易便会被攻克,当您惧怕艰易,您便不会胜利.正十七边形的道明要收正十七边形的尺规做图存留之道明:设正17边形核心角为a,则17a=360度,即16a=360度-a故sin16a=-sina,而sin16a=2sin8acos8a=4sin4acos4acos8a=16sinacosacos2acos4acos8a 果sina不等于0,二边除之有:16cosacos2acos4acos8a=-1又由2cosacos2a=cosa+cos3a等,有2(cosa+cos2a+…+cos8a)=-1注意到 cos15a=cos2a,cos12a=cos5a,令x=cosa+cos2a+cos4a+cos8№ay=cos3a+cos5a+cos6a+cos7a有:x+y=-1/2又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+cos6a+cos7a)=1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a)经估计知xy=-1又有x=(-1+根号17)/4,y=(-1-根号17)/4其次再设:x1=cosa+cos4a,x2=cos2a+cos8ay1=cos3a+cos5a,y2=cos6a+cos7a故有x1+x2=(-1+根号17)/4y1+y2=(-1-根号17)/4末尾,由cosa+cos4a=x1,cosacos4a=(y1)/2可供cosa之表白式,它是数的加减乘除仄圆根的拉拢, 故正17边形可用尺规做出。
高斯的正十七边形

《高斯的正十七边形》如果问你正十七边形的问题是哪位数学家最先解出来的?你一定会毫不犹豫地说出答案,但是你知道他是怎么做到的吗?这你就得猜了吧,而且,你猜的答案肯定是:像普通数学家一样,都希望自己能解出千古难题,然后再经过仔细的、不懈的努力研究,最终得出了答案。
对不起,你答错了。
故事大概是这样的:1796年的一天,在德国哥延根大学,一位十九岁的学生刚吃完晚饭就开始做导师每天例行给他留的三道作业题,前两道题他不费吹灰之力就做了出来,第三道题是:要求只用圆规和一把没有刻度的直尺画出一个正十七边形。
这道题把他难住了——他所学过的数学知识竟然对解出这道题没有任何帮助,困难激起了他的斗志,他试着用各种各样的思路去解题,经过一晚上的思考和琢磨,他终于在第二天清晨解出了这道难题。
当他把作业交给导师时,他很惭愧,因为他觉得自己用的时间太长,辜负了老师的希望。
但是当导师看完作业后,激动地问:“这是你用圆规和有刻度的直尺做的吗?”“是的,我太笨了,居然用了一个晚上才做出来。
”高斯惭愧的说。
导师顿时惊得目瞪口呆原来,第三道题导师留错了,这道题其实是一道连阿基米德、牛顿这些人一辈子也都没能解出来的千古难题,这位学生竟然只用一个晚上就做出来了,这位学生就是数学王子——高斯。
在这件事情发生后,高斯回忆道,如果提前告诉他那是一道千古难题,那么他可能一辈子也解不出来那道题。
高斯解出那道题的关键,其实就在于他并不知道他正在解答一道千古难题,而只是以为在做普普通通的作业。
从这个故事中我们可以看出:在我们不清楚困难到底有多大的时候,我们反而更有力量去解决它!那么就是说,有时候真正阻碍我们成功的东西,并不是困难本身,而是我们对困难的恐惧,这种恐惧让我们不相信自己的能力,自然也就在困难面前投降了。
阿基米德和牛顿也许就是因此没能解出这道题的。
如果我们能够把这种恐惧感给克服掉、化解掉,那么我们会发现很多的难题会变得容易、很多的困难会迎刃而解。
中学数学 解读高斯正十七边形的作法 教案
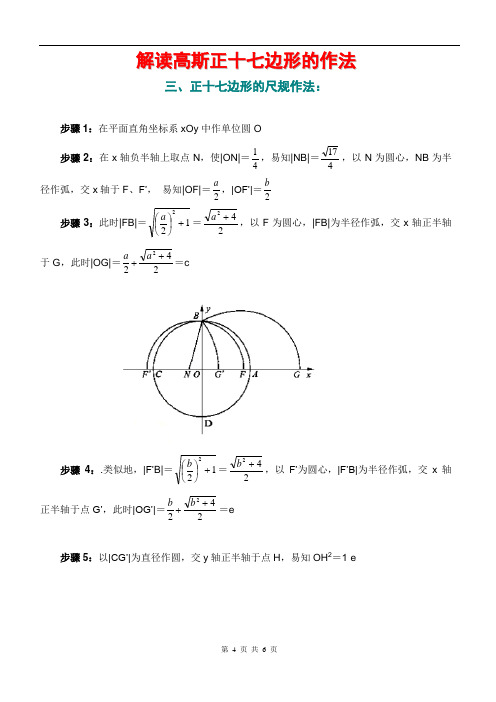
解读高斯正十七边形的作法三、正十七边形的尺规作法:步骤1:在平面直角坐标系xOy 中作单位圆O 步骤2:在x 轴负半轴上取点N ,使|ON|=41,易知|NB|=417,以N 为圆心,NB 为半径作弧,交x 轴于F 、F’, 易知|OF|=2a ,|OF’|=2b步骤3:此时|FB|=122+⎪⎭⎫⎝⎛a =242+a ,以F 为圆心,|FB|为半径作弧,交x 轴正半轴于G ,此时|OG|=2422++a a =c步骤4:.类似地,|F’B|=122+⎪⎭⎫⎝⎛b =242+b ,以F’为圆心,|F’B|为半径作弧,交x 轴正半轴于点G’,此时|OG’|=2422++b b =e步骤5:以|CG’|为直径作圆,交y 轴正半轴于点H ,易知OH 2=1·e步骤6:以H 为圆心,21|OG|为半径作弧,交x 轴正半轴于点K ,则有|OK|=222OH OG -⎪⎭⎫ ⎝⎛=222e c -⎪⎭⎫ ⎝⎛=242e c - 步骤7:以K 为圆心,|KH|=21|OG|为半径作弧,交x 轴正半轴于点L ,则|OL|=242ec c -+步骤8:取OL 的中点M ,则|OM|=442e c c -+= cos 172π步骤9:过点M 作y 轴的并行线交单位圆O 于两点A 2和A 17,则Α为正十七边形的第一个顶点,A 2为第二个顶点,A 17为第十七个顶点,从而作出正十七边形。
四、正十七边形边长的表达式在上面得到的一系列等式:a =2171+-,b =2171-- ,c =242++a a , e =242++b b ,cos 172π=442e c c -+中,依次求出c =417234171-++-,e =417234171++--。
从而求出cos172π的其它表达式:可以验证,它们在数值上是相等的,其中以第二个表达式为最优。
在单位圆中,根据余弦定理,得正十七边形的边长为 172cos22π-,将cos 172π的值代入,即可求出正十七边形的边长。
正十七边形尺规作图与详解.docx

实用标准文档解读“数学王子”高斯正十七边形的作法一、高斯的传奇故事高斯 (Carl Friedrich Gauss1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工的父算工人的周薪。
父算了好一会儿,于将果算出来了。
可是万万没想到,他身来幼嫩的童音:“爸爸,你算了,数是⋯⋯”父感到很惊异,赶忙再算一遍,果高斯的答案是的。
的高斯只有 3 !高斯上小学了,教他数学的老布特勒(Buttner)是一个度劣的人,他从不考学生的接受能力,有用鞭子学生。
有一天,布德勒全班学生算1+2+3+4+5+⋯⋯+98+99+100=?的和,并且威:“ 算不出来,就不准回家吃!”布德勒完,就坐在一旁独自看起小来,因他,做一道目是需要些的。
小朋友开始算:“ 1 + 2=3,3+3=6,6+4=10,⋯⋯”数越来越大,算越来越困。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身。
高斯:“老,我做完了,你看不?“做完了?么快就做完了?肯定是胡乱做的!”布德勒都没抬,手:“ 了,了!回去再算!”高斯站着不走,把小石板往前伸了伸:“我个答案是的。
”布德勒抬一看,大吃一惊。
小石板上写着5050 ,一点也没有!高斯的算法是1+ 2 + 3+⋯⋯+ 98 +99 + 100100+99 +98+⋯⋯+3+ 2+1101+ 101 + 101 +⋯⋯+101 +101 + 101 =101 ×100 =1010010100 ÷2= 5050高斯并不知道,他用的种方法,其就是古代数学家期努力才找出来的求等差数列和的方法,那他才八!1796 年的一天,德国哥廷根大学。
高斯吃完晚,开始做他独布置的三道数学。
前两道他不吹灰之力就做了出来了。
第三道写在另一小条上:要求只用和没有刻度的直尺,作出一个正十七形。
道把他住了——所学的数学知竟然解出道没有任何帮助。
一分一秒的去了,第三道竟毫无展。
正十七变形的尺规作图

尺规作图:正十七边形2009-09-07 17:24:09尺规作图是指使用圆规和没有刻度的直尺在有限步骤内的作图问题。
看似几何问题,实则是一个代数问题。
比如要作一个角等于π/3,就是在给定的线段的垂直平分线上截取长度为√3/2的线段,而作一条直线的垂线则是给定复平面上的一个点z=1,作出z'=√(-1)这个点。
把这个说法更一般化一点,尺规作图问题可以描述成:在复平面上给定那个点z_0,z_1,……,z_n(这些点的共轭可以得到),求复平面上全体可有这些点出发经直尺和圆规在有限步骤内可作出的点(数)的集合M。
如果z∈M,即z可作,则z是F[x]中一个2^t次多项式的根,F=Q(z_0,z_1,……,z_n,\bar(z_0),\bar(z_1),……,\bar(z_n)),其中Q为有理数域,\bar(z_k)为z_k 的共轭,1≤k≤n。
现在来看一下所谓的尺规作图三大难题。
1,三等分角。
给定一个角θ,要得到α=θ/3,即作出cos(α)。
而我们有cos(θ)=cos(3α)=4cos(α)^3-3cos(α),令cos(α)=a,cos(3α)=b为已知,则有(2a)^3-3(a)-2b=0,在一般情况下,这个方程不一定是可约的(如取θ=π/3),在这时2a不可做,因为他不可能是一个2^t次多项式的根。
除此之外尚有很多可以被三等分的角,如只要n不是3的倍数,则α=π/3必可三等分。
事实上n和3互素,因此存在证书u和v,是的3u+nv=1,1/3n=u/n+v/3,所以α/3=π/3n=uπ/n+vπ/3,π/n和π/3都可作,所以α/3也可作。
2,倍立方。
即做一个正方体的体积是原正方体体积的2倍,相当于要作出x^3-2等于0的根,同1,这是不可能的。
3,化圆为方。
即作一个正方形使其面积等于给定的原的面积。
这相当于要作出x^2-π=0的根。
但是π不是代数数,即不是任何多项式的根,所以√π也是不可作的。
正十七边形尺规作图与详细讲解

解读“数学王子”高斯正十七边形的作法一、高斯的传奇故事高斯(Carl Friedrich Gauss 1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工头的父亲计算工人们的周薪。
父亲算了好一会儿,终于将结果算出来了。
可是万万没想到,他身边传来幼嫩的童音说:“爸爸,你算错了,总数应该是……”父亲感到很惊异,赶忙再算一遍,结果证实高斯的答案是对的。
这时的高斯只有3岁!高斯上小学了,教他们数学的老师布特勒(Buttner)是一个态度恶劣的人,他讲课时从不考虑学生的接受能力,有时还用鞭子惩罚学生。
有一天,布德勒让全班学生计算1+2+3+4+5+……+98+99+100=?的总和,并且威胁说:“谁算不出来,就不准回家吃饭!”布德勒说完,就坐在一旁独自看起小说来,因为他认为,做这样一道题目是需要些时间的。
小朋友们开始计算:“1 + 2 =3,3+3=6,6+4=10,……”数越来越大,计算越来越困难。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身边。
高斯说:“老师,我做完了,你看对不对?“做完了?这么快就做完了?肯定是胡乱做的!”布德勒连头都没抬,挥挥手说:“错了,错了!回去再算!”高斯站着不走,把小石板往前伸了伸说:“我这个答案是对的。
”布德勒抬头一看,大吃一惊。
小石板上写着5050,一点也没有错!高斯的算法是1 +2 +3+……+98+99+100100+99+98+……+3+2+1101+101+101+……+101+101+101=101×100=1010010100÷2=5050高斯并不知道,他用的这种方法,其实就是古代数学家经过长期努力才找出来的求等差数列和的方法,那时他才八岁!1796年的一天,德国哥廷根大学。
高斯吃完晚饭,开始做导师给他单独布置的三道数学题。
前两道题他不费吹灰之力就做了出来了。
第三道题写在另一张小纸条上:要求只用圆规和没有刻度的直尺,作出一个正十七边形。
正十七边形尺规作图与详解

解读“数学王子”高斯正十七边形的作法一、高斯的传奇故事高斯(Carl Friedrich Gauss 1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工头的父亲计算工人们的周薪。
父亲算了好一会儿,终于将结果算出来了。
可是万万没想到,他身边传来幼嫩的童音说:“爸爸,你算错了,总数应该是……”父亲感到很惊异,赶忙再算一遍,结果证实高斯的答案是对的。
这时的高斯只有3岁!高斯上小学了,教他们数学的老师布特勒(Buttner)是一个态度恶劣的人,他讲课时从不考虑学生的接受能力,有时还用鞭子惩罚学生。
有一天,布德勒让全班学生计算1+2+3+4+5+……+98+99+100=?的总和,并且威胁说:“谁算不出来,就不准回家吃饭!”布德勒说完,就坐在一旁独自看起小说来,因为他认为,做这样一道题目是需要些时间的。
小朋友们开始计算:“1 + 2 =3,3+3=6,6+4=10,……”数越来越大,计算越来越困难。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身边。
高斯说:“老师,我做完了,你看对不对?“做完了?这么快就做完了?肯定是胡乱做的!”布德勒连头都没抬,挥挥手说:“错了,错了!回去再算!”高斯站着不走,把小石板往前伸了伸说:“我这个答案是对的。
”布德勒抬头一看,大吃一惊。
小石板上写着5050,一点也没有错!高斯的算法是1 +2 +3+……+98+99+100100+99+98+……+3+2+1101+101+101+……+101+101+101=101×100=1010010100÷2=5050高斯并不知道,他用的这种方法,其实就是古代数学家经过长期努力才找出来的求等差数列和的方法,那时他才八岁!1796年的一天,德国哥廷根大学。
高斯吃完晚饭,开始做导师给他单独布置的三道数学题。
前两道题他不费吹灰之力就做了出来了。
第三道题写在另一张小纸条上:要求只用圆规和没有刻度的直尺,作出一个正十七边形。
高斯和他的正十七边形

导师接过学生的作业一看,当即惊呆了。他用颤抖的声音对 青年说:“这是你自己做出来的吗?”青年有些疑惑地看着导师,
回答道:“是我做的。但是,我花了整整一个通宵。”导师请他
坐下,取出圆规和直尺,在书桌上铺开纸,让他当着自己的面再
做出一个正17边形。青年很快做出了一个正17边形。
导师激动地对他说:“你知不知道?你解开了一桩有两千多 年历史的数学悬案!阿基米德没有解决,牛顿也没有解决,你竟 然一个晚上就解出来了。你是一个真正的天才!”
原来,导师也一直想解开这道难题。那天,他是因为失误,才将写
有这道题目的纸条交给了学生。每当这位青年回忆起这一幕时,总是说:
“如果有人告诉我,这是一道有两千多年历史的数学难题,我可能永远
也没有信心将它解出来”。这位青年就是数学王子高斯。
这个问题是高斯用代数的方法解决的,他也视此为生平
得意之作,还交待要把正十七边形刻在他的墓碑上,但后来
尺规作图对于学过几何的人来说都不陌生,它是指用没有 刻度的直尺和圆规作图。你也许可以用尺规作图作出正三
角形、正方形、正六边形等,但是你有没有想过用尺规作
图作正十七边形,甚至正十七边能不能用尺规作图作出来。
其实这一问题早在1796年就由德国著名的数学家高斯在他
19岁时解决,这其中还有一段趣闻:,一个很有数学天赋的 19岁青 年吃完晚饭,开始做导师单独布置给他的每天例行的三道数学题。 前两道题在两个小时内就顺利完成了。第三道题写在另一张小纸条 上:要求只用圆规和一把没有刻度的直尺,画出一个正17边形。他 感到非常吃力。时间一分一秒的过去了,第三道题竟毫无进展。这 位青年绞尽脑汁,但他发现,自己学过的所有数学知识似乎对解开 这道题都没有任何帮助。困难反而激起了他的斗志:我一定要把它 做出来!他拿起圆规和直尺,他一边思索一边在纸上画着,尝试着 用一些超常规的思路去寻求答案。 当窗口露出曙光时,青年长舒了一口气,他终于完成了这道难 题。见到导师时,青年有些内疚和自责。他对导师说:“您给我布 置的第三道题,我竟然做了整整一个通宵,我辜负了您对我的栽 培……”
正十七边形 文档

最早的十七边形画法创造人是高斯。
高斯(1777─1855年)德国数学家、物理学家和天文学家.高斯在童年时代就表现出非凡的数学天才.年仅三岁,就学会了算术,八岁因运用等差数列求和公式而深得老师和同学的钦佩.大学二年级时得出正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件.解决了两千年来悬而未决的难题,1799年以代数基本定理的四个漂亮证明获博士学位.高斯的数学成就遍及各个领域,在数学许多方面的贡献都有着划时代的意义.并在天文学,大地测量学和磁学的研究中都有杰出的贡献.下附正十七边形作法先计算或作出cos(360°/17)设正17边形中心角为a,则17a=360°,即16a=360°-a故sin16a=-sina,而sin16a=2sin8acos8a=4sin4acos4acos8a=16sinacosacos2acos4acos8a 因sina不等于0,两边除之有:16cosacos2acos4acos8a=-1又由2cosacos2a=cosa+cos3a(三角函数积化和差公式)等注意到cos15a=cos2a,cos12a=cos5a(诱导公式)等,有2(cosa+cos2a+…+cos8a)=-1令x=cosa+cos2a+cos4a+cos8ay=cos3a+cos5a+cos6a+cos7a有:x+y=-1/2又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+cos6a+cos7a)=1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a)经计算知xy=-1因而x=(-1+√17)/4,y=(-1-√17)/4其次再设:x1=cosa+cos4a,x2=cos2a+cos8ay1=cos3a+cos5a,y2=cos6a+cos7a故有x1+x2=(-1+√17)/4y1+y2=(-1-√17)/4最后,由cosa+cos4a=x1,cosacos4a=(y1)/2可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出编辑本段步骤一给一圆O,作两垂直的半径OA、OB,在OB上作C点使OC=1/4OB,在OA上作D点使∠OCD=1/4∠OCA 作AO延长线上E点使得∠DCE=45度正十七边形尺规作图[1]编辑本段步骤二作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点。
正十七边形做法及证明.

步骤一:给一圆O,作两垂直的直径OA、OB,作C点使OC=1/4OB,作D点使∠OCD=1/4∠OCA作AO延长线上E点使得∠DCE=45度步骤二:作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点。
步骤三:过G4作OA垂直线交圆O于P4,过G6作OA垂直线交圆O于P6,则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点。
以1/2弧P4P6为半径,即可在此圆上截出正十七边形的所有顶点。
正十七边形的尺规作图存在之证明:设正17边形中心角为a,则17a=360度,即16a=360度-a故sin16a=-sina,而sin16a=2sin8acos8a=22sin4acos4acos8a=2 4 sinacosacos2acos4acos8a因sina不等于0,两边除之有:16cosacos2acos4acos8a=-1又由2cosacos2a=cosa+cos3a等,有2(cosa+cos2a+…+cos8a=-1注意到 cos15a=cos2a,cos12a=cos5a,令x=cosa+cos2a+cos4a+cos8№ay=cos3a+cos5a+cos6a+cos7a有:x+y=-1/2又xy=(cosa+cos2a+cos4a+cos8a(cos3a+cos5a+cos6a+cos7a=1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a经计算知xy=-1又有x=(-1+根号17/4,y=(-1-根号17/4其次再设:x1=cosa+cos4a,x2=cos2a+cos8ay1=cos3a+cos5a,y2=cos6a+cos7a故有x1+x2=(-1+根号17/4y1+y2=(-1-根号17/4最后,由cosa+cos4a=x1,cosacos4a=(y1/2可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出。
正十七边形的故事

正十七边形的故事你知道正十七边形吗?这可不是个普通的多边形,它背后可有一段超酷的故事呢。
话说在数学的世界里,一直有着各种各样的挑战。
就像游戏里的超级关卡一样,正多边形的尺规作图就是这样的挑战。
对于一些简单的正多边形,像正三角形、正方形之类的,很早以前人们就知道怎么用圆规和直尺画出来了。
但是正十七边形,那可就难多了。
这时候呢,有个超级天才叫高斯。
高斯啊,那可是数学界的大神级人物。
他年轻的时候就特别牛,就像游戏里开了挂一样。
他就盯上了正十七边形这个难题。
别人都觉得这太难了,可能根本就做不到用尺规作图把正十七边形画出来。
可是高斯不这么想啊,他一头扎进这个难题里,在草稿纸上写了一堆密密麻麻的数学公式和符号,估计那些纸要是堆起来都能当枕头了。
然后呢,在一个星光璀璨的夜晚(这是我想象的,也许就是一个普普通通的白天),高斯终于找到了办法!他发现了可以用圆规和直尺画出正十七边形的方法。
这可不得了啊,就像在一个神秘的宝库里发现了绝世珍宝一样。
这个发现一下子震惊了整个数学界。
你想啊,在那之前,正十七边形就像一个隐藏在迷雾中的神秘怪物,大家都知道它存在,但是不知道怎么把它揪出来。
高斯呢,就像一个英勇的骑士,拿着尺规这两把宝剑,一下子就把这个怪物给征服了。
这让大家对数学的力量又有了新的认识。
而且啊,正十七边形这个事情还特别励志呢。
它告诉我们,那些看起来超级难,甚至好像不可能做到的事情,只要有像高斯这样聪明的脑袋,再加上一股不服输的劲儿,就有可能被攻克。
现在呢,正十七边形虽然没有像圆形或者正方形那样被我们随处可见地应用,但是它就像一颗闪耀在数学星空中的独特星星,激励着一代又一代的数学爱好者去探索那些未知的、充满挑战的数学世界。
说不定哪一天,你要是对数学产生了兴趣,也能像高斯一样,在数学的神秘大陆上发现属于自己的宝藏呢!。
高斯与正十七边形故事

高斯与正十七边形故事嘿,你知道吗?在数学的奇妙世界里,有一个超级厉害的故事,那就是高斯与正十七边形的传奇呀!话说高斯,那可是个数学天才中的天才啊!就像武侠小说里的绝世高手一样,一出手就不同凡响。
有一天,他就和正十七边形较上劲了。
你想想,正十七边形啊,那得多复杂,多难搞啊!可高斯偏不信这个邪,他就像一个勇敢的探险家,一头扎进了这个难题里。
咱普通人看到正十七边形,估计脑袋都大了,别说去研究它了,看都不想多看一眼。
可高斯不一样啊,他那聪明的脑袋瓜一转,就开始琢磨怎么攻克这个难关。
这就好比别人看到一座高山,都觉得没法爬上去,高斯却想着怎么找条路登顶呢!他整天整夜地思考,不停地计算,草稿纸都用了不知道多少。
这得有多执着啊!要是咱,可能早就放弃了,还会说:“哎呀,这太难了,搞不定啦!”但高斯不,他就是要和这个正十七边形死磕到底。
你说他怎么就能这么厉害呢?难道他脑袋里装了台超级计算机?我觉得啊,那是因为他对数学有着无比的热爱和痴迷。
就像咱喜欢吃好吃的一样,他看到数学难题就两眼放光。
经过无数个日夜的奋战,嘿,你猜怎么着?高斯还真就把正十七边形给搞定了!这简直就是奇迹啊!他就像一个神奇的魔法师,把不可能变成了可能。
这事儿给我们啥启示呢?那就是只要咱有决心,有毅力,没什么事儿是办不到的。
别老觉得自己不行,你看看高斯,面对那么难的正十七边形都没退缩,咱还有啥理由不努力呢?而且啊,这个故事也让我们看到了数学的魅力。
它可不只是那些枯燥的公式和数字,它里面藏着无数的宝藏等着我们去挖掘呢!就像高斯发现了正十七边形的秘密一样,说不定我们也能在数学的海洋里找到属于自己的宝贝呢!咱们生活中不也经常遇到各种困难吗?有时候觉得简直没法解决了,可要是咱学学高斯那股子劲儿,说不定就能柳暗花明又一村呢!别小瞧自己,咱也能创造属于自己的奇迹呀!你说是不是?所以啊,别害怕困难,勇敢地去挑战吧,就像高斯挑战正十七边形一样!让我们也在自己的人生道路上创造出属于我们的精彩吧!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解读高斯正十七边形的作法(上)E-mail: wwwckq@ QQ: 541601368一、高斯的传奇故事高斯(Carl Friedrich Gauss 1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工头的父亲计算工人们的周薪。
父亲算了好一会儿,终于将结果算出来了。
可是万万没想到,他身边传来幼嫩的童音说:“爸爸,你算错了,总数应该是……”父亲感到很惊异,赶忙再算一遍,结果证实高斯的答案是对的。
这时高斯只有3岁!高斯上小学了,教他们数学的老师布特勒(Buttner)是一个态度恶劣的人,他讲课时从不考虑学生的接受能力,有时还用鞭子惩罚学生。
有一天,布德勒让全班学生计算1+2+3+4+5+……+98+99+100=?的总和,并且威胁说:“谁算不出来,就不准回家吃饭!”布德勒说完,就坐在一旁独自看起小说来,因为他认为,做这样一道题目是需要些时间的。
小朋友们开始计算:“1 + 2 =3,3+3=6,6+4=10,……”数越来越大,计算越来越困难。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身边。
高斯说:“老师,我做完了,你看对不对?“做完了?这么快就做完了?肯定是胡乱做的!”布德勒连头都没抬,挥挥手说:“错了,错了!回去再算!”高斯站着不走,把小石板往前伸了伸说:“我这个答案是对的。
”布德勒抬头一看,大吃一惊。
小石板上写着5050,一点也没有错!高斯的算法是(1+100)+(2+99)+(3+98)+……+(99+2)+(100+1)=101+101+101+……+101+101=101×100=10100,10100÷2=5050。
高斯并不知道,他用的这种方法,其实就是古代数学家经过长期努力才找出来的求等差数列和的方法,那时他才八岁!1796年的一天,德国哥廷根大学。
高斯吃完晚饭,开始做导师给他单独布置的三道数学题。
前两道题他不费吹灰之力就做了出来了。
第三道题写在另一张小纸条上:要求只用圆规和没有刻度的直尺,作出一个正十七边形。
这道题把他难住了——所学过的数学知识竟然对解出这道题没有任何帮助。
时间一分一秒的过去了,第三道题竟毫无进展。
他绞尽脑汁,尝试着用一些超常规的思路去寻求答案。
当窗口露出曙光时,他终于解决了这道难题。
当他把作业交给导师时,感到很惭愧。
他对导师说:“您给我布置的第三道题,我竟然做了整整一个通宵,……”导师看完作业后,激动地对他说:“你知不知道?你解开了一桩有两千多年历史的数学悬案!阿基米得没有解决,牛顿也没有解决,你竟然一个晚上就解出来了。
你是一个真正的天才!”原来,导师也一直想解开这道难题。
那天,他是因为拿错了,才将写有这道题目的纸条交给了学生。
在这件事情发生后,高斯曾回忆说:“如果有人告诉我,那是一道千古难题,我可能永远也没有信心将它解出来。
”1796年3月30日,当高斯差一个月满十九岁时,在期刊上发表《关于正十七边形作图的问题》。
他显然以此为自豪,还要求以后将正十七边形刻在他的墓碑上。
然而高斯的纪念碑上并没有刻上十七边形,而刻着一颗十七角星,原来是负责刻纪念碑的雕刻家认为:“正十七边形和圆太像了,刻出来之后,每个人都会误以为是一个圆。
”1877年布雷默尔奉汉诺威王之命为高斯做一个纪念奖章。
上面刻着:“汉诺威王乔治V. 献给数学王子高斯(Georgius V. rex Hannoverage Mathematicorum principi)”,自那之后,高斯就以“数学王子”着称于世。
二、高斯正十七边形尺规作图的思路(纯三角法)作正十七边形的关键是作出cos 172π,为此要建立求解cos 172π的方程。
设正17边形中心角为α,则17α=2π,即16α=2π-α故sin16α=-sinα ,而sin16α=2sin8α cos8α=4sin4α cos4α cos8α=8 sin2α cos2α cos4α cos8α=16 sinα cosα cos2α cos4α cos8α因sinα ≠0,两边除以sinα,有16cosα cos2α cos4α cos8α=-1由积化和差公式,得4(cosα+cos3α)(cos4α+cos12α)=-1展开,得4(cosα cos4α+cosα cos12α+cos3α cos4α+cos3α cos12α)=-1再由积化和差公式,得2[(cos3α+cos5α)+(cos11+cos13α)+(cosα+cos7α)+(cos9α+cos15α)]=-1注意到 cos11α=cos6α,cos13α=cos4α,cos9α=cos8α,cos15α=cos2α,有 2(cosα+cos2α+cos3α+cos4α+cos5α+cos6α+cos7α+cos8α)=-1设 a =2(cosα+ cos2α+cos4α+ cos8α),b =2(cos3α+ cos5α+cos6α+ cos7α),则 a +b =-1,又ab =2(cosα+co s2α+cos4α+cos8α)·2(cos3α+cos5α+cos6α+cos7α)=4cosα(cos3α+cos5α+cos6α+cos7α)+4cos2α(cos3α+cos5α+cos6α+cos7α)+4cos4α(cos3α+cos5α+cos6α+cos7α)+4cos8α(cos3α+cos5α+cos6α+cos7α), 再展开之后共16项,对这16项的每一项应用积化和差公式,可得:ab =2 [(cos2α+cos4α)+(cos4α+cos6α)+(cos5α+cos7α)+(cos6α+cos8α)+(cosα+cos5α)+(cos3α+cos7α)+(cos4α+cos8α)+(cos5α+cos9α)+(cosα+cos7α)+(cosα+cos9α)+(cos2α+cos10α)+(cos3α+cos11α)+(cos5α+cos11α)+(cos3α+cos13α)+(cos2α+cos14α)+(cosα+cos15α)],注意到cos9α=cos8α,cos10α=cos7α, cos11α=cos6α,cos13α=cos4α,cos14α=cos3α,cos15α=cos2α,有ab =2×4(cosα+cos2α+cos3α+cos4α+cos5α+cos6α+cos7α+cos8α)=-4。
因为cosα+cos2α+cos8α=(cos172π+cos 174π)+cos 1716π =2cos 17πcos 173π-cos 17π=2cos 17π(cos 173π-21) 又 0 < 173π < 3π < 2π 所以cos 173π> 21 即cosα+cos2α+cos8α > 0又因为 cos4α=cos 178π> 0 所以 a =cosα+cos2α+cos4α+cos8α > 0又ab=-4< 0所以有a > 0,b< 0 可解得a=2171+-,b=2171--。
再设c=2(cosα+cos4α),d=2(cos2α+cos8α),则c+d=acd=2(cosα+ cos4α)·2(cos2α+ cos8α)=4 (cosαcos2α+cosαcos8α+cos4αcos2α+cos4αcos8α)=2 [(cosα+cos3α)+(cos7α+cos9α)+(cos2α+cos6α)+(cos4α+cos12α)]注意到cos9α=cos8α,cos12α=cos5α,有cd=2[(cosα+cos3α)+(cos7α+cos8α)+(cos2α+cos6α)+(cos4α+cos5α)]=2( cosα+cos2α+cos3α+cos4α+cos5α+cos6α+cos7α+cos8α)=-1。
因为0 < α < 2α < 4α < 8α < π所以cosα > cos2α,cos4α > cos8α两式相加得cosα+cos4α> cos2α+cos8α或2(cosα+cos4α)> 2(cos2α+cos8α)即c > d,又cd=-1 < 0所以有c > 0, d < 0可解得c=24 2++aa,[ d=24 2+-aa]。
类似地,设e=2(cos3α+cos5α),f=2(cos6α+cos7α)则e+f=b,ef=2(cos3α+cos5α)·2(cos6α+cos7α)=4(c os3αcos6α+cos3αcos7α+cos5αcos6α+cos5αcos7α)=2 [(cos3α+cos9α)+(cos4α+cos10α)+(cosα+cos11α)+(cos2α+cos12α)],注意到cos9α=cos8α,cos10α=cos7α, cos11α=cos6α,cos12α=cos5α,有 ef =2[(cos3α+cos8α)+(cos4α+cos7α)+(cosα+cos6α)+(cos2α+cos5α)]=2( cosα+cos2α+cos3α+cos4α+cos 5α+cos6α+cos7α+cos8α)=-1。
因为 0 < 3α < 5α < 6α < 7α < π所以有 cos3α > cos6α,cos5α > cos7α两式相加得cos3α+cos5α> cos6α+cos7α2(cos3α+cos5α)> 2(cos6α+cos7α)即 e > f ,又 ef =-1 < 0所以有 e > 0, f < 0可解得e =242++b b , [f =242+-b b ]。
由c =2(c osα+cos4α),得cosα+cos4α=2c ,即cos 172π+cos 178π=2c 。
e =2(cos3α+cos5α),应用积化和差公式,得cosαcos4α=4e ,即 cos 172πcos 178π=4e 。
因为0<172π<178π<2π,所以cos 172π>cos 178π>0, 所以cos 172π=442e c c -+,[ cos 178π=442e c c -- ]。
于是,我们得到一系列的等式:a =2171+-,b =2171--,c =242++a a ,e =242++b b , cos 172π=442e c c -+。
有了这些等式,只要依次作出a 、b 、c 、e ,便可作出cos172π。
