第2章静电场
合集下载
电动力学第二章
R r
y
r R l 2 Rl cos
2 2 2
2l
x -Q
求近似值：
r R 1 2l cos / R 1 2l cos R (1 ) R l cos 2 R
(l R)
同理
r R l cos
1 1 r r 2l cos 2l cos 2 2 2 2 r r r r R l cos R
1 R 2 / M 2 1 1 R 2 / M 2 1 0 P P0 lim ln 1 R 2 / M 2 1 1 R 2 / M 2 1 M 4 0 0
R2 1 R2 1 2 1 2 M 2M R02 R P P0 ln 2 ln 4 0 R 2 0 R0
2Ql cos 2QlR cos PR ( P) 2 3 3 4 0 R 4 0 R 4 0 R
x- y
平面为等势面（Z = 0的平面）。
若电偶极子放在均匀介质 中（无限大介质）：
均匀介质中点电荷产生的束缚电荷分布在自由点电 荷附近，介质中电偶极子产生的势为自由偶极子与 束缚偶极子产生的势的迭加，设 Q p 为束缚电荷， 0 0 0 Q p (1 )Q Pp 2QP l ez 2Ql ez ( 1) ( 1) P
（4） W
1 dV中的 是由电荷分布 激发的电势； 2
（5）在静电场中，电场决定于电荷分布。在场内没有
独立的运动。因而场的能量就由电荷分布所决定。 （6）若全空间充满了介电常数为ε的介质，可得到电荷 分布ρ所激发的电场总能量
1 ( x) 1 ( x ) ( x) W ( x )dV dV dV r dV 2 4 r 8 与 点的距离。 式中r为 x x
第二章静电场恒定电场和恒定磁场
图2.1电介质的极化
介质中的高斯定理表示为 式中电位移矢量为
在线性的各向同性的电介质中
例2.1在空气中放入一个带电量为Q、半径为a的球体，该球体的 相对介电常数为εr。求该球体内、外任意一点的电场强度。
解（1） 球内任意一点，设到球心距离为r,做高斯面为以r为半径的球面， 如图2.2所示。
由电场的对称性可知，E和D的方向为er,所以
大小、它们之间的距离和周围的电介质，即可以不用电容器。
例2.10同心金属球与球壳系统如图2.12所示，内导体球半径为a，外导体 球壳的内外半径分别为b和c，导体球与导体球壳带有等量异号电荷，它
们之间充满相对介电常数为 r 的电介质，球外为空气。求该导体系统
的电容。
解:根据高斯定理不难求出空间各点的电场强度，设导体球和导体球壳的 带电量分别是q和-q，则导体和导体球壳之间的电场强度的大小为
电场能为
WeΒιβλιοθήκη 1 2dVv
（2） 对于多导体系统
We
1 2
dV
v
例2.12半径分别为a和b的同轴线，外加电压为U，内圆柱体电荷量为正，外圆柱 面单位长度上的电荷量与内圆柱体等值异号。如图2.16(a)所示，两电极间在θ1的 角度内填充介电常数为ε的电介质，其余部分为空气，求同轴线单位长度上储存 的电场能量。
示，求在l长度上的外电感。
图2.25例2.20用图
例2.21一个半径为a的无限长直导线，在导线均匀流过的电流为I，求这个导线
在单位长度上的内电感，如图2.26所示（设导体内部的磁导率近似为μ0）。 解:截面上的磁通并没有与全部电流I交链，而只是与一部分电流交链，交链的总 磁链为
图2.26
2. 互 有两感个回路l1和l2，如图2.27所示。
介质中的高斯定理表示为 式中电位移矢量为
在线性的各向同性的电介质中
例2.1在空气中放入一个带电量为Q、半径为a的球体，该球体的 相对介电常数为εr。求该球体内、外任意一点的电场强度。
解（1） 球内任意一点，设到球心距离为r,做高斯面为以r为半径的球面， 如图2.2所示。
由电场的对称性可知，E和D的方向为er,所以
大小、它们之间的距离和周围的电介质，即可以不用电容器。
例2.10同心金属球与球壳系统如图2.12所示，内导体球半径为a，外导体 球壳的内外半径分别为b和c，导体球与导体球壳带有等量异号电荷，它
们之间充满相对介电常数为 r 的电介质，球外为空气。求该导体系统
的电容。
解:根据高斯定理不难求出空间各点的电场强度，设导体球和导体球壳的 带电量分别是q和-q，则导体和导体球壳之间的电场强度的大小为
电场能为
WeΒιβλιοθήκη 1 2dVv
（2） 对于多导体系统
We
1 2
dV
v
例2.12半径分别为a和b的同轴线，外加电压为U，内圆柱体电荷量为正，外圆柱 面单位长度上的电荷量与内圆柱体等值异号。如图2.16(a)所示，两电极间在θ1的 角度内填充介电常数为ε的电介质，其余部分为空气，求同轴线单位长度上储存 的电场能量。
示，求在l长度上的外电感。
图2.25例2.20用图
例2.21一个半径为a的无限长直导线，在导线均匀流过的电流为I，求这个导线
在单位长度上的内电感，如图2.26所示（设导体内部的磁导率近似为μ0）。 解:截面上的磁通并没有与全部电流I交链，而只是与一部分电流交链，交链的总 磁链为
图2.26
2. 互 有两感个回路l1和l2，如图2.27所示。
第2章 静电场(5) 泊松方程和拉普拉斯方程
第二章 静电场
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 §2.7 §2.8
库仑定律与电场强度 静电场的无旋性与电位函数 静电场中的导体与电介质 高斯通量定理 泊松方程和拉普拉斯方程 分界面上的边界条件 导体系统的电容 静电场能量和静电力
★ 电位的泊松方程
2
★ 静电场的基本方程
一次积分
d
dx
1 2
0 x2 0d
C1
一次积分
边界条件： x 0,
0;
0 x3 6 0 d
C1x C2
C1
U0 d
0d 6 0
;
x d , U0 .
C2 0
21
0x3 6 0 d
U0 d
0d 6 0
x
E
0 x2 2 0 d
U0 d
0d 6 0
ax
22
填空题：
静电场电位所满足的微分方程是
E ()
（在均匀、线性、各向同性的电介质中，为常数。）
2
（电位的泊松方程）
12
2、拉普拉斯方程
对于场中没有电荷分布（=0）的区域内：
2
（电位的泊松方程）
0 2
(电位的拉普拉斯方程)
拉普拉斯方程是泊松方程的特例。
13
2是拉普拉斯算符：二阶微分算符
直角坐标系：
aU (a r ) r
19
例2-10 P66
两无限大平行板电极，板间距为d，电压
为U0，并充满密度为0x/d的体电荷。用 泊松方程的方法求板间的电场强度。
解：
2
0x 0d
x 0, 0
(0 x d)
x d, U0
0x d
2
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 §2.7 §2.8
库仑定律与电场强度 静电场的无旋性与电位函数 静电场中的导体与电介质 高斯通量定理 泊松方程和拉普拉斯方程 分界面上的边界条件 导体系统的电容 静电场能量和静电力
★ 电位的泊松方程
2
★ 静电场的基本方程
一次积分
d
dx
1 2
0 x2 0d
C1
一次积分
边界条件： x 0,
0;
0 x3 6 0 d
C1x C2
C1
U0 d
0d 6 0
;
x d , U0 .
C2 0
21
0x3 6 0 d
U0 d
0d 6 0
x
E
0 x2 2 0 d
U0 d
0d 6 0
ax
22
填空题：
静电场电位所满足的微分方程是
E ()
（在均匀、线性、各向同性的电介质中，为常数。）
2
（电位的泊松方程）
12
2、拉普拉斯方程
对于场中没有电荷分布（=0）的区域内：
2
（电位的泊松方程）
0 2
(电位的拉普拉斯方程)
拉普拉斯方程是泊松方程的特例。
13
2是拉普拉斯算符：二阶微分算符
直角坐标系：
aU (a r ) r
19
例2-10 P66
两无限大平行板电极，板间距为d，电压
为U0，并充满密度为0x/d的体电荷。用 泊松方程的方法求板间的电场强度。
解：
2
0x 0d
x 0, 0
(0 x d)
x d, U0
0x d
2
第二章 静电场中的导体和电介质：电容器的电容
D 0 E P 0 r E E
P e 0 E
§2.8 电容器的电容
一.孤立导体的电容
q C V
单位：F（法拉）
C是与导体的尺寸和形状以及周围的电介质有 关,与q，V无关的常数。
1F 10 F 10 PF
6 12
例1 .求半径为R的孤立导体球的电容。
q1:q2: · :qn = C1:C2: · :Cn · · · ·
q qi (V A VB ) C i ,
i 1 i 1
n
n
n q C Ci VA VB i 1
并联电容器的总电容等 于各电容器的电容之和 2. 串联
C Ci
i 1
n
A +
VA +q –q +q –q 。
q dA udq dq C
从开始极板上无电荷直到极板上电量为Q的过 程中，电源作的功为
2 q 1 Q 1Q dq 0 qdq C C 2 C
A dA 0
Q
Q CU
U为极板上电量为Q时两板间的电势差
1 Q2 1 1 2 A CU QU 2 C 2 2
E
0
( r R1 , r R2 )
λ er 2πεr
B A
( R1 r R2 )
2
VA VB
R E dl R Edr
1
λdr R1 2πεr
R2
R2 q R2 λ ln ln 2πε R1 2πεL R1
q 2πεL C V A VB ln( R2 / R1 )
②所求的C = q/VA–VB一定与q和VA–VB无关，仅 由电容器本身的性质决定。
P e 0 E
§2.8 电容器的电容
一.孤立导体的电容
q C V
单位：F（法拉）
C是与导体的尺寸和形状以及周围的电介质有 关,与q，V无关的常数。
1F 10 F 10 PF
6 12
例1 .求半径为R的孤立导体球的电容。
q1:q2: · :qn = C1:C2: · :Cn · · · ·
q qi (V A VB ) C i ,
i 1 i 1
n
n
n q C Ci VA VB i 1
并联电容器的总电容等 于各电容器的电容之和 2. 串联
C Ci
i 1
n
A +
VA +q –q +q –q 。
q dA udq dq C
从开始极板上无电荷直到极板上电量为Q的过 程中，电源作的功为
2 q 1 Q 1Q dq 0 qdq C C 2 C
A dA 0
Q
Q CU
U为极板上电量为Q时两板间的电势差
1 Q2 1 1 2 A CU QU 2 C 2 2
E
0
( r R1 , r R2 )
λ er 2πεr
B A
( R1 r R2 )
2
VA VB
R E dl R Edr
1
λdr R1 2πεr
R2
R2 q R2 λ ln ln 2πε R1 2πεL R1
q 2πεL C V A VB ln( R2 / R1 )
②所求的C = q/VA–VB一定与q和VA–VB无关，仅 由电容器本身的性质决定。
第二章-静电场与导体
第二章静电场与导体教学目的要求：1、深入理解并掌握导体的静电平衡条件及静电平衡时导体的基本性质，加深对高斯定理和环路定理的理解，结合应用电场线这一工具，会讨论静电平衡的若干现象，会结合静电平衡条件去理解静电感应、静电屏蔽等现象，并会利用前章的知识求解电场中有导体存在时的场强和电势分布。
2、确理解电容的概念，并能计算几种特殊形式的电容器的电容值。
3、进一步领会静电能的概念、会计算一些特殊带电导体的静电能。
4、深刻理解电场能量的概念，会计算电场能。
教学重点：1、静电场中的导体2、电容和电容器教学难点：1、静电场的唯一定理§2.1 静电场中的导体§2.2 电容和电容器§2.3 静电场的能量§2.1 静电场中的导体1、导体的特征功函数（1）金属导体的特征金属可以看作固定在晶格点阵上的正离子（实际上在作微小振动）和不规则运动的自由电子的集合。
①大量自由电子的运动与理想气体中分子的运动相同，服从经典的统计规律。
②自由电子在电场作用下将作定向运动，从而形成金属中的电流。
③自由电子的平均速率远大与定向运动速率。
（2）功函数金属表面存在一种阻止自由电子从金属逸出的作用，电子欲从金属内部逸出到外部，就要克服阻力作功。
一个电子从金属内部跑到金属外部必须作的最小功称为逸出功，亦称功函数。
2、导体的静电平衡条件（1）什么是静电感应？当某种原因（带电或置于电场中）使导体内部存在电场时，自由电子受到电场力的作用而作定向运动，使导体一侧因电子的聚集而出现负电荷布另一侧因缺少电子而有正电荷分布，这就是静电感应，分布在导体上的电荷便是感应电荷。
（2）静电平衡状态当感应电荷在导体内产生的场与外场完全抵消时，电子的定向运动终止，导体处于静电平衡状态。
（3）静电平衡条件所有场源包括导体上的电荷共同产生的电场的合场强在导体内部处处为零。
静电平衡时：①导体是等势体。
②导体外表面附近的电场强度与导体表面垂直。
015-2第2章 静电场-1-静电场的标势及其微分方程
₪静电场1.静电场的标势2.静电势的微分方程和边值关系3.静电场能量静电场2.1静电场的标势及其微分方程第2章₪静电场1.静电场的标势(２) 电标势的定义根据静电场无旋性，电场中任一闭合回路L 的环量等于零，C1、C 2是点a 到点b 的两条不同路径 1212d 0d d 0d d 功与路径无关L C C C C b a E l E l E l E l E l b a E dlC 1C 2a bL₪静电场1.静电场的标势(4) 电势参考点在有限的电荷分布于有限区域的情况下，可以选择无穷远处作为零电势参考点，则每一点的电势实际是该点与无穷远点的电势差，因而是有确定的物理意义的。
=PPP P E dl E dl1.静电场的标势(5) 零电势参考点的选取1.有限电荷分布于有限自由空间的情况，选取无穷远处作为零电势参考点；2.对于接地的带电体，选取地球或者接地处、或者接地的导体，作为零电势的参考点、或者参考面、或者参考体；QQ₪静电场₪静电场1.静电场的标势(5) 零电势参考点的选取3.对于电路而言，选取地线为零电势参考线；4.对于无限电荷分布于无限空间，根据题目条件选取参考点。
0地线火线零线拉线开关三孔插座₪静电场1.静电场的标势(6)电势与电场的关系PP E dl E 电势与电场可以由上面两个式子共同决定，相互制约的。
可以看出，只要确定电场分布或者电势的其中一个物理量，另外一个物理量就可以确定。
而且电场强度的方向是电势梯度方向（电势改变最快的方向）。
1.静电场的标势(７)关于电势的五点说明1.引入电势的优点：如果知道电势，只需要通过计算梯度，即可求出电场强度矢量。
这说明电势和电场强度矢量所包含的信息量是一样的，但是电场强度矢量有三个分量，而电势只是一个标量，因此通过引入电势这个量，可以将矢量问题约化为标量问题。
₪静电场₪静电场1.静电场的标势(７)关于电势的五点说明3.参考点的选择是任意的，选择不同的参考点电势会增加一个常数K ，K 是电场强度矢量在两个参考点之间的线积分。
第二章 静电场
ρ =0
(r > a ) (r < a ) 15 ρ = ε o E0 (a 2 − r 2 ) 2a3
第2章
§ 2.3
静电场的旋度与静电场的电位
1、静电场的电位与电场强度关系 静电场的电位与电场强度关系 电位与 体分布的电荷产生的电场强度为
E(r) =
→ →
1 4 πε
0
∫
1
ρ ( r ′ )( r − r ′ )
(2)表明：某点的电场强度散度正比该点的电荷 (2)表明：某点的电场强度散度正比该点的电荷 表明 电场强度 体密度！静电场是有散度的场， 体密度！静电场是有散度的场，其散度源为电荷 是所有电荷产生电场。 。 E 是所有电荷产生电场。
→
第2章
假设在半径为a 例1、P.24 假设在半径为a的球体内均匀分 的电荷， 在球内外的电场 布着密度为ρ0的电荷，求在球内外的电场 强度。 强度。 因为电场具有球对称性 球对称性， 球面为高斯面， 解：因为电场具有球对称性，以球面为高斯面，有 ρ 0 4π 3 2 E r 4π r = a r>a时 当r>a时， ε0 3
第2章
所以
E(r ) =
→ →
−1 4 πε 0
∫
V
ρ ( r ′) ∇ (
→
1
→
r − r′
→Leabharlann ) d V ′, d V ′ = d x ′d y ′d z ′
→
（ 因为算子 ∇ 半对场点坐标 r x , y , z ） 微分，积 微分， 因为算子 → 进行，所以将算子 分对源点坐标 r（ x ′, y ′, z ′） 进行，所以将算子 ∇ ′ 从积分符号里提出来 分符号里提出来！ 从积分符号里提出来！得
(r > a ) (r < a ) 15 ρ = ε o E0 (a 2 − r 2 ) 2a3
第2章
§ 2.3
静电场的旋度与静电场的电位
1、静电场的电位与电场强度关系 静电场的电位与电场强度关系 电位与 体分布的电荷产生的电场强度为
E(r) =
→ →
1 4 πε
0
∫
1
ρ ( r ′ )( r − r ′ )
(2)表明：某点的电场强度散度正比该点的电荷 (2)表明：某点的电场强度散度正比该点的电荷 表明 电场强度 体密度！静电场是有散度的场， 体密度！静电场是有散度的场，其散度源为电荷 是所有电荷产生电场。 。 E 是所有电荷产生电场。
→
第2章
假设在半径为a 例1、P.24 假设在半径为a的球体内均匀分 的电荷， 在球内外的电场 布着密度为ρ0的电荷，求在球内外的电场 强度。 强度。 因为电场具有球对称性 球对称性， 球面为高斯面， 解：因为电场具有球对称性，以球面为高斯面，有 ρ 0 4π 3 2 E r 4π r = a r>a时 当r>a时， ε0 3
第2章
所以
E(r ) =
→ →
−1 4 πε 0
∫
V
ρ ( r ′) ∇ (
→
1
→
r − r′
→Leabharlann ) d V ′, d V ′ = d x ′d y ′d z ′
→
（ 因为算子 ∇ 半对场点坐标 r x , y , z ） 微分，积 微分， 因为算子 → 进行，所以将算子 分对源点坐标 r（ x ′, y ′, z ′） 进行，所以将算子 ∇ ′ 从积分符号里提出来 分符号里提出来！ 从积分符号里提出来！得
第2章 静电场(8) 静电场的能量
2
400 R 5Q
2
―带电金属球”或“均匀带电球面”
We Q 80 R
400 R
35
均匀带电球体
We 6Q
2
400 R
―带电金属球”或“均匀带电球面”
We 5Q
2
400 R
36
[结论] 将“带电金属球”改为同样大小的 “均匀带电球面”，结果？
Answer: 改为球面, We不变； 同样大小的“均匀带电球体”？
20
能量体密度：
（定义）
1 we D E 2
we E 2 1
2
（2-103）
对于理想介质： （2-104）
物理意义：
电场是一种物质，它具有能量。
21
注释：
We 1
2
d V
（2-97）
V
★适用范围： 仅适用于静电场
★适用范围：
（反映了：静止电荷所具有的静电位能）
即位移是虚设的，故称为虚位移法。
45
★虚位移法
★原理：能量守恒
外力做的功=静电场能量的变化+电场力做功
d W d We f g d g
d W k dqk
与各带电导体 相连的外电源 提供的能量；
K
第p号导体作dg 位移后电场储 能We的增量；
f 在 g 方向 的分量。
46
★方法：
第二章 静电场
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 §2.7 §2.8 库仑定律与电场强度 静电场的无旋性与电位函数 静电场中的导体与电介质 高斯通量定理 泊松方程和拉普拉斯方程 分界面上的边界条件 导体系统的电容 静电场能量和静电力
第2章_静电场和恒定电场
3、电位函数
在静电场中，某点P处的电位定义为把单位正电荷 从P点移到参考点 Q的过程中电场力所作的功。若 正试验电荷 qt 从 P 点移到 Q 点的过程中电场力作功 为W，则P点处的电位为
Q W lim E dl P qt 0 q t
当电荷不延伸到无穷远处时，一般把电位参考点 Q 选在无限远处，这将给电位的计算带来很大的方便。 此时，任意P点的电位为
z
在直线上选一线元dz’，则其上的电荷为 ρl dz’,它在点P处产生的电场强度dE=
2
l 2
dz
d Ez
dE d E
z
R
P(, , z)
dE可以分解成两个分量：
Oyl 21例 :一个半径为a的均匀带电圆环，求轴线上的电场强度。 解： 取坐标系如图 ，圆环位于xoy平面，圆环中
1 4 0 1 4 0
S ( r)
S
l
R l ( r) dl R
dS
关于电位，要注意以下几个问题：
（1）电场中给定P点的电位φ ，表示单位正电荷 由给定点P移到参考点Q处时电场力所做的功。 （2）参考点Q的选取是任意的，但一般就遵循两 个原则：电位表达式有意义；电位表达式尽可能 简单。另外，同一静电场中只能选取一个参考点。 有意义，就是它能给出场中各点电位的确定值。 在点电荷的电场中，不能选取点电荷所在处为参 考点，同样，对于电荷分布延伸到无穷远处时 （如，无限长带电线、无限长带电圆柱面），也 不能把参考点Q选在无穷远处。
qi在该点产生的电场强度的矢量和，即 E=E1+E2+…+En=
分布电荷的电场强度：
第二章 静电场 镜像法
解：先考虑介质1 中的电势，设想将下半空间换成 与上半空间一样，并在z=-a处有Q的像电荷Q' 来代替分界面上极化电荷对上半空间场的影响。 则在Z>0的区域，空间一点的电势为
`1
1
4 1
(Q r
Q) r
(1)
1
4 1
x2
y2
Q (z
a)2
1 2
ez
3. 真空中有一半径R0的接地导体球，距球心 a > R0 处有一点电荷 Q，求空间各点电势。
解：（1）分析： 因导体球接地故球的电 势为零。根据镜象法原 则假想电荷应在球内。 因空间只有两个点电荷， 场应具有轴对称，故假 想电荷应在线上，即极 轴上。
1 [Q Q] 40 r r
这里要注意几点：
a) 唯一性定理要求所求电势必须满足原有电荷分布所满足的 Poisson’s equation or Laplace’s equation，即所研究空间的泊松方 程不能被改变（即自由点电荷位置、大小不能变）。因此，做替 代时，假想电荷必须放在所求区域之外。在唯一性定理保证下， 采用试探解，只要保证解满足泊松方程及边界条件即是正确解。
a=b
பைடு நூலகம்
由以上三式解得
所以
Q 1 2 Q 1 2
Q 2 2 Q 1 2
1
Q
4 1
1
1 2
x2 y2 (z a)2 1 2
2 2 (1 2 )
Q x2 y2 (z a)2
(8)
1
设电量为 Q，位置为（0，0，a ）
第二章静电场_第一部分
6
2. 静电场的散度方程和旋度方程
一.积分形式的静电场两个基本方程 1.高斯定理
uuur
uur r ∫ D0 • ds = ∑ q
表明 D 在闭合面S上通量特性，q为闭合面S包围的电 荷。 2.静电系统的守恒定理
0
∫
ur r E •dl = 0
ur 表明 E 在闭合回路上的环流量特性，电场具有守恒性。
2.3 泊松方程、拉普拉斯方程
1.泊松方程
推导
ρ ∇ ϕ= − ε0
2
泊松方程
uur u r u r ∴ ∇ • D 0 =∇ • (ε 0 E)=ε 0∇ • E =ε 0∇ • ( −∇ϕ ) = − ε 0∇ 2ϕ uur ∇ • D 0 = − ε 0∇ 2ϕ =ρ
)
此时电位函数
u ( z ) = ϕ ( z ) −ϕ ( z0)
σ ⎡ 2 2 2 2 ⎤ = + − + − + z a a z z z 0 ⎥ ⎣ ⎦ 2ε 0 ⎢
0
当
a→∞ u ( z) = 2ε 0
σ
(z
0
− z)
此时
ur E = −∇u ⎧ σ ur ez ⎪ ⎪ 2ε 0 =⎨ ur σ ⎪− ez ⎪ ⎩ 2ε 0 z>0 z<0
q2受到的电场力： F ( R, q1 , q2 ) 点电荷电场强度：
r R
q1
q2
r r q1 1 v E ( R, q1 ) = ⋅ 2 eR 4πε 0 R
u v v 1 1 R ⎛ ⎞ 利用： ∇ ⎜ ⎟ = −e R =− 3 2 R R ⎝R⎠
r r 1 q1 E ( R, q1 ) = − ∇( ) 4πε 0 R
第2章静电场和恒定电流电场
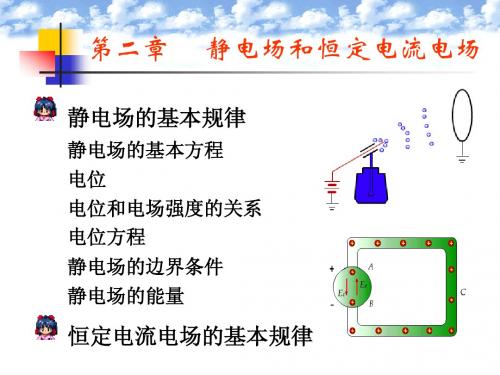
ϕ = C E1t = E2t Et = 0 ρs ⇒ ⇔ ∂ϕ D n − D2n = 1 Dn = ρs ε ∂n = −ρs 0
E = −∇ϕ, ∇⋅ D = ρ Q v v v ∇⋅ (ϕD) = ϕ∇⋅ D +∇ϕ ⋅ D v v v v v v ∴E ⋅ D = −∇ϕ ⋅ D = −∇⋅ (ϕD) +ϕ∇⋅ D = −∇⋅ (ϕD) + ρϕ v 1 1 ∴W = ∫∫∫ ρϕdv − ∫∫∫ ∇⋅ (ϕD)dv 2 2 v v v 高斯定理） Q∫∫∫ ∇⋅ (ϕD)dv = ∫∫ ϕD⋅ dS （高斯定理） v v 1 1 ∴W = ∫∫∫ ρϕdv − ∫∫ ϕD⋅ dS 2 2 1 v v 1 Q ∫∫ ϕD⋅ dS 通常 = 0 ∴W = ∫∫∫ ρϕdv （2） 2 2
−ρ 0 ≤ x ≤ d 2 , ∇ ϕ1 = 2 ε d ∇2ϕ = 0, ≤ x≤d 2 2 ϕ 因为ϕ1 ， 2与坐标y，z 无
+
x
d
−
2
ρ
2
O
关，电位方程可简化为： 电位方程可简化为：
d ϕ1 −ρ ∇ ϕ1 = = , 2 dx ε
2 2
d ϕ2 ∇ ϕ2 = = 0, 2 dx
v v 1 W = ∫∫∫ E ⋅ Ddv （1） 六 静电场的能量 v v 2
例1 平行板电容器极板平面的尺寸远大于它们之间的距 离d，两极板间加恒定电压 U 0 ，极板间的介电常数为ε， 其中一半空间有体电荷均匀分布， 其中一半空间有体电荷均匀分布，体电荷密度为 ρ ，分 界面与极板平行。试求极板间的电位分布。 界面与极板平行。试求极板间的电位分布。 解
当分界面为导体与电介质的交界 面时，由于导体的特殊性质， 面时，由于导体的特殊性质，在导体和介质的分解面上 的边界条件有其特点。导体在静电场中有以下性质： 的边界条件有其特点。导体在静电场中有以下性质： 1）导体内部不带电，电荷只分布在导体表面上； 导体内部不带电，电荷只分布在导体表面上； 导体内部电场为零； 2）导体内部电场为零； 3）导体表面电场方向为法线方向，导体是个等势体， 导体表面电场方向为法线方向，导体是个等势体， 表面是等势面。 表面是等势面。 导体和电介质分界面上的边界条件为： 导体和电介质分界面上的边界条件为：
电磁场与电磁波第二章讲义
(r )
第二章 静 电 场
当r<a时，
Er 4r2
0 0
4
3
r3
所以
Er
0r 30
(r )
第二章 静 电 场
例 2 - 3 已知半径为a的球内、 外的电场强度为
E
er E0
a2 r2
(r a)
E
er E0 5
r 2a
3
r3 2a3
(r a)
们的连线， 同号电荷之间是斥力， 异号电荷之间是引力。点电
荷q′受到q的作用力为F′，且F′=-F，可见两点电荷之间的作用力 符合牛顿第三定律。
第二章 静 电 场
库仑定律只能直接用于点电荷。所谓点电荷，是指当带电体 的尺度远小于它们之间的距离时，将其电荷集中于一点的理想化 模型。 对于实际的带电体， 一般应该看成是分布在一定的区域 内，称其为分布电荷。用电荷密度来定量描述电荷的空间分布情 况。电荷体密度的含义是，在电荷分布区域内，取体积元ΔV， 若其中的电量为Δq，则电荷体密度为
(r)
P(r' )V '
4 0
r r' r r' 3
整个极化介质产生的电位是上式的积分：
(r) 1
4 0
V
P(r' ) (r r r' 3
4 0R2
R
q' q
4 0
R R3
式中：R=r-r′表示从r′到r的矢量；R是r′到r的距离；R°是R的单
位矢量；ε0是表征真空电性质的物理量，称为真空的介电常数，
其值为
电磁场与电磁波 第2章静电场
如果电场由点电荷q单独产生
如果是一个闭合路径，则W=0 电场强度的环路线积分恒为零，即
应用斯托克斯定理
因此，静电场的电场强度 可以用一个标量函数 的梯度来表示，即定义
单位正实验电荷在电场中移动电场力做功
两点间的电位差定义为两点间的电压U，即
单位：V
电位函数不唯一确定，取
故可选空间某点Q作为电位参考点，空间任一点P的电位为 通常选取无限远作为电位参考点，则任一P点的电位为
在交界面上不存在 时，E、D满足折射定律。
D 1 n D 2 n 1 E 1 c1 o 2 E s 2 c2 os
E 1 t E 2 t E 1 si1 n E 2 si2n
图2.3.3 分界面上E线的折射
t电位函数 表示分界面上的衔接条件
Ax Ay Az
对应静电场的基本方程 E 0 ，矢量 A 可以表示一个静电场。
能否根据矢量场的散度来判断该矢量场是否是静电场?
2.3.2 分界面上的边界条件
1、 电位移矢量D的衔接条件 以分界面上点P作为观察点，作一
小扁圆柱高斯面（ L 0）。
图2.3.1 在电介质分界面上应用高斯定律
根据 DdSq
V ' P d ' V S 'P e n d ' S 0
• 在均匀极化的电介质内，极化电荷体密度 p 0。
• 有电介质存在的场域中，任一点的电位及电场强度表示为
(r) 4 1 0 V '( r f r 'p )d' V S '( r f r 'p )d' S E (r ) 4 1 0 V '( f r p r )'3 r( r ')d' V S '( f r p r ) '3 r( r ')d' S
如果是一个闭合路径，则W=0 电场强度的环路线积分恒为零，即
应用斯托克斯定理
因此，静电场的电场强度 可以用一个标量函数 的梯度来表示，即定义
单位正实验电荷在电场中移动电场力做功
两点间的电位差定义为两点间的电压U，即
单位：V
电位函数不唯一确定，取
故可选空间某点Q作为电位参考点，空间任一点P的电位为 通常选取无限远作为电位参考点，则任一P点的电位为
在交界面上不存在 时，E、D满足折射定律。
D 1 n D 2 n 1 E 1 c1 o 2 E s 2 c2 os
E 1 t E 2 t E 1 si1 n E 2 si2n
图2.3.3 分界面上E线的折射
t电位函数 表示分界面上的衔接条件
Ax Ay Az
对应静电场的基本方程 E 0 ，矢量 A 可以表示一个静电场。
能否根据矢量场的散度来判断该矢量场是否是静电场?
2.3.2 分界面上的边界条件
1、 电位移矢量D的衔接条件 以分界面上点P作为观察点，作一
小扁圆柱高斯面（ L 0）。
图2.3.1 在电介质分界面上应用高斯定律
根据 DdSq
V ' P d ' V S 'P e n d ' S 0
• 在均匀极化的电介质内，极化电荷体密度 p 0。
• 有电介质存在的场域中，任一点的电位及电场强度表示为
(r) 4 1 0 V '( r f r 'p )d' V S '( r f r 'p )d' S E (r ) 4 1 0 V '( f r p r )'3 r( r ')d' V S '( f r p r ) '3 r( r ')d' S
第二章 静电场中的导体与电介质
第二章 静电场中的导体与电介质2.1 导体与电介质的区别：（1）宏观上，它们的电导率数量级相差很大（相差10多个数量级，而不同导体间电导率数量级最多就相差几个数量级）。
（2）微观上导体内部存在大量的自由电子，在外电场下会发生定向移动，产生宏观上的电流而电介质内部的电子处于束缚状态，在外场下不会发生定向移动（电介质被击穿除外）。
2.2静电场中的导体1. 导体对电场的响应：静电场中的导体，其内部的自由电子会发生定向漂移，电荷分布会发生变化，这是导体对电场的响应方式称为静电感应，导体表面会产生感应电荷，感应电荷激发的附加场会在导体内部削弱外电场直至导体内部不再有自由电子定向移动，导体内电荷宏观分布不再随时间变化，这时导体处于静电平衡状态。
2. 导体处于静电平衡状态的必要条件:0i E =（当导体处于静电平衡状态时，导体内部不再有自由电子定向移动，导体内电荷宏观分布不再随时间变化，自然其内部电场（指外场与感应电荷产生的电场相叠加的总电场）必为0。
3. 静电平衡下导体的电学性质：（1）导体内部没有净电荷，电荷（包括感应电荷和导体本身带的电荷）只分布在导体表面。
这个可以由高斯定理推得：ii sq E ds ε⋅=⎰⎰，S 是导体内“紧贴”表面的高斯面，所以0i q =。
（2）导体是等势体，导体表面是等势面。
显然()()0b a b i a V V E dl -=⋅=⎰，a,b 为导体内或导体表面的任意两点，只需将积分路径取在导体内部即可。
（3）导体表面以处附近空间的场强为：0ˆEn δε=，δ为邻近场点的导体表面面元处的电荷密度，ˆn为该面元的处法向。
简单的证明下：以导体表面面元为中截面作一穿过导体的高斯柱面，柱面的处底面过场点，下底面处于导体内部。
由高斯定理可得：12i s s dsE ds E ds δε⋅+⋅=⎰⎰⎰⎰，1s ,2s 分别为高斯柱面的上、下底面。
因为导体表面为等势面所以ˆE En=，所以1s E ds Eds ⋅=⎰⎰而i E =0所以0ds Eds δε=，即0ˆE n δε=（0δ>E 沿导体表面面元处法线方向，0δ<E 沿导体表面面元处法线指向导体内部）。
第二章有导体时的静电场讲解
Q 2h C U A U A ln RB RA
§4 带电体系的静电能
一、带电体系的静电能 在引力场中，两物体相互靠近时，引力作正功， 势能减少；反之势能增加。类似地，对静电体系， 也可引入静电势能的概念。如，q1、q2构成的静电 体系，体系从状态 1 变化到状态 2 ，则电场力在这 一过程中做的功可定义为体系在新旧两种状态中 静电（势）能之差。进一步约定q1、q2处于无限远 离时的静电能为 0，则它们处于任意状态时的静电 能便有了明确值。对多个点电荷构成的静电电系 也可类似地定义静电能。
q
i
i
0
s
E 0
2.面电荷密度 和场强E 关系:
E dS ES S / 0
侧 上
下
E 0
E
S
注意: E 仅在导体表面附近适用 0
3.导体表面曲率和电荷密度的关系
U2
U1 4 0r Q1
4 0 R
1 2 3
1 EB ( 1 2 3 4 ) 0 2 0
A 1 2 B 3 4
§ 2.2 封闭金属壳内的静电场 1.腔内无电荷(无论导体是否带电) (a) 导体内场强为零； (b) 腔内空间场强处处为零； (c) 导体、空腔为等势体； (d) 内表面处处没有电荷，电荷只分布在外表面。 2. 腔内有电荷 q q (a)导体内场强处处为零； (b)腔内表面感应电荷为 - q,腔外壁总电荷为Q+q； (c)腔内电场不再为零，具体分布与腔内电荷有关； (d)导体外表面上的电荷分布与无空腔的导体相同。
而平行板电容器内部为体积V的均匀电场, 很明显,单位体积内能量,(电场能量密度):
1 2 w E 2
§4 带电体系的静电能
一、带电体系的静电能 在引力场中，两物体相互靠近时，引力作正功， 势能减少；反之势能增加。类似地，对静电体系， 也可引入静电势能的概念。如，q1、q2构成的静电 体系，体系从状态 1 变化到状态 2 ，则电场力在这 一过程中做的功可定义为体系在新旧两种状态中 静电（势）能之差。进一步约定q1、q2处于无限远 离时的静电能为 0，则它们处于任意状态时的静电 能便有了明确值。对多个点电荷构成的静电电系 也可类似地定义静电能。
q
i
i
0
s
E 0
2.面电荷密度 和场强E 关系:
E dS ES S / 0
侧 上
下
E 0
E
S
注意: E 仅在导体表面附近适用 0
3.导体表面曲率和电荷密度的关系
U2
U1 4 0r Q1
4 0 R
1 2 3
1 EB ( 1 2 3 4 ) 0 2 0
A 1 2 B 3 4
§ 2.2 封闭金属壳内的静电场 1.腔内无电荷(无论导体是否带电) (a) 导体内场强为零； (b) 腔内空间场强处处为零； (c) 导体、空腔为等势体； (d) 内表面处处没有电荷，电荷只分布在外表面。 2. 腔内有电荷 q q (a)导体内场强处处为零； (b)腔内表面感应电荷为 - q,腔外壁总电荷为Q+q； (c)腔内电场不再为零，具体分布与腔内电荷有关； (d)导体外表面上的电荷分布与无空腔的导体相同。
而平行板电容器内部为体积V的均匀电场, 很明显,单位体积内能量,(电场能量密度):
1 2 w E 2
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
“立个球面”的立体角＝？ 2. “任意曲面”dS对“某点”所张的立体角 (1) 以R0为半径的“球面”
3. “立体角”的重要结论
散度方程微分形式的引出：
请注意：此处的ρ 是指自由电荷的体密度ρvf ！
（强调）散度方程
• 物理意义： 它们描述了静电场的发散性，给出了通过封闭面的 电通量与面内所围电荷量之间的关系； • 积分形式说明： 任意封闭面的电通量＝面内所围电荷总量； 电通量为0，则封闭面内不包含电荷，即面内无源; 进而说明：静电场具有通量源，即自由电荷。 • 微分形式说明： 静电场(电位移)散度＝该点处电荷体密度; 进而，静电场具有散度源，即自由电荷的体密度。
例2. 求电荷分布
已知真空中电场分布,求各处电荷分布的体密度. 分析: 由电场分布可知, 球对称, 电场只有径向分量； 可以直接运用散度方程求解； 仍要分球内和球外两种情况；
作业
• 试计算电荷面密度为σ 的无限大平面周围 的电场。
静电场的旋度方程
• 首先应注意，这是静电场，不是任意电场； • 积分形式: 电场沿任意闭合曲线的积分为0； C指任意闭合曲线； C自身方向与C所围曲面方向满足右手规则； 积分式即电场的环流量； • 微分形式: 静电场的旋度为0 无论在有源区还是无源区； 电荷是静电场的什么源？体密度是什么源？
真空中距离为R的两点电荷q1，q2 q1对q2的作用力，电荷量正比，距离平方反比 矢量方向：q1指向q2 真空中介电常数(Dielectric Constant)
1 12 0 8.85 10 ( F / m) 9 4 9 10
真空中静止点电荷的电场强度
q 2受到的电场力：F R, q1 , q2
总结1：
库仑定律(真空中静止电荷电场)
q1 q2 F1 2 a 2 R 4 0 R 1 12 8.85 10 F / m 0 9 4 9 10 0 r
总结2：
E q1 q1 源点电量 1 2 2 4 0 R R 源场距离
2.3 两个方程
1. 泊松方程 Poisson’s Equation 2. 拉普拉斯方程 Laplace’s Equation
方程的来源——静电场的基本方程
拉普拉斯算符
笛卡儿坐标系
Laplace’s Equation
“条件”：空间内没有“体”电荷分布时：
例题
已知：导体球，半径a，球体电位U(基准?) 求：球外的电位？ • 分析： 对称性？——球对称！ 有几种方法可以求“电位”？ 直接求解——积分或代数叠加 场强求电位 拉氏方程
2.6 静电场中的介质
“电场”对外界的作用： • 对“导体”——“法拉第圆筒” • 对“电介质”——“极化” 介质中“束缚电荷”—— • 电子、离子或分子 • 受电场影响感应出：电偶极子——极化
微波炉的工作原理——介质极化
• 1946年，美国人斯潘瑟(Dr. Percy Spencer). • 食物中含有水分，水分子为极性分子，一端为正，一端为 负，其实就是电偶极子。 • 微波炉采用约2.45GHz的超短波来工作，该波的电场方向 在1秒钟内变换正负极2.45亿次，每换一次，由于极化效 应水分子方向随之反转一次；剧烈的运动产生了大量的热 能，也就是摩擦生热，热被食物分子吸收，食物就会变 热、变熟。 • 并不是任何容器都适合装食物放进微波炉内加热的，譬如 金属容器就不能。 • 大家今后不妨做个试验，把手机放进不锈钢饭盒，搁在微 波炉里加热！
• 由间距“很小”的2个等量正负“点”电荷组成 • 间距：l， “点”电荷：q1=q、q2=-q • 解决问题的入手点——矢量叠加原理！ ql r 1 E E E 4 0 r 3 1 q E 4 0 r 1 q E 4 0 R
• 物理意义： 它们说明静电场是一种保守场。 这种场做功的大小与路径无关，只与起始位置 有关,这种场的旋度为0, 又称无旋场或守恒场； • 积分形式说明： 任意封闭路径上静电场的环流量等于0； 电场力做功的大小与路径无关; • 微分形式说明： 静电场没有旋度源。
（强调）静电场的基本方程
2.2 电位及其梯度
2.2 静电场的基本方程
• 散度方程 • 旋度方程 • 物质本征方程
先认识一下这些方程
静电场的散度方程
散度方程积分形式的引出：
S
n q E dS
i 1
D E
0
S
n D dS q
i 1
请注意：此处的q 是指自由电荷！！！ 详细证明过程从略。 证明要点： 1. 仅一个电荷时，证明… 2. 多个电荷时，“叠加原理” 3. 任意曲面上求积分时，“立体角”
第2 章静电场
主要内容 电场强度 静电场基本方程: 旋度方程 散度方程 电位、电偶极子、电介质* 边界条件 导体系的电容 电场能和电场力*
2.1 电荷、库仑定理、电场强度
电荷 单位: 库仑(Coulomb) 1. 电子(Electron)： 静止质量：m e= 9.107 ×10−31 Kg 电荷量: e = −1.60 ×10−19 C 2. 质子(Proton) ： 静止质量：mP= 1.673×10−27 Kg 电荷量：p = +1.60 ×10−19 C 3. 电荷量是代数量——电荷分布是标量场
电荷分布
• 本章所要讨论的电荷分布都是静止的，稳定。 • 其中，“静止”针对空间，“稳定”针对时间。 3种电荷分布对应3种电荷密度 单位 q C 3 lim 1. 体密度： V r v 0 v m
q 2. 线密度： l r lim l 0 l q lim 3. 面密度： s r S 0 S
当场源不在坐标原点时：
1 q1 q1 1 E R, q1 4 0 R 4 0 R 1 q1 E r , r1 , q1 4 0 r r1
q1 1 E R, q1 2 aR 4 0 R
电场强度的矢量叠加
dq 1 2 aR dE r 4 0 R 微元dq=?
V / s / l，dq V dV 或 s ds或l dl
例1：电偶极子(Electric Dipole)
C C
m m
2
电场强度(Electric Field Intensity) 试验电荷q受到的静电力F E lim q 0 电荷电量q 伏 单位：E : V m 米
q
0的原因是什么？ 不使试验电荷的形状影响场的分布。
库仑定律——真空中静止电荷的电场
Coulomb's Law q1 q2 a F1 2 2 R 4 0 R
旋度方程积分形式的引出： • 根据大学物理知识，电场中的点电荷沿任 何轨迹移动后又回到原处，则电场力不做 功。 • 对于多个电荷或者任意电荷分布所形成的 电场，根据电场叠加原理，或者电场力做 功叠加的原理，不难证明旋度方程的积分 形式。
旋度方程微分的引出：
请注意：对于有源或无源区都成立！！！
（强调）旋度方程
静电场高斯定理
回忆：高斯定理Gauss’s Law ——散度定理
矢量场散度的体积分 ＝该矢量穿过包围该体积的封闭曲面的 总通量
静电场高斯定理(引言)
静电学的两个基本假设：或称之为公理
静电场高斯定理
要点： • 1. “左边” 电场在空间任意封闭面的总流出 通量 • 2. “右边” 封闭面包围的总电荷除以… • 重要用途——对称条件下，求解电场强 度！
为什么引入“电位”？ • 静电场是“有散无旋”场 • 也就是说，静电场是一种保守场。 • 回忆关于保守场的恒等式(可逆) • 标量场梯度的旋度为零。
逆定理…？ 一个无旋场一定可以用某个标量场的梯度来 表示。
1. 静电场是无旋场
2. 定义电位函数：ψ
梯度表示标量场最大空间增长率的大小和 方向。 而电场强度方向是电位下降最快的方向。
什么是边界条件？
边界条件就是不同介质(或导体)分界面两侧的场量 之间的关系。 边界的分类： 第1类: 已知整个边界上的电位 Dirichlet Problems 狄理赫利问题 第2类: 已知整个边界上电位的法导 Neumann Problems 纽曼问题 第3类: 已知部分边界电位+另一部分边界电位法 导 Hybrid Problems混合问题
2.4 电偶极子(Electric Dipole)
由间距“很小”的2个等量正负“点”电荷组成
球坐标系下
电偶极子的电力线
无极-太极-两仪-四象-六合-八方
……
• 用Matlab计算画 出的电偶极子电 位分布
2.5 静电场中的导体
• 从电磁场学科的角度看，什么是导体？ 带有大量自由电荷的物质. 静电场中, 平衡状态下, 导体内部电场处处为0. • 一些结论（适用于静电场）： 导体所带的含净电荷一定分布于表面； 是均匀分布？面电荷密度是常数？？ 导体是等势体，导体表面是等势面； 等势面与电力线相垂直。
3、各种坐标系下
4. 空间A、B两点间的电位差：
5. 电位的参考点——测量的参考点！
6. “点电荷”的电位 通常选择无穷远处电位为零。
复杂电荷分布下计算电势
若已知空间中的电荷分布 dq根据电荷分布不同来求 体电荷、面电荷、线电荷——积分 离散点电荷的集合——求和 若已知电场分布，则 • 若不知空间电荷或电场分布，仅知边界分 布，则……？
两种电荷概念
• “自由电荷”——free charge 能够自由运动并形成传导电流的电荷！ • “束缚电荷”——polarization charge 极化时，介质内出现的(正或负)电荷 不能随心所欲地自由运动，不能形成传 导电流！