3.2_一元二次不等式根的分布整理

合集下载

不等式一元二次方程根的分布

布2023-11-07•定义和公式•根的分布情况•图像表示目录•实例分析•解题技巧和注意事项•练习题与答案01定义和公式定义一元二次方程的标准形式是$ax^2 + bx + c = 0$，其中$a \neq 0$。

说明一元二次方程的标准形式是解决一元二次方程问题的基础，通过配方等方法可以将非标准形式的一元二次方程转化为标准形式，便于分析其根的分布情况。

一元二次方程的标准形式一元二次方程的解是满足方程的根，记作$x_{1}, x_{2}$。

定义根据判别式的性质，一元二次方程的解的情况分为三种：有两个不相等的实数根、有两个相等的实数根和没有实数根。

判别式$b^2 - 4ac$是判断一元二次方程解的分布情况的依据。

说明一元二次方程的解02根的分布情况当判别式Δ大于0时，一元二次方程有两个不相等的实根。

两根不等实根与系数关系图像表示两个实根的和为-b/a，两个实根的积为c/a。

在实数平面上表示为两个不相交的直线。

030201当判别式Δ等于0时，一元二次方程有两个相等的实根。

两根相等两个实根的和为-b/a，两个实根的积为c/a。

实根与系数关系在实数平面上表示为一条直线。

图像表示当判别式Δ小于0时，一元二次方程有两个不相等的虚根。

两根不等且虚根两个虚根的实部为0。

实部为0两个虚根的虚部为√(-Δ)/a。

虚部与系数关系在复数平面上表示为两个相交的直线。

图像表示当Δ < 0时，方程的根的分布03图像表示图像表示一元二次方程的解实数根对于一元二次方程 $ax^2 + bx + c = 0$，如果 $a > 0$，那么该方程有两个实数根，分别是 $x_1 = \frac{-b + \sqrt{\Delta}}{2a}$ 和 $x_2 = \frac{-b - \sqrt{\Delta}}{2a}$。

虚数根如果 $a < 0$，那么该方程有两个共轭虚数根，分别是 $x_1 = \frac{-b + i\sqrt{4ac - b^2}}{2a}$ 和 $x_2 = \frac{-b - i\sqrt{4ac - b^2}}{2a}$。

二次不等式,根的分布

二次不等式恒成立问题、二次方程根的分布、二次函数在闭区间最值一、恒成立问题“恒成立问题”一般是针对不等式而言的一个概念（本处主要研究二次不等式的恒成立），是指在已知不等式的解集为R 或Φ等的条件下，求解参数（异于变量的待定系数）的取值范围，不是解所给的不等式。

☆恒成立问题的解决方案：⎩⎨⎧易于作图的情况）、数形结合处理（针对理（本方法是通法）、转化为最值问题来处21)(x f y =在D x ∈上有最值，那么①a x f <)(恒成立a x f <⇔max )(②a x f >)(恒成立a x f >⇔min )(【注意】在计算最值时应该明确，不等式恒成立的范围，有的是R 上的恒成立，有些是某些区间上的恒成立，关系到最值的求解，故应关注到函数的定义域。

【例题1】已知不等式a x x >-+352在]2,1[上恒成立，求a 的取值范围。

【例题2】已知不等式1)42lg(2+>+-m x x 在]4,1[∈x 上恒成立，求m 的范围。

思考【例题3】已知a x x <--122，在],1[a x ∈上恒成立，求a 的取值范围。

基本思路：结合图像的相对位置关系，列出适合于条件的不等式求解参数的范围【例题4】已知不等式03)1(4)54(22>+---+x m x m m 对一切实数x 恒成立，求参数m 的取值范围．【例题5】当m 取何值时，关于x 的不等式m x x a ax x a >+++++1)1(22对任意的x ∈Ｒ恒成立．【例题6】x 取一切实数时，使3472+++kx kx kx 恒有意义，求实数k 的取值范围．二、二次方程根的分布二次方程根的分布是研究二次方程根的特殊性质的知识，该知识最终目标还是求某些参数的取值范围，主要有以下两种研究方法：⎩⎨⎧、数形结合解答点：数的关系）该方法的特、韦达定理（即根与系21图像的锁定依赖于：_____ _____ _____ _____等几个方面一些准备知识：1、方程()0f x =有实数根⇔函数()y f x =的图象与x 轴有 ⇔函数()y f x =有2、连续函数()y f x =在[,]a b 上存在零点⇔ ()()___0f a f b ⋅3、函数21y x mx =++在(,2]-∞为减函数⇔_________ 4、方程02=++c bx ax （0≠a ）根的个数与24b ac ∆=-有怎样的关系？5、韦达定理：若方程02=++c bx ax （0≠a ）的实根为1x 、2x ，则12x x +=12x x ⋅=【例题7】：已知2(3)0x m x m +-+=，根据一下条件求m 的取值范围⑴方程有两个不同实数根 ⑵方程有两正根⑶方程有两负根 ⑷两根都小于1⑸两根都大于12⑹一个根大于1，一个根小于1⑺两根都在(0,2) ⑻两根仅有1根在(0,2)⑼两根一个在(2,0)-另一根在(1,2)内 ⑽两根异号，且负根绝对值大于正根不论哪种题型，最关键的地方在于数形结合【练习】（1）已知关于x 的方程 2(2)(36)60k x k k --++=有两个负根，求k 的取值范围.（2）已知二次方程2(2)310m x mx -++=的两个根分别属于(-1,0)和(0,2),则m 的取值范围是（3）已知集合A ＝{x |x 2－5x ＋4≤0}与B ＝{x |x 2－2ax ＋a ＋2≤0，a ∈R}，若A ∪B ＝A ，求a 的取值范围．（4）已知函数3211()32f x x ax bx =++在区间[11)-，，(13]，内各有一个极值点．求24a b - 的最大值；三、二次函数在闭区间上的最值问题（值域问题）该部分知识同学们自我学习巩固1.二次函数在指定区间上的最值（值域）的解决方法：数形结合，切忌直接代入端点求解（只有当函数在区间上单调的时候方可代端点求最值）2.基本思路是：先作出二次函数在指定区间上的有效图像，从有效图像观察最值在何处取得才是最稳妥的方法。

不等式一元二次方程根的分布

不等式一元二次方程根的分布xx年xx月xx日•不等式与一元二次方程的联系•不等式在一元二次方程中的应用•不等式与一元二次方程的综合应用•不等式在一元二次方程中的拓展应用目录01不等式与一元二次方程的联系如果a>b，c>d，那么a+c>b+d。

不等式的基本性质不等式的性质1如果a>b，c>0，那么ac>bd。

不等式的性质2如果a>b，c<0，那么ac<bd。

不等式的性质3一元二次方程的根的判别式Δ=b²-4ac，当Δ>0时，方程有两个不同的实根；当Δ=0时，方程有两个相同的实根；当Δ<0时，方程没有实根。

一元二次方程的根与系数的关系x₁,x₂=[-b±√(b²-4ac)]/2a，其中x₁,x₂为一元二次方程ax²+bx+c=0的两个根。

一元二次方程的根与系数的关系不等式与一元二次方程的关联01不等式和一元二次方程的联系在于一元二次方程的根的分布情况可以由不等式来表示。

02对于一元二次方程ax²+bx+c=0，如果判别式Δ>0，那么这个方程有两个不同的实根，这两个实根可以用不等式来表示。

03如果a>0，那么方程的两个实根x₁和x₂满足x₁<x₂；如果a<0，那么方程的两个实根x₁和x₂满足x₁>x₂。

02不等式在一元二次方程中的应用利用不等式求根公式通过求解不等式，可以求得一元二次方程的实数根。

确定不等式的解集根据一元二次方程的系数和判别式的值，可以确定不等式的解集，进而求得一元二次方程的根。

利用不等式求解一元二次方程的根通过构造不等式，可以证明一元二次方程在某个区间内至少有一个实数根。

利用不等式证明根的存在通过构造不等式，可以证明一元二次方程在某个区间内只有一个实数根。

利用不等式证明根的唯一性利用不等式证明一元二次方程的根的分布利用不等式判断根的实数性质通过求解不等式，可以判断一元二次方程的实数根是否为整数、有理数、无理数等。

高中数学一元二次不等式根的分布

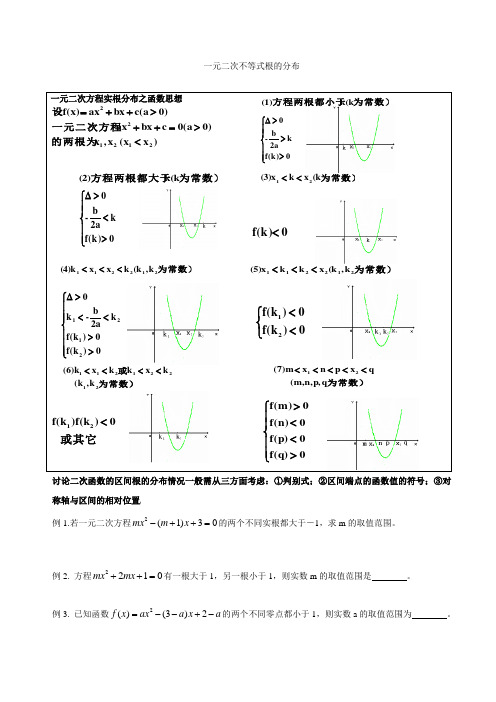
一元二次不等式根的分布讨论二次函数的区间根的分布情况一般需从三方面考虑：①判别式；②区间端点的函数值的符号；③对称轴与区间的相对位置例1.若一元二次方程2(1)30mx m x -++=的两个不同实根都大于－1，求m 的取值范围。

例2. 方程2210mx mx ++=有一根大于1，另一根小于1，则实数m 的取值范围是。

例3. 已知函数2()(3)2f x ax a x a =--+-的两个不同零点都小于1，则实数a 的取值范围为。

一元二次方程实根分布之函数思想 )x (x x ,x 0)0(a c bx ax 0)c(a bx ax f(x)212122<>=++>++=的两根为一元二次方程设为常数）212211k ,(k k x x (4)k <<<⎪⎪⎪⎩⎪⎪⎪⎨⎧>><<>∆0)f(k 0)f(k k 2a b -k 02121为常数）212211k ,(k x k k (5)x <<<⎩⎨⎧<<0)f(k 0)f(k 21为常数）或21221211k ,(k k x k k x (6)k <<<<或其它))f(k f(k 21<为常数）q p,n,(m, q x p n x (7)m 21<<<<<⎪⎪⎩⎪⎪⎨⎧><<>0f(q)0f(p)0f(n)0f(m)⎪⎪⎩⎪⎪⎨⎧>>>∆0f(k)k 2a b -0为常数）方程两根都小于k(k (1)为常数）方程两根都大于k(k (2)⎪⎪⎩⎪⎪⎨⎧><>∆0f(k)k2a b -0为常数）(k x k (3)x 21<<0f(k)<例4.若函数2()(2)(21)f x m x mx m =-+++的两个零点分别在区间(1,0),(1,2)-内，求m 的取值范围.例 5.已知方程2(1)40x a x a ++++=的两个实根为12,x x ，且1201x x <<<，则实数a 的取值范围为 .答案：例1. 令2()(1)3f x mx m x =-++，则方程2()(1)30f x mx m x =-++=有两个不同实根且都大于2(1)120112(1)0m m b m am mf ⎧∆=+->⎪+⎪-⇔-=>-⎨⎪->⎪⎩，解得5m >+或2m <-或05m <<-故实数m 的取值范围为(,2)(0,5(5)-∞-⋃-⋃++∞。

一元二次方程根的分布问题

而另一根不小于 1. 试求：
（1）参数 m 的取值范围；（2）方程两根的平方和的最大值和最小值.
5．设 m 是整数, 且方程 3x2 mx 2 0 的两根都大于
9 7 而小于，求 m 得值。 5 3
二次方程的应用二次方程最重要的性质是判别式和韦达定理 . 下面通过一些例题给出关于二次方程性质的应用. 对于与二次方程有关的问题，通常可以利用判别式、韦达定理和求根公式解决. 例 1 已知实数 a ， b （ a b ），且满足
练习： 1．若方程 x2 3x 1 0 的两根 α ， β 也是方程 x
4
px2 q 0的根，求 p q 的值。
2．设 x1 ， x2 二次方程 x2 x 3 0 的两个根，求 x1
3
4x2 19 的值。
3．已知 b ， c 满足 c b 0 的整数，方程 x2 bx c 0 有两个不等的实根 x1 ， x2 ，在
例 3 若实数 x ，
y 满足
x y x y 1，求 x y 得值。 3 3 3 1， 3 3 3 3 4 3 6 5 4 5 63
3
求根公式法例 4 已知 a 0， b 0 ， c 0，且
b2 4ac b 2ac，求 b2 4ac的最小值。
一元二次方程根的分布问题一元二次方程根的分布问题是初中数学竞赛的一个热点问题，它包括根的分布、求参数的范围等内容，涉及函数、不等式等知识，综合性较强。例 1 当 a 满足什么条件时，方程 (a 值较大？
2
1)x2 6(3a 1)x 72 0 的两根异号且负根的绝对
例 2 设关于
2b 3c 得 a

3.2.2《一元二次不等式的应用》课件(北师大版必修5)

的取值范围； • (2)对于x∈[1,3]，f(x)＜－m＋5恒成立，求m 的取值范围．
• [策略点睛]
[规范作答]
(1)要 mx2－mx－1＜0 恒成立，
若 m＝0，显然－1＜0. 若
m＜0， m≠0， Δ＝m2＋4m＜0
⇒－4＜m＜0.
∴－4＜m≤0.
(2)方法一：∵f(x)＝mx
方法二：原不等式即 f(x)＋m－5＜0，即令
12 3 mx－2 ＋4m－6＜0，x∈[1,3] 12 3 g(x)＝mx－2 ＋4m－6，x∈[1,3]，
当 m＞0 时，g(x)是增函数，∴g(x)max＝g(3)， 6 6 ∴7m－6＜0，得 m＜7.∴0＜m＜7. 当 m＝0 时，－6＜0 恒成立．当 m＜0 时，g(x)是减函数． ∴f(x)max＝g(1)＝m－6＜0，得 m＜6.∴m＜0.
x－3x＋2≥0 x＋2≠0
⇒x＜－2 或 x≥3.
所以原不等式的解集为{x|x＜－2 或 x≥3}，即(－∞，－2)∪[3，＋∞)．
4 (2)原不等式⇒ －(x－1)≤0 x－1
x－3x＋1x－1≥0 x－3x＋1 ⇒ ≥0⇒ x－1≠0 x－1
• (2)解分式不等式注意的问题： • ①解分式不等式一定要等价变形为标准形式，
就是右边为零，左边为分式再等价转化为不等式组或高次不等式来求解． • ②若分式不等式含等号，等价转化为整式不等式时，其分母不为零最易丢掉，这一点一定要注意． • ③当分式不等式分母正负不确定时不可通过不等式两边同乘以分母的方法转化为整式不等式．
• ． • 2．若ax2＋bx＋c＜0(a≠0)的解集是∅，则a，b，
c满足的条件是 . a＞0，b2－4ac＜0 • 3．二次函数y＝ax2 ＋bx＋c(x∈R)的部分对应值如表： x －3 －2 －1 0 1 2 3 4 y 6 0 －4 －6 －6 －4 0 6

一元二次方程实根的分布

一元二次方程实根的分布一元二次方程实根的分布是二次方程中的重要内容，在各类竞赛和中考中经常出现。

这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于一元二次方程根的判别式和根与系数关系（韦达定理）的运用。

本文将在前面方法的基础上，结合二次函数图象的性质，分两种情况系统地介绍一元二次方程实根分布的情况及其运用。

一．一元二次方程实根的基本分布——零分布一元二次方程实根的零分布，指的是方程的根相对于零的关系。

比如二次方程有一正根，有一负根，其实就是指这个二次方程一个根比零大，一个根比零小，或者说，这两个根分布在零的两侧。

对于这类问题，用一元二次方程根的判别式和根与系数关系（韦达定理）即可判别。

一元二次方程02=++c bx ax （0≠a ）的两个实数根为1x 、2x ，则1x 、2x 均为正⇔△≥0，1x ＋2x ＞0，1x 2x ＞0； 1x 、2x 均为负⇔△≥0，1x ＋2x ＜0，1x 2x ＞0；1x 、2x 一正一负⇔1x 2x ＜0。

例1．关于x 的一元二次方程28(1)70x m x m +++-=有两个负数根，求实数m 取值范围。

解：设两个实数根为1x 、2x ，依题意有1212000x x x x ∆⎧⎪+< ⎨⎪> ⎩≥ ①②③由①得：2(1)32(7)0m m +--≥，2(15)0m -≥，恒成立。

由②得：18m +-＜0，解之，m ＞1-。

由③得：78m -＞0，解之，m ＞7。

综上，m 的取值范围是m ＞7。

例2．若n ＞0，关于x 的方程21(2)04x m n x mn --+=有两个相等的正实数根，求mn 的值。

解：设两个实数根为1x 、2x ，依题意有1212000x x x x ∆= ⎧⎪+⎨⎪> ⎩①＞ ②③由①得：2(2)0m n mn --=，()(4)0m n m n --=，∴m n =或4m n =。

若m n =，则1x ＋2x 22m n n n n =-=-=-＜0，不符合②，舍去。

一元二次方程根的分布

【定理 4】有且仅有 k1<x1(或 x2)<k2(在(k1，k2)内有且仅有一个根)⇔f(k1)·f(k2)<0.
【定理 5】 k1<x1≤x2<k2(两个根都在(k1，k2)内)⇔ ffkΔa（（>1＝<0kk－，b122））2－ba>><400ka，，2c≥0，或Δaffk（（<1＝<0kk－，b122））2－ba<<<400ka，，2c.≥0，⇔aakΔff1≥（（<－0kk，122））ba<>>k002，，.
f（－2）＝0，上恰有一个零点，需满足①f(－2)·f(2)＜0 或②－2＜41m＜0 或 ③0f（＜24）1m＜＝20.，解①得－18＜m＜0 或 0＜m＜38；②无解；解③得 m＝38.综上可知－18<m≤38，故选 D.
例3 关于x的一元二次方程(m-1)x2+2(m+1)x-m=0 根据下列条件求实数m的取值范围
【定理 1】 x1>0，x2>0
Δ＝b2－4ac≥0， (两个正根)⇔x1＋x2＝－ba>0， x1x2＝ca>0.
Δ＝b2－4ac≥0， Δ＝b2－4ac≥0，
推论：x1>0，x2>0⇔af（>00，）＝c>0，或fa（<00，）＝c<0，
b<0
b>0.
上述推论结合二次函数图象不难得到．
【定理 2】 x1<0，x2<0
(m-1)f(2)<0 即m(m-1)<0
解得0<m<1
所以m的取值范围是0<m<1
（2）两根都在区间[-1,3）内

3.2.2《一元二次不等式的应用》课件(北师大版必修5)

• ． • 2．若ax2＋bx＋c＜0(a≠0)的解集是∅，则a，b，
c满足的条件是 . a＞0，b2－4ac＜0 • 3．二次函数y＝ax2 ＋bx＋c(x∈R)的部分对应值如表： x －3 －2 －1 0 1 2 3 4 y 6 0 －4 －6 －6 －4 0 6
1 {2} 1．不等式4x2－4x＋1≤0的解集是
解析：
原不等式等价于(2x－1)(3x＋1)＞0，
1 1 ∴x＜－3或 x＞2.
答案： A
x－1 2．不等式 log2 x ≥1 的解集为( A．(－∞，－1] C．[－1,0)
)
B．[－1，＋∞) D．(－∞，－1)∪(0，＋∞)
x－1 x＋1 解析：由已知得 x ≥2，即 x ≤0，由此解得－1≤x＜0.
其解集如图的阴影部分．
• ∴原不等式解集为{x|x<－5或－5<x<－4或
x>2}．
x2－4x＋1 x2－4x＋1－3x2＋7x－2 (2) 2 <1⇔ <0 3x －7x＋2 3x2－7x＋2 －2x2＋3x－1 2x－1x－1 ⇔ 2 <0⇔ >0 3x －7x＋2 3x－1x－2 ⇔(2x－1)(x－1)(3x－1)(x－2)>0.
[题后感悟]
(1)数形结合法解恒成立问题，
设 f(x)＝ax2＋bx＋c(a≠0) ①f(x)＞0 在 x∈R
a＞0 上恒成立⇔ Δ＜0 a＜0 上恒成立⇔ Δ＜0
；
②f(x)＜0 在 x∈R
；
③a＞0 时，f(x)＜0
fα＜0 在区间[α，β]上恒成立⇔ fβ＜0
1.解不等式： (1)(x＋4)(x＋5)2(2－x)3＜0； x2－4x＋1 (2) 2 ＜1； 3x －7x＋2 x2－2x＋1 (3) 2 ≥0. x ＋9x－10

一元二次方程实根的分布

第24页
第七章
不等式及推理与证明
高考调研
新课标版 ·数学（文） ·高三总复习
(5) 已知方程 x2 ＋ (m － 2)x ＋ 2m － 1 ＝ 0 有一实根在 0 和 1 之间，求m的取值范围．
1 2 【答案】 2<m<3
(6)已知方程x2＋(m－2)x＋2m－1＝0的较大实根在0和1之间，求m的取值范围．变式：改为较小实根．
【定理5】 k1<x1<k2≤p1<x2<p2⇔ a>0， fk1>0， fk2<0， fp1<0， fp2>0 a<0， fk1<0，或fk2>0， fp1>0， 0 . fp2<
此定理可直接由定理4推出，请读者自证．
第 4页
第七章
不等式及推理与证明
高考调研
新课标版 ·数学（文） ·高三总复习
【定理1】 x1>0，x2>0(两个正根)⇔ Δ＝b2－4ac≥0， x ＋x ＝－b>0， 1 2 a c x1x2＝ >0. a
第 5页
第七章
不等式及推理与证明
高考调研
新课标版 ·数学（文） ·高三总复习
推论： x1>0，x2>0⇔
Δ＝b2－4ac≥0， a>0， f0＝c>0， b<0
或
2 Δ ＝ b －4ac≥0， a<0， f0＝c<0， b>0.
上述推论结合二次函数图像不难得到．
第 6页
第七章
不等式及推理与证明
高考调研
新课标版 ·数学（文） ·高三总复习

微专题(一) 一元二次方程根的分布--2025年高考数学复习讲义及练习解析

所谓一元二次方程根的分布问题，就是已知一个一元二次方程根的分布情况，确定方程中系数的取值范围问题．解决一元二次方程根的分布问题，主要依据方程的根与函数零点间的关系，借助图象，从以下三个方面建立关于系数的不等式(组)进行求解．(1)判别式Δ的符号；(2)对称轴x＝－b2a与所给区间的位置关系；(3)区间端点处函数值的符号．一元二次方程根的分布问题，类型较多，情况复杂，但基本可以分为以下三类：类型一已知两根与实数k的大小关系例1(1)若关于x的方程x2－(m－1)x＋2－m＝0的两根为正数，则实数m的取值范围是________．答案[－1＋22，2)解析设f(x)＝x2－(m－1)x＋2－m，m－1）2－4（2－m）≥0，，2－m>0，解得－1＋22≤m<2.(2)(2024·湖北武汉华师第一附中模拟)若关于x的方程ax2＋(a＋2)x＋9a＝0有两个不相等的实数根x1，x2，且x1<1<x2，那么实数a的取值范围是________．答案－211，解析由于方程ax2＋(a＋2)x＋9a＝0有两个不相等的实数根，故a≠0，则ax2＋(a＋2)x＋9a ＝0可化为x2＋9＝0，令f(x)＝x2＋9，则f(1)＝1＋9<0，解得－211<a<0.当方程中二次项系数含有参数时，为避免讨论对应二次函数图象的开口方向，可将方程两边同时除以二次项系数，从而只需研究开口向上的情况，当然需要先判断二次项系数能否为0.1．(2023·黑龙江哈尔滨六中模拟)关于x的方程x2＋(m－2)x＋6－m＝0的两根都大于2，则实数m的取值范围是________．答案(－6，－25]解析令f(x)＝x 2＋(m－2)x＋6－m，＝（m－2）2－4（6－m）≥0，－m－22>2，2）＝4＋2（m－2）＋6－m>0，即≥25或m≤－25，<－2，>－6，解得－6<m≤－2 5.2．已知二次方程(2m＋1)x2－2mx＋(m－1)＝0有一正根和一负根，则实数m的取值范围是________．答案－12，解析解法一：显然2m＋1≠0，令f(x)＝x2－2m2m＋1x＋m－12m＋1，则f(0)<0，即m－12m＋1<0，所以(2m ＋1)(m－1)<0，解得－12<m<1.解法二：设x1，x2是方程(2m＋1)x2－2mx＋(m－1)＝0的两个根，则x1x2＝m－12m＋1<0，解得－12<m<1.类型二已知两根所在的区间f（m）<0，另外，根在区间上的分布还有一种情况：两根分别在区间(m，n)外，即在区间两侧x1<m，x2>n(图形分别如下)，需满足的条件是：(1)当a >0m ）<0，n ）<0；(2)当a <0m ）>0，n ）>0.例2已知关于x 的二次方程x 2＋2mx ＋2m ＋1＝0.若方程有两根，其中一根在区间(－1，0)内，另一根在区间(1，2)内，则实数m 的取值范围为________；若方程两根均在区间(0，1)内，则实数m 的取值范围为________．答案－56，－－12，1－2解析设函数f (x )＝x 2＋2mx ＋2m ＋1，则其图象与x 轴的交点分别在区间(－1，0)和(1，2)内，画出示意图如图1，由题意，得0）＝2m ＋1<0，1）＝2>0，1）＝4m ＋2<0，2）＝6m ＋5>0，<－12，∈R ，<－12，>－56，解得－56＜m ＜－12.由题意知函数f (x )＝x 2＋2mx ＋2m ＋1的图象与x 轴的交点落在区间(0，1)内，画出示意图如图2，由题意，得0）＝2m＋1>0，1）＝4m＋2>0，＝4m2－4（2m＋1）≥0，－m<1，>－12，>－12，≥1＋2或m≤1－2，1<m<0，解得－12＜m≤1－ 2.求解二次方程根的分布问题，最重要的是数形结合，即结合对应二次函数的图象，从以下角度考虑：①开口方向；②对称轴；③判别式；④在区间端点的函数值．注意以下两点：一是特殊点(含参的二次函数过的一些定点(比如与x，y轴的交点)或某些函数值的正负)的应用；二是对于一些特殊情况，还可以利用根与系数的关系、因式分解求出根再求解等方法．3．已知方程x2－(2a＋1)x＋a(a＋1)＝0的两根分别在区间(0，1)，(1，3)内，则实数a的取值范围为________．答案(0，1)解析解法一：设f(x)＝x2－(2a＋1)x＋a(a＋1)，则0）>0，1）<0，3）>0，即（a＋1）>0，2a＋a（a＋1）<0，－3（2a＋1）＋a（a＋1）>0，>0或a<－1，a<1，>3或a<2，所以0<a<1.解法二：由x2－(2a＋1)x＋a(a＋1)＝0，得(x－a)[x－(a＋1)]＝0，所以方程两根为x1＝a，x2＝a＋1，a<1，a＋1<3，解得0<a<1.4．已知关于x的方程ax2＋x＋2＝0的两个实根一个小于0，另一个大于1，则实数a的取值范围是________．答案(－3，0)解析显然a≠0，则方程ax2＋x＋2＝0可化为x2＋xa＋2a＝0，设f(x)＝x2＋xa＋2a，则0）<0，1）<0，，＋1a＋2a<0，解得－3<a<0，所以实数a的取值范围是(－3，0)．类型三可转化为一元二次方程根的分布的问题一元二次方程根的分布问题是高中数学的重要知识点之一，很多涉及函数零点个数问题或方程根的个数问题，经过换元后都能转化为根的分布问题求解．(2023·河北石家庄藁城一中模拟)设函数f (x )＝－32cos2x ＋a sin x ＋a ＋92，若方程f (x )＝0在(0，π)上有4个不相等的实数根，则实数a 的取值范围是________．答案(－3，6－62)解析f (x )＝－32(1－2sin 2x )＋a sin x ＋a ＋92＝3sin 2x ＋a sin x ＋a ＋3，x ∈(0，π)，令sin x ＝t ，t ∈(0，1]，h (t )＝3t 2＋at ＋a ＋3，当0<t <1时，sin x ＝t 有两个不相等的实数根，当t ＝1时，sin x ＝t 有且仅有一个实数根，因为方程f (x )＝0在(0，π)上有4个不相等的实数根，所以原问题等价于h (t )＝3t 2＋at ＋a ＋3＝0在区间(0，1)上有两个不相等的实数根，所以－a6<1，＝a 2－12（a ＋3）>0，（0）＝a ＋3>0，（1）＝2a ＋6>0，解得－3<a <6－6 2.本题中，令sin x ＝t ，将原问题转化为3t 2＋at ＋a ＋3＝0在区间(0，1)上有两个不相等的实数根，进而转化为一元二次方程根的分布问题是解决问题的关键，同时要注意区间端点是否满足题意．5．(2024·黑龙江哈尔滨南岗实验中学模拟)设函数f (x )x ＋1，x ≤0，4x |，x >0，若关于x 的函数g (x )＝[f (x )]2－(a ＋2)f (x )＋3恰好有六个零点，则实数a 的取值范围是________．答案23－2，32解析作出函数f (x )x ＋1，x ≤0，4x |，x >0的图象如图，令f (x )＝t ，则当t ∈(1，2]时，方程f (x )＝t 有3个不同的实数解，所以使关于x 的方程[f (x )]2－(a ＋2)f (x )＋3＝0恰好有六个不同的实数解，则方程t 2－(a ＋2)t ＋3＝0在(1，2]上有两个不同的实数根，令g (t )＝t 2－(a ＋2)t ＋3，则＝（a ＋2）2－12>0，1<a ＋22<2，（1）＝2－a >0，（2）＝3－2a ≥0，解得23－2<a ≤32，故实数a 23－2，32.。

一元二次方程实根的分布.

一元二次方程实根的分布一元二次方程实根的分布是二次方程中的重要内容，在各类竞赛和中考中经常出现。

这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于一元二次方程根的判别式和根与系数关系（韦达定理）的运用。

本文将在前面方法的基础上，结合二次函数图象的性质，分两种情况系统地介绍一元二次方程实根分布的情况及其运用。

一．一元二次方程实根的基本分布——零分布一元二次方程实根的零分布，指的是方程的根相对于零的关系。

比如二次方程有一正根，有一负根，其实就是指这个二次方程一个根比零大，一个根比零小，或者说，这两个根分布在零的两侧。

对于这类问题，用一元二次方程根的判别式和根与系数关系（韦达定理）即可判别。

一元二次方程02=++c bx ax （0≠a ）的两个实数根为1x 、2x ，则 1x 、2x 均为正⇔△≥0，1x ＋2x ＞0，1x 2x ＞0； 1x 、2x 均为负⇔△≥0，1x ＋2x ＜0，1x 2x ＞0；1x 、2x 一正一负⇔1x 2x ＜0。

例1．关于x 的一元二次方程28(1)70x m x m +++-=有两个负数根，求实数m 取值范围。

解：设两个实数根为1x 、2x ，依题意有1212000x x x x ∆⎧⎪+< ⎨⎪> ⎩≥ ①②③由①得：2(1)32(7)0m m +--≥，2(15)0m -≥，恒成立。

由②得：18m +-＜0，解之，m ＞1-。

由③得：78m -＞0，解之，m ＞7。

综上，m 的取值范围是m ＞7。

例2．若n ＞0，关于x 的方程21(2)04x m n x mn --+=有两个相等的正实数根，求m n的值。

解：设两个实数根为1x 、2x ，依题意有1212000x x x x ∆= ⎧⎪+⎨⎪> ⎩①＞ ②③由①得：2(2)0m n mn --=，()(4)0m n m n --=，∴m n =或4m n =。

若m n =，则1x ＋2x 22m n n n n =-=-=-＜0，不符合②，舍去。

专题二次函数根的分布问题、含参数一元二次不等式(解析版)

专题09 二次函数根的分布问题、含参数一元二次不等式【考点预测】1、实系数一元二次方程20(0)ax bx c a ++=≠的实根符号与系数之间的关系（1）方程有两个不等正根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=->⎨⎪⎪=>⎪⎩（2）方程有两个不等负根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=-<⎨⎪⎪=>⎪⎩（3）方程有一正根和一负根，设两根为12,x x ⇔120cx x a=< 2、一元二次方程20(0)ax bx c a ++=≠的根的分布问题一般情况下需要从以下4个方面考虑：（1）开口方向；（2）判别式；（3）对称轴2bx a=-与区间端点的关系；（4）区间端点函数值的正负．设12,x x 为实系数方程20(0)ax bx c a ++=>的两根，则一元二次20(0)ax bx c a ++=>的根的分布与其限定条件如表所示．根的分布图像限定条件12m x x <<2()0b m a f m ∆>⎧⎪⎪->⎨⎪⎪>⎩ 12x m x <<()0f m <12x x m <<02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪>⎩ 在区间(,)m n 内没有实根0∆<12120x x m x x m∆==≤=≥或02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪≥⎩02()0b n a f n ∆>⎧⎪⎪->⎨⎪⎪≥⎩()0()0f m f n ≤⎧⎨≤⎩ Onm yxOnmyxOnm yxOnm yxOnm yx在区间(,)m n 内有且只有一个实根()0()0f m f n >⎧⎨<⎩()0()0f m f n <⎧⎨>⎩在区间(,)m n 内有两个不等实根02()0()0b m n a f m f n ∆>⎧⎪⎪<-<⎪⎨⎪>⎪>⎪⎩ 3、解含参数的一元二次不等式需要对字母的取值进行分类讨论，常用的分类方法有以下三种：（1）按二次项系数a 的符号分类，即0,0,0a a a >=<；（2）按判别式的符号分类，即0,0,0∆>∆=∆<；（3）按方程20ax bx c ++=的根1x 、2x 的大小分类，即121212,,x x x x x x >=<．【典型例题】例1．（2022·辽宁·营口市第二高级中学高一期末）已知关于x 的不等式2320(R)ax x a ++>∈. (1)若2320ax x ++>的解集为{}1x b x <<，求实数,a b 的值； (2)求关于x 的不等式2321ax x ax -+>-的解集.【解析】（1）因为2320ax x ++>的解集为{}1x b x <<，所以方程2320ax x ++=的两个根为,1(1)b b <，由根与系数关系得:3121b ab a ⎧+=-⎪⎪⎨⎪⋅=⎪⎩，解得525a b =-⎧⎪⎨=-⎪⎩； OnmyxOn m yxOn myx（2）22321(3)30(3)(1)0ax x ax ax a x ax x -+>-⇒-++>⇒-->，当a =0，不等式为10x -<，不等式的解集为{}1x x <；当0a <时，不等式化为3()(1)0x x a --<，不等式的解集为31x x a ⎧⎫<<⎨⎬⎩⎭当0a >时，方程2321ax x ax -+=-的两个根分别为：3,1a.当3a =时，两根相等，故不等式的解集为{|1}x x ≠；当3a >时，31a <，不等式的解集为3{|x x a<或1}x >；当0<<3a 时，31a>，不等式的解集为{|1x x <或3}x a >，.综上：当0a <时，不等式的解集为31x x a ⎧⎫<<⎨⎬⎩⎭当a =0，不等式的解集为{}1x x <；当0<<3a 时，不等式的解集为{|1x x <或3}x a >.当3a =时，不等式的解集为{|1}x x ≠；当3a >时，不等式的解集为3{|x x a<或1}x >；例2．（2022·全国·高一专题练习）已知关于x 的不等式ax 2﹣x +1﹣a ＜0． (1)当a ＝2时，解关于x 的不等式； (2)当a ＞0时，解关于x 的不等式．【解析】（1）当a ＝2时，不等式2x 2﹣x ﹣1＜0可化为：（2x +1）（x ﹣1）＜0， ∴不等式的解集为1{|1}2x x -＜＜；（2）不等式ax 2﹣x +1﹣a ＜0可化为：（x ﹣1）（ax +a ﹣1）＜0，当a ＞0时，()1110x x a ⎛⎫-+- ⎪⎝⎭＜，()1110x x a ⎛⎫-+-= ⎪⎝⎭的根为：12111x x a==-，， ①当102a ＜＜时，111a -＜，∴不等式解集为1{|11}x x a-＜＜，②当12a =时，111a=-，不等式解集为∅， ③当12a ＞时，111a-＞，∴不等式解集为{x |11a -＜x ＜1}，综上，当102a ＜＜时，不等式解集为1{|11}x x a-＜＜，当a 12=时，不等式解集为∅，当12a ＞时，不等式解集为{x |11a-＜x ＜1}．．例3．（2022·河南·高一阶段练习）（1）若不等式210ax bx +-<的解集是113x x ⎧⎫-<<⎨⎬⎩⎭∣，求,a b的值；（2）若31b a =--，且关于x 的方程210+-=ax bx 有两个不同的负根，求a 的取值范围. 【解析】（1）由题意可得1-和13是方程210+-=ax bx 的两个实根，则11,3111,3b a a ⎧-+=-⎪⎪⎨-⎪-⨯=⎪⎩解得3,2a b ==.（2）因为31b a =--，所以()23110ax a x -+-=，由题可知Δ0>，则1a <-或19a >-，由题意，方程有两个负根，即310,10,a a a +⎧<⎪⎪⎨-⎪>⎪⎩解得103-<<a .综上，实数a 的取值范围是109aa ⎧⎫-<<⎨⎬⎩⎭∣. 例4．（2022·全国·高一课时练习）已知关于x 的方程220x x a -+=． (1)当a 为何值时，方程的一个根大于1，另一个根小于1？(2)当a 为何值时，方程的一个根大于1-且小于1，另一个根大于2且小于3？ (3)当a 为何值时，方程的两个根都大于0？【解析】（1）二次函数22y x x a =-+的图象是开口向上的抛物线，故方程220x x a -+=的一个根大于1，另一个根小于1，则2120a -+<，解得1a <，所以a 的取值范围是{}1a a <．（2）方程220x x a -+=的一个根大于1-且小于1，另一个根大于2且小于3，作满足题意的二次函数22y x x a =-+的大致图象，由图知，120120440960a a a a ++>⎧⎪-+<⎪⎨-+<⎪⎪-+>⎩ ，解得30a -<<．所以a 的取值范围是{}30a a -<<．（3）方程220x x a -+=的两个根都大于0，则Δ4400a a =-≥⎧⎨>⎩，解得01a <≤，所以a 的取值范围是{}01a a <≤．例5．（2022·全国·高一单元测试）求实数m 的范围，使关于x 的方程()221?260.x m x m +-++= (1)有两个实根，且一个比2大，一个比2小； (2)有两个实根 αβ，，且满足014αβ<<<<； (3)至少有一个正根. 【答案】(1)1m <- (2)7554m -<<- (3)1m ≤-【分析】设()()22126y f x x m x m ==+-++，一元二次方程根的分布主要从对称轴、判别式、端点值、开口方向这几个方面来确定. （1）设()()22126y f x x m x m ==+-++．依题意有()20f <，即()441260m m +-++<，得1m <-．（2）设()()22126y f x x m x m ==+-++．依题意有()()()02601450410140f m f m f m ⎧=+>⎪=+<⎨⎪=+>⎩，解得7554m -<<-．（3）设()()22126y f x x m x m ==+-++．方程至少有一个正根，则有三种可能：①有两个正根，此时可得()()Δ0002102f m ⎧⎪≥⎪⎪>⎨⎪-⎪>⎪-⎩，即153.311m m m m m ≤-≥⎧⎪>-∴-<≤-⎨⎪<⎩或． ②有一个正根，一个负根，此时可得()00f <，得3m <-．③有一个正根，另一根为0，此时可得()6203210m m m +=⎧∴=-⎨-<⎩，．综上所述，得1m ≤-．【过关测试】一、单选题1．（2022·湖北·华中师大一附中高一开学考试）关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ，且121x x ，那么a 的取值范围是（） A ．2275a -<<B ．25a > C ．27a <-D ．2011a -<< 【答案】D【解析】当0a =时，()2290ax a x a +++=即为20x =，不符合题意；故0a ≠，()2290ax a x a +++=即为22190x x a ⎛⎫+++= ⎪⎝⎭，令2219y x x a ⎛⎫=+++ ⎪⎝⎭，由于关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ，且121x x ，则()229y ax a x a =+++与x 轴有两个交点，且分布在1的两侧，故1x =时，0y <，即211190a ⎛⎫++⨯+< ⎪⎝⎭，解得211a <-，故2011a -<<，故选：D2．（2022·全国·高一课时练习）关于x 的方程()22210x m x m +-+-=恰有一根在区间()0,1内，则实数m 的取值范围是（） A ．13,22⎡⎤⎢⎥⎣⎦B ．12,23⎛⎤ ⎥⎝⎦C ．1,22⎡⎫⎪⎢⎣⎭D ．{}12,6723⎛⎤⋃- ⎥⎝⎦【答案】D【解析】方程2(2)210x m x m +-+-=对应的二次函数设为：()2(2)21f x x m x m =+-+-因为方程2(2)210x m x m +-+-=恰有一根属于(0,1)，则需要满足： ①()()010f f ⋅<，()()21320m m --<，解得：1223m <<； ②函数()f x 刚好经过点()0,0或者()1,0，另一个零点属于(0,1)，把点()0,0代入()2(2)21f x x m x m =+-+-，解得：12m =，此时方程为2302x x -=，两根为0，32，而()30,12∉，不合题意，舍去把点()1,0代入()2(2)21f x x m x m =+-+-，解得：23m =，此时方程为23410x x -+=，两根为1，13，而()10,13∈，故符合题意；③函数与x 轴只有一个交点，横坐标属于(0,1)， ()2(2)4210m m ∆=---=，解得67m =±当67m =+2(2)210x m x m +-+-=的根为27-- 若627m =-2(2)210x m x m +-+-=72，符合题意综上：实数m 的取值范围为{}12,6723⎛⎤⋃- ⎥⎝⎦故选：D3．（2022·江苏·高一专题练习）关于x 的方程222(1)0x m x m m +-+-=有两个实数根α，β，且2212αβ+=，那么m 的值为（） A ．1- B ．4- C ．4-或1 D ．1-或4【答案】A【解析】关于x 的方程()22210x m x m m +-+-=有两个实数根， ()()222141440∴∆=--⨯⨯-=-+⎡⎤⎣⎦m m m m ，解得：1m ，关于x 的方程()22210x m x m m +-+-=有两个实数根α，β，2(1)m αβ∴+=--，2m m αβ⋅=-，()()()22222221212αβαβαβ∴+=+-⋅=----=⎡⎤⎣⎦m m m ，即2340m m --=，解得：1m =-或4(m =舍去). 故选：A.4．（2022·江苏·高一）已知关于x 的方程230x kx k -++=有两个正根，那么两个根的倒数和最小值是（）A ．-2B ．23C ．89D ．1【答案】B【解析】由题意可得∆2()4(3)0k k =--+，解得6k 或2k ≤-，设两个为1x ，2x ，由两根为正根可得1212·30x x k x x k +=>⎧⎨=+>⎩，解得0k >，综上知，6k .故两个根的倒数和为12121211x xx x x x ++=1331k k k==++，6k ，∴1106k <，3102k <，故33112k <+， ∴12331k+，故两个根的倒数和的最小值是23. 故选：B5．（2022·全国·高一专题练习）已知方程240x x a -+=的两根都大于1，则a 的取值范围是（） A ．34a <≤ B ．14a <≤ C ．1a > D ．4a ≤【答案】A【解析】设方程240x x a -+=的两根为12,x x ，依题意有：121216404a x x x x a ∆=-≥⎧⎪+=⎨⎪=⎩，因12,x x 都大于1，则122x x +>，且12()1(1)0x x ->-，显然122x x +>成立，由12()1(1)0x x ->-得1212()10x x x x -++>，则有410a -+>，解得3a >，由1640a ∆=-≥解得：4a ≤，于是得34a <≤，所以a 的取值范围是34a <≤. 故选：A6．（2022·全国·高一期中）若关于x 的不等式()2330x m x m -++<的解集中恰有3个整数，则实数m 的取值范围为（） A ．(]6,7 B ．[)1,0- C ．[)(]1,06,7-⋃ D ．[]1,7-【答案】C【解析】不等式()2330x m x m -++<，即()()30x x m --<，当3m >时，不等式解集为()3,m ，此时要使解集中恰有3个整数，这3个整数只能是4，5，6，故67m <≤；当3m =时，不等式解集为∅，此时不符合题意；当3m <时，不等式解集为(),3m ，此时要使解集中恰有3个整数，这3个整数只能是0，1，2，故10m -≤<；故实数m 的取值范围为[)(]1,06,7-⋃．故选：C7．（2022·上海·高一专题练习）关于x 的不等式2320ax x -+>的解集为{|1x x <或}x b >，则关于x 的不等式2()0ax ac b x bx -++>，以下结论正确的是（） A ．当0c >时，解集为{}|0x x c << B ．当0c 时，解集为R C ．当0c <时，解集为{|x x c <或0}x > D ．以上都不正确【答案】C【解析】由题意，121,x x b ==为方程2320ax x -+=的两个根代入方程2320320a ab b -+=⎧⎨-+=⎩ 解得：1a =，2b =于是关于x 的不等式2()0ax ac b x bx -++>，即为20x cx ->令2120,0,x cx x x c -===，对应的二次函数开口向上当0c >时，解集为{|0x x <或}x c > 当0c 时，解集为{|0}x x ≠ 当0c <时，解集为{|x x c <或0}x > 故选：C8．（2022·全国·高一课时练习）若关于x 的不等式()210x a x a -++<的解集中恰有两个整数，则实数a 的取值范围是 A ．{}34a a << B ．{|21a a -<<-或}34a << C ．{}34a a <D ．{|21a a -<-或}34a <【答案】D【解析】由题意得，原不等式可转化为()()10x x a --<.当1a >时，解得1x a <<，此时解集中的整数为2，3，则34a <；当1a <时，解得1<<a x ，此时解集中的整数为0，-1，则21a -<-.当1a =时，不符合题意.故实数a 的取值范围是{|21a a -<-或}34a <，故选D ．二、多选题9．（2022·湖南·株洲二中高一开学考试）已知关于x 的不等式组222802(27)70x x x k x k ⎧-->⎨+++<⎩仅有一个整数解，则k 的值可能为（） A ．5- B ．3-C ．πD ．5【答案】ABD【解析】解不等式2280x x -->，得4x >或2x <- 解方程22(27)70x k x k +++=，得127,2x x k =-=-（1）当72k >，即72k -<-时，不等式22(27)70x k x k +++<的解为：72k x -<<-此时不等式组222802(27)70x x x k x k ⎧-->⎨+++<⎩的解集为7,2k ⎛⎫-- ⎪⎝⎭，依题意，则54k -≤-<-，即45k <≤；（2）当72k <，即72k ->-时，不等式22(27)70x k x k +++<的解为：72x k -<<-，要使不等式组222802(27)70x x x k x k ⎧-->⎨+++<⎩的解集中只有一个整数，则需满足：35k -<-≤，即53k -≤<；所以k 的取值范围为[5,3)(4,5]-. 故选：ABD.10．（2022·江苏·高一专题练习）已知函数23y ax bx =+-，则下列结论正确的是（） A ．关于x 的不等式230ax bx +-<的解集可以是{}3x x > B ．关于x 的不等式230ax bx +->的解集可以是∅ C ．函数23y ax bx =+-在()0,∞+上可以有两个零点D ．“关于x 的方程230ax bx +-=有一个正根和一个负根”的充要条件是“0a >” 【答案】BCD【解析】若不等式230ax bx +-<的解集是{}3x x >，则0a =且330b -=，得1b =，而当0a =，1b =时，不等式230ax bx +-<，即30x -<，得3x <，与3x >矛盾，故A 错误；取1a =-，0b =，此时不等式230x -->的解集为∅，故B 正确；取1a =-，4b =，则由2430y x x =-+-=，得1x =或3，故C 正确；若关于x 的方程230ax bx +-=有一个正根和一个负根，则0,30,a a≠⎧⎪⎨-<⎪⎩得0a >，若0a >，则2120b a ∆=+>，故关于x 的方程230ax bx +-=有两个不等的实根12,x x ，且1230x x a=-<，即关于x 的方程230ax bx +-=有一个正根和一个负根．因此“关于x 的方程230ax bx +-=有一个正根和一个负根”的充要条件是“0a >”，故D 正确．故选：BCD ．11．（2022·湖南·长沙市实验中学高一期中）已知关于x 的方程x 2＋(m －3)x ＋m ＝0，下列结论正确的是（）A ．方程x 2＋(m －3)x ＋m ＝0有实数根的充要条件是m ∈{m |m <1或m >9}B ．方程x 2＋(m －3)x ＋m ＝0有一正一负根的充要条件是m ∈{m |m <0}C ．方程x 2＋(m －3)x ＋m ＝0有两正实数根的充要条件是m ∈{m |0<m ≤1}D ．方程x 2＋(m －3)x ＋m ＝0无实数根的必要条件是m ∈{m |m >1} 【答案】BCD【解析】方程x 2＋(m －3)x ＋m ＝0有实数根的充要条件是()2340m m ∆=--≥，解得(][),19,m ∈-∞+∞，A 错误；方程x 2＋(m －3)x ＋m ＝0有一正一负根的充要条件是()23400m m m ⎧∆=-->⎪⎨<⎪⎩，解得(),0m ∈-∞，B 正确；方程x 2＋(m －3)x ＋m ＝0有两正实数根的充要条件是()2340030m m m m ⎧∆=--≥⎪>⎨⎪->⎩，解得(]0,1m ∈，C 正确；方程x 2＋(m －3)x ＋m ＝0无实数根的充要条件是()2340m m ∆=--<，解得()1,9m ∈，()()1,91,⊆+∞，故必要条件是m ∈{m |m >1}，故D 正确.故选：BCD.12．（2022·湖南·新化县教育科学研究所高一期末）已知a Z ∈，关于x 的一元二次不等式x 2-8x +a ≤0的解集中有且仅有3个整数，则a 的值可以是（） A ．13 B ．14C ．15D ．17【答案】ABC【解析】设二次函数f (x )=x 2-8x +a ，开口向上，其对称轴为x =4，因为一元二次不等式x 2-8x +a ≤0的解集中有且仅有3个整数∴3个整数解必然是3，4，5，∴根据对称性，满足f （2）>0且f （3）≤0，故4160a -+>，且9240a -+≤，即12<a ≤15，a =13，14，15. 故选：ABC. 三、填空题13．（2022·全国·高一单元测试）方程()2250x a x a --+-=的两根都大于2，则实数a 的取值范围是_____．【答案】54a -<≤-【解析】由题意，方程()2250x a x a +=－－－的两根都大于2，令()()225f x x a x a =+－－－，可得()020222f a⎧⎪≥⎪>⎨⎪-⎪>⎩，即2165024a a a ⎧≥⎪+>⎨⎪->⎩，解得54a <≤－－．故答案为：54a -<≤-.14．（2022·全国·高一专题练习）方程()2110mx m x --+=在区间()0,1内有两个不同的根，m 则的取值范围为__．【答案】322m >+【解析】令()()211f x mx m x =--+，图象恒过点()0,1，方程()211mx m x --+=0在区间()0,1内有两个不同的根，()()2010********Δ0m m m m m f m m >⎧⎧⎪>-⎪⎪<<⎪⎪∴⇒>⎨⎨⎪⎪>-->⎪⎪⎩>⎪⎩，解得322m >+ 故答案为：322m >+15．（2022·全国·高一专题练习）已知方程()()22110x a x a a -+++=的两根分别在区间()0,1，()1,3之内，则实数a 的取值范围为______．【答案】()0,1.【解析】方程()()()()2211010x a x a a x a x a ⎡⎤+++=⇒--+=⎣⎦－∴方程两根为12,1x a x a ==+，若要满足题意，则01113a a <<⎧⎨<+<⎩，解得01a <<，故答案为：()0,1.16．（2022·安徽·泾县中学高一开学考试）记关于x 的不等式220x x a a -+-≤的解集为A ，集合{}12B x x =-≤<，若A B ，则实数a 的取值范围为___________. 【答案】()1,2-【解析】原不等式220x x a a -+-≤可变形为()()10x a x a -+-≤，当1a a ，即12a =时，12A ⎧⎫=⎨⎬⎩⎭，满足题意；当1a a <-，即12a <时，{}1A x a x a =≤≤-，所以112a a ≥-⎧⎨-<⎩，解得1a >-，所以112a -<<；当1a a ，即12a >时，{}1A x a x a =-≤≤，所以21112a a a ⎧⎪<⎪-≥-⎨⎪⎪>⎩，解得122a <<.综上可得1a 2-<<，即()1,2a ∈-；故答案为：()1,2- 四、解答题17．（2022·四川成都·高一期末）设函数()()()3f x x x a =--，R a ∈. (1)解关于x 的不等式()0f x <；(2)当()3x ∈+∞，时，不等式()9f x ≥-恒成立，求a 的取值范围. 【解析】(1)当3a <时，不等式()0f x <的解集为(),3a ，当3a =时，不等式()0f x <的解集为∅，当3a >时，不等式()0f x <的解集为()3,a .(2)因为()3x ∈+∞，，所以由()9f x ≥-可得93x a x --≥-，93a x x ≤+-，因为()999332339333x x x x x x +=-++≥-⋅=---，当且仅当933x x -=-，即6x =时等号成立，所以9a ≤.18．（2022·全国·高一课时练习）已知函数()()21f x x x a a =++-，(1)当2a =时，求不等式()0f x <的解集. (2)求不等式()2f x x <的解集.【解析】（1）当2a =时，2()20f x x x =+-<，解得为21x -<<，所以解集为{|21}x x -<< （2）由()2f x x<可得2(1)0x x a a -+-<，[(1)]()0x a x a ---<①当1a a ->，即12a <时，不等式2(1)0x x a a -+-<解集为(,1)a a -； ②当1a a -=，即12a =时，不等式可化为2102x ⎛⎫-< ⎪⎝⎭，此时解集为∅；③当1a a -<，即12a >时，不等式2(1)0x x a a -+-<解集为(1,)a a - 综上所述，当12a <时，解集为(,1)a a -；当12a =时，解集为∅；当12a >时，解集为(1,)a a -. 19．（2022·江苏省天一中学高一期末）已知二次函数()()222,R f x ax bx b a a b =++-∈，当()1,3x ∈-时，()0f x >；当()(),13,x ∈-∞-⋃+∞，()0f x <. (1)求a ，b 的值；(2)解关于x 的不等式：()()220R ax b c x c c +-+>∈.【解析】(1)由题意可知：()2220f x ax bx b a =++-=的两根为1,3- ，故21323bab a a⎧-=-+⎪⎪⎨-⎪=-⎪⎩ ，即得12a b =-⎧⎨=⎩ ,即1,2a b =-= ； (2)由（1）可知：()()220R ax b c x c c +-+>∈，即2(2)20x c x c ---< ，解方程2(2)20x c x c ---=得两根为122,x x c ==- ，当2c -> ，即2c <-时，2(2)20x c x c ---<解集为{|2}x x c <<- ；当2c -= ，即2c =-时，2(2)20x c x c ---<解集为∅；当2c -< ，即2c >-时，2(2)20x c x c ---<解集为{|2}x c x -<< ；故2c <-时，解集为{|2}x x c <<-；2c =-时，解集为∅； 2c >-时，解集为{|2}x c x -<< .20．（2022·湖南·高一课时练习）当k 为何值时，关于x 的方程()22340x k x k +-+=分别满足：(1)无实数根？(2)有两正实根？【解析】(1)∵关于x 的方程()22340x k x k +-+=无实数根，∴()243440k k ∆=--⨯<， ∴21090k k -+<，解得19k <<，即()1,9k ∈.(2)∵关于x 的方程()22340x k x k +-+=有两正实根，∴()()2Δ4344023040k k k k ⎧=--⨯≥⎪-->⎨⎪>⎩，解得01k <≤，即(0,1]k ∈.21．（2022·全国·高一单元测试）关于x 的方程2220x mx m +++=分别满足下列条件： (1)当4m =时，两根分别为1x 、2x ，求2212x x +的值； (2)m 为何值时，有一正根一负根； (3)m 为何值时，有两个不相等的正根．【解析】（1）当4m =时，方程变为2860x x ++=，由韦达定理得，12128,6x x x x +=-=，所以212122122()2642652x x x x x x =+-=⨯=+-.（2）由题意，1200x x ∆>⎧⎨<⎩，即244(2)020m m m ⎧-+>⎨+<⎩，解得2m <-.（3）由题意1212000x x x x ∆>⎧⎪+>⎨⎪>⎩，即244(2)02020m m m m ⎧-+>⎪->⎨⎪+>⎩，解得21m -<<-.22．（2022·全国·高一专题练习）已知关于x 的方程2(21)70x m x m -+++=有两个不等的实根1x ，2x ．（1）两根一个根大于1，一个根小于1，求参数m 的取值范围；（2）113x <<，24x >，求参数m 的取值范围．【解析】令()2(21)7f x x m x m =-+++，（1）两根一个根大于1，一个根小于1，等价于()10f <，则()12170m m -+++<，解得7m >；（2）若113x <<，24x >，则(1)0(3)0(4)0f f f >⎧⎪<⎨⎪<⎩，即1(21)709(21)37016(21)470m m m m m m -+++>⎧⎪-+⋅++<⎨⎪-+⋅++<⎩，即7135197m m m ⎧⎪<⎪⎪>⎨⎪⎪>⎪⎩，解得1977m <<.。

高中数学第3章不等式3.2一元二次不等式第2课时一元二次不等式及其解法(二)数学

12/13/2021
第二十八页，共三十四页。
(1)若在①处忽视对二次项系数的讨论，则会漏掉 k＝0 的情况，从而错填(0，1]． (2)二次项系数含参数时要分系数为正、系数为零、系数为负三种情况进行讨论，尤其是当系数为零时，一元一次不等式要注意单独验证．如本例中当 k＝0 时，不等式为 3≥0，成立．因此，k＝0 符合题目要求．
12/13/2021
第六页，共三十四页。
3. 在如图所示的锐角三角形空地中，欲建一个面积不小于 300 m2 的内接矩形花园(阴影部分), 则其边长 x(单位：m)的取值范围是________．
12/13/2021
第七页，共三十四页。
解析：设矩形高为 y，由三角形相似得： 4x0＝404－0 y，且 x>0，y>0，x<40，y<40，xy≥300，整理得 y＋x＝40，将 y＝40－x 代入 xy≥300，整理得 x2－40x＋300≤0，解得 10≤x≤30. 答案：[10，30]
12/13/2021
第三十一页，共三十四页。
3．若产品的总成本 y(万元)与产量 x(台)之间的函数关系式是 y ＝3 000＋20x－0.1x2(0<x<240，x∈N)，若每台产品的售价为 25 万元，则生产者不亏本(销售收入不小于总成本)时的最低产量是________台．解析：y－25x＝－0.1x2－5x＋3 000≤0，所以 x2＋50x－30 000≥0，得 x≤－200(舍去)或 x≥150，又因为 0<x<240，x∈N，所以 150≤x<240，x∈N. 答案：150
12/13/2021
第八页，共三十四页。
简单的分式不等式的解法 (1)不等式2xx－＋11≤0 的解集为________． (2)不等式x＋x 1≤3 的解集是________．