2021全国统考数学(理)人教版一轮 54 直线与圆锥曲线

合集下载

2021年高考数学一轮复习第47讲直线与圆锥曲线

共点，例如：与双曲线的渐近线平行的直线与双曲线只有一个交点．故选 A.]
4．过点(0,1)作直线，使它与抛物线 y2＝4x 仅有一个公共点，这样的直线有________条．
3 [结合图形分析可知，满足题意的直线共有 3 条：直线 x＝0，过点(0,1)且平行于 x
轴的直线以及过点(0,1)且与抛物线相切的直线(非直线 x＝0). ]
(3)过抛物线 y2＝2px(p>0)焦点的弦中最短弦的弦长是 2p.( )
(4)若抛物线上存在关于直线 l 对称的两点，则 l 与抛物线有两个交点．( )
[答案] (1)√ (2)× (3)√ (4)×
x2 y2 2．(教材改编)直线 y＝k(x－1)＋1 与椭圆＋＝1 的位置关系是( )
94
A．相交
B．相切
C．相离
D．不确定
A [直线 y＝k(x－1)＋1 恒过定点(1,1)，又点(1,1)在椭圆内部，故直线与椭圆相交．]
3．“直线与双曲线相切”是“直线与双曲线只有一个公共点”的( )
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
A [直线与双曲线相切时，只有一个公共点，但直线与双曲线相交时，也可能有一个公
线和一条与对称轴平行或重合的直线；过抛物线内一点只有一条直线与抛物线有且只有一个
公共点：一条与对称轴平行或重合的直线．
[基础自测]
1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)
(1)直线 l 与椭圆 C 相切的充要条件是直线 l 与椭圆 C 只有一个公共点．( )
-1-
(2)直线 l 与双曲线 C 相切的充要条件是直线 l 与双曲线 C 只有一个公共点．( )

直线和圆、圆锥曲线综合测试卷(新高考专用)(解析版)—2025年高考数学一轮复习

直线和圆、圆锥曲线综合测试卷专练（考试时间：120分钟；满分：150分）注意事项：1.本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答第I卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3.回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4.考试结束后，将本试卷和答题卡一并交回。

第I卷（选择题）一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合要求的。

则由椭圆的中心对称性可知可知AF1BF2为平行四边形，则可得△ABF2的周长为|AF当AB位于短轴的端点时，当围成的等腰三角形底边在x轴上时，当围成的等腰三角形底边在直线l因为tanα=2tanα21―tan2α2=2，且tanα2>所以k=tanθ=tanα2=5―12，或故选：B．5．（5分）（2024·西藏拉萨的最小值为（）A．1453【解题思路】先设点的坐标，结合轨迹方程求参，再根据距离和最小值为两点间距离求解即可6．（5分）（2024·湖南邵阳点B在C上且位于第一象限，B．8 A．453【解题思路】由点A―1,8由点A―1,8在抛物线y23所以抛物线C的方程为y2设B(x0,y0)，则x0>0,y0>由题意知F p2,0，又OP 显然直线AB的斜率不为由y2=2pxx=ty+p2，得y2―2pty显然直线BD的斜率不为由y2=2pxλp，得y2故选：C.二、多项选择题：本题共3小题，每小题6分，共18分，在每小题给出的四个选项中，有多项符合题目的要求，全部选对的得6分，部分选对的得部分分，有选错的得0分。

如图，因为K OA=∠PDA=∠ODB，所以×|PA|⋅S△PAB=12故选：ABD.11．（6分）（2024·福建龙岩|AB|=8.过焦点F的直线C的准线与坐标轴的交点，则（A．若MF=3FN，则直线C．∠MON为钝角设M(x1,y1),N(x2,y 得y2―8my―16=所以y1y2=―16,x1∴x1x2+y1y2=4⟨⟩三、填空题：本题共3小题，每小题5分，共15分。

2021年高考数学一轮复习第三讲直线与圆锥曲线的综合问题讲练理新人教A版

2021年高考数学一轮复习第三讲直线与圆锥曲线的综合问题讲练理新人教A 版一、直线与圆锥曲线的位置关系的判断将直线方程与圆锥曲线方程联立，消去一个变量得到关于x (或y )的一元方程：ax 2＋bx ＋c ＝0(或ay 2＋by ＋c ＝0)．1．当a ≠0，可考虑一元二次方程的判别式Δ，有 ①Δ＞0⇔直线与圆锥曲线相交； ②Δ＝0⇔直线与圆锥曲线相切； ③Δ＜0⇔直线与圆锥曲线相离．2．当a ＝0，b ≠0时，即得到一个一元一次方程，则直线l 与圆锥曲线E 相交，且只有一个交点，①若E 为双曲线，则直线l 与双曲线的渐近线的位置关系是平行；②若E 为抛物线，则直线l 与抛物线的对称轴的位置关系是平行或重合．二、圆锥曲线的弦长设斜率为k (k ≠0)的直线l 与圆锥曲线C 相交于A 、B 两点，A (x 1，y 1)，B (x 2，y 2)，则|AB |＝1＋k 2|x 2－x 1|＝1＋1k2|y 2－y 1|.基础自测1．直线y ＝kx －k ＋1与椭圆x 29＋y 24＝1的位置关系为( )A ．相交B ．相切C ．相离D ．不确定【解析】直线y ＝kx －k ＋1＝k (x －1)＋1恒过定点(1,1)，又点(1,1)在椭圆内部，故直线与椭圆相交．【答案】 A2．若直线y ＝kx 与双曲线x 29－y 24＝1相交，则k 的取值范围是( )A.⎝ ⎛⎭⎪⎫0，23B.⎝ ⎛⎭⎪⎫－23，0 C.⎝ ⎛⎭⎪⎫－23，23 D.⎝ ⎛⎭⎪⎫－∞，－23∪⎝ ⎛⎭⎪⎫23，＋∞ 【解析】双曲线x 29－y 24＝1的渐近线方程为y ＝±23x ，若直线与双曲线相交，数形结合，得k ∈⎝ ⎛⎭⎪⎫－23，23. 【答案】 C3．已知倾斜角为60°的直线l 通过抛物线x 2＝4y 的焦点，且与抛物线相交于A 、B 两点，则弦AB 的长为________．【解析】直线l 的方程为y ＝3x ＋1，由⎩⎨⎧y ＝3x ＋1x 2＝4y得y 2－14y ＋1＝0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝14， ∴|AB |＝y 1＋y 2＋p ＝14＋2＝16. 【答案】 164．过椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的左顶点A 且斜率为1的直线与椭圆的另一个交点为M ，与y 轴的交点为B ，若|AM |＝|MB |，则该椭圆的离心率为________．【解析】由题意A 点的坐标(－a,0)，l 的方程为y ＝x ＋a ，∴B 点的坐标为(0，a )，故M 点的坐标为(－a 2，a2)，代入椭圆方程得a 2＝3b 2，∴c 2＝2b 2，∴e ＝63.【答案】63考点一中点弦、弦长问题例已知F 1(－1,0)、F 2(1,0)，圆F 2：(x －1)2＋y 2＝1，一动圆在y 轴右侧与y 轴相切，同时与圆F 2相外切，此动圆的圆心轨迹为曲线C ，曲线E 是以F 1，F 2为焦点的椭圆．(1)求曲线C 的方程；(2)设曲线C 与曲线E 相交于第一象限点P ，且|PF 1|＝73，求曲线E 的标准方程；(3)在(1)、(2)的条件下，直线l 与椭圆E 相交于A 、B 两点，若AB 的中点M 在曲线C 上，求直线l 的斜率k 的取值范围．【思路点拨】 (1)利用两圆外切的性质求曲线C 的方程．(2)利用|PF 1|＝73可求点P 的横坐标，进一步求|PF 2|的长，再结合椭圆的定义求出椭圆的方程．(3)设出直线l 的方程，与椭圆方程联立利用根与系数的关系求解或用点差法求解．【尝试解答】 (1)设动圆圆心的坐标为(x ，y )(x ＞0)因为动圆在y 轴右侧与y 轴相切，同时与圆F 2相外切，所以|CF 2|－x ＝1， ∴x －12＋y 2＝x ＋1，化简整理得y 2＝4x ，曲线C 的方程为y 2＝4x (x ＞0)；(2)依题意，c ＝1，|PF 1|＝73，可得x p ＝23，∴|PF 2|＝53，又由椭圆定义得2a ＝|PF 1|＋|PF 2|＝73＋53＝4，a ＝2.∴b 2＝a 2－c 2＝3，所以曲线E 的标准方程为x 24＋y 23＝1；(3)(方法一)设直线l 与椭圆E 交点A (x 1，y 1)，B (x 2，y 2)，A ，B 的中点M 的坐标为(x 0，y 0)，设直线l 方程为y ＝kx ＋m (k ≠0，m ≠0)，与x 24＋y 23＝1联立得(3＋4k 2)x 2＋8kmx ＋4m 2－12＝0，由Δ＞0得4k 2－m 2＋3＞0；①由韦达定理得x 1＋x 2＝－8km3＋4k2，∴x 0＝－4km 3＋4k 2，y 0＝3m3＋4k2，将M ⎝ ⎛⎭⎪⎫－4km 3＋4k 2，3m 3＋4k 2代入y 2＝4x ，整理得m ＝－16k 3＋4k 29，② 将②代入①得162k 2(3＋4k 2)＜81，令t ＝4k 2(t ＞0)，则64t 2＋192t －81＜0，∴0＜t ＜38. ∴－68＜k ＜68且k ≠0. (方法二)设直线l 与椭圆E 交点A (x 1，y 1)，B (x 2，y 2)，A ，B 的中点M 的坐标为(x 0，y 0)，将A ，B 的坐标代入椭圆方程中，得⎩⎪⎨⎪⎧3x 21＋4y 21－12＝0，3x 22＋4y 22－12＝0，两式相减得3(x 1－x 2)(x 1＋x 2)＋4(y 1－y 2)(y 1＋y 2)＝0，∴y 1－y 2x 1－x 2＝－3x 04y 0， ∵y 20＝4x 0，∴直线AB 的斜率k ＝y 1－y 2x 1－x 2＝－316y 0，由(2)知x p ＝23，∴y 2p ＝4x p ＝83，∴y P ＝±263，由题设－263＜y 0＜263(y 0≠0)，∴－68＜－316y 0＜68，即－68＜k ＜68(k ≠0)．方法与技巧 1.在第2问方法一中，根据Δ＞0求t 的范围，进而去求k 的取值范围，这是求解的关键.2.涉及弦的中点与直线的斜率问题，可考虑“点差法”，构造出k AB ＝y 1－y 2x 1－x 2和x 1＋x 2，y 1＋y 2，整体代换，求出中点或斜率，体现“设而不求”的思想.跟踪练习设抛物线过定点A (－1,0)，且以直线x ＝1为准线． (1)求抛物线顶点的轨迹C 的方程；(2)若直线l 与轨迹C 交于不同的两点M ，N ，且线段MN 恰被直线x ＝－12平分，设弦MN的垂直平分线的方程为y ＝kx ＋m ，试求m 的取值范围．【解】 (1)设抛物线顶点为P (x ，y )，则焦点F (2x －1，y ) 再根据抛物线的定义得|AF |＝2，即(2x )2＋y 2＝4，所以轨迹C 的方程为x 2＋y 24＝1.(2)设弦MN 的中点为P (－12，y 0)，M (x M ，y M )，N (x N ，y N )，则由点M ，N 为椭圆上的点，可知⎩⎪⎨⎪⎧4x 2M ＋y 2M ＝4，4x 2N ＋y 2N ＝4.两式相减，得4(x M －x N )(x M ＋x N )＋(y M －y N )(y M ＋y N )＝0，将x M ＋x N ＝2×(－12)＝－1，y M ＋y N ＝2y 0，y M －y N x M －x N ＝－1k 代入上式得k ＝－y 02. 又点P (－12，y 0)在弦MN 的垂直平分线上，所以y 0＝－12k ＋m .所以m ＝y 0＋12k ＝34y 0.由点P (－12，y 0)在线段BB ′上(B ′、B 为直线x ＝－12与椭圆的交点，如图所示)，所以y B ′＜y 0＜y B ，也即－3＜y 0＜ 3. 所以－334＜m ＜334，且m ≠0.考点二最值与范围问题例 (xx·课标全国卷Ⅱ)平面直角坐标系xOy 中，过椭圆M ：x 2a 2＋y 2b2＝1(a ＞b ＞0)右焦点的直线x ＋y －3＝0交M 于A ，B 两点，P 为AB 的中点，且OP 的斜率为12.(1)求M 的方程；(2)C ，D 为M 上的两点，若四边形ACBD 的对角线CD ⊥AB ，求四边形ACBD 面积的最大值．【思路点拨】 (1)涉及到弦AB 的中点问题，考虑点差法，建立关于a ，b 的方程组，解得a ，b 的值，确立M 的方程；(2)将四边形的面积表示出来，可转化为S ＝|AB |·h ，然后利用函数的知识求最值．【尝试解答】 (1)设A (x 1，y 1)，B (x 2，y 2)，P (x 0，y 0)，则x 21a 2＋y 21b 2＝1，x 22a 2＋y 22b 2＝1，y 2－y 1x 2－x 1＝－1，由此可得b 2x 2＋x 1a 2y 2＋y 1＝－y 2－y 1x 2－x 1＝1.因为x 1＋x 2＝2x 0，y 1＋y 2＝2y 0，y 0x 0＝12，所以a 2＝2b 2.又由题意知，M 的右焦点为(3，0)，故a 2－b 2＝3.因此a 2＝6，b 2＝3.所以M 的方程为x 26＋y 23＝1.(2)由⎩⎪⎨⎪⎧x ＋y －3＝0，x 26＋y 23＝1，解得⎩⎪⎨⎪⎧x ＝433，y ＝－33，或⎩⎨⎧x ＝0，y ＝ 3.因此|AB |＝463. 由题意可设直线CD 的方程为y ＝x ＋n ⎝ ⎛⎭⎪⎫－533＜n ＜3，设C (x 3，y 3)，D (x 4，y 4)．由⎩⎪⎨⎪⎧y ＝x ＋n ，x 26＋y23＝1，得3x 2＋4nx ＋2n 2－6＝0.于是x 3,4＝－2n ±29－n 23.因为直线CD 的斜率为1，所以|CD |＝2|x 4－x 3|＝439－n 2.由已知，四边形ACBD 的面积 S ＝12|CD |·|AB |＝869 9－n 2，当n ＝0时，S 取得最大值，最大值为863.所以四边形ACBD 面积的最大值为863.方法与技巧在利用代数法解决最值与范围问题时常从以下五个方面考虑： 1利用判别式来构造不等关系，从而确定参数的取值范围；2利用已知参数的范围，求新参数的范围，解这类问题的核心是在两个参数之间建立等量关系；3利用隐含或已知的不等关系建立不等式，从而求出参数的取值范围； 4利用基本不等式求出参数的取值范围；5利用函数的值域的求法，确定参数的取值范围.跟踪练习 (xx·玉溪模拟)已知定点A (1,0)和定直线x ＝－1上的两个动点E 、F ，满足AE →⊥AF →，动点P 满足EP →∥OA →，FO →∥OP →(其中O 为坐标原点)．(1)求动点P 的轨迹C 的方程；(2)过点B (0,2)的直线l 与(1)中轨迹C 相交于两个不同的点M 、N ，若AM →·AN →＜0，求直线l 的斜率的取值范围．【解】 (1)设P (x ，y )，E (－1，y 1)，F (－1，y 2)(y 1、y 2均不为0)，由EP →∥OA →得y 1＝y ，即E (－1，y )，由FO →∥OP →得y 2＝－y x，即F ⎝ ⎛⎭⎪⎫－1，－y x ，由AE →⊥AF →得AE →·AF →＝0⇒(－2，y 1)·(－2，y 2)＝0⇒y 1y 2＝－4⇒y 2＝4x (x ≠0)，∴动点P 的轨迹C 的方程为y 2＝4x (x ≠0)．(2)设直线l 的方程y ＝kx ＋2(k ≠0)，M ⎝ ⎛⎭⎪⎫y 214，y 1，N ⎝ ⎛⎭⎪⎫y 224，y 2，联立得⎩⎪⎨⎪⎧y ＝kx ＋2，y 2＝4x ，消去x 得ky 2－4y ＋8＝0，∴y 1＋y 2＝4k ，y 1y 2＝8k，且Δ＝16－32k ＞0即k ＜12.∴AM →·AN →＝⎝ ⎛⎭⎪⎫y 214－1，y 1·⎝ ⎛⎭⎪⎫y 224－1，y 2＝⎝ ⎛⎭⎪⎫y 214－1⎝ ⎛⎭⎪⎫y 224－1＋y 1y 2＝y 21y 2216－14(y 21＋y 22)＋y 1y 2＋1 ＝4k 2－14⎝ ⎛⎭⎪⎫16k 2－16k ＋8k ＋1＝k ＋12k.∵AM →·AN →＜0，∴－12＜k ＜0.考点三定值、定点问题例设M 、N 为抛物线C ：y ＝x 2上图8－8－1的两个动点，过M 、N 分别作抛物线C 的切线l 1、l 2，与x 轴分别交于A 、B 两点，且l 1与l 2相交于点P ，若|AB |＝1.(1)求点P 的轨迹方程；(2)求证：△MNP 的面积为一个定值，并求出这个定值．【思路点拨】 (1)设出M 、N 的坐标，再求出切线l 1，l 2的方程，然后求出交点P 的坐标，最后利用|AB |＝1可求得点P 的轨迹方程．(2)设出直线MN 的方程，再与抛物线方程联立，结合根与系数关系表示出弦长|MN |，再求出点P 到直线MN 的距离，证明△MNP 的面积为定值．【尝试解答】 (1)设M (m ，m 2)，N (n ，n 2)，则依题意知，切线l 1，l 2的方程分别为y ＝2mx －m 2，y ＝2nx －n 2，则A ⎝ ⎛⎭⎪⎫m2，0，B ⎝ ⎛⎭⎪⎫n2，0.设P (x ，y )，由⎩⎪⎨⎪⎧y ＝2mx －m 2，y ＝2nx －n 2，得⎩⎪⎨⎪⎧x ＝m ＋n 2，y ＝mn ，①因为|AB |＝1，所以|n －m |＝2，即(m ＋n )2－4mn ＝4，将①代入上式，得 y ＝x 2－1.∴点P 的轨迹方程为y ＝x 2－1.(2)证明设直线MN 的方程为y ＝kx ＋b (b ＞0)．联立方程⎩⎪⎨⎪⎧y ＝kx ＋b ，y ＝x 2，消去y ，得x 2－kx －b ＝0. 所以m ＋n ＝k ，mn ＝－b .② 点P 到直线MN 的距离d ＝|k ⎝ ⎛⎭⎪⎫m ＋n 2－mn ＋b |1＋k2，|MN |＝1＋k 2|m －n |，∴S △MNP ＝12d ·|MN |＝12|k ⎝ ⎛⎭⎪⎫m ＋n 2－mn ＋b |·|m －n | ＝14·(m －n )2·|m －n |＝2. 即△MNP 的面积为定值2.方法与技巧 1.求定值问题常见的方法有两种(1)从特殊入手，求出定值，再证明这个值与变量无关．(2)直接推理、计算，并在计算推理的过程中消去变量，从而得到定值． 2．定点的探索与证明问题(1)探索直线过定点时，可设出直线方程为y ＝kx ＋b ，然后利用条件建立b 、k 等量关系进行消元，借助于直线系的思想找出定点．(2)从特殊情况入手，先探求定点，再证明与变量无关．跟踪练习在平面直角坐标系xOy 中，直线l 与抛物线y 2＝4x 相交于不同的A 、B 两点．(1)如果直线l 过抛物线的焦点，求OA →·OB →的值；(2)如果OA →·OB →＝－4，证明直线l 必过一定点，并求出该定点．【解】 (1)由题意：抛物线焦点为(1,0)，设l ：x ＝ty ＋1，代入抛物线y 2＝4x ，消去x 得y 2－4ty －4＝0，设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝4t ，y 1y 2＝－4， ∴OA →·OB →＝x 1x 2＋y 1y 2＝(ty 1＋1)(ty 2＋1)＋y 1y 2＝t 2y 1y 2＋t (y 1＋y 2)＋1＋y 1y 2＝－4t 2＋4t 2＋1－4＝－3.(2)设l ：x ＝ty ＋b ，代入抛物线y 2＝4x ，消去x 得 y 2－4ty －4b ＝0.设点A (x 1，y 1)，B (x 2，y 2)．则y 1＋y 2＝4t ，y 1y 2＝－4b ， ∴OA →·OB →＝x 1x 2＋y 1y 2＝(ty 1＋b )(ty 2＋b )＋y 1y 2 ＝t 2y 1y 2＋bt (y 1＋y 2)＋b 2＋y 1y 2＝－4bt 2＋4bt 2＋b 2－4b ＝b 2－4b .令b 2－4b ＝－4，∴b 2－4b ＋4＝0，∴b ＝2， ∴直线l 过定点(2,0)．∴若OA →·OB →＝－4，则直线l 必过一定点(2,0).\ 31845 7C65 籥24786 60D2 惒40606 9E9E 麞34078 851E 蔞29528 7358 獘29082719A 熚S25148 623C 戼21660 549C 咜27827 6CB3 河Di。

2021版新高考数学一轮复习高考大题专项(五)直线与圆锥曲线新人教A版

2
........................ 优质文档..........................
5. (2019 浙江模拟,19)如图,不垂直于坐标轴的直线 l 与抛物线 y2=2px(p>0)有且只有一个公共点 M. (1)当 M 的坐标为(2,2)时,求 p 的值及直线 l 的方程; (2)若直线 l 与圆 x2+y2=1 相切于点 N,求|MN|的最小值.
+
2, 得
k1y2-4y-4k1+8=0,
由韦达定理知,2y1=8-k41k1,所以 y1=4-k21k1 = k41-2=4k2-2,同理可得 y2=4k1-2.
设线段 AB 的中点为 D,则点 D 的横坐标为 t,则 t=x1+x2 = y12+y22 = (4k2-2)2+(4k1-2)2
2
8
y2-1
设过点 G 的椭圆 C 的切线的斜率分别为 k1,k2,所以 k1k2=x02-3 . 0
因为两条切线相互垂直,所以x0y02-21-3=-1,即x02 + y02=4(x0≠± 3), 由①②知 G 在圆x2 + y2=4 上,又点 G 在直线 x+y+m=0 上,所以直线 x+y+m=0 与圆 x2+y2=4 有公共
圆锥曲线
突破 1 圆锥曲线中的
最值、范围问题
1.解(1)由题意,
c = 6,
a3
a2 = b2 +
解得 c2,
a2=3b2,又a12
+
32b2=1,解得
a2 b2
= =
3, 1,
所以椭圆 C 的标准方程为x2+y2=1.

专题50 直线与圆锥曲线的综合问题-备战2021年高考数学(理)一轮复习考点通

专题50 直线与圆锥曲线的综合问题典型例题剖析解析几何研究的问题是几何问题，研究的手法是代数法(坐标法)．因此，求解解析几何问题最大的思维难点是转化，即几何条件代数化．如何在解析几何问题中实现代数式的转化，找到常见问题的求解途径，即解析几何问题中的条件转化是如何实现的，是突破解析几何问题难点的关键所在．为此，从以下几个途径，结合数学思想在解析几何中的切入为视角，分析解析几何的“双管齐下”，突破思维难点．利用向量转化几何条件[典例] 如图所示，已知圆C ：x 2＋y 2－2x ＋4y －4＝0，问：是否存在斜率为1的直线l ，使l 与圆C 交于A ，B 两点，且以AB 为直径的圆过原点？若存在，写出直线l 的方程；若不存在，请说明理由．[解题观摩] 假设存在斜率为1的直线l ，使l 与圆C 交于A ，B 两点，且以AB 为直径的圆过原点．设直线l 的方程为y ＝x ＋b ，点A (x 1，y 1)，B (x 2，y 2)．联立22,2440.y x b x y x y =+⎧⎨+-+-=⎩ 消去y 并整理得2x 2＋2(b ＋1)x ＋b 2＋4b －4＝0，所以x 1＋x 2＝－(b ＋1)，x 1x 2＝2442b b +-.①因为以AB 为直径的圆过原点，所以OA ⊥OB ，即x 1x 2＋y 1y 2＝0.又y 1＝x 1＋b ，y 2＝x 2＋b ，则x 1x 2＋y 1y 2＝x 1x 2＋(x 1＋b )(x 2＋b )＝2x 1x 2＋b (x 1＋x 2)＋b 2＝0. 由①知，b 2＋4b －4－b (b ＋1)＋b 2＝0，即b 2＋3b －4＝0，解得b ＝－4或b ＝1. 当b ＝－4或b ＝1时，均有Δ＝4(b ＋1)2－8(b 2＋4b －4)＝－4b 2－24b ＋36＞0，即直线l 与圆C 有两个交点．所以存在直线l ，其方程为x －y ＋1＝0或x －y －4＝0. [关键点拨]以AB 为直径的圆过原点等价于OA ⊥OB ，而OA ⊥OB 又可以“直译”为x 1x 2＋y 1y 2＝0，可以看出，解此类解析几何问题的总体思路为“直译”，然后对个别难以“直译”的条件先进行“转化”，将“困难、难翻译”的条件通过平面几何知识“转化”为“简单、易翻译”的条件后再进行“直译”，最后联立“直译”的结果解决问题．[典例] (1)求动圆圆心的轨迹C 的方程；(2)已知点B (－1,0)，设不垂直于x 轴的直线l 与轨迹C 交于不同的两点P ，Q ，若x 轴是∠PB Q 的角平分线，求证：直线l 过定点．[解题观摩] (1)设动圆圆心为点P (x ，y )，则由勾股定理得x 2＋42＝(x －4)2＋y 2，化简即得圆心的轨迹C 的方程为y 2＝8x .(2)证明：法一：由题意可设直线l 的方程为y ＝kx ＋b (k ≠0)．联立2,8,y kx b y x =+⎧⎨=⎩得k 2x 2＋2(kb －4)x ＋b 2＝0.由Δ＝4(kb －4)2－4k 2b 2＞0，得kb ＜2. 设点P (x 1，y 1)，Q(x 2，y 2)，则x 1＋x 2＝－22(4)kb k-，x 1x 2＝22b k . 因为x 轴是∠PB Q 的角平分线，所以k PB ＋k Q B ＝0，即k PB ＋k Q B ＝111y x +＋221y x +＝12121222(1)(1)kx x k b x x b x x +++++++＝2128()(1)(1)k b x x k +++＝0，所以k ＋b ＝0，即b ＝－k ，所以l 的方程为y ＝k (x －1)．故直线l 恒过定点(1,0)．法二：设直线PB 的方程为x ＝my －1，它与抛物线C 的另一个交点为Q′，设点P (x 1，y 1)，Q′(x 2，y 2)，由条件可得，Q 与Q′关于x 轴对称，故Q(x 2，－y 2)．联立21,8x my y x=-⎧⎨=⎩消去x 得y 2－8my ＋8＝0，其中Δ＝64m 2－32＞0，y 1＋y 2＝8m ，y 1y 2＝8. 所以k P Q ＝1212128y y x x y y +=--，因而直线P Q 的方程为y －y 1＝128y y -(x －x 1)．又y 1y 2＝8，21y ＝8x 1，将P Q 的方程化简得(y 1－y 2)y ＝8(x －1)，故直线l 过定点(1,0)．法三：由抛物线的对称性可知，如果定点存在，则它一定在x 轴上，所以设定点坐标为(a,0)，直线P Q 的方程为x ＝my ＋a . 联立2,8x my a y x=+⎧⎨=⎩消去x ，整理得y 2－8my －8a ＝0，Δ＞0.设点P (x 1，y 1)，Q(x 2，y 2)，则12128.8y y m y y a +=⎧⎨=-⎩由条件可知k PB ＋k Q B ＝0，即k PB ＋k Q B ＝111y x +＋221y x + ＝1212122(1)()(1)(1)my y a y y x x +++++＝0，所以－8ma ＋8m ＝0.由m 的任意性可知a ＝1，所以直线l 恒过定点(1,0)．法四：设P 211,8y y ⎛⎫ ⎪⎝⎭，Q 222,8y y ⎛⎫⎪⎝⎭，因为x 轴是∠PB Q 的角平分线，所以k PB ＋k Q B ＝12221201188y y y y +=++，整理得(y 1＋y 2)1288y y ⎛⎫+⎪⎝⎭＝0. 因为直线l 不垂直于x 轴，所以y 1＋y 2≠0，可得y 1y 2＝－8. 因为k P Q ＝12221288y y y y --＝128y y +，所以直线P Q 的方程为y －y 1＝128y y +218y x ⎛⎫- ⎪⎝⎭，即y ＝128(1)x y y -+．故直线l 恒过定点(1,0)． [关键点拨]本题前面的三种解法属于比较常规的解法，主要是设点，设直线方程，联立方程，并借助判别式、根与系数的关系等知识解题，计算量较大．解法四巧妙地运用了抛物线的参数方程进行设点，避免了联立方程组，计算相对简单，但是解法二和解法四中含有两个参数y 1，y 2，因此判定直线过定点时，要注意将直线的方程变为特殊的形式．弦长条件的转化[典例] 如图所示，已知椭圆G ：2x ＋y 2＝1，与x 轴不重合的直线l 经过左焦点F 1，且与椭圆G 相交于A ，B 两点，弦AB 的中点为M ，直线OM 与椭圆G 相交于C ，D 两点．(1)若直线l 的斜率为1，求直线OM 的斜率．(2)是否存在直线l ，使得|AM |2＝|CM ||DM |成立？若存在，求出直线l 的方程；若不存在，请说明理由．[解题观摩] (1)由题意可知点F 1(－1,0)，又直线l 的斜率为1，故直线l 的方程为y ＝x ＋1. 设点A (x 1，y 1)，B (x 2，y 2)，由221,1,2y x x y =+⎧⎪⎨+=⎪⎩消去y 并整理得3x 2＋4x ＝0，则x 1＋x 2＝－43，y 1＋y 2＝23，因此中点M 的坐标为2133⎛⎫- ⎪⎝⎭，.故直线OM 的斜率为1323-＝－12.(2)假设存在直线l ，使得|AM |2＝|CM ||DM |成立．由题意，直线l 不与x 轴重合，设直线l 的方程为x ＝my －1.由221,1.2x my x y =-⎧⎪⎨+=⎪⎩消去x 并整理得(m 2＋2)y 2－2my －1＝0.设点A (x 1，y 1)，B (x 2，y 2)，则1221222,212m y y m y y m ⎧+=⎪⎪+⎨⎪=-⎪+⎩可得|AB ||y 1－y 2|221)2m m ++， x 1＋x 2＝m (y 1＋y 2)－2＝2222m m +－2＝242m -+，所以弦AB 的中点M 的坐标为22222m m m -⎛⎫ ⎪++⎝⎭，，故直线CD 的方程为y ＝－2m x . 联立222 1.2m y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩消去y 并整理得2x 2＋m 2x 2－4＝0，解得x 2＝242m +.由对称性，设C (x 0，y 0)，D (－x 0，－y 0)，则20x ＝242m +，可得|CD |0|2|x=因为|AM |2＝|CM ||DM |＝(|OC |－|OM |)(|OD |＋|OM |)，且|OC |＝|OD |，所以|AM |2＝|OC |2－|OM |2，故22||||44AB CD =－|OM |2，即|AB |2＝|CD |2－4|OM |2，则()222222222228(1)4(4)44(2)2(2)2m m m m m m m ⎡⎤++⎢⎥=--+⎢⎥++++⎣⎦，解得m 2＝2，故m ＝.所以直线l 的方程为xy ＋1＝0或xy ＋1＝0. [关键点拨]本题(2)的核心在于转化|AM |2＝|CM |·|DM |中弦长的关系．由|CM |＝|OC |－|OM |，|DM |＝|OD |＋|OM |，又|OC |＝|OD |，得|AM |2＝|OC |2－|OM |2.又|AM |＝12|AB |，|OC |＝12|CD |，因此|AB |2＝|CD |2－4|OM |2，转化为弦长|AB |，|CD |和|OM |三者之间的数量关系，易计算．面积条件的转化[典例] 设椭圆的中心在坐标原点，A (2,0)，B (0,1)是它的两个顶点，直线y ＝kx (k ＞0)与椭圆交于E ，F 两点，求四边形AEBF 的面积的最大值．[解题观摩] 法一：如图所示，依题意得椭圆的方程为214x ＋y 2＝1，直线AB ，EF 的方程分别为x ＋2y ＝2，y ＝kx (k ＞0)．设点E (x 1，kx 1)，F (x 2，kx 2)，其中x 1＜x 2，且x 1，x 2满足方程(1＋4k 2)x 2＝4，故x 2＝－x 1＝214k+ .①根据点到直线的距离公式和①，得点E ，F 到直线AB 的距离分别为h 1＝21122(1214)55(14)k k k +++=+，h 2＝22222(1214)55(14)k k k +-+=+.又|AB |＝2221=5+，所以四边形AEBF 的面积为S ＝12|AB |·(h 1＋h 2)＝12·5·222(12)145(14)k k k +=++＝22214414k kk +++＝224114k k ++＝24114k k++≤22，当且仅当1k ＝4k ，即k ＝12时取等号．因此四边形AEBF 的面积的最大值为22.法二：依题意得椭圆的方程为24x ＋y 2＝1.直线EF 的方程为y ＝kx (k ＞0)．设点E (x 1，kx 1)，F (x 2，kx 2)，其中x 1＜x 2.联立22, 1.4y kx x y =⎧⎪⎨+=⎪⎩消去y ，得(1＋4k 2)x 2＝4.故x 1，x 2，|EF |＝x 1－x 2|＝.根据点到直线的距离公式，得点A ，B 到直线EF 的距离分别为d 1，d 2＝.因此四边形AEBF 的面积为S ＝12|EF |·(d 1＋d 2)＝12＝，当且仅当1k ＝4k ，即k ＝12时取等号．因此四边形AEBF 的面积的最大值为. [关键点拨]如果利用常规方法理解为S四边形AEBF＝S △AEF ＋S △BEF ＝12|EF |·(d 1＋d 2)(其中d 1，d 2分别表示点A ，B 到直线EF 的距离)，则需要通过联立直线与椭圆的方程，先由根与系数的关系求出EF 的弦长，再表示出两个点线距，其过程很复杂．而通过分析，若把四边形AEBF 的面积拆成两个小三角形——△ABE 和△ABF 的面积之和，则更为简单．因为直线AB 的方程及其长度易求出，故只需表示出点E 与点F 到直线AB 的距离即可．[总结规律·快速转化]做数学，就是要学会翻译，把文字语言、符号语言、图形语言、表格语言相互转换，我们要学会对解析几何问题中涉及的所有对象逐个理解、表示、整理，在理解题意的同时，牢记解析几何的核心方法是“用代数方法研究几何问题”，核心思想是“数形结合”，牢固树立“转化”意识，那么就能顺利破解解析几何的有关问题．附几种几何条件的转化，以供参考1．平行四边形条件的转化长度相等，横(纵)坐标差相等2．直角三角形条件的转化几何性质代数实现3．等腰三角形条件的转化4．菱形条件的转化5．圆条件的转化6．角条件的转化达标检测要扎实一、解答题1．顺次连接椭圆2222:1(0)x y C a b a b+=>>的菱形，该菱形对角线长度之比为2（1）求椭圆C 的标准方程；（2）设椭圆C 的右焦点为F ，定点()4,0M ，过点F 的直线l 与椭圆C 交于两点A ，B ，设直线,AM BM 的斜率分别为12,k k ，求证：12k k +为定值.【答案】（1）22143x y +=；（2）证明见解析. 【解析】（1）依题意227a b a b ⎧+=⎪⎨=⎪⎩，解得224,3a b ==，所以椭圆C 的标准方程为22143x y +=.（2）当直线l 的斜率不存在时，直线AM ，BM 的倾斜角互补，所以120k k +=. 当直线l 的斜率存在时，设其方程为(1)y k x =-，代入椭圆C 的方程，整理得()22223484120kxk x k +-+-=，设()()1122,,,A x y B x y ，则221212228412,3434k k x x x x k k-+==++， ()()()()122112121221444444y x y x y yk k x x x x -+-+=+=----， ()()()()()()122121141444k x x x x x x --+--⎡⎤⎣⎦=--，因为()()()()()122112121414258x x x x x x x x --+--=-++，()2222223224412825880343434k k k k k k-+-=⨯-⨯+=+=+++，所以120k k +=.2．如下图，设抛物线方程为()220x py p =>，M 为直线2y p =-上任意一点，过M 引抛物线的切线，切点分别为A ，B ．（Ⅰ）设线段AB 的中点为N ；（ⅰ）求证：MN 平行于y 轴；（ⅱ）已知当M 点的坐标为()22p -，时，AB = （Ⅱ）是否存在点M ，使得点C 关于直线AB 的对称点D 在抛物线()220x py p =>上，其中，点C 满足OC OA OB =+（O 为坐标原点）．若存在，求出所有适合题意的点M 的坐标；若不存在，请说明理由．【答案】（Ⅰ）（ⅰ）证明见解析；（ⅱ）22x y =或24x y =；（Ⅱ）仅存在一点()0,2M p -适合题意.【解析】（Ⅰ）（ⅰ）证明：由题意设211,2x A x p ⎛⎫ ⎪⎝⎭，222,2x B x p ⎛⎫ ⎪⎝⎭，12x x <，()33,N x y ，()0,2M x p -．由22x py =得22x y p=，则x y p '=，所以1MA x k p =，2MB x k p =．因此直线MA 的方程为()102x y p x x p+=-，直线MB 的方程为()202x y p x x p+=-．所以()2111022x x p x x p p +=-，①()2222022x x p x x p p+=-．② 由①、②得121202x x x x x +=+-，因此1202x x x +=，即012322x x x x =+=，也即03x x =.所以MN平行于y 轴．（ⅱ）解：由（ⅰ）知，当02x =时，将其代入①、②并整理得：2211440x x p --=，2222440x x p --=，所以1x ，2x 是方程22440x x p --=的两根，因此124x x +=，2124x x p =-，又222101221222ABk x x x x x p p x x p p-+===-，所以2AB k p=．由弦长公式的AB ==又AB =，所以1p =或2p =，因此所求抛物线方程为22x y =或24x y =．（Ⅱ）解：设()44,D x y ，由题意得()1212,C x x y y ++，则CD 的中点坐标为124124,22x x x y y y Q ++++⎛⎫⎪⎝⎭，设直线AB 的方程为()011x y y x x p-=-，由点Q 在直线AB 上，并注意到点1212,22x x y y ++⎛⎫⎪⎝⎭也在直线AB 上，代入得044x y x p=．若()44,D x y 在抛物线上，则2440422x py x x ==，因此40x =或402x x =．即()0,0D 或2022,x D x p ⎛⎫ ⎪⎝⎭．（1）当00x =时，则12020x x x +==，此时，点()0,2M p -适合题意．（2）当00x ≠，对于()0,0D ，此时221202,2x x C x p ⎛⎫+ ⎪⎝⎭，2212221200224CDx x x x pk x px ++==，又0ABx k p =，AB CD ⊥，所以22220121220144AB CD x x x x x k k p px p++⋅=⋅==-，即222124x x p +=-，矛盾．对于20022,x D x p ⎛⎫ ⎪⎝⎭，因为221202,2x x C x p ⎛⎫+ ⎪⎝⎭，此时直线CD 平行于y 轴，又00AB x k p=≠，所以直线AB 与直线CD 不垂直，与题设矛盾，所以00x ≠时，不存在符合题意得M 点．综上所述，仅存在一点()0,2M p -适合题意．3．已知椭圆C ：22221x y a b+=（0a b >>）的左、右焦点分别为1F ，2F ，短轴长为A ，B是C 上关于x 轴对称的两点，1ABF 周长的最大值为8. （1）求C 的标准方程.（2）过C 上的动点M 作C 的切线l ，过原点O 作OP l ⊥于点P .问：是否存在直线l ，使得OMP 的面积为1？若存在，求出此时直线l 的方程；若不存在，请说明理由.【答案】（1）22143x y +=；（2）不存在，理由见解析. 【解析】（1）设AB 与x 轴的交点为H ，由题意可知2AH AF ≤，则112||2AF AH AF AF a +≤+=，当AB 过右焦点2F 时，1ABF 的周长取最大值48a =，所以2a =，且b =所以椭圆C 的方程为22143x y +=.（2）不存在直线l ，使得OMP 的面积为1.理由如下.显然直线l 斜率存在且不为0，设直线l ：y kx t =+，联立方程组223412y kx tx y =+⎧⎨+=⎩ 得()2223484120kxktx t +++-=，由()()2222644344120k t k t∆=-+-=，得2243t k =+，所以()284234M kt kx t k -==-+，因为直线OP l ⊥，所以直线OP 的方程为1=-y x k，由1y x k y kx t⎧=-⎪⎨⎪=+⎩，得21P kt x k =-+，所以()322244411k kt k k kt t k t k MP --+=-+==++又OP =，所以21111111222124OMPk S MP OP k k k=⋅==⋅=⋅≤++△，当且仅当1k =±时成立.因此不存在直线l ，使得OMP 的面积为1.4．在平面直角坐标系xOy 中，已知椭圆()2222:10x y C a b a b+=>>，其短轴长为2，右焦点为)，动点M 在椭圆C 上，点T 满足2MT MO =-，设点T 的轨迹为曲线C '. （1）求椭圆C 的方程和曲线C '的方程；（2）过点M 的直线()0y kx m m =+≠交C '于,P Q ，求PQT △面积的最大值.【答案】（1）椭圆C 的方程为：2214x y +=；曲线C '的方程为221369x y +=；（2）18. 【解析】（1）由题知：1b =，c =2222214a b c =+=+=，所以椭圆C 的方程为：2214x y +=.设00(,)M x y ，(),T x y ，因为2MT MO =-，所以000022x x x y y y -=⎧⎨-=⎩，所以0033x x y y ⎧=⎪⎪⎨⎪=⎪⎩. 又因为动点M 在椭圆C 上，所以220014x y +=，所以223143x y ⎛⎫⎪⎛⎫⎝⎭+= ⎪⎝⎭，化简得：221369x y +=，所以曲线C '的方程为221369x y +=.（2）因为点00(,)M x y 的过直线()0y kx m m =+≠，所以()000y kx m m =+≠. 设()()1122,,,P x y Q x y ，由()2201369y kx m m x y ⎧=+≠⎪⎨+=⎪⎩消去y ，并整理得：()2221484360k x kmx m +++-=.因为直线()0y kx m m =+≠交C '于,P Q ，所以>0∆，所以()()()22284144360km km-⋅+⋅->，化简得：229(14)k m +>，所以220914m k<<+. 所以21212228436,1414km m x x x x k k-+=-⋅=++. 由（1）知：00(,)M x y 时，()003,3T x y .PQ ===4=点()003,3T x y 到直线()0y kx m m =+≠的距离：d ===所以1122PQTSPQ d =⋅⋅=⋅422m =⋅4=4=设2214m t k=+，则09t <<，则PQTS===所以当92t =时，max944182PQT S ==⨯=. 所以PQT △的面积最大值为18.5．如图，已知椭圆2222:1x y C ab+=经过()2,0和(，过原点的一条直线l 交椭圆于A ，B 两点（A 在第一象限），椭圆C 上点D 满足AD AB ⊥，连直线BD 与x 轴、y 轴分别交于M 、N 两点，ABD △的重心在直线1321x =的左侧.（1）求椭圆的标准方程；（2）记AOM 、OMN 面积分别为1S 、2S ，求12S S -的取值范围.【答案】（1）22142x y +=；（2）0,8⎛⎫ ⎪ ⎪⎝⎭. 【解析】（1）椭圆2222:1x y C a b+=经过()2,0和(，∴224121a b ⎧=⎪⎪⎨⎪=⎪⎩，解得2242a b ⎧=⎨=⎩，∴椭圆的标准方程为22142x y +=；（2）设()11,A x y ，()11,B x y --，()22,D x y ，()0,0M x ，由22112222142142x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩作差得22221212042x x y y --+=即()()()()1212121212y y y y x x x x +-+=--，记AD 的中点为E ，则1212OE y y k x x ++=，由//OE BD 可得OE BD k k =，∴()()()()1212121212AD BD AD OE y y y y k k k k x x x x ⋅=⋅+-==-+-，又AD AB ⊥，∴1AD AB k k =-⋅，∴22AB BD BM k k k ==即11101222y y x x x =⋅+， ∴01x x =，AM ⊥x 轴，N 为BM 的中点，∴点()1,0M x ，直线()111:2y BM y x x x =-，则()111222142y y x x x x y ⎧=-⎪⎪⎨⎪+=⎪⎩，消去y 得222111211240212y y y x x x x -⎛⎫+ ⎭⋅⎝+-=⎪，>0∆， ∴21121212112y x x x y x -+=，结合2211142x y +=可得3112214123x x x x ++=，又ABD △的重心在直线1321x =的左侧，∴223131x <即311211341237x x x ++<，化简得()()21111732520x x x --+<，∴101x <<，11,22AOM BOM ONM BON AOM BOM S S S S S S ====△△△△△△，∴1111211112224AOM ONMAOM S S S S x y x S -==⋅⋅===-△△△⎛=⎝⎭， ∴12SS -的取值范围为0,8⎛⎫ ⎪ ⎪⎝⎭.6．如图，已知椭圆2222:1(0)x y a b a b Γ+=>>经过不同的三点13((,),2424A B C --(C 在第三象限），线段BC 的中点在直线OA 上．（Ⅰ）求椭圆Γ的方程及点C 的坐标；（Ⅱ）设点P 是椭圆Γ上的动点（异于点,,)A B C 且直线,PB PC 分别交直线OA 于,M N 两点，问||||OM ON ⋅是否为定值？若是，求出定值；若不是，请说明理由．【答案】（1）31(,).24--；（2）2516．【解析】（Ⅰ）由点,A B 在椭圆Γ上，得2222551,416{191416a b a b+=+=解得225,2{5.8a b ==所以椭圆Γ的方程为221.5528x y +=………………………3分由已知，求得直线OA 的方程为20,x y -=从而2 1.m n =-（1）又点C 在椭圆Γ上，故2228 5.m n +=（2）由（1）（2）解得34n =（舍去）或1.4n =-从而3,2m =-所以点C 的坐标为31(,).24--………………………………………6分（Ⅱ）设001122(,),(2,),(2,).P x y M y y N y y因,,P B M 三点共线，故10103344,11222y y y x ++=++整理得0010032.4(21)x y y y x -=-+ 因,,P C N 三点共线，故20201144,33222y y y x ++=++整理得002006.4(21)x y y y x -=--……………10分因点P 在椭圆Γ上，故2200285x y +=，即220054.2x y =-从而220000000012222000000(32)(6)3201216[(2)1]16(441)x y x y x x y y y y y x y x x y ---+==--+-- 220000000000533(4)20125(4)522.531616(41)16(4)22y x y y x y x y x y --+-===---所以121225||||||5||16OM ON y y y y ⋅===为定值． ………………………15分 7．已知纵坐标分别为M ，N 是抛物线2:2(0)C y px p =>上的两点，且点M ，N到直线2px =的距离相等. （1）求抛物线C 的方程；（2）若直线l 与抛物线C 交于点A ，B ，与抛物线C 的准线交于点D ，BO (点O 为坐标原点)的延长线与准线交于点E ，且2DA DE DE ⋅=，求证：直线AB 过定点P ，并求出定点P 的坐标. 【答案】（1）28y x =；（2）证明见解析，()2,0.【解析】（1）因为点M ，N 在抛物线C上，且纵坐标分别为所以点M ，N 的横坐标分别为824,22p p因为点M ，N 到直线2px =的距离相等，所以8242222p p p +=⨯，解得4p =，所以抛物线C 的方程为28y x =. （2）设直线AB 的方程为x my n =+，与28y x =联立得2880y my n --=，设221212,,,88y y A y B y ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭，则128y y n =-，由2DA DE DE ⋅=得()0DA DE DE -⋅=，即0AE DE ⋅=，所以AE DE ⊥，抛物线准线方程是2x =-，故()12,E y -，由B ，O ，E 三点共线得212228y y y =-，即816,2n n -=-=，直线AB 的方程为2x my =+ 所以直线AB 过定点()2,0，点P 的坐标为()2,0.8．如图，已知抛物线2:4E x y =上不同的两点()11,A x y ，()22,B x y ，关于直线:5l y kx =+对称，记l 与y 轴交于点C ．（1）若124x x +=-，求k 的值；（2）求ABC 面积的最大值．【答案】（1）1k =；（2. 【解析】（1）由题意，可设直线AB 的方程为1y x b k=-+，联立方程组214y x b kx y⎧=-+⎪⎨⎪=⎩，得2440x x b k +-=，故1244x x k+=-=-，所以1k =；（2）由（1）知，124x x k+=-，124x x b =- 1212214()22y y x x b b k k+=-++=+，则线段AB 的中点坐标为222,b k k ⎛⎫-+ ⎪⎝⎭，所以2225b k k k ⎛⎫+=-+ ⎪⎝⎭，即223b k =-亦即直线AB 的方程为2123y x k k=-+-， 124x x k +=-，122812x x k=-，，所以点C 到AB 的距离为d =||AB ===故ABC 面积2141S k ⎛=+⎝t =，则24(4)S t t =-，令3()416(0f t t t t =-+<<，则()21216f t t =+'-，易知()f t 在⎛ ⎝上递增，在递减，故max ()9f t f ==，即当235k =时，ABC 面积有最大值9． 9．如图，定义：以椭圆中心为圆心，长轴为直径的圆叫做椭圆的“辅助圆”．过椭圆第四象限内一点M 作x 轴的垂线交其“辅助圆”于点N ，当点N 在点M 的下方时，称点N 为点M 的“下辅助点”．已知椭圆2222:1(0)x y E a b a b +=>>上的点(1,2-的下辅助点为(1,1)-．（1）求椭圆E 的方程；（2）若OMN的面积等于8，求下辅助点N 的坐标．【答案】（1）2212x y +=；（2）(2，或．【解析】（1）椭圆2222:1(0)x y E a b a b +=>>上的点(1,2-的下辅助点为(1,1)-，∴辅助圆的半径为R ==a R ==将点(1,)2-代入椭圆方程22212x y b +=中，解得1b =，∴椭圆E 的方程为2212x y +=；（2）设点0(N x ，00)(1)y y <，则点0(M x ，11)(0)y y <，将两点坐标分别代入辅助圆方程和椭圆方程可得，2202x y +=，220112x y +=，故22012y y =，即01y =，又()01012OMNSx y y =-=，则01x y =，将014x y =-与220112x y +=，01y =联立可解得002x y ⎧=⎪⎪⎨⎪=⎪⎩或002x y ⎧=⎪⎪⎨⎪=-⎪⎩， ∴下辅助点N的坐标为，或，；10．已知椭圆()2222:10x y C a b a b+=>>的离心率为12，P 为椭圆C 上异于长轴端点的任意一点，12PF F △（1）求椭圆C 的标准方程；（2）已知A 为椭圆C 的右顶点，过左焦点F 的动直线交椭圆于B ，D 两点（异于点A ），直线AB ，AD 与定直线():0l x t t =≠的交点分别为M ，N ，若以MN 为直径的圆经过点F ，求直线l 的方程．【答案】（1）22143x y +=；（2）直线l 的方程为4x =-．【解析】（1）由离心率12e =得，2a c =，① 因为当点P 为短轴端点时，12PF F △面积最大，122c b bc ⨯⨯==，② 在椭圆中222a b c =+，③由①②③解得，24a =，23b =，所以椭圆的标准方程为22143x y +=．（2）由（1）知，()1,0F -，()2,0A ，设直线BD 的方程为1x my =-，联立221,431,x y x my ⎧+=⎪⎨⎪=-⎩消x 得()2234690m y my +--=，设()11,B x y ，()22,D x y ，则()()()222643491441440m m m ∆=--⨯+⨯-=+>，122634m y y m +=+，122934y y m -=+．设()1,M t n ，()2,N t n ，由A ，B ，M 三点共线得，11122y nx t =--，∴()11122t y n x -=-，同理得()22222t y n x -=-，因为以MN 为直径的圆经过点F ，所以NF MF ⊥，于是0NF MF ⋅=，由()21,NF t n =---，()11,MF t n =---，()21210t n n ∴++=．将()11122t y n x -=-，()22222t y n x -=-，代入上式，得()()()()22121221022y y t t x x -⋅++=--，∵111x my =-，221x my =-， ∴()()()()22121221033y y t t my my -⋅++=--，③将122634m y y m +=+，122934y y m -=+，代入③得()()222104t t --++=，解得4t =-，或0t =（舍去）．故直线l 的方程为4x =-．11．抛物线()2:20C y px p =>，抛物线上一点()2,P t 到抛物线焦点F 的距离为3.（1）求抛物线C 的方程；（2）若点Q 为抛物线C 上的动点，求点Q 到直线2y x =+距离的最小值以及取得最小值时点Q 的坐标；（3）若直线l 过点()4,0M 且与抛物线C 交于A ，B 两点，当ABF 与AOF 的面积之和取得最小值时，求直线l 的方程. 【答案】（1）24y x =；（2）2，()1,2Q ；（3）)4y x =±-.【解析】（1）由题意可得，抛物线的准线1:2pl x =-，由于3PF =，则12p=，即2p =，即抛物线C 的方程为：24y x =.（2）设平行于直线2y x =+且与抛物线相切的直线为y x b =+，则()()222242404y x b x b x x b x b y x=+⎧⇒+=⇒+-+=⎨=⎩，又()2224401b b b ∆=--=⇒=，则直线 2y x =+与直线 1y x =+的距离2d ==，此时点Q 的坐标为()1,2.（3）当直线l 的斜率不存在时，方程为：4x =，易得14ABF AOF S S +=△△；当直线l 的斜率存在时，设方程为()4y k x =-，设()()1122,,,A x y B x y ，由()244y k x y x⎧=-⎨=⎩消去x 并整理得：24160ky y k --=， 1212416y y k y y ⎧+=⎪∴⎨⎪=-⎩ ，则121143222ABFAOFAOMBFMSSSSy y +=+=⨯⨯+⨯⨯≥= 当且仅当1243y y =时取等号，又1216y y =，所以12y y ==或12y y ==-所以124y y k +==，解得：k =± 8314≤，所以当ABF 与AOF 的面积之和取得最小值时，直线l 的方程为)4y x =±-.12．如图所示，在直角坐标系xOy 中，A ，B 是抛物线21:2(0)C y pm p =>上两点，M ，N 是椭圆222:163x y C +=两点，若AB 与MN 相交于点()2,0E ，2OA OB p ⋅=-.（1）求实数p 的值及抛物线C 的准线方程.（2）设OMN 的面积为S ，OMN 、OAB 的重心分别为G ，T ，当GT 平行于x 轴时，求2||GT S +的最大值.【答案】（1）2，10x +=；（2）13126. 【解析】（1）设1122(,),(,)A x y B x y ，:2AB x ty =+与22y px =联立得2240y pty p --=，12122,4y y pt y y p +==-，2212121212()(2)42y y OA OB x x y y y y p p⋅=+=+=--，所以22(2)40p p --+=，解得2p =.抛物线C 的准线方程为10x +=；（2）设3344(,),(,)M x y N x y ，:2MN x my =+与22163x y +=联立得22(2)420m y my ++-=，34342242,22m y y y y m m +=-=-++，由GT 平行于x 轴可知3412y y y y +=+，由（1）知2p =，所以124y y t +=，代入得2442m t m =-+即22mt m =-+，所以12341|||()()|3GT x x x x =+-+ 12341|()()|3t y y m y y =+-+ 222242214|4()|()33m m m m t t m t =⋅-=+-++ 22224[()3]22m m m m +++=. 又22234341(||||)()2S OE y y y y =⋅-=-23434()4y y y y =+-222328(2)m m +=⋅+，于是22222222432||[()83(2)]22m m m m m GT S m +++=⋅++++42222142(2)31m m m +++=⋅，令22,2m u u +=>，得22241726||3u u GT S u+-+=⋅ 24117393[26()]352104u =⋅--+ 4393131310426≤⋅=当且仅当252217m u +==，即m =2||GT S +有最大值13126. 13．已知椭圆22221(0)x y a b a b +=>>的离心率为2．点在椭圆C 上．（1）求椭圆C 的标准方程；（2）过点(0,2)P -任作椭圆C 的两条相互垂直的弦AB 、CD ，设M 、N 分别是AB 、CD 的中点，则直线MN 是否过定点？若过，求出该定点坐标；若不过，请说明理由．【答案】（1）221123x y +=；（2）直线MN 过定点2(0,)5-．【解析】（1）由已知得22222421c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩，解得212a =，23b =，所以椭圆C 的方程为221123x y +=；（2）由题意知直线AB ，CD 的斜率存在且不为0，设直线AB 的方程为：11222(0),(,),(,)y kx k A x y B x y =-≠，由2221123y kx x y =-⎧⎪⎨+=⎪⎩得22(14)1640k x kx +-+=，由2221(16)44(14)012k k k ∆=--⨯⋅+>⇒>，且1221614kx x k +=+，所以1228214Mx x k x k +==+，22214M M y kx k=-=-+，即28(14k M k +，22)14k -+，同理28(4k N k -+，222)4k k -+，所以222222221144885144MNk k k k k k k k k k -+-++==+++，所以直线MN 的方程为222218()14514k ky x k k k -+=-++，由对称性可知定点必在y 轴上，令0x =，得2221822(0)514145k k y k k k -=--=-++，所以直线MN 过定点2(0,)5-． 14．已知221:(1)4M x y -+=，直线1:2l x =-，动圆N 与M 相外切，且与直线l 相切.设动圆圆心N 的轨迹为C ，过点(0,1)Q 的直线l 与曲线C 有两个不同的交点A 、B . （1）求直线l 的斜率的取值范围；（2）设O 为原点，点(1,2)P ，直线PA 交y 轴于M ，直线PB 交y 轴于N ，QM QO λ=，QN QO μ=，求证：11λμ+为定值.【答案】（1）(,0)(0,1)-∞；（2）证明见解析.【解析】（1）由题意设(,)N x y ，且12x >-，由题意可得1122x +=，整理可得：24y x =；所以曲线C 的方程为：24y x =；由题意可得直线AB 的斜率存在且不为0，设直线AB 的方程为：1y kx =+，设1(A x ，1)y ，2(B x ，2)y 联立直线与抛物线的方程：214y kx y x=+⎧⎨=⎩，整理可得：222(2)10k x k x +-+=，可得∆224(2)40k k =-->，解得1k <，且0k ≠，所以直线l 的斜率的取值范围(-∞，0)(0⋃，1). （2）证明：由（1）可得：1222(2)k x x k -+=-，1221x x k =，直线PA 的方程为：1122(1)1y y x x --=--，令0x =可得1111212211y kx y x x -+-+=+=+--，可得111(0,2)1kx M x -++-，同理可得N 的坐标22121N kx y x -+=+-，由QM QO λ=，QN QO μ=，可得1N y μ=-，1M y λ=-，所以()()()2212121212122224211111111··21111111M N k x x x x x x k k y y k x k x k x x k k λμ-+-+--+=+=+===------，所以11λμ+为定值2.【点睛】本题考查求轨迹方程，及直线与抛物线的综合，和直线与圆的位置关系，属于中档题.15．已知椭圆C ：()222210x y a b a b+=>>过点31,2⎛⎫ ⎪⎝⎭，过坐标原点O 作两条互相垂直的射线与椭圆C 分别交于M ，N 两点.（1）证明：当229a b +取得最小值时，椭圆C的离心率为2. （2）若椭圆C 的焦距为2，是否存在定圆与直线MN 总相切？若存在，求定圆的方程；若不存在，请说明理由.【答案】（1）证明见解析；（2）存在，22127x y += 【解析】（1）证明：∵椭圆C 经过点31,2⎛⎫ ⎪⎝⎭，∴221914a b +=， ∴()222222222219859999444b a a b a b a b a b ⎛⎫+=++=++ ⎪⎝⎭8512144≥+=，当且仅当2222994b a a b=，即222a b =时，等号成立，此时椭圆C的离心率2e ==. （2）解：∵椭圆C 的焦距为2，∴221a b -=，又221914a b+=，∴24a =，23b =. 当直线MN 的斜率不存在时，由对称性，设()00,M x x ，()00,N x x -.∵M ，N 在椭圆C 上，∴2200143x x +=，∴20127x =，∴O 到直线MN的距离07d x ===. 当直线MN 的斜率存在时，设MN 的方程为y kx m =+. 由22143y kx m x y =+⎧⎪⎨+=⎪⎩，得()2223484120k x kmx m +++-=， ()()()22284344120km k m ∆=-+->. 设()11,M x y ，()22,N x y ，则122834km x x k +=-+，212241234m x x k-=+. ∵OM ON ⊥，∴12120x x y y +=，∴()()1212x x kx m kx m +++()()22121210k x x km x x m =++++=，∴()22222224128103434m k m k m k k -+⋅-+=++，即()227121m k =+， ∴O 到直线MN的距离7d ===. 综上，O 到直线MN的距离为定值，且定值为7，故存在定圆O ：22127x y +=，使得圆O 与直线MN 总相切.16．如图，已知椭圆的左、右焦点分别为12(c,0),F (c,0)(c 0)F ->，短轴的两个端点为1B ，2112,B F B B △是边长为2的等边三角形.（1）求椭圆的标准方程；（2）点,,A B C 分别为椭圆C 上第一、二、四象限内的点，且//AB x 轴.①若ABC的重心坐标为12,36⎛- ⎝⎭，求直线AC 的斜率；②若直线AC 过点(1,0)，且90ACB ∠=︒，求直线AC 的斜率.【答案】（1）2214x y +=；（2；②1. 【解析】（1）设椭圆的方程为：22221(0)x y a b a b+=>>，112F B B △是边长为2的等边三角形，∴c =1b =，∴2224a b c =+=， ∴椭圆的标准方程为2214x y +=；（2）设()11,A x y ，()22,C x y ，//AB x 轴，∴()11,B x y -， ①ABC 的重心坐标为2122,33x y y +⎛⎫ ⎪⎝⎭，由题意可知2121332236x y y ⎧=⎪⎪⎨+⎪=⎪⎩，解得21x =，12212y y +=-， ∵点C 为椭圆上第四象限内的点，∴222214x y +=且20y <，将21x =代入可解得22y =-，∴1,2C ⎛- ⎝⎭，又12212y y +=-，∴112y =， ∵点A 为椭圆上第一象限内的点，∴221114x y +=且1>0x ，将112y =代入可解得1x =∴12A ⎫⎪⎭， ∴直线AC斜率12222AC k ⎛-- +==；②90ACB ︒∠=，∴0CA CB ⋅=即()2221212y y x x -=-.又点,A C 都在椭圆上，则221114x y +=，222214x y +=， ∴两式相减可得2222121204x x y y -+-=. ∴()()22212214y y y y -=-，12y y ≠，∴2153y y =-， ∵直线AC 过点(1,0)，设直线AC 的方程为1x ty =+， ∴22141x y x ty ⎧+=⎪⎨⎪=+⎩，整理可得()224230t y ty ++-=，>0∆，∴1221222434t y y t y y t ⎧+=-⎪⎪+⎨⎪=-⎪+⎩，2153y y =-，∴1221222345334t y t y t ⎧-=-⎪⎪+⎨⎪-=-⎪+⎩，消去1y 可得22154t t =+，解得1t =±，又10y >，∴0t >，∴1t =， ∴直线AC 的斜率为11t =.。

2021年高考数学一轮复习第三讲直线与圆锥曲线的综合问题习题理新人教A版

2021年高考数学一轮复习第三讲直线与圆锥曲线的综合问题习题理新人教A版1．（xx安徽）已知直线y＝a交抛物线y＝x2于A，B两点．若该抛物线上存在点C，使得∠ACB为直角，则a的取值范围为________．解析：本题考查直线与抛物线的位置关系，圆的性质，考查考生的转化与化归能力．法一：设直线y＝a与y轴交于点M，抛物线y＝x2上要存在C点，只要以|AB|为直径的圆与抛物线y＝x2有交点即可，也就是使|AM|≤|MO|，即a≤a(a>0)，所以a≥1.法二：易知a>0，设C(m，m2)，由已知可令A(a，a)，B(－a，a)，则＝(m－a，m2－a)，＝(m＋a，m2－a)，因为⊥，所以m2－a＋m4－2am2＋a2＝0，可得(m2－a)(m2＋1－a)＝0.因为由题易知m2≠a，所以m2＝a－1≥0，故a∈[1，＋∞)．答案：[1，＋∞)2．（xx浙江）设F为抛物线C：y2＝4x的焦点，过点P(－1,0)的直线l交抛物线C于A，B两点，点Q为线段AB的中点．若|FQ|＝2，则直线l的斜率等于________．解析：本题考查抛物线方程、性质，直线与抛物线的位置关系，考查数形结合思想及运算求解能力．法一：注意到|FQ|＝2，正好是抛物线通径的一半，所以点Q为通径的一个端点，其坐标为(1，±2)，这时A，B，Q三点重合，直线l的斜率为±1.法二：令直线l 的方程为x ＝ty －1，由⎩⎪⎨⎪⎧x ＝ty －1，y 2＝4x ，得y 2－4ty ＋4＝0，设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝4t ，y 1y 2＝4，x 1＋x 2＝4t 2－2，所以x Q ＝2t 2－1，y Q ＝2t ，|FQ |2＝(x Q－1)2＋y 2Q ＝4，代入解得，t ＝±1或t ＝0(舍去)，即直线l 的斜率为±1.答案：±13．（xx 辽宁）已知P ，Q 为抛物线x 2＝2y 上两点，点P ，Q 的横坐标分别为4，－2，过P ，Q 分别作抛物线的切线，两切线交于点A ，则点A 的纵坐标为( )A ．1B ．3C ．－4D ．－8解析：因为P ，Q 两点的横坐标分别为4，－2，且P ，Q 两点都在抛物线y ＝12x 2上，所以P (4,8)，Q (－2,2)．因为y ′＝x ，所以k PA ＝4，k QA ＝－2，则直线PA ，QA 的方程联立得⎩⎪⎨⎪⎧y －8＝4x －4y －2＝－2x ＋2，即⎩⎪⎨⎪⎧y ＝4x －8y ＝－2x －2，可得A 点坐标为(1，－4)．答案：C4．（xx 北京）在直角坐标系xOy 中，直线l 过抛物线y 2＝4x 的焦点F ，且与该抛物线相交于A ，B 两点，其中点A 在x 轴上方．若直线l 的倾斜角为60°，则△OAF 的面积为________．解析：直线l 的方程为y ＝3(x －1)，即x ＝33y ＋1，代入抛物线方程得y 2－433y －4＝0，解得y A ＝433＋ 163＋162＝23(y B ＜0，舍去)，故△OAF 的面积为12×1×23＝ 3.答案： 35．(xx·宁夏、海南)已知抛物线C 的顶点在坐标原点，焦点为F (1,0)，直线l 与抛物线C 相交于A 、B 两点．若AB 的中点为(2,2)，则直线l 的方程为________．解析：抛物线C 的顶点在坐标原点，焦点为F (1,0)，∴p2＝1，抛物线方程为y 2＝4x .设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝4，y 21＝4x 1① y 22＝4x 2②①－②得y 21－y 22＝4(x 1－x 2)， ∴(y 1＋y 2)(y 1－y 2)＝4(x 1－x 2)，∴y 1－y 2x 1－x 2＝1， ∴直线l 的斜率为1，且过点(2,2)，∴直线方程为y －2＝x －2，∴x －y ＝0. 答案：x －y ＝06．[xx·北京卷] 已知椭圆C ：x 2＋2y 2＝4. (1)求椭圆C 的离心率；(2)设O 为原点，若点A 在直线y ＝2上，点B 在椭圆C 上，且OA ⊥OB ，求线段AB 长度的最小值．解：(1)由题意，椭圆C 的标准方程为x 24＋y 22＝1.所以a 2＝4，b 2＝2，从而c 2＝a 2－b 2＝2. 因此a ＝2，c ＝ 2. 故椭圆C 的离心率e ＝c a ＝22. (2)设点A ，B 的坐标分别为(t ，2)，(x 0，y 0)，其中x 0≠0.因为OA ⊥OB ，所以OA →·OB →＝0，即tx 0＋2y 0＝0，解得t ＝－2y 0x 0.又x 20＋2y 20＝4，所以|AB |2＝(x 0－t )2＋(y 0－2)2＝⎝⎛⎭⎪⎫x 0＋2y 0x 02＋(y 0－2)2＝x 20＋y 20＋4y 2x 20＋4＝x 2＋4－x 202＋2（4－x 20）x 20＋4＝x 202＋8x 20＋4 (0＜x 20≤4)．因为x 202＋8x 20≥4(0＜x 20≤4)，当x 20＝4时等号成立，所以|AB |2≥8.故线段AB 长度的最小值为2 2.7．[xx·广东卷] 已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的一个焦点为(5，0)，离心率为53.(1)求椭圆C 的标准方程；(2)若动点P (x 0，y 0)为椭圆C 外一点，且点P 到椭圆C 的两条切线相互垂直，求点P 的轨迹方程．2222002222220.:1(0)(1);(2)(,),,.:(1)3,954,1.94(2),,4x yC a ba bCP x y C P C Pcc e a b a cax yCx y+=>>====∴==-=-=∴+=已知椭圆的一个焦点为求椭圆的标准方程若动点为椭圆外一点且点到椭圆的两条切线相互垂直求点的轨迹方程解椭圆的标准方程为:若一切线垂直轴则另一切线垂直于轴则这样的点P共个002200222000022222000000(3,2),(3,2).(),(),194(94)18()9()40,,0,(18)()36()4(94)0,4()4y y k x xx yy k x x yk x k y kx x y kxk y kx y kx k y kx-±±-=-=-++=⎡⎤++-+--=∆=⎣⎦⎡⎤----+=--⎣⎦,它们的坐标分别为若两切线不垂直于坐标轴,设切线方程为即将之代入椭圆方程中并整理得:依题意即:即2222200000122220022(94)0,4(9)240,,1,:1,913,(3,2),(3,2),13.kyx k x y k y k kxx yP x y+=-∴--+-=∴=-=--∴+=-±±∴+=两切线相互垂直即显然这四点也满足以上方程点的轨迹方程为8．(xx·辽宁，12分)已知，椭圆C经过点A(1，32)，两个焦点为(－1,0)，(1,0)．(1)求椭圆C的方程；(2)E，F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值．解：(1)由题意，c＝1，可设椭圆方程为x21＋b2＋y2b2＝1.因为A在椭圆上，所以11＋b2＋94b2＝1，解得b2＝3，b2＝－34(舍去)．所以椭圆方程为x24＋y23＝1.(2)设直线AE方程为y＝k(x－1)＋32，代入x24＋y23＝1，得(3＋4k 2)x 2＋4k (3－2k )x ＋4(32－k )2－12＝0.设E (x E ，y E )，F (x F ，y F )．因为点A (1，32)在椭圆上，所以x E ＝432－k 2－123＋4k 2，y E ＝kx E ＋32－k . 又直线AF 的斜率与AE 的斜率互为相反数，在上式中以－k 代k ，可得 x F ＝432＋k 2－123＋4k 2，y F ＝－kx F ＋32＋k . 所以直线EF 的斜率k EF ＝y F －y E x F －x E ＝－k x E ＋x F ＋2k x F －x E ＝12.即直线EF 的斜率为定值，其值为12.备选9．（xx 福建，13分）如图，椭圆E ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的左焦点为F 1，右焦点为F 2，离心率e ＝12.过F 1的直线交椭圆于A 、B 两点，且△ABF 2的周长为8.(1)求椭圆E 的方程；(2)设动直线l ：y ＝kx ＋m 与椭圆E 有且只有一个公共点P ，且与直线x ＝4相交于点Q .试探究：在坐标平面内是否存在定点M ，使得以PQ 为直径的圆恒过点M ？若存在，求出点M 的坐标；若不存在，说明理由．解：法一：(1)因为|AB |＋|AF 2|＋|BF 2|＝8，即|AF 1|＋|F 1B |＋|AF 2|＋|BF 2|＝8，又|AF 1|＋|AF 2|＝|BF 1|＋|BF 2|＝2a ，所以4a ＝8，a ＝2.又因为e ＝12，即c a ＝12，所以c ＝1，所以b ＝a 2－c 2＝ 3. 故椭圆E 的方程是x 24＋y 23＝1.(2)由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y23＝1，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0.因为动直线l 与椭圆E 有且只有一个公共点P (x 0，y 0)，所以m ≠0且Δ＝0，即64k 2m 2－4(4k 2＋3)(4m 2－12)＝0，化简得4k 2－m 2＋3＝0.(*) 此时x 0＝－4km 4k 2＋3＝－4k m ，y 0＝kx 0＋m ＝3m ，所以P (－4k m ，3m )．由⎩⎪⎨⎪⎧x ＝4，y ＝kx ＋m ，得Q (4,4k ＋m )．假设平面内存在定点M 满足条件，由图形对称性知，点M 必在x 轴上．设M (x 1,0)，则·＝0对满足(*)式的m ，k 恒成立．因为＝(－4k m －x 1，3m)，＝(4－x 1,4k ＋m )，由·＝0，得－16k m ＋4kx 1m －4x 1＋x 21＋12k m＋3＝0，整理，得(4x 1－4)km＋x 21－4x 1＋3＝0.(**)由于(**)式对满足(*)式的m ，k 恒成立，所以⎩⎪⎨⎪⎧4x 1－4＝0，x 21－4x 1＋3＝0，解得x 1＝1.故存在定点M (1,0)，使得以PQ 为直径的圆恒过点M . 法二：(1)同法一．(2)由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y23＝1，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0.因为动直线l 与椭圆E 有且只有一个公共点P (x 0，y 0)，所以m ≠0且Δ＝0，即64k 2m 2－4(4k 2＋3)(4m 2－12)＝0，化简得4k 2－m 2＋3＝0.(*)此时x 0＝－4km 4k 2＋3＝－4k m ，y 0＝kx 0＋m ＝3m ，所以P (－4k m ，3m )．由⎩⎪⎨⎪⎧x ＝4，y ＝kx ＋m ，得Q (4,4k ＋m )．假设平面内存在定点M 满足条件，由图形对称性知，点M 必在x 轴上．取k ＝0，m ＝3，此时P (0，3)，Q (4，3)，以PQ 为直径的圆为(x －2)2＋(y －3)2＝4，交x 轴于点M 1(1,0)，M 2(3,0)；取k ＝－12，m ＝2，此时P (1，32)，Q (4,0)，以PQ 为直径的圆为(x －52)2＋(y －34)2＝4516，交x 轴于点M 3(1,0)，M 4(4,0)．所以若符合条件的点M 存在，则M 的坐标必为(1,0)．以下证明M (1,0)就是满足条件的点：因为M 的坐标为(1,0)，所以＝(－4k m －1，3m )，＝(3,4k ＋m )，从而·＝－12k m －3＋12km＋3＝0，故恒有⊥，即存在定点M (1,0)，使得以PQ 为直径的圆恒过点M .CNa29802 746A 瑪P[40434 9DF2 鷲>26315 66CB曋19979 4E0B 下 26230 6676 晶 39094 98B6 颶1。

2021年全国统一高考数学试卷(理科)(新课标ⅰ)(含答案)

2021年普通高等学校招生全国统一考试（全国乙卷）数学（理）及答案一、选择题1.设2()3()46z z z z i ++-=+，则z =( ）A.12i -B.12i +C.1i +D.1i -2.已知集合{|21,}S s s n n Z ==+∈，{|41,}T t t n n Z ==+∈，则S T =( )A.∅B.SC.TD.Z3.已知命题:p x R ∃∈﹐sin 1x <；命题||:,1x q x R e∈∀≥，则下列命题中为真命题的是（） A.p q ∧ B.p q ⌝∧ C.p q ∧⌝D.()p q ⌝∨4.设函数1()1xf x x-=+，则下列函数中为奇函数的是（） A.1()1f x -- B.1()1f x -+ C.1()1f x +- D.1()1f x ++5.在正方体1111ABCD A B C D -中，P 为11B D 的中点，则直线PB 与1AD 所成的角为（）A.2π3C.4πD.6π6.将5名北京冬奥会志愿者分配到花样滑冰，短道速滑､冰球和冰壶4个项目进行培训，每名志愿者只分配到1个项目，每个项目至少分配1名志愿者，则不同的分配方案共有（） A.60种 B.120种 C.240种 D.480种7.把函数()y f x =图像上所有点的横坐标缩短到原来的12倍，纵坐标不变，再把所得曲线向右平移3π个单位长度，得到函数sin()4y x π=-的图像，则)(f x =（）A.7sin()212x π-B.sin()212x π+C.7sin(2)12x π-D.sin(2)12x π+8.在区间(0,1)与(1,2)中各随机取1个数，则两数之和大于74的概率为（） A.79 B.2332 C.93299.魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作.其中第一题是测量海岛的高.如图，点,,E H G 在水平线AC 上，DE 和FG 是两个垂直于水平面且等高的测量标杆的高度，称为“表高”，EG 称为“表距”，GC 和EH 都称为“表目距”.GC 与EH 的差称为“表目距的差”，则海岛的高AB =（）A.⨯+表高表距表高表目距的差B.⨯-表高表距表高表目距的差C.⨯+表高表距表距表目距的差 D.⨯-表高表距表距表目距的差10.设0a ≠，若x a =为函数2()()()f x a x a x b =--的极大值点，则A.a b <B.a b >C.2ab a <D.2ab a >11.设B 是椭圆C ：22221(0)x y a b a b+=>>的上顶点，若C 上的任意一点P 都满足，2PB b ≤，则C 的离心率的取值范围是（）A.2[,1)22C.2(0,]2D.1(0,]212.设2ln1.01a =，ln1.02b =， 1.041c =-，则（）A.a b c <<B.b c a <<C.b a c <<D.c a b << 综上，a c b >>. 二、填空题13.已知双曲线C ：221(0)x y m m-=>的一条渐近线为30x my +=，则C 的焦距为 .14.已知向量(1,3)a =，(3,4)b =，若()a b b λ-⊥，则λ= . 15.记ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，面积为3， 60B =︒，223a c ac +=，则b = .16.以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为（写出符合要求的一组答案即可）.三、解答题17.某厂研制了一种生产高精产品的设备，为检验新设备生产产品的某项指标有无提高，用一台旧设备和一台新设备各生产了10件产品，得到产品该项指标数据如下：旧设备和新设备生产产品的该项指标的样本平均数分别记为x 和y，样本方差分别己为21s 和22S . （1）求x ，y ，21s ，22s ：（2）判断新设备生产产品的该项指标的均值较旧设备是否有显著提高 ( 如果2212210s s y x +-≥，则认为新设备生产产品的该项指标的均值较旧设备有显著提高，否则不认为有显著提高 ) 。

数学一轮复习高考大题专项五直线与圆锥曲线课件新人教A版

∴直线 NB1:y+3=- 0 x,①
0
直线 NB2:y-3=-
0 +3
x.②
0 -3
02 -9
=
0 = -2,
02
由①②解得
又 18 + 9 =1,∴x=- 2 ,故
代入18 +
0 = -,
= -0 ,
02
9
2
=1 得
9
+
2
9
2
0
,
02
02
0
2
=1.∴点 N 的轨迹方程为
∴(2a- 2)2=2+(2c)2-2· 2·
2c·
cos 45°,即 a2- 2a=c2-c.①

又∵e= =

2
2
,∴a= 2c.②
联立①②有 a= 2,c=1,又 a2=b2+c2,∴b=1.∴椭圆 C 的方程为
2
2=1.
+y
2
-10-

方法三:∵e= =

2
2
,∴a2=2c2,又 a2=b2+c2,∴a= 2b= 2c.
1
2
|AA'||x2-1 |=y1|x2+1|=y1|my2|=|my1y2|=
||
2+ 2
2
=
1
2
+||
| |
≤
1
2
2
·||
| |
=
2
,当且仅当| |=|m|即|m|= 2时取等号.
4
2
∴△F1A'B 面积的最大值为 4 .
-12-
2 +1

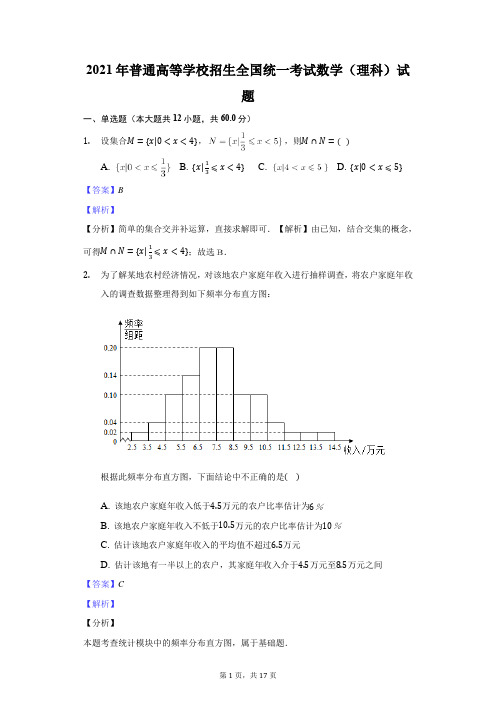
2021年普通高等学校招生全国统一考试数学(理科)试题-教师用卷

2021年普通高等学校招生全国统一考试数学（理科）试题一、单选题（本大题共12小题，共60.0分）1.设集合M={x|0<x<4}，，则M∩N=()⩽x<4} C. D. {x|0<x⩽5}A. B. {x|13【答案】B【解析】【分析】简单的集合交并补运算，直接求解即可．【解析】由已知，结合交集的概念，⩽x<4}；故选．可得M∩N={x|132.为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论中不正确的是()A. 该地农户家庭年收入低于4.5万元的农户比率估计为6％B. 该地农户家庭年收入不低于10.5万元的农户比率估计为10％C. 估计该地农户家庭年收入的平均值不超过6.5万元D. 估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间【答案】C【解析】【分析】本题考查统计模块中的频率分布直方图，属于基础题．利用频率分布直方图中频率的求解方法，通过求解频率即可判断选项A，B，D，利用平均值的计算方法，即可判断选项C．【解析】解：对于A，该地农户家庭年收入低于4.5万元的农户比率估计为0.02+0.04= 0.06= 6％，故A正确；对于B，该地农户家庭年收入不低于10.5万元的农户比率估计为0.02×3+0.04=0.10=10％，故B正确；对于C，估计该地农户家庭年收入的平均值为3×0.02+4×0.04+5×0.1+6×0.14+ 7×0.2+8×0.2+9×0.1+10×0.1+11×0.04+12×0.02+13×0.02+14×0.02=7.68>6.5万元，故C错误；对于D，家庭年收入介于4.5万元至8.5万元之间的频率为0.10+0.14+0.20×2=0.64=64％，故估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间，故D正确；故选C．3.已知，则A. −1−32i B. C. D. −32−i【答案】B【解析】【分析】复数模块，两边同除以(1−i)2后，再根据共轭复数定义，直接化简计算，难度不大．【解析】由(1−i)2z=3+2i，得z=3+2i(1−i)2=3+2i−2i=−1+32i，．4.青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为(√1010≈1.259)()A. 1.5B. 1.2C. 0.8D. 0.6【答案】C【解析】【分析】题干新颖，但考查的并不难，考查了指数和对数之间的互化，属于基础题．【解析】将L=4.9代入L=5+lg V，可得lg V=−0.1=−110．故V =10−110=1√1010≈11.529≈0.8．故选．5. 已知F 1,F 2是双曲线C 的两个焦点，P 为C 上一点，且∠F 1PF 2=60∘,|PF 1|=3|PF 2|，则C 的离心率为( )A. √72B. √132C. √7D. √13【答案】A 【解析】【分析】本题考查双曲线离心率的求法，求解过程中用到了余弦定理，综合性较强，属于中等偏难一点题，在前6题中出现，是一个不小的挑战．【解析】因为|PF 1⃗⃗⃗⃗⃗⃗⃗ |=3|PF 2⃗⃗⃗⃗⃗⃗⃗ |， |PF 1⃗⃗⃗⃗⃗⃗⃗ |−|PF 2⃗⃗⃗⃗⃗⃗⃗ |=2a ，所以|PF 1⃗⃗⃗⃗⃗⃗⃗ |=3a , |PF 2⃗⃗⃗⃗⃗⃗⃗ |=a ．在ΔF 1PF 2中，．可得(2c)2=(3a)2+a 2−2×3a ×a ×cos60∘,即e =c a =√72. 故选A.6. 在一个正方体中，过顶点A 的三条棱的中点分别为E,F,G.该正方体截去三棱锥A −EFG 后，所得多面体的三视图中，正视图如右图所示，则相应的侧视图是( )A. B. C. D.【答案】D 【解析】【分析】本题考查了三视图，但不是由三视图还原几何体，相对而言难度不是特别大，只要做出几何体直观图，便可直接画出侧视图．【解析】正视图与侧视图的高相等，能看见的用实线．故选D ．7. 等比数列{a n }的公比为q ，前n 项和为S n 设甲：q >0，乙：{S n }是递增数列，则( )A. 甲是乙的充分条件但不是必要条件B. 甲是乙的必要条件但不是充分条件C. 甲是乙的充要条件D. 甲既不是乙的充分条件也不是乙的必要条件【答案】B【解析】【分析】本题是一道综合题，考查了数列和简易逻辑，简易逻辑考查的是充分必要条件，数列考查的是等比数列的单调性，考查点都不难．【解析】a=−1，q=2时，{ S n}是递减数列，所以甲不是乙的充分条件；若{ S n}是递增数列，则a n= S n− S n−1>0，可以推出q>0，故甲是乙的必要条件．故选B．8.2020年12月8日，中国和尼泊尔联合公布珠程朗玛峰最新高程为8848.86(单位：m)，三角高程测量法是珠峰高程则量方法之一．右图是三角高程测量法的一个示意图，现有A，B，C三点，且A，B，C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45∘,∠A′B′C′=60∘.由C点测得B点的仰角为15∘,BB′与CC′的差为100；由B 点测得A点的仰角为45∘，则A，C两点到水平面A′B′C′的高度差AA′−CC′约为(√3≈1.732)( )A. 346B. 373C. 446D. 473【答案】B【解析】【分析】本题属于解三角形的范畴，题干复杂，做题时需要能提炼出有用信息，结合图去求解即可，整体上不失为一道好题，近年来大量的高考题和生活和文化相结合，是高考的命题方向，这道题很好的切合了最近几年的命题方向．【解析】过点C作BB′垂线，交BB′于点M，过点B作AA′垂线，交AA′于点N，设B′C′=CM=m,A′B′=BN=n.在ΔA′B′C′中，msin75∘=nsin45∘，在ΔCBM中，msin75∘=100sin15∘，联立两式求得n=√3−1≈273．可得A、C两点到水平面的高度差AA′−CC′约为273+100=373．故选B.9. 若α∈(0,π2),tan2α=cosα2−sinα,则tanα=( )A. √1515B. √55C. √53D. √153【答案】A 【解析】【分析】本题考查三角函数，做这道题需要用到弦切互化的技巧，以及同角三角函数关系的知识点，有一定的综合性，难度中等．【解析】由tan2α=sin2αcos2α=2sinαcosα1−2sin α=cosα2−sinα.化简可得,sinα=14,tanα=√1515. 故选A.10. 将4个1和2个0随机排成一行，则2个0不相邻的概率为( )A. 13B. 25C. 23D. 45【答案】C 【解析】【分析】本题考查的排列组合和概率，排列组合考察的是插空法，插空法是排列组合问题的基础求解方法，作为高考题非常合适，考察了学生的基本功．【解析】由将4个1和2个0随机排成一行共有C 62种，先将4个1全排列，再将2个0用插空法共有C 52种，则题目所求的概率为P =C 52C 62=23.故选C.11. 已知A ，B ，C 是半径为1的球О的球面上的三个点，且AC ⊥BC ，AC =BC =1，则三棱锥O −ABC 的体积为( )A. √212B. √312C. √24D. √34【答案】A 【解析】【分析】本题考查球的结构特征和三棱锥体积，属于中档题．求出球心到平面的距离，即可求解．【解析】解：记▵ABC 的外接圆的圆心为O 1，由于AC ⊥ BC ，又球的半径为1，则AB =√2，O 1C =√22；所以OA=OB=OC=1，所以OA2+OB2=AB2，OO1=√22.于是OO12+O1C2=OC2，所以OO1⊥O1C，OO1⊥AB.又O1C∩AB=O1，O1C、AB⊂平面ABC，易得OO1⊥平面ABC.所以V O−ABC=13×S△ABC×OO1=13×12×1×1×√22=√212.故选A.12.设函数f(x)的定义域为R，f(x+1)为奇函数，f(x+2)为偶函数，当x∈[1,2]时，f(x)=ax2+b.若f(0)+f(3)=6，则f(92)=( )A. −94B. −32C. 74D. 52【答案】A【解析】【分析】作为选择压轴题，这道题考查的是函数奇偶性和对称性、周期性的综合应用，有一定的难度，但求出的周期后，此题做的就基本差不多了，但整体而言，作为选择压轴题，还是很不错的．【解析】因为f(x+1)为奇函数，所以f(1)=0，即a+ b=0，所以b=− a.又f(0)= f(−1+1)=− f(1+1)=− f(2)=−4 a− b=−3 a.f(3)= f(1+2)= f(−1+2)=f(1)=0，由f(0)+ f(3)=6，得a=−2.f(92)=f(2+52)=f(2−52)=f(−12)=f(−32+1)=−f(32+1)=−f(12+2)=−f(−1+2)=−f(3)=−9a−b=−5a=5.故选A.二、单空题（本大题共4小题，共20.0分）13.曲线y=2x−1x+2在点(−1,−3)处的切线方程为_______________．【答案】【答案】y=2x+1．【解析】【分析】本题考查了利用导数研究函数的切线方程，是基础题．先根据函数解析式，得到导函数，再得到切线的斜率，即可得到结果．【解析】因为y=1−2x+2=xx+2，所以y′=x+2−x(x+2)2=2(x+2)2，所以曲线在点(−1,−1)处的切线斜率为2，所以所求切线方程为y+1=2(x+1)，即y=2x+1.14.已知向量a⃗=(3,1)，b⃗ =(1,0)，若a⃗⊥c⃗，则k=______．【答案】−103【解析】【分析】本题考查向量的数量积的应用，向量的垂直，考查计算能力．利用已知向量表示，通过a⃗⊥c⃗，向量的数量积为0，求解即可．【解析】解：因为a⃗=(3,1)，b⃗ =(1,0)，所以c⃗=a⃗+k b⃗ =(k+3,1)，因为a⃗⊥c⃗，则3(k+3)+1=0，解得k=−103.故答案为−103.15.已知F1,F2为椭圆C:x216+y24=1两个焦点，P，Q为C上关于坐标原点对称的两点，且|PQ|=|F1F2|，则四边形PF1QF2的面积为______．【答案】【答案】16．【解析】【分析】本题考查椭圆方程应用，考查椭圆的性质，属基础题【解析】根据题意，可得|OP|=3，设P(x1,y1)，所以x12+y12=9.又P在椭圆上，联立两方程，可求得|y1|=163，代入面积公式，即可求得答案解：因为P，Q是椭圆上关于原点对称的两个点，且|PQ|=6，所以|OP|=3，设P(x1,y1)，所以x12+y12=9，又P在椭圆上，所以x1225+y1216=1，联立方程{x12+y12=9x1225+y1216，可得y12=2569，即|y1|=163，所以▵PF1F2的面积S=12⋅|F1F2|⋅|y1|=12×6×163=16.故答案为16.16.已知函数f(x)=2cos(ωx+φ)的部分图像如图所示，则满足条件(f(x)−f(−7π4))(f(x)−f(4π3))>0的最小正整数x为______．【答案】【答案】2．【解析】【分析】本题考查正弦型函数的图像和性质以及相关应用，需要由图求出正弦型函数的解析式，然后解一个一元二次不等式，得到的范围，最后求解的范围．【解析】34T=13π12−π3=34π,可得T=π,φ=2.将x=π3代入f(x)=cos(2x+φ),得cos(2π3+φ)=0.故2π3+φ=π2,即φ=−π6.所以f(x)=cos(2x−π6).保存编辑所以题目条件可转化为(f(x)−1)(f(x)+√3)>0.等价于f(x)>1,f(x)<−√3.从图像可以看出:x∈(π2,3π4).故答案为x=2.三、解答题（本大题共7小题，共84.0分）17.甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了200件产品，产品的质量情况统计如下表：一级品二级品合计甲机床15050200乙机床12080200合计270130400(1)甲机床、乙机床生产的产品中一级品的频率分别是多少？(2)能否有99％的把握认为甲机床的产品质量与乙机床的产品质量有差异？附：K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，0.0500.0100.001k 3.841 6.63510.828【答案】【答案】(1)P1=150200=0.75,P2=120200=0.6；(2)没有．【解析】【分析】统计和概率作为第一道大题，难度不大，第一问由表格数据和频率计算公式可以直接得到，非常简单，送分题，第二问考查卡方分布，也是直接套公式，这套卷子的第一道大题可以说是非常简单了．【解析】(1)设甲机床、乙机床生产的产品中一级品的频率分P1、P2；则有P1=150200=0.75,P2=120200=0.6.(2)根据列联表中数据，可得K²的观测值；K2=400(150×80−120×50)2200×200×270×130=40039≈10.256.因为10.256<10.828，所以没有99％的把握认为甲机床的产品质量与乙机床的产品质量有差异．18.已知数列{a n}的各项均为正数，记S n为{a n}的前n项和，从下面①②③中选取两个作为条件，证明另外一个成立．①数列{a n}是等差数列；②数列{√S n}是等差数列；③a2=3a1.注：若选择不同的组合分别解答，则按第一个解答计分．【答案】【答案】▵.选择条件①和③．▵.选择条件①和②．▵.选择条件②和③．【解析】【解析】Ⅰ.选择条件①和③．数列{a n}是等差数列，a2=3a1，设公差为d.则a2=3a1=a1+d，即d=2a1.因为S n=na1+n(n−1)2d=n2a1，所以√S n=n√a1(a1>0).故{√S n}是等差数列．Ⅱ.选择条件①和②．已知数列{a n}是等差数列，数列{√S n}是等差数列；则a n=a1+(n−1)d，S n=na1+n(n−1)2d=12n2d+(a1−d2)n.因为数列{√S n}是等差数列，则a1=d2，所以a2=a1+d=3a1.Ⅲ.选择条件②和③．已知数列{√S n}是等差数列，a2=3a1.因为s2=a1+a2=4a1，所以√s2−√s1=√4a1−√a1=√a1(a1>0)．即{√S n}的公差d等于√a1，所以√s n=√a1+(n−1)d=n√a1．所以S n=n2a1，即数列{a n}是等差数列．19. 已知直三棱柱ABC −A 1B 1C 1中，侧面AA 1B 1B 为正方形．AB =BC =2,E,F 分别为AC 和CC 1的中点，D 为棱A 1B 1上的点，BF ⊥A 1B 1. (1)证明：BF ⊥DE ；(2)当B 1D 为何值时，面BB 1C 1C 与面DFE 所成的二面角的正弦值最小？【答案】解：(1)因为E,F 是直三棱柱ABC −A 1B 1C 1中AC 和CC 1的中点,且AB =BC =2;所以CF =1,BF =√5.，，于是AF =3，所以AC =2√2，由AB 2+BC 2=AC 2，；于是,A(2,0,0),B(0,0,0),C(0,2,0),E(1,1,0),F(0,2,1). 设B 1D =m,则D(m,0,2).于是,BF ⃗⃗⃗⃗⃗ =(0,2,1),DE⃗⃗⃗⃗⃗⃗ =(1−m,1,−2). BF ⃗⃗⃗⃗⃗ ⋅DE ⃗⃗⃗⃗⃗⃗ =0×(1−m)+2×1+1×(−2)=0，；(2)易知平面BB 1C 1C 的法向量为n 1⃗⃗⃗⃗ =(1,0,0)，而DE⃗⃗⃗⃗⃗⃗ =(1−m,1,−2),EF ⃗⃗⃗⃗⃗ =(−1,1,1).则{n 2⃗⃗⃗⃗ ·DE ⃗⃗⃗⃗⃗⃗ =0n 2⃗⃗⃗⃗ ·EF ⃗⃗⃗⃗⃗ =0，即{(1−m)x +y −2z =0−x +y +z =0, 于是,平面DFE 的法向量n 2⃗⃗⃗⃗ =(3,m +1,2−m).设面BB 1C 1C 与面DFE 所成的二面角的平面角为θ，于是|cosθ|=|cos <n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ >|=√2(m−12)2+272． sinθ=√1−cos 2θ=√1−92(m −12)2+272⩾√33 当m =12时，即当B 1D =12时，面BB 1C 1C 与面DFE 所成的二面角的正弦值最小，为．【解析】本题考查利用空间向量证明线线垂直，求二面角，属于中档题． (1)由已知证明建立空间直角坐标系，表示出BF ⃗⃗⃗⃗⃗ ,DE⃗⃗⃗⃗⃗⃗ ，可得BF ⃗⃗⃗⃗⃗ ⋅DE ⃗⃗⃗⃗⃗⃗ =0，即可得证；(2)分别求出面BB 1C 1C 与面DFE 的法向量，利用空间向量夹角公式即可求解．20. 抛物线C 的顶点为坐标原点O ，焦点在x 轴上，直线L ：x =1交C 于P ，Q 两点，且已知点，且⊙M 与L 相切．(1)求C ，⊙M 的方程； (2)设是C 上的三个点，直线A 1A 2，A 1A 3均与⊙M 相切．判断直线A 2A 3与⊙M 的位置关系，并说明理由．【答案】【答案】(1)C 的方程为y 2=x ，⊙M 的方程为(x −2)2+y 2=1；．【解析】【分析】圆锥曲线大题考查椭圆、双曲线、抛物线中最简单的一条抛物线；第一问求解抛物线方程和圆的方程难度不大；第二问考查设而不求的思路和韦达定理．可以先把抛物线上的三个点(a 2,a)、(b 2,b)、(c 2,c)都设出来；根据两个相切条件，得到2=1，2=1；进一步得到b 和c 是(a 2−1)x 2+2ax −a 2+3=0的两根；接下来算出圆心到A 2A 3的距离为d =√1+(b+c)2；再由韦达定理可知b +c 和bc ，带入计算求出d =1，即可得到A 2A 3和圆相切．【解析】(1)C 的方程为y 2=x ，⊙M 的方程为(x −2)2+y 2=1； (2)设A(x 1,y 1),B(x 2,y 2),C(x 3,y 3)．当A 1,A 2,A 3中有一个为坐标原点，另外两个点的横坐标的值均为3时，满足条件，且此时直线A 2A 3与⊙M 也相切．当x 1≠x 2≠x 3时，可知直线A 1A 2的方程为x −(y 1+y 2)y +y 1y 2=0，，即(y12−1)y22+2y1y2+3−y12=0；同理可得，(y12−1)y32+2y1y3+3−y12=0；由此可知，．依题意有，．M到直线A2A3的距离，d2=(|2+y1y2|√1+(y1+y2)2)2=(2+y1y2)21+(y1+y2)2=(2+3−y12y12−1)21+(−2y1y12−1)2=1．．21.已知且a≠1，函数．(1)当时，求f(x)的单调区间；(2)若曲线与直线有且仅有两个交点，求a的取值范围．【答案】【答案】；(2)a∈(1,e)∪(e,+∞)．【解析】【分析】导数作为压轴题的存在，考查了单调性和零点，第一问的单调性，难度不大，不含参数，不需要分类讨论；第二问交点问题最后转化成零点问题，构造函数后再看函数和直线相交的情况，构造出的函数不含参数，图像易得，最后求参数范围即可，这道导数压轴题和往年相比，相对难度不是特别大．【解析】(1)当a=2时,f(x)=x22x(x>0)，求导f′(x)=x(2−xln2)2x(x>0)，．令，即x>2ln 2，此时单调递减．单调递增区间为，单调递减区间为．(2)要使y=f(x)与y=1有2个交点,即x aa x =1有2解,故ln xx=ln aa有2解．令g(x)=ln xx ,求导g′(x)=1−ln xx2(x>0)．令g′(x)=0,解得x=e，令g′(x)>0,即0<x<e,此时g(x)单调递增，，故g(x)max =g(e)=1e ,当x >e 时,g(x)∈(0,1e )．因为g(1)=0,要使得条件成立.则0<ln a a<1．①当0<a <1,此时不符合条件． ②当1<a,g(x)max =g(e)=1e ．故a ∈(1,e)∪(e,+∞)．22. [选修4−4：坐标系与参数方程]在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ=2√2cosθ.(1)将C 的极坐标方程化为直角坐标方程；(2)设点A 的直角坐标为(1,0),M 为C 上的动点，点P 满足AP ⃗⃗⃗⃗⃗ =√2 AM ⃗⃗⃗⃗⃗⃗ ，写出P 的轨迹C 1的参数方程，并判断C 与C 1是否有公共点．【答案】【答案】(1)曲线C 的直角坐标方程为(x −√2)2+y 2=2；(2)C 1的参数方程为{x =3+√2+2cos αy =2sin α(α为参数,且α∈[0,2π))．【解析】【分析】极坐标和参数方程这道题，作为选做题，难度不大，第一问考查极坐标方程和直角坐标方程的互化，较为基础；第二问考查了轨迹方程的求法，考查的是相关点法，求出直角坐标系下的方程后，进一步化成极坐标方程即可，由圆心距小于半径差可得两个圆为内含关系，本题整体难度不大，考查的较为基础．【解析】(1)∵p =2√2 cos θ,∴p 2=2√2pcos θ.∵x =pcos θ,p =x 2+y 2,∴x 2+y 2=2√2x.即曲线C 的直角坐标方程为(x −√2)2+y 2=2．(2)设P 点坐标为(x,y),M 点坐标为(x ′,y′).则AP⃗⃗⃗⃗⃗ =(x −1,y),AM ⃗⃗⃗⃗⃗⃗ =(x ′−1,y′).∵AP⃗⃗⃗⃗⃗ =√2AM ⃗⃗⃗⃗⃗⃗ ,∵M 为上的动点,∴(x −1√2+1−√2)2+(y √2)2=2.即(x −√2−3)2+y 2=4.故C 1的参数方程为{x =3+√2+2cos αy =2sin α(α为参数,且α∈[0,2π)).∴|CC 1|=3,r 1=2,r =√2. ∴r 1−r <|CC 1|<r 1+r.故C 与C 1有公共点.23. [选修4−5：不等式选讲]23、已知函数f(x)=|x −2|,g(x)=|2x +3|−|2x −1|. (1)画出y =f(x)和y =g(x)的图象； (2)若f(x +a)≥g(x)，求a 的取值范围．【答案】【答案】(1)见解析；．【解析】【分析】不等式选讲这道选做题，考查了绝对值函数图像的画法和含参绝对值不等式的求法，绝对值函数图像作图相对简单，含参绝对值不等式的求解，主要用到分类讨论的思想，分类讨论的时候需要注意不重不漏．(1)通过对x 分类讨论，写出分段函数的形式，画出图像即可得出． (2)由图像可得：f(6)=4，f(12)=4，若满足题意，那么就需把函数f(x)的图像向左或向右平移|a|个单位以后，f(x)的图像不在g(x)图像的下方，由图像观察可得出结论．【解析】(1)当x<−32时，2x+3<0，2x−1<0，故g(x)=[−(2x+3)]−[−(2x−1)]=−4．当−32≤x≤12时，2x+3≥0，2x−1≤0，故g(x)=(2x+3)−[−(2x−1)]=4x+2．当x>12时，2x+3>0，2x−1>0，故g(x)=(2x+3)−(2x−1)=4．综上，g(x)={4x+2,−32≤x<12−4,x<−324,x≥32 ,y=f(x)和y=g(x)的图象为：(2)由上可知，y=f(x+a)是函数y=f(x)左右平移|a|个单位得到．观察图像，不难发现函数y=f(x)向右平移不符合题意．函数y=f(x)向左平移至图像右支恰好经过点(12,4)，此时为满足f(x+a)≥g(x)的临界状态．y=f(x+a)=|x−2|+a=x−2+a，代入点(12,4)，可得a=112．,+∞)．由上可得，a的取值范围为[112。

2021年高考数学人教B版(理)一轮复习专题9第7讲直线与圆锥曲线

2021年高考数学人教B版（理）一轮复习专题9第7讲直线与圆锥曲线高考数学精品复习资料2021.5第7讲直线与圆锥曲线的位置关系A级基础演练(时间：30分钟满分：55分)一、选择题(每小题5分，共20分)1．(20xx・潍坊一模)直线4kx－4y－k＝0与抛物线y2＝x交于A，B两点，若|AB|1＝4，则弦AB的中点到直线x＋2＝0的距离等于 7A.4B．29C.4( )．D．4?1?解析直线4kx－4y－k＝0，即y＝k?x－4?，即直线4kx－4y－k＝0过抛物线y2＝x的焦点?4，0?.设A(x1，y1)，B(x2，y2)，则|AB|＝x1＋x2＋2＝4，故x1＋x2??7717＝2，则弦AB的中点的横坐标是4，弦AB的中点到直线x＋2＝0的距离是4＋192＝4. 答案 C2x2y22．(20xx・台州质检)设斜率为2的直线l与椭圆a2＋b2＝1(a>b>0)交于不同的两点，且这两个交点在x轴上的射影恰好是椭圆的两个焦点，则该椭圆的离心率为( )．3A.31B.22C.21D.3解析由于直线与椭圆的两交点A，B在x轴上的射影分别为左、右焦点F1，b2F2，故|AF1|＝|BF2|＝a，设直线与x轴交于C点，又直线倾斜角θ的正切值为22|AF1||BF2|22b22，结合图形易得tan θ＝2＝|CF1|＝|CF2|，故|CF1|＋|CF2|＝a＝|F1F2|＝22c，整理并化简得2b2＝2(a2－c2)＝ac，即2(1－e2)＝e，解得e＝2. 答案 C3．(20xx・临沂二模)抛物线y2＝2px与直线2x＋y＋a＝0交于A，B两点，其中点A的坐标为(1,2)，设抛物线的焦点为F，则|FA|＋|FB|的值等于 ( )． A．7B．35D．5解析点A(1,2)在抛物线y2＝2px和直线2x＋y＋a＝0上，则p＝2，a＝－4，F(1,0)，则B(4，－4)，故|FA|＋|FB|＝7. 答案 Ax2y24．(20xx・宁波十校联考)设双曲线a2－b2＝1(a>0，b>0)的左、右焦点分别为F1，F2，离心率为e，过F2的直线与双曲线的右支交于A，B两点，若△F1AB是以A为直角顶点的等腰直角三角形，则e2＝ A．1＋22 C．5－22B．4－22 D．3＋22( )．解析如图，设|AF1|＝m，则|BF1|＝2m，|AF2|＝m－2a，|BF2|＝2m－2a，∴|AB|＝|AF2|＋|BF2|＝m－2a＋2m－2a＝m，得m＝22a，又由|AF1|2＋|AF2|2＝|F1F2|2，可得m2＋(m－2a)2c2＝4c，即得(20－82)a＝4c，∴e＝a2＝5－222222，故应选C. 答案 C二、填空题(每小题5分，共10分)x22?11?5．椭圆2＋y＝1的弦被点?2，2?平分，则这条弦所在的直线方程是________． ??解析设弦的两个端点为A(x1，y1)，B(x2，y2)，则x1＋x2＝1，y1＋y2＝1.x2x2122∵A，B在椭圆上，∴2＋y1＝1，2＋y22＝1. 两式相减得：?x1＋x2??x1－x2?＋(y1＋y2)(y1－y2)＝0，2y1－y2x1＋x2即＝－， x1－x22?y1＋y2?∵x1＋x2＝1，y1＋y2＝1，y1－y211∴＝－2，即直线AB的斜率为－2. x1－x211?1?∴直线AB的方程为y－2＝－2?x－2?，??即该弦所在直线的方程为2x＋4y－3＝0. 答案 2x＋4y－3＝0x2y26．(20xx・东北三省联考)已知椭圆C：a2＋b2＝1(a>b>0)，F(2，0)为其右焦点，过F垂直于x轴的直线与椭圆相交所得的弦长为2，则椭圆C的方程为________．c＝2，??b2由题意，得?＝1，a??a2＝b2＋c2，解析?a＝2，x2y2解得?∴椭圆C的方程为4＋2＝1.b＝2，?x2y2答案 4＋2＝1 三、解答题(共25分)7．(12分)在平面直角坐标系xOy中，直线l与抛物线y2＝4x相交于不同的A，B两点．→・→的值；(1)如果直线l过抛物线的焦点，求OAOB→・→＝－4，证明：直线l必过一定点，并求出该定点． (2)如果OAOB(1)解由题意：抛物线焦点为(1,0)，设l：x＝ty＋1，代入抛物线y2＝4x，消去x得y2－4ty－4＝0，设A(x1，y1)，B(x2，y2)，则y1＋y2＝4t，y1y2＝－4，→・→＝xx＋yy＝(ty＋1)(ty＋1)＋yy ∴OAOB12121212＝t2y1y2＋t(y1＋y2)＋1＋y1y2＝－4t2＋4t2＋1－4＝－3. (2)证明设l：x＝ty＋b，代入抛物线y2＝4x，消去x得y2－4ty－4b＝0，设A(x1，y1)，B(x2，y2)，则y1＋y2＝4t，y1y2＝－4b，→・→＝xx＋yy＝(ty＋b)(ty＋b)＋yy ∴OAOB12121212＝t2y1y2＋bt(y1＋y2)＋b2＋y1y2 ＝－4bt2＋4bt2＋b2－4b＝b2－4b.令b2－4b＝－4，∴b2－4b＋4＝0，∴b＝2，∴直线l过定点(2,0)．→・→＝－4，则直线l必过一定点．∴若OAOBy28．(13分)给出双曲线x－2＝1.2(1)求以A(2,1)为中点的弦所在的直线方程；(2)若过点A(2,1)的直线l与所给双曲线交于P1，P2两点，求线段P1P2的中点P的轨迹方程；(3)过点B(1,1)能否作直线m，使得m与双曲线交于两点Q1，Q2，且B是Q1Q2的中点？这样的直线m若存在，求出它的方程；若不存在，说明理由．22?2x1－y1＝2，解 (1)设弦的两端点为P1(x1，y1)，P2(x2，y2)，则?22两式相减得?2x2－y2＝2，到2(x1－x2)(x1＋x2)＝(y1－y2)(y1＋y2)，又x1＋x2＝4，y1＋y2＝2，所以直线斜率k＝y1－y2＝4. x1－x2故求得直线方程为4x－y－7＝0. (2)设P(x，y)，P1(x1，y1)，P2(x2，y2)， y1－y22x按照(1)的解法可得＝，x1－x2y①由于P1，P2，P，A四点共线， y1－y2y－1得＝， x1－x2x－2②2xy－1由①②可得y＝，整理得2x2－y2－4x＋y＝0，检验当x1＝x2时，x＝2，yx－2＝0也满足方程，故P1P2的中点P的轨迹方程是2x2－y2－4x＋y＝0. (3)假设满足题设条件的直线m存在，按照(1)的解法可得直线m的方程为y＝2x－1.y＝2x－1，??考虑到方程组?2y2x－2＝1??无解，因此满足题设条件的直线m是不存在的．B级能力突破(时间：30分钟满分：45分)一、选择题(每小题5分，共10分)1．(20xx・皖南八校联考)已知直线l：y＝k(x－2)(k>0)与抛物线C：y2＝8x交于A，B两点，F为抛物线C的焦点，若|AF|＝2|BF|，则k的值是 1A.322B.3C．222D.4( )．解析法一据题意画图，作AA1⊥l′，BB1⊥l′，BD⊥AA1.设直线l的倾斜角为θ，|AF|＝2|BF|＝2r，则|AA1|＝2|BB1|＝2|AD|＝2r，所以有|AB|＝3r，|AD|＝r，|BD|则|BD|＝22r，k＝tan θ＝tan∠BAD＝|AD|＝22.2y＝8x，?2法二直线y＝k(x－2)恰好经过抛物线y＝8x的焦点F(2,0)，由??y＝k?x－2?，可得ky2－8y－16k＝0，因为|FA|＝2|FB|，所以yA＝－2yB.则yA＋yB＝－2yB＋yB 感谢您的阅读，祝您生活愉快。

2021高考理科数学(人教A版)一轮复习高考大题专项(五) 直线与圆锥曲线

高考大题专项(五) 直线与圆锥曲线突破1 圆锥曲线中的最值、范围问题1.(2019广东深圳模拟,20)在平面直角坐标系xOy 中,离心率为√63的椭圆C :x 2a 2+y 2b2=1(a>b>0)过点M1,√63.(1)求椭圆C 的标准方程;(2)若直线x+y+m=0上存在点G ,且过点G 的椭圆C 的两条切线相互垂直,求实数m 的取值范围.2.(2019河北石家庄一模,20)已知抛物线C :y 2=2px (p>0)上一点P (x 0,2)到焦点F 的距离|PF |=2x 0. (1)求抛物线C 的方程;(2)过点P 引圆M :(x-3)2+y 2=r 2(0<r ≤√2)的两条切线PA 、PB ,切线PA 、PB 与抛物线C 的另一交点分别为A 、B ,线段AB 中点的横坐标记为t ,求t 的取值范围.3.(2019河南濮阳模拟,20)已知椭圆C :x 2a2+y 2b2=1(a>b>0)的两个焦点分别为F 1、F 2,|F 1F 2|=2,点Q 在椭圆上,且△QF 1F 2的周长为6. (1)求椭圆C 的方程;(2)若点P 的坐标为(2,1),不过原点O 的直线l 与椭圆C 相交于A ,B 两点,设线段AB 的中点为M ,点P 到直线l 的距离为d ,且M ,O ,P 三点共线,求1213|AB|2+1316d 2的最大值.4.(2019山东淄博三模,20)已知圆O :x 2+y 2=4,抛物线C :x 2=2py (p>0).(1)若抛物线C 的焦点F 在圆O 上,且A 为抛物线C 和圆O 的一个交点,求|AF|;(2)若直线l 与抛物线C 和圆O 分别相切于M ,N 两点,设M (x 0,y 0),当y 0∈[3,4]时,求|MN|的最大值. 5.(2019浙江模拟,19)如图,不垂直于坐标轴的直线l与抛物线y2=2px(p>0)有且只有一个公共点M.(1)当M的坐标为(2,2)时,求p的值及直线l的方程;(2)若直线l与圆x2+y2=1相切于点N,求|MN|的最小值.突破2圆锥曲线中的定点、定值与存在性问题1.在△ABC中,AB=2,C=π3,且S△ABC=√33,若以A,B为左右焦点的椭圆M经过点C.⃗⃗⃗⃗⃗ ·(2)设过M右焦点且斜率为k的动直线与M相交于E,F两点,探究在x轴上是否存在定点D,使得DE⃗⃗⃗⃗⃗ 为定值?若存在,试求出定值和点D的坐标;若不存在,请说明理由.DF2.(2019江西宜春模拟,19)已知抛物线C:y2=2px(p>0),过焦点F作垂直于x轴的直线l,l与抛物线C相交于A,B两点,E为C的准线上一点,且△ABE的面积为4.(1)求抛物线C的标准方程;(2)设Q(2,0),若点P是抛物线C上的一动点,则是否存在垂直于x轴的定直线被以PQ为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长;如果不存在,说明理由.3.(2019四川绵阳质检,20)在平面直角坐标系xOy中,抛物线C:y2=2px(p>0)的准线为l,其焦点为F,点B是抛物线C上横坐标为1的一点,若点B到l的距离等于|BO|.2(2)设A是抛物线C上异于顶点的一点,直线AO交直线l于点M,抛物线C在点A处的切线m交直线l于点N,求证:以点N为圆心,以|MN|为半径的圆经过x轴上的两个定点.4.(2019贵州遵义航天中学十一模,20)已知椭圆C:x 2a2+y2b2=1(a>b>0)的离心率e=√22,左、右焦点分别为F1,F2,抛物线y2=4√2x的焦点F恰好是该椭圆的一个顶点.(1)求椭圆C的方程;(2)已知圆M:x2+y2=23的切线l与椭圆相交于A,B两点,那么以AB为直径的圆是否经过定点?如果是,求出定点的坐标;如果不是,请说明理由.5.(2019湖北武汉模拟,20)如图,O为坐标原点,椭圆C:x 2a2+y2b2=1(a>b>0)的焦距等于其长半轴长,M,N为椭圆C的上、下顶点,且|MN|=2√3.(1)求椭圆C的方程;(2)过点P(0,1)作直线l交椭圆C于异于M,N的A,B两点,直线AM,BN交于点T.求证:点T的纵坐标为定值3.突破3圆锥曲线中的证明与探索性问题1.(2019湖南永州三模,20)已知直线l是经过点A(1,-2)且与抛物线E:y2=4x相切的直线.(1)求直线l的方程;(2)如图,已知点B(1,2),M,N是x轴上两个不同的动点,且满足|BM|=|BN|,直线BM,BN与抛物线E的另一个交点分别是P,Q,求证:直线PQ与l平行.2.(2018全国1,20)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.(1)当l与x轴垂直时,求直线BM的方程;(2)证明:∠ABM=∠ABN.3.(2019四川成都七中模拟,20)设圆x2+y2-4x-60=0的圆心为F2,直线l过点F1(-2,0)且与x轴不重合,交圆F2于C,D两点,过点F1作CF2的平行线交DF2于点E.(1)求|EF1|+|EF2|的值;(2)设点E的轨迹为曲线E1,直线l与曲线E1相交于A,B两点,与直线x=-8相交于M点,试问在椭圆E1上是否存在一定点N,使得k1,k3,k2成等差数列(其中k1,k2,k3分别指直线AN,BN,MN的斜率)?若存在,求出N点的坐标;若不存在,请说明理由.4.(2019重庆巴蜀中学模拟,20)已知椭圆C1:x 2a2+y2b2=1(a>b>0)的离心率为12,过点E(√7,0)的椭圆C1的两条切线相互垂直.(1)求椭圆C1的方程;(2)在椭圆C1上是否存在这样的点P,过点P引抛物线C2:x2=4y的两条切线l1,l2,切点分别为B,C,且直线BC过点A(1,1)?若存在,指出这样的点P有几个(不必求出点的坐标);若不存在,请说明理由.5.(2019广东广雅中学、执信、六中、深外四校联考,20)设斜率不为0的直线l与抛物线x2=4y交于A,B两点,与椭圆x 26+y24=1交于C,D两点,记直线OA,OB,OC,OD的斜率分别为k1,k2,k3,k4.(1)若直线l过(0,4),证明:OA⊥OB;(2)求证:k1+k2的值与直线l的斜率的大小无关.k3+k4参考答案高考大题专项(五)直线与圆锥曲线突破1圆锥曲线中的最值、范围问题1.解 (1)由题意,{ca=√63,a 2=b 2+c 2,解得a 2=3b 2,又1a 2+23b 2=1,解得{a 2=3,b 2=1,所以椭圆C 的标准方程为x 2+y 2=1.(2)①当过点G 的椭圆C 的一条切线的斜率不存在时,另一条切线必垂直于y 轴,易得G (±√3,±1).②当过点G 的椭圆C 的切线的斜率均存在时,设G (x 0,y 0),x 0≠±√3. 切线方程为y=k (x-x 0)+y 0,代入椭圆方程得(3k 2+1)x 2-6k (kx 0-y 0)x+3(kx 0-y 0)2-3=0, Δ=[6k (kx 0-y 0)]2-4(3k 2+1)·[3(kx 0-y 0)2-3]=0,化简得(kx 0-y 0)2-(3k 2+1)=0,由此得(x 02-3)k 2-2x 0y 0k+y 02-1=0,设过点G 的椭圆C 的切线的斜率分别为k 1,k 2,所以k 1k 2=y 02-1x 02-3.因为两条切线相互垂直,所以y 02-1x 02-3=-1,即x 02+y 02=4(x 0≠±√3),由①②知G 在圆x 02+y 02=4上,又点G 在直线x+y+m=0上,所以直线x+y+m=0与圆x 2+y 2=4有公共点,所以1+1≤2,所以-2√2≤m ≤2√2.综上所述,m 的取值范围为[-2√2,2√2]. 2.解 (1)由抛物线定义,得|PF|=x 0+p2,由题意得{2x 0=x 0+p2,2px 0=4,p >0,解得{p =2,x 0=1.所以抛物线C 的方程为y 2=4x.(2)由题意知,过P (1,2)引圆(x-3)2+y 2=r 2(0<r ≤√2)的切线斜率存在且不为0,设切线PA 的方程为y=k 1(x-1)+2,则圆心M 到切线PA 的距离d=1√k 1+1=r ,整理得(r 2-4)k 12-8k 1+r 2-4=0.设切线PB 的方程为y=k 2(x-1)+2,同理可得(r 2-4)k 22-8k 2+r 2-4=0.所以k 1,k 2是方程(r 2-4)k 2-8k+r 2-4=0的两根,k 1+k 2=8r 2-4,k 1k 2=1. 设A (x 1,y 1),B (x 2,y 2),由{y =k 1(x -1)+2,y 2=4x ,得k 1y 2-4y-4k 1+8=0, 由韦达定理知,2y 1=8-4k1k 1,所以y 1=4-2k1k 1=4k 1-2=4k 2-2,同理可得y 2=4k 1-2.设线段AB 的中点为D ,则点D 的横坐标为t ,则t=x 1+x22=y 12+y 228=(4k 2-2)2+(4k 1-2)28=2(k 12+k 22)-2(k 1+k 2)+1=2(k 1+k 2)2-2(k 1+k 2)-3.设λ=k 1+k 2,则λ=8r 2-4∈[-4,-2),所以t=2λ2-2λ-3,对称轴λ=12>-2,所以9<t ≤37. 3.解 (1)由题意得2c=2,2a+2c=6,解得a=2,c=1,∴b 2=a 2-c 2=3.∴椭圆C 的方程为x 24+y 23=1.(2)设A (x 1,y 1),B (x 2,y 2).当直线l 与x 轴垂直时,由椭圆的对称性可知,点M 在x 轴上,且与O 点不重合, 显然M ,O ,P 三点不共线,不符合题设条件, 故可设直线l 的方程为y=kx+m (m ≠0). 由{y =kx +m ,3x 2+4y 2=12,消去y 整理得:(3+4k2)x2+8kmx+4m2-12=0,①则Δ=64k2m2-4(3+4k2)(4m2-12)>0.∴x1+x2=-8km3+4k2,x1x2=4m2-123+4k2.∴点M的坐标为-4km3+4k 2,3m3+4k2.∵M,O,P三点共线,∴k OM=k OP,∴3m3+4k2-4km3+4k2=12.∵m≠0,∴k=-32,此时方程①为3x2-3mx+m2-3=0,则Δ=3(12-m2)>0.∴m∈(-2√3,2√3).则x1+x2=m,x1x2=m 2-33.∴|AB|2=(1+k2)(x1+x2)2-4x1x2=1312(12-m2).又d=√3+2=√13,∴12 13|AB|2+1316d2=(12-m2)+(m-4)24=-34(m+43)2+523.∴当m=-43∈(-2√3,2√3)时,1213|AB|2+1316d2取得最大值为523.4.解(1)由题意知F(0,2),所以p=4.所以抛物线C的方程为x2=8y.将x2=8y与x2+y2=4联立得点A的纵坐标为y A=2(√5-2),结合抛物线定义得|AF|=y A +p2=2√5-2. (2)由x 2=2py 得y=x 22p ,y'=x p ,所以直线l 的斜率为x0,故直线l 的方程为y-y 0=x(x-x 0).即x 0x-py-py 0=0. 又由|ON|=0√x 0+p=2得p=8y 0y 02-4且y 02-4>0, 所以|MN|2=|OM|2-|ON|2=x 02+y 02-4 =2py 0+y 02-4=16y 002-4y 0+y 02-4 =16y 02y 02-4+y 02-4=16(y 02-4+4)y 02-4+y 02-4 =16+64y 02-4+y 02-4. 令t=y 02-4,y 0∈[3,4],则t ∈[5,12],令f (t )=16+t+64t ,则f'(t )=1-64t2; 当t ∈[5,8]时f'(t )≤0,f (t )单调递减, 当t ∈(8,12]时f'(t )>0,f (t )单调递增,又f (5)=16+5+645=1695,f (12)=16+12+6412=1003<1695, 所以f (x )max =1695,即|MN|的最大值为13√55. 5.解 (1)点M (2,2)在抛物线y 2=2px 上,故有22=4p ,所以p=1,从而抛物线方程为y 2=2x. 设直线l 的方程为x=n (y-2)+2,代入y 2=2x ,得y 2-2ny+4n-4=0.由l 与抛物线相切可知,Δ=4n 2-4(4n-4)=0,解得n=2. 所以,直线l 的方程为x=2(y-2)+2,即x-2y+2=0. (2)设直线l 的方程为x=my+t (m ≠0),代入y 2=2px 得y 2-2pmy-2pt=0.由直线l 与抛物线相切可知,Δ=4p 2m 2+8pt=0. 所以t=-pm 22.①又因为直线l 与圆x 2+y 2=1相切,所以√2=1,即t 2=1+m 2.②将①式代入②式,得p 2m 44=1+m 2,所以p 2=4(1+m 2)m 4. 设M 的坐标为(x 0,y 0),由y 2-2pmy-2pt=0与t=-pm 22可知y 0=pm ,从而x 0=my 0+t=pm 22.所以|MN|2=|OM|2-|ON|2=x 02+y 02-1=p 2m 44+p 2m 2-1=1+m 2+4(1+m 2)m 2-1=m 2+4m 2+4≥8.因此,当|m|=√2时,|MN|有最小值,最小值为2√2.突破2 圆锥曲线中的定点、定值与存在性问题1.解 (1)在△ABC 中,由余弦定理得AB 2=CA 2+CB 2-2CA·CB·cos C=(CA+CB )2-3CA·CB=4.(*)又因为S △ABC =12CA·CB·sin C=√34CA·CB=√33,所以CA·CB=43, 代入(*)式得CA+CB=2√2,即椭圆长轴长2a=2√2,焦距2c=AB=2, 所以椭圆M 的标准方程为x 22+y 2=1.(2)存在.设直线方程为y=k (x-1),联立{x 22+y2=1,y =k (x -1),消去y ,得(1+2k 2)x 2-4k 2x+2k 2-2=0,Δ=8k 2+8>0,设交点E (x 1,y 1),F (x 2,y 2),所以x 1+x 2=4k21+2k 2,x 1x 2=2k 2-21+2k2.假设x 轴上存在定点D (x 0,0),使得DE ⃗⃗⃗⃗⃗ ·DF ⃗⃗⃗⃗⃗ 为定值,所以DE ⃗⃗⃗⃗⃗ ·DF ⃗⃗⃗⃗⃗ =(x 1-x 0,y 1)·(x 2-x 0,y 2)=x 1x 2-x 0(x 1+x 2)+x 02+y 1y 2 =x 1x 2-x 0(x 1+x 2)+x 02+k 2(x 1-1)(x 2-1) =(1+k 2)x 1x 2-(x 0+k 2)·(x 1+x 2)+x 02+k 2 =(2x 02-4x 0+1)k 2+(x 02-2)1+2k2, 要使DE ⃗⃗⃗⃗⃗ ·DF ⃗⃗⃗⃗⃗ 为定值,则DE ⃗⃗⃗⃗⃗ ·DF ⃗⃗⃗⃗⃗ 的值与k 无关,所以2x 02-4x 0+1=2(x 02-2),解得x 0=54,此时DE ⃗⃗⃗⃗⃗ ·DF ⃗⃗⃗⃗⃗ =-716为定值,定点为54,0.2.解 (1)∵S △ABE =12×2p×p=4.∴p 2=4, ∵p>0,∴p=2. ∴y 2=4x.(2)存在.设存在直线l 1:x=a 满足条件,P (x 0,y 0),则PQ 的中点Mx 0+22,y 02,|PQ|=√(x 0-2)2+y 02,因此以PQ 为直径的圆的半径r=12|PQ|=12√(x 0-2)2+y 02=12√x 02+4,M 点到直线x=a 的距离 d=x 0+22-a .所以所截弦长为222=2√14(x 02+4)-(x 0+22-a)2=√x 02+4-(x 0+2-2a )2=√-4(1-a )x 0+8a -4a 2,要使弦长与变量x 0无关,则令1-a=0即a=1时,弦长为定值2, 这时直线方程为x=1.故存在垂直于x 轴的定直线x=1,被以PQ 为直径的圆截得的弦长为定值2. 3.(1)解由题意,得|BF|=|BO|,则△BOF 为等腰三角形,因为点B 的横坐标为12,所以线段OF 的中点的横坐标为12, 从而点F 的横坐标为1,即p 2=1,所以p=2, 故所求抛物线C 的方程为y 2=4x.(2)证明设切线m 的方程为y=kx+b ,由{y =kx +b ,y 2=4x ,得k 2x 2+2(kb-2)x+b 2=0,(*)由题意知Δ=4(kb-2)2-4k 2b 2=0,即b=1k , 所以方程(*)的根为x=1k 2,从而A1k 2,2k .直线OA 的方程为y=2kx , 由{y =kx +1k ,x =-1,得N -1,1k -k ,由{y =2kx ,x =-1,得M (-1,-2k ),所以以点N 为圆心,以|MN|为半径的圆的方程为(x+1)2+(y -1+k)2=(k +1)2, 令y=0,得(x+1)2+(k -1)2=(k +1)2,解得x=1或x=-3, 所以圆N 经过x 轴上的两个定点(1,0)和(-3,0). 4.解 (1)因为椭圆C 的离心率e=√22,所以c a =√22,即a=√2c.因为抛物线y 2=4√2x 的焦点F (√2,0)恰好是该椭圆的一个顶点, 所以a=√2,所以b=1.所以椭圆C 的方程为x 22+y 2=1.(2)(i)当直线l 的斜率不存在时.因为直线l 与圆M 相切,故其中的一条切线方程为x=√63. 由{x =√63,x 22+y 2=1,不妨设A √63,√63,B √63,-√63,则以AB 为直径的圆的方程为(x -√63)2+y 2=23. (ii)当直线l 的斜率为零时.因为直线l 与圆M 相切,所以其中的一条切线方程为y=-√63. 由{y =-√63,x 22+y 2=1,不妨设A √63,-√63,B -√63,-√63,则以AB 为直径的圆的方程为x 2+(y +√63)2=23. 显然以上两圆都经过点O (0,0). (iii)当直线l 的斜率存在且不为零时. 设直线l 的方程为y=kx+m. 由{y =kx +m ,x 2+y 2=1消去y ,得(2k 2+1)x 2+4kmx+2m 2-2=0,所以设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-4km2k 2+1,x 1x 2=2m 2-22k 2+1.所以y 1y 2=(kx 1+m )(kx 2+m )=k 2x 1x 2+km (x 1+x 2)+m 2=m 2-2k22k 2+1.所以OA ⃗⃗⃗⃗⃗ ·OB⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2=3m 2-2k 2-22k 2+1.①因为直线l 和圆M 相切,所以圆心到直线l 的距离d=√1+k =√63,整理,得m 2=2(1+k 2),②将②代入①,得OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ =0,显然以AB 为直径的圆经过定点O (0,0). 综上可知,以AB 为直径的圆过定点(0,0). 5.(1)解由题意可知:2c=a ,2b=2√3,又a 2=b 2+c 2,有b=√3,c=1,a=2,故椭圆C 的方程为x 24+y 23=1.(2)证明由题意知直线l 的斜率存在,设其方程为y=kx+1,设A (x 1,y 1),B (x 2,y 2)(x 1x 2≠0),联立直线方程和椭圆方程得{y =kx +1,3x 2+4y 2-12=0,消去y 得(4k 2+3)x 2+8kx-8=0, x 1+x 2=-8k4k 2+3,x 1x 2=-84k 2+3,则有x 1+x 2=kx 1x 2,又l BN :y=y 2+√3x2·x-√3,l AM :y=y 1-√3x 1·x+√3,由{y =y 2+√3x 2·x -√3,y =y 1-√3x 1·x +√3,得√3y+√3=y 1-√3x 1·2y 2+√3,故√3y+√3=kx 1+1-√3x 1·2kx +1+√3=12√3)2kx x +(1+√3)x 整理得到y=√3[1212√3(1-x 2x -x +√3(x +x )=√3[12√3(12x -x +√3(x +x )=3.故点T 的纵坐标为3.突破3 圆锥曲线中的证明与探索性问题1.(1)解显然直线l 的斜率存在且不为0,设直线l 的方程为y+2=k (x-1),与y 2=4x 联立,消去x 整理得y 2-4k y-8k -4=0,令Δ=0,即-4k 2-4-8k -4=0, 解得k=-1,所以直线l 的方程为y=-x-1. (2)证明由题意知,两直线BM ,BN 的斜率互为相反数,设直线BM 的方程为y-2=t (x-1),与y 2=4x 联立,消去x 整理得y2-4t y+8t -4=0,则2y P =8t -4⇒y P =4t -2,从而P t 2-4t+4t 2,4-2t t ,将t 换成-t ,得Q t 2+4t+4t 2,-2t -4t ,k PQ =4-2t t --2t -4t t 2-4t+4t 2-t 2+4t+4t 2=8t -8t t 2=-1=k l , 所以直线PQ 与l 平行.2.(1)解当l 与x 轴垂直时,l 的方程为x=2,可得M 的坐标为(2,2)或(2,-2).所以直线BM 的方程为y=12x+1或y=-12x-1.(2)证明当l 与x 轴垂直时,AB 为MN 的垂直平分线,所以∠ABM=∠ABN.当l 与x 轴不垂直时,设l 的方程为y=k (x-2)(k ≠0),M (x 1,y 1),N (x 2,y 2),则x 1>0,x 2>0. 由{y =k (x -2),y 2=2x得ky 2-2y-4k=0,可知y 1+y 2=2k ,y 1y 2=-4. 直线BM ,BN 的斜率之和为k BM +k BN =y 1x 1+2+y 2x 2+2 =x 2y 1+x 1y 2+2(y 1+y 2)(x 1+2)(x 2+2).① 将x 1=y 1k +2,x 2=y 2k +2及y 1+y 2,y 1y 2的表达式代入①式分子,可得x 2y 1+x 1y 2+2(y 1+y 2)=2y 1y 2+4k (y 1+y 2)k =-8+8k =0. 所以k BM +k BN =0,可知BM ,BN 的倾斜角互补,所以∠ABM=∠ABN.综上,∠ABM=∠ABN.3.解 (1)因为圆x 2+y 2-4x-60=0的圆心为F 2,所以|F 2D|=|F 2C|且F 1E ∥CF 2,所以∠F 2DC=∠F 2CD=∠EF 1D ,所以|EF 1|=|ED|,所以|EF 1|+|EF 2|=|ED|+|EF 2|=|DF 2|,又因为圆F 2的半径为8,即|DF 2|=8,所以|EF 1|+|EF 2|=8.(2)存在.由(1)知,曲线E 1是以F 1,F 2为焦点的椭圆,且长轴长为8,所以曲线E 1的方程为x 216+y 212=1(y ≠0).设直线l 的方程为y=k (x+2),代入椭圆化简得(4k 2+3)x 2+16k 2x+16k 2-48=0,设A (x 1,y 1),B (x 2,y 2),N (x 0,y 0),则x 1+x 2=-16k 24k 2+3,x 1x 2=16k 2-484k 2+3, 所以k 1+k 2=y 0-y 1x 0-x 1+y 0-y 2x 0-x 2=(2y 0-4k )x 0+(2k -kx 0-y 0)(x 1+x 2)+2kx 1x 2x 02-x 0(x 1+x 2)+x 1x 2 =8y 0k 2(x 0+2)-12k (x 0+8)+6x 0y 04k 2(x 0+2)2+3x 0-48, 因为k 1,k 3,k 2成等差数列,所以2k 3=k 1+k 2,易知M (-8,-6k ),则k 3=y 0+6kx 0+8, 所以2×y 0+6kx 0+8 =8y 0k 2(x 0+2)-12k (x 0+8)+6x 0y 04k 2(x 0+2)2+3x 02-48, 化简得24k 3(x 0+2)2-24k 2y 0(x 0+2)+24k (x 0+2)2-24y 0(x 0+2)=0,对任意的k 该等式恒成立,所以x 0=-2,所以存在点N (-2,±3),使得k 1,k 3,k 2成等差数列.4.解 (1)由椭圆的对称性,不妨设在x 轴上方的切点为M ,x 轴下方的切点为N ,则k NE =1,NE 的直线方程为y=x-√7,因为椭圆C 1:x 2a 2+y 2b 2=1(a>b>0)的离心率为12, 所以椭圆C 1:x 22+y 22=1, 所以{y =x -√7,x 24c 2+y 23c 2=1,消去y 得7x 2-8√7x+28-12c 2=0.Δ=0,则c=1,所以椭圆方程为x 24+y 23=1.(2)设点B (x 1,y 1),C (x 2,y 2),P (x 0,y 0),由x 2=4y ,即y=14x 2,得y'=12x , ∴抛物线C 2在点B 处的切线l 1的方程为y-y 1=x 12(x-x 1),即y=x 12x+y 1-12x 12, ∵y 1=14x 12,∴y=x12x-y 1. ∵点P (x 0,y 0)在切线l 1上,∴y 0=x 12x 0-y 1.①同理,y 0=x22x 0-y 2.② 综合①、②得,点B (x 1,y 1),C (x 2,y 2)的坐标都满足方程y 0=x 2x 0-y. ∵经过B (x 1,y 1),C (x 2,y 2)两点的直线是唯一的,∴直线BC 的方程为y 0=x 2x 0-y ,∵点A (1,1)在直线BC 上,∴y 0=12x 0-1,∴点P 的轨迹方程为y=1x-1.又∵点P 在椭圆C 1上,又在直线y=12x-1上, ∴直线y=12x-1经过椭圆C 1内一点(0,-1),∴直线y=1x-1与椭圆C 1交于两点.∴满足条件的点P 有两个.5.证明 (1)设直线l 的方程为y=kx+4,设A (x 1,y 1),B (x 2,y 2),{x 12=4y 1,x 22=4y 2,两式相乘得(x 1x 2)2=16y 1y 2. 将直线l 的方程代入抛物线x 2=4y ,得x 2-4kx-16=0.∴x 1x 2=-16,∴y 1y 2=16,∴x 1x 2+y 1y 2=0,∴OA ⃗⃗⃗⃗⃗ ·OB⃗⃗⃗⃗⃗ =0. ∴OA ⊥OB.(2)设直线l :y=kx+m ,A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),D (x 4,y 4).联立y=kx+m 和x 2=4y ,得x 2-4kx-4m=0,则x 1+x 2=4k ,x 1x 2=-4m ,k 1+k 2=y 1x 1+y 2x 2=x 14+x24=k , 联立y=kx+m 和x 26+y 24=1得(2+3k 2)x 2+6kmx+3m 2-12=0,在Δ=(6km )2-4(2+3k 2)(3m 2-12)>0(即4+6k 2>m 2)可不求解的情况下, x 3+x 4=-6km 2+3k 2,x 3x 4=3m 2-122+3k 2,k 3+k 4=y 3x 3+y 4x 4=2k+m x 3+m x 4=2k+m (x 3+x 4)x 3x 4=2k+-6km 23m 2-12=-8k m 2-4, 所以k 1+k 2k 3+k 4=-m 2-48是一个与k 无关的值.快乐分享，知识无界！感谢您的下载!由Ruize收集整理！。

2021年高考数学一轮复习《直线与圆锥曲线的综合问题》精选练习(原卷版)

2021年高考数学一轮复习《直线与圆锥曲线的综合问题》精选练习一、选择题1.过抛物线y 2=8x 的焦点F 的直线交抛物线于A ，B 两点，交抛物线的准线于C ，若|AF|=6， BC →=λFB →，则λ的值为( ) A.34 B.32 C. 3 D.3 2.若直线ax ＋by －3=0与圆x 2＋y 2=3没有公共点，设点P 的坐标为(a ，b)，则过点P 的一条直线与椭圆x 24＋y 23=1的公共点的个数为( ) A.0 B.1 C.2 D.1或23.设F 1，F 2分别是椭圆x 2a 2＋y 2b2=1(a ＞b ＞0)的左、右焦点，过F 2的直线交椭圆于P ，Q 两点，若∠F 1PQ=60°，|PF 1|=|PQ|，则椭圆的离心率为( )A.13B.23C.233D.334.已知双曲线x 2a 2－y 2b2=1(a ＞0，b ＞0)与直线y=2x 有交点，则双曲线离心率的取值范围为( )A.(1，5)B.(1，5]C.(5，＋∞)D.[5，＋∞)5.如图，F 1，F 2是双曲线C ：x 2a 2－y 2b2=1(a ＞0，b ＞0)的左、右焦点，过F 1的直线l 与C 的两个分支分别交于点A ，B.若△ABF 2为等边三角形，则双曲线的离心率为( )A.4B.7C.233D. 3 6.已知不过原点O 的直线交抛物线y 2=2px 于A ，B 两点，若OA ，AB 的斜率分别为k OA =2，k AB =6，则OB 的斜率为( )A.3B.2C.－2D.－37.已知直线y=kx －1与双曲线x 2－y 2=4的右支有两个交点，则k 的取值范围为( )A.⎝ ⎛⎭⎪⎫0，52B.⎣⎢⎡⎦⎥⎤1，52C.⎝ ⎛⎭⎪⎫－52，52D.⎝⎛⎭⎪⎫1，52 8.过原点的直线l 与双曲线x 29－y 23=－1有两个交点，则直线l 的倾斜角的取值范围是( ) A.⎣⎢⎡⎦⎥⎤π6，5π6 B.⎝ ⎛⎭⎪⎫π6，5π6 C.⎝ ⎛⎭⎪⎫π6，π2∪⎝ ⎛⎭⎪⎫π2，5π6 D.⎣⎢⎡⎭⎪⎫π6，π2∪⎝ ⎛⎦⎥⎤π2，5π6 9.已知直线y=1－x 与双曲线ax 2＋by 2=1(a ＞0，b ＜0)的渐近线交于A 、B 两点，且过原点和线段AB 中点的直线的斜率为－32，则a b的值为( ) A.－32 B.－233 C.－932 D.－232710.已知双曲线x 23－y 2=1的右焦点是抛物线y 2=2px(p ＞0)的焦点，直线y=kx ＋m 与抛物线相交于A ，B 两个不同的点，点M(2,2)是线段AB 的中点，则△AOB(O 为坐标原点)的面积是( )A.4 3B.313C.14D.2 3 11.已知双曲线C ：x 2a 2－y 2b2=1(a ＞0，b ＞0)，F 是双曲线C 的右焦点，过F 作双曲线C 在第一、三象限的渐近线的垂线l ，若l 与双曲线C 的左、右两支分别交于点D ，E ，则双曲线C 的离心率e 的取值范围为( ) A.(2，3) B.(2，＋∞) C.(2，2) D.(1，62) 12.已知双曲线x 2a 2－y 2b2=1(a ＞0，b ＞0)上的一点到双曲线的左、右焦点的距离之差为4，若抛物线y=ax 2上的两点A(x 1，y 1)，B(x 2，y 2)关于直线y=x ＋m 对称，且x 1x 2=－12，则m 的值为( ) A.32 B.52C.2D.3 二、填空题13.设抛物线x 2=4y 的焦点为F ，点A ，B 在抛物线上，且满足AF ―→=λFB ―→，若|AF ―→|=32，则λ的值为________. 14.已知抛物线C ：y 2=2px(p ＞0)，直线l ：y=3(x －1)，l 与C 交于A ，B 两点，若|AB|=163，则p=________.15.已知双曲线E ：x 24－y 22=1，直线l 交双曲线于A ，B 两点，若线段AB 的中点坐标为(12,-1)，则l 的方程为________.16.已知抛物线C ：y 2=2px(p ＞0)的焦点为F ，过点F 且倾斜角为60°的直线l 与抛物线C在第一、四象限分别交于A ，B 两点，则|AF||BF|的值等于________. 三、解答题17.已知直线l ：y=x ＋m ，m ∈R .(1)若以点M(2，－1)为圆心的圆与直线l 相切于点P ，且点P 在x 轴上，求该圆的方程；(2)若直线l 关于x 轴对称的直线l ′与抛物线C ：x 2=1my(m ≠0)相切，求直线l 和抛物线C 的方程.18.已知椭圆C ：x 2a 2＋y 2b 2=1(a>b>0)的左、右焦点分别为F 1，F 2，且离心率为22，过左焦点F 1的直线l 与C 交于A ，B 两点，△ABF 2的周长为4 2.(1)求椭圆C 的方程；(2)当△ABF 2的面积最大时，求l 的方程.19.已知△ABC的顶点A(1,0)，点B在x轴上移动，|AB|=|AC|，且BC的中点在y轴上.(1)求点C的轨迹T的方程；(2)已知过P(0，－2)的直线l交轨迹Γ于不同两点M，N，求证：Q(1,2)与M，N两点连线QM，QN的斜率之积为定值.20.已知直线l过点P(2,0)且与抛物线E：y2=4x相交于A，B两点，与y轴交于点C，其中点A在第四象限，O为坐标原点.(1)当A是PC中点时，求直线l的方程；(2)以AB为直径的圆交直线OB于点D，求|OB|·|OD|的值.21.已知椭圆E ：x 2a 2＋y 2b 2=1(a>b>0)经过点⎝ ⎛⎭⎪⎫1，32，且离心率e=12. (1)求椭圆E 的方程；(2)设椭圆E 的右顶点为A ，若直线l ：y=kx ＋m 与椭圆E 相交于M 、N 两点(异于A 点)，且满足MA ⊥NA ，试证明直线l 经过定点，并求出该定点的坐标.22.已知椭圆C 1的焦点在x 轴上，中心在坐标原点；抛物线C 2的焦点在y 轴上，顶点在坐标原点.在C 1，C 2上各取两个点，将其坐标记录于表格中：(1)求C 1，C 2的标准方程；(2)已知定点C ⎝ ⎛⎭⎪⎫0，18，P 为抛物线C 2上一动点，过点P 作抛物线C 2的切线交椭圆C 1于A ，B 两点，求△ABC 面积的最大值.23.已知椭圆C ：x 2a 2＋y 2b 2=1(a ＞b ＞0)的焦距为4，P ⎝⎛⎭⎪⎫2，55是椭圆C 上的点. (1)求椭圆C 的方程；(2)O 为坐标原点，A ，B 是椭圆C 上不关于坐标轴对称的两点，设OD ―→=OA ―→＋OB ―→.证明：直线AB 的斜率与OD 的斜率的乘积为定值.。

2021高考数学一轮复习专练54曲线与方程含解析理新人教版

专练54 曲线与方程命题范围：求轨迹方程的常用方法：直接法、定义法、相关点法等[基础强化]一、选择题1．已知平面内动点P 满足|PA |＋|PB |＝4，其中|AB |＝4，则点P 点轨迹是( ) A ．直线 B ．线段 C ．圆 D ．椭圆2．已知点(0,0)，A (1，－2)，动点P 满足|PA |＝3|PO |，则P 点的轨迹方程是( )A ．8x 2＋8y 2＋2x －4y －5＝0B ．8x 2＋8y 2－2x －4y －5＝0C ．8x 2＋8y 2＋2x ＋4y －5＝0D ．8x 2＋8y 2－2x ＋4y －5＝03．若M ，N 为两个定点，且MN ＝6，动点P 满足PM →·PN →＝0，则P 点的轨迹是( ) A ．圆 B ．椭圆C ．双曲线D ．抛物线4．已知点A (1,0)，直线l ：y ＝2x －4，点R 是直线l 上的一点，若RA →＝AP →，则点P 的轨迹方程为( )A ．y ＝－2xB ．y ＝2xC ．y ＝2x －8D ．y ＝2x ＋45．若点P 到直线x ＝－1的距离比它到点(2,0)的距离小1，则点P 的轨迹为( ) A ．圆 B ．椭圆C ．双曲线D ．抛物线 6．设P 为双曲线x 24－y 2＝1上一动点，O 为坐标原点，M 为线段OP 的中点，则点M 的轨迹方程是( )A.x 28－y 22＝1 B ．x 2－4y 2＝1 C.x 24－y 2＝1 D.x 22－2y 2＝1 7．设A ，B 为椭圆x 22＋y 2＝1的左右顶点，O 为坐标原点，若|PO |是|PA |和|PB |的等比中项，则点P 的轨迹方程为( )A ．x 2－y 2＝1B ．x 2－y 2＝2C ．y 2－x 2＝1D ．y 2－x 2＝28．[2020·山东德州一中高三测试]已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的一个焦点在抛物线y 2＝16x 的准线上，且双曲线的一条渐近线过点(3，3)，则双曲线的方程为( )A.x 24－y 220＝1B.x 212－y 24＝1 C.x 24－y 212＝1 D.x 220－y 24＝1 9．已知点F (0,1)，直线l ：y ＝－1，P 为平面上的动点，过点P 作直线l 的垂线，垂足为Q ，且QP →·QF →＝FP →·FQ →，则动点P 的轨迹C 的方程为( )A ．x 2＝4yB ．y 2＝3xC ．x 2＝2yD ．y 2＝4x 二、填空题10．已知直线l 过点(1,0)且垂直于x 轴．若l 被抛物线y 2＝4ax 截得的线段长为4，则抛物线的焦点坐标为________．11．到点O (0,0)和A (1,0)的距离的平方和为1的轨迹方程为________．12．设F 是抛物线y ＝14x 2的焦点，P 是抛物线上的动点，则线段PF 中点的轨迹方程是________．[能力提升]13．已知两圆C 1：(x －4)2＋y 2＝169，C 2：(x ＋4)2＋y 2＝9.动圆M 在圆C 1内部且和圆C 1内切，和圆C 2相外切，则动圆圆心M 的轨迹方程为( )A.x 264－y 248＝1B.x 248＋y 264＝1C.x 248－y 264＝1 D.x 264＋y 248＝1 14．已知点Q 在椭圆C ：x 216＋y 210＝1上，点P 满足OP →＝12(OF 1→＋OQ →)(其中O 为坐标原点，F 1为椭圆C 的左焦点)，则点P 的轨迹为( )A ．圆B ．抛物线C ．双曲线D ．椭圆15．在平面直角坐标系中，O 为坐标原点，A (1,0)，B (2,2)，若点C 满足OC →＝OA →＋t (OB →－OA →)，其中t ∈R ，则点C 的轨迹方程是______________．16．曲线y ＝1kx －1与y ＝kx ＋1(k 为参数)的交点的轨迹方程为______________．专练54 曲线与方程1．B ∵|PA |＋|PB |＝4＝|AB |，∴点P 的轨迹是线段AB . 2．A 设P (x ，y )，∵|PA |＝3|PO |，∴(x －1)2＋(y ＋2)2＝9(x 2＋y 2)即：8x 2＋8y 2＋2x －4y －5＝0.3．A PM →·PN →＝0，∴PM ⊥PN ，∴点P 的轨迹是以MN 为直径的圆．4．B 设P (x ，y )，R (x 1，y 1)，由RA →＝AP →，得(1－x 1，－y 1)＝(x －1，y )，∴⎩⎪⎨⎪⎧x 1＝2－x ，y 1＝－y ，又(x 1，y 1)在直线l 上，∴－y ＝2(2－x )－4，即y ＝2x .5．D 由题意得P 到直线x ＝－2的距离与它到(2,0)的距离相等，∴点P 的轨迹为抛物线．6．B 设M (x ，y )，P (x 1，y 1)，∵M 为OP 的中点， ∴⎩⎪⎨⎪⎧2x ＝x 1，2y ＝y 1，又(x 1，y 1)在x 24－y 2＝1上，∴4x 24－4y 2＝1，即：x 2－4y 2＝1即为所求． 7．A 设P (x ，y )，又A (－2，0)，B (2，0)，且|PO |2＝|PA ||PB |， ∴x 2＋y 2＝x ＋22＋y 2·x －22＋y 2，化简得x 2－y 2＝1，∴点P 的轨迹方程为x 2－y 2＝1.8．C ∵y 2＝16x 的准线方程为x ＝－4，∴a 2＋b 2＝4， ①又双曲线的一条渐近线过(3，3)，∴3＝3ba，即b ＝3a ②将①②联立，得⎩⎪⎨⎪⎧a 2＝4，b 2＝12，∴双曲线方程为x 24－y 212＝1.9．A 设点P (x ，y )，则Q (x ，－1)，QP →＝(0，y ＋1)，QF →＝(－x,2)，FP →＝(x ，y －1)，FQ →＝(x ，－2)．∵QP →·QF →＝FP →·FQ →，∴(0，y ＋1)·(－x,2)＝(x ，y －1)·(x ，－2)，即2(y ＋1)＝x 2－2(y －1)，整理得 x 2＝4y ，∴动点P 的轨迹C 的方程为x 2＝4y . 10．(1,0)解析：由题意得a >0，设直线l 与抛物线的两交点分别为A ，B ，不妨令A 在B 的上方，则A (1,2a )，B (1，－2a )，故|AB |＝4a ＝4，得a ＝1，故抛物线方程为y 2＝4x ，其焦点坐标为(1,0)．11．x 2＋y 2－x ＝0解析：设P (x ，y )为所求曲线上一点，由题意得x 2＋y 2＋(x －1)2＋y 2＝1.整理得x 2＋y 2－x ＝0.12．x 2＝2y －1解析：由题意得F (0,1)，设PF 的中点为M (x ，y )，P (x 1，y 1)，由题意得⎩⎪⎨⎪⎧ x 1＝2x ，1＋y 1＝2y ，得⎩⎪⎨⎪⎧x 1＝2x ，y 1＝2y －1，又(x 1，y 1)在y ＝14x 2上，∴2y －1＝14×(2x )2＝x 2，即x 2＝2y －1.13．D 设圆M 的半径为r ，则由已知得|MC 1|＋|MC 2|＝(13－r )＋(3＋r )＝16，而|C 1C 2|＝8，且16>8，所以M 的轨迹是以C 1，C 2为焦点的椭圆，且2a ＝16,2c ＝8. 故所求的轨迹方程为x 264＋y 248＝1.14．D 由题意得：F 1(－2,0)，P 为F 1Q 的中点，设P (x ，y )，Q (x 1，y 1)则⎩⎪⎨⎪⎧－2＋x 1＝2x ，y 1＝2y ，得⎩⎪⎨⎪⎧x 1＝2x ＋2，y 1＝2y ，又(x 1，y 1)在椭圆C 上，∴2x ＋2216＋2y 210＝1，∴点P 的轨迹为椭圆．15．y ＝2x －2解析：设C (x ，y )，又OC →＝OA →＋t (OB →－OA →)， ∴⎩⎪⎨⎪⎧x ＝t ＋1，y ＝2t ，消去参数t ，得y ＝2x －2.16．y 2－x 2＝1 解析：由⎩⎪⎨⎪⎧y ＝1kx －1，y ＝kx ＋1，得(y ＋1)(y －1)＝1kx ·kx ＝x 2，整理得y 2－x 2＝1.。

2021届高考数学一轮温习阶段检测试题（五）理新人教版

阶段检测试题(五)(时间:120分钟满分:150分)【选题明细表】知识点、方法题号直线的方程、圆的方程3直线与直线、直线与圆、圆与圆的位置关系1,2,13,14椭圆定义、标准方程及简单几何性质的应用7,8,11,16双曲线定义、标准方程及简单几何性质的应用6,8,9,10抛物线定义、标准方程及简单几何性质的应用4,15轨迹方程5,12最值、范围问题、证明问题17,20定点、定值问题、存在性问题18,19,21,22 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.直线l1:2x-y-1=0与直线l2:mx+y+1=0彼此垂直的充要条件是( C )(A)m=-2 (B)m=- (C)m= (D)m=2解析:直线l1:2x-y-1=0与直线l2:mx+y+1=0垂直⇔2m-1=0⇔m=.故选C.2.过原点且与圆x2+y2-4x+3=0相切的直线的倾斜角为( B )(A)或(B)或(C)或(D)或解析:由x2+y2-4x+3=0,得(x-2)2+y2=1,所以圆心为(2,0),半径为1.设直线l的方程为kx-y=0,由圆与直线相切得=1,解得k=±.设直线l的倾斜角为θ(0≤θ<π),由tan θ=±,得θ=或.所以直线l的倾斜角为或.故选B.3.圆E通过三点A(0,1),B(2,0),C(0,-1),且圆心在x轴的正半轴上,则圆E的标准方程为( C )(A)（x-）2+y2= (B)(x+)2+y2=(C)(x-)2+y2= (D)(x-)2+y2=解析:按照题意,设圆E的圆心坐标为(a,0)(a>0),半径为r,则有解得a=,r2=,所以要求圆的方程为(x-)2+y2=.故选C.4.点M(5,3)到抛物线y=ax2的准线的距离为6,那么抛物线的方程是( D )(A)y=12x2 (B)y=12x2或y=-36x2(C)y=-36x2(D)y=x2或y=-x2解析:将y=ax2化为x2=y,准线y=-,由已知得|3+|=6,所以a=-或a=.所以抛物线方程为y=或y=-x2.故选D.5.已知动点P(x,y)知足5=|3x+4y-1|,则点P的轨迹是( B )(A)直线 (B)抛物线(C)双曲线(D)椭圆解析:动点P(x,y)知足5=|3x+4y-1|,可得=,表示动点P(x,y)到(1,2)与到直线3x+4y-1=0距离相等,又(1,2)不在直线3x+4y-1=0上,则点P的轨迹是以(1,2)为核心以直线3x+4y-1=0为准线的抛物线.故选B.6.已知双曲线-=1(a>0,b>0)与抛物线y2=8x有一个公共的核心F,且两曲线的一个交点为Ρ,若|ΡF|=5,则双曲线的渐近线方程为( D )(A)x±2y=0 (B)2x±y=0(C)x±y=0 (D)x±y=0解析:抛物线y2=8x的核心坐标为(2,0),准线方程为直线x=-2,因为双曲线-=1与抛物线y2=8x有一个公共的焦点F,则双曲线的半焦距c=2,a2+b2=4, ①又因为|PF|=5,所以点P的横坐标为3,代入抛物线y2=8x得,y=±2,则P(3,±2),因为点P在双曲线上,则有-=1, ②联立①②,解得a=1,b=,所以双曲线方程为x2-=1,其渐近线方程为y=±x.故选D.7.椭圆+=1的左核心为F,直线x=a与椭圆相交于点M,N,当△FMN的周长最大时,△FMN的面积是( C )(A)(B)(C)(D)解析:设右核心为F′,连接MF′,NF′.因为|MF′|+|NF′|≥|MN|,所以当直线x=a过右核心时,△FMN的周长最大.由椭圆的概念可得△FMN的周长的最大值4a=4,c==1.把c=1代入椭圆标准方程得+=1,解得y=±,所以此时△FMN的面积S=×2×2×=.故选C.8.已知双曲线C:-=1(a>0,b>0)与椭圆+=1的核心重合,离心率互为倒数,设F1,F2为双曲线C的左、右焦点,P为右支上任意一点,则的最小值为( A )(A)4 (B)8 (C)16 (D)32解析:由椭圆+=1,可得其核心F1(-1,0),F2(1,0),离心率为,所以双曲线的离心率e=2=,解得a=.设|PF2|=t,由|PF1|-|PF2|=2a,则|PF1|=2a+t,所以===t++2≥2+2=4,当且仅当t=即t=|PF2|=1时取等号,所以的最小值为4.故选A.9.已知双曲线E:-=1(a>0,b>0),若矩形ABCD的四个极点在E上,AB,CD的中点为双曲线E的两个核心,且双曲线E的离心率是2.直线BD的斜率为k.则|k|等于( B )(A)2 (B) (C) (D)3解析:令x=c,代入双曲线的方程可得y=±b=±.由双曲线E的离心率是2,可得e==2,即c=2a,b==a,直线AC的斜率为k,则|k|====.即有|k|=.故选B.10.已知点A,B是双曲线-=1(a>0,b>0)的左、右极点,P为双曲线上除极点外的一点,记k PA,k PB别离表示直线PA,PB的斜率,若k PA·k PB=,则该双曲线的离心率为( C )(A)3 (B)2 (C) (D)解析:由题意知A(-a,0),B(a,0),设P(m,n),所以k PA·k PB=·=,又点P在双曲线上,所以-=1,化简得n2=,所以k PA·k PB==.所以e==.故选C.11.如图,已知椭圆C1:+y2=1,曲线C2:y=x2-1与y轴的交点为M,过坐标原点O的直线l与C2相交于A,B两点,直线MA,MB别离与C1相交于D,E两点,则·的值是( B )(A)正数(B)0 (C)负数(D)皆有可能解析:设A(x1,y1),B(x2,y2),过原点的直线l:y=tx,联立得x2-tx-1=0,则x1+x2=t,x1x2=-1,所以·=(x1,y1+1)·(x2,y2+1)=x1x2+(y1+1)(y2+1)=(t2+1)x1x2+t(x1+x2)+1=-(t2+1)+t2+1=0.而=λ,=μ,所以·=λμ·=0.故选B.12.已知椭圆C:+=1(a>b>0)的左、右极点分別为A,B,点M,N是椭圆C上关于长轴对称的两点,若直线AM与BN相交于点P,则点P的轨迹方程是( D )(A) x=±a(y≠0)(B)y2=2b(|x|-a)(y≠0)(C)x2+y2=a2+b2(y≠0)(D)-=1(y≠0)解析:由题意可知A(-a,0),B(a,0),设M(x0,y0),N(x0,-y0),y0≠0,P(x,y),y≠0,则直线PA的斜率k=,直线PA的方程y=(x+a), ①同理直线PB的斜率k=,直线PB的方程y=(x-a), ②①×②得y2=(x2-a2).由+=1,=(a2-),则y2=(x2-a2),整理得-=1(a>b>0)(y≠0),即点P的轨迹方程为-=1(a>b>0)(y≠0).故选D.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.直线ax-y+3=0与圆(x-2)2+(y-a)2=4相交于M,N两点,若|MN|≥2,则实数a的取值范围是.解析:由圆的方程得圆心坐标为(2,a),半径r=2,由d2+()2=r2=4,所以d2=4-,又因为圆心到直线ax-y+3=0的距离d=,|MN|≥2,所以≤,解得a≤-.答案:(-∞,-]14.已知a,b为正数,且直线 ax+by-6=0与直线 2x+(b-3)y+5=0彼此平行,则2a+3b的最小值为.解析:因为直线 ax+by-6=0与直线 2x+(b-3)y+5=0彼此平行,所以a(b-3)-2b=0且5a+12≠0,所以3a+2b=ab,即+=1,又a,b均为正数,则2a+3b=(2a+3b)( +)=4+9++≥13+2=25.当且仅当a=b=5时上式等号成立.答案:2515.抛物线y2=4x的核心为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为.解析:设AB的中点为H,抛物线y2=4x的核心为F(1,0),准线为x=-1,设A,B,H在准线上的射影别离为A′,B′,H′,则|HH′|= (|AA′|+|BB′|),由抛物线的概念可得,|AF|=|AA′|,|BF|=|BB′|,|AF|+|BF|=6,即为|AA′|+|BB′|=6,|HH′|=×6=3,即有H的横坐标为2,设直线AB:y=kx+3,代入抛物线方程,可得k2x2+(6k-4)x+9=0,即有判别式(6k-4)2-36k2>0,解得k<且k≠0,又x1+x2==2x H=4,解得k=-2或 (舍去),则直线AB:y=-2x+3,AB的中点为(2,-1),AB的中垂线方程为y+1= (x-2),令y=0,解得x=4,则D(4,0).答案:416.已知椭圆C:+=1(a>b>0)的左核心为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|AF|=6,cos∠ABF=,则C的离心率e= .解析:设椭圆的右核心为F1,在△ABF中,由余弦定理可解得|BF|=8,所以△ABF为直角三角形,又因为斜边AB的中点为O,所以|OF|=c=5,连接AF1,因为A,B关于原点对称,所以|BF|=|AF1|=8,所以2a=14,a=7,所以离心率e=.答案:三、解答题(大本题共6小题,共70分.解承诺写出文字说明、证明进程或演算步骤)17.(本小题满分10分)已知椭圆C:+=1(a>b>0),焦距为2,离心率e为.(1)求椭圆C的标准方程;(2)过点P(,1)作圆O:x2+y2=的切线,切点别离为M,N,直线MN与x轴交于点F,过点F的直线l交椭圆C于A,B两点,点F关于y轴的对称点为G,求△ABG的面积的最大值.解:(1)因为椭圆C:+=1(a>b>0),焦距为2,离心率e为.所以由题意,2c=2,解得c=1.由e==,解得a=2.所以b==.所以椭圆C的标准方程为+=1.(2)由题意,得O,M,P,N四点共圆,该圆的方程为(x-)2+(y-)2=,又圆O的方程为x2+y2=,两圆的方程作差,得直线MN的方程为x+2y-1=0,令y=0,得x=1,即点F的坐标为(1,0),则点F关于y轴的对称点为G(-1,0).设A(x1,y1),B(x2,y2),则S△ABG=|GF||y1-y2|=|y1-y2|,所以S△ABG最大,|y1-y2|就最大.由题意知,直线l的斜率不为零,可设直线l的方程为x=my+1,由得(3m2+4)y2+6my-9=0,所以y1+y2=,y1y2=.则S△GAB=|GF||y1-y2|=|y1-y2|==.令t=,则t≥1,S△GAB===.令f(t)=3t+,则函数f(t)在[,+∞)上单调递增,在t∈[1,+∞)时单调递增,所以f(t)≥f(1)=,所以S△GAB≤3.故△ABG的面积的最大值为3.18.(本小题满分12分)已知直线y=-x+1与椭圆G: +=1(a>b>0)相交于A,B两点,且线段AB的中点在直线l:x-2y=0上,椭圆G的右核心关于直线l的对称点在圆x2+y2=4上.(1)求椭圆G的标准方程;(2)已知点C,D别离为椭圆G的右极点与上极点,设P为第三象限内一点且在椭圆G上,直线PC与y轴交于点M,直线PD与x轴交于点N,求证:四边形CDNM的面积为定值.(1)解:将直线y=1-x代入椭圆方程得,b2x2+a2(1-x)2=a2b2,即(b2+a2)x2-2a2x+a2-a2b2=0,设A(x1,y1),B(x2,y2),则x1+x2=,即AB中点的横坐标是,纵坐标是.由于线段AB的中点在直线l:x-2y=0上,则a2=2b2,又b2=a2-c2,则a2=2c2,设右核心(c,0)关于直线x-2y=0的对称点为(m,n),则解得由于椭圆的右核心关于直线l的对称点在圆x2+y2=4上,所以+=4, 得c2=4,a2=8,b2=4,故椭圆方程为+=1.(2)证明:设P(m,n)(m<0,n<0),+=1,又C(2,0),D(0,2),所以直线PC:y=(x-2),令x=0,得y M=,又直线PD:y=x+2,令y=0,得:x N=,|DM|=2+,|CN|=2+,所以四边形CDNM的面积S=|DM|·|CN|=2(1+)(+)=2×=2×,由+=1,所以m2+2n2=8,所以S=2×=2×2·=4=4(定值).所以四边形CDNM的面积为定值.19.(本小题满分12分)已知抛物线的对称轴为坐标轴,极点是坐标原点,准线方程为x=-1,直线l与抛物线相交于不同的A,B两点.(1)求抛物线的标准方程;(2)若是直线l过抛物线的核心,求·的值;(3)若是·=4,直线l是不是过必然点,若过必然点,求出该定点;若不过必然点,试说明理由.解:(1)已知抛物线的对称轴为坐标轴,极点是坐标原点,准线方程为x=-1,所以=1,p=2.所以抛物线的标准方程为y2=4x.(2)设l:my=x-1,与y2=4x联立,得y2-4my-4=0,设A(x1,y1),B(x2,y2),所以y1+y2=4m,y1y2=-4,所以·=x1x2+y1y2=·+y1y2=()2+y1y2=-3.(3)假设直线l过定点,设l:my=x+n,得y2-4my+4n=0,设A(x1,y1),B(x2,y2),所以y1+y2=4m,y1y2=4n.由·=()2+y1y2=n2+4n=-4,解得n=-2,所以l:my=x-2过定点(2,0).20.(本小题满分12分)已知椭圆E:+=1(a>b>0)的焦距为4,过核心且垂直于x轴的弦长为2.(1)求椭圆E的方程;(2)过椭圆E右核心的直线l交椭圆于点M,N,设椭圆的左核心为F,求·的取值范围.解:(1)因为椭圆E:+=1(a>b>0)的焦距是4,所以核心坐标是(-2,0),(2,0).由题意可得,椭圆E过(2,)点,所以2a=+=4,则a=2,b==2,所以椭圆E的方程是+=1.(2)由题意得,左核心F(-2,0),右核心坐标为(2,0).若直线l垂直于x轴,则点M(2,),N(2,-).·=(4,)·(4,-)=14;若直线l不垂直于x轴,可设l的方程为y=k(x-2),设点M(x1,y1),N(x2,y2).联立取得(1+2k2)x2-8k2x+8k2-8=0.则x1+x2=,x1x2=.所以·=(x1+2,y1)·(x2+2,y2)=(x1+2)(x2+2)+y1y2=(x1+2)(x2+2)+k(x1-2)·k(x2-2)=(1+k2)x1x2+2(1-k2)(x1+x2)+4(1+k2)==14-,因为0<<18,所以-4<·<14,所以·的取值范围是[-4,14].21.(本小题满分12分)已知椭圆E:+=1(a>b>0)的离心率是,过E的右核心且垂直于椭圆长轴的直线与椭圆交于A,B两点,|AB|=2.(1)求椭圆方程;(2)过点P(0,)的动直线l与椭圆E交于两点M,N(不是椭圆的极点),是不是存在实数λ,使·+λ·为定值?若存在,求出λ的值;若不存在,请说明理由.解:(1)由椭圆的离心率e===,则a2=2b2,则|AB|==2,则b2=a,解得a=2,b=,所以椭圆的标准方程为+=1.(2)当直线l的斜率存在时,设直线l的方程为y=kx+,M(x1,y1),N(x2,y2),联立得(1+2k2)x2+4kx+2=0,由韦达定理可知x1+x2=-,x1x2=,从而,·+λ·=x1x2+y1y2+λ[x1x2+(y1-)(y2-)]=(1+λ)(1+k2)x1x2+k(x1+x2)+3=(1+λ)(1+k2)×+k×(-)+3===λ-2+,所以当λ=-7时,·+λ·=-9,故存在常数λ=-7,使得·+λ·为定值-9.22.(本小题满分12分)已知椭圆C:+ =1(a>b>0)的左、右极点别离为A1,A2,左、右核心分别为F1,F2,离心率为,点B(4,0),F2为线段A1B的中点.(1)求椭圆C的方程;(2)若过点B且斜率不为0的直线l与椭圆C交于M,N两点,已知直线A1M与A2N相交于点G,试判断点G是否在定直线上?若是,请求出定直线的方程;若不是,请说明理由.解:(1)设点A1(-a,0),F2(c,0),由题意可知c=,即a=4-2c. ①又因为椭圆的离心率e==,即a=2c. ②联立方程①②可得a=2,c=1,则b2=a2-c2=3,所以椭圆C的方程为+=1.(2)按照椭圆的对称性猜想点G在与y轴平行的直线x=x0上.假设当点M为椭圆的上极点时,直线l的方程为x+4y-4=0,此时点N(,),则联立直线:x-2y+2=0和直线:3x+2y-6=0可得点G(1,),据此猜想点G在直线x=1上,下面对猜想给予证明:设M(x1,y1),N(x2,y2),联立方程可得(3+4k2)x2-32k2x+64k2-12=0,Δ>0.由韦达定理可得x1+x2=,x1x2=.(*)因为直线:y=(x+2),:y=(x-2),联立两直线方程得(x+2)=(x-2)(其中x为G点的横坐标),即证:=,即3k(x1-4)·(x2-2)=-k(x2-4)·(x1+2),即证2x1x2-5(x1+x2)+8=0.将(*)代入上式可得-+8=0⇔16k2-3-20k2+3+4k2=0, 此式明显成立,原命题得证.所以点G在定直线x=1上.。

2021届高考数学一轮复习考点规范练：52直线与圆锥线【含解析】

2021届高考数学一轮复习考点规范练：52直线与圆锥线基础巩固1.双曲线=1的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为()A B.5 C D答案:D解析:不妨设=1的渐近线y=x与y=x2+1只有一个交点,由得ax2-bx+a=0,所以Δ=b2-4a2=0,即c2-a2-4a2=0,=5,e=故选D.2.设A(x1,y1),B(x2,y2)是抛物线y=2x2上的两点,直线l是AB的垂直平分线.当直线l的斜率为时,直线l在y轴上的截距的取值范围是()A B C.(2,+∞) D.(-∞,-1)答案:A解析:设直线l在y轴上的截距为b,则直线l的方程为y=x+b,过点A,B的直线可设为y=-2x+m,联立方程得2x2+2x-m=0,从而有x1+x2=-1,Δ=4+8m>0,m>-又AB的中点在直线l上,即m+1=-+b,得m=b-,将m=b-代入4+8m>0,得b>,所以直线l 在y轴上的截距的取值范围是3.过双曲线=1(a>0,b>0)的右焦点F(1,0)作x轴的垂线与双曲线交于A,B两点,O为坐标原点,若△AOB的面积为,则双曲线的渐近线方程为()A.y=±xB.y=±2xC.y=±2xD.y=±2x答案:B解析:由题意得|AB|=,∵S△AOB=,1=,①∵a2+b2=1,②解①②得a=,b=,∴双曲线的渐近线方程为y=±x=±2x.故选B.4.斜率为1的直线l与椭圆+y2=1相交于A,B两点,则|AB|的最大值为()A.2 B C D答案:C解析:设A,B两点的坐标分别为(x1,y1),(x2,y2),直线l的方程为y=x+t,由消去y,得5x2+8tx+4(t2-1)=0.则x1+x2=-t,x1x2=所以|AB|=|x1-x2|===,当t=0时,|AB|max=5.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为()A.16B.14C.12D.10答案:A解析:方法一:由题意,易知直线l1,l2斜率不存在时,不合题意.设直线l1方程为y=k1(x-1),联立抛物线方程,得消去y,得x2-2x-4x+=0,所以x1+x2=同理,直线l2与抛物线的交点满足x3+x4=由抛物线定义可知|AB|+|DE|=x1+x2+x3+x4+2p=+4=+8≥2+8=16,当且仅当k1=-k2=1(或-1)时,取得等号.方法二:如图所示,由题意可得F(1,0),设AB倾斜角为作AK1垂直准线,AK2垂直x轴,结合图形,根据抛物线的定义,可得所以|AF|·cosθ+2=|AF|,即|AF|=同理可得|BF|=,所以|AB|=又DE与AB垂直,即DE的倾斜角为+θ,则|DE|=,所以|AB|+|DE|=16,当θ=时取等号,即|AB|+|DE|最小值为16,故选A.6.在平面直角坐标系xOy中,P为双曲线x2-y2=1右支上的一个动点.若点P到直线x-y+1=0的距离大于c恒成立,则实数c的最大值为.答案:解析:直线x-y+1=0与双曲线的渐近线y=x平行,且两平行线间的距离为由图形知,双曲线右支上的动点P到直线x-y+1=0的距离的最小值无限趋近于,要使距离d大于c 恒成立,只需c即可,故c的最大值为7.已知椭圆C:=1(a>b>0)的左焦点F(-2,0),上顶点B(0,2).(1)求椭圆C的方程;(2)若直线y=x+m与椭圆C交于不同的两点M,N,且线段MN的中点G在圆x2+y2=1上,求m的值.解:(1)由题意可得,c=2,b=2,由a2=b2+c2得a2=22+22=8,所以a=2故椭圆C的方程为=1.(2)设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点G(x0,y0),由消去y得3x2+4mx+2m2-8=0,则Δ=96-8m2>0,所以-2<m<2x0==-,y0=x0+m=,因为点G(x0,y0)在圆x2+y2=1上,所以=1.解得m=±8.在平面直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连接ON并延长交C于点H.(1)求;(2)除H以外,直线MH与C是否有其他公共点?说明理由.解:(1)由已知得M(0,t),P又N为M关于点P的对称点,故N,ON的方程为y=x,代入y2=2px整理得px2-2t2x=0,解得x1=0,x2=因此H所以N为OH的中点,即=2.(2)直线MH与C除H以外没有其他公共点.理由如下:直线MH的方程为y-t=x,即x=(y-t).代入y2=2px得y2-4ty+4t2=0,解得y1=y2=2t,即直线MH与C只有一个公共点,所以除H以外直线MH与C没有其他公共点.能力提升9.(2019广东六校第一次联考)抛物线y=2x2上有一动弦AB,中点为M,且弦AB的长为3,则点M的纵坐标的最小值为()A B C D.1答案:A解析:由题意设A(x1,y1),B(x2,y2),M(x0,y0),直线AB的方程为y=kx+b.由题意知y0≥b>0.联立得整理得2x2-kx-b=0,Δ=k2+8b>0,x1+x2=,x1x2=-,则|AB|=,点M的纵坐标y0=+b.因为弦AB的长为3,所以=3,即(1+k2)=9,故(1+4y0-4b)(y0+b)=9,即(1+4y0-4b)(4y0+4b)=36.由基本不等式得,(1+4y0-4b)+(4y0+4b)≥2=12,当且仅当时取等号,即1+8y0≥12,y0,所以点M的纵坐标的最小值为故选A.10.已知双曲线C:-y2=1,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M,N.若△OMN为直角三角形,则|MN|=()A B.3 C.2 D.4答案:B解析:由条件知F(2,0),渐近线方程为y=±x,所以∠NOF=∠MOF=30°,∠MON=60°≠90°.不妨设∠OMN=90°,则|MN|=|OM|.又|OF|=2,在Rt△OMF中,|OM|=2cos30°=,所以|MN|=3.11.平面直角坐标系xOy中,双曲线C1:=1(a>0,b>0)的渐近线与抛物线C2:x2=2py(p>0)交于点O,A,B.若△OAB的垂心为C2的焦点,则C1的离心率为.答案:解析:如图,双曲线的渐近线为y=±x.由得A由得B∵F为△OAB的垂心,∴k AF·k OB=-1.即=-1,解得,,即可得e=12.在平面直角坐标系xOy中,曲线C:y=与直线l:y=kx+a(a>0)交于M,N两点.(1)当k=0时,分别求C在点M和N处的切线方程;(2)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.解:(1)由题设可得M(2,a),N(-2,a)或M(-2,a),N(2,a).又y'=,故y=在x=2处的导数值为,C在点(2,a)处的切线方程为y-a=(x-2),即x-y-a=0.y=在x=-2处的导数值为-,C在点(-2,a)处的切线方程为y-a=-(x+2),即x+y+a=0.故所求切线方程为x-y-a=0和x+y+a=0.(2)存在符合题意的点,证明如下:设P(0,b)为符合题意的点,M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为k1,k2.将y=kx+a代入C的方程得x2-4kx-4a=0.故x1+x2=4k,x1x2=-4a.从而k1+k2=当b=-a时,有k1+k2=0,则直线PM的倾斜角与直线PN的倾斜角互补,故∠OPM=∠OPN,所以点P(0,-a)符合题意.高考预测13.已知椭圆E:=1(a>b>0)的左、右顶点分别为A1,A2,右焦点F的坐标为(,0),点P坐标为(-2,2),且直线PA1⊥x轴,过点P作直线与椭圆E交于A,B两点(A,B在第一象限且点A在点B的上方),直线OP与AA2交于点Q,连接QA1.(1)求椭圆E的方程;(2)设直线QA1的斜率为k1,直线A1B的斜率为k2,问:k1k2的斜率乘积是否为定值?若是,求出该定值;若不是,说明理由.解:(1)由题意可知所以b=1.所以椭圆的方程为+y2=1.(2)是定值,定值为-设A(x1,y1),B(x2,y2),因为直线AB过点P(-2,2),设直线AB的方程为x=my-2m-2,联立(m2+4)y2-(4m2+4m)y+(4m2+8m)=0,所以y1+y2=,y1y2=因为点Q在直线OP上,所以可设Q(-t,t).又Q在直线AA2上,所以t=-,所以k1k2==-=-=-=-。