1.5事件的独立性(课件)
合集下载
概率论及数理统计:1.5 事件的独立性

同时成立:
P( AB) P( A)P(B)
两两相互独立
P( AC ) P( A)P(C )
(1)
P(C ) P( A)P(B)P(C ) (2)
注1:三个事件A,B,C相互独立的性质类似两个事件的性质.
例 八组事件 A, B,C; A, B,C; A, B,C 任何一组相互独立,则其它各组也相互独立
解 设取出的5个数按由小到大排列为
x1 x2 x3 x4 x5
令 ( x3 4) 表示所求的事件 ( x3 4) ( x3 4) ( x3 3)
( x3 4) : 1,1,2,3,3; 1,1,2,3,4;
1,1,4,4,5; 1,1,4,5,8;
— 所取的5个数字中至少有3个数字不大于4
P( AB) P( AC ) P( ABC ) P( A) P(B) P(C ) P(BC )
P( A)P(B C )
结论:
若 n 个事件 A1, A2, …, An 相互独立,将这 n个事件 任意分成 k 组,同一个事件不能同时 属于两个不 同的组,则对每组的事件进行求和、积、差、对立 等运算所得到的 k 个事件也相互独立
P( A1 A2 An ) P( A1 )P( A2 ) P( An )
事件独立性的判别: 常根据实际问题的意义
例 已知事件 A, B, C 相互独立,证明事件
A 与 B C 也相互独立
证 P A(B C ) P(B C ) P A(B C )
P(B) P(C ) P(BC )
Pn(k ) k = 0, 1 , 2, …, n
例 八门炮同时独立地向一目标各射击一发炮 弹, 若有不少于2发炮弹命中目标时, 目标 就被击毁. 如果每门炮命中目标的概率为
1.5事件的独立性(课件)

定义 两个事件 A 与 B , 如果其中任何一个 事件发生的概率, 都不受另一个事件发生与否 的影响,则称事件 A 与 B 是相互独立的.
例 掷一枚均匀的骰子,(1)A表示“点数小于 则 B表示“点数为奇数” 5”,
P ( A)
4 6
2 3
P(B)
1 2 1 3
3 6
P ( AB )
一个独立试验序列.
定义1.8 由一个贝努利试验 独立重复进行,形成 的随机试验序列称为贝努利试验序列. 由一个贝努利试验 独立重复进行n次,形成的 随机试验序列 称为n 重贝努利试验. 在n 重贝努利试验中, 事件A发生 每一次试验, 的概率都是 p , 事件 A 发生的概率都是 q 1 p
P ( A1 ) P ( A 5 ) P ( A 6 )
A1 , A 2 , ..., A n 两两独立.
A1 , A 2 , ..., A n 相互独立
例 一个袋中装有4个球,其中全红、全黑、全白色 的球 各一个,另一个是涂有红、黑、白三色的彩球. 事件A、B、C 分别表示取到的球上 从中任取一个, 有红色、黑色、 白色, 判别A,B,C的独立性. 2 2 解 P(A) 2 P(B ) P (C )
§1.5 事件的独立性
一般地
P ( A B ) P ( A)
但在有些情况下, 事件B发生与否并不影响事件 A发生的机会. 如 甲、乙两人各掷一次硬币,
B表示 “乙掷出正面”,
A表示 “甲掷出正面”, 又如, 某校毕业班进行统考,
B表示 “乙同学英语及格.” A表示 “甲同学数学及格.”
一、两个事件的独立性 当事件B对事件A 发生的概率 没有任何影响时, 应有 P A B P ( A ) 其中 P ( B ) 0 当事件A对事件B 发生的概率 没有任何影响时, 应有 P B A P ( B ) 其中 P ( A ) 0 当 P ( B ) 0 时,
15事件的独立性课件-PPT课件
即AB同时发生 影响了C发生的机会.
P( A B C ) P( A)
例 设开关A,B,C闭合的概率分别为 0 . 7 , 0 . 8 , 求指示灯亮 0 . 8 , 且各开关是否闭合彼此独立, 的概率.
解 设 A, B,C分别表示 开关A、B、C有闭合. A 则指示灯亮的概率为
PA B C
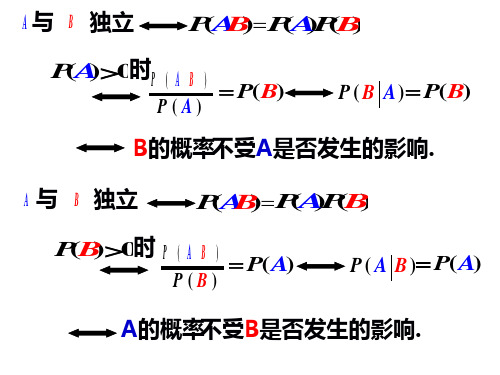
A 与 B 独立
P (A B ) PAPB ( ) ( )
时P ( A B ) P (A )0 P(B) P ( A)
P ( B A ) P(B)
B的概率不受A是否发生的影响.
A 与 B 独立
P (A B ) PAPB ( ) ( )
时P (A B ) PB ( )0 P( A) P(B)
P ( Ai A j )
P(Aj)
P( Ai )
j
PA iA
j
P( 发生的影响.
n个事件两两独立,即其中任何一个事件发生的 概率都不受另一个事件是否发生的影响.
, 2,. . . ,A 定义1.6 对n个事件 AA 1 n( n2),如果对其 中任意k个事件 A . . ,A 2 k n ) , 都有 i ,A i ,. i (
AA , 2,. . . ,A 相互独立 1 n
AA , 2,. . . ,A 两两独立. 1 n
( n 2)如果对其中 , 2,. . . ,A 定义1.6 对n个事件AA 1 n
. . ,A k n ) 任意 k 个事件 A i ,A i ,. i (2 都有
则称这 n 个事件 相互独立.
P ( A B ) P( A)
A的概率 不受B是否发生的影响.
定义
两个事件 A 与 B , 如果其中任何一个
概率论§1.5 事件独立性

例1 三人独立地去破译一份密码, 已知每个人 能译出的概率分别为1/5,1/3,1/4。问三人中 至少有一人能将密码译出的概率是多少?
解:将三人分别编号为1, 2, 3, 记 Ai ={第i个人破译出密码},i=1, 2, 3。
故,所求为 P(A1∪A2∪A3)
已知 P(A1)=1/5, P(A2)=1/3, P(A3)=1/4,
P ( A) P ( B) P (C ) 1 2
说明事件A,B,C两两相互独立,但不是总体相互独立。
定理8
A1, A2, …, An 相互独立,则
Ai1 , Ai2 , , Ai m , Ai m1 , Ai n 也相互独立
(1≤m≤n, i1, i2, …, in为1, 2, …, n 的一个全排 列) 注意: 在实际应用中,对于n个事件的相互独立性, 我们往往不是根据定义来判断,而是根据实际意义 来加以判断的
A 与 B 也相互独立
证明:(1) A AB AB 且 AB AB
P ( A) P ( AB) P ( AB )
又 P(AB)=P(A)P(B) 则有:
P ( AB ) P ( A) P ( A) P ( B ) P ( A) P ( B )
故, A与 B 相互独立
等价定义
定理6 设A,B是两个随机事件,若P(A)>0,则 事件B关于事件A独立的充要条件是 P(AB)=P(A)P(B)
证明:若事件B关于事件A独立,即P(B|A)=P(B)
则由乘法公式可得 P(AB)=P(A)P(B|A)=P(A)P(B) 反之,若P(AB)=P(A)P(B),已知P(A)>0
且 A1,A2,A3相互独立 可得 P(A1∪A2∪A3) 1 P ( A1 A2 An )
1.5独立性及伯努利概型 《概率论与数理统计》课件

则称 A1,A2,An 相互独立.
n 个事件相互独立,则必须满足 2n n1个等式.
显然 n 个事件相互独立,则它们中的任意
m (2 mn)个事件也相互独立.
2.事件独立性的性质
定理1.5.1 四对事件{A、B},{ A , B },{A,B }、
{ A 、B }中有一对相互独立,则其它三对也相互独立.
证明 不失一般性.设事件 A 与 B 独立,仅证 A 与 B
相互独立,其余情况类似证明 因为 P ( A B ) P ( B A ) P ( B A ) P B ( B ) P ( A )B
又 A 与 B 独立,所以 P (A)B P (A )P (B )
从而 P ( A B ) P ( B ) P ( A ) P ( B ) P ( B ) 1 P ( ( A ) P ) ( A ) P ( B ) 所以, A 与 B 相互独立.
AB={(男、女),(女、男)}
于是
P(A)= 1 , P(B)= 3 , P(AB)= 1
2
4
2
由此可知 P(AB) P(A) P(B).
所以 A与B 不独立.
2)有三个小孩的家庭,样本空间Ω={(男、
男、男),(男、男、女),(男、女、男),
(女、男、男)(男、女、女),(女、女、男),
(女、男、女),(女、女、女)}
= 1 P(A1A2An) = 1 P(A 1)P(A 2)P(A n)
这个公式比起非独立的场合,要简便的多,它 在实际问题中经常用到.
例1.5.6 假若每个人血清中含有肝炎病的概率为 0.4%,混合100个人的血清,求此血清中含有肝炎病 毒的概率?
解: 设 A i={第 i 个人血清中含有肝炎病毒}
n 个事件相互独立,则必须满足 2n n1个等式.
显然 n 个事件相互独立,则它们中的任意
m (2 mn)个事件也相互独立.
2.事件独立性的性质
定理1.5.1 四对事件{A、B},{ A , B },{A,B }、
{ A 、B }中有一对相互独立,则其它三对也相互独立.
证明 不失一般性.设事件 A 与 B 独立,仅证 A 与 B
相互独立,其余情况类似证明 因为 P ( A B ) P ( B A ) P ( B A ) P B ( B ) P ( A )B
又 A 与 B 独立,所以 P (A)B P (A )P (B )
从而 P ( A B ) P ( B ) P ( A ) P ( B ) P ( B ) 1 P ( ( A ) P ) ( A ) P ( B ) 所以, A 与 B 相互独立.
AB={(男、女),(女、男)}
于是
P(A)= 1 , P(B)= 3 , P(AB)= 1
2
4
2
由此可知 P(AB) P(A) P(B).
所以 A与B 不独立.
2)有三个小孩的家庭,样本空间Ω={(男、
男、男),(男、男、女),(男、女、男),
(女、男、男)(男、女、女),(女、女、男),
(女、男、女),(女、女、女)}
= 1 P(A1A2An) = 1 P(A 1)P(A 2)P(A n)
这个公式比起非独立的场合,要简便的多,它 在实际问题中经常用到.
例1.5.6 假若每个人血清中含有肝炎病的概率为 0.4%,混合100个人的血清,求此血清中含有肝炎病 毒的概率?
解: 设 A i={第 i 个人血清中含有肝炎病毒}
§1.5事件的独立性

16
甲、乙两个乒乓球运动员进行乒乓球单打比赛,已知 练习2: 每一局甲胜的概率为0.6,乙胜的概率为0.4。比赛时 可以采用三局两胜或五局三胜,问在哪一种比赛制度 下,甲获胜的可能性较大? 解 (1)三局两胜,设 A1 甲∶乙=2:0 甲净胜二局
A2
甲∶乙=2:1
前两局中各胜一局,第三局甲胜
P A1 0.62 0.36
立的射击一次, 已知目标被命中, 则它是乙命中的概率是多少? 解: 设
12
二、独立试验序列
n次重复试验
每次试验相互独立 每次试验的结果只有两个: A, A
这样的试验类型叫做n重独立试验序列或n重伯努利(Bernoulli)概型。 在n重独立试验序列中,A出现 m 次的概率为:
m m n m P ( m ) C n n p q
3 i 0
2
P( A | B1 ) 0.992 (1 0.95) P( A | B3 ) (1 0.95)3
P( A) P( Bi ) P( A | Bi ) 0.8629
10
例3 若干人独立地向一游动目标射击,每人击中目标的概率都是 0.6,问至少需要多少人,才能以0.99以上的概率击中目标? 解
p K N
k K P ( A) Cn N k
K 1 N
nk
, k 0,1, 2,..., n.
14
例5 一张英语试卷,有10道选择题,每题有4个选择答案,且其 中只有一个是正确答案. 某同学投机取巧,随意填空,试问他 至少填对6道题的概率是多大? 解 B =“他至少填对6道题”. 作10道题就是10重伯努利试验,
P( A) 0.9
P( A
P( B) 0.8
甲、乙两个乒乓球运动员进行乒乓球单打比赛,已知 练习2: 每一局甲胜的概率为0.6,乙胜的概率为0.4。比赛时 可以采用三局两胜或五局三胜,问在哪一种比赛制度 下,甲获胜的可能性较大? 解 (1)三局两胜,设 A1 甲∶乙=2:0 甲净胜二局
A2
甲∶乙=2:1
前两局中各胜一局,第三局甲胜
P A1 0.62 0.36
立的射击一次, 已知目标被命中, 则它是乙命中的概率是多少? 解: 设
12
二、独立试验序列
n次重复试验
每次试验相互独立 每次试验的结果只有两个: A, A
这样的试验类型叫做n重独立试验序列或n重伯努利(Bernoulli)概型。 在n重独立试验序列中,A出现 m 次的概率为:
m m n m P ( m ) C n n p q
3 i 0
2
P( A | B1 ) 0.992 (1 0.95) P( A | B3 ) (1 0.95)3
P( A) P( Bi ) P( A | Bi ) 0.8629
10
例3 若干人独立地向一游动目标射击,每人击中目标的概率都是 0.6,问至少需要多少人,才能以0.99以上的概率击中目标? 解
p K N
k K P ( A) Cn N k
K 1 N
nk
, k 0,1, 2,..., n.
14
例5 一张英语试卷,有10道选择题,每题有4个选择答案,且其 中只有一个是正确答案. 某同学投机取巧,随意填空,试问他 至少填对6道题的概率是多大? 解 B =“他至少填对6道题”. 作10道题就是10重伯努利试验,
P( A) 0.9
P( A
P( B) 0.8
1.5事件独立性

概率论 . 第一章. 事件独立性
概率论 . 第一章. 事件独立性
二、伯努利试验概型 伯努利 Jacob Bernoulli 1654-1705 瑞士数学家 概率论的奠基人
伯努利家族祖孙三代出过十多位数学家. 这 在世界数学史上绝无仅有. 伯努利幼年遵从父亲意见学神学,当读了 R 笛 卡尔的书后,顿受启发,兴趣转向数学.
1. P(B|A)>0 3. P(A|B)=0 2. P(A|B)=P(A) 4. P(AB)=P(A)P(B)
设A、B为独立事件,且P(A)>0,P(B)>0, 下面四个结论中,正确的是: 1. P(B|A)>0 3. P(A|B)=0 2. P(A|B)=P(A) 4. P(AB)=P(A)P(B)
概率论 . 第一章. 事件独立性
注意互斥与独立的区别 互斥 指 事件不可能同时发生。 独立 指 事件的发生互不影响,但并不一定事 件不可能同时发生.
概率论 . 第一章. 事件独立性
前面我们看到独立与互斥的区别,再请你做个小练习 .
设A、B为互斥事件,且P(A)>0,P(B)>0, 下面四个结论中,正确的是:
k
k k
nk n k k ( P 1 ( k p ) ) C,n n
k n k p k (1 0p ,1 ), 2, , , nk 0,1,2 个事件两两互
Pn ( k ) C p (1 p)
k n k
n k
,
k 0,1,2,, n
概率论 . 第一章. 事件独立性
A、B、C、D、E、F、G、H是电路中的独立元件.
它们下方的数是它们各自正常工作的概率.
求电路正常工作的概率.
0.70
事件的独立性讲义

例2 三人独立地去破译一份密码,已知各人能 译出的概率分别为1/5,1/3,1/4,问三人中至 少有一人能将密码译出的概率是多少?
解:将三人编号为1,2,3,
记 Ai={第i个人破译出密码} i=1,2,3
所求为 P(A1+A2+A3)
1
记 Ai={第i个人破译出密码} 所求为 P(A1+A2+A3)
P(A2∪B2)=P(A2)+P(B2)-P(A2)P(B2)=2r-r2,
……
第n对元件的可靠性 P(An∪Bn)=P(An)+P(Bn)-P(An)P(Bn)=2r-r2 于是 RⅡ=[r(2-r)]n=rn(2-r)n
Ⅲ 比较大小.比较2-rn与(2-r)n的大小。 n>1时,2-rn<(2-r)n,
由于 P(A)=1/13, P(A|B)=2/26=1/13
P(A)= P(A|B), 所以事件A、B独立.
练:投掷一枚均匀的骰子。 (1)设A表示“掷得点数小于5”,B表示“掷 得 奇数点”,问A,B是否独立? 独立。 (2)设A表示“掷得点数小于4”,B表示“掷 得奇数点”,问A,B是否独立? 不独立。
P(AB)= P(A)P(B)
四个等式同时
P(AC)= P(A)P(C)
成立,则称事件
P(BA)P(B)P(C) 独立。
其中,前三个等式成立时,称A、B、C两两
独立。
如: 将一枚骰子掷两次,设
A:“第一次掷得偶数点”,
B:“第二次掷得奇数点”, C:“两次都掷得奇数或偶数点”。 容易算出 P(A)=1/2, P(B)=1/2, P(C)=1/2, P(AB)=1/4, P(AC)=1/4, P(BC)=1/4, P(ABC)=0. 于是
1.5事件的独立性

相互独立
两两独立
例2.设一个人开枪击中低空飞机的概率为0.4%, 求100个人同时开枪击中飞机概率. 解: 记 B={飞机被击中} Ai ={第i个人击中飞机}, 则 P ( B ) P ( Ai ) 1 P ( Ai )
1 1 P ( Ai )
iห้องสมุดไป่ตู้1
100
不难发现, 与任何事件都独立.
前面我们看到独立与互斥的区别和联系, 再请你做个小练习. 设A、B为互斥事件,且P(A)>0,P(B)>0, 下面四个结论中,正确的是: 1. P(B|A)>0 2. P(A|B)=P(A) 3. P(A|B)=0 4. P(AB)=P(A)P(B) 设A、B为独立事件,且P(A)>0,P(B)>0, 下面四个结论中,正确的是:
第一章
随机事件及其概率
1.1 基本概念 1.2 随机事件的概率 1.3 概率的定义与性质 1.4 条件概率 1.5 事件的独立性
1.5.1 两个事件的独立性 1.5.2 多个事件的独立性
§1.5
事件的独立性
一、两个事件的独立性
引例: 将一颗均匀骰子连掷两次, 设 A={第一次掷出6点}, B={第二次掷出6点}, 易见
由定义判断独立性 例1 从一副不含大小王的扑克牌中任取一张, 记 A={抽到K}, B={抽到的牌是红色的} 问事件A、B是否独立? 解: P(AB)=2/52=1/26 P(B)=26/52=1/2 P(A)=4/52=1/13,
P(A)= P(A|B) P(A|B)=2/26=1/13 说明事件A、B独立.
100 i 1
i 1 100
1 (1 0.004)
n
概率论1.5

推广到n个事件的独立性定义 可类似写出 推广到 个事件的独立性定义,可类似写出: 个事件的独立性定义 可类似写出: 设A1,A2, …,An是 n个事件,如果对任意 个事件,如果对任意k (1<k n),任意 ≤ 1<i2< …<ik ≤ 具有等式 任意1 i n,具有等式 任意
P( Ai1 Ai2 ⋯Ain ) = P( Ai1 )P( Ai2 )⋯P( Ain )
前面我们是根据两事件独立的定义作 出结论的,也可以通过计算条件概率去做: 出结论的,也可以通过计算条件概率去做 从一副不含大小王的扑克牌中任取一张,记 从一副不含大小王的扑克牌中任取一张 记 A={抽到 抽到K}, B={抽到的牌是黑色的 抽到的牌是黑色的} 抽到 抽到的牌是黑色的 则 由于 P(A)=1/13, P(A|B)=2/26=1/13 P(A)= P(A|B), 说明事件 、B独立 说明事件A 独立. 独立 在实际应用中, 往往根据问题的实际意 在实际应用中 往往根据问题的实际意 义去判断两事件是否独立. 义去判断两事件是否独立
1
个人破译出密码} 记 Ai={第i个人破译出密码 i=1,2,3 第 个人破译出密码 所求为 P(A1+A2+A3) 已知, 已知 P(A1)=1/5,P(A2)=1/3,P(A3)=1/4 P(A1+A2+A3) = 1− P( A + A + A ) 1 2 n
3
2
= 1− P( A A2 A ) 1 3
p1 = p + 2 p (1− p).
2 2
采用五局三胜制, 甲最终获胜, 采用五局三胜制, 甲最终获胜, 至少需比赛 3 局 (可能赛 3 局, 也可能赛 4 局或 5 局), 可能赛
第五讲事件的独立性PPT课件

若A与B互不相容, AB即 :
0 则: P(A/B)P(AB) P(B)
事件独立的性质(P15)
P(B)=P(B|A),则称事件B对A独立。 此时 A对B是否独立?
?
P ( A) P(A/ B)
P ( AB ) P(B)
P(A)P(B/ A)P(A)P(B)P(A)
P(B)
P(B)
性质1:若事件B对A独立,则A对B独立
P(A)1[P ( AP ) (B)]P(PA() A)P(B)P(A)
P(A)P(A)P(B)
பைடு நூலகம்
1P(B)
P(A)
性质3:若事件A、B独立,则
A 与 B, A与 B, A与B都是相互独立的 (P15)
例1:甲、乙两人分别同时向同一固定目标射击,已知甲击 中目标 的概率为0.82,乙击中目标的概率为0.60,求目标被 击中的概率。
(1)某时有机床需要工人照管:
P(ABC)P(ABC ) 1 P ( A) B 1 P ( A C ) P ( B ) P ( C )
ABC
P ( A ) P ( B ) P ( C ) P ( A B ) P ( B C ) P ( A C ) P ( A B C )
P ( A 0 B . 1 A 0 C . 2 0 B . 1 C ) 0 . 5 1 P ( 0 A . 2 B ) 0 . 2 P ( 0 A . 1 C )0 . 5 1 P ( 0 B . 1 C ) 0 . 5 P 1 2 ( P0 A (. 2 A B B A 0 C C . 1 ))
一、条件概率与乘法公式
定义(P9):已知事件B发生的条件下,事件A发生的概 率,称为A对B的条件概率,记作P(A/B)
0 则: P(A/B)P(AB) P(B)
事件独立的性质(P15)
P(B)=P(B|A),则称事件B对A独立。 此时 A对B是否独立?
?
P ( A) P(A/ B)
P ( AB ) P(B)
P(A)P(B/ A)P(A)P(B)P(A)
P(B)
P(B)
性质1:若事件B对A独立,则A对B独立
P(A)1[P ( AP ) (B)]P(PA() A)P(B)P(A)
P(A)P(A)P(B)
பைடு நூலகம்
1P(B)
P(A)
性质3:若事件A、B独立,则
A 与 B, A与 B, A与B都是相互独立的 (P15)
例1:甲、乙两人分别同时向同一固定目标射击,已知甲击 中目标 的概率为0.82,乙击中目标的概率为0.60,求目标被 击中的概率。
(1)某时有机床需要工人照管:
P(ABC)P(ABC ) 1 P ( A) B 1 P ( A C ) P ( B ) P ( C )
ABC
P ( A ) P ( B ) P ( C ) P ( A B ) P ( B C ) P ( A C ) P ( A B C )
P ( A 0 B . 1 A 0 C . 2 0 B . 1 C ) 0 . 5 1 P ( 0 A . 2 B ) 0 . 2 P ( 0 A . 1 C )0 . 5 1 P ( 0 B . 1 C ) 0 . 5 P 1 2 ( P0 A (. 2 A B B A 0 C C . 1 ))
一、条件概率与乘法公式
定义(P9):已知事件B发生的条件下,事件A发生的概 率,称为A对B的条件概率,记作P(A/B)
概率论与数理统计1.5 事件的独立性

1.5
甲、乙两人轮流射击目标。 乙是否击中与甲是否击中有关系吗?
袋中5个红球、3个黑球,从中有放回地 取出两球。 第一次取到球的颜色与第二次取到球的 颜色有联系吗?
事件的独立性
若两事件A、B满足 P(AB)= P(A) P(B), 则称A、B相互独立。 概率为零的事件与任何事件相互独立。 概率为1的事件与任何事件相互独立。
k n k
nk
补 (2007, 数一)某人向一目标射击,每次击中
目标的概率为p, 则此人第4次射击恰好第2次 击中目标的概率是多少?
设每次试验成功的概率为p, 重复进行试验 直到第n次才取得r次成功的概率是多少?
注意要点
n重伯努利试验是概率论中非常重要的模型, 只要题目中出现“将……重复进行n次”, “对……重复观察n次”等说法时,可考虑用 n重伯努利试验;
注意要点
事件的独立性与事件在样本空间中的位置没 有直接关系,一般不能通过画图来描述;
有时独立性是根据问题背景判断出来。
定理:若两事件A、B独立,则
A与B 、 A 与B、 A 与B 也相互独立.
证:
独立性
什么关系? 互不相容
若AB独立,则P(AB)=P(A) P(B) 若AB=Φ,则P(A+B)=P(A)+P(B)
若P(A)>0,P(B)>0,则A、B互不相容
和A、B相互独立不能同时成立。 互不相容是对一次试验的可能结果之 间的关系而言; 相互独立可看作是对两次试验的可能 结果之间的关系判断.
例1.设甲、乙两人分别破译同一个密码, 设甲、乙能独自译出的概率分别是
0.4与0.25,现各破译一次,试求
1.此密码能被译出的概率。
P(AB)= P(A)P(B)
甲、乙两人轮流射击目标。 乙是否击中与甲是否击中有关系吗?
袋中5个红球、3个黑球,从中有放回地 取出两球。 第一次取到球的颜色与第二次取到球的 颜色有联系吗?
事件的独立性
若两事件A、B满足 P(AB)= P(A) P(B), 则称A、B相互独立。 概率为零的事件与任何事件相互独立。 概率为1的事件与任何事件相互独立。
k n k
nk
补 (2007, 数一)某人向一目标射击,每次击中
目标的概率为p, 则此人第4次射击恰好第2次 击中目标的概率是多少?
设每次试验成功的概率为p, 重复进行试验 直到第n次才取得r次成功的概率是多少?
注意要点
n重伯努利试验是概率论中非常重要的模型, 只要题目中出现“将……重复进行n次”, “对……重复观察n次”等说法时,可考虑用 n重伯努利试验;
注意要点
事件的独立性与事件在样本空间中的位置没 有直接关系,一般不能通过画图来描述;
有时独立性是根据问题背景判断出来。
定理:若两事件A、B独立,则
A与B 、 A 与B、 A 与B 也相互独立.
证:
独立性
什么关系? 互不相容
若AB独立,则P(AB)=P(A) P(B) 若AB=Φ,则P(A+B)=P(A)+P(B)
若P(A)>0,P(B)>0,则A、B互不相容
和A、B相互独立不能同时成立。 互不相容是对一次试验的可能结果之 间的关系而言; 相互独立可看作是对两次试验的可能 结果之间的关系判断.
例1.设甲、乙两人分别破译同一个密码, 设甲、乙能独自译出的概率分别是
0.4与0.25,现各破译一次,试求
1.此密码能被译出的概率。
P(AB)= P(A)P(B)
1.5 事件的独立性

请问:如图的两个事件是否独立? 我们来计算: 因 P(AB)=0, 而 P(A) ≠ 0, P(B) ≠0。 即 P(AB) ≠ P(A)P(B)。 故 A与B不独立。
即: 若A、B互斥,且P(A)>0, P(B)>0, 则 A
与B不独立。
其逆否命题是:若A与B独立,且 P(A)>0, P(B)>0, 则 A与B一定不互斥。
1. P(B|A)>0, 3. P(A|B)=0,
2. P(A|B)=P(A), 4. P(AB)=P(A)P(B)。
设A, B为独立事件,且P(A)>0, P(B)>0, 下面四个结论中,正确的是:
1. P(B|A)>0, 3. P(A|B)=0 ,
2. P(A|B)=P(A), 4. P(AB)=P(A)P(B)。
k 个事件 Ai1 , Ai2 , Aik 也相互独立;
◎ 若事件A1, A2, …, An相互独立,则B1, B2, …, Bn也相互独立,其中 Bi 或为Ai ,或为Āi , i=1, 2, …, n 。
1.5.3 独立性概念在计算概率中的应用
对独立事件,许多概率的计算可得到简化。
例2: 三人独立地去破译一份密码, 已知每个人 能译出的概率分别为1/5,1/3,1/4。问三人中 至少有一人能将密码译出的概率是多少?
解 : 设事件 Ai( i=1,2,3,4 ) 为“第 i 个继电器 接点闭合”, L 至 R 为通路这一事件可表示为:
A A1 A2 A3 A4.
1
2
L
3
4R
由和事件的概率公式及 A1, A2, A3, A4的相互独 立性,得到
P( A) P( A1A2 A3 A4 ) P( A1A2 ) P( A3 A4 ) P( A1A2 A3 A4 )
事件的独立性与相关性ppt课件

5
例1.5.1 某高校的一项调查表明:该校有30%的学生 视力有缺陷. 7%的学生听力有缺陷,3%的学生视力与 听力都有缺陷,记
A =“学生视力有缺陷”P,( A) 0.30 B =“学生听力有缺陷”P,(B) 0.07 AB=“学生听力与视力都有缺陷”,P( AB) 0.03 现在来研究下面三个问题: (1)事件 A与 B 是否独立? 由于
概率论与数理统计
1
1.5 事件的独立性与相关性
1.5.1 两个事件的独立性与相关性 1.5.2 有限个事件的独立性 1.5.3 相互独立事件的性质 1.5.4 Bernoulli概型
2
1.5.1 两个事件的独立性与相关性
例如 箱中装有10件产品:7件正品,3件次品,甲买走1件 正品,乙要求另开一箱,也买走1件正品.
(3)如果已知一学生听力有缺陷,那么他视力也有缺 陷的概率是多少?
类似地可算条件概率 P( A B) P( AB) 0.03 3 P(B) 0.07 7
7
定义 设 0 P( A) 1,0 P(B) 1, 称
( A, B)
P( AB) P( A)P(B)
P( A)(1 P( A))P(B)(1 P(B))
A表示电路断电,
则A1,A2,A3相互独立,A= A1+A2+A3, P(A)=P(A1+A2+A31)= P( A1 A2 A3 )
1 P( A1 )P( A2 )P( A3 )
=1-0.168=0.832
12
例1.5.4 已知事件 A, B, C 相互独立,证明:事件
事件 A 与 B C 也相互独立.
P(Bn) 1 (1 )n, 0 1 n 1,2,
lim
例1.5.1 某高校的一项调查表明:该校有30%的学生 视力有缺陷. 7%的学生听力有缺陷,3%的学生视力与 听力都有缺陷,记
A =“学生视力有缺陷”P,( A) 0.30 B =“学生听力有缺陷”P,(B) 0.07 AB=“学生听力与视力都有缺陷”,P( AB) 0.03 现在来研究下面三个问题: (1)事件 A与 B 是否独立? 由于
概率论与数理统计
1
1.5 事件的独立性与相关性
1.5.1 两个事件的独立性与相关性 1.5.2 有限个事件的独立性 1.5.3 相互独立事件的性质 1.5.4 Bernoulli概型
2
1.5.1 两个事件的独立性与相关性
例如 箱中装有10件产品:7件正品,3件次品,甲买走1件 正品,乙要求另开一箱,也买走1件正品.
(3)如果已知一学生听力有缺陷,那么他视力也有缺 陷的概率是多少?
类似地可算条件概率 P( A B) P( AB) 0.03 3 P(B) 0.07 7
7
定义 设 0 P( A) 1,0 P(B) 1, 称
( A, B)
P( AB) P( A)P(B)
P( A)(1 P( A))P(B)(1 P(B))
A表示电路断电,
则A1,A2,A3相互独立,A= A1+A2+A3, P(A)=P(A1+A2+A31)= P( A1 A2 A3 )
1 P( A1 )P( A2 )P( A3 )
=1-0.168=0.832
12
例1.5.4 已知事件 A, B, C 相互独立,证明:事件
事件 A 与 B C 也相互独立.
P(Bn) 1 (1 )n, 0 1 n 1,2,
lim
1.5事件的独立性

例1:
甲,乙,丙三人在同一时间分别 破译某一个密码 .设甲译出的概率为 0.8, 乙译出的概率为 0.7,丙译出的概率为 0.6.求密码可以译出的概率 .
解 : P( A + B + C ) = 1 − P( A ∪ B ∪ C ) = 1 − P( A) P( B ) P(C ) = 1 − 0.2 × 0.3 × 0.4 = 0.976
2 1 1 3 P( AB ) = = , P( A) = , P( B ) = 4 2 2 4 所以, P( AB ) ≠ P( A) ⋅ P( B ) 即A与B不独立.
( 2) Ω 2 = {(男,男,男), (男,男, 女 ), (男, 女 , 女 ), (男, 女 ,男), (女 , 女 , 女 ), (女 , 女 ,男), (女 ,男,男), (女 ,男, 女 )} − − − 23 个
由A, B独立的条件 , P( A) = P( A) P( B ) + P( AB )
所以, P( A B ) = P( A)(1 − P( B )) = P( A) P( B ),即A与B独立. 其余的可类似证明.
Def 2 : 直观定义 两个事件 A 与 B , 如果其中任何一个事件 发生的概率不受另外 一个事件发生与否的影 响, 则称事件 A 与 B 是相互独立的 .
对这种只描述了两种对 立结果的随机试验 , 称为伯努利试验 .习惯上, 把伯努利试验的一种结 果 , 称作" 成功" , 另一种结果称为"失败".
特别的,由一个伯努利试验独立 地重复n次称为一个 n重伯努利试验 .
*
Th1 :在n重伯努利试验中, 事件A恰好发生 k次的概率是
k Cn p k q n −k − − − 二项分布
中南大学概率论与数理统计课件(1.5事件的独立性与独立试验概型)

设A1 ,A2 ,A3 分别表示第一、第二、第三道工 序出现次P品(A,1则)=依2题%意, :PA(A1 2,)A=21,%A,3 P相(互A独3)立=,5%且 又设A表示加工出来的零件是次品, 则
A=A1∪A2∪A3 方法2 (用对立事件的概率关系)
P(A) 1 P(A) 1 P(A1 A2 A3 )
P( AB AB) P( A)P(B) P( A)P(B) 0.5
P(AU B) P(A) P(B) P(A)P(B) 0.8
有限多个事件的独立性
定义1.9 如果事件A,B,C满足
P(AB)=P(A)P(B) P(AC)=P(A)P(C)
P(BC)=P(B)P(C)
P(ABC)=P(A)P(B)P(C)
n
P( A1A2 L An ) P( A1)P( A2 )L P( An ) P( Ai ) i 1
(2) 若 A1, A2,L , An 相互独立,则
n
n
P(U Ai ) 1 P( Ai )
i 1
i 1
例 加工某一种零件需要经过三道工序,设三道工序 的次品率分别为2%,1%,5% ,假设各道工序是互不 影响的.求加工出来的零件的次品率. 解
由 题 设A1, A2 , A3 , A4 , A5相 互 独 立 , 故 对 任 意k
(k =2,3,4,5) 所以
P(B) 2 p2 2 p3 5 p4 2 p5.
补例(练习1.5第一题)
证明:若P( A) 1,则A与任意事件相互独立。
证 因为A B A, P( A) 1, 所以P( A B) P( A) 1, P( A B) 1, 而P( A B) P( A) P(B) P( AB)
1 P(A1)P(A2 )P(A3 )
A=A1∪A2∪A3 方法2 (用对立事件的概率关系)
P(A) 1 P(A) 1 P(A1 A2 A3 )
P( AB AB) P( A)P(B) P( A)P(B) 0.5
P(AU B) P(A) P(B) P(A)P(B) 0.8
有限多个事件的独立性
定义1.9 如果事件A,B,C满足
P(AB)=P(A)P(B) P(AC)=P(A)P(C)
P(BC)=P(B)P(C)
P(ABC)=P(A)P(B)P(C)
n
P( A1A2 L An ) P( A1)P( A2 )L P( An ) P( Ai ) i 1
(2) 若 A1, A2,L , An 相互独立,则
n
n
P(U Ai ) 1 P( Ai )
i 1
i 1
例 加工某一种零件需要经过三道工序,设三道工序 的次品率分别为2%,1%,5% ,假设各道工序是互不 影响的.求加工出来的零件的次品率. 解
由 题 设A1, A2 , A3 , A4 , A5相 互 独 立 , 故 对 任 意k
(k =2,3,4,5) 所以
P(B) 2 p2 2 p3 5 p4 2 p5.
补例(练习1.5第一题)
证明:若P( A) 1,则A与任意事件相互独立。
证 因为A B A, P( A) 1, 所以P( A B) P( A) 1, P( A B) 1, 而P( A B) P( A) P(B) P( AB)
1 P(A1)P(A2 )P(A3 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 由n个人组成的小组, 同时分别破译一个密码, 假设每人能译出的概率都是0.7 若要以 99.9999% 的把握能够译出,问n至少为几? i 人译出密码” ( i 1,2,..., n ) 解 设 Ai 表示 “第 则A1 , A2 ,..., An互相独立,从而 A1 , A2 ,..., An也互相独立. B A1 A2 ... An 设B表示 “密码被破译” 要求 P ( B ) 99.9999%
K ” B, 为 “抽到的牌是黑色 则 记A为 “抽到 的”, 1 4 26 2
P ( A)
52
P( B)
52
2
P ( AB )
52
4 1 2 P ( A) P ( B ) P ( AB ) 52 2 52
所以A,B独立.
在实际应用中,常根据问题的实际意义去判断 两个事件是否独立.
k 3 时, P ( Ai Ai Ai ) P ( Ai1 ) P ( Ai2 ) P ( Ai3 ) 1 2 3 k 4 时, P ( Ai Ai Ai Ai ) P ( Ai ) P ( Ai ) P ( Ai ) P ( Ai ) 1 2 3 4 1 2 3 4 k n 时, P ( A1 , A2 ,..., An ) P( A1 ) P( A2 )... P( An )
例 一个袋中装有4个球,其中全红、全黑、全白色 的球 各一个,另一个是涂有红、黑、白三色的彩球. 事件A、B、C 分别表示取到的球上 从中任取一个, 有红色、黑色、 白色,判别A,B,C的独立性. 解 P ( A ) 2 , P ( B ) 2 , P (C ) 2 ,
即AB同时发生影响了C发生的机会.
二、有限个事件的独立性 定义1.5 对n个事件 A1 , A2 ,..., An ( n 2 )如果其中 两任意个都互相独立,即对于 i , j 1,2,..., n, i j 有 P ( Ai A j ) P ( Ai ) P ( Aj )
则称这 n 个事件 两两独立.
2 C 这里共有 n 个等式.
四、贝努利概型 定义 如果一个随机试验 只有两种对立结果 这样的试验称为贝努利试验.相应的概率模型称为 贝努利概型. 例如, 一批产品的次品率为15% 从中随机抽取一个 进行检验,抽取的结果只有两个:正品或次品 P 抽到次品 0.15 P 抽到正品 0.85 又如, 抛掷一枚硬币一次,结果只有两个:出正面 或出反面. P 出正面 0.5 P 出反面 0.5 又如,一射手的命中率为 p ( 0 p 1 ) 他射击一次, 结果只有两个:击中或没击中. P 击中 p P 没击中 1 p
A1 , A2 ,..., An 相互独立
A1 , A2 ,..., An 两两独立.
可以证明,n个事件相互独立,即其中任何一个 事件的概率 都不受另外一个或几个事件是否发生 的影响. 如
P ( A2 A1 A5 A6 ) P ( A2 ) P( A1 ) P( A5 ) P( A6 ) P ( A2 A1 A5 A6 ) P ( A1 A5 A6 ) P ( A1 ) P ( A5 ) P ( A6 ) P ( A2 )
P ( A B ) P ( A)
P ( AB ) P ( A) P( B) P ( AB ) P ( B ) P ( A) P ( AB ) P ( A) P ( B ) P ( AB ) P ( A) P ( B )
当 P ( A) 0 时 ,
P ( B A) P ( B )
4 4 4 1 1 P ( A ) P ( B ), P ( A) P (C ), P ( AB ) P ( AC ) 4 4 1 A, B , C 两两独立. P ( B ) P (C ), P ( BC ) 4 1 P ( ABC ) P ( A) P ( B ) P (C ), A, B , C 不相互独立. 4 P (CAB ) P( B AC ) P( B) 同样 P ( C ) P ( C A B ) 此时, 1 P ( AB ) P ( A B C ) P ( A)
当P ( A j ) 0 时, P ( Ai A j ) P ( Ai ) P ( Aj )
P ( Ai A j ) P ( Ai ) P ( Aj )
P Ai A j P ( Ai )
n个事件两两独立,即其中任何一个事件发生的 概率都不受另一个事件是否发生的影响.
定义1.6 对n个事件 A1 , A2 ,..., An ( n 2 ) 如果对其中
定义1.4 如果两个事件 A, B 满足等式
P ( AB ) P ( A) P ( B )
则称事件 A 与 B 是相互独立的,简称 A 与 B 独立. 推论1 对于两个事件A与B 若P ( B ) 0 则 若 P ( A) 0 则
A 与 B 独立 A 与 B 独立
P ( A B ) P ( A) P ( B A) P ( B )
一个独立试验序列.
定义1.8 由一个贝努利试验 独立重复进行,形成 的随机试验序列称为贝努利试验序列. 由一个贝努利试验 独立重复进行n次,形成的 随机试验序列 称为n 重贝努利试验. 在n 重贝努利试验中, 事件A发生 每一次试验, 的概率都是 p, 事件 A 发生的概率都是 q 1 p
定义 两个事件 A 与 B , 如果其中任何一个 事件发生的概率, 都不受另一个事件发生与否 的影响,则称事件 A 与 B 是相互独立的.
例 掷一枚均匀的骰子,(1)A表示“点数小于 则 5”, B表示“点数为奇数” 2 4 3
P ( A)
6
P( B)
2 1 1 P ( A) P ( B ) P ( AB ) 3 2 3
解 设 A, B, C分别表示开关A、B、C有闭合. A 则指示灯亮的概率为
P A BC P A P BC P ABC P A P B P C P A P B P C
B
C
0.7 0.8 0.8 0.7 0.8 0.8
1 P A1 P A2 P An
0.3 1 0.999999 10
n 6
n 0.3 1 0.999999 n 6
n 11.47 设0.3 10 n至少为12, 才能保证译出的概率超过 99.9999%
例 设开关A,B,C 闭合的概率分别为 0.7, 0.8, 0.8, 且各开关是否闭合彼此独立, 求指示灯亮 的概率.
思考: 两事件相互独立与它们互斥这两个概念有何联系?
A、B独立 事件A发生与否不影响B发生的概率; 事件B发生与否也不影响A发生的概率. A、B互斥
AB
事件A与B不能同时发生.
当 P ( A) 0, P ( B ) 0 时,
A,B互斥 AB
P ( AB ) 0 P ( A) P ( B ) A,B不独立
§1.5
事件的独立性
一般地 P ( A B ) P ( A) 但在有些情况下, 事件B发生与否并不影响事件 A发生的机会. 如 甲、乙两人各掷一次硬币,
B表示 “乙掷出正面”,
A表示 “甲掷出正面”, 又如, 某校毕业班进行统考,
B表示 “乙同学英语及格.” A表示 “甲同学数学及格.”
一、两个事件的独立性 当事件B对事件A 发生的概率 没有任何影响时, 应有 P A B P ( A) 其中 P ( B ) 0 当事件A对事件B 发生的概率 没有任何影响时, 应有 P B A P ( B ) 其中 P ( A) 0 当 P ( B ) 0 时,
1 P A B C P A P B P C
4 2 3 3 1 0.6 5 3 4 5
P ( B ) 1 P ( B) 1 P A1 A2 ... An 1 P A1 A2 An
A, B , C 相互独立 A, B , C 相互独立 A, B , C 相互独立
实际意义:
A与B独立
A 与 B 独立
A 与 B 独立
A 与 B独立
证 设A与B独立,
P A B P ( A B ) P A AB P A P AB
P A P A P ( B ) P A 1 P ( B )
1 1 1 概率分别为 5 , 3 , 4问能将密码译出的概率是多少?
例 三人独立地去破译一个密码, 他们能译出的
解 设 A, B, C 分别表示 甲、乙、丙译出密码
A, B, C 相互独立.
D 表示 “译出密码” 则 D A B C
P( D) P A B C 1 P A B C
任意 k 个事件 Ai , Ai ,..., Ai ( 2 k n ) 都有
1 2 k
P ( Ai1 Ai2 ... Aik ) P ( Ai1 ) P ( Ai2 )... P ( Aik )
则称这 n 个事件 相互独立.
2 4 n 3 C C ... C 这里共有 n C n n n 个等式. k 2 时, P ( Ai A j ) P ( Ai ) P ( Aj )
A,B独立 P ( AB ) P ( A) P ( B ) 0 AB A,B不互斥
三、相互独立的性质 性质1 如果 n 个事件A1 , A2 ,..., An相互独立.则它们 中的任意一部分事件 换成各自的对立事件后, 所得 的n个事件也相互独立. n=2时, A 与 B 独立 A 与 B 独立 A 与 B独立 A与B独立 n=3时, A,B,C相互独立
