第4章动量与角动量
第4章 动量和角动量

0
N
f
Mg
u
θ mg y x
∫ (Mg + mg + N + f )dt = Mv + m(v +u) −0 τ (1) x方向: ∫ fdt = −Mv + m(−v + u cosθ )— 方向: 方向 τ y方向: 方向: 方向 ∫ (N − Mg − mg)dt = musinθ —(2)
mv = ( M + m)u
m
m M
细绳张力始终垂直于其位移方向,不作功; 细绳张力始终垂直于其位移方向,不作功; 只有重力作功 机械能守恒! 机械能守恒! 1 ( m + M ) u 2 = ( m + M ) g l (1 − c o s α ) 2 入射物体的速度: 入射物体的速度:
N
dP F= dt
∑ F + ∑∑
i =1 i i =1 j ≠ i
N
N
dpi d N f ij = ∑ = ∑ pi dt i =1 iቤተ መጻሕፍቲ ባይዱ=1 dt
N
质点系的动量定理: 质点系的动量定理:
∫ (∑ F )dt = ∑ p − ∑ p
tf ti i f i i i
i
或: I = ∑ I i = P f − P i
P = ∑ pi = 常矢量
i= i =1
N
注意
——质点系动量守恒定律 质点系动量守恒定律
1. 合外力沿某一方向为零;可得到该方向上的动量守恒。 合外力沿某一方向为零;可得到该方向上的动量守恒。 尽管总动量不守恒) (尽管总动量不守恒)
∑ p α = const.
i i
2. 在某些情况下,如碰撞、打击、爆炸等过程,外力 在某些情况下,如碰撞、打击、爆炸等过程, 与内力相比小很多。 与内力相比小很多。 在极短的时间内,外力的时间积累(冲量) 在极短的时间内,外力的时间积累(冲量)相比之 下可以忽略不计。 下可以忽略不计。 我们可以有近似的动量守恒。 我们可以有近似的动量守恒。 3. 动量定理只适用于惯性系 4. 在牛顿力学的理论体系中,动量守恒定律是牛顿定 在牛顿力学的理论体系中, 律的推论。 律的推论。 但动量守恒定律是更普遍、更基本的定律, 但动量守恒定律是更普遍、更基本的定律,它在宏观 和微观领域、低速和高速范围均适用。 和微观领域、低速和高速范围均适用。
动量与角动量

r p
得 即 质点 对某定点 的
r p
mv
p
角动量的时间变化率 称为质点的
所受的合外力矩
角动量定理
的微分形式
质点的角动量定理也可用积分形式表达
由微分形式
积分形式
即
称为 冲量矩 这就是质点的
角动量的增量
角动量定理
的积分形式
冲量矩的单位是
牛顿 · 米 · 秒 ( N · m · s )
质点的动量矩定理表明,合外力矩是引起角动量变化的原因。 合外力矩的时间积累效果(冲量矩)可用动量矩的增量来量度。 动量矩定理也只有在惯性系中才适用。
凡例
再用三角 公式算出
原子系统衰变,内力远大于外力(重力) 。 系统动量守恒。 选实验室坐标系
例p.49
动量
剩 余 核 中微子静止 放射性原子核 电子
发生衰变
1
动量
设 剩余核 反冲动量为 则 即 大小
。
= 6.4×10 -23 kg · m · s 1
= 1.2×10 -22 kg · m · s -
重力
本题的合外力是向心力
由a到b 绕行半周 的 冲量 的 冲量
对应的冲量式为 方向 可用 于是 待求 已求 标识 然后合成 求出 的 大小和方向
3.2
质点系
系动量定理
p.47例 人车之间的作用为
内力,不影响系统 建立坐标系:
质点系:人,车
系统受
外力: 重 力 支持力 側向力
跳车后车速 轨车侧向力 应用质点系 的动量定理
喷出燃料
主体质量不断减少
变质量问题的牛顿定律可用
运行装料
主体质量不断增加
此类问题并非惯性质量随 速度而变,而是物质的流动 称为质量的流动问题。
大学物理动量与角动量

I F (t2 t1)
运动员在投掷标 枪时,伸直手臂,尽 可能的延长手对标枪 的作用时间,以提高 标枪出手时的速度。
变力的冲量:
I
t
2
F
(
t
)
dt
单位:N·s
t1
牛顿运动定律:
F
ma
F
d(mv)
dp
dt dt
动量定理的微分式:
dp
解:(1) 设沙袋抛到船上后,共同运动的初速度为V, 并设此运动方向为x轴正方向,忽略沙袋撞击船时受 水的阻力,则可认为沙袋+船在沙袋落到船上前后水 平方向动量守恒,因而有
(M m)V mv0
3分
V m v0
2分
Mm
(2) 由 k d x (M m) d v 得 d x M m d v
动量与角动量
研究: 力的时间积累作用
对平动——动量定理 对转动——角动量定理
基础:牛顿定律(牛顿力学)
1 动量
2 动量定理
3 动量守恒定律
*4 火箭飞行原理
*5 质心与质心运动定理 6 质点的角动量
7 力矩
8 角动量定理 角动量 守恒定律
2-2 动量守恒定律
动量
车辆超载容易 引发交通事故
车辆超速容易 引发交通事故
t
v2 x
mv 2
sin
Ft sin105
sin 0.7866 51.86 51.86 45 6.86
动量守恒定律
质点系的动量定理: t t0
Fidt P P0
当 Fi 0 时,
第4章动量和角动量

用多大的牵引力拉车厢? (摩擦忽略不计)
解 选取车厢和车厢里的煤 m 和即将 落入车厢的煤 d m 为研究的系统。取水平
v
dm
向右为正。
m
F
t 时刻系统的水平总动量:
m v dm 0mv
t + dt 时刻系统的水平总动量: m d v m (v m d m )v
dt 时间内水平总动量的增量: d p (m d m )v m v d v m
④ 动量和力是矢量,可沿坐标轴分解,当沿某坐标方向所受合 外力为零时,总动量沿该方向的分量守恒。
N
当Fx 0时,
mivix px 常量
i=1
当Fy 0时,
N
miviy py 常 量
i=1
当Fz 0时,
N
miviz pz 常 量
i=1
⑤ 动量守恒定律只适用于惯性系。
例题4-3 质量为M,仰角为α的炮车发射了一枚质量为m的炮
dt
F dtdp — 动量定理的微分式
2)积分形式: 对上式积分,
t2
v Fdt
t1
pv2 pv1
dpv
即:
t2
v Fdt
pv
— 动量定理的积分式
t1
在一个过程中,质点所受合力的冲量等于质点动量的增量。
说明
1、反映了过程量与状态量的关系。 2、I 与p 同向3、。 只适用于惯性系。
从动量定理可以知道,在相等的冲量作用下,不同质量的物体, 其速度变化是不相同的,但它们的动量的变化却是一样的,所以从 过程角度来看,动量比速度能更能恰当地反映了物体的运动状态。 因此,一般描述物体作机械运动时的状态参量,用动量比用速度更 确切些。动量是描述物体机械状态的状态参量。
大学物理第四章

解:利用功能原理:
A=DE
q
kF
m
Fl0tgq
=
1 2
k (l0 setq
- l0 )2
1 2
mv2
F
m
解得:
v=
2 m
Fl0tgq
-
1 m
k (l0 setq
-
l0
)2
[例13] 作业、p-55 功和能 自-20
一质量为m的球,从质量为M的圆弧
形槽中由A位置静止滑下,设圆弧形槽的半
径为R,(如图)。所有摩擦都略,试求:
+12 MV2
l
L
解得:
vr=
2(m +M) gR M
V= m
2gR M(m +M)
(2)小球到最低点B处时,槽滑行的距离。
∵ SFx = 0 ∴ DPx = 0
mvx = MVx
Am
m vxdt = M Vxdt
R
ml=ML
MB
l+L=R
L
=
mR m+M
lL
(3)小球在最低点B处时,槽对球的作用力;
1、动量: P
P = mv 2、第二定律:
F
=
dP dt
= ma
3、冲量: I
I
=
F t 2
t1
dt
4、动量原理
I = DP
5、力矩 M M = r × F
6、动量矩 L
L = r × P = r × mv
7、角动量原理:
t 2 t1
M dt
=
ω ω
2 1
J
dω
= Jω 2
大学物理学上册资料09 动量和角动量

冲量的方向就不能决定于某一瞬时外力的方向,然而总 决定于这段时间内动量增量的方向。 而冲量的量值,尽管在运动过程中外力随时改变, 质点的速度也逐点不同,冲量大小却完全决定于质点在 始末两点动量矢量差的绝对值,而与运动过程中物体在 各点处的动量无关。 ② 定理在碰撞、打击问题中的应用:求平均力 碰撞:力的作用时间很短 t 冲力:随时间变化很大又很复杂 t F d t 平均冲力:冲力对碰撞时间的平均值 F
例2 两个相互作用的物体A和B,无摩擦地在一条水平直 线上运动,A的动量是PA=P0-bt。在下列两种情况下,写 出B的动量:⑴开始时,若B静止,则PB1=______; ⑵开始时,若B的动量为-P0 , 则PB2=____。 易知 (A+B)系统动量守恒: 解:
P A PB P A 0 PB 0 P B P A 0 P B 0 P A
Px F x t Py F y t Pz F z t
p1 x t1
④ 当t 很小时,由于冲力很大,有时有的有限大小的 力(如重力)可忽略不计。 ⑤ 动量与参考系有关,但动量差值与参考系无关。因 此,动量定理适用于所有惯性系。
例1:质量为 2. 5g 的乒乓球以10 m/s v2 y 的速率飞来,被板推挡后,又以 20 m/s的速率飞出。设两速度在垂直于 板面的同一平面内,且它们与板面法 30o x ˆ O n 线的夹角分别为45o和30o,求: o 45 (1)乒乓球得到的冲量; (2)若撞击时间为0.01s,求板施于 v1 球的平均冲力的大小和方向。 解: (1)分量式法取挡板和球为研究对象,忽 略重力。 设挡板对球的冲力为F 则有: I m v 2 m v 1 取坐标系,将上式投影,有:
物理学概念知识:动量定理和动量角动量定理

物理学概念知识:动量定理和动量角动量定理动量定理和动量角动量定理是物理学中非常基本的两个概念。
它们的内容涉及到我们对物体运动规律的认识,不仅有助于我们更好地理解物理学知识,还可以应用于现实生活中的一些问题。
下面,我们将分别介绍这两个概念及其应用。
一、动量定理动量定理是描述物体运动过程中动量变化的一个基本定理。
它指出:在总外力作用下,物体的动量就会发生变化,这种变化的大小跟作用力和时间的乘积成正比。
这个定理的表达方式为:Δp=Ft其中,Δp表示物体动量的变化量,F表示物体所受的总外力,t 表示外力作用的时间。
式子的意义是:在总外力作用下,物体动量的变化量等于总外力作用时间的乘积。
重物移动时,如果外力越大,或者作用时间越长,那么物体的动量就会发生更大的变化。
从而可以更快地推动物体运动起来。
同样,如果要让运动中的物体停下来,也可以利用动量定理的知识。
通过对物体施加一个与它的运动方向相反的恒定力,也就是反向加速度,可以让物体的动量逐渐减小,直到物体停下来。
二、动量角动量定理动量角动量定理是物理学中另一个基本的概念。
它是通过描述物体绕某一点旋转的行为,来了解物体运动过程中动量变化的定理。
它指出:在物体绕某一点旋转时,物体的角动量就会发生变化,这种变化的大小跟作用力矩和时间的乘积成正比。
这个定理的表达方式为:ΔL=Mt其中,ΔL表示物体角动量的变化量,M表示作用力矩,t表示外力作用的时间。
式子的意义是:在物体绕某一点旋转时,物体角动量的变化量等于力矩作用时间的乘积。
个陀螺时,如果外力越大,或者作用时间越长,那么陀螺的角动量也会发生更大的变化。
从而可以更快地让陀螺旋转。
同样,如果要让旋转中的陀螺停下来,也可以利用动量角动量定理的知识。
通过对陀螺施加一个与它的旋转方向相反的外力矩,也就是反向加速度矩,可以让陀螺的角动量逐渐减小,直到陀螺停下来。
总之,动量定理和动量角动量定理是物理学中非常重要的两个概念。
它们既可以帮助我们更好地理解物理学知识,也可以用于实际生活中的问题解决。
线性动量与角动量

线性动量与角动量动量是物体运动状态的物理量,描述了物体在空间中的运动和速度。
线性动量和角动量是动量的两种不同表现形式,它们在物理学中有着重要的作用。
一、线性动量的概念与特性线性动量是描述物体直线运动状态的物理量。
它是物体质量与速度的乘积,用公式表示为:动量(p)= 质量(m)×速度(v)其中,动量的单位是千克·米/秒(kg·m/s)或牛顿·秒(N·s)。
线性动量具有以下特性:1. 动量守恒定律:在一个封闭系统中,当外力不产生作用时,物体的总动量保持不变。
即物体在相互作用过程中,动量的代数和保持不变。
2. 动量改变率与力的关系:牛顿第二定律指出,力是物体动量改变率的原因。
力与动量的改变率成正比,可以用公式表示为:力(F)= 动量改变率(Δp)/ 时间变化率(Δt)由此可见,力的作用会改变物体的动量,使其发生加速度或减速度。
二、角动量的概念与特性角动量是描述物体旋转状态的物理量。
它是物体质量、速度和转动半径的乘积,用公式表示为:角动量(L)= 质量(m)×速度(v)×转动半径(r)其中,角动量的单位是千克·米²/秒(kg·m²/s)或牛顿·米·秒(N·m·s)。
角动量具有以下特性:1. 角动量守恒定律:在一个封闭系统中,当外力矩不产生作用时,物体的总角动量保持不变。
即物体在相互作用过程中,角动量的代数和保持不变。
2. 角动量改变率与力矩的关系:力矩是物体角动量改变率的原因。
力矩与角动量的改变率成正比,可以用公式表示为:力矩(τ)= 角动量改变率(ΔL)/ 时间变化率(Δt)根据这个关系式,力矩的作用会改变物体的角动量,使其发生加速度或减速度。
三、线性动量与角动量之间的关系线性动量和角动量之间存在着密切的关系。
对于直线运动,物体的线性动量可以看作是角动量在该直线方向上的分量。
角动量和动量的转化关系

角动量和动量的转化关系角动量和动量是物理学中两个重要的概念,它们之间存在着转化关系。
本文将详细解释角动量和动量的含义,并探讨它们之间的转化关系。
我们来了解一下角动量的概念。
角动量是描述物体旋转状态的物理量。
对于一个质点,其角动量可以通过其质量、速度和距离旋转轴的位置来确定。
角动量的大小与旋转物体的质量、速度和旋转半径有关。
当旋转物体的质量增加、速度增加或旋转半径增加时,角动量也会增加。
而动量是描述物体运动状态的物理量。
动量等于物体的质量乘以其速度。
动量是一个矢量量,具有大小和方向。
当物体的质量增加或速度增加时,动量也会增加。
在物理学中,角动量和动量之间存在着转化关系。
在旋转运动中,物体的角动量可以转化为动量,而动量也可以转化为角动量。
这种转化关系可以通过以下两种情况来解释:情况一:物体的角动量转化为动量。
当一个旋转物体突然停止旋转,其角动量会转化为线性动量。
这是因为旋转物体在旋转时具有角动量,当它停止旋转时,角动量会转化为物体的线性动量。
这就是我们常说的角动量守恒定律。
情况二:动量转化为角动量。
当一个物体在运动过程中受到外力的作用,其动量会转化为角动量。
这是因为外力的作用会改变物体的运动状态,使其发生旋转运动,从而产生角动量。
通过上述两种情况可以看出,角动量和动量之间存在着转化关系。
它们之间的转化是相互联系的,不可分割的。
这种转化关系在物理学中具有重要的意义,可以帮助我们更好地理解物体的运动规律。
在实际应用中,角动量和动量的转化关系被广泛应用于航天、机械工程、天文学等领域。
例如,火箭发射时,燃料的动量转化为火箭的角动量,从而使火箭得以旋转并产生推力。
再如,地球的自转使得地球具有角动量,而地球自转的角动量又转化为地球的动量,影响地球的运动轨迹。
角动量和动量是物理学中两个重要的概念,它们之间存在着转化关系。
角动量描述物体的旋转状态,而动量描述物体的运动状态。
角动量可以转化为动量,动量也可以转化为角动量。
第四章角动量守恒定律

的子弹, 例6、质量为 、质量为20g的子弹,以400m/s的速度沿 的子弹 的速度沿 图示方向射入一原来静止的质量为980g的摆球 图示方向射入一原来静止的质量为 的摆球 设摆线长度不可伸缩, 中,设摆线长度不可伸缩,则子弹入射后与摆 球一起运动的速度为多少? 球一起运动的速度为多少? 碰撞的瞬间, 碰撞的瞬间,对子弹和摆球组成的系统 所收的外力矩为零,角动量守恒。 所收的外力矩为零,角动量守恒。
2、合力矩: 、合力矩:
单位: 单位:N·m
v v v 矢量和 F = F1 + F2 + L v v v v v v v v M = r × F = r × ( F1 + F2 + L) = M 1 + M 2 + L
注意:所有力矩相对于同一参考点。 同一参考点 注意:所有力矩相对于同一参考点。 3、力矩的计算: 、力矩的计算:
初
初
则
p =c
r r r 则 r×p=L=c
例:跳水运动
跳水运动员为了使身体快速旋转双手抱 膝尽量蜷缩,当入水时必须把手脚舒展 膝尽量蜷缩, 开使转速变慢入水。 开使转速变慢入水。
例:花样滑冰
花样滑冰运动员把手脚伸展开时旋 转速度较小, 转速度较小,当把手脚收回时转速 变快。 变快。
t 用下运动, 质点位于坐标原点,且静止; 用下运动, = 0 时,质点位于坐标原点,且静止; 求:此质点在2秒时相对于坐标原点的角动量。 此质点在 秒时相对于坐标原点的角动量。 秒时相对于坐标原点的角动量
点由静止释放, 例2、一质量为 的小球在 ( x1 ,0,0) 点由静止释放, 、一质量为m的小球在 设重力加速度沿Z轴负向 轴负向; 设重力加速度沿 轴负向;求:小球所受重力相对 于坐标原点O的角动量 的角动量。 于坐标原点 的角动量。 例3、求做匀速圆周运动的物体对圆心的角动量。 、求做匀速圆周运动的物体对圆心的角动量。
物理动量和角动量

02
角动量
定义
总结词
角动量是描述旋转运动的物理量,表示物体转动惯量和角速度的乘积。
详细描述
角动量是描述旋转运动的物理量,它等于物体转动惯量和角速度的乘积。转动惯量是描述物体转动惯 性的物理量,与物体的质量分布和旋转轴的位置有关。角速度是描述物体旋转快慢的物理量,等于物 体转过的角度与时间的比值。
乒乓球的旋转速度和方向决定了球的 轨迹和落点,对于比赛结果具有重要 影响。因此,乒乓球运动员需要熟练 掌握各种旋转球技术,以提高比赛水 平。
感谢您的观看
THANKS
动量的计算公式
总结词
动量的计算公式是质量与速度的乘积 。
详细描述
动量的计算公式为 P=mv,其中 P 表示 动量,m 表示质量,v 表示速度。这个 公式用于计算物体的动量,是物理学中 常用的基本公式之一。
动量的矢量性
总结词
动量是一个矢量,具有方向和大小。
详细描述
动量具有矢量性,表示物体运动的方向和大小。在物理学中,动量的方向与速度 的方向一致,大小等于质量与速度的乘积。矢量性是动量最基本的性质之一,对 于描述物体的运动状态和变化趋势非常重要。
角动量的计算公式
总结词
角动量的计算公式为 L = Iω,其中 L 是角动 量,I 是转动惯量,ω 是角速度。
详细描述
角动量的计算公式为 L = Iω,其中 L 是角动 量,I 是转动惯量,ω 是角速度。转动惯量 I 是由物体的质量分布和旋转轴的位置决定的, 可以通过质心坐标系和刚体转动轴的垂直距 离计算得出。角速度 ω 是描述物体旋转快慢 的物理量,等于物体转过的角度与时间的比
动量的守恒定律
总结词
在没有外力作用的情况下,封闭系统中的总动量保持不变。
第3、4章动量和角动量守恒定律

Iy Ix
0.1148
6.54
为 I 与x方向的夹角。
Fx 6.1N Fy 0.7N
F F F 6.14N
2 x
2 y
知识回顾
运动状态的变化是力 持续作用的累积效应 力对空间的累积作用的规律 力对时间的累积作用的规律 ( )
动量 P P mv
冲量 I
I y Fy t mv2 sin 30 mv sin 45 1
y
O
v2 30o 45o x v1 n
t 0.01s v1 10m/s v2 20m/s m 2.5g
I x 0.061Ns
I y 0.007Ns
I
tg
2 2 I x I y 6.14 102 Ns
系统的内力对于系统内的每一质点均属于外力
一. 质点系的动量定理
P 表示质点系在时刻 t 的动量
P miv i
i
问题: 系统从P状态 思路:
Q状态 P ?
叠加
对每个质点讨论 Pi
?
质点系 Pi
?
一. 质点系的动量定理 1、两个质点的情况 t2 F1+F12 dt m1v1 m1v10
t1
t2 P P= Fdt 2 1
t1
即
t1
F合dt I 合 p2 p1 mv2 mv1
在给定的时间间隔内,外力作用在质点上的冲量, 等于该质点在此时间内动量的增量——动量定理
说明
动量定理从牛顿第二定律导出, 此定理只适用于惯性参照系 动量定理说明质点动量的 改变是由外力和外力作用时 其定量关系为: 间两个因素,即冲量决定的
(高考系列)高中物理竞赛教程(超详细)_第九讲_动量_角动量..

第四讲动量角动量和能量§4.1动虽与冲量动童定理4. 1. 1.动量在牛顿定律建立以前,人们为了量度物体作机械运动的“运动量”,引入了动量的概念。
当时在研究碰撞和打击问题时认识到:物体的质量和速度越大,其“运动量”就越大。
物体的质量和速度的乘积mv遵从一定的规律,例如,在两物体碰撞过程中,它们的改变必然是数值相等、方向相反。
在这些事实基础上,人们就引用mv来星度物体的“运动量”,称之为动量。
4. 1. 2.冲量要使原来静止的物体获得某一速度,可以用较大的力作用较短的时间或用较小的力作用较长的时间,只要力F和力作用的时间也的乘积相同,所产生的改变这个物体的速度效果就一样,在物理学中把F△,叫做冲量。
4. 1. 3.质点动量定理由牛顿定律,容易得出它们的联系:对单个物体:FAi=ma^t=/nAv=mv x-mv Q FZ=Np即冲量等于动量的增量,这就是质点动定理.在应用动量:定理时要注意它是矢量式,速度的变化前后的方向可以在一条直线上,也可以不在一条直线上,当不在一宣线上时,可将矢景投影到某方向上,分量式为:F4=mv tt-mv Qs气&=-mv Qy F=Z=mv c-mv0:对于多个物体组成的物体系,按照力的作用者划分成内力和外力。
对各个质点用动量定理:第1个,外+L内=扪十1,一川+|。
第2个匕外+4内='"2四一华玲0第n个/“外+/”内=""”一〃"”0由牛顿第三定律:,内+匕内+....+A»内=0因此得到:L外+】2外+……+.外=(WiV l/+zn2v2/+......+m n v n,)_(w,v,0+/n2v20+......m…v nQ)即:质点系所有外力的冲量和等于物体系总动量的增量。
§4,2角动虽角动虽守值定律动量对空间某点或某轴线的矩,叫动量矩,也叫角动量。
它的求法跟力矩完全一样,只要把力F换成动量P即可,故B点上的动量P对原点O的动量矩J为J=rxP(尸=OB)以下介绍两个定理:O(1).角动量定理:质点对某点或某轴线的动景矩对时间的微商,等于作用在该质点上的力对比同点或同轴的力矩,即dJ u出(M为力矩)。
第四章 动量

④动量守恒定律
当 F合外力 0 时, p 恒矢量
§4-3 碰撞 一.碰撞
t (S)
0.1
10
-2
10
-3
10
-4
FN mg 6.5 56 5.5 102 5.5 103 两个或几个物体相遇,在较短时间内发生 较强的相互作用,称为″碰撞″。
二.碰撞的共同规律 碰撞系统大都满足外力远小于内力,即F外 F内, 故碰撞物体组成的系统动量守恒。 三.分类 1.弹性碰撞: 机械能守恒的碰撞称为弹性碰撞,又称 完全弹性碰撞。 2.非弹性碰撞:机械能不守恒的碰撞称为非弹性碰撞。 如果两物体碰撞后合二为一,以共同的 速度运动,则称为完全非弹性碰撞。
( M m )v0 cos MV m(V 例5.一运动员质量为M,手中拿着质量为m的篮球自地面 u) V球地 V球人 V人地 以仰角 、初速度 v 斜向前跳起,跳至最高点时,以相
对于人的速率u将球水平向后抛出,问运动员向前的距离 与不抛球时相比,增加多少? (书P106 4 - 14) 解:①系统: m+M
1 I 5 40 (10 5) 20 20 2 200(N s)
I p mv 0
v 40 m s
O
5
10
t(s)
1 WF mv 2 0 4000J 2
t2 I Fdt
t1
§4-2 dt t f12dt t ( f 21 f12 )dt 0 t f 21动量守恒定律
②条件分析:抛球前后
0
F水平 0
p水平 恒量
③状态分析: 抛球前
抛球后
v0
动量和角动量

x20 - x10 = l
整理后得:
A
t
ΔX1
x
O
m1 (x20 x10 ) = 1 + v1dt 0 m2
l
ΔX2
B
x = x1 = x10 + v1dt
0
m1 t l = 1 + 0 v1dt m2
t
m 2l 0 v1dt = m1 + m2
F = 400 4 10 t/3 = 0
5
得:t=0.003s
0.003 0
2)由冲量定义: I=
0.003
0
Fdt =
(400 4 105 t/3)dt
0.003
= 400t 2 10 t /3 0
5 2
= 0.6N s
3)由动量定理:
I=
0.003
0
Fdt = ΔP = mv = 0.6N s
合外力 合内力
fij = f ji
F
+
0
=
d P dt
总动量
dP 质点系的动力学方程: F = dt
质点系的动量定理的微分形式: Fdt
= dP
ii
t1→t2 积分,得质点系的动量定理积分形式:
( F )dt = p p
t2 t1 i if i i i
总冲量
或:
末、始时刻的总动量
F1
t 1Δt 1Δt 2
F2
Δt i
Fi
t2
ΔIi = F(t i )Δti
F(t )Δt
i i
i
I
近似为 t1→t2 时间段的冲量
力学动量与角动量

力学动量与角动量在物理学中,力学动量和角动量是两个重要的概念。
它们描述了物体或系统的运动特性,并且在许多物理问题的分析中起着至关重要的作用。
本文将深入探讨力学动量和角动量的定义、性质以及在力学中的应用。
一、力学动量力学动量是描述物体线性运动状态的物理量。
它由物体的质量和速度决定,可以用数学公式p = mv来表示,其中p表示动量,m表示质量,v表示速度。
动量的单位是千克·米/秒(kg·m/s),在国际单位制中被广泛采用。
动量具有一些重要的性质。
首先,动量是矢量量,具有大小和方向。
其次,根据牛顿第一定律(惯性定律),一个物体的动量在不受外力作用的情况下保持恒定。
第三,根据牛顿第二定律(力学定律),物体所受外力等于动量的变化率,即F = dp/dt,其中F表示力,t表示时间。
力学动量在力学中具有重要的应用。
例如,在碰撞问题中,动量守恒定律指出,碰撞前后物体的总动量保持不变。
这个定律帮助我们理解物体碰撞时的运动情况。
此外,在运动过程中,动量变化率可以帮助我们分析物体所受的力和物体的运动轨迹。
二、角动量角动量是描述物体旋转运动状态的物理量。
它由物体的质量、速度和距离旋转轴的距离决定,可以用公式L = Iω表示,其中L表示角动量,I表示质量关于旋转轴的转动惯量,ω表示角速度。
角动量的单位是千克·米^2/秒(kg·m^2/s^2)。
角动量也具有一些重要的性质。
与动量类似,角动量也是矢量量,具有大小和方向。
在没有外力矩作用的情况下,角动量守恒,即角动量的大小和方向保持不变。
对于刚体的旋转运动,由于质量分布的不同,转动惯量会有所变化,从而影响角动量的大小。
角动量在力学中也有广泛的应用。
例如,在天体力学中,角动量守恒定律有助于我们研究行星和卫星的运动。
此外,在旋转体的稳定性分析、陀螺仪的原理以及核物理中的粒子自旋等问题中,角动量也发挥着重要的作用。
三、力学动量与角动量的关系力学动量和角动量之间存在一定的联系。
第04章 动量和角动量 部分例题

(3) t=6 秒时刻木箱速度。 解:(1) 根据动量定理: 30
0
m
F/N
4
7
t/s
2
F/N 30
0 4 7 t/s
3
[例4-2] 一物体质量为m,受到方向不变的力F = a + bt 的作用, 求从开始到时刻 t1内,此力的冲量为多少?若物体的初速度 大小为v0,方向与力F相同,求在t1时刻的物体速度大小。
14
mv0 (m M )V
v2 (m M ) g (m M ) l 1 1 (m M )V 2 2(m M ) gl (m M )v 2 2 2
O l m M
解这三个方程式,得
mM v0 5 gl m 若m = 10g,M = 1kg,l = 0.5m,则有
0
x
x方向: y方向:
fdt Mv m(v u cos ) — (1) ( N Mg mg ) d t mu sin — ( 2 )
0
9
θ
10
讨论:
1. 若炮车与地面没有摩擦
2. 若炮车与地面有摩擦,但水平发射炮弹
3. 自锁现象,即 v=0 时
11
解: t1 1 冲量大小 I Fdt a bt dt at1 bt12 0 2 冲量等于动量的增量 I p2 p1 mv mv0
∴物体的速度大小 1 1 1 2 v p2 p1 v0 at1 bt1 v0 m m 2
0.01 1 v0 5 9.8 0.5 500(m / s) 0.01
15
[例4-13]考察如图示两物体间的碰撞,求弹簧对地面的最大压力。
4_3角动量 角动量守恒定律
m
14
第四章 刚体的转动
4-3角动量 角动量守恒定律
3 刚体定轴转动的角动量原理 d ( mi ri 2 ω ) dLi 质点mi 所受合力矩:M i = = dt dt
所有 质 点 所 受 合 外 力矩 :
zω
O
ri
mi
vi
1 r0 L0 = mr ω0 = mr02 ω L = m ω 4 2 1 2 2 mr0 ω0 = mr0 ω ω = 4ω 0 4 3 2 2 由质点的动能定理 W = E k − E k 0 = mr0 ω0
v
θ
r
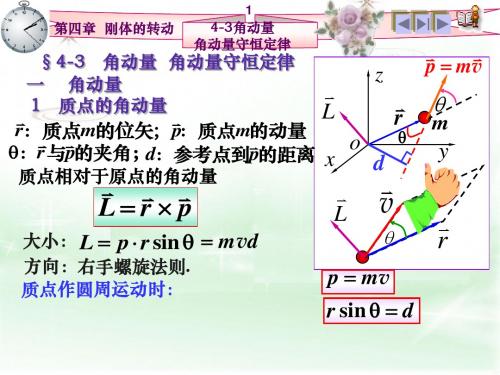
p = mv
r sin θ = d
2
第四章 刚的转动
§4-3 角动量 角动量守恒定律 一 角动量 1 质点的角动量 r:质点m的位矢; p:质点m的动量 θ:r 与p的夹角;d:参考点到p的距离 质点相对于原点 相对于原点的 质点相对于原点的角动量
4-3角动量 角动量守恒定律
z
L
p = mv
o Jr L= ω
m
3
第四章 刚体的转动
4-3角动量 角动量守恒定律
质点的角动量与参考点的位置有关, 质点的角动量与参考点的位置有关,在计 算质点的角动量时必须说明参考点的位置。 算质点的角动量时必须说明参考点的位置。 2 刚体定轴转动的角动量 质量 元 m i 相 对 于转 轴 的 角动 量 : Li = mi ri vi 注意
dL 问题: 问题: =? dt L=r× p
4-3角动量 角动量守恒定律
合力矩
dt
质点的角动量原理
dL M= dt
作用于质点的合力对参考点 的力矩 作用于质点的合力对参考点O的力矩,等于质点对该 参考点 的力矩, 点O的角动量随时间的变化率。 的角动量随时间的变化率。 随时间的变化率
动量和角动量守恒原理

动量和角动量守恒原理一、动量守恒原理动量是描述物体运动状态的物理量,它等于物体的质量乘以速度,用数学公式表示为:动量= 质量× 速度。
动量守恒原理指的是,在一个孤立系统中,系统的总动量在相互作用过程中保持不变。
动量守恒原理可由牛顿第二定律推导得到。
根据牛顿第二定律,物体的加速度与施加在物体上的合外力成正比,与物体的质量成反比。
当物体的质量不变时,可以得到物体的加速度与物体受到的合力成正比。
根据牛顿第三定律,物体受到的合力等于其他物体对它施加的力的矢量和。
因此,在相互作用过程中,物体受到的合力等于其他物体对它施加的力的矢量和,根据物体的加速度与物体受到的合力成正比的关系,可以得到物体的加速度等于其他物体对它施加的力的矢量和除以物体的质量。
将物体的加速度代入动量的定义式中,可以得到物体的动量在相互作用过程中保持不变。
动量守恒原理在物理学中有广泛的应用。
例如,在碰撞过程中,根据动量守恒原理可以计算物体碰撞前后的速度和质量。
在火箭发射过程中,根据动量守恒原理可以计算火箭推进剂的质量和速度,以及火箭的推力。
在运动中的摩擦力、阻力等问题中,也可以利用动量守恒原理进行分析和计算。
二、角动量守恒原理角动量是描述物体旋转状态的物理量,它等于物体的惯性力矩乘以角速度,用数学公式表示为:角动量= 惯性力矩× 角速度。
角动量守恒原理指的是,在一个孤立系统中,系统的总角动量在相互作用过程中保持不变。
角动量守恒原理可由角动量定理推导得到。
根据角动量定理,物体的角动量的变化率等于物体所受的力矩。
当物体受到的合力矩为零时,物体的角动量保持不变。
在一个孤立系统中,由于没有外力矩的作用,因此系统的总角动量保持不变。
角动量守恒原理同样在物理学中有广泛的应用。
例如,在刚体的旋转运动中,根据角动量守恒原理可以计算刚体旋转的角速度和惯性力矩。
在天体运动中,根据角动量守恒原理可以计算行星的轨道半径和角速度。
在自行车、滑板等运动装置的稳定性问题中,也可以利用角动量守恒原理进行分析和计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t2 t1
t2
t1
M dt L2 L1
称为“冲量矩”
33
Mdt
n n 质点系的角动量: L Li (ri pi ) i 1 i 1
12
4-2-3 质心运动定理 质心位置公式:
mrC mi ri
drC dri m mi dt dt
mvC mi vi
结论: 质点系的总动量等于总质量与其质心运动速度 的乘积。
由质点系动量定理的微分式可得:
dp dvi dvC d Fi dt dt mi vi mi dt m dt
p0
t dp F dt t0
4
t I F dt p p0 mv mv 0
t0
质点动量定理: 质点在运动过程中,所受合外力的冲量等 于质点动量的增量。 说明: p (1) 冲量的方向 I 与动量增量 的方向一致。 (2) 动量定理中的动量和冲量都是矢量,符合矢量叠加 原理。常把动量和冲量投影在坐标轴上以分量形式 进行计算。
r
27
质点对参考点的角动量在通过点的任意轴线上的投 影,称为质点对轴线的角动量。
质点系的角动量 L
Lz L cos
L
设各质点对O点的位矢分别为
r1 , r2 , , rn
O
z Lz
动量分别为
p1 , p2 , , pn
n n L Li (ri pi ) i 1 i 1
14
(2)
例5 求腰长为a的等腰直角三角形均匀薄板质心的 位置坐标。
y
解
取如图坐标轴
a x
对称性分析可知
yC 0
O
x dx
取宽度为dx的面积元,设薄板每单位面 积的质量为,则此面积元的质量为
dm 2 ydx 2xdx
xc
xdm dm
0
a
2
a
0
2 a 2 3 2xdx
第4章
动量和角动量
1
§4-1 动量和动量定理
4-1-1 冲量 反映力对时间的累积效应。 冲量:作用力与作用时间的乘积。 恒力的冲量:
I F (t2 t1 )
t2 I F (t ) dt
t1
变力的冲量:
单位:N· s
2
4-1-2 动量 物体的运动状态不仅取决于速度,而且与物体的质 量有关。 动量:运动质点的质量与速度的乘积。
t
6
结论:物体动量变化一定的情况下,作用时间越长, 物体受到的平均冲力越小;反之则越大。
海绵垫子可以 延长运动员下落时 与其接触的时间, 这样就减小了地面 对人的冲击力。
7
§4-2 质点系动量定理
4-2-1 质点系动量定理 设n个质点构成系统 第i个质点: 内力 F内i 初速度
质心运动定理
Fi
22
1. 完全弹性碰撞
1 1 1 1 2 2 2 m1 v10 m2 v 20 m1 v12 m2 v 2 2 2 2 2
m1 v10 m2 v 20 m1 v1 m2 v 2
(m1 m2 ) v10 2m2 v 20 v1 m1 m2 (m2 m1 ) v 20 2m1 v10 v2 m1 m2
v 0 sin t g 跳跃增加的水平距离:
x x 2 x1 ( v1 v 0 cos )t muv 0 sin ( m m) g
20
§4-4 碰撞
两个或两个以上的物体在运动中发生极 其短暂的相互作用,使物体的运动状态 发生急剧变化,这一过程称为碰撞。
21
系统总末动量:
系统总初动量:
F1
F内12 m2 F内21
m1
F2
合外力的冲量:
t
t0
Fi dt
9
t
t0
Fi dt p p0 p
质点系的动量定理:
质点系所受合外力的冲量等于系统总动量的增量。
微分式:
dp Fi dt
注意:系统的内力不能改变整个系统的总动量。
解 水平方向所受合外力为零, 因此系统动量守恒:
MV mv 0
小球、槽、地球组成的系统在运动 过程中机械能守恒: 1 1 2 mgR mv MV 2 2 2 小球速度: v
2MgR M m
2 gR 槽速度:V m M ( M m)
18
例9 质量为m'的人拿着质量为m的物体,与地面成角 的方向向前跳跃,初速率为v0,在跳到最高点P处时,人 将物体相对于人以u的速率水平向后抛出,问人的跳跃 水平距离增加了多少?
y
解 最高点P抛前和抛后过程,水平运动满 足动量守恒条件.设抛后人对地的速率 为v1,物体对地的速率为v2,则有:
v0
P
v 2 (v1 u)
(m m)v0 cos mv1 m(v1 u)
O
x1
x
x2
19
m v1 v 0 cos u m m
从最高点落到地面所需的时间:
定义:外力 F 对参考点O的力矩:
M r F
单位:Nm 力矩的大小:
z
M
F
O
M rF sin
力矩的方向由右手螺旋关系 确定,垂直于 r 和 F 确定的 平面。
r
θ
y
x
30
设作用于质点系的作用力分别为:F1 , F2 , , Fn
e
v 2 v1 v10 v 20
e 为恢复系数
e = 0,则v2 = v1,为完全非弹性碰撞。 e =1,则分离速度等于接近速度,为完全弹性碰撞。 一般非弹性碰撞:0 < e < 1
25
§4-5 质点的角动量
4-5-1 质点的角动量
设:t 时刻质点的位矢 r 质点的动量 mv
运动质点相对于参考点O的 角动量定义为:
作用点相对于参考点O的位矢分别为: r1 , r2 , , rn
F1
z
r1
O
Fi
相对于参考点O的合力矩为:
M ri Fi
x
ri
r2
F2
y
31
2.力对轴的矩
力 F 对轴的力矩:
Z
M
力 F 对点的力矩 M 在过点的任一
轴线上的投影。
(1)如果m1= m2 ,则v1 = v20 ,v2 = v10,即两物体在碰撞时 速度发生了交换。
(2) 如果v20 = 0 , 且 m2 >> m1, 则v1 = - v10, v2 = 0
23
2.完全非弹性碰撞 由动量守恒定律
m1 v10 m2 v 20 v m1 m2
完全非弹性碰撞中动能的损失
28
4-5-2 力矩 1.力对参考点的力矩
质点的角动量 L 随时间的变化率为
式中
而且与参考点O到质点的位矢 r 有关。
质点角动量的改变不仅与所受的作用力 F 有关,
29
dL dr p dr dp pr dt dt dt dt dr dp p v p 0 F dt dt dL rF dt
vi 0
t
质量 mi 外力 Fi
i
末速度 vi
质点动量定理:
F内i
t0
Fi F内i dt mi vi mi vi 0
8
t
t0
Fi F内i dt mi vi mi vi0
其中:
F内i 0
p mi vi p0 mi vi 0
r2
m2
y
x
11
质心位置的分量式:
xC
mx m
i
i i
yC
my m
i i
i
zC
mz m
i
i i
连续体的质心位置:
xC
xdm dm
yC
ydm dm
zC
zdm dm
说明: 对于密度均匀,形状对称的物体,其质心都在 它的几何对称中心。
动量守恒的分量式:
p x mi vix 常量 p y mi viy 常量 p z mi v iz 常量
F 0 F 0 F 0
x y z
动量守恒定律是自然界最普遍的规律之一,它 不仅适合宏观物体,同样也适合微观物体。
17
例8 一质量为m的小球在质量为M的圆弧形槽上,圆 弧形槽半径为R,放在水平地面上,小球与槽间、槽与 地面间的摩擦忽略,现小球从圆弧形槽顶端静止滑下, 求刚离开槽时,小球和木块的速度等于多少?
13
质心运动定理:
Fi maC
作用于质点系上的合外力等于质点系的总质 量与质心加速度的乘积。 质心的两个重要性质:
(1) 系统所受合外力为零时,质心的速度为一恒矢量, 内力既不能改变质点系的总动量,也就不能改变质心 的运动状态 。 系统在外力作用下,质心的加速度等于外力的矢量 和除以系统的总质量。
1 1 1 2 2 E ( m1 v10 m2 v 20 ) (m1 m2 )v 2 2 2 2
m1 m2 ( v10 v 20 ) 2 2(m1 m2 )
24
