2.2.2对数函数及其性质(第一课)
2.2.2对数函数及其性质1

质
x>1时, y>0
(5) 在(0,+∞)上是增函数 (5)在(0,+∞)上是减函数
例1:求下列函数的定义域: (1)y=logax2 ; (2)y=loga(4-x).
分析:主要利用对数函数y=logax的定义域为 (0,+∞)求解.
解 (1)由x2>0 得x≠0, ∴函数y=logax2的定义域是 {x│x≠0}. (2)由4-x>0 得x<4,
(2)真数位置是自变量x,且x的系数是1,x>0;
(3)logax的系数是1.
常用对数函数与自然对数函数
(1).常用对数函数:以10为底的对数函数
常用对数函数;
y lg x 为
(2).自然对数函数:以无理数
e 为底的对数函数
y ln x
为自然对数函数.
探索研究:在同一坐标系中画出下列对数函数的图象
首先想到要做什么?
要使函数有意义
依据: (1)若a 1,loga m loga n m n 0
(2)若0 a 1,loga m loga n 0 m n
[典例3]
(1)解方程:log2(x2-2x-3)=log2(x+1);
[思路点拨] 首先注意定义域的问题,然后解方程.
图象位于y轴右方
定义域 : ( 0,+∞)
图象向上、向下无限延伸 值 域 :
R
自左向右看图象逐渐上升 在(0,+∞)上是:增函数
探索发现:认真观察 函数 y log 1 x
2
y 2 1 11
42
的图象填写下表
图象特征
0 -1 -2
1 2 3 4
2.2.2对数函数及其性质1

学习目标:
1.理解对数函数的含义,认识对数函数与指数函数的 关系;
2.类比指数函数的性质探究过程,用同样的方法探究对 数函数图像及其性质,并能再具体实例中指出其性质;
3.提高归纳演绎能力.
【导入】
一、创设情景,引入概念
某种细胞分裂时,每次每个细胞分裂为2个,则1个这样的细胞第1次分裂后 变为2个细胞,第2次分裂后就得到4个细胞,…,问:经过多少次分裂以后,变
成 y 个细胞? 解:设通过 x 次分裂以后,变成 y 个细胞,则
y 2x
解得
x log2 y
所以,通过log2 y 次分裂以后,变成 y 个细胞。
【导入】
一、创设情景,引入概念
已知函数 y 2x :
x R, y (0, )
1. 反解 x : x log2 y x R, y (0, )
2. x, y 互换: y log2 x x (0, ), y R
3. 定义域: (0, )
二、对数函数的定义
一般地,我们把函数 y = loga x a 0且a 1 叫做对数函数,其中
x 是自变量,函数的定义域是 0, .
三、对数函数的图象与性质
【学习新知】
对数函数的图像和性质 y = loga x a 0且a 1
五、课堂小结
谈谈这节课你的收获?
【小结】
【学习新知】
a 的范围
0 a 1
a 1
图像
定义域
(0, )
值域
R
定点
(1, 0)
单调性
在(0,)单调递减
在(0,)单调递增
奇偶性 函数值的变化范围
非奇非偶函数
当 0 x 1时,y 0 当 x 1 时,y 0
课件21:2.2.2 对数函数及其性质 第一课时

2
2.对数函数 y=logax(a>0,且 a≠1)的图象特征和性质
a>1
0<a<1
图 象
(1)定义域:(0,+∞)
(2)值域:R
性
(3)当 x=1 时,y=0,即过定点_(_1_,0_)__
质 (4)当 x>1 时,__y>__0__;
【问题探究】 1.比较下列两组数的大小: (1)log108与log1015; (2)log0.50.9与log0.50.6. 答案:(1)log1015>log108;(2)log0.50.6>log0.50.9.
2.求下列函数的定义域: (1)y=loga(2x+8); (2)y=1-l1og32x. 答案:(1)x>-4;(2)x>0,且 x≠32.
2
2
A.y<x<1
B.x<y<1
C.1<x<y
D.1<yg 1 y⇒x>y,log 1 y<0⇒y>1,即 1<y<x.
2
2
2
5.下列关系式成立的是( C ) A.0.32<log20.3<20.3 B.0.32<20.3<log20.3 C.log20.3<0.32<20.3 D.log20.3<20.3<0.32
【变式与拓展】
2.函数f(x)=log2(3x+1)的值域为( A )
A.(0,+∞)
B.[0,+∞)
C.(1,+∞)
D.[1,+∞)
解析:∵3x>0,3x+1>1,∴log2(3x+1)>0.
2.2.2对数函数及其性质(一)第一课时

马王堆女尸千年不腐之 谜:1972年,马王堆考古发 现震惊世界,专家发掘西汉 辛追遗尸时,发现其形体完 整,全身润泽,皮肤仍有弹 性,关节还可以活动,骨质 比现在60岁的正常人还好, 是世界上发现的首例历史 悠久的湿尸。
古长沙国丞相夫人辛追
马王堆辛追夫人在湿润的环境中保存了 2200多年之久,人们最关注的两个问题是:
1 1
2
3
4
5
6
7
8
定义域 :
( 0,+∞)
值域:
R
性
过定点 在(0,+∞)上是
增函数
(1 ,0) 即当x =1时,y=0
在(0,+∞)上是 减函数
当x>1时, y>0
质
当x=1时, y=0 当0<x<1时,y<0
当x>1时, y<0
当x=1时, y=0 当0<x<1时, y>0
学点一 求定义域
例 求下列函数的定义域:
表 y=log2x -2 -1 0 1 2
y
描2
点1 11
0 42 1 2 3 4
x
连线 1-
2
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与
性质
x … 1/4 1/2 1 2 4 …
列 表
y
y
log 2
log 1
x…
x…
2
-2 2
-1 1
0 0
1 -1
2… -2 …
y
描
2
点
P74 A组7、10
作业
谢谢市教研所各位专家和教研组 各位老师的光临指导!
数学:2.2.2《对数函数及其性质》教案(新人教版A必修1)

2.2.2对数函数及其性质一、教学内容分析《普通高中课程标准数学教科书·必修(1)》(人民教育出版社)高中一年级第二单元2.2.2《对数函数的图象和性质》第一课时。
函数是高中数学的主体内容——变量数学的主要研究对象之一,是中学数学的重点知识,研究函数的一般理论和基本方法,用函数的思想方法解决实际问题,是函数教学的主要目标。
必修(Ⅰ)2.2.2对数函数及其性质,按课标要求教学时间为3个学时,本节课为第1课时,本节课教学是学生在学过正比例函数、一次函数、二次函数、反比例函数和指数函数的基础上进一步学习的一种新函数,对对数函数概念的理解,图象和性质的掌握和应用有利于学生对初等函数认识的系统性,有利于进一步加深对函数思想方法的理解。
为后面进一步探究对数函数的应用及指数函数、对数函数的综合应用起到承上启下的作用。
二、学情与教材分析对数函数是高中引进的第二个初等函数,是本章的重点内容。
学生在前面的函数性质、指数函数学习的基础上,用研究指数函数的方法,进一步研究和学习对数函数的概念、图象和性质以及初步应用,有利于学生进一步完善初等函数的认识的系统性,加深对函数的思想方法的理解,在教学过程中,虽然学生的认知水平有限,但只要让学生体验对数函数来源于实践,通过教师课件的演示,通过数形结合,让学生感受y=log a x(a>0且a≠1)中,a取不同的值时反映出不同的函数图象,让学生观察、小组讨论、发现、归纳出图象的共同特征、函数图象的规律,进而探究学习对数函数的性质。
最后将对数函数、指数函数的图象和性质进行比较,以便加深对对数函数的概念、图象和性质的理解,同时也为后面教学作准备。
三、设计思想在本节课的教学过程中,通过古遗址上死亡生物体内碳14含量与生物死亡年代关系的探索,引出对数函数的概念。
通过对底数a的分类讨论,探究总结出对数函数的图象与性质,使学生经历从特殊到一般的过程,体验知识的产生、形成过程,通过例题的分析与练习,进一步培养学生自主探索,合作交流的学习方式,通过学生经历直观感知,观察、发现、归纳类比,抽象概括等思维过程,落实培养学生积极探索学习习惯,提高学生的数学思维能力的新课程理念。
高中数学第二章基本初等函数(ⅰ)2.2对数函数2.2.2第一课时对数函数的图象及性质aa高一数学

[点睛] 形如 y=2log2x,y=log2 x3都不是对数函数,可 称其为对数型函数.
2021/12/12
第二页,共十八页。
2.对数函数的图象及性质
a 的范围
0<a<1
4.已知 y=ax 在 R 上是增函数,则 y=logax 在(0,+∞)上是 ________函数.(填“增”或“减”)
答案:增
2021/12/12
第六页,共十八页。
对数函数(duìshù hán shù)的概念
[例 1] 指出下列函数哪些是对数函数? (1)y=3log2x; (2)y=log6x;(3)y=logx5; (4)log2x+1.
[活学活用] 1.函数 f(x)=(a2-a+1)log(a+1)x 是对数函数,则实 数 a=________.
解析:a2-a+1=1,解得 a=0 或 1. 又 a+1>0,且 a+1≠1,∴a=1. 答案:1
2021/12/12
第九页,共十八页。
求对数(duìshù)型函数的定义域
[例 2] 求下列函数的定义域: (1)y=log5(1-x); (2)y=log(1-x)5; (3)y=lnx4--3x; (4)y= log0.54x-3.
2.2.2 对数函数及其性质
第一课时 对数函数的图象及性质
预习课本 P 70~73,思考并完成以下问题
(1)对数函数的概念是什么?它的解析式具有什么特点?
(2)对数函数的图象是什么,通过图象可观察到对数函数具有 哪些性质?
(3)反函数的概念是什么?
2021/12/12
2.2.2 对数函数及其性质(一)

1 >0 1 1-3x (3)由 ,得 x< ; 3 1-3x≠0
1 ∴所求函数定义域为x|x< ; 3
x>0 (4)由 log3x≥0 x>0 ,得 x≥1
;
∴x≥1,∴所求函数定义域为{x|x≥1}.
小结
此题主要利用对数函数 y=logax 的定义域为(0,
2.2.2 对数函数及其性质(一)
问题: 某种细胞分裂时,由1个分裂为2个,2个分为4
个,……,一个这样的细胞分裂x次后,得到的细胞的
个数 y 与 x 的函数关系是:
y2 .
x
现在我们来研究相反的问题.如果要求这种细胞 经过多少次分裂,大约可以得到1万个,10万个…… 细胞,那么,分裂次数 x 就是要得到的细胞个数 y 的函数. 即 x log y .
∴ 函数的定义域为 (1,2)∪(2,3) .
例 2:比较大小 例3:
(1) log2 3 , log2 3.5 (3) log3 2 , log3.5 2 (2) log0.7 1.6 , log0.7 1.8 (4) log1.6 0.7 , log1.8 0.7
( 解:1) y log2 x 在 (0 , ) 上是增函数,
∴函数 y=loga(9-x2)的定义域是{x|-3<x<3}. (4)由 16-4x>0,得 4x<16=42,由指数函数的单调性得
x<2, ∴函数 y=log2(16-4x)的定义域为{x|x<2}.
例2.求下列函数的定义域 :
(1) y loga x ;
2
(2) y loga (4 x 2 );
否
否 否
2.2.2 对数函数及其性质 第1课时 对数函数的图象及性质

探究1:对数函数的定义 一般地,我们把函数_y_=_l_o_g_a_x_(_a_>_0_,_且__a_≠_1_)_叫
做对数函数,其中x是自变量,函数的定义域是 _〔__0_,__+_∞__〕__.__ 注意:〔1〕对数函数定义的严格形式;
〔2〕对数函数对底数的限制条件:
a 0且a 1.
思考1.对数函数的解析式具有什么样的结构特征呢? 提示:对数函数的解析式具有以下三个特征: (1)底数a为大于0且不等于1的常数; (2)真数位置是自变量x,且x的系数是1; (3)logax的系数是1.
1
2
4
……
y=2x
反过来,1个细胞经过多少次分裂,大约可以 等于1万个、10万个细胞?细胞个数y,如何求细 胞分裂次数x?得到怎样一个新的函数?
1
2
4 ……
y=2x
x=? x log2 y y 2x
现在就让我们一起进入本节的学习来解决这些 问题吧!
1.理解对数函数的概念,掌握对数函数的图像与 性质.〔重点〕 2.知道对数函数是一类重要的函数模型; 3.了解指数函数y=ax与对数函数y=logax互为反函 数〔a>0,且a≠1).〔难点〕
4,
1 2
.
①求f(x)的解析式; ②解方程f(x)=2. 分析:(1)根据对数函数的形式定义确定参数m所满足的条件求解 即可;(2)根据设出函数解析式,代入点的坐标求出对数函数的底数; 然后利用指对互化解方程.
变式训练1(1)假设函数f(x)=log(a+1)x+(a2-2a-8)是对数函数,那么 a= .
所以函数 y 1 的定义域为{x|x>0,且x≠1}. log2 x
〔3〕因为
2.2.2 对数函数及其性质

3 y x ( x R) 的反函数,并且画出原来的函数和它 例13:求函数
的反函数的图象。
解:由y x 3,得 x 3 y ∴函数 y x 的反函数是: y 3 x ( x R)
3 3 y x ( x R)和它的反函数 y 3 x ( x R) 的图象如图所示: 函数
(2)在定义域上是增函数
注:函数 y log a x(a 0且a 1) 的图象与 y log 1 x(a 0且a 1) 的 a 图象关于 x轴对称。 练习: 1. 函数 y log 4.3 x 的值域是( D )
A.(0,) C义:
一般地,我们把函数 y log a x(a 0, 且a 1) 叫做对数函数, 其中 x 是自变量,函数的定义域是(0,) 。
注:
x y a 1.由于指数函数 中的底数a满足a 0且a 1 ,则对数函数 y log a x 中的底数 a 也必须满足 a 0且a 1。
二、对数函数的图象和性质:
例2:函数 y log2 x 和 y log1 x 的图象。
2
一般地,对数函数y log a x(a 0,且a 1)的图象和性质 如下表所示:
0 a 1
图象
a 1
定义域 值域 性质 (2)在定义域上是减函数
(0,)
R
(1)过定点(1,0),即x=1时,y=0
x f 1 ( y)
y 注:在函数 x f 1 ( y)中,表示自变量,表示函数。但在习惯上, x 我们一般用 x 表示自变量,用 y表示函数,为此我们常常对调函数 x f 1 ( y)中的字母 x, y,把它改写为 y f 1 ( x)。
2.如果函数 y f ( x)有反函数 f 1 ( x) ,那么函数 y f 1 ( x) 的反函 数就是y f ( x) 。
高中数学人教A版必修1课件:2、2、2对数函数及其性质

个元素和它对应,那么这样的对应(包括集合A,B以及A到B
的对应法则f)叫做集合A到集合B的映射,记作: f : A B
其中,如果 a A,b B ,且元素a和元素b对应,那么我们
把元素b叫做元素a的象,元素a叫做元素b的原象
说明:1 映射 f : A B有方向性,即它只表示从集合A
a 1
0 a 1
y
y
图
y loga x
(1,0)
像
o (1,0)
xo
x
y loga x
定义域 性值 域 质 单调性
奇偶性 过定点
(0,)
(0,)
R 在(0,)上递增
R 在(0,)上递减
非奇非偶
非奇非偶
(1,0), 即x=1时,y=0
单调性的应用
例 比较对数值大小
1. 同底的两个对数比较
⑴ log 23.4 , log 28.5 ⑵ log 0.31.8 , log 0.32.7 ⑶ log a5.1 , log a5.9 ( a>0 , a≠1 ) 解:(3)当a>1时,函数y=log ax在(0,+∞)上是增函数, log a5.1<log a5.9 当0<a<1时,函数y=log ax在(0,+∞)上是减函数, log a5.1>log a5.9
⑧ y log 1 x
概念辨析
例2 下列函数是对数函数的是(D) A. y=log2(3x-2) B. y=log(x-1)x C. y=log0.3x2 D. y=lnx
2.对数函数的图像和性质
用描点法作y=log2x与y=log0.5x的图象.
x
1 4
2019-2020年人教版高中数学必修一说课稿:2-2对数函数及其性质

2019-2020年人教版高中数学必修一说课稿:2-2对数函数及其性质一、教材分析本节课选自人教版高一数学(必修一)第二单元2.2.2《对数函数及其性质》第一课时。
对数函数是重要的基本初等函数之一,是指数函数知识的拓展和延伸. 它的教学过程,体现了“数形结合”的思想,同时蕴涵丰富的解题技巧,这对培养学生的观察、分析、概括的能力、发展学生严谨论证的思维能力有重要作用.本节课也为后面进一步探究对数函数的应用及指数函数、对数函数的综合应用起到承上启下的作用。
二、学情分析学生前面已经学习了指数函数,用研究指数函数的方法,进一步研究和学习对数函数的概念、图像和性质以及初步应用,启发引导学生进一步完善初等函数的知识的系统性,加深对函数的思想方法的理解。
教学过程中,发挥大多数学生动手能力较强的特点,让学生自己通过列表、描点、连线画对数函数图像。
这样也利于对对数函数性质的理解。
三、教学目标1.知识目标:让学生掌握对数函数的概念,能正确描绘对数函数的图象,掌握对数函数的性质.2.能力目标:通过对对数函数的学习,培养学生观察,思考,分析,归纳的思维能力.3.情感目标:培养学生勇于探索的精神,让学生主动融入学习.四、教学重点和难点重点:在理解对数函数定义的基础上,掌握对数函数的图象和性质。
难点:对数函数性质的应用。
五、教法与学法说教法教学过程是教师和学生共同参与的过程,启发学生自主性学习,教师主导,学生为主体,根据这样的原则和所要完成的教学目标,我采用如下的教学方法:(1)启发引导学生思考、分析、实验、探索、归纳。
(2)采用“从特殊到一般”、“从具体到抽象”的方法。
(3)体现“对比联系”、“数形结合”及“分类讨论”的思想方法。
(4)多媒体演示法。
说学法教给学生方法比教给学生知识更重要,本节课注重调动学生积极思考、主动探索,尽可能地增加学生参与教学活动的时间和空间,我进行了以下学法指导:(1)对照比较学习法:学习对数函数,处处与指数函数相对照。
2.2.2 第一课时对数函数及其性质

(
)
x-1>0, 解析:由题意得 解得 2-x>0.
1<x<2.
答案:B
3.求下列函数的定义域: (1)y=log5(1+x); (2)y=log(1-x)5; (3)y= log2x; (4)y= log0.5(4x+3). 3
3.求下列函数的定义域: (1)y=log5(1+x);
大,图象向右越靠近x轴;0<a<1时,a越小,图象向
右越靠近x 轴. (2)左右比较:比较图象与y=1的交点,交点的 横坐标越大,对应的对数函数的底数越大.
答案:[1,2]
[例3] 求函数y=log2(x2-4x+6)的值域.
[思路点拨] 先确定真数的取值范围,再运用对数函数的单调
性求解.
解: ∵x2-4x+6=(x-2)2+2≥2, 又f(x)=log2u在(0,+∞)上是增函数, ∴log2(x2-4x+6)≥log22=1. ∴函数的值域是[1,+∞).
[一点通] 解决与对数函数有关的定义域问题时,经常 需要考虑的问题 1 (1) 中 f(x)≠0; f(x) (2) 2n f(x)(n∈N*)中 f(x)≥0;
(3)logaf(x)(a>0,且 a≠1)中 f(x)>0; (4)logf(x)a 中 f(x)>0 且 f(x)≠1; (5)[f(x)]0 中 f(x)≠0; (6)实际应用问题中自变量的取值要有实际意义.
8.求下列函数的值域: (1)y=log2(x +4); (2)y=log1(3+2x-x ).
2
2
2
(2)设 u=3+2x-x2,则 u=-(x-1)2+4≤4.
2+4)的定义域为R. 解:(1) y = log ( x ∵u >0 , ∴ 0 < u≤4. 2 2+4)≥log 又 y= log1u 在 (0 ,+ ∞)上是减函数, ∵ x 2+ 4≥4 ,∴ log ( x 2 24=2.
2.2.2 对数函数及其性质

第一课时 对数函数的概念、图象与性质
学习目标
1. 理解对数函数的概念;
2. 掌握对数函数的图象与性质; 3. 对数函数的图象与性质应用.
北京青年报曾报道:潮 白河底挖出冰冻古树可 能是山杨,专家经过检 测可推断树的埋藏时 间.
• 你知道专家是根据什 么推断树的埋藏时间 的吗?
y
描 点
2
1 11
42
0 1 23 4
连 -1
线
-2
2 4 ….. 1 2…
x
作y=log0.5x图像
列
x
1/4 1/2 1 2 4
表 y log 2 x -2 -1 0 1 2
y log 1 x
2
1 0 -1 -2
y
2
描
2
点
1 11
42
0 1 23 4
x 这两个函
连
-1
线
-2
数的图象 有什么关
系呢?
关于x轴对称
(3)根据对称性(关于x轴对称)已知 f (x) log3 x
的图象,你能画出 f (x) log 1 x
3
y
的图象吗?
1
o
1
x
(4)当 0<a<1时与a>1时的图象又怎么画呢?
对数函数y=logax (a>0,且a≠1) 的图象与性质
a>1 图
0<a<1
象
定义域 : 值域:
3.已知对数函数过点(16,4)则函数解析式为—
2. 对数函数:y = loga x (a>0,且a≠ 1)
图象与性质
在同一坐标系中用描点法画出对数函数
y log2 x和y log 1 x 的图象。
必修一同步2.2.2第1课时对数函数及其性质

5.函数y=lnx的反函数是________. [答案] y=ex
高效课堂
●互动探究
对数函数概念
下列函数表达式中,是对数函数的有(
y=logx(x+2);⑥y=2log4x;⑦y=log2(x+1). A.1个 C.3个 B.2个 D.4个
)
①y=logx2;②y=logax(a∈R);③y=log8x;④y=lnx;⑤
1 -1 0 ,logaa=___ 1 ,loga =____(a>0,且 a≠1). 2.loga1=___ a 指数 函 3.一般地,我们把函数 y=ax(a>0 且 a≠1)叫做______
(0,+∞) .把指数式 y=ax 化 数,它的定义域为 R,值域为___________
为对数式为 x=logay.
A.a>b>1>c>d
B.b>a>1>d>c C.1>c>a>b>c>d D.a>b>1>d>c
[解析]
解法一:观察在x轴上方的图象,从右至左依次为
②①④③,故b>a>d>c. 解法二:在上图中画出直线 y = 1 ,发现分别与①,②,
③ , ④ 交 于 A(a,1) , B(b,1) , C(c,1) , D(d,1) 四 点 , 由 图 可 知
(2) 左右比较,在 x 轴
上方,图象从左至右底 数依次增大.
如图所示, 曲线是对数函数 y=logax 的图象, 已知 a 取 3、 4 3 1 3、5、10,则相应于 C1、C2、C3、C4 的 a 值依次为( 4 3 1 A. 3、3、5、10 4 1 3 B. 3、3、10、5 4 3 1 C.3、 3、5、10 4 1 3 D.3、 3、10、5 )
高一数学人教A版必修1课件:2.2.2 对数函数及其性质(第1课时)

∴函数 y loga x2 的定义域是x | x 0
二、例题讲解
例1、求下列函数的定义域
(3) y log(2x1)(4x 8)
2x 1>0
(3)
由题意可得
2
x
1
1
4x 8>0
解得
x> 1 2
x1
1、函数 y loga x (其中a 0, a 1)的图象恒过
定点__(_1_,0_)__
2、函数 y loga (x 2)(其中a 0, a 1)的图象恒过
定点__(_3_,0_)__ 定 3、点函_数_(_3_y,_0_)_loga (5x 2)(其中a 0, a 1)的图象恒过 4、函数5 y 3loga (5x 2)+1(其中a 0, a 1)的图象 恒过定点__( _5_,_1_)_
七y 、lo小g结a x与y log1 x 的图象关于x轴对称
y loga x
a
a>1
0<a<1
y
y
y log a x
图
(a 1)
(1, 0)
象
o (1, 0)
xo
y loga x x
(0 a 1)
当 x > 1 时, y > 0
定义当域0<x <1 时,y < 0
当 x > 1 时, y < 0
定义当域0<x <1 时,y < 0
当 x > 1 时, y < 0
(0,) 当0< x<1 时, y>0
第二章 2.2.2 第1课时 对数函数及其性质(一)
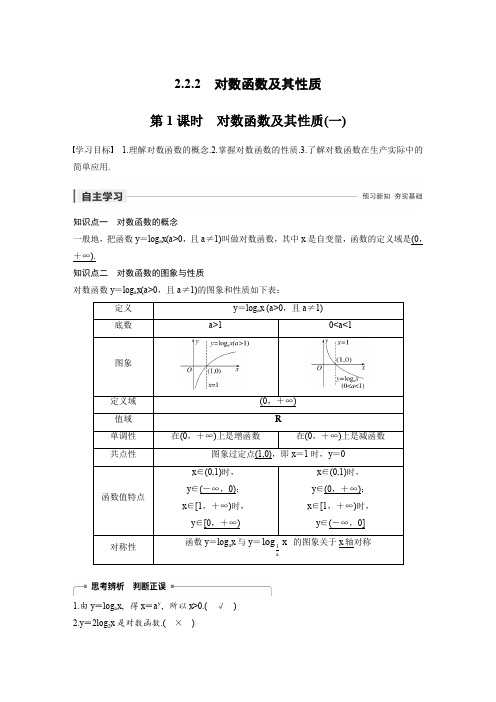
2.2.2 对数函数及其性质 第1课时 对数函数及其性质(一)学习目标 1.理解对数函数的概念.2.掌握对数函数的性质.3.了解对数函数在生产实际中的简单应用.知识点一 对数函数的概念一般地,把函数y =log a x (a >0,且a ≠1)叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞).知识点二 对数函数的图象与性质对数函数y =log a x (a >0,且a ≠1)的图象和性质如下表:1.由y =log a x ,得x =a y ,所以x >0.( √ )2.y =2log 2x 是对数函数.( × )3.y =a x 与y =log a x 的单调区间相同.( × )4.由log a 1=0,可得y =log a x 恒过定点(1,0).( √ )题型一 对数型函数的定义域 例1 求下列函数的定义域. (1)y =log a (3-x )+log a (3+x ); (2)y =log 2(16-4x ). 考点 对数函数的定义域 题点 对数函数的定义域解 (1)由⎩⎪⎨⎪⎧3-x >0,3+x >0,得-3<x <3,∴函数的定义域是(-3,3). (2)由16-4x >0,得4x <16=42, 由指数函数的单调性得x <2,∴函数y =log 2(16-4x )的定义域为(-∞,2).反思感悟 求含对数式的函数定义域关键是真数大于0,底数大于0且不为1.如需对函数式变形,需注意真数底数的取值范围是否改变. 跟踪训练1 求下列函数的定义域. (1)y =x 2-4lg (x +3);(2)y =12-x+ln(x +1). 考点 对数函数的定义域 题点 对数函数的定义域解 (1)要使函数有意义,需⎩⎪⎨⎪⎧x 2-4≥0,x +3>0,x +3≠1,即⎩⎪⎨⎪⎧x ≤-2或x ≥2,x >-3,x ≠-2,即-3<x <-2或x ≥2,故所求函数的定义域为(-3,-2)∪[2,+∞).(2)要使函数有意义,需⎩⎪⎨⎪⎧2-x >0,x +1>0,即⎩⎪⎨⎪⎧x <2,x >-1,∴-1<x <2. 故所求函数的定义域为(-1,2). 题型二 对数型函数的求值问题例2 已知函数f (x )=⎩⎪⎨⎪⎧2x ,x ≤0,log 3x ,x >0,(1)求f ⎝⎛⎭⎫f ⎝⎛⎭⎫127的值; (2)若f (a )=12,求a 的值.解 (1)∵f ⎝⎛⎭⎫127=log 3127=-3, ∴f ⎝⎛⎭⎫f ⎝⎛⎭⎫127=f (-3)=2-3=18. (2)当a >0时,由f (a )=12,得log 3a =12.∴a =123= 3.当a ≤0时,由f (a )=12,得2a =12,∴a =-1,综上所述a 的值为-1或 3.反思感悟 理解运算对象,选择运算方法即对于分段函数要注意分类讨论,掌握运算法则,即指数、对数的运算法则,求得运算结果,所以本题充分体现了数学运算的核心素养. 跟踪训练2 已知函数f (x )=log 3(x +1),若f (a )=1,则a 等于( ) A.0 B.1 C.2 D.3 答案 C解析 ∵f (a )=log 3(a +1)=1,∴a +1=3,∴a =2.题型三 对数函数的图象问题例3 (1)函数y =x +a 与y =log a x 的图象只可能是下图中的( )答案 C(2)画出函数y =lg|x -1|的图象. 考点 对数函数的图象题点 含绝对值的对数函数的图象 解 (1)先画出函数y =lg x 的图象(如图).(2)再画出函数y =lg|x |的图象(如图).(3)最后画出函数y =lg|x -1|的图象(如图).延伸探究1.把本例(1)的条件“y =log a x ”改为“y =log a (-x )”,则函数y =a -x 与y =log a (-x )的图象可能是( )答案 C解析 ∵在y =log a (-x )中,-x >0,∴x <0, ∴图象只能在y 轴的左侧,故排除A ,D ; 当a >1时,y =log a (-x )是减函数, y =a -x =⎝⎛⎭⎫1a x 是减函数,故排除B ; 当0<a <1时,y =log a (-x )是增函数, y =a -x =⎝⎛⎭⎫1a x 是增函数,∴C 满足条件,故选C. 2.把本例(2)改为f (x )=|log 2(x +1)|+2,试作出其图象. 解 第一步:作y =log 2x 的图象,如图①所示.第二步:将y=log2x的图象沿x轴向左平移1个单位长度,得y=log2(x+1)的图象,如图②所示.第三步:将y=log2(x+1)的图象在x轴下方的部分作关于x轴的对称变换,得y=|log2(x+1)|的图象,如图③所示.第四步:将y=|log2(x+1)|的图象沿y轴向上平移2个单位长度,即得到所求的函数图象,如图④所示.反思感悟现在画图象很少单纯依靠描点,大多是以基本初等函数为原料加工,所以一方面要掌握一些常见的平移、对称变换的结论,另一方面要关注定义域、值域、单调性、关键点.1.下列函数为对数函数的是()A.y=log a x+1(a>0且a≠1)B.y=log a(2x)(a>0且a≠1)C.y=log(a-1)x(a>1且a≠2)D.y=2log a x(a>0且a≠1)考点对数函数的概念题点对数函数的概念答案 C2.函数y=log2(x-2)的定义域是()A.(0,+∞)B.(1,+∞)C.(2,+∞)D.[4,+∞)考点对数函数的定义域题点对数函数的定义域答案 C3.函数f(x)=3-x+lg(x+1)的定义域为()A.[-1,3)B.(-1,3)C.(-1,3]D.[-1,3] 答案 C4.已知a >0,且a ≠1,函数y =a x 与y =log a (-x )的图象只能是下图中的( )答案 B解析 由y =log a (-x ),知-x >0,即x <0,可排除A ,C.当a >1时,B 适合. 5.若函数f (x )=2log a (2-x )+3(a >0,且a ≠1)过定点P ,则点P 的坐标是__________. 考点 对数函数的性质 题点 对数函数图象过定点问题 答案 (1,3)1.含有对数符号“log ”的函数不一定是对数函数.判断一个函数是否为对数函数,不仅要含有对数符号“log ”,还要符合对数函数的概念,即形如y =log a x (a >0,且a ≠1)的形式.如:y =2log 2x ,y =log 5x5都不是对数函数,可称其为对数型函数.2.研究y =log a f (x )的性质如定义域、值域、比较大小,均需依托对数函数的相应性质.一、选择题 1.给出下列函数:①223log y x ;②y =log 3(x -1);③y =log (x +1)x ;④y =log πx .其中是对数函数的有( ) A.1个 B.2个 C.3个 D.4个 考点 对数函数的概念 题点 对数函数的概念 答案 A解析 ①②不是对数函数,因为对数的真数不是只含有自变量x ;③不是对数函数,因为对数的底数不是常数;④是对数函数.2.已知函数f (x )=11-x的定义域为M ,g (x )=ln(1+x )的定义域为N ,则M ∩N 等于( ) A.{x |x >-1} B.{x |x <1} C.{x |-1<x <1}D.∅考点 对数函数的定义域 题点 对数函数的定义域 答案 C解析 ∵M ={x |1-x >0}={x |x <1}, N ={x |1+x >0}={x |x >-1}, ∴M ∩N ={x |-1<x <1}.3.函数y =log 2(x -1)2-x 的定义域是( )A.(1,2]B.(1,2)C.(2,+∞)D.(-∞,2) 答案 B解析 由⎩⎪⎨⎪⎧ x -1>0,2-x >0,得⎩⎪⎨⎪⎧x >1,x <2,∴1<x <2.∴函数的定义域为(1,2).4.下列函数中,与函数y =x 相等的是( ) A.y =(x )2 B.y =x 2 C.2log 2xy =D.y =log 22x答案 D解析 因为y =log 22x 的定义域为R ,且根据对数恒等式知y =x . 5.函数y =log a (2x -3)+1的图象恒过定点P ,则点P 的坐标是( ) A.(2,1) B.(2,0) C.(2,-1) D.(1,1) 答案 A解析 令2x -3=1,则x =2.∴y =log a (2x -3)+1的图象恒过定点(2,1).6.函数y =a x 与y =-log a x (a >0,且a ≠1)在同一坐标系中的图象形状可能是( )答案 A7.已知函数f (x )=log a (x +2),若图象过点(6,3),则f (2)的值为( ) A.-2 B.2 C.12 D.-12考点 对数函数的性质 题点 对数函数图象过定点问题 答案 B解析 代入(6,3),3=log a (6+2)=log a 8, 即a 3=8,∴a =2.∴f (x )=log 2(x +2),∴f (2)=log 2(2+2)=2.8.若函数f (x )=log a (x +b )的图象如图所示,其中a ,b 为常数,则函数g (x )=a x +b 的图象大致是( )考点 对数函数的图象题点 同一坐标系下的指数函数与对数函数的图象 答案 D解析 由f (x )的图象可知0<a <1,0<b <1, ∴g (x )的图象应为D. 二、填空题9.函数f (x )=log 2x -2的定义域是________. 答案 [4,+∞)解析 由题意知⎩⎪⎨⎪⎧ x >0,log 2x -2≥0,即⎩⎪⎨⎪⎧x >0,x ≥4,∴x ≥4,∴函数f (x )的定义域为[4,+∞). 10.已知0<a <1,0<b <1,若log (3)1b x a -<,则x 的取值范围是__________.考点 对数不等式 题点 解对数不等式 答案 (3,4)解析 ∵0<a <1, ∴log (3)1b x a-<=a 0等价于log b (x -3)>0=log b 1.∵0<b <1,∴⎩⎪⎨⎪⎧x -3>0,x -3<1,解得3<x <4.11.函数12log (3)y x a =- 的定义域是⎝⎛⎭⎫23,+∞,则a =________. 答案 2解析 由12log (3)y x a =-知,3x -a >0,即x >a3.∴a 3=23,即a =2. 三、解答题12.求下列函数的定义域: (1)f (x )=log (x -1)(3-x ); (2)f (x )=2x +3x -1+log 2(3x -1). 解 (1)由题意知⎩⎪⎨⎪⎧3-x >0,x -1>0,x -1≠1,解得1<x <3,且x ≠2,故f (x )的定义域是(1,2)∪(2,3). (2)由题意知⎩⎪⎨⎪⎧2x +3≥0,x -1≠0,3x -1>0,解得x >13,且x ≠1.故f (x )的定义域是⎝⎛⎭⎫13,1∪(1,+∞).13.若函数f (x )为定义在R 上的奇函数,且x ∈(0,+∞)时,f (x )=lg(x +1),求f (x )的解析式,并画出大致图象.解 ∵f (x )为R 上的奇函数,∴f (0)=0. 又当x ∈(-∞,0)时,-x ∈(0,+∞), ∴f (-x )=lg(1-x ).又f (-x )=-f (x ), ∴f (x )=-lg(1-x ),∴f (x )的解析式为f (x )=⎩⎪⎨⎪⎧lg (x +1),x >0,0,x =0,-lg (1-x ),x <0,∴f (x )的大致图象如图所示,14.已知log a (3a -1)恒为正,则a 的取值范围是________. 考点 对数函数的图象 题点 对数函数的图象答案 ⎩⎨⎧⎭⎬⎫a ⎪⎪13<a <23或a >1 解析 由题意知log a (3a -1)>0=log a 1. 当a >1时,y =log a x 是增函数, ∴3a -1>1,解得a >23,∴a >1;当0<a <1时,y =log a x 是减函数,∴⎩⎪⎨⎪⎧3a -1<1,3a -1>0,解得13<a <23.∴13<a <23. 综上所述,a 的取值范围是⎩⎨⎧⎭⎬⎫a ⎪⎪13<a <23或a >1. 15.已知函数f (x )=log 21+x1-x .(1)求证:f (x 1)+f (x 2)=f ⎝ ⎛⎭⎪⎫x 1+x 21+x 1x 2;(2)若f ⎝⎛⎭⎪⎫a +b 1+ab =1,f (-b )=12,求f (a )的值.(1)证明 左边=log 21+x 11-x 1+log 21+x 21-x 2=log 2⎝ ⎛⎭⎪⎫1+x 11-x 1·1+x 21-x 2=log 21+x 1+x 2+x 1x 21-x 1-x 2+x 1x 2.右边=log 21+x 1+x 21+x 1x 21-x 1+x 21+x 1x 2=log 21+x 1+x 2+x 1x 21+x 1x 2-x 1-x 2. 所以左边=右边.(2)解 因为f (-b )=log 21-b 1+b =-log 21+b 1-b =12, 所以f (b )=log 21+b 1-b=-12, 利用(1)可知f (a )+f (b )=f ⎝⎛⎭⎪⎫a +b 1+ab ,所以f (a )-12=1, 解得f (a )=32.。
2.2.2对数函数及其性质1

3.(2015·无锡高一检测)如图所示的曲线是对数函数y=logax,
y=logbx,y=logcx,y=logdx的图象,则a,b,c,d与1的大小关系
为
.
【解题探究】1.典例1中由lga+lgb=0会得到a与b怎样的关系式,需要 对a的范围进行分情况讨论吗? 提示:由lga+lgb=0可得lg(ab)=0,则ab=1,即a= 行讨论.
1 a
x(a>0且a≠1)的图象关于x轴(即直线y=0)对称.
【拓展延伸】对数函数单调性的记忆口诀 对数增减有思路,函数图象看底数; 底数要求大于0,但等于1却不行; 底数若是大于1,图象从左往右增; 底数0到1之间,图象从左往右减; 无论函数增和减,图象都过(1,0)点.
【题型探究】 类型一 对数函数概念的应用
1 2 1 (a ) , 当a=- 时, 底数小于 2 4 0,故(4)不是对数函数. 1 答案:(3) 2
类型二
求对数型函数的定义域、函数值问题 )
【典例】1.已知函数f(x)=log5(x+1),若f(a)=1,则a= ( A.3 B.4 C.5 D.6
2.(2015·邢台高一检测)函数f(x)=log(x-1)
答案:y=log4x
a 2 5a 4 0, 3.由题意可得, 2a 1 0, 解得a=4. 2a 1 1,
答案:4
【方法技巧】判断一个函数是对数函数的方法
【变式训练】已知下列函数.
(1)y=log
1 2
(-x)(x <0).
(2)y=2log4(x-1)(x>1). (3)y=lnx(x>0). (4)y=
x 2 0, 必须 4 x 0, 4 x 解得-2<x<4 且x≠3, 1.
2.2.2对数函数及其性质(第一课时)

2.2.2对数函数及其性质(第一课时)1、函数f(x)=lg(x -1)+4-x 的定义域为( )A .(1,4]B .(1,4)C .[1,4]D .[1,4)2、函数y =x |x|l og 2|x|的大致图象是()3、已知函数f(x)=|lgx|,若a≠b,且f(a)=f(b),则ab =( )A .1B .2 C.12 D.144、下列各组函数中,定义域相同的一组是( )A .y =a x 与y =log a x(a >0,且a≠1)B .y =x 与y =xC .y =lgx 与y =lg xD .y =x 2与y =lgx 25、函数y =log 2x 与y =log 12x 的图象关于( )A .x 轴对称B .y 轴对称C .原点对称D .直线y =x 对称6、已知a>0且a≠1,则函数y =a x 与y =log a (-x)的图象可能是()7、对数函数的图象过点M(16,4),则此对数函数的解析式为( )A .y =log 4xB .y =log 14xC .y =log 12x D .y =log 2x8、已知图中曲线C 1,C 2,C 3,C 4分别是函数y =loga 1x ,y =loga 2x ,y =loga 3x ,y =loga 4x 的图象,则a 1,a 2,a 3,a 4的大小关系是( )A .a 4<a 3<a 2<a 1B .a 3<a 4<a 1<a 2C .a 2<a 1<a 3<a 4D .a 3<a 4<a 2<a 19、函数y =log 2x 在[1,2]上的值域是( )A .RB .[0,+∞)C .(-∞,1]D .[0,1] 10、函数y =log a (x +2)+3(a >0且a≠1)的图象过定点________.11、函数y =log12x -1的定义域是________.12、若函数f(x)=log a x(0<a<1)在区间[a,2a]上的最大值是最小值的3倍,则a 的值为________.13、已知g(x)=⎩⎨⎧e x x≤0lnx x>0,则g[g(13)]=________. 14、.求下列函数的定义域:(1)y =log 333x +4;(2)y =log (x -1)(3-x).15、已知f(x)=log 3x.(1)作出这个函数的图象;(2)当0<a <2时,有f(a)>f(2),利用图象求a 的取值范围.16、函数f(x)=log 2(32-x 2)的定义域为A ,值域为B.试求A∩B.17、求证:函数f (x )=lgxx +-11是奇函数.18、求函数)416(log )1(x x y -=+的定义域.19、 求函数y = log 2|x|的定义域,并画出它的图象.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
返回
再来一遍
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
O
性 质
定义域 R;值域(0,+∞) 过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数 x>0时,ax>1; x>0时,0<ax<1; x<0时,0<ax<1 x<0时,ax>1
湖南省长沙市一中卫星远程学校
3. 某种细胞分裂时,得到的细胞的 个数y是分裂次数x的函数,这个函数 可以用指数函数y=2x表示.
3
y
y log 3 x
O
y log 1 x
3
湖南省长沙市一中卫星远程学校
x
3. 对数函数的性质:a>1 0<a<1y图 象yO
x
O
x
性 x∈(0, 1)时,y<0; x∈(0, 1)时,y>0 质 x∈(1, +∞)时,y>0. x∈(1, +∞)时,y<0.
在(0,+∞)上是增函数
定义域:(0, +∞); 值域:R 过点(1, 0),即当x=1时,y=0.
2.2.2对数函数 及其性质
湖南省长沙市一中卫星远程学校
复习引入
1. 指数与对数的相互转化 ab=N logaN=b.
湖南省长沙市一中卫星远程学校
2. 指数函数的图象和性质
a>1
图 象
y (0,1) y=ax (a>1) y=1 x
0<a<1
y=ax (0<a<1) y (0,1) O y=1 x
练习
1. 教材P.73练习第2、3题
2. 函数y=loga(x+1)-2 (a>0, a≠1)
的图象恒过定点 .
湖南省长沙市一中卫星远程学校
课堂小结
对数函数定义、图象、性质;
湖南省长沙市一中卫星远程学校
课后作业
1、教材P74:7、8 2、选作
已知函数y=loga(x+1) (a>0, a≠1) 的定义域与值域都是[0, 1],求a的值.
2
y
思 考:
y log 2 x
x
y log 1 x
湖南省长沙市一中卫星远程学校
两图象有什么 关系?
O
2
练习:教材P.73:练习1
湖南省长沙市一中卫星远程学校
练习 教材P.73练习第1题 画出函数 y log 3 x 及 y log 1 x 的图象,并且说明这两个函数的相 同点和不同点.
且a≠1)叫做对数函数,其中x是自变量,
函数的定义域为(0,+∞),
湖南省长沙市一中卫星远程学校
例1 求下列函数的定义域:
(1) y log a x
2
( 2) y log a (4 x )
( 3) y log a (9 x )
2
湖南省长沙市一中卫星远程学校
2. 对数函数的图象: 通过列表、描点、连线作 y log 2 x 与 y log 1 x 的图象.
在(0,+∞)上是减函数
湖南省长沙市一中卫星远程学校
例2 比较下列各组数中两个值的大小:
(1) log 2 3.4, log 2 8.5
( 2) log 0.3 1.8, log 0.3 2.7
( 3) log a 5.1, log a 5.9(a 0, a 1)
湖南省长沙市一中卫星远程学校
这种细胞经过多少次分裂,大约 可以得到1万个,10万个……细胞? 分裂次数x就是细胞个数y的函 数.这个函数写成对数的形式是x= log2y.
湖南省长沙市一中卫星远程学校
x=log2y
如果用x表示自变量,y表示函 数,这个函数就是y=log2x.
湖南省长沙市一中卫星远程学校
讲授新课
1. 对数函数的定义: 一般的,我们把函数y=logax (a>0
