2009年学而思杯六年级数学试题及答案(A卷)
2008年学而思杯六年级一试A卷解析

2008年第一届“学而思杯”综合素质测评六年级1试数学试题(A卷)1.计算:11111 200820092010201120121854108180270++++= 。
2.如图,相同的汉字代表相同的数字,不同的汉字代表不同的数字,那么四位数“奥林匹克”最大是奥林匹克+奥数网20083.三个连续的自然数,从小到大依次是4、7、9的倍数,这三个自然数的和最小是。
4.在循环小数中类似于10.1428577••=,10.07692313••=等,循环节是从小数点右边的第一位(即十分位)就开始的小数,叫做纯循环小数,包括7和13在内,共有个正整数,其倒数是循环节恰好为六位的纯循环小数。
5.已知ABCD是平行四边形,:3:2BC CE=,三角形ODE的面积为6平方厘米。
则阴影部分的面积是平方厘米。
6.三位数A满足:它的所有质因数之和是26。
这样的三位数A有个。
7.电子玩具车A与B在一条轨道的两端同时出发相向而行,在轨道上往返行驶。
已知A比B的速度快50%,根据推算,第20072007次相遇点与第20082008次相遇点相距58厘米,轨道长厘米。
8.一块电子手表,显示时与分,使用12小时计时制,例如中午12点和半夜12点都显示为12:00。
如果在一天(24小时)中的随机一个时刻看手表,至少看到一个数字“1”的概率是。
9.欢欢和贝贝是同班同学,并且住在同一栋楼里。
早晨7:40,欢欢从家出发骑车去学校,7:46追上了一直匀速步行的贝贝;看到身穿校服的贝贝才想起学校的通知,欢欢立即调头,并将速度提高到原来的2倍,回家换好校服,再赶往学校;欢欢8:00赶到学校时,贝贝也恰好到学校。
如果欢欢在家换校服用去6分钟且调头时间不计,那么贝贝从家里出发时是点分。
10. 某个班的20个学生的家庭住址在城市中的分布如图(圆点是各个学生的家庭住址,线段是街道),如果这个班的学生举行一个聚会,为了尽量减少每个学生行走路程总和,那么他们应该选择 十字路口附近的地点。
2009年秋季学而思入学测试题

2009年秋季学而思入学测试题五年级姓名所在区学校年级答题计时要求:1、请在40分钟内独立完成,并写出详细解答过程。
2、做完试题后,请携带试题到学而思前台与老师核对答案,选择合适的班级。
1、(09年市奥校入学考试题)计算:101×33-101×662、(07年育才小学四年级期末试题)如果把被减数、减数和差加起来,用它们的和除以被减数,商一定是多少?3、一个偶数各个数位的和是40,这个数最小是多少?4、(09年16校联考试题)一个正方形的边长增加2cm,面积增加20c㎡,扩大后正方形面积为()c㎡。
5、(08年市奥校入学考试题)将一根绳子对折再对折,然后用剪刀在中间剪一刀,这条绳子被剪成几段?6、(07年16校联考试题)甲乙两人以匀速绕圆形跑道相向跑步,出发点在圆直径的两端,如果他们同时出发,并在甲跑完60米时第一次相遇,乙跑一圈还差80米时两人第二次相遇,求跑道的长多少米?7、(09年16校联考试题)有甲、乙两堆煤,从甲中取出12吨放到乙中,两堆煤重量相等;从乙中取出12吨放到甲中,甲是乙的两倍。
甲、乙两堆煤共重多少吨?8、(第八届华杯赛初赛题)一个车队以5米/秒的速度缓缓通过一座长250米的大桥,共用105秒。
已知每辆车长5米,两车间隔10米。
这个车队共有多少辆车?9、(08年16校联考试题)下图中大小正方形的边长分别是9厘米和4厘米,求阴影部分的面积。
10、(第十三届华杯赛决赛试题)黑板上写着1至2008共2008个自然数,小明每次擦去两个奇偶性相同的数,再写上他们的平均数,最后黑板上只剩下一个自然数,这个自然数可能的最大值和最小值的差是多少?入学测试评价报告书入学测试综合评价内容建议班次:教师签字:。
小学六年级数学竞赛训练题--流水行船问题

小学六年级数学竞赛训练--流水行船【例1】乙船顺水航行2小时,行了120千米,返回原地用了4小时.甲船顺水航行同一段水路,用了3小时.甲船返回原地比去时多用了几小时?【解析】乙船顺水速度:120÷2=60(千米/小时).乙船逆水速度:120÷4=30(千米/小时)。
水流速度:(60-30)÷2=15(千米/小时).甲船顺水速度:12O÷3=4O(千米/小时)。
甲船逆水速度:40-2×15=10(千米/小时).甲船逆水航行时间:120÷10=12(小时)。
甲船返回原地比去时多用时间:12-3=9(小时).【例2】船往返于相距180千米的两港之间,顺水而下需用10小时,逆水而上需用15小时。
由于暴雨后水速增加,该船顺水而行只需9小时,那么逆水而行需要几小时?【解析】本题中船在顺水、逆水、静水中的速度以及水流的速度都可以求出.但是由于暴雨的影响,水速发生变化,要求船逆水而行要几小时,必须要先求出水速增加后的逆水速度.船在静水中的速度是:(180÷10+180÷15)÷2=15(千米/小时).暴雨前水流的速度是:(180÷10-180÷15)÷2=3(千米/小时).暴雨后水流的速度是:180÷9-15=5(千米/小时).暴雨后船逆水而上需用的时间为:180÷(15-5)=18(小时).【例3】(2009年“学而思杯”六年级)甲、乙两艘游艇,静水中甲艇每小时行1千米,乙艇每小时行54千米.现在甲、乙两游艇12于同一时刻相向出发,甲艇从下游上行,乙艇从相距27千米的上游下行,两艇于途中相遇后,又经过4小时,甲艇到达乙艇的出发地.水流速度是每小时千米.【解析】两游艇相向而行时,速度和等于它们在静水中的速度和,所以它们从出发到相遇所用的时间为10小时.相遇后又经过4小时,甲艇到达乙艇的出发地,说明甲艇逆水行驶27千米需要10小时,那么甲艇的逆水速度为1(千米/小时),则水流速度为24(千米/小时).【例4】一艘轮船顺流航行120千米,逆流航行80千米共用16时;顺流航行60千米,逆流航行120千米也用16时。
燕尾定理详细解析.题库教师版

燕尾定理:在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.OFE DCBA上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.通过一道例题证明一下燕尾定理:如右图,D 是BC 上任意一点,请你说明:1423:::S S S S BD DC ==S 3S 1S 4S 2EDCBA【解析】 三角形BED 与三角形CED 同高,分别以BD 、DC 为底,所以有14::S S BD DC =;三角形ABE 与三角形EBD 同高,12::S S ED EA =;三角形ACE 与三角形CED 同高,43::S S ED EA =,所以1423::S S S S =;综上可得1423:::S S S S BD DC ==.【例 1】 (2009年第七届希望杯五年级一试试题)如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .FED CBA33321F E DC BAABCDEF【解析】 方法一:连接CF ,例题精讲燕尾定理根据燕尾定理,12ABF ACF S BD S DC ==△△,1ABF CBF S AES EC==△△, 设1BDF S =△份,则2DCF S =△份,3ABF S =△份,3AEF EFC S S ==△△份,如图所标所以551212DCEF ABC S S ==△方法二:连接DE ,由题目条件可得到1133ABD ABC S S ==△△,11212233ADE ADC ABC S S S ==⨯=△△△,所以11ABD ADE S BF FE S ==△△, 111111122323212DEF DEB BEC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211323CDE ABC S S =⨯⨯=△△.所以则四边形DFEC 的面积等于512.【巩固】如图,已知BD DC =,2EC AE =,三角形ABC 的面积是30,求阴影部分面积.【解析】 题中条件只有三角形面积给出具体数值,其他条件给出的实际上是比例的关系,由此我们可以初步判断这道题不应该通过面积公式求面积. 又因为阴影部分是一个不规则四边形,所以我们需要对它进行改造,那么我们需要连一条辅助线,(法一)连接CF ,因为BD DC =,2EC AE =,三角形ABC 的面积是30,所以1103ABE ABC S S ==△△,1152ABD ABC S S ==△△.根据燕尾定理,12ABF CBF S AE S EC ==△△,1ABF ACF S BDS CD==△△,所以17.54ABF ABC S S ==△△,157.57.5BFD S =-=△,所以阴影部分面积是30107.512.5--=.(法二)连接DE ,由题目条件可得到1103ABE ABC S S ==△△,11210223BDE BEC ABC S S S ==⨯=△△△,所以11ABE BDE S AF FD S ==△△, 1111112.5223232DEF DEA ADC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211032CDE ABC S S =⨯⨯=△△.所以阴影部分的面积为12.5.【巩固】如图,三角形ABC 的面积是2200cm ,E 在AC 上,点D 在BC 上,且:3:5AE EC =,:2:3BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .FED CBAABC DEF FEDCBA【解析】 连接CF ,根据燕尾定理,2639ABF ACF S BD S DC ===△△,36510ABF CBF S AE S EC ===△△, 设6ABF S =△份,则9ACF S =△份,10BCF S =△份,5459358EFC S =⨯=+△份,310623CDF S =⨯=+△份,所以24545200(6910)(6)8(6)93(cm )88DCFE S =÷++⨯+=⨯+=【巩固】如图,已知3BD DC =,2EC AE =,BE 与CD 相交于点O ,则ABC △被分成的4部分面积各占ABC △面积的几分之几?OE DCBA13.54.59211213O E D CBA【解析】 连接CO ,设1AEO S =△份,则其他部分的面积如图所示,所以1291830ABC S =+++=△份,所以四部分按从小到大各占ABC △面积的12 4.5139313.59,,,30306030103020+===【巩固】(2007年香港圣公会数学竞赛)如图所示,在ABC △中,12CP CB =,13CQ CA =,BQ 与AP 相交于点X ,若ABC △的面积为6,则ABX △的面积等于 .XQPABC XQPAB C4411XQPCBA【解析】 方法一:连接PQ .由于12CP CB =,13CQ CA =,所以23ABQ ABC SS =,1126BPQ BCQABCS S S ==.由蝴蝶定理知,21:::4:136ABQ BPQ ABC ABC AX XP S S S S ===,所以441226 2.455255ABX ABP ABC ABC S S S S ==⨯==⨯=.方法二:连接CX 设1CPX S =△份,根据燕尾定理标出其他部分面积, 所以6(1144)4 2.4ABX S =÷+++⨯=△【巩固】如图,三角形ABC 的面积是1,2BD DC =,2CE AE =,AD 与BE 相交于点F ,请写出这4部分的面积各是多少?ABCDE F48621ABCDEF【解析】 连接CF ,设1AEFS =△份,则其他几部分面积可以有燕尾定理标出如图所示,所以121AEF S =△,62217ABF S ==△,821BDF S =△,242217FDCE S +==【巩固】如图,E 在AC 上,D 在BC 上,且:2:3AE EC =,:1:2BD DC =,AD 与BE 交于点F .四边形DFEC的面积等于222cm ,则三角形ABC 的面积 .A BCDE FA BCDEF 2.41.62A BC DE F 12【解析】 连接CF ,根据燕尾定理,12ABF ACF S BD S DC ==△△,23ABF CBF S AE S EC ==△△, 设1BDF S =△份,则2DCF S =△份,2ABF S =△份,4AFC S =△份,24 1.623AEF S =⨯=+△ 份,34 2.423EFC S =⨯=+△份,如图所标,所以2 2.4 4.4EFDC S =+=份,2349ABC S =++=△份 所以222 4.4945(cm )ABCS =÷⨯=△【巩固】三角形ABC 中,C 是直角,已知2AC =,2CD =,3CB =,AM BM =,那么三角形AMN (阴影部分)的面积为多少?【解析】 连接BN .ABC △的面积为3223⨯÷=根据燕尾定理,::2:1ACN ABN CD BD ==△△; 同理::1:1CBN CAN BM AM ==△△设AMN △面积为1份,则MNB △的面积也是1份,所以ANB △的面积是112+=份,而ACN △的面积就是224⨯=份,CBN △也是4份,这样ABC △的面积为441110+++=份,所以AMN △的面积为31010.3÷⨯=.【巩固】如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米?y B CD EGE D CBAEDB A【解析】 设1DEF S =△份,则根据燕尾定理其他面积如图所示551212BCD S S ==△阴影平方厘米.【例 2】 如图所示,在四边形ABCD 中,3AB BE =,3AD AF =,四边形AEOF 的面积是12,那么平行四边形BODC 的面积为________.OFE DBA684621O F E DB A【解析】 连接,AO BD ,根据燕尾定理::1:2ABO BDO S S AF FD ==△△,::2:1AOD BOD S S AE BE ==△△,设1BEO S =△,则其他图形面积,如图所标,所以221224BODC AEOF S S ==⨯=.【例 3】 ABCD 是边长为12厘米的正方形,E 、F 分别是AB 、BC 边的中点,AF 与CE 交于G ,则四边形AGCD 的面积是_________平方厘米.GFE DCBAGFE D CBA【解析】 连接AC 、GB ,设1AGC S =△份,根据燕尾定理得1AGB S =△份,1BGC S =△份,则11126S =++⨯=正方形()份,314ADCG S =+=份,所以22126496(cm )ADCG S =÷⨯=【例 4】 如图,正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是_____平方厘米.EDCBEDCB【解析】 连接BH ,根据沙漏模型得:1:2BG GD =,设1BHC S =△份,根据燕尾定理2CHD S =△份,2BHD S =△份,因此122)210S =++⨯=正方形(份,127236BFHG S =+=,所以712010146BFHG S =÷⨯=(平方厘米).【例 5】 如图所示,在ABC △中,:3:1BE EC =,D 是AE 的中点,那么:AF FC = .FE D C B AFE DCB A【解析】 连接CD .由于:1:1ABD BED S S =△△,:3:4BED BCD S S =△△,所以:3:4ABD BCD S S =△△,根据燕尾定理,::3:4ABD BCD AF FC S S ==△△.【巩固】在ABC ∆中,:3:2BD DC =, :3:1AE EC =,求:OB OE =?A BCDE OABCDE O【解析】 连接OC .因为:3:2BD DC =,根据燕尾定理,::3:2AOB AOC S S BD BC ∆∆==,即32AOB AOC S S ∆∆=; 又:3:1AE EC =,所以43AOC AOE S S ∆∆=.则3342223AOB AOC AOE AOE S S S S ∆∆∆∆==⨯=, 所以::2:1AOB AOEOB OE S S ∆∆==.【巩固】在ABC ∆中,:2:1BD DC =, :1:3AE EC =,求:OB OE =?A B CDE O【解析】 题目求的是边的比值,一般来说可以通过分别求出每条边的值再作比值,也可以通过三角形的面积比来做桥梁,但题目没告诉我们边的长度,所以应该通过面积比而得到边长的比.本题的图形一看就联想到燕尾定理,但两个燕尾似乎少了一个,因此应该补全,所以第一步要连接OC . 连接OC .A B CDE O因为:2:1BD DC =,根据燕尾定理,::2:1AOB AOC S S BD BC ∆∆==,即2AOB AOC S S ∆∆=; 又:1:3AE EC =,所以4AOC AOE S S ∆∆=.则2248AOB AOC AOE AOE S S S S ∆∆∆∆==⨯=, 所以::8:1AOB AOE OB OE S S ∆∆==.【例 6】 (2009年清华附中入学测试题)如图,四边形ABCD 是矩形,E 、F 分别是AB 、BC 上的点,且13AE AB =,14CF BC =,AF 与CE 相交于G ,若矩形ABCD 的面积为120,则AEG ∆与CGF ∆的面积之和为 .BEH BEBE【解析】 (法1)如图,过F 做CE 的平行线交AB 于H ,则::1:3EH HB CF FB ==,所以122AE EB EH ==,::2AG GF AE EH ==,即2AG GF =,所以122311033942AEG ABF ABCD S S S ∆∆=⨯⨯=⨯⨯=.且22313342EG HF EC EC ==⨯=,故CG GE =,则1152CGF AEG S S ∆∆=⨯⨯=.所以两三角形面积之和为10515+=. (法2)如上右图,连接AC 、BG .根据燕尾定理,::3:1ABG ACG S S BF CF ∆∆==,::2:1BCG ACG S S BE AE ∆∆==,而1602ABC ABCD S S ∆==,所以3321ABG S ∆=++,160302ABC S ∆=⨯=,2321BCG S ∆=++,160203ABC S ∆=⨯=,则1103AEG ABG S S ∆∆==,154CFG BCG S S ∆∆==,所以两个三角形的面积之和为15.【例 7】 如右图,三角形ABC 中,:4:9BD DC =,:4:3CE EA =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::4:912:27AOB AOC S S BD CD ===△△::3:412:16AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:27:16:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【巩固】如右图,三角形ABC 中,:3:4BD DC =,:5:6AE CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::3:415:20AOB AOC S S BD CD ===△△ ::5:615:18AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:20:1810:9:AOC BOC S S AF FB ===△△【巩固】如图,:2:3BD DC =,:5:3AE CE =,则:AF BF =GF EDCBA【解析】 根据燕尾定理有:2:310:15ABG ACG S S ==△△,:5:310:6ABG BCGS S ==△△,所以:15:65:2:ACG BCG S S AF BF ===△△【巩固】如右图,三角形ABC 中,:2:3BD DC =,:5:4EA CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::2:310:15AOB AOC S S BD CD ===△△::5:410:8AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:15:8:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【例 8】 (2008年“学而思杯”六年级数学试题)如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形ABC 的面积是1,则三角形ABE 的面积为______,三角形AGE 的面积为________,三角形GHI 的面积为______.I HGFEDC BAI HG FEDCBA【分析】 连接AH 、BI 、CG .由于:3:2CE AE =,所以25AE AC =,故2255ABE ABC S S ∆∆==; 根据燕尾定理,::2:3ACG ABG S S CD BD ∆∆==,::3:2BCG ABG S S CE EA ∆∆==,所以::4:6:9ACG ABG BCG S S S ∆∆∆=,则419ACG S ∆=,919BCG S ∆=;那么2248551995AGE AGC S S ∆∆==⨯=;同样分析可得919ACH S ∆=,则::4:9ACG ACH EG EH S S ∆∆==,::4:19ACG ACB EG EB S S ∆∆==,所以::4:5:10EG GH HB =,同样分析可得::10:5:4AG GI ID =,所以5521101055BIE BAE S S ∆∆==⨯=,55111919519GHI BIE S S ∆∆==⨯=.【巩固】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形GHI 的面积是1,求三角形ABC 的面积.IH G FEDCBA IH G FEDCBA【解析】 连接BG ,AGC S △=6份根据燕尾定理,::3:26:4AGC BGC S S AF FB ===△△,::3:29:6ABG AGC S S BD DC ===△△得4BGC S =△(份),9ABG S =△(份),则19ABC S =△(份),因此619AGC ABC S S =△△,同理连接AI 、CH 得619ABH ABC S S =△△,619BIC ABC S S =△△,所以1966611919GHI ABC S S ---==△△ 三角形GHI 的面积是1,所以三角形ABC 的面积是19【巩固】(2009年第七届“走进美妙的数学花园”初赛六年级)如图,ABC ∆中2BD DA =,2CE EB =,2AF FC =,那么ABC ∆的面积是阴影三角形面积的 倍.BCB【分析】 如图,连接AI .根据燕尾定理,::2:1BCI ACI S S BD AD ∆∆==,::1:2BCI ABI S S CF AF ∆∆==,所以,::1:2:4ACI BCI ABI S S S ∆∆∆=,那么,221247BCI ABC ABC S S S ∆∆∆==++.同理可知ACG ∆和ABH ∆的面积也都等于ABC ∆面积的27,所以阴影三角形的面积等于ABC ∆面积的211377-⨯=,所以ABC ∆的面积是阴影三角形面积的7倍.【巩固】如图在ABC △中,12DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值. IHG FEDCBAIHG FEDCB A【解析】 连接BG ,设BGC S △=1份,根据燕尾定理::2:1AGC BGC S S AF FB ==△△,::2:1ABG AGC S S BD DC ==△△,得2AGC S =△(份),4ABG S =△(份),则7ABC S =△(份),因此27AGC ABC S S =△△,同理连接AI 、CH 得27ABH ABC S S =△△,27BIC ABC S S =△△, 所以7222177GHI ABC S S ---==△△ 【点评】如果任意一个三角形各边被分成的比是相同的,那么在同样的位置上的图形,虽然形状千变万化,但面积是相等的,这在这讲里面很多题目都是用“同理得到”的,即再重复一次解题思路,因此我们有对称法作辅助线.【巩固】如图在ABC △中,13DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值. IHG FEDCBAIH G FEDCB A【解析】 连接BG ,设BGC S △=1份,根据燕尾定理::3:1AGC BGC S S AF FB ==△△,::3:1ABG AGC S S BD DC ==△△,得3AGC S =△(份),9ABG S =△(份),则13ABC S =△(份),因此313AGC ABC S S =△△,同理连接AI 、CH 得13ABH ABC S S =△△,313BIC ABC S S =△△, 所以1333341313GHI ABC S S ---==△△【巩固】如右图,三角形ABC 中,:::4:3AF FB BD DC CE AE ===,且三角形ABC 的面积是74,求角形GHI的面积.IH G FEDCBAIH G FEDCBA【解析】 连接BG ,AGC S △=12份根据燕尾定理,::4:312:9AGC BGC S S AF FB ===△△,::4:316:12ABG AGC S S BD DC ===△△得9BGC S =△(份),16ABG S =△(份),则9121637ABC S =++=△(份),因此1237AGC ABC S S =△△,同理连接AI 、CH 得1237ABH ABC S S =△△,1237BIC ABC S S =△△, 所以3712121213737GHI ABC S S ---==△△ 三角形ABC 的面积是74,所以三角形GHI 的面积是174237⨯=【例 9】 两条线段把三角形分为三个三角形和一个四边形,如图所示, 三个三角形的面积 分别是3,7,7,则阴影四边形的面积是多少?【解析】方法一:遇到没有标注字母的图形,我们第一步要做的就是给图形各点标注字母,方便后面的计算.再看这道题,出现两个面积相等且共底的三角形.设三角形为ABC,BE和CD交于F,则BF FE=,再连结DE.所以三角形DEF的面积为3.设三角形ADE的面积为x,则()():33:10:10x AD DB x+==+,所以15x=,四边形的面积为18.方法二:设ADFS x=△,根据燕尾定理::ABF BFC AFE EFCS S S S=△△△△,得到3AEFS x=+△,再根据向右下飞的燕子,有(37):7:3x x++=,解得7.5x=四边形的面积为7.57.5318++=【巩固】右图的大三角形被分成5个小三角形,其中4个的面积已经标在图中,那么,阴影三角形的面积是.【解析】方法一:整个题目读完,我们没有发现任何与边长相关的条件,也没有任何与高或者垂直有关系的字眼,由此,我们可以推断,这道题不能依靠三角形面积公式求解.我们发现右图三角形中存在一个比例关系:()2:13:4S=+阴影,解得2S=阴影.方法二:回顾下燕尾定理,有2:41:3S+=阴影(),解得2S=阴影.【例 10】如图,三角形ABC被分成6个三角形,已知其中4个三角形的面积,问三角形ABC的面积是多少?35304084OFED CBA【解析】设BOFS x=△,由题意知:4:3BD DC=根据燕尾定理,得::4:3ABO ACO BDO CDOS S S S==△△△△,所以33(84)6344ACOS x x=⨯+=+△,再根据::ABO BCO AOE COES S S S=△△△△,列方程3(84):(4030)(6335):354x x++=+-解得56x=:35(5684):(4030)AOES=++△,所以70AOES=△所以三角形ABC的面积是844030355670315+++++=【例 11】三角形ABC的面积为15平方厘米,D为AB中点,E为AC中点,F为BC中点,求阴影部分的面积.F CBA F CBA【解析】 令BE 与CD 的交点为M ,CD 与EF 的交点为N ,连接AM ,BN .在ABC △中,根据燕尾定理,::1:1ABM BCM S S AE CE ==△△,::1:1ACM BCM S S AD BD ==△△,所以13ABM ACM BCN ABC S S S S ===△△△△由于1122AEM AMC ABM S S S ==△△△S ,所以:2:1BM ME =在EBC △中,根据燕尾定理,::1:1BEN CEN S S BF CF ==△△::1:2CEN CBN S S ME MB ==△△设1CEN S =△(份),则1BEN S =△(份),2BCN S =△(份),4BCE S =△(份),所以1124BCN BCE ABC S S S ==△△△,1148BNE BCE ABC S S S ==△△△,因为:2:1BM ME =,F 为BC 中点,所以221133812BMN BNE ABC ABC S S S S ==⨯=△△△△,11112248BFN BNC ABC S S S ==⨯=△△△,所以115515 3.1251282424ABC ABC S S S ⎛⎫=+==⨯= ⎪⎝⎭△△阴影(平方厘米)【例 12】 如右图,ABC △中,G 是AC 的中点,D 、E 、F 是BC 边上的四等分点,AD 与BG 交于M ,AF 与BG 交于N ,已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米,则ABC △的面积是多少平方厘米?N M GA BCD EFNMGA BCD EF【解析】 连接CM 、CN .根据燕尾定理,::1:1ABM CBM S S AG GC ==△△,::1:3ABM ACM S S BD CD ==△△,所以15ABM ABC S S =△△;再根据燕尾定理,::1:1ABN CBN S S AG GC ==△△,所以::4:3ABN FBN CBN FBN S S S S ==△△△△,所以:4:3AN NF =,那么1422437ANG AFC S S =⨯=+△△,所以2515177428FCGN AFC ABC ABC S S S S ⎛⎫=-=⨯= ⎪⎝⎭△△△.根据题意,有157.2528ABCABC S S -=△△,可得336ABC S =△(平方厘米)【巩固】(2007年四中分班考试题)如图,ABC ∆中,点D 是边AC 的中点,点E 、F 是边BC 的三等分点,若ABC ∆的面积为1,那么四边形CDMF 的面积是_________.F ABCDE M NFABCDEMN【解析】 由于点D 是边AC 的中点,点E 、F 是边BC 的三等分点,如果能求出BN 、NM 、MD 三段的比,那么所分成的六小块的面积都可以求出来,其中当然也包括四边形CDMF 的面积. 连接CM 、CN .根据燕尾定理,::2:1ABM ACM S S BF CF ∆∆==,而2ACM ADM S S ∆∆=,所以24ABM ACM ADM S S S ∆∆∆==,那么4BM DM =,即45BM BD =.那么421453215BMF BCD BM BF S S BD BC ∆∆=⨯⨯=⨯⨯=,14721530CDMF S =-=四边形. 另解:得出24ABM ACM ADM S S S ∆∆∆==后,可得111155210ADM ABD S S ∆∆==⨯=,则11731030ACF ADM CDMF S S S ∆∆=-=-=四边形.【例 13】 如图,三角形ABC 的面积是1,BD DE EC ==,CF FG GA ==,三角形ABC 被分成9部分,请写出这9部分的面积各是多少?GFE D CBAN MQPGF EDCBA【解析】 设BG 与AD 交于点P ,BG 与AE 交于点Q ,BF 与AD 交于点M ,BF 与AE 交于点N .连接CP ,CQ ,CM ,CN .根据燕尾定理,::1:2ABP CBP S S AG GC ==△△,::1:2ABP ACP S S BD CD ==△△,设1ABP S =△(份),则1225ABC S =++=△(份),所以15ABP S =△同理可得,27ABQ S =△,12ABN S =△,而13ABG S =△,所以2137535APQ S =-=△,1213721AQG S =-=△.同理,335BPM S =△121BDM S =△,所以1239273570PQMN S =--=四边形,139********MNED S =--=四边形,1151321426NFCE S =--=四边形,1115321642GFNQ S =--=四边形【巩固】如图,ABC ∆的面积为1,点D 、E 是BC 边的三等分点,点F 、G 是AC 边的三等分点,那么四边形JKIH 的面积是多少?K JI HABC D EF GKJI HA BCD EFG【解析】 连接CK 、CI 、CJ .根据燕尾定理,::1:2ACK ABK S S CD BD ∆∆==,::1:2ABK CBK S S AG CG ∆∆==,所以::1:2:4ACK ABK CBK S S S ∆∆∆=,那么111247ACK S ∆==++,11321AGK ACK S S ∆∆==.类似分析可得215AGI S ∆=.又::2:1ABJ CBJ S S AF CF ∆∆==,::2:1ABJ ACJ S S BD CD ∆∆==,可得14ACJ S ∆=. 那么,111742184CGKJ S =-=. 根据对称性,可知四边形CEHJ 的面积也为1784,那么四边形JKIH 周围的图形的面积之和为172161228415370CGKJ AGI ABES S S ∆∆⨯++=⨯++=,所以四边形JKIH 的面积为61917070-=.【例 14】 如右图,面积为1的ABC △中,::1:2:1BD DE EC =,::1:2:1CF FG GA =,::1:2:1AH HI IB =,求阴影部分面积.CBB【解析】 设IG 交HF 于M ,IG 交HD 于N ,DF 交EI 于P .连接AM , IF .∵:3:4AI AB =,:3:4AF AC =,916AIF ABC S S ∴=△△∵::2FIM AMF S S IH HA ==△△,::2FIM AIM S S FG GA ==△△,∴19464AIM AIF ABC S S S ==△△△ ∵:1:3AH AI = ∴364AHM ABC S S =△△,∵:1:4AH AB = :3:4AF AC = ∴316AHF ABC S S =△△ .同理 316CFD BDH ABC S S S ==△△△ ∴716FDH ABC S S =△△ 33::1:46416HM HF ==,∵ :3:4,:3:4AI AB AF AC ==, ∴IF BC ∥ ,又∵:3:4,:1:2IF BC DE BC ==,∴:2:3,:2:3DE IF DP PF ==,同理 :2:3HN ND =,∵:1:4HM HF =,∴:2:5HN HD =,∴17710160160HMN HDF ABC S S S ===△△△. 同理 6个小阴影三角形的面积均为7160.阴影部分面积721616080=⨯=.【例 15】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.GCBAGCBA【解析】 三角形在开会,那么就好好利用三角形中最好用的比例和燕尾定理吧!令BI 与CD 的交点为M ,AF 与CD 的交点为N ,BI 与AF 的交点为P ,BI 与CE 的交点为Q ,连接AM 、BN 、CP⑴求ADMI S 四边形:在ABC △中,根据燕尾定理,::1:2ABM CBM S S AI CI ==△△::1:2ACM CBM S S AD BD ==△△设1ABM S =△(份),则2CBM S =△(份),1ACM S =△(份),4ABC S =△(份),所以14ABM ACM ABC S S S ==△△△,所以11312ADM ABM ABC S S S ==△△△,112AIM ABC S S =△△,所以111()12126ABC ABC ADMI S S S =+=△△四边形,同理可得另外两个顶点的四边形面积也分别是ABC △面积的16⑵求DNPQE S 五边形:在ABC △中,根据燕尾定理::1:2ABN ACN S S BF CF ==△△::1:2ACN BCN S S AD BD ==△△,所以111133721ADN ABN ABC ABC S S S S ==⨯=△△△△,同理121BEQ ABC S S =△△在ABC △中,根据燕尾定理::1:2ABP ACP S S BF CF ==△△,::1:2ABP CBP S S AI CI ==△△所以15ABP ABC S S =△△所以1111152121105ABP ADN BEP ABC ABC DNPQE S S S S S S ⎛⎫=--=--= ⎪⎝⎭△△△△△五边形同理另外两个五边形面积是ABC △面积的11105所以11113133610570S =-⨯-⨯=阴影【例 16】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.GCBAGCBA【解析】 设深黑色六个三角形的顶点分别为N 、R 、P 、S 、M 、Q ,连接CR在ABC △中根据燕尾定理,::.2:1ABR ACR S S BG CG ==△△,::1:2ABR CBR S S AI CI ==△△所以27ABR ABC S S =△△,同理27ACS ABC S S =△△,27CQB ABC S S =△△所以222117777RQS S =---=△同理17MNP S =△根据容斥原理,和上题结果11131777010S =+-=六边形【例 17】(2009年数学解题能力大赛六年级初试试题)正六边形1A ,2A ,3A ,4A ,5A ,6A 的面积是2009平方厘米,1B ,2B ,3B ,4B ,5B ,6B 分别是正六边形各边的中点;那么图中阴影六边形的面积是 平A 4B 5A 3A 45A 3【解析】 (方法一)因为空白的面积等于23A A G △面积的6倍,所以关键求23A A G △的面积,根据燕尾定理可得2312333117732A A G A A A S S S ==⨯⨯△△正六边形,但在123A A A △用燕尾定理时,需要知道13,A D A D 的长度比,连接1363,A A A A ,1A G ,过6B 作12A A 的平行线,交13A A 于E ,根据沙漏模型得1A D DE =,再根据金字塔模型得13A E A E =,因此13:1:3A D A D =,在123A A A △中,设121A A G S =△份,则233A A G S =△份,313A A G S =△份,所以2312333111773214A A G A A A S S S S ==⨯⨯=△△正六边形正六边形,因此141620091148147S S =-⨯=⨯=阴影正六边形()(平方厘米)(方法二)既然给的图形是特殊的正六边形,且阴影也是正六边形我们可以用下图的割补思路,把正六边形分割成14个大小形状相同的梯形,其中阴影有8个梯形,所以阴影面积为82009114814⨯=(平方厘米)A 3A【例 18】已知四边形ABCD ,CHFG 为正方形,:1:8S S =乙甲,a 与b 是两个正方形的边长,求:?a b =baHFEDbaMED【解析】 观察图形,感觉阴影部分像蝴蝶定理,但是细细分析发现用蝴蝶定理无法继续往下走,注意到题目条件中给出了两个正方形的边长,有边长就可以利用比例,再发现在连接辅助线后可以利用燕尾,那么我们就用燕尾定理来求解 连接EO 、AF ,根据燕尾定理:::AOE AOF S S a b =△△,::AOF EOF S S a b =△△所以 22::AOE EOF S S a b =△△,作OM ⊥AE 、ON ⊥EF ,∴22=OM ON a b::∴33==::1:8 S S a b乙甲∴:1:2a b=。
六年级学而思杯数学试卷

一、选择题(每题5分,共50分)1. 下列哪个数是质数?A. 16B. 17C. 18D. 192. 下列哪个图形是轴对称图形?A. 长方形B. 正方形C. 三角形D. 梯形3. 一个长方形的长是8厘米,宽是5厘米,它的周长是多少厘米?A. 26B. 28C. 30D. 324. 下列哪个数是偶数?A. 15B. 16C. 17D. 185. 一个圆形的半径是5厘米,它的周长是多少厘米?A. 15πB. 25πC. 10πD. 20π6. 下列哪个数是奇数?A. 15B. 16C. 17D. 187. 一个正方形的边长是6厘米,它的面积是多少平方厘米?A. 36B. 42C. 48D. 548. 下列哪个图形是平行四边形?A. 长方形B. 正方形C. 三角形D. 梯形9. 一个长方体的长、宽、高分别是5厘米、4厘米、3厘米,它的体积是多少立方厘米?A. 60B. 72C. 80D. 9010. 下列哪个数是质数?A. 19B. 20C. 21D. 22二、填空题(每题5分,共50分)1. 下列数列的下一个数是多少?2,4,8,16,()。
2. 一个长方形的长是12厘米,宽是6厘米,它的周长是多少厘米?3. 一个圆形的半径是7厘米,它的面积是多少平方厘米?4. 下列数列的下一个数是多少?3,6,9,12,()。
5. 一个正方形的边长是10厘米,它的面积是多少平方厘米?6. 一个长方体的长、宽、高分别是7厘米、5厘米、3厘米,它的体积是多少立方厘米?7. 下列数列的下一个数是多少?5,10,15,20,()。
8. 一个圆形的半径是4厘米,它的周长是多少厘米?9. 下列数列的下一个数是多少?7,14,21,28,()。
10. 一个长方形的面积是24平方厘米,长是8厘米,它的宽是多少厘米?三、解答题(每题20分,共60分)1. 一个长方形的长是15厘米,宽是8厘米,求它的周长和面积。
2. 一个正方形的边长是12厘米,求它的周长、面积和体积。
2009年秋季学而思竞赛班选拔考试

2009年秋季学而思竞赛班选拔考试学校 姓名 得分 所在学而思班次 春季 暑期 秋季 考试说明 1.考试时间:60分钟. 2.试卷分值:本试卷共15道题,每题8分,共120分.快乐的暑假即将结束了,灰太郎向羊村的村民们发出了挑战:进行一场数学大赛,如果羊村的代表输给灰太郎,就要被吃掉.为了打败灰太郎,羊村派出最聪明的喜羊羊和他的伙伴们组成了数学学习小组,每天集中学习和讨论经典的数学题型.现在,就让我们也来一起研究这些题目,帮助羊村一起度过难关吧!小朋友们一定要睁大眼睛,耐心仔细地看好题目,躲过其中的小陷阱,最后不要忘记一定要认真检查!加油!!1.684291+++++= .2.用2,4这两张卡片可以组成 个不同的数.3. 数一数.(必须全答对才给分哦!)个正方体个正方体.4. 早上9:00刚到学校,懒羊羊就饿了,但是中午11:00才能吃午饭,请你帮他算一算,再过 分钟懒羊羊才能吃上午饭.新二年级5.慢羊羊在去给病人看病的路上,两只手各拎了1个药箱,每个药箱里各装着3瓶药,请问:慢羊羊带了瓶药去看病.6.☆+▼=22,▼-☆=12,则▼= .7.妹妹今年4岁,哥哥今年10岁,再过5年,哥哥比妹妹大岁.8.把一根绳子先对折,再对折,然后从正中剪断,这根绳子被剪成了段.9.小红借给灰灰10元钱后还剩下20元,这时两人的钱数同样多,灰灰原来有元钱.10.小红和小明共有42张画片,如果小红给小明5张,两人的画片张数就同样多,原来小红有张.11.羊村为庆祝国庆六十周年特地彩排了一个舞蹈,他们按1红、1蓝、1紫、1白的服装颜色依次列队,如果这列小羊共有23只,那么最后一只小羊穿颜色的服装.12.有三根铁丝,第一根长15米,第二根长24米,第三根的长度和前两根的总和同样长,这三根铁丝一共长米.13.暖羊羊和美羊羊一共有20块糖,美羊羊有12块,两人相差块糖,如果想让两人的糖数一样多,那么美羊羊要给暖羊羊块糖.(必须全答对才给分哦!)14.一只蜗牛从12厘米深的空穴底部往上爬,每爬3厘米要用3分钟,然后停1分钟休息一下,再继续往上爬,蜗牛从洞底爬到洞口一共要用分钟.15.在50以内(包括50),十位上的数字比个位上的数字大的两位数一共有个.。
六年级学而思奥数

2.连锁约分: 多分数连乘,将分子、分母都化成乘积形式,伺机约分。
测试题
例 1 测: 计算:
2 3
1 2
35
23 21
35
11 A.1
8
11 B.
8
1 C. 1
8
5 D.1
8
124 24 5 357 478
例 2 测: 计算:
3
5
7
9
11 1 1
35 7 9
A.2
B.4
C. 3
D.1
例 3 测:
123 2 46 369
测试题
【例 1】 (★★ ) 计算1
1 3
1 5
1 7
1 9
1 11
_____.
6 12 20 30 42
5 A . 36
14
7 B. 5
12
41 C.
21
【例 2】 (★★★ )计算: 2 3 3 7
9 11 ()
3 4 5 12 20 30
32 A.
27
41 B.
12
41 C.
21
17 D.
12 23 D. 12
2 / 28
【例 3】 (★★★★ )1 1
1
1
12 12 3 12 3 4
1 _____
1 2 3 10
11 A.
13
1 B.
11
【例 4】 (★★★★ )计算: 12 32 22 1
22 42 32 1
7 A . 20
19
151 B . 38
190
7 C.
12 32 52 42 1
1 C. 40
11 +2 1+3 1 +4 1 + +20 1
2009年学而思杯赛试题

2009年“学而思杯”六年级一试试题一、填空题1.10.810.9810.99810.999810.99998a=++++,a的整数部分是.2.前四个质数的乘积为210.200到220之间有唯一的质数,它是________.3.如图,棱长分别为1厘米、2厘米、3厘米的三个正方体紧贴在一起,则所得到的立体图形的表面积是________平方厘米.4.12个人围成一圈,从中选出3个人,其中恰有两人相邻,共有种不同的选法.5.18,29,310,……,20022009中,共有个最简分数.二、填空题6. 计算:1122426153577++++= .7. 放满一个水池,如果同时打开1,2号阀门,则12分钟可以完成;如果同时打开1,3号阀门,则15分钟可以完成;如果单独打开1号阀门,则20分钟可以完成;那么,如果同时打开1,2,3号阀门, 分钟可以完成.8. 6支球队进行足球比赛,每两支队之间都要赛一场,规定胜一场得3分,平一场各得1分,负一场不得分.全部比赛结束后,发现共有4场平局,且其中5支球队共得了31分,则第6支球队得了 分.9. 如图,三角形ABC 的面积为1,且13A D A B =,14BE BC =,15CF CA =,则三角形DEF 的面积是 .FE CDB A10.如果一个至少两位的自然数N满足下列性质:在N的前面任意添加一些数字,使得得到的新数的数字和为N,但无论如何添加,这样得到的新数一定不能被N整除,则称N为“破坏数”.那么最小的“破坏数”是________.三、填空题11.甲、乙两艘游艇,静水中甲艇每小时行3.3千米,乙艇每小时行2.1千米.现在甲、乙两游艇于同一时刻相向出发,甲艇从下游上行,乙艇从相距27千米的上游下行,两艇于途中相遇后,又经过4小时,甲艇到达乙艇的出发地.水流速度是每小时千米.12.差为2的两个正整数,如果每个数的各位数字之和都能被7整除,我们就称它们为一对幸运数.在200到300的范围内,有对幸运数.13.三个连续三位数的和能够被13整除,且这三个数中最大的数被9除余4,那么符合条件的三个数中最小的数的最大值是.14.能被3整除且至少有一个数字是6的四位数有个.15.有77个人站成一排,每个人要么是总说实话的老实人,要么是总说谎话的骗子.从第5个人开始,问每一个人,“你前面的四个人里面的骗子人数是奇数还是偶数?”结果,这73个人全部回答“偶数”.那么老实人和骗子中人数较少的那一类最多有________人.。
行程问题(题答案)

一、 相遇与追及1、路程和路程差公式【例 1】 如下图,某城市东西路与南北路交会于路口A .甲在路口A 南边560米的B 点,乙在路口A .甲向北,乙向东同时匀速行走.4分钟后二人距A 的距离相等.再继续行走24分钟后,二人距A 的距离恰又相等.问:甲、乙二人的速度各是多少?【考点】行程问题 【难度】3星 【题型】解答【关键词】2003年,明心奥数挑战赛【解析】 本题总共有两次距离A 相等,第一次:甲到A 的距离正好就是乙从A 出发走的路程.那么甲、乙两人共走了560米,走了4分钟,两人的速度和为:5604140÷=(米/分)。
第二次:两人距A 的距离又相等,只能是甲、乙走过了A 点,且在A 点以北走的路程=乙走的总路程.那么,从第二次甲比乙共多走了560米,共走了42428+=(分钟),两人的速度差:5602820÷=(米/分),甲速+乙速140=,显然甲速要比乙速要快;甲速-乙速20=,解这个和差问题,甲速14020280=+÷=()(米/分),乙速1408060=-=(米/分).【答案】甲速80米/分,乙速60米/分2、多人相遇【例 2】 有甲、乙、丙3人,甲每分钟走100米,乙每分钟走80米,丙每分钟走75米.现在甲从东村,乙、丙两人从西村同时出发相向而行,在途中甲与乙相遇6分钟后,甲又与丙相遇. 那么,东、西两村之间的距离是多少米?【考点】行程问题 【难度】2星 【题型】解答【解析】 甲、丙6分钟相遇的路程:()1007561050+⨯=(米);甲、乙相遇的时间为:()10508075210÷-=(分钟);东、西两村之间的距离为:()1008021037800+⨯=(米).【答案】37800米3、多次相遇【例 3】 甲、乙两车分别同时从A 、B 两地相对开出,第一次在离A 地95千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B 地25千米处相遇.求A 、B 两地间的距离是多少千米?【考点】行程问题 【难度】2星 【题型】解答【解析】 画线段示意图(实线表示甲车行进的路线,虚线表示乙车行进的路线):可以发现第一次相遇意味着两车行了一个A 、B 两地间距离,第二次相遇意味着两车共行了三个A 、B 两地间的距离.当甲、乙两车共行了一个A 、B 两地间的距离时,甲车行了95千米,当它们共行三个A 、B 两地间的距离时,甲车就行了3个95千米,即95×3=285(千米),而这285千米比一个A 、B 两地间的距离多25千米,可得:95×3-25=285-25=260(千米).【答案】260千米二、典型行程专题1、火车过桥【例4】某列车通过250米长的隧道用25秒,通过210米长的隧道用23秒,若该列车与另一列长150米.时速为72千米的列车相遇,错车而过需要几秒钟?【考点】行程问题之火车问题【难度】3星【题型】解答a)根据另一个列车每小时走72千米,所以,它的速度为:72000÷3600=20(米/秒),某列车的速度为:(25O-210)÷(25-23)=40÷2=20(米/秒)某列车的车长为:20×25-250=500-250=250(米),两列车的错车时间为:(250+150)÷(20+20)=400÷40=10(秒)。
奥数 六年级 千份讲义 25 1[1].学而思杯考前辅导
![奥数 六年级 千份讲义 25 1[1].学而思杯考前辅导](https://img.taocdn.com/s3/m/8183ac10c5da50e2524d7fe1.png)
模块一、计算【例 1】(2008年学而思杯6年级1试第1题)计算:11111200820092010201120121854108180270++++= 。
【例 2】(2009年学而思杯6年级第6题)计算:1122426153577++++=____。
【例 3】(2008年学而思杯6年级第1题)计算:3413441344413444444441344444444412389275277527775277777777527777777775+⨯+⨯++⨯+⨯=。
【巩固】(第五届《小数报》数学竞赛初赛计算题第3题)计算:11111 123420 261220420 +++++【巩固】计算:1111111 315356399143195++++++学而思杯考前辅导【巩固】 111111212312100++++++++++【巩固】 234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 111111212312100++++++++++【巩固】 234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 (仁华学校入学测试题) 22222211111131517191111131+++++=------ .【巩固】 计算:222222223571512233478++++⨯⨯⨯⨯【巩固】 计算:222222222231517119931199513151711993119951++++++++++=----- .【巩固】计算:222212350133********++++=⨯⨯⨯⨯.【巩固】11111 (......) 1200722006(2008)200622007120071111 (......) 20081200622005(2007)20061n nn n+++++-⨯⨯⨯-⨯⨯+++++⨯⨯⨯-⨯【巩固】1 2【例 4】(2009年学而思杯6年级第1题)a=10.8+10.98+10.998+10.9998+10.99998,的整数部分是。
天津2009秋学而思入学测试题(六年级数学)

1 ▎入学测试题·学生版 ▎各位家长和同学:45分钟完成,共12道题,一定要独立完成!试卷说明:答案完全正确的得分,多解、漏解、错解都不得分.1. 将如下五个分数从小到大排列:10121520601719233337、、、、 ______<______<______<______<______。
2. 一件工作,甲、乙合做需4小时完成,乙、丙合做需5小时完成。
现在先请甲、丙合做2小时后,余下的乙还需做6小时完成。
乙单独做完这件工作要_______小时3. 有两筐桔子,如果从甲筐取出10千克给乙筐,则两筐重量相等;如果两筐各取出10千克,则甲筐剩下的重量的30%比乙筐剩下重量的13多5千克,乙筐原来有__________.4. 如右图,已知BD DC =,2CE AE =,三角形ABC 的面积是60,那么阴影部分面积是 .2009秋季6年级数学入学测试题E F2 ▎入学测试题·学生版 ▎5. 有一个分数,分子加2可约为85,分子减1可约为21,则这个分数是6. 已知哥哥5年后的年龄与弟弟3年前的年龄和恰好是29岁,而弟弟现在的年龄是两人年龄差的4倍,那么试问哥哥今年______岁。
7. 一个三位数,抹去它的首位数字之后剩下的两位数的4倍比它大25,这个三位数是 .8. 用1,2,3,4,5,6这六个数字组成两个三位数,这两个三位数的最大乘积是______。
9. 用2,4,6三个数字来构造四位数,但是不允许有两个连着的2出现在四位数中(例如6442、4242是允许的,2264、4222就不允许),这样的四位数共有 个.10. 甲、乙、丙三人赛跑,同时从起点出发后,甲比乙早10分钟到达终点,乙比丙早10分钟到达终点.已知甲比乙每小时快3千米,乙比丙每小时快2千米.这次比赛的路程是 千米.11. 把170分成8个正整数的和,且每个数都不超过22,那么这样的分法共有多少种?12. 蓝天小学举行“迎春”环保知识大赛,一共有100名男、女选手参加初赛,经过初赛、复赛,最后确定了参加决赛的人选.已知参加决赛的男选手的人数,占初赛的男选手人数的20%;参加决赛的女选手的人数,占初赛的女选手人数的12.5%,而且比参加决赛的男选手的人数多.参加决赛的男、女选手共有 人。
学而思 2009春季 第二讲 带答案
A
Bቤተ መጻሕፍቲ ባይዱ
P
C
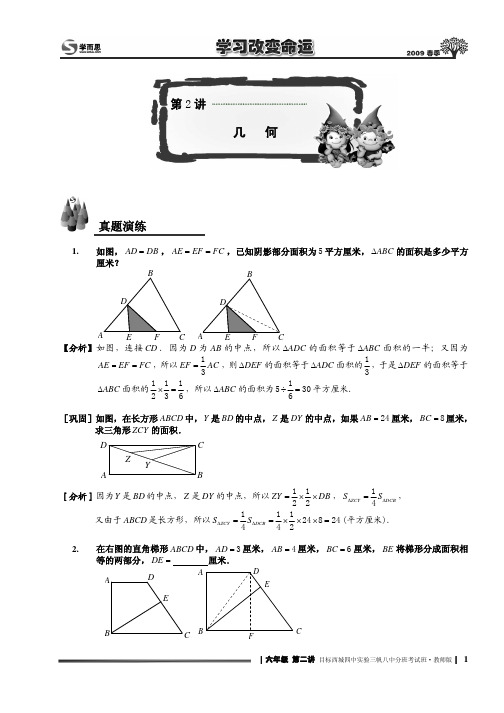
【分析】如图所示,连接 AP . 三角形 ABC 的面积等于三角形 APB 与三角形 APC 的面积之和, 而这两个三角形的底 AB 、AC 相 1 等,高分别为 x 和 y ,所以 12 x y 42 ,可得 x y 7 . 2 1 本题也可运用特殊值法,设 P 在 B 点,则此时 x 0 ,那么 SABC AC y 42 ,得到 y 7 , 2 x y 7. 4. 图中的大直角三角形被分割成两个小直角三角形和一个正方形, 如果两个小直角三角形的斜边长 分别为 20 厘米和 l0 厘米,那么这两个小直角三角形的面积之和是 平方厘米.
A D E
A D E
B
C B
F
C
|六年级 第二讲 目标西城四中实验三帆八中分班考试班·教师版| 1
【分析】首先可运用梯形面积公式求出: S梯形ABCD ( 3 6 ) 4 2 18 平方厘米,它的一半为 9 平方厘米. 连接 BD,则 SABD 3 4 2 6 平方厘米, SBED 9 6 3 平方厘米, 则 DE : EC S BED : S BEC 3 : 9 1: 3 . 再过 D 作 DF BC 于 F , 则 DF AB 4 厘米,FC 6 3 3 厘米, 根据勾股定理可得 CD 5 厘 1 1 5 米,所以 DE CD 5 厘米. 4 4 4 [巩固]如图所示,在四边形 ABCD 中,线段 BC 长为 6 厘米,角 ABC 为直角,角 BCD 为 135 ,而且点 A 到边 CD 的垂线 AE 的长为 12 厘米,线段 ED 的长为 5 厘米,求四边形 ABCD 的面积. A
C
学而思六年级数学试卷

学而思六年级数学试卷1.一件商品原价125元,先涨价 20% 后,再降 20% ,现价比原价()。
[单选题] *A.降低了(正确答案)B.升高了C.不变D.无法判断3.直径是6cm的半圆的周长是()cm。
[单选题] *A.18.84B.9.42C.15.42(正确答案)D.12.424.下面图形中,()可能不是轴对称图形。
[单选题] *A.等边三角形B.长方形C.平行四边形(正确答案)D.圆5.与“北偏东65°”表示的方向相同的是()。
[单选题] *A.东偏北65°B.北偏东25°C.南偏西65°D.东偏北25°(正确答案)6.右图中圆的半径是15cm,长方形的面积是()cm²。
[单选题] *A.225B.450C.900D.1350(正确答案)[填空题]_________________________________7.右图正方形中阴影部分的周长()空白部分的周长。
[单选题] *B.等于(正确答案)C.小于D.无法比较8.一个圆环,外圆半径是内圆半径的2倍,这个圆环的面积和内圆的面积之比是()。
[单选题] *A.1∶4B.4∶1C.3∶1(正确答案)D.1∶39.甲城市的绿化率是10%,乙城市的绿化率是15%,甲、乙两城市的绿化面积相比,()。
[单选题] *A.甲城市绿化面积大B.乙城市绿化面积大C.无法确定(正确答案)10.若2∶3的前项增加6,要使比值不变,后项要()。
[单选题] *A.增加9(正确答案)B.扩大6倍C.缩小6倍11.同学们种花,活了100棵,有5棵没有成活,成活率约是()。
[单选题] *A.100%C.95.2%(正确答案)12.一个三角形中三个内角的度数比是1∶4∶5,这个三角形是() [单选题] *A.锐角三角形B.直角三角形(正确答案)C.钝角三角形13.在一个周长为100厘米的正方形纸片内,要画一个最大的圆,这个圆的半径是()。
2009年秋季学而思竞赛班选拔考试题目汇编-高年级

2009年秋季学而思竞赛班选拔考试学校姓名得分所在学而思班次春季暑期秋季考试说明1.考试时间:90分钟.2.试卷分值:本试卷共20道题,第1—16题,每题5分;第17—20题,每题10分,共120分.1.计算:1111111111 2481632641282565121024+++++++++=.2.分数57化成小数后,小数点后第2009位数字是.3.如图,长方形ABCD的面积为12,CDP∆的面积为4,则阴影三角形的面积是.P4.自然数N是一个两位数,也是一个质数,而且N的个位数字与十位数字都是质数,这样的自然数N有个.5.三个连续自然数的平方和等于365,则这三个连续自然数的和为________.6.一个两位数,其十位上的数字与个位上的数字交换以后,所得的两位数与原来的两位数之和为121,则满足条件的两位数中最大的是.新六年级7.用0、1、2、3、4、5这六个数字可以组成个没有重复数字的三位数.8.将1、2、3、……、10顺次写成一排得到一个多位数:12345678910,这个多位数除以3的余数是.9.小张从家到公园,原打算每分钟走50米,30分钟走到.为了提早10分钟到达,他把速度加快了,则小张实际上每分钟走米.10.一项工程,甲单独完成需12天,乙单独完成需9天.若甲先做4天后乙接着做,乙还需要天可以完成.11.甲、乙、丙、丁坐在同一排相邻的四个座位上,座位号从左到右依次是1、2、3、4,已知甲和乙不相邻,丙和丁不相邻,而且甲的座位号比乙大,比丙小.那么丁坐在号座位上.12.六位数2009□2能被24整除,则□中应该填的数是.13.轮船用同一速度往返于两码头之间,它顺流而下行了8个小时,逆流而上行了10个小时,如果水流速度是每小时3千米,两码头之间的距离是千米.14.图中是一个棱长为5厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个棱长为1厘米的正方体,做成一种玩具.这种玩具的表面积是平方厘米.15.某装订车间的工人要将一批书打包后送进邮局,每包书中所装的数目一样多.第一次他们领来了这批书的712,结果打了14个包还多35本;第二次他们把剩下的书全部取来,连同第一次多的零头一起,刚好又打了11包.那么这批书共有本.16.一个水池有一根进水管不间断地进水,还有若干根相同的抽水管.若用24根抽水管抽水,6小时即可把池中的水抽干;若用21根抽水管抽水,8小时可水池中的水抽干.若用16根抽水管,需要 小时水池中的水抽干.17. 如图所示,在三角形ABC 中,3DC BD =,DE EA =.若三角形ABC 的面积是1.则阴影部分的面积是 . CF E18. 1995的数字和是199524+++=.问:小于2000的四位数中数字和等于24的数共有 个.19. 某校有150名学生要到离校21千米的博物馆去参观,只有一辆能载50人的汽车,已知人步行速度为每小时5千米,汽车速度为每小时45千米,为使全体同学尽快到达博物馆,他们采用步行与乘车相结合的办法前往,那么到达博物馆所用的最短时间是多少小时?(上、下车所用时间忽略不计)20. 把数字1到9各使用一次,组成一个被555667整除的9位数,这个9位数是 .。
【例1】 ()2009年学而思六年级试题

牛吃草问题(二)【例1】(★★★)2009年学而思六年级试题一个水池有一根进水管不间断地进水,还有若干根相同的抽水管。
若用24根抽水管抽水,6小时即可把池中的水抽干;若用21根抽水管抽水,8小时可把池中的水抽干。
若用16根抽水管,需要____小时可把水池中的水抽干。
【例2】(★★★)一个水池装一个进水管和三个同样的出水管。
先打开进水管,等水池存了一些水后,再打开出水管。
如果同时打开2个出水管,那么8分钟后水池空;如果同时打开3个出水管,那么5分钟后水池空。
那么出水管比进水管晚开多少分钟?【例3】(★★★)(2010年希望杯六年级初赛)某超市平均每小时有60人排队付款,每一个收银台每小时能应付80人。
某天某时间段内,该超市只有一个收银台工作,付款开始4小时就没有顾客排队了。
如果当时有两个收银台工作,那么付款开始_____小时就没有人排队了。
【例4】(★★★)画展9点开门,但早有人来排队入场,从第一个观众来到时起,若每分钟来的观众一样多,如果开3个入场口,9点9分就不再有人排队;如果开5个入场口,9点5分就没有人排队。
求第一个观众到达的时间。
【例5】(★★★★)佳佳从甲地步行去乙地,出发一段时间后,海海有事去追赶她,若骑自行车,每小时行15千米,3小时可以追上;若骑摩托车,每小时行35千米,1小时可以追上;若开汽车,每小时行45千米,多少分钟可以追上佳佳?【例6】(★★★★)有一牧场,17头牛30天可将草吃完,19头牛则24天可以吃完。
现有若干头牛吃了6天后,卖掉了4头牛,余下的牛再吃两天便将草吃完。
问:原来有多少头牛吃草(草均匀生长)?本讲总结揭开“牛吃草”问题的面纱牛吃草——消长问题重点例题:例1,例3,例5。
学而思六年级数学选拔试卷

一、选择题(每题5分,共20分)1. 下列各数中,有理数是()A. $\sqrt{2}$B. $\pi$C. $-1/3$D. $0.333...$2. 一个长方形的长是4厘米,宽是3厘米,它的面积是()A. 7平方厘米B. 12平方厘米C. 15平方厘米D. 16平方厘米3. 若一个数的平方是81,则这个数可能是()A. 9B. -9C. 9或-9D. 9或94. 已知三角形ABC中,∠A=45°,∠B=60°,则∠C的度数是()A. 45°B. 60°C. 75°D. 90°5. 在等差数列{an}中,a1=2,d=3,则第10项an的值是()A. 29C. 31D. 32二、填空题(每题5分,共20分)6. 若x²+4x+3=0,则x的值是__________。
7. 在直角坐标系中,点P(-2,3)关于x轴的对称点坐标是__________。
8. 已知圆的半径是5厘米,其周长是__________厘米。
9. 若一个数的倒数是1/2,则这个数是__________。
10. 在梯形ABCD中,AD∥BC,AB=CD,则∠ABC和∠DCB的关系是__________。
三、解答题(每题10分,共30分)11. (10分)解下列方程:(1)2x - 3 = 7(2)5(x + 2) = 3x + 2012. (10分)已知等差数列{an}中,a1=3,d=2,求第10项an的值。
13. (10分)在直角坐标系中,点A(2,3)和B(-4,-1),求线段AB的长度。
四、应用题(每题10分,共20分)14. (10分)一个长方体的长、宽、高分别为4厘米、3厘米、2厘米,求它的体积。
15. (10分)甲、乙两人同时从同一点出发,甲向东走,乙向西走,甲的速度是每分钟30米,乙的速度是每分钟20米。
经过多少分钟后,两人相距1200米?答案:一、选择题1. C2. B4. C5. A二、填空题6. -1或-37. (-2,-3)8. 31.49. 210. 相等或互补三、解答题11. (1)x = 5(2)x = 1012. an = 3 + (n - 1) 2 = 2n + 113. AB = $\sqrt{(-4 - 2)^2 + (-1 - 3)^2}$ = $\sqrt{36 + 16}$ =$\sqrt{52}$ = 2$\sqrt{13}$四、应用题14. 体积 = 长× 宽× 高= 4 × 3 × 2 = 24立方厘米15. 两人相距1200米时,甲、乙两人所走的路程之和为1200米。
学而思数学六年级上册试卷

一、选择题(每题5分,共25分)1. 下列各数中,有理数是()A. $\sqrt{2}$B. $\pi$C. $\frac{1}{3}$D. $\sqrt{5}$2. 下列图形中,是轴对称图形的是()A. 正方形B. 等腰三角形C. 平行四边形D. 梯形3. 一个等腰三角形的底边长为6cm,腰长为8cm,那么这个三角形的面积是()A. 24cm²B. 27cm²C. 30cm²D. 32cm²4. 下列函数中,定义域为全体实数的是()A. $y=2x+3$B. $y=\sqrt{x-1}$C. $y=\frac{1}{x}$D. $y=x^2$5. 下列各式中,最简二次根式是()A. $\sqrt{18}$B. $\sqrt{25}$C. $\sqrt{50}$D.$\sqrt{49}$二、填空题(每题5分,共25分)6. $\frac{3}{4}$的倒数是__________。
7. $\sqrt{36}$等于__________。
8. 下列图形中,是平行四边形的是__________。
9. 一个长方形的长是8cm,宽是5cm,那么这个长方形的面积是__________cm²。
10. 函数$y=2x-3$在$x=2$时的函数值是__________。
三、解答题(每题15分,共45分)11. (1)已知:$a+b=5$,$ab=4$,求$a^2+b^2$的值。
(2)已知:$x^2-5x+6=0$,求$x^2-5x$的值。
12. (1)已知:$a=3$,$b=-2$,求$2a-b$的值。
(2)已知:$x^2-2x+1=0$,求$x^2+1$的值。
13. (1)已知:$a=5$,$b=2$,求$(a+b)^2$的值。
(2)已知:$x^2-4x+4=0$,求$x^2-4x$的值。
四、应用题(每题15分,共30分)14. 小明家到学校的距离是1200米,他骑自行车上学,每分钟骑行的速度是200米,求小明骑自行车上学需要多少分钟?15. 一块长方形菜地,长是20米,宽是15米,菜地四周种了篱笆,篱笆的总长度是多少米?。
学而思六年级数学教材

学而思六年级数学测试1·计算篇1.计算=⨯+++++++128)288122411681120180148124181(2.=++⨯++++-+++⨯+++)1119171()131111917151()1311119171()111917151(3.计算:2004×2003-2003×2002+2002×2001-2001×2000+…+2×1= 4.有一列数:……第2008个数是________ .5.看规律13 = 12,13 + 23 = 32,13 + 23 + 33 = 62 ……,试求63 + 73 + …+ 143第1讲 小升初专项训练·计算 四五年级经典难题回顾例1 求下列算式计算结果的各位数字之和:2576666666200562006⨯⨯个个例2 求数1911211111011++++ 的整数部分是几?小升初重点题型精讲例1=÷+÷+÷595491474371353251 .例2 =+⨯⨯÷+--+)19956.15.019954.01993(22.550276951922.510939519例3 =++÷++)25118100412200811()25138100432200831( .巩固 计算:=+⨯+⨯+⨯+⨯416024340143214016940146 .例4 计算:=⨯++⨯+⨯+⨯10199507535323112222.拓展计算:=⨯⨯++⨯⨯+⨯⨯10981943273215.例5 1⨯2+2⨯3+3⨯4+4⨯5+5⨯6+6⨯7+7⨯8+8⨯9+9⨯10= . 巩固:2⨯3+3⨯4+4⨯5+…+100⨯101= .拓展计算:1⨯2⨯3+2⨯3⨯4+3⨯4⨯5+…+9⨯10⨯11= .例6 [2007 –(⨯⨯1.5)÷10]÷160-0.3= .巩固计算:53×57 –47×43 = .例7 计算:11×19 + 12×18 + 13×17 + 14×16 = .拓展计算:1×99 + 2×98 + 3×97 + …+ 49×51 = . 例8 计算:1×99 + 2×97 + 3×95 + …+ 50×1 = . 家庭作业1.=÷+÷+÷797291585381373172.2.=-⨯⨯+÷)5246.5(402323153236.3.=++÷++)2231966913200711()2237966973200771(.4. 计算:=-++-+++-++-++-+119951199511993119931717151513132222222222.5. 计算:11×29 + 12×28 + …+ 19×21 = .名校真题1. 如图,AD = DB,AE = EF = FC,已知阴影部分面积为5平方厘米,△ABC的面积是_________平方厘米.2. 如图,ABCD与AEFG均为正方形,三角形ABH的面积为6平方厘米,图中阴影部分的面积为_________.3. 如图,长方形ABCD的面积是36,E是AD的三等分点,AE = 2ED,则阴影部分的面积是 .4. 如图,边长为1的正方形ABCD中,BE = 2EC,CF = FD,求三角形AEG的面积.5. 如图,3个边长为3的正方形,甲的中心在乙的一个顶点上,乙的中心在丙的一个顶点上,甲与丙不重叠,求甲、乙、丙叫共覆盖的面积是。
