第九届高数竞赛(医学类)试题
数学竞赛高数试题及答案

数学竞赛高数试题及答案试题一:极限的计算问题:计算极限 \(\lim_{x \to 0} \frac{\sin x}{x}\)。
解答:根据洛必达法则,我们可以将原式转换为 \(\lim_{x \to 0} \frac{\cos x}{1}\),由于 \(\cos 0 = 1\),所以极限的值为 1。
试题二:导数的应用问题:若函数 \( f(x) = 3x^2 - 2x + 1 \),求其在 \( x = 1 \) 处的导数值。
解答:首先求导数 \( f'(x) = 6x - 2 \),然后将 \( x = 1 \) 代入得到 \( f'(1) = 6 \times 1 - 2 = 4 \)。
试题三:不定积分的求解问题:求不定积分 \(\int \frac{1}{x^2 + 1} dx\)。
解答:这是一个基本的积分形式,可以直接应用反正切函数的积分公式,得到 \(\int \frac{1}{x^2 + 1} dx = \arctan(x) + C\),其中\( C \) 是积分常数。
试题四:级数的收敛性判断问题:判断级数 \(\sum_{n=1}^{\infty} \frac{1}{n^2} \) 是否收敛。
解答:根据比值测试,我们有 \(\lim_{n \to \infty}\frac{1}{(n+1)^2} / \frac{1}{n^2} = \lim_{n \to \infty}\frac{n^2}{(n+1)^2} = 1\),由于极限值为 1,小于 1,所以级数收敛。
试题五:多元函数的偏导数问题:设函数 \( z = f(x, y) = x^2y + y^3 \),求 \( f \) 关于\( x \) 和 \( y \) 的偏导数。
解答:对 \( x \) 求偏导,保持 \( y \) 为常数,得到 \( f_x =2xy \)。
对 \( y \) 求偏导,保持 \( x \) 为常数,得到 \( f_y = x^2 + 3y^2 \)。
医药高等数学试卷及答案

中医学院 20-20学年第一学期《医药高等数学》课程期末考试卷命题教师: 试卷编号: 审核人:适用专业考试班级考生姓名学号班级一、单项选择题:本大题共 8小题,每小题 3分,共 24分。
在每题给出的四个选项中,只有一项是符合题目要求的,把正确选项填在括号内。
1、 =+-+-++∞→113 2(3 2(lim n n nn n (。
A 、31 B 、 32C 、 1D 、和 n 取值有关 2、当1→x 时, ( 是 x -1的高阶无穷小。
A 、 231(x - B 、xx+-11 C 、 1(2x - D 、 1-x 3、⎪⎩⎪⎨⎧=≠=0, 9,0, sin (x x x Ax x f 在 x =0处连续,则 A =( 。
A 、 0B 、 -6C 、 -9D 、 94、 0=x 是函数 xxx f sin (=的( 。
A 、不是间断点B 、无穷间断点C 、跳跃间断点D 、可去间断点 5、若函数4(3(2(1( (----=x x x x x f ,则方程 0 (' =x f 的实根个数( 。
A 、 1 B 、 2 C 、 3 D 、 4 6、下列等式中正确的是( 。
A 、 d ⎰= ( (x f dx x fB 、 d ⎰=dx x f dx x f ( (C 、⎰=dx x f dx x f dx d ( ( D 、⎰+=c x f dx x f dxd( (7、满足 0 , (0 , (00' 00' ==y x f y x f y x 且的点 , (00y x 一定是( 。
A 、驻点B 、极值点C 、最大值点D 、最小值点8、σσd y x I d y x I DD221][ln( , ln(⎰⎰⎰⎰+=+=, 其中 D 是矩形闭区域53≤≤x ,10≤≤y ,则 1I 与 2I 之间的关系( 。
A 、21I I ≤B 、21I I ≥C 、 21I I =D 、无法比较二、填空题:本大题共 7小题,每小题 2分,共 14分。
高数竞赛试题及答案

高数竞赛试题及答案在高等数学领域中,竞赛试题的编写与解答一直是学生们提高自己数学水平的重要方式之一。
本文将提供一些高等数学竞赛试题,并附上详细的解答过程,以帮助读者更好地理解和应用数学知识。
1. 竞赛试题一考虑函数f(x) = |x^2 - 4x + 3|,其中x为实数。
(1)求函数f(x)的定义域。
(2)求函数f(x)的最大值和最小值。
解答过程:(1)为了求函数f(x)的定义域,我们需要确定使函数的值有意义的x 的范围。
由于函数f(x)中包含了一个绝对值,我们可以将其拆分成两种情况讨论:当x^2 - 4x + 3 ≥ 0时,函数f(x) = x^2 - 4x + 3;当x^2 - 4x + 3 < 0时,函数f(x) = -(x^2 - 4x + 3)。
对于第一种情况,我们需要求解不等式x^2 - 4x + 3 ≥ 0。
通过因式分解或配方法,我们可以得到(x-1)(x-3) ≥ 0。
解这个不等式可以得到x ≤ 1或x ≥ 3。
对于第二种情况,我们需要求解不等式x^2 - 4x + 3 < 0。
同样通过因式分解或配方法,可以得到(x-1)(x-3) < 0。
解这个不等式可以得到1< x < 3。
综上所述,函数f(x)的定义域为x ≤ 1或x ≥ 3,且1 < x < 3。
(2)为了求函数f(x)的最大值和最小值,我们可以分别考虑函数f(x)在定义域的两个区间内的取值情况。
当x ≤ 1时,函数f(x) = x^2 - 4x + 3。
通过求导可以知道,函数f(x)在x = 2处取得最小值。
代入可得最小值为f(2) = 1。
当x ≥ 3时,函数f(x) = -(x^2 - 4x + 3)。
同样通过求导可以知道,函数f(x)在x = 2处取得最大值。
代入可得最大值为f(2) = -1。
综上所述,函数f(x)的最大值为-1,最小值为1。
2. 竞赛试题二已知函数f(x) = 2^(x+1) - 3^(x-2),其中x为实数。
2017-2018学年度第九届高等数学竞赛(答案)

中山大学新华学院第九届高等数学竞赛姓名 学号 班级 成绩一、填空题(每题3分,共18分) 1.函数()11y ln x =++()()1,00,-⋃+∞。
2. 2111.dx x+∞=⎰。
3.曲线236x x y +=的拐点横坐标为=x 2-;4. 11(1x x -+=⎰2π. 5.a =6.设A =“某人投注的号码中一等奖”,则P (A )=861331615.64310C C -=⨯二、计算题(每题7分,共49分) 1. 设)1ln(2x x y ++=,求dy . )1ln(2++=x x d dy )1(1122++++=x x d x x ............3分dx x xx x ⎪⎪⎭⎫⎝⎛++++=111122 ----------5分.112dx x +=------------7分2、已知函数32()f x x ax bx =++在1x =处有极小值2-,(1) 求a 与b 的值; (2) 求()f x 的极大值点与极大值。
解:(1)由(1)2f =-且为极小值知,12320a b a b ++=-⎧⎨++=⎩,解得0;3a b =⎧⎨=-⎩------------------ 2分(2)322()3,()333(1)3(1)(1),f x x x f x x x x x '=-=-=-=+-由上表可得,极大值(1)2f -=。
------------------ 7分 3.设函数()f x 在0x =处有二阶导数,且 0()lim0,x f x x→=(0)4,f ''= 求(0),(0),f f '10()lim 1.xx f x x →⎛⎫+ ⎪⎝⎭解:4、设211()x x f x e-⎧⎪+=⎨⎪⎩00x x >≤,求31(2)d f x x -⎰. 解:令2=-t x,则d d =x t ,当1=x 时,1=-t ; 当3=x 时,1=t ------------------ 3分3101111(2)d ()d ()d ()d ---==+⎰⎰⎰⎰f x x ft t f t t f t t 0211d 1+x x -=⎰1-0e d x x +⎰114eπ=-+ ------------------ 7分5. 计算40⎰t =,则2,2x t dx tdt == ------------------ 2分4202t te dt =⎰⎰ ------------------- 4分222220002()2422(1)t t t te e dt e e e =-=-=+⎰ -----------------7分2000011()1()()lim ln 1lim lim 0000()1()(0)1limlim (0)222002()(0)lim ()lim 000,()(0)()(0)lim lim 0,()lim 1.x x x x f x f x f x xx x xx xx x x x f x f x f f xxx x f x f f x x xf x f f x f x xf x e eex eeee →→→→⎛⎫+•⎪⎝⎭→→→==→'''-''→→===⨯=-'===⎛⎫+= ⎪⎝⎭====6.解:)1ln(y xe e xzy x y x +++=∂∂++, ------------------ 2分yx xe y z y x +++=∂∂+11, ------------------ 4分 于是 =)0,1(dz dy e edx )2(2++. ------------------ 7分7. 计算二次积分 23120y xx I dx e dy =⎰⎰.解:被积函数是22y e ,对于y 而言,它的原函数不能用初等函数表示,需改变积分次序才能进行.区域D : 3,01,y x y y ⎧≤≤⎨≤≤⎩ 如图所示.--------- 2分2312y xxI dx e dy=⎰⎰2312y yye dy dx=⎰⎰=2122201(1)2y e y dy -⎰, 令22y u =, 由上式得----- 4分 1112220111222(12)212()|23uuu u u I e u du e du ue du e ue e e =-=-=---=-⎰⎰⎰------------------ 7分 三、(10分)0()()()()2.().设有任意阶导数,且满足试求xf x x t f t dt f x x f x -=-⎰12()()()2()+()()()2()=()2()()()xxxxx x f t dt tf t dt f x xx f t dt x f x xf x f x f t dt f x x f x f x f x c e c e -=-'⋅-'-''==+⎰⎰⎰⎰000解:由题意: 等式两端对变量求导:-=即:等式两端再次对变量求导: 上式微分方程对应通解为:12 0,(0)0,(0)21,()xx x x f f c c f x e e --'=====-令可得,从而=-1,故.四、应用题(每题9分,共18分)3x y =oxy x=-111 1y o1. 解:如图(略),曲线与x 轴的交点为)0,1(-和)0,1(,..........2分(1) ⎰112)1(--=dx x S 34=............5分(2) 12V dy π=⎰()12101122y dy y y πππ⎛⎫=-=-= ⎪⎝⎭⎰ .......9分 2. 解:设L 为获得的总利润,L R C =-= 1p 1q +2p 2q -C=1p ()1120.1p -+2p ()220.01p --(())123540q q ++=2211220.1160.01 2.4595p p p p -+-+- (2)分解方程组1112220.2160,0.02 2.40,p p L p p L p p =-+=⎧⎪⎨=-+=⎪⎩解得1p =80, 2p =120,唯一驻点是(80,120).又 ..........6分A =L 11=-0.2<0,B =L 12=0,C =L 22=-0.02<0,因此 Δ=AC -B 2=0.004>0.故L 在驻点(80,120)处有极大值. .........8分于是可以断定,当两个市场售价分别为80和120个单位时,利润最大,最大利润为L (80,120)=189. ...............9分五、综合拓展题(5分)兄妹二人沿某街分别在离家3公里与2公里处同向散步回家,家中的狗一直在二人之间来回奔跑。
高数竞赛练习

高数竞赛练习试卷(一)1. 求极限1101lim21arctantt t te te t π→+-。
2. 求极限0tan(sin )sin(tan )lim tan sin t x x x x →--。
3. 设()f x 具有二阶连续导数,且(0)0,(0)(0)0f f f '''>==,t 是曲线()y f x =上点(,())x f x 处的切线在x 轴的截距,求0()lim()x xf t tf x →。
4. 设()f x 在[0,)+∞二阶可导,且(0)1,(0)1,()(),(0f f f x f x x '''=>>>.求证:()x f x e >。
5. 已知()234111ydx ydx y dx y dxdx y -+++=--⎰⎰⎰⎰⎰,求()x f y =的表达式。
6. 设tan 20()()x F x f tx dt=⎰,其中()f x 为连续函数,求()F x ',并讨论()F x '的连续性。
7. 计算ln(sin )x x dxπ⎰。
8. 设()f x连续可导,证明:[]10(1)(0)x dx f f π'=-⎰⎰。
9. 设非负函数()f x 在[]0,1上连续,且单调上升,[]0,1,()t y f x ∈=与直线(1)y f =及x t =围成图形的面积为1()S t ,()y f x =与直线(0)y f =及x t =围成图形的面积为2()S t .⑴ 证明:存在唯一的(0,1)t ∈,使得12()()S t S t =.⑵ t 取何值时两部分面积之和取最小值? 10.求函数xyz ω=+()1,0,1P -处沿直线11:111x y z L --==-在平面:210x y z π-+-=上的投影直线l 方向的方向导数。
11.已知01n <<,证明级数2211nn m a m n ∞∞==+∑∑收敛.12. 计算曲线积分[][]()cos ()sin ACBf y x y dx f y x dyππ'-+-⎰,其中ACB 为连结点(,2)A π与点(3,4)B π的线段AB 之下方的任意路线,且该路线与线段AB 所围图形的面积为1,()f x 是连续可导的函数.13. 设(),()f x g x 可微,且()()z yf xy dx xg xy dy =+. ⑴ 若存在u ,使du z =,求()()f x g x -;⑵ 若()()f x F x '=,求u ,使z du =.14. 设()f u 在[)1,+∞上有连续的二阶导数,(1)1f =-,3(1)2f '=,且函数()()222222x y z f x y z ω=++++满足:2222220x y z ωωω∂∂∂++=∂∂∂,求()f u 在[)1,+∞上的最小值。
医用高数精选习题含答案

医用高数精选习题含答案医学生需要学习数学,尤其是高数。
然而,高数知识对于许多医学生来说是非常困难的。
因此,许多医学生需要精选的高数练习题目来加强他们的高数技能。
这里,我们提供一些医用高数精选习题和答案,这些习题涵盖了各种高数问题:导数、极值、曲率、微积分和微分方程。
1. 给出函数f(x) = 3x^2 + 2x的导函数答案:f’(x) = 6x + 2解析:对f(x)求导即可得到f’(x)。
2. 给出函数f(x) = x^3 - 3x^2 - 45的极值点答案:f(x)在x=-3和x=5处达到极小值和极大值解析:对f(x)求导,令f’(x)=0,解得x=-3和x=5,分别代入f(x)求得f(-3)和f(5),即得到极值。
3. 给出函数f(x) = sin(x),在x = 0处的曲率答案:f”(x) = -sin(x),因此,f”(0) = 0,所以曲率为0。
解析:对f(x)求两次导即可得到曲率公式f”(x) = -sin(x),将x=0代入公式即可得到曲率为0。
4. 求以下函数的不定积分:f(x) = 6x^2 - 8x + 9答案:∫f(x)dx = 2x^3 - 4x^2 + 9x + C(其中C为常数)解析:对f(x)进行积分,即可得到不定积分。
5. 给出微分方程dy/dx = 9x^2 - 12x,求其通解答案:y = 3x^3 - 6x^2 + C(其中C为常数)解析:对微分方程求解,得到y的一般解,再带入初始条件求得一个特定解。
练习以上高数习题能够帮助医学生们掌握高数知识并加强自己的技能。
如果你感到这些习题有些困难,可以不断的练习,直到完全理解并掌握。
只要你通过努力,这些数学技能就会变得相对容易了。
医学高数期末考试试题

医学高数期末考试试题### 医学高数期末考试试题#### 一、选择题(每题2分,共20分)1. 以下哪项不是微积分的基本定理?A. 牛顿-莱布尼茨公式B. 泰勒级数展开C. 定积分的性质D. 不定积分的计算2. 函数 \( f(x) = x^2 + 3x - 2 \) 在区间 \( [1, 3] \) 上的最大值是:A. 2B. 4C. 6D. 83. 以下哪个选项是 \( e^x \) 的泰勒级数展开式?A. \( 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots \)B. \( 1 - x + \frac{x^2}{2!} - \frac{x^3}{3!} + \ldots \)C. \( 1 + x - \frac{x^2}{2!} + \frac{x^3}{3!} - \ldots \)D. \( 1 + x + \frac{x^2}{2} + \frac{x^3}{3} + \ldots \)4. 已知 \( \lim_{x \to 0} \frac{\sin x}{x} = 1 \),求\( \lim_{x \to 0} \frac{\sin 2x}{x} \) 的值是:A. 0B. 1C. 2D. 45. 方程 \( y'' - 2y' + y = 0 \) 的通解是:A. \( y = e^{t} \)B. \( y = e^{t} + e^{2t} \)C. \( y = e^{t} + e^{-t} \)D. \( y = e^{t} + e^{2t} + e^{-t} \)#### 二、填空题(每题2分,共20分)6. 若 \( f(x) = \ln(x) \),则 \( f'(x) = ________ \)。
7. 函数 \( g(x) = x^3 - 6x^2 + 11x - 6 \) 的导数 \( g'(x) \) 是 ________。
大学医用高等数学习题

求解复杂函数的极限、导数、积分等,以及解决 一些实际问题。
解析方法
通过分析题目要求,引导学生逐步推导和证明, 让学生掌握解题思路和方法。
答案与解析
答案与解析
提供习题的答案和解析,帮助学生自我检测和巩固所学知识。
内容
包括每道习题的答案和详细的解析过程,让学生能够对照答案进行自我评估和纠正错误。
05 总结与展望
01
随着大数据和人工智能的兴起,医学高等数学将更多地应用于
数据分析和机器学习等领域。
跨学科融合
02
医学高等数学将与生物学、物理学、化学等其他学科进一步融
合,促进多学科交叉研究。
数学建模在医学研究中的应用
03
数学建模在医学研究中具有重要地位,未来将有更多复杂模型
应用于医学领域。
对未来学习的建议
01
02
流行病学模型是利用数学方法描述疾病在人 群中传播规律的模型,通过对疾病流行趋势 的预测和分析,为防控措施的制定提供依据。 流行病学模型在传染病防控、慢性病管理等 领域有广泛应用。
医学影像处理中的数学方法
总结词
利用数学方法对医学影像进行分析和处理的 手段。
详细描述
医学影像处理中的数学方法包括图像增强、 图像分割、特征提取和模式识别等技术。这 些技术可以帮助医生更准确地解读和分析医 学影像,提高诊断的准确性和可靠性。在放 射学、病理学和医学成像等领域,医学影像
不定积分与定积分
不定积分概念
不定积分是求函数原函数的运算,不定 积分的结果是一组原函数,它们之间相 差一个常数。不定积分的基本公式和运 算法则是学习定积分的基础。
VS
定积分概念
定积分是求函数在某个区间上的积分和的 运算。定积分的值与被积函数和积分的区 间有关,可以用来计算面积、体积等实际 问题。
高数竞赛题

1、设函数 f(x) 在区间 [a, b] 上连续,在 (a, b) 内可导,且 f(a) = 0,f(b) = 1。
若存在ξ∈ (a,b) 使得 f'(ξ) = 2,则以下哪个结论必然成立?A. ∀x ∈ (a, b), f(x) ≤ 2x - aB. ∃x₁, x₂∈ (a, b), f(x₁) < f(x₂)C. ∀x ∈ (a, ξ), f(x) < (x - a)/(b - a)D. ∃x₀∈ (a, b), f(x₀) = 1/2 且 f'(x₀) = 0(答案)2、设数列 {a_n} 满足 a_1 = 1,a_{n+1} = a_n + 2/a_n,则以下关于数列 {a_n} 的说法正确的是?A. {a_n} 是递减数列B. 对任意正整数 n,有 a_n < n + 1C. 存在正整数 k,使得 a_k < k 但 a_{k+1} > k + 1D. 对任意正整数 n,有 a_n ≥√(2n + 1)(答案)3、设函数 f(x, y) = x2 + y2 - 2x - 2y + 1,则 f(x, y) 在区域 D = {(x, y) | x2 + y2 ≤ 2} 上的最小值为?A. -1B. 0C. 1 - √2(答案)D. 2 - 2√24、设向量 a = (1, 2),b = (2, 1),c = (1, -2),若 (a + λb) ⊥ c,则实数λ的值为?A. -1/2B. 1/2(答案)C. -2D. 25、设函数 f(x) = x3 - 3x2 + 2,则 f(x) 的极值点个数为?A. 0B. 1C. 2(答案)D. 36、设矩阵 A = [1 2; 3 4],B = [2 0; 1 1],则 AB - BA =?A. [0 -2; 2 0](答案)B. [2 2; -2 -2]C. [0 2; -2 0]D. [-1 -2; 3 4]7、设函数 f(x) = ex - x - 1,则不等式 ex > x2 + x + 1 的解集为?A. (-∞, 0)B. (0, +∞)(答案)C. (-∞, -1) ∪ (1, +∞)D. (-1, 0) ∪ (0, 1)8、设函数 f(x) = (x - a)(x - b)(x - c),其中 a, b, c 是互不相等的实数。
医学高等数学试卷A

医学高等数学试卷A学号: 姓名: 院: 专业:一、计算下列各题(本题满分36分,每小题6分) (1) 20ln(1)lim .3x x x x →+- (2) 24lim .2xx x x →∞+⎛⎫ ⎪+⎝⎭ (3)1sin x y e =,求y ' . (4)2ln x xdx ⎰.(5) 40.(6) 设工厂A 和工厂B 的产品次品率分别为1%和2%,现从由A 和B 的产品分别占60%和40%的一批产品中抽取一件,求(1)抽取的是次品的概率;(2)如果抽取的一件发现是次品,该次品是A 厂生产的概率。
二、解答下列各题(本题满分42分,每小题7分)(1)求函数sin1z =的全微分。
(2)(我班做)设400001550,022,666333AB B ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭求(1);(2).B A 行列式矩阵(3)(别人班做)设连续型随机变量X 的概率密度为2,01;(=0,.x x f x <<⎧⎨⎩)其它 以Y 表示对x 三次独立的重复观察中事件12A X ⎧⎫=≤⎨⎬⎩⎭出现的次数,求概率(2)p Y =.. (4)设(ln ,)xz f x y =,求,.z z x y∂∂∂∂(5)求22,D x dxdy y ⎰⎰其中12,D x y x x==是由直线及曲线y=所围区域。
(6)求微分方程1y y x x'''-=的通解. 三、设函数21sin ,0,(),0x x f x xa x x ⎧>⎪=⎨⎪+≤⎩,试确定a 的值使函数()f x 在分断点处连续 (7分).四、求函数()3211y x =-+的单调区间,极值点(7分). 五、求由抛物线2,2y x y x y x ===与直线所围成的图形的面积。
(8分).一、计算下列各题(本题满分36分,每小题6分)(1)13-;(2)2e ;(3)1sin 211cos x e x x -. (4)3211ln 33x x x c -+.(5). 321122,=(3)23t t dx =+=⎰原式 (6)(a )7500全概率公式,(b )37贝叶斯公式, 二、解答下列各题(本题满分42分,每小题7分).(1)232222.()y dx xydydz x y -=+(2)(a) 6B =.(b)1106640002424113305501515306620066661636B A B ----⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦(3)1222301139()2,(2)()44464P A xdx p y C =====⎰ (4)121211,.z z x f f f x x y y y∂∂'''=+=-∂∂ (5)222119=4xx x dx dy y =⎰⎰原式. (6)2132121,,,13y p p p x y x c x x y x c x c '''=-==+=++一阶线性,.三、(7分)0a =四、(7分)2222()6(1),0-1,1()6(1)(51)f x x x f x x x '''=-=--驻点,;0+∞(,)函数单调增,(-∞,0)函数单调减. (0)0,f =极小值 五、(7分)122017(2)(2)6S x x dx x x dx =-+-=⎰⎰面积。
全国大学生数学竞赛赛试题(1-9届)

一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(__ ,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域. 2.设)(x f 是连续函数,且满足⎰--=222d )(3)(x x f x x f , 则=)(x f ____________.3.曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 4.设函数)(x y y =由方程29ln )(yy f e xe=确定,其中f 具有二阶导数,且1≠'f ,则=22d d xy_____.二、(5分)求极限xenx x x x ne e e )(lim 20+++→Λ,其中n 是给定的正整数.三、(15分)设函数)(x f 连续,⎰=10d )()(t xt f x g ,且A xx f x =→)(lim,A 为常数,求)(x g '并讨论)(x g '在0=x 处的连续性.四、(15分)已知平面区域}0,0|),{(ππ≤≤≤≤=y x y x D ,L 为D 的正向边界,试证:(1)⎰⎰-=---Lx y L x y x ye y xe x ye y xe d d d d sin sin sin sin ; (2)2sin sin 25d d π⎰≥--L y y x ye y xe .五、(10分)已知x x e xe y 21+=,x x e xe y -+=2,x x x e e xe y --+=23是某二阶常系数线性非齐次微分方程的三个解,试求此微分方程.六、(10分)设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时,0≥y ,又已知该抛物线与x 轴及直线1=x 所围图形的面积为31.试确定c b a ,,,使此图形绕x 轴旋转一周而成的旋转体的体积最小.七、(15分)已知)(x u n 满足),2,1()()(1Λ=+='-n e x x u x u xn n n, 且n eu n =)1(, 求函数项级数∑∞=1)(n n x u 之和. 八、(10分)求-→1x 时, 与∑∞=02n n x 等价的无穷大量.一、(25分,每小题5分)(1)设22(1)(1)(1),n n x a a a =+++L 其中||1,a <求lim .n n x →∞(2)求21lim 1x x x e x -→∞⎛⎫+ ⎪⎝⎭。
第九届全国大学生数学竞赛决赛试题参考答案及评分标准

第九届全国大学生数学竞赛决赛试题参考答案及评分标准(非数学类, 2018 年 3 月)一、 填空题(满分 30 分,每小题 6 分):(1) 极限lim tan x - sin x =1.x →0 x ln(1+ s in 2 x )2(2) 设一平面过原点和点(6, -3, 2) ,且与平面4x - y + 2z = 8 垂直,则此平面方 程为 2x + 2 y - 3z = 0 .(3) 设函数 f (x , y ) 具有一阶连续偏导数,满足d f (x , y ) = ye y d x + x (1+ y )e y d y , 及 f (0, 0) = 0 ,则 f (x , y ) =xye y .d u (t ) 1 2e t - e +1 (4) 满足 d t = u (t ) + ⎰0 u (t )d t 及u (0) = 1的可微函数u (t ) =3 - e.(5) 设a , b , c , d 是互不相同的正实数,x , y , z , w 是实数,满足a x = bcd ,b y = cda , c z = dab , d w = abc ,则行列式= 0.二、(本题满分 11 分) 设函数 f (x ) 在区间(0,1) 内连续,且存在两两互异的点 x 1, x 2 , x 3, x 4 ∈(0,1) ,使得α =f (x 1) - f (x 2 ) < x 1 - x 2 f (x 3 ) - f (x 4 ) =β ,x 3 - x 4证明:对任意λ ∈(α , β ) ,存在互异的点 x , x ∈(0,1) ,使得λ = f (x 5 ) - f (x 6 ) . 5 6 x - x56【证】 不妨设 x 1 < x 2 , x 3 < x 4 ,考虑辅助函数F (t ) =f ((1- t )x 2 + tx 4 ) - f ((1- t )x 1 + tx 3 ),……… 4 分(1- t )(x 2 - x 1) + t (x 4 - x 3 )则 F (t ) 在闭区间[0, 1] 上连续,且 F (0) = α < λ < β = F (1) . 根据连续函数介值定理,存在t 0 ∈(0,1) ,使得 F (t 0 ) = λ .………………… 3 分-x 11 1 1 - y11 1 1 -z11 11 -wn n !1⎣ ⎦- ∑π令 x 5 = (1- t 0 )x 1 + t 0 x 3 , x 6 = (1- t 0 )x 2 + t 0 x 4 ,则 x 5, x 6 ∈(0,1) , x 5 < x 6 ,且λ = F (t ) = f (x 5 ) - f (x 6 ).………………… 4 分x - x5 6三、(本题满分 11 分)设函数 f (x ) 在区间[0,1] 上连续且⎰1f (x )d x ≠ 0 ,证明: 在区间[0,1] 上存在三个不同的点x 1,x 2,x 3 ,使得π1f (x )d x =⎡ 1x 1f (t ) d t + f (x ) arctan⎤8 ⎰⎢1 + x 2 ⎰01x 1 ⎥ x 3⎣ 1 = ⎡ 1x 2 f (t ) d t + f (x ) a rctan x ⎦ ⎤ (1 - x ). ⎢1 + x 2 ⎰0 2 2 ⎥ 3 ⎣ 2 ⎦【证】 令 F (x ) = 4 arctan x ⎰0 ,则F (0) = 0, F (1) = 1且函数F (x )在闭⎰f (t )d t区间[0,1] 上可导. 根据介值定理,存在点x 3 ∈(0,1) ,使F (x 3 ) = 1. 2………………… 5 分再分别在区间[0, x 3 ] 与[x 3,1]上利用拉格朗日中值定理,存在x 1 ∈(0,x 3) , 使得F (x 3) - F (0) = F '(x 1)(x 3 - 0) ,即π1⎡ 1 x 1⎤8 ⎰0 f (x )d x = ⎢1 + x 2 ⎰0 f (x ) d x + f (x 1) arctan x 1 ⎥ x 3 ; ……… 3 分⎣ 1 ⎦且存在x 2 ∈(x 3 ,1) ,使F (1) - F (x 3) = F '(x 2 )(1 - x 3) ,即π1f (x )d x =⎡ 1x 2f (x ) d x + f (x) arctan x ⎤(1 - x ) .8 ⎰⎢1 + x 2 ⎰022⎥ 3⎣2⎦………………… 3 分四、(本题满分 12 分) 求极限: lim ⎡n +1 (n +1)! - n n !⎤ .n →∞【解】 注意到n +1(n +1)! - n⎡ n +1 (n +1)! n !=n ⎢ ⎤ 1⎥ , 而 ………… 3 分 ⎢ nn ! ⎦⎥ nlim1 nk lnln x d x1lim= en →∞ n k =1n = e ⎰0= ,…………… 3 分nn !xf (t )d t1n n en n ! nn ! ∑∑ 【证】 (1) 二次型 H (x ) = ∑ x -⎝ ⎭n -1 ⎭n n +1- 1 ⋅1 ∑n +1lnk=(n +1)n[(n +1)!] (n !)n +1 = (n +1)n (n +1)= e(n +1)!n n +1k =1 n +1, …… 3 分利用等价无穷小替换e x -1 x (x → 0) ,得lim ⎡ n +1 (n +1)! ⎤ n - 1 n +1 k 1n →∞ nn ! 1⎥ = - lim n +1∑ln n +1 = -⎰0 ln x d x = 1 , ⎢⎣因此,所求极限为⎦⎥ n →∞⎤k =1⎡ n +1 (n +1)! ⎤ 1lim - = limlim n ⎢ -1⎥ = . …… 3 分n →∞⎦ n →∞ n n →∞ ⎢⎣n n ! ⎦⎥ enn -1五、(本题满分 12 分) 设 x = (x , x , , x )T ∈ R n ,定义 H (x ) =x 2 -xx,n ≥ 2 .1 2 ni =1ii i +1i =1(1)证明:对任一非零 x ∈ R n , H (x ) > 0 ;(2)求 H (x ) 满足条件 x n = 1的最小值.nn -1 2ii i 1的矩阵为i =1⎛i =11 ⎫2 ⎪ ⎪ - 1 1 - 1 ⎪ 2 2 ⎪ 1 ⎪A = -2 ⎪ , ……………3 分⎪ 1 ⎪ 1 - ⎪2 ⎪ - 11⎪⎪ ⎝ 2 ⎭因为 A 实对称,其任意k 阶顺序主子式∆k > 0 ,所以 A 正定,故结论成立. ………………… 3 分 (2) 对 A 作分块如下 A = ⎛ A n -1 α ⎫ ,其中α = (0, , 0, - 1)T ∈ R n -1 ,取可逆矩⎛ I - A -1 α ⎫α T 1 ⎪ ⎛ A n -1 2 0 ⎫ ⎛ A n -1 0 ⎫ 阵 P = n -1 n -1 ⎪ ,则 P T AP = ⎪ = ⎪ ,其中⎝ 01 ⎭ ⎝ 0 1- α T A -1α ⎝ 0 a ⎭ n +1(n +1)!nn !⎡n +1 (n +1)! ⎣⎢ 1 -n -1 ⎛ f ⎫ ∂x ∂y a = 1- α T A -1α .………………… 3 分记 x = P (x ,1)T ,其中 x = (x , x , , x )T ∈ R n -1 ,因为12n -1H (x ) = x T Ax = (x T ,1)P T (P T )-1 ⎛ An -10 ⎫ P -1P ⎛ x 0 ⎫ = x TA x + a ,0 0a ⎪ 1 ⎪ 0 n -1 0⎝⎭ ⎝ ⎭且 A 正定,所以 H (x ) = x T A x + a ≥ a ,当 x = P (x ,1)T = P (0,1)T 时, H (x ) = a .n -10 n -1 0因此, H (x ) 满足条件 x n = 1的最小值为a .………………… 3 分六、(本题满分 12 分) 设函数 f (x , y ) 在区域 D = {(x , y ) x 2 + y 2 ≤ a 2}上具有一阶连续偏导数,且满足 f (x , y )⎡ ∂ 2 = a 2,以及 max ⎢⎛ ∂f ⎫2⎤ +⎥ = a 2 ,其x 2 + y 2 =a 2中a > 0 . 证明: ⎰⎰ f (x , y )d x d y ≤ 4π a 4 .( x , y )∈D⎪ ⎢⎣⎝ ⎭ ⎪ ⎝ ⎭ ⎥⎦D3 【解】 在格林公式P (x , y )d x + Q (x , y )d y = ⎛ ∂Q - ∂P ⎫d x d y ⎰ ⎰⎰ ∂x ∂y ⎪C D ⎝⎭中,依次取 P = yf (x , y ) , Q = 0 和取 P = 0 , Q = xf (x , y ) ,分别可得⎰⎰ f (x , y )d x d y = - ⎰ yf (x , y )d x - ⎰⎰ y ∂fd x d y , D C D ∂y⎰⎰ f (x , y )d x d y = ⎰ xf (x , y )d y - ⎰⎰ x ∂fd x d y .两式相加,得D C D ∂x= a 2 -+- 1⎛ ∂f +∂f ⎫= + ⎰⎰ f (x , y )d x d y2⎰ y d x x d y 2 ⎰⎰ x∂x y ∂y ⎪d x d y I 1 I 2DCD ⎝ ⎭ ………………… 4 分a224对 I 1 再次利用格林公式,得 I 1 =2⎰ - y d x + x d y = a ⎰⎰ d x d y = π a , …… 2 分CD对 I 2 的被积函数利用柯西不等式,得I 2 ≤ 1⎰⎰ x∂f+ yd x d y ≤1 ⎰⎰d x d y∂f ∂y2 D ∂x2 Dn n =1≤ax d y = 1π a 4 ,………………… 4 分2 D3因此,有⎰⎰f (x , y )d x d y ≤ π a 4 + 1 π a 4= 4 π a 4 . …………… 2 分D七、(本题满分 12 分) 设0 < a 3 3ln 1< 1 ,n = 1, 2, ,且lim a n= q (有限或+ ∞ ).nn →∞ln n∞∞(1)证明:当q > 1 时级数∑ a n 收敛,当q < 1 时级数∑ a n 发散;n =1n =1(2)讨论q = 1 时级数∑ a n 的收敛性并阐述理由.n =1证: (1)若 q > 1 ,则∃ p ∈ R ,s.t. q > p > 1 .根据极限性质, ∃N ∈ Z + ,s.t.ln 1a n1 ∞1∞∀n > N ,有ln n> p ,即a n <n p,而 p > 1时∑n p 收敛,所以∑ a n 收敛.n =1n =1若q < 1 ,则 ………………… 3 分∃ p ∈ R ,s.t. q < p < 1. 根据极限性质,∃N ∈ Z + ,s.t. ∀n > N ,ln 1a n1∞1∞有 ln n < p ,即a n > n p ,而 p < 1时∑ n p 发散,所以∑ a n 发散. n =1 n =1………………… 3 分(2) 当q = 1 时,级数∑ an可能收敛,也可能发散.n =11∞例如: a n = 满足条件,但级数∑ a n 发散; ………………… 3 分n =11 ∞又如: a n =n ln 2 n满足条件,但级数∑ a n 收敛. ………………… 3 分∞∞。
高等数学竞赛模拟试题【精品】
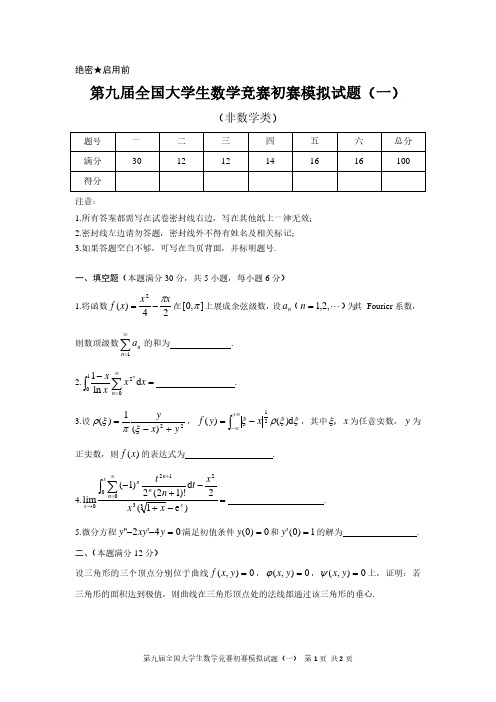
1 1 a + b f (b) = f (a) + (b − a ) f ' (a ) + f ' (b) + 4 f ' − (b − a ) 5 f (5) (ξ ). 6 2 2880
四、 (本题满分 14 分) 求经过三条平行直线 L1 : x = y = z , L2 : x − 1 = y = z + 1 , L3 : x = y + 1 = z − 1 的圆柱 面的方程.
(2)求
∑
k =1
1
∏ ( k + m)
m =0
2017
.
第九届全国大学生数学竞赛初赛模拟试题(二) 第 1 页 共 2 页
三、 (本题满分 14 分) 计算三重积分
∫∫∫ xyzdxdydz ,其中 Ω 位于第一象限,由下列曲面所围成:x
Ω
2
+ y 2 = mz ,
x 2 + y 2 = nz , xy = a 2 , xy = b 2 , y = αx , y = βx ,其中 0 < a < b , 0 < α < β ,
.
(−1) n 2.使级数 ∑ ln 1 + n p n=2
( p > 0) 条件收敛的 p 的取值范围为
.
3.设 f (u , v) 具有一阶连续偏导数,且满足 f (tu , tv ) = t 2 f (u , v) , f (1,2) = 0, f u (1,2) = 3 ,
n →∞
. .
2.设 f ( x) =
∫
1
0
ln x − t dt ,则 max f ( x) =
医用高等数学题库(供参考)

医用高等数学题库第一章函数与极限1.设,求,并作出函数的图形。
2.设,,求,并作出这两个函数的图形。
3.设,求。
4.试证下列函数在指定区间内的单调性:(1)(2)5.下列函数中哪些是是周期函数?对于周期函数,指出其周期:(1)(2)6.设。
试求下列复合函数,并指出x的取值范围。
7.已知对一切实数x均有,且f(x)为单调增函数,试证:8.计算下列极限:(1)(2)(3)9.(1)设,求常数a,b。
(2)已知,求a,b。
10.计算下列极限:(1)(2)(x为不等于零的常数)(3)(4)(5)(k为正整数)11.计算下列极限:(1)(2)(3)(4)(k为常数)(5)(6)(7)(8)(a>0,b>0,c>0)(9)(10)(11)(12)(13)(14)(15)(16)(17)(18)(19)(20)(21)(22)(23)(24)12.当时,无穷小1-x和(1)(2)是否同阶?是否等价?13.证明:当时,有(1)(2)14.利用等价无穷小的性质求下列极限:(1)(n,m为正整数)(2)15.试确定常数a,使下列各函数的极限存在:(1)(2)16.讨论下列函数的连续性:(1)的连续性(2)在x=0处的连续性17.设函数在[0,2a]上连续,,试证方程在[0,a]内至少存在一个实根。
18.设函数在开区间(a,b)内连续,,试证:在开区间(a,b)内至少有一点c,使得(其中)。
第二章导数与微分1.讨论下列函数在x=0处的连续性与可导性:(1)(2)2.设存在,求3.设,问a,b为何值时,在x=0处可导?4.已知,求及,并问:是否存在?5.证明:双曲线上任一点处的切线与两坐标轴构成的三角形的面积都等于。
6.问当系数a为何值时,抛物线与曲线相切?7.求下列各函数的导数:(1)(2)(3)(4)(5)(6)(7)(8)(a>0)(9)(10)(11)(12)(13)(14)(15)(16)(17)(18)(19)(20)(21)(22)(23)(24)8.求曲线在点处的切线方程和法线方程。
中专医学数学考试题及答案

中专医学数学考试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是函数y=f(x)的奇函数?A. f(-x) = f(x)B. f(-x) = -f(x)C. f(-x) = xD. f(-x) = -x答案:B2. 求下列哪个函数的导数是f'(x) = 3x^2?A. f(x) = x^3B. f(x) = x^3 + 1C. f(x) = x^3 - 1D. f(x) = 3x^3答案:D3. 以下哪个选项是复数z = 3 + 4i的共轭复数?A. 3 - 4iB. -3 + 4iC. -3 - 4iD. 3 + 4i答案:A4. 已知等差数列的前三项分别为2,5,8,那么第四项是多少?A. 11B. 12C. 13D. 14答案:A5. 圆的标准方程为(x-2)^2 + (y-3)^2 = 9,圆心坐标为?A. (2, 3)B. (-2, 3)C. (2, -3)D. (-2, -3)答案:A二、填空题(每题2分,共10分)1. 函数y = 2x + 1在x = 2处的值为______。
答案:52. 等比数列的第二项为3,第三项为6,公比为______。
答案:23. 已知圆的半径为5,圆心到直线的距离为3,则直线与圆的位置关系是______。
答案:相切4. 函数f(x) = x^2 - 4x + 4的最小值为______。
答案:05. 已知向量a = (3, 4),向量b = (-4, 3),则向量a与向量b的点积为______。
答案:-7三、计算题(每题5分,共15分)1. 计算定积分∫(0到1) (3x^2 - 2x + 1) dx。
答案:(1/3x^3 - x^2 + x) | 0到1 = 4/3 - 1 + 1 = 1/32. 求函数f(x) = x^3 - 6x^2 + 9x + 15在x = 2处的导数值。
答案:f'(x) = 3x^2 - 12x + 9,f'(2) = 3(4) - 12(2) + 9 = 12 - 24 + 9 = -33. 已知函数f(x) = sin(x),求f'(x)。
医学院知识竞赛题目

医学院知识竞赛题目
题目一
1.什么是心肺复苏术?请详细描述其步骤和操作方法。
题目二
2.人体免疫系统是如何工作的?请简要介绍其主要组成部分及作用。
题目三
3.请解释人类血液中的不同类型血细胞的功能及特点。
题目四
4.什么是传染病?请列举一些常见的传染病及其传播途径。
题目五
5.请介绍心脑血管疾病的常见症状、治疗方法及预防措施。
题目六
6.什么是急救知识?请解释在日常生活中常见的急救措施。
题目七
7.请解释药物滥用的危害,并列举一些常见的药物滥用情况。
题目八
8.人体中的主要器官有哪些?请简要介绍它们的结构和功能。
题目九
9.什么是医学伦理?请讨论医生在临床实践中应该遵循的道德准则。
题目十
10.请介绍医学检查的常见方法和意义,以及如何正确解读检查报告。
以上是医学院知识竞赛题目,希望能够帮助大家更深入地了解医学知识,为未来的医学实践打下坚实的基础。
医药高等数学试题及答案

医药高等数学试题及答案一、选择题(每题2分,共10分)1. 函数 \( f(x) = x^2 - 4x + 3 \) 的零点是:A. 1B. 2C. 3D. 42. 曲线 \( y = e^x \) 在 \( x = 0 \) 处的切线斜率是:A. 0B. 1C. \( e \)D. \( e^2 \)3. 以下哪个函数是奇函数:A. \( f(x) = x^2 \)B. \( f(x) = x^3 \)C. \( f(x) = x^4 \)D. \( f(x) = \sin(x) \)4. 以下哪个积分是发散的:A. \( \int_0^1 \frac{1}{x} dx \)B. \( \int_1^\infty \frac{1}{x^2} dx \)C. \( \int_0^\infty e^{-x} dx \)D. \( \int_0^\infty \frac{1}{x} dx \)5. 矩阵 \( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \) 的行列式是:A. 5B. -2C. 7D. -5二、填空题(每题3分,共15分)1. 函数 \( f(x) = \ln(x) \) 的导数是 ________。
2. 极限 \( \lim_{x \to 0} \frac{\sin(x)}{x} \) 的值是________。
3. 函数 \( f(x) = x^3 - 3x^2 + 2 \) 的极值点是 ________。
4. 函数 \( y = \ln(x) \) 的反函数是 ________。
5. 矩阵 \( A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \) 的逆矩阵是 ________。
三、解答题(每题10分,共30分)1. 求函数 \( f(x) = x^3 - 6x^2 + 9x + 1 \) 的极值点和极值。
第九届高数竞赛(医学类)试题

第九届高数竞赛(医学类)试题二、单项选择题(每题3分,共15分)得分评阅人1、设函数f(某)在[1,2]上具有二阶导数,且f(1)f(2)0,F(某)(某1)2f(某),则F(2)(某)在开区间(1,2)内()(A)没有零点;(B)至少有一个零点;(C)恰好有两个零点;2、设lim某1(D)有且仅有一个零点.f(某)f(a)1,则(某a)2f(某)在某a处().(B)导数不存在;(D)取得极大值.(A)可导且f(1)(a)0;(C)取得极小值;3、设函数f(某)与g(某)在开区间(a,b)内可导,考虑如下两个命题,''''(1)若f(某)g(某),则f(某)g(某);(2)若f(某)g(某),则f(某)g(某).则()(A)两个命题均正确;(C)命题(1)正确,命题(2)不正确;(B)两个命题均不正确;(D)命题(2)正确,命题(1)不正确.)4、设函数(A)f(某)连续,则下列函数中必为偶函数的是(某[f(t)]2dt;f(t2)dt;(B)某t[f(t)f(t)]dt;某某(C)(D)t[f(t)f(t)]dt.5、考虑二元函数f(某,y)在点(某0,y0)处的下面四条性质:a.连续;b.可微;f(某,y)f(某,y)f(某,y)f(某,y)|(某0,y0)存在;d.|(某0,y0)与c.与yy连续;某某若用“PQ”表示可由性质P推出性质Q,则有((A)bca;(B)dba;)(D)dcb.(C)bda;第2页共7页得分评阅人三、(本题满分6分)求常数a,b,使1a某1,某0,某f(某)a某b,某1,1arctan,某1某1在所定义的区间上连续。
得分评阅人四、(本题满分6分)对t的不同取值,讨论函数f(某)t,上是否有最大值或最小值,若存在最大值或最小值,求出相应的最大值点和最大值或最小值点和最小值。
12某2某2在区间第3页共7页得分评阅人3某2lim五、(本题满分7分)求极限某3某12某1.得分评阅人某e某d某.六、(本题满分7分)计算(某1)2第4页共7页得分评阅人七、(本题满分8分)设某产品的边际成本为边际收入dC(某)某4(万元/百台),d某4dR(某)8某(万元/百台),求:d某(1)产量由1百台增到5百台的总成本与总收入的增量;(2)产量为多少时,总利润最大?得分评阅人八、(本题满分7分)设函数f(某,y)在点(1,)处可微,且f(1,1)1,d3ff|(1,1)2,|(1,1)3,(某)f(某,f(某,某)),求(某)|某1.某yd某第5页共7页得分评阅人九、(本题满分7分)z设f(u,v)有一阶连续偏导数,u某2y2,vco(某y),某rco,yrin,证明:z1zzzcoin2某yin(某,y).rruv得分评阅人十、(本题满分7分)设函数f(某)连续,求d某220tf(某t)dt.d某第6页共7页得分评阅人十一、(本题满分8分)设f(某)在[0,)上可导,f(0)0,其反函数为g(某),若某f(某)某g(t某)dt某2ln(1某),求f(某).得分评阅人十二、(本题满分7分)计算定积分22(|某|某)e|某|d某.第7页共7页。
医用高等数学资料 医科大学 测试题(答案)

《高 等 数 学》测试题(A )不定项选择题:将你认为正确的答案填入括号中,可单选,多选,每题4分,共24题。
1. 当0x →时,下列变量中( B )是无穷小量。
xx sin .A x e 1.B - x x x .C 2- x )x 1ln(.D +2. 22x 2sin lim 2sin x x xx x →∞+-=+( A ). A 12 B 2 C 0 D 不存在3.半径为R 的金属圆片,加热后伸长了R ∆,则面积S 的微分dS 是( B )A 、RdR πB 、RdR π2C 、dR πD 、dR π2注:dS=RdR π2;4.cos x xdx ππ-=⎰( C )A 、 1B 、 2C 、 0D 、 4注:偶倍奇零10121111105.12,().(12);.2(12);.2(12);.(2).x t f x dx ABCD A f t dt B f t dt C f t dt D f t dt --=-≠-----⎰⎰⎰⎰⎰作变量替换 则().6. 设)(x f 在区间[]b a ,上连续,⎰≤≤=xa b x a dt t f x F )()()(,则)(x F 是)(x f 的( B). A 、不定积分 B 、一个原函数C 、全体原函数D 、在[]b a ,上的定积分7.若()(),f x x φ''=则下列各式 AD 不成立。
()()0A f x x φ-= ()()B f x x C φ-=()()C d f x d x φ=⎰⎰ ()()ddD f x dx x dx dx dx φ=⎰⎰注:()()()().()()()()f x x f x x C d f x f x C d x x Cφφφφ''=⇒-==+=+⎰⎰8.设e -x 是f (x )的一个原函数,则⎰dx x xf )(=( B)。
A. C x e x +--)(1B. C x e x ++-)(1C. C x e x +--)(1D. C x e x ++--)(1注:()x x x x x xf x dx xde xe e dx xe e C -----==-=++⎰⎰⎰9.设()()⎪⎩⎪⎨⎧=≠+=0,0,11x x x x f x α,要使()x f 在0=x 处连续,则=α( C )A .1B .0C .eD .e 110.函数1+=x y 在0=x 处满足条件( A )A .连续但不可导B .可导但不连续C .不连续也不可导D .既连续已可导注:0100()1lim 11(0)010()1010()101,0()(0)(0)lim lim 01,0x x x y f x x x f x x f x x x x f x x x x f x f f x x x →+-→→==+⎡+⎤==⇒⎣⎦+≥⎧=⎨-<⎩>⎧'=⎨-<⎩⎧→-'===⎨--→⎩在点连续。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
评阅人
四、(本题满分6分)对 的不同取值,讨论函数 在区间 上是否有最大值或最小值,若存在最大值或最小值,求出相应的最大值点和最大值或最小值点和最小值。
得分
评阅人
五、(本题满分7分)求极限 .
得分
评阅人
六、(本题满分7分)计算
得分
评阅人
七、(本题满分8分)设某产品的边际成本为 (万元/百台),边际收入 (万元/百台),求:
南昌大学第九届高等数学竞赛(医学类)试题
序号:姓名:学号:学院:
班级:第考场考试日期:2012年10月14日
题号
一
二
三
四
五
六
七
八
九
十
十一十二总分累人签名题分15
15
6
6
7
7
8
7
7
7
8
7
100
得分
注:本卷共七页,十二个大题,考试时间为8:30——11:30.
一、填空题(每空3分,共15分)
得分
评阅人
2、设 ,则 在 处().
(A)可导且 ;(B)导数不存在;
(C)取得极小值;(D)取得极大值.
3、设函数 与 在开区间 内可导,考虑如下两个命题,
(1)若 ,则 ;(2)若 ,则 .
则( )
(A)两个命题均正确;(B)两个命题均不正确;
(C)命题(1)正确,命题(2)不正确;(D)命题(2)正确,命题(1)不正确.
得分
评阅人
十二、(本题满分7分)计算定积分 .
(1)产量由1百台增到5百台的总成本与总收入的增量;
(2)产量为多少时,总利润最大?
得分
评阅人
八、(本题满分7分)设函数 在点 处可微,且
求
得分
评阅人
九、(本题满分7分)设 有一阶连续偏导数,
, 证明:
得分
评阅人
十、(本题满分7分)设函数 连续,求 .
得分
评阅人
十一、(本题满分8分)设 在 上可导, ,其反函数为 ,若 ,求 .
1、 ;
2、设函数 为可导函数,则函数 的导数为;
3、 ;
4、设 ,则 _____________;
5、设 则
.
二、单项选择题(每题3分,共15分)
得分
评阅人
1、设函数 在 上具有二阶导数,且 ,则 在开区间 内()
(A)没有零点;(B)至少有一个零点;
(C)恰好有两个零点;(D)有且仅有一个零点.
4、设函数 连续,则下列函数中必为偶函数的是()
(A) ;(B) ;
(C) ;(D) .
5、考虑二元函数 在点 处的下面四条性质:
连续; 可微;
与 存在; 与 连续;
若用“ ”表示可由性质 推出性质 ,则有()
(A) ;(B) ;(C) ;(D) .
得分
评阅人
三、(本题满分6分)求常数 ,使
在所定义的区间上连续。
