江西省2019年中考数学总复习第四单元三角形第18课时相似三角形(高效集训本)课件
第四单元三角形(新)中考数学第一轮中考考点复习公开课PPT2
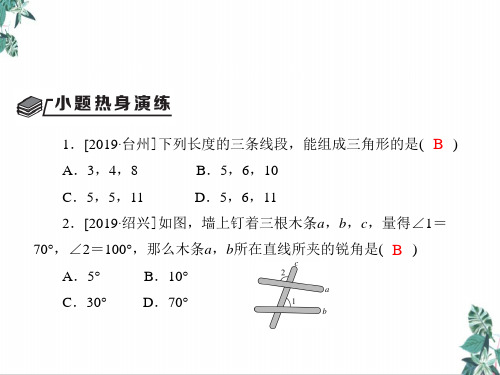
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
命题的真假:正确的命题是_真__命__题___,错误的命题是 _假___命__题__.判断一个命题为假命题时,只需举出一个反例;要 论证一个命题是真命题时,则需要加以推理和证明.
AC∥EF,∠C=∠F.求证:BC=DF.
证明:∵AD=BE, ∴AD-BD=BE-BD,∴AB=ED.
∵AC∥EF,∴∠A=∠E.
∠C=∠F, 在△ABC 和△EDF 中, ∠A=∠E,
AB=ED, ∴△ABC≌△EDF(AAS),∴BC=DF.
1.三角形的有关概念及分类
定 义:由不在同一条直线上的三条线段首尾顺次相接所
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
特 征:任意一个三角形都有三条角平分线,这三条角 平分线交于三角形内一点,这一点叫做三角形的_内__心___.
规 律:(1)三角形两条角平分线的交点一定在第三条角 平分线上.
(不添加其他字母及辅助线),你添加的条件是_A_C__=__B_C__.
【解析】添加AC=BC.∵△ABC的两条高线AD,BE, ∴∠ADC=∠BEC=90°.在△ ADC和△ BEC中,
∠ ∠AC=DC∠=C∠,BEC,∴△ADC≌△BEC(AAS). AC=BC,
5.[2019·山西]如图,已知点B,D在线段AE上,AD=BE,
逆命题:若命题2与命题1的题设、结论正好相反,则这样 的两个命题叫做互逆命题.如果把其中的一个命题叫做原命 题,那么另一个命题叫做它的逆命题.
初三《相似三角形》知识点总结

相似三角形知识点总结知识点1、三角对应相等,三边对应成比例的三角形叫相似三角形。
如△ABC 与△A /B /C /相似,记作: △ABC ∽△A /B /C /。
相似三角形的比叫相似比相似三角形的定义既是相似三角形的性质,也是三角形相似的判定方法。
注意:(1)相似比是有顺序的。
(2)对应性,两个三角形相似时,通常把对应顶点写在对应位置,这样写比较容易找到相似三角形的对应角和对应边。
(3)顺序性:相似三角形的相似比是有顺序的,若△ABC ∽△A /B /C /,相似比为k ,则△A /B /C /与△ABC 的相似比是1k知识点2、相似三角形与全等三角形的关系(1)两个全等的三角形是相似比为1的相似三角形。
(2)两个等边三角形一定相似,两个等腰三角形不一定相似。
(3)二者的区别在于全等要对应边相等,而相似要求对应边成比例。
知识点3、平行线分线段成比例定理1. 比例线段的有关概念:在比例式::中,、叫外项,、叫内项,、叫前项,a bc da b c d a d b c a c ()b 、d 叫后项,d 叫第四比例项,如果b=c ,那么b 叫做a 、d 的比例中项。
把线段AB 分成两条线段AC 和BC ,使AC 2=AB ·BC ,叫做把线段AB 黄金分割,C 叫做线段AB 的黄金分割点。
2. 比例性质:①基本性质:a bc dadbc ②合比性质:±±a b c d a b b c d d③等比性质:……≠……a bc dm nb dn a c m bdna b()03. 平行线分线段成比例定理(1)平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.已知l1∥l2∥l3,A D l1B E l2CF l3可得EF BC DEAB DFEF ACBC DFEF ABBC DFDE ACAB EFDE BCAB或或或或等.(2)推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. AD EBC由DE ∥BC 可得:AC AEABAD EAEC ADBD ECAE DBAD 或或.此推论较原定理应用更加广泛,条件是平行.(3)推论的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即:利用比例式证平行线.(4)定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例. 知识点4:相似三角形的性质①相似三角形的对应角相等②相似三角形的对应边成比例③相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比④相似三角形周长的比等于相似比⑤相似三角形面积的比等于相似比的平方知识点5:相似三角形的判定:①两角对应相等,两个三角形相似②两边对应成比例且夹角相等,两三角形相似③三边对应成比例,两三角形相似④如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角形相似⑤平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似⑥直角三角形被斜边上的高分成的两个直角三角形和原三角形相似如果两个三角形的两角分别于另一个三角形的两角对应相等,那么这两个三角形相似。
人教版中考数学复习《第18讲:相似三角形》课件

相似三角形
考点梳理自清
考题体验感悟
考法互动研析
考点一
考点二
考点三
考点一比例线段及比例的性质 1.定义 在四条线段中,如果其中两条线段的比等于另外两条线段的比, 那么这四条线段叫作成比例线段,简称比例线段. 2.比例的基本性质
(1)如果 = ,则 ad=bc
������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������
������
������
;
d ������ c c±d d
(2)如果 = ,ac ≠0,那么 = ; (3)如果 = ,那么
������ ± ������ ������ ������ ������
=
;
(4)如果 = =…= (b+d+…+n ≠0),那么
������ +������ +…+������ ������ +������ +…+������
∴������������ = ������������ ,
������������ 4
������������
∵AD 是中线,∴CD=2BC=4, ∴ 8 = ������������ ,解得 AC=4 2,故选 B.
9
1
考点梳理自清
考题体验感悟
考法互动研析
命题点
2.(2013· 安徽,13,5分)如图,P为平行四边形ABCD边AD上一点,E,F分 别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2,若 S=2,则S1+S2=8 .
九年级数学相似三角形知识点及习题(最新整理)

EF+DF)的相似比为( ).下列说法中:①所有的等腰三角形都相似;②所有的正三角形都相似;③所有的正方形都相似;④所________cm.10.(湖南常德)如图X6-4-4,已知四边形ABCD是平行四边形.(1)求证:△MEF∽△MBA;(2)若AF,BE分别是∠DAB,∠CBA的平分线,求证:DF=EC.11.(广西来宾)如图X6-4-5,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC,AB交于点D,E.(1)用圆规和直尺在图中作出AB的垂直平分线DE,并连接BD;(2)证明:△ABC∽△BDC.12.已知如图X6-4-6,在矩形ABCD中,E是BC上一点,F是BC的延长线上一点,且BE=CF,BD 与AE相交于点G.求证:(1)△ABE≌△DCF;(2)CF·AE=BF·GE.B级 中等题13.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3,4和x,那么x的值( )A.只有1个 B.可以有2个C.有2个以上但有限D.有无数个14.如图X6-4-7,已知在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.15.如图X6-4-8,在△ABC中,AB=AC,BD⊥AC于点D,试证明:BC2=2CD·AC.的面积最大?并求出这个最大值.图“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
相似三角形中考复习(知识点+题型分类练习)

相似三角形知识概述1. 平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。
2. 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例。
3. 相似三角形的定义对应边成比例、对应角相等的两个三角形叫做相似三角形.4. 相似三角形的基本性质①相似三角形的对应边成比例、对应角相等.②相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
③相似三角形的周长比等于相似比④面积比等于相似比的平方温馨提示:①全等三角形一定是相似三角形,其相似比k=1.所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等,而相似要求对应边成比例.②相似比具有顺序性. 例如△ AB(^A A B' C'的对应边的比,即相似比为k,则△ A B' C ABC的相似比元,当且仅当它们全等时,才有k=k' =1.③相似比是一个重要概念,后继学习时出现的频率较高,其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出.5. 相似三角形的判定定理①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;②三边对应成比例的两个三角形相似;③两角对应相等的两个三角形相似;④两边对应成比例且夹角相等的两个三角形相似。
温馨提示:(1) 判定三角形相似的几条思路:①条件中若有平行,可采用判定定理1;②条件中若有一对角相等(包括隐含的公共角或对顶角),可再找一对角相等或找夹边对应成比例;③条件中若有两边对应成比例,可找夹角相等;但是,在选择利用判定定理2时,一对对应角相等必—须是成比例两边的夹角对应相等.④条件中若有等腰关系,可找顶角相等或底角相等,也可找腰和底对应成比例。
(2) 在综合题中,注意相似知识的灵活运用,并熟练掌握线段代换、等比代换、等量代换技巧的应用,培养综合运用知识的能力。
(3) 运用相似的知识解决一些实际问题,要能够在理解题意的基础上,把它转化为纯数学知识的问题,要注意培养当数学建模的思想。
专题4.4 相似三角形中考数学第一轮总复习课件

= 2,
h2 BC
A
h1
P h2 F
h3
E
C
中考数学第一轮总复习
专题4.4 相似三角形
知识梳理
典例精讲
考点聚焦
查漏补缺
提升能力
01 比 例 线 段
02 相 似 三 角 形 的 判 定
03 相 似 三 角 形 的 性 质
04 相 似 三 角 形 的 应 用
精讲精练
考点聚焦
比例线段
知识点一
线段的比 在同一单位长度下,两条线段长度的比叫做两条线段的比。
4
9
或
部分,连接BE,AC相交于F,则S△AEF:S△CBF25
=_______.
25
B(1,0)
x
强化训练
相似三角形
提升能力
3.如图,在△ABC中,点G为△ABC的重心,过点G作DE∥BC,分别交AB,AC于
4:5
点D,E,则△ADE与四边形DBCE的面积比为_____.
4.如图,在Rt△ABC中,∠C=90º,点D,E,F,分别在边AC,AB,BC上,且四边形
A
2
1
D
B.AB:AD=AC:AE
D.AB:AD=BC:DE
B
E
C
01
比例线段
02
相似三角形的判定
考点聚焦
03
相似三角形的性质
04
相似三角形的应用
精讲精练
考点聚焦
定义
相似三角形的性质
知识点三
相等
成比例
如果两个三角形的各角对应____各边对应______,那么这两个三角形
相似.
相等
ቤተ መጻሕፍቲ ባይዱ成比例
2019年新课标人教版初中数学中考复习《相似三角形》精品课件.ppt

M
B
E
C
如图,平行四边形ABCD中,E是BC上一点, BE:EC=1:2,AE与BD相交于F,则BF:FD= 1:3 S△ABF:S△FBE= 3:1 .
A D
,
F
B E
C
1、已知D,E分别是△ABC的边AB,AC上的点,
且AD=2,AC=3,AE=2.4,AB=3.6,
则S△ADE :S 四边形BCED=
S 1 时,求 3 S
BPQ ABC
的值
(3)以A、P、Q为顶点的三角形能否与以C、Q、B为顶 点的三角形相似?若能,求出AP的长,若不能,请说明 理由
A.
1
C
D
A
B
2 5
5
B.
4 5
5
2 3 C. 5
4 D. 5
3
(第2题图)
3、(2008临沂)如图,□ABCD中,E是CD的延 长线上一点,BE与AD交于点F,DE=
1
CD。
2
⑴求证:△ABF∽△CEB; ⑵若△DEF的面积为2,求□ABCD的面积。
E A F D
21题图 B 第3
C
解:⑴证明:∵四边形ABCD是平行四边形, ∴∠A=∠C,AB∥CD,∴∠ABF=∠CEB, ∴△ABF∽△CEB. ……………………2分 ⑵∵四边形ABCD是平行四边形, ∴AD∥BC,ABCD, ∴△DEF∽△CEB,△DEF∽△ABF,……………3分 A
(2)设BD=x,AE=y,求y关于x的函数关系式;
A E B D C
1.(2006临沂)如图,在矩形ABCD中,E在 AD上,EF⊥BE,交CD于F,连接BF,则图中与 △ABE一定相似的三角形是 ( B ) A.△EFB B.△DEF C.△CFB D.△EFB和△DEF 2、(20ቤተ መጻሕፍቲ ባይዱ7临沂)如图,在△ABC中,AB=2, AC=1,以AB为直径的圆与AC相切,与边BC交 于点D,则AD的长为( A )。
【中考数学夺分大模块复习权威课件】-第4模块《几何基础、三角形与全等、相似及解直角三角形》名师大串讲

第14讲 三角形与全等三角形 第15讲 等腰三角形 第16讲 直角三角形 第17讲 图形的相似 第18讲 锐角三角函数
第13讲
几何初步、相交线与 平行线
┃考点自主梳理与热身反馈 ┃
考点1 点和线
1.下列说法错误的是 ( D ) A.平面内过一点有且只有一条直线与已知直线垂直 B.两点之间的所有连线中,线段最短 C.经过两点有且只有一条直线 D.经过一点,有且只有一条直线
第13讲┃ 几何初步、相交线与平行线
考点2
角
1.点 P 在∠MAN 内部,现在四个等式:①∠PAM=∠ NAP; 1 1 ②∠PAN= ∠ MAN;③∠MAP= ∠MAN;④∠MAN= 2 2 2∠ MAP,其中能表示 AP 是角平分线的等式有 ( D ) A. 1 个 B. 2 个 C. 3 个 D.4 个
第13讲┃ 几何初步、相交线与平行线
变式题 如图 13- 7,直线 AB, CD 相交于点 O, OE 平分∠ AOD,若∠ BOD= 100°,则∠ AOE= ________ 40° .
第13讲┃ 几何初步、相交线与平行线
考点3 相交线与对顶角 1. 如图 13- 1,已知直线 AB,CD 相交于点 O,OA 平分 ∠ EOC,∠ EOC= 110°,则∠BOD 的度数是 ( D ) A.25° B.35° C. 45° D. 55°
第13讲┃ 几何初步、相交线与平行线
2.如图 13- 2,直线 AB,CD 相交于点 O,OE⊥ AB, 48° 垂足为 O,如果∠ EOD= 42°,则∠ AOC= _____.
第13讲┃ 几何初步、相交线与平行线
50 2.若∠ α= 40°,则∠ α 的余角是________ °,∠α 的补 140 角是 ________ °.
2019中考初三数学相似三角形知识点

2019中考初三数学相似三角形知识点
各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢
初三数学相似三角形知识点
1.相似三角形的定义
对应角相等、对应边成比例的两个三角形叫做相似三角形。
如果三边分别对应A,B,C和a,b,c:那么:A/a=B/b=C/c
即三边边长对应比例相同。
2.相似三角形判定
对应角相等,对应边成比例的两个三角形叫做相似三角形。
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似
判定定理2:如果两个三角形的两组对应边成比例,并且对应的夹角相等,那么这两个三角形相似
判定定理3:如果两个三角形的三组
对应边成比例,那么这两个三角形相似判定定理4:两三角形三边对应平行,则两三角形相似。
判定定理5:两个直角三角形中,斜边与直角边对应成比例,那么两三角形相似。
其他判定:由角度比转化为线段比:h1/h2=Sabc
3.相似三角形性质
相似三角形的对应角相等。
相似三角形的对应边成比例。
相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
相似三角形的周长比等于相似比。
相似三角形的面积比等于相似比的平方。
各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢。
中考总复习:相似三角形

学生: 科目: 数 学 教师: 刘美玲知识点1 有关相似形的概念(1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多 边形.相似多边形对应边长度的比叫做相似比(相似系数).知识点2 比例线段的相关概念(1)如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=.注:在求线段比时,线段单位要统一。
(2)在四条线段dc b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注:①比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:a d c b =.②()a ca b c d b d==在比例式::中,a 、d 叫比例外项,b 、c叫比例内项, a 、c 叫比例前项,b 、d 叫比例后项,d 叫第四比例项,如果b=c ,即 a b b d=::那么b 叫做a 、d 的比例中项, 此时有2b ad =。
(3)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =⋅,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB .即512AC BC AB AC -== 简记为:512-长短==全长注:黄金三角形:顶角是360的等腰三角形。
黄金矩形:宽与长的比等于黄金数的矩形知识点3 比例的性质(注意性质立的条件:分母不能为0) (1) 基本性质:①bc ad d c b a =⇔=::;②2::a b b c b a c =⇔=⋅.注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除 了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d cb d b ad bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项课 题中考总复习 : 相似三角形教学内容(3)反比性质(把比的前项、后项交换): a c b d b d a c=⇔=.(4)合、分比性质:a c abcd b d b d±±=⇔=.注:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=dc d c b a b a ccd a a b d c b a 等等.(5)等比性质:如果)0(≠++++====n f d b nmf e d c b a ,那么b a n f d b m e c a =++++++++ .注:①此性质的证明运用了“设k 法”(即引入新的参数k )这样可以减少未知数的个数,这种方法是有关比例计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零.③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:ba f db ec a f ed c b a fe d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b .知识点4 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.由DE ∥BC 可得:ACAEAB AD EA EC AD BD EC AE DB AD ===或或注:①重要结论:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边......与原三角形三.....边.对应成比例. ②三角形中平行线分线段成比例定理的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即:利用比例式证平行线.③平行线的应用:在证明有关比例线段时,辅助线往往做平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.2.平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例.已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或等.FE D CB A EAB C D注:平行线分线段成比例定理的推论:平行线等分线段定理:两条直线被三条平行线所截,如果在其中一条上截得的线段相等,那么在另一条上截得的线段也相等。
江西省2019届中考数学总复习第1部分基础过关第四单元三角形课时18图形的相似作业

课时18 图形的相似(时间:30分钟 分值:60分)评分标准:选择填空每题3分.基础过关1.已知a b =513,则a -ba +b的值是( )A .-23B .-32C .-94D .-492.黄金分割在实际生活中有广泛的应用,比如在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高为2 m ,设它的下部的高度应设计为x m ,则x 满足的关系式为( )A .(2-x )∶x =x ∶2B .x ∶(2-x )=(2-x )∶2C .(1-x )∶x =x ∶1D .(1-x )∶x =1∶x3.(2017枣庄)如图1,在△ABC 中,∠A =78°,AB =4,AC =6,将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )图14.(2017张家界)如图2,D ,E 分别是△ABC 的边AB ,AC 上的中点,如果△ADE 的周长是6,则△ABC 的周长是( )图2A .6B .12C .18D .245.如图3,身高为1.5米的小星想测量一棵大树的高度,她沿着树影BA 由B 向A 走去.当走到C 点时,她的影子顶端正好与树的影子顶端重合,测得BC =3米,CA =1米,则树的高度为( )图3A.3米B.4米C.4.5米D.6米6.(2017河北)若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )A.增加了10% B.减少了10%C.增加了(1+10%) D.没有改变7.如图4,△ABC中,DE∥FG∥BC,AD∶DF∶FB=2∶3∶4,若EG=4,则AC=__________.图48.如图5,在△ABC中,点D,E分别为边AC,AB上的点,且∠ADE=∠B,AE=3,BE =4,则AD·AC=__________.图59.如图6,将一副直角三角板(含45°角的直角三角板ABC及含30°角的直角三角板DCB)按图示方式叠放,斜边交点为O,则△AOB与△COD的面积之比等于__________.图610.如图7,已知点B,E,C,F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是__________.(只需写一个条件,不添加辅助线和字母)图711.如图8,在大小为4×4的正方形网格中,所画三角形相似的是__________.图812.一天晚上,某人在路灯下距路灯竿6米远时,发现他在地面上的影子是3米长,则当他离路灯竿10米远时,他的影子长是__________米.13.(8分)(2017杭州)如图9,在锐角三角形ABC 中,点D ,E 分别在边AC ,AB 上,AG ⊥BC 于点G ,AF ⊥DE 于点F ,∠EAF =∠GAC .图9(1)求证:△ADE ∽△ABC ; (2)若AD =3,AB =5,求AF AG的值.拓展提升1.如图10,△ABC 中,AC =6,AB =4,点D 与点A 在直线BC 的同侧,且∠ACD =∠ABC ,CD =2,点E 是线段BC 延长线上的动点,当△DCE 和△ABC 相似时,线段CE 的长为( )图10A .3B .43C .3或43D .4或342.如图11,已知两点A (6,3),B (6,0),以原点O 为位似中心,相似比为1∶3把线段AB 缩小,则点A 的对应点坐标是__________.图113.(10分)如图12,一条东西走向的笔直公路,点A,B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路南侧直线PQ上行走,当他到达点P 时,树A恰好挡住电视塔,即点P,A,C在一条直线上,当他继续走180米到达点Q时,以同样方法观察电视塔,树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧所在直线PQ的距离.图12课时18 图形的相似基础过关 1.D 2.A 3.C 4.B 5.D 6.D 7.12 8.21 9.1∶310.∠B=∠DEC(答案不唯一) 11.①③12.513.(1)证明:∵AG⊥BC,AF⊥DE,∴∠AFE=∠AGC=90°.∵∠EAF=∠GAC,∴∠AED=∠ACB.∵∠EAD=∠BAC,∴△ADE∽△ABC.(2)解:由(1)可知,△ADE∽△ABC,且AG⊥BC,AF⊥DE,∴AFAG=ADAB=35.拓展提升 1.C 2.(2,1)或(-2,-1)3.解:如图1所示,作CE⊥PQ于点E,交AB于点D,设CD=x,则CE=x+60,图1 ∵AB∥PQ,∴△ABC∽△PQC.∴CDAB=CEPQ,即x150=x+60180,解得x=300.∴x+60=360.答:电视塔C到公路南侧所在直线PQ的距离是360米.。
通用2019中考数学总复习第四章三角形第5节相似三角形课件

◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
◆教材回顾 ◆突破考点(考点一
考点二 )
