初二数学八年级各种经典难题例题非常经典
(完整版)八年级数学经典难题

经典难题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥C O.求证:CD=GF.(初二)2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15度求证:△PBC是正三角形.(初二)3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA 1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典难题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二)3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初二)4、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离等于AB的一半.(初二)经典难题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二)2、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.(初二)3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.求证:PA=PF.(初二)4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO 相交于B、D.求证:AB=DC,BC=AD.(初三)经典难题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:√3≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=80度,D、E分别是AB、AC上的点,∠DCA =30度,∠EBA=20度,求∠BED的度数.答案经典难题(一)4.如下图连接AC并取其中点Q,连接QN和QM,所以可得∠QMF=∠F,∠QNM=∠D EN和∠QMN=∠QNM,从而得出∠DEN=∠F。
八年级下册数学好题难题精选

数学好题难题精选分式:一:如果abc=1,求证11++a ab +11++b bc +11++c ac =1二:已知a 1+b 1=)(29b a +,则a b +ba等于多少?三:一个圆柱形容器的容积为V 立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水。
向容器中注满水的全过程共用时间t 分。
求两根水管各自注水的速度。
五:已知M =222yx xy -、N =2222yx y x -+,用“+”或“-”连结M 、N,有三种不同的形式,M+N 、M-N 、N-M ,请你任取其中一种进行计算,并简求值,其中x :y=5:2。
解:选择一:22222222()()()x y xy x y x yM N xyxy x y x yx y++++=+==--+--, 当x ∶y =5∶2时,52xy =,原式=572532y yy y +=-.选择二:22222222()()()x y xy x y y xM N xyxy x y x yx y+----=-==--+-+, 当x ∶y =5∶2时,52xy =,原式=532572y yy y -=-+.选择三:22222222()()()xy x y x y x yN M xyxy x y x yx y+---=-==--+-+, 当x ∶y =5∶2时,52x y =,原式=532572y yy y -=+.勾股定理:一:清朝康熙皇帝是我国历史上对数学很有兴趣的帝王.近日,•西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,•设其面积为S ,则第一步:6S =m ;第二步:m =k ;第三步:分别用3、4、5乘以k ,得三边长”.(1)当面积S 等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.二:一张等腰三角形纸片,底边长l5cm ,底边上的高长22.5cm .现沿底边依次从下往上裁剪宽度均为3cm 的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )A .第4张B .第5张C .第6张D .第7张 三:如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的处目测得点与甲、乙楼顶B C 、刚好在同一直线上,且A 与B 相距350米,若小明的身高忽略不计,则乙楼的高度是 米. A 与B 相距350米,若小明的身高忽略不计,则乙楼的高度是米.四:恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧,50k m A B A =,、到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区,向、两景运送游客.小民设计了两种方案,图(1)是一的示意A P 与直线X 垂直,足为)到、的距离之和1S P A P B =+,图(2)是方案二的示意点关于直线X 的对称点是A ',连接B A '交直线X 于点),到、的距离之和2S P A P B =+. 别为10km 和40km ,要在沪渝高速公路旁修建一服务区,向、两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(A P 与直线X 垂直,垂足为),到、的距离之和1S P A P B =+,图(2)是方案二的示意图(点关于直线X 的对称点是A ',连接B A '交直线X 于点),到、的距离之和2S P A P B =+. 区运送游客.小民设计了两种方案,图(1)是方案一的示意图(A P 与直线X 垂直,垂足为),到、的距离之和1S P A P B =+,图(2)是方案二的示意图(点关于直线X 的对称点是A ',连接B A '交直线X 于点),到、的距离之和2S P A P B =+. (2)是方案二的示意图(点关于直线X 的对称点是A ',连接B A '交直线X 于点),到、的距离之和2S P A P B =+. 交直线X 于点),到、的距离之和2S P A P B =+.20乙C B A甲10?20(1)求1S 、2S ,并比较它们的大小; (2)请你说明2S P A P B =+的值为最小; (3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区、,使、、、组成的四边形的周长最小.并求出这个最小值. 在X 旁和Y 旁各修建一服务区、,使、、、组成的四边形的周长最小.并求出这个最小值. 最小.并求出这个最小值.五:已知:如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,BA PX图(1)YXBAQP O图(3)BAP X A '图(2) D AFDE⊥AC于点F,交BC于点G,交AB的延长线于点E,且A E A C=.(1)求证:B G F G=;(2)若2==,求AB的长.ACD D二:如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF。
(完整版)八年级数学经典难题

经典难题(一)1、已知:如图,O 是半圆的圆心,C、E 是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二)2、已知:如图,P 是正方形 ABCD 内点,∠PAD=∠PDA=15 度求证:△PBC是正三角形.(初二)3、如图,已知四边形 ABCD、A1B1C1D1 都是正方形,A2、B2、C2、D2 分别是 AA 1、BB1、CC1、DD1 的中点.求证:四边形 A2B2C2D2 是正方形.(初二)4、已知:如图,在四边形 ABCD 中,AD=BC,M、N 分别是 AB、CD 的中点,AD、BC 的延长线交 MN 于E、F.求证:∠DEN=∠F.经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM⊥BC 于 M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设 MN 是圆 O 外一直线,过 O 作OA⊥MN 于 A,自 A 引圆的两条直线,交圆于B、C 及D、E,直线 EB 及CD 分别交 MN 于P、Q.求证:AP=AQ.(初二)3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:设 MN 是圆 O 的弦,过 MN 的中点 A 任作两弦 BC、DE,设 CD、EB 分别交 MN 于 P 、Q.求证:AP=AQ.(初二)4、如图,分别以△ABC的AC 和BC 为一边,在△ABC的外侧作正方形 ACDE 和正方形 CBFG,点P 是EF 的中点.求证:点 P 到边 AB 的距离等于 AB 的一半.(初二)经典难题(三)1、如图,四边形 ABCD 为正方形,DE∥AC,AE=AC,AE 与 CD 相交于 F.求证:CE=CF.(初二)2、如图,四边形 ABCD 为正方形,DE∥AC,且 CE=CA,直线 EC 交 DA 延长线于F.求证:AE=AF.(初二)3、设 P 是正方形 ABCD 一边BC 上的任一点,PF⊥AP,CF 平分∠DCE.求证:PA=PF.(初二)4、如图,PC 切圆 O 于 C,AC 为圆的直径,PEF 为圆的割线,AE、AF 与直线 PO 相交于 B、D.求证:AB=DC,BC=AD.(初三)经典难题(四)1、已知:△ABC是正三角形,P 是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设 P 是平行四边形 ABCD 内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设 ABCD 为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形 ABCD 中,设 E、F 分别是 BC、AB 上的一点,AE 与CF 相交于 P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设 P 是边长为 1 的正△ABC 内任一点,L=PA+PB+PC,求证:√3≤L<2.2、已知:P 是边长为 1 的正方形 ABCD 内的一点,求 PA+PB+PC 的最小值.3、P 为正方形 ABCD 内的一点,并且 PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC 中,∠ABC=∠ACB=80 度,D、E 分别是 AB、AC 上的点,∠DC A=30 度,∠EBA=20 度,求∠BED 的度数.答案经典难题(一)4.如下图连接 AC 并取其中点 Q,连接 QN 和QM,所以可得∠QMF=∠F,∠QNM=∠ DEN 和∠QMN=∠QNM,从而得出∠DEN=∠F。
(完整版)初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
初二数学八年级各种经典难题例题(含答案)非常经典

1 已知一个等腰三角形两内角的度数之比为1 : 4 ,则这个等腰三角形 顶角的度数为()A. 2 0 B.1 2 0C. 2 0 或1 2 0D.3 61.一个凸多边形的每一个内角都等于 150°,则这个凸多边形所有对角线的条数总共有()A.42 条 B.54 条 C.66 条 D.78 条3、若直线 y k1x 1与 y k2x4的交点在 x轴上,那么 k 1k2等于()(竞赛)1正实数x,y 满足xy 1,那么1 x41 4y4的最小值为:()(A) 1 (B) 5 (C)1(D) 228(竞赛)在△ABC 中,若∠A>∠B,则边长 a 与 c 的大小关系是( )A、a>cB、c>aC、a>1/2c16.如图,直线 y=kx+6 与 x 轴 y 轴分D、c>1/2a别交于点 E,F.点 E 的坐标为(-8,0),点 A 的坐标为(-6,0).(1)求 k 的值;(2)若点 P(x,y)是第二象限内的直线上的一个动点,当点 P 运动过程中,试写出△OPA 的面积 S 与 x 的函数关系式,并写出自变量 x 的取值范围; (3)探究:当 P 运动到什么位置时,△OPA 的面积为 27 ,并说明8理由.6、已知,如图,△ABC 中,∠BAC=90°,AB=AC,D 为 AC 上一点,且∠BDC=124°,延长 BA 到点 E,使 AE=AD,BD 的延长线交 CE 于点 F,求∠E 的度数。
7.正方形 ABCD 的边长为 4,将此正方形置于平面直角坐标系中,使AB 边落在 X 轴的正半轴上,且 A 点的坐标是(1,0)。
①直线 y=x-经过点 C,且与 x 轴交与点 E,求四边形 AECD 的面积;②若直线l 经过点 E 且将正方形 ABCD 分成面积相等的两部分求直线l 的解析式,③若直线l1经过点F 3 2.0 且与直线y=3x平行,将②中直线l沿着y轴向上平移2 3个单位交x轴于点M,交直线l1于点N,求NMF的面积.(竞赛奥数)如图,在△ABC 中,已知∠C=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC 形外的等边三角形,而点 D 在 AC 上,且 BC=DC(1)证明:△C′BD≌△B′DC; (2)证明:△AC′D≌△DB′A;9.已知如图,直线 y 3x 4 3 与 x 轴相交于点 A,与直线 y 3x 相交 于点 P. ①求点 P 的坐标. ②请判断 OPA的形状并说明理由. ③动点 E 从原点 O 出发,以每秒 1 个单位的速度沿着 O→P→A 的路线 向点 A 匀速运动(E 不与点 O、A 重合),过点 E 分别作 EF⊥x 轴于 F, EB⊥y 轴于 B.设运动 t 秒时,矩形 EBOF 与△OPA 重叠部分的面积为 S.求:S 与 t 之间的函数关系式.16y多边形内角和公式等于(n-2)×180根据题意即(n-2)×180=150n,求得 n=12,多边形的对角线的条数公式等于 n(n-3)/2 带入 n=12,则这个多边形所有对角线的条数共有 54 条BE因为两直线交点在 x 轴上,则 k1 和 k2 必然不为 0,且交点处 OFx=-1/k1=4/k2,所以 k1:k2=-1:41/x^4+1/4y^4=(y^4+x^4)/x^4y^4 因为 xy=1 所以 x^4y^4=1 所以原式=y^4+x^4 因为(x^2-y^2)^2>0 且(x^2-y^2)^2=y^4+x^4-x^2y^2 大于或等于 0 所以 y^4+x^4 大于或等于 x^2y^2 即 1 所以 y^4+x^4 的最小值为 1竞赛解:在△ABC 中, ∵∠A>∠B, ∴a>b, ∵a+b>c, ∴2a>a+b>c, ∴a>12c. 故选 C.P Ax1、y=kx+6 过点 E(-8,0)则 -8K+6=0 K=3/4 2、 因点 E(-8,0) 则 OE=8 直线解析式 Y=3X/4+6 当 X=0 时,Y=6,则点 F(0,6) 因点 A(0,6),则 A、F 重合 OA=6 设点 P(X,Y) 则点 P 对于 Y 轴的高为|X| 当 P 在第二象限时,|X|=-X S=OA×|X|/2=-6X/2=-3X 3、 S=3|X| 当 S=278 时 278=±3X X1=278/3,X2=-278/3 Y1=3X1/4+6=3/4×278/3+6=151/2 Y2=3X2/4+6=-3/4×278/3+6=-127/2 点 P1(278/3,151/2),P2(-278/3,-127/2)6 解:在△ABD 和△ACE 中, ∵AB=AC,∠DAB=∠CAE=90°AD=AE, ∴△ABD≌△ACE(SAS), ∴∠E=∠ADB. ∵∠ADB=180°-∠BDC=180°-124°=56°, ∴∠E=56°. 7(1)由题意知边长已经告诉,易求四边形的面积; (2)由第一问求出 E 点的坐标,设出 F 点,根据直线 l 经过点 E 且将正方形 ABCD 分成面积相等的两部分,其实是两个直角梯形,根据梯形面积公式,可求 出 F 点坐标,从而解出直线 l 的解析式.解:(1)由已知条件正方形 ABCD 的 边长是 4, ∴四边形 ABCD 的面积为:4×4=16; (2)由第一问知直线 y=4/3x-8/3 与 x 轴交于点 E, ∴E(2,0), 设 F(m,4),直线 l 经过点 E 且将正方形 ABCD 分成面积相等的两部分,由图知是两个直角 梯形, ∴S 梯形 AEFD=S 梯形 EBCF=1/2(DF+AE)?AE=1/2(FC+EB) ∴m=4, ∵F(4,4),E(2,0), ∴直线 l 的解析式为:y=2x-4 竞赛奥数 (1)先证△ABC≌△C1BD:∵AB=C1B,∠ABC=∠C1BD(因为都是 60°+∠ ABD),BD=BC。
(完整版)初中数学经典难题(含答案)
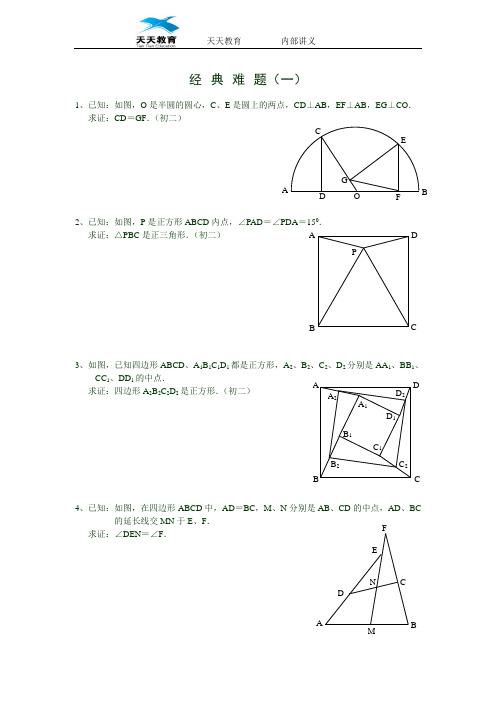
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A N FE CDMBP CG FB QA D E1、已知:△ABC 中,H 为垂心(各边高线的交点),O (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DEC N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F A E PC B A OD BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、Ptolemy (托勒密)定理:设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD . (初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)AP C B P A D CB C B DAF PD E C B A1、设P 是边长为1的正△ABC 内任一点,l =PA +PB +PC ,求证:3≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典难题(一)1、2、3、4、经典难题(二)1、2、4、经典难题(三)1、3、4、1、2、3、4、证明:过D 作DQ ⊥AE ,DG ⊥CF,并连接DF 和DE ,如右图所示 则S △ADE =21S ABCD =S △DFC ∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线,∴∠DPA=∠DPC1、2、3、3、4、。
八年级数学经典难题及答案

精心整理页脚内容APCDBP CGFBQA DE初二数学经典题型1.已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.证明如下。
首先,PA=PD ,∠PAD=∠PDA=(180°-150°)÷2=15°,∠PAB=90°-15°=75°。
在正方形ABCD 之外以AD 为底边作正三角形ADQ ,连接PQ ,则∠PDQ=60°+15°=75°,同样∠PAQ=75°,又AQ=DQ,,PA=PD ,所以△PAQ ≌△PDQ ,那么∠PQA=∠PQD=60°÷2=30°,在△PQA 中,∠APQ=180°-30°-75°=75°=∠PAQ=∠PAB ,于是PQ=AQ=AB ,显然△PAQ ≌△PAB ,得∠PBA=∠PQA=30°,PB=PQ=AB=BC ,∠PBC=90°-30°=60°,所以△ABC 是正三角形。
2.已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN=∠F .证明:连接AC,并取AC 的中点G,连接GF,GM.又点N 为CD 的中点,则GN=AD/2;GN ∥AD,∠GNM=∠DEM;(1) 同理:GM=BC/2;GM ∥BC,∠GMN=∠CFN;(2)又AD=BC,则:GN=GM,∠GNM=∠GMN.故:∠DEM=∠CFN. 3、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.证明:分别过E 、C 、F 作直线AB 的垂线,垂足分别为M 、O 、N ,在梯形MEFN 中,WE 平行NF 因为P 为EF 中点,PQ 平行于两底所以PQ 为梯形MEFN 中位线,所以PQ =(ME +NF )/2 又因为,角0CB +角OBC =90°=角NBF +角CBO所以角OCB=角NBF 而角C0B =角Rt =角BNF CB=BF所以△OCB 全等于△NBF △MEA 全等于△OAC (同理)所以EM =AO ,0B =NF 所以PQ=AB/2. 4、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .过点P 作DA 的平行线,过点A 作DP 的平行线,两者相交于点E ;连接BE因为DP//AE ,AD//PE 所以,四边形AEPD 为平行四边形所以,∠PDA=∠AEP 已知,∠PDA=∠PBA 所以,∠PBA=∠AEP 所以,A 、E 、B 、P 四点共圆所以,∠PAB=∠PEB 因为四边形AEPD 为平行四边形,所以:PE//AD ,且PE=AD 而,四边形ABCD 为平行四边形,所以:AD//BC ,且AD=BCAN FECD MBPADCB精心整理页脚内容所以,PE//BC ,且PE=BC 即,四边形EBCP 也是平行四边形所以,∠PEB=∠PCB 所以,∠PAB=∠PCB5.P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC=3a 正方形的边长.?解:将△BAP 绕B 点旋转90°使BA 与BC 重合,P 点旋转后到Q 点,连接PQ因为△BAP ≌△BCQ所以AP =CQ ,BP =BQ ,∠ABP =∠CBQ ,∠BPA =∠BQC 因为四边形DCBA 是正方形所以∠CBA =90°,所以∠ABP +∠CBP =90°,所以∠CBQ +∠CBP =90°即∠PBQ =90°,所以△BPQ 是等腰直角三角形所以PQ =√2*BP ,∠BQP =45 因为PA=a ,PB=2a ,PC=3a所以PQ =2√2a ,CQ =a ,所以CP^2=9a^2,PQ^2+CQ^2=8a^2+a^2=9a^2 所以CP^2=PQ^2+CQ^2,所以△CPQ 是直角三角形且∠CQA =90°所以∠BQC =90°+45°=135°,所以∠BPA =∠BQC =135°作BM ⊥PQ则△BPM 是等腰直角三角形所以PM =BM =PB/√2=2a/√2=√2a 所以根据勾股定理得:AB^2=AM^2+BM^2 =(√2a +a)^2+(√2a)^2=[5+2√2]a^2所以AB =[√(5+2√2)]a 6.一个圆柱形容器的容积为V 立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水。
初二数学经典难题

初二数学经典难题1.〔10分〕:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
专题:证明题。
分析:在正方形内做△DGC与△ADP全等,根据全等三角形的性质求出△PDG为等边,三角形,根据SAS证出△DGC≌△PGC,推出DC=PC,推出PB=DC=PC,根据等边三角形的判定求出即可.解答:证明:∵正方形ABCD,∴AB=CD,∠BAD=∠CDA=90°,∵∠PAD=∠PDA=15°,∴PA=PD,∠PAB=∠PDC=75°,在正方形内做△DGC与△ADP全等,∴DP=DG,∠ADP=∠GDC=∠DAP=∠DCG=15°,∴∠PDG=90°﹣15°﹣15°=60°,∴△PDG为等边三角形〔有一个角等于60度的等腰三角形是等边三角形〕,∴DP=DG=PG,∵∠DGC=180°﹣15°﹣15°=150°,∴∠PGC=360°﹣150°﹣60°=150°=∠DGC,在△DGC和△PGC中,∴△DGC≌△PGC,∴PC=AD=DC,和∠DCG=∠PCG=15°,同理PB=AB=DC=PC,∠PCB=90°﹣15°﹣15°=60°,∴△PBC是正三角形.点评:此题考查了正方形的性质,等边三角形的性质和判定,全等三角形的性质和判定等知识点的应用,关键是正确作出辅助线,又是难点,题型较好,但有一定的难度,对学生提出了较高的要求.2.〔10分〕:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.考点:三角形中位线定理。
(完整版)初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
初中数学难题精选(附答案)

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)APCDB AFGCEBOD3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=BC,M、NBC的延长线交MN于E、F.求证:∠DEN=∠F.D2C2B2A2D1C1B1C BD AA1B经典难题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二)F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.4、如图,PC切圆O于C,AC为圆的直径,B、D.求证:AB=DC,BC=AD.(初三)经典难题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.FP DE CBAA2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC 上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
初二数学各类经典难题(含答案)
简单的极端原理1 钟面上有十二个数1,2,3,…,12.将其中某些数的前面添上一个负号,使钟面上所有数之代数和等于零,则至少要添n个负号,这个数n是()A、4B、5C、6D、72、学生甲、乙、丙三人竞选学校的学生会主席,选举时收到有效选票1500张,统计其中1000张选票的结果是:甲350张,乙370张,丙280张,则甲在剩下的500张选票中至少再得票,才能保证以得票最多当选该校的学生会主席.3 已知a、b、c为实数.证明:(a+b+c)2、(a+b-c)2、(b+c-a)2、(c+a-b)2这四个代数式的值中至少有一个不小于a2+b2+c2的值,也至少有一个不大于a2+b2+c2的值.4如果a,b,c是正实数且满足abc=1,则代数式(a+1)(b+1)(c+1)的最小值是()A、64B、8 2C、8D、25如图,在矩形ABCD中,AE,AF三等分∠BAD,若BE=2,CF=1,则最接近矩形面积的是()A、13B、14C、15D、166.正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2, …按如图所示的方式放置.点A 1,A 2,A 3, …和点C 1,C2,C 3,…分别在直线y=kx+b(k >0)和x 轴上,已知点B 1(1,1),B 2(3,2),则Bn 的坐标是_________.7(2005•烟台)(1)如图1,以△ABC 的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ,连接EG ,试判断△ABC 与△AEG 面积之间的关系,并说明理由. (2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a 平方米,内圈的所有三角形的面积之和是b 平方米,这条小路一共占地多少平方米.yxO C1 B2A2C3B1A3B3A1 C8 已知,如图,等边三角形ABC中,AB=4,点P为AB边上的任意一点(点P可以与点A 重合,但不与点B重合),过点P作PE⊥BC,垂足为E,过点E作EF⊥AC,垂足为F,过点F作FQ⊥AB,垂足为Q,设BP=x,AQ=y.(1)写出y与x之间的函数关系式;(2)当BP的长等于多少时,点P与点Q重合.9(2001•苏州)如图,L甲、L乙分别是甲、乙两弹簧的长ycm与所挂物体质量xkg之间函数关系的图象,设甲弹簧每挂1kg物体伸长的长度为k甲cm,乙弹簧每挂1kg物体伸长的长度为k乙cm,则k甲与k乙的关系是()A、k甲>k乙B、k甲=k乙C、k甲<k乙D、不能确定10 如图,在平面直角坐标系中,直线y=- x + 3 交x轴于A点,交y轴于B点,点C是线段AB 的中点,连接OC,然后将直线OC绕点C顺时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥OC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依次类推,后面的三角形面积分别是S3,S4…,那么S1= ,若S=S1+S2+S3+…+S n,当n无限大时,S的值无限接近于.11 如图,正方形ABCD和正方形CGEF(CG>BC),连接AE,取线段AE的中点M.证明:FM⊥MD,且FM=MD.解答:证明:如图,过点E作AD的平行线分别交DM、DC的延长线于N、H,连接DF、FN.∴∠ADC=∠H,∠3=∠4.∵AM=ME,∠1=∠2,∴△AMD≌△EMN∴DM=NM,AD=EN.∵ABCD和CGEF是正方形,∴AD=DC,FC=FE,∠ADC=∠FCG=∠CFE=90°,∠5=∠6=90°-∠NEG=∠NEF,DC=AD=NE.又∵∠H=90°,∴∠DCF+∠7=∠5+∠7=90°∴∠DCF=∠5=∠NEF∵FC=FE,∴△DCF≌△NEF.∴FD=FN,∠DFC=∠NEF.∵∠CFE=90°,∴∠DFN=90°,即△DFN为等腰直角三角形.又DM=MN,∴FM⊥MD,MF=MD.点评:本题考查了正方形各边相等且各内角为直角的性质,考查了全等三角形的判定和对应边、对应角相等的性质,本题中求证△DCF≌△NEF是解题的关键.。
初二数学难题及答案

t(h)4· 8· 1216S(km) 4 0AB· · 第22题图EDABC题目:一:小王与小李两人同时由甲地出发,小王匀速步行到乙地后原路返回,小李由甲地匀速步行经乙地后继续前行,到丙地后原路返回.设步行的时间为t (h ),两人离乙地的距离分别为S 1(km )和S 2(km),图中的折线分别表示S 1、S 2与t 之间的函数关系.问: (1)甲、乙两地之间的距离为多少km ?乙、丙两地之间的距离为多少km ? (2)求小李由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少? (3)求图中线段AB 所表示的S 与t 间的函数关系式,并写出自变量t 的取值范围.二:如今,餐馆常用一次性筷子,有人说这是浪费资源,破坏生态环境.已知用来生产一次性筷子的大树的数量(万棵)与加工后一次性筷子的数量(亿双)成正比例关系,且100万棵大树能加工成18亿双一次性筷子.(1)求用来生产一次性筷子的大树的数量y (万棵)与加工后一次性筷子的数量x (亿双)的函数关系式.(2)据统计,我国一年要耗费一次性筷子约450亿双,生产这些一次性筷子约需要多少万棵大树?每1万棵大树占地面积约为0.08平方千米,照这样计算,我国的森林面积每年因此将会减少大约多少平方千米?三:如图, △ABC 和△ECD 都是等腰直角三角形,∠ACB=∠ECD=900,D 为AB 上一点. (1)△ACE 与△BCD 全等吗?为什么? (2)等式AD 2+BD 2=DE 2成立吗?请说明理由.四:已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
⑴求证:BF =AC ; ⑵求证:CE =12BF ; ⑶连结GC ,试判断GC 与BG 的数量关系,并说明理由;CE 与BG 的大小关系如何?试证明你的结论。
(完整版)初二数学八年级各种经典难题例题(含答案)非常经典

1 已知一个等腰三角形两内角的度数之比为1: 4 ,则这个等腰三角形顶角的度数为( )A . 20B .120C . 20 或120D . 361.一个凸多边形的每一个内角都等于 150°,则这个凸多边形所有对角线的条数总共有( )A .42 条B .54 条C .66 条D .78 条3、若直线 y = k x +1 与 y = k x - 4 的交点在 x 轴上,那么 k 1 等于() 1 2 2A .4 B. - 4 C. 1 41 1 D. - 1 4 (竞赛)1 正实数 x , y 满足 xy = 1,那么 x 4 + 4 y 4的最小值为:( ) 15(A) (B) (C)1 (D) 2 8(竞赛)在△ABC 中,若∠A >∠B ,则边长 a 与 c 的大小关系是()A 、a >cB 、c >aC 、a >1/2cD 、c >1/2a16. 如图,直线 y=kx+6 与 x 轴 y 轴分别交于点 E ,F.点 E的坐标为(-8,0),点 A 的坐标为(-6,0).(1)求 k 的值;(2) 若点 P(x ,y)是第二象限内的直线上的一个动点,当点 P 运动过程中,试写出△OPA 的面积 S 与 x 的函数关系式,并写出自变量 x 的取值范围;27(3) 探究:当 P 运动到什么位置时,△OPA 的面积为 ,并说明理由.8 2k⎝ ⎭ 6、已知,如图,△ABC 中,∠BAC=90°,AB=AC,D 为 AC 上一点,且∠BDC=124°,延长 BA 到点 E ,使 AE=AD,BD 的延长线交 CE 于点 F ,求∠E 的度数。
7.正方形 ABCD 的边长为 4,将此正方形置于平面直角坐标系中,使 AB 边落在 X 轴的正半轴上,且 A 点的坐标是(1,0)。
4 8 ①直线 y=3x-3经过点 C ,且与 x 轴交与点 E ,求四边形 AECD 的面积;②若直线l 经过点 E 且将正方形 ABCD 分成面积相等的两部分求直线l 的解析式, ③若直线l 经过点 F ⎛- 3 .0⎫ 且与直线 y=3x 平行,将②中直线l 沿着 y 轴向上平移 2 个单位1 2 ⎪ 3交 x 轴于点 M ,交直线l 1 于点 N ,求∆NMF 的面积.(竞赛奥数)如图,在△ABC 中,已知∠C=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC 形外的等边三角形,而点D 在AC 上,且BC=DC(1)证明:△C′BD≌△B′DC;(2)证明:△AC′D≌△DB′A;3x + 4 与x 轴相交于点A,与直线y = 3x 相交于点P.9.已知如图,直线y =-3①求点P 的坐标.②请判断∆OPA 的形状并说明理由.③动点E 从原点O 出发,以每秒1 个单位的速度沿着O→P→A 的路线向点A 匀速运动(E 不与点O、A 重合),过点E 分别作EF⊥x 轴于F,EB⊥y 轴于B.设运动t 秒时,矩形EBOF 与△OPA 重叠部分的面积为S.求:S 与t 之间的函数关系式.yPEBO F A x16多边形内角和公式等于(n -2)×180根据题意即(n -2)×180=150n,求得n=12,多边形的对角线的条数公式等于 n(n-3)/2 带入 n=12,则这个多边形所有对角线的条数共有 54 条因为两直线交点在x 轴上,则k1 和k2 必然不为0,且交点处x=-1/k1=4/k2,所以k1:k2=-1:41/x^4+1/4y^4=(y^4+x^4)/x^4y^4因为xy=1所以x^4y^4=1所以原式=y^4+x^4因为(x^2-y^2)^2>0且(x^2-y^2)^2=y^4+x^4-x^2y^2 大于或等于0所以y^4+x^4 大于或等于x^2y^2 即1所以 y^4+x^4 的最小值为 1竞赛解:在△ABC 中,∵∠A>∠B,∴a>b,∵a+b>c,∴2a>a+b>c,∴a>12c.故选C.1、y=kx+6 过点E(-8,0)则-8K+6=0K=3/42、因点E(-8,0)则OE=8直线解析式Y=3X/4+6当X=0 时,Y=6,则点F(0,6)因点A(0,6),则A、F 重合OA=6设点P(X,Y)则点P 对于Y 轴的高为|X|当P 在第二象限时,|X|=-XS=OA×|X|/2=-6X/2=-3X3、S=3|X|当S=278 时278=±3XX1=278/3,X2=-278/3 Y1=3X1/4+6=3/4×278/3+6=151/2 Y2=3X2/4+6=-3/4×278/3+6=-127/2点 P1(278/3,151/2),P2(-278/3,-127/2)6解:在△ABD 和△ACE 中,∵AB=AC,∠DAB=∠CAE=90°AD=AE,∴△ABD≌△ACE(SAS),∴∠E=∠ADB.∵∠ADB=180°-∠BDC=180°-124°=56°,∴∠E=56°.7(1)由题意知边长已经告诉,易求四边形的面积;(2)由第一问求出E 点的坐标,设出F 点,根据直线l 经过点E 且将正方形ABCD 分成面积相等的两部分,其实是两个直角梯形,根据梯形面积公式,可求出F 点坐标,从而解出直线l 的解析式.解:(1)由已知条件正方形ABCD 的边长是4,∴四边形ABCD 的面积为:4×4=16;(2)由第一问知直线y=4/3x-8/3 与x 轴交于点E,∴E(2,0),设F(m,4),直线l 经过点E 且将正方形ABCD 分成面积相等的两部分,由图知是两个直角梯形,∴S 梯形AEFD=S 梯形EBCF= 1/2(DF+AE)•AE= 1/2(FC+EB)∴m=4,∵F(4,4),E(2,0),∴直线 l 的解析式为:y=2x-4竞赛奥数(1) 先证△ABC≌△C1BD:∵AB=C1B, ∠ABC=∠C1BD (因为都是60°+∠ABD), BD=BC。
八年级数学经典难题(答案+解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC 是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M (﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P 与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD 于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B 两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1已知一个等腰三角形两内角的度数之比为,则这个等腰三角形顶角的度数为( )
A .
B .
C .或
D .
1.一个凸多边形的每一个内角都等于150°,则这个凸多边形所有对角线的条数总共有( )
A .42条
B .54条
C .66条
D .78条
3、若直线与的交点在轴上,那么等于( )
(竞赛)1 正实数,x y 满足1xy =,那么44
114x y +的最小值为:( )
(A)
12 (B)58
16.如图,直线y=kx+6与x 轴y 轴分别交于点E ,F.点E 的
坐标为(-8,0),点A 的坐标为(-6,0).
(1)求k 的值;
(2)若点P(x ,y)是第二象限内的直线上的一个动点,当
点P 运动过程中,试写出△OPA 的面积S 与x 的函数
关系式,并写出自变量x 的取值范围;
(3)探究:当P 运动到什么位置时,△OPA 的面积为8
27,并说明理由.
6、已知,如图,△ABC 中,∠BAC=90°,AB=AC,D 为AC 上一点,且∠BDC=124°,延长BA 到点E ,使AE=AD,BD 的延长线交CE 于点F ,求∠E 的度数。
7.正方形ABCD 的边长为4,将此正方形置于平面直角坐标系中,使AB 边落在X 轴的正半轴上,且A 点的坐标是(1,0)。
①直线y=43x-83
经过点C ,且与x 轴交与点E ,求四边形AECD 的面积; ②若直线l 经过点E 且将正方形ABCD 分成面积相等的两部分求直线l 的解析式, ③若直线1l 经过点F ⎪⎭
⎫ ⎝⎛-0.23且与直线y=3x 平行,将②中直线l 沿着y 轴向上平移32个单位交x 轴于点M ,交直线1l 于点N ,求NMF ∆的面积.
(竞赛奥数)如图,在△ABC 中,已知∠C=60°,AC >BC ,又△ABC ′、△BCA ′、△CAB ′都是△ABC 形外的等边三角形,而点D 在AC 上,且BC=DC
(1)证明:△C ′BD ≌△B ′DC ;
(2)证明:△AC ′D ≌△DB ′A ;
9.
已知如图,直线y=+与x轴相交于点A
,与直线y=相交于点P.
①求点P的坐标.
②请判断OPA
∆的形状并说明理由.
③动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.求:S与t之间的函数关系式.
16
多边形内角和公式等于(n - 2)×180
根据题意即(n - 2)×180=150n,求得n=12,
多边形的对角线的条数公式等于 n(n-3)/2带入n=12,则这个多边形所有对角线的条数共有54条
因为两直线交点在x轴上,则k1和k2必然不为0,且交点处x=-1/k1=4/k2,
所以k1:k2=-1:4
1/x^4+1/4y^4=(y^4+x^4)/x^4y^4
因为xy=1
所以x^4y^4=1
所以原式=y^4+x^4
因为(x^2-y^2)^2>0
且(x^2-y^2)^2=y^4+x^4-x^2y^2大于或等于0所以y^4+x^4大于或等于x^2y^2 即1
所以y^4+x^4的最小值为1
竞赛解:在△ABC中,
∵∠A>∠B,
∴a>b,
∵a+b>c,
∴2a>a+b>c,
∴a>12c.
故选C.
1、y=kx+6过点E(-8,0)则
-8K+6=0
K=3/4
2、
因点E(-8,0)
则OE=8
直线解析式Y=3X/4+6
当X=0时,Y=6,则点F(0,6)
因点A(0,6),则A、F重合
OA=6
设点P(X,Y)
则点P对于Y轴的高为|X|
当P在第二象限时,|X|=-X
S=OA×|X|/2=-6X/2=-3X
3、
S=3|X|
当S=278时
278=±3X
X1=278/3,X2=-278/3
Y1=3X1/4+6=3/4×278/3+6=151/2
Y2=3X2/4+6=-3/4×278/3+6=-127/2
点P1(278/3,151/2),P2(-278/3,-127/2)
6
解:在△ABD和△ACE中,
∵AB=AC,∠DAB=∠CAE=90°AD=AE,
∴△ABD≌△ACE(SAS),
∴∠E=∠ADB.
∵∠ADB=180°-∠BDC=180°-124°=56°,
∴∠E=56°.
7
(1)由题意知边长已经告诉,易求四边形的面积;
(2)由第一问求出E点的坐标,设出F点,根据直线l经过点E且将正方形ABCD 分成面积相等的两部分,其实是两个直角梯形,根据梯形面积公式,可求出F 点坐标,从而解出直线l的解析式.解:(1)由已知条件正方形ABCD的边长是4,
∴四边形ABCD的面积为:4×4=16;
(2)由第一问知直线 y=4/3x-8/3与x轴交于点E,
∴E(2,0),
设F(m,4),
直线l经过点E且将正方形ABCD分成面积相等的两部分,由图知是两个直角梯形,
∴S梯形AEFD=S梯形EBCF= 1/2(DF+AE)•AE= 1/2(FC+EB)
∴m=4,
∵F(4,4),E(2,0),
∴直线l的解析式为:y=2x-4
竞赛奥数
(1) 先证△ABC≌△C1BD:∵AB=C1B, ∠ABC=∠C1BD (因为都是60°+∠ABD), BD=BC。
(SAS)
(得出:∠C1DB=∠C=60°)
再证:△ABC≌△B1DC:∵AC=B1C, ∠C=∠B1CA=60°, BC=DC。
(SAS)
∴△C1BD≌△B1DC
(得出:B1C=C1D)
(2) ∵B1C=C1D,B1C=AB1,∴AB1=C1D
∠C1DB=60°,∠BDC=60°,∴∠ADC1=60°=∠B1AD
AD是公共边
∴△AC1D≌△DB1A (SAS)
(3) S△B1CA > S△ABC1 > S△ABC > S△BCA1
y=-(3^½)x+4*(3^½)与x轴相交于A,即x=4,y=0,则A点坐标为:(4,0)
又与y=(3^½)x相交于P,则联列解得:
x=2,y=2*(3^½)
即P点坐标为:(2,2*(3^½))
|OP|={2²+[2*(3^½)]²}^½=4
|AP|={(2-4)²+[2*(3^½)]²}^½=4
而|OA|=4
所以△OAP为等边三角形。
