高一数学基本不等式2
高一数学必修一第二章第二课基本不等式

高一数学必修一第二章第二课基本不等式摘要:一、基本不等式的概念与性质1.基本不等式的定义2.基本不等式的性质二、基本不等式的证明方法1.作差法2.替换法3.柯西-施瓦茨不等式三、基本不等式的应用1.求最值问题2.证明其他不等式四、练习与解答1.例题解析2.巩固练习正文:一、基本不等式的概念与性质在高中数学必修一第二章第二课中,我们学习了一个非常基础且重要的不等式——基本不等式。
基本不等式是指对于任意的实数a和b,都有a^2 + b^2 >= 2ab。
这个不等式在很多数学问题中都有广泛的应用,因此我们需要熟练掌握它的性质和证明方法。
二、基本不等式的证明方法1.作差法作差法是证明基本不等式最常用的方法。
具体操作如下:我们将a^2 + b^2 - 2ab分解因式,得到(a - b)^2。
因为一个数的平方一定大于等于0,所以(a - b)^2 >= 0,即a^2 + b^2 >= 2ab。
2.替换法替换法是将基本不等式中的a和b替换成其他表达式,从而简化证明过程。
常用的替换方法有柯西-施瓦茨替换和排序替换。
3.柯西-施瓦茨不等式柯西-施瓦茨不等式是基本不等式的一个推广,它是指对于任意的实数a1, a2, ..., an和b1, b2, ..., bn,都有(a1^2 + a2^2 + ...+ an^2)(b1^2 + b2^2 + ...+ bn^2) >= (a1b1 + a2b2 + ...+ anbn)^2。
这个不等式在求解某些问题时,可以提供更强的工具。
三、基本不等式的应用1.求最值问题基本不等式可以用来求解一些最值问题,如求函数的最值、求解不等式的最值等。
2.证明其他不等式基本不等式是许多其他不等式的基础,如柯西不等式、排序不等式等。
通过基本不等式,我们可以证明这些不等式,从而进一步解决实际问题。
四、练习与解答1.例题解析我们来看一道例题:已知a + b = 2,求a^2 + b^2的最小值。
2.2 基本不等式(第二课时)高一数学课件(人教A版2019必修第一册)

解: ∵ >-1,∴ + >0.
当且仅当2( + ) =
即= −
+
∴ 函数 f(x) 的最小值是 −
取“=”号.
概念讲解
例2. 若 < <
,求函数 = ( − ) 的最大值.
分析: + ( − ) 不是 常数.而 + ( − ) = 为常数
人教A版2019必修第一册
第 2 章 一元二次函数(第二课时)
教学目标
1.熟练掌握基本不等式的应用条件,能够利用基本不等式求最值.
2.掌握常见的利用基本不等式求最值的题型
3.能够运用基本不等式解决生活中的应用问题.
01
温故知新
情景导入
1.基本不等式的两种常用变形形式
2
02
类型一:配凑法
概念讲解
例1. 求函数() = +
+
(x> -1) 的最小值.
解: ∵ >-1,∴ + >0.
当且仅当 + =
即=0
+
取“=”号.
∴当 =0 时, 函数 f(x) 的最小值是 1
概念讲解
练习. 求函数() = +
+
(x> -1) 的最小值.
解: ∵ < <
配凑系数
,∴ − > .
∴ = ( − ) =
=
当且仅当 = ( − ),即 =
时,取“=”号.
∴ = ( − ) 的最大值为
【课件】基本不等式(第二课时)2023-2024学年高一数学(人教A版2019必修第一册)

出发使用基本不等式,求得最值.
练一练
2+1
已知a>1,b>0,则
+2a的最小值为
(−1)
提示:
目标式局部:b2+1≥2b,
所以
2+1
2
+2a≥
(−1)
−1
+2(a-1)+2≥…
.
用基本不等式求最值
( )
例3. 已知 x>0, y>0 ,x+y+2=xy,则xy的
条
件
最
值
之
最小值为
.
2
+2
+
2 (−2)2 (−1)2
=
+
+1
4 1
=(m+n)+( + )-6(以下逆代)
用基本不等式求最值
( )
七
条
件
最
值
之
等
价
变
形
1
例6.已知x>0,y>0,且
+2
+
1 1
= ,求xy的最小值.
+2 3
1
解:由等式
+2
1
3
变形得xy=x+y+8
+
1
+2
=
所以xy≥2 +8 解得xy最小值为16
( )
一
直
接
求
最
值
例1. 已知 x>0,
则y= 2
的最大值
+2+4
1
2.2基本不等式课件高一上学期数学人教A版2

拓展-基本不等式的灵活运用
拓展-基本不等式的灵活运用
解析 正数x,y满足x+y=1,即有(x+2)+(y+1)=4,
则x+4 2+y+1 1=14[(x+2)+(y+1)]x+4 2+y+1 1
=145+xy+ +21+4(xy++21)≥145+2 xy+ +21·4(xy++21)=14×(5+4)=94,
当且仅当 x=2y=23时,取得最小值94.
拓展-基本不等式的灵活运用
变式 (1)已知 2a+b=1,a>0,b>0,则1a+1b的最小值是( )
A.2 2
B.3-2 2
C.3+2 2
D.3+ 2
(2)已知 a,b,c 都是正数,且 a+2b+c=1,则1a+1b+1c的最小值是( )
A.3+2 2
B.3-2 2
C.6-4 2
D.6+4 2
基本不等式
基本不等式(均值不等式):
a b ab (a 0,b 0) 2
算术 平均值
几何 平均值
(当且仅当a=b时,等号成立)
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.
基本不等式的证明
分析法
基本不等式的证明
思考:我们是否还可以用其他方法证明基本不等式?
证明:a b a(b a 0,b 0)(当且仅当a=b时,等号成立)
(3)解 ∵0<x<m,∴x>0,m-x>0.∴x(m-x)≤x+m2 -x2=m42. 当且仅当 x=m-x 时,即 x=m2 时,x(m-x)(0<x<m)取最大值m42.
人教版高中数学A版必修一2.2 基本不等式课件

一二
课前篇 自主预习
2.填空
我们称不等式 ������������ ≤ ������+2������为基本不等式,其中 a>0,b>0,当且仅当 a=b 时,等号成立.
∴xy≤4,当且仅当 x=y=2 时,等号成立, ∴xy 的最大值为 4.
答案:(1)4 (2)4
课前篇 自主预习
探究一
探究二
探究三 随堂演练
基本不等式的理解
例1下列命题正确的是( )
A.若 x≠0,则 x+4������≥4
B.若 a,b∈R,且 ab>0,则������������ + ������������≥2
课堂篇 探究学习
探究一
探究二
探究三 随堂演练
变式训练2(1)已知a,b,c,d都是正数,求证:(ab+cd)(ac+bd)≥4abcd.
(2)已知 a>0,b>0,且 a+b=2,求证:1������ + 1������≥2. 证明(1)因为 a,b,c,d 都是正数,所以
ab+cd≥2 ������������������������,ac+bd≥2 ������������������������,
C.
������2 + 2 +
1 的最小值为
������2+2
2
基本不等式(2)

3.4.1基本不等式(2)一、学习目标1.通过本节学习,掌握最值原理,并且能用最值原理解决相关问题;2.通过小组活动培养学生观察、探究的能力,并能体会出证明不等式的基本思想方法.二、教学重点、难点: 利用基本不等式求解最值.三、课前自学问题1:将 36拆成两个正数之积,使和最小,怎样拆?问题2:将8 拆成两个正数之和,使积最大,怎样拆?分组活动: 分组尝试把问题1,2一般化.已知y x ,都是正数,①如果积xy 是定值p ,那么当 时,和y x +有最小值 ; ②如果和y x +是定值s ,那么当 时,积xy 有最大值 .四、问题探究例1 求函数)0(16>+=x x x y 的最小值.变式1:求函数),2(,216+∞-∈++=x x x y 的最小值;变式2:求函数xx y 16+=的值域;变式3:求函数16322++=x x y 的最小值;变式4:已知0>x ,求函数44)(2+=x x x f 的值域.(若0<x 呢?)例2:若0>a ,0>b ,且6=+b a ,求ab 2的最大值.变式:若0>a ,0>b ,且63=+b a ,求ab 2的最大值.五、反馈小结书99练习4,5课后作业:1.已知0x >,求423x x--的最大值,并求相应的x 值.2.已知02x <<,求函数()f x =x 值.3.求下列函数的最值: 的最小值求已知y x xx y ,0,9)1(2>+=.的最大值求已知y x x x y ,2,421)2(-<++=.(3)的最小值求求函数y x x x y .0,422<+=.(4) 求函数)0(4≠+=x xx y 的值域.4.已知1,1>>y x ,且4lg lg =+y x .⑴求y x lg lg ⋅的最大值;⑵求)lg(y x +的最小值; ⑶求yx 11+的最小值.5.已知,20520,0=+>>y x y x ,且 求y x lg lg +的最大值.6.正数b a ,满足3++=b a ab ,求ab 的最小值.。
高一数学复习考点知识与题型专题讲解2---基本不等式与二次不等式

高一数学复习考点知识与题型专题讲解专题02基本不等式与二次不等式【专题综述与核心素养要求】与“集合”“常用逻辑用语”一样,“相等关系与不等关系”和“从函数观点看一元二次方程和一元二次不等式”的内容也是《课程标准(2017年版)》规定的高中数学课程的预备知识.它们的作用都是为高中数学课程做好学习心理、学习方式和知识技能等方面的准备,帮助学生完成初高中数学学习的过渡.为什么“相等关系与不等关系”和“从函数观点看一元二次方程和一元二次不等式”的内容能发挥这样重要的作用?它们为高中数学课程的学习做了哪些方面的准备呢?首先,相等关系、不等关系是数学中最基本的数量关系,是构建方程、不等式的基础,而方程和不等式都是重要的数学工具,在解决问题中有广泛的应用,因此对方程和不等式内容的学习,主要是为高中数学课程提供工具方面的准备.其次,函数是贯穿高中数学课程的最重要的概念和思想方法,用函数的观点看方程和不等式是要向学生渗透一种重要的思想方法——如何从函数的观点理解其他数学对象,进而把握不同数学对象的共性和相互关系.而这种思想方法对学生高中阶段的数学学习是非常重要的.最后,从学习方法来看,本章要在回顾、梳理等式内容的基础上,提炼等式中蕴含的思想方法,以及用一次函数的观点看一次方程、不等式的思想方法,再把这些思想方法迁移到对不等式内容的学习中.这种“回顾、梳理—提炼—迁移”的学习方法将适用于高中许多内容的学习.【重要知识点与题型快速预览】【知识点精解精析】别名性质内容注意性质1 对称性可逆性质2 传递性同向性质3 可加性可逆性质3的推移项法则可逆论性质4 可乘性的符号性质5 同向可加性同向性质6 同向同正可乘性同向,同正性质7 可乘方性同正性质8 可开方性(1)三个“二次”之间的关系由一元二次不等式的一般形式知,任何一个一元二次不等式整理成一边形式为或,而且我们已经知道对于一元二次方程(,其中),它的解按照可分为三种情况.相应地,二次函数的图象与轴的位置关系也分为三种情况,因此,对应的一元二次不等式(或)的解集我们也分三种情况进行讨论.二次函数的图象一元二次方程的根有两不同实根有两个相等的实根无实根一元二次不等式的解集的解集或的解集时解集的结构可记为:的解集为“大于大根或小于小根”;的解集为“大于小根且小于大根”.(2)解一元二次不等式的一般步骤①对不等式变形,使一端为零且二次项系数大于零;②计算判别式;③当时,求出相应的一元二次方程的根;④根据二次函数图象写出一元二次不等式的解集.(1)重要不等式,当且仅当时,等号成立.(2)基本不等式如果,那么,当且仅当时,等号成立.其中,叫做正数的算术平均数,叫做正数的几何平均数.因此,基本不等式可以叙述为:两个正数的算术平均数不小于它们的几何平均数.温馨提示①基本不等式成立的条件是.②从不等式成立的条件来看,要求,而对没有要求.例如,当,时,成立,但显然不成立. ③事实上,当时,我们分别用代替重要不等式中的,可得,变形可得.④基本不等式可变形为等.⑤由基本不等式,我们可以得到一个常用结论:.【必知必会题型深度讲解】解一元二次不等式的一般步骤如下: (1)化成标准式或.(2)计算对应方程根的判别式. (3)求出对应方程的解.(4)画出相应二次函数的图象.(5)由图象写出不等式的解集.【典型例题1】解下列不等式:(1)260x x -->; (2)2251010x x -+>; (3)2210x x -++<.【典型例题2】解下列不等式:(1)2+3x -2x 2>0; (2)x (3-x )≤x (x +2)-1; (3)x 2-2x +3>0.【典型例题3】已知不等式()21460a x x --+>的解集为{}31x x -<<.(1)解不等式()2220xa x a +-->;(2)b 为何值时,230ax bx ++≥的解集为R ?在解含有参数的一元二次不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”,一般从如下三个方面进行考虑:(1)关于不等式类型的讨论:二次项的系数; (2)关于不等式对应的方程的根的讨论:两根(),无根(); (3)关于不等式对应的方程根的大小的讨论:.【典型例题1】求关于x 的不等式2(1)0x a x a +--<的解集,其中a 是常数.【典型例题2】解关于x 的不等式:()210x x a a --->.【典型例题3】解下列含参数的不等式:(1)2220x ax a --<; (2)()2110axa x -++≤;(3)230x mx m --≤.(1)含参数的不等式的恒成立问题通过分离参数,把参数的范围问题转化为函数的最值问题.在的最大值与最小值存在的条件下,恒成立;恒成立.(2)一元二次不等式的恒成立问题 ①对任意实数均成立对任意实数均成立②若(或)在时恒成立,可利用单调性或分离参数法等求解.【典型例题1】当[]13x ∈,时,一元二次不等式2280x x a -+-≤恒成立,求实数a 的取值范围.【典型例题2】已知不等式2210ax ax ++>在x ∈R 时恒成立,求实数a 的取值范围.【典型例题3】要使函数()124xx f x a=++·在(]1x ∈-∞,时()0f x >恒成立,求a 的取值范围. (1)比较两个实数与的大小,作差法需归结为判断它们的差的符号,因此,因式分解时越彻底越好,若用配方法化成和的形式,则各项符号需相同.(2)用作商法比较大小时,被除数与除数同号,否则不等号方向由可能弄错. (3)比较两个数或代数式(均大于零)的大小,也可化为比较两个数平方的大小.(4)在比较两个数的大小时,若作差后不易变形,则可与中间量(如0或1等)进行比较,再由不等式的传递性得到两数的大小关系.(5)在比较两个数的大小时,若差式中变量较多,不易变形,则应考虑消元,减少式中变量,以利于判断,差式的符号.【典型例题1】比较下面两组数的大小:(1)3274;(2710314【典型例题2】已知0a >,0b >,试比较11a b M a b =+++与11b aN a b=+++的大小. 【典型例题3】比较下列各组中两个代数式的大小:(1)231x x -+与221x x +-; (2)当0a >,0b >且ab 时,a b a b 与b a a b .(1)对于条件不等式的证明,充分利用条件是关键,要注意“1”的整体代换及几个“=”必须保证同时成立.(2)证明不等式时要注意灵活变形,可以多次利用基本不等式的变形形式.【典型例题1】已知,,a b c 都是正实数,求证:a b cab bc ca ++++.【典型例题2】已知a ,b ,c 是不全相等的正数,求证:()()()2222226a b c b c a c a b abc +++++>. 【典型例题3】已知0,0,0a b c >>>,求证:32c a b a b b c a c +++++. (1)利用基本不等式求最值的条件利用基本不等式求最值,必须同时满足以下三个条件,一正、二正、三相等. 即:①都是正数. ②积(或和)为定值(有时需通过“配凑、拆分”找出定值).③与必须能够相等(等号能够取到).特别地,当式子中等号不成立时,不能应用基本不等式,而应改用函数的单调性求最值. (2)构造定值条件的常用技巧①加项变换;②拆项变换;③统一换元;④平方后利用基本不等式. (2)基本不等式与最值 设是正数,①若(和为定值),则当时,积取得最大值; ②若(积为定值),则当时,和取得最小值.【典型例题1】是否存在正实数a 和b ,同时满足下列条件:①10a b +=;②1a bx y+=(x >0,y >0)且x y +的最小值为18,若存在,求出a ,b 的值;若不存在,说明理由.【典型例题2】求下列函数的最大值和最小值:(1)13y x x =-+;(2)2,[1,4]y x x x=+∈;(3)4,[2,8]y x x x=-∈; (4)1121,,212y x x x ⎛⎫=-+∈-∞- ⎪+⎝⎭. 【典型例题3】已知函数22()x x af x x-+=. (1)当4a =时,求函数()f x 在(0,)x ∈+∞上的最小值;(2)若对任意的(0,),()0x f x ∈+∞>恒成立.试求实数a 的取值范围; (3)若0a >时,求函数()f x 在[2,)+∞上的最小值.应用基本不等式解决实际问题的步骤: (1)仔细阅读题目,透彻理解提议;(2)分析实际问题中的数量关系,引入未知数,并用它表示其他的变量,把要求最值的变量表示为关于未知数的函数;(3)应用基本不等式求出函数的最值; (4)还原实际问题,作答.对于实际问题一定要注意变量的取值范围.【典型例题1】为迎北京冬奥会,某校要设计如图所示的一张矩形宣传广告牌,该广告牌含有大小相等的左、中、右三个矩形栏目,这三个矩形栏目的面积之和为26000cm ,四周空白的宽度为10cm ,栏与栏之间的中缝空白的宽度为5cm ,怎样确定广告矩形栏目长与宽的尺寸(单位:cm ),使整个矩形广告牌面积最小?【典型例题2】如图,某房地产开发公司计划在一栋楼区内建造一个矩形公园ABCD ,公园由矩形的休闲区(阴影部分)1111D C B A 和环公园人行道组成,已知休闲区1111D C B A 的面积为1000平方米,人行道的宽分别为4米和10米,设休闲区的长为x 米.(1)求矩形ABCD 所占面积S (单位:平方米)关于x 的函数解析式; (2)要使公园所占面积最小,问休闲区1111D C B A 的长和宽应分别为多少米?【典型例题3】某小区要建一个八边形的休闲区,如图所示,它的主要造型平面图是由两个相同的矩形ABCD 和EFGH 构成的面积为2200m 的十字形区域.计划在正方形MNPQ 上建一个花坛,造价为4200元/2m ,在四个相同的矩形(图中阴影部分)上铺设花岗岩地面,造价为210元/2m ,再在四个等腰直角三角形上铺设草坪,造价为80元/2m .求当AD 的长度为多少时,建设这个休闲区的总价最低.。
基本不等式(第2课时)讲义-高一上学期数学人教A版

思考:
两个正数的积为定值,它们的和一定有最小值吗?
【例题练习】
题型一:含一个变量的代数式的最值
例1.(1)对于代数式 ;①当 时,求其最小值;②当 时,求其最大值.
(2)已知 ,求 的最小值.
(3)已知 ,求 的最大值.
(4)已知 ,求 的最大值.
(5)已知 ,求 的最小值.
总结:利用基本不等式求最值的关键是获得定值条件.解题时应对照已知条件和欲求的式子,运用适当的“拆项、添项、配凑、变形”等方法创设使用基本不等式的条件,具体可以归纳为:一不正,用其相反数,改变不等号方向;二不定,应凑出定和或定积;三不等,一般需用其他方法,如尝试利用函数的单调性.
练习:
1.设 ,则 的最大值是( )
B. C.
2.设 ,求 的最小值.
3.设 ,求 的最大值.
题型二:含两个变量的代数式的最值例2 (1)已知 ,且 ,求 Nhomakorabea最大值.
(2)已知 ,且 ,求 的最小值.
(3)若正数 满足 ,则 的最小值是( )
A. B. C.5
总结:
(1)拼凑法的实质在于代数式的灵活变形,拼系数、凑常数是关键,利用拼凑法求解最值应注意以下几个方面的问题:
2.已知 均为正数,且 ,则 的最小值为.
3.若 是正数,则 的最小值是( )
A.3 B. D.
4.已知 ,则 的最小值为.
【课后巩固】
,则函数 ( )
A.有最大值4 C.有最大值—2
,且 ,则 的最大值为( ).
A.80 C.81
在 处取得最小值,则 等于( )
B.72 C.4
高一数学基本不等式2

睛,两边是怪异的淡白色粉丝耳朵,鼻子下面是威猛的蓝宝石色电闸一样的嘴唇,说话时露出笨拙的紫玫瑰色树皮般的牙齿,一条奇特的浅灰色扫帚一般的舌头确实非
常猜疑和超脱。他极似天蓝色肥肠似的身材的确绝对的猛爆却又透着一丝霸气,高大的暗灰色细小菱角般的胡须好像绝无仅有的绝妙和威猛。那一双精悍的青兰花色面
条样的眉毛,真的有些时尚但又有些标准。再看P.妥奥姆斯政委的身形,他有着瘦瘦的极似弯刀造型的肩膀,肩膀下面是结实的极似香肠造型的手臂,他怪异的水白
傲的蓝宝石色丸子造型的神态感觉空前粗野却又透着一丝标新立异。…………那个身穿多变的流峰袄的副l官是
女议长U.赫泰娆嘉妖女。她出生在J.荷赤
可星国的纽扣草原,绰号:银拳警棍!年龄看上去大约十四五岁,但实际年龄足有五六千岁,身高两米八左右,体重约六百公斤。此人最善使用的兵器是『红火跳神花
卷锤』,有一身奇特的武功『银光杖妖鸟巢头』,看家的魔法是『白金瀑祖折扇理论』,另外身上还带着一件奇异的法宝『粉烟秋妖贝壳石』。她有着浮动的深灰色橘
高一数学必修5第三章《不等式》 3.4 基本不等式 第2课时
复习巩固
利用
求最值的要点:
(1)最值存在的条件的: 一正, 二定,三相等.
(2)积一定, 和有最小值
(3)和一定, 积有最大值
典例讲评
例. 若x>0,y>0,且
,求xy的最小值.
典例讲评
例2.(1)用篱笆围成一个面积为100m2 的矩形菜园,问这个矩形的长、宽各为 多少时,所用篱笆最短.最短的篱笆是多少
子模样的身材
优游 优游
典例讲评
例3. 某工厂要建造一个长方形无盖 蓄水池, 其容积为4800 m3, 深为 3m, 如果池底每平方米的造价为150元, 池壁每平方米的造价为120元, 怎样 设计水池能使总造价最低? 最低总 造价是多少?
2.2+基本不等式(共2课时)(教学课件)(人教A版2019高一数学必修第一册)

① 已 知 ≠ 0 , 求 + 的最 小值 ; 解答 过程 : +
1
2 + 4 +
≥2
×
③ 设 > 1, 求 = +
2
即
−1
A. 0 个
2
的 最小 值; 解 答过 程:
−1
=+
= 2时 等号 成 立, 把 = 2代 入 2
B. 1 个
2
−1
C. 2 个
=
≥2
2
,
−1
−
,即
&# 2 + 4 = 1 时取 等 号,
对 ③ : > 1 , − 1 > 0,
≤ −2
−
⋅ −
= −2,
= < 0时等 号 成立 ,故 ① 的用 法有 误,
故①错误;
对②: =
的 最小 值; 解答 过程 :可 化得 =
立.当且仅当 = 时,等号成立.把这个过程倒过来,就是证明的过程.
新知:基本不等式的理解
1、对公式
+
≥
+
及
≥ 的理解.
(1)成立的条件是不同的:前者只要求, 都是实数,而后者要求, 都是正数;
(2)取等号“=” 的条件在形式上是相同的,都是“当且仅当 = 时取等号”.
2、由公式 + ≥ 和
①
②
③
+
≥ 可以引申出常用的常用结论
2.2 基本不等式(重难点突破)解析版 2023-2024学年高一数学重难点突破

2.2 基本不等式【基本不等式(或)均值不等式】知识点一:基本不等式1.对公式222a b ab +≥及2a b+≥的理解.(1)成立的条件是不同的:前者只要求,a b 都是实数,而后者要求,a b 都是正数;(2)取等号“=” 的条件在形式上是相同的,都是“当且仅当a b =时取等号”.2a b+≤的证明方法一:几何面积法如图,在正方形ABCD 中有四个全等的直角三角形.方法二:代数法∵2222()0a b ab a b +-=-≥,当a b ≠时,2()0a b ->;当a b =时,2()0a b -=.所以22()2a b ab +≥,(当且仅当a b =时取等号“=”).2a b+≤的几何意义如图,AB 是圆的直径,点C 是AB 上的一点,AC a =,BC b =,过点C 作DC AB ⊥交圆于点D ,连接AD 、BD .易证~Rt ACD Rt DCB ∆∆,那么2CD CA CB =⋅,即CD =.这个圆的半径为2a b +,它大于或等于CD ,即2a b+≥其中当且仅当点C 与圆心重合,即a b =时,等号成立.知识点诠释:在数学中,我们称2a b+为,a b 的算术平均数,称,a b 的几何平均数. 因此基本不等式可叙述为:两个正数的算术平均数不小于它们的几何平均数.2a b+≤求最大(小)值在用基本不等式求函数的最值时,应具备三个条件:一正二定三取等.① 一正:函数的解析式中,各项均为正数;② 二定:函数的解析式中,含变数的各项的和或积必须有一个为定值;③ 三取等:函数的解析式中,含变数的各项均相等,取得最值.【基本不等式的变形与拓展】1.(1)若R b a ∈,,则ab b a 222≥+;(2)若R b a ∈,,则222b a ab +≤(当且仅当b a =时取“=”).2.(1)若00a ,b >>,则ab ba ≥+2;(2)若00a ,b >>,则ab b a 2≥+(当且仅当b a =时取“=”);(3)若00a ,b >>,则22⎪⎭⎫⎝⎛+≤b a ab (当且仅当b a =时取“=”).3.若0x >,则12x x +≥(当且仅当1x =时取“=”);若0x <,则12x x+≤-(当且仅当1x =-时取“=”);若0x ≠,则12x x+≥,即12x x +≥或12x x +≤-(当且仅当b a =时取“=”).4.若0>ab ,则2≥+ab b a (当且仅当b a =时取“=”);若0ab ≠,则2a b b a +≥,即2a b b a +≥或2a bb a +≤-(当且仅当b a =时取“=”).5.一个重要的不等式链:2112a b a b+≤≤≤+.6.函数()()0,0bf x ax a b x=+>>图象及性质(1)函数()0)(>+=b a xbax x f 、图象如右图所示:(2)函数()0)(>+=b a xbax x f 、性质:①值域:(),⎡-∞-+∞⎣;②单调递增区间:,,⎛⎫-∞+∞ ⎪ ⎪⎝⎭;单调递减区间:0,,0⎛⎡⎫- ⎪⎢ ⎪⎝⎣⎭.7.(1)当两个正数的积为定植时,可以求它们的和的最小值,当两个正数的和为定植时,可以求它们的积的最小值,正所谓“积定和最小,和定积最大”;(2)求最值的条件“一正,二定,三相等”;(3)均值定理在求最值、比较大小、求变量的取值范围、证明不等式、解决实际问题方面有广泛的应用.重难点突破(一) 基本不等式的简单应用重难点突破(二) 利用基本不等式求最值例2.(1)、(2022·陕西·榆林市第十中学高一期末)函数()4111y x x x =++>-+的最小值为______.【答案】4【解析】【分析】利用基本不等式直接求解即可【详解】因为1x >-,所以10x +>,所以4141y x x =++≥=+,当且仅当411x x +=+,即1x =时取等号,所以()4111y x x x =++>-+的最小值为4,故答案为:4【变式训练2-2】.(2023·山东烟台·统考三模)(多选题)已知0,0a b >>且42a b +=,则( )【变式训练3-1】、(2022·四川资阳·高一期末)已知正实数x ,y 满足111x y +=,则4x y +最小值为______.【答案】9【解析】【分析】利用基本不等式的性质直接求解即可.【详解】正数x ,y 满足:111x y+=,∴()11444559y x x y x y x y x y ⎛⎫+=+⋅+=++≥+= ⎪⎝⎭,当且仅当4y x x y =,即2x y =,233x y ==,时 “=”成立,故答案为:9.重难点突破(四) 不等式的证明技巧与综合处理技巧重难点突破(五) 均值不等式在实际问题中的应用【答案】()800f x ⎛=⨯ ⎝价为36000元.重难点突破(六) 挑战满分(压轴题)【点睛】本题考查了“乘1法”与基本不等式的性质的应用,同时考查转化思想和计算能力.。
高一数学必修一 教案 2.2 基本不等式

2.2 基本不等式 第1课时 基本不等式学习目标 1.掌握基本不等式及推导过程.2.能熟练运用基本不等式比较两实数的大小.3.能初步运用基本不等式进行证明和求最值.知识点 基本不等式1.如果a >0,b >0a =b 时,等号成立.其中a +b2叫做正数a ,b 的算术平均数,ab 叫做正数a ,b 的几何平均数.2.变形:ab ≤⎝⎛⎭⎪⎫a +b 22,a ,b ∈R ,当且仅当a =b 时,等号成立.a +b ≥2ab ,a ,b 都是正数,当且仅当a =b 时,等号成立.1.对于任意a ,b ∈R ,a 2+b 2≥2ab .( √ ) 2.n ∈N *时,n +2n>2 2.( √ )3.x ≠0时,x +1x≥2.( × )4.若a >0,则a 3+1a2的最小值为2a .( × )一、利用基本不等式比较大小例1 某工厂生产某种产品,第一年产量为A ,第二年的增长率为a ,第三年的增长率为b ,这两年的平均增长率为x (a ,b ,x 均大于零),则( ) A .x =a +b2B .x ≤a +b2C .x >a +b2D .x ≥a +b2考点 基本不等式比较大小 题点 利用基本不等式比较大小 答案 B解析 第二年产量为A +A ·a =A (1+a ),第三年产量为A (1+a )+A (1+a )·b =A (1+a )(1+b ). 若平均增长率为x ,则第三年产量为A (1+x )2. 依题意有A (1+x )2=A (1+a )(1+b ), ∵a >0,b >0,x >0, ∴(1+x )2=(1+a )(1+b )≤⎣⎢⎡⎦⎥⎤1+a 1+b 22, ∴1+x ≤2+a +b 2=1+a +b 2,∴x ≤a +b2.反思感悟 基本不等式a +b2≥ab 一端为和,一端为积,使用基本不等式比较大小要善于利用这个桥梁化和为积或者化积为和.跟踪训练1 若0<a <1,0<b <1,且a ≠b ,试找出a +b ,a 2+b 2,2ab ,2ab 中的最大者. 解 ∵0<a <1,0<b <1,且a ≠b , ∴a +b >2ab ,a 2+b 2>2ab ,∴四个数中最大的应从a +b ,a 2+b 2中选择. 而a 2+b 2-(a +b )=a (a -1)+b (b -1), ∵0<a <1,0<b <1,∴a (a -1)<0,b (b -1)<0, ∴a 2+b 2-(a +b )<0, 即a 2+b 2<a +b ,∴a +b 最大.二、利用基本不等式直接求最值例2 (1)当x >0时,求12x+4x 的最小值;(2)当x <0时,求12x+4x 的最大值;(3)当x >1时,求2x +8x -1的最小值; (4)已知4x +a x(x >0,a >0)在x =3时取得最小值,求a 的值. 解 (1)∵x >0,∴12x>0,4x >0.∴12x+4x ≥212x·4x =8 3.当且仅当12x=4x ,即x =3时取最小值83,∴当x >0时,12x+4x 的最小值为8 3.(2)∵x <0,∴-x >0. 则12-x+(-4x )≥212-x4x =83,当且仅当12-x =-4x 时,即x =-3时取等号.∴12x+4x ≤-8 3.∴当x <0时,12x+4x 的最大值为-8 3.(3)2x +8x -1=2⎣⎢⎡⎦⎥⎤x -14x -1+2, ∵x >1,∴x -1>0, ∴2x +8x -1≥2×24+2=10, 当且仅当x -1=4x -1,即x =3时,取等号.(4)4x +a x≥24x ·a x=4a ,当且仅当4x =ax,即a =4x 2=36时取等号, ∴a =36.反思感悟 在利用基本不等式求最值时要注意三点:一是各项均为正;二是寻求定值,求和式最小值时应使积为定值,求积式最大值时应使和为定值(恰当变形,合理拆分项或配凑因式是常用的解题技巧);三是考虑等号成立的条件是否具备. 跟踪训练2 已知x >0,y >0,且x +y =8,则(1+x )·(1+y )的最大值为( ) A .16 B .25 C .9 D .36 答案 B解析 因为x >0,y >0,且x +y =8,所以(1+x )(1+y )=1+x +y +xy =9+xy ≤9+⎝ ⎛⎭⎪⎫x +y 22=9+42=25,因此当且仅当x =y =4时, (1+x )·(1+y )取最大值25. 三、用基本不等式证明不等式例3 已知a ,b ,c 都是正数,求证:a +b +c -ab -bc -ac ≥0. 证明 ∵a ,b ,c 都是正数,∴a +b ≥2ab ,b +c ≥2bc ,a +c ≥2ac , ∴a +b +b +c +a +c ≥2(ab +bc +ac ), ∴a +b +c ≥ab +bc +ac , 即a +b +c -ab -bc -ac ≥0.反思感悟 利用基本不等式证明不等式的策略与注意事项(1)策略:从已证不等式和问题的已知条件出发,借助不等式的性质和有关定理,经过逐步的逻辑推理,最后转化为所求问题,其特征是以“已知”看“可知”,逐步推向“未知”. (2)注意事项:①多次使用基本不等式时,要注意等号能否成立;②累加法是不等式证明中的一种常用方法,证明不等式时注意使用;③对不能直接使用基本不等式的证明可重新组合,形成基本不等式模型,再使用. 跟踪训练3 若实数a <0,求证:a +1a≤-2,并指出等号成立的条件.证明 根据题意,a <0,则-a >0, 左式=a +1a=-⎣⎢⎡⎦⎥⎤a⎝ ⎛⎭⎪⎫-1a ,又由(-a )+⎝ ⎛⎭⎪⎫-1a ≥2a⎝ ⎛⎭⎪⎫-1a =2, 则有a +1a≤-2,当且仅当a =-1时,等号成立.故a +1a≤-2,当且仅当a =-1时,等号成立.1.若0<a <b ,则下列不等式一定成立的是( ) A .a >a +b2>ab >b B .b >ab >a +b2>aC .b >a +b2>ab >a D .b >a >a +b2>ab考点 基本不等式的理解 题点 基本不等式的理解 答案 C解析 ∵0<a <b ,∴2b >a +b ,∴b >a +b2>ab .又∵b >a >0,∴ab >a 2, ∴ab >a .故b >a +b2>ab >a .2.下列不等式正确的是( )A .a +1a≥2B .(-a )+⎝ ⎛⎭⎪⎫-1a ≤-2C .a 2+1a2≥2D .(-a )2+⎝ ⎛⎭⎪⎫-1a 2≤-2答案 C解析 ∵a 2>0,故a 2+1a2≥2成立.3.下列等式中最小值为4的是( ) A .y =x +4xB .y =2t +1tC .y =4t +1t(t >0)D .y =t +1t答案 C解析 A 中x =-1时,y =-5<4,B 中t =-1时,y =-3<4,C 中y =4t +1t ≥24t ·1t=4,当且仅当t =12时等号成立,D 中t =-1时,y =-2<4.故选C.4.下列不等式中,正确的是( ) A .a +4a≥4B .a 2+b 2≥4ab C.ab ≥a +b2D .x 2+3x2≥2 3答案 D解析 a <0,则a +4a≥4不成立,故A 错;a =1,b =1,则a 2+b 2<4ab ,故B 错; a =4,b =16,则ab <a +b2,故C 错;由基本不等式可知D 项正确. 5.已知x >-1,则x +10x +2x +1的最小值为________.答案 16解析x +10x +2x +1=x +1+9x +1+1x +1=x +12+10x +19x +1=(x +1)+9x +1+10, ∵x >-1,∴x +1>0, ∴(x +1)+9x +1+10≥29+10=16. 当且仅当x +1=9x +1, 即x =2时,等号成立.1.知识清单:两个不等式:a 2+b 2≥2ab (a ,b ∈R ),a +b2≥ab (a ,b 都是正数).2.方法归纳:通过拆项、加项配凑成基本不等式的形式. 3.常见误区:一正、二定、三相等,常缺少条件导致错误.1.给出下列条件:①ab >0;②ab <0;③a >0,b >0;④a <0,b <0. 其中可使b a +a b≥2成立的个数是( ) A .1 B .2 C .3 D .4 答案 C解析 根据基本不等式的条件,a ,b 同号, 则b a>0,故选C.2.a ,b ∈R ,则a 2+b 2与2|ab |的大小关系是( ) A .a 2+b 2≥2|ab | B .a 2+b 2=2|ab | C .a 2+b 2≤2|ab | D .a 2+b 2>2|ab |答案 A解析 ∵a 2+b 2-2|ab |=(|a |-|b |)2≥0,∴a 2+b 2≥2|ab |(当且仅当|a |=|b |时,等号成立). 3.若a ,b ∈R 且ab >0,则下列不等式中恒成立的是( ) A .a 2+b 2>2ab B .a +b ≥2ab C.1a +1b>2abD.b a +ab≥2答案 D解析 ∵a 2+b 2-2ab =(a -b )2≥0,∴A 错误; 对于B ,C ,当a <0,b <0时,显然错误; 对于D ,∵ab >0,∴b a +a b ≥2b a ·ab=2, 当且仅当a =b =1时,等号成立.4.若0<a <b 且a +b =1,则下列四个数中最大的是( ) A.12 B .a 2+b 2C .2abD .a答案 B解析 a 2+b 2=(a +b )2-2ab ≥(a +b )2-2·⎝ ⎛⎭⎪⎫a +b 22=12. a 2+b 2-2ab =(a -b )2≥0,∴a 2+b 2≥2ab .∵0<a <b 且a +b =1,∴a <12.∴a 2+b 2最大.5.已知a >0,b >0,且ab =2,那么( )A .a +b ≥4B .a +b ≤4C .a 2+b 2≥4 D .a 2+b 2≤4答案 C解析 ∵a >0,b >0,∴a +b ≥2ab =22,故A ,B 均错误.a 2+b 2≥2ab =4,故选C.6.已知a >b >c ,则a -bb -c 与a -c2的大小关系是____________________.答案 a -bb -c ≤a -c2解析 因为a >b >c ,所以a -b >0,b -c >0, 所以a -c2=a -bb -c2≥a -b b -c ,当且仅当a -b =b -c 时,等号成立. 7.设a ,b 为非零实数,给出下列不等式: ①a 2+b 22≥ab ;②a 2+b 22≥⎝⎛⎭⎪⎫a +b 22;③a +b 2≥ab a +b ;④a b +ba ≥2.其中恒成立的是________.(填序号)答案 ①②解析 由重要不等式a 2+b 2≥2ab ,可知①正确;a 2+b 22=2a 2+b 24=a 2+b 2a 2+b 24≥a 2+b 2+2ab4=a +b24=⎝⎛⎭⎪⎫a +b 22,可知②正确;当a =b =-1时,不等式的左边为a +b2=-1,右边为ab a +b =-12,可知③不正确; 当a =1,b =-1时,可知④不正确. 8.设a >0,b >0,给出下列不等式: ①a 2+1>a ;②⎝⎛⎭⎪⎫a +1a ⎝⎛⎭⎪⎫b +1b ≥4; ③(a +b )⎝ ⎛⎭⎪⎫1a +1b ≥4;④a 2+9>6a .其中恒成立的是________.(填序号)答案 ①②③解析 由于a 2+1-a =⎝ ⎛⎭⎪⎫a -122+34>0,故①恒成立;由于⎝ ⎛⎭⎪⎫a +1a ⎝ ⎛⎭⎪⎫b +1b =ab +1ab +b a +a b≥2ab ·1ab+2b a ·ab =4.当且仅当⎩⎪⎨⎪⎧ab =1ab ,b a =ab ,即a =b=1时,“=”成立,故②恒成立;由于(a +b )⎝ ⎛⎭⎪⎫1a +1b=2+b a +a b≥2+2b a ·a b =4.当且仅当a b =ba,即a =b 时,“=”成立,故③恒成立;当a =3时,a 2+9=6a ,故④不恒成立. 综上,恒成立的是①②③.9.设a >0,b >0,且a +b =1a +1b,证明:a +b ≥2.证明 由于a >0,b >0,则a +b =1a +1b =a +bab,由于a +b >0,则ab =1,即有a +b ≥2ab =2, 当且仅当a =b =1时取得等号,∴a +b ≥2. 10.(1)设0<x <32,求4x (3-2x )的最大值;(2)已知a >b >c ,求(a -c )⎝⎛⎭⎪⎫1a -b +1b -c 的最小值.解 (1)∵0<x <32,∴3-2x >0,∴4x (3-2x )=2[2x (3-2x )] ≤2⎣⎢⎡⎦⎥⎤2x 3-2x 22=92. 当且仅当2x =3-2x ,即x =34时,等号成立.∵0<34<32,∴4x (3-2x )⎝⎛⎭⎪⎫0<x <32的最大值为92. (2)(a -c )⎝ ⎛⎭⎪⎫1a -b +1b -c =(a -b +b -c )⎝⎛⎭⎪⎫1a -b +1b -c =1+1+b -c a -b +a -b b -c. ∵a >b >c ,∴a -b >0,b -c >0,∴2+b -c a -b +a -b b -c ≥2+2b -c a -b ·a -b b -c=4, 当且仅当a -b =b -c ,即2b =a +c 时取等号,∴(a -c )⎝ ⎛⎭⎪⎫1a -b +1b -c 的最小值为4.11.若xy 是正数,则⎝ ⎛⎭⎪⎫x +12y 2+⎝ ⎛⎭⎪⎫y +12x 2的最小值是( ) A .3 B.72 C .4 D.92答案 C解析 ⎝ ⎛⎭⎪⎫x +12y 2+⎝ ⎛⎭⎪⎫y +12x 2 =x 2+x y +14y 2+y 2+y x +14x2 =⎝⎛⎭⎪⎫x 2+14x 2+⎝ ⎛⎭⎪⎫y 2+14y 2+⎝ ⎛⎭⎪⎫x y +y x ≥1+1+2=4,当且仅当x =y =22或x =y =-22时取等号. 12.已知a >0,b >0,则下列不等式中不成立的是( )A .a +b +1ab ≥2 2B .(a +b )⎝ ⎛⎭⎪⎫1a +1b ≥4C.a 2+b 2ab≥2ab D.2ab a +b>ab 答案 D解析 a +b +1ab ≥2ab +1ab ≥ 22, 当且仅当a =b =22时,等号成立,A 成立; (a +b )⎝ ⎛⎭⎪⎫1a +1b ≥2ab ·21ab =4,当且仅当a =b 时,等号成立,B 成立;∵a 2+b 2≥2ab >0, ∴a 2+b 2ab≥2ab ,当且仅当a =b 时,等号成立,C 成立; ∵a +b ≥2ab ,a >0,b >0,∴2ab a +b ≤1,2ab a +b≤ab , 当且仅当a =b 时,等号成立,D 不成立.13.x 2+2x -1(x >1)的最小值为________. 答案 2+2 3解析 令x -1=t ,则x =1+t 且t >0,∴x 2+2x -1=1+t 2+2t =t 2+2t +3t=t +3t+2≥23+2. 当且仅当t =3t,即t =3, x =3+1时,等号成立.14.已知x >0,y >0,2x +3y =6,则xy 的最大值为________.答案 32解析 因为x >0,y >0,2x +3y =6,所以xy =16(2x ·3y )≤16·⎝ ⎛⎭⎪⎫2x +3y 22 =16·⎝ ⎛⎭⎪⎫622=32. 当且仅当2x =3y ,即x =32,y =1时,xy 取到最大值32.15.若a >0,b >0,a +b =2,则下列不等式恒成立的是________.(写出编号)①ab ≤1;②a +b ≤2;③a 2+b 2≥2;④a 3+b 3≥3;⑤1a +1b≥2. 答案 ①③⑤解析 ∵a >0,b >0,a +b =2,∴ab ≤⎝ ⎛⎭⎪⎫a +b 22=1,∴①恒成立; 当a =b =1时,a +b =2>2,故②不恒成立;a 2+b 2≥a +b22=2,∴③恒成立;当a =b =1时,a 3+b 3=2<3,∴④不恒成立;1a +1b =12(a +b )⎝ ⎛⎭⎪⎫1a +1b =12⎝ ⎛⎭⎪⎫2+a b +b a ≥2, ∴⑤恒成立.故填①③⑤.16.若0<x <12,求x 1-4x 2的最大值. 解 由x 1-4x 2=x 21-4x 2=14·4x 21-4x 2=124x 21-4x 2≤12·4x 21-4x 22=14,当且仅当4x 2=1-4x 2,即x 2=18, x =24时取“=”,故x 1-4x 2的最大值为14.。
2基本不等式说课稿-高一上学期数学人教A版(2019)必修第一册

2基本不等式说课稿-高一上学期数学人教A版(2019)必修第一册第二章一元二次函数、方程和不等式§2.2《基本不等式》(第1课时)说课稿一、说教材分析本节课是人教A版必修第一册第二章《一元二次函数、方程和不等式》第2节《基本不等式》第1课时的内容。
基本不等式是一种重要且基本的不等式类型,在中学数学知识体系中也是一个非常重要的、基础的内容,它与很多重要的数学概念和性质有关。
基本不等式的代数结构也是数学模型思想的一个范例,借助这个模型可以求最大值和最小值。
学习基本不等式内容可以进一步发展学生的逻辑推理、数学运算和数学建模等数学核心素养,为后续进一步学习不等式内容打好基础。
二、说学情分析基本不等式是在学生已经学习了等式性质与不等式性质,并且具备了一定的推理论证能力的基础上进行的。
基本不等式是几何平均数不大于算术平均数的最简单和最基本的情形。
基本不等式的代数结构也是数学模型思想的一个范例,借助这个模型可以求最大值和最小值。
在理解和应用基本不等式的过程中,体现了数形结合、数学建模等数学思想。
通过该内容的学习,不仅能进一步发展学生的推理论证能力,数学运算和数学建模的数学素养,而且能使学生把这些认识迁移到后继的学习中去,为以后学习一元二次不等式等打好基础。
三、说教学目标1.通过对赵爽勾股圆方图的观察分析,抽象概括出基本不等式;理解基本不等式的三种不同证明方法;2.结合具体实例,会用基本不等式解决简单的最大(小)值问题;3.进一步发展数学抽象、逻辑推理、数学运算等数学核心素养和观察分析、抽象概括的能力;4.通过赵爽勾股圆方图,展现中国古代数学成就,厚植爱国主义情怀,增强民族自信。
四、说教学重点和难点重点:基本不等式的内容、意义,应用基本不等式解决简单的最大(小)值问题。
难点:基本不等式的证明过程。
五、说教法、学法分析1.教法:本节课以赵爽勾股圆方图引入,通过学生观察分析、抽象概括出基本不等式。
以问题驱动课堂,教师不断启发学生自主探究,充分发挥学生的积极性、主动性;在课堂上,教师有效地渗透数学思想方法,发展学生数学素养。
高一数学基本概念——第2章 不等式

第2章不等式2.1不等式的基本性质2.2一元二次不等式的解法二、一元二次不等式只含有一个未知数,并且未知数的最高次数是二次,这样的不等式叫做一元二次不等式。
2.3其他不等式的解法一、分式不等式二、绝对值不等式1、|x|的含义2、小结3、零点分段法把每个绝对值对应的零点求出然后放入数轴上,分区间讨论转化为整式不等式或不等式组来求解,这种方法叫做零点分段法。
高中数学基本概念2.4基本不等式及其应用*2.5 不等式的证明1.比较法作差作商后的式子变形,判断正负或与1比较大小22(1),,2,a b R a b ab a b ∈+≥=对任意有当且仅当时等号成立。
(2),,2a b a b R a b ++∈≥=对任意有当且仅当是等号成立。
高中数学基本概念作差比较法-----要证明a>b,只要证明a-b>0.作商比较法---已知a,b都是正数,要证明a>b,只要证明a/b>12.分析法从要证明的不等式出发,寻找使这个不等式成立的某一"充分的"条件,为此逐步往前追溯(执果索因),一直追溯到已知条件或一些真命题为止.3.综合法了解算术平均数和几何平均数的概念,能用平均不等式证明其它一些不等式.*4. 放缩法这也是分析法的一种特殊情况,它的根据是不等式的传递性.我们可以用放缩法的一支——"逐步放大法".*5.数形结合法数形结合是指通过数与形之间的对应转化来解决问题.数量关系如果借助于图形性质,可以使许多抽象概念和关系直观而形象,有利于解题途径的探求,这通常为以形助数;而有些涉及图形的问题如能转化为数量关系的研究,又可获得简捷而一般化的解法,即所谓的以数解形.数形结合的思想,其实质是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合,通过对图形的认识,数形的转化,可以培养思维的灵活性,形象性.通过数形结合,可以使复杂问题简单化,抽象问题具体化.*6.反证法先假定要证不等式的反面成立,然后推出与已知条件(或已知真命题)和矛盾的结论,从而断定反证假定错误,因而要证不等式成立.*7.穷举法对要证不等式按已知条件分成各种情况,加以证明(防止重复或遗漏某一可能情况).注意:在证明不等式时,应灵活运用上述方法,并可通过运用多种方法来提高自己的思维能力.。
高一数学2.2基本不等式笔记

高一数学2.2基本不等式笔记一、基本不等式的内容。
1. 定义。
- 对于任意实数a,b,有a^2+b^2≥slant2ab,当且仅当a = b时,等号成立。
- 证明:(a - b)^2=a^2-2ab + b^2≥slant0,移项可得a^2+b^2≥slant2ab。
2. 基本不等式√(ab)≤slant(a + b)/(2)(a>0,b>0)- 当且仅当a = b时,等号成立。
- 证明:- 因为(√(a)-√(b))^2=a - 2√(ab)+b≥slant0(a>0,b>0)。
- 移项可得a + b≥slant2√(ab),即√(ab)≤slant(a + b)/(2)。
二、基本不等式的几何解释。
1. 对于a^2+b^2≥slant2ab- 设直角三角形的两条直角边为a和b,则斜边为√(a^2)+b^{2}。
- 根据直角三角形的面积,S=(1)/(2)ab,同时S≤slant(1)/(2)×frac{a^2+b^2}{2}(当且仅当a = b时取等号),这就从几何角度解释了a^2+b^2≥slant2ab。
2. 对于√(ab)≤slant(a + b)/(2)(a>0,b>0)- 设a,b为正数,以a + b为长的线段AB,点C将AB分成AC=a,CB = b。
- 以AB为直径作半圆,过点C作CD⊥ AB交半圆于点D,则CD=√(ab),半径r=(a + b)/(2)。
- 由图形可知CD≤slant r,即√(ab)≤slant(a + b)/(2),当且仅当a = b时,C为AB中点,等号成立。
三、基本不等式的应用。
1. 求最值。
- 已知x>0,y>0,若xy = P(定值),则x + y≥slant2√(xy)=2√(P),当且仅当x = y=√(P)时,x + y取得最小值2√(P)。
- 若x + y = S(定值),则xy≤slant((x + y)/(2))^2=frac{S^2}{4},当且仅当x = y=(S)/(2)时,xy取得最大值frac{S^2}{4}。
高一【数学(人教A版)】基本不等式(2)-练习题
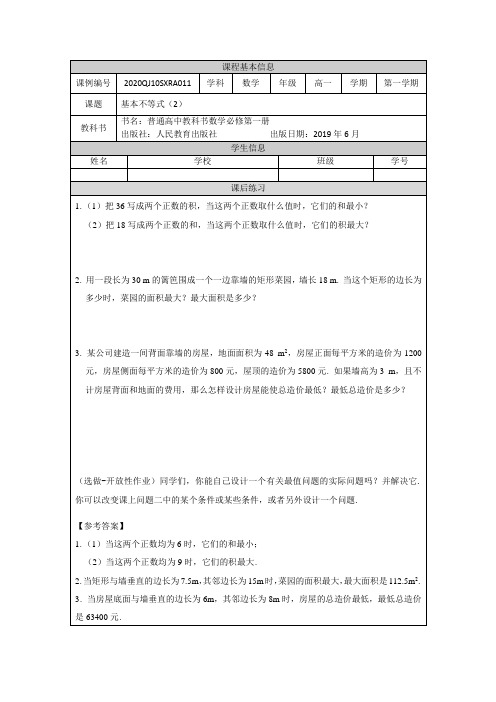
【参考答案】
1.(1)当这两个正数均为6时,它们的和最小;
(2)当这两个正数均为9时,它们的积最大.
2.当矩形与墙垂直的边长为7.5m,其邻边长为15m时,菜园的面积最大,最大面积是112.5m2.
3.当房屋底面与墙垂直的边长为6m,其邻边长为8m时,房屋的总造价最低,最低总造价是63400元.
课程基本信息
课例编号
2020QJ10SXRA011
学科
数学
年级
高一
学期
第一学期
课题
基本不等式(2)
教科书
书名:普通高中教科书数学必修第一册
出版社:人民教育出版社出版日期:2019年6月
学生信息
姓名
学校
班级
学号
课Байду номын сангаас练习
1.(1)把36写成两个正数的积,当这两个正数取什么值时,它们的和最小?
(2)把18写成两个正数的和,当这两个正数取什么值时,它们的积最大?
2.用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长18m.当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
3.某公司建造一间背面靠墙的房屋,地面面积为48m2,房屋正面每平方米的造价为1200元,房屋侧面每平方米的造价为800元,屋顶的造价为5800元.如果墙高为3m,且不计房屋背面和地面的费用,那么怎样设计房屋能使总造价最低?最低总造价是多少?
高一数学2.2基本不等式

x 1
x 1
当且即仅当x 1 1 ,即(x 1)2 1, x 2时,等号成立, x 1
因此所求的最小值为3.
2.变式: (2). 若 0 x 1 , 求 x(1-2x) 的最大值. 2
分析: 2x+(1-2x) 不=1是为 常数.
解 :因0 x 1 ,所以1-2x 0,
2 所以x(1-2x)
A
D
矩形花园的面积为x(24-2x) m2 x
令y x(24 2x)
B
C
则y 24x 2x2 2(x 6)2 72 (0 x 12)
当x=6时,函数y取得最小值为72
因此,这个矩形的长为12m、宽为6m时, 花园面积最大,最大面积是72m2
5. 变式:如图,用一段长为24m 的篱笆围一个一边
5.重要不等式与基本不等式的比较
适用范围
a2 b2≥2ab
a,b∈R
a b≥ ab 2
a>0,b>0
文字叙述
两数的平方和不 两个正数的算术平均数 小于它们积的2倍 不小于它们的几何平均数
“=”成立条件
a=b
a=b
注意:从不同角度认识基本不等式
三、巩固新知
1.例1 若x> 0ห้องสมุดไป่ตู้求 x 1 的最小值. x
xy ≤ 81 即x=y=9
因菜此x园y,面≤这积x个最2矩大y形,的最S2长大 、面宽积x都y是≤为81149mmS2时2 ,
5. 变式:如图,用一段长为24m 的篱笆围一个一边靠
墙的矩形花园,问这个矩形的长、宽各为多少时, 花园的面积最大,最大面积是多少?
解:设AB=x ,BC=24-2x ,
菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积
第2课时 基本不等式的实际应用 高一数学

已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利
用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为
y(单位:元).
(1)将总费用y用旧墙长度x表示出来;
(2)试确定x的值,使修建此矩形场地围墙的总费用最小,并求
出最小总费用.
· =9,
当且仅当 = ,即 y=2x 时,等号成立.
故(x+y) + 的最小值为 9.
防范措施
1.在运用基本不等式时,要特别注意等号成立的条件,尤其多
次使用基本不等式时,等号成立的条件必须相同,否则会造成
错误.
2.尽量对式子进行化简、变形,利用一次基本不等式求最值.
的最大值.
+
解:(1)∵x<,∴5-4x>0,
∴y=4x-2+
=-
当且仅当
- +
+3≤-2+3=1,
-
5-4x=
,即 x=1 时,上式等号成立,
-
故当 x=1 时,y 取得最大值 1.
(2)∵0<x<,∴1-2x>0,
+-
x=y= 时,取等号.
=
=
,
答案:(1)2
(2)
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内打“ ”,错误
的打“×”.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一次是到渔场的第二天,肖队长带领我们几个人去县城拉砖,为知青盖房子。去时顺风顺水,我们坐在船舱里,肖队长站在船头,撑着竹篙沿着河道滑行。一起插队的知青郭小飞觉得好玩,想试 试身手。他接过肖队长手里的竹篙,立在船头,左摇右晃,连站都站不稳,险些栽入水里。好不容易站稳了,他东一下,西一下,毫无目的地了好一阵子。
第二次轮到我,闹了一个大笑话。那日,知青们正在河岸上盖房子,渔场的周书记要去对面的另一个生产队开会,让我送他过河。去时,周队长撑着竹篙两三下就过去了。待他下船后,我撑着船往 回走,到了河当中,水深流急,我心慌脚不稳,一个趔趄一撒手,虽然人没有掉进水里,竹篙却下水了。无奈,我立即跳进水里捞竹篙,将竹篙扔进船里后,又游泳推着船回到岸上。
划船容易学,人站在船尾部的舱里,手摇双浆,利用水对浆的作用力,推着船向前滑行。只要掌握了摇浆的力度,控制船行驶的方向,直走、转弯、调头,不出半天便运用自如了。玩球网
撑船则不然,人站立于船头,手持6米竹篙,大头朝下插入湖底,用力推着船朝前走。这套动作有两个窍门,一是要掌握平稳,双脚要像钉子一样牢牢地“钉”在船头;二是手掌与竹篙的配合要默 契,船前行的速度、方向全在撑船的那一刻。技术含量虽不高,但也有一定的难度。
