人教版八年级下册数学正方形-课件.ppt
合集下载
《丰富多彩的正方形》教学PPT课件 初中数学(人教版) 八年级下册 公开课
感谢指导!
如图,正方形ABCD的对角线交于点O, 点E、F分别在AB 、BC上(AE<BE),且∠EOF=90°, OE与DA的延长线交于点M,OF与AB的延长线交于点N. (1)求证:OM=ON (2)若正方形ABCD的边长为4,E为OM的中点,求MN得长.
D
C
O
AE M
F
N B
课堂小结
• 1 本节课你学到了哪些数学知识? • 2 本节课你体验到了什么数学方法或数学 思想?
实验1 猜想→特殊情形→
探究:正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶 点,而且这两个正方形的边长相等, 现将正方形 A1B1C1O绕点O转动. (1)当OA1与OA重合,OC1与OB重合时,重叠部分的面积与一个正方 形的面积有何关系?
实验2
猜想→特殊情形→
探究:正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶 点,而且这两个正方形的边长相等, 现将正方形 A1B1C1O绕点O转动 . (2)当OA1⊥AB于点E,OC1⊥BC于点F时,它们之间的关系会改变吗?
实验 猜想→特殊情形→一般情形证明→结论
• (4)从以上你能得出什么结论
1
S 4 s 重叠
正方形ABCD
把正方形A1B1C1O改为矩形,直角三角形结果怎样?
归纳建模(一)
小试牛刀
如图(1),将三角板放在正方形ABCD上,使三角板的 直角顶点E与正方形ABCD的顶点A重合,三角板的一边交 CD于点F,另一边交CB的延长线于点G.
义务教育课程标准实验教科书(人教版) 八年级下册
知识回顾
正方形的性质
边: 四边相等,对边平行 角: 四角相等,都是直角
新人教版数学初中八年级下册18.2.3《正方形》公开课优质课课件

且
的四边形是正方形; 的四边形是
且有三个角是
三、应用新知 解决问 题:
相交于点O,
例1 已知:如图,四边形ABCD是正方形,对角线AC、BD
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三
角形.
证明:∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO. ∴△ABO,△BCO,△CDO,△DAO都是等腰直 角三角形, △ABO≌△BCO≌△CDO≌△DAO.
人民教育出版社 八年级 | 下册
第十八章 · 平行四边
18.2.3 正方 形
形
一、创设情境 引入新知:
活动1:把一张长方形的纸片(如图)中,如何通过折纸的方法, 截出正方形纸片,你有几种方法? 如果是长方形木板,又怎样从中截出面积最大的 正方形木板呢?
一、创设情境 引入新知:
活动2:如图,某一拉门在完全关闭时,其相应的菱形变成正 方形.请说说图中∠1的变化过程.
一、创设情境 引入新知:
小结:正方形既是矩形, 又是菱形. 有一组邻边相等的矩形是 正方形;
有一个角是直角的菱形是 正方形.
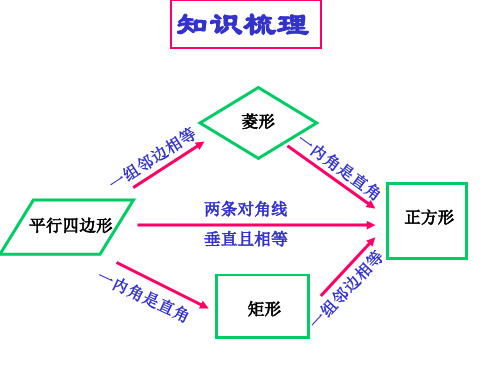
二、回顾思考 梳理关系:
1.通过前面的探究,我们知道正方形既是矩形,又是菱形,还是 平行四边形,它们之间的关系如图:
二、回顾思考 梳理关系:
2.理解上面的关系图,填写下面的表格: 图形 平行四 边形 矩形 菱形 对边 平行、相等 平行、相等 平行、 四条边 都相等 平行、 四条边 都相等 对角 相等 四个角 都是直 角 相等 对角线 互相平分 对称性
不是轴对称图形
正方形
轴对称图 互相平分且相等 形,有两条对 互相垂直且 称轴 轴对称图形, 平分,每条对 有两条对称 角线平分一 轴 组对角 互相垂直、 四个角都 轴对称图形, 平分且相等, 是直角 有四条对称轴 每条对角线 平分一组对
18.2.3正方形 正方形的判定(教学课件)-人教版数学八年级下册

探究点
正方形的判定
归纳总结:
(1)四条边相等、四个角都是直角的四边形是正方形 从四边形出发
(2)对角线互相垂直平分且相等的四边形是正方形 (1)有一组邻边相等并且有一个角是直角的平行四边 从平行四边形 形是正方形 出发 (2)对角线互相垂直且相等的平行四边形是正方形 从矩形出发 对角线互相垂直的矩形是正方形 从菱形出发 对角线相等的菱形是正方形
A
D
∴AB=BC=CD=DA,∠A=∠C,∠B=∠D.
又∠A=90°,
ቤተ መጻሕፍቲ ባይዱ
B
C
∴易得∠A=∠B=∠C=∠D=90°.
∴四边形ABCD是正方形.
归纳总结:有一个角是直角的菱形是正方形
探究点
正方形的判定
在上面的证明过程中,是分别从矩形、菱形出 发,添加边或角的条件后得到正方形,那么还有没 有通过添加边、角、对角线的条件可以得到其他 判定正方形的方法呢? 大家想一想.
课堂总结
知识结构
四边形
平行四边形
正 矩形 方 菱形
形
课堂总结
知识结构
课堂总结
1. 教材P62习题18.2第13题.
课后作业
1. 如图,E,F,M,N 分别是正方形ABCD四条边上的
点,且AE=BF=CM=DN,试判断四边形EFMN是什么
图形,并证明你的结论. 【选自教材P62,习题18.2第13题】
把能活动的菱形木框的一个角变为直角(如图),
能否得到正方形?
探究点
正方形的判定
2. 有一个角是直角的菱形是正方形
正方形
可以看到,这个变化过程中只要改变菱形的一 个角,就能得到正方形.
下面我们进行证明:
探究点
人教版八年级数学下册第十八章《正方形》优课件(共17张PPT)

(1) AB=AD;
A
(2) AC=BD;
(3) ∠BAD=90;
(4) AC⊥BD。
B
D O
C
判断对错
1. 四边相等的四边形是正方形 2.四角相等的四边形是正方形 3.四条边相等且有一个角是直角的四边 形是正方形 4.对角线互相垂直平分且相等的四边形 是正方形 5.对角线垂直的平行四边形是正方形
判断对错
6.对角线互相垂直且相等的四边形是正 方形。 7.对角线互相垂直的矩形是正方形。 8.对角线相等的菱形是正方形。
活动
1.从长方形木板中怎样截出最大的正方形木板?
2.怎样使菱形的衣帽架变成正方形的衣帽架?
3.昨天,我去超市买了一条方巾,现在想请同学们帮助检验 一下方巾是否是正方形的。
1.已知:正例方形题AB解CD中析,点E、F、G 、H
正方形
菱形
这一 样个 的人 人所 才受 有的 学教 问育 。超
过 了 自 己 的 智 力 ,
You made my day!
我们,还在路上……
每一条对角线平分一组对角
对称性---- 是轴对称图形.
D O
C
根据图形所具有的性质,在下表相应的空格中打 ”√”
对边平行且相 等
四边都相等
四个角都是直 角
对角线互相平 分
对角线互相垂 直
对角线相等
平行四边 形
√
√
矩形
√
√ √
√
菱形
√ √
√ √
正方形
√ √ √ √ √ √
你觉得什么样的四 边形是正方形呢?
分别是AB 、BC 、CD 、DA的中点,试判断四
边形EFGH是正方形吗?为什么?
正方形的性质+课件+2023-2024学年人教版数学八年级下册

OA=OB=OC=OD
∴△ABO,△BCO,△CDO,△DAO是
等腰直角三角形
先证
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ ,△ ,△ ,△ 是全等的等腰直角三角形 .
思考:图中
共有多少个
等腰直角三
角形?
同理:△ BCO ≌△ CDO, △ CDO ≌△ DAO
四个角
都是直角
对角线相等,
对角线互相平分
对角相等,
邻角互补
对角线互相垂直,
对角线互相平分,
每条对角线
平分一组对角
菱
形
对边平行,
四边相等
正方形性质
边
角
图形
语言
文字
语言
Hale Waihona Puke o对边平行,四条边相等
四个角都是直角
∵四边形ABCD是正方形 ∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
几何 ∴AB∥CD, AD∥BC,
第一部分 新课内容
第十八章 平行四边形
第11课时 §18.2.3 正方形的性质
学习目标
1、理解并掌握正方形的概念及性质。
2、探索正方形的性质。
3、利用正方形的性质解决实际问题。
重点
探索正方形的性质。
难点
能利用正方形的性质解决实际问题。
类比、归纳思想
回顾:矩形、菱形的性质
矩
形
边
角
对角线
对边平行
对边相等
正方形ABCD的周长为________,面积为________;
3 2
2
变式1-1:正方形的一条对角线的长为3,则此正方形的边长是____
∴△ABO,△BCO,△CDO,△DAO是
等腰直角三角形
先证
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ ,△ ,△ ,△ 是全等的等腰直角三角形 .
思考:图中
共有多少个
等腰直角三
角形?
同理:△ BCO ≌△ CDO, △ CDO ≌△ DAO
四个角
都是直角
对角线相等,
对角线互相平分
对角相等,
邻角互补
对角线互相垂直,
对角线互相平分,
每条对角线
平分一组对角
菱
形
对边平行,
四边相等
正方形性质
边
角
图形
语言
文字
语言
Hale Waihona Puke o对边平行,四条边相等
四个角都是直角
∵四边形ABCD是正方形 ∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
几何 ∴AB∥CD, AD∥BC,
第一部分 新课内容
第十八章 平行四边形
第11课时 §18.2.3 正方形的性质
学习目标
1、理解并掌握正方形的概念及性质。
2、探索正方形的性质。
3、利用正方形的性质解决实际问题。
重点
探索正方形的性质。
难点
能利用正方形的性质解决实际问题。
类比、归纳思想
回顾:矩形、菱形的性质
矩
形
边
角
对角线
对边平行
对边相等
正方形ABCD的周长为________,面积为________;
3 2
2
变式1-1:正方形的一条对角线的长为3,则此正方形的边长是____
第18章第12课正方形的判定课件-人教版八年级数学下册

又∠A=90°, AC=BD(答案不唯一)
试说明四边形AEDF是正方形.
选①
B.选②
C.选③ D.选④
∴四边形 AEDF 是矩形. 试说明四边形AEDF是正方形.
7.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
AB=AC,D 是 BC 的中点, (1)求证:∠ADB=∠CDB;
第12课 正方形的判定
目录
温故知新 新课学习 重难易错
三级检测练
温故知新
1.正方形的性质: ①边:四条边都__相__等____; ②角:四个角都是__直__角____; ③对角线:对角线_垂__直__平__分ຫໍສະໝຸດ _且__相__等___,且对角线平分
每一组__对__角____.
新课学习
知识点1 正方形的判定1
形 ACED 是正方形.
证明:(1)在□ABCD 中,AD∥BC,
∴∠DAO=∠CEO. ∵O 为 CD 的中点,∴OC=OD.
∠DAO=∠CEO, 在△AOD 和△EOC 中, ∠AOD=∠EOC,
OD=OC, ∴△AOD≌△EOC(AAS).
三级检测练
一级基础巩固练 9.下列判断中,正确的是( D ) A.有一个角是直角的平行四边形是正方形 B.四角相等的四边形是正方形 C.对角线相等的平行四边形是正方形 D.对角线互相垂直平分且相等的四边形是正方形
13.如图,在△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
∠A=90°,DF⊥AB,DE⊥AC,垂足分别为F, ∴矩形CFDE是正方形.
试说明四边形AEDF是正方形. 如果一个平行四边形要成为一个正方形,需要增加的条件是( )
正方形的性质及判定人教版八年级数学下册课件

形
根如据图角 所平示分,线一上共的有点多都少两对边全的等距三离角相形等(, )
求证: : △四A边BO形、CF△DBEC是O正、方△形C.DO、 △DAO是全等的
志(不1)立先,证天它下是无矩可形成,之再事证。它有一组邻边相等;
正方形
有根一据组 角邻平边分相线等上且的有点一都个两角边是的直距角离相等,
有一组邻边相等且有一个角是直角
有一组邻边相等并且有一个角是直角的平行四边形是正方形
第十八章 根据角平分线上的点都两边的距离相等,
(1)对角线互相垂直且相等的平行四边形. 正方形具有而菱形不一定具有的性质是( )
平行四边
求证:四边形CFDE是正方形.
∴△BOM≌△CON, 是正轴方对 形称是图一形个,完有美的4条图对形称轴. 有正志方始 形知的蓬四莱个近角,都无是为直总角觉咫尺远。
角 正方形的四个角都是直角
对角线 正方形的对角线相等,互相垂直平分,每条 对角线平分一组对角。
正方形是中心对称图形,它也是轴对称图形
正方形是一个完美的图形
正方形判定:
(1)正方形的定义 (2)先证它是矩形,再证它有一组邻边相等; (3)先证它是菱形,再证它有一个角为直角.
(1)先证它是矩形,再证它有一组邻边相等;
(2)先证它是菱形,再证它有一个角为直角.
正方形的判定方法: (可从平行四边形、矩形、菱形为基础)
1、
平行四边形
一组邻边相等 一内角是直角
正方形
定义法
2、
菱形
一内角是直角
正方形
菱形法
3、
矩形
一组邻边相等
正方形
矩形法
平行四边形、矩形、菱形、正方形之间关系
四边形 平行四边形
最新人教版数学八年级下册《正方形的判定》优质教学课件

吧!
·数学
谢谢聆听
∴矩形ABCD是正方形.
3.【例1】已知四边形ABCD,则下列说法中正确的是( A )
A.若AB∥CD,AB=CD,则四边形ABCD是平行四边形
B.若AC⊥BD,AC=BD,则四边形ABCD是矩形
C.若AC⊥BD,AB=AD,CB=CD,则四边形ABCD是菱形
D.若AB=BC=CD=AD,则四边形ABCD是正方形
∴AC=BD,AC⊥BD,
∵点E,F,G,H分别是正方形ABCD各边的中点,
∴EH是△ABD的中位线,
∴EH∥BD,EH= BD,
同理:FG= BD,EF∥AC,EF= AC,GH= AC,∴EH
=EF=FG=GH,
∴四边形EFGH是菱形,
又∵AC⊥BD,∴EH⊥EF,
∴四边形EFGH是正方形.
小结:菱形+对角线相等(或有一个角为90°)→正方形.
6.小明在学习了正方形之后,给同桌小文出了一道题,从下
列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,
④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形
(如图),现有下列四种选法,你认为其中错误的是( B )
A.①②
B.②③
C.①③
(2)∵ME⊥AC,MF⊥AD,∠CAD=90°,
即∠CAD=∠AEM=∠AFM=90°,
∴四边形AEMF是矩形.
又∵∠CAB=∠DAB,ME⊥AC,MF⊥AD,
∴ME=MF,∴矩形AEMF是正方形.
★8.(创新题)如图,在四边形ABCD中,AD∥BC,AD=CD,
E是对角线BD上一点,且EA=EC.
新课标人教版初中数学八年级下册第十九章19.2特殊的平行四边形--正方形的判定-精品课件
∴∠CEA=∠ABG
练习1:判断 (1)四个角都相等的四边形是正方形 (2)四条边都相等的四边形是正方形 (3)对角线相等的菱形正方形 (4)对角线互相垂直的矩形是正方形 (5)对角线垂直且相等的四边形是正方形 (6)四边相等,有一角是直角的四边形是 正方形
例2 已知:在正方形ABCD中,A′、B ′、C ′、 D ′分别从顶点A、B、C、D沿AB、BC、CD、 DA方向同时以同样速度向B、C、D、A移动。
D
M
A
E
F
C
N
B
练习2(2019年山东省济南市中考试题)如图,是 一块在电脑屏幕上出现的矩形色块图,由5种颜色 不同的正方形组成。设中间最小的一个正方形边 长为1,则这个矩形的面积是
练习4 (2019年陕西省中考题)如图,在矩形 ABCD中,点E、F分别在AB、CD上,BF平行 于DE。若AD=12cm,AB=7cm,且AE:EB=5: 2,求阴影部分的面积。
例题3:已知正方形ABCD中,Q在CD上,且 DQ=QC,P在BC上,AP=CD+CP; 求证:AQ 平分∠DAP.
证明:延长AQ交BC延长线与E,
∵四边形ABCD是正方形, ∴AD=CD,AD∥CD;
A
D
∴∠D=∠QCE,∠DAQ=∠E, 又∵DQ=CQ,
Q
∴⊿ADQ≌⊿ECQ (AAS).
∴∴ACDD==CCEE,,又∴AADP==CCDD,+CP=CE+CP=EPB.
①AE与BF相等吗?为什么?
②AE与BF是否垂直?说明你的理由。
A
D
F G
BE
C
练习7:如图,已知正方形ABCD中,
E、F分别为BC和DC上的点,且
练习1:判断 (1)四个角都相等的四边形是正方形 (2)四条边都相等的四边形是正方形 (3)对角线相等的菱形正方形 (4)对角线互相垂直的矩形是正方形 (5)对角线垂直且相等的四边形是正方形 (6)四边相等,有一角是直角的四边形是 正方形
例2 已知:在正方形ABCD中,A′、B ′、C ′、 D ′分别从顶点A、B、C、D沿AB、BC、CD、 DA方向同时以同样速度向B、C、D、A移动。
D
M
A
E
F
C
N
B
练习2(2019年山东省济南市中考试题)如图,是 一块在电脑屏幕上出现的矩形色块图,由5种颜色 不同的正方形组成。设中间最小的一个正方形边 长为1,则这个矩形的面积是
练习4 (2019年陕西省中考题)如图,在矩形 ABCD中,点E、F分别在AB、CD上,BF平行 于DE。若AD=12cm,AB=7cm,且AE:EB=5: 2,求阴影部分的面积。
例题3:已知正方形ABCD中,Q在CD上,且 DQ=QC,P在BC上,AP=CD+CP; 求证:AQ 平分∠DAP.
证明:延长AQ交BC延长线与E,
∵四边形ABCD是正方形, ∴AD=CD,AD∥CD;
A
D
∴∠D=∠QCE,∠DAQ=∠E, 又∵DQ=CQ,
Q
∴⊿ADQ≌⊿ECQ (AAS).
∴∴ACDD==CCEE,,又∴AADP==CCDD,+CP=CE+CP=EPB.
①AE与BF相等吗?为什么?
②AE与BF是否垂直?说明你的理由。
A
D
F G
BE
C
练习7:如图,已知正方形ABCD中,
E、F分别为BC和DC上的点,且
人教版初中八年级下册数学课件 《正方形》课件

1
1
01 探究
现在,你对正方形有哪些新的认识? 正方形的四条边都相等,四个角都是直角, 它既是矩形又是菱形,既具有矩形的性质,又有菱形的性质
矩形 正方形
菱形
01 知识回顾
怎样判定一个平行四边形是正方形? 怎样判定一个矩形是正方形? 怎样判定一个菱形是正方形?
平行四边形
矩形 菱形
正方形
01 知识回顾
O
B
C
02
练一练
LEARNING OBJECTIVES
02 练一练
1.如图,正方形ABCD中,对角线AC, BD相交于点O,则图中的等腰三角形有( )
C
A、4个 C、8个
B、6个 D、10个
02 练一练
2.如图,在正方形ABCD的外侧,作等边三角形ADE,
连接BE,则∠AEB的度数为__1__5_°.
定义 性质 逆向猜想 判定
01 知识回顾
在小学,什么样的四边形是正方形? 正方形与矩形和菱形分别有什么关系? 四个角都是直角,四条边都相等的四边形叫做正方形. 你能用一张矩形纸片,折出一个最大的正方形吗?
说说折出的四边形是正方形的依据.
01 知识回顾
如图,某一拉门在完全关闭时,其相应的菱形变成正方形. 请说说图中∠1的变化过程.
第十八章 平行四边形 正方形
CHAPTER
18
SECTION
03
SQUARE
目 录 CONTENS
01
学习目标 LEARNING OBJECTIVES
1、理解正方形与平行四边形、矩形、菱形概念之间的 联系和区别; 2、能用正方形的定义、性质和判定进行推理与计算.
02
重点A KEY
人教版八年级数学下册第十八章《18.2.3 正方形》优质公开课课件

角三角形.
A
D
思考:图中共有__四____个
O
等腰直角三
B
C
证明:∵四边形ABCD是_正__方__形_____,
∴AC=_B_D___,AC__⊥__BD,AO=_C_O___=_B_O___=_D_O___. ∴△ABO、△_B__C_O__、△_C_D__O__、△_D_A_O___是等腰直角三角 形,且△ABO≌△BCO__≌___△CDO__≌___△DAO.
“引导学生读懂数学书”课题 研究成果配套课件
新课引入 展示目标 研读课文 归纳小结 强化训练
第十课时 § 18.2.3 正方形
一、新课引入
矩形
1.四个角都___相__等___ 性 质
2.对角线__互__相__平__分__
1.有一个角是_直__角___的 __平__行__四__边__形_
判 2.有三个角是_直__角__的 定 ___四__边__形__
_______________
五、强化训练
已知:如图,△ABC中,∠C=90°,CD平分
∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
C
解:∵∠C=90°,DE⊥BC于E,
DF⊥AC于F
E
∴四边形CEDF有三个直角F,
它是矩形
A
又∵CD平分∠ACB
D
B
根据角平分线上的点都两边的距离相等,可知
二
2、正方形与平行四边形、矩形、菱形之间的关系有怎样的
包含关系?请填入下图中.
正
方
平行四边形
形
的 性
菱形
正方形 矩形
质
三、研读课文
例5 求证:正方形的两条对角线把这个正方形分成四个全
八年级数学下册课件: 正方形(第课时) 公开课一等奖课件

高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校:
北京大学光华管理学院
北京市理科状元杨蕙心
班主任 孙烨:杨蕙心是一个目标高远 的学生,而且具有很好的学习品质。学 习效率高是杨蕙心的一大特点,一般同 学两三个小时才能完成的作业,她一个 小时就能完成。杨蕙心分析问题的能力 很强,这一点在平常的考试中可以体现。 每当杨蕙心在某科考试中出现了问题, 她能很快找到问题的原因,并马上拿出 解决办法。
班主任: 我觉得何旋今天取得这样的成绩, 我觉得,很重要的是,何旋是土生土长的北京 二中的学生,二中的教育理念是综合培养学生 的素质和能力。我觉得何旋,她取得今天这么 好的成绩,一个来源于她的扎实的学习上的基 础,还有一个非常重要的,我觉得特别想提的, 何旋是一个特别充满自信,充满阳光的这样一 个女孩子。在我印象当中,何旋是一个最爱笑 的,而且她的笑特别感染人的。所以我觉得她 很阳光,而且充满自信,这是她突出的这样一 个特点。所以我觉得,这是她今天取得好成绩 当中,心理素质非常好,是非常重要的。
zx``x````````k
6
六、应用新知
已知:点E、F、G、 H分别是正方形ABCD四 条边上的中点,并且E、F、 G、H分别是AB、BC、 CD、AD的中点.求证:四 边形EFGH是正方形.
A E B
H
D G
F
C
7
七、小结
1.正方形的判定方法. 2.了解正方形、矩形、菱形之间的联系与 区别,体验事物之间是相互联系但又有区别的 辩证唯物主义观点.
青 春 风 采
高考总分:
692分(含20分加分) 语文131分 数学145分 英语141分 文综255分
