14黑体辐射
14黑体辐射详解PPT课件

公式在短波区域 明显与实验不符, 而理论上却找不出 错误
16
第
十
五
新实验
章
尖锐矛盾
量
经典物理
子
物
理
0 结果
相对论
紫外灾难
安宏
量子论
’s formula)
章量1900.10.19年德国物理学家普朗克根据实验数据拼凑了 子一个公式:“普朗克公式”
物
M理 (T)
12
安宏
第热辐射的实验曲线
十
五 章
热辐射的实验规律
量
子
M (T)
物
60
2200K
理
50
21080000000度度度 火 炉
40 2000K
30
20
1800K
炉火纯青
10
1600K
1.0 2.0 3.0 4.0 5.0
13
安宏
第热辐射规律的理论解释
十
五
章
量
实验规律——找到了
子 物
实验曲线——画出来了
理
下一步
要上升到理论:从理论上找到符合实验曲线
的函数式
14
安宏
第热辐射规律的理论解释
十五热辐射的理论解释M (T)
章
量当时经典物理占统治地位,人们自然用经典学
子理论来解释热辐射并建立了两个公式:
物
理
1.02.0 3.04.05.0 6.0 7.08.0 9.0
1)维恩公式(Wien’s formula)
物理种方“式我来试消图除将hEn纳入nh经典这理一论关的系范式围。,它但写一道切:
这样的尝试都失败了,这个量非常顽固”。后来 他又说:“在好几年内我花费了很大的劳动,徒 劳地去尝试如何将作用量子引入到经典理论中去。 我的一些同事把这看成是悲剧,但我有自已的看 法,因为我从这种深入剖析中获得了极大的好处 ,起初我只是倾向于认为,而现在是确切地知道
普朗克黑体辐射公式推导(精.选)

普朗克黑体辐射公式的推导所谓的黑体是指能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。
黑体辐射:由这样的空腔小孔发出的辐射就称为黑体辐射。
辐射热平衡状态:处于某一温度T 下的腔壁,单位面积所发射出的辐射能量和它所吸收的辐射能量相等时,辐射达到热平衡状态。
实验发现:热平衡时,空腔辐射的能量密度,与辐射的波长的分布曲线,其形状和位置只与黑体的绝对温度T 有关而与黑体的形状和材料无关。
实验得到: 1.Wien 公式从热力学出发加上一些特殊的假设,得到一个分布公式:Wien 公式在短波部分与实验还相符合,长波部分则明显不一致。
2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符,但是在高频区公式与实验不符,并且∞→=⎰∞v v d E E ,既单位体积的能量发散,而实验测得的黑体辐射的能量密度是4T E σ=,该式叫做Stefan-Bolzmann 公式,σ叫做Stefan-Bolzmann 常数。
3. Planck 黑体辐射定律1900年12月14日Planck 提出如果空腔内的黑体辐射和腔壁原子处于平衡,那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。
作为辐射原子的模型,Planck 假定:(1)原子的性能和谐振子一样,以给定的频率v 振荡; (2)黑体只能以E=hv 为能量单位不连续的发射和吸收辐射能量,而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。
得到:νννπνρνd kT h C h d ⎪⎪⎭⎫ ⎝⎛-=1)/exp(1833该式称为Planck 辐射定律 h 为普朗克常数,h=s j .10626.634-⨯4,普朗克的推导过程:把空窖内的电磁波分解为各个频率的简振振动,简振模的形式最后为).(),(wt r K i k k e C t r -=αβψ,为常系数振方向,表示两个互相垂直的偏ααk C 2,1=每一个简振模在力学上等价于一个自由度,记频率在()νννd +,内的自由度数为()ννd g ,则(0,v )范围内的总自由度数G(v)与g(v)的关系为()()ννννd g G ⎰=0。
黑体辐射的原理和应用

黑体辐射的原理和应用1. 黑体辐射的基本概念黑体是指具有完美吸收和辐射性能的物体,它能够吸收所有入射到其表面的辐射能量,而且能够以最高效率将能量辐射出去。
黑体辐射是指黑体表面上的电磁波辐射,它是由于黑体内部原子或分子的热运动而产生的,具有各种波长的辐射光谱。
黑体辐射的特点是它的辐射能量与波长之间的关系是确定的。
2. 黑体辐射的原理黑体辐射的原理可以用普朗克辐射定律来描述,该定律是由德国物理学家马克斯·普朗克在20世纪初提出的。
普朗克辐射定律表明,黑体辐射的能量密度与波长的关系符合普朗克分布函数。
该函数在不同波长范围内的峰值位置和强度有所不同,但都是由辐射体的温度所决定的。
当温度较低时,黑体辐射的能量主要集中在长波段;当温度较高时,能量则主要分布在短波段。
普朗克辐射定律的数学表达式如下:$$B(\\lambda,T)=\\frac{2hc^2}{\\lambda^5}\\frac{1}{e^{hc/\\lambda kT}-1}$$其中,$B(\\lambda,T)$表示波长为$\\lambda$的辐射能量密度,ℎ为普朗克常数,c为光速,k为玻尔兹曼常数,T为黑体的温度。
3. 黑体辐射的应用黑体辐射在许多领域都有广泛的应用。
以下列举了一些常见的应用领域:3.1 热辐射和能量转换黑体辐射是热辐射的基础,它在能量转换和传递过程中起着重要的作用。
例如,太阳光是由黑体辐射引起的,地球上的太阳能利用就是通过能源转换将太阳辐射的能量转换为电能或其他形式的能量。
3.2 红外线技术黑体辐射的波长范围覆盖了红外线区域,红外线技术利用了黑体辐射的特性。
红外线技术在军事、医学、安防等领域有广泛的应用,如红外线热成像、红外线测温、红外线通信等。
3.3 热辐射测量和光谱分析利用黑体辐射的特点,可以进行热辐射测量和光谱分析。
例如,利用红外光谱技术可以对物质的成分进行分析和检测,而红外辐射测温技术可以测量物体的温度。
p141黑体辐射的规律

[解析]在任何温度下对任意波长的电磁波只吸 收不反射的物体称为绝对黑体,简称黑体。
{范例14.1} 黑体辐射的规律
黑体的单色辐射本领是在单位时间内从物体表
面单位面积上所发射的波长在λ到λ + dλ范围内 的辐射能量dP(λ,T)与波长间隔dλ之比
{范例14.1} 黑体辐射的规律
根据实验得出两个黑体辐射实验规律。黑体的总辐射本 领(能力)为P(T) = σT4,这就是斯特藩-玻尔兹曼定律, 其中,σ = 5.67×10-8W/(m2·K4),σ称为斯特藩常数。
黑体的单色辐射本领(能力)的峰值波长与温 度的关系为Tλm = b,这就是维恩位移定律, 其中,b = 2.897×10-3m·K,b称为维恩常数。
M(,T)dP(,T) d
M(λ,T)表示在单位时间内从物体表面单位面积
发射的波长在附近单位波长间隔内的辐射本 其中,k为玻
领,是波长和温度的函数,其单位是W/m3。 尔兹曼常数,
普朗克提出的 黑体单色辐射 本领的公式为
M(,T)
2πhc2
5[exp( hc )1]
kT
h为普朗克常 数,c为真空 中的光速。
由此可得CI = 5.6688×10-8, 这就是斯特藩常数。
{范例14.1} 黑体辐射的规律
x hc , kT
M(x,T)
2πk4T4x5 h3c2(ex1)
当波长趋于零时, x趋于无穷大,单色辐射本领M趋于零;
当波长趋于无穷大时, x趋于零,单色辐射本领M也趋于零。
因此单色辐射本领随波长的变化有极值。
kT
h3c2(ex1)
dx hc d kT2
14黑体辐射详解

安宏
18.10.12
量子概念的诞生
第十五章 量子物理
量子理论带来了出人意料的 科学上
hν
技术上
社会上
哲学上
的多种多样的新鲜成果
揭示了微观世界中一个重要规律,
开创了物理学的一个全新领域。 安宏
18.10.12
也逐渐成了20世纪物理学中的“唯一思想模式”
量子概念的诞生
第十五章 量子物理
“这一发现成为20世纪整个物理研究的基础, 从那时起,几乎完全决定了物理学的发展”。 ——爱因斯坦
相对论
紫外灾难
安宏
量子论
18.10.12
量子概念的诞生
第十五章 量子物理
普朗克公式(Planck’s formula)
1900.10.19年德国物理学家普朗克根据实验数据拼凑了 一个公式:“普朗克公式”
M (T )
普朗克
普朗克公式曲线
1.02.0 3.04.0 5.0 6.0 7.0 8.0 9.0
hν
事实上正是这一理论导致了量子力学的诞生, 1918年因此而获得诺贝尔奖。
普朗克诞辰100周年德国发行的2马克面值的纪念硬币
哥庭根市公墓: h = 6.6310-34J· s 安宏
18.10.12
量子概念的诞生
第十五章 量子物理
注意:普朗克这一思想是完全背离经典物理,并 受到当时许多人的怀疑和反对,包括当时的物理 学泰斗---洛仑兹。乃至当时普朗克自已也想以某 种方式来消除 En n h 这一关系式。它写道: “我试图将h 纳入经典理论的范围,但一切 这样的尝试都失败了,这个量非常顽固”。后来 他又说:“在好几年内我花费了很大的劳动,徒 劳地去尝试如何将作用量子引入到经典理论中去。 我的一些同事把这看成是悲剧,但我有自已的看 法,因为我从这种深入剖析中获得了极大的好处 ,起初我只是倾向于认为,而现在是确切地知道 作用量子 将在物理中发挥出巨大作用”。
普朗克黑体辐射公式的详细推导

普朗克黑体辐射公式的详细推导辐射是物体由于内部热运动而产生的电磁波。
普朗克假设黑体辐射是由许多振动的谐振子(即电磁振子)组成的,每个谐振子只能具有离散能量值。
普朗克假设这些能量是量子化的,即能量E只能取整数倍的基本能量hν,其中ν为辐射频率。
设一个振子的能量为E,频率为ν,则E=hν。
普朗克认为振子的能量只能取整数倍的基本能量hν,因此振子的能量只能是离散的。
假设在单位时间内,频率在ν到ν+dν范围内,能量在E到E+dE范围内的谐振子数为n(E,ν)。
则单位体积内频率在ν到ν+dν范围内,能量在E到E+dE范围内的谐振子数为:n(E,ν)dEdν为了求解n(E,ν),我们需要引入玻尔兹曼分布和玻尔兹曼常数k。
在热平衡状态下,系统中具有能量E的状况数(即相同的谐振子数)为:W(E)=n(E,ν)*e^(-E/kT)其中,T为系统的温度,n(E,ν)为单位体积内频率在ν到ν+dν范围内,能量在E到E+dE范围内的谐振子数。
根据统计物理学的理论,系统的熵S与状况数W的关系为:dS = k * ln W(E)将W(E)代入上式并对E求微分,我们可以得到:dS = k * [ d(n(E,ν)) - (E/kT) * dn(E,ν) ]根据熵的最大化原理,熵是关于能量的单调递增函数,即dS>=0,即有:d(n(E,ν)) - (E/kT) * dn(E,ν) >= 0 (式1)我们将式1两边对E积分,可得:∫(d(n(E,ν)) - (E/kT) * dn(E,ν)) = ∫0到E dn(E,ν) (式2)其中,积分区间为0到E。
对式2进行变换,得到:n(E,ν) - (∫0到E (E/kT) * dn(E,ν)) = ∫0到E dn(E,ν)整理后,我们可以得到:n(E,ν)=[∫0到E(1/e^(E/kT))]*n(E,ν)令x=E/(kT),则式子变为:n(E,ν)=[∫0到x(1/e^x)]*n(E,ν)通过计算可知,上式的积分结果为:∫0到x(1/e^x)=1-(1+x)e^(-x)将该结果代入n(E,ν)的表达式中,我们可以得到:n(E,ν)=(1-(1+x)e^(-x))*n(E,ν)(式3)进一步简化,我们可以得到:n(E,ν)=(1-(1+E/(kT))e^(-E/(kT)))*n(E,ν)(式4)根据统计物理学的经验公式,单位体积频率为ν到ν+dν范围内,能量为E到E+dE范围内的谐振子数n(E,ν)与能量E的关系为:n(E,ν)=C*E^3*1/(e^(E/(kT))-1)(式5)其中,C为常数。
普朗克黑体辐射公式推导

普朗克黑体辐射公式的推导所谓的黑体是指能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。
黑体辐射:由这样的空腔小孔发出的辐射就称为黑体辐射。
辐射热平衡状态:处于某一温度T 下的腔壁,单位面积所发射出的辐射能量和它所吸收的辐射能量相等时,辐射达到热平衡状态。
实验发现:热平衡时,空腔辐射的能量密度,与辐射的波长的分布曲线,其形状和位置只与黑体的绝对温度T 有关而与黑体的形状和材料无关。
实验得到: 1.Wien 公式从热力学出发加上一些特殊的假设,得到一个分布公式:Wien 公式在短波部分与实验还相符合,长波部分则明显不一致。
2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符,但是在高频区公式与实验不符,并且∞→=⎰∞v v d E E ,既单位体积的能量发散,而实验测得的黑体辐射的能量密度是4T E σ=,该式叫做Stefan-Bolzmann 公式,σ叫做Stefan-Bolzmann 常数。
3. Planck 黑体辐射定律1900年12月14日Planck 提出如果空腔内的黑体辐射和腔壁原子处于平衡,那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。
作为辐射原子的模型,Planck 假定:(1)原子的性能和谐振子一样,以给定的频率v 振荡; (2)黑体只能以E=hv 为能量单位不连续的发射和吸收辐射能量,而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。
得到:νννπνρνd kT h C h d ⎪⎪⎭⎫ ⎝⎛-=1)/exp(1833该式称为Planck 辐射定律 h 为普朗克常数,h=s j .10626.634-⨯4,普朗克的推导过程:把空窖内的电磁波分解为各个频率的简振振动,简振模的形式最后为).(),(wt r K i k k e C t r -=αβψ,为常系数振方向,表示两个互相垂直的偏ααk C 2,1=每一个简振模在力学上等价于一个自由度,记频率在()νννd +,内的自由度数为()ννd g ,则(0,v )范围内的总自由度数G(v)与g(v)的关系为()()ννννd g G ⎰=0。
14激光产生的必要条件
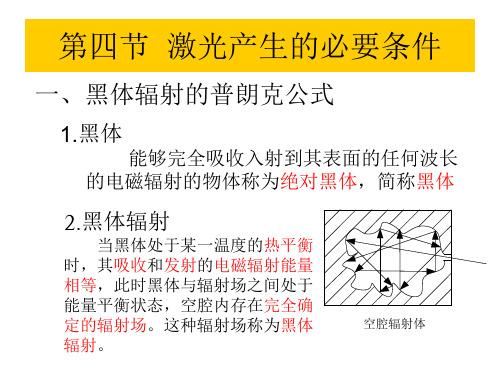
辐射出的光子能量满足 波尔条件: h E2 E1
其频率为 E2 E1 h
2) 自发辐射跃迁几率
从E2自发跃迁到下能级 E1的原子数 dn21 sp 应正比于 n2和dt, t时刻处于上能级 E2的原子数为 n2,则在 t ~ t dt时刻
dn21 sp A21n2dt
三、A21、B12、B21的关系
物质原子是一个二能级 系统,达到 温度为 T的热平衡时,有
( 1)腔内黑体辐射场单色 能量密度为 8h 3 1 h 3 c e KT 1
(2)各能级上原子数服从 玻耳兹曼分布 n2 g 2 e n1 g1
E 2 E1 KT
(3)在热平衡状态下, n1和n2应保持不变 dn21 dn21 dn12 dt sp dt st dt st
当物质处于热平衡时, 各能级上的原子数服从 玻耳兹曼分布 dn12 E2 E1 B n n g dt st 12 1 1 2 e KT 1 B21 n2 n2 g1 dn21 dt st
在热平衡状态下,物质以吸收光子为主,光通过物质被衰减
1)定义
处于能级E2的原子在频率为的辐射场作用下,向 E1能级跃迁并发射与外来光子能量相同的光子的过程 称为受激辐射跃迁。
2) 受激辐射跃迁几率
在的作用下,从 E2受激辐射跃迁到能级 E1的原子数 dn21 st 应正比于 、n2和dt, t时刻处于能级 E2的原子数为 n2,则在 t ~ t dt时间内
dn21 st B21 n2dt
其中,B21——受激辐射跃迁爱因斯坦系数
受激辐射跃迁几率
dn21 1 W21 B21 dt st n2
14-1黑体辐射

平衡态时 黑体辐射只依赖于物体的温度
与构成黑体的材料 形状无关
• 实验和理论均证明:
在各种材料中 黑体的光谱辐射度最大
15
维恩设计的黑体
空腔上的小孔
炼钢炉上的小洞
向远处观察打开 的窗子 近似黑体
16
2.黑体辐射实验规律 1) 实验规律一 维恩位移定律
m T b
b = 2.897756×10-3 m· K 或
物理学晴朗天空中的一朵乌云!
25
五、普朗克的能量子假说和黑体辐射公式 1.黑体辐射公式 1900.10.19 普朗克在德国 物理学会会议上提出一个 黑体辐射公式
2πh M (T ) 2 h / kT c e 1
3
h 6.55 1034 J s
M.Planck 德国人 1858-1947 26
热辐射与温度有关激光日光灯发光不是热辐射11光谱辐射出射度也称单色辐射本领单位时间内从物体单位表面向前方半球发出的波长在附近单位波长间隔内的电磁波的能量单位面积12或按频率定义单位时间内从物体单位表面向前方半球发出的频率在附近单位频率间隔内的电磁波的能表面情况物质种类单位面积13表面情况物质种类辐射出射度与有关14二平衡热辐射加热一物体物体的温度恒定时物体所吸收的能量等于在同一时间内辐射的能量这时得到的辐射称为平衡热辐射讨论平衡热辐射的规律15三黑体辐射的实验规律研究热辐射的理想模型黑体黑体
•物体发射或吸收电磁辐射时 交换能量 的最小单位是“能量子” = h
E (n)h
29
由此得到了普朗克的热辐射公式:
2πh M (T ) 2 h / kT c e 1
3
h 6.55 1034 J s
大时: 小时: 维恩公式 瑞利-金斯公式
黑体辐射

不同温度的黑体辐射频谱。
随着温度下降,频谱峰值波长增加地球溫度的黑體輻射黑体辐射维基百科,自由的百科全书黑体辐射指处于热力学平衡态的黑体发出的电磁辐射。
黑体辐射的电磁波谱只取决于黑体的温度。
或許我們換一個角度來說: 所謂黑體輻射其實就是光和物質達到平衡所表現出的現象。
物質達到平衡,所以可以用一個溫度來描述物質的狀態,而光和物質的交互作用很強,如此光和光之間也可以用一個溫度來描述(光和光之間本身不會有交互作用,但光和物質的交互作用很強)。
而描述這關係的便是普朗克分佈(Planck distribution )。
黑体辐射能量按波长的分布仅与温度有关。
黑体不仅仅能全部吸收外来的电磁辐射,且散射电磁辐射的能力比同温度下的任何其它物体强。
对于黑体的研究,使自然现象中的量子效应被發现。
而在現實上黑體輻射是不存在的,只有非常近似的黑體【好比在一顆恆星或一個只有單一開口的空腔之中】 舉個例來說,我們觀測到宇宙背景輻射,對應到一個約3K 的黑體輻射,這暗示宇宙早期光是和物質達到平衡的。
而隨著時間演化,溫度慢慢降了下來,但方程式依然存在。
(頻率和溫度的效應抵銷)目录1黑體輻射方程1.1黑体辐射本领1.2黑體輻射的普朗克公式1.3黑體輻射的維恩位移定律1.4黑體輻射的斯特藩玻爾茲曼定律2人體的輻射3行星和其衛星之間的熱力學關係3.1因素3.2推導3.3地球的溫度4運動黑體的多普勒效應5參考文獻6參閱黑體輻射方程黑体辐射本领基尔霍夫(G. R. Kirchhoff)证明,对于任意一个物体,辐射本领与吸收率之比是一个与组成物体的物质无关的普适函数(以表示)其中,辐射本领为单位时间内从辐射体表面的单位面积上发射出的辐射能量的频率分布,所以,在人體的大多數能量以紅外線的形式散射掉了。
一些材料對地球(雲層,大氣和地面)的長波熱輻射強度可以認為地球受到太陽照射的地區仅等於一個二維的圆形面積而非整個球面。
黑體輻射定理的應用之一是用於概略的估計一個行星的溫度。
p141黑体辐射的规律

因此单色辐射本领随波长的变化有极值。
令dM(x,T)/dx = 0,可得方程 xm = 5[1 – exp(-xm)] ,
一般用迭代算法计算上式之值,除了 零解之外,可得xm的值为4.965。
可得
T m
hc kxm
0.0029
这就是维恩常数。
理论值与实验值 也符合得很好。
取温度为 参数,黑 体的单色 辐射本领 与波长的 关系如图 所示。
{范例14.1} 黑体辐射的规律
黑体的单色辐射本领是在单位时间内从物体表
面单位面积上所发射的波长在λ到λ + dλ范围内 的辐射能量dP(λ,T)与波长间隔dλ之比
M
(,T
)
dP(,T d
)
M(λ,T)表示在单位时间内从物体表面单位面积
发射的波长在附近单位波长间隔内的辐射本 其中,k为玻
领,是波长和温度的函数,其单位是W/m3。 尔兹曼常数,
n1 n4 90
理论值与实验 值符合得很好。
由此可得CI = 5.6688×10-8, 这就是斯特藩常数。
{范例14.1} 黑体辐射的规律
x hc ,
kT
2πk 4T 4 x5 M (x,T ) h3c2 (ex 1)
当波长趋于零时, x趋于无穷大,单色辐射本领M趋于零;
当波长趋于无穷大时, x趋于零,单色辐射本领M也趋于零。
不论温度是多少,单 色辐射本领随波长的 增加先增加再减小。
峰值波长与温度的关系 遵守维恩位移定律:峰 值波长与温度成反比。
温度升高时,峰值 波长变短,峰变高。
曲线下的面积表示总 辐射本领,温度越高, 曲线下的面积越大, 总辐射本领越强。
x3
dx
0 ex 1
《黑体辐射》课件
结论
通过本次《黑体辐射》PPT课件,我们深入了解了黑体辐射的定义、特点、计算方法和应用领域。黑体辐射在 物理学、工程学以及众多领域中都具有重要的作用。
《黑体辐射》PPT课件
欢迎来到《黑体辐射》PPT课件!在本课程中,我们将探讨黑体辐射的定义、 特点、计算方法以及应用领域。让我们一起深入了解这一重要的物理现象吧!
导言
导言部分将介绍《黑体辐射》这一主题的背景和目的,并介绍黑体辐射的基本概念。
黑体辐射的定义
黑体辐射是指具有各个温度下均匀辐射任意波长的 理想化物体。通过研究黑体辐射,我们可以深入了 解物体在不同温度下的发光特性。
2 斯特藩-玻尔兹曼定律
斯特藩-玻尔兹曼定律表明黑体辐射的总辐射 功率与温度的四次方成正比。我们可以利用 这一定律计算黑体辐射的总功率。
黑体辐射的应用领域
黑体辐射在许多领域中都有重要的应用。本部分将介绍一些常见的应用领域,并探讨黑体辐射在这些领域中的 作用。
热辐射学
热辐射学利用黑体辐射的理 论和实践应用,研究物体的 热辐射特性以及与其它物体 的相互作用。
红外成像技术
通过探测物体发出的红外辐 射,红外成像技术可以实现 对远距离目标的探测和成像, 具有广泛的军事和工业应用。
天体物理学
天体物理学研究天体的辐射 特性和物质的相互作用,黑 体辐射是天体物理学中不可 或缺的基本概念。
实例分析:黑体辐射的应用案例
让我们通过实际案例来更好地了解黑体辐射在现实生活中的应用。以下是一些有趣的案例分析。
1
黑体辐射在太阳能热发电中的应用
太阳能热发电利用太阳辐射产生的热能,其中包括黑体辐射,转换成电能。我们将分 析太阳能热发电的原理和工作机制。
2
黑体辐射在热能战略中的应用
黑体辐射计算的数值计算方法

黑体辐射计算的数值计算方法在物理学中,黑体辐射是指能够完全吸收所有入射光线并以最高效率辐射出来的物体。
黑体模型被广泛运用于天体物理学、能源传输和光学领域等。
黑体辐射计算是指对于黑体物理特性进行计算和模拟的过程,是物理学和工程学研究实践中不可或缺的技术。
在本文中,我们将重点探讨黑体辐射计算的数值计算方法。
1、黑体辐射的基本概念理论上,在热力学中,热辐射只与温度有关,而与物体自身性质无关。
一个与辐射恒定的物体,它的总辐射通量(每秒放射出的能量)完全取决于它的温度,且不依赖于物体材质的种类和形状。
这个独立于物体自身性质的热辐射称为黑体辐射。
2、数值计算方法计算黑体辐射的方法有多种,其中主要有下列几种数值计算方法:(1)直接确定辐射场:这是计算黑体辐射的最常用方法。
它采用区域划分技术,将区域分割成若干个互补的单元,然后通过微分方程、积分方程、离散化等数学方法,求解单元之间的辐射通量及温度场。
直接确定辐射场的方法具有计算量大、准确度高等特点。
(2)行列式计算:该方法用到了行列式的交替和定理,可以通过行列式的组合得到辐射通量的表达式,但不适合分析复杂的物理过程。
(3)离散截面法:传统的离散截面法是指将介质吸收、散射、反射等过程描述为离散作用,在几何形状相同时,通过计算表面所接受单元体和单位输出辐射通量的比例,进而计算出辐射通量。
但该方法不能同时解决介质透明性和不透明性以及非均匀性等问题。
(4)经验公式法:采用积分公式、试探分析等方法,建立数学模型,来模拟辐射现象,使能够在一定误差范围内,模拟出真实的辐射通量。
总之,黑体辐射计算的数值计算方法在实际工程应用中有着多样化和灵活的表现形式。
在具体应用中,应当结合被研究物体的实际情况,选择适合的计算方法,以提高计算效率和准确度。
3、结尾黑体辐射计算是物理学和工程学研究实践中必不可少的技术,而合适的计算方法可以提高计算效率和准确度。
本文详细介绍了黑体辐射的基本概念和主要的数值计算方法。
黑体辐射:夜空中最亮的星

黑体辐射:夜空中最亮的星1. 什么是黑体辐射?黑体辐射(black body radiation)是指在特定温度下的物体所发出的辐射。
一个理想的黑体是一个能完全吸收所有辐射能量,并且无损地将其转化为热能的物体。
由于吸收了所有辐射能量,黑体也会以同样的强度将能量辐射出去,因此被称为黑体辐射。
2. 黑体辐射的性质根据普朗克发现的普朗克辐射公式,黑体辐射具有以下几个特性:频率分布:处于热平衡状态的黑体发出的辐射能量,不同频率下的辐射功率与频率成正比。
也就是说,黑体辐射呈现出连续的频谱分布。
辐射强度:随着温度升高,黑体的辐射功率密度会增加,即黑体辐射的强度会变大。
峰值频率:随着温度升高,黑体辐射的峰值频率会向高频方向移动。
频谱分布与温度关系:根据普朗克定律,不同温度下的黑体辐射频谱形状不同,高温下偏向紫外光,低温下偏向红外光。
3. 夜空中最亮的星夜空中最亮的星指的是对人眼来说,在天空中最明亮、最突出、最容易被察觉的星星。
然而,这些所谓“夜空中最亮的星”实际上并不完全由星星本身发出的可见光构成。
在天文学中,我们主要使用视星等(apparent magnitude)来描述星星的亮度。
视星等是基于人眼对天体亮度感知的一种量表,数值越小表示亮度越大。
然而,夜空中最亮的星并不一定符合视星等最小的条件。
众所周知,夜空中最明亮的天体实际上是我们家门口那颗耀眼炫目的太阳。
然而,在日间观察时无法看到其他星星。
而在夜晚,为什么我们会注意到其他更加暗淡、视星等更大一些的“夜空中最亮的星”呢?原因在于黑体辐射和人眼感受到亮度之间存在着复杂关系。
虽然某些恒星可能在可见光范围内很亮,但它们可能在其他波长范围内发出了更大数量或者更高能量级别的黑体辐射。
也就是说,尽管这些恒星可能在可见光下并不显眼,但它们在其他波长范围内可能非常明亮。
其中一个例子是天狼星。
天狼星是位于南半球最亮、最接近地球和太阳系最大的恒星之一。
然而,它看起来并不是地球上着名“夜空中最亮的星”。
普朗克黑体辐射公式推导

普朗克黑体辐射公式推导TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】普朗克黑体辐射公式的推导所谓的黑体是指能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。
黑体辐射:由这样的空腔小孔发出的辐射就称为黑体辐射。
辐射热平衡状态: 处于某一温度 T 下的腔壁,单位面积所发射出的辐射能量和它所吸收的辐射能量相等时,辐射达到热平衡状态。
实验发现:热平衡时,空腔辐射的能量密度,与辐射的波长的分布曲线,其形状和位置只与黑体的绝对温度 T 有关而与黑体的形状和材料无关。
实验得到: 1. Wien 公式从热力学出发加上一些特殊的假设,得到一个分布公式:Wien 公式在短波部分与实验还相符合,长波部分则明显不一致。
2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符,但是在高频区公式与实验不符,并且∞→=⎰∞v v d E E ,既单位体积的能量发散,而实验测得的黑体辐射的能量密度是4T E σ=,该式叫做Stefan-Bolzmann 公式,σ叫做Stefan-Bolzmann 常数。
3. Planck 黑体辐射定律1900年12月14日Planck 提出如果空腔内的黑体辐射和腔壁原子处于平衡,那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。
作为辐射原子的模型,Planck 假定:(1)原子的性能和谐振子一样,以给定的频率 v 振荡;(2)黑体只能以 E = hv 为能量单位不连续的发射和吸收辐射能量,而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。
得到:νννπνρνd kT h C h d ⎪⎪⎭⎫ ⎝⎛-=1)/exp(1833该式称为 Planck 辐射定律 h 为普朗克常数,h=s j .10626.634-⨯4,普朗克的推导过程:把空窖内的电磁波分解为各个频率的简振振动,简振模的形式最后为).(),(wt r K i k k e C t r -=αβψ,为常系数振方向,表示两个互相垂直的偏ααk C 2,1=每一个简振模在力学上等价于一个自由度,记频率在()νννd +,内的自由度数为()ννd g , 则(0,v )范围内的总自由度数G(v)与g(v)的关系为()()ννννd g G ⎰=0。
物理学中的黑体辐射理论

物理学中的黑体辐射理论黑体辐射是热物理学中的基本现象,它的理论研究始于19世纪,在发展中产生了很多有价值的理论成果。
黑体辐射的理论研究不仅对热物理学,还对其他物理学分支产生了深远的影响,被誉为“现代物理学之母”。
一、黑体辐射概述黑体是指一种理想的物体,它能够完全吸收所接受的辐射能量,不产生反射和透射。
经过一个一定时间后,黑体达到热平衡状态,它呈现出一个“黑色”的外表,因此称为黑体。
黑体辐射现象,是指黑体对辐射场的反应,辐射场包括电磁波、光线等等。
在特定温度下,黑体辐射的能量密度与波长有关,呈现出一定的特征谱线,这种谱线称为黑体辐射谱线。
二、黑体辐射规律的提出19世纪末至20世纪初,物理学家们开始对黑体辐射进行深入的研究。
1896年,维恩发现黑体辐射的波长与温度有关,即波峰位置随温度的变化而移动。
维恩的研究使得物理学家们开始探索黑体辐射规律,并且得到了准确的定律。
1900年,普朗克推导出了黑体辐射规律,此后被称为普朗克辐射定律。
它对黑体辐射功率谱密度进行了整体描述。
普朗克通过黑体的热力学平衡状态、量子化假设等方法,揭示了能量与频率有关,辐射的功率谱密度与波长及温度有关。
三、黑体辐射谱线的研究在普朗克定律的基础上,维恩和瑞利也提出了有关黑体辐射谱线的定律。
维恩定律是指在同一温度下,黑体辐射谱线的峰位波长与绝对温度呈反比关系。
这条定律的实验验证与研究已经相对成熟,可以用来作为恒星光谱的计算依据。
瑞利定律是指在同一温度下,黑体辐射的总辐射能量密度与绝对温度的四次方呈正比关系。
瑞利的研究使得我们能够更加准确地描述黑体辐射运动规律。
四、经典物理学中黑体辐射理论的局限性在黑体辐射理论的发展中,人们发现了经典物理学的局限性,无法描述黑体辐射场的真实过程。
为了更好地描述黑体辐射,物理学家们必须重新审视传统物理理论。
这种由于经典物理学的局限性而引发的科学革命,在20世纪初期的物理学发展中居于重要的地位。
爱因斯坦、玻尔等学者在量子力学、相对论等领域都做出了突出的贡献,物理学的发展呈现出前所未有的繁荣态势。
黑体会辐射

黑体会辐射
黑体辐射是指温度高于绝对零度的物体会发出电磁波的现象。
根据黑体辐射定律,黑体辐射能量与温度的四次方成正比。
在真实世界中,没有绝对的黑体,但我们可以近似地将某些物体视为黑体来研究其辐射行为。
黑体辐射是由物体内部分子和原子的热运动导致的。
当物体的温度升高时,分子和原子的热运动加剧,它们释放出的能量以电磁波的形式传播出去。
这些电磁波包括可见光、红外线、紫外线等。
辐射的能量和频率之间存在着特定的关系,即普朗克公式。
普朗克公式揭示了辐射能量随频率的变化规律,即高频率的辐射能量较弱,低频率的辐射能量较强。
这也解释了为什么高温物体的辐射呈现出白炽光,而低温物体的辐射主要是红外线。
黑体辐射存在着辐射能量密度和辐射功率密度的概念。
辐射能量密度是指黑体单位体积或单位面积内的辐射能量,而辐射功率密度是指单位时间内黑体单位体积或单位面积内的辐射能量。
这两个概念量化了黑体辐射的强弱。
在实际应用中,黑体辐射有着广泛的应用。
例如,热成像技术利用物体的红外辐射来生成热图像,用于检测异常热量的分布。
太阳能电池利用太阳辐射中的可见光能量来产生电能。
此外,黑体辐射对于了解宇宙射线的起源和性质也起到了重要的作用。
总之,黑体辐射是物体在高温状态下释放电磁波的现象。
它是
热物理学和光学领域的重要研究课题,有着广泛的应用价值。
通过对黑体辐射的研究,我们能够更好地了解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黑体实验
(一)、实验目的要求
1、掌握黑体基本理论
2、掌握黑体辐射能量的测量和任意发射光源的辐射能量的测量
3、学会利用相同的装置验证黑体的辐射定律
(二)、实验原理与设备
黑体的基本理论
物体在一定的温度下发出电磁辐射,如果理想热辐射体表面温度已知,那么其辐射特性就可以完全确定。
黑体在温度T时的光谱辐射出射度M等于普适函数。
1900年,普朗克根据他提出的量子理论建立了的准确表达式,得到了与实验完全相同的结果。
这就是著名的普朗克辐射公式。
式中:__第一辐射常量,其值为3.7418
___第二辐射常量,其值为1.4388;
M__单位为.
普朗克公式是光辐射的一个重要的基本公式。
从这个公式出发,可以推导出其他有关的辐射公式。
根据基尔霍夫定律可知,绝对黑体的总辐射出射度只是温度的函数,1879年斯忒藩根据实验得到一条经验定律:绝对黑体的积分辐射出射度与其热力学温度的四次方成正比。
1884年,玻尔兹曼根据热力学理论推导出了与斯忒藩经验定律相一致的结果,因此,称为斯-玻定律。
将上式对所有波长积分,就得到绝对黑体的积分辐射出射度,
即=
此式为斯忒藩-玻耳兹曼定律,其中称为斯忒藩-玻尔兹曼常量。
斯忒藩-玻尔兹曼定律表明,黑体的全辐射出射度与热力学温度的四次方成正比。
因此,温度T微小的变化,就会引起辐射出射度很大的变化。
凡温度在绝对零度以上的物体均能够发出红外辐射,其辐射的峰值波长与物体的温度有确定的关系:
式中λm ——物体辐射的峰值波长
T——物体的温度
B——常数(2898μm·K)
此为辐射度学中的维恩位移定律,意为只要物体有温度,则一定有固定波长的辐射,自然界的物体温度如果在
-40℃~3000℃(233K~3273K)范围,则根据上述公式,峰值辐射波长在0.88~12μm之间,即人们通常所说的红外波段。
2.实验装置及工作原理
WGH–10性黑体实验装置,油光栅单色仪,接受单元,扫描系统,电子放大器,A/D采集单元,电压可调的稳压溴钨灯光源,计算机及打印机组成.该设备集光学,精密机械,电子学,计算机技术与一体. 溴钨灯光源,可调溴钨灯供电源,红外光栅单色器,红外滤光片,硫化铅(PbS)光接收器,光调制器,信号采集单元,数据采集与单色仪控制软件及计算机等。
主机部分有以下几部分组成:单色器,狭缝,接收单元,光学系统以及光栅驱动系统等。
红外单色器光路采用C -T型,如图1。
图1红外单色器光学原理图
M1反射镜、M2准光镜、M3物镜,M4反射镜、M5 深椭球镜
G平面衍射光栅、S1入射狭缝、S2,S3出射狭缝、T调制器
狭缝为直狭缝,宽度范围0—2.5mm连续可调,顺时针旋转为狭缝宽度加大,反之减小,每旋转一周狭缝宽度变化0.5mm。
为延长使用受命,调节时注意最大不超过2.5mm,平时不使用时,狭缝最好开到0.1-0.5 mm左右。
为去除光栅光谱仪中的高级次光谱,在使用过程中,操作者可根据需要把备用的滤光片插入入缝插板上。
图2WGH-10型黑体实验装置
本实验装置的工作区间在800-2500nm,所以选用硫化铅(PbS)为光信号接收器,
从单色仪出缝射出的单色光信号经调制器,调制成50HZ的频率信号被PbS接收,选用的PbS是晶体管外壳结构、该系列探测器是将硫化铅元件封装在晶体管壳内,充以干燥的氮气或其它惰性气体,并采用熔融或焊接工艺,以保证全密封。
该器件可在高温,潮湿条件下工作且性能稳定可靠。
标准黑体应是黑体实验的主要设置,一个标准黑体其价格太高,所以本实验装置采用稳压溴钨灯作光源。
钨丝灯是一种选择性的辐射体,它产生的光谱是连续的它的总辐射本领RT可由下式求出。
式中为温度T时的总辐射系数,它是给定温度钨丝的辐射强度与绝对黑体的辐射强度之比,因此
或
式中B为常数,1.47×10-4钨丝灯的辐射光谱分布RλT为:
本次实验的钨灯光源,有实测的工作电流与色温度对应关系的数据。
(三)、实验步骤与内容
1、仔细阅读实验讲义,按要求正确连接电路。
检查无误后,打开溴钨灯电源预热;打开主机电源,连接好USB 数据线。
2、建立传递函数曲线
(1)将标准光源电流调整为―溴钨灯的色温‖表中色温为2940K时电流所在位置;
(2)预热20分钟后,在系统上记录该条件下全波段图谱;该光谱曲线包含了传递函数的影响;
(3)点击―验证黑体辐射定律‖菜单,选―计算传递函数‖命令,将该光谱曲线与已知的光源能量曲线相除,即得到传递函数曲线,并自动保存。
以后用户在做测量时,只要将菜单栏中右上方―传递函数‖点击成―传递函数‖。
后再测未知光源辐射能量线时,此时测量的结果已扣除了仪器传递的影响。
3、修正为黑体
任意发光体的光谱能量辐射本领与黑体辐射都有一系数关系软件内提供了钨的发射系数,并能通过点击修正黑体的菜单进行修正,此时,测量溴钨灯的辐射能量曲线将自动修正为同温度下黑体的曲线。
4、验证黑体辐射定律
(1)验证普朗克辐射定律
(2)验证斯特藩-波尔兹曼定律
(3)验证维恩位移定律
(综合性实验是指实验内容涉及本课程的综合知识或与本课程相关知识的实验,不是单一的。
设计性实验是指给定实验目的要求和条件,由学生自己设计实验方案并加以实现的实验。
)
本实验相关知识点:
红外物理(光度学与辐射度学):涉及黑体的基本概念、普朗克辐射定律、斯特藩-波尔兹曼定律、维恩位移定律等,几乎贯穿红外技术领域中各个环节。
