数字5版习题2章解答
《电子技术基础》数字部分第五版课后答案

第一章数字逻辑习题1.1数字电路与数字信号1.1.2图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0121112(ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制2−1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于4(2)127(4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43(3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+(2)@(3)you(4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1.6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
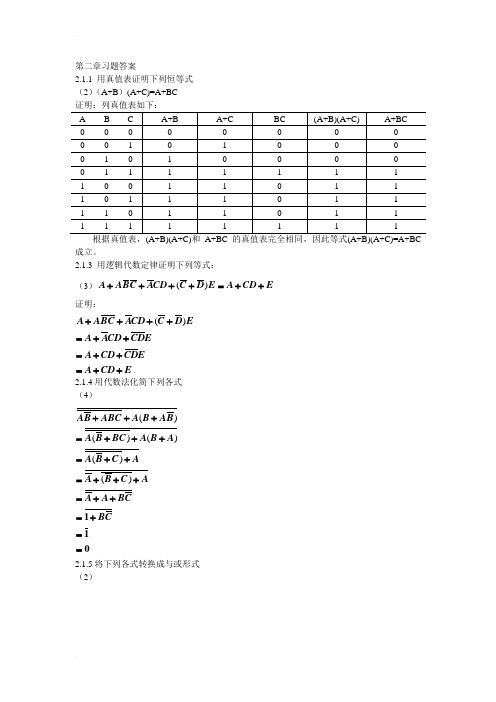
解:(a)为与非,(b)为同或非,即异或第二章逻辑代数习题解答2.1.1用真值表证明下列恒等式(3)A B AB AB ⊕=+(A⊕B)=AB+AB 解:真值表如下A B A B⊕ABAB A B⊕AB +AB00010110110000101000011111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
数值分析课程第五版课后习题答案

=
1 = 1.7863 × 10 − 2 。 55.982
8、当 N 充分大时,怎样求 ∫ [解]因为 ∫
N +1 N
1 dx ? 1+ x2
1 dx = arctan( N + 1) − arctan N ,当 N 充分大时为两个相近数相 1+ x2
减,设 α = arctan( N + 1) , β = arctan N ,则 N + 1 = tan α , N = tan β ,从而 tan(α − β ) = 因此 ∫
5、计算球体积要使相对误差限为 1%,问度量半径 R 允许的相对误差是多少? 4 ε * ( π (R* )3 ) 4 3 [解]由 1% = ε r* ( π ( R * ) 3 ) = 可知, 4 3 * 3 π (R ) 3 ′ 4 4 4 ε * ( π ( R * ) 3 ) = 1% × π ( R * ) 3 = π ( R * ) 3 ε * ( R * ) = 4π ( R * ) 2 × ε * ( R * ) , 3 3 3
ε * ( y n ) = 10ε * ( y n −1 ) = 10 n ε * ( y 0 ) ,
1 1 从而 ε * ( y10 ) = 1010 ε * ( y 0 ) = 1010 × × 10 − 2 = × 10 8 ,因此计算过程不稳定。 2 2 12、计算 f = ( 2 − 1) 6 ,取 2 ≈ 1.4 ,利用下列公式计算,哪一个得到的结果最 好? 1 ( 2 + 1)
* r
x= x
*
ε ( x * ) = n( x * ) n −1 2% x * = 2n% ⋅ x * ,
数值分析第五版课后答案2篇

数值分析第五版课后答案2篇数值分析第五版课后答案(一)第一章1.1 机器精度的数值为2^-52 ≈2.22 × 10^-16。
1.2 Example 1.2设f(x) = (1 - cosx)/sinx,则f(0)的分母为0,无法进行数值计算。
1.3 Example 1.3设f(x) = (1 - cosx)/sinx,则f(0)的分子为0,因此有f(0) = 0。
1.4 Example 1.4(a) 将x的值从1.8改为1.799,则f(x)的值由-0.000000000000159为0.000000000000313,差值为0.000000000000472。
(b) 我们有f'(x) = sinx/(1 - cosx) - 1/sin^2x。
将x的值从1.8改为1.799,利用f(x)和f'(x)的值可以得到下面的近似式:f(x + Δx) ≈ f(x) + f'(x)Δx = -0.000000000000159 + 0.449787416887455×0.001 = -0.000000000000137。
与(a)中的结果相近。
1.5 Example 1.5(a) 当x很接近于0时,函数值的符号取决于cosx的符号,其中cosx接近于1。
因此,函数值为正。
(b) 当x很接近于π时,函数值的大小趋于无穷大,因为分母趋向于0,而分子不为0。
1.6 Example 1.6(a) 因为函数在x = 0处是奇函数,所以它的导数为偶函数。
(b) 首先,我们有f''(0) = -2,因此x = 0是最大值。
其次,我们有f''(x) = -2 - 8sin^2x。
由于-f''(x)在x = 0处是正的,我们有当x越接近0时,f''(x)越小,也就意味着函数在x = 0处是严格的最大值。
1.7 Example 1.7(a) 我们有f(x) = x^3 - 2x^2 - 5x + 6,f'(x) =3x^2 - 4x - 5和f''(x) = 6x - 4。
第2章习题解答

第二章习题解答2.01 试给出数据通信系统的基本模型并说明其主要组成构件的作用。
答:1)信源和信宿信源就是信息的发送端,是发出待传送信息的设备;信宿就是信息的接收端,是接收所传送信息的设备,在实际应用中,大部分信源和信宿设备都是计算机或其他数据终端设备(data terminal equipment,DTE)。
2)信道信道是通信双方以传输媒体为基础的传输信息的通道,它是建立在通信线路及其附属设备(如收发设备)上的。
该定义似乎与传输媒体一样,但实际上两者并不完全相同。
一条通信介质构成的线路上往往可包含多个信道。
信道本身也可以是模拟的或数字方式的,用以传输模拟信号的信道叫做模拟信道,用以传输数字信号的信道叫做数字信道。
3)信号转换设备其作用是将信源发出的信息转换成适合于在信道上传输的信号,对应不同的信源和信道,信号转换设备有不同的组成和变换功能。
发送端的信号转换设备可以是编码器或调制器,接收端的信号转换设备相对应的就是译码器或解调器。
2.02 试解释以下名词:数据,信号,模拟数据,模拟信号,数字数据,数字信号。
答:数据:通常是指预先约定的具有某种含义的数字、符号和字母的组合。
信号:信号是数据在传输过程中的电磁波的表示形式。
模拟数据:取值是连续的数据。
模拟信号:是指幅度随时间连续变化的信号。
数字数据:取值是离散的数据。
数字信号:时间上是不连续的、离散性的信号2.03 什么叫传信速率?什么叫传码速率?说明两者的不同与关系。
答:传信速率又称为比特率,记作R b,是指在数据通信系统中,每秒钟传输二进制码元的个数,单位是比特/秒(bit/s,或kbit/s或Mbit/s)。
传码速率又称为调制速率、波特率,记作N Bd,是指在数据通信系统中,每秒钟传输信号码元的个数,单位是波特(Baud)。
若是二电平传输,则在一个信号码元中包含一个二进制码元,即二者在数值上是相等的;若是多电平(M电平)传输,则二者在数值上有R b=N Bd×log2 M的关系。
数值分析课程第五版课后习题答案(李庆扬等)1之欧阳与创编

第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x xx x x ,相对误差为****ln ln )(ln )(ln xxx x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x n x n x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++;[解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫⎝⎛∂∂=++∑x x x x x f x x x e n k k kεεεε;(2)*3*2*1x x x ; [解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e nk k kεεεε;(3)*4*2/x x 。
数字电路第五版课后答案

第一章数字逻辑习题1.1 数字电路与数字信号图形代表的二进制数1.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%数制将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于2−4(2)127 (4)解:(2)(127)D= 27 -1=()B-1=(1111111)B=(177)O=(7F)H(4)()D=B=O=H二进制代码将下列十进制数转换为 8421BCD 码:(1)43 (3)解:(43)D=(01000011)BCD试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为 0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,33逻辑函数及其表示方法在图题 1. 中,已知输入信号 A,B`的波形,画出各门电路输出 L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答用真值表证明下列恒等式(3)A⊕ =B AB AB+ (A⊕B)=AB+AB解:真值表如下由最右边2栏可知,A⊕B与AB+AB的真值表完全相同。
用逻辑代数定律证明下列等式(3)A+ABC ACD C D E A CD E++ +( ) = + +解:A+ABC ACD C D E++ +( )=A(1+BC ACD CDE)+ += +A ACD CDE+= +A CD CDE+ = +A CD+ E用代数法化简下列各式 (3)ABC B( +C)解:ABCB( +C)= + +(A B C B C)( + )=AB AC BB BC CB C+ + + + +=AB C A B B+ ( + + +1)=AB C+(6)(A + + + +B A B AB AB ) ( ) ( )() 解:(A + + + +B A B AB AB ) () ( )( )= A B ⋅+ A B ⋅+(A + B A )(+ B )=AB(9)ABCD ABD BCD ABCBD BC + + + +解:ABCD ABD BCD ABCBD BC +++ +=ABC D D ABD BC D C ( + +) + ( + ) =B AC AD C D ( + + + ) =B A C AD ( + + + ) =B A C D ( + + ) =AB BC BD + +画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门B AB AB = + + AB B = + A B = +(1)L AB AC =(2) ( ) L DAC = +已知函数L (A ,B ,C ,D )的卡诺图如图所示,试写出函数L 的最简与或表达式用卡诺图化简下列个式(3) ( )() L ABCD=+ +解: ( , , , ) L ABCDBCDBCDBCDABD = + + +(1)ABCD ABCD AB AD ABC+ + + +解:ABCD ABCD AB AD ABC+ + + +=ABCD ABCD ABC C D D AD B B C C ABC D D++ ( + )( + +)( + )( + +)( + )=ABCD ABCD ABCD ABCD ABCD ABCD ABCD+ + + + + +(6)L A B C D( , , , )=∑m(0,2,4,6,9,13)+∑d(1,3,5,7,11,15)解:L= +A D(7)L A B C D( , , , )=∑m(0,13,14,15)+∑d(1,2,3,9,10,11)解:L AD AC AB= + +已知逻辑函数L AB BC CA=+ + ,试用真值表,卡诺图和逻辑图(限用非门和与非门)表示解:1>由逻辑函数写出真值表用摩根定理将与或化为与非表达式L = AB + BC + AC = AB BC AC ⋅ ⋅4>由已知函数的与非-与非表达式画出逻辑图2> 由真值表画出卡诺图3> 由卡诺图,得逻辑表达式 LABBCAC = + +第三章习题MOS 逻辑门电路根据表题所列的三种逻辑门电路的技术参数,试选择一种最合适工作在高噪声环境下的门电路。
高中数学必修5第二章课后习题解答新版

新课程标准数学必修5第二章课后习题解答第二章 数列2.1数列的概念与简单表示法 练习(P31) 1、2、前5项分别是:1,0,1,0,1--.3、例1(1)1(2,)1(21,)n n m m N n a n m m N n⎧-=∈⎪⎪=⎨⎪=-∈⎪⎩**; (2)2(2,)0(21,)n n m m N a n m m N ⎧=∈⎪=⎨=-∈⎪⎩**说明:此题是通项公式不唯一的题目,鼓励学生说出各种可能的表达形式,并举出其他可能的通项公式表达形式不唯一的例子.4、(1)1()21n a n Z n +=∈-; (2)(1)()2n n a n Z n +-=∈; (3)121()2n n a n Z +-=∈ 习题2.1 A 组(P33) 1、(1)2,3,5,7,11,13,17,19;(2) (3)1,1.7,1.73,1.732,…1.732050; 2,1.8,1.74,1.733,…,1.732051.2、(1)11111,,,,491625; (2)2,5,10,17,26--.3、(1)(1),4-,9,(16-),25,(36-),49; 12(1)n n a n +=-; (2)1,(,2;n a =.4、(1)1,3,13,53,2132; (2)141,5,,,5454--.5、对应的答案分别是:(1)16,21;54n a n =-;(2)10,13;32n a n =-;(3)24,35;22n a n n =+.6、15,21,28; 1n n a a n -=+. 习题2.1 B 组(P34)1、前5项是1,9,73,585,4681.该数列的递推公式是:1118,1n n a a a +=+=.通项公式是:817n n a -=.2、110(10.72)10.072a =⨯+=﹪; 2210(10.72)10.144518a =⨯+=﹪; 3310(10.72)10.217559a =⨯+=﹪; 10(10.72n n a =⨯+﹪.3、(1)1,2,3,5,8; (2)358132,,,,2358.2.2等差数列 练习(P39)1、表格第一行依次应填:0.5,15.5,3.75;表格第二行依次应填:15,11-,24-.2、152(1)213n a n n =+-=+,1033a =.3、4n c n =4、(1)是,首项是11m a a md +=+,公差不变,仍为d ;(2)是,首项是1a ,公差2d ;(3)仍然是等差数列;首项是716a a d =+;公差为7d . 5、(1)因为5375a a a a -=-,所以5372a a a =+. 同理有5192a a a =+也成立; (2)112(1)n n n a a a n -+=+>成立;2(0)n n k n k a a a n k -+=+>>也成立. 习题2.2 A 组(P40)1、(1)29n a =; (2)10n =; (3)3d =; (4)110a =.2、略.3、60︒.4、2℃;11-℃;37-℃.5、(1)9.8s t =; (2)588 cm ,5 s. 习题2.2 B 组(P40)1、(1)从表中的数据看,基本上是一个等差数列,公差约为2000,52010200280.2610a a d =+=⨯ 再加上原有的沙化面积5910⨯,答案为59.2610⨯;(2)2021年底,沙化面积开始小于52810 hm ⨯. 2、略. 2.3等差数列的前n 项和 练习(P45) 1、(1)88-; (2)604.5.2、59,11265,112n n a n n ⎧=⎪⎪=⎨+⎪>⎪⎩ 3、元素个数是30,元素和为900.习题2.3 A 组(P46)1、(1)(1)n n +; (2)2n ; (3)180个,和为98550; (4)900个,和为494550.2、(1)将120,54,999n n a a S ===代入1()2n n n a a S +=,并解得27n =; 将120,54,27n a a n ===代入1(1)n a a n d =+-,并解得1713d =.(2)将1,37,6293n d n S ===代入1(1)n a a n d =+-,1()2n n n a a S +=,得111237()6292n n a a a a =+⎧⎪⎨+=⎪⎩;解这个方程组,得111,23n a a ==.(3)将151,,566n a d S ==-=-代入1(1)2n n n S na d -=+,并解得15n =;将151,,1566a d n ==-=代入1(1)n a a n d =+-,得32n a =-.(4)将2,15,10n d n a ===-代入1(1)n a a n d =+-,并解得138a =-;将138,10,15n a a n =-=-=代入1()2n n n a a S +=,得360n S =-. 3、44.5510⨯m. 4、4.5、这些数的通项公式:7(1)2n -+,项数是14,和为665.6、1472.习题2.3 B 组(P46)1、每个月的维修费实际上是呈等差数列的. 代入等差数列前n 项和公式,求出5年内的总共的维修费,即再加上购买费,除以天数即可. 答案:292元.2、本题的解法有很多,可以直接代入公式化简,但是这种比较繁琐. 现提供2个证明方法供参考. (1)由 61615S a d =+,1211266S a d =+,18118153S a d =+ 可得61812126()2()S S S S S +-=-.(2)1261212126()()S S a a a a a a -=+++-+++7812a a a =+++ 126(6)(6)(6)a d a d a d =++++++ 126()36a a a d =++++636S d =+同样可得:1812672S S S d -=+,因此61812126()2()S S S S S +-=-.3、(1)首先求出最后一辆车出发的时间4时20分;所以到下午6时,最后一辆车行驶了1小时40分.(2)先求出15辆车总共的行驶时间,第一辆车共行驶4小时,以后车辆行驶时间依次递减,最后一辆行驶1小时40分. 各辆车的行驶时间呈等差数列分布,代入前n 项和公式,这个车队所有车的行驶时间为2418531522S +=⨯= h. 乘以车速60 km/h ,得行驶总路程为2550 km.4、数列1(1)n n ⎧⎫⎨⎬+⎩⎭的通项公式为111(1)1na n n n n ==-++ 所以111111111()()()()1122334111n nS n n n n =-+-+-++-=-=+++ 类似地,我们可以求出通项公式为1111()()n a n n k k n n k==-++的数列的前n 项和.2.4等比数列练习(P52) 1、2、由题意可知,每一轮被感染的计算机台数构成一个首项为180a =,公比为20q =的等比数列,则第5轮被感染的计算机台数5a 为 447518020 1.2810a a q ==⨯=⨯.3、(1)将数列{}n a 中的前k 项去掉,剩余的数列为12,,k k a a ++ . 令,1,2,k i b a i +== ,则数列12,,k k a a ++ 可视为12,,b b .因为11(1)i k i i k ib a q i b a ++++==≥,所以,{}n b 是等比数列,即12,,k k a a ++ 是等比数列. (2){}n a 中的所有奇数列是135,,,a a a ,则235211321(1)k k a a aq k a a a +-===== ≥. 所以,数列135,,,a a a 是以1a 为首项,2q 为公比的等比数列. (3){}n a 中每隔10项取出一项组成的数列是11223,,,a a a , 则1112231111121110(1)k k a a aq k a a a +-===== ≥ 所以,数列11223,,,a a a 是以1a 为首项,11q 为公比的等比数列.猜想:在数列{}n a 中每隔m (m 是一个正整数)取出一项,组成一个新的数列,这个数列是以1a 为首项,1m q +为公比的等比数列.4、(1)设{}n a 的公比为q ,则24228511()a a q a q ==,而262837111a a a q a q a q ⋅=⋅=所以2537a a a =⋅,同理2519a a a =⋅ (2)用上面的方法不难证明211(1)nn n a a a n -+=⋅>. 由此得出,n a 是1n a -和1n a +的等比中项. 同理:可证明,2(0)nn k n k a a a n k -+=⋅>>. 由此得出,n a 是n k a -和n k a +的等比中项(0)n k >>. 5、(1)设n 年后这辆车的价值为n a ,则13.5(110)n n a =-﹪. (2)4413.5(110)88573a =-≈﹪(元). 用满4年后卖掉这辆车,能得到约88573元.习题2.4 A 组(P53)1、(1)可由341a a q =,得11a =-,6671(1)(3)729a a q ==-⨯-=-. 也可由671a a q =,341a a q =,得337427(3)729a a q ==⨯-=-(2)由131188a q a q =⎧⎪⎨=⎪⎩,解得12723a q =⎧⎪⎨=⎪⎩,或12723a q =-⎧⎪⎨=-⎪⎩(3)由416146a q a q ⎧=⎪⎨=⎪⎩,解得232q =,862291173692a a q a q q a q ==⋅==⨯= 还可由579,,a a a 也成等比数列,即2759a a a =,得22795694a a a ===.(4)由411311156a q a a q a q ⎧-=⎪⎨-=⎪⎩ ①②①的两边分别除以②的两边,得2152q q +=,由此解得12q =或2q =. 当12q =时,116a =-. 此时2314a a q ==-. 当2q =时,11a =. 此时2314a a q ==. 2、设n 年后,需退耕n a ,则{}n a 是一个等比数列,其中18(110),0.1a q =+=﹪. 那么2005年需退耕5551(1)8(110)13a a q =+=+≈﹪(万公顷) 3、若{}n a 是各项均为正数的等比数列,则首项1a 和公比q 都是正数. 由11n n a a q-=11(1)22)n n q --=.那么数列{}n a12q 为公比的等比数列.4、这张报纸的厚度为0.05 mm ,对折一次后厚度为0.05×2 mm ,再对折后厚度为0.05×22 mm ,再对折后厚度为0.05×32 mm. 设00.05a =,对折n 次后报纸的厚度为n a ,则{}n a 是一个等比数列,公比2q =. 对折50次后,报纸的厚度为50505013100.052 5.6310 m m 5.6310 m a a q ==⨯≈⨯=⨯ 这时报纸的厚度已经超出了地球和月球的平均距离(约83.8410 m ⨯),所以能够在地球和月球之间建一座桥.5、设年平均增长率为1,105q a =,n 年后空气质量为良的天数为n a ,则{}n a 是一个等比数列.由3240a =,得2231(1)105(1)240a a q q =+=+=,解得10.51q =≈ 6、由已知条件知,,2a bA G +==,且02a b A G +-=- 所以有A G ≥,等号成立的条件是a b =. 而,a b 是互异正数,所以一定有A G >.7、(1)2±; (2)22()ab a b ±+. 8、(1)27,81; (2)80,40,20,10. 习题2.4 B 组(P54)1、证明:由等比数列通项公式,得11m m a a q -=,11n n a a q -=,其中1,0a q ≠所以 1111m m n m n n a a q q a a q---== 2、(1)设生物体死亡时,体内每克组织中的碳14的原子核数为1个单位,年衰变率为q ,n 年后的残留量为n a ,则{}n a 是一个等比数列. 由碳14的半衰期为5730则 57305730112n a a qq===,解得157301()0.9998792q =≈ (2)设动物约在距今n 年前死亡,由0.6n a =,得10.9998790.6n n a a q ===. 解得 4221n ≈,所以动物约在距今42213、在等差数列1,2,3,…中,有7108917a a a a +==+,1040203050a a a a +==+ 由此可以猜想,在等差数列{}n a 中若*(,,,)k s p q k s p q N +=+∈,则k s p q a a a a +=+. 从等差数列与函数之间的联系的角度来分析这个问题:由等差数列{}n a 的图象,可以看出k p a k a p =,s q a sa q=根据等式的性质,有k s p q a a k sa a p q++=++,所以k s p q a a a a +=+. 猜想对于等比数列{}n a ,类似的性质为:若*(,,,)k s p q k s p q N +=+∈,则k s p q a a a a ⋅=⋅. 2.5等比数列的前n 项和 练习(P58) 1、(1)6616(1)3(12)189112a q S q --===--. (2)1112.7()9190311451()3n n a a qS q----===----. 2、设这个等比数列的公比为q(第3题)所以 101256710()()S a a a a a a =+++++++ 555S q S =+55(1)q S =+50= 同理 1015105S S q S =+.因为 510S =,所以由①得 5101051416S q q S =-=⇒= 代入②,得1015105501610210S S q S =+=+⨯=.3、该市近10年每年的国内生产总值构成一个等比数列,首项12000a =,公比 1.1q =设近10年的国内生产总值是10S ,则10102000(1 1.1)31874.81 1.1S -=≈-(亿元) 习题2.5 A 组(P61) 1、(1)由34164641a q a ===--,解得4q =-,所以144164(4)5111(4)a a q S q ---⨯-===---. (2)因为2131233(1)S a a a a q q --=++=++,所以2113q q --++=,即2210q q --=解这个方程,得1q =或12q =-. 当1q =时,132a =;当12q =-时,16a =.2、这5年的产值是一个以1138 1.1151.8a =⨯=为首项, 1.1q =为公比的等比数列所以5515(1)151.8(1 1.1)926.75411 1.1a q S q -⨯-==≈--(万元) 3、(1)第1个正方形的面积为42cm ,第2个正方形的面积为22cm ,…,这是一个以14a =为首项,12q =为公比的等比数列所以第10个正方形的面积为99710114()22a a q -==⨯=(2cm )(2)这10个正方形的面积和为77110101422821112a a qS q---⨯-===---(2cm )4、(1)当1a =时,2(1)(1)(2)()12(1)2n n na a a n n --+-++-=-----=-当1a ≠时,22(1)(2)()()(12)n n a a a n a a a n -+-++-=+++-+++(1)(1)12n a a n n a -+=--(2)1212(235)(435)(35)2(12)3(555)n n n n -------⨯+-⨯+-⨯=+++-+++11(1)5(15)323(1)(15)2154n nn n n n ----+-⨯-⨯=+--- (3)设21123n n S x x nx -=++++ ……①则 212(1)n n n xS x x n x nx -=+++-+ ……②①-②得,21(1)1n n n x S x x x nx --=++++- ……③当1x =时,(1)1232n n n S n +=++++= ;当1x ≠时,由③得,21(1)1n n n x nx S x x -=--- 5、(1)第10次着地时,经过的路程为91002(50251002)-++++⨯1291911002100(222)2(12)100200299.61 (m)12------=+⨯+++-=+⨯≈- (2)设第n 次着地时,经过的路程为293.75 m ,则1(1)12(1)12(12)1002100(222)100200293.7512n n ---------+⨯+++=+⨯=- 所以130********.75n --⨯=,解得120.03125n -=,所以15n -=-,则6n =6、证明:因为396,,S S S 成等差数列,所以公比1q ≠,且9362S S S =+即,936111(1)(1)(1)2111a q a q a q q q q---⨯=+--- 于是,9362q q q =+,即6321q q =+ 上式两边同乘以1a q ,得741112a q a q a q =+ 即,8252a a a =+,故285,,a a a 成等差数列 习题2.5 B 组(P62)1、证明:11111()(1())1n n n n n n n n n bb b a b a a a b b a a b a a a b a+++---+++=+++==-- 2、证明:因为7714789141277()S S a a a q a a a q S -=+++=+++=141421141516211277()S S a a a q a a a q S -=+++=+++=所以71472114,,S S S --成等比数列3、(1)环保部门每年对废旧物资的回收量构成一个等比数列,首项为1100a =,公比为 1.2q =. 所以,2010年能回收的废旧物资为89100 1.2430a =⨯≈(t )(2)从2002年到2010年底,能回收的废旧物资为9919(1)100(1 1.2)208011 1.2a q S q --==≈--(t )可节约的土地为165048320⨯=(2m ) 4、(1)依教育储蓄的方式,应按照整存争取定期储蓄存款利率计息,免征利息税,且若每月固定存入a 元,连续存n 个月,计算利息的公式为()2a na n+⨯月利率.因为整存整取定期储蓄存款年利率为2.52﹪,月利率为0.21﹪故到期3年时一次可支取本息共(505036)360.2118001869.932+⨯⨯⨯+=﹪(元)若连续存6年,应按五年期整存整取定期储蓄存款利率计息,具体计算略. (2)略.(3)每月存50元,连续存3年按照“零存整取”的方式,年利率为1.89﹪,且需支付20﹪的利息税所以到期3年时一次可支取本息共1841.96元,比教育储蓄的方式少收益27.97元.(4)设每月应存入x 元,由教育储蓄的计算公式得36(36)0.2136100002x x x +⨯+=﹪解得267.39x ≈(元),即每月应存入267.39(元) (5)(6)(7)(8)略 5、设每年应存入x 万元,则2004年初存入的钱到2010年底利和为7(12)x +﹪,2005年初存入的钱到2010年底利和为6(12)x +﹪,……,2010年初存入的钱到2010年底利和为(12)x +﹪. 根据题意,76(12)(12)(12)40x x x ++++++= ﹪﹪﹪根据等比数列前n 项和公式,得7(12)(1 1.02)401 1.02x +-=-﹪,解得52498x ≈(元) 故,每年大约应存入52498元第二章 复习参考题A 组(P67)1、(1)B ; (2)B ; (3)B ; (4)A .2、(1)212n n n a -=; (2)12(1)(21)1(2)n n n a n +--=+;(3)7(101)9n n a =-; (4)n a =n a3、4、如果,,a b c 成等差数列,则5b =;如果,,a b c 成等比数列,则1b =,或1-.5、n a 按顺序输出的值为:12,36,108,324,972. 86093436sum =.6、81381.9(10.13)1396.3⨯+≈﹪(万) 7、从12月20日到次年的1月1日,共13天. 每天领取的奖品价值呈等差数列分布.110,100d a ==. 由1(1)2n n n S a n d -=+得:1313121001310208020002S ⨯=⨯+⨯=>. 所以第二种领奖方式获奖者受益更多.8、因为28374652a a a a a a a +=+=+=所以34567285450()2a a a a a a a +++++==+,则28180a a +=.9、容易得到101010,1012002n n na n S +==⨯=,得15n =.10、212212()()()n n n n S a a a a nd a nd a nd ++=+++=++++++2121()n a a a n nd S n d =++++⨯=+32122312(2)(2)(2)n n n nS a a a a n d a n d a n d ++=+++=++++++ 2121()22n a a a n n d S n d =++++⨯=+ 容易验证2132S S S =+. 所以,123,,S S S 也是等差数列,公差为2n d . 11、221(1)(1)4(1)221a f x x x x x =+=+-++=-- 223(1)(1)4(1)267a f x x x x x =-=---+=-+ 因为{}n a 是等差数列,所以123,,a a a 也是等差数列. 所以,2132a a a =+. 即,20286x x =-+. 解得1x =或3x =. 当1x =时,1232,0,2a a a =-==. 由此可求出24n a n =-. 当3x =时,1232,0,2a a a ===-. 由此可求出42n a n =-.第二章 复习参考题B 组(P68)1、(1)B ; (2)D .2、(1)不成等差数列. 可以从图象上解释. ,,a b c 成等差,则通项公式为y pn q =+的形式,且,,a b c 位于同一直线上,而111,,a b c 的通项公式却是1y pn q =+的形式,111,,a b c不可能在同一直线上,因此肯定不是等差数列.(2)成等比数列. 因为,,a b c 成等比,有2b ac =. 又由于,,a b c 非零,两边同时取倒数,则有21111b ac a c==⨯. 所以,111,,a b c也成等比数列.3、体积分数:60.033(125)0.126⨯+≈﹪,质量分数:60.05(125)0.191⨯+≈﹪.4、设工作时间为n ,三种付费方式的前n 项和分别为,,n n n A B C . 第一种付费方式为常数列;第二种付费方式为首项是4,公差也为4的等差数列;第三种付费方式为首项是0.4,公比为2的等比数列. 则38n A n =,2(1)44222n n n B n n n -=+⨯=+, 0.4(12)0.4(21)12n n n C -==--. 下面考察,,n n n A B C 看出10n <时,380.4(21)n n >-.因此,当工作时间小于10天时,选用第一种付费方式.10n ≥时,,n n n n A C B C ≤≤因此,当工作时间大于10天时,选用第三种付费方式.5、第一星期选择A 种菜的人数为n ,即1a n =,选择B 种菜的人数为500a -.所以有以下关系式:2118030a a b =⨯+⨯﹪﹪3228030a a b =⨯+⨯﹪﹪……118030n n b a a b --=⨯+⨯﹪﹪500n n a b += 所以111502n n a a -=+,115003502n n n b a a -=-=- 如果1300a =,则2300a =,3300a =,…,10300a =6、解:由1223n n n a a a --=+得 1123()n n n n a a a a ---+=+以及1123(3)n n n n a a a a ----=--所以221213()37n n n n a a a a ---+=+=⨯,221213(1)(3)(1)13n n n n a a a a ----=--=-⨯.由以上两式得,11437(1)13n n n a --=⨯+-⨯ 所以,数列的通项公式是11137(1)134n n n a --⎡⎤=⨯+-⨯⎣⎦ 7、设这家牛奶厂每年应扣除x 万元消费基金2002年底剩余资金是1000(150)x +-﹪2003年底剩余资金是2[1000(150)](150)1000(150)(150)x x x x +-+-=+-+-﹪﹪﹪﹪ ……5年后达到资金 54321000(150)(150)(150)(150)(150)2000x x x x +-+-+-+-+=﹪﹪﹪﹪﹪ 解得 459x ≈(万元)。
电子技术基础数字部分(第五版)康光华主编第二章习题答案
第二章习题答案2.1.1 用真值表证明下列恒等式 (2)(A+B )(A+C)=A+BC 证明:列真值表如下:成立。
2.1.3 用逻辑代数定律证明下列等式:(3)()A ABC ACD C D E A CD E ++++=++ 证明:()A ABC ACD C D E A ACD CDE A CD CDE A CD E++++=++=++=++2.1.4用代数法化简下列各式 (4)()()()()()110AB ABC A B AB A B BC A B A A B C A A B C A A A BC BC +++=+++=++=+++=++=+==2.1.5将下列各式转换成与或形式 (2)()()()()A B C D C D A DA B C D C D A D AC AD BC BD AC CD AD D AC BC AD BD CD D AC BC D+++++++=+++++=+++++++=+++++=++2.1.7 画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门。
(1)L=AB+AC解:先将逻辑表达式化为与非-与非式:L AB AC AB AC AB AC =+=+=根据与非-与非表达式,画出逻辑图如下:LA B C2.1.8 已知逻辑函数表达式为L AB AC =+,画出实现该式的逻辑电路图,限使用非门和二输入或非门。
解:先将逻辑函数化为或非—或非表达式L AB A C AB A C A B A C =+=+=+++根据或非—或非表达式,画出逻辑图如下:A B CL另一种做法:用卡诺图化简变换为最简或与式A+B()()()()L A C A B A C A B A C A B =++=++=+++根据或非—或非表达式,画出逻辑图如下:AC BL2.2.1将下列函数展开为最小项表达式 (1)()()(,,,,)29101315L ACD BC D ABCD A B B CD ABCD A A BC D ABCD ABCD ABCD ABC D ABC D ABCD m =++=+++++=++++=∑(2)()L A B C =+()()()(,,)023L A B C AB AC AB C C A B B CABC ABC ABC ABC ABC ABC ABC m =+=+=+++=+++=++=∑(,,,,)14567L L m ==∑2.2.3用卡诺图化简下列各式(1) ABCD ABCD AB AD ABC ++++ 解:由逻辑表达式作卡诺图如下:ABAD由卡诺图得到最简与或表达式如下:L AB AC AD =++(5)(,,,)(,,,,,,,,,)0125689101314L A B C D m =∑解:由逻辑表达式作卡诺图如下:由卡诺图得到最简与或表达式如下:(,,,)L A B C D BD CD C D =++(7) (,,,)(,,,)(,,,,,)013141512391011L A B C D m d =+∑∑解:由逻辑表达式作卡诺图如下:A BAD AC由卡诺图得到最简与或表达式如下:=++(,,,)L A B C D AB AC AD。
数字电子技术基础课后习题答案第2章习题答案

思考题:题2.1.1 答:肖特基二极管(SBD)、分流。
题2.1.2 答:基区、滞后。
题2.1.3 答:(A)、(B) 。
题2.1.4 答:对。
题2.2.1 答:A、B。
题2.2.2 答:C、D。
题2.2.3 答:4ns。
题2.2.4 答:(A)、(C)、。
题2.2.5 答:降低、降低。
题2.2.6 答:0、1和三态题2.2.7 答:若一个输出高电平,另一个输出低电平时,会在T4和T5间产生一个大电流,烧毁管子。
OC门“线与”在输出接一电阻和一5-30V电源电压。
题2.2.8 答:能、分时。
题2.2.9 答:1. 为了缩短传输延迟时间,电路中使用肖特基管和有源泄放电路,另外,还将输入级的多发射极管改用SBD代替,由于SBD没有电荷存储效应,因此有利于提高电路的工作速度。
电路中还接入了D3和D4两个SBD,当电路的输出端由高电平变为低电平时,D4经T2的集电极和T5的基极提供了一条通路,一是为了加快负载电容的放电速度,二是为了加速T5的导通过程。
另外,D3经T2的集电极为T4的基极提供了一条放电通路,加快了T4的截止过程。
2. 为降低功耗,提高了电路中各电阻的阻值,将电阻R5原来接地的一端改接到输出端,以减小T3导通时电阻R5上的功耗。
题2.3.1 答:A。
题2.3.2 答:A。
题2.3.3 答:A。
题2.3.4 答:导通。
题2.3.5 答:B、C。
思考题:题2.4.1 答:(A)分流。
题2.4.2 答:(B) 内部电阻和容性负载。
题2.4.3 答:(B) 3.3V;(C)5V;(D) 30V。
题2.4.4 答:CMOS反相器和CMOS传输门。
题2.4.5 答:加入缓冲器保证输出电压不抬高或者降低,正逻辑变负逻辑或者相反,与非变成或非,或者或非变为与非。
题2.4.6 答:(C)低、高。
题2.4.7答:(A) OD门;(B) OC门;(C)三态门。
16题2.4.8 答:(A)驱动大负载;(B)电平移位。
计算机网络(第5版)课后习题答案:第2章 物理层

第二章物理层2-01 物理层要解决哪些问题?物理层的主要特点是什么?答:物理层要解决的主要问题:(1)物理层要尽可能地屏蔽掉物理设备和传输媒体,通信手段的不同,使数据链路层感觉不到这些差异,只考虑完成本层的协议和服务。
(2)给其服务用户(数据链路层)在一条物理的传输媒体上传送和接收比特流(一般为串行按顺序传输的比特流)的能力,为此,物理层应该解决物理连接的建立、维持和释放问题。
(3)在两个相邻系统之间唯一地标识数据电路。
物理层的主要特点:①由于在OSI之前,许多物理规程或协议已经制定出来了,而且在数据通信领域中,这些物理规程已被许多商品化的设备所采用,加之,物理层协议涉及的范围广泛,所以至今没有按OSI的抽象模型制定一套新的物理层协议,而是沿用已存在的物理规程,将物理层确定为描述与传输媒体接口的机械、电气、功能和过程特性。
②由于物理连接的方式很多,传输媒体的种类也很多,因此,具体的物理协议相当复杂。
2-02 归层与协议有什么区别?答:规程专指物理层协议。
2-03 试给出数据通信系统的模型并说明其主要组成构建的作用。
答:源点:源点设备产生要传输的数据。
源点又称为源站。
发送器:通常源点生成的数据要通过发送器编码后才能在传输系统中进行传输。
接收器:接收传输系统传送过来的信号,并将其转换为能够被目的设备处理的信息。
终点:终点设备从接收器获取传送过来的信息。
终点又称为目的站。
传输系统:信号物理通道。
2-04 试解释以下名词:数据,信号,模拟数据,模拟信号,基带信号,带通信号,数字数据,数字信号,码元,单工通信,半双工通信,全双工通信,串行传输,并行传输。
答:数据:是运送信息的实体。
信号:则是数据的电气的或电磁的表现。
模拟数据:运送信息的模拟信号。
模拟信号:连续变化的信号。
基带信号(即基本频带信号):来自信源的信号。
像计算机输出的代表各种文字或图像文件的数据信号都属于基带信号。
带通信号:把基带信号经过载波调制后,把信号的频率范围搬移到较高的频段以便在信道中传输(即仅在一段频率范围内能够通过信道)。
数值分析课程第五版课后习题答案

第一章 绪论3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(2.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++;[解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ; [解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
[解]53232323*42*4*2*2*41***4*2*1088654.01021)430.56(461.561021)430.56(461.561021)430.56(031.01021430.561)()()(1)()/(-----=⨯≈⨯⨯=⨯⨯=⨯⨯+⨯⨯=+=⎪⎪⎭⎫⎝⎛∂∂=∑x x x x x x x f x x e n k k kεεε。
数字设计:原理与实践第五版习题答案

数字设计:原理与实践第五版习题答案第一章:数字系统基础1. 哪些数学符号代表布尔逻辑运算?分别代表哪些逻辑操作?布尔逻辑运算包括与(AND)、或(OR)、非(NOT)、异或(XOR)等运算。
它们的对应数学符号表示如下:•与(AND):$\\cdot$ 或 $\\land$•或(OR):+或 $\\lor$•非(NOT):$\\overline{A}$ 或eee•异或(XOR):$\\oplus$2. 简述数字系统的信号表示和信号处理单元。
数字系统的信号表示使用离散量来表示连续或离散的信号,其中离散量指代具有离散数值的量。
信号处理单元是指对输入信号进行处理和操作的硬件模块,用于实现特定的功能或执行特定的任务。
3. 什么是布尔函数?它可以用哪些方法表示?布尔函数是指以布尔逻辑运算为基础,将一个或多个布尔变量映射为单一布尔值的函数。
布尔函数可以用真值表、逻辑表达式和逻辑图等方法表示。
4. 简述数字系统的设计方法。
数字系统的设计方法包括以下几个步骤:1.确定问题的需求和约束条件。
2.将问题抽象为逻辑功能的实现。
3.设计逻辑电路并进行仿真验证。
4.实现电路设计并进行实验验证。
5.优化电路设计并进行性能评估。
6.完成设计文档和报告。
第二章:组合逻辑电路设计1. 什么是组合逻辑电路?简述其基本特征。
组合逻辑电路是指将组合逻辑块进行组合形成的电路,其输出仅依赖于当前的输入。
它的基本特征包括:•输入输出之间无时序关系。
•只有组合逻辑块,没有存储元件。
•输出仅取决于当前输入。
2. 简述逻辑门的功能和特点。
逻辑门是实现布尔逻辑运算的基本构件,其功能和特点如下:•与门(AND):多个输入信号全部为高时,输出高;否则输出低。
•或门(OR):多个输入信号有一个为高时,输出高;否则输出低。
•非门(NOT):输入信号为高时,输出低;否则输出高。
•异或门(XOR):多个输入信号中奇数个为高时,输出高;否则输出低。
3. 什么是选择器和解码器?选择器是一种组合逻辑电路,根据选择信号将一组输入信号中的某一个作为输出。
计算方法与实习第五版-习题答案

方程求根
习题2——3:用简单迭代法求方程ex-4x=0的 根,并验证收敛性,精确到4位有效数字。
解:2.在区间[0,1]上构造收敛的公式并计算
x=ln(4x)= φ2(x) (1)两种等价形式: x=ex/4=φ1(x); xk (2) x=ex/4=φ1(x): e |φ1’(x)|=ex/4<1 (收敛), 迭代公式为: xk 1
(3) x=ln(4x)= φ2(x): |φ2’(x)|=1/x<1 (收敛),
迭代公式为:
xk 1 ln(4xk )
x3=2.137 x8=2.153
(4) 计算:x0=2 x4=2.146 x5=2.150
x1=2.079 x2=2.118 x6=2.152 x7=2.153 ∴ x ≈ 2.153
绪论
习题1——1:指出下列各数有几位有效数字
4.8675 4.08675 0.08675 96.4730 96*105 5 6 4 6 2
0.00096
2
绪论
习题1——2:对下列各数写出具有5位有效数 字的近似值
3.25894 3.25896 4.382000 0.000789247
3.2589
1.《计算方法》课程主要研究以计算 机为工具的 数值 分析方法 ,并评价 该算法的计算误差。 2.近似值作四则运算后的绝对误差限 公式为 ( x1 x2 ) ( x1 ) ( x2 ) ,近似值 1.0341的相对误差限不大于 1 10 2 , 则它至少有三位有效数字。 4
2 3
| x 0 1.5
=0.4557 <1(收敛) ∴2比1收敛快
∵ | 2’(x)|<|1’(x)|
数据通信与计算机网络第五版(习题答案)——第二章物理层

数据通信与计算机网络第五版第二章物理层2-1物理层要解决哪些问题?物理层协议的主要任务是什么?解答:物理层考虑的是怎样才能在连接各种计算机的传输媒体上传输数据比特流,而不是指具体的传输媒体。
因此物理层要考虑如何用电磁信号表示“1”或“0”;考虑所采用的传输媒体的类型,如双绞线、同轴电缆、光缆等;考虑与物理媒体之间接口,如插头的引脚数目和排列等;考虑每秒发送的比特数目,即数据率。
物理层协议的主要任务就是确定与传输媒体的接口有关的一些特性,即机械特性、电气特性、功能特性和过程特性。
2-2规程与协议有什么区别?解答:用于物理层的协议也常称为物理层规程(procedure)。
其实物理层规程就是物理层协议。
只是在“协议”这个名词出现之前人们就先使用了“规程”这一名词。
2-3物理层的接口有哪几个方面的特性?各包含些什么内容?解答:(1)机械特性指明接口所用接线器的形状和尺寸、引脚数目和排列、固定和锁定装置等。
常见的各种规格的电源接插件都有严格的标准化的规定。
(2)电气特性指明在接口电缆的各条线上出现的电压的范围。
(3)功能特性指明某条线上出现的某一电平的电压表示何种意义。
(4)过程特性指明对于不同功能的各种可能事件的出现顺序。
典,用户目的系统一般也包括以下两个部分:接收器:接收传输系统传送过来的信号,并把它转换为能够被目的设备处理的信息。
典型的接收器就是解调器,它把来自传输线路上的模拟信号进行解调,提取出在发送端置入的消息,还原出发送端产生的数字比特流。
终点:终点设备从接收器获取传送来的数字比特流,然后进行信息输出(例如,把汉字在PC 屏幕上显示出来)。
终点又称为目的站或信宿。
在源系统和目的系统之间的传输系统可以是简单的传输线,也可以是连接在源系统和目的系统之间的复杂网络系统。
2-5 请画出数据流1 0 1 0 0 0 1 1的不归零编码、曼彻斯特编码和差分曼彻斯特编码的波形(从高电平开始)。
解答:所求波形图如图所示。
《电子技术基础》数字部分第五版课后答案

第一章数字逻辑习题1.1数字电路与数字信号1.1.2图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0121112(ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制2−1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于4(2)127(4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43(3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+(2)@(3)you(4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1.6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解:(a)为与非,(b)为同或非,即异或第二章逻辑代数习题解答2.1.1用真值表证明下列恒等式(3)A B AB AB ⊕=+(A⊕B)=AB+AB 解:真值表如下A B A B⊕ABAB A B⊕AB +AB00010110110000101000011111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
数字电子技术第2章习题解答

第2章习题解答题2-1 用真值表证明下列恒等式。
(1) ()A B C AB AC ⊕=⊕(2) ()()()()()A B A C B C A B A C ''+++=++ (3) ()0A B A B A B '⊕==⊕⊕解:将输入变量所有的取值逐一代入公式两边计算,然后将计算结果列成真值表。
如果两边的真值表相同,则等式成立。
(1)证明()A B C AB AC ⊕=⊕表JT2-1(2) 证明 ()()()()()A B A C B C A B A C ''+++=++表JT2-2(3) 证明()0A B A B A B '⊕==⊕⊕表JT2-3题2-2 证明下列逻辑等式(证明方法不限)。
(1)()()BC D D B C AD B B D '''++++=+(2) A C A B BC A C D A BC ''''''''+++=+(3) ()ABCD A B C D AB BC CD A D '''''''''+=+++ (4) ()()()A C B D B D AB BC '''+++=+解:在实际应用中,除非逻辑式很简单、而且逻辑变量数很少的情况下,一般不宜用列真值表的方法。
对多变量、复杂的逻辑等式、通常采用公式推演或公式推演与画卡诺图相结合的方法去证明。
如果有条件使用Multisim 等EDA 软件进行证明,则更简单、便捷。
(1)()()()()BC D D B C AD B BC D B C AD B BC D AB D AC D BB BC B D'''''++++=++++''''=+++++=+(2)()A C A B BC A C D A C A B BC A BC BC A BC ''''''''''''''+++=++=+=+(3)()()()()()()()()()()()AB BC CD A D AB BC CD A D A B B C C D A D A B A C BC AC AD C D ABCD A B C D '''''''''''''+++=''''''''''=++++=++++''''=+ (4)()()()()()()A C B D B D A C B BD BD A C B AB BC ''''''+++=+++=+=+题2-3已知逻辑函数Y 1和Y 2的真值表如表JT2-4(a )、(b )所示,试写出Y 1和Y 2的逻辑函数式。
《高等数学第五版》上下册习题答案.pdf

习题1−11. 设A =(−∞, −5)∪(5, +∞), B =[−10, 3), 写出A ∪B , A ∩B , A \B 及A \(A \B )的表达式. 解 A ∪B =(−∞, 3)∪(5, +∞),A ∩B =[−10, −5),A \B =(−∞, −10)∪(5, +∞),A \(A \B )=[−10, −5).2. 设A 、B 是任意两个集合, 证明对偶律: (A ∩B )C =A C ∪B C .证明 因为x ∈(A ∩B )C ⇔x ∉A ∩B ⇔ x ∉A 或x ∉B ⇔ x ∈A C 或x ∈B C ⇔ x ∈A C ∪B C ,所以 (A ∩B )C =A C ∪B C .3. 设映射f : X →Y , A ⊂X , B ⊂X . 证明(1)f (A ∪B )=f (A )∪f (B );(2)f (A ∩B )⊂f (A )∩f (B ).证明 因为y ∈f (A ∪B )⇔∃x ∈A ∪B , 使f (x )=y⇔(因为x ∈A 或x ∈B ) y ∈f (A )或y ∈f (B )⇔ y ∈ f (A )∪f (B ),所以 f (A ∪B )=f (A )∪f (B ).(2)因为y ∈f (A ∩B )⇒ ∃x ∈A ∩B , 使f (x )=y ⇔(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )⇒ y ∈ f (A )∩f (B ), 所以 f (A ∩B )⊂f (A )∩f (B ).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使, , 其中I X I f g =D Y I g f =D X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f −1.证明 因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射.又因为对于任意的x 1≠x 2, 必有f (x 1)≠f (x 2), 否则若f (x 1)=f (x 2) ⇒g [ f (x 1)]=g [f (x 2)] ⇒ x 1=x 2. 因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y →X , 因为对每个y ∈Y , 有g (y )=x ∈X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X →Y , A ⊂X . 证明:(1)f −1(f (A ))⊃A ;(2)当f 是单射时, 有f −1(f (A ))=A .证明 (1)因为x ∈A ⇒ f (x )=y ∈f (A ) ⇒ f −1(y )=x ∈f −1(f (A )),所以 f −1(f (A ))⊃A .(2)由(1)知f −1(f (A ))⊃A .另一方面, 对于任意的x ∈f −1(f (A ))⇒存在y ∈f (A ), 使f −1(y )=x ⇒f (x )=y . 因为y ∈f (A )且f 是单射, 所以x ∈A . 这就证明了f −1(f (A ))⊂A . 因此f −1(f (A ))=A .6. 求下列函数的自然定义域:(1)23+=x y ;解 由3x +2≥0得32−>x . 函数的定义域为) ,32[∞+−. (2)211xy −=; 解 由1−x 2≠0得x ≠±1. 函数的定义域为(−∞, −1)∪(−1, 1)∪(1, +∞).(3)211x xy −−=; 解 由x ≠0且1−x 2≥0得函数的定义域D =[−1, 0)∪(0, 1].(4)241x y −=; 解 由4−x 2>0得 |x |<2. 函数的定义域为(−2, 2).(5)x y sin =;解 由x ≥0得函数的定义D =[0, +∞).(6) y =tan(x +1);解 由21π≠+x (k =0, ±1, ±2, ⋅ ⋅ ⋅)得函数的定义域为 12−+≠ππk x (k =0, ±1, ±2, ⋅ ⋅ ⋅). (7) y =arcsin(x −3);解 由|x −3|≤1得函数的定义域D =[2, 4].(8)xx y 1arctan 3+−=; 解 由3−x ≥0且x ≠0得函数的定义域D =(−∞, 0)∪(0, 3).(9) y =ln(x +1);解 由x +1>0得函数的定义域D =(−1, +∞).(10)x e y 1=.解 由x ≠0得函数的定义域D =(−∞, 0)∪(0, +∞).7. 下列各题中, 函数f (x )和g (x )是否相同?为什么?(1)f (x )=lg x 2, g (x )=2lg x ;(2) f (x )=x , g (x )=2x ;(3)334)(x x x f −=,31)(−=x x x g .(4)f (x )=1, g (x )=sec 2x −tan 2x .解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x <0时, g (x )=−x .(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ−, ϕ(−2), 并作出函数y =ϕ(x )的图形. 解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=−=−ππϕ, 0)2(=−ϕ. 9. 试证下列函数在指定区间内的单调性:(1)xx y −=1, (−∞, 1); (2)y =x +ln x , (0, +∞).证明 (1)对于任意的x 1, x 2∈(−∞, 1), 有1−x 1>0, 1−x 2>0. 因为当x 1<x 2时,0)1)(1(112121221121<−−−=−−−=−x x x x x x x x y y , 所以函数xx y −=1在区间(−∞, 1)内是单调增加的. (2)对于任意的x 1, x 2∈(0, +∞), 当x 1<x 2时, 有 0ln)()ln ()ln (2121221121<+−=+−+=−x x x x x x x x y y , 所以函数y =x +ln x 在区间(0, +∞)内是单调增加的.10. 设 f (x )为定义在(−l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(−l , 0)内也单调增加.证明 对于∀x 1, x 2∈(−l , 0)且x 1<x 2, 有−x 1, −x 2∈(0, l )且−x 1>−x 2.因为f (x )在(0, l )内单调增加且为奇函数, 所以f (−x 2)<f (−x 1), − f (x 2)<−f (x 1), f (x 2)>f (x 1),这就证明了对于∀x 1, x 2∈(−l , 0), 有f (x 1)< f (x 2), 所以f (x )在(−l , 0)内也单调增加.11. 设下面所考虑的函数都是定义在对称区间(−l , l )上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明 (1)设F (x )=f (x )+g (x ). 如果f (x )和g (x )都是偶函数, 则F (−x )=f (−x )+g (−x )=f (x )+g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的和是偶函数.如果f (x )和g (x )都是奇函数, 则F (−x )=f (−x )+g (−x )=−f (x )−g (x )=−F (x ),所以F (x )为奇函数, 即两个奇函数的和是奇函数.(2)设F (x )=f (x )⋅g (x ). 如果f (x )和g (x )都是偶函数, 则F (−x )=f (−x )⋅g (−x )=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的积是偶函数.如果f (x )和g (x )都是奇函数, 则F (−x )=f (−x )⋅g (−x )=[−f (x )][−g (x )]=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个奇函数的积是偶函数.如果f (x )是偶函数, 而g (x )是奇函数, 则F (−x )=f (−x )⋅g (−x )=f (x )[−g (x )]=−f (x )⋅g (x )=−F (x ),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y =x 2(1−x 2);(2)y =3x 2−x 3;(3)2211x xy +−=; (4)y =x (x −1)(x +1);(5)y =sin x −cos x +1;(6)2x x a a y −+=. 解 (1)因为f (−x )=(−x )2[1−(−x )2]=x 2(1−x 2)=f (x ), 所以f (x )是偶函数.(2)由f (−x )=3(−x )2−(−x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+−=−+−−=−, 所以f (x )是偶函数. (4)因为f (−x )=(−x )(−x −1)(−x +1)=−x (x +1)(x −1)=−f (x ), 所以f (x )是奇函数.(5)由f (−x )=sin(−x )−cos(−x )+1=−sin x −cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=−−−−−, 所以f (x )是偶函数.13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期:(1)y =cos(x −2);(2)y =cos 4x ;(3)y =1+sin πx ;(4)y =x cos x ;(5)y =sin 2 x .解 (1)是周期函数, 周期为l =2π.(2)是周期函数, 周期为2π=l . (3)是周期函数, 周期为l =2.(4)不是周期函数.(5)是周期函数, 周期为l =π.14. 求下列函数的反函数:(1)31+=x y ;(2)xx y +−=11; (3)dcx b ax y ++=(ad −bc ≠0); (4) y =2sin3x ;(5) y =1+ln(x +2);(6)122+=x xy . 解 (1)由31+=x y 得x =y 3−1, 所以31+=x y 的反函数为y =x 3−1.(2)由x x y +−=11得yy x +−=11, 所以x x y +−=11的反函数为x x y +−=11. (3)由d cx b ax y ++=得a cy b dy x −+−=, 所以d cx b ax y ++=的反函数为acx b dx y −+−=. (4)由y =2sin 3x 得2arcsin 31y x =, 所以y =2sin 3x 的反函数为2arcsin 31x y =. (5)由y =1+ln(x +2)得x =e y −1−2, 所以y =1+ln(x +2)的反函数为y =e x −1−2.(6)由122+=x x y 得y y x −=1log 2, 所以122+=x x y 的反函数为xx y −=1log 2. 15. 设函数f (x )在数集X 上有定义, 试证: 函数f (x )在X 上有界的充分必要条件是它在X 上既有上界又有下界.证明 先证必要性. 设函数f (x )在X 上有界, 则存在正数M , 使|f (x )|≤M , 即−M ≤f (x )≤M . 这这就证明了f (x )在X 上有下界−M 和上界M .再证充分性. 设函数f (x )在X 上有下界K 1和上界K 2, 即K 1≤f (x )≤ K 2 . 取M =max{|K 1|, |K 2|}, 则 −M ≤ K 1≤f (x )≤ K 2≤M ,即 |f (x )|≤M .这就证明了f (x )在X 上有界.16. 在下列各题中, 求由所给函数复合而成的函数, 并求这函数分别对应于给定自变量值x 1和x 2的函数值:(1) y =u 2, u =sin x , 61π=x , 32π=x ; (2) y =sin u , u =2x , ,81π=x ,42π=x ; (3)u y =, u =1+x 2, x 1=1, x 2= 2;(4) y =e u , u =x 2, x 1 =0, x 2=1;(5) y =u 2 , u =e x , x 1=1, x 2=−1.解 (1)y =sin 2x , 41)21(6sin 221===πy ,3)3(sin 222===πy . (2)y =sin2x , 224sin )82sin(1==⋅=ππy ,12sin )42sin(2==⋅=ππy . (3)21x y +=, 21121=+=y , 52122=+=y .(4), , .2x e y =1201==e y e e y ==212 (5)y =e 2x , y 1=e 2⋅1=e 2, y 2=e 2⋅(−1)=e −2.17. 设f (x )的定义域D =[0, 1], 求下列各函数的定义域:(1) f (x 2);(2) f (sin x );(3) f (x +a )(a >0);(4)f (x +a )+f (x −a )(a >0).解 (1)由0≤x 2≤1得|x |≤1, 所以函数f (x 2)的定义域为[−1, 1].(2)由0≤sin x ≤1得2n π≤x ≤(2n +1)π (n =0, ±1, ±2⋅ ⋅ ⋅), 所以函数f (sin x )的定义域为[2n π, (2n +1)π] (n =0, ±1, ±2⋅ ⋅ ⋅) .(3)由0≤x +a ≤1得−a ≤x ≤1−a , 所以函数f (x +a )的定义域为[−a , 1−a ].(4)由0≤x +a ≤1且0≤x −a ≤1得: 当210≤<a 时, a ≤x ≤1−a ; 当21>a 时, 无解. 因此当210≤<a 时函数的定义域为[a , 1−a ], 当21>a 时函数无意义.18. 设⎪⎩⎪⎨⎧>−=<=1|| 11|| 01|| 1)(x x x x f , g (x )=e x , 求f [g (x )]和g [f (x )], 并作出这两个函数的图形.解 ⎪⎩⎪⎨⎧>−=<=1|| 11|| 01|| 1)]([x x x e e e x g f , 即⎪⎩⎪⎨⎧>−=<=010 00 1)]([x x x x g f ., 即()⎪⎩⎪⎨⎧>=<==−1|| 1|| e 1|| ][101)(x e x x e e x f g x f ()⎪⎩⎪⎨⎧>=<=−1|| 1|| 11|| ][1x e x x e x f g .19. 已知水渠的横断面为等腰梯形, 斜角ϕ=40°(图1−37). 当过水断面ABCD 的面积为定值S 0时, 求湿周L (L =AC +CD +DB)与水深h 之间的函数关系式, 并说明定义域. 图1−37解 D 40sin hDC Ab ==, 又从0)]40cot 2([21S h BC BC h =⋅++D 得h hS BC ⋅−=D 40cot 0, 所以 h hS L D D 40sin 40cos 20−+=. 自变量h 的取值范围应由不等式组h >0,040cot 0>⋅−h hS D 确定, 定义域为D 40cot 00S h <<. 20. 收敛音机每台售价为90元, 成本为60元. 厂方为鼓励销售商大量采购, 决定凡是订购量超过100台以上的, 每多订购1台, 售价就降低1分, 但最低价为每台75元.(1)将每台的实际售价p 表示为订购量x 的函数;(2)将厂方所获的利润P 表示成订购量x 的函数;(3)某一商行订购了1000台, 厂方可获利润多少?解 (1)当0≤x ≤100时, p =90.令0. 01(x 0−100)=90−75, 得x 0=1600. 因此当x ≥1600时, p =75.当100<x <1600时,p =90−(x −100)×0. 01=91−0. 01x .综合上述结果得到.⎪⎩⎪⎨⎧≥<<−≤≤=1600 751600100 01.0911000 90x x x x p(2).⎪⎩⎪⎨⎧≥<<−≤≤=−=1600 151600100 01.0311000 30)60(2x x x x x x x x p P (3) P =31×1000−0. 01×10002=21000(元).习题1−21. 观察一般项x n 如下的数列{x n }的变化趋势, 写出它们的极限:(1)n n x 21=; (2)nx n n 1)1(−=; (3)212nx n +=; (4)11+−=n n x n ; (5) x n =n (−1)n .解 (1)当n →∞时, n n x 21=→0, 021lim =∞→n n .(2)当n →∞时, n x nn 1)1(−=→0, 01)1(lim =−∞→nn n . (3)当n →∞时, 212n x n +=→2,2)12(lim 2=+∞→nn . (4)当n →∞时, 12111+−=+−=n n n x n →0,111lim =+−∞→n n n . (5)当n →∞时, x n =n (−1)n 没有极限. 2. 设数列{x n }的一般项nn x n 2cos π=. 问=? 求出N , 使当n >N 时, x n n x ∞→lim n 与其极限之差的绝对值小于正数ε , 当ε =0.001时, 求出数N .解 . 0lim =∞→n n x n n n x n 1|2cos ||0|≤=−π. ∀ε >0, 要使|x n −0|<ε , 只要ε<n 1, 也就是ε1>n . 取]1[ε=N , 则∀n >N , 有|x n −0|<ε .当ε =0.001时, ]1[ε=N =1000. 3. 根据数列极限的定义证明:(1)01lim 2=∞→nn ; (2)231213lim =++∞→n n n ;(3)1lim 22=+∞→na n n (4). 19 999.0lim =⋅⋅⋅∞→ 个n n (1)分析 要使ε<=−221|01|n n , 只须ε12>n , 即ε1>n . 证明 因为∀ε>0, ∃]1[ε=N , 当n >N 时, 有ε<−|01|2n, 所以01lim 2=∞→n n . (2)分析 要使ε<<+=−++n n n n 41)12(21|231213|, 只须ε<n41, 即ε41>n . 证明 因为∀ε>0, ∃41[ε=N , 当n >N 时, 有ε<−++231213|n n , 所以231213lim =++∞→n n n . (3)分析 要使ε<<++=−+=−+n a n a n n a n n a n n a n 22222222)(|1|, 只须ε2a n >. 证明 因为∀ε>0, ∃][2εa N =, 当∀n >N 时, 有ε<−+|1|22n a n , 所以1lim 22=+∞→n a n n . (4)分析 要使|0.99 ⋅ ⋅ ⋅ 9−1|ε<=−1101n , 只须1101−n <ε , 即ε1lg 1+>n . 证明 因为∀ε>0, ∃]1lg 1[ε+=N , 当∀n >N 时, 有|0.99 ⋅ ⋅ ⋅ 9−1|<ε , 所以. 19 999.0lim =⋅⋅⋅∞→ n 个n 4. , 证明. 并举例说明: 如果数列{|x a u n n =∞→lim ||||lim a u n n =∞→n |}有极限, 但数列{x n }未必有极限.证明 因为, 所以∀ε>0, ∃N ∈N , 当n >N 时, 有, 从而 a u n n =∞→lim ε<−||a u n ||u n |−|a ||≤|u n −a |<ε .这就证明了|. |||lim a u n n =∞→ 数列{|x n |}有极限, 但数列{x n }未必有极限. 例如, 但不存在. 1|)1(|lim =−∞→n n n n )1(lim −∞→ 5. 设数列{x n }有界, 又, 证明: . 0lim =∞→n n y 0lim =∞→n n n y x 证明 因为数列{x n }有界, 所以存在M , 使∀n ∈Z , 有|x n |≤M .又, 所以∀ε>0, ∃N ∈N , 当n >N 时, 有0lim =∞→n n y M y n ε<||. 从而当n >N 时, 有εε=⋅<≤=−MM y M y x y x n n n n n |||||0|,所以.0lim =∞→n n n y x 6. 对于数列{x n }若x 2k →a (k →∞), x 2k +1→a (k →∞), 证明: x n →a (n →∞). 证明 因为x 2k →a (k →∞), x 2k +1→a (k →∞), 所以∀ε>0, ∃K 1, 当2k >2K 1时, 有| x 2k −a |<ε ;∃K 2,当2k +1>2K 2+1时, 有| x 2k +1−a |<ε..取N =max{2K 1, 2K 2+1}, 只要n >N , 就有|x n −a |<ε . 因此x n →a (n →∞).习题1−31. 根据函数极限的定义证明: (1);8)13(lim 3=−→x x (2);12)25(lim 2=+→x x (3)424lim22−=+−−→x x x ; (4)21241lim321=+−−→x x x . 证明 (1)分析 |(3x −1)−8|=|3x −9|=3|x −3|, 要使|(3x −1)−8|<ε , 只须ε31|3|<−x .证明 因为∀ε >0, ∃εδ31=, 当0<|x −3|<δ时, 有|(3x −1)−8|<ε , 所以.8)13(lim 3=−→x x (2)分析 |(5x +2)−12|=|5x −10|=5|x −2|, 要使|(5x +2)−12|<ε , 只须ε51|2|<−x .证明 因为∀ε >0, ∃εδ51=, 当0<|x −2|<δ时, 有|(5x +2)−12|<ε , 所以.12)25(lim 2=+→x x (3)分析 |)2(||2|244)4(2422−−=+=+++=−−+−x x x x x x x , 要使ε<−−+−)4(242x x , 只须ε<−−|)2(|x .证明 因为∀ε >0, ∃εδ=, 当0<|x −(−2)|<δ时, 有ε<−−+−)4(242x x , 所以424lim 22−=+−−→x x x .(4)分析|)21(|2|221|212413−−=−−=−+−x x x x , 要使ε<−+−212413x x , 只须ε21|)21(|<−−x . 证明 因为∀ε >0, ∃εδ21=, 当δ<−−<|)21(|0x 时, 有ε<−+−212413x x , 所以21241lim321=+−−→x x x . 2. 根据函数极限的定义证明: (1)2121lim33=+∞→x x x ; (2)0sin lim=+∞→xxx .证明 (1)分析333333||21212121x x x x x x =−+=−+, 要使ε<−+212133x x , 只须ε<3||21x , 即321||ε>x .证明 因为∀ε >0, ∃321ε=X , 当|x |>X 时, 有ε<−+212133x x , 所以2121lim 33=+∞→x x x .(2)分析 xxx xx 1|sin |0sin ≤=−, 要使ε<−0sin x x, 只须ε<x1, 即21ε>x .证明 因为∀ε>0, ∃21ε=X , 当x >X 时, 有ε<−0sin xx, 所以0sin lim=+∞→x xx .3. 当x →2时, y =x 2→4. 问δ等于多少, 使当|x −2|<δ时, |y −4|<0. 001?解 由于x →2, |x −2|→0, 不妨设|x −2|<1, 即1<x <3. 要使|x 2−4|=|x +2||x −2|<5|x −2|<0. 001, 只要0002.05001.0|2|=<−x , 取δ=0. 0002, 则当0<|x −2|<δ时, 就有|x 2−4|<0. 001. 4. 当x →∞时, 13122→+−=x x y , 问X 等于多少, 使当|x |>X 时, |y −1|<0.01?解 要使01.034131222<+=−+−x x x , 只397301.04||=−>x , 397=X . 5. 证明函数f (x )=|x | 当x →0时极限为零.6. 求,)(xxx f = x x x ||)(=ϕ当x →0时的左﹑右极限, 并说明它们在x →0时的极限是否存在.证明 因为11lim lim )(lim 000===−−−→→→x x x x xx f ,11lim lim )(lim 000===+++→→→x x x x xx f ,,)(lim )(lim 0x f x f x x +→→=−所以极限存在.)(lim 0x f x → 因为1lim ||lim )(lim 00−=−==−−−→→→x xx x x x x x ϕ, 1lim ||lim )(lim 00===+++→→→xx x x x x x x ϕ, ,)(lim )(lim 0x x x x ϕϕ+→→≠−所以极限不存在.)(lim 0x x ϕ→ 7. 证明: 若x →+∞及x →−∞时, 函数f (x )的极限都存在且都等于A , 则.A x f x =∞→)(lim证明 因为, , 所以∀ε>0,A x f x =−∞→)(lim A x f x =+∞→)(lim ∃X 1>0, 使当x <−X 1时, 有|f (x )−A |<ε ; ∃X 2>0, 使当x >X 2时, 有|f (x )−A |<ε .取X =max{X 1, X 2}, 则当|x |>X 时, 有|f (x )−A |<ε , 即.A x f x =∞→)(lim 8. 根据极限的定义证明: 函数f (x )当x →x 0 时极限存在的充分必要条件是左极限、右极限各自存在并且相等.证明 先证明必要性. 设f (x )→A (x →x 0), 则∀ε>0, ∃δ>0, 使当0<|x −x 0|<δ 时, 有|f (x )−A |<ε .因此当x 0−δ<x <x 0和x 0<x <x 0+δ 时都有|f (x )−A |<ε .这说明f (x )当x →x 0时左右极限都存在并且都等于A . 再证明充分性. 设f (x 0−0)=f (x 0+0)=A , 则∀ε>0, ∃δ1>0, 使当x 0−δ1<x <x 0时, 有| f (x )−A <ε ; ∃δ2>0, 使当x 0<x <x 0+δ2时, 有| f (x )−A |<ε .取δ=min{δ1, δ2}, 则当0<|x −x 0|<δ 时, 有x 0−δ1<x <x 0及x 0<x <x 0+δ2 , 从而有| f (x )−A |<ε ,即f (x )→A (x →x 0).9. 试给出x →∞时函数极限的局部有界性的定理, 并加以证明.解 x →∞时函数极限的局部有界性的定理: 如果f (x )当x →∞时的极限存在, 则存在X >0及M >0, 使当|x |>X 时, |f (x )|<M .证明 设f (x )→A (x →∞), 则对于ε =1, ∃X >0, 当|x |>X 时, 有|f (x )−A |<ε =1. 所以 |f (x )|=|f (x )−A +A |≤|f (x )−A |+|A |<1+|A |.这就是说存在X >0及M >0, 使当|x |>X 时, |f (x )|<M , 其中M =1+|A |.习题1−41. 两个无穷小的商是否一定是无穷小?举例说明之. 解 不一定.例如, 当x →0时, α(x )=2x , β(x )=3x 都是无穷小, 但32)()(lim 0=→x x x βα, )()(x x βα不是无穷小.2. 根据定义证明:(1)392+−=x x y 当x →3时为无穷小;(2)xx y 1sin =当x →0时为无穷小.证明 (1)当x ≠3时|3|39||2−=+−=x x x y . 因为∀ε >0, ∃δ=ε , 当0<|x −3|<δ时, 有εδ=<−=+−=|3|39||2x x x y ,所以当x →3时392+−=x x y 为无穷小.(2)当x ≠0时|0|1sin |||||−≤=x xx y . 因为∀ε >0, ∃δ=ε , 当0<|x −0|<δ时, 有εδ=<−≤=|0||1sin |||||x xx y ,所以当x →0时xx y 1sin =为无穷小.3. 根据定义证明: 函数xxy 21+=为当x →0时的无穷大. 问x 应满足什么条件, 能使|y |>104证明 分析2||11221||−≥+=+=x x x x y , 要使|y |>M , 只须M x >−2||1, 即21||+<M x .证明 因为∀M >0, ∃21+=M δ, 使当0<|x −0|<δ时, 有M xx>+21, 所以当x →0时, 函数xxy 21+=是无穷大. 取M =104, 则21014+=δ. 当2101|0|04+<−<x 时, |y |>104.4. 求下列极限并说明理由: (1)xx n 12lim+∞→;(2)xx x −−→11lim 20.解 (1)因为x x x 1212+=+, 而当x →∞ 时x 1是无穷小, 所以212lim =+∞→xx n .(2)因为x xx +=−−1112(x ≠1), 而当x →0时x 为无穷小, 所以111lim 20=−−→x x x .5. 根据函数极限或无穷大定义, 填写下表:6. 函数y =x cos x 在(−∞, +∞)内是否有界?这个函数是否为当x →+∞ 时的无穷大?为什么?解 函数y =x cos x 在(−∞, +∞)内无界.这是因为∀M >0, 在(−∞, +∞)内总能找到这样的x , 使得|y (x )|>M . 例如y (2k π)=2k π cos2k π=2k π (k =0, 1, 2, ⋅ ⋅ ⋅),当k 充分大时, 就有| y (2k π)|>M .当x →+∞ 时, 函数y =x cos x 不是无穷大.这是因为∀M >0, 找不到这样一个时刻N , 使对一切大于N 的x , 都有|y (x )|>M . 例如022cos()22()22(=++=+ππππππk k k y (k =0, 1, 2, ⋅ ⋅ ⋅),对任何大的N , 当k 充分大时, 总有N k x >+=22ππ, 但|y (x )|=0<M .7. 证明: 函数x x y 1sin 1=在区间(0, 1]上无界, 但这函数不是当x →0+时的无穷大.证明 函数xx y 1sin 1=在区间(0, 1]上无界. 这是因为∀M >0, 在(0, 1]中总可以找到点x k , 使y (x k )>M . 例如当221ππ+=k x k (k =0, 1, 2, ⋅ ⋅ ⋅)时, 有22)(ππ+=k x y k ,当k 充分大时, y (x k )>M .当x →0+ 时, 函数xx y 1sin 1=不是无穷大. 这是因为∀M >0, 对所有的δ>0, 总可以找到这样的点x k , 使0<x k <δ, 但y (x k )<M . 例如可取πk x k 21=(k =0, 1, 2, ⋅ ⋅ ⋅), 当k 充分大时, x k <δ, 但y (x k )=2k πsin2k π=0<M .习题1−51. 计算下列极限: (1)35lim 22−+→x x x ;解 9325235lim 222−=−+=−+→x x x .(2)13lim 223+−→x x x ;解 01)3(3)3(13lim 22223=+−=+−→x x x . (3)112lim 221−+−→x x x x ;解 02011lim )1)(1()1(lim 112lim121221==+−=+−−=−+−→→→x x x x x x x x x x x .(4)xx xx x x 2324lim 2230++−→;解 2123124lim 2324lim 202230=++−=++−→→x x x x x x x x x x .(5)hx h x h 220)(lim−+→;解 x h x hx h hx x h x h x h h h 2)2(lim 2lim )(lim02220220=+=−++=−+→→→.(6))112(lim 2xx x +−∞→; 解 21lim 1lim 2)112(lim 22=+−=+−∞→∞→∞→x x x x x x x . (7)121lim22−−−∞→x x x x ; 解 2111211lim 121lim 2222=−−−=−−−∞→∞→x x x x x x x x .(8)13lim242−−+∞→x x x x x ; 解 013lim242=−−+∞→x x x x x (分子次数低于分母次数, 极限为零)或 012111lim13lim 4232242=−−+=−−+∞→∞→xx x x x x xx x x . (9)4586lim 224+−+−→x x x x x ;解 32142412lim )4)(1()4)(2(lim 4586lim 44224=−−=−−=−−−−=+−+−→→→x x x x x x x x x x x x x .(10))12)(11(lim 2xx x −+∞→; 解 221)12(lim )11(lim )12)(11(lim 22=×=−⋅+=−+∞→∞→∞→x x x x x x x . (11))21 41211(lim n n +⋅⋅⋅+++∞→; 解 2211)21(1lim )21 41211(lim 1=−−=+⋅⋅⋅++++∞→∞→n n n n .(12)2)1( 321limn n n −+⋅⋅⋅+++∞→;解 211lim 212)1(lim )1( 321lim 22=−=−=−+⋅⋅⋅+++∞→∞→∞→n n n n n n n n n n . (13)35)3)(2)(1(lim n n n n n +++∞→;解 515)3)(2)(1(lim3=+++∞→n n n n n (分子与分母的次数相同, 极限为最高次项系数之比).或 51)31)(21)(11(lim 515)3)(2)(1(lim3=+++=+++∞→∞→n n n n n n n n n . (14))1311(lim 31xx x −−−→; 解 112lim )1)(1()2)(1(lim )1)(1(31lim )1311(lim 212122131−=+++−=++−+−−=++−−++=−−−→→→→x x x x x x x x x x x x x x x x x x x .2. 计算下列极限: (1)2232)2(2lim −+→x x x x ; 解 因为01602)2(lim 2322==+−→x x x x , 所以∞=−+→2232)2(2lim x x x x .(2)12lim 2+∞→x x x ;解 ∞=+∞→12lim 2x x x (因为分子次数高于分母次数).(3).)12(lim 3+−∞→x x x 解 (因为分子次数高于分母次数).∞=+−∞→)12(lim 3x x x 3. 计算下列极限: (1)xx x 1sin lim 20→;解 01sin lim 20=→x x x (当x →0时, x 2是无穷小, 而x 1sin 是有界变量). (2)xx x arctan lim ∞→. 解 0arctan 1lim arctan lim =⋅=∞→∞→x x x x x x (当x →∞时, x 1是无穷小, 而arctan x 是有界变量). 4. 证明本节定理3中的(2).习题1−61. 计算下列极限: (1)xx x ωsin lim 0→;解 ωωωωω==→→x x x x x x sin lim sin lim 00. (2)xx x 3tan lim 0→; 解 33cos 133sin lim 33tan lim 00=⋅=→→x x x x x x x . (3)xx x 5sin 2sin lim 0→; 解 52525sin 522sin lim 5sin 2sin lim 00=⋅⋅=→→x x x x x x x x .(4);x x x cot lim 0→ 解 1cos lim sin lim cos sin lim cot lim 0000=⋅=⋅=→→→→x x x x x x x x x x x x . (5)xx x x sin 2cos 1lim 0−→; 解法一 ()2sin lim 2sin 2lim 2cos1lim sin 2cos 1lim 20220200===−=−→→→→xx x x x x x x x x x x x .解法二 2sin lim 2sin sin 2lim sin 2cos 1lim 0200===−→→→xx x x x x x x x x x .(6)nn n x2sin2lim ∞→(x 为不等于零的常数). 解 x x xxx nn n n n n =⋅=∞→∞→22sinlim2sin 2lim . 2. 计算下列极限:(1)xx x 1)1(lim −→;解{}11)(10)1)(11)](1[lim )](1[lim )1(lim −−−→−−→→=−+=−+=−e x x x x x x x x x .(2)x x x 1)21(lim +→;解[]22210221010)21(lim )21(lim )21(lim e x x x x x x x x x =+=+=+→→→.(3)x x xx 2)1(lim +∞→;解 []222)11(lim )1(lim e x x x xx x x =+=+∞→∞→.(4)kx x x)11(lim −∞→(k 为正整数). 解 k k x x kx x e xx −−−∞→∞→=−+=−))(()11(lim )11(lim . 3. 根据函数极限的定义, 证明极限存在的准则I ′. 解4. 利用极限存在准则证明:(1)111lim =+∞→nn ;证明 因为n n 11111+<+<,而 且11lim =∞→n 1)11(lim =+∞→nn ,由极限存在准则I, 111lim =+∞→n n .(2)()11211lim 222=++⋅⋅⋅++++∞→πππn n n n n n ; 证明 因为()πππππ+<++⋅⋅⋅++++<+22222221 211n n n n n n n n n n , 而 1lim22=+∞→πn n n n , 1lim 22=+∞→πn n n ,所以 ()11211lim 222=++⋅⋅⋅++++∞→πππn n n n n n . (3)数列2, 22+, 222++, ⋅ ⋅ ⋅ 的极限存在;证明 21=x , n n x x +=+21(n =1, 2, 3, ⋅ ⋅ ⋅).先证明数列{x n }有界. 当n =1时221<=x , 假定n =k 时x k <2, 当n =k +1时,22221=+<+=+k k x x ,所以x n <2(n =1, 2, 3, ⋅ ⋅ ⋅), 即数列{x n }有界.再证明数列单调增.nn n n n n nn n n n n x x x x x x x x x x x x +++−−=++−+=−+=−+2)1)(2(22221,而x n −2<0, x n +1>0, 所以x n +1−x n >0, 即数列{x n }单调增.因为数列{x n }单调增加有上界, 所以此数列是有极限的. (4)11lim 0=+→n x x ;证明 当|x |≤1时, 则有 1+x ≤1+|x |≤(1+|x |)n , 1+x ≥1−|x |≥(1−|x |)n , 从而有 ||11||1x x x n +≤+≤−. 因为 ,1|)|1(lim |)|1(lim 0=+=−→→x x x x 根据夹逼准则, 有 11lim 0=+→n x x .(5)[]11lim 0=+→xx x . 证明 因为[]xx x 1111≤<−, 所以[]111≤<−x x x .又因为, 根据夹逼准则, 有11lim )1(lim 0==−++→→x x x []11lim 0=+→xx x .习题 1−71. 当x →0时, 2x −x 2 与x 2−x 3相比, 哪一个是高阶无穷小? 解 因为02lim 2lim 202320=−−=−−→→xx x x x x x x x ,所以当x →0时, x 2−x 3是高阶无穷小, 即x 2−x 3=o (2x −x 2).2. 当x →1时, 无穷小1−x 和(1)1−x 3, (2))1(212x −是否同阶?是否等价? 解 (1)因为3)1(lim 1)1)(1(lim 11lim 212131=++=−++−=−−→→→x x xx x x x x x x x ,所以当x →1时, 1−x 和1−x 3是同阶的无穷小, 但不是等价无穷小.(2)因为1)1(lim 211)1(21lim 121=+=−−→→x x x x x , 所以当x →1时, 1−x 和)1(212x −是同阶的无穷小, 而且是等价无穷小.3. 证明: 当x →0时, 有: (1) arctan x ~x ; (2)2~1sec 2x x −.证明 (1)因为1tan lim arctan lim00==→→y y xxy x (提示: 令y =arctan x , 则当x →0时, y →0),所以当x →0时, arctan x ~x .(2)因为()122sin2lim 22sin 2limcos cos 1lim 2211sec lim20222020===−=−→→→→x xx x x x xx x x x x x ,所以当x →0时, 2~1sec 2x x −.4. 利用等价无穷小的性质, 求下列极限: (1)xxx 23tan lim0→;(2)mn x x x )(sin )sin(lim0→(n , m 为正整数);(3)xx x x 30sin sin tan lim −→;(4))1sin 1)(11(tan sin lim320−+−+−→x x x x x .解 (1)2323lim 23tan lim 00==→→x x x x x x .(2) ⎪⎩⎪⎨⎧<∞>===→→mn m n m n x x x x mn x m n x 0 1lim )(sin )sin(lim00. (3)21cos 21lim sin cos cos 1lim sin )1cos 1(sin lim sin sin tan lim 220203030==−=−=−→→→→x x x x x x xx x x x x x x x x . (4)因为32221)2(2~2sin tan 2)1(cos tan tan sin x x x x x x x x x −=⋅−−=−=−(x →0), 23232223231~11)1(11x x x x x ++++=−+(x →0),x x x x x ~sin ~1sin 1sin 1sin 1++=−+(x →0),所以 33121lim )1sin 1)(11(tan sin lim 230320−=⋅−=−+−+−→→xx x x x xx x x .5. 证明无穷小的等价关系具有下列性质: (1) α ~α (自反性);(2) 若α ~β, 则β~α(对称性); (3)若α ~β, β~γ, 则α~γ(传递性). 证明 (1)1lim=αα, 所以α ~α ; (2) 若α ~β, 则1lim =βα, 从而1lim =αβ. 因此β~α ;(3) 若α ~β, β~γ, 1lim lim lim =⋅=βαγβγα. 因此α~γ.习题1−81. 研究下列函数的连续性, 并画出函数的图形:(1);⎩⎨⎧≤<−≤≤=21 210 )(2x x x x x f (2).⎩⎨⎧>≤≤−=1|| 111 )(x x x x f 解 (1)已知多项式函数是连续函数, 所以函数f (x )在[0, 1)和(1, 2]内是连续的. 在x =1处, 因为f (1)=1, , 1lim )(lim 211==−−→→x x f x x 1)2(lim )(lim 11=−=++→→x x f x x 所以, 从而函数f (x )在x =1处是连续的.1)(lim 1=→x f x 综上所述,函数f (x )在[0, 2]上是连续函数. (2)只需考察函数在x =−1和x =1处的连续性.在x =−1处, 因为f (−1)=−1, , , 所以函数在x =−1处间断, 但右连续.)1(11lim )(lim 11−≠==−−−→−→f x f x x )1(1lim )(lim 11−=−==++−→−→f x x f x x 在x =1处, 因为f (1)=1, =f (1), =f (1), 所以函数在x =1处连续.1lim )(lim 11==−−→→x x f x x 11lim )(lim 11==++→→x x x f 综合上述讨论, 函数在(−∞, −1)和(−1, +∞)内连续, 在x =−1处间断, 但右连续.2. 下列函数在指出的点处间断, 说明这些间断点属于哪一类, 如果是可去间断点, 则补充或改变函数的定义使它连续:(1)23122+−−=x x x y , x =1, x =2;(2)x xy tan =, x =k , 2ππ+=k x (k =0, ±1, ±2, ⋅ ⋅ ⋅); (3),1cos 2xy = x =0;(4), x =1.⎩⎨⎧>−≤−=1 311x x x x y 解 (1))1)(2()1)(1(23122−−−+=+−−=x x x x x x x y . 因为函数在x =2和x =1处无定义, 所以x =2和x =1是函数的间断点.因为∞=+−−=→→231lim lim 2222x x x y x x , 所以x =2是函数的第二类间断点;因为2)2()1(limlim 11−=−+=→→x x y x x , 所以x =1是函数的第一类间断点, 并且是可去间断点. 在x =1处,令y =−2, 则函数在x =1处成为连续的. (2)函数在点x =k π(k ∈Z)和2ππ+=k x (k ∈Z)处无定义, 因而这些点都是函数的间断点. 因∞=→x xk x tan limπ(k ≠0), 故x =k π(k ≠0)是第二类间断点;因为1tan lim 0=→xxx ,0tan lim2=+→x x k x ππ(k ∈Z), 所以x =0和2ππ+=k x (k ∈Z) 是第一类间断点且是可去间断点.令y |x =0=1, 则函数在x =0处成为连续的; 令2 ππ+=k x 时, y =0, 则函数在2ππ+=k x 处成为连续的. (3)因为函数x y 1cos 2=在x =0处无定义, 所以x =0是函数xy 1cos 2=的间断点. 又因为xx 1cos lim 2→不存在, 所以x =0是函数的第二类间断点. (4)因为, 所以x =1是函数的第一类不可去间断点.0)1(lim )(lim 11=−=−−→→x x f x x 2)3(lim )(lim 11=−=++→→x x f x x 3. 讨论函数x x x x f n n n 2211lim )(+−=∞→的连续性, 若有间断点, 判别其类型.解 ⎪⎩⎪⎨⎧<=>−=+−=∞→1|| 1|| 01|| 11lim )(22x x x x x x x x x f nnn . 在分段点x =−1处, 因为, , 所以x =−1为函数的第一类不可去间断点.1)(lim )(lim 11=−=−−−→−→x x f x x 1lim )(lim 11−==++−→−→x x f x x 在分段点x =1处, 因为, , 所以x =1为函数的第一类不可去间断点.1lim )(lim 11==−−→→x x f x x 1)(lim )(lim 11−=−=++→→x x f x x 4. 证明: 若函数f (x )在点x 0连续且f (x 0)≠0, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.证明 不妨设f (x 0)>0. 因为f (x )在x 0连续, 所以, 由极限的局部保号性定理,存在x 0)()(lim 00>=→x f x f x x 0的某一去心邻域, 使当x ∈时f (x )>0, 从而当x ∈U (x )(0x U D )(0x U D0)时, f (x )>0. 这就是说, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.5. 试分别举出具有以下性质的函数f (x )的例子:(1)x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅是f (x )的所有间断点, 且它们都是无穷间断点;(2)f (x )在R 上处处不连续, 但|f (x )|在R 上处处连续;(3)f (x )在R 上处处有定义, 但仅在一点连续. 解 函数x x x f ππcsc )csc()(+=在点x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅处是间断的, 且这些点是函数的无穷间断点.解(2)函数在R 上处处不连续, 但|f (x )|=1在R 上处处连续.⎩⎨⎧∉∈−=Q Qx x x f 1 1)( 解(3)函数在R 上处处有定义, 它只在x =0处连续.⎩⎨⎧∉−∈=Q Qx x x x x f )(习题1−91. 求函数633)(223−+−−+=x x x x x x f 的连续区间, 并求极限, 及.)(lim 0x f x →)(lim 3x f x −→)(lim 2x f x → 解 )2)(3()1)(1)(3(633)(223−++−+=−+−−+=x x x x x x x x x x x f , 函数在(−∞, +∞)内除点x =2和x =−3外是连续的, 所以函数f (x )的连续区间为(−∞, −3)、(−3, 2)、(2, +∞). 在函数的连续点x =0处, 21)0()(lim 0==→f x f x .在函数的间断点x =2和x =−3处,∞=−++−+=→→)2)(3()1)(1)(3(lim )(lim 22x x x x x x f x x , 582)1)(1(lim )(lim 33−=−+−=−→−→x x x x f x x .2. 设函数f (x )与g (x )在点x 0连续, 证明函数 ϕ(x )=max{f (x ), g (x )}, ψ(x )=min{f (x ), g (x )}在点x 0也连续.证明 已知, .)()(lim 00x f x f x x =→)()(lim 00x g x g x x =→ 可以验证] |)()(|)()([21)(x g x f x g x f x −++=ϕ,] |)()(|)()([21)(x g x f x g x f x −−+=ψ.因此 ] |)()(|)()([21)(00000x g x f x g x f x −++=ϕ,] |)()(|)()([21)(00000x g x f x g x f x −−+=ψ.因为] |)()(|)()(21lim )(lim 00x g x f x g x f x x x x x −++=→→ϕ] |)(lim )(lim |)(lim )(lim [210000x g x f x g x f x x x x x x x x →→→→−++=] |)()(|)()([210000x g x f x g x f −++==ϕ(x 0),所以ϕ(x )在点x 0也连续.同理可证明ψ(x )在点x 0也连续.3. 求下列极限: (1)52lim 20+−→x x x ;(2)34)2(sin lim x x π→;(3))2cos 2ln(lim 6x x π→(4)xx x 11lim 0−+→; (5)145lim1−−−→x xx x ;(6)ax ax a x −−→sin sin lim; (7))(lim 22x x x x x −−++∞→.解 (1)因为函数52)(2+−=x x x f 是初等函数, f (x )在点x =0有定义, 所以 55020)0(52lim 220=+⋅−==+−→f x x x .(2)因为函数f (x )=(sin 2x )3是初等函数, f (x )在点x =4π有定义, 所以142(sin )4()2(sin lim 334=⋅==→πππf x x .(3)因为函数f (x )=ln(2cos2x )是初等函数, f (x )在点x =6π有定义, 所以0)62cos 2ln()6()2cos 2ln(lim 6=⋅==→πππf x x . (4)211101111lim )11(lim )11()11)(11(lim 11lim0000=++=++=++=++++−+=−+→→→→x x x xx x x x x x x x x x . (5))45)(1(44lim )45)(1()45)(45(lim 145lim111x x x x x x x x x x x x x x x x x +−−−=+−−+−−−=−−−→→→ 214154454lim1=+−⋅=+−=→xx x .(6)ax ax a x ax ax a x a x −−+=−−→→2sin 2cos2limsin sin lima a a a x ax ax ax ax cos 12cos 22sinlim 2coslim =⋅+=−−⋅+=→→. (7))())((lim)(lim 22222222x x x x x x x x x x x x x x x x x x −++−++−−+=−−++∞→+∞→1)1111(2lim)(2lim22=−++=−++=+∞→+∞→xx x x x x xx x .4. 求下列极限: (1)x x e 1lim ∞→;(2)xxx sin lnlim 0→; (3)2)11(lim xx x+∞→;(4);x x x 2cot 20)tan 31(lim +→ (5)21)63(lim −∞→++x x xx ;(6)xx x x x x −++−+→20sin 1sin 1tan 1lim.解 (1) 1lim 01lim1===∞→∞→e ee xxx x .(2) 01ln sin lim ln(sin lnlim 00===→→x xxx x x .(3) []e e xx xx xx ==+=+∞→∞→21212)11(lim 11(lim .(4) []33tan312cot 222)tan 31(lim )tan 31(lim ex x xx xx =+=+→→.(5)21633621)631()63(−+−⋅−+−+−+=++x x x x xx x . 因为。
计算机组成原理第五版白中英(详细)第2章作业参考答案解析

第2章作业参考答案1、(1) -35(=23)16 (2)127 (3)-127 (4)-1[-35]原=10100011[127]原=01111111 [-127]原=11111111 [-1]原=10000001[-35]反=11011100[127]反=01111111 [-127]反=10000000 [-1]反=11111110[-35]补=11011101[127]补=01111111 [-127]补=10000001 [-1]补=111111112 当a 7=0时,x ≥0,满足x>-0.5的条件,即:若a 7=0,a 6~ a 0可取任意值 当a 7=1时,x<0,若要满足x>-0.5的条件,则由补码表示与其真值的关系,可知:7061524334251676022222221)2(1--------=*+*+*+*+*+*+*+-=*+-=∑a a a a a a a a x i i i 要使x>-0.5 ,所以要求a 6=1,并且a 5~a 0不能全部为0所以,要使x>-0.5,则要求a 7=0;或者a 7= a 6=1,并且a 5~a 0至少有一个为13、由题目要求可知,该浮点数的格式为:31 30 23 22 0注:由于S是数符,已表示了尾数的符号,所以为了提高表示精度,M(23位)不必存储符号位,只需存小数点后面的有效数值位即可。
(1)最大数的二进制表示为:0 11111111 1111……111(23个1)(2)最小数的二进制表示为:1 11111111 0000……000(23个0)(3)非IEEE754标准的补码表示的规格化数是指其最高有效位与符号位相反故有:最大正数为:0 11111111 1111……111(23个1)=+(1-2-23)⨯2127最小正数为:0 00000000 1000……000(22个0)=+0.5⨯2-128最大负数为:1 00000000 0111……111(22个1)=-(0.5+2-23)⨯2-128最小负数为:1 11111111 0000……000(23个0)=-1⨯2127所以其表示数的范围是:+0.5⨯2-128~+(1-2-23)⨯2127以及-1⨯2127~-(0.5+2-23)⨯2-1284、IEEE754标准32位浮点的规格化数为X=(-1)S⨯1.M⨯2E-127(1)27/6427/64=27⨯2-6=(11011)2⨯2-6=(1.1011)2⨯2-2所以S=0,E=e+127=125=(01111101)2,M=101132位的规格化浮点数为:00111110 11011000 00000000 00000000,即十六进制的(3ED80000)16(2)-27/64-27/64=-(1.1011)2 2-2所以S=1,E=e+127=125=(01111101)2,M=101132位的规格化浮点数为:10111110 11011000 00000000 00000000,即十六进制的(BED80000)165、[x+y]补=[x]补+[y]补(1)x=11011,y=00011[x+y]补=0011011+0000011=0011110;没有溢出,x+y=11110(2)x=11011,y=-10101[x+y]补=0011011+1101011=0000110;0 0 1 1 0 1 1+ 1 1 0 1 0 1 10 0 0 0 1 1 0没有溢出,x+y=00110(3)x=-10110,y=-00001[x+y]补=1101010+1111111=1101001;没有溢出,x+y=-101116、[x-y]补=[x]补+[-y]补(1)x=11011,y=-11111[-y]补=0011111[x-y]补=0011011+0011111=0111010;0 0 1 1 0 1 1+ 0 0 1 1 1 1 10 1 1 1 0 1 0正溢出,x-y=+111010(2)x=10111,y=11011[-y]补=1100101[x-y]补=0010111+1100101=1111100;0 0 1 0 1 1 1+ 1 1 0 0 1 0 11 1 1 1 1 0 0没有溢出,x-y=-00100(3)x=11011,y=-10011[-y]补=0010011[x-y]补=0011011+0010011=0101110;正溢出,x-y=+1011107、(1)x=11011,y=-11111用原码阵列乘法器1 1 0 1 11 1 1 1 11 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 0 0 0 1 0 1[x⨯y]符号=0⊕1=1所以 [x⨯y]原=1 1101000101用直接补码阵列乘法器:[x]补=011011,[y]补=100001(0) 1 1 0 1 1⨯ (1) 0 0 0 0 1(0) 1 1 0 1 1(0) 0 0 0 0 0(0) 0 0 0 0 0(0) 0 0 0 0 0(0) 0 0 0 0 00 (1) (1) (0) (1) (1)0 (1) (1) 0 (1) (1) 1 1 0 1 1将乘积中的符号位用负权表示,其他的负权位化为正权,得:[x⨯y]补=1 0010111011(2) x=-11111,y=-11011用原码阵列乘法器1 1 1 1 1⨯ 1 1 0 1 11 1 1 1 11 1 1 1 10 0 0 0 01 1 1 1 11 1 1 1 11 1 0 1 0 0 0 1 0 1[x⨯y]符号=1⊕1=0所以 [x⨯y]原=0 1101000101用直接补码阵列乘法器:[x]补=100001,[y]补=100101(1) 0 0 0 0 1⨯ (1) 0 0 1 0 1(1) 0 0 0 0 1(0) 0 0 0 0 0(1) 0 0 0 0 1(0) 0 0 0 0 0(0) 0 0 0 0 01 (0) (0) (0) (0) (1)1 0 0 (1) (1) 0 0 0 1 0 1将乘积中的符号位用负权表示,其他的负权位化为正权,得:[x⨯y]补=0 11010001018、(1) x=11000,y=-11111用原码阵列除法器计算,符号位单独处理,商的符号位=0⊕1=1设a=(|x|⨯2-5),b=(|y|⨯2-5),则a,b均为正的纯小数,且x÷y的数值=(a÷b);余数等于(a÷b)的余数乘以25下面用不恢复余数法的原码阵列除法器计算a÷b[a]补=[|x|⨯2-5]补=0.11000,[b]补=[|y|⨯2-5]补=0.11111,[-b]补=1.00001过程如下:0. 1 1 0 0 0+[-b]补 1. 0 0 0 0 11. 1 1 0 0 1 ——余数为负,商为01. 1 0 0 1 0 ——余数和商左移一位(0)+[b]补 0. 1 1 1 1 10. 1 0 0 0 1 ——余数为正,商为11. 0 0 0 1 0 ——余数和商左移一位(01)+[-b]补 1. 0 0 0 0 10. 0 0 0 1 1 ——商为10. 0 0 1 1 0 ——(011)+[-b]补 1. 0 0 0 0 11. 0 0 1 1 1 ——商为00. 0 1 1 1 0 ——(0110)+[b]补 0. 1 1 1 1 11. 0 1 1 0 1 ——商为00. 1 1 0 1 0 ——(01100)+[b]补 0. 1 1 1 1 11. 1 1 0 0 1 ——商为0——(011000)即:a÷b的商为0.11000;余数为1.11001⨯2-5,因为1.11001为负数,加b处理为正数,1.11001+b=1.11001+0.11111=0.11000,所以a÷b的余数为0.11000⨯2-5所以,(x÷y)的商=-0.11000,原码为:1.11000;余数为0.11000(2) x=-01011,y=11001商的符号位=1⊕0=1设a=|x|⨯2-5,b=|y|⨯2-5,则a,b均为正的纯小数,且x÷y的数值=a÷b;余数等于(a÷b)的余数乘以25下面用不恢复余数法的原码阵列除法器计算a÷b[a]补=[|x|⨯2-5]补=0.01011,[b]补=[|y|⨯2-5]补=0.11001,[-b]补=1.00111过程如下:0. 0 1 0 1 1+[-b]补 1. 0 0 1 1 11. 1 0 0 1 0 ——余数为负,商为01. 0 0 1 0 0 ——余数和商左移一位(0)+[b]补 0. 1 1 0 0 11. 1 1 1 0 1 ——余数为负,商为01. 1 1 0 1 0 ——余数和商左移一位(00)+[b]补 0. 1 1 0 0 10. 1 0 0 1 1 ——商为11. 0 0 1 1 0 ——(001)+[-b]补 1. 0 0 1 1 10. 0 1 1 0 1 ——商为10. 1 1 0 1 0 ——(0011)+[-b]补 1. 0 0 1 1 10. 0 0 0 0 1 ——商为10. 0 0 0 1 0 ——(00111)+[-b]补 1. 0 0 1 1 11. 0 1 0 0 1 ——商为0——(001110)即:a÷b的商为0.01110;余数为1.01001⨯2-5,因为1.01001为负数,加b处理为正数,1.01001+b=1.01001+0.11001=0.00010,所以a÷b的余数为0.00010⨯2-5所以,(x÷y)的商=-0.01110,原码为:1.01110;余数为0.000109、(1)x=2-011⨯0.100101,y=2-010⨯(-0.011110)E X=-011,E y=-010,所以 [E X]补=1101,[E y]补=1110M X=0.100101,M y=-0.011110,所以[M X]补=0.100101,[M y]补=1.100010 [x]浮=1101 0.100101,[y]浮=1110 1.100010E X<E y,E y-E X = E y+(-E X)=1110+0011=0001对阶后[x]浮=1110 0.010010(1),[y]浮=1110 1.100010对阶后的尾数相加:M X+M y=0.010010(1)+1.1000100. 0 1 0 0 1 0 (1)+ 1. 1 0 0 0 1 01. 1 1 0 1 0 0 (1)x+y=1.110100(1)⨯21110,化为规格化数(左移2位)为:x+y=1.010010⨯21100,即:x+y=-0.101110⨯2-4对阶后的位数相减:M X-M y=M X+(-M y)=0.010010(1)+0.0111100. 0 1 0 0 1 0 (1)+ 0. 0 1 1 1 1 00. 1 1 0 0 0 0 (1)x-y=0.110000(1)⨯21110,已经是规格化数,采用0舍1入法进行舍入处理:x-y=0.110001⨯21110,即:x-y=0.110001⨯2-2(2)x=2-101⨯(-0.010110),y=2-100⨯(0.010110)E X=-101,E y=-100,所以 [E X]补=1011,[E y]补=1100M X=-0.010110,M y=0.010110,所以[M X]补=1.101010,[M y]补=0.010110[x]浮=1011 1.101010,[y]浮=1100 0.010110E X<E y,E y-E X = E y+(-E X)=1100+0101=0001对阶后[x]浮=1100 1.110101(0),[y]浮=1100 0.010110对阶后的尾数相加:M X +M y =1.110101+0.0101101. 1 1 0 1 0 1 + 0. 0 1 0 1 1 00. 0 0 1 0 1 1x+y=0.001011⨯21100,化为规格化数(左移2位)为:x+y=0.101100⨯21010,即: x+y=0.101100⨯2-6对阶后的位数相减:M X -M y =M X +(-M y )=1.110101+1.1010101. 1 1 0 1 0 1 + 1. 1 0 1 0 1 01. 0 1 1 1 1 1x-y=1.011111⨯21100,已经是规格化数,所以x-y=-0.100001⨯2-410、 (1) ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⨯⎪⎭⎫ ⎝⎛⨯16921613243 M x =110100.02110116134=⨯=-,Ex=0011 M y =100100.021*******-=⨯-=--,Ey=0100 Ex+Ey=0011+0100=0111[x ⨯y]符=0⊕1=1,乘积的数值=|M x |⨯|M y |:0. 1 1 0 1⨯ 0. 1 0 0 10 1 1 0 10 0 0 0 00 0 0 0 00 1 1 0 1 0 0 0 0 00 0 1 1 1 0 1 0 1所以,x ⨯y =-0.01110101⨯20111,规格化处理(左移一位),并采用0舍1入法进行舍入:x ⨯y =-0.111011⨯20110 即:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⨯⎪⎭⎫ ⎝⎛⨯16921613243=-0.111011⨯26 (2) ⎪⎭⎫ ⎝⎛⨯÷⎪⎭⎫ ⎝⎛⨯-161523213232 将x 、y 化为规格化数:M x =011010.02110132135=⨯=-,Ex=1110 M y =111100.021********=⨯=-,Ey=0011 Ex-Ey=Ex+(-Ey)=1110+1101=1011[x ÷y]符=0⊕0=0,下面用加减交替法计算尾数M x ÷M y :[Mx]补=0.011010,[My]补=0.111100,[-My]补=1.0001000. 0 1 1 0 1 0+[-My]补 1. 0 0 0 1 0 01. 0 1 1 1 1 0 ——余数为负,商为00. 1 1 1 1 0 0 ——余数和商左移一位(0)+[My]补 0. 1 1 1 1 0 01. 1 1 1 0 0 0 ——余数为负,商为01. 1 1 0 0 0 0 ——余数和商左移一位(00)+[My]补 0. 1 1 1 1 0 00. 1 0 1 1 0 0 ——余数为正,商为11. 0 1 1 0 0 0 ——余数和商左移一位(001)+[-My]补 1. 0 0 0 1 0 00. 0 1 1 1 0 0 ——商为10. 1 1 1 0 0 0 ——(0011)+[-My]补 1. 0 0 0 1 0 01. 1 1 1 1 0 0 ——商为01. 1 1 1 0 0 0 ——(00110)+[My]补 0. 1 1 1 1 0 00. 1 1 0 1 0 0 ——商为11. 1 0 1 0 0 0 ——(001101)+[-My]补 1. 0 0 0 1 0 00. 1 0 1 1 0 0 ——商为11. 0 1 1 0 0 0 ——(0011011)+[-My]补 1. 0 0 0 1 0 00. 0 1 1 1 0 0 ——商为1——(00110111)Mx÷My的商为0.0110111,余数为0.011100⨯2-7,由于x化为0.01101(Mx)是尾数右移2位才得到,所以x÷y真正的余数是0.011100⨯2-7再尾数左移2位,即0.011100⨯2-9=0.111000⨯2-10所以,x÷y的商为:0.0110111⨯21011,规格化处理后为:0.110111⨯21010=0.110111⨯2-6,余数为0.111000⨯2-1011、不考虑181ALU的函数发生器,而是从简单的全加器出发,则:若设4位的二进制数为A=A3A2A1A0,B=B3B2B1B0,并设G i=A i B i,P i=A i⊕B i,由全加器进位输出的逻辑函数C i+1=A i B i+C i(A i⊕B i)可知:(由于进位输出函数还可以写成C i+1=A i B i+C i(A i+B i),故P i=A i+B i也可)(1) 串行进位方式:C1=A0B0+C0(A0⊕B0)=G0+P0C0C2=A1B1+C1(A1⊕B1)=G1+P1C1C3=A2B2+C2(A2⊕B2)=G2+P2C2C4=A3B3+C3(A3⊕B3)=G3+P3C3(2) 并行进位方式:C1=G0+P0C0C2=G1+P1C1=G1+P1(G0+P0C0)=G1+P1G0+P1P0C0C3=G2+P2C2=G2+P2(G1+P1G0+P1P0C0)=G2+P2G1+P2P1G0+P2P1P0C0C4=G3+P3C3=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0C012、(1) -5-5=-(101)2=-(1.01)2⨯22所以S=1E=e+127=2+127=129=(81)16=(10000001)2M=(010 0000 0000 0000 0000 0000)2故浮点格式为:1 10000001 010 0000 0000 0000 0000 0000,用十六进制表示为:(C0A00000)16(2) -1.5-1.5=-(1.1)2=-(1.1)2⨯20所以S=1E=e+127=0+127= (7F)16=(01111111)2M=(100 0000 0000 0000 0000 0000)2故浮点格式为:1 01111111 100 0000 0000 0000 0000 0000,用十六进制表示为:(BFC00000)16 (3) 384384=(180)16=(1 1000 0000)2=(1.1)2⨯28所以S=0E=e+127=8+127=135= (87)16=(10000111)2M=(100 0000 0000 0000 0000 0000)2故浮点格式为:0 10000111 100 0000 0000 0000 0000 0000,用十六进制表示为:(43C00000)16 (4) 1/161/16= (1.0)2⨯2-4所以S=0E=e+127=-4+127= (7B)16=(01111011)2M=(000 0000 0000 0000 0000 0000)2故浮点格式为:0 01111011 000 0000 0000 0000 0000 0000,用十六进制表示为:(3D800000)16 (5) -1/32-1/32=-(1.0)2⨯2-5所以S=1E=e+127=-5+127= (7A)16=(01111010)2M=(000 0000 0000 0000 0000 0000)2故浮点格式为:1 01111010 000 0000 0000 0000 0000 0000,用十六进制表示为:(BD000000)1613、(1) 1 10000011 110 0000 0000 0000 0000 0000S=1E=(83)16=131 e=E-127=131-127=41.M=(1.11)2所以,该浮点数为 -(1.11)2⨯24=-(11100)2=-28(2) 0 01111110 101 0000 0000 0000 0000 0000S=0E=(7E)16=126 e=E-127=126-127=-11.M=(1.101)2所以,该浮点数为 (1.101)2⨯2-1=(0.1101)2=0.812514、IEEE754标准中,32位二进制数仍然有232种不同的组合,但是由于在IEEE754标准中,阶码为全1并且尾数为非0的情况不表示一个数。
