理论力学-11-动能定理及其应用
理论力学-11-动能定理及其应用

F FN
0
F
滑动摩擦力做负功!
O
M
C
又滚又滑
11.1.2 各种力做功的计算
约束力的功
只滚不滑 纯滚动时,静滑动摩擦力 (约束力)作功为零!
vO
O
C* FN
F
WF F drC F vC dt
0
11.1.2 各种力做功的计算
约束力的功
理想约束:
约束力作功等于零的约束。 ◆ 不可伸长的柔索约束 ◆ 光滑的固定支承面 ◆ 光滑铰链: 轴承、滚动铰支座 ◆ 纯滚动时的静摩擦力
例题2
分别选轮和物体为研究对象?
FOy
圆轮:
1 T2 J O 2 2
T1 0
FT R
O
FOx
T2 T1 W12
物体:
T1 0
T2 1W 2 v 2 g
mg
FT
F'T
Ws FT s
P v W
11.3 动能定理及其应用
例题3
l-b
b
一长为 l , 质量密度为 ρ 的链条放置在光滑的水 平桌面上,有长为b的一段 悬挂下垂,如图。初始链 条静止,在自重的作用下 运动。 求:当末端滑离桌面时, 链条的速度。
1 2 1 2 mv2 mv1 W12 2 2
1 2 d( mv ) δW 2
11.3 动能定理及其应用
质点系
1 2 微分形式: d T d ( mi vi ) Fi d ri δ Wi 2
1 1 2 2 m v - m v 积分形式: i i2 i i1 W12 i 2 i 2 i
3 2 T mvC 4
动能定理的应用讲

汽车加速和减速
在汽车加速时,发动机产生的力大于 阻力,使汽车速度增加,动能增大。
在汽车减速时,制动器产生的力大于 驱动力,使汽车速度减小,动能减小 。
投掷物体的距离和速度
在投掷物体时,物体的速度越大,飞行距离越远。 动能定理可以用来计算投掷物体的最大距离和最佳出手角度。
滑冰和滑雪的速度控制
在滑冰和滑雪时,通过改变身体姿态和施加外力来控制速 度。
动能定理的应用
在自由落体运动中,物体的动能变化等于重力所做的功。通过测量物体下落的高度和时间,可以计算 出物体的速度和动能的变化,进一步验证动能定理的正确性。
火箭实验和宇宙速度的计算
火箭实验
为了研究火箭发动机的性能和原理,需 要进行火箭实验。通过测量火箭发动机 的推力和工作时间,可以计算出火箭的 初速度和末速度,进一步验证动能定理 的正确性。
动能定理的应用
目
CONTENCT
录
• 动能定理简介 • 动能定理的基本应用 • 动能定理在生活中的应用 • 动能定理在工程中的应用 • 动能定理在科学实验中的应用 • 动能定理的发展与展望
01
动能定理简介
动能定理的定义
动能定理是指合外力对物体所做的功等于物体动能的变化量,数学 表达式为:W总=ΔEK。
动能定理在未来科技发展中的前景
01
在新能源领域,利用动能定理优化能源转换和利用效率,推 动可持续发展。
02
在人工智能领域,运用动能定理研究机器学习算法和智能控 制技术。
03
在太空探索领域,运用动能定理分析航天器的运动轨迹和优 化太空任务。
THANK YOU
感谢聆听
物体在运动过程中受到的平均功率P_avg可以通过下式计算:$P_{avg} = frac{W}{t}$,其中W是力做的功,t是运动的时间。
动能定理的应用

动能定理的应用在物理学中,动能定理是一个非常重要的概念,它在解决各种力学问题中发挥着关键作用。
动能定理指出:合外力对物体所做的功等于物体动能的变化量。
这个定理看似简单,但其应用却十分广泛且精妙。
让我们先从一个简单的例子来理解动能定理。
想象有一个质量为 m 的物体,在一个水平面上受到一个恒力 F 的作用,沿着力的方向移动了一段距离 s。
如果物体的初速度为 v₁,末速度为 v₂,那么根据牛顿第二定律 F = ma(其中 a 为加速度),以及运动学公式 2as = v₂²v₁²,我们可以得到:Fs = ½mv₂² ½mv₁²。
这就是动能定理的表达式。
在实际问题中,动能定理的应用场景多种多样。
比如在自由落体运动中,物体只受到重力的作用。
假设一个物体从高度 h 处自由下落,其质量为 m,到达地面时的速度为 v。
重力做的功为 mgh,根据动能定理,mgh = ½mv² 0,从而可以很容易地求出物体到达地面时的速度 v=√(2gh)。
再来看一个涉及多个力的问题。
假设一个物体在粗糙水平面上受到一个水平拉力 F 的作用,同时还受到摩擦力 f 的阻碍。
物体移动了一段距离 s,初速度为 v₁,末速度为 v₂。
拉力做的功为 Fs,摩擦力做的功为 fs,合力做的功为(F f)s。
根据动能定理,(F f)s =½mv₂² ½mv₁²。
通过这个式子,我们可以求出物体在这个过程中的末速度 v₂。
动能定理在解决曲线运动问题时也非常有用。
例如一个物体在竖直平面内做圆周运动,在最低点时,绳子对物体的拉力和物体的重力共同做功,使得物体的动能增加。
根据动能定理,我们可以计算出拉力和重力做功的总和与动能变化之间的关系。
在碰撞问题中,动能定理同样能发挥作用。
当两个物体发生碰撞时,虽然碰撞过程中的内力非常复杂,但如果我们只关心碰撞前后物体动能的变化,就可以运用动能定理。
理论力学第13章动能定理

在理论力学中,动能被定义为物体运动时的能量,其大小与物体的质量和速度有关。根据牛顿第二定律,物体的动量改变量等于作用在物体上的外力的冲量。因此,如果一个力在一段时间内作用在一个物体上,那么这个力就会使物体的动量发生改变,从而产生动能的变化。
动能的定义
外力的功
外力的功等于力的大小与物体在力的方向上发生的位移的乘积。
总结词
外力的功是指力对物体运动所产生的效应,其大小等于力的大小与物体在力的方向上发生的位移的乘积。这是物理学中功的定义,也是计算外力对物体所做功的基本方法。
详细描述
VS
系统动能的增量等于合外力对系统所做的功。
详细描述
系统动能的增量是指在一个过程中,系统动能的增加量。这个增量可以通过计算合外力对系统所做的功来得到。如果合外力对系统做正功,则系统动能增加;如果合外力对系统做负功,则系统动能减少。因此,系统动能的增量与合外力对系统所做的功有直接的关系。
总结词
系统动能的增量
03
CHAPTER
动能定理的应用
适用于单个质点在力的作用下运动的情况,计算质点的动能变化。
单个质点的动能定理指出,质点在力的作用下运动时,外力对质点所做的功等于质点动能的增量。这个定理是理论力学中研究质点运动的基本定理之一,可以用来解决各种实际问题。
总结词
详细描述
单个质点的动能定理
动能定理是能量守恒定律在动力学中的具体表现,是解决动力学问题的有力工具。
动能定理适用于一切宏观低速的物体,对于微观、高速适用于狭义相对论。
动能定理适用于直线运动,对于曲线运动需要积分形式进行处理。
动能定理的适用范围
02
CHAPTER
动能定理的基本内容
总结词
动能定理及其应用

动能定理及其应用引言:动能定理是物理学中的一项重要理论,它描述了物体的动能与力的关系。
动能定理不仅在理论物理学领域具有广泛的应用,还在实际生活中发挥着重要的作用。
本文将探讨动能定理的基本原理,并介绍其在不同领域中的应用。
一、动能定理的原理动能定理是基于牛顿第二定律和功的定义推导得出的。
根据牛顿第二定律,力的作用将改变物体的加速度。
而根据功的定义,力对物体所做的功等于力与物体位移的乘积。
结合这两个定律,可以得出动能定理的基本公式:物体的动能等于力对物体所做的功。
二、动能定理在机械工程中的应用在机械工程中,动能定理有着广泛的应用。
例如,在机械设备的设计和优化中,动能定理可以用来分析和评估物体的运动状态和能量转换的效率。
通过计算物体受到的力和位移的乘积,可以得出物体的动能变化情况,进而对机械系统进行合理的设计和改进。
三、动能定理在运动学中的应用在运动学中,运用动能定理可以推导出物体在不同条件下的运动规律。
例如,根据动能定理可以推导出机械系统的动力学方程,并通过求解这些方程,可以预测物体的运动轨迹和速度变化等。
这对于研究运动学问题和进行科学实验具有重要意义。
四、动能定理在能源领域中的应用动能定理在能源领域中也有着重要的应用。
例如,通过应用动能定理,可以计算出流体在流动过程中的动能变化,帮助研究人员优化水力发电站的设计和运行效率。
此外,动能定理还可以用来分析和评估其他能源转换装置,如风力发电机和光伏发电板等。
五、动能定理在体育运动中的应用动能定理在体育运动中也具有广泛的应用。
例如,在跳高比赛中,运动员需要将自身的动能转化为势能,从而跳过跳杆。
通过运用动能定理,可以帮助运动员合理调整起跳速度和身体姿势,从而获得更好的跳远成绩。
同样,在其他运动项目中,运用动能定理也可以帮助运动员优化运动技巧和能量利用,提高竞技成绩。
结论:动能定理作为物理学的基本理论之一,不仅在理论物理学中有着广泛的应用,还在实际生活中发挥着重要的作用。
理论力学 动能定理

第11章动能定理即质点系的动能等于其随质心平BCθABθCPA2rOr C力的功2rOr CAP2rOr CAP2rOr CAPs汽车驱动问题能量角度:汽缸内气体爆炸力是内力,不改变汽车的动量,但使汽车的动能增加。
动量角度:地面对后轮的摩擦力是驱动力,使汽车的动量增加,但不做功,不改变汽车的动能。
内力不能改变质点系的动量和动量矩,但可以改变能量;外力能改变质点系的动量和动量矩,但不一定能改变能量。
例题11-8水平悬臂梁AB,B端铰接滑轮B,匀质滑轮质量m1,半径r;绳一端接滚,轮C,半径r,质量m2视为质量集中在边缘;绳另端接重物D,质量m3。
求重物加速度。
CωDv BωCv 解:末位置是一般位置hconst 01==T T =2T 2321D v m 221B B J ω+221CP J ω+运动学关系rr v v B C C D ωω===2121rm J B =2222222rm r m r m J P=+=2321222121Dv m m m T ⎟⎠⎞⎜⎝⎛++=gh m W 312=CωDv BωCv h1212W T T =−gh m T v m m m D 30232122121=−⎟⎠⎞⎜⎝⎛++对t 求导h g m vv m m m D D &&33210)221(=−++Dv h =&D D a v=&gm m m m a D 3213221++=例11-9匀质圆盘和滑块的质量均为m。
圆盘的半径为r。
杆平行于斜面,其质量不计。
斜面的倾斜角为θ。
圆盘、滑块与斜面的摩擦因数均为μ。
圆盘在斜面上作纯滚动。
试求滑块下滑加速度。
1212W T T =−01=T 2222212121mvJ mv T A ++=ω解()sF F mgs mgs W B A +−+=θθsin sin 12θμcos mg F F B A ==取导221,mrJ v r A ==ω2245mvT =()θμθcos sin 2452−=gs v a v v s==&&,()θμθcos sin 54−=g a F A 是静摩擦力,理想约束,不作功。
理论力学13-动能定理

动能定理是理论力学中重要的定理之一,描述了物体动能的变化与外力做功 的关系。它为解决各种实际问题提供了有力的工具。
动能的定义与计算方法
动能定义
动能是物体由于运动而具有的能量。
动能计算方法
动能等于物体质量与速度平方的乘积乘以常数1/2。
举例
例如,一个质量为m的物体速度为v,它的动能为Ek=1/2mv^2。
碰撞实验
通过观察简谐摆的运动过程, 可以验证动能定理在实验中 的有效性和准确性。
利用碰撞实验可以验证动能 定理在不同碰撞情况下的适 用性。
滚动小球实验
通过观察滚动小球的动能变 化,可以验证动能定理在滚 动运动中的应用。
结论和要点
结论
动能定理是描述物体动能变化与外力做功关系的重要定理。
要点
动能定理的表达式是功等于动能的变化量,可以通过实验验证。
动能定理的提出及其重要性
1 提出背景
动能定理最早由牛顿提出,是牛顿运动定律的一部分。
2 重要性
动能定理能够精确描述物体动能的变化与外力做功的关系,对研究运动学和动力学等科 学领域具有重要意义。
动能定理的表达式及推导过程
动能定理表达式 推导过程 推导公式
功等于动能的变化量 根据牛顿第二定律和功的定义推导得出 W = ΔK = (1/2)mvf^2 - (1/2)mvi^2
动能定理在实际问题中的应用
1
碰撞问题
2
动能定理在研究碰撞问题中起到关 键作用,如弹性碰撞和非弹性碰撞。
3
机械能守恒
动能定理与势能定理结合可以帮助 解决机械能守恒的问题。
动能定理与其他物理定律的 关系
动能定理与动量定理、能量守恒定 律等相互关联,共同构成了理论力 学的核心部分。
理论力学课件:动能定理

动能定理
【例12-8】 C618车床的主轴转速n=42r/min时,其切削力
P=14.3kN,若工件直径d=115mm,电动机到主轴的机械效率
η=0.76。求此时电动机的功率为多少?
解 由式(12-12)得切削力P 的功率:
动能定理
12.5 势力场 势能及机械能守恒定理
动能定理
动能定理
12.4 功率 功率方程
1.功率
在单位时间内力所做的功称为功率。它是衡量机器工作
能力的一个重要指标。
δW 是dt时间内力的元功,则功率为
动能定理
由于元功为δW =Ft·ds,因此
即,力的功率等于切向力与力作用点速度的乘积
力矩的元功为δW =M·dφ,则
即,力矩的功率等于力矩与物体转动角速度的乘积。
动能定理
动能定理
12.1 力的功
12.2 质点 质点系的动能
12.3 质点与质点系的动能定理
12.4 功率 功率方程
12.5 势力场 势能及机械能守恒定理
12.6 动力学普遍定理及综合应用
思考题
动能定理
12.1 力 的 功
工程实际中,一物体受力的作用所引起运动状态的变化,
不仅取决于力的大小和方向,而且与物体在力的作用下经过
的功。
动能定理
图12-15
动能定理பைடு நூலகம்
【例12-4】 在图12-16中,为测定摩擦系数f,把矿车置于
斜坡上的A 点处,让其无初速下滑。当它达到B 点时,靠惯性
又往前滑行一段路程,在C 点处停止。求摩擦系数f0,已知S1、
S2 和h。
图12-16
动能定理
理论力学课后习题答案-第10章--动能定理及其应用-)

理论力学课后习题答案-第10章--动能定理及其应用-)(a)v ϕABC rv 1v 1v 1ωϕ(a)CCωCvωO第10章 动能定理及其应用10-1 计算图示各系统的动能:1.质量为m ,半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时,若已知圆盘上A 、B 两点的速度方向如图示,B 点的速度为v B ,θ = 45º(图a )。
2.图示质量为m 1的均质杆OA ,一端铰接在质量为m 2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动,圆心速度为v (图b )。
3.质量为m 的均质细圆环半径为R ,其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动,图示瞬时角速度为ω(图c )。
解:1.222222163)2(2121)2(212121BBB CCCmv r v mr v m J mv T =⋅+=+=ω 2.222122222214321)(21212121v m v m r v r m v m vm T +=⋅++= 3.22222222)2(212121ωωωωmR R m mR mR T =++=10-2 图示滑块A 重力为1W ,可在滑道内滑动,与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ,杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时,试求系统的动能。
解:图(a ) B AT T T +=)2121(21222211ωC CJ vgWv g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10-3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
理论力学基础 动能定理

M2 M1
(
Fx
dx
Fy
dy
Fzdz)
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第十二章 动能定理
三、重力之功 Fx Fy 0 Fz mg
W12
z2 z1
mgdz
mg(z1
z2 )
质点系
第
一 节
W m g(z z )
12
i
i1
i2
力
的
功
由 mzC mi zi
量分别为m和2m,且OC=AC=BC=l,滑块A和
第 B重量均为m。常力偶M作用在曲柄上,设=0
三 节 动
时系统静止,求曲柄角速度和角加速度 (以转角
表示)。
vB
能
定 理
K
vA
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第十二章 动能定理
例题六 图示系统中,滚子A 、滑轮B 均质,重
量和半径均为Q 及r,滚子沿倾角为 的斜面向
W d r F
三
节 m d v d r mdv d r mdv v mvdv
动 能 定
dt
d
(
1
dt
mv2 )
理
2
动能定理的微分形式: W d ( 1 mv2 )
2
动能定理的积分形式:
W
1 2
mv22
1 2
mv12
鞍山科技大学机械工程与自动化学院工程力学系
下滚动而不滑动,借跨过滑轮B的不可伸长的绳
第 索提升重P的物体,同时带动滑轮B绕O轴转动,
理论力学动能定理

光滑铰链(中间铰链)、刚性二力杆及不可伸长的细 绳作为系统内的约束时,约束力作功之和等于零。 滑动摩擦力作负功。
当轮子在固定面上只滚不滑时,滚动摩擦力不作功。
变形元件的内力(气缸内气体压力、弹簧力等)作功; 刚体所有内力作功的和等于零。
例2 卷扬机如图,鼓轮在常力偶M的作用下将圆柱上拉。已 知鼓轮的半径为R1,质量为m1,质量分布在轮缘上;圆柱 的半径为R2,质量为m2,质量均匀分布。设斜坡的倾角为α, 圆柱只滚不滑。系统从静止开始运动,求圆柱中心C经过路 程S 时的速度。 解:以系统为研究对象, 受力如图。系统在运动过程中 所有力所作的功为
vC 1 R1
2 1
1 2 J c m2 R2 2
vC 2 R2
m2g
FS
FN
于是
2 vC T2 (2m1 3m2 ) 4
FOy M O C m1g FOx
由 T2 T1 W12 得
m2g
FS
FN
2 vC s (2m1 3m2 ) 0 M m2 g sin s 4 R1
1 2 d mv W 2
--质点动能定理微分式
即:质点动能的增量等于作用于质点上外力所作的 元功。
1 1 2 2 积分后得: mv2 mv1 W 2 2 或: T2 T1 W
即:在一段路程中,质点动能的改变量等于作用于质 点上外力在路程上所作的功。
二、质点系的动能定理
的联系,这是一种能量传递的规律。
§13-1 力的功
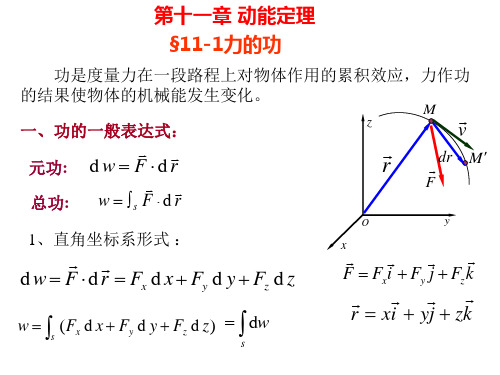
一、力的功
力的功是力在一段路程内对物体作用的积累效应
的度量。力做功的结果是使物体的机械能发生变化
1、常力功的计算
理论力学——动能定理

解:在运动过程中,T 的大小不变,但方向 在变,因此T 的元功为
δWT T cosa d x
cosa (20 x) (20 x)2 152
因此T在整个过程中所作的功为
O
力F在刚体从角j1转到j2所作的功为
W12
j2 j1
M
zdj
Mz可视为作用在刚体上的力偶
例1 如图所示滑块重P=9.8 N,弹 簧刚度系数k=0.5 N/cm,滑块在A 位置时弹簧对滑块的拉力为2.5 N, 滑块在20 N的绳子拉力作用下沿光 滑水平槽从位置A运动到位置B,求 作用于滑块上所有力的功的和。
OC作定轴转动,规尺AB作平面运动。首先对 vA
运动进行分析,O1是AB的速度瞬心,因:
运动分析
A
vc O1C AB OC AB
AB
O1
系vA统分O析1AAB 2a cosj a
TA
1 2
mAvA2
ma 2 2
2
vC C
vB O1BAB 2asinj 3a
T
A
15 cm
B
20 cm
PT
F
a
N
20
20
WT 0 T cosa d x 0 20
20 x d x 200 N cm
(20 x)2 152
再计算F的功:
由题意:
d1
2.5 0.5
5cm
T
A
15 cm
B
20 cm
理论力学课件 第十二章 动能定理

FRO
r1 r2 O
mg
解:取整体为研究对象,受力分析如图所示。 v1
A
v2
B
系统对O点的动量矩为
m1 g
m2 g
LO m1v1r1 m2v2r2 J0 (m1r12 m2r22 JO )
系统所受全部外力对O点的动量矩为
MO (F e ) m1gr1 m2gr2
质点系的动量矩定理为 dLO dt
WFN 0
WF F s fmgs cos 30 8.5 J
WF
1 2
k
(12
2 2
)
100 (0 0.52) 2
12.5 J
W Wi 24.5 0 8.512.5 3.5 J
12.2 质点和质点系的动能
12.2.1 质点的动能
设质量为m的质点,某瞬时的速度为v,则质点质量与其速度平方乘积的
路径无关。若质点下降,重力的功为正;若质点上升,重力的功为负。
对于质点系,重力的功等于各质点的重力功的和,即
上式也可写为
W12 mi g(zi1 zi2) W12 mg(zC1 zC2 )
2.弹力的功
设有一根刚度系数为k,自由长为l0的弹 簧, 一端固定于点O, 另一端与物体相连接,
如图所示。求物体由M1移动到M2过程中,弹 力F所做的功。
W12
M2 M1
(Fx
d
x
Fy
d
y
Fz
d
z)
12.1.3 常见力的功
1.重力的功
z M1 M
mg
设质点M的重力为mg,沿曲线由M1运动到
M2
M2,如图所示。因为重力在三个坐标轴上的
投影分别为Fx=Fy=0,Fz=-mg,故重力的功为
理论力学第十一章动能定理
由于刚体上任意两点之间的距离始终保持不变。因此
d rB
cos
d rA
cos
d w 0
5、约束力的功 (1)光滑固定面力的功 d w FN d r 0 (2)摩擦力的功
FN dr
FN
静滑动摩擦力不做功
纯滚动摩擦力: dW F dr F vI dt 0
IF
动滑动摩擦力的功:dW F ds fd FN ds
1 2
mivr2i
柯尼希定理: 质点系的动能等于随同其质心平动的动 能与相对其质心运动的动能之和。
三、刚体的动能
1、平移刚体的动能:
T
1 2
mi
vi2
1 2
mi
v
2
1 mv2 2
2、定轴转动刚体的动能:
T
1 2
mi
vi2
1 2
(mi
i
2
)
2
1 2
J z 2
3、刚体作平面运动
设刚体上任一质点到瞬心的垂直距离为 i,则该
/
h2
a |90 3.14m/s 2 ( 90 )
例5:已知:mA=m,mB=m/2,mC=m/3,鼓轮的回转半径为,质 量为m,鼓轮小半径为r,大半径为R,外力偶M,C轮的半径为r, 物体A接触的摩擦系数为fd,系统初始静止,求物体A的速度(表 示成物体A位移xA的函数)。
解: “系统” T1 0
解 :BC杆及重物D(以 杆BC的水平位置为零势能位 )
V1
P1
l 2
cos
P2l
cos
( P1 2
P2 )l
cos
弹簧(选弹簧的原长处为势能的零位置)
B
V2
动能定理的原理和应用

动能定理的原理和应用一、动能定理的原理动能定理是物理学中的一个重要定理,它描述了物体的动能与作用在物体上的净力之间的关系。
动能定理可以用来分析物体在运动过程中的能量转化和能量变化情况。
动能定理的核心原理是:物体的动能的变化率等于作用在物体上的净力乘以物体在该力下移动的距离。
动能定理的数学表示如下:W = ΔK其中,W表示净力所做的功,ΔK表示物体动能的变化。
二、动能定理的应用动能定理在物理学中有着广泛的应用,下面将介绍一些常见的应用场景。
1. 车辆碰撞分析动能定理可以用来分析车辆碰撞的力量和能量变化情况。
通过对碰撞之前和之后车辆的动能变化进行计算,可以推断碰撞的严重程度和造成的损伤情况。
这对于交通事故的调查和事故重建非常重要。
2. 物体自由下落当一个物体从高处自由下落时,可以利用动能定理计算物体的速度和落地时的动能。
这在物理实验和工程设计中经常用到。
3. 弹性碰撞动能定理也可以应用于弹性碰撞的分析。
在弹性碰撞中,物体的动能会发生变化,而动能定理可以帮助我们计算碰撞前后物体的速度和动能变化情况。
4. 机械能守恒动能定理与机械能守恒定律密切相关。
机械能守恒定律指出,在没有外力做功的情况下,物体的机械能(动能和势能之和)保持不变。
动能定理可以帮助我们理解物体机械能的变化和转化情况,从而应用于机械系统的分析和优化设计。
三、总结动能定理是物理学中的一个重要定理,它描述了物体的动能与作用在物体上的净力之间的关系。
动能定理可以用于分析物体在不同情况下的能量变化和转化。
它的应用场景广泛,包括车辆碰撞分析、物体自由下落、弹性碰撞和机械能守恒等方面。
掌握了动能定理的原理和应用,有助于我们深入理解物理学中的能量概念,并能在实际问题中进行定量分析。
理论力学课后习题答案 第10章 动能定理及其应用 )

(a)A(a)O第10章 动能定理及其应用10-1 计算图示各系统的动能:1.质量为m ,半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时,若已知圆盘上A 、B 两点的速度方向如图示,B 点的速度为v B ,θ = 45º(图a )。
2.图示质量为m 1的均质杆OA ,一端铰接在质量为m 2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动,圆心速度为v(图b )。
3.质量为m 的均质细圆环半径为R ,其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动,图示瞬时角速度为ω(图c )。
解:1.222222163)2(2121)2(212121BB BC C C mv r v mr v m J mv T =⋅+=+=ω 2.222122222214321)(21212121v m v m r v r m v m v m T +=⋅++=3.22222222)2(212121ωωωωmR R m mR mR T =++=10-2 图示滑块A 重力为1W ,可在滑道内滑动,与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ,杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时,试求系统的动能。
解:图(a )B A T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10-3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
曲柄的重力为Q F ,角速度为ω,齿轮可视为匀质圆盘。
试求行星齿轮机构的动能。
理论力学11动能定理

F dr Xdx Ydy Zdz)
力 F 在曲线路程 M1M 2 中作功为
M2
M2
W F cosds F ds (自然形式表达式)
M1
M1
M2
F dr
(矢量式)
M1
M2
Xdx Ydy Zdz (直角坐标表达式)
9
M1
三.合力的功
质点M 受n个力 F1,F2 ,,Fn 作用合力为 R Fi 则合力 R
F d (rA rB ) F d (BA)
只要A、B两点间距离保持不变,内力的元功和就等于零。
不变质点系的内力功之和等于零。刚体的内力功之和等于零。
不可伸长的绳索内力功之和等于零。
功的计算公式中力作用点的含义应包括三方面: (1)受力点:受力物体(分析对象)上直接受到力的那个点; (2)加力点:施力物体上加力的那个点,该瞬时与受力点的接触点; (3)力点:力作用点的空间位置。 任何瞬时这三个点都是重合的,但在很多情况下,这三个点具有不同的运 动和轨迹。 功的正确计算: dr 和 v应当为受力点的位移和速度。
即 dT Wi 质点系动能定理的微分形式 将上式沿路径 M1M 2 积分,可得
T2 T1 W 质点系动能定理的积分形式
在理想约束的条件下,质点系的动能定理可写成以下的形式
dT W (F) ; T2 T1 W (F)
5
若将质点系中的受力分为外力、内力,则有外力功和内力功
T2 T1 W12
W12 i
ri 2 ri1
F (e)
i
dri
i
ri 2 ri1
F (i)
i
dri
动能定理在力学中的应用

动能定理在力学中的应用在物理学的广阔天地中,力学无疑是其中最为基础且重要的一个分支。
而动能定理,作为力学领域中的一颗璀璨明珠,为我们理解和解决众多力学问题提供了强大而有效的工具。
要理解动能定理,首先得明白什么是动能。
简单来说,动能就是物体由于运动而具有的能量。
其大小与物体的质量和速度的平方成正比,表达式为$E_k =\frac{1}{2}mv^2$,其中$m$是物体的质量,$v$是物体的速度。
那动能定理又是什么呢?动能定理指出:合外力对物体所做的功等于物体动能的变化量。
用数学表达式写出来就是:$W =\DeltaE_k$,其中$W$是合外力做的功,$\Delta E_k$是动能的变化量。
为了更清楚地看到动能定理在实际问题中的应用,让我们先来看一个简单的例子。
假设有一个质量为$m$的物体,在一个水平光滑的表面上,受到一个水平方向的恒力$F$的作用,从静止开始运动,经过一段距离$x$后,速度达到$v$。
由于物体在水平方向上只受到一个力$F$的作用,根据功的定义,力$F$所做的功$W = Fx$。
而物体的初动能为$0$,末动能为$\frac{1}{2}mv^2$,根据动能定理,$Fx =\frac{1}{2}mv^2 0$,通过这个式子,我们就可以很容易地求出物体的末速度$v$。
再来看一个稍微复杂一点的例子。
一个质量为$m$的物体从高度为$h$的斜面顶端由静止滑下,到达斜面底端时的速度为$v$。
忽略摩擦力的作用。
在这个过程中,重力做功$W = mgh$,物体的初动能为$0$,末动能为$\frac{1}{2}mv^2$,根据动能定理,$mgh =\frac{1}{2}mv^2 0$,从而可以求出物体到达底端时的速度$v$。
从上面两个例子可以看出,动能定理的应用大大简化了我们解决力学问题的过程。
特别是在涉及到多个力做功或者物体的运动轨迹比较复杂的情况下,动能定理的优势就更加明显了。
比如,一个物体在粗糙水平面上受到一个水平拉力$F$和摩擦力$f$的作用,做直线运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.2 质点与质点系的动能
1、质点系的动能 2、刚体的动能
11.2 质点与质点系的动能 1、质点系的动能
质点动能——
T 1 2 mv
2
(标量)
质点系的动能——
T
2m v
i i
1
2 i
动能是度量质点系整体运动的另一物理量。动能是正 标量,其数值与速度的大小有关,但与速度的方向无关。
1 l m ml 3 2 2
2
T总
1 12
9M
4m v
2
第11章 动能定理及其应用
11.3 动能定理及其应用
11.3 动能定理及其应用
1、质点系的动能定理 2、动能定理的应用举例
11.3 动能定理及其应用
质点系的动能定理
1、质点系的动能定理
例题3
例题3
一长为l,质量密度为 ρ 的链条放置在光滑的水平桌面 上,有长为b的一段悬挂下垂,如图。初始链条静止,在自 重的作用下运动。求当末端滑离桌面时,链条的速度。 lb 解:链条在初始及终止两状态的动能 分别为 1 2
T1 0
T2
2
lv 2
b
在运动过程中所有的力所作的功为 由
根据运动学补充关系
v A R A
11.3 动能定理及其应用
例题4
解: 对象:整个系统 受力:如图所示 运动:轮A作平面运动;轮B 作定轴转动;物块C作平移。 方程: 1. 系统的动能为:
T1 0 , 1 1 1 1 2 2 2 2 T2 mv A J A A J B B mvC 2 2 2 2
2
1
k d
1
2
k1
2
1
2
k 2
2
11.1 力的功 3、内力的功
内力作功的情形 日常生活中,人的行走和奔跑是腿的肌肉内力作功; 弹簧力作功等等;摩擦力做功损耗能量。 刚体的内力不作功 刚体内任何两点间的距离始终保持不变,所以刚体 的内力所作功之和恒等于零。
O x
W = mgdz
W12 mg( z1 z 2 )
11.1 力的功
对于质点系:
W 1 2 m i g ( z i1 z i 2 ) ( m i z i1 m i z i 2 ) g ( M zC1 M zC 2 ) g M g ( zC1 zC 2 )
11.2 质点与质点系的动能
刚体的动能
2、刚体的动能 平移刚体的动能
T
i
1 2
m ivi
2
i
1 2
m iv
2
2 C
1 2
2 m i v C i
1 2
mvC
刚体平移时的动能,相当于将刚体的质量集中于 质心时的动能。
11.2 质点与质点系的动能
刚体的动能
mv
1 2
2 C
2
1 2
J C
2
JC
mR , v C R
2
T
3 4
mvC
11.2 质点与质点系的动能
刚体的动能
例题1 均质细杆长为l,质量为m,上端B靠在光滑的墙上,
下端A用铰与质量为M半径为R且放在粗糙地面上的圆柱中心 相连,在图示位置圆柱作纯滚动,中心速度为v,杆与水平线 的夹角=45o,求该瞬时系统的动能。 I B 解(法1): T总 T A T A B
11.3 动能定理及其应用
2、动能定理的应用举例
11.3 动能定理及其应用
例题2
已知: m ,R, f , 。圆盘初始静止。求纯滚动时盘心的加速度。 解:对象:圆盘 受力:如图 运动:平面运动 s C 方程:取系统为研究对象,假设圆 F vC 盘中心向下产生位移 s时速度达到vc。
2
2
1 2
J C
2
1 2
m (d )
2
因为d· =vC ,于是得
T
1
mv
2 C
1
2 2 平面运动刚体的动能等于随质心平移的动能与绕 质心转动的动能的和。
J C
2
11.2 质点与质点系的动能
刚体的动能
思考题:求均质圆盘在地面上作纯滚动时的 动能。
C
vC
T
1 2
11.1 力的功
理想约束力的功 理想约束:约束力不作功或约束力作功之和等于零的约束。
1、不可伸长的柔性约束也是理想约束。
2、光滑的固定支承面 3、光滑的铰链(轴承、光滑的活动铰链支座、二力杆)
11.1 力的功
4、纯滚动时,摩擦力(约束力)不作功 C* 为瞬时速度中心, 在这一瞬时C*点的速度为 零。作用在C*点的摩擦力 F所作元功为 F
TA 1 Mv 2
2 C
1
2
J C
2
3 4
Mv C
2
I 为AB杆的瞬心
v
v AB IA
v C AB
T AB 1 4 1 2
2
l sin v l v IC l sin 2 2 sin
2
v A
2
C
mv C 1 12
1 2
4 m v
2
11.2 质点与质点系的动能
刚体的动能
解(法2):T
TA 3 4
总
2
T A T AB
I
B C
Mv
I 为AB杆的瞬心 v IA AB
v l sin
JI
T AB 1 2 J I AB
2
v A
2 2
1 12
ml
2
1 1 v 1 2 ml mv 2 3 l sin 45 3
d( mv ) W12 2
2
1
积分形式动能定理为
1 2
mv
2 2
1 2
mv1 W12
2
质点动能的改变量等于作用于质点的力作的功。
11.3 动能定理及其应用
质点系的动能定理
对于质点系:
1
2
d( mv ) δW 2
2
1
d T d ( mi vi ) Fi d ri δ Wi 2
Nanjing University of Technology
理论力学课堂教学软件(11)
理论力学
第三篇 动力学
第三篇 动力学
第11章 动能定理及其应用
第11章 动能定理及其应用
11.1 力的功 11.2 质点与质点系的动能 11.3 动能定理及其应用 11.4 势能的概念 机械能守恒定律及其应用 11.5 动力学普遍定理的综合应用 11.6 结论与讨论
定轴转动刚体的动能
T
i
1 2 1
2
m ivi
2
i
m i ri
2
1 2
m r
2 i i i
2
1 2
J z
2
11.2 质点与质点系的动能
刚体的动能
平面运动刚体的动能
T
J P J C md
1 2
2
J P
2
C
P
T
1 2
( J C md )
第11章 动能定理及其应用
11.1 力的功
11.1 力的功
1、力的功的定义 2、定轴转动刚体上力的功、力偶的功 3、内力的功
11.1 力的功 1、力的功的定义
M1
力Fi的元功
δW Fi d ri Fi dscos Fi ,d ri
Fx dx Fy dy Fz dz
M z (F ) F R
——力F对轴z的矩
刚体由角度1转到角度2时F所作的功为
W12
2
1
M z ( F )d
11.1 力的功
W12
外力偶的功 若力偶矩矢M与z轴平行,则M所作之功为
W12
2
1
M z ( F )d
2
1
M d
若力偶矩矢M为任意矢量,则M所作之功为
重力的功仅与重心的始末位置有关,而与重心走过的路径无 关。 重力的功 对于质点: W12 mg( z1 z 2 ) 对于质点系:
W12 Mg ( z C1 z C 2 )
11.1 力的功
弹性力的功 弹性力的元功
W = F d r = k ( r l 0 ) r0 d r
W12
Mz——力偶矩矢M在z轴上的投影
2
1
M z d
11.1 力的功
扭转弹簧力矩的功 假设扭簧上的杆处于 水平时扭簧未变形,且变 形时在弹性范围之内。变 形时扭簧作用于杆上的力 对点O之矩为
M k
其中k为扭簧的刚度系数。当杆从角度θ1转到角度θ 2时所 作的功为
W12
vO O
C*
FN
WF F drC F v dt 0 C
约束力为无功力的约束称为理想约束
11.1 力的功
总结: 内力不能改变质点系的动量和动量矩,但 它可能改变质点系的能量; 外力能改变质点系的动量和动量矩,但不 一定能改变其能量。
第11章 动能定理及其应用
11.2 质点与质点系的动能
