(完整word版)湖南省高中历年学考数学试题

合集下载

年湖南省普通高中学业水平考试数学试卷及答案,推荐文档

2012 年湖南省普通高中学业水平考试数学试卷一、选择题：本大题共10 小题，每小题4 分，满分40 分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知等差数列{ a n}的前3 项分别为2、4、6，则数列{ a n}的第4 项为A．7 B．8 C．10 D．12 2.如图是一个几何体的三视图，则该几何体为A．球B．圆柱C．圆台D．圆锥正视图俯视图3.函数f (x) = (x -1)(x + 2) 的零点个数是A．0 B．1 C．2 D．3（第 2 题图）4．已知集合A= {-1,0,2} ，B= {x,3}，若A B= {2}，则x 的值为A．3 B．2 C．0 D．-15.已知直线l1：y = 2x +1，l2：y = 2x + 5 ，则直线l1与l2的位置关系是A.重合B．垂直C．相交但不垂直D．平行6.下列坐标对应的点中，落在不等式x +y - 1 < 0 表示的平面区域内的是A．（0，0）B．（2，4）C．（-1，4）D．（1，8）7.某班有50 名同学，将其编为1、2、3、…、50 号，并按编号从小到大平均分成5 组．现用系统抽样方法，从该班抽取5 名同学进行某项调查，若第1 组抽取的学生编号为3，第2 组抽取的学生编号为13，则第4 组抽取的学生编号为A．14 B．23 C．33 D．438.如图，D 为等腰三角形ABC 底边AB 的中点，则下C列等式恒成立的是A．CA ⋅CB = 0 B．CD ⋅AB = 0C．CA ⋅CD = 0 D．CD ⋅CB = 09.将函数y = sin x 的图象向左平移个单位长度，得到3的图象对应的函数解析式为A D B（第8 题图）A.y = sin(x +)B.y = sin(x -3 3))C. y = sin(x + 2 )D. y = sin(x - 23 310. 如图，长方形的面积为 2，将 100 颗豆子随机地撒在长方形内，其中恰好有 60 颗豆子落在阴影部分内，则用随机模拟的方法可以估计图中阴影部分的面积为A. 2 3 C ． 6 5 B ． 45D ． 43（第 10 题图）二、填空题：本大题共 5 小题，每小题 4 分，满分 20 分．11. 比较大小： log 2 5log 2 3 （填“＞”或“＜”）．12．已知圆(x - a )2 + y 2 = 4 的圆心坐标为(3,0) ，则实数 a =．13. 某程序框图如图所示，若输入的a , b , c 值分别为 3，4，5，则输出的 y 值为．14. 已知角的终边与单位圆的交点坐标为（ 1,3 ），2 2则cos = ．15. 如图，A ，B 两点在河的两岸，为了测量 A 、B 之间的距离，测量者在 A 的同侧选定一点 C ，测出 A 、C 之间的距离是 100 米，∠BAC=105º，∠ACB=45º，则 A 、B 两点之间的距离为米．B（第 13 题图）（第 15 题图）三、解答题：本大题共 5 小题，满分 40 分．解答应写出文字说明、证明过程或演算步骤． 16．（本小题满分 6 分）已知函数 y = f (x ) （ x ∈[-2,6]）的图象如图．根据图象写出：（1）函数 y = f (x ) 的最大值；（2）使 f (x ) = 1的 x 值．开始输入 a ,b ,c输出 y 结束y =a +b +c 3河105ºA45ºCy21 -2-1 O -1256x2 B 1D B4 55 6 6 90 0 0 1 1 217．（本小题满分 8 分）一批食品，每袋的标准重量是 50 g ，为了了解这批食品的实际重量情况，从中随机抽取 10 袋食品，称出各袋的重量（单位： g ），并得到其茎叶图（如图）．（1）求这 10 袋食品重量的众数，并估计这批食品实际重量的平均数；（2）若某袋食品的实际重量小于或等于 47 g ，则视为不合格产品，试估计这批食品重量的合格率．（第 17 题图）18．（本小题满分 8 分）如图，在四棱柱 ABCD -A 1B 1C 1D 1 中，D 1D ⊥底面 ABCD ，底面 ABCD 是正方形，且 AB=1，D 1D= ．（1）求直线 D 1B 与平面 ABCD 所成角的大小；（2）求证：AC ⊥平面 BB 1D 1D ．D 1C 1A 1CA（第 18 题图）19．（本小题满分 8 分）已知向量 a =（ sin x ，1），b =（ cos x ，1）， x ∈R ．（1）当 x = 时，求向量 a + b 的坐标；4（2）若函数 f (x ) = |a + b |2 + m 为奇函数，求实数m 的值．20．（本小题满分 10 分）已知数列{ a n }的前n 项和为S n= 2n + a ( a 为常数， n ∈N *)．（1）求a 1 ， a 2 ， a 3 ；（2）若数列{ a n }为等比数列，求常数a 的值及a n ；（3）对于（2）中的a n ，记 f (n ) = ⋅ a 2n +1 - 4⋅ a n +1 - 3 ，若 f (n ) < 0 对任意的正整数n 恒成立，求实数的取值范围．2 2 1 2012 年湖南省普通高中学业水平考试数学试卷参考答案一、选择题（每小题 4 分，满分 40 分）二、填空题（每小题 4 分，满分 20 分）11．＞； 12． 3； 13．4； 14．三、解答题（满分 40 分）1 ； 15．2100 ．16. 解：（1）由图象可知，函数 y = 分f (x ) 的最大值为 2； (3)（2）由图象可知，使 f (x ) = 1的 x 值为-1 或 5． ..................................... 6 分 17．解：（1）这 10 袋食品重量的众数为 50（ g ）， ....................................... 2 分因为这 10 袋食品重量的平均数为45 + 46 + 46 + 49 + 50 + 50 + 50 + 51 + 51 + 52 = 49 （ g ），10所以可以估计这批食品实际重量的平均数为 49（ g ）； .......................... 4 分（2）因为这 10 袋食品中实际重量小于或等于 47 g 的有 3 袋，所以可以估计这批食品重量的不合格率为 3 ，故可以估计这批食品重量的合格率为 7．10 108 分 18．（1）解：因为 D 1D ⊥面 ABCD ，所以 BD 为直线 B D 1 在平面 ABCD 内的射影，所以∠D 1BD 为直线 D 1B 与平面 ABCD 所成的角， ................................... 2 分又因为 AB=1，所以 BD= ，在 Rt △D DB 中， tan ∠D BD = D 1 D= 1，1 BD所以∠D 1BD=45º，所以直线 D 1B 与平面 ABCD 所成的角为 45º； 4 分（2）证明：因为 D 1D ⊥面 ABCD ，AC 在平面 ABCD 内，所以 D 1D ⊥AC ，又底面 ABCD 为正方形，所以 AC ⊥BD ， ............................................... 6 分因为 BD 与 D 1D 是平面 BB 1D 1D 内的两条相交直线，所以 AC ⊥平面 BB 1D 1D ． ........................................................................... 8 分 19．解：（1）因为 a =（ sin x ，1），b =（ cos x ，1）， x = ，4所以 a + b = (sin x + cos x ,2) = ( 2,2) ； ......................................................... 4 分（2）因为 a + b = (sin x + cos x ,2) ，题号 1 2 3 4 5 6 7 8 9 10 答案 B D C B D A CBAC1 n n n -1所以 f (x ) = (sin x + cos x )2 + 4 + m = sin 2x + 5 + m ， ............................... 6 分因为 f (x ) 为奇函数，所以 f (-x ) = - f (x ) ，即sin(-2x ) + 5 + m = -sin 2x - 5 - m ，解得m = -5 ． ............................... 8 分注：由 f (x ) 为奇函数，得 f (0) = 0 ，解得m = -5 同样给分．20．解：（1） a 1 = S 1 = a + 2 ， ........................................................................ 1 分由S 2 = a 1 + a 2 ，得a 2 = 2 ， ......................................................................... 2 分由S 3 = a 1 + a 2 + a 3 ，得a 3 = 4 ； .............................................................. 3 分（2）因为a = a + 2 ，当n ≥ 2 时， a = S - S = 2n -1 ，又{ a n }为等比数列，所以a 1 = 1 ，即a + 2 = 1，得a = -1， ..................... 5 分故a n = 2n -1 ； ............................................................................................... 6 分（3）因为a n = 2n -1 ，所以 f (n ) = ⋅22n - 4⋅2n - 3 ， .................................... 7 分令t = 2n ，则t ≥ 2 ， f (n ) = ⋅ t 2 - 4⋅ t - 3 =(t - 2)2 - 4- 3 ，设 g (t ) = (t - 2)2 - 4- 3 ，当= 0 时， f (n ) = -3 < 0 恒成立，........................................................... 8 分当> 0 时， g (t ) =(t - 2)2 - 4- 3 对应的点在开口向上的抛物线上，所以f (n ) < 0 不可能恒成立， ................................................................................. 9 分当< 0 时， g (t ) = (t - 2)2 - 4- 3 在t ≥ 2 时有最大值- 4- 3 ，所以要使f (n ) < 0- 3< < 0 ， 4对任意的正整数n 恒成立，只需- 4- 3 < 0 ，即> - 3，此时 4综上实数的取值范围为- 3< ≤ 0 ． ..................................................... 10 分4说明：解答题如有其它解法，酌情给分．“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

湖南省长沙市2020届高三12月联考数学(理)试题 Word版含答案

湖南省长沙市2017届高三12月联考数学（理科）本试题卷共6页，23题（含选考题）全卷满分150分，考试用时120分钟第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．（1）设集合{|A x x =≥2}，1{|0}4x B x x -=>-，则A B =（） A ．∅ B ．[2,4)C ．[2,)+∞D ．(4,)+∞（2）已知复数z 满足11zi z-=+，则||z =（） A ．1BC ． 2D．（3）已知数列{}n a 的前n 项和nn S Aq B =+(0)q ≠，则“A B =-”是“数列{}n a 是等比数列”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分且不必要条件（4）在矩形ABCD 中，2AB AD =，在CD 上任取一点P ，ABP ∆的最大边是AB 的概率是（）AB ．C1 D1（5）如图为某几何体的三视图，则该几何体的外接球的表面积为（）正视图侧视图俯视图A BCD PA ．272π B ． 27π C．D（6）若变量,x y 满足约束条件4400y x y x y ≤⎧⎪+-≥⎨⎪-≥⎩，则2z x y =+的最小值是__ __．A ．4B ．6C ．8D ．12（7）已知12,F F 是双曲线2222:1x y E a b-=的左，右焦点，过点1F 且与x 垂直的直线与双曲线左支交于点,M N ，已知2MF N ∆是等腰直角三角形，则双曲线的离心率是（） AB ．2C．1D．2（8）ABC ∆是边长为2的等边三角形，向量a ，b 满足2AB a =，2AC a b =+，则向量a ，b 的夹角为（）A ．30B ．60C ．120D ．150 （9）执行如图所示程序框图，若输出的S 值为20-，则条件框内应填写（） A ．3?i > B ．4?i < C ．4?i > D ．5?i <（10）等差数列{}n a 的前n 和为n S ，且1a ＜0，若存在自然数m ≥3，使得m m a S =，则当n ＞m 时，n S 与n a 的大小关系是（）A ．n S ＜n aB ．n S ≤n aC ．n S ＞n aD ．大小不能确定（11）已知函数()sin()f x x ωϕ=+（0ω>，||2πϕ<）的部分图象如图，则20161()6n n f π==∑（） A ．1- B ．0 C ．12D ．1（12）已知函数21()(0)2x f x x e x =+-<与()()2ln g x x x a =++的图象上存在关于y 轴对称的点，则a 的取值范围是（）A．⎛-∞ ⎝ B．(-∞C．⎛ ⎝ D．⎛ ⎝第II 卷本卷包括必考题和选考题两部分．第（13）～（21）题为必考题，每个试题考生都必须作答．第（22）、（23）题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每小题5分，共20分．（13）已知直线:0l mx y ++=与圆22(1)2x y ++=相交，弦长为2，则m =________．（14）在5(21)(1)x x +-的展开式中含3x 项的系数是___________（用数字作答）．（15）有共同底边的等边三角形ABC 和BCD 所在平面互相垂直，则异面直线AB 和CD 所成角的余弦值为___________．（16）有一支队伍长L 米，以一定的速度匀速前进．排尾的传令兵因传达命令赶赴排头，6π 512π 1-1到达排头后立即返回，且往返速度不变．如果传令兵回到排尾后，整个队伍正好前进了L 米，则传令兵所走的路程为___________．三、解答题：本大题共6小题，共70分，解答应写出必要的文字说明，证明过程或演算步骤．（17）（本小题满分12分）已知,,a b c 分别为ABC ∆三个内角,,A B C的对边，且cos sin 0a C C b c --= （I ）求A ；（II ）若AD 为BC 边上的中线，1cos 7B =，2AD =，求ABC ∆的面积．（18）（本小题满分12分）为响应国家“精准扶贫，产业扶贫”的战略，进一步优化能源消费结构，某市决定在一地处山区的A 县推进光伏发电项目．在该县山区居民中随机抽取50户，统计其年用电量得到以下统计表．以样本的频率作为概率．（I ）在该县山区居民中随机抽取10户，记其中年用电量不超过600度的户数为X ，求X 的数学期望；（II ）已知该县某山区自然村有居民300户．若计划在该村安装总装机容量为300千瓦的光伏发电机组，该机组所发电量除保证该村正常用电外，剩余电量国家电网以0.8元/度进ABD行收购．经测算以每千瓦装机容量年平均发电1000度，试估计该机组每年所发电量除保证正常用电外还能为该村创造直接收益多少元？（19）（本小题满分12分）如图，在四棱锥中P ABCD -，PA ⊥平面ABCD ，//AD BC ，AD CD ⊥，且AD CD ==BC =2PA =．（I ）求证：AB PC ⊥；（II ）在线段PD 上，是否存在一点M ，使得二面角M AC D --的大小为45，如果存在，求BM 与平面MAC 所成的角的正弦值，如果不存在，请说明理由．PBCDMA（20）（本小题满分12分）如图，设点,A B的坐标分别为(0)，0)，直线AP ，BP 相交于点P ，且它们的斜率之积为23-．（I ）求点P 的轨迹方程；（II ）设点P 的轨迹为C ，点M 、N 是轨迹为C 上不同于,A B 的两点，且满足//AP OM ，//BP ON ，求证：MON ∆的面积为定值．（21）（本小题满分12分），函数31()||3f x x x a =+-（x R ∈，a R ∈）．（I ）若函数()f x 在R 上为增函数，求a 的取值范围；（II ）若函数()f x 在R 上不单调时：（i ）记()f x 在[1,1]-上的最大值、最小值分别为()M a 、()m a ，求()()M a m a -；（ii ）设b R ∈，若2|()|3f x b +≤对[1,1]x ∀∈-恒成立，求a b -的取值范围．请考生在第（22）、（23）题中任选一题作答，如果多做，那么按所做的第一个题记分．（22）（本小题满分10分）（选修4-4：坐标系与参数方程）在直角坐标系xoy 中，设倾斜角为α的直线l 的参数方程为3cos sin x t y t αα=+⎧⎨=⎩（t 为参数）与曲线1:cos tan x C y θθ⎧=⎪⎨⎪=⎩（θ为参数）相交于不同的两点A 、B ．（I ）若3πα=，求线段AB 的中点的直角坐标；（II ）若直线l 的斜率为2，且过已知点(3,0)P ，求||||PA PB ⋅的值．（23）（本小题满分10分）（选修4-5：不等式选讲）已知函数()|||3|f x x a x =-+-（3a <）．（I ）若不等式()4f x ≥的解集为1{|2x x ≤或9}2x ≥，求a 的值．（II ）若对x R ∀∈，()|3|1f x x +-≥，求实数a 的取值范围．数学（理科）参考答案1．命题依据：以一元二次、一元一次不等式的解法切入，然后考查集合的交并运算．答案：D ．2．命题依据：考查复数代数形式及其乘法、除法、模运算．答案：A ．1(1)(1)1(1)(1)i i i z i i i i ---===-++-．，故选A ． 3．命题依据：具体情境中识别数列的性质，充分条件与必要条件．答案：B ．若0A B ==，则0n S =，故数列{}n a 不是等比数列；若数列{}n a 是等比数列，则1a A q B =+，22a Aq Aq =-，323a Aq Aq =-，由3221a a a a =，得A B =-．选B ．4．命题依据：几何概型．答案：D ．分别以A 、B 为圆心，AB 为半径作弧，交CD 于1P 、2P ，则当P 在线段12P P 间运动时，能使得ABP ∆的最大边是AB，易得121PP CD=，即ABP ∆的最大边是AB1．5．命题依据：由三视图认识空间几何体的结构特征，球的表面积计算．答案：B ．由三视图可知，该几何体是一个正方体切割成的一个四棱锥，则该几何体的外接球的半径为2，从而计算得表面积为24()272ππ=．故选B ． 6．命题依据：线性规划的应用．答案：B ．作出可行域为开放区域，2z x y =+在直线40x y +-=与直线0x y -=的交点(2,2)处取得最小值6．故选B ．7．命题依据：双曲线的标准方程及简单几何性质，离心率求解．答案：C ．由已知22b c a=，即2220c ac a --=，得2210e e --=，解得1e =故选C ．8．命题依据：平面向量基本定理，向量的数量积运算．答案：C ．易得120． 9．命题依据：算法，程序框图．答案：D ．ABD PCP 1 P 210．命题依据：等差数列的性质，等差数列的单调性答案：C ．若1a ＜0，存在自然数m ≥3，使得m m a S =，则0d >．因为若d ＜0，则数列是递减数列，则m m S a <，不会有m m a S =．由于1a ＜0，0d >，当m ≥3，有m m a S =，则0m a >，0m S >，而1n m m n S S a a +=+++，显然n n S a >．故选C ．11．命题依据：()sin()f x A x ωϕ=+的图象与性质．答案：B ．易得2ω=，由五点法作图可知262ππϕ⨯+=，得6πϕ=．即()sin(2)6f x x π=+．故()16f π=，21()62f π=，31()62f π=-，4()16f π=-，51()62f π=-，61()62f π=，201611111()336(11)062222n n f π==⨯+---+=∑．故选B ． 12．命题依据：函数的零点、方程的根的关系．答案：B ．由题意得即方程()221ln 2x x e x x a -+-=++有正根，即()1ln 2x e x a --=+有正根，作函数12x y e -=-与()ln y x a =+的图象，则可知0x =时，()1ln 2x a +<故a <B ．13．命题依据：直线方程，圆的方程，直线与圆的位置关系．答案：3m =．由已知可得圆心(1,0)-到直线的距离为d =，所以212+=，解得3m =． 14．命题依据：二项式定理的应用．答案：223355(1)2(1)10C C -+-=-．15．命题依据：线线角，面面垂直．答案：14． 16．命题依据：数学应用，数学建模．答案：(1L +．思路一：设传令兵的速度为v '，队伍行进速度为v ，则传令兵从队尾到排头的时间为L v v '-，从排头到队尾的时间为L v v '+，往返共用时间为L Lt v v v v=+''-+，则传令兵往返路程S v t '=．由于传令兵回到排尾后，整个队伍正好前进了L 米，则L vt =．故22()2t v v v L ''-=，可得222()2t v v v tL ''-=．即22()2()0v t L v t L ''--=，解得(1v t L '=+，传令兵所走的路程为(1L ．思路二：设传令兵的速度为v '，队伍行进速度为v ，则传令兵从队尾到排头的时间为L v v '-，从排头到队尾的时间为Lv v '+，则易得 L L Lv v v v v +=''-+，化简得222v v v v ''-=，得1v v'=，由于队伍与传令兵行进时间相等，故传令兵所走路程为(1L +．17．命题依据：三解形中的恒等变换，正、余弦定理．【分析】（I ）利用正弦定理将边的关系化为角的关系，利用三角恒等变换求出B 值．（II ）先根据两角和差的正弦公式求出sin C ，再根据正弦定理得到边长,,a b c 的比值关系，再在ABD ∆或ACD 利用余弦定理可求,b c 的值，再由三角形面积公式可求结果．【解答】（I ）因为cos sin 0a C C b c --= ，由正弦定理得：sin cos sin sin sin A C A C B C +=+，即sin cos sin sin()sin A C A C A C C +=++，……3分cos 1A A -=，所以1sin(30)2A ︒-=．……5分在ABC ∆中，0180A ︒︒<<，所以3030A ︒︒-=，得60A ︒=．……6分（II ）在ABC ∆中，1cos 7B =，得sin B =．……7分则11sin sin()72C A B =+=+=8分由正弦定理得sin 7sin 5a A c C ==．……9分设7a x =，5c x =，在ABD ∆中，由余弦定理得： 2222cos AD AB BD AB BD B =+-⋅，则2212911125492574427x x x x =+⨯-⨯⨯⨯⨯，解得1x =，即7,5a c ==，……11分故1sin 2ABC S ac B ∆==．……12分18．命题依据：统计与概率，离散型随机变量的期望，统计思想的应用．数学抽象与应用意识．解：（I ）记在该县山区居民中随机抽取1户，其年用电量不超过600度为事件A ．由抽样可知， 3()5P A =．……3分由已知可得从该县山区居民中随机抽取10户，记其中年用电量不超过600度的户数为X 服从二项分布，即3~(10,)5X B ，故3()1065E X =⨯=．……6分（II ）设该县山区居民户年均用电量为()E Y ，由抽样可得51510155()1003005007009005005050505050E Y =⨯+⨯+⨯+⨯+⨯=（度）……10分则该自然村年均用电约150000度．又该村所装发电机组年预计发电量为300000度，故该机组每年所发电量除保证正常用电外还能剩余电量约150000度，能为该村创造直接收益120000元．……12分19．命题依据：垂直的判定与证明，空间角的求解，空间向量的应用．【分析】（I ）利用几何图形的特点，将空间问题平面化后，找出垂直关系，进行证明；（II ）假设存在点M ，利用二面角M AC D --的大小为45确定点M 的位置，再利用平面MAC 的法向量求线面角．【解答】（I ）如图，由已知得四边形ABCD 是直角梯形，由已知AD CD ==BC =可得ABC ∆是等腰直角三角形，即AB AC ⊥，又PA ⊥平面ABCD ，则PA AB ⊥，所以AB ⊥平面PAC ，所以AB PC ⊥．……4分（II ）存在．法一：（猜证法）观察图形特点，点M 可能是线段PD 的中点．下面证明当M 是线段PD 的中点时，二面角M AC D --的大小为45．……5分过点M 作MN AD ⊥于N ，则//MN PA ，则MN ⊥平面ABCD ．过点M 作MG AC ⊥于G ，连接NG ，则M G N ∠是二面角M AC D --的平面角．因为M 是线段PD 的中点，则1MN =，A DBCAN =在四边形ABCD 求得1NG =，则45MGN ∠=．……8分在三棱锥M ABC -中，可得13M ABC ABC V S MN -∆=⋅，设点B 到平面MAC 的距离是h ，13B MAC MAC V S h -∆=⋅，则ABC MAC S MN S h ∆∆⋅=⋅，解得h =．……10分在Rt BMN ∆中，可得BM =．设BM 与平面MAC 所成的角为θ，则sin h BM θ==．……12分法二：（作图法）过点M 作MN AD ⊥于N ，则//MN PA ，则MN ⊥平面ABCD ．过点M 作MG AC ⊥于G ，连接NG ，则MGN ∠是二面角M AC D --的平面角．若45MGN ∠=，则NG MN =，又AN ==，易求得1MN =．即M 是线段PD 的中点．……8分（以下同解法一）法三：（向量计算法）建立如图所示空间直角坐标系．则(0,0,0)A，C，(0,D ，(0,0,2)P，B，(0,2)PD =-．设PM tPD =（01t ≤≤），则M的坐标为(0,,22)t -．……6分设(,,)n x y z =是平面AMC 的一个法向量，则00n AC n AM ⎧⋅=⎪⎨⋅=⎪⎩，得0(22)0t z ⎧+=⎪⎨+-=⎪⎩，则可取(1,1,)1n t =--．……8分又(0,0,1)m =是平面ACD 的一个法向量，所以|||||cos ,|cos 45||||m n m n mn ⋅<>===解得12t =．即点M 是线段PD 的中点．……10分此时平面AMC 的一个法向量可取(1,n =-，(BM =-．BM 与平面MAC 所成的角为θ，则sin |cos ,|n BM θ=<>=．……12分20．命题依据：椭圆的方程、轨迹的求解，解析几何中的定值问题，运算能力。

2021年湖南省普通高中学业水平考试数学试题(附解析)

湖南省普通高中学业水平考试数学试题（附解析）一、单选题1．如图示意的几何体是（）A ．圆锥B ．棱锥C ．圆台D ．棱柱2．已知向量()2,1a =，()11b =-,，若(),2a b x +=，则x =（） A ．0 B ．1 C ．2 D ．33．圆C : x 2+y 2= 1的面积是（）A ．4πB ．2πC ．πD ．2π4．盒子里装有大小相同的2个红球和1个白球，从中随机取出1个球，取到白球的概率是（） A ．13 B ．12 C ．23 D ．15．要得到函数y =1+sin x 的图象，只需将函数y =sin x 的图象（）A ．向上平移1个单位长度B ．向下平移1个单位长度C ．向右平移1个单位长度D ．向左平移1个单位长度6．已知数列{a n }满足a 1=1，a n +1=2a n ，则a 4=（）A ．4B ．8C ．16D ．327．已知函数2,0(),0x x f x x x +≤⎧⎪=⎨>⎪⎩，若f (0)=a ，则f (a )=（） A ．4 B ．2 C ．2 D ．08．函数()2sin cos f x x x =的最小正周期是（）A ．2π B ．π C ．2π D ．4π9．用12cm 长的铁丝折成一个面积最大的矩形，则这个矩形的面积是（）A ．3cm 2B ．6cm 2C ．9cm 2D ．12cm 210．已知定义在[3,3]-上的函数y =f (x )的图象如图 .下述四个结论:①函数y =f (x )的值域为[2,2]-②函数y =f (x )的单调递减区间为[1,1]-③函数y =f (x )仅有两个零点④存在实数a 满足()()0f a f a +-=其中所有正确结论的编号是（）A ．①②B ．②③C ．③④D ．②④二、填空题11．已知集合2{|1},{|}A x x B x x a ====，若A B ⊆，则a =______________.12．某班视力近视的学生有15人，视力正常的学生有30人.为了解该班学生近视形成的原因，拟采用分层抽样的方法抽取部分学生，调查相关信息，则抽取的学生中视力近视与视力正常的人数之比为_____________13．已知直线l 1:y =x ，l 2:y =kx .若l 1⊥l 2，则k =______________.14．已知等差数列{a n }满足a 1=1，a 2=2，则{ a n }的前5项和S 5= __________.15．已知角α的终边经过点(3，4)，则cos α=______________.三、解答题16．2020年春季，受疫情的影响，学校推迟了开学时间.上级部门倡导“停课不停学”，鼓励学生在家学习，复课后，某校为了解学生在家学习的周均时长(单位:小时)，随机调查了部分学生，根据他们学习的周均时长，得到如图的频率分布直方图.（1）求该校学生学习的周均时长的众数的估计值;（2）估计该校学生学习的周均时长不少于30小时的概率.17．如图，△ABC中，AB=AC=2，BC=23.（1）求内角B的大小;（2）设函数f(x)=2sin(x+B)，求f(x)的最大值，并指出此时x的值.18．如图，三棱锥P -ABC 中，PA ⊥平面ABC ，AB ⊥AC ，且E ，F 分别为BC ，PC 的中点.（1）求证: EF //平面PAB ;（2）已知AB =AC =4，PA =6，求三棱锥F -AEC 的体积.19．已知函数(())x x f x a g x a -==，，其中0a >，且1a ≠.（1）判断()f x 的奇偶性，并说明理由;（2）若不等式()()f x g x ≥对x ∈R 都成立，求a 的取值范围;（3）设(1)2f =，直线1y t =与()y f x =的图象交于A B ，两点，直线2y t =与()y g x =的图象交于C D ，两点，得到四边形ABCD .证明:存在实数12t t ，，使四边形ABCD 为正方形.2020年湖南省普通高中学业水平考试数学试题（解析）一、单选题1．如图的几何体是（）A ．圆锥B ．棱锥C ．圆台D ．棱柱【答案】D 【详解】由图形可知，该几何体有两个面平行且全等，侧棱平行且相等，故该几何体为棱柱.故选：D.2．已知向量()2,1a =，()11b =-,，若(),2a b x +=，则x =（） A ．0B ．1C ．2D ．3【答案】B 【详解】已知向量()2,1a =，()11b =-,，则()()1,2,2a b x +==，因此，1x =.故选：B. 3．圆C : x 2+y 2= 1的面积是（）A ．4πB ．2πC ．πD ．2π【答案】C【详解】由圆的方程知：圆C 的半径为1，所以面积2S r ππ==，故选：C4．盒子里装有大小相同的2个红球和1个白球，从中随机取出1个球，取到白球的概率是（） A ．13 B ．12 C ．23 D ．1【答案】A【详解】由题意可知盒子里装有大小相同的红球和白球共3 个，其中1个白球，所以从中随机取出1个球，取到白球的概率是13, 故选：A5．要得到函数y =1+sin x 的图象，只需将函数y =sin x 的图象（）A ．向上平移1个单位长度B ．向下平移1个单位长度C ．向右平移1个单位长度D ．向左平移1个单位长度【答案】A 【详解】根据“左加右减，上加下减”的原则，将函数y =sin x 的图象向上平移1个单位可得y =1+sin x 的图象，故选：A.6．已知数列{a n }满足a 1=1，a n +1=2a n ，则a 4=（）A ．4B ．8C ．16D ．32 【答案】B【详解】由题意a n +1=2a n 可知，数列{a n }是首项为1，公比为2的等比数列，故可得数列的通项公式为12n n a ，∴3428a ==，故选：B.7．已知函数2,0(),0x x f x x x +≤⎧⎪=⎨>⎪⎩，若f (0)=a ，则f (a )=（） A ．4B ．2C ．2D ．0 【答案】C【详解】因为f (0)=a ，代入分段函数中可得02a +=，得2a =，所以()(2)2f a f ==，故选：C 8．函数()2sin cos f x x x =的最小正周期是（）A ．2πB ．πC ．2πD ．4π【答案】B【详解】()2sin cos sin 2f x x x x ==，所以，函数()f x 的最小正周期为22T ππ==. 故选：B.9．用12cm 长的铁丝折成一个面积最大的矩形，则这个矩形的面积是（）A ．3cm 2B ．6cm 2C ．9cm 2D ．12cm 2 【答案】C【详解】设矩形的长、宽分别为,x y cm ，则有2()12x y +=，即6x y +=，∵矩形的面积S xy =， ∴2()94x y S xy +=≤= cm 2，当且仅当3x y ==时等号成立，故选：C10．已知定义在[3,3]-上的函数y =f (x )的图象如图 .下述四个结论:①函数y =f (x )的值域为[2,2]-②函数y =f (x )的单调递减区间为[1,1]-③函数y =f (x )仅有两个零点④存在实数a 满足()()0f a f a +-=其中所有正确结论的编号是（）A ．①②B ．②③C ．③④D ．②④【答案】D【详解】由图像可知函数的最大值大于2，最小值小于2-，所以①错误；由图像可知函数y =f (x )的单调递减区间为[1,1]-，所以②正确；由图像可知其图像与x 轴交点的个数为3，所以函数有3个零点，所以③错误；当1a =时，有()()(1)(1)220f a f a f f +-=+-=-+=，所以④正确，故选：D二、填空题11．已知集合2{|1},{|}A x x B x x a ====，若A B ⊆，则a =______________.【答案】1【详解】由题意，集合2{|1},{|}A x x B x x a ====，因为A B ⊆，所以1B ∈，即1是方程2x a =是方程的根，解得1a =，当1a =，可得集合{}1,1b =-,此时满足A B ⊆，所以1a =.故答案为：1.12．某班视力近视的学生有15人，视力正常的学生有30人.为了解该班学生近视形成的原因，拟采用分层抽样的方法抽取部分学生，调查相关信息，则抽取的学生中视力近视与视力正常的人数之比为_____________ 【答案】12【详解】因为某班视力近视的学生有15人，视力正常的学生有30人，所以用分层抽样的方法抽取部分学生中，视力近视与视力正常的人数之比为151302=，故答案为：1213．已知直线l 1:y =x ，l 2:y =kx .若l 1⊥l 2，则k =______________.【答案】-1【详解】由l 1⊥l 2，知：1k =-，故答案为：-1.14．已知等差数列{a n }满足a 1=1，a 2=2，则{ a n }的前5项和S 5= __________.【答案】15.【详解】由等差数列{a n }满足a 1=1，a 2=2，知：公差1d =，∴{a n }是首项为1，公差为1的等差数列，故通项公式为1(1)n a a n d n =+-=，∴由等差数列前n 项和公式1()(1)22n n n a a n n S ++==，即可得55(51)152S ⨯+==，故答案为：15.15．已知角α的终边经过点(3，4)，则cos α=______________. 【答案】35【详解】因为角α的终边经过点(3，4)，所以2233cos 534x r α===+，故答案：35三、解答题16．2020年春季，受疫情的影响，学校推迟了开学时间.上级部门倡导“停课不停学”，鼓励学生在家学习，复课后，某校为了解学生在家学习的周均时长(单位:小时)，随机调查了部分学生，根据他们学习的周均时长，得到如图的频率分布直方图.（1）求该校学生学习的周均时长的众数的估计值;（2）估计该校学生学习的周均时长不少于30小时的概率.【详解】（1）根据直方图知：频率最大的区间中点横坐标即为众数，∴由频率最大区间为[20,30)，则众数为2030252+=；（2）由图知：不少于30小时的区间有[30,40)、[40,50)，∴该校学生学习的周均时长不少于30小时的概率0.03100.3P=⨯=. 17．如图，△ABC中，AB=AC=2，BC=23.（1）求内角B的大小;（2）设函数f(x)=2sin(x+B)，求f(x)的最大值，并指出此时x的值.【详解】解：（1）因为△ABC中，AB=AC=2，BC=23.所以2222222(23)23cos 222223AB BC AC B AB BC +-+-===⋅⨯⨯，因为(0,)B π∈，所以6B π=，（2）由（1）可知()2sin()6f x x π=+，所以当2,62x k k Z πππ+=+∈时，()f x 取最大值2，即2,3x k k Z ππ=+∈18．如图，三棱锥P -ABC 中，PA ⊥平面ABC ，AB ⊥AC ，且E ，F 分别为BC ，PC 的中点.（1）求证: EF //平面PAB ;（2）已知AB =AC =4，PA =6，求三棱锥F -AEC 的体积.【详解】（1）连接EF ，在△PBC 中EF 为中位线，故//EF PB ，∵EF ⊄面PAB ，PB ⊂面PAB∴//EF 面PAB ；（2）过F 作//FG PA 交AC 于G ，如下图示：∵P A ⊥平面ABC ，∴FG ⊥平面ABC ，即FG 是三棱锥F -AEC 的高，又F 为PC 的中点， ∴由P A =6，则32PA FG ==，又AB =AC =4，E 为BC 的中点且AB ⊥AC ，知：44424ABC AEC S S⨯===， ∴三棱锥F -AEC 的体积143AEC V FG S =⋅⋅=. 19．已知函数(())x x f x a g x a -==，，其中0a >，且1a ≠.（1）判断()f x 的奇偶性，并说明理由;（2）若不等式()()f x g x ≥对x ∈R 都成立，求a 的取值范围; （3）设(1)2f =，直线1y t =与()y f x =的图象交于A B ，两点，直线2y t =与()y g x =的图象交于C D ，两点，得到四边形ABCD .证明:存在实数12t t ，，使四边形ABCD 为正方形.【详解】 (1) ()f x 是偶函数 ()x f x a =，))((x x f x aa f x -∴==-=,()f x ∴是偶函数（2）))((x x f x a g a x -==，(())x x x f x g a a -≥⇔≥∴ 当1a >时0x x x x R ≥-⇒≥⇒∈ 满足题意，当01a <<时00x x x x ≥-⇒≤⇒= 不满足题意所以1a >（3）(1)2,2f a =∴= ()22()x x f x g x -∴==，因为四边形ABCD 为正方形，所以AB BC = ,设01(,)B x t 则02(,)C x t 0122x t t ∴=- ，又00122,2,x x t t -==02122log log x t t ∴==-212212log log 01t t t t ∴+=⇒=故存在实数12t t ，当121t t =使得四边形ABCD 为正方形.。

2020年6月普通高中学业水平合格性考试数学试题 Word版含答案

2020年6月福建省普通高中学业水平合格性考试数学试题(考试时间:90分钟;满分:100分)参考公式：样本数据x1，x2，…，x 。

的标准差s =√1n [(x 1−x ̅)2+(x 2−x ̅)2+⋯+(x n −x ̅)2] ,其中x ̅为样本平均数锥体体积公式V=13Sh ，其中S 为底面面积，h 为高球的表面积公式S=4πR 2,球的体积公式V=43πR 3,其中R 为球的半径柱体体积公式V=Sh ，其中S 为底面面积，h 为高台体体积公式V =13(S ′+√S ′S +S)h ，其中S ＇，S 分别为上、下底面面积，h 为高第Ⅰ卷 (选择题45)一、选择题(本大题有15小题，每小题3分，共45分.每小题只有一个选项符合题意)1.已知集合A=｛3｝，B=｛1，2，3｝，则A ∩B=A.{1,2,3}B.{1,3}C.{3}D. φ2.右图是某圆锥的三视图，则该圆锥底面圆的半径长是A.1B.2C.3D. √103.若三个数1，3，a 成等比数列，则实数a=A.1B.3C.5D.94.一组数据3，4，4，4，5，6的众数为A.3B.4C.5D.65.如图，在正方形上随机撒一粒黄豆，则它落到阴影部分的概率为A. 14B. 12C. 34 D.1 6.函数y=cosx 的最小正周期为A. π2B. πC. 3π2D. 2π 7.函数y= 1X−2的定义域为A.(-∞，2)B.(2，+∞)C.(-∞，2)U(2，+∞)D. R8.不等式2x+y-4≤0表示的平面区域是9.已知直线l 1:y =x-2，l 2:y=kx ，若l 1∥l 2，则实数k=A.-2B.-1C.0D.110.化简MN ⃗⃗⃗⃗⃗⃗⃗ + MP ⃗⃗⃗⃗⃗⃗ +QP ⃗⃗⃗⃗⃗ =A. MP ⃗⃗⃗⃗⃗⃗B. NQ ⃗⃗⃗⃗⃗⃗C. MQ ⃗⃗⃗⃗⃗⃗D. PM ⃗⃗⃗⃗⃗⃗10.不等式(x+2)(x-3)＜0的解集是A.｛x | x ＜-2，或x ＞3｝B. {x |-2<x<3｝C.｛−12 < x < 13｝D. ｛x|x <−12，或x ＞1312.化简tan(π+α)=A. sinαB.cos αC. –sinαD.tanα13.下列函数中，在(0，+∞)上单调递减的是A. y=x-3B.y= 2xC.y=x 2D.y=2x14.已知a=40.5，b=42，c=log 40.5，则a ，b ，c 的大小关系是Aa < b<c B .c<b<a Cc<a < b D a<c< b15.函数y={1, |x|＜2，log2|x|,|x|≥2的图象大致为第Ⅱ卷(非选择题55分)二、填空题(本大题有5小题，每小题3分，共15分)16.已知向量a=(0，2)，则2a= 。

(完整word版)高中数学新定义类型题

同步练习学校:___________姓名：___________班级：___________考号：___________第I 卷（选择题）一、选择题（本题共22道小题，每小题5分，共110分）1.定义,max{,},a a b a b b a b ≥⎧=⎨<⎩，设实数,x y 满足约束条件22x y ⎧≤⎪⎨≤⎪⎩，则max{4,3}z x y x y =+-的取值范围是（）（A ）[8,10]- （B ） [7,10]-（C ）[6,8]- （D ）2.对于复数a,b,c,d ,若集合{}S=a,b,c,d 具有性质“对任意x,y S ∈,必有xy S ∈”,则当22a=1b =1c =b ⎧⎪⎨⎪⎩时,b+c+d 等于 ( ) A 、1 B 、-1 C 、0 D 、i 3.在实数集R 中定义一种运算“*”，R b a ∈∀,，a b *为唯一确定的实数，且具有性质：（1）对任意R a ∈，0a a *=；（2）对任意,R a b ∈，(0)(0)a b ab a b *=+*+*．关于函数1()()x x f x e e=*的性质，有如下说法：①函数)(x f 的最小值为3；②函数)(x f 为偶函数；③函数)(x f 的单调递增区间为(,0]-∞．其中正确说法的序号为（） A ．①B ．①②C ．①②③D ．②③4.设A 是整数集的一个非空子集，对于k ∈A ，如果k －1∉A 且k ＋1∉A ，那么称k 是集合A 的一个“好元素”．给定集合S ＝{1,2,3,4,5,6,7,8}，由S 的3个元素构成的所有集合中，不含“好元素”的集合共有（）A ．2个B ．4个C ．6个D ．8个 5.对于集合∈+==k k x x S ，12{N }和集合}{S b a b a x x T ∈⊕==，，，若满足S T ⊆，则集合T 中的运算“⊕”可以是A ．加法B ．减法C ．乘法D ．除法 6.设函数)(x f 的定义域为R ，如果存在函数()(g x ax a =为常数），使得)()(x g x f ≥对于一切实数x 都成立，那么称)(x g 为函数)(x f 的一个承托函数. 已知对于任意(0,1)k ∈，()g x ax =是函数()e x kf x =的一个承托函数，记实数a 的取值范围为集合M ，则有（）A. 1e ,e M M -∉∉B. 1e ,e M M -∉∈C.1e ,e M M -∈∉ D.1e ,e M M -∈∈ 7.用C (A )表示非空集合A 中的元素个数，定义⎩⎨⎧<-≥-=-)()(),()()()(),()(||B C A C A C B C B C A C B C A C B A . 若}2,1{=A ，2{|23|}B x x x a =+-=，且|A-B|=1，由a 的所有可能值构成的集合为S ，那么C (S )等于( )A ．1B ．2C ．3D ．48.对于集合M 、N ，定义M －N ＝{x |x ∈M 且x ∉N }，M ⊕N ＝(M －N )∪(N －M )，设A ＝{y |y ＝3x ， x ∈R}，B ＝{y |y ＝－122++x x ，x ∈R}，则A ⊕B 等于( )A ．[0,2)B ．(0,2]C ．(－∞，0]∪(2，＋∞)D ．(－∞，0)∪[2，＋∞)9.在实数集R 中定义一种运算“*”，R b a ∈∀,，a b *为唯一确定的实数，且具有性质：（1）对任意R a ∈，0a a *=；（2）对任意,R a b ∈，(0)(0)a b ab a b *=+*+*．的性质，有如下说法：①函数)(x f 的最小值为3；②函数)(x f 为偶函数；③函数)(x f 的单调递增区间为(,0]-∞．其中所有正确说法的个数为( ) A ．0B．1C ．2．310.给出定义:（其中m 则m 叫做与实数x “亲密的整数”, 记作{}x m =,数()y f x =在(0,1)x ∈上是增函数;②函数()y f x =的图象关于直线称;③函数()y f x =是周期函数,最小正周期为1;④当(0,2]x ∈时，函数()()ln g x f x x =-有两个零点. 其中正确命题的序号是____________.A ．②③④B ．①③C ．①②D ．②④ 11.定义运算a b ad bc c d=-，若函数()123x f x xx -=-+在(,)m -∞上单调递减，则实数m 的取值范围是A ．(2,)-+∞B ．[2,)-+∞C ．(,2)-∞-D ． (,2]-∞-12.对于函数()f x ，若,,a b c R ∀∈，()()(),,f a f b f c 为某一三角形的三边长，则称()f x 为“可构造三角形函数”，已知函数()1x xe tf x e +=+是“可构造三角形函数”，则实数t 的取值范围是A ．[)0,+∞B ．[]0,1C ．[]1,2D ．1[,2]213.对于集合A ，如果定义了一种运算“⊕”，使得集合A 中的元素间满足下列4个条件：（ⅰ）,a b A ∀∈，都有a b A ⊕∈；（ⅱ）e A ∃∈，使得对a A ∀∈，都有e a a e a ⊕=⊕=；（ⅲ）a A ∀∈，a A '∃∈，使得a a a a e ''⊕=⊕=；（ⅳ）,,a b c A ∀∈，都有()()a b c a b c ⊕⊕=⊕⊕，则称集合A 对于运算“⊕”构成“对称集”．下面给出三个集合及相应的运算“⊕”： ①{}A =整数，运算“⊕”为普通加法；②{}A =复数，运算“⊕”为普通减法；③{}A =正实数，运算“⊕”为普通乘法．其中可以构成“对称集”的有( ) A ①②B ①③C ②③D ①②③14.设()f x 与()g x 是定义在同一区间[a ，b]上的两个函数，若函数()()y f x g x =-在[,]x a b ∈上有两个不同的零点，则称()f x 和()g x 在[,]a b 上是“关联函数”，区间[,]a b 称为“关联区间”．若2()34f x x x =-+与()2g x x m =+在[0,3]上是“关联函数”，则m 的取值范围是( )A. 9,24⎛⎤-- ⎥⎝⎦ B ．[－1,0] C ．(－∞，－2] D. 9,4⎛⎫--∞ ⎪⎝⎭ 15.设函数()f x 的定义域为D，如果对于任意的1x D ∈，存在唯一的2x D ∈，使得12()()2f x f x C+= 成立（其中C 为常数），则称函数()y f x =在D 上的均值为C ，现在给出下列4个函数： ①3y x = ②4sin y x = ③lg y x = ④2x y = ，则在其定义域上的均值为 2的所有函数是下面的（）A. ①②B. ③④C. ①③④D. ①③16.对任意实数,a b 定义运算""*如下()()a ab a b b a b ≤⎧⎪*=⎨>⎪⎩，则函数x x x f 221log )23(log )(*-=的值域为（）A. [)0,+∞B. (],0-∞C. ⎥⎦⎤ ⎝⎛0,32log 2D. 22log ,3⎛⎫+∞ ⎪⎝⎭ 17.设B A ,是非空集合，定义},|{B A x B A x x B A ⋂∉⋃∈=⨯且，已知}20|{≤≤=x x A ，}0|{≥=x x B ，则B A ⨯等于（）.A ),2(+∞ .B ),2[]1,0[+∞⋃ .C ),2()1,0[+∞⋃ .D ),2(]1,0[+∞⋃18.设集合A ⊆R ，如果x 0∈R 满足：对任意a ＞0，都存在x ∈A ，使得0＜|x ﹣x 0|＜a ，那么称x 0为集合A 的一个聚点．则在下列集合中：（1）Z +∪Z ﹣；（2）R +∪R ﹣；（3）{x|x=，n ∈N *}；（4）{x|x=，n ∈N *}．其中以0为聚点的集合有（） A ． 1个B ． 2个C ． 3个D ．4个19.若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，例如解析式为y ＝2x 2＋1，值域为{9}的“孪生函数”三个：（1）y ＝2x 2＋1，}2{-∈x ；（2）y ＝2x 2＋1，}2{∈x ；（3）y ＝2x 2＋1，}2,2{-∈x 。

湖南省普通高中学业水平考试数学试题(Word版)

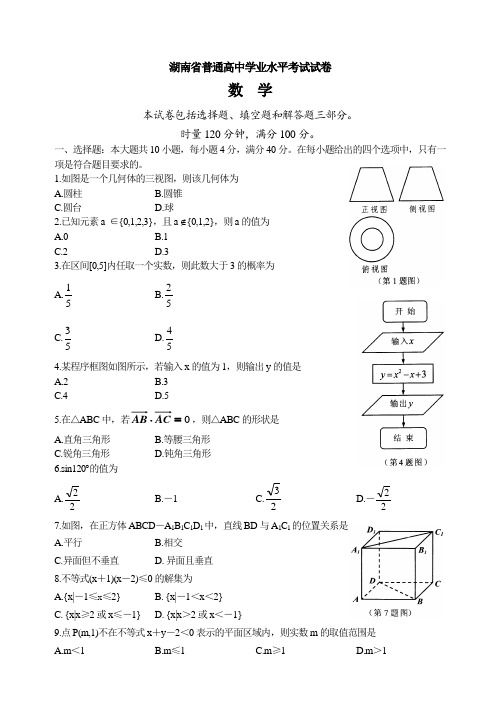
机密★启用前湖南省普通高中学业水平考试数学本试题卷包括选择题、填空题和解答题三部分，时量120分钟满分100分一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的1．下列几何体中为圆柱的是2．执行如图1所示的程序框图，若输入x 的值为10，则输出y 的值为 A ．10 B ．15 C ．25 D ．353．从1，2，3，4，5这五个数中任取一个数，则取到的数为偶数的概率是A ．45 B ．35 C ．25 D ．154．如图2所示，在平行四边形ABCD 中中，AB AD +=u u u r u u u rA ．AC uuu rB ．CA u u u rC ．BD u u u r D ．DB u u u r5．已知函数y ＝f （x ）（[1,5]x ∈-）的图象如图3所示，则f （x ）的单调递减区间为 A ．[1,1]- B ．[1,3] C ．[3,5] D ．[1,5]- 6．已知a ＞b ，c ＞d ，则下列不等式恒成立的是 A ．a +c ＞b ＋d B ．a +d >b +c C ．a -c >b -d D ．a -b >c-d 7．为了得到函数cos()4y x π=+的图象象只需将cos y x =的图象向左平移A ．12个单位长度 B ．2π个单位长度C ．14个单位长度 D ．4π个单位长度 8．函数(1)2()log x f x -=的零点为A ．4B ．3C ．2D ．1 9．在△ABC 中，已知A ＝30°，B ＝45°，AC，则BC ＝A ．12BCD ．110．过点M （2，1）作圆C ：22(1)2x y -+=的切线，则切线条数为A ．0B ．1C ．2D ．3 二、填空题；本大题共5小题，每小题4分，共20分， 11．直线3y x =+在y 轴上的截距为_____________。

【精选高中试题】高中数学黄金100题系列——专题05 函数定义域(解析版) Word版(含解析)

I ．题源探究·黄金母题例1 求函数)34(log )(5.0-=x x f 的定义域. 【解析】要使式子有意义，则0)34(log 5.0≥-x ，即1log 0)34(log 5.05.0=≥-x ，根据对数函数的单调性，则1340≤-<x ，解得143≤<x ，所以函数)(x f 的定义域为]1,43(.II ．考场精彩·真题回放【例2】【2016高考江苏卷】函数y义域是 ▲ . 【答案】[]3,1-【解析】要使函数有意义，必须2320x x --≥，即2230x x +-≤，31x ∴-≤≤．故答案应填：[]3,1-，【例3】【2016高考新课标2文数】下列函数中，其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是（）（A ）y =x （B ）y =lg x （C ）y =2x （D）y =【答案】D 【解析】lg 10xy x ==，定义域与值域均为()0,+∞，只有D 满足，故选D ．精彩解读【试题来源】人教版A 版必修一第74页习题2.2 A 组第7题【母题评析】本题以求函数定义域为载体，考查根式的概念及利用对数函数的性质解简单对数不等式.本类考查方式是近几年高考试题常常采用的命题形式，达到一箭双雕的目的.【思路方法】由函数式有意义得到关于自变量的不等式，利用有关函数的性质或不等式性质，解出自变量的取值范围，即为函数的定义域.【命题意图】本类题通常主要考查函数定义域的求法.【考试方向】这类试题在考查题型上，通常基本以选择题或填空题的形式出现，难度较小，往往与特殊函数的图像与性质、值域、解不等式、集合运算有联系. 【难点中心】对求函数定义域问题，首项要确定使函数式子有意义的条件，列出关于自变量的不等式（组），其次利用有关不等式性质和相关函数的性质解不等式（组），注意：①函数解析式含有几个式子，这几个式子都必须有意义，其交集即为函数的定义域；②解不等式时要等价变形；③抽象函数的定义域是难点.本题是简单函数定义域的求法，是基础题.III ．理论基础·解题原理考点一函数定义域的概念1．在函数y ＝f (x )，x ∈A 中，x 叫做自变量，x 的取值范围A 叫做函数的定义域；考点二常见函数的定义域1.一次函数b kx y +=的定义域为R ；2.二次函数c bx ax y ++=2的定义域为R ； 3.指数函数x a y =（0>a 且1≠a ）定义域为R ；4.对数函数x y a log =（0>a 且1≠a ）的定义域为),0(+∞；（1）当Z m ∈，n 为奇数且0>mn 时，定义域为R ；（2）当m 为奇数n 为偶数且0>mn 时，定义域为),0[+∞；（3)当*Z m ∈，n 为奇数且0<mn 时，定义域为),0()0,(+∞⋃-∞；（4）当m 是奇数，n 为偶数且0<mn 时，定义域为),0(+∞； 6.正弦函数x y sin =、余弦函数x y cos =定义域都为R ；考点三函数定义域的求法 1.已知函数解析式，求定义域紧扣“函数定义域是函数自变量的取值范围”这一概念。

湖南省常德市2018届高三上学期检测考试(期末)数学(文)试题Word版含答案

湖南省常德市2018届高三上学期检测考试(期末)数学(文)试题Word版含答案常德市2017-2018学年度上学期高三数学（文科）检测考试第Ⅰ卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项符合题目要求。

1.已知集合$A=\{1,2,3\},B=\{2,3,4,5\}$，则$A\cap B$中元素的个数为（）。

A．2.B．3.C．4.D．5.2.在复平面内，复数$z=1+2i$（$i$为虚数单位）对应的点所在的象限为（）。

A．第一象限。

B．第二象限。

C．第三象限。

D．第四象限。

3.在某学校图书馆的书架上随意放着有编号为1,2,3,4,5的五本史书，若某同学从中任意选出两本史书，则选出的两本史书编号相连的概率为（）。

A．$\frac{1}{10}$。

B．$\frac{1}{5}$。

C．$\frac{2}{5}$。

D．$\frac{1}{2}$。

4.元朝著名数学家XXX《四元玉鉴》中有一首诗：“我有一壶酒，携着XXX走，遇店添一倍，逢友饮一斗，店友经三处，没了壶中酒，借问此壶中，当原多少酒？”其意思为：“诗人带着装有一倍分酒的壶去春游，先遇到酒店就将酒添加一倍，后遇到朋友饮酒一斗，如此三次先后遇到酒店和朋友，壶中酒恰好饮完，问壶中原有多少酒？”用程序框图表达如图所示，即最终输出的$x=$，那么在这个空白框中可以填入（）。

A．$x=x-1$。

B．$x=2x-1$。

C．$x=2x$。

D．$x=2x+1$。

5.已知向量$a=(x,y),b=(1,2),c=(-1,1)$，若满足$a\parallel b,b\perp(a-c)$，则向量$a$的坐标为（）。

A．$(\frac{5}{11},\frac{5}{11})$。

B．$(-\frac{5}{11},-\frac{5}{11})$。

C．$(\frac{6}{11},\frac{3}{11})$。

D．$(\frac{5}{11},\frac{6}{11})$。

(完整版)湖南省普通高中学业水平考试数学试卷

湖南省普通高中学业水平考试试卷数学本试卷包括选择题、填空题和解答题三部分。

时量120分钟，满分100分。

一、选择题：本大题共10小题，每小题4分，满分40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.如图是一个几何体的三视图，则该几何体为A.圆柱B.圆锥C.圆台D.球2.已知元素a ∈{0,1,2,3}，且a ∉{0,1,2}，则a 的值为A.0B.1C.2D.33.在区间[0,5]内任取一个实数，则此数大于3的概率为 A.51 B.52 C.53 D.54 4.某程序框图如图所示，若输入x 的值为1，则输出y 的值是A.2B.3C.4D.55.在△ABC 中，若0=⋅AC AB ，则△ABC 的形状是A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形 6.sin120︒的值为A.22B.－1C.23D.－22 7.如图，在正方体ABCD －A 1B 1C 1D 1中，直线BD 与A 1C 1的位置关系是A.平行B.相交C.异面但不垂直D. 异面且垂直 8.不等式(x ＋1)(x －2)≤0的解集为 A.{x|－1≤x ≤2} B. {x|－1＜x ＜2}C. {x|x ≥2或x ≤－1}D. {x|x ＞2或x ＜－1} 9.点P(m,1)不在不等式x ＋y －2＜0表示的平面区域内，则实数m 的取值范围是10.某同学从家里骑车一路匀速行驶到学校，只是在途中遇到一次交通堵塞，耽搁了一些时间，下列函数的图像最能符合上述情况的是二、填空题：本大题共5小题，每小题4分，满分20分。

11.样本数据－2，0，6，3，6的众数是＿＿＿＿＿＿。

12.在△ABC 中，角A 、B 、C 所对应的边分别为a 、b 、c ，已知a ＝1，b ＝2，sinA ＝31，则sinB ＝＿＿＿＿＿＿。

13.已知a 是函数f(x)＝2－log 2x 的零点，则实数a 的值为＿＿＿＿＿＿。

14.已知函数y ＝sin ωx(ω＞0)在一个周期内的图像如图所示，则ω的值为＿＿＿＿＿＿。

2006年湖南省高考数学试卷(文科)【附答案、word版本,可再编辑;B4纸型两栏】

2006年湖南省高考数学试卷（文科）一、选择题（共10小题，每小题5分，满分50分） 1. 函数y =√2x 的定义域是（） A.(0, 1]B.(0, +∞)C.[1, +∞)D.(1, +∞)2. 已知向量a →=(2,t)，b →=(1,2)，若t =t 1时，a → // b →；t =t 2时，a →⊥b →，则（） A.t 1=−4，t 2=−1 B.t 1=−4，t 2=1 C.t 1=4，t 2=−1D.t 1=4，t 2=13. 若(ax −1)5的展开式中x 3的系数是80，则实数a 的值是（） A.−2B.2√2C.√43D.24. 过半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是60∘则该截面的面积是（） A.πB.2πC.2√3πD.3π5. “a ＝1”是“函数f(x)＝|x −a|在区间[1, +∞)上为增函数”的（） A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件6. 在数字1，2，3与符号+，-五个元素的所有全排列中，任意两个数字都不相邻的全排列个数是（） A.6B.12C.24D.187. 圆x 2+y 2−4x −4y −10=0上的点到直线x +y −14=0的最大距离与最小距离的差是( ) A.36B.18C.5√2D.6√28. 设点P 是函数f(x)=sin ωx 的图象C 的一个对称中心，若点P 到图象C 的对称轴上的距离的最小值π4，则f(x)的最小正周期是（） A.2πB.πC.π4D.π29. 过双曲线M:x 2−y 2b 2=1的左顶点A 作斜率为1的直线l ，若l 与双曲线M 的两条渐近线分别相交于点B ，C ，且|AB|=|BC|，则双曲线M 的离心率是（） A.√10B.√5C.√103D.√5210. 如图，OM // AB ，点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内（不含边界）．且OP →=xOA →+yOB →，则实数对(x, y)可以是（）A.(14，34)B.(−23，23)C.(−14，34)D.(−15，75)二、填空题（共5小题，每小题4分，满分20分）11. 若数列{a n }满足：a 1=1，a n+1=2a n ．n =1，2，3…．则a 1+a 2+...+a n =________．12. 某高校有甲、乙两个数学建模兴趣班．其中甲班有40人，乙班50人．现分析两个班的一次考试成绩，算得甲班的平均成绩是90分，乙班的平均成绩是81分，则该校数学建模兴趣班的平均成绩是________分．13. 已知{x ≥1x −y +1≤02x −y −2≤0，则x 2+y 2的最小值是________．14. 过三棱柱ABC −A 1B 1C 1的任意两条棱的中点作直线，其中与平面ABB 1A 1平行的直线共有________条．15. 若f(x)=a sin (x +π4)+3sin (x −π4)是偶函数，则a =________．三、解答题（共6小题，满分80分） 16. 已知√3sin θ−sin (π2−2θ)cos (π+θ)⋅cos θ=1，θ∈(0, π)，求θ的值．17. 某安全生产监督部门对5家小型煤矿进行安全检查（简称安检）．若安检不合格，则必须进行整改．若整改后经复查仍不合格，则强行关闭．设每家煤矿安检是否合格是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率是0.8，计算（结果精确到0.01）：（1）恰好有两家煤矿必须整改的概率；（2）平均有多少家煤矿必须整改；（3）至少关闭一家煤矿的概率．18. 如图，已知两个正四棱锥P−ABCD与Q−ABCD的高分别为1和2，AB=4．（1）证明PQ⊥平面ABCD；（2）求异面直线AQ与PB所成的角；（3）求点P到平面QAD的距离．19. 已知函数f(x)=ax3−3x2+1−3a．（1）讨论函数f(x)的单调性；（2）若曲线y=f(x)上两点A、B处的切线都与y轴垂直，且线段AB与x轴有公共点，求实数a的取值范围．。

(完整word)湖南省高中历年学考数学试题

湖南省2009年普通高中学业水平考试数学一、选择题1. 已知集合A={-1，0，1，2}，B={-2，1，2}则A I B=（）A{1} B.{2} C.{1，2} D.{-2，0，1，2} 2.若运行右图的程序，则输出的结果是（） A.4， B. 9 C. 13 D.223.将一枚质地均匀的子抛掷一次，出现“正面向上的点数为6”的概率是（） A.31 B.41 C.51 D.61 4.4cos4sinππ的值为（）A.21B.22C.42D.25.已知直线l 过点（0，7），且与直线y=-4x+2平行，则直线l 的方程为（） A.y=-4x-7 B.y=4x-7 C.y=-4x+7 D.y=4x+76.已知向量),1,(),2,1(-==x b a 若b a ⊥，则实数x 的值为（） A.-2 B.2 C.-1 D.17.已知函数f(x)的图像是连续不断的，且有如下对应值表： x 1 2 3 4 5 f(x)-4-2147在下列区间中，函数f(x)必有零点的区间为（） A.（1，2） B.（2，3） C.(3,4) D. (4,5)8.已知直线l ：y=x+1和圆C ：x 2+y 2=1,则直线l 和圆C 的位置关系为（） A.相交 B.相切 C.相离 D.不能确定 9.下列函数中，在区间（0，+∞）上为增函数的是（） A.xy )31(= B.y=log 3x C.xy 1=D.y=cosx 10.已知实数x,y 满足约束条件⎪⎩⎪⎨⎧≥≥≤+,0,0,1y x y x 则z=y-x 的最大值为（）A=9 A=A+13 PRINT A ENDA.1B.0C.-1D.-2 二、填空题11.已知函数f(x)=⎩⎨⎧<+≥-),0(1)0(2x x x x x 则f(2)=___________.12.把二进制数101（2）化成十进制数为____________.13.在△ABC 中，角A 、B 的对边分别为a,b,A=600,a=3,B=300,则b=__________. 14.如图是一个几何体的三视图，该几何体的体积为_________.15.如图，在△ABC 中，M 是BC 的中点，若,AM AC AB λ=+则实数λ=________.三、解答题16.已知函数f(x)=2sin(x-3π), (1)写出函数f(x)的周期；（2）将函数f(x)图像上所有的点向左平移3π个单位，得到函数g(x)的图像，写出函数g(x)的表达式，并判断函数g(x)的奇偶性.2 223 3BMC17.某市为了节约生活用水，计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准，有关部门抽样调查了100位居民.右表是这100位居民月均用水量（单位：吨）的频率分布表，根据右表解答下列问题：（1）求右表中a 和b 的值；（2）请将下面的频率分布直方图补充完整，并根据直方图估计该市每位居民月均用水量的众数.18.在四棱锥P-ABCD 中，底面ABCD 是正方形，PA ⊥底面ABCD ，且PA=AB. （1）求证：BD ⊥平面PAC ；（2）求异面直线BC 与PD 所成的角.分组频数频率 [0,1) 10 0.1 [1,2) a 0.2 [2,3) 30 0.3 [3,4) 20 b [4,5) 10 0.1 [5,6) 10 0.1 合计10010 1 2 3 4 5 60.3 0.4 频率/组距月均用水量BCDAP19.如图，某动物园要建造两间完全相同的矩形熊猫居室，其总面积为24平方米，设熊猫居室的一面墙AD 的长为x 米（2≤x ≤6）. (1)用x 表示墙AB 的长；（2）假设所建熊猫居室的墙壁造价（在墙壁高度一定的前提下）为每米1000元，请将墙壁的总造价y(元)表示为x(米)的函数；（3）当x 为何值时，墙壁的总造价最低？20.在正项等比数列{a n }中，a 1=4,a 3=64. (1)求数列{a n }的通项公式a n ;(2)记b n =log 4a n ,求数列{b n }的前n 项和S n ;(3)记y=-λ2+4λ-m,对于（2）中的S n ,不等式y ≤S n 对一切正整数n 及任意实数λ恒成立，求实数m 的取值范围.Ex参考答案一、选择题二、填空题11.2 12.5 13.1 14.3π 15.2 三、解答题 16.（1）2π（2）g(x)=2sinx ,奇函数. 17.（1）a=20,b=0.2 (2)2.5吨 18.（1）略（2）450 19.（1）AB=24/x; (2)y=3000(x+x16) (3)x=4,y min =24000. 20.(1)a n =4n ; (2)S n =2)1(+n n (3)m ≥3.2010年湖南省普通高中学业水平考试数学本试题卷包括选择题、填空题和解答题三部分，时量120分钟.满分100分.一、选择题：本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。

湖南省三湘名校教育联盟2020-2021学年高一上学期期中考试数学试题 Word版含答案

绝密★启用前湖南省三湘名校教育联盟2020-2021高一期中考试试题数学本试卷共4页。

全卷满分150分，考试时间120分钟。

注意事项：1.答题前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡，上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、单项选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合A＝{2，3，4，6，7}，B＝{2，3，5，7}，则A∩B＝A.{2，3，5}B.{2，3，7}C.{2，3，5，7}D.{2，3，4，5，6，7}2.“a>c且b>d”是“a＋b>c＋d”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.中文“函数(function)”一词，最早是由近代数学家李善兰翻译出来的，之所以这么翻译，他给出的原因是“凡此变数中函彼变数者，则此为彼之函数”，即函数指一个量随着另一个量的变化而变化，下列选项中两个函数相等的是A.f(x)g(x)＝|x| B.f(x)＝x(x∈R)与g(x)＝x(x∈Z)C.f(x)＝|x|与g(x)＝x0x x0≥⎧⎨-<⎩，，D.f(x)＝x－1与g(x)＝2x1x1-+4.设a－b<0，c<0，则下列结论中正确的是A.ac2<bc2B.a2c>b2cC.11ab bc< D.c ca b>5.函数y的单调递增区间为A.(－∞，32] B.[32，＋∞) C.[32，2] D.[1，32] 6.若不等式x 2＋1>2mx 在R 上恒成立，则实数m 的取值范围是A.(－∞，－1)∪(1，＋∞)B.(－∞，－1]∪[1，＋∞)C.[－1，1]D.(－1，1)7.已知函数f(x)＝()2x 4ax x 12a 3x 4a 5x 1⎧-+≤⎪⎨+-+>⎪⎩，，，若f(x)在R 上是增函数，则实数a 的取值范围是 A.(12，1] B.[12，32] C.(12，＋∞) D.[1，2] 8.在R 上定义运算：A B ＝(A －2)·B ，若不等式(t －x)(x ＋t)<4对任意的x ∈R 恒成立，则实数t 的取值范围是A.(－3，1)B.(－1，2)C.(－1，3)D.(－∞，－1)∪(3，＋∞)二、多项选择题：本题共4小题，每小题5分，共20分。

湖南省(XXX)、江西省(XXX)等十四校2018届高三第二次联考数学(理)试题+Word版含答案

湖南省(XXX)、江西省(XXX)等十四校2018届高三第二次联考数学(理)试题+Word版含答案2018届高三·十四校联考第二次数学（理科）考试第Ⅰ卷一、选择题：本大题共12个小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项符合题目要求。

1.设集合A={x|x≥2}，B={x|1<−x≤2}，则A∩B=（）A。

(-4,+∞) B。

[-4,+∞) C。

[-2,-1] D。

[-4,-2]2.复数z=xxxxxxxxxxxxxxxxi的共轭复数为（）A。

3+i B。

-i C。

+i D。

-i3.下列有关命题的说法中错误的是（）A。

设a,b∈R，则“a>b”是“aa>bb”的充要条件B。

若p∨q为真命题，则p，q中至少有一个为真命题C。

命题：“若y=f(x)是幂函数，则y=f(x)的图象不经过第四象限”的否命题是假命题D。

命题“∀n∈N，f(n)∈N且f(n)≤n”的否定形式是“∃n∈N*，f(n)∉N*且f(n)>n”4.已知不等式ax+1/x+2<0的解集为(-2,-1)，则二项式(x+2)(ax-2)展开式的常数项是（）A。

-15 B。

15 C。

-5 D。

55.若函数f(x)=3sin(π-ωx)+sin(5π+ωx/2)，且f(α)=2，f(β)=3，α-β的最小值是π，则f(x)的单调递增区间是（）A。

(2kπ-5π/3,2kπ-π/3) (k∈Z)B。

(2kπ-,2kπ+) (k∈Z)C。

(kπ-,5π/3+kπ) (k∈Z)D。

(kπ-π/3,5π/3+kπ) (k∈Z)6.某几何体的三视图如图所示（单位：cm），则该几何体的表面积（单位：cm）是（）A。

40+125 B。

40+245 C。

36+125 D。

36+2457.甲、乙、丙、丁、戊五位同学相约去学校图书室借A、B、C、D四类课外书（每类课外书均有若干本），已知每人均只借阅一本，每类课外书均有人借阅，且甲只借阅A类课外书，则不同的借阅方案种类为（）A。

湖南省普通高中学业水平考试数学试卷(word).doc

（第3题图）俯视图侧视图正视图（第10题图）2013年湖南省普通高中学业水平考试数学试卷本试题卷包括选择题、填空题和解答题三部分，时量120分钟，满分100分一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合M={0,1,2}，N={x}，若M ∪N={0,1,2,3}，则x 的值为( ) A ．3 B ．2 C ．1 D ．02．已知函数()1,12,1x f x x x ⎧≥⎪=⎨⎪<⎩，则f (1)的值为( )A ．0B ．1C ．2D ．-13．如图是一个几何体的三视图，则该几何体为( ) A ．球 B ．圆锥 C ．圆柱 D ．圆台 4．函数y=2cosx-1，x ∈R 的最小值是( )A ．-3B ．-1C ．1D ．3 5．已知向量()()1,2,4//a b x a b ==，，若，则实数x 的值为( )A ．8B ．2C ．-2D ．-86．某学校高一、高二、高三年级的学生人数分别为600，400，800。

为了了解教师的教学情况，该校采用分层抽样的方法从这三个年级中抽取45名学生进行座谈，则高一、高二、高三年级抽取的人数分别为( )A ．15,5,25B ．15,15,15C ．10,5,30D ．15,10,207．某袋中有9个大小相同的球，其中有5个红球，4个，则取出的球恰好是白球的概率为( ) A ．15 B ．14 C ．49 D ．598．已知点(x ,y )在如图所示的平面区域（阴影部分）内运动，则z=x+y 的最大值是( )A ．1B ．2C ．3D ．59．已知两点P (4,0)，Q (0,2)，则以线段PQ A ．(x +2)2+(y +1)2=5 B ．(x -2)2+(y -1)2=10 C ．(x -2)2+(y -1)2=5 D ．(x +2)2+(y +1)2=10 10．如图，在高速公路建设中需要确定隧道的长度，工程技术人员已测得隧道两端的两点A ,B 到点C 的距离AC=BC=1km ，且∠ACB=120°，则A ,B 两点间的距离为( ) A ． B C ．1.5km D ．2km 二、填空题：本大题共5小题，每小题4分，共20分.11．计算：log 21+ log 24=_________. 12．若1,x ,9成等比数列，则实数x =_______.13．某程序框图如图所示，若输入的x 值为2，则输出的y 值为__________.（第17题图）F ED CBA（第18题图）14．经过点A (0,3)，且与直线y= -x +2垂直的直线方程是__________.15．已知向量,||24||4a b a a b b π=⋅==与的夹角为，且，则_____.三、解答题：本大题共5小题，共40分．解答应写出文字说明,证明过程或演算步骤. 16．（本小题满分6分）已知1cos ,(0,)22παα=∈。

(完整word版)高二数学期末考试试题及其答案

禄劝一中高中2018-2019学年高二（上）期末数学模拟试卷、选择题：本大题共 12个小题，每小题 5分，共60分.1. （5分）已知集合 M={1, 2, 3}, N={2, 3, 4},则下列式子正确的是（ A. M?NB. N?MC. MAN={2, 3} D. M U N={1 , 4}C.向左平移单位B.向右平移单位 ……冗、,D.向右平移亏单位7 .下表提供了某厂节能降耗技术改造后在生产A 产品过程中记录的产量 x （吨）与相应的生产能耗y （吨）的几组对应数据：根据上表提供的数据，若求出y关于x 的线性回归方程为 ? 0.7x 0.35 ,那么表中t 的值为B. 3.158 .已知 f (x) = (x — m) (x — n) +2,并且 m, n, a, 3的大小关系可能是（2.已知向量 a=(-b l)f 正⑵ -3),则 2%-b 等于（） A. (4, - 5) B. (—4, 5) C. (0, T) D. (0, 1) 3.在区间（1, 7）上任取一个数，这个数在区间 5, 8）上的概率为4.要得到函数B-i7Ty=sin （4x-F-）的图象，只需将函数y=sin4x 的图象 5.已知两条直线m, n,两个平面鹏 8给出下面四个命题:①m H n, m± a? n± a ② a// & m? a, n?仅 m // n @ aJ & m " n, m± ? n± 3 其中正确命题的序号是 A.①③B.②④C.①④D.②③ 6.执行如图所以的程序框图，如果输入 a=5 ,那么输出 n=（A. 2B. 3C. 4D. 5A.向左平移，单位x 3 4 5 6y 2.5 t 4 4.5A. 3 a 、 D. 4.53是方程f （x ） =0的两根，则实数A. a< mvnv 3 B- m< a< 3< n C. m< a< n< 3 D. a< mv 3< n 9 .已知某锥体的三视图（单位： cm ）如图所示，则该锥体的体积为（）10 .在等月ABC 中，/BAC=90°, AB=AC=2,同=2而I,菽=3凝，则前■刘的值为（）Dy11 .已知一个三角形的三边长分别是 5, 5, 6, 一只蚂蚁在其内部爬行，若不考虑蚂蚁的大小,13.若直线 2X + (m+1) y+4=0 与直线 mX+3y+4=0 平行，则 m=y<l15 .若变量x 、y 满足约束条件 y+y>口 ,则z=x-2y 的最大值为bkx 3,x 016 .已知函数f X 1k，若方程f f X 2 0恰有三个实数根，则实数k 的-,x 02取值范围是三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17 .在△ ABC 中，a, b, c 分别为内角 A, B, C 的对边，2bsinB= (2a+c) sinA+ (2c+a) sinC. (I) 求B 的大小；(n) 若 b=" A=T\求^ ABC 的面积.r . ..-18 .已知：a 、b 、c是同一平面上的三个向量，其中a=(l, 2).A. 2cm 3B. 4cm 3C. 6cm 3D . 8cm 3B.则某时刻该蚂蚁距离三角形的三个顶点的距离均超过 2的概率是（B. 1-C. 1 -12.已知函数f （x ）= ,X 1 , X 2 , X 3, X 4, X 5 是方程 f (x) =m 的五个不等的实数根，则 X 1+X 2+X 3+X 4+X 5的取值范围是（A. (0,同 B .（一兀，兀） C. (lg ，兀 1) D. ( 为 10)二、填空题（每题 5分，，茜分20分）14.已知sinOL IcosCl①若|C 1=2 j5,且c // a,求C的坐标.… .. 5②右|b |=——,且a +2 b与2 a -b垂直，求a,与b的夹角219.设S n是等差数列｛a n｝的前n项和，已知S3=6, a4=4.(1)求数列｛a n｝的通项公式；(2) 若bn=3 — 3 %,求证：—+---+ , , •+ ——<—.b L b2 L 420为了了解某省各景点在大众中的熟知度，随机对15〜65岁的人群抽样了n人，回答问题15 25 35 45 55 e5 学龄(1)分别求出a,b,x,y的值;(2)从第2, 3, 4组回答正确的人中用分层抽样的方法抽取6人，求第2, 3, 4组每组各抽取多少人？(3)在(2)抽取的6人中随机抽取2人，求所抽取的人中恰好没有第3组人的概率.21.在三柱ABC-A i B i C i中，△ ABC是边长为2的正三角形，侧面BB i C i C是矩形，D、E分别是线段BB i、AC i的中点.(i)求证：DE//平面A i B i C i；(2)若平面ABC，平面BB i C i C, BB i=4 ,求三棱锥A- DCE的体积.22.已知圆C: x2+y2+2x- 3=0.(i)求圆的圆心C的坐标和半径长；(2)直线l经过坐标原点且不与y轴重合，l与圆C相交于A (xi, yi)、B (X2, y2)两点, 求证：1 :工为定值;町K2(3)斜率为i的直线m与圆C相交于D、E两点，求直线m的方程，使^ CDE的面积最大.禄劝一中高中2018-2019学年高二（上）期末数学模拟试卷参考答案选择题（每小题分，共分） 1 2 3 4 5 6 7 8 9 10 11 12 CBCBCBABAACD、填空题（每小题 5分，共12分）,、M A TV - n 2n 兀兀 n 解：A =——，，C =兀- =———4 q 3 3 2••,|b=V3, B =-^-JbsinC V5 ^/218.解：①设 c (x, y) • •• c // a 且|C |二2 J52x y 0•• 2 2 x 2 y 2 202 c =(2,4)或 c =(-2, -4).13.-3 14. — 15. 3 16.1,17 (I)解：:2bsinB= (2a+c) sinA+ (2c+a) sinC,由正弦定理得, 2b 2= (2a+c) a+ (2c+a) c, 化简彳导,a 2+c 2B=2TT...sinC=sin (2L 』)=、3 「 JT由正弦定理得,SliTT-COS-^-COS-SLIT^ bI sinC sinBcsinBsin号X 炳乂配yXsin-TT 3^/3b 2+ac=0.・•.△ABC 的面积②「( a+2b ) ± (2a-b)，( a+2b) (2a-b) =0,-r -to- -► —*■• -2a 2+3a b-2 b 2=0• •.2|a |2+3| a | b||cos -2|b |2=02X 5+3X v -'5 X — cos -2X - =0, cos = -1 2 4打九 2k Tt, 长［0,兀］「. 0 =Tt.9 CL— 2520解：（1）由频率表中第 4组数据可知，第 4组总人数为 —再结合频率分布直方图可知n ----------- 1000.025 10a 100 0.01 10 0.5 519.解：（1）设公差为 d,则解得=1-a n =n. (2)证明：b n =3—3 、=3n+1— 3n=2?3n,0.36 (1分)•｝是等比数列.，q1b 100 0.03 10 0.9 2乙x 180.9, y — 0,220 15(2)因为第2, 3, 4组回答正确的人数共有 54人，所以利用分层抽样在 54人中抽取6人,每组分别抽取的人数为:(3)设第2组2人为：A 1, A 2；第3组3人为：B 1, B 2, B 3；第4组1人为：C 1 .则从6人中随机抽取2人的所有可能的结果为：(A1,A 2), (A 1,B 1), (A 1,B 2), (A 1,B 3), (A 1C1),(A 2,B 1), (A 2, B 2), (A 2,B 3), (A2,C I ), (B I ,B2), (B I ,B3), (B 1,C 1), (B 2,B 3), (B2,C I ), (B 3,C I )共15个基本事件，其中恰好没有第3组人共3个基本事件, ……，一，…— …31，所抽取的人中恰好没有第 3组人的概率是：P - -155贝U 由EF 是△ AA 1C 1的中位线得 EF // AA 1, 又 DB 1//AA 1, DB 1卷AA 1 所以 EF // DB 1, EF = DB 1所以DE //平面A 1B 1C 1(n)解：因为E 是 AC 1 的中点，所以 V A DCE =V D ACE =2过A 作AH ，BC 于H 因为平面平面 ABC ，平面BB 1C 1C,所以AHL 平面BB 1C 1C,所以 V A DCE =V D —ACE =「5二「7 (4)第2组:18 54 2人;第3组:27 54 3人;第4组:9 54…(8分)21. (1)证明：取棱A i C i 的中点F,连接EF 、B 1F…(10分)…(12分)故四边形DEFB 1是平行四边形，从而 DE// B1FEF122.解：（1）圆 C: x 2+y 2+2x-3=0,配方得（x+1） 2+y 2=4,则圆心C 的坐标为（-1,0）,圆的半径长为 2;（2）设直线l 的方程为y=kx,联立方程组工卜了 +2x3=。

历年高考试题及答案word版校长网

历年高考试题及答案word版校长网一、语文1. 阅读下面的文字，完成（1）-（4）题。

（1）请解释文中“饕餮”一词的含义。

（2）文中“他”的动机是什么？（3）文中描绘了哪些场景？（4）作者通过这篇文章想要传达的主题是什么？答案：（1）饕餮：古代传说中的一种凶猛的野兽，比喻贪婪的人。

（2）“他”的动机是追求个人利益。

（3）文中描绘了市场、家庭和学校三个场景。

（4）作者通过这篇文章传达了对人性贪婪的批判。

二、数学2. 解下列方程组：\[\begin{cases}x + y = 5 \\2x - y = 1\end{cases}\]答案：\[\begin{cases}x = 2 \\y = 3\end{cases}\]三、英语3. 翻译以下句子：（1）This is the best time to learn English.（2）The weather is getting warmer and warmer.答案：（1）这是学习英语的最佳时机。

（2）天气越来越暖和。

四、物理4. 在一个没有摩擦的平面上，一个质量为2kg的物体以10m/s的速度运动，求物体的动量。

答案：\[p = mv = 2 \times 10 = 20 \, \text{kg} \cdot \text{m/s} \]五、化学5. 写出下列化学反应方程式：（1）铁与稀盐酸反应。

（2）碳酸钠与盐酸反应。

答案：（1）\[ \text{Fe} + 2\text{HCl} \rightarrow \text{FeCl}_2 + \text{H}_2 \]（2）\[ \text{Na}_2\text{CO}_3 + 2\text{HCl} \rightarrow 2\text{NaCl} + \text{H}_2\text{O} + \text{CO}_2 \]六、生物6. 描述细胞分裂的过程。

答案：细胞分裂的过程包括有丝分裂和减数分裂。