交流电的相量表示法(2)
正弦交流电的相量表示法

之一,广泛应用于交流电的分析、设计和控制中。
02
正弦交流电的基础知识
正弦交流电的定义
总结词
正弦交流电是指电压和电流随时间按 正弦规律变化的电能。
详细描述
正弦交流电是现代电力系统中最常用 的电能形式,其电压和电流的大小和 方向随时间变化,且变化规律呈正弦 波形。
正弦交流电的特性
总结词
正弦交流电具有周期性、频率、幅值、相位等特性。
THANKS
性等特性。
相量表示法在交流电机、电力系 统、通信和控制等领域有广泛应 用,是现代电力电子和通信技术
中不可或缺的工具。
04
相量表示法与正弦交流电的 关系
相量与正弦交流电的对应关系
相量是复数,其实部表示正弦交流电 的幅度,虚部表示正弦交流电的相位 。
相量长度(模)表示正弦交流电的有 效值或最大值,相量的角度表示正弦 交流电的相位。
02
相量运算能够简化正弦交流电的分析过程,使得复 杂的三角函数运算转化为简单的复数运算。
03
相量运算在交流电路的分析、设计与控制中有广泛 应用。
相量在电路分析中的应用
在交流电路分析中,相量表示法 能够将时域的三角函数形式转换 为复数形式,便于计算和分析。
通过相量图和相量运算,可以分 析交流电路的阻抗、功率和稳定
复数几何意义
复数在平面坐标系中可以用点或 向量表示,实部为x轴坐标,虚部 为y轴坐标。
阻抗和导纳
阻抗定义
阻抗是电路中阻碍电流流动的量,表示为复数 形式Z=R+jX,其中R是电阻,X是电抗。
导纳定义
导纳是类似于阻抗的量,表示为复数形式Y=G+jB, 其中G是电导,B是电纳。
阻抗和导纳的关系
交流电的向量表示法

2j
U a jb
U(cos j sin) 代数式
U e j
指数式
U
极坐标形式
HOME
10
设a、b为正实数
U a jb U e j U a jb U e j
在第一象限 在第二象限
在一、二象限,一般取值:180° 0 °
U a jb U e j U a jb U e j
在第三象限 在第四象限
在三、四象限,一般取值:0° -180 °
HOME
11
U2 j
U1
2=120°
1=60° +1
3= -120°
U3
HOME
12
例 计算相量的相位角时,要注意所在 象限。如:
U 3 j4
U 3 j4 U 3 j4
U 3 j4
u 5 2 sin( t 53 1)
2
相量的书写方式
最大值
Um 或 U
有效值
1. 描述正弦量的有向线段称为相量 (phasor )。若其
幅度用最大值表示 ,则用符号:Um I m
2. 在实际应用中,幅度更多采用有效值,则用符号:
UI
3.
相量符号U、I
包含幅度与相位信息。
HOME
3
正弦量的相量表示法举例
例1:将 u1、u2 用相量表示
i1 100 2 sin(6280t 60) A
i2 10 2 sin(6280t 30) A
HOME
18
小结:正弦波的四种表示法
波形图 瞬时值 相量图
i
Im
t
T
u Um sin t
U
I
复数 符号法
U a jbUej U
交流电的三种表示方法

同期工作原理
一、同期的概念:两个系统之间的电压,频率,相序,
相角相等时,称为同期。
把发电机并入电网时,必须对发电
机并网前的电压进行控制,只有满足同期条件后才能同期
并列,而用来同期并网的装置叫做同期装置。
二、同期原理
1、交流电的产生
二、交流电的三种表示方法
1、数学式表达方法
U=U m sin(ωt+ψi)
2、波形表示法
3、相位表示法
三、交流电的三要素:电压幅值、频率、初相位角
U
U1 △U
0 U2
U
U
U1
△U
U2
0 T
T
T
电压频率不一样
我公司二期同期整定值:允许频差0.15HZ;允许压差5%U n;初相角20度以内。
四、同期操作票:先调电压,再调频率,初相位不用调,提前合闸时间发出合闸脉冲。
五、同期过程(视频)
1、相量旋转原理:假设系统3000转/分,发电机3006转/分,1÷50×X=1÷50.1×(X+1)得X=500转500×0.02=10秒
2、同期装置和同期表的区别
六、同期二次图(图纸)
八、开关的合闸/跳闸回路(图纸)
1、同期合闸
2、NCS合闸
九、同期事故(内蒙古通辽电厂和湖北襄樊电厂和贵州鸭溪电厂)发电机中性点断线分析:(图纸)
课堂习题:
1、同期三要素?
2、5012开关合闸先后经过了哪些设备?。
三相电压的相量表示

三相电压的相量表示是将时间上连续变化的三相正弦交流电压以复数形式表达,这种方法可以直观地描述各相电压在幅值、频率以及相位上的关系。
在电力系统分析中,通常采用极坐标或直角坐标(也称作笛卡尔坐标)来表示。
极坐标表示:
对于星形连接(Y接法)的三相电源或负载,其相电压相对于同一基准(例如A相)的相量表示为:
- A相:UA = V∠0°
- B相:UB = V∠-120°
- C相:UC = V∠120°
这里的V代表每相的有效电压幅值,角度表示的是相对于A 相的相位差,按照逆时针方向,B相滞后A相120度,C相超前A相120度。
直角坐标表示:
在静止对称坐标系(如αβγ坐标系或dq0坐标系)中,也可以转换成直角坐标形式表示,但此处不涉及具体的坐标变换过程。
对于三角形连接(Δ接法)的三相电压,线电压与相电压之间的关系如下:
- 线电压UAB = UA - UB = 380∠30° (假设有效线电压为380V)
- 线电压UBC = UB - UC = 380∠-90°
- 线电压UCA = UC - UA = 380∠150°
相量图中,三个电压相量按照120度均匀分布,且同时绕着同一个轴以相同的角速度逆时针旋转,这个角速度对应的就是系统的角频率ω(对于50Hz的交流电,ω=2π×50 rad/s)。
通过相量图和相量计算,能够简化复杂电路的分析和计算。
简述正弦交流电的三种表示方法

简述正弦交流电的三种表示方法1.引言1.1 概述概述部分的内容可以按照以下方式编写:引言部分是文章的开篇,目的是为读者提供对后续内容的整体了解。
在这篇文章中,我们将讨论正弦交流电的三种表示方法。
正弦交流电是工程技术领域中常见的电信号类型之一,广泛应用于电力系统、电子电路和通信系统等领域。
正弦交流电具有周期性的特点,可以表示为周期性变化的信号。
对于正弦交流电的表示方法,研究者们提出了多种不同的方式。
本文将详细介绍其中的三种主要表示方法,分别是:1. 直角坐标系表示法:通过在直角坐标系中绘制电压或电流随时间的变化曲线,来表示正弦交流电的变化规律。
这种方法直观且易于理解,可以清晰展示电压或电流的振幅、频率和相位等重要参数。
2. 极坐标系表示法:将正弦交流电视为一个旋转的向量,通过描述其振幅和相位差来表示。
极坐标系表示法适用于描述相位关系的问题,对于分析电路中的相位差和频率变化等现象非常有用。
3. 复数表示法:利用复数的实部和虚部,将正弦交流电转化为复数形式进行表示。
这种表示方法在电路分析和计算中非常高效,可以通过简单的复数运算得到电流和电压的各种参数,极大地简化了电路分析的过程。
本文将分别对上述三种表示方法进行详细阐述,分析其优缺点以及适用场景,旨在让读者全面了解正弦交流电的不同表示方法,并为进一步深入研究和应用提供参考。
接下来,我们将介绍文章的结构以及各个章节的具体内容。
1.2文章结构文章结构部分的内容可以包括以下内容:文章结构是指整篇文章内容的组织和安排方式,它包括了引言、正文和结论三个主要部分。
通过清晰的文章结构,读者可以更好地理解文章的内容,把握文章的逻辑关系和主旨。
引言部分为文章提供了一个引人注目的开篇,引发读者的兴趣,并对正文的内容进行简单概述。
在这个部分,我们将对正弦交流电的三种表示方法进行简要的介绍。
正文部分是文章的重点,用来详细阐述正弦交流电的三种表示方法。
在正文中,我们将分别介绍第一种、第二种和第三种表示方法,详细讲解它们的原理、特点和应用场景。
电路分析基础第4章 相量法(2h)

Im
U 2
U
U 1
41.9
60 30
Re
U
Im
U 2
首
U 1
60 尾
41.9
相 接
30
Re
/38 章目录 上一页 下一页 返回 退出
第4章 正弦稳态电路分析
4.3 基尔霍夫定律的相量形式和基本
元件伏安关系的相量形式
一. 电阻 i(t)
+
uR(t) R -
•
I
+
•
UR
R
-
相量模型
已知 i(t) 2I cos(wt y i )
设 i(t)=Imcos(w t+ )
I
1 T
T 0
I
2 m
cos2
(
wt
Ψ
) dt
def
I
1 T i 2 (t )dt
T0
cos2 ( wt Ψ ) 1 cos2(wt Ψ )
2
I 0.707Im Im 2I
i(t) Im cos(wt Ψ ) 2I cos(wt Ψ )
10/38 章目录 上一页 下一页 返回 退出
u2 (t) 4 2cos(314t 60o ) V
U1 630o V U 2 460o V
U U1 U 2 630 460 5.19 j3 2 j3.46
7.19 j6.46 9.6441.9o V
u(t) u1(t) u2 (t) 9.64 2cos(314 t 41.9o ) V
dt
C 相量形式:
•
U Uy u
•
IC
wCUy u
π 2
1 相量关系:
正弦交流电的相量表示法
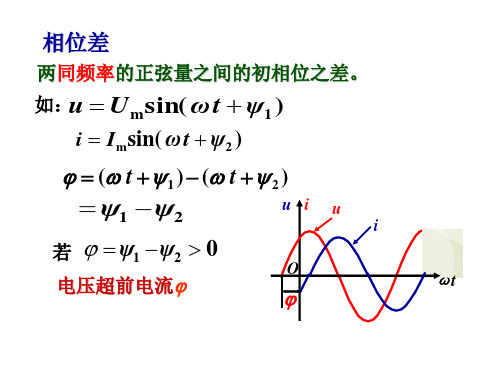
u
波形图
O
ωt
瞬时值表达式 u Umsin( t )
相量 U Uψ
必须 小写
重点
前两种不便于运算,重点介绍相量表示法。
2.正弦量用旋转有向线段表示
设正弦量: y
u
Umsin(
t ψ)
u
u0ω
O
x
u1
U
O
m
ψ
ω t1
ωt
若:有向线段长度 = Um
有向线段与横轴夹角 =
初相位
有向线段以速度ω 按逆时针方向旋转
②只有正弦量才能用相量表示, 非正弦量不能用相量表示。
③只有同频率的正弦量才能画在同一相量图上。
I
U
④相量的两种表示形式
相量式: U Uejψ U ψ U( cos ψ jsin ψ)
相量图: 把相量表示在复平面的图形
可不画坐标轴
I
U
⑤相量的书写方式
• 模用最大值表示 ,则用符号:U m 、Im
• 实际应用中,模多采用有效值,符号: U 、I
如:已知 u 220 sin(ω t 45)V
则U m 220e j45V或 U 220 e j45V 2
⑥“j”的数学意义和物理意义
e 旋转 90 因子: j90
ej90 cos 90 jsin90 j
设相量 A rejψ B
+j
则:该旋转有向线段每一瞬时在纵轴上的投影即表示
相应时刻正弦量的瞬时值。
3. 正弦量的相量表示
实质:用复数表示正弦量 复数表示形式
设A为复数: (1) 代数式A =a + jb
+j
b
r
0
A
正弦交流电路的相量表示法

直观,但不便于分析计算。
便于完成正弦量的加减乘除运算
【 重点与难点 】
1.正弦量的三要素。
2.正弦量各种表达方法之间的互相转换
Im
对应
新中国成立后,我国的整个工业行业师从前苏联,电力行业也不例外,完全执行前苏联的国家标准。苏联当时采用的频率是50赫兹,这个标准与IEC国际电工委员会推荐值之一,并不矛盾,所以我国一直采用50赫兹。 这是一种国家制定的标准,从此以后,所有生产的发电及用电设备,都按50赫芝控制.这样全国就统一了,就不会乱.否则你北京造的电视机是50HZ的,天津造的是30HZ的,上海造的是100HZ的.那不乱套了嘛.这就和秦始皇统一汉字,度量衡是一个目的.现在有的日本电器,是60HZ的.在中国用还要连接变频器,多麻烦啊! 其实其它频率也是有的,以前日本在东北使用的是25Hz;我国电网是50Hz;香港沿袭英国的习惯使用60Hz。 使用低于50Hz的电网供电时的照明光源往往存在一个频闪问题;如果给电机供电其同步速仅为1500rpm。 50或60是有政治因素的,学苏联的肯定不可能学日本的, 100,1000高频率的话对硅钢片材料的要求更高,危险性更大,损耗大,那将是现在技术不行的, 如果现在提高频率肯定不利的,大量设备将不能用。
知识链接
相量的加、减、乘、除运算公式
设:U1、U2均为正实数。
U1±U2 =
(U1a±U2a)+j ( U1b±U2b)
ψ1+ ψ2
U1×U2 =
U1×U2
U1÷U2 =
ψ1- ψ2
U1÷U2
有U1=U1 ψ1=U1a+jU1b;
U2=U2 ψ2=U2a+jU2b;
平行四边形法则可以用于相量运算,但不方便。故引入相量的复数运算法。
电工技术:正弦交流电的相量表示法

同频率正弦量的相量运算:知识点小结
两个同频率的正弦交流电相加(减): 方法一:都化成相量,变为复数的相加(减) 方法二:相量图法(平行四边形或首尾相接法)
正弦交流电的相量表示法
正弦交流电有哪些表达形式?
(1)正弦函数(瞬时值表达式)如
i I m sin (ω t ψ )
Im
(2)正弦曲线波形,如
i
-Im
O
2
T
t
t
这两种表达形式直观,但运算繁琐,绘制困难。
正弦交流电为什么要用相量表示?
两个正弦量
i1 2 I1m sin ( t 1 )
实际应用更多的是有效值形式的相量表示!
一、正弦量的相量表示法
2.注意事项 (1)表示正弦量的复数称相量
(2)相量只是表示正弦量,而不等于正弦量。
u U m sin ( ω t ψ) =
(3)一个正弦量与一个复数是一一对应的关系。 (4)只有正弦周期量才能用相量表示,相量不能表示非正弦周期量。
u2 110 2sin(ω t 450 ) V
(2) 相量图
+j
U 2
U2
超前 U1
U 1
+1
45 20
正弦交流电的相量表示法(1):知识点小结
(1)正弦交流电用相量(复数)表示方法
u U m sin ( ω t ψ )
(2)相量图
U U ψ
U
ψ
正弦交流电的相量运算
同频率正弦量的相量运算
• 同频率正弦量相加减
同频率的两个正弦量相位差为一些 特殊角时,用相量图中的几何关系 很方便求相量和、相量差。 例:题3: 已知 解:
正弦交流电的相量表示法(2)

正弦量的表示法:
解析式: i(t ) I m sin(t ) A
i
Im
最大值相量: I m I m
有效值相量: I I
最大值: I m
I
Im
I
有效值: I
平均值:
I
I
电工基础
例:写出下列正弦量的相量形式:
i1 (t ) 5 2 sin(t 53.1) A
2
虚数
用 j 代替
虚部 实部
i
B a jb
j
复数 A a jb 代数式
0
D
b
A
C a jb
D a jb
复数的模
r
0
1
r a 2 b2
复数矢量与实轴正方向的夹角
a
C
0
取值在正180度到负180度之间
a r cos
0
电工基础
三、正弦量的相量表示法: re j r cos jr sin
Im
t
正弦交流电
I me j (t ) I m cos(t ) jI m sin(t )
用 I me
I me
j (t )
代
jt
替
I m sin(t ) I mt
加减用代 数式运算
A B a1 jb1 a2 jb2 (a1 a2 ) j (b1 b2 ) A B a1 jb1 (a2 jb2 ) (a1 a2 ) j (b1 b2 )
A B
A
A B
A
B B
1
1
对称三相交流电压的时域表达式和相量表达式

对称三相交流电压的时域表达式和相量表达式在电力系统中,三相交流电压是一种常见的电力信号。
了解对称三相交流电压的时域表达式和相量表达式对于电力系统的分析和运行非常重要。
本文将深入探讨这一主题,从简到繁,由浅入深地介绍对称三相交流电压的时域表达式和相量表达式,以便读者能更深入地理解。
1. 对称三相交流电压的时域表达式对称三相交流电压由三个正弦波电压相位相差120度组成。
对称三相交流电压的时域表达式可表示为:\[V_a = V_m \cdot \sin(\omega t)\]\[V_b = V_m \cdot \sin(\omega t - \frac{2}{3} \pi)\]\[V_c = V_m \cdot \sin(\omega t + \frac{2}{3} \pi)\]其中,\(V_a\)、\(V_b\)、\(V_c\) 分别代表A相、B相、C相的电压;\(V_m\) 代表电压的峰值;\(\omega\) 代表角频率;\(t\) 代表时间。
时域表达式告诉我们,对称三相交流电压是随着时间周期性变化的正弦波电压。
A相、B相、C相的电压之间相位差120度,呈现对称关系。
2. 对称三相交流电压的相量表达式对称三相交流电压的相量表达式是一种通过向量表示三个电压之间相互关系的方法。
相量表达式可以更直观地展示电压之间的幅值和相位关系。
假设三相电压的相量分别为\(V_a\)、\(V_b\)、\(V_c\),则其相量表达式为:\[V_a = V_{an} \angle 0^\circ\]\[V_b = V_{bn} \angle (-120^\circ)\[V_c = V_{cn} \angle 120^\circ\]其中,\(V_{an}\)、\(V_{bn}\)、\(V_{cn}\) 分别代表A相、B相、C相的电压幅值;角度表示电压之间的相位差。
相量表达式可以将三相电压用向量形式表示,从而清晰地展示电压之间的相位关系。
3.2相量表示法
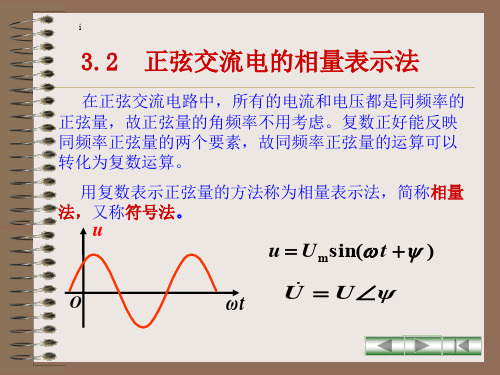
例已知正弦电量的瞬时值表达式分别为
,
e 180 2 sin(t 60) V i 10 2 sin(t 30) A
要求(1)写出各正弦量对应的最大值相量和有效值相量。
(2)画出各正弦量对应相量的相量图。
方法2:用图解法求总电流i
① 根据电流i1、i2的瞬时值表达式,写出对应的相量表
达式。
I1
630
A
I 2 8 60 A
② 画出 I1 I 2 ,用矢
量求和法作出电流的相量
图,如图(b)所示。由
相量图确定正弦电流的有
效值和初相位
I 10 A 23.1
③ 写出电流对应的相量表达式
最大值
3.已知:
I 4 e
j30
A
复数
4 2 sin (ω t 30 )A?
瞬时值
4.已知:
U 100 15V
U 100V ? ? U 100 ej15 V
负号
3.2.3相量的计算
(1)复数的加减运算 设两个复数分别为A1 = a1 + jb1,A2 = a2 + jb2,
② 用复数符号法求和,得到电流i对应的相量表达式
I I1 I2
(5.196 j3) (4 j6.928)
I 10 23.1A
9.296 j3.928 10 23.1A
③写出电流i的瞬时值表达式。
i 10 2 sin(t 23.1)A
解:(1)写出各正弦量对应的最大值相量和有效值相量。
第3章 相量法 (2)

Sin t Im e ut U m sin t
其中:
j t
j t j t j ImU m e ImU m e e U m U m j t ImU m e ImU m t 相量是复数
• 有效值相量, 即相量的模取有 效值。
–最大值与有效值的关系 U m 2U • 正弦量与相量的互化
相量图:相量是一个复数,它在复平面上的图形称为 相量图
I I i U U
+j
u
0
+1
同频率的正弦量,才能 画在同一பைடு நூலகம்相量图上。
例i(t)=141.4sin(314t+300)A,u(t)=311.1sin(314t-600)V 。 试分别用相量表示该电压、电流,并作图 。 解:
0
Ri 2 dt RI 2
p(t)= u i = R i 2
b)大多数电器设备的铭牌数据由于要反映其温升和平均功率,因 此均以有效值给出铭牌数据。比如交流电压380V,电流20A等。
小结
1、正弦量:指电压或电流随时间按正弦规律变化。 2、三要素:Im ω 和Φ ,我们将这三个量称作正弦量 的三要素。 三要素是正弦量之间进行比较和区分的主要依据 3 、相位差:两个同频率正弦量的相位角之差称为 相位差 4 、有效值
i( 所以正弦量也常写作:t ) 2I sin(t i ) , u(t ) 2U sin(t u )
因此,三要素也可称作是 I,ω ,φ i ③引入有效值的意义:a)计算功率简单方便 平均有效功率: 1 0 P T
T
p (t )dt
和直流功率表达式一样 。
第4讲正弦交流电的基本概念、相量表示法

P 1
T pdt 1
T
UI(1 cos 2 ωt)dt
UI
T0
T0
P UI I 2R U 2 p R
+
+
单位:瓦(W)
O
P
ωt
通常测量的或铭牌标注的功率均指有功功率
作业
P49 练习题2.2.1、 P87 练习题3.1.1。
u Ri RI m sin ωt Um sin ωt
⑴电压与电流同频率、同相 ψu ψi 0
⑵最大值、有效值伏安关系: Um U R
Im I
⑶波形关系
ui u
⑷相量关系
i
U U0 I I0 O
ωt
UI
U I
R
欧姆定律的相量表示式: U RI
则 Um 220 2e V j30
U 220 e V j30
⒉ 相量图
相量图:按照各个正弦量的大小和相位关系画出的
若干个相量的图形。
例:U 22030V I 560 A
只有同频率的正弦量才能
I
U
画在同一相量图上,可不画坐
60
标轴。
30
⒊ 旋转因子“j” 当 90时,则
ui
i
i
_
_
+
O
-
+
+
t
_
u
-
R
u
-
R
正半周
负半周
图中虚线箭头代表电流的实际方向; 代表电压的实际方向(极性)。
正弦量:正弦电压和电流等物理量统称为正弦量。
正弦量的特征表现在:
变化的快慢 大小 初始值
交流电的相量表示法

幅度用最大值表示 ,则用符号:Um I m
2. 在实际应用中,幅度更多采用有效值,则用符号:
UI
3.
相量符号U、I
包含幅度与相位信息。
HOME
正弦量的相量表示法举例
例1:将 u1、u2 用相量表示
u1 2U1 sin t 1 u2 2U2 sin t 2
设: 幅度:相量大小 U2 U1
HOME
例2:已知相量,求瞬时值。
已知两个频率都为 1000 Hz 的正弦电流其相量形
式为: I1 100 60 A I 2 10 e j 30 A
求: i1、i2
解:
2
f
2 1000 6280
rad s
i1 100 2 sin(6280t 60 ) A
1. 复数加 、减运算
设: U 1 a1 jb1 U 2 a 2 jb 2
则:
U U1±U2 (a1±a2 ) j(b1±b2 )
Ue j
U
HOME
2. 复数乘、除法运算
设: A 1 A 1e j 1
A
2
A
e j 2
2
乘法: A A 1 A 2
U 3 j4
U 3 j4 U 3 j4
U 3 j4
u 5 2 sin( t 53 1 )
u 5 2 sin( t 53 1 )
u 5 2 sin( t 126 9 )
u 5 2 sin( t 126 9 )
HOME
3.2.3相量的运算
代数型 三角函数型
指数型 极坐标型
HOME
3.2.2相量与复数
将相量 U 放到复平面上,可如下表示:
交流电的相量表示法

a
U a jb U cos jU sin
j
bU
a
U
欧 拉
cos e j e j
2
公
+1 式
sin e j e j
2j
U a jb
U(cos j sin) 代数式
U e j
指数式
U
极坐标形式
设a、b为正实数
U a jb U e j U a jb U e j
i2 10 2 sin(6280t 30) A
HOME
小结:正弦波的四种表示法
波形图 瞬时值 相量图
i
Im
t
T
u Um sin t
U
I
复数 符号法
U a jbUej U
幅度用最大值表示 ,则用符号:Um I m
2. 在实际应用中,幅度更多采用有效值,则用符号:
UI
3. 相量符号U、I 包含幅度与相位信息。
正弦量的相量表示法举例
例1:将 u1、u2 用相量表示
u1 2U1 sin t 1
U2
u2 2U2 sin t 2
设: 幅度:相量大小 U2 U1
可将复数A表示成代数型、三角函数型、指 数型和极坐标型4种形式。
A a1 ja2 a cos ja sin ae j a
代数型 三角函数型 指数型 极坐标型
相量与复数
将相量 U 放到复平面上,可如下表示:
j
a、b分别为U在实轴
U
和虚轴上的投影
bU
a
U a2 b2
+1
tg 1 b
交流电的相量表示法
概念 :一个正弦量的瞬时值可以用一个旋转矢量
在纵轴上的投影值来表示。
正弦交流电的相量图表示法ppt课件

u1 2U1sint 1
u2 2U2 sint 2 u= u1 +u2 = 2U sint
U 同频率正弦波的
U2
相量画在一起,
构成相量图。
2
1
U1
U U1 U2
HOME
7
注意 :
1. 只有正弦量才能用相量表示,非正弦量不可以。 2. 只有同频率的正弦量才能画在一张相量图上,
不同频率不行。 3. 一般取直角坐标轴的水平正方向为参考方向,逆 时针转动的角度为正,反之为负。 4. 用相量表示正弦交流电后,它们的加减运算可按 平行四边形法则进行。
在直角坐标系上可表示为.
A = a + jb
用极坐标系则表示为.
0 ax
A=r/
变换关系为:r a2 b2
arctg b a
或: a r cos b r sin
3
5.2 正弦交流电的相量图表示法
概念 :一个正弦量的瞬时值可以用一个旋转矢量
在纵轴上的投影值来表示。
u Um sin t
正弦交流电的相量图表示法矢量长度矢量与横轴夹角初相位矢量以角速度按逆时针方向旋转homehome描述正弦量的有向线段称为相量phasor幅度用最大值表示则用符号
5.2 正弦交流电的相量图表示法
1
正弦量的相量表示法
• 正弦量具有幅值、频率及初相位三个基 本特征量,表示一个正弦量就要将这三
要素表示出来。
包含幅度与相位信息。
HOME
5
正弦量的相量表示法举例
例1:将 u1、u2 用
设: 幅度:相量大小 U2 U1
相位: 2 1
U2 领先于 U1
U2
2
1
U1
7.2交流电的表示法
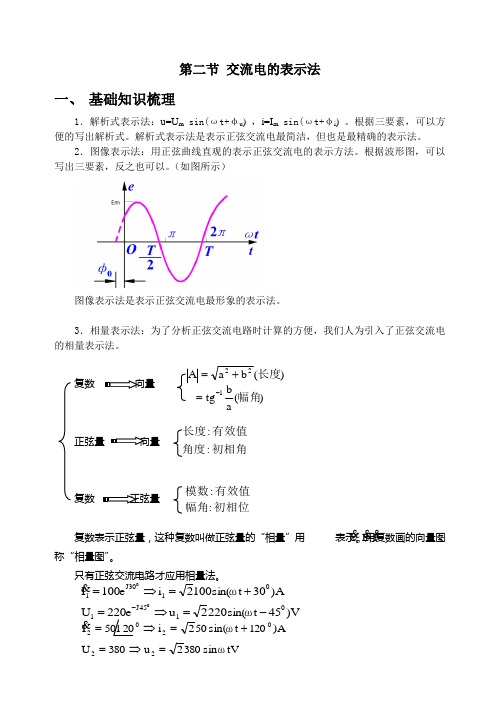
第二节 交流电的表示法一、 基础知识梳理1.解析式表示法:u=U m sin(ωt+φu ) ,i=I m sin(ωt+φi ) 。
根据三要素,可以方便的写出解析式。
解析式表示法是表示正弦交流电最简洁,但也是最精确的表示法。
2.图像表示法:用正弦曲线直观的表示正弦交流电的表示方法。
根据波形图,可以写出三要素,反之也可以。
(如图所示)图像表示法是表示正弦交流电最形象的表示法。
3.相量表示法:为了分析正弦交流电路时计算的方便,我们人为引入了正弦交流电的相量表示法。
复数正弦量复数复数表示正弦量,这种复数叫做正弦量的“相量”用 表示。
用复数画的向量图称“相量图”。
只有正弦交流电路才应用相量法。
)(b a A 22长度+=)(a b tg 1幅角-=有效值:初相角角度:有效值模数:初相位幅角:I,E ,U A )30t ωsin(1002i e 100I 0130J 10+=⇒= V )45t ωsin(2202u e 220U 0145J 10-=⇒=-A)120t ωsin(502i 20501I 0202+=⇒= tV ωsin 3802u 380U 22=⇒=相量形式是当频率一定时,正弦量瞬时值表达式的代表符。
所以,采用相量法后,交流电路和直流电路中的定律和公式在形式上是相似的。
所不同的是,交流电在计算时应按复数运算法则进行。
二、 应用举例应用一:相量表示法应用分析:相量形式:用复数的极坐标形式来表示交流量正弦量可以用振幅相量或有效值相量表示,但通常用有效值相量表示。
有效值相量表示法是用正弦量的有效值做为相量的模(长度大小)、用初相角做为相量的幅角,通式为:e E E ϕ∠= u U U ϕ∠= iI I ϕ∠=相量图形式:把交流电的相量画到复平面中。
(同频率的可画在同一复平面中)例1:写出下列正弦电压的相量(1) .U =10∠0 V(2) .U =10∠/2V (3) .U =10∠-/2V(4) .U =10∠-3/4 V 举一反三:如图所示为两个同频率的正弦交流电压u 1、u 2的波形,求u 1、u 2的解析式和相量形式,并画出相量图。
