银川一中第二次模拟数学(理科)试卷答案
2022届宁夏回族自治区银川一中高三下学期二模考试数学(理)试题及答案

故选:D.
3. 命题“ ,则 ”及其逆命题、否命题和逆否命题这四个命题中,真命题的个数为()
A. 0B. 2C. 3D. 4
【3题答案】
【答案】D
【解析】
首先判断原命题的真假,写出其逆命题,即可判断其真假,再根据互为逆否命题的两个命题同真假,即可判断;
【详解】解:因为命题“ ,则 ”为真命题,所以其逆否命题也为真命题;
对于C选项,当 时,不等式显然不成立,故错误;
对于D选项,由于 ,故 ,正确.
故选:D
6. 下列四个函数中,在其定义域上既是奇函数又是增函数的是()
A. B.
C. D.
【6题答案】
【答案】D
【解析】
A.利用指数函数的性质判断;B.利用正切函数的性质判断;C.利用正弦函数的性质判断;D.利用函数的图象判断.
A. B. C. D.
【7题答案】
【答案】D
【解析】
先将4人分成3组,其一组有2人,然后将3个项目进行排列,可求出每个项目至少安排一名志愿者进行志愿服务的方法数,再求出4名志愿者参加3个项目比赛的志愿服务的总方法数,再利用古典概型的概率公式求解即可
【详解】先将4人分成3组,其一组有2人,另外两组各1人,共有 种分法,
秘密★启用前
2022届宁夏回族自治区银川一中高三下学期二模考试
数学(理)试题
★祝考试顺利★
(含答案)
一、选择题:本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 若全集 ,集合 , ,则图中阴影部分表示的集合为()
A. B. C. D.
【1题答案】
【答案】A
A. B.
宁夏银川一中2019届高三数学第二次模拟考试试题理(含解析)

银川一中届高三年级第二次模拟考试理科数学试题卷注意事项:. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
. 作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
. 考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的..设集合,,则(). . . .【答案】【解析】【分析】化简集合,进而求交集即可得到结果.【详解】由题意可得,又∴故选:【点睛】本题考查交集的求法,解题时要认真审题,是基础题..复数,则(). . -2 . .【答案】【解析】【分析】把代入,再由复数代数形式的乘除运算化简得答案.【详解】解:,,故选:.【点睛】本题考查复数代数形式的乘除运算,是基础的计算题..高铁、扫码支付、共享单车、网购被称为中国的“新四大发明”,为评估共享单车的使用情况,选了座城市作实验基地,这座城市共享单车的使用量(单位:人次天)分别为,,…,,下面给出的指标中可以用来评估共享单车使用量的稳定程度的是(). ,,…,的平均数. ,,…,的标准差. ,,…,的最大值. ,,…,的中位数【答案】【解析】【分析】平均数反应的是水平,而方差和标准差反映的是稳定性.【详解】标准差能反映一个数据集的离散程度,因此可以用来评估共享单车使用量的稳定性,故选.【点睛】本道题目考查了平均数和标准差的概念和意义,注意两者反映总体的水平不同..已知等比数列中,有,数列是等差数列,其前项和为,且,则(). . 52 . .【答案】【解析】【分析】设等比数列的公比为,利用等比性质可得,即,再结合,即可得到结果.【详解】设等比数列的公比为,∵,∴≠,解得=,数列是等差数列,且.∴故选:.【点睛】本题考查了等比数列与等差数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题..如图,在中,,是上一点,若,则实数的值为(). . . .【答案】【解析】【分析】由题意,可根据向量运算法则得到(﹣),从而由向量分解的唯一性得出关于的方程,求出的值.【详解】由题意及图,,又,,所以,∴(﹣),又,所以,解得,,故选:.【点睛】本题考查平面向量基本定理,根据分解的唯一性得到所求参数的方程是解答本题的关键,本题属于基础题..学校就如程序中的循环体,送走一届,又会招来一级。
2020届宁夏回族自治区银川一中高三第二次模拟考试数学(理)试题及答案

1 2 2015
t 1 1 1
1
2(1 1 1 1 1 1 )
1 2 1 23
1 2 2015
223
2015 2016
2(1 1 ) 2015 ,选 D. 2016 1008
点睛:算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,
包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通
c
3 2
a
b2 4
c2
3 a2 4
a2
c2 4
3 c2 4
1 a2 2
0.
所以 3c2 2a2 ,所以 e c 6 , a3
故选:A.
点评:
本题考查了直线与椭圆的交点,考查了向量垂直的坐标表示,考查了椭圆的离心率公式,属于基础
题.
12.已知函数
f
(
x)
(
x
2)
x ex
3, (x ln 2) , 当 x [m, ) 时 , f (x) 的 取 值范 围 为
则 y 4 cos x ex 在 0, 上单调递减,
故选:A. 点评: 本题主要考查函数的图象,可以通过函数的性质进行排除,属于中档题.
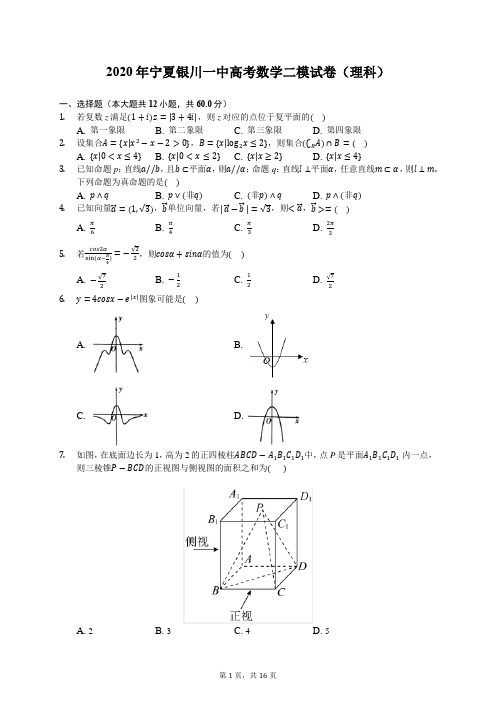
7.如图,在底面边长为 1,高为 2 的正四棱柱 ABCD A1B1C1D1 中,点 P 是平面 A1B1C1D1 内一 点,则三棱锥 P BCD 的正视图与侧视图的面积之和为()
间想象能力与计算能力,属于基础题.
8.抛物线
的准线与双曲线
的两条渐近线所围成的三角形面积为 ,则 的
值为()
A.
B.
C.
D.
答案:A
求得抛物线的准线方程和双曲线的渐近线方程,解得两交点,由三角形的面积公式,计算即可得到
宁夏银川一中高三第二次模拟数学(理) 含答案

绝密★启用前2019年普通高等学校招生全国统一考试理科数学试题卷 ( 银川一中第二次模拟考试 )注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.如果复数iai+-21(R a ∈,i 为虚数单位)的实部与虚部相等,则a 的值为 A .1 B .-1 C .3 D .-32.若{}{}0,1,2,|2,aA B x x a A ===∈,则A B =UA .{0,1,2} B. {0,1,23}, C. {0,1,24}, D. {1,24},3. 向量)3,1(),,2(-==b t ρ,若b ρ,的夹角为钝角,则t 的范围是A .t<32 B .t>32 C .t<32且t≠-6 D .t<-6 4.直线kx-2y+1=0与圆x 2+(y-1)2=1的位置关系是A .相交B .相切C .相离D .不确定5.有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组, 则不同的选法共有 A .60种B .70种C .75种D .150种6.已知某个几何体的三视图如下,根据图中 标出的尺寸,可得这个几何体的表面积是 A .162B .122226+C .1822+D .1622+7. 下列函数中,最小正周期为π,且图象关于直线x=3对称的函数是2 422A .y=2sin(2x+3π) B .y=2sin(2x-6π) C .y=2sin(32π+x ) D .y=2sin(2x-3π) 8.我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截 取一半,永远都截不完.现将该木棍依此规律截取,如图 所示的程序框图的功能就是计算截取20天后所剩木棍的 长度(单位:尺),则①②③处可分别填入的是 A .i i ,iS S ,i 2120=-=< B .i i ,iS S ,i 2120=-=≤ C .1220+==<i i ,S S ,i D . 1220+==≤i i ,S S ,i 9.已知α是第二象限角,且sin(53)-=+απ,则tan2α的值为 A .54B .723-C .724- D .924-10.已知函数xx x f -+=)1ln(1)(,则)(x f y =的图像大致为A. B. C. D.11.已知抛物线x 2=4y 焦点为F,经过F 的直线交抛物线于A(x 1,y 1),B(x 2,y 2),点A,B 在抛物线准线上的射影分别为A 1,B 1,以下四个结论:①x 1x 2=4-, ②AB =y 1+y 2+1, ③11FB A ∠=2π,④AB 的中点到抛物线的准线的距离的最小值为2 其中正确的个数为A .1B .2C .3D . 412.已知函数ax x e x f x-=)(,),0(∞+∈x ,当12x x >时,不等式1221)()(x x f x x f <恒成立,则实数a 的取值范围为A .],(e -∞B .),(e -∞C .)2,(e-∞ D .]2,(e -∞ 二、填空题:本大题共4小题,每小题5分. 13.(x+y)(2x-y)5的展开式中x 3y 3的系数为_______.14.在锐角三角形ABC 中,c b a ,,分别为角A 、B 、C 所对的边,且A c a sin 23=11y xo 11y xo 11y xo 11y xoc=7,且ΔABC 的面积为233,b a +的值为_______. 15.如图所示,有三根针和套在一根针上的n 个金属片,按下列规则,把金属片从一根针上全部移到另一根针上. (1)每次只能移动一个金属片;(2)在每次移动过程中,每根针上较大的金属片不能放在 较小的金属片上面.将n 个金属片从1号针移到3号针 最少需要移动的次数记为f (n ),则f (n )=________.16.一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是A (0,0,5),B (3,0,0),C (0,1,0),D (3,1,5),则该四面体的外接球的体积 为______.三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答;第22、23题为选考题,考生根据要求作答。
2020年宁夏银川一中高考数学二模试卷(理科)(有答案解析)
2020年宁夏银川一中高考数学二模试卷(理科)一、选择题(本大题共12小题,共60.0分)1.若复数z满足(1+i)z=|3+4i|,则z对应的点位于复平面的()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.设集合A={x|x2−x−2>0},B={x|log2x≤2},则集合(∁R A)∩B=()A. {x|0<x≤4}B. {x|0<x≤2}C. {x|x≥2}D. {x|x≤4}3.已知命题p:直线a//b,且b⊂平面α,则a//α;命题q:直线l⊥平面α,任意直线m⊂α,则l⊥m.下列命题为真命题的是()A. p∧qB. p∨(非q)C. (非p)∧qD. p∧(非q)4.已知向量a⃗=(1,√3),b⃗ 单位向量,若|a⃗−b⃗ |=√3,则<a⃗,b⃗ >=()A. π6B. π4C. π3D. 2π35.若cos2αsin(α−π4)=−√22,则cosα+sinα的值为()A. −√72B. −12C. 12D. √726.y=4cosx−e|x|图象可能是()A. B.C. D.7.如图,在底面边长为1,高为2的正四棱柱ABCD−A1B1C1D1中,点P是平面A1B1C1D1内一点,则三棱锥P−BCD的正视图与侧视图的面积之和为()A. 2B. 3C. 4D. 58. 抛物线y 2=ax(a >0)的准线与双曲线C :x 28−y 24=1的两条渐近线所围成的三角形面积为2√2,则a 的值为( ) A. 8 B. 6 C. 4 D. 29. 《九章算术》勾股章有一“引葭赴岸”问题“今有饼池径丈,葭生其中,出水两尺,引葭赴岸,适与岸齐,问水深,葭各几何?”,其意思是:有一个直径为一丈的圆柱形水池,池中心生有一颗类似芦苇的植物,露出水面两尺,若把它引向岸边,正好与岸边齐,问水有多深,该植物有多高?其中一丈等于十尺,如图若从该葭上随机取一点,则该点取自水下的概率为( )A. 1213B. 1314C. 2129D. 141510. 执行如图所示的程序框图,则输出的结果为( )A. 40322017B. 20152016C. 20162017D. 2015100811. 如图,在平面直角坐标系xOy 中,F 是椭圆x 2a2+y 2b 2=1(a >b >0)的右焦点,直线y =b2与椭圆交于B ,C 两点,且∠BFC =90°,则该椭圆的 离心率为( )A. √63B. 2√33C. 12D. √2212. 已知函数f(x)={(x −2)(x −e x )+3,(x ≥ln2)3−2x,(x <ln2),当x ∈[m,+∞)时,f(x)的取值范围为(−∞,e +2],则实数m 的取值范围是( )A. (−∞,1−e 2] B. (−∞,1] C. [1−e 2,1] D. [ln2,1]二、填空题(本大题共4小题,共20.0分)13. 在一次医疗救助活动中,需要从A 医院某科室的6名男医生、4名女医生中分别抽调3名男医生、2名女医生,且男医生中唯一的主任医师必须参加,则不同的选派案共有______种.(用数字作答)14. 若x ,y 满足|x|≤1−y ,且y ≥−1,则3x +y 的最大值为______.15. 在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,∠ABC =120°,∠ABC 的平分线交AC 于点D ,且BD =1,则4a +c 的最小值为______.16.棱长为a的正四面体ABCD与正三棱锥E−BCD的底面重合,若由它们构成的多面体ABCDE的顶点均在一球的球面上,则正三棱锥E−BCD的内切球半径为______.三、解答题(本大题共7小题,共82.0分)S n+1(n∈N∗).17.已知数列的前n项和为S n,且满足a n=12(1)求数列{a n}的通项公式;(2)若b n=log2a n,c n=1,且数列{c n}的前n项和为T n,求T n的取值范围.b n b n+118.棉花的纤维长度是评价棉花质量的重要指标,某农科所的专家在土壤环境不同的甲、乙两块实验地分别种植某品种的棉花,为了评价该品种的棉花质量,在棉花成熟后,分别从甲、乙两地的棉花中各随机抽取20根棉花纤维进行统计,结果如下表:(记纤维长度不低于300mm的为“长)为“纤维长度与土壤环境有关系”.;附:(1)k2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)抽取8根进行检测,在这8根纤维中,记乙地“短纤维”的根数为X,求X的分布列及数学期望.19. 在底面为菱形的四棱柱ABCD −A 1B 1C 1D 1中,AB =AA 1=2,A 1B =A 1D ,∠BAD =60°,AC ∩BD =O ,AO ⊥平面A 1BD . (1)证明:B 1C//平面A 1BD ;(2)求二面角B −AA 1−D 的正弦值.20. 如图,点T 为圆O :x 2+y 2=1上一动点,过点T 分别作x 轴,y 轴的垂线,垂足分别为A ,B ,连接BA 延长至点P ,使得BA ⃗⃗⃗⃗⃗ =AP⃗⃗⃗⃗⃗ ,点P 的轨迹记为曲线C . (1)求曲线C 的方程;(2)若点A ,B 分别位于x 轴与y 轴的正半轴上,直线AB 与曲线C 相交于M ,N 两点,|AB|=1,试问在曲线C 上是否存在点Q ,使得四边形OMQN 为平行四边形,若存在,求出直线l 方程;若不存在,说明理由.21. 已知函数f(x)=x 3−3ax +e ,g(x)=1−lnx ,其中e 为自然对数的底数.(1)讨论函数f(x)的单调性;(2)用max{m,n}表示m ,n 中较大者,记函数ℎ(x)=max{f(x),g(x)},(x >0).若函数ℎ(x)在(0,+∞)上恰有2个零点,求实数a 的取值范围.22. 在平面直角坐标系中,曲线C 1:x 2−y 2=2,曲线C 2的参数方程为{x =2+2cosθy =2sinθ(θ为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系. (Ⅰ)求曲线C 1,C 2的极坐标方程;(Ⅱ)在极坐标系中,射线θ=π6与曲线C 1,C 2分别交于A ,B 两点(异于极点O),定点M(3,0),求△MAB的面积.23.设不等式−2<|x−1|−|x+2|<0的解集为M,a、b∈M,(1)证明:|13a+16b|<14;(2)比较|1−4ab|与2|a−b|的大小,并说明理由.-------- 答案与解析 --------1.答案:D解析:解:z=|3+4i|1+i =√32+42(1−i)(1+i)(1−i)=52−52i.∴z对应的点(52,−52)位于复平面的第四象限.故选:D.利用复数的运算法则、几何意义即可得出.本题考查了复数的运算法则、几何意义,考查了推理能力与计算能力,属于基础题.2.答案:B解析:【分析】考查描述法的定义,对数函数的单调性,补集和交集的运算.可解出集合A,B,然后进行交集、补集的运算即可.【解答】解:A={x|x<−1或x>2},B={x|0<x≤4};∴∁R A={x|−1≤x≤2};∴(∁R A)∩B={x|0<x≤2}.故选B.3.答案:C解析:解:根据线面平行的判定,我们易得命题p:若直线a//b,直线b⊂平面α,则直线a//平面α或直线a在平面α内,命题p为假命题;根据线面垂直的定义,我们易得命题q:若直线l⊥平面α,则若直线l与平面α内的任意直线都垂直,命题q为真命题;故:A命题“p∧q”为假命题;B命题“p∨(¬q)”为假命题;C命题“(¬p)∧q”为真命题;D命题“p∧(¬q)”为假命题.故选:C.根据空间线面平行及线面垂直的判定与性质,我们易判断命题p与命题q的真假,进而根据复合命题的真假,对题目中的四个结论逐一进行分析,即可得到答案.本题考查的知识点是空间线面平行的判定,及空间线面垂直的定义,及复合命题的真假,其中根据空间点线关系的定义,判断命题p与命题q的真假,是解答本题的关键.属于基础题.4.答案:C解析:解:向量a⃗=(1,√3),b⃗ 单位向量,若|a⃗−b⃗ |=√3,可得|a⃗−b⃗ |2=3,即a⃗2−2a⃗⋅b⃗ +b⃗ 2=3.4−2|a⃗|⋅|b⃗ |cos<a⃗,b⃗ >+1=3,cos<a⃗,b⃗ >=12.∴<a⃗,b⃗ >=π3.故选:C.通过向量的模的平方,结合数量积求解即可.本题考查平面向量的数量积以及向量的夹角的求法,考查计算能力.5.答案:C解析:【分析】本题考查两角和与差的三角函数及二倍角公式,属基础题.由cos2α=cos2α−sin2α及sin(α−π4)=√22(sinα−cosα)即可得解.【解答】解:∵cos2αsin(α−π4)=22√22(sinα−cosα)=−√2(sinα+cosα)=−√22,∴cosα+sinα=12,故选C.6.答案:D解析:解:显然y=4cosx−e|x|是偶函数,图象关于y轴对称,当x>0时,y′=−4sinx−e x=−(4sinx+e x),显然当x∈(0,π]时,y′<0,当x∈(π,+∞)时,e x>eπ>e3>4,而4sinx≥−4,∴y′=−(4sinx+e x)<0,∴y′=−(4sinx+e x)<0在(0,+∞)上恒成立,∴y=4cosx−e|x|在(0,+∞)上单调递减.故选:D.判断函数的奇偶性,利用导数判断函数在(0,+∞)上的单调性即可得出结论.本题考查了函数图象的判断,一般从奇偶性,单调性,特殊值等方面判断,属于基础题.7.答案:A解析:【分析】本题考查的知识点是简单空间图形的三视图的面积计算,属于简单题.分析三棱锥P−BCD的正视图与侧视图的形状,并求出面积,相加可得答案.【解答】解:三棱锥P−BCD的正视图是底面边长为1,高为2的三角形,面积为1,三棱锥P−BCD的侧视图也是底面边长为1,高为2的三角形,面积为1,故三棱锥P−BCD的正视图与侧视图的面积之和为2,故选:A.8.答案:A解析:【分析】求得抛物线的准线方程和双曲线的渐近线方程,解得两交点,由三角形的面积公式,计算即可得到所求值.本题考查三角形的面积的求法,注意运用抛物线的准线方程和双曲线的渐近线方程,考查运算能力,属于基础题.【解答】解:抛物线y2=ax的准线为x=−a4,双曲线C:x28−y24=1的两条渐近线为y=±√22x,可得两交点为(−a4,√28a),(−a4,−√28a),即有三角形的面积为12⋅a4⋅√24a=2√2,解得a=8,故选:A.9.答案:C解析:解:设水深为x尺,则(x+2)2=x2+52,解得x=214,即水深214尺.又葭长214+2=294尺,则所求概率P=214294=2129,故选:C.设水深为x尺,利用勾股定理求出水深,结合葭长214+2=294尺,代入几何概型概率计算公式,可得答案.本题考查几何概型概率的求法,考查勾股定理的应用,是基础题.10.答案:D解析:解:第1次执行循环体后:S=1,t=22,i=2,不满足退出循环的条件;第2次执行循环体后:S=3,t=43,i=3,不满足退出循环的条件;第3次执行循环体后:S=6,t=64,i=4,不满足退出循环的条件;第4次执行循环体后:S=10,t=85,i=5,不满足退出循环的条件;…第n 次执行循环体后:S =n(n+1)2,t =2nn+1,i =n +1,不满足退出循环的条件;…第2014次执行循环体后:S =2039180,t =40282015,i =2015,不满足退出循环的条件; 第2015次执行循环体后:S =2041195,t =40302016=20151008,i =2016,满足退出循环的条件; 故输出的t 值为20151008,故选:D .由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量i 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题. 11.答案:A解析:【分析】本题考查椭圆的离心率的求法,注意运用两直线垂直的条件:斜率之积为−1,考查化简整理的运算能力,属于中档题.设右焦点F(c,0),将y =b2代入椭圆方程求得B ,C 的坐标,运用两直线垂直的条件:斜率之积为−1,结合离心率公式,计算即可得到所求值.【解答】解:设右焦点F(c,0),将y =b2代入椭圆方程可得x =±a √1−b 24b 2=±√32a , 可得B(−√32a,b 2),C(√32a,b2),由∠BFC =90°,可得k BF ⋅k CF =−1, 即有b 2−√32a−c ⋅b 2√32a−c =−1,化简为b 2=3a 2−4c 2,由b 2=a 2−c 2,即有3c 2=2a 2, 由e =ca ,可得e 2=c 2a 2=23,可得e =√63,故选:A . 12.答案:C解析:解:当x ≥ln2时,f(x)=(x −2)(x −e x )+3的导数为f′(x)=(x −1)(2−e x ),当ln2≤x ≤1时,f′(x)≤0,f(x)递减;x >1时,f′(x)>0,f(x)递增,x =1处f(x)取得极大值2+e , 作出y =f(x)的图象,由当x ∈[m,+∞)时,f(x)的取值范围为(−∞,e +2], 由3−2x =2+e ,可得x =1−e 2,可得1−e 2≤m ≤1.故选:C .当x ≥ln2时,求得f(x)的导数和单调性、极大值,画出f(x)的图象,求得3−2x =2+e 的x 的值,结合额图象和条件可得m 的范围.本题考查分段函数的图象和性质,注意运用导数判断单调性和极值,考查数形结合思想方法和运算能力,属于中档题. 13.答案:60解析:解:男医生中唯一的主任医师必须参加,则从剩余5名男医生中选2名,从4名女医生中选2名,共有C 52C 42=10×6=60, 故答案为:60男主任医师必选,则从剩余5名男医生中选2名,从4名女医生中选2名,利用组合的公式进行计算即可.本题主要考查组合的应用,利用组合数公式是解决本题的关键.比较基础. 14.答案:5解析:解:由|x|≤1−y ,且y ≥−1,作出可行域如图,联立{y =−1x +y −1=0,解得A(2,−1),令z =3x +y ,化为y =−3x +z ,由图可知,当直线y =−3x +z 过点A 时,z 有最大值为3×2−1=5. 故答案为:5.由约束条件作出可行域,令z =3x +y ,化为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题. 15.答案:9解析:【分析】本题主要考查基本不等式的应用,利用1的代换结合基本不等式是解决本题的关键.根据面积关系建立条件等式,结合基本不等式利用1的代换的方法进行求解即可.【解答】解:由题意得12acsin120°=12asin60°+12csin60°,即ac=a+c,得1a +1c=1,得4a+c=(4a+c)(1a +1c)=ca+4ac+5≥2√ca⋅4ac+5=4+5=9,当且仅当ca =4ac,即c=2a,亦即a=32,c=3时,取等号,故答案为:9.16.答案:3√2−√612a解析:解:∵棱长为a的正四面体ABCD与正三棱锥E−BCD的底面重合,由它们构成的多面体ABCDE的顶点均在一球的球面上,∴多面体ABCDE的外接球即正四面体ABCD的外接球,且其外接球的直径为AE,由题意得正四面体ABCD的高为√63a,外接球的半径为√64a,设正三棱锥E−BCD的高为h,∵AE=√62a=√63a+ℎ,∴ℎ=√66a,∵底面△BCD的边长为a,∴EB=EC=ED=√22a,则正三棱锥E−BCD的三条侧棱两两垂直,由题意得正棱锥E−BCD的表面积S=3+√34a2,体积V E−BCD=13×12×√22a×√22a×√22a=√224a3,设正三棱锥E−BCD的内切球的半径为r,由13S⋅r=√224a3,得r=3√2−√612a.故答案为:3√2−√612a.多面体ABCDE的外接球即正四面体ABCD的外接球,且其外接球的直径为AE,由题意得正四面体ABCD的高为√63a,外接球的半径为√64a,正三棱锥E−BCD的高为√66a,EB=EC=ED=√22a,则正三棱锥E−BCD的三条侧棱两两垂直,求出正棱锥E−BCD的表面积S=3+√34a2,体积为V E−BCD=√224a3,由此能求出正三棱锥E−BCD的内切球的半径.本题考查正三棱锥内切球的半径的求法,考查正四面体、正三棱锥及内切球性质等基础知识,考查运算求解能力和空间想象能力,是中档题.17.答案:解:(1)当n=1时,a1=12S1+1,解得a1=2当n≥2时,a n−1=12S n−1+1…①a n=12S n+1…②②−①得a n−a n−1=12a n即a n=2a n−1∴数列{a n}是以2为首项,2为公比的等比数列∴a n=2n(2)b n=log2a n=log22n=nc n=1b n b n+1=1n(n+1)=1n−1n+1T n=1−12+12−13+13−14+⋯+1n−1n+1=1−1n+1∵n∈N∗∴1n+1∈(0,12]∴T n∈[12,1)解析:(1)由a1=12S1+1,可求a1,然后由n≥2时,a n=s n−s n−1可得a n=2a n−1,根据等比数列的通项可求(2)由b n=log2a n=log22n=n,而c n=1b n b n+1=1n(n+1)=1n−1n+1,利用裂项可求T n,即可求解本题主要考查了递推公式,a n=s n−s n−1,(n≥2)在数列的通项求解中的应用,等比数列的通项公式的应用及裂项求和方法的应用,属于数列知识的综合应用.18.答案:9;16;25;11;4;15;20;20;402×2列联表:根据2×2列联表中的数据,可得K2=40(9×4−16×11)225×15×20×20≈5.227>5.024所以,在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.(Ⅱ)由表可知在8根中乙地“短纤维”的根数为1540×8=3,X的可能取值为:0,1,2,3,P(X=0)=C 113C 153=3391,P(X =1)=C 112C 41C 153=4491,P(X =2)=C 111C 42C 153=66455,P(X =3)=C 43C 153=4455. X 0 1 2 3 P33914491654554455∴E(X)=0×3391+1×4491+2×65455+3×4455=364455=45. (I)利用k 2的计算公式即可得出.(Ⅱ)由表可知在8根中乙地“短纤维”的根数为1540×8=3,X 的可能取值为:0,1,2,3,利用P(X =k)=∁113−k ∁4k∁153即可得出.本题考查了独立性检验原理、超几何分布列的概率计算公式与数学期望计算公式,考查了推理能力与计算能力,属于中档题.19.答案:解:(1)依题意,A 1B 1//AB ,A 1B 1C =AB ,AB//CD ,AB =CD ,∴A 1B 1=CD ,A 1B 1//CD ,∴四边形A 1B 1CD 是平行四边形, ∴B 1C//A 1D ,∵B 1C ⊄平面A 1BD ,A 1D ⊂平面A 1BD , ∴B 1C//平面A 1BD ;(2)∵AO ⊥平面A 1BD ,∴AO ⊥A 1O ,∵A 1B =A 1D 且O 为BD 的中点,∴A 1O ⊥BD , ∵AO 、BD ⊂平面ABCD ,且AO ∩BD =O , ∴A 1O ⊥平面ABCD ,以O 为原点,分别以OA ⃗⃗⃗⃗⃗ ,OB ⃗⃗⃗⃗⃗⃗ ,OA 1⃗⃗⃗⃗⃗⃗⃗⃗ 为x 轴、y 轴、z 轴的正方向,建立如图所示的空间直角坐标系O −xyz , 则A(√3,0,0),B(0,1,0),D(0,−1,0),A 1(0,0,1),∴AA 1⃗⃗⃗⃗⃗⃗⃗ =(−√3,0,1),AB ⃗⃗⃗⃗⃗ =(−√3,1,0),AD⃗⃗⃗⃗⃗⃗ =(−√3,−1,0), 设平面A 1AB 的法向量为n⃗ =(x,y,z), 则{n ⃗ ⋅AA 1⃗⃗⃗⃗⃗⃗⃗ =0n⃗ ⋅AB ⃗⃗⃗⃗⃗ =0,∴{−√3x +z =0−√3x +y =0,取x =1,则n ⃗ =(1,√3,√3),设平面A 1AD 的法向量为m⃗⃗⃗ =(x 1,y 1,z 1), 则{m ⃗⃗⃗ ⋅AA 1⃗⃗⃗⃗⃗⃗⃗ =0m ⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ =0,∴{−√3x +z =0−√3x −y =0,取x =1,则m ⃗⃗⃗ =(1,−√3,√3)∴cos <m ⃗⃗⃗ ,n ⃗ >=m ⃗⃗⃗ ⋅n ⃗⃗|m ⃗⃗⃗ |⋅|n ⃗⃗ |=√7×√7=17, 设二面角B −AA 1−D 的平面角为α,则sinα=√1−(17)2=4√37, ∴二面角B −AA 1−D 的正弦值为4√37.解析:(1)根据题意,得到四边形A 1B 1CD 是平行四边形,得到B 1C//A 1D ,再根据线面平行的判定定理证明即可;(2)根据题意,以O 为原点,分别以OA ⃗⃗⃗⃗⃗ ,OB ⃗⃗⃗⃗⃗⃗ ,OA 1⃗⃗⃗⃗⃗⃗⃗⃗ 为x 轴、y 轴、z 轴的正方向,建立如图所示的空间直角坐标系O −xyz ,求出平面A 1AB 的法向量和平面A 1AD 的法向量,利用夹角公式求出即可. 本题主要考查直线与直线、直线与平面的位置关系,二面角等基础知识,意在考查直观想象、逻辑推理与数学运算的数学核心素养,中档题. 20.答案:解:(1)设T(x 0,y 0),P(x,y), 由A(x 0,0),B(0,y 0)由题意BA ⃗⃗⃗⃗⃗ =AP⃗⃗⃗⃗⃗ ,即A 为PB 的中点 ∴x =2x 0,y =−y 0, 即x 0=12x ,y 0=−y ,∵x 02+y 02=1故点P 的轨迹C 的方程为x 24+y 2=1,(2)由题意知l 的斜率存在且不为零,设直线l 的方程为y =kx +t , ∵|AB|=1, ∴(−tk )2+t 2=1,即t 2k 2+t 2=1,① 联立{y =kx +tx 24+y 2=1,消y 可得(4k 2+1)x 2+8ktx +4(t 2−1)=0,设M(x 1,y 1),N(x 2,y 2), ∴x 1+x 2=−8kt1+4k 2,x 1x 2=4(t 2−1)4k 2+1, ∴y 1+y 2=k(x 1+x 2)+2t =2t4k 2+1,∵四边形OMQN 为平行四边形,故Q(−8kt1+4k 2,2t4k 2+1), ∴14(−8kt 1+4k2)2+(2t 4k 2+1)2=1,整理可得4t 2=4k 2+1,②,将①代入②可得4k 4+k 2+1=0,该方程无解, 故这样的直线不存在.解析:(1)设T(x 0,y 0),P(x,y),通过BA⃗⃗⃗⃗⃗ =AP ⃗⃗⃗⃗⃗ ,即A 为PB 的中点,转化求解,点P 的轨迹C 的方程.(2)设直线l 的方程为y =kx +t ,先根据|AB|=1,可得t 2k 2+t 2=1,①,再根据韦达定理,点在椭圆上可得4t 2=4k 2+1,②,将①代入②可得4k 4+k 2+1=0,该方程无解,问题得以解决 本题考查点的轨迹方程的求法,考查满足条件的点是否存在的判断与直线方程的求法,体现了数学转化思想方法,是中档题.21.答案:解:(1)f′(x)=3x 2−3a ,当a ≤0时,f′(x)≥0,f(x)在R 上单调递增, 当a >0时,f′(x)=3(x +√a)(x −√a),当x ∈(−∞,−√a),(√a,+∞),f′(x)>0,f(x)单调递增, 当x ∈(−√a,√a),f′(x)<0,f(x)单调递减;(2)当x ∈(0,e)时,g(x)>0,ℎ(x)≥g(x)>0,ℎ(x)在(0,e)无零点, 当x =e 时,g(e)=0,f(e)=e 3−3ae +e , 若f(e)≤0,即a ≥e 2+13,则e 是ℎ(x)的一个零点, 若f(e)>0,即a <e 2+13,则e 不是ℎ(x)的零点,当x ∈(e,+∞)时,g(x)<0,所以此时只需考虑函数f(x)的零点的情况.因为f′(x)=3x 2−3a >3e 2−3a ,①当a ≤e 2时,f′(x)>0,f(x)在(e,+∞)上单调递增. 所以:(ⅰ)当a ≤e 2+13时,f(e)≥0,f(x)在(e,+∞)上无零点;(ⅰ)当e 2+13<a ≤e 2时,f(e)<0,又f(2e)=8e 3−6ae +e ≥8e 3−6e 2+e >0,所以此时f(x)在(e,+∞)上恰有一个零点;②当a >e 2时,由(1)知,f(x)在(e,√a)递减,(√a,+∞)递增,又因为f(e)=e 3−3ae +e <e 3−3e 3+e <0,f(2a)=8a 3−6a 2+e >8a 2−6a 2+e =2a 2+e >0,所以此时f(x)恰有一个零点. 综上,a >e 2+13.解析:(1)含参的求导判断单调性;(2)ℎ(x)=max{f(x),g(x)},(x >0),对x ∈(0,e),x =e ,x ∈(e,+∞)三种情况讨论函数f(x),与g(x)的零点问题,得出结论.本题考查用导数法判断含参问题的单调性,函数的零点问题,是一道函数与导数综合性很高的题,难度大,注意分类讨论的细节.22.答案:解:(Ⅰ)∵曲线C 1:x 2−y 2=2,∴曲线C 1的极坐标方程为:ρ2cos 2θ−ρ2sin 2θ=2,---------(2分) ∵曲线C 2的参数方程为{x =2+2cosθy =2sinθ(θ为参数).∴曲线C 2的普通方程为:(x −2)2+y 2=4,---------(3分) ∴x 2+y 2−4x =0,∴曲线C 2的极坐标方程为ρ=4cosθ.---------------(4分) (Ⅱ)由(Ⅰ)得:点A 的极坐标为(2,π6),---------(5分) 点B 的极坐标为(2√3,π6),----------(6分)∴|AB|=|2−2√3|=2√3−2,------------------(7分)M(3,0)点到射线θ=π6(ρ≥0)的距离为d =3sin π6=32,--------------------------(8分) ∴△MAB 的面积为:S △MAB =12|AB|d =12×(2√3−2)×32=3√3−32.---------(10分)解析:(Ⅰ)由曲线C 1的普通方程能求出曲线C 1的极坐标方程;由曲线C 2的参数方程能求出曲线C 2的普通方程,由此能求出曲线C 2的极坐标方程.(Ⅱ)点A 的极坐标为(2,π6),点B 的极坐标为(2√3,π6),从而|AB|=|2−2√3|=2√3−2,M(3,0)点到射线θ=π6(ρ≥0)的距离为d =3sin π6=32,由此能求出△MAB 的面积.本题考查曲线的极坐标方程的求法,考查三角形面积的求法,考查直角坐标方程、极坐标方程、参数方程的互化等基础知识,考查运算求解能力,考查函数与方程思想,是中档题. 23.答案:解:(1)记f(x)=|x −1|−|x +2|={3,x ≤−2−2x −1,−2<x <1−3,x ≥1,由−2<−2x −1<0解得−12<x <12,则M =(−12,12).…(3分) ∵a 、b ∈M ,∴|a|<12,|b|<12所以|13a +16b|≤13|a|+16|b|<13×12+16×12=14.…(6分) (2)由(1)得a 2<14,b 2<14.因为|1−4ab|2−4|a −b|2=(1−8ab +16a 2b 2)−4(a 2−2ab +b 2) =(4a 2−1)(4b 2−1)>0,…(9分)所以|1−4ab|2>4|a −b|2,故|1−4ab|>2|a −b|.…(10分)解析:(1)利用绝对值不等式的解法求出集合M ,利用绝对值三角不等式直接证明:|13a +16b|<14; (2)利用(1)的结果,说明ab 的范围,比较|1−4ab|与2|a −b|两个数的平方差的大小,即可得到结果.本题考查不等式的证明,绝对值不等式的解法,考查计算能力.。
2023届宁夏回族自治区银川一中高三下学期第二次模拟考试 数学(理)答案

银川一中2023届高三第二次模拟数学(理科)参考答案一、单选题1.【答案】A【分析】根据给定条件,求出复数z 及z ,再利用复数除法运算求解作答.【详解】依题意,12z i =+,则12i z =-,所以12i (12i)(12i)34i 34i 12i (12i)(12i)555z z +++-+====-+--+.故选:A2.【答案】D 【分析】由已知可推得2B ∈,代入即可解得2m =-,代入即可得出答案.【详解】由题意可知,2B ∈,即2220m -+=,所以2m =-,所以,{}{}2202,1B x x x =--==-.故选:D.3.【答案】C【分析】根据含量词命题的否定形式可得到原命题,通过反例可说明原命题为假命题.【详解】 命题P 的否定为特称命题,P ∴:x ∀∈R ,211x +>,当0x =时,211x +=,P ∴为假命题,ABD 错误,C 正确.故选:C.4.【答案】B【分析】求出基本事件总数,再求出和为奇数事件所包含的基本事件个数,根据古典概型求解.【详解】不超过17的质数有:2,3,5,7,11,13,17,共7个,随机选取两个不同的数,基本事件总数27C 21n ==,其和为奇数包含的基本事件有:(2,3),(2,5),(2,7),(2,11),(2,13),(2,17),共6个,所以62217P ==.故选:B 5.【答案】B【分析】执行程序即可算出其输出值结果.【详解】由题意可知,流程图的功能为计算111111223344556S =++++⨯⨯⨯⨯⨯的值,裂项求和可得:111111111122334455566S ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+-= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.故选:B.6.【答案】D【分析】根据一次函数、反比例函数、幂函数和分段函数的性质,逐个选项进行判断即可得到答案.【详解】对于A :函数2y x =-+的定义域为R ,值域也为R ,不符合题意;对于B:函数y =的定义域和值域都为[)0,∞+,不符合题意;对于C :2y x =的定义域和值域都为{}0x x ≠,不符合题意;对于D :2,02,0x x y x x -≤⎧=⎨+>⎩的定义域为R ;当0x ≤时,22y x =-≤-;当0x >时,22y x =+>;所以值域为(](),22,∞∞--⋃+,定义域和值域不相同,符合题意;故选:D .7.【答案】A【分析】利用向量垂直的坐标表示,结合数量积公式,即可求解.【详解】因为()2cos 75cos152sin 75sin152cos 15750a b ⋅=-=+=,2a = ,1b = .所以()()222280a b a b a b λλλ+⋅-=-=-= .所以8λ=.故选:A 8.【答案】A 【分析】由题意求出双曲线的一条渐近线的倾斜角,可得渐近线的斜率,根据离心率的计算公式可得答案.【详解】由题意设一条渐近线的倾斜角为π,(0,)2αα∈,则另一条渐近线的倾斜角为5α,由双曲对称性可得π5π,=6ααα+=∴,则一条渐近线的斜率为πtan 6=设双曲线的长半轴长为a ,短半轴长为b,则b a =,故离心率为3e ==,故选:A 9.【答案】C 【分析】根据已知条件求得123R h =,243R h =,代入体积公式计算即可.【详解】设小球缺的高为1h ,大球缺的高为2h ,则122h h R +=,①由题意可得:122π12π2Rh Rh =,即:212h h =,②所以由①②得:123R h =,243R h =,所以小球缺的体积23112228ππ333381R R R V R ⎛⎫⎛⎫=-⨯= ⎪ ⎝⎭⎝⎭,大球缺的体积23214480ππ333381R R R V R ⎛⎫⎛⎫=-⨯= ⎪ ⎪⎝⎭⎝⎭,所以小球缺与大球缺体积之比为313228π78180π2081R V R V ==.故选:C.10【答案】B 【分析】由判别式可解得6k ,由根与系数关系可得121212111331x x k x x x x k k ++===++ ,由k 的范围结合不等式的性质变形可得答案.【详解】由题意可得∆2()4(3)0k k =--+,解得6k 或2k ≤-,设两个为1x ,2x ,由两根为正根可得12120·30x x k x x k +=>⎧⎨=+>⎩,解得0k >,综上知,6k .故两个根的倒数和为12121211x x x x x x ++=1331kk k==++,6k ,∴1106k <,3102k <,故33112k <+,∴12331k+,故两个根的倒数和的最小值是23.故选:B 11.【答案】B 【分析】根据二倍角公式得到11tan 10γ=,代入式子得到22111061410hhD d ==++,解得答案.【详解】10sin 211cos 21γγ=+,即220sin cos 10tan 112cos γγγγ==,所以11tan 10γ=,22111061410h h D d ==++,解得66h =,故选:B.12.【答案】B【分析】结合229x y +≥可确定曲线上的点的位置,结合双曲线和圆的图象可确定曲线Γ的图象,采用数形结合的方式可求得结果.【详解】由题意得:2290x y +-≥,即229x y +≥,即曲线Γ上的点(),x y 为圆229x y +=上或圆229x y +=外的点,由221033x y ⎛⎫-- ⎪⎝⎭得:22133y x -=或229x y +=,由22221339x y x y ⎧-=⎪⎨⎪+=⎩得:xy ⎧=⎪⎨=⎪⎩x y ⎧=⎪⎨=⎪⎩x y ⎧⎪⎨⎪⎩x y ⎧=⎪⎨=⎪⎩由此可得曲线Γ的图象如下图所示,由图象可知:当()3,m ∈- 时,直线y m =与曲线Γ有四个不同交点;∴实数m的取值范围为()3,- .故选:B.二、填空题13.【答案】11【分析】根据题设的抽取方式,结合随机表法依次写出所得编号,即可得答案.【详解】由题设,依次取出的编号为08、02、14、07、11、05,所以第5个个体的编号为11.故答案为:1114.【答案】2【分析】由题,利用导数及韦达定理可得37a a,后利用等比中项性质可得答案.【详解】()284f x x x '=-+,由题37a a ,是方程2840x x -+=的两个不等实根,则由韦达定理373740,80a a a a =>+=>,所以370,0a a >>又5a 是37a a ,的等比中项且5a 与37a a ,同号,则2555402a a a =>⇒=,.故答案为:2.15.【答案】60︒【分析】把展开图恢复到原正方体,得到AE //DC ,从而得到∠BAE 或其补角是异面直线AB 与CD 所成的角,从而可解.【详解】如图所示,把展开图恢复到原正方体.连接AE ,BE .由正方体可得//CE AD 且CE AD =,∴四边形ADCE 是平行四边形,∴AE //DC .∴BAE ∠或其补角是异面直线AB 与CD 所成的角.由正方体可得:AB AE BE ==,∴ABE 是等边三角形,∴60=︒∠BAE .∴异面直线AB 与CD 所成的角是60°.故答案为:60°16.【答案】1【分析】构造函数()x f x e =,设切点为11(,)x y ,设()ln g x x =,设切点为22(,)x y ,结合条件得到12,x x 是函数()f x e x =和()ln g x x =的图象与曲线1y x =交点的横坐标,利用对称性得出1122(,),(,)x y x y 关于直线y x =对称,从而得出12e x x =,12ln x x =,然后计算出12k k .【详解】设()x f x e =,则()e x f x '=,设切点为11(,)x y ,则11e x k =,则切线方程为111e ()x y y x x -=-,即111e e ()x x y x x -=-,直线1(1)1y k x =+-过定点(1,1)--,所以1111e e (1)x x x --=--,所以11e 1x x =,设()ln g x x =,则1()g x x '=,设切点为22(,)x y ,则221k x =,则切线方程为2221()y y x x x -=-,即2221ln ()y x x x x -=-,直线1(1)1y k x =+-过定点(1,1)--,所以22211ln (1)x x x --=--,所以22ln 1x x =,则12,x x 是函数()f x e x =和()ln g x x =的图象与曲线1y x =交点的横坐标,易知()f x 与()g x 的图象关于直线y x =对称,而曲线1y x =也关于直线y x =对称,因此点1122(,),(,)x y x y 关于直线y x =对称,从而12e x x =,12ln x x =,所以1122e 1x k k x ==.故答案为:1.三、解答题17.【答案】(1)21n a n =+;(2)详见解析.【分析】(1)设数列{}n a 的公差为d ,将已知条件转化为1,a d 关系,即可求解;(2)根据{}n b 通项公式,用裂项相消法求出和n T ,即可证明结论.【详解】(1)由设数列{}n a 的公差为d ,则11393315a d a d +=⎧⎨+=⎩解得2d =,13a =,所以{}n a 是首项为3,公差为2的等差数列,所以21n a n =+;(2)由21n a n =+,可得111111()(21)(23)22123n n n b a a n n n n +===-++++,所以12n n T b b b =+++ 1111111()()()235572123n n ⎡⎤=-+-++-⎢⎥++⎣⎦11111()2323646n n =-=-++,又1046n >+,故.18.【答案】(1)12(2)分布列见解析,()87E X =(3)3月3日【分析】(1)根据古典概型公式求解即可.(2)根据题意得到0,1,2X =,()2327C 10C 7P X ===,()113427C C 41C 7P X ===,()2427C 22C 7PX ===,再写出分布列数学期望即可.(3)根据折线图和频率分布直方图求解即可.【详解】(1)令时间A 为“职工甲和职工乙微信记步数都不低于10000”,从3月2日至3月7日这6天中,3月2日、5日、7日这3天中,甲乙微信记步数都不低于10000,故()3162P A ==.(2)由(1)知:0,1,2X =,()2327C 10C 7P X ===,()113427C C 41C 7P X ===,()2427C 22C 7P X ===,X的分布列为:X 012P 174727()14280127777E X =⨯+⨯+⨯=(3)根据频率分步直方图知:微信记步数落在[]20,25,[)15,20,[)10,15,[)5,10,[)0,5(单位:千步)区间内的人数依次为2000.1530⨯=人,2000.2550⨯=人,2000.360⨯=人,2000.240⨯=人,2000.120⨯=人,由甲微信记步数排名第68,可知当天甲微信记步数在15000到20000万之间,根据折线图知:只有3月2日,3月3日,3月7日.由乙微信记步数排名第142,可知当天乙微信记步数在5000到10000万之间,根据折线图知:只有3月3日和3月6日,所以3月3日符合要求.19.【答案】(1)26y x =(2)证明见解析【分析】(1)将(6,6)M -代入抛物线即可求解;(2)设()()1122,,,A x y B x y ,直线l 的方程为,(0)my x t t =-≠,将直线l 与抛物线进行联立可得12126,6y y m y y t +==-,结合OA OB ⊥可得6t =,即可求证【详解】(1)因为抛物线C 过点(6,6)M -,∴2(6)26p -=⨯,解得3p =,∴抛物线C 的标准方程为26y x =.(2)设()()1122,,,A x y B x y ,直线l 的方程为,(0)my x t t =-≠,联立26my x ty x =-⎧⎨=⎩,化为2660y my t --=,236240m t ∆=+>,∴12126,6y y m y y t +==-,∵OA OB ⊥,∴()212121236y y OA OB x x y y ⋅=+= 12661036t y y t -⎛⎫+=-+= ⎪⎝⎭,0t ≠,16n T <解得6t =,满足236240m t ∆=+>,∴直线l的方程为6my x =-,∴直线过定点()6,0.20.【答案】(1)存在,理由见解析【分析】(1)根据面面平行的判定定理、性质定理分析证明;(2)根据题意结合长方体的外接球可得12AA =,建系,利用空间向量求二面角.【详解】(1)当点D 为AB 的中点时,1O D 平面1A AC ,证明如下:取AB 的中点D ,连接OD ,∵O ,D 分别为BC ,AB 的中点,则OD AC ,OD ⊄平面1A AC ,AC ⊂平面1A AC ,∴OD 平面1A AC ,又∵1OO 1AA ,1OO ⊄平面1A AC ,1AA ⊂平面1A AC ,∴1OO 平面1A AC ,1O O OD O ⋂=,1,O O OD ⊂平面1OO D ,∴平面1OO D 平面1A AC ,由于1O D ⊂平面1OO D ,故1O D ∥平面1A AC .(2)∵BC 是O 的直径,可得90BAC ∠=︒,即AB AC ⊥,且2BC =,30ABC ∠=︒,故AB =1AC =,又∵1AA ⊥平面ABC ,且,AB AC 平面ABC ,∴11,AA AB AA AC ⊥⊥,即AB ,AC ,1AA 两两垂直,且点1A ,A ,B ,C 可知该球为以AB 、AC 、1AA 则(22221AB AC AA ++=,可得12AA =,以A为原点,AB ,AC ,1AA 所在直线分别为x ,y ,z 轴建立直角坐标系,则()0,0,0A,)B ,()0,1,0C ,()10,0,2A ,得)12A B =- ,()10,1,2AC=- ,设(),,n x y z =r 为平面1A BC 的一个法向量,则112020n A B z n A C y z ⎧⋅=-=⎪⎨⋅=-=⎪⎩ ,令2x=,则y z =,可得(2,=r n ,且()0,1,0AC = 为平面1A AB 的一个法向量,设二面角1C A B A--为θ,则cos cos ,19AC n AC n AC n θ⋅===uuu r r uuu r r uuu r r ,所以二面角1C A B A --的余弦值为19.21.【答案】(1)存在,22m -≤≤;(2)①证明见解析;②证明见解析.【分析】(1)根据微积分基本定理求得()f x ,由()10f '=,求得参数a ;利用导数求函数的在区间上的最值,结合一次不等式在区间上恒成立问题,即可求得参数m 的范围;(2)①求得()F x ',利用导数求得()F x 的单调性,即可容易证明;②由①中所求,可得12ln()11k k k +>++,利用对数运算,即可证明.【详解】由题可知2()ln(1)(1)f x a x x =+++,∴()221a f x x x '=+++.(1)由()01f '=,可得2202a ++=,8a =-.又当8a =-时,()()()2311x x f x x +'-=+,故()f x 在区间()0,1单调递减,在()1,+∞单调递增.故函数()f x 在1x =处取得极值,所以8a =-.∵11e <-,82(1)(3)()2211x x f x x x x --+'=++=++.∴()0f x '>,当[]1,x e e ∈-时,由上述讨论可知,()f x 单调递增,故2min ()(1)8f x f e e =-=-+不等式2214()m tm e f x ++-≤对任意[]1,x e e ∈-及[]1,1t ∈-恒成立,即:22222min 14()148m tm e f x m tm e e ++-≤⇔++-≤-+,即:260m tm +-≤对[]1,1t ∈-恒成立,令2()6g t m mt =+-,(1)0g ⇒-≤,(1)0g ≤即260m m --≤,且260m m +-≤,整理得()()320m m -+≤,且()()320m m +-≤,解得:22m -≤≤,即为所求.(2)①∵2()()(1)ln(1)F x f x x x x x =-+-=+-,∴()1xF x x-'=+当0x >时,()0F x '<,∴()F x 在(0,)+∞上单调递减,()(0)0F x F ∴<=即证.②由①可得:ln(1)(0)x x x +<>令:11x k =+,得11ln(111k k +<++,即:12ln()11k k k +>++∴1112322ln ln ln 12(1)1221n n n n n n n n n n +++++⋅⋅⋅+>++⋅⋅⋅++++++++=ln 2即证.【点睛】本题考查由极值点求参数值,利用导数由恒成立问题求参数范围,以及利用导数证明不等式以及数列问题,属压轴题.22.【答案】(1)C 的极坐标方程为2sin22ρθλ=,ππ,Z 2k k θ≠+∈,l的直角坐标方程为40x +=(2)1λ=【分析】(1)消去参数得到C 的普通方程,再利用公式得到极坐标方程,注意定义域,再求出l 的直角坐标方程;(2)将()π12θρ=∈R 代入C 的极坐标方程,求出,A B 的坐标,得到AB 为直径的圆的圆心和半径,根据相切关系得到方程,求出答案.【详解】(1)将曲线C 的参数方程x ty tλ=⎧⎪⎨=⎪⎩消去t ,得C 的普通方程为xy λ=,且因为0t ≠,所以0x ≠,将cos ,sin x y ρθρθ==,ππ,Z 2k k θ≠+∈,代入xy λ=,得2sin cos ρθθλ=,即2sin22ρθλ=,ππ,Z 2k k θ≠+∈,即为C 的极坐标方程,由直线l 的方程πsin 26ρθ⎛⎫-= ⎪⎝⎭化简得1sin cos 222ρθρθ-=,化简得40x +=,即为l 的直角坐标方程.(2)将直线π12θ=代入2sin22ρθλ=,得24ρλ=,即12ρρ==-故以AB 为直径的圆圆心为O,半径r =圆心O 到直线l的距离2d =,由已知得2=,解得1λ=.23.【答案】(1)(0,4)【分析】(1)根据零点分区间,分类求解即可,(2)根据绝对值三角不等关系可得21a =,进而结合基本不等式即可求解.【详解】(1)当1a =-时,()4f x <等价于|1||3|4x x -+-<,当1x ≤时,13420x x x -+-<⇒-<,则01x <≤,当13x <<时,13424x x -+-<⇒<,则13x <<,当3x ≥时,134244x x x -+-<⇒-<,则34x ≤<,综上所述,不等式()4f x <的解集为(0,4).(2)()3(3)2f x x a x a x a x a a =+++≥+-+= ,当且仅当()(3)0x a x a ++≤等号成立,min ()|2|2f x a ∴==,即21a =,24()()a m a m n -+= ,∴22241a m n =+=,∴2222222211445()59()n n m mn m m n mn ⎛⎫⎛⎫+=++=++≥+ ⎪⎪⎝⎭⎝⎭,当且仅当224()()mn mn =,即2()2mn =,即213m =,26n =时,等号成立,故221n m +的最小值为9。
2020年宁夏银川一中高考数学二模试卷(理科) (含答案解析)

2020年宁夏银川一中高考数学二模试卷(理科)一、单项选择题(本大题共12小题,共60.0分)1. 若z =1−i ,则复数z +z 2在复平面上对应的点的坐标为( )A. (1,−3)B. (−3,1)C. (1,1)D. (−1,1)2. 设集合A ={x|(x +3)(x −6)≥0},B ={x|2x ≤14},则(∁R A)∩B =( )A. (−3,6)B. [6,+∞)C. (−3,−2]D. (−∞,−3)U(6,+∞)3. 设α、β是两个不同的平面,l 、m 为两条不同的直线,命题p :若α//β,l ⊂α,m ⊂β,则l//m ,命题q :l//α,m ⊥l ,m ⊂β,则α⊥β则下列命题为真命题的是( )A. p ∨qB. p ∧qC. (¬p)∨qD. p ∧(¬q)4. △ABC 中,BA ⃗⃗⃗⃗⃗ =(√3,1),BC ⃗⃗⃗⃗⃗ =(0,1),则AB ⃗⃗⃗⃗⃗ 与BC ⃗⃗⃗⃗⃗ 的夹角大小为( )A. 2π3B. π4C. π3D. π65. 已知sin (α−π4)=7√210,cos 2α=725,则sin α=( )A. 45B. −45C. 35D. −356. 函数y =3cos x −e |x|的图象可能是( )A. B. C. D.7. 如图,在正四棱柱ABCD −A 1B 1C 1D 1中,AB =1,AA 1=2,点P 是平面A 1B 1C 1D 1内的一个动点,则三棱锥P −ABC 的正视图与俯视图的面积之比的最大值为( )A. 1B. 2C. 12D. 148.抛物线x2=16y的准线与双曲线x29−y23=1的两条渐近线所围成的三角形的面积是()A. 16√3B. 8C. 4D. 29.“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”其意思是:有一个正方形的池塘,池塘的边长为一丈,有一颗芦苇生长在池塘的正中央.露出水面一尺,若把它引向岸边,正好与岸边齐(如图所示),问水有多深,芦苇有多长?其中一丈为十尺.若从该芦苇上随机取一点,则该点取自水上的概率为()A. 1213B. 113C. 314D. 21310.如图所示,执行如图的程序框图,输出的S值是()A. 1B. 10C. 19D. 2811.在平面直角坐标系xOy中,以椭圆x2a2+y2b2=1(a>b>0)上的一点A为圆心的圆与x轴相切于椭圆的一个焦点,与y轴相交于B,C两点,若△ABC是锐角三角形,则该椭圆的离心率的取值范围是()A. (√6−√22,√5−12) B. (√6−√22,1)C. (√5−12,1)D. (0,√5−12) 12. 函数f(x)={2x 3+3x 2 x ≤0ax ex ,x >0在[−2,2]上的最大值为1,则实数a 的取值范围是( )A. [0,+∞)B. [0,e]C. (−∞,0]D. (−∞,e]二、填空题(本大题共4小题,共20.0分)13. 新冠病毒爆发初期,全国支援武汉的活动中,需要从A 医院某科室的6名男医生(含一名主任医师)、4名女医生(含一名主任医师)中分别选派3名男医生和2名女医生,要求至少有一名主任医师参加,则不同的选派方案共有___________种.(用数字作答) 14. 已知实数x ,y 满足{x +y ≥3x +2y ≤5x ≥0y ≥0,则y −2x 的最大值是__________.15. 在面积为2的△ABC 中,a 2+2b 2+c 2的最小值_________.16. 已知正三棱锥P −ABC 的侧面是直角三角形,P −ABC 的顶点都在球O 的球面上,正三棱锥P −ABC 的体积为36,则球O 的表面积为__________. 三、解答题(本大题共7小题,共82.0分)17. 已知数列{a n }的前n 项和S n 与通项a n 满足S n =12(1−a n ).(1)求数列{a n }的通项公式;(2)设函数f(x)=log 13x ,b n =f(a 1)+f(a 2)+⋯+f(a n ),求T n =1b 1+1b 2+1b 3+⋯1b n的值.18. 为推行“新课堂”教学法,某地理老师分别用传统方法和“新课堂”两种不同的教学方法,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.分数[50,59)[60,69)[70,79)[80,89)[90,100)甲班频数56441乙班频数1365(1)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.025的前提下认为“成绩优良与教学方式有关”?甲班乙班总计成绩优良成绩不优良总计,(n=a+b+c+d)附:K2=n(ad−bc)2(a+c)(b+d)(a+b)(c+d)临界值表:P(K2≥k0)0.100.050.0250.010k0 2.706 3.841 5.024 6.635(2)先从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核,在这8人中,记成绩不优良的乙班人数为X,求X的分布列及数学期望.19.如图,在四棱柱ABCD−A1B1C1D1中,底面ABCD为直角梯形,其中AD//BC,且AD=2BC=2AB=4,AB⊥AD,侧面ABB1A1⊥平面ABCD,且四边形ABB1A1是菱形,∠B1BA=π,M为A1D的中点.3(1)证明:CM//平面AA1B1B;(2)求二面角A1−CD−A的余弦值.20.已知点A(−√2,0)和圆B:(x−√2)2+y2=16,点Q在圆B上,线段AQ的垂直平分线角BQ于点P.(1)求点P的轨迹C的方程;(2)轨迹C上是否存在直线2x+y+1=0对称的两点,若存在,设这两个点分别为S,T,求直线ST的方程,若不存在,请说明理由.21.已知函数f(x)=e x−ax(其中e为自然对数的底数).(1)讨论函数f(x)的单调性.(2)当a=e2时,设x1,x2是函数f(x)的两个零点,证明:x1+x2<4.22.已知平面直角坐标系中,曲线C的参数方程为{x=1+√5cosα(α为参数),直线l1:x=0,直y=2+√5sinα线l2:x−y=0,以原点O为极点,x轴的正半轴为极轴(取相同的长度单位)建立极坐标系.(1)求曲线C和直线l1,l2的极坐标方程;(2)若直线l1与曲C交于O,A两点,直线l2与曲线C交于O,B两点,求线段AB的长.23.设f(x)=−x+|2x+1|,不等式f(x)<2的解集是M.(1)求集合M;(2)设a,b∈M,证明:2|ab|+1>|a|+|b|.【答案与解析】1.答案:A解析:本题考查复数的运算以及复数的几何意义,属于基础题.根据复数的运算得z+z2=1−3i,在复平面上对应点的坐标为(1,−3).解:z+z2=1−i+(1−i)2=1−i−2i=1−3i,在复平面上对应点的坐标为(1,−3),故选A.2.答案:C解析:解:A={x|x≤−3,或x≥6},B={x|x≤−2};∴∁R A={x|−3<x<6};∴(∁R A)∩B={x|−3<x≤−2}=(−3,−2].故选:C.可解出集合A,B,然后进行补集、交集的运算即可.考查描述法、区间表示集合的概念,以及补集、交集的运算.3.答案:C解析:解:在长方体ABCD−A1B1C1D1中命题p:平面AC为平面α,平面A1C1为平面β,直线A1D1,和直线AB分别是直线m,l,显然满足α//β,l⊂α,m⊂β,而m与l异面,故命题p为假命题;则¬p真命题;命题q:平面AC为平面α,平面A1C1为平面β,直线A1D1,和直线A1B1分别是直线m,l,显然满足l//α,m⊥l,m⊂β,而α//β,故命题q假命题;¬q为真命题,∴p∨q是假命题,p∧q是假命题,¬p∨q是真命题,p∧¬q是假命题,故选:C对于命题p ,q ,只要把相应的平面和直线放入长方体中,找到反例即可.此题是个基础题.考查面面平行的判定和性质定理,要说明一个命题不正确,只需举一个反例即可,否则给出证明;考查学生灵活应用知识分析解决问题的能力.4.答案:A解析:本题考查了平面向量的数量积与夹角的计算问题,是基础题.根据平面向量的夹角公式求出BA ⃗⃗⃗⃗⃗ 与BC ⃗⃗⃗⃗⃗ 的夹角,再求出AB ⃗⃗⃗⃗⃗ 与BC ⃗⃗⃗⃗⃗ 的夹角大小. 解:△ABC 中,BA ⃗⃗⃗⃗⃗ =(√3,1),BC ⃗⃗⃗⃗⃗ =(0,1), ∴BA ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =√3×0+1×1=1, |BA ⃗⃗⃗⃗⃗ |=√3+1=2,|BC ⃗⃗⃗⃗⃗ |=1,∴cos <BA ⃗⃗⃗⃗⃗ ,BC ⃗⃗⃗⃗⃗ >=BA ⃗⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ |BA ⃗⃗⃗⃗⃗⃗ |×|BC ⃗⃗⃗⃗⃗ |=12×1=12, ∴BA ⃗⃗⃗⃗⃗ 与BC ⃗⃗⃗⃗⃗ 的夹角为π3, ∴AB ⃗⃗⃗⃗⃗ 与BC ⃗⃗⃗⃗⃗ 的夹角为2π3. 故选A .5.答案:C解析:利用两角差的正弦公式和二倍角公式把条件等式都转化为 α角的正弦余弦函数,联立可解得sin α.解:由sin (α−π4)=7√210得sin α−cos α=75,① 由cos 2α=725得cos 2α−sin 2α=725,所以(cos α−sin α)·(cos α+sin α)=725,②由①②可得cos α+sin α=−15,③由①③可得sinα=35.故选C.6.答案:B解析:本题考查了函数图象的判断,一般从奇偶性,单调性,特殊值等方面判断,属于基础题.判断函数的奇偶性,利用导数判断函数在(0,+∞)上的单调性即可得出结论.解:显然y=3cosx−e|x|是偶函数,图象关于y轴对称,当x>0时,y′=−3sinx−e x=−(3sinx+e x),显然当x∈(0,π]时,y′<0,当x∈(π,+∞)时,e x>eπ>e3>4,而3sinx≥−3,∴y′=−(3sinx+e x)<0,∴y′=−(3sinx+e x)<0在(0,+∞)上恒成立,∴y=3cosx−e|x|在(0,+∞)上单调递减.只有B符合,故选B.7.答案:B解析:解:由题意可知,P在正视图中的射影是在C1D1上,AB在正视图中,在平面CDD1C1上的射影是CD,P的射影到CD的距离是AA1=2,所以三棱锥P−ABC的正视图的面积为12×1×2=1;三棱锥P−ABC的俯视图的面积的最小值为12×1×1=12,所以三棱锥P−ABC的正视图与俯视图的面积之比的最大值为112=2,故选:B.由题意确定棱锥P−ABC的正视图的面积,三棱锥P−ABC的俯视图的面积的最小值,即可求出三棱锥P−ABC的正视图与俯视图的面积之比的最大值.本题考查三视图与直观图形的关系,正确处理正射影与射影图形是解题的关键,考查空间想象能力,计算能力.8.答案:A解析:解:抛物线x2=16y的准线方程为y=−4,双曲线x29−y23=1的两条渐近线方程为y=√3∴抛物线的准线与双曲线的两条渐近线的交点坐标为(±4√3,−4)∴抛物线的准线与双曲线的两条渐近线所围成的三角形的面积是12×8√3×4=16√3故选A.确定抛物线的准线与双曲线的两条渐近线的方程,求得交点坐标,即可求得面积.本题考查抛物线的准线与双曲线的两条渐近线,考查学生的计算能力,属于基础题.9.答案:B解析:解:设水深为x尺,根据勾股定理得:(x+1)2=x2+52,解得x=12,∴水深12尺,芦苇长13尺,根据几何概型概率公式得:从芦苇上随机取一点,该点取自水上的概率为p=113.故选:B.设水深为x尺,根据勾股定理求出水深12尺,芦苇长13尺,根据几何概型概率公式能求出从芦苇上随机取一点,该点取自水上的概率.本题考查概率的求法,考查几何概型等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.10.答案:C解析:本题考查了循环结构的程序框图,属于基础题.模拟程序运行,正确写出每次循环得到的S,A的值可得答案.解:模拟执行程序框图,A =1,S =1,满足条件A ≤2, S =10,A =2,满足条件A ≤2, S =19,A =3,不满足条件A ≤2, 退出循环,输出S 的值为19. 故选C .11.答案:A解析:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、锐角三角形,考查了推理能力与计算能力,属于中档题.设椭圆的右焦点F(c,0),代入椭圆的标准方程可得A(c,b 2a ).根据△ABC 是锐角三角形,可得∠BAD <45°,且1>cb 2a>√22,化为{e 2+√2e −1>0e 2+e −1<0,解出即可. 解:如图所示,设椭圆的右焦点F(c,0),代入椭圆的标准方程可得:y 2=b 4a 2, 取y =b 2a ,A(c,b 2a). ∵△ABC 是锐角三角形, ∴∠BAD <45°, ∴1>cb 2a>√22,化为{e 2+√2e −1>0e 2+e −1<0,解得√6−√22<e <√5−12. 故选A .12.答案:D解析:分别讨论x≤0,x>0时的情况,x≤0时,通过求导得到f(x)max=f(−1)=1,x>0时,讨论①a> 0时,②a≤0时a的范围,综合得出结论.本题考察了函数的单调性,导数的应用,求函数的最值问题,求参数的范围,是一道基础题.解:x≤0时,f′(x)=6x(x+1),令f′(x)=0,解得:x=−1,x=0,∴f(x)在(−∞,−1)递增,在(−1,0)递减,∴f(x)max=f(−1)=1,x>0时,f′(x)=ae x(1−x),e2x①a>0时,若f′(x)>0,则0<x<1,若f′(x)<0,则x>1,≤1,∴f(x)max=f(1)=ae解得:a≤e,②a≤0时,f(x)≤0,符合题意,综上:a≤e,故选D.13.答案:90解析:解:根据题意,从A医院某科室的6名男医生和4名女医生中分别选派3名男医生和2名女医生,有C63C42=120种取法,若其中没有主任医师参加,即从不是主任医师的5名男医生中选出3名男医生,从不是主任医师的3名女医生中选出2名女医生,其取法有C53C32=30种,则至少有一名主任医师参加的取法有120−30=90种,故答案为:90.根据题意,先计算从A 医院某科室的6名男医生和4名女医生中分别选派3名男医生和2名女医生的取法数目,再排除其中没有主任医师参加的取法,由此分析可得答案. 本题考查排列组合的应用,注意用间接法分析,避免分类讨论,属于基础题.14.答案:0解析:本题考查了简单的线性规划,考查了数形结合的解题思想方法,属于中档题.由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,求得最优解的坐标,代入目标函数得答案.解:由约束条件{x +y −3≥0x +2y −5≤0x ≥0y ≥0作出可行域如图,令z =y −2x ,化为y =2x +z ,由图可知,当直线y =2x +z 过点C 时,y −2x 取得最大值, 联立{x +2y −5=0x +y −3=0,解得C(1,2).所以y −2x 的最大值为2−2×1=0. 故答案为:0.15.答案:8√5解析:本题考查解三角形的实际应用,属于较难题. 构造三角形,再运用基本不等式即可求得最小值. 解:作图如下:a2+2b2+c2=x2+y2+2ℎ2+2b2⩾12(x+y)2+2ℎ2+2b2=5b2+2ℎ2⩾2√5bℎ,第一个等号当且仅当x=y时取到,第二个等号当且仅当5b2=4ℎ2时取到,∵△ABC的面积为2,则bℎ=4则2√5bℎ=8√5.故答案为8√5.16.答案:108π解析:本题考查正三棱锥外接球的表面积,关键是求球的半径,属于中档题.依据题目条件求出三棱锥的侧棱长,将棱锥置于正方体中求出球半径,即可求解.解:设正三棱锥的侧棱长为a,球O的半径为R,正三棱锥P−ABC的侧面是直角三角形,∴13×12a3=36,解得a=6,把正三棱锥补形为正方体,则其体对角线长为2R=√62+62+62=6√3,解得R=3√3,所以球O的表面积为4πR2=4π×27=108π.故答案为108π.17.答案:解:(1)n≥2时,a n=12(1−a n) −12(1−a n−1) =−12a n+12a n−1,2a n=−a n+a n−1a n a n−1=13, S 1=a 1=12(1−a 1)得a 1=13,∴数a n 是以首a 1=13,公比13的等比数列,∴a n =(13)n(2)∵f(x)=log 13x ,b n =f(a 1)+f(a 2)+⋯+f(a n ),∴b n =log 13a 1+log 13a 2 +⋯+log 13a n =log 13(a 1⋅a 2…⋅a n )即log 13(13)1+2+⋯+n=1+2+⋯+n =n(n+1)2∴1b n=2n(n+1)=2(1n −1n+1),∴T n =11+12 +⋯+1n =2[(1−1)+(1−1)+⋯+(1−1)]=2n解析:(1)n ≥2时由a n =s n −s n−1,再利用S 1=a 1=12(1−a 1)求得a 1,分析可求数列{a n }的通项公式;(2)由f(x)=log 13x ,b n =f(a 1)+f(a 2)+⋯+f(a n ),a n =(13)n 可求得b n ,再用裂项法可求T n 的值. 本题考查数列求和,重点考查裂项法求和,考查学生的理解与转化及运算能力,属于中档题.18.答案:解:(1)根据2×2列联表中的数据,得K 2的观测值为k =40(9×4−16×11)225×15×20×20≈5.227>5.024,∴能在犯错概率不超过0.025的前提下认为“成绩优良与教学方式有关”.(2)由表可知在8人中成绩不优良的人数为1540×8=3,则X 的可能取值为0,1,2,3,P(X =0)=C 113C 153=3391,P(X =1)=C 112C 41C 153=4491,P(X =2)=C 111C 42C 153=66455,P(X =0)=C 43C 153=4455.∴X 的分布列为:∴E(X)=0×3399+1×4499+2×66455+3×4455=364455.解析:(1)利用频数与频率,求解两个班的成绩,得到2×2列联表中的数据,求出K 2的观测值,判断即可.(2)由表可知在8人中成绩不优良的人数为1540×8=3,则X 的可能取值为0,1,2,3,求出概率,得到分布列,然后求解期望即可.本题考查离散性随机变量的分布列以及期望的求法,独立检验的应用,考查计算能力.19.答案:(1)证明:取AA 1的中点N ,连接MN ,BN .在△ADA 1中,MN//AD 且MN =12AD ,又BC//AD 且BC =12AD ,所以MN//BC 且MN =BC , 所以四边形MNBC 是平行四边形,从而CM//BN ,又BN ⊂平面AA 1B 1B ,MC ⊄平面AA 1B 1B ,所以CM//平面AA 1B 1B . (2)解:取A 1B 1的中点P ,连接AP ,AB 1, 因为在菱形AA 1B 1B 中,∠B 1BA =π3, 所以AB =AA 1=AB 1=A 1B 1, 所以AP ⊥A 1B 1, 又AB//A 1B 1, 所以AP ⊥AB ,又侧面ABB 1A 1⊥平面ABCD ,侧面ABB 1A 1∩平面ABCD =AB , 所以AP ⊥平面ABCD ,又AB ⊥AD ,故以A 为原点,AB ,AD ,AP 所在直线分别为x ,y ,z 轴 建立空间直角坐标系A −xyz(如图所示),则A(0,0,0),D(0,4,0),C(2,2,0),P(0,0,√3), A 1(−1,0,√3),CD ⃗⃗⃗⃗⃗ =(−2,2,0),CA 1⃗⃗⃗⃗⃗⃗⃗ =(−3,−2,√3).因为AP ⊥平面ABCD ,所以AP⃗⃗⃗⃗⃗ =(0,0,√3)为平面ABCD 的一个法向量.设平面A 1CD 的法向量为n ⃗ =(x,y,z),由{n ⃗ ⊥CD⃗⃗⃗⃗⃗ n ⃗ ⊥CA 1⃗⃗⃗⃗⃗⃗⃗ ,即{−2x +2y =0−3x −2y +√3z =0,取n ⃗ =(1,1,5√33)为平面A 1CD 的一个法向量, 所以cos <AP ⃗⃗⃗⃗⃗ ,n ⃗ >=AP ⃗⃗⃗⃗⃗ ⋅n ⃗⃗ |AP ⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |=√3×5√33√3×√12+12+(5√33)2=5√3131.设二面角A 1−CD −A 大小为θ,θ∈(0,π2),故cosθ=5√3131,解析:本题考查二面角的平面角的求法,空间向量的数量积的应用,直线与平面平行的判断定理的应用,考查计算能力.(1)取AA 1的中点N ,连接MN ,BN.证明四边形MNBC 是平行四边形,推出CM//BN ,然后证明CM//平面AA 1B 1B .(2)取A 1B 1的中点P ,连接AP ,AB 1,以A 为原点,AB ,AD ,AP 所在直线分别为x ,y ,z 轴建立空间直角坐标系A −xyz(如图所示),求出平面ABCD 的一个法向量.平面A 1CD 的法向量,利用空间向量的数量积求解即可.20.答案:解:(1)因为|PA|+|PB|=|PQ|+|PB|=4>|AB|= 2√2 ,所以点P 的轨迹是以A ,B 为焦点的椭圆,方程为x 24+y 22=1 ;(2)若存在满足条件的点S ,T ,设直线ST 的方程为 y =12x +m ,与 x 24+y 22=1联立,消去y 并化简可得3x 2+4mx −4m 2−8=0,由已知知Δ>0,即16m 2−4×3×4(m 2−2)>0,解得 −√3<m <√3, 设点S (x 1,y 1),T (x 2,y 2),则 x 1+x 2=−43m , x 1x 2=4(m 2−2)3,∵线段ST 的中点 (−23m,23m) 在对称轴2x +y +1=0上, ∴ −43m +23m +1=0,解得 m =32 ,且 32∈(−√3,√3),所以满足条件的点S ,T 是存在的, 直线ST 的方程为 y =12x +32 ,即x −2y +3=0.解析:本题主要考查圆锥曲线的综合问题,难度较大.(1)根据题干描述可以知道|PA|、|PB|、|PQ|、|PB|的关系,即|PA|+|PB|=|PQ|+|PB|=4>|AB|= 2√2,再根据椭圆的定义,可以求出点P的轨迹方程;(2)假设满足条件的点S、T存在,则根据这两点关于直线2x+y+1=0对称,可以设出直线ST的方程,将其与(1)中求出的椭圆方程联立,消去y,利用Δ>0,求出m的范围以及点S、T的横坐标之和、之积,利用线段ST的中点在对称轴2x+y+1=0上,可以求出m,从而得到直线ST的方程.21.答案:(1)解:由题得f′(x)=e x−a.当a⩽0时,f′(x)>0对x∈R恒成立,所以f(x)在R上单调递增.当a>0时,令f′(x)=0,.当时,则f(x)单调递减;,则f(x)单调递增.综上,当a⩽0时,f(x)在R上单调递增;当a>0时,f(x)在区间内单调递减,在区间内单调递增.(2)证明:不妨设x1<x2,由f(x)=e x−e2x,得f′(x)=e x−e2,令f′(x)=0,得x=2.f(x)在区间内单调递减,在区间内单调递增,f(0)=1>0,f(4)=e4−4e2=(e2−4)e2>0,所以0<x1<2<x2<4,构造函数F(x)=f(4−x)−f(x)(0<x<2),+e x)+2e2⩽−2e2+2e2=0,则F′(x)=−(e4−x−e2)−(e x−e2)=−e4−x−e x+2e2=−(e4e x所以函数F(x)在区间(0,2)内单调递减.因为0<x1<2,所以2<4−x1<4,所以F(x1)=f(4−x1)−f(x1)>F(2)=0,又f(x1)=f(x2)=0,所以f(4−x1)>f(x2).因为函数f(x)在区间内单调递增,所以4−x1>x2,即x1+x2<4.解析:本题考查利用导数判断函数的单调性以及研究函数的零点问题,难度较大.(1)利用导函数的定义分类讨论即可;(2)首先利用函数单调性求出x1、x2的取值范围,再通过构造新函数求解即可.22.答案:解:(1)∵曲线C的参数方程为{x=1+√5cosαy=2+√5sinα(α为参数),∴曲线C的普通方程为(x−1)2+(y−2)2=5,即x2+y2−2x−4y=0,将x=ρcosθ,y=ρsinθ代入上式,得曲线C的极坐标方程为ρ=2cosθ+4sinθ.∵直线l1:x=0,∴直线l1的极坐标方程为θ=π2(ρ∈R),∵直线l2:x−y=0,∴直线l2的极坐标方程为θ=π4(ρ∈R).(2)设A,B两点对应的极径分别为ρ1,ρ2,在ρ=2cosθ+4sinθ中,令θ=π2,得ρ1=2cosθ+4sinθ=4,令θ=π4,得ρ2=2cosθ+4sinθ=3√2,∵π2−π4=π4,∴|AB|=√ρ12+ρ22−2ρ1ρ2cosπ4=√10.解析:本题考查曲线的直线的极坐标方程的求法,考查弦长的求法,考查直角坐标方程、极坐标方程、参数方程的互化等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.(1)由曲线C的参数方程消去参数,求出曲线C的普通方程,由此能求出曲线C的极坐标方程,由直线l1:x=0,能求出直线l1的极坐标方程,由直线l2:x−y=0,能求出直线l2的极坐标方程.(2)设A,B两点对应的极径分别为ρ1,ρ2,在ρ=2cosθ+4sinθ中,令θ=π2,得ρ1=2cosθ+4sinθ=4,令θ=π4,得ρ2=2cosθ+4sinθ=3√2,由此能求出|AB|.23.答案:(1)解:当x≥−12时,f(x)=−x+2x+1=x+1.由f(x)<2,得x<1,所−12≤x<1.当x<−12时,f(x)=−x−2x−1=−3x−1.由f(x)<2,得x>−1,所以−1<x<−12.综上可知,M={x|−1<x<1}.(2)证明:因为a,b∈M,所以−1<a<1,−1<b<1,即|a|<1,|b|<1.于是2|ab|+1−(|a|+|b|)=|ab|+|ab|+1−(|a|+|b|)=|ab|+(|a|−1)·(|b|−1)>0,故2|ab|+1>|a|+|b|.解析:本题考查含绝对值不等式的解法和不等式的证明,属中档题.(1)讨论x和−1的大小去绝对值,解不等式即可;2(2)分析2|ab|+1−(|a|+|b|)与0的关系即可得2|ab|+1>|a|+|b|.。
2020年宁夏银川一中高考数学二模试卷(理科)

2020年宁夏银川一中高考数学二模试卷(理科)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若复数z 满足(1)|34|i z i +=+,则z 对应的点位于复平面的( ) A .第一象限B .第二象限C .第三象限D .第四象限2.(5分)设集合2{|20}A x x x =-->,2{|log 2}B x x =„,则集合()(R A B =I ð ) A .{|04}x x <„B .{|02}x x <„C .{|2}x x …D .{|4}x x „3.(5分)已知命题p :直线//a b ,且b ⊂平面α,则//a α;命题q :直线l ⊥平面α,任意直线m α⊂,则l m ⊥.下列命题为真命题的是( ) A .p q ∧B .p ∨(非)qC .(非)p q ∧D .p ∧(非)q4.(5分)已知向量(1,3)a =r ,b r 是单位向量,若||3a b -=r r ,则a <r ,(b >=r ) A .6πB .4π C .3π D .23π 5.(5分)若cos 22sin()4απα=--,则cos sin αα+的值为( ) A .7-B .12-C .12D .7 6.(5分)||4cos x y x e =-图象可能是( )A .B .C .D .7.(5分)如图,在底面边长为1,高为2的正四棱柱1111ABCD A B C D -中,点P 是平面1111A B C D 内一点,则三棱锥P BCD -的正视图与侧视图的面积之和为( )A .2B .3C .4D .58.(5分)抛物线2(0)y ax a =>的准线与双曲线22:184x y C -=的两条渐近线所围成的三角形面积为22,则a 的值为( ) A .8B .6C .4D .29.(5分)《九章算术》勾股章有一“引葭赴岸”问题“今有饼池径丈,葭生其中,出水两尺,引葭赴岸,适与岸齐,问水深,葭各几何?”,其意思是:有一个直径为一丈的圆柱形水池,池中心生有一颗类似芦苇的植物,露出水面两尺,若把它引向岸边,正好与岸边齐,问水有多深,该植物有多高?其中一丈等于十尺,如图若从该葭上随机取一点,则该点取自水下的概率为( )A .1213B .1314C .2129D .141510.(5分)执行如图所示的程序框图,则输出的结果为( )A .40322017B .20152016C .20162017D .2015100811.(5分)如图,在平面直角坐标系xOy 中,F 是椭圆22221(0)x y a b a b+=>>的右焦点,直线2by =与椭圆交于B ,C 两点,且90BFC ∠=︒,则该椭圆的离心率为( ) A 6B 23C .12D 2 12.(5分)已知函数(2)()3,(2)()32,(2)x x x e x ln f x x x ln ⎧--+=⎨-<⎩…,当[x m ∈,)+∞时,()f x 的取值范围为(-∞,2]e +,则实数m 的取值范围是( ) A .1(,]2e--∞ B .(-∞,1]C .1[,1]2e -D .[2ln ,1]二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)在一次医疗救助活动中,需要从A 医院某科室的6名男医生、4名女医生中分别抽调3名男医生、2名女医生,且男医生中唯一的主任医师必须参加,则不同的选派案共有 种.(用数字作答)14.(5分)若x ,y 满足||1x y -„,且1y -…,则3x y +的最大值为 .15.(5分)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,120ABC ∠=︒,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为 .16.(5分)棱长为a 的正四面体ABCD 与正三棱锥E BCD -的底面重合,若由它们构成的多面体ABCDE 的顶点均在一球的球面上,则正三棱锥E BCD -的内切球半径为 . 三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分)17.(12分)已知数列的前n 项和为n S ,且满足*11()2n n a S n N =+∈.(1)求数列{}n a 的通项公式; (2)若2log n n b a =,11n n n c b b +=,且数列{}n ð的前n 项和为n T ,求n T 的取值范围. 18.(12分)棉花的纤维长度是评价棉花质量的重要指标,某农科所的专家在土壤环境不同的甲、乙两块实验地分别种植某品种的棉花,为了评价该品种的棉花质量,在棉花成熟后,分别从甲、乙两地的棉花中各随机抽取20根棉花纤维进行统计,结果如下表:(记纤维长度不低于300mm 的为“长纤维”,其余为“短纤维” )(1)由以上统计数据,填写下面22⨯列联表,并判断能否在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.附:(1)2()()()()()n ad bc k a b c d a c b d -=++++;(2)临界值表;(2)现从上述40根纤维中,按纤维长度是否为“长纤维”还是“短纤维”采用分层抽样的方法抽取8根进行检测,在这8根纤维中,记乙地“短纤维”的根数为X ,求X 的分布列及数学期望. 19.(12分)在底面为菱形的四棱柱1111ABCD A B C D -中,12AB AA ==,11A B A D =,60BAD ∠=︒,AC BD O =I ,AO ⊥平面1A BD .(1)证明:1//B C 平面1A BD ; (2)求二面角1B AA D --的正弦值.。
银川一中2020高三第二次模拟数学(理科)试卷答案(1)

e x a ;由 f (x) 0 ,得 x a ,所以 f (x) 在 (e, a ) 上单调递减,在 ( a , ) 上单调递
增,
………10 分
因为 f (e) e3 3ae e e3 3e3 e 0 ,
3 6 32 62 4
(2)由(1)得 a2<1,b2<1. 44
………6 分
因为|1-4ab|2-4|a-b|2=(1-8ab+16a2b2)-4(a2-2ab+b2)
=(4a2-1)(4b2-1)>0,
所以|1-4ab|2>4|a-b|2,故|1-4ab|>2|a-b|. ………10 分
2
2
22
3,x≤-2,
………10 分
23.解:(1)证明:记 f(x)=|x-1|-|x+2|= -2x-1,-2<x<1,
-3,x≥1.
由-2<-2x-1<0,解得-1<x<1, 22
………3 分
| | -1,1
则 M= 2 2 . 所以
1a+1b 36
≤1|a|+1|b|<1×1+1×1=1. ………5 分
∵ B1C 平面 A1BD , A1D 平面 A1BD ,
∴ B1C ∥平面 A1BD .············································································ 4 分
(2)∵ AO 平面 A1BD ,∴ AO A1O ,
1
,
2t 4k 2 1
,
银川一中第二次模拟考试-理科数学

绝密★启用前2014年普通高等学校招生全国统一考试理 科 数 学(银川一中第二次模拟考试)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~24题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U=R ,集合⎭⎬⎫⎩⎨⎧<-=01|A x x x ,{}1|≥=x x B ,则集合{}0|≤x x 等于 A .A B ⋂B .A B ⋃C .U C A B ⋂()D .U C A B ⋃() 2.若复数z 满足i iz 42+=,则z = A .i 42+B .i 42-C .i 24-D .i 24+3.已知等比数列{}n a 的公比大于1,7273=a a ,2782=+a a ,则=12a A .96B .64C .72D .484.设l ,m ,n 表示不同的直线,α、β、γ表示不同的平面,给出下列四个命题:①若m ∥l ,且m ⊥α,则l ⊥α; ②若m ∥l ,且m ∥α,则l ∥α; ③若α∩β=l ,β∩γ=m ,γ∩α=n ,则l ∥m ∥n ; ④若α∩β=m ,β∩γ=l ,γ∩α=n ,且n ⊂β,则l ∥m . 其中正确命题的个数是A .2B .1C .3D .4 5.从抛物线x y 42=上一点P 引抛物线准线的垂线, 垂足为M ,且|PM|=5,设抛物线的焦点为F , 则△MPF 的面积( )A .5B .10C .20D .156.阅读如图所示的程序框图,若输入919a =,则输出的k A .9 B . 10 C . 11 D . 127.将甲、乙、丙等六人分配到高中三个年级,每个年级2人,要求甲必须在高一年级,乙和丙均不能在高三年级,则不同的安排种数为 A .18 B .15 C .12 D .9 8.某几何体的三视图如图所示,则该几何体的表面积为 A .π2 B .π22C .(212+)πD .(222+)π9.△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若cb<cos A ,则△ABC 为A .钝角三角形B .直角三角形C .锐角三角形D .等边三角形10.现有四个函数:①sin y x x =⋅;②cos y x x =⋅;③|cos |y x x =⋅;④2xy x =⋅的图象A .①④②③B .①④③②C .④①②③D .③④②①11.过双曲线12222=-by a x )0,0(>>b a 的右顶点A 作斜率为1-的直线,该直线与双曲线的两条渐近线的交点分别为B , C .若BC AB =2,则双曲线的离心率是 A .2B .3C .5D .1012.设函数)(x f y =在(-∞,+∞)内有定义,对于给定的正数k ,定义函数:x⎩⎨⎧>≤=))(()(()()(k x f kkx f x f x f k ,取函数x e x x f ---=2)(,若对任意的),(∞+-∞∈x ,恒有)()(x f x f k =,则 A. k 的最大值为2 B. k 的最小值为2 C. k 的最大值为1D. k 的最小值为1第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.已知向量)1,(z x -=,),2(z y +=,且⊥,若变量x ,y 满足约束条件⎪⎩⎪⎨⎧≤+≥-≥5231y x xy x ,则z 的最大值为 14.6)1xx -(的二项展开式中含3x 的项的系数为15.若(0,)απ∈,且3cos 2sin()4παα=-,则sin 2α的值为 .16.在平面直角坐标系中,记抛物线2y x x =-与x 轴所围成的平面区域为M ,该抛物线与直线y =kx (k >0)所围成的平面区域为A ,向区域M 内随机抛掷一点P ,若点P 落在区域A 内的概率为827,则k 的值为三、解答题:解答应写出文字说明.证明过程或演算步骤17.(本小题满分12分)设数列{}n a 的各项均为正数,它的前n 项的和为n S ,点(,)n n a S 在函数2111822y x x =++的图像上;数列{}n b 满足1111,()n n n n b a b a a b ++=-=.其中n N *∈. (Ⅰ)求数列{}n a 和{}n b 的通项公式; (Ⅱ)设n n na cb =,求证:数列{}n c 的前n 项的和59n T >(n N *∈).理科数学试卷 第3页(共6页)18 (本题满分12分)今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁。
2020年宁夏银川一中高考数学二模试卷(理科)(有答案解析)

当 P 与线段 BC1 的端点重合时,A1P 与 ad1 所成角取得最小值 ,当 P
13. (1﹣x)10 的展开式中,x3 的系数等于_______.
D. (1,+∞)
14. 已知实数 x,y 满足约束条件
,若目标函 z=2x+ay,仅在点(3,4)取得最小值,则 a
的取值范围是______. 15. 已知抛物线 y2=8x 的焦点为 F,直线 l 过 F 且依次交抛物线及圆(x-2)2+y2=1 于点 A,B,C,D
2020 年宁夏银川一中高考数学二模试卷(理科)
题号 得分
一
二
三
总分
一、选择题(本大题共 12 小题,共 60.0 分)
1. 设集合 A={0,2,4,6,8,10},B={x|2x-3<4},则 A∩B=( )
A. {4,8}
B. {0,2,6}
C. {0,2}
D. {2,4,6}
2. 复数 z=1-2i,则 =( )
则 S13= ×13(b1+b13)=13b7=13×4=52.
故选 B.
5.答案:C
解析:【分析】 本题考查平面向量基本定理,根据分解的唯一性得到所求参数的方程是解答本题的关键,属于中档 题.
第 7 页,共 19 页
由题意,可根据向量运算法则得到 =
求出 t 的值. 【解答】
解:设
,
+(1-m) ,从而由向量分解的唯一性得出关于 t 的方程,
B. x1,x2,…xn 的标准差
C. x1,x2,…xn 的最大值
D. x1,x2,…xn 的中位数
4. 已知等比数列{an}中,有 a3a11=4a7,数列{bn}是等差数列,其前 n 项和为 Sn,且 b7=a7,则 S13=
2020-2021学年度宁夏银川高考第二次模拟考试数学(理)试题及答案

普通高等学校招生全国统一考试理 科 数 学(银川一中第二次模拟考试)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~23题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.考生必须按照题号在答题卡各题号相对应的答题区域内(黑色线框)作答,写在草稿纸上、超出答题区域或非题号对应的答题区域的答案一律无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数2(1)i i-= A .22i -+B .2C .2-D .22i -2.设集合2{|0}M x x x =->,1|1N x x ⎧⎫=<⎨⎬⎩⎭,则 A .φ=⋂N M B .φ=⋃N MC .M N =D .M N R =U3.已知1tan 2α=-,且(0,)απ∈,则sin 2α= A .45 B .45-C .35 D .35-4.若两个单位向量a r ,b r 的夹角为120o,则2a b +=r rA .2B .3C D5.从标有数字1、2、3、4、5的五张卡片中,依次抽出2张(取后不放回),则在第一次抽到卡片是奇数的情况下,第二次抽到卡片是偶数的概率为 A .14B .12C .13D .236.已知233a -=,432b -=,ln3c =,则 A .a c b <<B .a b c <<C .b c a <<D .b a c <<7.中心在原点,焦点在y 轴上的双曲线的一条渐近线经过点()2,4-,则它的离心率为A 5B .2C 3D 58.三棱锥P-ABC 中,PA ⊥面ABC ,PA=2,AB=AC=3,∠BAC=60°,则该棱锥的外接球的表面积是A .π12B .π8C .π38D .π349.20世纪70年代,流行一种游戏——角谷猜想,规则如下:任意写出一个自然数n ,按照以下的规律进行变换:如果n 是个奇数,则下一步变成31n +;如果n 是个偶数,则下一步变成2n,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确地说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设 计的,如果输出的i 值为6,则输入的n 值为 A .5B .16C .5或32D .4或5或32 10.已知P 是△ABC 所在平面外的一点,M 、N 分别是AB 、PC 的中点,若MN =BC =4,PA =43, 则异面直线PA 与MN 所成角的大小是A .30°B .45°C .60°D .90° 11.若将函数f(x)=sin(2x +φ)+3cos(2x +φ)(0<φ<π)的图象向左平移π4个单位长度,平移后的图象关于点⎝ ⎛⎭⎪⎫π2,0对称,则函数g(x)=cos(x +φ)在⎣⎢⎡⎦⎥⎤-π2,π6上的最小值是A .-12B .-32C .22D .12 12.已知函数f(x)=(3x +1)ex +1+mx(m ≥-4e),若有且仅有两个整数使得f(x)≤0,则实数m 的取值范围是20120120120120120A .⎥⎦⎤ ⎝⎛2,5eB .⎪⎭⎫⎢⎣⎡--238,25e eC .⎪⎭⎫⎢⎣⎡--238,21eD .⎪⎭⎫⎢⎣⎡--e e 25,4第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第23题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.已知函数f(x)=log 21-x 1+x ,若f(a)=12,则f(-a)=________.14.设221(32)a x x dx =⎰-,则二项式261()ax x-展开式中的第6项的系数为__________.15.若目标函数2z kx y =+在约束条件2122x y x y y x -≤⎧⎪+≥⎨⎪-≤⎩下当且仅当在点(1,1)处取得最小值,则实数k 的取值范围是__________.16.已知点A(0,1),抛物线C :y 2=ax(a>0)的焦点为F ,连接FA ,与抛物线C 相交于点M ,延长FA ,与抛物线C 的准线相交于点N ,若|FM|∶|MN|=1∶3,则实数a 的值为________. 三.解答题17.(本小题满分12分){a n }的前n 项和S n 满足:a n +S n =1 (1)求数列{a n }的通项公式; (2)若1+=n nn a a C ,数列{C n }的前n 项和为T n ,求证:T n <1. 18.(本小题满分12分)随着互联网的快速发展,基 于互联网的共享单车应运而生, 某市场研究人员为了了解共享单 车运营公司M 的经营状况,对 该公司最近六个月的市场占有 率进行了统计,并绘制了相应 的折线图:(1)由折线图可以看出,可用线性回归模型拟合月度市场占 有率y 与月份代码x 之间的关系, 求y 关于x 的线性回归方程,并 预测M 公司2017年4月的市场占 有率;(2)为进一步扩大市场,公司拟再采购一批单车,现有采购成本分别为1000元/辆和 1200元/辆的A 、B 两款车型可供选择,按规定每辆单车最 多使用4年,但由于多种原因(如骑行频率等)会导致单车使 用寿命各不相同,考虑到公司运营的经济效益,该公司决定 先对这两款车型的单车各100辆进行科学模拟测试,得到两 款单车使用寿命的频数表如右表:经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率,如果你是M 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型? 参考公式:回归直线方程为$$y bx a =+$,其中2121121)())((ˆx n xyx n y xx xy y x xb n i ini i in i ii ni i--=---=∑∑∑∑====,$ay bx =-$. 19.(本小题满分12分)如图,在四棱锥P-ABCD 中,底面ABCD 是平行四边形,∠BCD=135°,侧面PAB ⊥底面ABCD ,∠BAP=90°,AB=AC=PA=2,E 、F 分别为BC 、AD 的中点,点M 在线段PD 上.(1)求证:EF ⊥平面PAC ;(2)如果直线ME 与平面PBC 所成的角和直线ME 与平 面ABCD 所成的角相等,求PDPM的值. 20.(本小题满分12分)已知椭圆C 的中心在原点,焦点在x 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q)(1)求椭圆C 的方程;(2)设点P 是直线x=-4与x 轴的交点,过点P 的直线l 与椭圆C 相交于M 、N 两点,当线段MN 的中点落在正方形Q 内(包括边界)时,求直线l 斜率的取值范围. 21.(本小题满分12分)已知函数()()()21,ln f x x ax g x x a a R =++=-∈.(1)当1a =时,求函数()()()h x f x g x =-的极值;(2)若存在与函数()(),f x g x 的图象都相切的直线,求实数a 的取值范围.请考生在第22-23题中任选一题作答,如果多做,则按所做的第一题计分. 22.【选修4-4:坐标系与参数方程】(本小题满分10分)在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C :2sin 2cos (0)a a ρθθ=>,过点(24)P --,的直线l的参数方程为:24x y ⎧=-⎪⎪⎨⎪=-⎪⎩ (t 为参数),直线l 与曲线C 分别交于M 、N 两点.(1)写出曲线C 的直角坐标方程和直线l 的普通方程; (2)若|PM |,|MN|,|PN|成等比数列,求a 的值 23选修4-5:不等式选讲(本小题满分10分)已知函数|1|||)(--=x x x f .(1)若|1|)(-≥m x f 的解集非空,求实数m 的取值范围;(2)若正数y x ,满足M y x =+22,M 为(1)中m 可取到的最大值,求证:xy y x 2≥+.高三第二次模拟理科数学试题参考答案一、选择题:本大题共12小题,每小题5分. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CCBDBDABCADB二.填空题:13. —2114.—24; 15.24<<-k ; 16. 212.已知函数f(x)=(3x +1)e x +1+mx(m ≥-4e),若有且仅有两个整数使得f(x)≤0,则实数m 的取值范围是( )A.⎝ ⎛⎦⎥⎤5e ,2B.⎣⎢⎡⎭⎪⎫-52e ,-83e 2C.⎣⎢⎡⎭⎪⎫-12,-83e 2D.⎣⎢⎡⎭⎪⎫-4e ,-52e 答案 B解析 由f(x)≤0,得(3x +1)·e x +1+mx ≤0,即mx ≤-(3x +1)ex +1,设g(x)=mx ,h(x)=-(3x +1)e x +1,则h ′(x)=-[3e x +1+(3x +1)ex +1]=-(3x +4)e x +1,由h ′(x)>0,得-(3x +4)>0,即x<-43,由h ′(x)<0, 得-(3x +4)<0,即x>-43,故当x =-43时,函数h(x) 取得极大值.在同一平面直角坐标系中作出y =h(x), y =g(x)的大致图象如图所示,当m ≥0时,满足 g(x)≤h(x)的整数解超过两个,不满足条件;当m<0时, 要使g(x)≤h(x)的整数解只有两个,则需满足()()()()⎩⎨⎧-<--≥-,33,22g h g h即⎩⎨⎧5e -1≥-2m ,8e -2<-3m ,即⎩⎪⎨⎪⎧m ≥-52e ,m<-83e 2,即-52e ≤m<-83e 2,即实数m 的取值范围是⎪⎭⎫⎢⎣⎡--238,25e e ,故选B.16已知点A(0,1),抛物线C :y 2=ax(a>0)的焦点为F ,连接FA ,与抛物线C 相交于点M ,延长FA ,与抛物线C 的准线相交于点N ,若|FM|∶|MN|=1∶3,则实数a 的值为________.答案2解析 依题意得焦点F 的坐标为⎝ ⎛⎭⎪⎫a 4,0,设M 在抛物线的准线上的射影为K ,连接MK ,由抛物线的定义知|MF|=|MK|,因为|FM|∶|MN|=1∶3,所以|KN|∶|KM|=22∶1,又k FN =0-1a 4-0=-4a ,k FN =-|KN||KM|=-22,所以4a =22,解得a = 2.三.解答题:17.解析:(1)由a n +S n =1得a n-1+S n-1=1(n ≥2) 两式相减可得:2a n =a n-1即211=-n n a a ,又211=a ∴{a n }为等比数列,∴a n =n )21((2)n n n nn C 211211)21()21(<+=+= 故12112112112121212121321<-=-⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛<++++=n n nn n C C C C T ΛΛ 18.解:(1)由题意: 3.5x =,16y =,()()6135i i i x x y y =--=∑,()62117.5i i x x=-=∑,35217.5b ==$,$162 3.59a y b x =-⋅=-⨯=$,∴$29y x =+, 7x =时,$27923y =⨯+=.即预测M 公司2017年4月份(即7x =时)的市场占有率为23%.(2)由频率估计概率,每辆A 款车可使用1年,2年,3年,4年的概率分别为0.2、0.35、0.35、0.1, ∴每辆A 款车的利润数学期望为()()()()50010000.2100010000.35150010000.35200010000.1175-⨯+-⨯+-⨯+-⨯=(元)每辆B 款车可使用1年,2年,3年,4年的概率分别为0.1,0.3,0.4,0.2, ∴每辆B 款车的利润数学利润为()()()()50012000.1100012000.3150012000.4200012000.2150-⨯+-⨯+-⨯+-⨯=(元)∵175150>, ∴应该采购A 款车. 19.(1)证明:在平行四边形中,因为,, 所以.由分别为的中点,得,所以.因为侧面底面,且,所以底面.又因为底面,所以.又因为,平面,平面,所以平面.(2)解:因为底面,,所以两两垂直,以分别为、、,建立空间直角坐标系,则,所以,,,设,则,所以,,易得平面的法向量.设平面的法向量为,由,,得令,得.因为直线与平面所成的角和此直线与平面所成的角相等, 所以,即,所以,解得,或(舍).综上所得:20.【解析】(1)依题意,设椭圆C 的方程为)0(12222>>=+b a by a x ,焦距为c 2。
银川一中2020届高三第二次模拟数学(理科)试卷答案

1银川一中2020届高三年级第二次模拟考试(理科)参考答案13、60 14、5 15、9 16、a 12623- 三、解答题(解答应写出文字说明,证明过程或演算步骤) 17.(1)当1n =时,11112a S =+,解得12a = ……………1分 当2n ≥时,11112n n a S --=+……① 112n n a S =+ ……② ……………3分 ②-①得112n n na a a --= 即12n n a a -= ……………5分∴数列{}na 是以2为首项,2为公比的等比数列 ∴2n na = ……………6分(2)22log log 2n n n b a n === ……………7分11111(1)1n n n c b b n n n n +===-++ ……………8分11111111...223341n T n n =-+-+-++-+=111n -+ ……………10分n N *∈ 110,12n ⎛⎤∴∈ ⎥+⎝⎦ 1,12n T ⎡⎫∴∈⎪⎢⎣⎭……………12分 18.试题分析:(1)可以根据所给表格填出列联表,利用列联表求出2K,结合所给数据,应用独立性检验知识可作出判断;(2)写出X 的所有可能取值,并求出对应的概率,可列出分布列并进一步求出X 的数学期望. 根据22⨯列联表中的数据,可得()2240941611 5.227 5.024********K ⨯-⨯=≈>⨯⨯⨯所以,在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.……6分(Ⅱ)由表可知在8根中乙地“短纤维”的根数为158340⨯=, X 的可能取值为:0,1,2,3, ……………7分()31131533091C P X C ===,()2111431544191C C P X C ===,()12114315662455C C P X C ===,()3431543455C P X C ===. ……………9分 ∴ ()33446543644012391914554554555E X =⨯+⨯+⨯+⨯==. ……………12分 19.方法一:(1)依题意,11//,A B AB 且//,AB CD ∴11//A B CD ,····················································································· 1分 ∴四边形11A B CD 是平行四边形, ···························································· 2分 ∴11B C A D ∥, ··················································································· 3分 ∵1B C ⊄平面1A BD ,1A D ⊂平面1A BD ,∴1B C ∥平面1A BD . ··········································································· 4分 (2)∵AO ⊥平面1A BD ,∴1AO AO ⊥, ∵11A B A D =且O 为BD 的中点,∴1AO BD ⊥, ∵AO BD ⊂、平面ABCD 且AO BD O =,∴1A O ⊥平面ABCD , · (5)分 以O 为原点,分别以1,,OA OB OA 为x 轴、y 轴、z 正方向,建立如图所示的空间直角坐标系O xyz -,则()3,0,0A,()0,1,0B ,()0,1,0D -,()10,0,1A ,∴()()()13,0,13,1,,0,3,1,0,AB AA AD =-=-=-- 设平面1A AB 的法向量为(),,n x y z =,则1n AA n AB ⎧⊥⎪⎨⊥⎪⎩,∴00z y ⎧+=⎪⎨+=⎪⎩,取1x =,则(1,3,n =. ························· 7分 设平面1A AD 的法向量为()111,,m x y z =,则1n AA n AD ⎧⊥⎪⎨⊥⎪⎩,∴030z x y ⎧+=⎪⎨--=⎪⎩,取1x =,则(1,m=. ······················ 9分∴11cos ,77m n m n m n⋅<>===⨯⋅, ·················································· 11分 设二面角1B AA D --的平面角为α,则sin α= ∴二面角1B AA D --················································· 12分20.(1)设(),P x y ,()00,T x y ,则()0,0A x ,()00,B y , ……………1分 由题意知BA AP =,所以A 为PB 中点,由中点坐标公式得00202x x y y ⎧=⎪⎪⎨+⎪=⎪⎩,即002x x y y ⎧=⎪⎨⎪=-⎩,又点T 在圆O :221x y +=上,故满足22001x y +=, ……………3分得2214x y +=. ……………4分(2)由题意知直线l 的斜率存在且不为零,设直线l 的方程为y kx t =+, 因为1AB OT ==,故221t t k ⎛⎫-+= ⎪⎝⎭,即2221t t k += ①,联立2214y kx t x y =+⎧⎪⎨+=⎪⎩,消去y 得:()()222418410k x ktx t +++-=, 设()11,M x y ,()22,N x y ,122841kt x x k +=-+,()21224141t x x k -=+, ……………8分()1212282241kt y y k x x t k t k ⎛⎫+=++=-+ ⎪+⎝⎭2241t k =+, ……………9分因为OMQN 为平行四边形,故2282,4141kt t Q k k ⎛⎫- ⎪++⎝⎭,点Q 在椭圆上,故222282411441kt t k k ⎛⎫- ⎪+⎛⎫⎝⎭+= ⎪+⎝⎭,整理得22441t k =+,②,……10分 将①代入②,得42410k k ++=,该方程无解,故这样的直线不存在. ……12分21.(1)()233f x x a '=-,①当0a ≤时,0f x ()≥,∴函数()f x 在∞∞(-,+)内单调递增; ………2分②当0a >时,令()3(0f x x x '=-=,解得x =x =当x <x >,()0f x '>,则()f x 单调递增,当x <<,()0f x '<,则()f x 单调递减, ………4分 ∴函数()f x的单调递增区间为(,-∞和)+∞,单调递减区间为(…5分 (2)(Ⅰ)当(0,e)x ∈时,0)()(,0)(>≥>x g x h x g 所以()h x 在(0,)e 上无零点; ……6分 (Ⅱ)当x e =时,3()0,()3g e f e e ae e ==-+,①若03)(3≤+-=e ae e e f ,即312+≥e a ,则e 是()h x 的一个零点; ②若3()30f e e ae e =-+>,即2e 13a +<,则e不是()h x 的零点 ………8分 (Ⅲ)当(,)x e ∈+∞时,()0<g x ,所以此时只需考虑函数()f x 在(,)e +∞上零点的情况,因为22()333e 3f x x a a '=->-,所以①当2e a ≤时,()0,()f x f x '>在(,)e +∞上单调递增。
宁夏银川一中高考数学二模试卷(理科)解析版

k0
2.072
P(K2≥k0) 0.15
2.706 0.10
3.841 0.05
5.024 0.025
6.635 0.010
7.879 0.005
10.828 0.001
参考公式:
,n=a+b+c+d.
19. 如图所示,ABCD 是边长为 2 的正方形,AE⊥平面 BCE,且 AE=1.
(Ⅰ)求证:平面 ABCD⊥平面 ABE;
③异面直线 A1P 与 AD1 所成角的取值范围是
;
④三棱锥 D1-APC 的体积不变.
A. ①②
B. ①②④
C. ③④
D. ①④
12. 已知函数 f(x)=
若函数 g(x)=f(f(x))-2 恰有 5 个零点,且最
小的零点小于-4,则 a 的取值范围是( )
A. (-∞,-1)
B. (0,+∞)
A. x1,x2,…xn 的平均数
B. x1,x2,…xn 的标准差
C. x1,x2,…xn 的最大值
D. x1,x2,…xn 的中位数
4. 已知等比数列{an}中,有 a3a11=4a7,数列{bn}是等差数列,其前 n 项和为 Sn,且 b7=a7
,则 S13=( )
A. 26
B. 52
C. 78
D. 104
5. 如图,在
中,
,则实数 的值为( )
, 是 上一点,若
A. B. C. D.
6. 学校就如程序中的循环体,送走一届,又会招来一级.老师们目送着大家远去,渐 行渐远…执行如图所示的程序框图,若输入 x=64,则输出的结果为( )
第 1 页,共 19 页
(全优试卷)宁夏银川一中高三第二次模拟考试数学(理)试题Word版含答案

绝密★启用前2018年普通高等学校招生全国统一考试理科数学(银川一中第二次模拟考试)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~23题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.考生必须按照题号在答题卡各题号相对应的答题区域内(黑色线框)作答,写在草稿纸上、超出答题区域或非题号对应的答题区域的答案一律无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑。
第I卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1A B C D2A B C D3A B C D4bA B CD5.从标有数字1、2、3、4、5的五张卡片中,依次抽出2张(取后不放回),则在第一次抽到卡片是奇数的情况下,第二次抽到卡片是偶数的概率为A B C D6A B C D7A B.2 C D8.三棱锥P-ABC中,PA⊥面ABC,PA=2,BAC=60°,则该棱锥的外接球的表面积是A B C D9.20世纪70年代,流行一种游戏——更准确地说是落入底部的4-2-1循环,而永远也 跳不出这个圈子,下列程序框图就是根据这个游戏而设ABC D 10.已知P 是△ABC 所在平面外的一点,M 、N 分别是AB 、PC 的中点,若MN =BC =4,PA =43, 则异面直线PA 与MN 所成角的大小是A .30°B .45°C .60°D .90° 11.若将函数f (x )=sin(2x +φ)+3cos(2x +φ)(0<φ<π)的图象向左平移π4个单位长度,平移后的图象关于点⎝⎛⎭⎫π2,0对称,则函数g (x )=cos(x +φ)在⎣⎡⎦⎤-π2,π6上的最小值是A .-12B .-32C .22D .1212.已知函数f (x )=(3x +1)e x +1+mx (m ≥-4e),若有且仅有两个整数使得f (x )≤0,则实数m 的取值范围是A B C D 第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第23题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13.已知函数f (x )=log 21-x 1+x ,若f (a )=12,则f (-a )=________.14__________. 15的取值范围是__________.16.已知点A (0,1),抛物线C :y 2=ax (a >0)的焦点为F ,连接FA ,与抛物线C 相交于点M ,延长FA ,与抛物线C 的准线相交于点N ,若|FM |∶|MN |=1∶3,则实数a 的值为________. 三.解答题17.(本小题满分12分){a n }的前n 项和S n 满足:a n +S n =1 (1)求数列{a n }的通项公式; (2){C n }的前n项和为T n ,求证:T n <1. 18.(本小题满分12分)随着互联网的快速发展,基 于互联网的共享单车应运而生, 某市场研究人员为了了解共享单 该公司最近六个月的市场占有 率进行了统计,并绘制了相应 的折线图:(1)由折线图可以看出,可用线性回归模型拟合月度市场占2017年4月的市场占 有率;(2)为进一步扩大市场,公/辆和 1200元/多使用4年,但由于多种原因(如骑行频率等)会导致单车使 用寿命各不相同,考虑到公司运营的经济效益,该公司决定 先对这两款车型的单车各100辆进行科学模拟测试,得到两 款单车使用寿命的频数表如右表:经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型? 参考公式:bx19.(本小题满分12分)如图,在四棱锥P -ABCD 中,底面ABCD 是平行四边形,∠BCD =135°,侧面PAB ⊥底面ABCD ,∠BAP =90°,AB =AC =PA =2,E 、F 分别为BC 、AD 的中点,点M 在线段PD 上.(1)求证:EF ⊥平面PAC ;(2)如果直线ME 与平面PBC 所成的角和直线ME 与平面ABCD20.(本小题满分12分)已知椭圆C 的中心在原点,焦点在x 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q )(1)求椭圆C 的方程;(2)设点P 是直线x = -4与x 轴的交点,过点P 的直线l 与椭圆C 相交于M 、N 两点,当线段MN 的中点落在正方形Q 内(包括边界)时,求直线l 斜率的取值范围. 21.(本小题满分12分)(1)(2)请考生在第22-23题中任选一题作答,如果多做,则按所做的第一题计分.22.【选修4-4:坐标系与参数方程】(本小题满分10分)在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C :l(t 为参数),直线l 与曲线C 分别交于M 、N 两点.(1)写出曲线C 的直角坐标方程和直线l 的普通方程; (2)若|PM |,|MN |,|PN |成等比数列,求a的值 23选修4-5:不等式选讲(本小题满分10分)(1)(2)1)中m银川一中2018届高三第二次模拟理科数学试题参考答案一、选择题:本大题共12小题,每小题5分. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CCBDBDABCADB二.填空题:13. 14. —24; 15. 16. 12.已知函数f (x )=(3x +1)e x +1+mx (m ≥-4e),若有且仅有两个整数使得f (x )≤0,则实数m 的取值范围是( )A.⎝⎛⎦⎤5e ,2B.⎣⎡⎭⎫-52e ,-83e 2C.⎣⎡⎭⎫-12,-83e 2D.⎣⎡⎭⎫-4e ,-52e 答案 B解析 由f (x )≤0,得(3x +1)·e x +1+mx ≤0,即mx ≤-(3x +1)e x +1,设g(x )=mx ,h(x )=-(3x +1)e x +1, 则h′(x )=-[3ex +1+(3x +1)ex +1]=-(3x +4)e x +1,由h′(x )>0,得-(3x +4)>0,即x <-43,由h′(x )<0, 得-(3x +4)<0,即x >-43,故当x =-43时,函数h(x ) 取得极大值.在同一平面直角坐标系中作出y =h(x ), y =g(x )的大致图象如图所示,当m ≥0时,满足 g(x )≤h(x )的整数解超过两个,不满足条件;当m <0时, 要使g(x )≤h(x )即⎩⎪⎨⎪⎧5e -1≥-2m ,8e -2<-3m ,即⎩⎨⎧m ≥-52e ,m <-83e 2,即-52e ≤m <-83e 2,即实数m故选B.16已知点A (0,1),抛物线C :y 2=ax (a >0)的焦点为F ,连接FA ,与抛物线C 相交于点M ,延长FA ,与抛物线C 的准线相交于点N ,若|FM |∶|MN |=1∶3,则实数a 的值为________.答案2解析 依题意得焦点F 的坐标为⎝⎛⎭⎫a 4,0,设M 在抛物线的准线上的射影为K ,连接MK ,由抛物线的定义知|MF |=|MK |,因为|FM |∶|MN |=1∶3,所以|KN |∶|KM |=22∶1,又k FN =0-1a 4-0=-4a ,k FN =-|KN ||KM |=-22,所以4a =22,解得a = 2.三.解答题:17.解析:(1)由a n +S n =1得a n -1+S n -1=1(n ≥2)两式相减可得:2a n =a n -1∴{a n }为等比数列,∴a n18.解:(1)3517.5b ==16b x ⋅=-2017年4月份()(2)由频率估计概率,1年,2年,3年,4元)1年,2年,3年,4元).19.(1,所以平面.(2令20.【解析】(1(2y =k (x+4)21.(1(222. (1)∴曲线C a > 0)t 得直线l(2)解:将直线l6分设M 、N 两点对应的参数分别为t 1、t 2分23.(本小题满分10分)选修4—5;不等式选讲.解法一:【命题意图】本题旨在考查绝对值不等式的解法、分析法在证明不等式中的应用,考查考生的推理论证能力与运算求解能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
银川一中届高三第二次模拟数学(理科)试卷参考答答案
一、选择题:
二、填空题:
13.1 16. 1 三、解答题: 17. 18.
.
19.
20.解:(1)依题意,设椭圆C 的方程为22
221x y a b
+=.
1122PF F F PF 、
、构成等差数列, ∴1122224a PF PF F F =+==, 2a =.
又1c = ,2
3b ∴=.
∴椭圆C 的方程为
2
2
143x y +=.
(2) 将直线l 的方程y kx m =+代入椭圆C 的方程2
2
3412x y +=中,得
01248)34(222=-+++m kmx x k . ……………………5分
由直线l 与椭圆C 仅有一个公共点知,2
2
2
2
644(43)(412)0k m k m ∆=-+-=, 化简得:2
2
43m k =+. …………………………7分 设11d F M ==
22d F M ==
, …………………………9分
(法一)当0k ≠时,设直线l 的倾斜角为θ,则1d 12d d MN k
-∴=
, 2212
1212221()221
m d d d d S d d k k k --=+==+
m
m m m 1814
3
22+
=
+-=
,……11分
2243m k =+,∴当0k ≠时,3>m ,3343
31=+>+
m m ,32<S . 当0=k 时,四边形12F MNF 是矩形,S =. …………………………13分 所以四边形12F MNF 面积S 的最大值为 ……………………………14分
(法二) 2222
2
2
2
1
2222()2(53)
11m k k d d k k +++=+==++, 222122233311m k k d d k k -+====++.
MN ∴===
四边形12F MNF 的面积121
()2S MN d d =+)(1
1212d d k ++=, ………11分 2
2
2212
22122
)1(1216)2(11++=+++=k k d d d d k S
12)21
1
(41622≤-+-=k . …………………………………………13分
当且仅当0k =时,2
12,S S ==max S =
所以四边形12F MNF 的面积S 的最大值为
21.解:由已知函数)(),(x f x g 的定义域均为),1()1,0(+∞ ,且ax x
x
x f -=
ln )(. …1分 (Ⅰ)函数2
2)(ln 1ln )(ln 1
ln )(x x x x x x x g -=⋅
-=
', 当e 0<<x 且1≠x 时,0)(<'x g ;当e >x 时,0)(>'x g .
所以函数)(x g 的单调减区间是)e ,1(),1,0(,增区间是),e (+∞. ………………3分
(Ⅱ)因f (x )在(1,)+∞上为减函数,故2
ln 1()0(ln )
x f x a x -'=-≤在(1,)+∞上恒成立.
所以当(1,)x ∈+∞时,max ()0f x '≤.
又()
2
2ln 111()ln ln (ln )
x f x a a x x x -'=-=-+-()
2
111ln 24a x =--+-,
故当11ln 2
x =,即2e x =时,max 1()4f x a '=-.
所以10,4a -≤于是14a ≥,故a 的最小值为14
. …………………………6分
(Ⅲ)命题“若2
12,[e,e ],x x ∃∈使()12()f x f x a '≤+成立”等价于
“当2[e,e ]x ∈时,有()min max ()f x f x a '≤+”.
由(Ⅱ),当2[e,e ]x ∈时,max 1()4f x a '=-,∴()max 14
f x a '+=.
问题等价于:“当2[e,e ]x ∈时,有min 1()4
f x ≤”. ………………………8分
01当14
a ≥时,由(Ⅱ)
,()f x 在2[e,e ]上为减函数, 则min ()f x =2
22e 1(e )e 24
f a =-≤,故21124e a ≥-.
02当0<14a <时,由于()f x '()
2
111ln 24
a x =--+-在2[e,e ]上为增函数,
故()f x '的值域为2[(e),(e )]f f '',即1[,]4
a a --.
由()f x '的单调性和值域知,
∃唯一20(e,e )x ∈,使0()0f x '=,且满足:
当0(e,)x x ∈时,()0f x '<,()f x 为减函数;当20(,e )x x ∈时,()0f x '>,()f x 为增函数;
所以,min ()f x =00001()ln 4
x
f x ax x =-≤,20(e,e )x ∈.
所以,2001111111ln 44e 244
ln e a x x ≥->->-=,与104a <<矛盾,不合题意.
综上,得21124e a ≥-. …………………………13分。
