§2.1数列极限
合集下载
2.1.数列极限概念
lim an a 或 → a (n →∞) na
n
注: 上述定义称为“ε义
lim an a 0,
n
N N＋ , n N , 有
| an a | .
？
求实
创新
团结
奉献
n 1 例1：证明 lim . n n 1
奉献
三、数列极限 -N定义
分析： 数列{an}的极限为a ⇔ 随着n的无限增大，通项an无限接近于a ⇔ 当n充分大时，an与a的距离|an − a|可以任意小
求实
创新
团结
奉献
定义: 设 {an}为数列，a为定数，若对任给的ε >0，总存在
正整数N，使得当n>N时，有 |an − a|< ε，则称数列{an}收敛 于a，a称为{an}的极限. 记作
求实
创新
团结
奉献
例如, 当 n >N 时, 有
| an a | ,
则当 n > N1 = 2N 时, 对于同样的 , 更应有
| an a | .
也就是说, 在这里只是强调 N 的存在性, 而不追求 N 的 “ 最佳性 ” .
求实
创新
团结
奉献
xn
A
A
越来越 ，N越来越大！
an U (a ; ) , 即 lim an a .
n
求实
创新
团结
奉献
2
a x2 x1 x N 1
a
a
x N 2 x3
x
当n N时, 所有的点 x n都落在 (a , a )内, 只有有限个 (至多只有N个) 落在其外.
求实
2.1 数列的极限
第二节 极限的概念与性质
数学系 贺 丹
2.1 数列极限的概念
.
一的 尺《 之庄 棰子
·
日 天战
取 下国
其 篇时
半 》代
万 世 不 竭
引哲 用学 过家 一庄 句周
话所
:
著
2.1 数列极限的概念
战国时代哲学家庄周著的《庄子·天下 篇》引用过一句话：
一尺之棰 日取其半 万世不竭.
{an } ：剩余的长度
例
4．证明：
lim
n
n2 2n2
1 3n
1 2
。
证明：
0 ，要使
n2 1 2n2 3n
1 2
2 3n
3n 2
2(2n2 3n) 2(2n2 3n)
3n 2(2n2
3n)
3 2(2n 3)
3 4n
1 n
放大
放大 放大
即 n 1 ，故取 N [1] ，
∵
0 ， N
[1]，
1
0 ，要使 n a 1 n a 1 ，只要 (a)n 1 ，
即只要 1 ln a ln(1 ) ，从而有 n ln a ，
n
ln(1 )
取
N
ln a
ln(1
)
。
∵
0 ， N
ln a
ln(1
)
，
n
N
时，恒有
n
a
1
，
∴ lim n a 1 。 n
2.1 数列极限的概念
A 1 ， A 2 ， A 3 ，…， An ，…，
当 n 无限增大时，正 6 2n1 边形无限地接近于圆， An 就无限地接近于常数 A R2 。
数学系 贺 丹
2.1 数列极限的概念
.
一的 尺《 之庄 棰子
·
日 天战
取 下国
其 篇时
半 》代
万 世 不 竭
引哲 用学 过家 一庄 句周
话所
:
著
2.1 数列极限的概念
战国时代哲学家庄周著的《庄子·天下 篇》引用过一句话：
一尺之棰 日取其半 万世不竭.
{an } ：剩余的长度
例
4．证明：
lim
n
n2 2n2
1 3n
1 2
。
证明：
0 ，要使
n2 1 2n2 3n
1 2
2 3n
3n 2
2(2n2 3n) 2(2n2 3n)
3n 2(2n2
3n)
3 2(2n 3)
3 4n
1 n
放大
放大 放大
即 n 1 ，故取 N [1] ，
∵
0 ， N
[1]，
1
0 ，要使 n a 1 n a 1 ，只要 (a)n 1 ，
即只要 1 ln a ln(1 ) ，从而有 n ln a ，
n
ln(1 )
取
N
ln a
ln(1
)
。
∵
0 ， N
ln a
ln(1
)
，
n
N
时，恒有
n
a
1
，
∴ lim n a 1 。 n
2.1 数列极限的概念
A 1 ， A 2 ， A 3 ，…， An ，…，
当 n 无限增大时，正 6 2n1 边形无限地接近于圆， An 就无限地接近于常数 A R2 。
§2.1 数列极限的概念与性质
\\ 2.1.2 数列极限的算术定义 数列极限与数值级数 映射与函数
例２ 用数列极限定义验证 分析 对于任意给定的正数
， 要使
只需 证 对于任意给定的正数 当 时，恒有 存在正整数 ， ，则
因此，由定义知
．
\\ 2.1.2 数列极限的算术定义 数列极限与数值级数 映射与函数
N 极限“
”定义简洁形式： 当 时，恒有
祖冲之 公元429-500
第二章 数列极限与数值级数
极限的定义 基本性质 收敛性判定 收敛与发散的定义 基本性质 收敛性判定
数列极限
数值级数
数列极限与数值级数 映射与函数
§2.1 数列极限的概念与性质
2.1.1 数列极限的直观描述 2.1.2 数列极限算术定义 2.1.3 数列极限的几何解释 2.1.4 数列极限的基本性质 内容小结与作业
an
.
.
. . . . . . . .. ..... . .... .... .... . ..
n
.
O
上图说明对任意给定的两平行线 一定可以找到正整数 ，对于 均落在这两条平行线之间．
与 的所有点
，
数列极限与数值级数 映射与函数
重点回顾
§2.1 数列极限的概念与性质
数列极限算术定义 数列极限的基本性质
n Sin n n Sin n
1 2 3 4 0.8415 0.9093 0.1411 0.7568 6 7 8 9 0.2794 0.6570 0.9894 0.4121
5 0.9589 10 0.5440
\\ 2.1.1 数列极限的直观描述 数列极限与数值级数 映射与函数
几何法：
方法一：将数列 的项所对应数值表示在数轴上
数列极限
a n 2 n；
1 1 1 ( 2) 1, , , , , 2 3 n
1 { }； n
{a n }；
(3) 0, 1, 0, 2,,0, n,
1 an ； n a2 k 1 0， k 1, 2, a 2 k k，
整序函数： 数列是以正整数集合 N { 1,2,} 为定义域的一个 函数，若记此函数为 f ( n)，则数列可以记为 a1 f (1) , a2 f ( 2) ,, an f ( n) ,, 或 {an } , 每个数an 称为数列的项 。
注： 1. 如果an an1 (an an1 )，则称数列为严格单调 增加（减少） 数列。
二. 数列极限
观察：
1 {1 } n 3 4 5 n1 2, , , ,, , 2 3 4 n 1 1 1 1, 0, , 0, , 0 , , 3 5 7
n
1
n sin 2 } { n
1
例 3 对于数列{q n }，试证当| q | 1 时为收敛数列 , 且有
n
lim q n 0 .
n
证明
n 若 q 0， 则恒有 q n 0， lim q 0．
若 0 | q | 1， 则必存在 a 0，使 | q |
0， 要使
n n
1 ． 1 a
1
所以 lim 1
n
1 1。 n
( 1)n 例 2 已知 an ， 证明数列 {an } 的极限为 0． 2 ( n 1)
证明 0 1， 要使
| an 0 |
1 1 2 ( n 1) n 1
1 则 n 1， 可取 N 1 ．
【高等数学】2.1 数列的极限
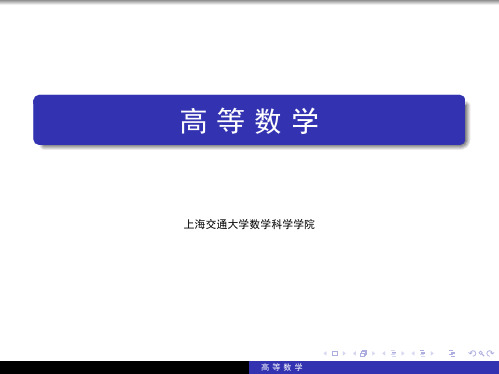
0.001 |xn − 1| < 0.001 n > 1000
1
ϵ
|xn − 1| < ϵ
n>[ ] ϵ
.
.
.
.
.
.
高等数学
定义(数列极限) 对数列 {xn}, 若 ∃A ∈ R, ∀ϵ > 0, ∃N ∈ N+, 当 n > N 时,
|xn − A| < ϵ,
则称 A 为 {xn} 的极限, 或称 {xn} 收敛于 A, 记为
xn
=
n+(−1)n n
ϵ = 0.1 N = 10?
0.9
1
1.1
x10
.
.
.
.
.
.
高等数学
xn
=
n+(−1)n n
0.9
1
x11
ϵ = 0.1 N = 10?
1.1
.
.
.
.
.
.
高等数学
xn
=
n+(−1)n n
0.9
ϵ = 0.1 N = 10?
1
1.1
x12
.
.
.
.
.
.
高等数学
xn
=
n+(−1)n n
.
.
.
.
.
.
高等数学
注 1. 若不存在这样的 A, 则称 {xn} 无极限, 或 称为发散(不收敛). 2. ϵ 具有任意性, 说明 xn 与 A 的接近程度可以 任意小; ϵ 具有相对固定性, 一旦给出就固定. 3. N 存在即可, 其选取通常依赖于 ϵ, 常写作 N = N(ϵ), 但这不是真正的函数, 因为 N 不具 有唯一性, 也不需要最小. 4. 几何意义 无论 ϵ 多小, 第 N 项后的所有 xn 都在邻域 (A − ϵ, A + ϵ) 内, 即在此邻域外只有 有限项.
§2.1 数列的极限
二①
15/18
2n 例1. 用分析的定义证明 lim =2 n→∞ n + 1
分析：由数列极限的定义可知，对给定的ε 分析：由数列极限的定义可知，对给定的ε，要找 到正整数N， 成立. 到正整数 ，使得当 n>N 时，恒有 |yn-2|< ε 成立 为此， 为此，我们可以通过解上述不等式的方法找到 N.
二①
8/18
⑵有界性 若存在某一个正数A,使数列 使数列{y 中的一切项 若存在某一个正数 使数列 n}中的一切项 均满足不等式|y 则称数列 是有界的,否则 均满足不等式 n |≤A,则称数列 n}是有界的 否则 则称数列{y 是有界的 称数列{y 是无界的 是无界的. 称数列 n}是无界的 n−1 − 1 n−1 n + (−1) n }则是有界的 则是有界的. 是无界数列; 例如{2 }是无界数列 { n }{(−1) }{ n 2 使得对一切n,恒有 注:⑴上界: 若存在常数 使得对一切 恒有 n≤M, ⑴上界: 若存在常数M,使得对一切 恒有y 则称数列{y 有上界 并称M 是它的一个上界; 有上界， 则称数列 n}有上界，并称 是它的一个上界; 下界: 若存在常数m,使得对一切 恒有y 使得对一切n,恒有 ⑵下界: 若存在常数 使得对一切 恒有 n≥m, 则称数列{y 有下界 并称m是它的一个下界 有下界， 是它的一个下界. 则称数列 n}有下界，并称 是它的一个下界. 结论: 若存在两个常数m和 ，使得对一切n， 结论 若存在两个常数 和M，使得对一切 ，恒有 m≤ yn ≤M, 有界. 则称数列 {yn} 有界
2n 2 2 2 | − 2 |= < < ε ⇒n > n+1 n+1 n ε
证明： 证明：对任意给定的 ε > 0,存在 N=[2/ ε],当n>N时 存在 当 时 恒有
15/18
2n 例1. 用分析的定义证明 lim =2 n→∞ n + 1
分析：由数列极限的定义可知，对给定的ε 分析：由数列极限的定义可知，对给定的ε，要找 到正整数N， 成立. 到正整数 ，使得当 n>N 时，恒有 |yn-2|< ε 成立 为此， 为此，我们可以通过解上述不等式的方法找到 N.
二①
8/18
⑵有界性 若存在某一个正数A,使数列 使数列{y 中的一切项 若存在某一个正数 使数列 n}中的一切项 均满足不等式|y 则称数列 是有界的,否则 均满足不等式 n |≤A,则称数列 n}是有界的 否则 则称数列{y 是有界的 称数列{y 是无界的 是无界的. 称数列 n}是无界的 n−1 − 1 n−1 n + (−1) n }则是有界的 则是有界的. 是无界数列; 例如{2 }是无界数列 { n }{(−1) }{ n 2 使得对一切n,恒有 注:⑴上界: 若存在常数 使得对一切 恒有 n≤M, ⑴上界: 若存在常数M,使得对一切 恒有y 则称数列{y 有上界 并称M 是它的一个上界; 有上界， 则称数列 n}有上界，并称 是它的一个上界; 下界: 若存在常数m,使得对一切 恒有y 使得对一切n,恒有 ⑵下界: 若存在常数 使得对一切 恒有 n≥m, 则称数列{y 有下界 并称m是它的一个下界 有下界， 是它的一个下界. 则称数列 n}有下界，并称 是它的一个下界. 结论: 若存在两个常数m和 ，使得对一切n， 结论 若存在两个常数 和M，使得对一切 ，恒有 m≤ yn ≤M, 有界. 则称数列 {yn} 有界
2n 2 2 2 | − 2 |= < < ε ⇒n > n+1 n+1 n ε
证明： 证明：对任意给定的 ε > 0,存在 N=[2/ ε],当n>N时 存在 当 时 恒有
§2.1 数列的极限-13页PPT精选文档
A , A 内 ， 而 在 开 区 间 以 外 ， 至 多 只 有 有 限 个 点
x1,x2,,xN
目录 上一页 下一页 退 出
介绍几个常用的符号： 符 号 “ ” 表 示 ： “ 对 于 任 意 的 ” 、 “ 对 于 所 有 的 ” ；
符 号 “ ” 表 示 ： “ 存 在 ” 、 “ 有 一 个 ” ；
目录 上一页 下一页 退 出
下面给出数列极限的定义
定义2 对 于 数 列 x n ， 如 果 当 n 无 限 增 大 时 ， 一 般 项 x n
的 值 无 限 接 近 于 一 个 确 定 的 常 数 A ， 则 称 A 为 数 列 x n 当 n 趋 向 于 无穷大时的极限，记为 l n i m x n A ， 或 者 x n A n
x n . 数 列 中 的 每 个 数 称 为 数 列 的 项，其中xn称为数列源自的一般项或通项...
目录 上一页 下一页 退 出
下 面 考 察 当 n 无 限 增 大 时 ( 记 为 n ， 符 号 读 作
趋 向 于 ） 一 般 项 x n 的 变 化 趋 势 : 11n1
定义3 设 有 数 列 x n ， 若 M 0 ， 使 对 一 切 n 1 , 2 , , 有 x n M ， 则 称 数 列 x n 是 有 界 的 ， 否 则 称 它 为 无 界 的 。
例 如 数 列 n 2 1 1 、 (-1 )n有 界 ， 数 列 n 2无 界 。
符 号 “ m a x X ” 表 示 数 集 X 中 的 最 大 数 ；
符 号 “ m i n X ” 表 示 数 集 X 中 的 最 小 数 .
x1,x2,,xN
目录 上一页 下一页 退 出
介绍几个常用的符号： 符 号 “ ” 表 示 ： “ 对 于 任 意 的 ” 、 “ 对 于 所 有 的 ” ；
符 号 “ ” 表 示 ： “ 存 在 ” 、 “ 有 一 个 ” ；
目录 上一页 下一页 退 出
下面给出数列极限的定义
定义2 对 于 数 列 x n ， 如 果 当 n 无 限 增 大 时 ， 一 般 项 x n
的 值 无 限 接 近 于 一 个 确 定 的 常 数 A ， 则 称 A 为 数 列 x n 当 n 趋 向 于 无穷大时的极限，记为 l n i m x n A ， 或 者 x n A n
x n . 数 列 中 的 每 个 数 称 为 数 列 的 项，其中xn称为数列源自的一般项或通项...
目录 上一页 下一页 退 出
下 面 考 察 当 n 无 限 增 大 时 ( 记 为 n ， 符 号 读 作
趋 向 于 ） 一 般 项 x n 的 变 化 趋 势 : 11n1
定义3 设 有 数 列 x n ， 若 M 0 ， 使 对 一 切 n 1 , 2 , , 有 x n M ， 则 称 数 列 x n 是 有 界 的 ， 否 则 称 它 为 无 界 的 。
例 如 数 列 n 2 1 1 、 (-1 )n有 界 ， 数 列 n 2无 界 。
符 号 “ m a x X ” 表 示 数 集 X 中 的 最 大 数 ；
符 号 “ m i n X ” 表 示 数 集 X 中 的 最 小 数 .
04.数列的极限的性质汇总
.
A
.
. . . . . . . . .... .... . .... . . . . . . .. .
n
.
o
§2.1 数列的极限
xn lim zn A, 定理5（夹逼性）设 xn yn zn (n 1,2,) ，且 nlim n yn A. 则nlim
思考题：
作业 P23: 7, 8(1), 9,10,12
lim f ( x) A 0, 0, 当 x x0 0 时, 有 f ( x) A .
f ( x) A lim f ( x) lim f ( x) A 定理1 xlim x x
定理2
x x0
lim f ( x) A lim f ( x) lim f ( x) A
un A
§2.2 函数的极限
定义1 设 f ( x)在 (a,) 内有定义,若存在常数 A ,使得对于 N 任意的正数 , 存在正数 ,N 当时 x ,恒有
f ( x) A
则称 f ( x) 在过程 x 中存在极限 A ,记为
x
lim f ( x) A
定义2 设 f ( x)在 x0 的某去心邻域内有定义,若存在常数 A , 使得 0 , 0 ,当时 0 x x0 ,恒有
f ( x) A
则称 f ( x)在过程中 x x0 存在极限 A ,记为
xx0
lim f ( x) A 或 f ( x) A ( x x0 ) .
x x0 x x0
总结与练习
本讲主要内容：
子数列的概念及其收敛性 函数极限的定义（6种情形） 各种极限之间的关系
理学21数列极限
当n 时的极限，记作
lim
n
xn
a
或
xn a (n 时)
如不存在这样的常数 a,则称数列{xn }发散，或不收敛，也可
以说极限
lim
n
xn不存在。
例 求以下数列的极限： 数列的项不一定取到它的极限值.
(1) 2, 4, 8, L , 2n , L 2n 无限增大; lim 2n不存在， 记为 lim 2n
数列极限严格的数学定义： N语言
0 , 若 N 0 ,使当 n N 时,
| xn a | 成立, 则称数 a 为数列{xn}当n 时的极限,
记为
lim
n
xn
a,
或
xn a
(n ) .
几何意义： 0,N, 使得 N 项以后的所有项
xN 1, xN 2 , xN 3 ,
3、随着n的无限增大，数列的变化趋势可大致分为两类： 一类，无限接近某个常数， 另一类，不趋近某个常数。
问题 当 n 的无限增大时，数列是否无限接近于某一确定的 数值，如果是，如何描述之？
数列极限的定义：
当n无限增大时,数列xn的通项 xn 无限趋于一个确定
的常数 a,则称数列xn收敛于a，或称 a 为数列xn
(1)n n
无限接近于0;
(5) 1 , 2 , 3 , L , n , L
234
n1
通项 :
n
xn
n
. 1
n
n
1
x1 x2 x3 … xn …
••••• •••••
x
0
1 2
2 3
3 4
…
n n 1
…
1
由图可知,当n无限增大时, 表示数列(5)的点逐渐密集
lim
n
xn
a
或
xn a (n 时)
如不存在这样的常数 a,则称数列{xn }发散，或不收敛，也可
以说极限
lim
n
xn不存在。
例 求以下数列的极限： 数列的项不一定取到它的极限值.
(1) 2, 4, 8, L , 2n , L 2n 无限增大; lim 2n不存在， 记为 lim 2n
数列极限严格的数学定义： N语言
0 , 若 N 0 ,使当 n N 时,
| xn a | 成立, 则称数 a 为数列{xn}当n 时的极限,
记为
lim
n
xn
a,
或
xn a
(n ) .
几何意义： 0,N, 使得 N 项以后的所有项
xN 1, xN 2 , xN 3 ,
3、随着n的无限增大，数列的变化趋势可大致分为两类： 一类，无限接近某个常数， 另一类，不趋近某个常数。
问题 当 n 的无限增大时，数列是否无限接近于某一确定的 数值，如果是，如何描述之？
数列极限的定义：
当n无限增大时,数列xn的通项 xn 无限趋于一个确定
的常数 a,则称数列xn收敛于a，或称 a 为数列xn
(1)n n
无限接近于0;
(5) 1 , 2 , 3 , L , n , L
234
n1
通项 :
n
xn
n
. 1
n
n
1
x1 x2 x3 … xn …
••••• •••••
x
0
1 2
2 3
3 4
…
n n 1
…
1
由图可知,当n无限增大时, 表示数列(5)的点逐渐密集
微积分第2章极限与连续
2. 用定义只能验证极限，不能求极限.
第二章 极限与连续
7
三、数列极限的运算法则 (课本p.66§2.5 )
定理 设
则
会应用
证明
特别地，
第二章 极限与连续
8
例2 求极限：
注意: 极限四则运算只适用于 有限项运算，且各项极限存在!
(上下同除以n3)
例3 设函数
(先求括号内各项之和)
，求极限 (考研题)
例4 证明方程 x3 - 4x2 + 1=0 在 (0,1) 内至少有一个根.
函数极限的计算方法
1. 图像观察 2. 按定义验证 3. 四则运算（拆分后各部分极限应存在） 4. 夹逼准则 5. 两个重要极限及其应用 6. 无穷小、无穷大的性质 7. 无穷小等价代换 8. f 在连续点 x0 处的极限为 f(x0) 9. 多重复合函数，遇连续函数，极限符号可向内移位 10. 变量替换
例2 比较 x→0 时下列各无穷小量的阶：
1) sinx 与 x, tanx 与 x；
等价
2)
与 x；
同阶
3)
与 x (x→0+) ；
4) 1-cos x 与 x2/2；
等价
x→0 时常用等价无穷小量
要记
x ~ sin x ~ tan x ~ arcsin x ~ arctan x ~ ln(1+x) ~ ex -1
一、无穷小量 二、无穷大量 三、无穷小量的阶 四、无穷小量等价代换
一、无穷小量
定义 若
，则称 f(x) 为当x→X 时的无穷小量.
若 f(x) 在 X 某邻域内有界，则称 f(x) 为x→X 时的有界量.
例: x2, sinx, 0 是 x→0 时的无穷小量；
2.1数列的极限
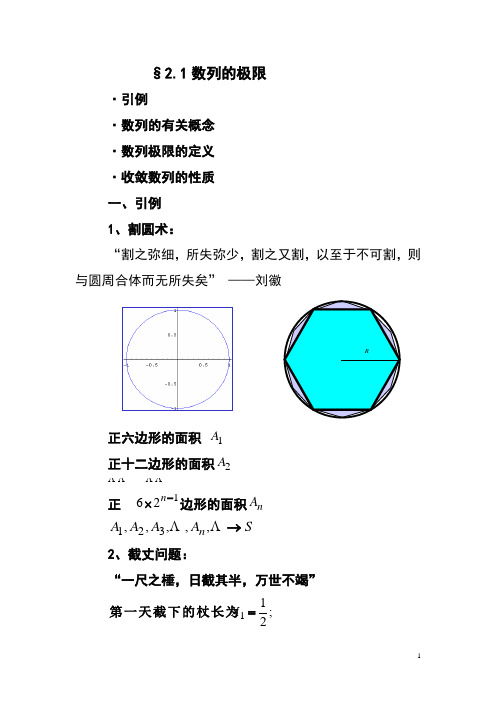
§2.1数列的极限·引例·数列的有关概念 ·数列极限的定义 ·收敛数列的性质 一、引例 1、割圆术：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣” ——刘徽正六边形的面积 1A 正十二边形的面积2A 正 126-⨯n 边形的面积n AS A A A A n → ,,,,,3212、截丈问题：“一尺之棰，日截其半，万世不竭”;211=X 第一天截下的杖长为;212122+=X 为第二天截下的杖长总和;2121212nn X n +++=天截下的杖长总和为第1211→-=nn X二、数列的有关概念 1、定义:以正整数集+N为定义域的函数)(n f 按,)(,,)2(,)1(n f f f 排列的一列数称为数列，通常用 ,,,,21n x x x 表示，其中 )(n f x n=，n x 称为通项 例如：（1） 11111, , , , , ,234n 1n ⎧⎫⎨⎬⎩⎭（2） 2, 4, 8, , 2, n{}2n (3) 12313, 3, 3, 3, , 4, 234n -14n ⎧⎫-⎨⎬⎩⎭(4) 11, 1, 1, 1, , (1), n +--- {}1(1)n +-注意：(1) 一个数列对应着数轴上的一个点列.(2) 数列是整标函数 ).(n f x n =2、有界性定义: 对数列n x , 若存在正数M , 使得一切自然数n , 恒有M x n ≤成立, 则称数列n x 有界, 否则, 称为无界.例如, 1+=n nx n 数列 有界，nn x 2=数列无界. 数轴上对应于有界数列的点n x 都落在闭区间],[M M -上.，都满足，对一切若存在实数A x n A n ≥,}{为下有界称n x ；的下界是}{n x A同样, ，都满足，对一切若存在B x n B n ≤,}{为上有界称n x ．的上界是}{n x A3、单调性,}{21n n x x x x ≤≤≤ 若满足数列 }{n x 称数列为单调增数列；,21n x x x ≥≥≥ 若满足为则称数列}{n x 单调减数列．单调增数列和单调减数列统称为单调数列． 4、子数列 (subsequence) {}{}列，简称子列．的子数新数列称为取其中无穷多项构成的，任在保持原有顺序情况下定义：将数列n n x x例如， ,,,,,21n i x x x x,,,,21kn n n x x x 注意： {}{}.k n n x x k x x k k n n n n kkk≥项，显然，中却是第在原数列而项，是第中，一般项在子数列三、数列极限的定义(Limit of a sequence)我们来观察⎭⎬⎫⎩⎨⎧+n n 1的情况。
第二节 数列的极限课件
机动 目录 上页 下页 返回 结束
例3. 证明数列 证: 用反证法. 假设数列
是发散的.
xn 收敛 ,
2
则有唯一极限 a 存在 .
取 1 , 则存在 N , 使当 n > N 时 , 有 2
a 1 xn a 1
但因
2
xn 交替取值 1 与－1 ,
2
而此二数不可能同时落在
( 0) . (用反证法证明)
4. 收敛数列的任一子数列收敛于同一极限 . 证: 设数列 若 是数列
的任一子数列 .
时, 有
则 0 , N , 当
现取正整数 K , 使
于是当 k K 时, 有
nk nK N
*********************
xN
N
从而有 x n a , 由此证明 lim x nk a . k
所以xn 单调递增 .
18
例6
证明数列 xn 3 3
n
3
(n重根式)
的极限存在并求 . lim xn
(2)再证 xn 的有界性
x1 3 3,
xn 有上界;
lim x n 存在.
n
假定 xk 3,
x k 1 3 x k 3 3 3,
(1) n 1 0 故 lim xn lim x 0 也可由 2 n n n ( n 1) ( n 1) 2 说明: N 与 有关, 但不唯一. 取 N 1 1 不一定取最小的 N . 1] 故也可取 N [
机动 目录 上页 下页 返回 结束
xn (1) n1 趋势不定
机动 目录 上页
散
下页 返回 结束
例3. 证明数列 证: 用反证法. 假设数列
是发散的.
xn 收敛 ,
2
则有唯一极限 a 存在 .
取 1 , 则存在 N , 使当 n > N 时 , 有 2
a 1 xn a 1
但因
2
xn 交替取值 1 与－1 ,
2
而此二数不可能同时落在
( 0) . (用反证法证明)
4. 收敛数列的任一子数列收敛于同一极限 . 证: 设数列 若 是数列
的任一子数列 .
时, 有
则 0 , N , 当
现取正整数 K , 使
于是当 k K 时, 有
nk nK N
*********************
xN
N
从而有 x n a , 由此证明 lim x nk a . k
所以xn 单调递增 .
18
例6
证明数列 xn 3 3
n
3
(n重根式)
的极限存在并求 . lim xn
(2)再证 xn 的有界性
x1 3 3,
xn 有上界;
lim x n 存在.
n
假定 xk 3,
x k 1 3 x k 3 3 3,
(1) n 1 0 故 lim xn lim x 0 也可由 2 n n n ( n 1) ( n 1) 2 说明: N 与 有关, 但不唯一. 取 N 1 1 不一定取最小的 N . 1] 故也可取 N [
机动 目录 上页 下页 返回 结束
xn (1) n1 趋势不定
机动 目录 上页
散
下页 返回 结束
2.1 数列极限
n
定理2.1（夹逼定理） 假设存在正整数 N 0 , 使得
n N 0 时, 数列 { xn }, { yn }, { zn } 满足不等式 yn x n z n 如果 lim yn lim zn a , 那么数列 { xn } 收敛 , 且
n n
lim xn a
n 时, an 始终为 1,
因此 lim an 1 ,
n
即 lim 1 1 .
n
( 2) 数列an ( 1)n , n 1,2,,
当 n 按奇数无限增大时, an 始终为 1;
n 按偶数无限增大时, an 始终为 1;
因此, n 时, an 没有明确的趋势,
即 lim( 1)n 不存在.
n
( 3) 数列 an 3n 2, n 1, 2, , 是正整数数列, n 无限增大时, an 也无限增大,
且 an 的趋势不是一个确定的数,
因此 lim(3n 2) 不存在. 记为 lim(3n 2) .
n
n
1 (4) 数列 an , n 1,2,, 当 n 无限增大时, an 无限 n 1 趋于 0, 因此 lim 0. n n 1 (5) 数列 an n , n 1,2,, 当n无限增大时, an 无限 2 1 趋于 0, 因此 lim n 0. n 2
n n
(3) 由于
3 n 2 n1 n 2 n1
因为 lim n( n 2 n 1)
n
3 n lim n n 2 n 1
3 lim . n 2 1 2 1 1 n n
3
1 2n 1 ln( 2n 1) ln n ln ln 2 (4) 由于 n n 1 lim 因此 n[ln( 2n 1) ln n] lim ln 2 ln 2 n n n 3 1 3 n n1 4 3 4 (5) 由于 2 n1 n n 2 3 3 2 4
定理2.1（夹逼定理） 假设存在正整数 N 0 , 使得
n N 0 时, 数列 { xn }, { yn }, { zn } 满足不等式 yn x n z n 如果 lim yn lim zn a , 那么数列 { xn } 收敛 , 且
n n
lim xn a
n 时, an 始终为 1,
因此 lim an 1 ,
n
即 lim 1 1 .
n
( 2) 数列an ( 1)n , n 1,2,,
当 n 按奇数无限增大时, an 始终为 1;
n 按偶数无限增大时, an 始终为 1;
因此, n 时, an 没有明确的趋势,
即 lim( 1)n 不存在.
n
( 3) 数列 an 3n 2, n 1, 2, , 是正整数数列, n 无限增大时, an 也无限增大,
且 an 的趋势不是一个确定的数,
因此 lim(3n 2) 不存在. 记为 lim(3n 2) .
n
n
1 (4) 数列 an , n 1,2,, 当 n 无限增大时, an 无限 n 1 趋于 0, 因此 lim 0. n n 1 (5) 数列 an n , n 1,2,, 当n无限增大时, an 无限 2 1 趋于 0, 因此 lim n 0. n 2
n n
(3) 由于
3 n 2 n1 n 2 n1
因为 lim n( n 2 n 1)
n
3 n lim n n 2 n 1
3 lim . n 2 1 2 1 1 n n
3
1 2n 1 ln( 2n 1) ln n ln ln 2 (4) 由于 n n 1 lim 因此 n[ln( 2n 1) ln n] lim ln 2 ln 2 n n n 3 1 3 n n1 4 3 4 (5) 由于 2 n1 n n 2 3 3 2 4
2.1数列极限
一、数列极限的定义
设有一圆，其内接
正六边形的面积 A1
R
正十二边形的面积 A2
正6 2n1形的面积 An
则得一数列：
A1 , A2 , A3 ,, An ,
显然，An却不会等于圆面积，但是，这些正多 边形的面积必将随着边数的增加而不断接近圆的面
积，这个“不断接近”的过程就是一个极限的过程。 而且，当 n 时，An无限接近于圆的面积。
证
反证法 设
lim
n
xn
a, lim n
xn
b,
且a b
取
b
2
a
，由定义有
自然数N1,当
n
N1 时
xn
a
ba 2
a
ba 2
x
a
ba 2
(1)
自然数N2, 当 n N2 时
ba
ba
ba
xn b 2 b 2 x b 2 (2)
取 N max{N1, N2}, 当 n N 时，(1)与(2)同时成立
1
xn
1
; 10000
显然 1 , 1 , 1 一个比一个小，但毕竟是确定数。 10 100 10000
一般地，要使 xn 1 ( 可以任意小), 只要
n
1
1
即可，即从第[
1
1]
项开始，以后所有项
都满足 xn 1 .
同理可观察数列(2)，用数学语言表达为：
定义2 设{xn}是一个数列，a为一个确定的数。若
2 ,,
,1 (1)n , ;
n
23
n
(3) {2n},
即 2,4,6, ,2n, ;
1 (1)n
(4) {
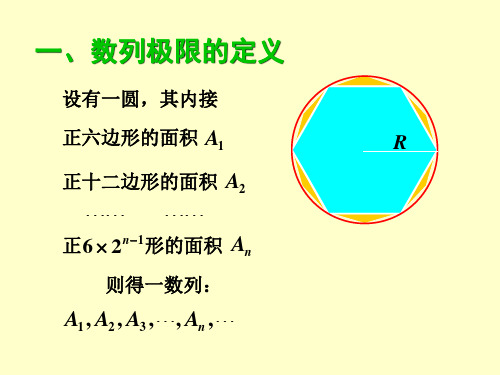
设有一圆，其内接
正六边形的面积 A1
R
正十二边形的面积 A2
正6 2n1形的面积 An
则得一数列：
A1 , A2 , A3 ,, An ,
显然，An却不会等于圆面积，但是，这些正多 边形的面积必将随着边数的增加而不断接近圆的面
积，这个“不断接近”的过程就是一个极限的过程。 而且，当 n 时，An无限接近于圆的面积。
证
反证法 设
lim
n
xn
a, lim n
xn
b,
且a b
取
b
2
a
，由定义有
自然数N1,当
n
N1 时
xn
a
ba 2
a
ba 2
x
a
ba 2
(1)
自然数N2, 当 n N2 时
ba
ba
ba
xn b 2 b 2 x b 2 (2)
取 N max{N1, N2}, 当 n N 时，(1)与(2)同时成立
1
xn
1
; 10000
显然 1 , 1 , 1 一个比一个小，但毕竟是确定数。 10 100 10000
一般地，要使 xn 1 ( 可以任意小), 只要
n
1
1
即可，即从第[
1
1]
项开始，以后所有项
都满足 xn 1 .
同理可观察数列(2)，用数学语言表达为：
定义2 设{xn}是一个数列，a为一个确定的数。若
2 ,,
,1 (1)n , ;
n
23
n
(3) {2n},
即 2,4,6, ,2n, ;
1 (1)n
(4) {
2.1数列的极限
注:一般地分段函数不是初等函数,形式上分段但可 化为一个解析表达式的函数可能是初等函数.
如:y x
x2
x
x
x0 x0
构建函数模型的步骤和方法
一、构建函数模型的步骤和方法 二、函数模型举例
函数关系是一种变量相依关系的数 学模型.数学模型方法是处理科学理论问 题的一种经典方法,也是处理各类实际问 题的一般方法.我们对数学模型方法作一 简述
1 2
[
g(
x
)
g(x) ]
=
1 2
(
x
x)
=0
, x<0
1 2
(
x
2
x 2 ) =x2
,
x≥0
f(x) , f(x)<0 g[f(x)]=
[f(x)]2 , f(x)≥0
1 2
(
x
x) =0
, x<0
f(x)=
f(x)≥0
1 2
(
x
x)
=x
,
x≥0
0 , x<0
g[f(x)]=[f(x)]2 = x2 , x≥0
n
观察数列{1 (1)n1 }当n时的变化趋势
n
通过上面演示实验的观察: 当 n 无限增大时，
(Ⅰ) 2, 1 , 4 ,, n (1)n1 ,;
(Ⅱ)
1 2
2 ,1 4
3 ,1 8
,,
n
{xn }
1 2n
,;
{1
(1)n1 }
1
n1 {2n
}
0
不能无限接近于
数列 {n n}：1, 2，3 3，4 4， ，n n，
数列极限概念的引入1数列的概念若数列的定义域为全体正...
第二章
极限
§２.１. 数列极限 一、数列极限概念的引入 1．数列的概念 若数列 f 的定义域为全体正整数集合 N+ ，则称
f :Z+ → R
或 f ( n), n ∈ N +
为数列。因为正整数集可以由小到大排列，故数列 f ( n ) 也可以写作
a1 , a 2 , ⋯, a n ,⋯
简记为 {a n } ，其中 a n 称为该数列的通项。 注:(1) 根据函数的记号，数列也可记为 f ( n), n ∈ N + ； (2) 记 f ( n) = an ，则数列 { f ( n)} 就可写作为： a1 , a2 ,⋯ , an ,⋯ ，简记为 {an } , 即 { f (n) | n ∈ N+ } = {an } . 2．极限概念引入 极限概念，是数学分析中最重要、最基础的概念，在后面要讲的连续、微分、 积分等等中都要用到极限概念．极限方法是从已知认识未知，从有限认识无限， 从近似认识精确的一种数学方法．这种方法，早在我国古代就被采用了． 例如 战国时代哲学家庄周所著的《庄子。天下篇》引用过一句话：“一尺之棰，日取 其半，万世不竭。”也就是说一根一尺长的木棒，每天截去一半，这样的过程可 以一直无限制的进行下去。将每天截后的木棒排成一列,如图所示
1 以后的所有项： 10
n
18
−
1 1 1 , , − , ... 11 12 13
n
都能满足这个不等式。 对
1 ( −1) − 0 = 1 < 1 ，只须 ，能够做到 n > 102 即可，即数列(1)的第 102 项 2 2 n n 10 10
1 以后的所有项： 102 − 1 1 1 , , − , ... 101 102 103
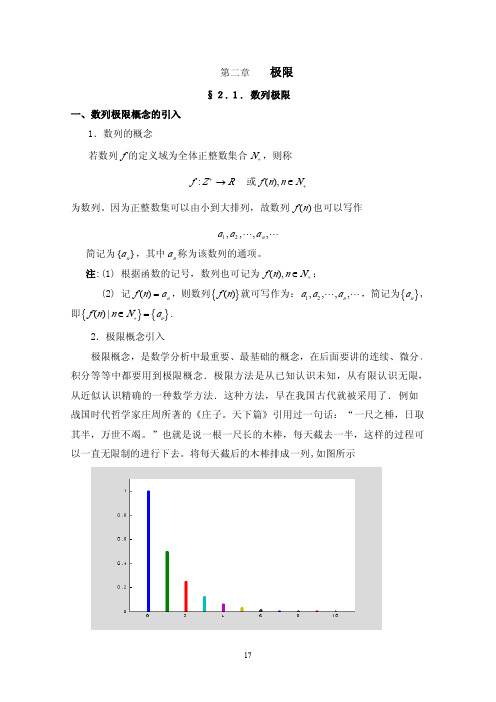
极限
§２.１. 数列极限 一、数列极限概念的引入 1．数列的概念 若数列 f 的定义域为全体正整数集合 N+ ，则称
f :Z+ → R
或 f ( n), n ∈ N +
为数列。因为正整数集可以由小到大排列，故数列 f ( n ) 也可以写作
a1 , a 2 , ⋯, a n ,⋯
简记为 {a n } ，其中 a n 称为该数列的通项。 注:(1) 根据函数的记号，数列也可记为 f ( n), n ∈ N + ； (2) 记 f ( n) = an ，则数列 { f ( n)} 就可写作为： a1 , a2 ,⋯ , an ,⋯ ，简记为 {an } , 即 { f (n) | n ∈ N+ } = {an } . 2．极限概念引入 极限概念，是数学分析中最重要、最基础的概念，在后面要讲的连续、微分、 积分等等中都要用到极限概念．极限方法是从已知认识未知，从有限认识无限， 从近似认识精确的一种数学方法．这种方法，早在我国古代就被采用了． 例如 战国时代哲学家庄周所著的《庄子。天下篇》引用过一句话：“一尺之棰，日取 其半，万世不竭。”也就是说一根一尺长的木棒，每天截去一半，这样的过程可 以一直无限制的进行下去。将每天截后的木棒排成一列,如图所示
1 以后的所有项： 10
n
18
−
1 1 1 , , − , ... 11 12 13
n
都能满足这个不等式。 对
1 ( −1) − 0 = 1 < 1 ，只须 ，能够做到 n > 102 即可，即数列(1)的第 102 项 2 2 n n 10 10
1 以后的所有项： 102 − 1 1 1 , , − , ... 101 102 103
数学分析(第二版)上册第二章第二节《数列极限概念》课件
1，
一般地，任给 0 ，想要 1 -0 ， n
只要n
N
:
1
1，就有
1 n
0
.
1 0n
n
几何直观：当n无限增大时，1 无限接近0. n
一般地，任给 0 ，想要 1 -0 ， n
只要n
N
:
1
1，就有
1 n
0
.
把
1 n
抽象为an
,
把 0 抽象 a.
K.T.W. Weierstrass 德, 1815-1897
23
n
1 an n
0 (n )
收
敛
an
1
(1)n1 n
1 n
(3) 2 , 4 , 8 ,
, 2n ,
an 2n (n )发Βιβλιοθήκη an (1)n1散
趋势不定
数列极限的直观定义
定性描述: 一般地，当 n 无限增大时，若 an 无
限接近某常数
a
，则称
a
为
{an
}
的极限(Limit). I.Newton,
n
天剩下的长度
1 2n
1
1
1
1
2
22
23
24
……
1 2n
引例2.抛物线弓形面积问题.
元前287-212《阿基米德方法》：
弓形面积为与其同底等高三角形面积的 4 倍. 3
逐次作出与弓形同底等高的三角形，再累加三角形面积.
穷竭法:
S弓形
4 3
A.
记 Sn 为第 n 次累加面积值,
A
当 n 越来越大时，
几点说明
注：1.正数 以小为贵。取之前有任意性，取后有（暂时）确定性.
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
华北科技学院理学院
2017年11月29日星期三
8
《数学分析》(1)
§2.1 数列极限概念
引例②截丈问题
战国时代哲学家庄周著的《庄子· 天下 篇》引用过一句话：
一尺之棰 日取其半 万世不竭. 1 第一天截下后的杖长为 X1 ; 2 1 第二天截下后的杖长为 X2 2 ; 2
1 第n天 截 下 后 的 杖 长 为 Xn n ; 2 1 0 Xn n
2
……
9
华北科技学院理学院
2017年11月29日星期三
《数学分析》(1)
§2.1 数列极限概念
两个引例共同点是出现了无限接近思想，这正是 极限概念的原始面貌. 极限概念是由于求某些问题的 精确答案而产生的, 割圆术和杖棰问题使用的都是极 限的方法. 第一个是把一个固定不变的量看作是一系 列变化着的多边形面积的趋向，从而确定出面积的 大小. 第二个是杖棰剩余问题，看作一系列变化着的 剩余趋向于一个确定量的问题. 无论是内接正多边形的面积 ，还是杖棰的剩余长 度，都可以看作是关于 n 的一个数列{ an }，而这个数 列中的项随着 n 增加产生一个什么样的变化过程则是 人们最关心的，极限就是讨论这一类问题的数学模型.
16
《数学分析》(1)
§2.1 数列极限概念
(4) 对 0, 2 , , 2 , M ( M正常数 )等, 虽与 在 形式上有差异 ， 但在本质上都与 起着同样的作用 .
lim a n a 0, N N , 当n N时, 有 a n a M .
2017年11月29日星期三
12
《数学分析》(1)
§2.1 数列极限概念
下面给出数列极限严格的数学定义. ( N定义)
定义1
设 { an } 为一个数列, a 为一个常数,
0, N N , 当n N时, 有 a n a .
则称数列 { an } 收敛于a , 或称 a 为数列 { an }的极限,
记作
lim an a ( 或 an a , n ) . n
也可简单定义为
0, N 0, n N , 有 an a .
若 { an } 不收敛, 则称 { an }为发散数列.
华北科技学院理学院
2017年11月29日星期三
13
《数学分析》(1)
§2.1 数列极限概念
0, N N , 当n N时, 有 a n a .
数列极限的几何解释: 由 定 义 a n a ， 得
a an a .
a a N 3
a
a2 a1 a N 1
a
aN 2
a3
x
对任意给定的 邻 域 (a , a ) , 总 存 在 项 a N， 第N项 以 后 的 所 有 项 a N 1 , a N 2, 全 位 于 这 个 邻 域 内 ;只 有 有 限 个 (至 多 只 有 N个) 落 在 其 外 .
可见：数列是否有极限，只与它从某一项以后有 关，而与它前面的有限个项无关。因之，在讨论数列 极限时，可添加、去掉或改变其有限个项的数值，对 收敛性和极限都无影响。 注意：数列极限的定义未给出求极限的方法.
华北科技学院理学院
2017年11月29日星期三
15
《数学分析》(1)
§2.1 数列极限概念
关于数列极限定义的几点理解 （1）正数 的任意性和相对固定性。
1,1,1, , ( 1)
n1
,;
n 1
1 { n} 2 n 1 {(1) }
n 1
1 4 n ( 1) 2, , , , 2 3 n
n ( 1) ,; { n
}
注： 数列对应着数轴上一个点列.可看作一动 点在数轴上依次取 a1 , a 2 , , a n , .
1 得n 1 ， 取N 1
1，
lim 1 0. n n
当n N时, 有 1 0 ,
n
注意： 使用定义验证极限的过程就是求解不等式.
华北科技学院理学院
2017年11月29日星期三
19
《数学分析》(1)
§2.1 数列极限概念
《数学分析》(1)
§2.1 数列极限概念 数列极限概念
二、数列的极限
引例①割圆术 正六边形的面积 A1 正十二边形的面积 A2
R
正 6 2 n 1形的面积 An
依次下去，得到数列： A1 , A2 , A3 ,, An , 随着 n 的无限增大，多边形的面积 An 将 无限接近圆面积 .
华北科技学院理学院
2017年11月29日星期三
1
《数学分析》(1)
§2.1 数列极限概念
CH2 数列极限
教学内容： 1、数列极限的概念 2、收敛数列的性质 3、数列极限存在的条件 教学重点与难点： 用定义证明数列极限，极限的性质， 柯西收敛准则.
华北科技学院理学院
2017年11月29日星期三
2
《数学分析》(1)
1 练习 用定义验证: lim n 0. n
证
1 1 0, 由 0 ， n n
得n ，
1
1 1 取N 1， 当n N时, 有 0 , n
1 li m 0. n n
华北科技学院理学院
2017年11月29日星期三
§2.1 数列极限概念
一、数列的定义 二、数列的极限 三、无穷小与无穷大数列
华北科技学院理学院
2017年11月29日星期三
3
《数学分析》(1)
§2.1 数列极限概念
一、数列的定义
若函数 f 的定义域为全体正整数的集合 N + , 则称
f : N+ R 或 f ( n), n N+
为数列. 因为N+的所有元素可以从小到大排列出来,
递增
无限趋近
1 3 0
递减
摆动
无限趋近
1 1 ( 1) n ， ， ， （3） 1，， ２ 3 n
无限趋近
-1
.
.... . ... . . 1 .. 0
3
. 1
2
共同特性：不论这些变化趋势如何，随着项数n 的无限增大，数列的项an无限地趋近于常数a.
华北科技学院理学院
n
(5) lim a n a与 lim a n a的比较.
n n
lim a n a 0, N N , n N , 有 a n a .
n
lima n a 0 0, N N , n0 N , 有 a n0 a 0 .
《数学分析》(1)
§2.1 数列极限概念
CH2 数列极限
极限(Limit ) 是数学分析中最基本的概念之一, 用 以描述变量在一定的变化过程中的终极状态. 早在中 国古代, 极限的朴素思想和应用就已在文献中有记载. 随着微积分的诞生, 极限作为数学中的一个概念也就 明确提出. 但最初提出的这一概念是含糊不清的,因此 在数学界引起不少争论甚至怀疑. 直到19世纪, 由柯西 和维尔斯特拉斯等人的工作, 才将其置于严密的理论 基础之上, 从而得到举世一致的公认. 凡本质上与极限概念有关的数学分支统称分析数 学,以区别于完全不用这一概念的代数学.几何学的各 分支绝大部分也直接或间接地与极限概念密切相关。
n
{a n }发散 a R, 0 0, N N , n0 N , 有 a n0 a 0 .
华北科技学院理学院
2017年11月29日星期三
17
《数学分析》(1)
§2.1 数列极限概念
例1
n ( 1) n1 1. 证明:lim n n
正数是任意给定的 , 说明an与a接进程度可任意小；
但是具有相对固定性，一旦给出之后, 就确定了.
(2) 不等式an a 刻划了 an与a的无限接近 .
（3）N的存在性与非唯一性.
N与有关, 而与n无关，只强调存在性 .
一般地， 越小, N将越大 .
华北科技学院理学院
2017年11月29日星期三
所以我们也将数列写成
a1 , a2 ,, an , ,
或简记为 {an}.
a2
..
. .
a1
2
an
an1
.
an称为数列 {an} 的通项.
华北科技学院理学院
O
1
n 1
n
2017年11月29日星期三
4
《数学分析》(1)
§2.1 数列极限概念
1 1 1 1 例如 , , ,, n ,; 2 4 8 2
a3
a1
a2 a4
an
5
华北科技学院理学院
2017年11月29列极限概念
二、数列的极限
引例①割圆术
割之弥细， 所失弥少，割 之又割，以至 于不可割，则 与圆合体而无 所失矣.
魏晋时刘徽提出的 “割圆术”.他把圆周六等分、十 二等分、二十四等分、· · · ，并作内接正多边形，这样一直 分割下去, 所得内接正多边形的面积就无限接近于圆的面 积. 2017年11月29日星期三 6 华北科技学院理学院
华北科技学院理学院
2017年11月29日星期三
11
《数学分析》(1)
§2.1 数列极限概念
分析 当n无限增大时，下列数列的项an的变化趋势 及共同特征:
1 2 3 n ，，， ， ， （1） 2 3 4 n1 1 1 1 3 2， ， 3 n， （2） 3 ， 10 10 10