C15 南京市2017届高三年级三模数学卷
江苏省南京市2017-2018学年高三下学期三模数学试卷Word版含解析

2017-2018学年江苏省南京市高考数学三模试卷一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题纸相应位置上.1.已知复数z=﹣1,其中i为虚数单位,则z的模为.2.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:排队人数0 1 2 3 4 ≥5概率0.1 0.16 0.3 0.3 0.1 0.04则该营业窗口上午9点钟时,至少有2人排队的概率是.3.若变量x,y满足约束条件则z=2x+y的最大值.4.如图是一个算法流程图,则输出k的值是.5.如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是.6.记不等式x2+x﹣6<0的解集为集合A,函数y=lg(x﹣a)的定义域为集合B.若“x∈A”是“x∈B”的充分条件,则实数a的取值范围为.7.在平面直角坐标系xOy中,过双曲线C:x2﹣=1的右焦点F作x轴的垂线l,则l与双曲线C的两条渐近线所围成的三角形的面积是.8.已知正六棱锥P﹣ABCDEF的底面边长为2,侧棱长为4,则此六棱锥的体积为.9.在△ABC中,∠ABC=120°,BA=2,BC=3,D,E是线段AC的三等分点,则?的值为.10.记等差数列{a n}的前n项和为S n.若S k﹣1=8,S k=0,S k+1=﹣10,则正整数k= .11.若将函数f(x)=|sin(ωx﹣)|(ω>0)的图象向左平移个单位后,所得图象对应的函数为偶函数,则实数ω的最小值是.12.已知x,y为正实数,则+的最大值为.13.在平面直角坐标系xOy中,圆C的方程为(x﹣1)2+(y﹣1)2=9,直线l:y=kx+3与圆C 相交于A,B两点,M为弦AB上一动点,以M为圆心,2为半径的圆与圆C总有公共点,则实数k的取值范围为.14.已知a,t为正实数,函数f(x)=x2﹣2x+a,且对任意的x∈[0,t],都有f(x)∈[﹣a,a].若对每一个正实数a,记t的最大值为g(a),则函数g(a)的值域为.二、解答题:本大题共6小题,共计90分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知acosC+ccosA=2bcosA.(1)求角A的值;(2)求sinB+sinC的取值范围.16.在四棱锥P﹣ABCD中,BC∥AD,PA⊥PD,AD=2BC,AB=PB,E为PA的中点.(1)求证:BE∥平面PCD;(2)求证:平面PAB⊥平面PCD.17.如图,摩天轮的半径OA为50m,它的最低点A距地面的高度忽略不计.地面上有一长度为240m的景观带MN,它与摩天轮在同一竖直平面内,且AM=60m.点P从最低点A处按逆时针方向转动到最高点B处,记∠AOP=θ,θ∈(0,π).(1)当θ=时,求点P距地面的高度PQ;(2)试确定θ的值,使得∠MPN取得最大值.18.在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.(1)已知点(,1)在椭圆C上,求实数m的值;(2)已知定点A(﹣2,0).①若椭圆C上存在点T,使得=,求椭圆C的离心率的取值范围;②当m=1时,记M为椭圆C上的动点,直线AM,BM分别与椭圆C交于另一点P,Q,若=λ,=μ,求证:λ+μ为定值.19.已知函数f(x)=x2﹣x+t,t≥0,g(x)=lnx.(1)令h(x)=f(x)+g(x),求证:h(x)是增函数;(2)直线l与函数f(x),g(x)的图象都相切.对于确定的正实数t,讨论直线l的条数,并说明理由.20.已知数列{a n}的各项均为正数,其前n项的和为S n,且对任意的m,n∈N*,都有(S m+n+S1)2=4a2m a2n.(1)求的值;(2)求证:{a n}为等比数列;(3)已知数列{c n},{d n}满足|c n|=|d n|=a n,p(p≥3)是给定的正整数,数列{c n},{d n}的前p项的和分别为T p,R p,且T p=R p,求证:对任意正整数k(1≤k≤p),c k=d k.选修4-1:几何证明选讲21.如图,AB,AC是⊙O的切线,ADE是⊙O的割线,求证:BE?CD=BD?CE.选修4-2:矩阵与变换22.已知矩阵A=,直线l:x﹣y+4=0在矩阵A对应的变换作用下变为直线l′:x﹣y+2a=0.(1)求实数a的值;(2)求A2.选修4-4:坐标系与参数方程23.在极坐标系中,设圆C:ρ=4cosθ与直线l:θ=(ρ∈R)交于A,B两点,求以AB 为直径的圆的极坐标方程.选修4-5:不等式选讲24.已知实数x,y满足x>y,求证:2x+≥2y+3.七、解答题(共2小题,满分20分)25.如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=,AB=1,BD=PA=2.(1)求异面直线BD与PC所成角的余弦值;(2)求二面角A﹣PD﹣C的余弦值.26.已知集合A是集合P n={1,2,3,…,n}(n≥3,n∈N*)的子集,且A中恰有3个元素,同时这3个元素的和是3的倍数.记符合上述条件的集合A的个数为f(n).(1)求f(3),f(4);(2)求f(n)(用含n的式子表示).。
2017年江苏省南京市、淮安市高三三模数学试卷

2017年江苏省南京市、淮安市高三三模数学试卷一、填空题(共14小题;共70分)1. 已知全集,集合,,则.2. 甲盒子中有编号分别为,的两个乒乓球,乙盒子中有编号分别为,,,的四个乒乓球.现分别从两个盒子中随机地各取出个乒乓球,则取出的乒乓球的编号之和大于的概率为.3. 若复数满足,其中为虚数单位,为复数的共轭复数,则复数的模为.4. 执行如下所示的伪代码,若输出的值为,则输入的值为.Read xIf x≥0 Theny←Elsey←End IfPrint y5. 如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为.6. 在同一直角坐标系中,函数的图象和直线的交点的个数是.7. 在平面直角坐标系中,双曲线的焦距为,则所有满足条件的实数构成的集合是.8. 已知函数是定义在上且周期为的偶函数,当时,,则的值为.9. 若等比数列的各项均为正数,且,则的最小值为.10. 如图,在直三棱柱中,,,,,点为侧棱上的动点,当最小时,三棱锥的体积为.11. 函数在区间上单调递增,则实数的最大值为.12. 在凸四边形中,,且,,则四边形的面积为.13. 在平面直角坐标系中,圆,圆(为实数).若圆和圆上分别存在点,,使得,则的取值范围为.14. 已知,,为正实数,且,,则的取值范围为.二、解答题(共6小题;共78分)15. 如图,在三棱锥中,,分别为,上的点,且 平面.(1)求证: 平面;(2)若平面,,求证:平面平面.16. 已知向量,,,为实数.(1)若,求的值;(2)若,且,求的值.17. 在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域,及矩形表演台四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以,为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的倍,矩形表演台中,米,三角形水域的面积为平方米,设.(1)求的长(用含的式子表示);(2)若表演台每平方米的造价为万元,求表演台的最低造价.18. 如图,在平面直角坐标系中,椭圆的右顶点和上顶点分别为点,,是线段的中点,且.(1)求椭圆的离心率;(2)若,四边形内接于椭圆,,记直线,的斜率分别为,,求证:为定值.19. 已知常数,数列满足,.(1)若,,①求的值;②求数列的前项和;(2)若数列中存在三项,,(,)依次成等差数列,求的取值范围.20. 已知,函数的导数为.(1)求曲线在处的切线方程;(2)若函数存在极值,求的取值范围;(3)若时,恒成立,求的最大值.答案第一部分1.2.3.4.5.6.7.8.9.10.【解析】将直三棱柱展开成矩形,如图,连接,交于,此时最小,因为,,,,点为侧棱上的动点,所以当最小时,,此时三棱锥的体积:11.12.【解析】因为,所以,因为,所以所以,所以.所以四边形的面积.13.14.第二部分15. (1) 平面,平面,平面平面,,又平面,平面,平面.(2)平面,平面,,由()可知,又,,又,平面,平面,平面,又平面,平面平面.16. (1)向量,,,为实数.若,则,可得,平方可得,即为,由,解得即有,.则;(2)若,且,即有,即有,由为锐角,可得,即有,则,.17. (1)因为看台Ⅰ的面积是看台Ⅱ的面积的倍,所以,所以,因为,所以,所以,在中,由余弦定理得,所以.(2)设表演台的造价为万元,则,设,则,所以当时,,当时,,所以在上单调递减,在上单调递增,所以当时,取得最小值,所以的最小值为,即表演台的最小造价为万元.18. (1),,线段的中点.,.因为.所以,化为:.所以椭圆的离心率.(2)由,可得,所以椭圆的标准方程为:,,.直线的方程为:,联立化为:,解得,所以.即.直线的方程为:,联立化为:,所以,解得,,可得.所以,化为:.所以,所以.19. (1)①因为,所以,,.②因为,,所以当时,,当时,,即从第二项起,数列是以为首项,以为公比的等比数列,所以数列的前项和(),显然当时,上式也成立,所以.(2)因为,所以,即单调递增.(i)当时,有,于是,所以,所以.若数列中存在三项,,(,)依次成等差数列,则有,即(),因为,所以,因此()不成立.因此此时数列中不存在三项,,(,)依次成等差数列.(ii)当时,有.此时.于是当时,,从而,所以.若数列中存在三项,,(,)依次成等差数列,则有,同(i)可知:,于是有,因为,所以.因为是整数,所以,于是,即,与矛盾.故此时数列中不存在三项,,(,)依次成等差数列.(iii)当时,有,.于是,.此时数列中存在三项,,依次成等差数列.综上可得:.20. (1)的定义域为.,,又.曲线在处的切线方程为.(2)因为(),.函数存在极值,即方程有正实数根,(),令,在恒成立.时,,所以函数存在极值,的取值范围为.(3)由(),()可知,,结合()时,,可得(),,则在恒成立.所以单调递增,从而.所以时,,在递增,.故在递增,所以.当时,存在,使,所以时,,即时,递减,而,所以时,,此时递减,而,所以在,,故当时,不恒成立;综上时,恒成立,的最大值为.。
2017模拟卷-江苏省南京市2017届高三上学期学情调研数学试题解析02(解析版)Word版含解斩

江苏省南京市2017届高三上学期学情调研数学试题一、填空题:本大题共14个小题,每小题5分,共70分.1.已知集合{0,1,2}A =,2{|0}B x x x =-≤,则A B = . 【答案】{0,1} 【解析】试题分析:2{|0}[0,1]B x x x =-≤=,A B = {0,1} 考点:集合运算 【方法点睛】1.用描述法表示集合,首先要弄清集合中代表元素的含义,再看元素的限制条件,明确集合类型,是数集、点集还是其他的集合.2.求集合的交、并、补时,一般先化简集合,再由交、并、补的定义求解.3.在进行集合的运算时要尽可能地借助Venn 图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn 图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍.1 2.设复数满足()34z i i i +=-+(为虚数单位),则的模为 .【答案】考点:复数的模【名师点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()()(),(,,.)++=-++∈a bi c di ac bd ad bc i a b c d R . 其次要熟悉复数相关基本概念,如复数(,)+∈a bi a b R 的实部为、虚部为、对应点为(,)a b 、共轭为.-a bi 3.为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有 辆.【答案】80 【解析】试题分析:时速在区间[40,60)内的汽车有200(0.010.03)1080.⨯+⨯= 1 考点:频率分布直方图 4.若函数()sin()6f x x πω=+(0)ω>的最小正周期为π,则()3f π的值是 . 【答案】12考点:三角函数周期【方法点睛】已知函数sin()(A 0,0)y A x B ωϕω=++>>的图象求解析式(1)max min maxmin,22y y y y A B -+==. (2)由函数的周期T 求2,.T πωω= (3)利用“五点法”中相对应的特殊点求.5.下图是一个算法的流程图,则输出的值是 .【答案】5考点:循环结构流程图【名师点睛】算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.6.设向量(1,4)a =- ,(1,)b x =-,3c a b =+ ,若//a c ,则实数的值是 .【答案】4 【解析】试题分析:由题意得(1,4)//(2,43x)843x x 4---+⇒=-+⇒= 1 考点:向量平行7.某单位要在四名员工(含甲乙两人)中随机选两名到某地出差,则甲乙两人中,至少有一人被选中的概率是 .【答案】56考点:古典概型概率【方法点睛】古典概型中基本事件数的探求方法 (1)列举法.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法:适用于限制条件较多且元素数目较多的题目.8.在平面直角坐标系xOy 中,双曲线222:1(0)4x y C a a -=>的一条渐近线与直线21y x =+平行,则实数的值是 . 【答案】1 【解析】试题分析:由题意得221a a=⇒= 考点:双曲线渐近线9.在平面直角坐标系xOy 中,若直线20ax y +-=与圆心为C 的圆22(1)()16x y a -+-=相交于,A B 两点,且ABC ∆为直角三角形,则实数的值是 . 【答案】-1 【解析】试题分析:由题意得C 到直线20ax y +-=1.a =⇒=- 考点:直线与圆位置关系10.已知圆柱M 的底面半径为2,高为6,圆锥N 的底面直径和母线长相等,若圆柱M 和圆锥N 的体积相同,则圆锥N 的高为 . 【答案】6考点:圆锥体积【方法点睛】(1)求锥体的体积要充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题求解,注意求体积的一些特殊方法——分割法、补形法、等体积法. (2)涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.111.各项均为正数的等比数列{}n a ,其前项和为n S ,若2578a a -=-,313S =,则数列{}n a 的通项公式n a = . 【答案】3n -1 【解析】试题分析:由题意得321111(1)78,(1)13(1)6,03,1,3n n a q q a q q q q q q a a --=++=⇒-=>∴===考点:等比数列通项公式12.已知函数312,0()2,0x x x f x x x ⎧-≤=⎨->⎩,当(,]x m ∈-∞时,()f x 的取值范围为[16,)-+∞,则实数m 的取值范围是 . 【答案】1-2,8] 【解析】试题分析:320,1212402x y x x y x x '≤=-⇒=-=⇒=-(正舍),(2)16f -=-;由2168x x -=-⇒=,所以当2m <-时,()16f x >-;当28m -≤≤时,()16f x ≥-;当8m >时,min ()16f x <-;因此实数m 的取值范围是28m -≤≤ 考点:利用导数研究函数值域【思路点睛】(1)运用函数图象解决问题时,先要正确理解和把握函数图象本身的含义及其表示的内容,熟悉图象所能够表达的函数的性质.(2)在研究函数性质特别是单调性、最值、零点时,要注意用好其与图象的关系,结合图象研究.13.在ABC ∆中,已知3AB =,2BC =,D 在AB 上,13AD AB = ,若3DB DC ∙=,则AC 的长是 .考点:向量投影【方法点睛】平面向量数量积的类型及求法(1)求平面向量数量积有三种方法:一是夹角公式a ·b =|a ||b |cos θ;二是坐标公式a ·b =x 1x 2+y 1y 2;三是利用数量积的几何意义.1(2)求较复杂的平面向量数量积的运算时,可先利用平面向量数量积的运算律或相关公式进行化简.14.已知(),()f x g x 分别是定义在R 上的奇函数和偶函数,且1()()()2xf xg x +=,若存在01[,1]2x ∈,使得等式00()(2)0af x g x +=成立,则实数的取值范围是 .【答案】 【解析】试题分析:11()()()()()()()()222x xx f x g x f x g x f x g x -+=⇒-+-=⇒-+=,所以11()2()222(),()22x x x xf xg x -+==,所以00000022200(2)22223,22[]()2222x x x x x x g x t a t t f x t t ---++=-===+=-∈-,所以minmax 22t a t a ====即实数的取值范围是 考点:函数值域【思路点睛】已知方程有解求参数取值范围常用的方法和思路(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.二、解答题 (本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.(本小题满分14分)如图,在平面直角坐标系xOy 中,以轴正半轴为始边的锐角α和钝角β的终边分别与单位圆交于点,A B ,若点A,点B(1)求cos()αβ-的值; (2)求αβ+的值.【答案】(1)-10(2)34π(1)cos(α-β)=cos αcos β+sin αsin β=10×(-5)+10×5=-10. …………………… 8分(2)sin(α+β)=sin αcos β+cos αsin β2. …………………… 11分因为α为锐角,β为钝角,故α+β∈(2π,32π),所以α+β=34π. …………………… 14分 考点:三角函数的定义,给值求角【思路点睛】在求角的某个三角函数值时,应注意根据条件选择恰当的函数,尽量做到所选函数在确定角的范围内为一对一函数。
南京市2017届高三年级三模数学附加卷(第三稿)

南京市2017届高三年级第三次模拟考试数学附加题 2017.05注意事项:1.附加题供选修物理的考生使用.2.本试卷共40分,考试时间30分钟.3.答题前,请务必将自己的姓名、学校写在答题卡上.试题的答案写在答题卡...上对应题目的答案空格内.考试结束后,交回答题卡.21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答.卷卡指...定区域内....作答.解答应写出文字说明、证明过程或演算步骤.A .选修4—1:几何证明选讲如图,AD 是△ABC 的高,AE 是△ABC 的外接圆的直径,点B 和点C 在直线AE 的两侧. 求证:AB ·AC =AD ·AE .B .选修4—2:矩阵与变换已知矩阵 A =⎣⎢⎡⎦⎥⎤ 2 x y 2 ,X =⎣⎡⎦⎤-1 1 ,且AX =⎣⎡⎦⎤12 ,其中x ,y ∈R . (1)求x ,y 的值;(2)若 B =⎣⎢⎡⎦⎥⎤1 -10 2 ,求(AB )-1.C .选修4—4:坐标系与参数方程已知曲线C 的极坐标方程是 ρ2-8ρcos θ+15=0,直线l 的极坐标方程是θ=π4(ρ∈R ).若P ,Q 分别为曲线C 与直线l 上的动点,求PQ 的最小值.(第21(A)图)D .选修4—5:不等式选讲已知x >0,求证:x 3+y 2+3≥3x +2y .【必做题】第22题、第23题,每题10分,共计20分.请在答.卷卡指定区域内.......作答.解答应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)在平面直角坐标系xOy 中,直线l :x =-1,点T (3,0).动点P 满足PS ⊥l ,垂足为S ,且OP →·ST →=0.设动点P 的轨迹为曲线C .(1)求曲线C 的方程;(2)设Q 是曲线C 上异于点P 的另一点,且直线PQ 过点(1,0),线段PQ 的中点为M ,直线l与x 轴的交点为N .求证:向量SM →与NQ →共线.23.(本小题满分10分)已知数列{a n }共有3n (n ∈N *)项,记f (n )=a 1+a 2+…+a 3n .对任意的k ∈N *,1≤k ≤3n ,都有a k ∈{0,1},且对于给定的正整数p (p ≥2),f (n )是p 的整数倍.把满足上述条件的数列{a n }的个数记为T n .(1)当p =2时,求T 2的值;(2)当p =3时,求证:T n =13[8n +2(-1)n ].。
江苏省南京市高考数学三模考试数学(理)试卷有答案

)A B=______________.乙盒子中有编号分别为3则取出的乒乓球的编号之和大于6的概率为的值为______________.π190,点D11.函数2((2))f x ex x x a =++﹣在区间[],1a a +上单调递增,则实数a 的最大值为______________. 12.在凸四边形ABCD 中,2BD =且0,()()5AC BD AB DC BC AD ⋅=+⋅+=,则四边形ABCD 的面积为______________.13.在平面直角坐标系xOy 中,圆221:x O y +=,圆22:121M x a y a +++=()(﹣)(a 为实数).若圆O 和圆M 上分别存在点,P Q ,使得30OQP ∠=︒,则a 的取值范围为______________. 14.已知,,a b c 为正实数,且23228,a b c a b c +≤+≤,则38a bc+的取值范围是______________. 二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程. 15.(本小题满分14分)如图,在三棱锥A BCD -中,,E F 分别为,BC CD 上的点,且BD ∥平面AEF . (1)求证:EF ∥平面ABD ;(2)若AE ⊥平面BCD ,BD CD ⊥,求证:平面AEF ⊥平面ACD .16.(本小题满分14分)已知向量2π(2cos ,sin ),(2sin ,),(0,),t 2a a ab a t a ==为实数. (1)若2(,0)5a b -=,求t 的值;(2)若1t =,且1a b ⋅=,求πtan(2)4a +的值.17.(本小题满分14分)在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC ,及矩形表演台BCDE 四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以,AB AC 为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,10CD =米,三角形水域ABC 的面积为平方米,设BAC θ∠=. (1)求BC 的长(用含θ的式子表示);(2)若表演台每平方米的造价为0.3万元,求表演台的最低造价.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆22221(0)x y a b a b+=>>的右顶点和上顶点分别为点,,A B M 是线段AB的中点,且232OM AB b =.(1)求椭圆的离心率;(2)若2a =,四边形ABCD 内接于椭圆,AB CD ∥,记直线,AD BC 的斜率分别为1,2k k ,求证:1?2k k 为定值.19.(本小题满分16分)已知常数0p >,数列{}n a 满足*1|2,|n n n a a p p a n +=++∈N -. (1)若n S a 1=﹣1,p=1, ①求4a 的值;②求数列{}n a 的前n 项和n S ;(2)若数列{}n a 中存在三项*,,,,(,)ar as at r s t r s t ∈<<N 依次成等差数列,求1a p的取值范围. 20.(本小题满分16分)已知λ∈R ,函数()(ln 1)xf x e ex x x x λ=+﹣﹣﹣的导数为()g x .(1)求曲线()y f x =在1x =处的切线方程; (2)若函数()g x 存在极值,求λ的取值范围; (3)若1x ≥时,()0f x ≥恒成立,求λ的最大值.江苏省南京市2017届高考数学三模考试数学(理)试卷答 案1.{2}二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程. 15.证明:(1)∵BD ∥平面AEF ,BD ⊂平面BCD ,平面BCD 平面AEF EF =,∴BD EF ∥,又BD ⊂平面ABD ,EF ⊄平面ABD , ∴EF ∥平面ABD .(2)∵AE ⊥平面BCD ,CD ⊂平面BCD , ∴AE CD ⊥,由(1)可知BD EF ∥,又BD CD ⊥,∴EF CD ⊥, 又,AEEF E AE =⊂平面AEF ,EF ⊂平面AEF ,∴CD ⊥平面AEF ,又CD ⊂平面ACD , ∴平面AEF AEF ⊥平面ACD .16.解:(1)向量2π(2cos ,sin ),(2sin ,),(0,),t 2a a ab a t a ==为实数,若2(,0)5a b -=,则2(2cos 2sin ,sin 2)=(,0)5a a a t --,可得1cos sin =5a a -,平方可得1sin 2cos22cos sin =25a a a a +-,即为1242cos sin =1,(cos 0,sin 0)2525a a a a -=>>,由sin2cos2=1a a +,解得7cos sin 5a a +, 即有34cos =,sin =55a a .则16sin 2=25t a =;(2)若1t =,且1a b ⋅=,即有4cos sin sin21a a a +=, 即有4cos sin 1sin2cos2a a a a =-=,由a 为锐角,可得(c s 1)o 0,α∈,即有sin 1tan cos 4a a α==, 则212tan 82tan 211tan 15116a a α===--,81tan 212315tan(2)81t π4an 27115a a α+++===--. 17.解:(1)∵看台Ⅰ的面积是看台Ⅱ的面积的3倍,∴22π()31122π()22AB AC =⨯,∴AB =,∵1sin 22ABC S AB AC sin θθ∆=⋅⋅= ∴228002400,sin sin AC AB θθ==, 在ABC ∆中,由余弦定理得2222cos BC AB AC AB AC θ=⋅=+-∴BC =(2)设表演台的造价为y 万元,则y =设()π)0f θθ=<<,则()f θ'∴当0π6θ<<时,0()f θ'<,当π6πθ<<时,0()f θ'>, ∴()f θ在(0,π)6上单调递减,在(π,6π)上单调递增,∴当=6πθ时,()f θ取得最小值1π(6)=f ,∴y 的最小值为120,即表演台的最小造价为120万元.(,),(,)22a bAB a b OM =-=.∵232OM AB b ⋅=-.∴22213222ab b -+=-,化为:2a b =.∴椭圆的离心率c e a===. (2)证明:由2a =,可得1b =,∴椭圆的标准方程为:221,(2,0),(0,1)4x y A B +=.直线BC 的方程为:21y k x =+,联立222114y k x x y =+⎧⎪⎨+=⎪⎩,化为:2222(14)80k x k x ++=, 解得222814c k x k -=+,∴22221414c k y k -=+.即2222222814(,)1414k k C k k --++. 直线AD 的方程为:1()2y k x =-,联立122(2)14y k x x y =-⎧⎪⎨+=⎪⎩,化为:2222111(14)161640k x k x k +-+-=, ∴2121164214D k x k -=+,解得2112211824,1414D D k k x y k k --==++,可得2112211824(,)1414k k D k k --++∴12C D CD C D y y k x x -==--,化为:222221211122111622880k k k k k k k k -+-+-=∴1212121()4440()14k k k k k k -++=-,∴121=4k k .19.解:(1)①∵12||n n n a p a a p +=++-, ∴211||1212211a a a =++=+=--, 322||1210213a a a =++=++=-, 433||1212619a a a =++=++=-, ②∵2111||21n n n a a a a +==++,-, ∴当2n ≥时,1n a ≥,当2n ≥时,11213n n n n a a a a +=+++=-,即从第二项起,数列{}n a 是以1为首项,以3为公比的等比数列, ∴数列{}n a 的前n 项和11123413111321322n n n n a a n S a a a ---=++++⋯+=+=⨯≥---,(), 显然当1n =时,上式也成立,∴113322n n S -=⨯-; (2)∵1||20n n n n n n a a p a a p p a a p p +=++≥++=--->,∴1n n a a +>,即{}n a 单调递增. (i )当11a p≥时,有1a p ≥,于是1n a a p ≥≥, ∴1|223|n n n n n n a p a a p a p a p a +=++=++=--,∴113n n a a -=⋅.若数列{}n a 中存在三项*,)(r s t a a a r s t r s t ∈<<N ,,,,依次成等差数列,则有2s r t a a a =+,即111233*3()s r t ---⨯=+∵1s t ≤-,∴111122333333s st r t ---⨯=⨯<<+-.因此(*)不成立.因此此时数列{}n a 中不存在三项*,)(r s t a a a r s t r s t ∈<<N ,,,,依次成等差数列.(ii )当111a p-<<时,有1p a p <<-.此时211111||222a P a a p p a a p a p p =++=++=+>--. 于是当2n ≥时,2n a a p ≥>.从而1|223|n n n n n n a p a a p a p a p a +=++=++=--.∴2221((3)2)32n n na a a p n --==+≥若数列{}n a 中存在三项*,)(r s t a a a r s t r s t ∈<<N ,,,,依次成等差数列,则有2s r t a a a =+,同(i )可知:1r =.于是有2211123(2)3(2)s t a p a a p ⨯+=++﹣﹣,∵21S t ≤≤-,∴211212 2333329103s t s t a a p --=⨯=⨯⨯+<﹣﹣-.∵22233s t ⨯﹣﹣-是整数,∴11 12a a p≤+.于是112a a p ≤--,即1a p ≤-.与1p a p <<-矛盾. 故此时数列{}n a 中不存在三项*,)(r s t a a a r s t r s t ∈<<N ,,,,依次成等差数列.(iii )当11a p≤时,有110a p p a p ≤<+≤-,. 于是211111||222a P a a p p a a p a p =++=++=+--.32211111|2252|54||a p a a p a p a p a p a p a p =++=+++=++=+---此时数列{}n a 中存在三项123a a a ,,依次成等差数列. 综上可得:11a p≤-. 20.解:(1)()(ln 1)x f x e ex x x x λ=+---的定义域为(0)+∞,. ()ln (1)0x f x e e x f λ'='=--,,又(1)0f =. 曲线()y f x =在1x =处的切线方程为0y =.(2)∵()()ln ,(0)x g x f x e e x x λ='=>﹣﹣,()xg x e xλ'=-函数()g x 存在极值,即方程0x e xλ-=有正实数根,,(0)x xe x λ⇒=>,令()x G x xe =,()(1)0x G x x e '=+>在(0)+∞,恒成立. (0)x ∈+∞,时,()0G x >, ∴函数()g x 存在极值,λ的取值范围为(0)+∞,. (3)由(1)、(2)可知(1)0,(1)(1)0f f g '=== 结合(2)1x ≥时,()0x g x e xλ'=-≥,可得(1)x xe x λ≤≥,,()x G x xe =,在(1)+∞,恒成立. ∴e λ≤时,()0g x '≥,()g x 在[1)+∞,递增,()(1)0g x g ≥= 故()f x 在[1)+∞,递增,∴()(1)=0f x f ≥.当e λ>时,存在01x ≥,使()=0g x ',∴0(1)x x ∈,时,()<0g x ', 即0(1,)x x ∈时,()g x 递减,而(1)=0g ,∴0(1,)x x ∈时,()<0g x ,此时()f x 递减,而(1)=0f , ∴在0(1,)x ,()<0f x ,故当e λ>时,()0f x ≥不恒成立; 综上1x ≥时,()0f x ≥恒成立,λ的最大值为e【点评】本题考查了导数的综合应用,利用导数求极值、证明函数恒等式,属于难题江苏省南京市2017届高考数学三模考试-数学(理)试卷解 析1.【考点】交、并、补集的混合运算.【分析】根据已知中集合,,U A B ,结合集合的并集和补集运算的定义,可得答案. 【解答】解:∵集合1,4,{}{}3,4A B ==, ∴1,}4{3,A B =,又∵全集1,2{},3,4U =, ∴{2()}U A B ⋃=ð, 故答案为:{2}【点评】本题考查的知识点是集合的交集,并集,补集运算,难度不大,属于基础题. 2.【考点】古典概型及其概率计算公式.【分析】列举基本事件,即可求出概率.【解答】解:分别从每个盒子中随机地取出1个乒乓球,可能出现以下情况:()()()()()()(1314151623242)6)52(、、、、、、、,,,,,,,,共8种情况,其中编号之和大于6的有:1+6=7,2+5=7,2+6=8,共3种情况,∴取出的乒乓球的编号之和大于6的概率为38,故答案为:38.【点评】本题考查古典概型,考查学生的计算能力,确定基本事件的个数是关键.3.【考点】复数代数形式的乘除运算.【分析】设z a bi =+,得到z a bi =-,根据系数相等求出,a b 的值,从而求出||z 即可. 【解答】解:设z a bi =+,则z a bi =-,由232z z i +=+,得332abi i =+﹣, ∴1,2a b ==﹣,∴||z【点评】本题考查了复数求模问题,考查共轭复数,是一道基础题. 4.【考点】伪代码.【分析】分析出算法的功能是求分段函数()f x 的值,根据输出的值为1,分别求出当0x ≤时和当0x >时的x 值即可. 【解答】解:由程序语句知:算法的功能是求122,0()=2,0x x x x f x +⎧≥⎪⎨-<⎪⎩的值, 当0x ≥时,211y x =+=,解得1x =-,不合题意,舍去; 当0x <时,221y x ==﹣,解得1x =±,应取1x =-;综上,()f x x 的值为1-.故答案为:1-.【点评】本题考查了选择结构的程序语句应用问题,根据语句判断算法的功能是解题的关键. 5.【考点】茎叶图.【分析】根据茎叶图中的数据求出甲、乙二人的平均数,再根据方差的定义得出乙的方差较小,求出乙的方差即可.【解答】解:根据茎叶图中的数据,计算甲的平均数为11(7791418)115x =⨯++++=,乙的平均数为21(89101315)115x =⨯++++=;根据茎叶图中的数据知乙的成绩波动性小,较为稳定(方差较小),计算乙成绩的方差为:222222134[(811)(911)(1011)(1311)(1511)]55x =⨯-+-+-+-+-=故答案为:345.【点评】本题考查了茎叶图、平均数与方差的应用问题,是基础题. 6.【考点】正弦函数的图象.【分析】令π1sin()=32y x =+,求出在[π)0,2x ∈内的x 值即可.【解答】解:令π1sin()=32y x =+,解得ππ=2π36x k ++,或π5π=2π,k 36x k ++∈Z ;即π=2π6k x +-,或π=2π,k 2k x +∈Z ;∴同一直角坐标系中,函数y 的图象和直线12y =在[π)0,2x ∈内的交点为(π2,12)和(11π6,12),共2个.故答案为:2.【点评】本题考查了正弦函数的图象与性质的应用问题,是基础题.7.【考点】双曲线的简单性质.【分析】根据题意,先由双曲线的方程分析可得m 的取值范围,进而又由该双曲线的焦距为6,则有3c =,即,解可得m 的值,结合m 的范围可得m 的值,用集合表示即可得答案.【解答】解:根据题意,双曲线的方程为:222123x y m m -= ,则有22030m m ⎧>⎨>⎩,解可得0m >,则有c =又由该双曲线的焦距为6,则有c=3,, 解可得:=3m -或32, 又由0m >, 则3=2m ; 即所有满足条件的实数m 构成的集合是{32}; 故答案为{32}. 【点评】本题考查双曲线的几何性质,注意焦距是2c . 8.【考点】函数的周期性.【分析】由函数的奇偶性与周期性把1()2f 转化为求7()2f 的值求解.【解答】解:∵函数()f x 是定义在R 上且周期为4的偶函数,∴1117()=()=(4)=()2222f f f f --,又当4[]2,x ∈时,43()=|log ()|2f x x -,∴441773lg 2lg 21()=()=|log ()||log 2|2222lg 42lg 22f f -====.故答案为:12. 【点评】本题考查函数的周期性和奇偶性的应用,考查数学转化思想方法,是基础题. 9.【考点】等比数列的通项公式.【分析】由已知把首项用公比q 表示,再由等比数列的通项公式可得5a ,然后利用配方法求得5a 的最小值. 【解答】解:∵0n a >,且312a a -=, ∴2112a q a -=,则122(0)1a q q =>-, ∴445122422===111q a a q q q q --. 令21(t 0)t q=>,则522a t t=-+,又22111()244t t t -+=--+≤,∴58[),a ∈+∞.∴5a 的最小值为8. 故答案为:8.【点评】本题考查等比数列的通项公式,考查了利用配方法求函数的最值,是中档题. 10.【考点】棱柱、棱锥、棱台的体积.【分析】将直三棱柱111ABC A B C -展开成矩形11ACC A ,如图,连结1AC ,交1BB 于D ,此时1AD DC +最小,当1AD DC +最小时,1BD =,此时三棱锥1D ABC ﹣的体积:11D C V ABC V ABD -=-,由此能求出结果.【解答】解:将直三棱柱111ABC A B C -展开成矩形11ACC A ,如图, 连结1AC ,交1BB 于D ,此时1AD DC +最小,∵11,2,3,90AB BC BB ABC ===∠=︒,点D 为侧棱1BB 上的动点, ∴当1AD DC +最小时,1BD =, 此时三棱锥1D ABC ﹣的体积:111111111111112332323D C ABD V ABC V ABD S B C AB BD B C ∆-=-=⨯⨯=⨯⨯⨯⨯=⨯⨯⨯⨯=.故答案为:13.【点评】本题考查几何体的体积的求法,考查空间中线线、线面、面面的位置关系等基础知识,考查推理论证能力、运算求解能力、空间思维能力,考查数数结合思想、函数与方程思想、化归与转化思想,是中档题. 11.【考点】利用导数研究函数的单调性.【分析】求出函数的导数,问题转化为22a x +≥在[],1a a +恒成立,求出a 的范围即可. 【解答】解:2((2))f x ex x x a =++﹣,2()()2f x ex x x a '=++﹣, 若()f x 在[],1a a +上单调递增, 则220x a ++≥-在[],1a a +恒成立, 即22a x +≥在[],1a a +恒成立,①10a +<即1a <-时,2y x =在[],1a a +递减,2y x =的最大值是2y a =,故22a a +≥,解得:220a a ≤--,解得:12a <<-,不合题意,舍; ②10a ≤≤-时,2y x =在[),0a 递减,在(0,1]a +递增, 故2y x =的最大值是2a 或2()1a +,③0a >时,2y x =在[],1a a +递增,y 的最大值是2()1a +,故221()a a +≥+,解得:0a <≤,则实数a ,综上,a ,. 【点评】本题考查了函数的单调性问题,考查导数的应用以及函数恒成立问题,是一道中档题. 12.【考点】平面向量数量积的运算.【分析】用,AC BD 表示出括号内的和向量,化简得出AC ,从而可求得四边形的面积. 【解答】解:∵0AC BD ⋅=,∴AC BD ⊥, ∵()()5AC DC BC AD +⋅+=,∴22()()()()5AB BC DC CB BC CD AD DC AC DB BD AC AC BD +++⋅+++=+⋅+=⋅=, ∴2259AC BD =+=,∴3AC =.∴四边形ABCD 的面积1132322S AC BD =⨯⨯=⨯⨯=.故答案为:3.【点评】本题考查了平面向量的运算,数量积运算,属于中档题.13.【考点】直线与圆的位置关系.【分析】从圆M 上的点向圆上的点连线成角,当且仅当两条线均为切线时才是最大的角,1OP =,利用圆O 和圆M 上分别存在点,P Q ,使得30OQP ∠=︒,可得||2OM ≤,进而得出答案. 【解答】解:由题意,圆22()(121)M x a y a +++=:﹣(a 为实数),圆心为1(),2M a a -- 从圆M 上的点向圆上的点连线成角,当且仅当两条线均为切线时才是最大的角,1OP =. ∵圆O 和圆M 上分别存在点,P Q ,使得30OQP ∠=︒, ∴||2OM ≤,∴22144()a a ++≤, ∴315a ≤≤-,故答案为:3 15a≤≤-.【点评】本题考查了直线与圆相切的性质、两点间的距离的计算公式、数形结合思想方法,属于中档题.14.【考点】不等式的基本性质.【分析】令axc=,byc=,38z x y=+,将条件转化为关于,x y的不等式,并求出,x y的范围,作出平面区域,根据平面区域得出z取得最值时的位置,再计算z的最值.【解答】解:∵2328,a b ca b c +≤+≤,∴28232a bc cc ca b⎧+≤⎪⎪⎨⎪+≤⎪⎩,设axc=,byc=,则有28232x yx y+≤⎧⎪⎨+≤⎪⎩,∴142322 18y xxyxx⎧≤-⎪⎪⎪≥⎨-⎪<<⎪⎪⎩,作出平面区域如图所示:令38=38a bz x yc+=+,则388zy x=+,由图象可知当直线388zy x=+经过点A时,截距最大,即z最大;当直线388zy x=+与曲线322xyx=-相切时,截距最小,即z最小.解方程组142322y xxyx⎧=-⎪⎪⎨⎪=⎪-⎩得(2,3)A,∴z的最大值为328330⨯+⨯=,设直线388z y x =+与曲线322xy x =-的切点为00(,)x y ,则03()|3282x x x x ==--',即026223()8x -=-,解得0=3x , ∴切点坐标为(93,4),∴z 的最小值为9338274⨯+⨯=.∴2730z ≤≤,故答案为:[27,30].【点评】本题考查了线性规划的应用,将三元不等式转化为二元不等式,转化为线性规划问题是解题的关键,属于中档题.二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程. 15.【考点】平面与平面垂直的判定;直线与平面平行的判定.【分析】(1)利用线面平行的性质可得BD EF ∥,从而得出EF ∥平面ABD ; (2)由AE ⊥平面BCD 可得AE CD ⊥,由BD CD ⊥,BD EF ∥可得EF CD ⊥,从而有CD ⊥平面AEF ,故而平面AEF ⊥平面ACD .【解答】证明:(1)∵BD ∥平面AEF ,BD ⊂平面BCD ,平面BCD 平面AEF EF =,∴BD EF ∥,又BD ⊂平面ABD ,EF ⊄平面ABD , ∴EF ∥平面ABD .(2)∵AE ⊥平面BCD ,CD ⊂平面BCD , ∴AE CD ⊥,由(1)可知BD EF ∥,又BD CD ⊥, ∴EF CD ⊥, 又,AEEF E AE =⊂平面AEF ,EF ⊂平面AEF ,∴CD ⊥平面AEF ,又CD ⊂平面ACD , ∴平面AEF AEF ⊥平面ACD .【点评】本题考查了线面平行、线面垂直的性质,面面垂直的判定,属于中档题. 16.【考点】平面向量数量积的运算;三角函数中的恒等变换应用.【分析】(1)运用向量的加减运算和同角的平方关系,即可求得3cos 5α=,4sin 5α=.进而得到t 的值; (2)运用向量的数量积的坐标表示,结合条件的商数关系,求得tanα,再由二倍角的正切公式和和角公式,计算即可得到所求值.【解答】解:(1)向量2π(2cos ,sin ),(2sin ,),(0,),t 2a a ab a t a ==为实数,若2(,0)5a b -=,则2(2cos 2sin ,sin 2)=(,0)5a a a t --,可得1cos sin =5a a -,平方可得1sin 2cos22cos sin =25a a a a +-,即为1242cos sin =1,(cos 0,sin 0)2525a a a a -=>>,由sin2cos2=1a a +,解得7cos sin 5a a +,即有34cos =,sin =55a a .则16sin 2=25t a =;(2)若1t =,且1a b ⋅=,即有4cos sin sin21a a a +=, 即有4cos sin 1sin2cos2a a a a =-=,由a 为锐角,可得(c s 1)o 0,α∈,即有sin 1tan cos 4a a α==, 则212tan 82tan 211tan 15116a a α===--,81tan 212315tan(2)81t π4an 27115a a α+++===--. 【点评】本题考查向量的加减运算和数量积的坐标表示,考查同角的基本关系式和二倍角正切公式及和角公式的运用,考查化简整理的运算能力,属于中档题.17.【考点】三角函数中的恒等变换应用;在实际问题中建立三角函数模型. 【分析】(1)根据看台的面积比得出,AB AC 的关系,代入三角形的面积公式求出,AB AC 再利用余弦定理计算BC ;(2)根据(1)得出造价关于θ的函数,利用导数判断函数的单调性求出最小造价. 【解答】解:(1)∵看台Ⅰ的面积是看台Ⅱ的面积的3倍,∴22π()31122π()22AB AC =⨯,∴AB =,∵1sin 22ABC S AB AC sin θθ∆=⋅⋅= ∴228002400,sin sin AC AB θθ==, 在ABC ∆中,由余弦定理得2222cos BC AB AC AB AC θ=⋅=+-∴BC =(2)设表演台的造价为y 万元,则y =设()π)0f θθ=<<,则()f θ'∴当0π6θ<<时,0()f θ'<,当π6πθ<<时,0()f θ'>, ∴()f θ在(0,π)6上单调递减,在(π,6π)上单调递增,∴当=6πθ时,()f θ取得最小值1π(6)=f ,∴y 的最小值为120,即表演台的最小造价为120万元.【点评】本题考查了解三角形,函数最值计算,余弦定理,属于中档题.18.【考点】椭圆的简单性质. 【分析】(1),0,()(0),A a B b ,线段AB 的中点(,)22a b M .利用232OM AB b ⋅=-与离心率的计算公式即可得出.(2)由2a =,可得1b =,可得椭圆的标准方程为:221,(2,0),(0,1)4x y A B +=.直线BC 的方程为:21y k x =+,直线AD 的方程为:1()2y k x =-,分别于同一方程联立解得,C D ,坐标,利用12C D CD C D y y k x x -==--,即可得出.【解答】(1)解:,0,()(0),A a B b ,线段AB 的中点(,)22a bM .(,),(,)22a bAB a b OM =-=.∵232OM AB b ⋅=-.∴22213222a b b -+=-,化为:2a b =.∴椭圆的离心率c e a===. (2)证明:由2a =,可得1b =,∴椭圆的标准方程为:221,(2,0),(0,1)4x y A B +=.直线BC 的方程为:21y k x =+,联立222114y k x x y =+⎧⎪⎨+=⎪⎩,化为:2222(14)80k x k x ++=, 解得222814c k x k -=+,∴22221414c k y k -=+.即2222222814(,)1414k k C k k --++. 直线AD 的方程为:1()2y k x =-,联立122(2)14y k x x y =-⎧⎪⎨+=⎪⎩,化为:2222111(14)161640k x k x k +-+-=, ∴2121164214D k x k -=+,解得2112211824,1414D D k k x y k k --==++,可得2112211824(,)1414k k D k k --++∴12C D CD C D y y k x x -==--,化为:222221211122111622880k k k k k k k k -+-+-=∴1212121()4440()14k k k k k k -++=-,∴121=4k k .【点评】本题考查了椭圆的标准方程与性质、直线与椭圆相交问题、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于难题.19.【考点】数列的求和;数列递推式.【分析】(1)①12||n n n a p a a p +=++-,可得211||1212211a a a =-++=+=-,同理可得343,9a a ==. ②21,112|1|n n n a a a a =+=++-,当2n ≥时,1n a ≥,当2n ≥时,11213n n n n a a a a +=+++=-,即从第二项起,数列{}n a 是以1为首项,以3为公比的等比数列,利用等比数列的求和公式即可得出n S . (2)1||20n n n n n n a a p a a p p a a p p +=++≥++=>---,可得1n n a a +>,即{}n a 单调递增.(i )当11a p≥时,有1a p ≥,于是1n a a p ≥≥,可得1|223|n n n n n n a p a a p a p a p a +=++=++=--,113n n a a -=⋅.利用反证法即可得出不存在. (ii )当111a p-<<时,有1p a p <<-.此时211111||222a P a a p p a a p a p p =++=++=+>--.于是当2n ≥时,2n a a p ≥>.从而2212122333(2)(||2)n n n n n n n n n a p a a p a p a p a a a a p n +=++=++===+≥﹣﹣--..假设存在2s r t a a a =+,同(i)可知:1r =.得出矛盾,因此不存在.(iii )当11a p≤时,有110a p p a p ≤<+≤-,.于是21111131||2224a P a a p p a a p a p a a p =++=++=+=+--..即可得出结论. 【解答】解:(1)①∵12||n n n a p a a p +=++-, ∴211||1212211a a a =++=+=--, 322||1210213a a a =++=++=-, 433||1212619a a a =++=++=-, ②∵2111||21n n n a a a a +==++,-, ∴当2n ≥时,1n a ≥,当2n ≥时,11213n n n n a a a a +=+++=-,即从第二项起,数列{}n a 是以1为首项,以3为公比的等比数列, ∴数列{}n a 的前n 项和11123413111321322n n n n a a n S a a a ---=++++⋯+=+=⨯≥---,(), 显然当1n =时,上式也成立,∴113322n n S -=⨯-; (2)∵1||20n n n n n n a a p a a p p a a p p +=++≥++=--->,∴1n n a a +>,即{}n a 单调递增.(i )当11a p≥时,有1a p ≥,于是1n a a p ≥≥,∴1|223|n n n n n n a p a a p a p a p a +=++=++=--,∴113n n a a -=⋅.若数列{}n a 中存在三项*,)(r s t a a a r s t r s t ∈<<N ,,,,依次成等差数列,则有2s r t a a a =+,即111233*3()s r t ---⨯=+∵1s t ≤-,∴111122333333s st r t ---⨯=⨯<<+-.因此(*)不成立.因此此时数列{}n a 中不存在三项*,)(r s t a a a r s t r s t ∈<<N ,,,,依次成等差数列.(ii )当111a p-<<时,有1p a p <<-.此时211111||222a P a a p p a a p a p p =++=++=+>--. 于是当2n ≥时,2n a a p ≥>.从而1|223|n n n n n n a p a a p a p a p a +=++=++=--.∴2221((3)2)32n n na a a p n --==+≥若数列{}n a 中存在三项*,)(r s t a a a r s t r s t ∈<<N ,,,,依次成等差数列,则有2s r t a a a =+,同(i )可知:1r =.于是有2211123(2)3(2)s t a p a a p ⨯+=++﹣﹣,∵21S t ≤≤-,∴211212 2333329103s t s t a a p --=⨯=⨯⨯+<﹣﹣-.∵22233s t ⨯﹣﹣-是整数,∴11 12a a p≤+.于是112a a p ≤--,即1a p ≤-.与1p a p <<-矛盾. 故此时数列{}n a 中不存在三项*,)(r s t a a a r s t r s t ∈<<N,,,,依次成等差数列.(iii )当11a p≤时,有110a p p a p ≤<+≤-,.于是211111||222a P a a p p a a p a p =++=++=+--.32211111|2252|54||a p a a p a p a p a p a p a p =++=+++=++=+---此时数列{}n a 中存在三项123a a a ,,依次成等差数列.综上可得:11a p≤-.【点评】本题考查了等差数列与等比数列的通项公式与求和公式、方程的解法、数列递推关系、分类讨论方法、反证法,考查了推理能力与计算能力,属于难题.20.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的极值.【分析】(1)求出()ln (1)0x f x e e x f λ'=-'=-,,得到曲线()y f x =在1x =处的切线方程为0y =.(2)()()ln ,(0)x g x f x e e x x λ='=>﹣﹣,()xg x e xλ'=-,函数()g x 存在极值,即方程0x e xλ-=有正实数根,,(0)x xe x λ⇒=>,可得λ的取值范围.(3)由(1)、(2)可知(1)0(1)(1)0f f g ='==,,结合(2)分e e λλ≤,>,讨论1x ≥时,是否()0f x ≥恒成立,即可.【解答】解:(1)()(ln 1)x f x e ex x x x λ=+---的定义域为(0)+∞,. ()ln (1)0x f x e e x f λ'='=--,,又(1)0f =. 曲线()y f x =在1x =处的切线方程为0y =.(2)∵()()ln ,(0)x g x f x e e x x λ='=>﹣﹣,()xg x e xλ'=-函数()g x 存在极值,即方程0x e xλ-=有正实数根,,(0)x xe x λ⇒=>,令()x G x xe =,()(1)0x G x x e '=+>在(0)+∞,恒成立. (0)x ∈+∞,时,()0G x >, ∴函数()g x 存在极值,λ的取值范围为(0)+∞,. (3)由(1)、(2)可知(1)0,(1)(1)0f f g '=== 结合(2)1x ≥时,()0x g x e xλ'=-≥,可得(1)x xe x λ≤≥,,()x G x xe =,在(1)+∞,恒成立. ∴e λ≤时,()0g x '≥,()g x 在[1)+∞,递增,()(1)0g x g ≥= 故()f x 在[1)+∞,递增,∴()(1)=0f x f ≥.当e λ>时,存在01x ≥,使()=0g x ',∴0(1)x x ∈,时,()<0g x ', 即0(1,)x x ∈时,()g x 递减,而(1)=0g ,∴0(1,)x x ∈时,()<0g x ,此时()f x 递减,而(1)=0f , ∴在0(1,)x ,()<0f x ,故当e λ>时,()0f x ≥不恒成立; 综上1x ≥时,()0f x ≥恒成立,λ的最大值为e【点评】本题考查了导数的综合应用,利用导数求极值、证明函数恒等式,属于难题。
【江苏省南京市】2017届高考数学三模考试数学(理)试卷-答案

2 3s﹣2 -3t﹣2
2 9
3s
1 3t1 3
0
.∵
2 3s﹣2 -3t﹣2
是整数,∴
a1
a1 2p
1.
于是 a1 -a1-2 p ,即 a1 - p .与 - p a1 p 矛盾.
故此时数列{an}中不存在三项 ar ,as ,at (r,s,t N*,r s t) 依次成等差数列.
江苏省南京市 2017 届高考数学三模考试数学(理)试卷
答案
1.{2} 2. 3 .
8 3. 5
4. 1.
5. 34 . 5
6.2.
7.{ 3 }. 2
8. 1 . 2
9.8 .
10. 1 . 3
11. 1 5 . 2
12. 3 .
13. -1 a 3 . 5
14.[27,30] . 二、解答题:本大题共 6 小题,共 90 分.解答应写出必要的文字说明或推理、验算过程.
(iii)当
a1 p
1时,有 a1
-p
p,a1
p
0.
于是 a2 | P-a1 | 2a1 p p-a1 2a1 p a1 2 p . a3 | p-a2 | 2a2 p | a1 p | 2a1 5 p -a1-p 2a1 5 p a1 4 p 此时数列{an} 中存在三项 a1,a2,a3 依次成等差数列.
若 a b ( 2 ,0) ,则 (2cos a 2sin a,sin 2a t)=( 2 ,0) ,
5
5
1 / 17
可得 cos a sin a= 1 ,平方可得 sin 2a cos 2a 2cos asin a= 1 ,
【江苏省南京市】2017届高考数学三模考试数学(理)试卷-答案

.即
C
( 1
8k2 4k2
2
,1 1
4k22 4k22
)
.
y k1 (x 2)
直线
AD
的方程为:
y
k1
(
x-2)
,联立
x
2
4
y2
1
,化为: (1 4k12 )x2 16k12 x 16k12 4 0 ,
∴ 2xD
16k12 4 1 4k12
由 a 为锐角,可得 cos (0,1) ,即有 tan sin a 1 , cos a 4
1
则
tan
2
2 tan a 1 tan2 a
2 1 1
8
, tan(2
π)
tan
2a
1
1
8 15
15
4 1 tan 2a 1 8
23 . 7
16
15
17.解:(1)∵看台Ⅰ的面积是看台Ⅱ的面积的 3 倍,
sin
∴ BC 40 2 3 cos . sin
(2)设表演台的造价为 y 万元,则 y 120 2 3 cos ,
sin
设 f ( ) 2 3 cos (0<<π) ,则 f ( )
sin
3 2cos sin2
∴当 0 π 时, f ( ) 0 ,当 π π 时, f ( ) 0 ,
(iii)当
a1 p
1时,有 a1
-p
p,a1
p
0.
于是 a2 | P-a1 | 2a1 p p-a1 2a1 p a1 2 p . a3 | p-a2 | 2a2 p | a1 p | 2a1 5 p -a1-p 2a1 5 p a1 4 p 此时数列{an} 中存在三项 a1,a2,a3 依次成等差数列.
【江苏省南京市】2017届高考数学三模考试数学(理)试卷

U A B=______________.则()乙盒子中有编号分别为3则取出的乒乓球的编号之和大于6的概率为为复数z的共轭复数的值为______________.π190,点D11.函数2((2))f x ex x x a =++﹣在区间[],1a a +上单调递增,则实数a 的最大值为______________. 12.在凸四边形ABCD 中,2BD =且0,()()5AC BD AB DC BC AD ⋅=+⋅+=,则四边形ABCD 的面积为______________.13.在平面直角坐标系xOy 中,圆221:x O y +=,圆22:121M x a y a +++=()(﹣)(a 为实数).若圆O 和圆M 上分别存在点,P Q ,使得30OQP ∠=︒,则a 的取值范围为______________.14.已知,,a b c 为正实数,且23228,a b c a b c+≤+≤,则38a b c +的取值范围是______________. 二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程. 15.(本小题满分14分)如图,在三棱锥A BCD -中,,E F 分别为,BC CD 上的点,且BD ∥平面AEF .(1)求证:EF ∥平面ABD ;(2)若AE ⊥平面BCD ,BD CD ⊥,求证:平面AEF ⊥平面ACD .16.(本小题满分14分)已知向量2π(2cos ,sin ),(2sin ,),(0,),t 2a a a b a t a ==为实数.(1)若2(,0)5a b -=,求t 的值;(2)若1t =,且1a b ⋅=,求πtan(2)4a +的值.17.(本小题满分14分)在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC ,及矩形表演台BCDE 四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以,AB AC 为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,10CD =米,三角形水域ABC 的面积为平方米,设BAC θ∠=.(1)求BC 的长(用含θ的式子表示);(2)若表演台每平方米的造价为0.3万元,求表演台的最低造价.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆22221(0)x y a b a b+=>>的右顶点和上顶点分别为点,,A B M 是线段AB 的中点,且232OM AB b =. (1)求椭圆的离心率;(2)若2a =,四边形ABCD 内接于椭圆,AB CD ∥,记直线,AD BC 的斜率分别为1,2k k ,求证:1?2k k 为定值.19.(本小题满分16分)已知常数0p >,数列{}n a 满足*1|2,|n n n a a p p a n +=++∈N -.(1)若n S a 1=﹣1,p=1,①求4a 的值;②求数列{}n a 的前n 项和n S ;(2)若数列{}n a 中存在三项*,,,,(,)ar as at r s t r s t ∈<<N 依次成等差数列,求1a p的取值范围. 20.(本小题满分16分) 已知λ∈R ,函数()(ln 1)xf x e ex x x x λ=+﹣﹣﹣的导数为()g x . (1)求曲线()y f x =在1x =处的切线方程;g x存在极值,求λ的取值范围;(2)若函数()f x≥恒成立,求λ的最大值.(3)若1x≥时,()0。
南京市2017届高三期初模拟考试数学卷
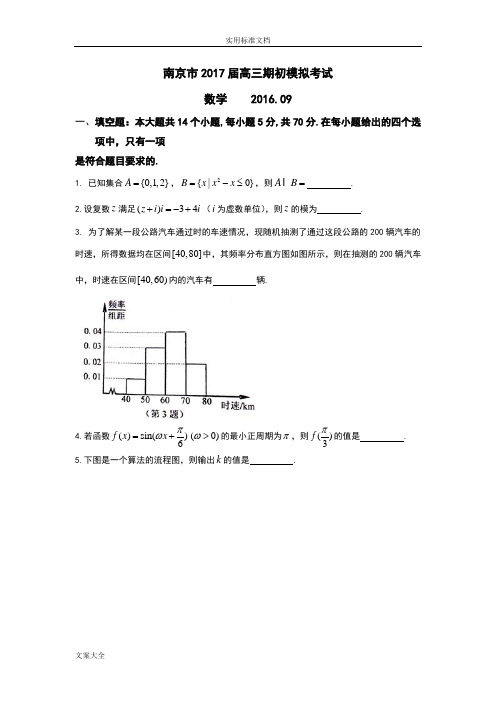
南京市2017届高三期初模拟考试数学 2016.09一、填空题:本大题共14个小题,每小题5分,共70分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1. 已知集合{0,1,2}A =,2{|0}B x x x =-≤,则AB = .2.设复数z 满足()34z i i i +=-+(i 为虚数单位),则z 的模为 .3. 为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有 辆.4.若函数()sin()6f x x πω=+(0)ω>的最小正周期为π,则()3f π的值是 .5.下图是一个算法的流程图,则输出k 的值是 .6.设向量(1,4)a =-,(1,)b x =-,3c a b =+,若//a c ,则实数x 的值是 .7. 某单位要在四名员工(含甲乙两人)中随机选两名到某地出差,则甲乙两人中,至少有一人被选中的概率是 .8. 在平面直角坐标系xOy 中,双曲线222:1(0)4x y C a a -=>的一条渐近线与直线21y x =+平行,则实数a 的值是 .9. 在平面直角坐标系xOy 中,若直线20ax y +-=与圆心为C 的圆22(1)()16x y a -+-=相交于,A B 两点,且ABC ∆为直角三角形,则实数a 的值是 .10. 已知圆柱M 的底面半径为2,高为2,圆锥N 的底面直径和母线长相等,若圆柱M 和圆锥N 的体积相同,则圆锥N 的高为 .11. 各项均为正数的等比数列{}n a ,其前n 项和为n S ,若2578a a -=-,313S =,则数列{}n a 的通项公式n a = .12. 已知函数312,0()2,0x x x f x x x ⎧-≤=⎨->⎩,当(,]x m ∈-∞时,()f x 的取值范围为[16,)-+∞,则实数m 的取值范围是 .13.在ABC ∆中,已知3AB =,2BC =,D 在AB 上,13AD AB =,若3DB DC ∙=,则AC 的长是 .14.已知(),()f x g x 分别是定义在R 上的奇函数和偶函数,且1()()()2xf xg x +=,若存在01[,1]2x ∈,使得等式00()(2)0af x g x +=成立,则实数a 的取值范围是 .二、解答题 (本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15. (本小题满分14分)如图,在平面直角坐标系xOy 中,以x 轴正半轴为始边的锐角α和钝角β的终边分别与单位圆交于点,A B ,若点A 的横坐标是10,点B 的纵坐标是5. (1)求cos()αβ-的值; (2)求αβ+的值.16. (本小题满分14分)如图,在直三棱柱111ABC A B C -中,点,M N 分别为线段11,A B AC 的中点. (1)求证://MN 平面11BB C C ;(2)若D 在边BC 上,1AD DC ⊥,求证:MN AD ⊥.17. (本小题满分14分)如图,某城市有一块半径为40m 的半圆形(以O 为圆心,AB 为直径)绿化区域,现计划对其进行改建,在AB 的延长线上取点D ,使80OD m =,在半圆上选定一点C ,改建后的绿化区域由扇形区域AOC 和三角形区域COD 组成,其面积为2Sm ,设A O C x r a d ∠=.(1)写出S 关于x 的函数关系式()S x ,并指出x 的取值范围; (2)试问AOC ∠多大时,改建后的绿化区域面积S 最大.18. (本小题满分12分)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b +=>>的左、右焦点分别为12,F F ,P 为椭圆上一点(在x 轴上方),连结1PF 并延长交椭圆于另一点Q ,设11PF FQ λ=.(1)若点P 的坐标为3(1,)2,且2PQF ∆的周长为8,求椭圆C 的方程;(2)若2PF 垂直于x 轴,且椭圆C 的离心率1[22e ∈,求实数λ的取值范围.19. (本小题满分12分)已知数列{}n a 是公差为正数的等差数列,其前n 项和为n S ,且2315a a =,416S =. (1)求数列{}n a 的通项公式; (2)数列{}n b 满足11b a =,111n n n n b b a a ++-=. ①求数列{}n b 的通项公式;②是否存在正整数,()m n m n ≠,使得2,,m n b b b 成等差数列?若存在,求出,m n 的值;若不存在,请说明理由. 20. (本小题满分16分)已知函数2()ln ,(,)f x ax bx x a b R =-+∈.(1)当1a b ==时,求曲线()y f x =在1x =处的切线方程; (2)当21b a =+时,讨论函数()f x 的单调性;(3)当1,3a b =>时,记函数()f x 的导函数'()f x 的两个零点是1x 和2x (12x x <),求证:123()()ln 24f x f x ->-.南京市2017届高三年级学情调研数学参考答案及评分标准说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题5分,计70分.)1.{0,1} 2..80 4.125.5 6.47.568.1 9.-1 10.6 11.3n-1 12.[-2,8]13.二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)15.(本小题满分14分)从而sinα==10.…………………… 2分因为钝角β的终边与单位圆交于点B,且点B的纵坐标是5,所以sinβ=,从而cosβ=-n=-…………………… 4分 (1)cos(α-β)=cos αcos β+sin αsin β=10×(-5)+10×5=-10. …………………… 8分 (2)sin(α+β)=sin αcos β+cos αsin β=×(-)+×=. …………………… 11分 因为α为锐角,β为钝角,故α+β∈(2π,32π),所以α+β=34π. …………………… 14分 16.(本小题满分14分) 证明:(1)如图,连结A 1C .在直三棱柱ABC -A 1B 1C 1中,侧面AA 1C 1C 为平行四边形. 又因为N 为线段AC 1的中点, 所以A 1C 与AC 1相交于点N ,即A 1C 经过点N ,且N 为线段A 1C 的中点. ……………… 2分 因为M 为线段A 1B 的中点,所以MN ∥BC . ……………… 4分 又MN ⊄平面BB 1C 1C ,BC ⊂平面BB 1C 1C ,所以MN ∥平面BB 1C 1C . …………………… 6分(2)在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC.又AD⊂平面ABC,所以CC1⊥AD. (8)分因为AD⊥DC1,DC1⊂平面BB1C1C,CC1⊂平面BB1C1C,CC1∩DC1=C1,所以AD⊥平面BB1C1C. (10)分又BC⊂平面BB1C1C,所以AD⊥BC. (12)分又由(1)知,MN∥BC,所以MN⊥AD. (14)分17.(本小题满分14分)解:(1)因为扇形AOC的半径为40 m,∠AOC=x rad,所以扇形AOC的面积S扇形AOC=22x OA∙=800x,0<x<π.……………………2分在△COD中,OD=80,OC=40,∠COD=π-x,所以△COD 的面积S△COD=12·OC·OD·sin∠COD=1600sin(π-x)=1600sin x.……………………4分从而 S=S△COD+S扇形AOC=1600sin x+800x,0<x<π. (6)分(2)由(1)知,S(x)=1600sin x+800x,0<x<π.S ′(x )=1600cos x +800=1600(cos x +12). …………………… 8分 由 S ′(x )=0,解得x =23π.从而当0<x <23π时,S ′(x )>0;当23π<x <π时, S ′(x )<0 .因此 S (x )在区间(0,23π)上单调递增;在区间(23π,π)上单调递减. …………………… 11分所以 当x =23π,S (x )取得最大值. 答:当∠AOC 为23π时,改建后的绿化区域面积S 最大. ……………………14分18.(本小题满分16分)解:(1)因为F 1,F 2为椭圆C 的两焦点,且P ,Q 为椭圆上的点,所以PF 1+PF 2=QF 1+QF 2=2a ,从而△PQF 2的周长为4a .由题意,得4a =8,解得a =2. …………………… 2分因为点P 的坐标为 (1,32),所以221914a b +=,解得b 2=3.所以椭圆C 的方程为22143x y +=. …………………… 5分(2)方法一:因为PF 2⊥x 轴,且P 在x 轴上方,故设P (c ,y 0),y 0>0.设Q (x 1,y 1).因为P 在椭圆上,所以220221y c a b +=,解得y 0=2b a,即P (c ,2b a). …………………… 7分 因为F 1(-c ,0),所以1PF =(-2c ,-2b a),1FQ =(x 1+c ,y 1).由1PF =λ1FQ ,得-2c =λ(x 1+c ),-2b a=λy 1, 解得x 1=-2λλ+c ,y 1=-2b a λ,所以Q (-2λλ+c ,-2b aλ). …………………… 11分 因为点Q 在椭圆上,所以(2λλ+)2e 2+222b a λ=1,即(λ+2)2e 2+(1-e 2)=λ2,(λ2+4λ+3)e 2=λ2-1, 因为λ+1≠0,所以(λ+3)e 2=λ-1,从而λ=3e 2+11-e 2=41-e2-3.…………………… 14分因为e ∈[12],所以14≤e 2≤12,即73≤λ≤5.所以λ的取值范围为[73,5]. …………………… 16分方法二:因为PF 2⊥x 轴,且P 在x 轴上方,故设P (c ,y 0),y 0>0.因为P 在椭圆上,所以22c a +202y b =1,解得y 0=2b a,即P (c ,2b a). …………………… 7分 因为F 1(-c ,0),故直线PF 1的方程为y =22b ac(x +c ).由22222()21b y x c ac x y a b ⎧=+⎪⎪⎨⎪+=⎪⎩,得(4c 2+b 2)x 2+2b 2cx +c 2(b 2-4a 2)=0.因为直线PF 1与椭圆有一个交点为P (c ,2b a).设Q (x 1,y 1),则x 1+c =-22224b c c b +,即-c -x 1=22224b cc b+. …………………… 11分 因为1PF =λ1FQ , 所以λ=12cc x --=2224c b b +=22223c a a c +-=22311e e +-=2431e--. …………………… 14分 因为e ∈[12,2],所以14≤e 2≤12,即73≤λ≤5.所以λ的取值范围为[73,5]. …………………… 16分19.(本小题满分16分)解:(1)设数列{a n }的公差为d ,则d >0.由a 2·a 3=15,S 4=16,得111()(2)154616a d a d a d ++=⎧⎨+=⎩解得112a d =⎧⎨=⎩或172a d =⎧⎨=-⎩(舍去)所以a n =2n -1. …………………… 4分(2)①因为b 1=a 1,b n +1-b n =11n n a a +, 所以b 1=a 1=1,b n +1-b n =11n n a a +=1111()(21)(21)22121n n n n =--+-+, …………………… 6分即 b 2-b 1=11(1)23-, b 3-b 2=111()235-,……b n-b n-1=111()22321n n---,(n≥2)累加得:b n-b1=111(1)22121nn n--=--,……………………9分所以b n=b1+121nn--=1+121nn--=3221nn--.b1=1也符合上式.故b n=3221nn--,n∈N*.……………………11分②假设存在正整数m、n(m≠n),使得b2,b m,b n成等差数列,则b2+b n=2b m.又b2=43,b n=3221nn--=32-142n-,b m=32-142m-,所以43+(32-142n-)=2(32-142m-),即121m-=16+142n-,化简得:2m=721nn-+=7-91n+.……………………14分当n+1=3,即n=2时,m=2,(舍去);当n+1=9,即n=8时,m=3,符合题意.所以存在正整数m=3,n=8,使得b2,b m,b n成等差数列. (16)分20.(本小题满分16分)解:(1)因为a=b=1,所以f(x)=x 2-x+ln x,从而f ′(x)=2x -1+1x.因为f(1)=0,f ′(1)=2,故曲线y=f(x)在x=1处的切线方程为y-0=2(x-1),即2x-y-2=0.…………………… 3分(2)因为b=2a+1,所以f(x)=ax2-(2a+1)x+ln x,从而 f ′(x )=2ax -(2a +1)+1x=22(21)1ax a x x -++=(21)(1)ax x x --,x >0. ………… 5分当a ≤0时,x ∈(0,1)时,f ′(x )>0,x ∈(1,+∞)时,f ′(x )<0,所以,f (x )在区间(0,1)上单调递增,在区间(1,+∞)上单调递减.…………………… 7分当0<a <12时, 由f ′(x )>0得0<x <1或x >12a ,由f ′(x )<0得1<x <12a , 所以f (x )在区间(0,1)和区间(12a ,+∞)上单调递增,在区间(1,12a)上单调递减.当a =12时,因为f ′(x )≥0(当且仅当x =1时取等号), 所以f (x )在区间(0,+∞)上单调递增. 当a >12时, 由f ′(x )>0得0<x <12a 或x >1,由f ′(x )<0得12a <x <1, 所以f (x )在区间(0,12a )和区间(1,+∞)上单调递增,在区间(12a,1)上单调递减.……………………10分(3)方法一:因为a =1,所以f (x )=x 2-bx +ln x ,从而f ′(x )=221x bx x-+ (x >0).由题意知,x 1,x 2是方程2x 2-bx +1=0的两个根,故x 1x 2=12. 记g (x ) =2x 2-bx +1,因为b >3,所以g (12)=32b -<0,g (1)=3-b <0,所以x 1∈(0,12),x 2∈(1,+∞),且bx i =22i x +1 (i =1,2). …………………… 12分f (x 1)-f (x 2)=(2212x x -)-(bx 1-bx 2)+ln12x x =-(2212x x -)+ln 12x x .因为x 1x 2=12,所以f (x 1)-f (x 2)=22x -2214x -ln(222x ),x 2∈(1,+∞). ……………… 14分令t =222x ∈(2,+∞),φ(t )=f (x 1)-f (x 2)=122t t--ln t . 因为φ′(t )=22(1)2t t -≥0,所以φ(t )在区间(2,+∞)单调递增,所以φ(t )>φ(2)=34-ln2,即f (x 1)-f (x 2)>34-ln2. …………………… 16分方法二:因为a =1,所以f (x )=x 2-bx +ln x ,从而f ′(x )=221x bx x-+ (x >0).由题意知,x 1,x 2是方程2x 2-bx +1=0的两个根. 记g (x ) =2x 2-bx +1,因为b >3,所以g (12)=32b -<0,g (1)=3-b <0,所以x 1∈(0,12),x 2∈(1,+∞),且f (x )在[x 1,x 2]上为减函数. …………………… 12分所以f (x 1)-f (x 2)>f (12)-f (1)=(14-2b +ln 12)-(1-b )=-34+2b-ln2. 因为b >3,故f (x 1)-f (x 2)>-34+2b -ln2>34-ln2. …………………… 16分南京市2017届高三年级学情调研数学附加参考答案及评分标准21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.A .选修4—1:几何证明选讲证明:因为点A 、D 、E 、B 在圆O 上,即四边形ADEB 是圆内接四边形,所以∠B =∠EDC . ……………………… 3分因为AB =AC ,所以∠B =∠C . ……………………… 5分所以∠C =∠EDC ,从而ED =EC . ……………………… 7分又因为EF ⊥DC 于点F ,所以F 为线段DC 中点. ……………………… 10分B .选修4—2:矩阵与变换解:(1)M =AB =⎣⎢⎡⎦⎥⎤ 2 -2 1 -3 ⎣⎢⎡⎦⎥⎤ 1 0 0 -1 = ⎣⎢⎡⎦⎥⎤ 2 2 1 3 . ………………………5分(2)矩阵M 的特征多项式为f (λ)= ⎪⎪⎪⎪⎪⎪ λ-2 -2 -1 λ-3 =(λ-2)(λ-3)-2令f (λ)=0,解得λ1=1,λ2=4,所以矩阵M 的特征值为1或4. ……………………… 10分C .选修4—4:坐标系与参数方程 解:曲线C 的极坐标方程为 ρ=2cos θ,化为直角坐标方程为x 2+y 2=2x .即(x -1)2+y 2=1,表示以(1,0)为圆心,1为半径的圆. ……………………… 3分直线l 的极坐标方程是 ρ sin(θ+π6)=m ,即12ρcos θ+32ρsin θ=m ,化为直角坐标方程为x +3y -2m =0. ………………………6分因为直线l 与曲线C 有且只有一个公共点, 所以|1-2m |2=1,解得m =-12或m =32.所以,所求实数m 的值为-12 或 32. ………………………10分D .选修4—5:不等式选讲 解:原不等式等价于⎩⎨⎧x ≤0,1-x -2x ≤4x或⎩⎨⎧0<x ≤1,1-x +2x ≤4x或⎩⎨⎧x >1,x -1+2x ≤4x .……………………… 6分 解⎩⎨⎧x ≤0,1-x -2x ≤4x ,得x ∈∅;解⎩⎨⎧0<x ≤1,1-x +2x ≤4x ,得 13≤x ≤1;解⎩⎨⎧x >1,x -1+2x ≤4x .得x >1.所以原不等式的解集为 [13,+∞). ………………………10分【必做题】第22题、第23题,每题10分,共计20分. 22.(本小题满分10分)解:(1)在四棱锥P -ABCD 中,底面ABCD 为正方形,侧棱PD ⊥底面ABCD ,所以DA 、DC 、DP 两两垂直,故以{DA →,DC →,DP →}为正交基底,建立空间直角坐标系D -xyz .因为PD =DC ,所以DA =DC =DP ,不妨设DA =DC =DP =2,则D (0,0,0),A (2,0,0),C (0,2,0),P (0,0,2),B (2,2,0).因为E 是PC 的中点,所以E (0,1,1). 所以AP →=(-2,0,2),BE →=(-2,-1,1),所以cos<AP →,BE →>=AP →·BE →|AP →|·|BE →|=32,从而<AP →,BE →>=π6.因此异面直线AP 与BE 所成角的大小为π6. (4)分(2)由(1)可知,DE →=(0,1,1),DB →=(2,2,0),PB →=(2,2,-2).设PF →=λPB →,则PF →=(2λ,2λ,-2λ),从而DF →=DP →+PF →=(2λ,2λ,2-2λ).设m =(x 1,y 1,z 1)为平面DEF 的一个法向量,则⎩⎪⎨⎪⎧m ·DF →=0, m ·DE →=0,即⎩⎨⎧λx 1+λy 1+(1-λ)z 1=0,y 1+z 1=0,取z 1=λ,则y 1=-λ,x 1=2λ-1.所以m =(2λ-1,-λ,λ)为平面DEF 的一个法向量. ……………………… 6分设n =(x 2,y 2,z 2)为平面DEB 的一个法向量,则⎩⎪⎨⎪⎧n ·DB →=0,n ·DE →=0,即⎩⎨⎧2x 2+2y 2=0,y 2+z 2=0,取x 2=1,则y 2=-1,z 2=1.所以n =(1,-1,1)为平面BDE 的一个法向量. ………………………… 8分因为二面角F -DE -B 的正弦值为33,所以二面角F -DE -B 的余弦的绝对值为63, 即 |cos<m ,n >|=63, 所以 |m ·n || m |·| n |=63, |4λ-1|3·(2λ-1)2+2λ2=63, 化简得,4λ2=1,因为点F 在线段PB 上,所以0≤λ≤1,所以λ=12,即PF PB =12. (10)分23.(本小题满分10分)解:(1)设甲第i 次投中获胜的事件为A i (i =1,2,3),则A 1,A 2,A 3彼此互斥.甲获胜的事件为A 1+A 2+A 3.P (A 1)=25;P (A 2)=35×13×25=225; P (A 3)=(35)2×(13)2×25=2125. 所以P (A 1+A 2+A 3)=P (A 1)+P (A 2)+P (A 3)=25+225+2125=62125.答:甲获胜的概率为62125. ………………………4分(2)X 所有可能取的值为1,2,3.则 P (X =1)=25+35×23=45;P (X =2)=225+35×13×35×23=425; P (X =3)=(35)2×(13)2×1=125.即X 的概率分布列为……………………… 8分所以X 的数学期望E (X )=1×45+2×425+3×125=3125. ………………………10分。
江苏省南京市2017届高三三模数学试卷(含解析)

2017年江苏省南京市高考数学三模试卷一、填空题:(本大题共14小题,每小题5分,共70分)1.已知全集U={1,2,3,4},集合A={1,4},B={3,4},则∁U(A∪B)= .2.甲盒子中有编号分别为1,2的两个乒乓球,乙盒子中有编号分别为3,4,5,6的四个乒乓球.现分别从两个盒子中随机地各取出1个乒乓球,则取出的乒乓球的编号之和大于6的概率为.3.若复数z满足,其中i为虚数单位,为复数z的共轭复数,则复数z的模为.4.执行如图所示的伪代码,若输出的y值为1,则输入x的值为.5.如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为.6.在同一直角坐标系中,函数的图象和直线y=的交点的个数是.7.在平面直角坐标系xoy中,双曲线的焦距为6,则所有满足条件的实数m 构成的集合是.8.已知函数f(x)是定义在R上且周期为4的偶函数,当x∈[2,4]时,,则的值为.9.若等比数列{a n}的各项均为正数,且a3﹣a1=2,则a5的最小值为.10.如图,在直三棱柱ABC﹣A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D﹣ABC1的体积为.11.函数f(x)=e x(﹣x2+2x+a)在区间[a,a+1]上单调递增,则实数a的最大值为.12.在凸四边形ABCD中,BD=2,且,,则四边形ABCD 的面积为.13.在平面直角坐标系xoy中,圆O:x2+y2=1,圆M:(x+a+1)2+(y﹣2a)2=1(a为实数).若圆O和圆M上分别存在点P,Q,使得∠OQP=30°,则a的取值范围为.14.已知a,b,c为正实数,且,则的取值范围为.二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程. 15.(14分)如图,在三棱锥A﹣BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.(1)求证:EF∥平ABD面;(2)若AE⊥平面BCD,BD⊥CD,求证:平面AEF⊥平面ACD.16.(14分)已知向量为实数.。
【江苏省南京市】2017届高考数学三模考试数学(理)试卷

......( 如图 ), 看台Ⅰ, 看台Ⅱ是分别以AB, AC 为直径的两个半圆形区域 , 且看台Ⅰ的面积是看台Ⅱ的面积的 3 倍 ,矩形表演台 BCDE 中, CD 10 米 , 三角形水域 ABC 的面积为 400 3 平方米 ,设BAC .( 1) 求 BC 的长(用含 的式子表示);( 2) 假设表演台每平方米的造价为 0.3万元,求表演台的最低造价.1816分 ).( 本小题总分值如图 , 在平面直角坐标系xOy 中,椭圆x 2y 2 1(a b 0) 的右顶点和上顶点分别为点 A,B,M 是线段ABa 2b 2的中点 ,且OM AB3 b 2.2( 1) 求椭圆的离心率;( 2) 假设 a 2 ,四边形 ABCD 内接于椭圆,AB ∥CD ,记直线 AD, BC 的斜率分别为 k1,k 2 , 求证:k1?k2为定值.19.( 本小题总分值16 分 )常数 p0 ,数列 { a n } 满足 a n 1 | p- a n | 2a np,n N *.( 1) 假设S n a1=﹣ 1, p=1, ①求 a 4的值;②求数列 { a n } 的前n 项和 S n ;( 2) 假设数列{ a n }中存在三项ar , as, at ( r , s,t N *, rs t ) 依次成等差数列,求a 1的取值X 围 .p20.( 本小题总分值 16分 )R ,函数f( ) e x( x ln ﹣ 1)的导数为 g( x).﹣ ﹣x exx x-3-/4...( 如图 ), 看台Ⅰ, 看台Ⅱ是分别以AB, AC 为直径的两个半圆形区域, 且看台Ⅰ的面积是看台Ⅱ的面积的 3 倍 ,矩形表演台 BCDE 中, CD 10米 , 三角形水域 ABC的面积为 400 3 平方米 ,设BAC.( 1)求 BC 的长(用含的式子表示);( 2)假设表演台每平方米的造价为0.3万元,求表演台的最低造价.1816分 ).( 本小题总分值如图 , 在平面直角坐标系xOy 中,椭圆x2y21(a b 0) 的右顶点和上顶点分别为点A,B,M是线段AB a 2b2的中点 ,且OM AB 3 b2.2( 1)求椭圆的离心率;( 2)假设 a 2 ,四边形 ABCD 内接于椭圆,AB∥CD ,记直线 AD, BC 的斜率分别为 k1,k 2, 求证:k1?k2为定值.19.( 本小题总分值16 分 )常数 p 0 ,数列 { a n } 满足 a n 1| p- a n | 2a n p,n N*.( 1) 假设S n a1=﹣ 1, p=1,①求 a4的值;②求数列 { a n } 的前n项和 S n;( 2) 假设数列{ a n}中存在三项ar , as, at ( r , s,t N *, r s t ) 依次成等差数列,求a1的取值X围 . p20.( 本小题总分值16分 )R ,函数f ()ex(xln ﹣1)的导数为g( x).﹣﹣x ex x x-3-/4。
江苏省南京淮安市2017届高三第三次模拟考试数学试题及答案

南京市2017届高三年级第三次模拟考试数 学注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部份.本试卷总分值为160分,考试时刻为120分钟.2.答题前,请务必将自己的姓名、学校写在答题卡上.试题的答案写在答题卡...上对应题目的答案空格内.考试终止后,交回答题卡. 参考公式:方差s 2=1n[(x 1-x )2+(x 2-x )2+…+(x n -x )2],其中x 为x 1,x 2,…,x n 的平均数.柱体的体积公式:V =Sh ,其中S 为柱体的底面积,h 为柱体的高. 锥体的体积公式:V =13Sh ,其中S 为锥体的底面积,h 为锥体的高.一、填空题:本大题共14小题,每题5分,共70分.请把答案填写在答.题卡..相应位置....上. 1.已知全集U ={1,2,3,4},集合A ={1,4},B ={3,4},那么∁U (A ∪B )=▲ .2.甲盒子中有编号别离为1,2的2个乒乓球,乙盒子中有编号别离为3,4,5,6的4个乒乓球.现别离从两个盒子中随机地各掏出1个乒乓球,那么掏出的乒乓球的编号之和大于6的概率为 ▲ .3.假设复数z 知足z +2-z =3+2i ,其中i 为虚数单位,-z 为 复数z 的共轭复数,那么复数z 的模为 ▲ . 4.执行如下图的伪代码,假设输出y 的值为1, 那么输入x 的值为 ▲ .5.如图是甲、乙两名篮球运动员在五场竞赛中所得分数的茎叶图,则在这五场竞赛中得分较为稳固(方差较小)的那名运动员的得分的方差为 ▲ .7 7 9 0 8 9 48 1 0 3 5 甲 乙 (第5题图)(第4题图)6.在同一直角坐标系中,函数y =sin(x +π3) (x ∈[0,2π])的图象和直线y =12 的交点的个数是 ▲ .7.在平面直角坐标系xOy 中,双曲线x 22m 2-y 23m =1的焦距为6,那么所有知足条件的实数m组成的集合是 ▲ .8.已知函数f (x )是概念在R 上且周期为4的偶函数.当x ∈[2,4]时,f (x )=|log 4(x -32)|,则f (12)的值为 ▲ .9.若等比数列{a n }的各项均为正数,且a 3-a 1=2,那么a 5的最小值为 ▲ . 10.如图,在直三棱柱ABC -A 1B 1C 1中,AB =1,BC =2,BB 1=3,∠ABC =90°,点D 为侧棱BB 1上的动点.当AD +DC 1最小时, 三棱锥D -ABC 1的体积为 ▲ .11.假设函数f (x )=e x (-x 2+2x +a )在区间[a ,a +1]上单调递增,那么实数a 的最大值为 ▲ .12.在凸四边形ABCD 中, BD =2,且AC →·BD →=0,(AB →+→DC )•(→BC +→AD )=5,那么四边形ABCD 的面积为 ▲ .13. 在平面直角坐标系xOy 中,圆O :x 2+y 2=1,圆M :(x +a +3)2+(y -2a )2=1(a 为实数).假设圆O 与圆M 上别离存在点P ,Q ,使得∠OQP =30 ,则a 的取值范围为 ▲ . 14.已知a ,b ,c 为正实数,且a +2b ≤8c ,2a +3b ≤2c ,那么3a +8b c的取值范围为 ▲ .二、解答题:本大题共6小题,共计90分.请在答.题卡..指定区域内.....作答,解答时应写出文字说明、证明进程或演算步骤. 15.(本小题总分值14分)如图,在三棱锥A -BCD 中,E ,F 别离为棱BC ,CD 上的点,且BD ∥平面AEF . (1)求证:EF ∥平面ABD ;(2)假设BD ⊥CD ,AE ⊥平面BCD ,求证:平面AEF ⊥平面ACD .ACB A 1B 1C 1D(第10题图) ABCFED16.(本小题总分值14分)已知向量a =(2cos α,sin 2α),b =(2sin α,t ),α∈(0,π2).(1)假设a -b =(25,0),求t 的值;(2)若t =1,且a • b =1,求tan(2α+π4)的值.17.(本小题总分值14分)在一水域上建一个演艺广场.演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC ,及矩形演出台BCDE 四个部份组成(如图).看台Ⅰ,看台Ⅱ是别离以AB ,AC 为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍;矩形演出台BCDE 中,CD =10米;三角形水域ABC 的面积为4003平方米.设∠BAC =θ.(1)求BC 的长(用含θ的式子表示);(2)假设演出台每平方米的造价为万元,求演出台的最低造价.(第17题图)18.(本小题总分值16分)如图,在平面直角坐标系xOy 中,椭圆x 2a 2+y 2b 2=1(a >b >0)的右极点和上极点别离为A ,B ,M 为线段AB 的中点,且OM →·AB →=-32b 2.(1)求椭圆的离心率;(2)已知a =2,四边形ABCD 内接于椭圆,AB ∥DC .记直线AD ,BC 的斜率别离为k 1,k 2,求证:k 1·k 2为定值.19.(本小题总分值16分)已知常数p >0,数列{a n }知足a n +1=|p -a n |+2 a n +p ,n ∈N *. (1)假设a 1=-1,p =1, ①求a 4的值;②求数列{a n }的前n 项和S n .(2)假设数列{a n }中存在三项a r ,a s ,a t (r ,s ,t ∈N *,r <s <t )依次成等差数列,求a 1p的取值范围.20.(本小题总分值16分)已知λ∈R ,函数f (x )=e x -e x -λ(x ln x -x +1)的导函数为g (x ). (1)求曲线y =f (x )在x =1处的切线方程; (2)假设函数g (x )存在极值,求λ的取值范围; (3)假设x ≥1时,f (x )≥0恒成立,求λ的最大值.南京市2017届高三第(第18题图)三次模拟考试数学参考答案及评分标准一、填空题(本大题共14小题,每题5分,计70分.)1.{2} 2.383. 5 4.-1 5. 6.27.{32} 8.12 9.8 10.13 11.-1+52 12.313.[-65,0] 14.[27,30]二、解答题(本大题共6小题,计90分.解许诺写出必要的文字说明,证明进程或演算步骤)15.(本小题总分值14分) 证明:(1)因为BD ∥平面AEF ,BD ⊂平面BCD ,平面AEF ∩平面BCD =EF ,因此 BD ∥EF . …………………… 3分 因为BD ⊂平面ABD ,EF ⊄平面ABD ,因此 EF ∥平面ABD . …………………… 6分 (2)因为AE ⊥平面BCD ,CD ⊂平面BCD ,因此 AE ⊥CD . …………………… 8分 因为 BD ⊥CD ,BD ∥EF ,因此 CD ⊥EF , …………………… 10分 又 AE ∩EF =E ,AE ⊂平面AEF ,EF ⊂平面AEF ,因此 CD ⊥平面AEF . …………………… 12分 又 CD ⊂平面ACD ,因此 平面AEF ⊥平面ACD . …………………… 14分16.(本小题总分值14分)解:(1)因为向量a =(2cos α,sin 2α),b =(2sin α,t ),且a -b =(25,0),因此cos α-sin α=15,t =sin 2α. …………………… 2分由cos α-sin α=15 得 (cos α-sin α)2=125,即1-2sin αcos α=125,从而2sin αcos α=2425.因此(cos α+sin α)2=1+2sin αcos α=4925.因为α∈(0,π2),因此cos α+sin α=75. …………………… 5分因此sin α=(cos α+sin α)-(cos α-sin α)2=35,从而t =sin 2α=925. …………………… 7分(2)因为t =1,且a • b =1,因此4sin αcos α+sin 2α=1,即4sin αcos α=cos 2α.因为α∈(0,π2),因此cos α≠0,从而tan α=14. …………………… 9分因此tan2α=2tan α1-tan 2α=815. …………………… 11分 从而tan(2α+π4)=tan2α+tanπ41-tan2α·tan π4=815+11-815=237. …………………… 14分17.(本小题总分值14分)解:(1)因为看台Ⅰ的面积是看台Ⅱ的面积的3倍,因此AB =3AC .在△ABC 中,S △ABC =12AB •AC •sin θ=4003,因此AC 2=800sin θ . …………………… 3分由余弦定理可得BC 2=AB 2+AC 2-2AB •AC •cos θ,=4AC 2-23AC 2 cos θ. =(4-23cos θ)800sin θ, 即BC =(4-23cos θ)•800sin θ=402-3cos θsin θ.因此 BC =402-3cos θsin θ,θ∈(0,π). …………………… 7分(2)设演出台的总造价为W 万元.因为CD =10m ,演出台每平方米的造价为万元, 因此W =3BC =1202-3cos θsin θ,θ∈(0,π). …………………… 9分记f (θ)=2-3cos θsin θ,θ∈(0,π).则f ′(θ)=3-2cos θsin 2θ. …………………… 11分由f ′(θ)=0,解得θ=π6.当θ∈(0,π6)时,f ′(θ)<0;当θ∈(π6,π)时,f ′(θ)>0.故f (θ)在(0,π6)上单调递减,在(π6,π)上单调递增,从而当θ=π6 时,f (θ)取得最小值,最小值为f (π6)=1.因此W min =120(万元).答:演出台的最低造价为120万元. …………………… 14分18.(本小题总分值16分)解:(1)A (a ,0),B (0,b ),由M 为线段AB 的中点得M (a 2,b2).因此OM →=(a 2,b 2),AB →=(-a ,b ).因为OM →·AB →=-32b 2,因此(a 2,b 2)·(-a ,b )=-a 22+b 22=-32b 2,整理得a 2=4b 2,即a =2b . …………………… 3分 因为a 2=b 2+c 2,因此3a 2=4c 2,即3a =2c .因此椭圆的离心率e =c a =32. …………………… 5分(2)方式一:由a =2得b =1,故椭圆方程为x 24+y 2=1.从而A (2,0),B (0,1),直线AB 的斜率为-12. …………………… 7分因为AB ∥DC ,故可设DC 的方程为y =-12x +m .设D (x 1,y 1),C (x 2,y 2).联立⎩⎨⎧y =-12x +m ,x 24+y 2=1,消去y ,得x 2-2mx +2m 2-2=0,因此x 1+x 2=2m ,从而x 1=2m -x 2. ……………………… 9分 直线AD 的斜率k 1=y 1x 1-2=-12x 1+m x 1-2,直线BC 的斜率k 2=y 2-1x 2=-12x 2+m -1x 2,……………………… 11分因此k 1·k 2=-12x 1+m x 1-2·-12x 2+m -1x 2=14x 1x 2-12(m -1)x 1-12mx 2+m (m -1)(x 1-2)x 2=14x 1x 2-12m (x 1+x 2)+12x 1+m (m -1)x 1x 2-2x 2=14x 1x 2-12m ·2m +12(2m -x 2)+m (m -1)x 1x 2-2x 2=14x 1x 2-12x 2x 1x 2-2x 2=14, 即k 1·k 2为定值14. ………………………16分方式二:由a =2得b =1,故椭圆方程为x 24+y 2=1.从而A (2,0),B (0,1),直线AB 的斜率为-12. …………………… 7分设C (x 0,y 0),那么x 024+y 02=1.因为AB ∥CD ,故CD 的方程为y =-12(x -x 0)+y 0.联立⎩⎨⎧y =-12(x -x 0)+y 0,x 24+y 2=1,消去y ,得x 2-(x 0+2y 0)x +2x 0y 0=0,解得x =x 0(舍去)或x =2y 0.因此点D 的坐标为(2y 0,12x 0). ……………………… 13分因此k 1·k 2=12x 02y 0-2·y 0-1x 0=14,即k 1·k 2为定值14. ……………………… 16分19.(本小题总分值16分)解:(1)因为p =1,因此a n +1=|1-a n |+2 a n +1. ① 因为 a 1=-1,因此a 2=|1-a 1|+2 a 1+1=1, a 3=|1-a 2|+2 a 2+1=3,a 4=|1-a 3|+2 a 3+1=9. …………………………… 3分 ② 因为a 2=1,a n +1=|1-a n |+2 a n +1, 因此当n ≥2时,a n ≥1,从而a n +1=|1-a n |+2 a n +1=a n -1+2 a n +1=3a n ,于是有 a n =3n -2(n ≥2) . …………………………… 5分 当n =1时,S 1=-1;当n ≥2时,S n =-1+a 2+a 3+…+a n =-1+1-3n -11-3=3n -1-32 .因此 S n =⎩⎪⎨⎪⎧1,n =1,3n -1-32,n ≥2,n ∈N *, 即S n =3n -1-32,n ∈N *. ………………………… 8分(2)因为a n +1-a n =|p -a n |+a n +p ≥p -a n +a n +p =2 p >0,因此a n +1>a n ,即{a n }单调递增. ………………………… 10分 (i )当a 1p≥1时,有a 1≥p ,于是a n ≥a 1≥p ,因此a n +1=|p -a n |+2 a n +p =a n -p +2 a n +p =3a n ,因此a n =3n -1a 1.假设{a n }中存在三项a r ,a s ,a t (r ,s ,t ∈N *,r <s <t )依次成等差数列,那么有2 a s =a r +a t ,即2×3s -1=3r -1+3t -1. (*)因为s ≤t -1,因此2×3s -1=23×3s <3t -1<3r -1+3t -1,即(*)不成立.故现在数列{a n }中不存在三项依次成等差数列. ……………………… 12分 (ii )当-1<a 1p<1时,有-p <a 1<p .现在a 2=|p -a 1|+2 a 1+p =p -a 1+2 a 1+p =a 1+2 p >p , 于是当n ≥2时,a n ≥a 2>p ,从而a n +1=|p -a n |+2 a n +p =a n -p +2 a n +p =3a n . 因此a n =3n -2a 2=3n -2(a 1+2p ) (n ≥2).假设{a n }中存在三项a r ,a s ,a t (r ,s ,t ∈N *,r <s <t )依次成等差数列, 同(i )可知,r =1,于是有2×3s -2(a 1+2 p )=a 1+3t -2(a 1+2p ).因为2≤s ≤t -1,因此a 1 a 1+2 p =2×3s -2-3t -2=29×3s -13×3t -1<0.因为2×3s -2-3t-2是整数,因此a 1a 1+2 p≤-1,于是a 1≤-a 1-2p ,即a 1≤-p ,与-p <a 1<p 相矛盾.故现在数列{a n }中不存在三项依次成等差数列. ………………… 14分 (iii )当a 1p ≤-1时,那么有a 1≤-p <p ,a 1+p ≤0,于是a 2=| p -a 1|+2a 1+p =p -a 1+2 a 1+p =a 1+2p ,a 3=|p -a 2|+2a 2+p =|p +a 1|+2a 1+5p =-p -a 1+2a 1+5p =a 1+4p , 现在有a 1,a 2,a 3成等差数列.综上可知:a 1p ≤-1. ……………………………… 16分20.(本小题总分值16分) 解:(1)因为f ′(x )=e x -e -λln x ,因此曲线y =f (x )在x =1处的切线的斜率为f ′(1)=0, 又切点为(1,f (1)),即(1,0),因此切线方程为y =0. ………………………… 2分 (2)g (x )=e x -e -λln x ,g ′(x )=e x -λx.当λ≤0时,g ′(x )>0恒成立,从而g (x )在(0,+∞)上单调递增,故现在g (x )无极值. ………………………… 4分 当λ>0时,设h (x )=e x -λx ,那么h ′(x )=e x +λx2>0恒成立,因此h (x )在(0,+∞)上单调递增. ………………………… 6分 ①当0<λ<e 时,h (1)=e -λ>0,h (λe)=e λe -e <0,且h (x )是(0,+∞)上的持续函数, 因此存在唯一的x 0∈(λe ,1),使得h (x 0)=0.②当λ≥e 时,h (1)=e -λ≤0,h (λ)=e λ-1>0,且h (x )是(0,+∞)上的持续函数, 因此存在唯一的x 0∈[1,λ),使得h (x 0)=0.故当λ>0时,存在唯一的x 0>0,使得h (x 0)=0. …………………… 8分 且当0<x <x 0时,h (x )<0,即g ′(x )<0,当x >x 0时,h (x )>0,即g ′(x )>0, 因此g (x )在(0,x 0)上单调递减,在(x 0,+∞)上单调递增, 因此g (x )在x =x 0处有极小值.因此当函数g (x )存在极值时,λ的取值范围是(0,+∞). …………………… 10分 (3)g (x )=f ′(x )=e x -e -λln x ,g ′(x )=e x -λx .若g ′(x )≥0恒成立,那么有λ≤x e x 恒成立.设φ(x )=x e x (x ≥1),那么φ′(x )=(x +1) e x >0恒成立, 因此φ(x )单调递增,从而φ(x )≥φ(1)=e ,即λ≤e . 于是当λ≤e 时,g (x )在[1,+∞)上单调递增,现在g (x )≥g (1)=0,即f ′(x )≥0,从而f (x )在[1,+∞)上单调递增.因此f (x )≥f (1)=0恒成立. …………………………… 13分 当λ>e 时,由(2)知,存在x 0∈(1,λ),使得g (x )在(0,x 0)上单调递减, 即f ′(x )在(0,x 0)上单调递减. 因此当1<x <x 0时,f ′(x )<f ′(1)=0,于是f (x )在[1,x 0)上单调递减,因此f (x 0)<f (1)=0. 这与x ≥1时,f (x )≥0恒成立矛盾.因此λ≤e ,即λ的最大值为e . …………………………… 16分南京市2017届高三第三次模拟考试数学附加参考答案及评分标准21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每题10分,共计20分.请在答卷卡指定区域内作答.解许诺写出文字说明、证明进程或演算步骤.A .选修4—1:几何证明选讲 证明:连结BE .因为AD 是边BC 上的高,AE 是△ABC 的外接圆的直径, 因此∠ABE =∠ADC =90°. …………… 4分∠AEB =∠ACD , …………… 6分 因此△ABE ∽△ADC , …………… 8分 因此AB AD = AE AC.即AB ·AC =AD ·AE . …………… 10分 B .选修4—2:矩阵与变换 解:(1)AX =⎣⎢⎡⎦⎥⎤ 2 x y 2 ⎣⎡⎦⎤-1 1 = ⎣⎢⎡⎦⎥⎤x -22-y . …………… 2分因为AX =⎣⎡⎦⎤12,因此⎩⎨⎧x -2=1,2-y =2,解得x =3,y =0. …………… 4分(2)由(1)知A =⎣⎢⎡⎦⎥⎤2 30 2 ,又B =⎣⎢⎡⎦⎥⎤1 -10 2 ,因此AB = ⎣⎢⎡⎦⎥⎤2 30 2 ⎣⎢⎡⎦⎥⎤1 -10 2 = ⎣⎢⎡⎦⎥⎤2 40 4 . …………… 6分设(AB )-1= ⎣⎢⎡⎦⎥⎤a b c d ,那么 ⎣⎢⎡⎦⎥⎤2 40 4 ⎣⎢⎡⎦⎥⎤a b c d = ⎣⎢⎡⎦⎥⎤1 00 1 ,即 ⎣⎢⎡⎦⎥⎤2a +4c 2b +4d 4c 4d = ⎣⎢⎡⎦⎥⎤1 00 1 . …………… 8分 因此 ⎩⎨⎧2a +4c =1,4c =0,2b +4d =0,4d =1, 解得a =12,b =-12,c =0,d =14,即 (AB )-1= ⎣⎢⎡⎦⎥⎤12 -120 14 .…………… 10分(第21(A)图)(说明:逆矩阵也能够直接利用公式求解,但要求呈现公式的结构) C .选修4—4:坐标系与参数方程 解:由于ρ2 = x 2+y 2,ρcos θ = x ,因此曲线C 的直角坐标方程为 x 2+y 2-8x +15=0,即 (x -4)2+y 2=1,因此曲线C 是以 (4,0) 为圆心,1为半径的圆.…………… 3分 直线l 的直角坐标方程为 y =x ,即x -y =0. …………… 6分 因为圆心 (4,0) 到直线l 的距离d =|4-0|2=22>1. …………… 8分因此直线l 与圆相离,从而PQ 的最小值为d -1=22-1. …………… 10分D .选修4—5:不等式选讲证明:因为x >0,因此x 3+2 = x 3+1+1 ≥ 33x 3×1×1 = 3x ,当且仅当x 3=1,即x =1时取“=”. …………… 4分 因为y 2+1-2y =(y -1)2≥0,因此y 2+1≥2y ,当且仅当y =1时取“=”. …………… 8分 因此 (x 3+2)+(y 2+1)≥3x +2y ,即x 3+y 2+3≥3x +2y ,当且仅当x =y =1时,取“=”. …………… 10分【必做题】第22题、第23题,每题10分,共计20分.请在答.卷卡指定区域内.......作答.解许诺写出文字说明、证明进程或演算步骤. 22.(本小题总分值10分)解:(1)设P (x ,y )为曲线C 上任意一点 .因为PS ⊥l ,垂足为S ,又直线l :x =-1,因此S (-1,y ). 因为T (3,0),因此OP →=(x ,y ), ST →=(4,-y ). 因为OP →·ST →=0,因此4x -y 2=0,即y 2=4x .因此曲线C 的方程为y 2=4x . …………… 3分 (2)因为直线PQ 过点(1,0),故设直线PQ 的方程为x =my +1.P (x 1,y 1),Q (x 2,y 2).联立⎩⎨⎧y 2=4x ,x =my +1,消去x ,得y 2―4my ―4=0.因此y 1+y 2=4m ,y 1y 2=―4. …………… 5分 因为M 为线段PQ 的中点,因此M 的坐标为(x 1+x 22,y 1+y 22),即M (2m 2+1,2m ).又因为S (-1,y 1),N (-1,0),因此SM →=(2m 2+2,2m -y 1),NQ →=(x 2+1,y 2)=(my 2+2,y 2). …………… 7分 因为(2m 2+2) y 2-(2m -y 1)(my 2+2)=(2m 2+2) y 2-2m 2y 2+my 1y 2-4m +2y 1=2(y 1+y 2)+my 1y 2-4m =8m -4m -4m =0.因此向量SM →与NQ →共线. …………… 10分 23.(本小题总分值10分)解:(1)由题意,当n =2时,数列{a n }共有6项.要使得f (2)是2的整数倍,那么这6项中,只能有0项、2项、4项、6项取1,故T 2=C 06+C 26+C 46+C 66=25=32. ……………………… 3分 (2)T n =C 03n +C 33n +C 63n +…+C 3n 3n . ……………………… 4分当1≤k ≤n ,k ∈N *时,C 3k 3n +3=C 3k 3n +2+C 3k -13n +2=C 3k -13n +1+C 3k 3n +1+C 3k -13n +1+C 3k -23n +1=2C 3k -13n +1+C 3k 3n +1+C 3k -23n +1 =2 (C 3k -13n +C 3k -23n )+C 3k -13n +C 3k 3n +C 3k -33n +C 3k -23n=3 (C 3k -13n +C 3k -23n )+C 3k 3n +C 3k -33n , ……………………… 6分 于是T n +1=C 03n +3+C 33n +3+C 63n +3+…+C 3n +33n +3=C 03n +3+C 3n +33n +3+3(C 13n +C 23n +C 43n +C 53n +…+C 3n -23n +C 3n -13n )+T n -C 03n +T n -C 3n 3n=2 T n +3(23n -T n )=3×8n -T n . ……………………… 8分 下面用数学归纳法证明T n =13[8n +2(-1)n ].当n =1时,T 1=C 03+C 33=2=13[81+2(-1)1],即n =1时,命题成立.假设n =k (k ≥1,k ∈N *) 时,命题成立,即T k =13[8k +2(-1)k ].那么当n =k +1时,T k +1=3×8k -T k =3×8k -13[8k +2(-1)k ]=13[9×8k -8k -2(-1)k ]=13[8k +1+2(-1)k +1],即n =k +1时,命题也成立.于是当n ∈N *,有T n =13[8n +2(-1)n ]. ……………………… 10分。
【江苏省南京市】2017届高考数学三模考试数学(理)试卷

的值为______________.π111.函数2((2))f x ex x x a =++﹣在区间[],1a a +上单调递增,则实数a 的最大值为______________. 12.在凸四边形ABCD 中,2BD =且0,()()5AC BD AB DC BC AD ⋅=+⋅+=u u u r u u u r u u u r u u u r u u u r u u u r,则四边形ABCD 的面积为______________.13.在平面直角坐标系xOy 中,圆221:x O y +=,圆22:121M x a y a +++=()(﹣)(a 为实数).若圆O 和圆M 上分别存在点,P Q ,使得30OQP ∠=︒,则a 的取值范围为______________.14.已知,,a b c 为正实数,且23228,a b c a b c +≤+≤,则38a b c+的取值范围是______________. 二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.15.(本小题满分14分)如图,在三棱锥A BCD -中,,E F 分别为,BC CD 上的点,且BD ∥平面AEF .(1)求证:EF ∥平面ABD ;(2)若AE ⊥平面BCD ,BD CD ⊥,求证:平面AEF ⊥平面ACD .16.(本小题满分14分)已知向量2π(2cos ,sin ),(2sin ,),(0,),t 2a a ab a t a ==r r 为实数. (1)若2(,0)5a b -=r r ,求t 的值; (2)若1t =,且1a b ⋅=r r ,求πtan(2)4a +的值. 17.(本小题满分14分)在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC ,及矩形表演台BCDE 四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以,AB AC 为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,10CD =米,三角形水域ABC 的面积为平方米,设BAC θ∠=.(1)求BC 的长(用含θ的式子表示);(2)若表演台每平方米的造价为0.3万元,求表演台的最低造价.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆22221(0)x y a b a b +=>>的右顶点和上顶点分别为点,,A B M 是线段AB 的中点,且232OM AB b =u u u u r u u u r g . (1)求椭圆的离心率;(2)若2a =,四边形ABCD 内接于椭圆,AB CD ∥,记直线,AD BC 的斜率分别为1,2k k ,求证:1?2k k 为定值.19.(本小题满分16分)已知常数0p >,数列{}n a 满足*1|2,|n n n a a p p a n +=++∈N -.(1)若n S a 1=﹣1,p=1,①求4a 的值;②求数列{}n a 的前n 项和n S ;(2)若数列{}n a 中存在三项*,,,,(,)ar as at r s t r s t ∈<<N 依次成等差数列,求1a p的取值范围. 20.(本小题满分16分) 已知λ∈R ,函数()(ln 1)xf x e ex x x x λ=+﹣﹣﹣的导数为()g x . (1)求曲线()y f x =在1x =处的切线方程;g x存在极值,求λ的取值范围;(2)若函数()f x≥恒成立,求λ的最大值.(3)若1x≥时,()0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京市2017届高三年级第三次模拟考试数 学 2017.05注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、学校写在答题卡上.试题的答案写在答题卡...上对应题目的答案空格内.考试结束后,交回答题卡. 参考公式:方差s 2=1n [(x 1-x )2+(x 2-x )2+…+(x n -x )2],其中x 为x 1,x 2,…,x n 的平均数.柱体的体积公式:V =Sh ,其中S 为柱体的底面积,h 为柱体的高. 锥体的体积公式:V =13Sh ,其中S 为锥体的底面积,h 为锥体的高.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置.......上.1.已知全集U ={1,2,3,4},集合A ={1,4},B ={3,4},则∁U(A ∪B )= ▲ .2.甲盒子中有编号分别为1,2的2个乒乓球,乙盒子中有编号分别为3,4,5,6的4个乒乓球.现分别从两个盒子中随机地各取出1个乒乓球,则取出的乒乓球的编号之和大于6的概率为 ▲ .3.若复数z 满足z +2-z =3+2i ,其中i 为虚数单位,-z 为复数z 的共轭复数,则复数z 的模为 ▲ .4.执行如图所示的伪代码,若输出y 的值为1,则输入x 的值为 ▲ .5.如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为 ▲ .7 7 9 0 8 94 8 10 3 5 甲 乙 (第5题图)(第4题图)6.在同一直角坐标系中,函数y =sin(x +π3) (x ∈[0,2π])的图象和直线y =12 的交点的个数是 ▲ .7.在平面直角坐标系xOy 中,双曲线x 22m 2-y 23m =1的焦距为6,则所有满足条件的实数m构成的集合是 ▲ .8.已知函数f (x )是定义在R 上且周期为4的偶函数.当x ∈[2,4]时,f (x )=|log 4(x -32)|,则f (12)的值为 ▲ .9.若等比数列{a n }的各项均为正数,且a 3-a 1=2,则a 5的最小值为 ▲ . 10.如图,在直三棱柱ABC -A 1B 1C 1中,AB =1,BC =2,BB 1=3,∠ABC =90°,点D 为侧棱BB 1上的动点.当AD +DC 1最小时,三棱锥D -ABC 1的体积为 ▲ . 11.(2017南京三模)若函数f (x )=e x (-x 2+2x +a )在区间[a ,a +1]上单调递增,则实数a 的最大值为 ▲ .12.(2017南京三模)在凸四边形ABCD 中, BD =2,且AC →·BD →=0,(AB →+→DC )•(→BC +→AD )=5,则四边形ABCD 的面积为 ▲ .13.(2017南京三模) 在平面直角坐标系xOy 中,圆O :x 2+y 2=1,圆M :(x +a +3)2+(y -2a )2=1(a 为实数).若圆O 与圆M 上分别存在点P ,Q , 使得∠OQP =30 ,则a 的取值范围为 ▲ .14.(2017南京三模)已知a ,b ,c 为正实数,且a +2b ≤8c ,2a +3b ≤2c ,则3a +8b c 的取值范围为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.15.(2017南京三模)(本小题满分14分)如图,在三棱锥A -BCD 中,E ,F 分别为棱BC ,CD 上的点, 且BD ∥平面AEF .(1)求证:EF ∥平面ABD ;(2)若BD ⊥CD ,AE ⊥平面BCD ,求证:平面AEF ⊥平面ACD .ACB A 1B 1C 1D(第10题图) A BCFED(第15题图)16.(2017南京三模)(本小题满分14分)已知向量a =(2cos α,sin 2α),b =(2sin α,t ),α∈(0,π2). (1)若a -b =(25,0),求t 的值;(2)若t =1,且a • b =1,求tan(2α+π4)的值.17.(2017南京三模)(本小题满分14分)在一水域上建一个演艺广场.演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC ,及矩形表演台BCDE 四个部分构成(如图).看台Ⅰ,看台Ⅱ是分别以AB ,AC 为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍;矩形表演台BCDE 中,CD =10米;三角形水域ABC 的面积为4003平方米.设∠BAC =θ. (1)求BC 的长(用含θ的式子表示);(2)若表演台每平方米的造价为0.3万元,求表演台的最低造价.(第17题图)18.(2017南京三模)(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆x 2a 2+y 2b 2=1(a >b >0)的右顶点和上顶点分别为A ,B ,M 为线段AB 的中点,且OM →·AB →=-32b 2.(1)求椭圆的离心率;(2)已知a =2,四边形ABCD 内接于椭圆,AB ∥DC .记直线AD ,BC 的斜率分别为k 1,k 2,求证:k 1·k 2为定值.(第18题图)19.(2017南京三模)(本小题满分16分)已知常数p >0,数列{a n }满足a n +1=|p -a n |+2 a n +p ,n ∈N *.(1)若a 1=-1,p =1,①求a 4的值;②求数列{a n }的前n 项和S n .(2)若数列{a n }中存在三项a r ,a s ,a t (r ,s ,t ∈N *,r <s <t )依次成等差数列,求a 1p 的取值范围.20.(2017南京三模)(本小题满分16分)已知λ∈R,函数f(x)=e x-e x-λ(x ln x-x+1)的导函数为g(x).(1)求曲线y=f (x)在x=1处的切线方程;(2)若函数g (x)存在极值,求λ的取值范围;(3)若x≥1时,f (x)≥0恒成立,求λ的最大值.南京市2017届高三第三次模拟考试数学参考答案及评分标准一、填空题(本大题共14小题,每小题5分,计70分.)1.{2} 2.383. 5 4.-1 5.6.8 6.27.{32} 8.12 9.8 10.13 11.-1+52 12.313.[-65,0] 14.[27,30]二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤)15.(本小题满分14分)证明:(1)因为BD ∥平面AEF ,BD ⊂平面BCD ,平面AEF ∩平面BCD =EF , 所以 BD ∥EF . …………………… 3分因为BD ⊂平面ABD ,EF ⊄平面ABD ,所以 EF ∥平面ABD . …………………… 6分 (2)因为AE ⊥平面BCD ,CD ⊂平面BCD ,所以 AE ⊥CD . …………………… 8分因为 BD ⊥CD ,BD ∥EF ,所以 CD ⊥EF , …………………… 10分 又 AE ∩EF =E ,AE ⊂平面AEF ,EF ⊂平面AEF ,所以 CD ⊥平面AEF . …………………… 12分又 CD ⊂平面ACD ,所以平面AEF ⊥平面ACD . …………………… 14分 16.(本小题满分14分)解:(1)因为向量a =(2cos α,sin 2α),b =(2sin α,t ),且a -b =(25,0),所以cos α-sin α=15,t =sin 2α. …………………… 2分由cos α-sin α=15 得 (cos α-sin α)2=125,即1-2sin αcos α=125,从而2sin αcos α=2425.所以(cos α+sin α)2=1+2sin αcos α=4925. 因为α∈(0,π2),所以cos α+sin α=75. (5)分所以sin α=(cos α+sin α)-(cos α-sin α)2=35,从而t =sin 2α=925. ……… 7分(2)因为t =1,且a • b =1,所以4sin αcos α+sin 2α=1,即4sin αcos α=cos 2α.因为α∈(0,π2),所以cos α≠0,从而tan α=14. …………………… 9分所以tan2α=2tan α1-tan 2α=815. …………………… 11分 从而tan(2α+π4)=tan2α+tanπ41-tan2α·tan π4=815+11-815=237. …………………… 14分17.(本小题满分14分)解:(1)因为看台Ⅰ的面积是看台Ⅱ的面积的3倍,所以AB =3AC .在△ABC 中,S △ABC =12AB •AC •sin θ=4003,所以AC 2=800sin θ . ………… 3分由余弦定理可得BC 2=AB 2+AC 2-2AB •AC •cos θ,=4AC 2-23AC 2 cos θ=(4-23cos θ) 800sin θ , 即BC =(4-23cos θ)•800sin θ=402-3cos θsin θ.所以 BC =402-3cos θsin θ,θ∈(0,π). …………………… 7分(2)设表演台的总造价为W 万元.因为CD =10m ,表演台每平方米的造价为0.3万元, 所以W =3BC =1202-3cos θsin θ,θ∈(0,π). …………………… 9分记f (θ)=2-3cos θsin θ,θ∈(0,π).则f ′(θ)=3-2cos θsin 2θ. …………………… 11分由f ′(θ)=0,解得θ=π6.当θ∈(0,π6)时,f ′(θ)<0;当θ∈(π6,π)时,f ′(θ)>0.故f (θ)在(0,π6)上单调递减,在(π6,π)上单调递增,从而当θ=π6 时,f (θ)取得最小值,最小值为f (π6)=1.所以W min =120(万元).答:表演台的最低造价为120万元. …………………… 14分 18.(本小题满分16分)解:(1)A (a ,0),B (0,b ),由M 为线段AB 的中点得M (a 2,b 2).所以OM →=(a 2,b 2),AB →=(-a ,b ).因为OM →·AB →=-32b 2,所以(a 2,b 2)·(-a ,b )=-a 22+b 22=-32b 2,整理得a 2=4b 2,即a =2b . …………………… 3分因为a 2=b 2+c 2,所以3a 2=4c 2,即3a =2c .所以椭圆的离心率e =c a =32. ……… 5分(2)方法一:由a =2得b =1,故椭圆方程为x 24+y 2=1.从而A (2,0),B (0,1),直线AB 的斜率为-12. …………………… 7分因为AB ∥DC ,故可设DC 的方程为y =-12x +m .设D (x 1,y 1),C (x 2,y 2).联立⎩⎨⎧y =-12x +m ,x 24+y 2=1,消去y ,得x 2-2mx +2m 2-2=0,所以x 1+x 2=2m ,从而x 1=2m -x 2.………… 9分 直线AD 的斜率k 1=y 1x 1-2=-12x 1+m x 1-2,直线BC 的斜率k 2=y 2-1x 2=-12x 2+m -1x 2,……………… 11分所以k 1·k 2=-12x 1+m x 1-2·-12x 2+m -1x 2=14x 1x 2-12(m -1)x 1-12mx 2+m (m -1)(x 1-2)x 2=14x 1x 2-12m (x 1+x 2)+12x 1+m (m -1)x 1x 2-2x 2=14x 1x 2-12m ·2m +12(2m -x 2)+m (m -1)x 1x 2-2x 2=14x 1x 2-12x 2x 1x 2-2x 2=14, 即k 1·k 2为定值14. ………………………16分方法二:由a =2得b =1,故椭圆方程为x 24+y 2=1.从而A (2,0),B (0,1),直线AB 的斜率为-12. …………………… 7分设C (x 0,y 0),则x 024+y 02=1.因为AB ∥CD ,故CD 的方程为y =-12(x -x 0)+y 0.联立⎩⎨⎧y =-12(x -x 0)+y 0,x 24+y 2=1,消去y ,得x 2-(x 0+2y 0)x +2x 0y 0=0,解得x =x 0(舍去)或x =2y 0.所以点D 的坐标为(2y 0,12x 0). ……………………… 13分所以k 1·k 2=12x 02y 0-2·y 0-1x 0=14,即k 1·k 2为定值14. ……………………… 16分19.(本小题满分16分)解:(1)因为p =1,所以a n +1=|1-a n |+2 a n +1.① 因为 a 1=-1,所以a 2=|1-a 1|+2 a 1+1=1,a 3=|1-a 2|+2 a 2+1=3, a 4=|1-a 3|+2 a 3+1=9. …………………………… 3分 ② 因为a 2=1,a n +1=|1-a n |+2 a n +1,所以当n ≥2时,a n ≥1,从而a n +1=|1-a n |+2 a n +1=a n -1+2 a n +1=3a n ,于是有 a n =3n -2(n ≥2) . …… 5分当n =1时,S 1=-1;当n ≥2时,S n =-1+a 2+a 3+…+a n =-1+1-3n -11-3=3n -1-32 .所以 S n =⎩⎪⎨⎪⎧1,n =1,3n -1-32,n ≥2,n ∈N *,即S n =3n -1-32,n ∈N *. ………… 8分 (2)因为a n +1-a n =|p -a n |+a n +p ≥p -a n +a n +p =2 p >0,所以a n +1>a n ,即{a n }单调递增. ………………………… 10分 (i )当a 1p≥1时,有a 1≥p ,于是a n ≥a 1≥p ,所以a n +1=|p -a n |+2 a n +p =a n -p +2 a n +p =3a n ,所以a n =3n -1a 1.若{a n }中存在三项a r ,a s ,a t (r ,s ,t ∈N *,r <s <t )依次成等差数列,则有2 a s =a r +a t , 即2×3s -1=3r -1+3t -1.(*),因为s ≤t -1,所以2×3s -1=23×3s <3t -1<3r -1+3t -1,即(*)不成立.故此时数列{a n }中不存在三项依次成等差数列. ……………………… 12分 (ii )当-1<a 1p <1时,有-p <a 1<p .此时a 2=|p -a 1|+2 a 1+p =p -a 1+2 a 1+p =a 1+2p >p ,于是当n ≥2时,a n ≥a 2>p ,从而a n +1=|p -a n |+2 a n +p =a n -p +2 a n +p =3a n . 所以a n =3n -2a 2=3n -2(a 1+2p ) (n ≥2).若{a n }中存在三项a r ,a s ,a t (r ,s ,t ∈N *,r <s <t )依次成等差数列,同(i )可知,r =1, 于是有2×3s -2(a 1+2 p )=a 1+3t -2(a 1+2p ).因为2≤s ≤t -1,所以a 1 a 1+2 p =2×3s -2-3t -2=29×3s -13×3t -1<0.因为2×3s -2-3t -2是整数,所以a 1 a 1+2 p ≤-1,于是a 1≤-a 1-2p ,即a 1≤-p ,与-p <a 1<p 相矛盾.故此时数列{a n }中不存在三项依次成等差数列. ………………… 14分(iii )当a 1p≤-1时,则有a 1≤-p <p ,a 1+p ≤0,于是a 2=| p -a 1|+2a 1+p =p -a 1+2 a 1+p =a 1+2p ,a 3=|p -a 2|+2a 2+p =|p +a 1|+2a 1+5p =-p -a 1+2a 1+5p =a 1+4p ,此时有a 1,a 2,a 3成等差数列.综上可知:a 1p≤-1. ……………………………… 16分 20.(本小题满分16分)解:(1)因为f ′(x )=e x -e -λln x ,所以曲线y =f (x )在x =1处的切线的斜率为f ′(1)=0,又切点为(1,f (1)),即(1,0),所以切线方程为y =0. ………………………… 2分(2)g (x )=e x -e -λln x ,g ′(x )=e x -λx. 当λ≤0时,g ′(x )>0恒成立,从而g (x )在(0,+∞)上单调递增,故此时g (x )无极值. ………………………… 4分当λ>0时,设h (x )=e x -λx ,则h ′(x )=e x +λx 2>0恒成立, 所以h (x )在(0,+∞)上单调递增. ………………………… 6分 ①当0<λ<e 时,h (1)=e -λ>0,h (λe)=e λe -e <0,且h (x )是(0,+∞)上的连续函数, 因此存在唯一的x 0∈(λe,1),使得h (x 0)=0. ②当λ≥e 时,h (1)=e -λ≤0,h (λ)=e λ-1>0,且h (x )是(0,+∞)上的连续函数,因此存在唯一的x 0∈[1,λ),使得h (x 0)=0.故当λ>0时,存在唯一的x 0>0,使得h (x 0)=0. …………………… 8分 且当0<x <x 0时,h (x )<0,即g ′(x )<0,当x >x 0时,h (x )>0,即g ′(x )>0, 所以g (x )在(0,x 0)上单调递减,在(x 0,+∞)上单调递增,因此g (x )在x =x 0处有极小值.所以当函数g (x )存在极值时,λ的取值范围是(0,+∞). …………………… 10分(3)g (x )=f ′(x )=e x -e -λln x ,g ′(x )=e x -λx.若g′(x)≥0恒成立,则有λ≤x e x恒成立.设φ(x)=x e x(x≥1),则φ′(x)=(x+1) e x>0恒成立,所以φ(x)单调递增,从而φ(x)≥φ(1)=e,即λ≤e.于是当λ≤e时,g (x)在[1,+∞)上单调递增,此时g (x)≥g (1)=0,即f′(x)≥0,从而f (x)在[1,+∞)上单调递增.所以f (x)≥f (1)=0恒成立.……………………………13分当λ>e时,由(2)知,存在x0∈(1,λ),使得g (x)在(0,x0)上单调递减,即f′(x)在(0,x0)上单调递减.所以当1<x<x0时,f′(x)<f′(1)=0,于是f (x)在[1,x0)上单调递减,所以f (x0)<f (1)=0.这与x≥1时,f (x)≥0恒成立矛盾.因此λ≤e,即λ的最大值为e.……………………………16分。
