材料力学第2版 课后习题答案 第6章 弯曲应力
《材料力学 第2版》_顾晓勤第06章第4节 弯曲时的正应力
纯弯曲的概念
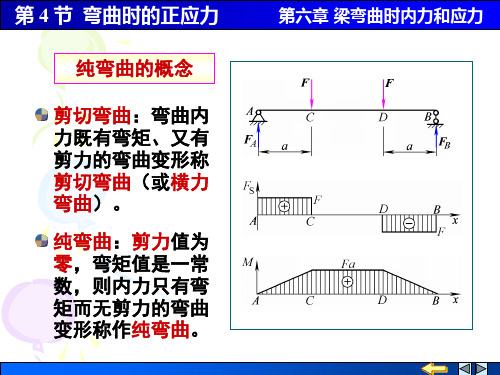
剪切弯曲:弯曲内 力既有弯矩、又有 剪力的弯曲变形称 剪切弯曲(或横力 弯曲)。
纯弯曲:剪力值为 零,弯矩值是一常 数,则内力只有弯 矩而无剪力的弯曲 变形称作纯弯曲。
第六章 梁弯曲时内力和应力
第 4 节 弯曲时的正应力
第六章 梁弯曲时内力和应力
一、实验现象及假设
梁表面 mm 、nn 等一组横向直线变形后仍为直 线,并与已变成弧线的 ab 、cd 等一组横向直线 正交,只是相对地转了一个角度。
纵向线变成圆弧线,位于中间位置的纵向线长度 不变,上部的纵向线缩短,下部的纵向线伸长。
变形后横截面的高度不变,而宽度在纵向线伸长 区减小,在纵向线缩短区增大,如图所示 b)。
第 4 节 弯曲时的正应力
第六章 梁弯曲时内力和应力
假设
平面假设:梁变形后横截面依然保持平面,且与梁 变形后的轴线垂直,横截面绕自身某轴作了转动。
纵向纤维单向受力假设:梁内各纵向纤维只产生轴 向拉伸或压缩变形。
中性层:梁在弯曲变形 时,一部分纤维伸长, 一部分纤维缩短,必然 有一部分纤维既不伸长 也不缩短的层。
中性轴:中性层与横截面的交线。
第 4 节 弯曲时的正应力
二、变形几何关系
bb oo
oo
(
y) d d
d
y
三、物理关系
根据纵向纤维假设,各
纵向“纤维”处于单向受 力状态。当应力不超过材 料的比例极限时,应用胡 克定律可得横截面上距中 性轴为 y 处的正应力
第六章 梁弯曲时内力和应力
E
E
第六章 梁弯曲时内力和应力
截面所有微面积上的力对 z 轴的合力矩即为作用在该截 面上的弯矩:
材料力学课后答案

由平衡方程,解得:
FBy 5KN; M B 13KN m
微分法画弯矩图
( M B 13KN m; M C M C 3KN m; M D 0)
2.根据强度要求确定 b
max WZ 2 bh 2 3 WZ b 6 3 M
弯矩图
M
(+)
x
3.绘制挠曲轴略图并计算wmax, A , B 令 dw 0 得 x l (0 x l ) 2 dx 所以 wmax w x l
2
挠曲轴略图
w
5ql 4 384 EI
x0
(-)
B
ql 3 24 EI
x
由式(3)知 A
max
M max ymax 176MPa IZ
max
M WZ
K
M max yK 132MPa IZ
3
5-5.图示简支梁,由 NO18 工字钢制成,在集度为q的均匀载荷作用下测得横截 4 面C底边的纵向正应变 =3.0 10 ,试计算梁内的最大弯曲正应力,已知刚的弹 FAy FBy 性模量E=200GPa,a=1m。
M yA Wy 6 M yA M zA 6M zA Wz 2b b 2 b (2b) 2
由 max 解得 b 35.6mm 故
h 2b 71.2mm
14
2.截面为圆形,确定d 由分析图及叠加原理可知: 在1,3区边缘某点分别有最大拉应力,最大压应力 其值均为:
I Z I Z 1 2 I Z 2 1.02 104 m4
2.画弯矩图 由平衡方程得 微分法画弯矩图
FCy 10KN; M C 10KN m
材料力学第六章 弯曲变形

4
2
C
B
)
=
A
( A)q C
l q
( B )q
(b)
B
( wC )q
l
θ B ( θ B )q ( θ B ) M e
+
Me
(c)
Mel ql 24 EI 6 EI
3
A
B
( B ) M e
( A ) MC ( wC ) M
e
e
l
例题3
AB梁的EI为已知,求梁中间C截面挠度.
F1l 2 F2 la 0.4 400 200 B ( ) 16 EI 3 EI 210 1880 16 3 +0.423 10-4 (rad)
F1l a F2a F2a l wC 5.19 106 m 16 EI 3 EI 3 EI wmax w (3)校核刚度: l l
x A
dx
F
x
C' dω
B
d tg dx
二、挠曲线的微分方程
1.纯弯曲时曲率与弯矩的关系
M EI
1
横力弯曲时, M 和 都是x的函数.略去剪力对梁的位移的影 响, 则
1 M ( x) ( x) EI
2.由数学得到平面曲线的曲率
F
1 | w | 3 2 2 ( x) (1 w )
q
A x B
w w F wq
+
w wF wq
例1 已知:EI, F,q .求C点挠度 F q
A
C a a
B
Fa 3 ( wC )F 6 EI
《材料力学》第6章 简单超静定问题 习题解
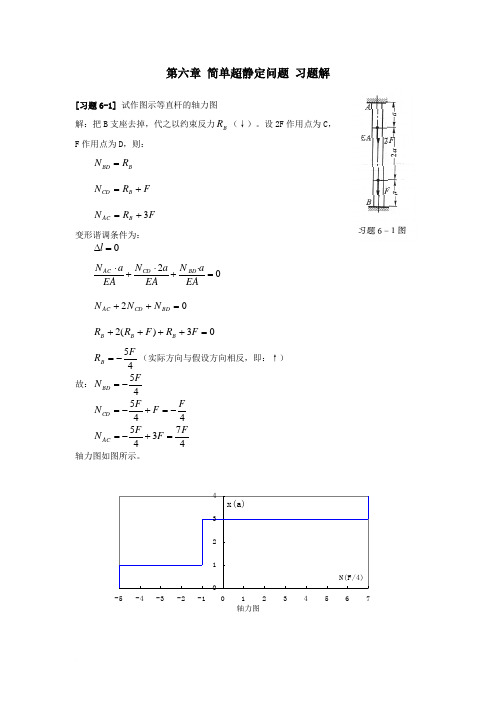
第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解:把B 支座去掉,代之以约束反力B R (↓)。
设2F 作用点为C , F 作用点为D ,则:B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为:0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=(实际方向与假设方向相反,即:↑) 故:45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=,1,2,3各杆由同一种材料制成,其横截面面积分别为21100mm A =,22150mm A =,23200mm A =。
试求各杆的轴力。
解:以节点A 为研究对象,其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件:设A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b )可知:00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31,则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得:kN N 45.81=;kN N 68.22=;kN N 54.111=(方向如图所示,为压力,故应写作:kN N 54.111-=)。
材料力学第6章弯曲应力

图6.5
页 退出
材料力学
出版社 理工分社
例6.1如图6.6所示,矩形截面悬臂梁受集中力和集中力偶作用。试求Ⅰ—Ⅰ 截面和固定端Ⅱ—Ⅱ截面上A,B,C,D 4点处的正应力。
图6.6
页 退出
材料力学
出版社 理工分社
解矩形截面对中性轴的惯性矩为 对于Ⅰ—Ⅰ截面,弯矩MⅠ=20 kN·m,根据式(6.2),各点正应力分别为
页 退出
材料力学
出版社 理工分社
(1)变形几何关系 弯曲变形前和变形后的梁段分别表示于图6.4(a)和(b)。以梁横截面的对称 轴为y轴且向下为正(见图6.4(c))。以中性轴为z轴,但中性轴的位置尚待确 定。在中性轴尚未确定之前,x轴只能暂时认为是通过原点的横截面的法 线。根据弯曲平面假设,变形前相距为dx的两个横截面,变形后各自绕中性 轴相对旋转了一个角度dθ ,且仍然保持为平面。这就使得距中性层为y的纵 向纤维bb的长度变为
式中积分
是横截面对y轴和z轴的惯性积。由于y轴是横截面的对
称轴,必然有Iyz=0(见附录)。所以式(g)是自然满足的。 将式(b)代入式(e),得
式中积分∫Ay2dA=Iz是横截面对z轴(中性轴)的惯性矩。于是式(h)改写为 式中 ——梁轴线变形后的曲率。
页 退出
材料力学
出版社 理工分社
式(6.1)表明,EIz越大,则曲率 越小,故EIz称为梁的抗弯刚度。从式 (6.1)和式(b)中消去 ,得
而对于变截面梁,虽然是等截面梁但中性轴不是横截面对称轴的梁,在计算 最大弯曲正应力时不能只注意弯矩数值最大的截面,应综合考虑My/Iz的值 (参看例6.5和例6.8)。
页 退出
材料力学
出版社 理工分社
引用记号
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
材料力学第6章弯曲应力习题答案

- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯曲应力6-1求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力。
题6-1图解:(a )m KN M m m ⋅=−5.2mKN M ⋅=75.3max 48844108.49064101064m d J x −−×=××==ππ(压)MPa A 37.20108.490104105.2823=××××=−−σMPa 2.38108.4901051075.3823max=××××=−−σ(b )m KN M m m ⋅=−60mKN M ⋅=5.67max 488331058321210181212m bh J x −−×=××==(压)MPa A 73.611058321061060823=××××=−−σMPa 2.104105832109105.67823max=××××=−−σ(c )m KN M m m ⋅=−1mKN M ⋅=1max 48106.25m J x −×=36108.7m W x −×=cmy A 99.053.052.1=−=(压)MPa A 67.38106.251099.0101823=××××=−−σMPa 2.128106.2510183max=××=−σ6-2图示为直径D =6cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ−=D W x⎟⎠⎞⎜⎝⎛−×××=−463)64(110326π361002.17m −×=3463321021.213210632m D W x −−×=××==ππMPa 88.521002.17109.0631=××=−σMPa 26.551021.2110172.1631=××=−σMPa26.55max =σ6-3T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。
解:A 截面:(拉)Mpa 95.371065.9101017010402831max =××××=−−σ(压)Mpa 37.501035.15101017010402831min −=××××−=−−σE 截面(拉)Mpa 19.301035.15101017010202832max =××××=−−σ(压)Mpa 98.181065.9101017010202832min −=××××−=−−σ6-4一根直径为d 的钢丝绕于直径为D 的圆轴上。
(1)求钢丝由于弯曲而产生的最大弯曲正应力(设钢丝处于弹性状态)(2)若d =lmm ,材料的屈服极限=700MPa ,弹性模量E =210GPa ,求不使钢丝产生s σ残余变形的轴径D 。
解:EJM =ρ1Dd E EJ M 324πρ==D d E d M W M ⋅===3max 32πσcm m d E D s 303.01070010110210639==××××=⋅≥−σ6-5矩形悬臂梁如图示.已知l =4m ,,q =10kN/m ,许用应力[σ]=10Mpa 。
32=h b 试确定此梁横截面尺寸。
解:m KN ql M ⋅=××==80410212122max963266322h h h h W =×==910101080263h M W W M =××==⇒=σσcmm h 6.41416.0==cmb 7.27=6-620a 工字钢梁的支承和受力情况如图所示。
若[σ]=160MPa ,试求许用载荷P 。
解:3237cm W =32m KN P M ⋅=32max (M 图)[][]P WM 32102371016066=×××=⋅=−σP 32[]KN P 880.5623716023=××=6-7压板的尺寸和载荷情况如图所示。
材料为45钢,=380MPa ,取安全系数s σ。
试校核压板强度。
5.1=n解:2331568)121230122030(101mmW =×−××=mN M ⋅=×××=−3601020101833[]σσ<=×==−MPa W M6.22910156836096-8由两个槽钢组成的梁受力如图示。
已知材料的许用应力[σ]=150MPa ,试选择槽钢号码。
解:mKN M ⋅=60max []33363max400104.010*******cm m MW x =×=××==−σ查表:(22a ,)332006.217cm cm W x >=(M 图)6-9割刀在切割工件时,受到P =1kN 的切销力的作用。
割刀尺寸如图所示。
试求割刀内最大弯曲应力。
解:mN p M ⋅=××=−Ι81083mN p M ⋅=××=−∏30103033242.706135.2mm W =×=Ι321506154mm W =×=∏()MPa W M 114104.7089max =×==−ΙΙΙσ()MPa W M 20010150309max =×==−∏∏∏σ6-10图示圆木,直径为D ,需要从中切取一矩形截面梁。
试问(1)如要使所切矩形截面的抗弯强度最高,h 、b 分别为何值?(2)如要使所切矩形截面的抗弯刚度最高,h 、b 又分别为何值?解:6)(6222b D b bh W −==0=dbdW ∴06322=−b D ∴322D b =2222323D D D h =−=从强度讲:∴Db 57735.0=∴Dh 8165.0=12)(123222b D b bh J −==0=dbdJ 0)2()(23)(21222322=−×−××+−b b D b b D从刚度讲∴Db 50.0=Dh 866.0=6-11T 字形截面的铸铁梁受纯弯曲如图示,欲使其最大压应力为最大拉应力的3倍,巳知h =12cm ,t =3cm ,试确定其翼板宽度b 之值。
解:3max max =下上拉压y y =σσ下上=y y 312=h y y =+下上cm y 3412==下05.4)39()233)(3(=××−−×=b S cm b 275.135.439=×××=6-12图示简支梁,由No.18工字钢制成,在外载荷作用下,测得横截面A 处梁底面的纵向正应变,试计算梁的最大弯曲正应力σmax 。
已知钢的弹性模量E =200GPa,4100.3−×=εa =1m。
解:MPaE A 60100.31020049=×××==−εσ28/34/3max max ===A A M M σσMPaA 1206022max =×==σσ243qa 283qa 241qa (M 图)6-13试计算图示矩形截面简支梁的1-1面上a 点和b 点的正应力和剪应力。
解:1-1截面KNQ 6364.3=mKN M ⋅=6364.3433375.210912155.712cm bh J =×==283105.310375.2109106364.3−−××××==y J M a σMPa03.6=82310375.2109105.7106364.3−−××××=b σMPa93.12=2863105.710375.2109105.5)5.74(106364.3−−−××××××××==Jb QS a τMPa379.0=6-14计算在均布载荷q =10kN /m 作用下,圆截面简支梁的最大正应力和最大剪应力,并指出它们发生在何处。
解:232max 110108181×××==ql M mN ⋅×=31025.11101021213max ×××==ql Q N3105×=633max 105321025.1−×××==πσWM 在跨中点上、下边缘MPa86.101=34105410534423max××××=×=−πτA Q 在梁端,中性轴上MPa46.25=6-15试计算6-12题工字钢简支梁在图示载荷下梁内的最大剪应力。
解:MPaWqa 60832=qa 413185cmW =KN q 6.29123810185106066=×××××=−43(Q图)KN qa Q2.2216.294343max=××==MPa Jt QS 12.22105.6104.15102.22323max=××××==−−τ6-16矩形截面木梁所受载荷如图示,材料的许用应力[σ]=10Mpa 。
试选择该梁的截面尺寸,设1:2:=b h KN19(Q 图)(M 图)解:KN R A 19=KN R B 29=126132h bhW ==[]σσ≤×==12101433maxhW M cmm h 6.25256.01010121014363==×××=cm b 8.12=[]ττ<=××××==−MPa A Q 961.0106.258.1210215.15.143max6-17试为图示外伸梁选择一工字形截面,材料的许用应力[σ]=160MPa ,[τ]=80Mpa 。
