七年级数学第十四周周周清试卷
七年级下第14周数学测试卷(附答案)

121 2021学年第二学期第14周教研联盟测试试卷七年级数学科说明:l .本卷共4页,满分为120分,考试用时为90分钟.2.解答过程写在答题卡上,监考教师只收答题卡.3. 非选择题必须用黑色字迹的钢笔或签字笔作答;画图时用2B 铅笔并描清晰.一、选择题(本大题共10小题,每小题3分,共30分)1.已知三角形的两边长分别为1和4,则第三边长可能是( ) A .3B .4C .5D .62.在人体血液中存在着大量的血红细胞,一个血红细胞的直径大约是0.00077厘米,则数0.00077用科学记数法可以表示为( ) A .7.7×10﹣4B .7.7×10﹣5C .0.77×10﹣5D .7.7×1043.下列图形中,∠1与∠2是对顶角的有( )A .1个B .2个C .3个D .4个 4.下列计算错误的是( )A .(a 2)5=a 10B .m 7•m =m 8C .(3cd )3=9c 3d 3D .3a 2﹣4a 2=﹣a 2 5.如图,直线b ,c 被直线a 所截,则∠1与∠2是( )A .对顶角B .同位角C .内错角D .同旁内角 6.下列说法不正确的是( )A .如果两个图形全等,那么它们的形状和大小一定相同B .面积相等的两个图形是全等图形C .图形全等,只与形状、大小有关,而与它们的位置无关D .全等三角形的对应边相等,对应角相等7.下列多项式的乘法中,能用平方差公式计算的是( )A .))((a b b a ++B .))((n m n m -+-C .)21)(21(x y y x +- D .))((22y x y x +- 8.如图,直线l 1∥l 2,点A ,C ,D 分别是l 1,l 2上的点,且CA ⊥AD 于点A ,若∠ACD =30°,则∠1度数为( )A .30°B .50°C .60°D .70°题5图9.小亮在放学回家的路上,看到同学小明在前方,便加快速度追赶小明,在距离学校60米处追上了小明,如图反映了这一过程,其中s (单位:米)表示与学校的距离,t (单位:秒)表示时间.根据相关信息,以下说法错误的是( ) A .开始时小明与小亮之间的距离是30米B .15秒时小亮追上了小明C .小亮走了60米追上小明D .小亮追上小明时,小明走了60米10.如图,在△ABC 中,∠BAC =90°,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,下面说法正确的是( )①△ABE 的面积=△BCE 的面积;②∠AFG =∠AGF ;③∠FAG =2∠ACF ; ④BH =CH . A .①②③④ B .①②③ C .②④D .①③二、填空题(本大题共7小题,每小题4分,共28分) 11.∠α 的余角是40°,则∠α= 度.12.若2=ma ,则ma 3的值为 .13.已知422+-mx x 是关于x 的完全平方式,则m 的值为 .14.如图,已知BC AD //,BD 平分∠ABC ,∠A =112°,且BD ⊥CD ,则∠ADC = .15.如图,在△ABC 中,如果过点B 作PB ⊥BC 交边AC 于点P ,过点C 作CQ ⊥AB 交AB 的延长线于点Q ,那么图中线段 是△ABC 的一条高.16.若某地打长途电话3分钟之内收费1.8元,每增加1分钟加收0.5元,当通话时间为t 分钟时(t ≥3且t 为整数),电话费y (元)与通话时间t (分)之间的关系式为 .题10图题14图题15图17.如图,在△ABC 中,点D ,E ,F 分别在三边上,E 是AC 的中点,AD ,BE ,CF 交于一点G ,BC =3DC ,S △GEC =3,S △GBD =8,则△ABC 的面积是 . 三、解答题(一)(本大题共3小题,每小题6分,共18分) 18.计算下列各式:(1)220210)31()1(8)2(-+-----π(2)2842232)3(m m m m m ÷-•+.19.先化简[]x y x x y x y x y x ÷---+-+)3(2)()2)(2(2,再求值,其中21,2-==y x .20.逻辑填空:已知:如图,AB ∥CD ,BC 平分∠ABD ,∠1=52°,求∠2的度数. 解:∵AB ∥CD (已知),∴∠1=∠ABC =52°( ). ∠ABD +∠CDB =180°( ). ∵BC 平分∠ABD ,(已知),∴∠ =2∠ABC =104°( ). ∴∠CDB =180°﹣∠ =76°(补角的定义). ∴∠2=∠CDB =76°( ).四、解答题(二)(本大题共3小题,每小题8分,共24分) 21.如图,利用尺规,在△ABC 的边AC 上方作∠CAE =∠ACB , 在射线AE 上截取AD =BC ,连接CD ,并证明:CD ∥AB (尺规作图要求保留作图痕迹,不写作法)22.新冠病毒防疫期间,草莓摊主小钱为避免交叉感染的风险,建议顾客选择微信支付,尽量不使用现金,早上开始营业前,他查看了自己的微信零钱;销售完20kg 后,他又一次查看了微信零钱,由于草莓所剩不多,他想早点卖完回家,于是每千克降价10元销售,很快销售一空,小钱弟弟根据小钱的微信零钱(元)与销售草莓数量(kg )之间的关系绘制了下列图象,请你根据以上信息回答下列问题: (1)图象中A 点表示的意义是什么? (2)降价前草莓每千克售价多少元?(3)小钱卖完所有草莓微信零钱应有多少元?题17图题20图 题21图 1223. 在四边形ABCD 中,E 为BC 边中点.已知:如图,若AE 平分∠BAD ,∠AED =90°,点F 为AD 上一点,AF =AB .求证:(1)△ABE ≌△AFE ;(2)AD =AB +CD .五、解答题(三)(本大题共2小题,每小题10分,共20分)24.你会求)1)(1(2201920202021+++⋅⋅⋅+++-a a a a a a 的值吗? 这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律: (a ﹣1)(a +1)=a 2﹣1 (a ﹣1)(a 2+a +1)=a 3﹣1 (a ﹣1)(a 3+a 2+a +1)=a 4﹣1(1)由上面的规律我们可以大胆猜想,得到)1)(1(2201820192020+++⋅⋅⋅+++-a a a a a a = . 利用上面的结论求 (2)求 1222222201820192020+++⋅⋅⋅+++ 的值.(3)求 455552201820192020++⋅⋅⋅+++ 的值.25.在△ABC 中,AB =AC ,点D 是射线CB 上的一动点(不与点B 、C 重合),以AD 为一边在AD 的右侧作△ADE ,使AD =AE ,∠DAE =∠BAC ,连接CE .(1)如图1,当点D 在线段CB 上,且∠BAC =90°时,那么∠DCE = 度; (2)设∠BAC =α,∠DCE =β.①如图2,当点D 在线段CB 上,∠BAC ≠90°时,请你探究α与β之间的数量关系,并证明你的结论;②如图3,当点D 在线段CB 的延长线上,∠BAC ≠90°时,请将图3补充完整,写出此时α与β之间的数量关系并证明.题23图图1图2图32020学年第二学期第14周教研联盟测试七年级数学科参考答案及评分标准一、选择题(每题3分,共30分) 1 2 3 4 5 6 7 8 9 10 B A A C B BCCDB二、填空题:(每题4分,共28分)11. 50 12. 8 13. 2±14. 124°15. CQ 16. t y 5.03.0+= 17. 30三、解答题(一)(本大题3小题,每小题6分,共18分) 18.计算:(1)解:原式=1﹣8﹣(﹣1)+9=﹣7+1+9=3 ---------------- 3分(2)解:原式=9m 6+m 6﹣2m 6=8m 6.---------------- 3分19.解:原式=[]x xy x y xy x y x ÷+-+-+-622422222=(3x 2+4xy )÷x=3x +4y ,---------------- 4分当21,2-==y x 时,原式=3×2+4×21=6﹣2=4.----------------6分20.解:∵AB ∥CD (已知),∴∠1=∠ABC =52°( 两直线平行,同位角相等 ). ∠ABD +∠ CDB =180°( 两直线平行,同旁内角互补 ). ∵BC 平分∠ABD ,(已知),∴∠ ABD =2∠ABC = 104 °( 角平分线的定义 ). ∴∠CDB =180°﹣∠ ABD = 76 °(补角的定义).∴∠2=∠CDB = 76 °( 对顶角相等 ). --------------每空1分,共6分四、解答题(二)(本大题共3小题,每小题8分,共24分) 21解:图象如图所示,----------------作图3分,结论1分,共4分 ∵∠EAC =∠ACB ,∴AD ∥CB , ----------------5分∵AD =BC ,∠DAC =∠ACB ,AC =CA , ∴△ACD ≌△CAB (SAS ),----------------6分 ∴∠ACD =∠CAB ,----------------7分 ∴AB ∥CD .----------------8分22.解:(1)由图象可知,小钱开始营业前微信零钱有50元;-------------2分 (2)由图象可知,销售草莓20kg 后,小钱的微信零钱为650元, ∴销售草莓20kg ,销售收入为650﹣50=600元,∴降价前草莓每千克售价为:600÷20=30(元);------------5分 (3)降价后草莓每千克售价为:30﹣10=20元,∴小钱卖完所有草莓微信零钱为:650+5×20=750(元), 答:小钱卖完所有草莓微信零钱应该有750元. -------------8分23.解(1)证明:∵AE 平分∠BAD , ∴∠BAE =∠F AE , 在△ABE 和△AFE 中,⎪⎩⎪⎨⎧=∠=∠=AE AE FAE BAE AF AB , ∴△ABE ≌△AFE (SAS ); -------------3分 (2)证明:由(1)知,△ABE ≌△AFE , ∴EB =EF ,∠AEB =∠AEF , ∵∠BEC =180°,∠AED =90°,∴∠AEB +∠DEC =90°,∠AEF +∠DEF =90°, ∴∠DEC =∠DEF , ∵点E 为BC 的中点,∴EB =EC , ∴EF =EC ,在△ECD 和△EFD 中,⎪⎩⎪⎨⎧=∠=∠=ED ED DEF DEC EF EC , ∴△ECD ≌△EFD (SAS ), ∴DC =DF ,∵AD =AF +DF ,AB =AF , ∴AD =AB +CD . -------------8分 (注意可以用不同方法证明)五、解答题(三)(本大题共2小题,每小题10分,共20分) 24.解:(1) a 2021﹣1 ; -------------2分 (2)1222222201820192020+++⋅⋅⋅+++ =)122222()12(2201820192020+++⋅⋅⋅+++⨯-) =20212; -------------5分(3)∵1555552201820192020+++⋅⋅⋅+++=)155555()15(412201820192020+++⋅⋅⋅+++⨯-⨯ =)15(412021-⨯ -------------7分 ∴455552201820192020++⋅⋅⋅+++ =21555552201820192020-+++⋅⋅⋅+++=2)15(412021--⨯ =4952021- -------------10分25.解:(1) 90° -------------2分(2)∵∠BAD +∠DAC =α,∠DAC +∠CAE =α, ∴∠BAD =∠CAE , 在△BAD 和△CAE 中,⎪⎩⎪⎨⎧=∠=∠=AE AD CAE BAD AC AB , ∴△BAD ≌△CAE (SAS ), ∴∠ACE =∠B ,∵∠B +∠ACB =180°﹣α,∴∠DCE =∠ACE +∠ACB =180°﹣α=β, ∴α+β=180°; -------------6分 (3)作出图形,∵∠BAD +∠BAE =α,∠BAE +∠CAE =α, ∴∠BAD =∠CAE , 在△BAD 和△CAE 中,⎪⎩⎪⎨⎧=∠=∠=AE AD CAE BAD AC AB , ∴△BAD ≌△CAE (SAS ), ∴∠AEC =∠ADB ,∵∠ADE +∠AED +α=180°,∠CDE +∠CED +β=180°, ∠CED =∠AEC +∠AED , ∴α=β. -------------10分。
初一数学周周清试卷

初一数学周周清试卷一、选择题(每题3分,共15分)1.下列数中,是负数的是()⏹ A. 0 B. -3 C. 2.5 D. +71.下列哪项运算的结果是 $3a - 2a$?()⏹ A. $a$ B. $5a$ C. $0$ D. $1$1.下列哪个方程表示 $x$ 和 $y$ 之间的关系?()⏹ A. $x + 3 = y$ B. $x - y = 5$ C. $2x = 3$ D. $y = 0$1.下列哪个图形是轴对称的?()⏹ A. 三角形 B. 平行四边形 C. 梯形 D. 圆形1.下列哪个选项是方程 $2x + 3 = 11$ 的解?()⏹ A. $x = 4$ B. $x = 2$ C. $x = 5$ D. $x = 8$二、填空题(每题4分,共16分)1.如果 $x$ 的值是方程 $3x - 2 = 10$ 的解,那么 $x =$ _______。
2.用科学记数法表示 567,000 为 _______。
3.在数轴上,点 A 表示 -3,点 B 表示 5,则 A、B 两点之间的距离是 _______。
4.一个角的余角比这个角的补角的一半小 $15^\circ$,则这个角的度数是 _______。
三、计算题(每题6分,共18分)1.计算:$(-2) \times 3 + 4 \div 2$2.解方程:$x - 2(x - 3) = 5$3.化简:$(x^2 - 4x + 4) \div (x - 2)$四、应用题(每题8分,共16分)1.一辆汽车以 60 km/h 的速度行驶了 3 小时,求这辆汽车行驶的总路程。
2.某商店进了一批苹果,进价是每千克 5 元,售价是每千克 7.5 元。
如果该商店售出了 100 千克苹果,那么它赚了多少钱?五、作图题(每题10分,共10分)1.用直尺和圆规作一个角,使其等于已知角 $\angle AOB$。
七年级数学周清测试卷(第14周)
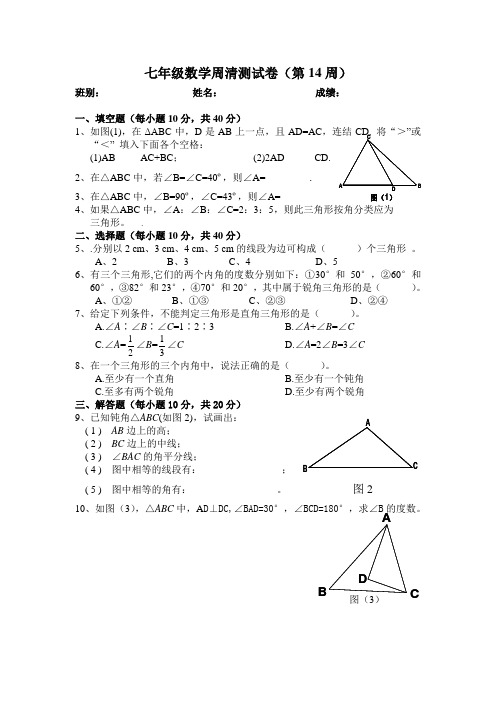
C A B AD C B图(1)AB DC 七年级数学周清测试卷(第14周)班别:_______________ 姓名:_______________ 成绩:________________一、填空题(每小题10分,共40分)1、如图(1),在ΔABC 中,D 是AB 上一点,且AD=AC ,连结CD. 将“>”或“<” 填入下面各个空格:(1)AB_____AC+BC ; (2)2AD _____ CD.2、在△ABC 中,若∠B=∠C=40º,则∠A= ____ .3、在△ABC 中,∠B=90º,∠C=43º,则∠A= _____4、如果△ABC 中,∠A :∠B :∠C=2:3:5,则此三角形按角分类应为 _____三角形。
.二、选择题(每小题10分,共40分)5、.分别以2 cm 、3 cm 、4 cm 、5 cm 的线段为边可构成( )个三角形 。
A 、2B 、3C 、4D 、56、有三个三角形,它们的两个内角的度数分别如下:①30°和50°,②60°和60°,③82°和23°,④70°和20°,其中属于锐角三角形的是( )。
A 、①②B 、①③C 、②③D 、②④7、给定下列条件,不能判定三角形是直角三角形的是( )。
A.∠A ∶∠B ∶∠C =1∶2∶3B.∠A +∠B =∠CC.∠A =21∠B =31∠C D.∠A =2∠B =3∠C 8、在一个三角形的三个内角中,说法正确的是( )。
A.至少有一个直角B.至少有一个钝角C.至多有两个锐角D.至少有两个锐角三、解答题(每小题10分,共20分)9、已知钝角△ABC (如图2),试画出: ( 1 ) AB 边上的高;( 2 ) BC 边上的中线;( 3 ) ∠BAC 的角平分线;( 4 ) 图中相等的线段有:_______________ ; ( 5 ) 图中相等的角有:________________ 。
第十四周数学试卷七年级

一、选择题(每题3分,共30分)1. 下列各数中,绝对值最小的是()A. -2B. 1C. 0D. -32. 下列方程中,解为整数的是()A. x + 3 = 5B. 2x - 1 = 7C. 3x + 2 = 9D. 4x - 3 = 103. 若a > b,则下列不等式中成立的是()A. a + 2 > b + 2B. a - 2 > b - 2C. a + 2 < b + 2D. a - 2 < b - 24. 下列函数中,图象是一条直线的是()A. y = 2x + 1B. y = x^2 + 1C. y = 3x - 4D. y = 2x^2 - 15. 一个长方体的长、宽、高分别为a、b、c,若a=2,b=3,c=4,则该长方体的体积为()A. 12B. 24C. 36D. 486. 若一个数的平方根是2,则这个数是()A. 4B. -4C. 2D. -27. 下列数中,是质数的是()A. 9B. 10C. 11D. 128. 下列图形中,对称轴最多的是()A. 等腰三角形B. 矩形C. 正方形D. 圆9. 若一个等腰三角形的底边长为8,腰长为6,则该三角形的面积为()A. 24B. 36C. 48D. 6010. 下列各式中,表示圆的周长的公式是()A. C = πdB. C = 2πrC. C = πr^2D. C = 2πr^2二、填空题(每题3分,共30分)11. 2的平方根是______,3的立方根是______。
12. 若a = 3,b = -2,则a + b的值是______。
13. 下列方程的解是x = 2,则该方程是______。
14. 若一个数的相反数是-5,则这个数是______。
15. 一个长方形的对角线长为10,长为6,则宽为______。
16. 若一个数的平方是4,则这个数是______。
17. 下列各数中,是偶数的是______。
七上第14周周统练数学试题

祝你取得好成绩,相信自己!但要仔细审题哟!第 1 页 共 2 页2017——2018学年度第一学期初一学年周统练数学试卷(满分100分;时间60分钟)一、选择题:(本题共5小题,每小题5分,共25分) 1.下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线; ③从A 地到B 地架设电线,总是尽可能沿着线段AB 架设; ④把弯曲的公路改直,就能缩短路程,其中可用公理“两点之间,线段最短”来解释的现象有( )A .①②B .①③C .②④D .③④ 2.下列语句正确的是( )A .画直线AB=10厘米B .画直线l 的垂直平分线C .画射线OB=3厘米D .延长线段AB 到点C ,使得BC=AB3.长度为12cm 的线段AB 的中点为M ,C 点将线段MB 分成MC :CB=1:2,则线段AC 的长度为( )A .2cmB .8cmC .6cmD .4cm4.同一平面内有四点,过每两点画一条直线,则直线的条数是 ( ) (A)1条 (B)4条 (C)6条 (D)1条或4条或6条5.如图3,C 是线段AB 的中点,D 是CB 上一点,下列说法中错误的是( ).A .CD=AC-BDB .CD=21BCC .CD=21AB-BD D .CD=AD-BC二.填空题:(本题共5小题,每小题5分,共25分)6.往返于甲、乙两地的火车中途要停靠三个站,则有_______种不同的票价(来回票价一样),需准备 _________种车票.7.在同一平面内的3个点,过任意2个点作一条直线,则可作直线的条数为______。
8.如图,C ,D 是线段AB 上两点,若CB=4cm ,DB=7cm ,且D 是AC 的中点,则AC 的长等于____________9.下列说法中不正确的有①一条直线上只有两个点;②射线没有端点;③如图,点A 是直线a 的中点; ④射线OA 与射线AO 是同一条射线;⑤延长线段AB 到C ,使AB=BC ;⑥延长直线CD 到E ,使DE=CD . 10.若线段AB=10㎝,在直线AB 上有一点C ,且BC=4㎝,M 是线段AC 的中点,则AM= ㎝.三、解答题:(本大题共4小题,共50分) 11、①如图(1)直线l 上有2个点,则图中有2条可用图中字母表示的射线,有1条线段 ②如图(2)直线l 上有3个点,则图中有 条可用图中字母表示的射线,有 条线段。
北师大版七年级数学上第14周周清试卷考试内容:4.1——5.2
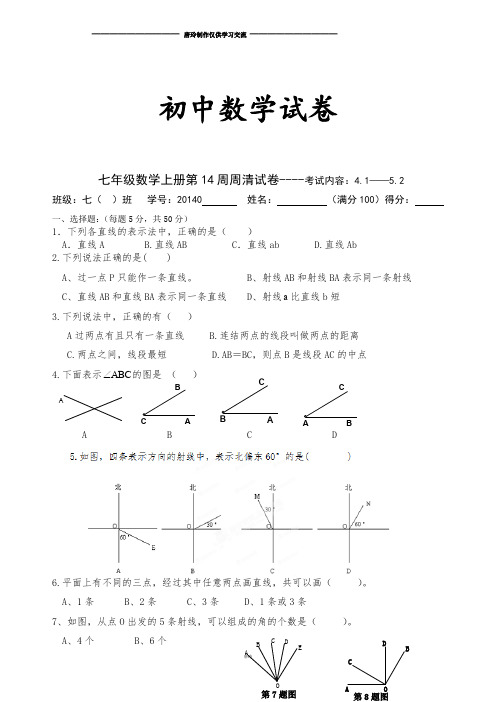
初中数学试卷七年级数学上册第14周周清试卷----考试内容:4.1——5.2班级:七( )班 学号:20140 姓名: (满分100)得分:一、选择题:(每题5分,共50分)1.下列各直线的表示法中,正确的是( )A .直线A B.直线ABC .直线ab D.直线Ab 2.下列说法正确的是( )A 、过一点P 只能作一条直线。
B 、射线AB 和射线BA 表示同一条射线C 、直线AB 和直线BA 表示同一条直线D 、射线a 比直线b 短 3.下列说法中,正确的有( )A 过两点有且只有一条直线 B.连结两点的线段叫做两点的距离 C.两点之间,线段最短 D.AB =BC ,则点B 是线段AC 的中点 4.下面表示ABC 的图是 ( )AA B C D6.平面上有不同的三点,经过其中任意两点画直线,共可以画( )。
A 、1条 B 、2条 C 、3条 D 、1条或3条7、如图,从点O 出发的5条射线,可以组成的角的个数是( )。
A 、4个 B 、6个ABC ACB BCA B C ED DBC 、8个D 、10个8.如图,∠AOB =120°,AO ⊥DO BO ⊥CO , 则∠COD 的度数是( )。
A 、30°B 、40°C 、45°D 、60°9.如果线段AB =7.2cm , 点C 在线段AB 上,且3AC =AB 。
点M 是线段AB 的中点,则MC =( )。
3.62.47.2M CBAA 、1.2cmB 、2.4cmC 、3.6cmD 、4.8cm10.点A ,B ,C 在同一条直线上,AB =4cm ,BC =5cm ,则AC =( )。
A 、1cm B 、9cm C 、1cm 或9cm D 、以上都不对二、填空题:(每题5分,共25分)11.将弯曲的河道改直,可以缩短航程,其依据是_ 。
12.时钟表面5时15分,时针与分针所夹角的度数是_ 。
七年级人教版上册第(14)周周考数学试卷

长汀五中第(14)周周考数学试卷 一、精心选一选(每题4分,共计24分)每小题给出的4个选项中只有一个符合题意,请将所选选项的字母代号写在题目后的括号内. 1、下列四个式子中,是方程的是( ) A .1 + 2 + 3 + 4 = 10 B .2x -3 C .x = 1 D .|1-0. 5|= 0. 5 2、方程12 x - 3 = 2 + 3x 的解是( ) A.-2 B.2 C.-12 D.12 3、下列方程中是一元一次方程的是( ) A.x+3=y+2 B.x+3=3-x C. 11=x D.x 2=1 4、下列等式变形错误的是( ) A.若x-1=3,则x=4; B.若12x-1=x,则x-1=2x C.若x-3=y-3,则x-y=0; D.若3x+4=2x,则3x-2x=-4 5、在解方程123123x x -+-=时,去分母正确的是( ) A .3(1)2(23)1x x --+= B .3(1)2(23)6x x --+= C .31431x x --+= D .31436x x --+= 6、小明和小刚从相距25.2千米的两地同时相向而行,小明每小时走4千米,3小时后两人相遇,设小刚的速度为x 千米/小时,列方程得( ) A 、4+3x=25.2 B 、3×4+x =25.2 C 、3(4+x) =25.2 D 、3(4-x) =25.2 二、细心填一填(每小题3分,共24分)在题中的横线上把答案直接写出来。
7、5与x 的差的13比x 的2倍大1的方程是__________. 8、写出一个系数为-3,解为x=1的一元一次方程 。
9、当x = ________时,代数式12x -与113x +-的值相等. 10、已知某商品降价20﹪后的售价为2800元,则该商品的原价为 元。
11、飞机在A 、B 两城之间飞行,顺风速度是每小时a 千米,逆风速度是每小时b 千米,则风的 速度是每小时______________千米. 12、方程267y y -=+变形为276y y -=+,这种变形叫___________,根据是____________. 13、若x = -3是方程3(x - a) = 7的解,则a = ________. 14、一次工程,甲独做m 天完成,乙独做比甲晚3天才能完成,甲、乙二人合作需要______天完成. 三、用心做一做,你一定是最好的 15.解下列方程(每题5分,共20分) (1)2x+8=x-3 (2)2(x-1)-3(x+2)=2x+1(3)341125x x-+-=(4)341.60.50.2x x-+-=16、(6分)已知2y+ m = my - m. (1)当 m = 4时,求y的值. (2)当y = 4时,求m的值.17、某校将3400元奖学金按两种奖项奖给25名学生,其中一等奖每人200元,二等奖每人120元,问获得一等奖的学生有多少人? (8分)18、某种商品的进价是215元,标价是258元,现要最低获得14﹪的利润,这种商品应最低打几折销售?(8分)19、(10分)某单位计划“五一”组织员工到某地旅游,A、B两旅行社的服务质量相同,且组织到该地旅游的价格都是每人300元。
初一数学初一数学十四周周周清试卷

第十四周数学周周清试卷班级_________姓名_________一、 细心填一填(每空2分)1、方程ax-2=6-x 的解为x=2 .则a= 把方程872=-y x 变形;用含y 的代数式表示x ;则 ___2、多边形的内角和为1080°;则这个多边形的边数为_______________。
3、已知三角形三边的长分别为4.5cm 、6.5cm 、(2a-3)cm ;(a 是整数).则a 的值为_____________.4、在△ABC 中;∠C+∠A=2∠B;∠C -∠A=80°;则△ABC 的最大内角为____°;按角分类此三角形为_____。
5、用正三角形和正方形能够铺满地面;每个顶点周围有______个正三角形和_____个正方形。
6、如右图是一块四边形钢板缺了一个角;根据图中所标出的测量结果;得所缺损的∠A的度数为_________.7、身高1.80米的人站在平面镜前2米处;它在镜子中的像高______米;人与像之间距离为_______米;如果他向前走0.2米;人与像之间距离为_________米.8、一个汽车车牌在水中的倒影为 该车的牌照号码是__________.9、适合不等式0x 312 -的自然数的和等于______已知方程组{x+y=5x y=2-,则3x -y =__ 10仔细观察下列图案;并按规律在横线上画出合适的图形.11、如图,等腰△ABC 的腰长AB=10cm ;AB 的垂直平分线交另一腰AC 于D ; △BCD 的周长为26cm ;则底边BC 的长是__________cm 12、如图;一块四边形绿化园地;四角都做有半径为R 的圆形喷水池;则这四个喷水池占去的绿化园地的面积为 .二、你能选得又快又准吗(每题3分)1、如果a >b ;那么下列结论正确的是( )A 、ac 2>bc 2 B 、3-a <4-b C 、a -3>b -2 D 、ba 11< 2、四边形ABCD 中;若∠A+∠C =180°且∠B :∠C :∠D =3:5:6;则∠A 为( ).°°. C. 60°°.3、一个多边形的边数每增加一条;这个多边形的( )4、当x=1;y =-1时ax +by=3;那么当x =-1;y=l 时;ax+ by + 3的值为( ) A .3 B .-3 C .0 D .15、如图;直线a ;b ;c 表示交叉的公路;现要建一货物中转站;要求它到三条公路的距离相等;则可供选择的站址有 ( ) A.一处 B .两处 C.三处 D .四处6、用绳子量井深;把绳子三折来量;井外余4尺;把绳子四折来量;井外余1尺;则井深和绳长分别是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学第十四周周周清试卷
一、细心填一填(每空2分)
1、方程ax-2=6-x 的解为x=2 .则
a= 把方程872=-y x 变形,用含y 的代数式表示x ,则 ___
2、多边形的内角和为1080°,则这个多边形的边数为_______________。
3、已知三角形三边的长分别为4.5cm 、6.5cm 、(2a-3)cm ,(a 是整数).则a 的值为_____________.
4、在△ABC 中,∠C+∠A=2∠B ,∠C-∠A=80°,则△ABC 的最大内角为____°,按角分类此三角形为_____。
5、用正三角形和正方形能够铺满地面,每个顶点周围有______个正三角形和_____个正方
形。
6、如右图是一块四边形钢板缺了一个角,根据图中所标出的测量结果,得所缺损的∠A
的度数为_________.
7、身高1.80米的人站在平面镜前2米处,它在镜子中的像高______米,人与像之
间距离为_______米;如果他向前走0.2米,人与像之间距离为_________米.
8、一个汽车车牌在水中的倒影为 该车的牌照号码是__________.
9、适合不等式0x 3
12 -的自然数的和等于______已知方程组{x+y=5x y=2-,则3x -y =__ 10仔细观察下列图案,并按规律在横线上画出合适的图形.
11、如图,等腰△ABC 的腰长AB=10cm ,AB 的垂直平分线交另一腰AC 于D , △BCD 的周长为26cm ,则底边BC 的长是__________cm 12、如图,一块四边形绿化园地,四角都做有半径为R 的圆形喷水池,
则这四个喷水池占去的绿化园地的面积为 .
二、你能选得又快又准吗(每题3分)
1、如果a >b ,那么下列结论正确的是( )A 、ac 2>bc 2 B 、3-a <4-b C 、a-3>b-2 D 、
b
a 11< 2、四边形ABCD 中,若∠A+∠C =180°且∠B:∠C:∠D =3:5:6,则∠A 为( ).
A.80°.
B.70°.
C. 60°.
D.50°.
3、一个多边形的边数每增加一条,这个多边形的( )
A.内角和增加360度
B.外角和增加360度
C.对角线增加一条
D.内角和增加180度
4、当x=1,y=-1时ax +by=3,那么当x=-1,y=l 时,ax+ by + 3的值为( ) A .3 B .-3 C .0
D .1
5、如图,直线a ,b ,c 表示交叉的公路,现要建一货物中转站,要求它到三条公路的距离相等,则可供选择的站址有 ( ) A.一处 B .两处 C.三处 D .四处
6、用绳子量井深,把绳子三折来量,井外余4尺,把绳子四折来量,井外余1尺,则井深和绳长分别是( )。
A .8尺,36尺 B.3尺,13尺 C.10尺,34尺 D.11尺,17尺
11题图
绿化12题图
7、用折纸的方法,可以直接剪出一个正五边形(如下图).方法是:拿一张长方形纸对折,折痕为AB ,以AB 的中点O 为顶点将平角五等份,并沿五等份的线折叠,再沿CD 剪开,使展开后的图形为正五边形,则∠OCD 等于( ) A .108° B .90°
C .72°
D .60°
三、 计算(每题4分) 1、12
223x x x -+-=- 2、3262317x y x y -=⎧⎨+=⎩ 3、⎪⎪⎩⎪⎪⎨⎧+<->--213
12,221x x x x
四、探索发现(每题5分)
1、 如图,△ABC 中,∠C=90°(1)画出斜边上的中线CD 并观察,图中有____个等腰三角形.
(2)量一量线段CD 和斜边AB 的长度,你发现了斜边上的中线与斜边的数量关系吗?____________(用式子表示);请你用一句准确的句子来叙述这个结论.___________________________ B
(3)当AC=BC 时,对于斜边上的中线CD,你有什么新的发现吗?
______________________________________________________ ______________
2小明发现:如果将4棵树栽于正方形的四个顶点上,如下图所示,恰好构 C
成一轴对称图形.你还能找到其他两种栽树的方法,也使其组成一个轴对称图形吗?
请在下面图上表示出来.如果是栽5棵,又如何呢?6棵、7棵呢?请分别在⑷、⑸、⑹上表示出来. 五、已知方程ax+12=0的解是x=3, 六、如图,沿着边长为90米的正方形,按逆时针方向,甲从
求不等式(a+2)x< -6的解集(5分) A 出发 ,每分钟走70米,乙从B 出发,每分钟走55米。
当甲第一次追上乙时在正方形的哪一条边上?(5分)
七、如右图,在ΔABC 中,∠ACB=90°,CD ⊥AB ,点E 在CB 的延长线上,
已知∠ACD=55°,求∠ABE 的度数。
(5分)
八、(6分)如图(1),有一块直角三角板XYZ 放在△ABC 上恰好三角板XYZ 的两条直角边XY ,XZ 分别经过点B ,C ,△ABC 中,∠A=30°,则∠ABC+∠ACB=________,∠XBC+∠XCB=________度.
A
D O
(2)如图(2)改变制角三角板XYZ的位置,使三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C.那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明,若不变化,请求出∠ABX+∠ACX的大小.。
