微分的概念
微分和积分

微分和積分微分和積分是高等数学中的两个重要概念,它们的相互关系在许多领域中都具有重要意义。
微分和積分不仅在数学中有重要的应用,而且在物理学、工程学、经济学、生物学等领域中也有广泛的应用。
一、微分微分是函数的一个基本操作,它是求一个函数在某一点处的导数,表示函数在该点的斜率。
微分可以帮助我们求解一些关键的问题,比如求极值、求曲率等。
微分是微积分中最基本的部分,也是微积分的基础。
1.1 导数导数是函数在某一点处的斜率。
在微积分中,导数可以通过求函数的极限来求解。
函数f(x)在点x=a处的导数可以记为f'(a),表示函数在该点处的斜率。
1.2 微分基本公式微分是通过求导数来实现的,因此,微分的基本公式就是函数导数的基本公式。
对于常见的函数,我们可以通过常见的微分公式来求它们的微分,比如:常数函数、幂函数、指数函数、对数函数、三角函数等。
1.3 微分应用微分在实际生活中有许多应用,比如对于速度、加速度、曲率等量的求解,都可以通过微分来实现。
在物理学中,微分可以帮助我们求解速度、加速度等的变化率,而在经济学中,微分可以帮助我们求解变化率与边际效应等的问题。
二、積分積分是函数运算的另一个基本操作,積分可以将函数从某一个点到另一个点之间的面积或体积求出。
積分的概念可以归于微积分学中的一个重要部分,预测与解决一些具体问题。
2.1 定积分定积分是積分的一种类型,它可以求解函数在一定区间内的面积。
根据古典微积分中的定理,我们可以通过复合函数和曲线斜率来解决面积问题。
需要注意的是,定积分可以为内点的式子整合,通常使用牛顿-莱布尼茨公式表示。
2.2 不定积分不定积分不同于定积分,不定积分一般不是某个变量的确定值,通常是某个函数的解集,这个解集中的每一个元素,都可以通过微积分的基本原理及函数导数的方法来实现。
不定积分一般表示为f(x)dx,它表示求解出一个函数f(x)及其导数f'(x)的关系。
2.3 積分应用積分也在实际有广泛的应用,比如计算材料强度、流体力学、统计学中的分布、物理学、生物学等领域都可以通过積分来实现。
微积分基本公式16个

微积分基本公式16个1. 微分:微分是数学中最重要的概念之一,它指的是在一定时间内几何形状的变化率。
可以理解为小步长地移动拟合函数,接近曲线本身。
可以表示为\frac{dy}{dx} 或f'(x) 。
2. 泰勒公式:泰勒公式是一个重要的微积分工具,它可以在某一特定点附近对任意连续函数进行展开,也就是说任意设定一个位置x0,可以根据它附近的数值向量求出函数在该位置的平均值。
可以用公式表示为:f(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)(x-x_0)^2}{2!} + \frac{f^{n}(x_0)(x-x_0)^n}{n!} + ...3. 高斯积分公式:高斯积分是指将函数抽象为一次多项式曲线,采用指数型或线性型积分方法求解积分。
它可以用公式f(x)=\sum_{i=0}^n a_i x^i 表示,其中a_i为积分下限、上限和积分点x_i处函数值相乘所得到的系数。
4. 黎曼积分:黎曼积分是一种常用的积分方法,它通过对连续函数求和,来确定函数在给定区间上的定积分。
可以用公式表示为:\int_{a}^{b}f(x)dx=\sum_{i=1}^{n}f(x_i)\Delta x_i ,其中n为梯形的节点数。
5. Stokes公式:Stokes公式是一种将多变量函数投影到多方向进行积分的方法,可以用公式表示为:\int_{\Omega}\nabla\times{\bf F} dA =\int_{\partial\Omega}{\bf F}\cdot{\bf n}dS,其中\nabla\times{\bf F} 为梯度矢量场,\partial\Omega 为边界,{\bfn}dS 为单位向量与边界面积的乘积。
6. Γ函数:Γ函数是一种重要的数学函数,通常用来表示非负整数的排列组合,也可以表示实数的阶乘,可以用公式表示为:\Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}dt7. 方阵的行列式:方阵的行列式是指一个n阶矩阵的行列式,可以用公式表示为:D= |a_{i,j}| = \begin{vmatrix} a_{1,1} & a_{1,2} & ... & a_{1,n} \\ a_{2,1} & a_{2,2} & ... & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & ... & a_{n,n} \end{vmatrix} ,其中a_{i,j} 为矩阵中的元素。
数学微分知识点总结

数学微分知识点总结微分是微积分的一个基础概念,它是研究函数的局部性质的一种重要工具。
微分的概念最早由牛顿和莱布尼兹等数学家引入,是微积分学的重要内容之一。
微分的概念不仅在数学中有着广泛的应用,还在物理、工程、经济等领域都有着重要的意义。
微分可以帮助我们理解函数的变化率、极值、凹凸性等重要性质,从而为我们研究问题提供了重要的手段。
本文将对微分的基本概念、微分法则、微分应用、微分方程等知识点进行系统总结,希望能够帮助读者对微分有一个系统、全面的认识。
一、微分基本概念1. 极限极限是微分的基本概念之一,也是微积分的核心概念。
在微分中,我们经常需要研究函数在某一点的变化情况,而极限则提供了一种严格的方式来描述函数在该点附近的性质。
在数学中,我们通常用“x趋于a时,函数f(x)的极限是L”来表示函数f(x)在点a处的极限为L。
通过对极限的研究,我们可以得到函数在某一点的斜率,从而引出了微分的概念。
2. 导数导数是微分的基本概念之一,它是用来描述函数在某一点的变化率的概念。
它在数学中有着广泛的应用,不仅可以帮助我们理解函数的变化规律,还可以用在求解最优化问题、解微分方程等领域。
在微分中,我们通常用f'(x)或dy/dx来表示函数f(x)的导数。
导数表示了函数在某一点的斜率,它是研究微分的基本工具。
3. 微分微分是微积分的一个重要概念,它是用来研究函数的局部性质的一种工具。
微分的概念最早由牛顿和莱布尼兹等数学家引入,是微积分学的一个基础概念。
在微分中,我们通常用dy来表示函数f(x)的微分。
微分可以帮助我们理解函数的局部性质,如凹凸性、极值等重要性质。
通过对微分的研究,我们可以得到函数在某一点的切线方程,从而更好地理解函数在该点的性质。
二、微分法则微分法则是微分求导的基本规则,它是研究微分的重要工具。
微分法则可以帮助我们求解各种函数的微分,从而更好地理解函数的性质。
微分法则包括常数法则、幂函数法则、指数函数法则、对数函数法则、三角函数法则、复合函数法则等,它们为我们研究微分提供了重要的工具。
微分公式和运算法则

(cos x)sin x
d(cos x)sin xdx
(tan x)sec2 x
d(tan x)sec2xdx
(cot x)csc2x
d(cot x)csc2xdx
(sec x)sec x tan x
d(sec x)sec x tan xdx
(csc x)csc x cot x
d(csc x)csc x cot xdx
§ 2.2.1 微分概念
一、微分的定义
引例: 一块正方形金属薄片受温度变化的影响, 其
边长由 变到
问此薄片面积改变了多少?
设薄片边长为 x , 面积为 A , 则
当x在 取
得增量 时, 面积的增量为
关于△x 的
时为
线性主部 高阶无穷小
故
称为函数在 的微分
1
定义1: 若函数
在点 的增量可表示为
( A 为不依赖于△x 的常数)
解: 已知球体体积为
镀铜体积为 V 在
时体积的增量
因此每只球需用铜约为 (g)
17
2.误差估计 某量的精确值为 A , 其近似值为 a , 称为a 的绝对误差 称为a 的相对误差 若 称为测量 A 的绝对误差限 称为测量 A 的相对误差限
18
误差传递公式 :
若直接测量某量得 x , 已知测量误差限为
12
§ 2.2.3 高阶微分
1、二阶微分:一阶微分的微分称为二阶微分。记作
且有
(1)
2、n 阶微分:n-1阶微分的微分称为n阶微分,记作
且有
(2)
3、高阶微分:二阶以及二阶以上的微分统称为高阶微分。
例设
(2)求
解由
得
依公式(1)得 类似地,依公式(2)得
第二章第3节-函数的微分

故 在点 可导, 且
定理 2.6 函数 在点
在点 x0 可微的充要条件是 处可导, 且 即
d y f ( x0 )x
“充分性” 已知 在点 的可导, 则
y lim f ( x0 ) x 0 x y f ( x0 ) x
Hale Waihona Puke d y 3 x x.2 0
(1)
( 2)
2 当x 很小时, y dy 3 x0 x.
定理 2.6 函数 在点
在点 x0 可微的充要条件是 处可导, 且 即
d y f ( x0 )x
证: “必要性”
已知
在点
可微 , 则
y f ( x0 x) f ( x0 ) A x o(x)
dy f ( x) 导数也叫作微商 dx
例1.
求 y x 2 在 x 1, x 0.01 时的微分。
x 1 x 0.01
解: d y
2 x x
x 1
0.02
x 0.01
例2. 求y=x3在x=2处的微分, 以及当x=0.1时在x=2 处的微分。
dx 3 x 2 dx 3x 2 x ( x dx ) 解: dy ( x )
1 x2 dx ; (16) d (arccot x) dx 2 . (15) d (arctan x) 1 x2 1 x
2.四则运算微分法则
设 u(x) , v(x) 均可微 , 则
du dv vdu udv
3. 复合函数的微分法则 均可导 , 则
(C 为常数)
(10)d (cot x) csc 2 xdx ;
函数的 微分

o x
lim x0 x
y lim x0 x
f ' x0
也就是说,如果函数y f x 在点 x0 处可微,那么函数在点 x0 处就可导, 且 A f ' x0 ;反之,如果函数 y f x 在点 x0处可导,即
lim y x0 x
f ' x0
存在,那么根据无穷小与函数极限的关系,有
高等数学
函数的微分
1.1 微分的概念
定义1.1 设函数 y f x在 点 x0 的某邻域内有定义,自变量 x 在点 x0 处
有一个改变量 Δx,如果相应的函数改变量 y f x0 x f x0
可以表示为
y Ax ox
其中,A 是不依赖于 Δx 的常数,ox 是比 Δx 高阶的无穷小 x 0时 那么称函数 y f x 在点 x0 处是可微的, Ax称为函数 y f x 在点
解 (1)先求函数的导数
y'
1
x2
1 '
2x 1 x2
2
因为 dy y' dx
所以
dy
2x 1 x2
2 dx
(2)
dy
x1
f ' 1dx
1 dx 2
(3)
dy
x1 x0.01
f ' 1
x
1 2
0.01 0.005
例1.2 求函数 y sinln的x 微分。
解法一 直接利用公式 dy y' dx ,得
dy sinlnx' dx 1 coslnxdx
x
解法二 利用微分形式不变性,得
dy dsinlnx coslnxd lnx 1 coslnxdx
微分方程知识点

微分方程知识点微分方程是数学中的一种重要工具,用于描述自然界中许多现象的变化规律。
它是关于未知函数及其导数之间的关系式。
在物理、工程、经济等领域中,微分方程广泛应用。
本文将介绍微分方程的基本概念和常见类型,帮助读者对微分方程有更深入的了解。
一、微分方程的定义微分方程是包含一个或多个未知函数及其导数的方程。
一般形式为:F(x, y, y', ..., y^(n)) = 0其中,x 是自变量,y 是未知函数,y' 是 y 对 x 的导数,y^(n) 是 y 的 n 阶导数(n 为正整数)。
二、常见的微分方程类型1. 一阶微分方程一阶微分方程是只包含一阶导数的微分方程。
常见的一阶微分方程类型包括:(1)可分离变量型dy/dx = f(x)g(y)这类微分方程可以通过变量分离的方法求解。
(2)齐次型dy/dx = f(y/x)这类微分方程可以通过令 y = ux 来化简,得到一阶线性微分方程。
(3)一阶线性微分方程dy/dx + P(x)y = Q(x)其中 P(x) 和 Q(x) 是已知函数。
该类型的一阶微分方程可以通过积分因子法求解。
2. 二阶线性微分方程二阶线性微分方程是包含二阶导数的微分方程。
一般形式为:a(d^2y/dx^2) + b(dy/dx) + cy = f(x)其中 a、b、c 是常数,f(x) 是已知函数。
这类微分方程可以通过特征方程的根的情况来分类,并利用特解和齐次解的线性叠加原理求解。
3. 高阶线性微分方程和常系数线性微分方程除了二阶线性微分方程,还存在高阶线性微分方程。
当系数为常数时,称之为常系数线性微分方程。
求解方法与二阶线性微分方程类似,但需要考虑更多的特征方程根的情况。
4. 线性微分方程组线性微分方程组是多个未知函数相互依赖的微分方程的集合。
一般形式为:dy1/dx = a11y1 + a12y2 + ... + a1ny_n + F1(x)dy2/dx = a21y1 + a22y2 + ... + a2ny_n + F2(x)...dyn/dx = an1y1 + an2y2 + ... + anny_n + Fn(x)其中,a_ij 和 F_i(x) 是已知函数。
综述微分和泰勒展开公式的关系

微分和泰勒展开公式是数学分析中两个重要的概念和工具,它们在数学推导和物理问题求解中起着至关重要的作用。
本文将综述微分和泰勒展开公式的关系,旨在深入探讨它们之间的内在通联和应用。
一、微分的基本概念1.微分的定义和性质2.微分在函数求导和近似计算中的应用3.微分的几何意义和物理意义二、泰勒展开公式的基本原理1.泰勒展开公式的定义和表达形式2.泰勒展开公式在函数逼近和级数求和中的应用3.泰勒展开公式的推导和证明方法三、微分和泰勒展开公式的关系1.微分与泰勒展开公式的通联和区别2.微分在泰勒展开公式中的角色和作用3.泰勒展开公式的导出过程中涉及微分的应用四、微分和泰勒展开公式在数学分析中的应用1.微分和泰勒展开公式在函数极值和凹凸性判定中的应用2.微分和泰勒展开公式在函数逼近和近似计算中的应用3.微分和泰勒展开公式在泛函分析和微分方程求解中的应用五、微分和泰勒展开公式在物理问题中的应用1.微分和泰勒展开公式在力学和动力学中的应用2.微分和泰勒展开公式在电磁学和热力学中的应用3.微分和泰勒展开公式在量子力学和相对论中的应用六、结论微分和泰勒展开公式作为数学分析中的重要概念和工具,不仅在理论研究中发挥着重要作用,也在物理问题求解中具有广泛的应用前景。
深入理解微分和泰勒展开公式的关系,对于加深对数学分析和物理学知识的理解和应用具有重要意义。
通过以上关于微分和泰勒展开公式的综述,我们可以更全面深入地了解它们的内在通联和应用,希望本文能对相关领域的研究者和学习者有所启发和帮助。
七、微分的基本概念微分是微积分学中的一个基本概念,它源自导数的概念。
在数学上,微分可以解释为函数的局部线性逼近,可以用来求函数的变化率、切线方程、极值点等等。
微分的定义和性质是我们理解微分和泰勒展开公式的基础。
微分的定义是指当自变量的增量趋于0时,函数增量与自变量增量之比的极限,即:\[ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}微分的一些基本性质包括线性性、乘积法则、商法则等,这些性质对于微分求导以及在泰勒展开中的应用都起着重要的作用。
微分

第二节 微分§2.1 微分的概念一、微分概念的引入在实际测量中,由于受到仪器精度的限制,往往会产生误差。
例如x 0为准确数,实际测量出是x *=x 0+Δx 为x 0的近似数,由此产生的误差为Δx 相应产生的函数值的误差Δy =f(x 0+Δx)-f(x 0),往往需要估计Δy 的值。
如果f(x 0+Δx),f(x 0)计算很复杂。
因此计算Δy 也很麻烦或者实际中只知道近似数x *与误差|Δx |≤δ,又如何估计Δy?假设f ′(x)存在,则0x lim→∆x )x (f )x x ("f 00∆-∆+=0x lim →∆x y∆∆=f ′(x 0),有 xy∆∆=f ′(x 0)+α,0x lim →∆α=0,于是Δy =f ′(x 0)Δx +αΔx ,而0x lim →∆xx∆∆∂=0(1)即 αΔx =0(Δx)(Δx →0)因此,当|Δx |很小时,Δy ≈f ′(x 0)Δx在实际中如果不知道x 0,只知道x *,由x 0,x *相差很小,则Δy ≈f ′(x *)Δx ,从而可以估计出Δy 。
从(1)式我们看到,f ′(x 0)相对Δx 是一个常数,αΔx 是Δx 的高阶无穷小,如果Δy =A Δx +0(Δx)(Δx →0),则Δy ≈A Δx ,由此得到微分的概念。
二、微分的概念定义 设y =f(x)在x 0的某领域U(x 0)内有定义,若Δy =f(x +Δx)-f(x)可表示为Δy =A Δx +o(Δx) (Δx →0)其中A 是写Δx 无关的常数,A Δx 称为Δy 的线性部。
则称y =f(x)在点x 处可微,称线性部A Δx 为y =f(x)在点x 处的微分,记为dy ,即dy =A Δx 。
三、可微与可导的关系从概念的引入,我们可以看到可导必可微,反之也是正确的。
因此有定理 函数y =f(x)在点x 可微的充要条件是函数y =f(x)在点x 处可导。
一、微分的概念

f ( x ) (Δ x )2 f ( x ) (d x )2 .
或写作 d 2 y f ( x )d x 2 , 称为 f 的二阶微分.
注 由于 Δ x 与 x 无关, 因此 x 的二阶微分 d(Δ x )
d(d x ) d 2 x 0, 它与 d x 2 (d x )2 , d( x 2 ) 2 x d x
sin x x, tan x x, ln1 x x , e x 1 x .
例5 试求 sin 33o 的近似值 ( 保留三位有效数字 ). π π π ), 取 f ( x ) sin x , x0 , 解 sin 33 sin( 6 60 6 x π , 由公式 (9) 得到 60
果已知测量值 x0 的误差限为 x , 即
| Δ x | | x x0 | x ,
则当 x 很小时, 量 y0 的绝对误差估计式为:
| Δ y | | f ( x ) f ( x0 ) | | f ( x0 )Δ x | | f ( x0 ) | x .
Δ x 的线性部分 2 xΔ x 和 Δ x 的高阶部分( Δ x )2.因
此, 当边长 x 增加一个微小量 Δ x 时, Δ S 可用 Δ x
的线性部分来近似. 由此产生的误差是一个关于
2 ( Δ x ) 的高阶无穷小量 , 即以 Δ x 为边长的小 Δx
正方形(如图).
x2
2
xΔ x
Δx
xΔ x
d (sin x ) cos x dx ;
ห้องสมุดไป่ตู้
d (a ) a ln a dx .
x
x
二、微分的运算法则
由导数与微分的关系,可方便得出微分运算法则:
函数的微分

微分与增量的关系
定理:当f ( x0 ) 0 时,微分是增量的线性 主部。
主部:设 , 均为无穷小,若 o
则称 是 的主部,有 o 结论: 若 o ,则 ~ 。
。
证: 若 f ( x 0 ) 0 ,则 Δy f ( x 0 Δx ) f ( x 0 ) 0
得
当
3 x 2 d x 3 y 2 d y 3 cos 3 x d x 6 d y 0 1 由上式得 d y x 0 d x x 0 时 y 0, 2
返回
称为a 的相对误差
若 称为测量 A 的绝对误差限 称为测量 A 的相对误差限
误差传递公式 :
若直接测量某量得 x , 按公式 已知测量误差限为 计算 y 值时的误差
x ,
d y f ( x) x
故 y 的绝对误差限约为
y f ( x) x
y
f ( x) x y f ( x)
整理并移项即得: x (dy dx ) y (dy dx ) #
思考: 若 y=e
sin x
dy ,怎样求 ? d cos x
返回
三、 微分在近似计算中的应用
y f ( x0 )x o( x)
当
x
很小时,
得近似等式:
y f ( x0 x) f ( x0 ) f ( x0 )x f ( x0 x) f ( x0 ) f ( x0 ) x
y 2 2 例 3 推证等式 arctan =ln x +y 满足 x 关系式 x dy-dx = y dy+dx .
证:
利用微分的形式不变性 对等式两边求微分 1 xdy ydx 1 1 2 (2 xdx 2 ydy ) 2 2 2 2 x y x y 1 x
函数的微分

边长由 x0 变到 x0 x , 问此薄片面积改变了多少? 设薄片边长为 x , 面积为 A , 则 A x 2 , 当 x 在 x0 取 得增量 x 时, 面积的增量为 2 x x ( x ) 0 x
关于△x 的线性 时为 主部 高阶无穷小
x 0
x0
2 A x0
所以
dy 2 1 0.01 0.02.
例 2 求函数 y x 3 在 x 2 处的微分; 解 函数 y x 3 在 x 2 处的微分为
dy ( x 3 )' x 2 dx 12dx.
基本初等函数的微分公式 (见 P60表)
完
二、 微分运算法则
设 u(x) , v(x) 均可微 , 则
即 d y f ( x0 ) x
可微的条件
定理 : 函数 在点
在点 x0 可微的充要条件是
处可导, 且 即
d y f ( x0 )x
证: “必要性” 已知 在点 可微 , 则
y f ( x0 x) f ( x0 ) A x o(x)
y o(x) lim lim ( A )A x 0 x x 0 x
3.004938
(1 x) 1 x
2. 求函数 y 解
x x 的微分 dy .
dy
1 d(x x) 2 x x
1 (dx d x ) 2 x x 1 (dx 1 dx ) 2 x 2 x x
ห้องสมุดไป่ตู้
2 x 1 1 . dx 2 x x 2 x 2 x 1 dx . 4 x x x
然而, 对于较复杂的函数 f ( x ), 差值
f ( x x ) f ( x )
微积分—微分

数 f ( x)在点 x0处可导, 且 A f ( x0 ).
证 (1) 必要性 f ( x )在点x0可微,
y A x o( x ),
y o( x ) A , x x
y o( x ) 则 lim A lim A. x 0 x x 0 x
函数 f ( x)在点 x0可微, 且 f ( x0 ) A.
令y x, dy dx ( x)x x.
dy f ( x)dx.
dy dy f ( x )dx. f ( x ). dx 即函数的微分 dy与自变量的微分 dx之商等于
该函数的导数. 导数也叫 " 微商".
(微分的实质) 微分 dy叫做函数增量 y的线性主部.
由定义知:
dy A x y A x o (x)
(1) dy是自变量的改变量 x的线性函数 ;
( 2) y dy o( x )是比x高阶无穷小 ; ( 3) 当A 0时, dy与y是等价无穷小 ;
即函数 f ( x )在点 x0可导, 且A f ( x0 ).
(2) 充分性 函数f ( x )在点x0 可导,
y lim f ( x 0 ), x 0 x
li m y A
从而 y f ( x0 ) x ( x ), f ( x0 ) x o( x ),
d (C ) 0 d (sin x ) cos xdx d (tan x ) sec2 xdx d ( x ) x 1 dx d (cos x ) sin xdx d (cot x ) csc2 xdx
第二章第五节 函数的微分

高等数学
二、微分的几何意义
当x从x0变到x0+∆x时, ∆y是曲线上点的纵坐 标的增量; dy是过点(x0, f(x0))的切 线上点的纵坐标的增量. 当|∆x|很小时, |∆y−dy|比|∆x|小得多. 因此, 在点M的邻近, 我们可以用切线段来近似代 替曲线段. 记 自变量的微分, ∆y = ∆x = dx 称∆x为 自变量的微分 记作 dx dy = f ′(x) 导数也叫作微商 则有 dy = f ′(x) dx 从而 dx
高等数学
§2.5函数的微分 函数的微分
一、微分的概念 二、微分的几何意义 三、微分的运算法则 四、微分在近似计算中的应用
高等数学
一、微分的概念 引例: 引例 一块正方形金属薄片受温度变化的影响, 其 边长由 x0 变到 x0 + ∆x , 问此薄片面积改变了多少? 设薄片边长为 x , 面积为 A , 则 A= x2 , 当 x 在 x0 取 得增量 ∆x 时, 面积的增量为 (∆x)2 x0∆x ∆x 关于△x 的 ∆x →0时为 线性主部 高阶无穷小 故 称为函数在 x0 的微分
高等数学
2、 微分的四则运算法则 、 设 u(x) , v(x) 均可微 , 则
= du ± dv = vdu + udv
3. 复合函数的微分 分别可微 , 则复合函数 的微分为
(C 为常数)
= f ′(u) ϕ′(x) dx dy = f ′(u) du
du
微分形式不变
高等数学
若y=f(u), u=j(x), 则dy=f ′(u)du. 例3 y=sin(2x+1), 求dy. 解 把2x+1看成中间变量u, 则 dy=d(sin u) =cos udu =cos(2x+1)d(2x+1) =cos(2x+1)⋅2dx =2cos(2x+1)dx. 在求复合函数的导数时, 可以不写出中间变量. 例4. y =ln(1+ex2 ) , 求 dy. 解 dy =d ln(1+ex2 ) = 1 2 d(1+ex2 ) 1+ex 1 ⋅ex2d(x2) = 1 ⋅ex2 ⋅2xdx = 2xex2 dx = . x2 x2 x2 1+e 1+e 1+e
微分的概念
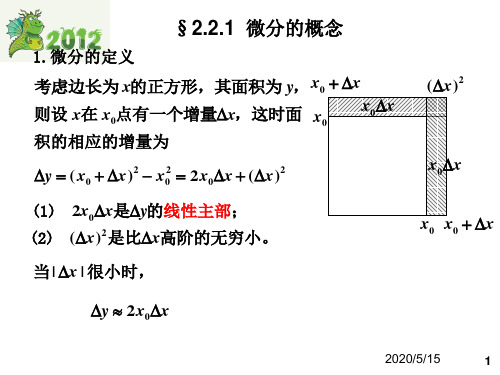
(1) 2x0 x是y的线性主部;
(2) ( x ) 是比x高阶的无穷小。
2
当 | x | 很小时, y 2 x0 x
2013-9-23 1
§2.2.1 微分的概念
定义1:若函数 y f ( x )在 x0的改变量 y与自变量 x的改变量
x有下列关系, y Ax o(x ),
(1)
其中 A是仅依赖于 x0而与 x无关的常数,o( x )是比 x高阶 的无穷小量,则称函数 y f ( x )在 x0可微,Ax称为函数 f ( x ) 在点 x0处的微分,记作dy | x x0 ,即 dy | x x0 Ax .
注:函数在一点的微分就是函数在该点的增量的线性主部。
1
dx( 1 x 1);
2013-9-23
10
§2.2.1 微分的概念
4.微分法则 a.函数的和、差、积、商的微分法则
设 u u(x ), v v (x ) 都可导,则有
(1) d( u v)=d u d v ; (2) d( uv) vd u ud v;
u vdu udv (3) d( ) (v 0). 2 v v
dy f (u)du
注1:这说明,y作为自变量 x的函数的微分与 y作为中间变量
u的函数的微分是相等的,这一性质称为微分形式不变性。 dy dy 注2:值得注意的是导数没有这种不变性。即 . dx du
2013-9-23 12
§2.2.1 微分的概念
例3 求下列函数的微分:
(1) y a
cos 2 x
;
(2) y arctan x ;
(3) y lncot 3 x;
tan x (4) y . x 1 e
函数的微分和泰勒展开

函数的微分和泰勒展开微积分是数学的一个重要分支,研究函数的微分和泰勒展开是微积分中的基本内容。
本文将介绍函数微分的概念以及泰勒展开的基本原理和应用。
一、函数的微分函数的微分是研究函数在某一点附近的局部变化率的方法。
对于一元函数f(x),其在点x=a处的微分表示为dy=f'(a)dx,其中f'(a)为函数f(x)在x=a处的导数。
微分可以看作是函数在某一点附近的线性逼近,并且刻画了函数在该点的局部变化特征。
二、泰勒展开泰勒展开是将一个函数表示为多项式的形式来近似表示的方法。
对于给定的函数f(x),在点x=a处的n阶泰勒展开式可以表示为:f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + f'''(a)(x-a)^3/3! + ... + f^n(a)(x-a)^n/n!其中,f'(a)表示函数在点x=a处的导数,f''(a)表示二阶导数,以此类推。
当n趋向于正无穷时,泰勒展开可以无限逼近函数的真实形式。
泰勒展开在计算机科学、物理学等领域中有着广泛的应用。
通过截取泰勒展开的前几项,可以将复杂的函数在某一点进行简化,从而方便计算和分析。
三、泰勒展开的应用1. 函数近似:通过截取泰勒展开的前几项,可以对函数进行近似表示,从而简化计算和分析过程。
特别是在计算机科学中,常常使用泰勒展开来近似计算一些复杂函数,提高计算效率。
2. 极值求解:通过泰勒展开可以对函数的极值进行求解。
通过求解泰勒展开的导数为零的点,可以得到函数的极值点的近似值。
3. 曲线绘制:通过泰勒展开可以绘制函数的近似曲线。
通过截取泰勒展开的前几项,可以在图表中绘制出函数在某一点附近的近似曲线,帮助我们直观了解函数的特征。
四、总结函数的微分和泰勒展开是微积分中的重要内容。
微分可以刻画函数在某一点的局部变化特征,而泰勒展开可以将函数近似表示为多项式形式。
全微分和微分

全微分和微分
摘要:
1.引言
2.全微分的概念
3.微分的概念
4.全微分与微分的关系
5.应用示例
6.结论
正文:
1.引言
微积分是数学中的一个重要分支,它在物理、工程、经济学等各种领域中都有广泛的应用。
微积分的主要内容包括微分和积分两个方面。
本文将介绍微分和全微分的概念及其关系。
2.全微分的概念
全微分是指函数在某一点的变化率,也可以理解为该函数在这一点的切线斜率。
全微分是微分的一种推广,它可以用来描述多元函数在某一点的变化情况。
全微分的概念可以通过泰勒公式来解释,即函数在某一点附近的近似值可以表示为该点的各阶导数的和。
3.微分的概念
微分是指函数在某一点的局部近似,可以用来描述函数在某一点的变化情况。
微分是微积分的基础概念,它在微积分中起着重要作用。
微分的概念可以
通过导数来解释,即函数在某一点的导数就是该函数在这一点的局部近似。
4.全微分与微分的关系
全微分与微分有着密切的关系,全微分可以看作是微分的一种推广。
全微分可以用来描述多元函数在某一点的变化情况,而微分只能描述单变量函数在某一点的变化情况。
此外,全微分还可以用来求解微分方程,微分方程是微积分中的一个重要内容。
5.应用示例
微分和全微分在实际应用中有很多例子,例如在物理学中,可以用微分来求解物体在某一点的速度,用全微分来求解物体在某一点的加速度。
在经济学中,可以用微分来求解成本函数的极值,用全微分来求解生产函数的极值。
6.结论
微分和全微分是微积分中的两个重要概念,它们在实际应用中有广泛的应用。
