数学实验第一章e
数学实验概率论与数理统计分册习题1-推荐下载

数学实验概率论与数理统计分册习题第1章古典概率2.碰运气能否通过英语四级考试大学英语四级考试是全面检验大学生英语水平的一种综合考试,具有一定难度。
这种考试包括听力、语法结构、阅读理解、写作等。
除写作占15分外,其余85道为单项选择题,每道题附有A、B、C、D四个选项。
这种考试方法使个别学生产生碰运气和侥幸心理,那么,靠运气能通过英语四级考试吗?解:假设学生作文得满分,即15分,85道选择题每道题都靠蒙,即每道题做对的概率为1/4,得60分则通过考试。
则该同学通过考试的概率为:P=4540 45851344C⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭>> nchoosek(85,40)*(1/4)^45*(3/4)^40ans =2.3448e-008即:82.344810-⨯由此可见,即使该同学作文满分,靠运气通过考试的概率也是如此的低,所以可以认为靠运气不能通过英语四级考试。
3.在区域H={(x,y)| (x,y)∈Q,x2+y2≤1},Q={(x,y) |0≤x≤1,0≤y≤1}上考虑计算二重积分(利用Monte-carlo法):⎰⎰++=HdxdyyxyxI) sin(解:积分区域如右图所示:>> n = 10000; % 模拟次数x = rand(n,1); % 点的x坐标y = rand(n,1); % 点的y坐标m = sum(sin(x+y)./(x+y) & x.^2 + y.^2 <= 1); Vn = m/n % 落到所求面积内的点的频率,即概率的模拟值Vn =0.7891第2章 随机变量及其分布4.公共汽车车门的高度是按成年男子与车门碰头的机会在0.01以下的标准来设计的。
根据统计资料,成年男子的身高X 服从均值为168厘米,方差为7厘米的正态分布,那么车门的高度应该至少设计为多少厘米?解:>> norminv(0.99, 168, 7)ans =184.2844则车门的高度应该至少设计为184.3厘米5.某研究中心有同类型仪器300台,各仪器工作相互独立,而且发生故障的概率均为0.01,通常一台仪器的故障由一人即可排除。
数学实验(电子版)

数学实验实验班级____资环12级植保检测2班____________学生姓名__ 黄诗宇_ _____________学生学号____201230200407____________ 指导老师________________华南农业大学理学院应用数学系2013-4-10一、MABLAB支持下的数学实验实验(一)MABLAB的基本命令、初等数值运算及图形班级专业:姓名:学号:日期:实验(二)MABLAB的MATLAB的程序结构班级专业:姓名:学号:日期:实验(三)MABLAB的线性代数运算班级专业:姓名:学号:日期:1A; (2) B, A B,>> a=[1 -2 2;3 0 5;1 5 3];实验(四) MATLAB的微积分运算班级专业:姓名:学号:日期:实验(五) 微分方程建模问题(综合实验1)班级专业:姓名:学号:日期:图1.5紫果云杉树高生长拟合曲线模拟结果显示,随着时间的演变,林木大小呈上升趋势,因此,树高随着树龄的增大而不断增加.二、动力学模型参考《数学实验》P78~80实验(六) 优化模型(综合实验二)班级专业:姓名:学号:日期:一、实验目的了解最优化思想,熟悉优化建模思路,学习建立和求解一些简单的优化模型,学习用适当的数学软件实现优化模型二、阅读《数学试验》P85~886 2,6实验(七) 矩阵模型(综合实验三)班级专业:姓名:学号:日期:二、统计实验实验(八) MINITAB(或SPSS)的基本操作班级专业:姓名:学号:日期:(SPSS)班级专业:姓名:学号:日期:班级专业:姓名:学号:日期:五、SPSS样题1 . 设灯泡的使用寿命为因变量,灯丝的配料为因子,四种配料方案为四水平,为单因子四水平的实验。
表10-1灯泡灯丝 1 2 3 4 5 6 7 8甲1600 1610 1650 1680 1700 1700 1780乙1500 1640 1400 1700 1750丙1640 155 **** **** 1640 1600 17401800丁1510 1520 1530 1570 1640 1680用SPSS作单因素方差分析1、不使用选择项操作步骤1)定义两个变量:Filament变量,取值1、2、3、4分别代表甲、乙、丙、丁,标签为“灯丝”Hours变量其值为灯泡的使用寿命,标签为“灯泡使用寿命”2)按Analyze Compared Means One-Way Anova顺序打开“单因素分析”主对话框。
大学数学实验

大学数学实验项目一矩阵运算与方程组求解实验1行列式与矩阵实验目的掌握矩阵的输入方法.掌握利用Mathematica(4.0以上版本)对矩阵进行转置、加、减、数乘、相乘、乘方等运算,并能求矩阵的逆矩阵和计算方阵的行列式.基本命令在Mathematica 中,向量和矩阵是以表的形式给出的.1.表在形式上是用花括号括起来的若干表达式,表达式之间用逗号隔开.如输入{2,4,8,16}{x,x+1,y,Sqrt[2]}则输入了两个向量.2.表的生成函数(1) 最简单的数值表生成函数Range,其命令格式如下:Range[正整数n]—生成表{1,2,3,4,…,n };Range[m,n]—生成表{m ,…,n };Range[m,n,dx]—生成表{m ,…,n },步长为d x .(2)通用表的生成函数Table.例如,输入命令Table[n^3,{n,1,20,2}]则输出{1,27,125,343,729,1331,2197,3375,4913,6859}输入Table[x*y,{x,3},{y,3}]则输出{{1,2,3},{2,4,6},{3,6,9}}3.表作为向量和矩阵一层表在线性代数中表示向量,二层表表示矩阵.例如,矩阵可以用数表{{2,3},{4,5}}表示.输入A={{2,3},{4,5}}则输出{{2,3},{4,5}}命令MatrixForm[A]把矩阵A 显示成通常的矩阵形式.例如,输入命令:MatrixForm[A]则输出⎪⎪⎭⎫ ⎝⎛5432 但要注意,一般地,MatrixForm[A]代表的矩阵A 不能参与运算.输入B={1,3,5,7}输出为{1,3,5,7}输入MatrixForm[B]输出为虽然从这个形式看向量的矩阵形式是列向量,但实质上Mathematica 不区分行向量与列向量.或者说在运算时按照需要,Mathematica 自动地把向量当作行向量或列向量.下面是一个生成抽象矩阵的例子.输入Table[a[i,j],{i,4},{j,3}]MatrixForm[%]则输出注:这个矩阵也可以用命令Array 生成,如输入Array[a,{4,3}]//MatrixForm则输出与上一命令相同.4.命令IdentityMatrix[n]生成n 阶单位矩阵.例如,输入IdentityMatrix[5]则输出一个5阶单位矩阵(输出略).5.命令DiagonalMatrix[…]生成n 阶对角矩阵.例如,输入DiagonalMatrix[{b[1],b[2],b[3]}]则输出{{b[1],0,0},{0,b[2],0},{0,0,b[3]}}它是一个以b[1],b[2],b[3]为主对角线元素的3阶对角矩阵.6.矩阵的线性运算:A+B 表示矩阵A 与B 的加法;k*A 表示数k 与矩阵A 的乘法;A.B 或Dot[A,B]表示矩阵A 与矩阵B 的乘法.7.求矩阵A 的转置的命令:Transpose[A].8.求方阵A 的n 次幂的命令:MatrixPower[A,n].9.求方阵A 的逆的命令:Inverse[A].10.求向量a 与b 的内积的命令:Dot[a,b].实验举例矩阵A 的转置函数Transpose[A]例1.1求矩阵的转置.输入ma={{1,3,5,1},{7,4,6,1},{2,2,3,4}};Transpose[ma]//MatrixForm输出为如果输入Transpose[{1,2,3}]输出中提示命令有错误.由此可见,向量不区分行向量或列向量.矩阵线性运算例1.2设,291724,624543⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=B A 求.24,A B B A -+ 输入A={{3,4,5},{4,2,6}};B={{4,2,7},{1,9,2}};A+B//MatrixForm4B-2A//MatrixForm输出为如果矩阵A 的行数等于矩阵B 的列数,则可进行求AB 的运算.系统中乘法运算符为“.”,即用A.B 求A 与B 的乘积,也可以用命令Dot[A,B]实现.对方阵A ,可用MatrixPower[A,n]求其n 次幂.例1.3设,148530291724,36242543⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=mb ma 求矩阵ma 与mb 的乘积. 输入Clear[ma,mb];ma={{3,4,5,2},{4,2,6,3}}; mb={{4,2,7},{1,9,2},{0,3,5},{8,4,1}};ma.mb//MatrixForm输出为矩阵的乘法运算例1.4设,101,530291724⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=B A 求AB 与,A B T 并求.3A输入Clear[A,B];A={{4,2,7},{1,9,2},{0,3,5}};B={1,0,1};A.B输出为{11,3,5}这是列向量B 右乘矩阵A 的结果.如果输入B.A输出为{4,5,12}这是行向量B 左乘矩阵A 的结果,A B T 这里不需要先求B 的转置.求方阵A 的三次方,输入MatrixPower[A,3]//MatrixForm输出为例1.5设,421140123,321111111⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=B A 求A AB 23-及.B A T 输入A={{?1,1,1},{1,?1,1},{1,2,3}}MatrixForm[A]B={{3,2,1},{0,4,1},{?1,2,?4}}MatrixForm[B]3A.B ?2A//MatrixFormTranspose[A].B//MatrixForm则输出A AB 23-及B A T 的运算结果分别为求方阵的逆例1.6设,5123641033252312⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=A 求.1-A输入Clear[ma]ma={{2,1,3,2},{5,2,3,3},{0,1,4,6},{3,2,1,5}};Inverse[ma]//MatrixForm则输出注:如果输入Inverse[ma//MatrixForm]则得不到所要的结果,即求矩阵的逆时必须输入矩阵的数表形式例1.7求矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--027926243043286345248127的逆矩阵. 解A={{7,12,8,24},{5,34,6,-8},{32,4,30,24},{-26,9,27,0}}MatrixForm[A]Inverse[A]//MatrixForm例1.8设,221331317230,5121435133124403⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=B A 求.1B A - 输入Clear[A,B];A={{3,0,4,4},{2,1,3,3},{1,5,3,4},{1,2,1,5}};B={{0,3,2},{7,1,3},{1,3,3},{1,2,2}};Inverse[ma].B//MatrixForm输出为对于线性方程组,b AX =如果A 是可逆矩阵,X ,b 是列向量,则其解向量为.1b A -例1.9解方程组⎪⎩⎪⎨⎧-=-+=+-=++.2442,63,723z y x z y x z y x输入Clear[A,b];A={{3,2,1},{1,-1,3},{2,4,-4}};b={7,6,-2};Inverse[A].b输出为{1,1,2}求方阵的行列式例1.10求行列式.3351110243152113------=D 输入Clear[A];A={{3,1,-1,2},{-5,1,3,-4},{2,0,1,-1},{1,-5,3,-3}};Det[A]输出为40例1.11求.11111111111122222222d d d d c c c c b b b b a a a a D ++++= 输入Clear[A,a,b,c,d];A={{a^2+1/a^2,a,1/a,1},{b^2+1/b^2,b,1/b,1},{c^2+1/c^2,c,1/c,1},{d^2+1/d^2,d,1/d,1}};Det[A]//Simplify则输出例1.12计算范德蒙行列式.1111145444342413534333231252423222154321x x x x x x x x x x x x x x x x x x x x 输入Clear[x]; Van=Table[x[j]^k,{k,0,4},{j,1,5}]//MatrixForm输出为再输入Det[van]则输出结果比较复杂(项很多)若改为输入Det[van]//Simplify或Factor[Det[van]]则有输出(x[1]-x[2])(x[1]-x[3])(x[2]-x[3])(x[1]-x[4])(x[2]-x[4])(x[3]-x[4])(x[1]-x[5])(x[2]-x[5])(x[3]-x[5])(x[4]-x[5])例1.13设矩阵,60975738723965110249746273⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=A 求.),(|,|3A A tr A 输入A={{3,7,2,6,?4},{7,9,4,2,0},{11,5,?6,9,3},{2,7,?8,3,7},{5,7,9,0,?6}}MatrixForm[A]Det[A]Tr[A]MatrixPower[A,3]//MatrixForm则输出3),(|,|A A tr A 分别为115923向量的内积向量内积的运算仍用“.”表示,也可以用命令Dot 实现例1.14求向量}3,2,1{=u 与}0,1,1{-=v 的内积.输入u={1,2,3};v={1,-1,0};u.v输出为-1或者输入Dot[u,v]所得结果相同.实验习题1.设,150421321,111111111⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=B A 求A AB 23-及.B A ' 2.设,001001⎪⎪⎪⎭⎫ ⎝⎛=λλλA 求.10A 一般地?=k A (k 是正整数). 3.求⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++++a a a a a 1111111111111111111111111的逆. 4.设,321011324⎪⎪⎪⎭⎫ ⎝⎛-=A 且,2B A AB +=求.B 5.利用逆矩阵解线性方程组⎪⎩⎪⎨⎧=++=++=++.353,2522,132321321321x x x x x x x x x实验2矩阵的秩与向量组的极大无关组实验目的学习利用Mathematica 求矩阵的秩,作矩阵的初等行变换;求向量组的秩与极大无关组.基本命令1.求矩阵M 的所有可能的k 阶子式组成的矩阵的命令:Minors[M,k].2.把矩阵A 化作行最简形的命令:RowReduce[A].3.把数表1,数表2,…,合并成一个数表的命令:Join[list1,list2,…].例如输入Join[{{1,0,?1},{3,2,1}},{{1,5},{4,6}}]则输出{{1,0,?1},{3,2,1},{1,5},{4,6}}实验举例求矩阵的秩例2.1设,815073*********⎪⎪⎪⎭⎫ ⎝⎛-------=M 求矩阵M 的秩. 输入Clear[M];M={{3,2,?1,?3,?2},{2,?1,3,1,?3},{7,0,5,?1,?8}};Minors[M,2]则输出{{?7,11,9,?5,5,?1,?8,8,9,11},{?14,22,18,?10,10,?2,?16,16,18,22},{7,?11,?9,5,?5,1,8,?8,?9,?11}}可见矩阵M 有不为0的二阶子式.再输入Minors[M,3]则输出{{0,0,0,0,0,0,0,0,0,0}}可见矩阵M 的三阶子式都为0.所以.2)(=M r例2.2已知矩阵⎪⎪⎪⎭⎫ ⎝⎛----=1t 0713123123M 的秩等于2,求常数t 的值. 左上角的二阶子式不等于0.三阶子式应该都等于0.输入Clear[M];M={{3,2,-1,-3},{2,-1,3,1},{7,0,t,-1}};Minors[M,3]输出为{{35-7t,45-9t,-5+t}}当5=t 时,所有的三阶子式都等于0.此时矩阵的秩等于2.例2.3求矩阵⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----3224211631095114047116的行最简形及其秩. 输入A={{6,1,1,7},{4,0,4,1},{1,2,?9,0},{?1,3,?16,?1},{2,?4,22,3}}MatrixForm[A]RowReduce[A]//MatrixForm则输出矩阵A 的行最简形根据矩阵的行最简形,便得矩阵的秩为3.矩阵的初等行变换命令RowfReduce[A]把矩阵A 化作行最简形.用初等行变换可以求矩阵的秩与矩阵的逆.例2.4设,41311221222832A ⎪⎪⎪⎭⎫ ⎝⎛--=求矩阵A 的秩. 输入Clear[A];A={{2,-3,8,2},{2,12,-2,12},{1,3,1,4}};RowReduce[A]//MatrixForm输出为因此A 的秩为2.例2.5用初等变换法求矩阵⎪⎪⎪⎭⎫ ⎝⎛343122321的逆矩阵.输入A={{1,2,3},{2,2,1},{3,4,3}}MatrixForm[A]Transpose[Join[Transpose[A],IdentityMatrix[3]]]//MatrixFormRowReduce[%]//MatrixFormInverse[A]//MatrixForm则输出矩阵A 的逆矩阵为向量组的秩矩阵的秩与它的行向量组,以及列向量组的秩相等,因此可以用命令RowReduce 求向量组的秩.例2.6求向量组)0,3,0,2(),2,5,4,0(),1,1,2,1(231=--=-=ααα的秩.将向量写作矩阵的行,输入Clear[A];A={{1,2,-1,1},{0,-4,5,-2},{2,0,3,0}};RowReduce[A]//MatrixForm则输出这里有两个非零行,矩阵的秩等于2.因此,它的行向量组的秩也等于2.例2.7向量组)7,5,1,3(),5,4,3,1(),1,1,1,1(),3,2,1,1(4321==-==αααα是否线性相关?输入Clear[A];A={{1,1,2,3},{1,?1,1,1},{1,3,4,5},{3,1,5,7}};RowReduce[A]//MatrixForm则输出向量组包含四个向量,而它的秩等于3,因此,这个向量组线性相关.例2.8向量组)3,1,1(),2,1,3(),7,2,2(321=-==ααα是否线性相关?输入Clear[A];A={{2,2,7},{3,-1,2},{1,1,3}};RowReduce[A]//MatrixForm则输出向量组包含三个向量,而它的秩等于3,因此,这个向量组线性无关.向量组的极大无关组例2.9求向量组的极大无关组,并将其它向量用极大无关组线性表示.输入Clear[A,B];A={{1,?1,2,4},{0,3,1,2},{3,0,7,14},{1,?1,2,0},{2,1,5,0}};B=Transpose[A];RowReduce[B]//MatrixForm则输出在行最简形中有三个非零行,因此向量组的秩等于3.非零行的首元素位于第一、二、四列,因此421,,ααα是向量组的一个极大无关组.第三列的前两个元素分别是3,1,于是.3213ααα+=第五列的前三个元素分别是,25,1,21-于是.25214215αααα++-= 向量组的等价可以证明:两个向量组等价的充分必要条件是:以它们为行向量构成的矩阵的行最简形具有相同的非零行,因此,还可以用命令RowReduce 证明两个向量组等价.例2.10设向量求证:向量组21,αα与21,ββ等价.将向量分别写作矩阵A ,B 的行向量,输入Clear[A,B];A={{2,1,-1,3},{3,-2,1,-2}};B={{-5,8,-5,12},{4,-5,3,-7}};RowReduce[A]//MatrixFormRowReduce[B]//MatrixForm则输出与两个行最简形相同,因此两个向量组等价.实验习题1.求矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=12412116030242201211A 的秩. 2.求t ,使得矩阵⎪⎪⎪⎭⎫ ⎝⎛-=t A 23312231的秩等于2.3.求向量组)0,0,1(),1,1,1(),1,1,0(),1,0,0(4321====αααα的秩.4.当t 取何值时,向量组),3,1(),3,2,1(),1,1,1(321t ===ααα的秩最小?5.向量组)1,1,1,1(),1,1,1,1(),1,1,1,1(),1,1,1,1(4321-=--=--==αααα是否线性相关?6.求向量组)6,5,4,3(),5,4,3,2(),4,3,2,1(321===ααα的最大线性无关组.并用极大无关组线性表示其它向量.7.设向量),6,3,3,2(),6,3,0,3(),18,3,3,8(),0,6,3,1(2121=-=-=-=ββαα求证:向量组21,αα与21,ββ等价.实验3线性方程组实验目的熟悉求解线性方程组的常用命令,能利用Mathematica 命令各类求线性方程组的解.理解计算机求解的实用意义.基本命令1.命令NullSpace []A ,给出齐次方程组0=AX 的解空间的一个基.2.命令LinearSolve []b A ,,给出非齐次线性方程组b AX =的一个特解.3.解一般方程或方程组的命令Solve 见Mathematica 入门.实验举例求齐次线性方程组的解空间设A 为n m ⨯矩阵,X 为n 维列向量,则齐次线性方程组0=AX 必定有解.若矩阵A 的秩等于n ,则只有零解;若矩阵A 的秩小于n ,则有非零解,且所有解构成一向量空间.命令NullSpace 给出齐次线性方程组0=AX 的解空间的一个基.例3.1求解线性方程组⎪⎪⎩⎪⎪⎨⎧=---=++=+--=--+.0532,0375,023,02432143243214321x x x x x x x x x x x x x x x 输入Clear[A];A={{1,1,?2,?1},{3,?2,?1,2},{0,5,7,3},{2,?3,?5,?1}};NullSpace[A]则输出{{?2,1,?2,3}}说明该齐次线性方程组的解空间是一维向量空间,且向量(?2,1,?2,3)是解空间的基. 注:如果输出为空集{},则表明解空间的基是一个空集,该方程组只有零解.例3.2求解线性方程组⎪⎪⎩⎪⎪⎨⎧=---=++=+--=-++053203750232302432143243214321x x x x x x x x x x x x x x x 输入Clear[A];A={{1,1,2,-1},{3,-2,-3,2},{0,5,7,3},{2,-3,-5,-1}};Nullspace[A]输出为{}因此解空间的基是一个空集,说明该线性方程组只有零解.例3.3向量组)7,5,1,3(),5,4,3,1(),1,1,1,1(),3,2,1,1(4321==-==αααα是否线性相关? 根据定义,如果向量组线性相关,则齐次线性方程组有非零解.输入Clear[A,B];A={{1,1,2,3},{1,?1,1,1},{1,3,4,5},{3,1,5,7}};B=Transpose[A];NullSpace[B]输出为{{?2,?1,0,1}}说明向量组线性相关,且02421=+--ααα非齐次线性方程组的特解例3.4求线性方程组⎪⎪⎩⎪⎪⎨⎧=----=++=+--=--+45322375222342432143243214321x x x x x x x x x x x x x x x 的特解.输入Clear[A,b];A={{1,1,?2,?1},{3,?2,?1,2},{0,5,7,3},{2,?3,?5,?1}};b={4,2,?2,4}LinearSolve[A,b]输出为{1,1,?1,0}注:命令LinearSolve 只给出线性方程组的一个特解.例3.5求线性方程组⎪⎪⎩⎪⎪⎨⎧=---=++=+--=--+45322375222342432143243214321x x x x x x x x x x x x x x x 的特解.输入Clear[A,b];A={{1,1,2,-1},{3,-2,-1,2},{0,5,7,3},{2,-3,-5,-1}};b={4,2,2,4}Linearsolve[A,b]输出为Linearsolve::nosol:Linearequationencounteredwhichhasnosolution.说明该方程组无解.例3.6向量)4,3,1,2(-=β是否可以由向量)1,3,2,1(1-=α,)11,12,5,5(2-=α,()3,6,3,13-=α线性表示?根据定义,如果向量β可以由向量组32,1,ααα线性相关,则非齐次线性方程组有解.输入Clear[A,B,b];A={{1,2,-3,1},{5,-5,12,11},{0,5,7,3},{1,-3,6,3}};B=Transpose[A];b={2,-1,3,4};Linearsolve[B,b]输出为 {31,31,0} 说明β可以由32,1,ααα线性表示,且213131ααβ+= 例3.7求出通过平面上三点(0,7),(1,6)和(2,9)的二次多项式,2c bx ax ++并画出其图形.根据题设条件有,924611700⎪⎩⎪⎨⎧=+⋅+⋅=+⋅+⋅=+⋅+⋅c b a c b a c b a 输入Clear[x];A={{0,0,1},{1,1,1},{4,2,1}}y={7,6,9}p=LinearSolve[A,y]Clear[a,b,c,r,s,t];{a,b,c}.{r,s,t}f[x_]=p.{x^2,x,1};Plot[f[x],{x,0,2},GridLines ?>Automatic,PlotRange ?>All];则输出c b a ,,的值为{2,?3,7}并画出二次多项式7322+-x x 的图形(略).非齐次线性方程组的通解用命令Solve 求非齐次线性方程组的通解.例3.8求出通过平面上三点(0,0),(1,1),(-1,3)以及满足9)1(,20)1(='=-'f f 的4次多项式).(x f解设,)(234e dx cx bx ax x f ++++=则有输入Clear[a,b,c,d,e];q[x_]=a*x^4+b*x^3+c*x^2+d*x+e;eqs=[q[0]==0,q[1]==1,q[-1]==3,q ’[-1]==20,q ’[1]==9];{A,y}=LinearEquationsToMatrices[eqs,{a,b,c,d}];p=LinearSolve[A,y];f[x_]=p.{x^4,x^3,x^2,x,1};Plot[f[x],{x,-1,1},GridLines->Automatic,PlotRange->All];则输出所求多项式非齐次线性方程组的通解用命令solve 求非齐次线性方程组的通解.例3.9解方程组⎪⎪⎩⎪⎪⎨⎧=+-=+-=++-=++-53323221242143143214321x x x x x x x x x x x x x x输入solve[{x-y+2z+w==1,2x-y+z+2w==3,x-z+w==2,3x-y+3w==5},{x,y,z,w}]输出为{{x →2-w+z,y →1+3z}}即3412x x x +-=,3231x x +=.于是,非齐次线性方程组的特解为(2,1,0,0).对应的齐次线性方程组的基础解系为(1,3,1,0)与(-1,0,0,1).例3.10解方程组⎪⎪⎩⎪⎪⎨⎧-=++-=++-=+-=-+-33713344324324214324321x x x x x x x x x x x x x 解法1用命令solve输入solve[{x-2y+3z-4w==4,y-z+w==-3,x+3y+w==1,-7y+3z+3w==-3},{x,y,z,w}]输出为{{x →-8,y →3,z →6,w →0}}即有唯一解81-=x ,32=x ,63=x ,04=x .解法2这个线性方程组中方程的个数等于未知数的个数,而且有唯一解,此解可以表示为b A x 1-=.其中A 是线性方程组的系数矩阵,而b 是右边常数向量.于是,可以用逆阵计算唯一解.输入Clear[A,b,x];A={{1,-2,3,-4},{0,1,-1,1},{1,3,0,1},{0,-7,3,1}};b={4,-3,1,-3};x=Inverse[A].b输出为{-8,3,6,0}解法3还可以用克拉默法计算这个线性方程组的唯一解.为计算各行列式,输入未知数的系数向量,即系数矩阵的列向量.输入Clear[a,b,c,d,e];a={1,0,1,0};b={-2,1,3,-7};c={3,-1,0,3};d={-4,1,1,1};e={4,-3,1,-3};Det[{e,b,c,d}]/Det[{a,b,c,d}]Det[{a,e,c,d}]/Det[{a,b,c,d}]Det[{a,b,e,d}]/Det[{a,b,c,d}]Det[{a,b,c,e}]/Det[{a,b,c,d}]输出为-836例3.10当a 为何值时,方程组⎪⎩⎪⎨⎧=++=++=++111321321321ax x x x ax x x x ax 无解、有唯一解、有无穷多解?当方程组有解时,求通解.先计算系数行列式,并求a ,使行列式等于0.输入Clear[a];Det[{{a,1,1},{1,a,1},{1,1,a}}];Solve[%??0,a]则输出{{a →?2},{a →1},{a →1}}当a 2-≠,a 1≠时,方程组有唯一解.输入Solve[{a*x ?y ?z ??1,x ?a*y ?z ??1,x ?y ?a*z ??1},{x,y,z}]则输出{{x →,21a +y →,21a+z →a +21}} 当a ??2时,输入Solve[{?2x+y+z==1,x ?2y+z==1,x+y ?2z==1},{x,y,z}]则输出{}说明方程组无解.当a =1时,输入Solve[{x+y+z==1,x+y+z==1,x+y+z==1},{x,y,z}]则输出{{x →1?y ?z}}}说明有无穷多个解.非齐次线性方程组的特解为(1,0,0),对应的齐次线性方程组的基础解系为为(?1,1,0)与(?1,0,1).例3.11求非齐次线性方程组⎪⎩⎪⎨⎧-=+-+=-+-=+-+2534422312432143214321x x x x x x x x x x x x 的通解.解法1输入A={{2,1,?1,1},{3,?2,1,?3},{1,4,?3,5}};b={1,4,?2};particular=LinearSolve[A,b]nullspacebasis=NullSpace[A]generalsolution=t*nullspacebasis[[1]]+k*nullspacebasis[[2]]+Flatten[particular]generalsolution//MatrixForm解法2输入B={{2,1,?1,1,1},{3,?2,1,?3,4},{1,4,?3,5,?2}}RowReduce[B]//MatrixForm根据增广矩阵的行最简形,易知方程组有无穷多解.其通解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛007/57/6107/97/1017/57/14321t k x x x x (k ,t 为任意常数)实验习题1.解方程组⎪⎩⎪⎨⎧=++=++=+-.024,02,032321321321x x x x x x x x x2.解方程组⎪⎩⎪⎨⎧=++-=++-=++-.0111784,02463,03542432143214321x x x x x x x x x x x x3.解方程组⎪⎩⎪⎨⎧-=-+-=+-=-+-.22,3,44324314324321x x x x x x x x x x4.解方程组⎪⎩⎪⎨⎧=++-=+++=-++.254,32,22432143214321x x x x x x x x x x x x5.用三种方法求方程组⎪⎪⎩⎪⎪⎨⎧=-+=-+=-+=-+127875329934,8852321321321321x x x x x x x x x x x x 的唯一解.6.当b a ,为何值时,方程组⎪⎪⎩⎪⎪⎨⎧-=+++=--+-=++=+++1232)3(122043214324324321ax x x x b x x a x x x x x x x x 有唯一解、无解、有无穷多解?对后 者求通解.实验4交通流模型(综合实验)实验目的利用线性代数中向量和矩阵的运算,线性方程组的求解等知识,建立交通流模型.掌握线性代数在交通规划方面的应用.应用举例假设某城市部分单行街道的交通流量(每小时通过的车辆数)如图4.1所示.300300300200500x x 8x 图4?1 试建立数学模型确定该交通网络未知部分的具体流量.假定上述问题满足下列两个基本假设(1)全部流入网络的流量等于全部流出网络的流量;(2)全部流入一个节点的流量等于流出此节点的流量.于是,根据图4.1及上述基本两个假设,可建立该问题的线性方程组即若将上述矩阵方程记为b Ax =,则问题就转化为求b Ax =的全部解.下面我们利用Mathmatica 软件来求解1、输入矩阵A ,并利用RowReduce[A ]命令求得A 的秩为8.输入RowReduce[A]//MatrixFormOut[2]//MatrixForm=则输出2、应用命令NullSpace[A]求出齐次线性方程组0=Ax 的基础解系.输入In[3]:=NullSpace[A]//MatrixFormOut[3]//MatrixForm=则输出由此即得到所求齐次线性方程组的基础解系:⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=+=00000110110011100000212211C C c c ξξη,(21,C C 为任意常数). 3、输入增广阵(Ab ),求出其秩为8,由,108)()(=<==n Ab r A r 知方程组有无穷多个解.输入RowReduce[Ab]//MatrixFormOut[5]//MatrixForm=则输出4、应用命令LinearSolve[A,b],求得非齐次线性方程组b Ax =的一个特解.输入LinearSolve[A,b]Out[9]={{800},{0},{200},{500},{0},{800},{1000},{0},{400},{600}}则得到所求非齐次线性方程组的一个特解:综上所述,我们就得到了非齐次线性方程组b Ax =的全部解为,*2211*ξξξξη++++=C C x (21,C C 为任意常数).在解的表示式中,x 的每一个分量即为交通网络中未知部分的具体流量,该问题有无穷多解(为什么?并思考其实际意义).本模型具有实际应用价值,求出该模型的解,可以为交通规划设计部门提供解决交通堵塞、车流运行不畅等问题的方法,知道在何处应建设立交桥,那条路应设计多宽等,为城镇交通规划提供科学的指导意见.但是,在本模型中,我们只考虑了单行街道这样一种简单情形,更复杂的情形留待读者在更高一级的课程中去研究.此外,本模型还可推广到电路分析中的网络节点流量等问题中.实验报告请读者应用本模型的思想方法,为你所在或你熟悉的城镇建立一个区域的交通流量模型.并提供一个具体的解决方案,即从无穷多个解中根据具体限制确定出一个具体的解决方案.。
高等数学数学实验报告(两篇)

引言概述:高等数学数学实验报告(二)旨在对高等数学的相关实验进行探究与研究。
本次实验报告共分为五个大点,每个大点讨论了不同的实验内容。
在每个大点下,我们进一步细分了五到九个小点,对实验过程、数据收集、数据分析等进行了详细描述。
通过本次实验,我们可以更好地理解高等数学的概念和应用。
正文内容:一、微分方程实验1.利用欧拉法求解微分方程a.介绍欧拉法的原理和步骤b.详细阐述欧拉法在实际问题中的应用c.给出具体的实例,展示欧拉法的计算步骤2.应用微分方程建立模型求解实际问题a.介绍微分方程模型的建立方法b.给出一个具体的实际问题,使用微分方程建立模型c.详细阐述模型求解步骤和结果分析3.使用MATLAB求解微分方程a.MATLAB求解微分方程的基本语法和函数b.给出一个具体的微分方程问题,在MATLAB中进行求解c.分析结果的准确性和稳定性二、级数实验1.了解级数的概念和性质a.简要介绍级数的定义和基本概念b.阐述级数收敛和发散的判别法c.讨论级数的性质和重要定理2.使用级数展开函数a.介绍级数展开函数的原理和步骤b.给出一个函数,使用级数展开进行近似计算c.分析级数近似计算的精确度和效果3.级数的收敛性与运算a.讨论级数收敛性的判别法b.介绍级数的运算性质和求和法则c.给出具体的例题,进行级数的运算和求和三、多元函数极值与最值实验1.多元函数的极值点求解a.介绍多元函数的极值点的定义和求解方法b.给出一个多元函数的实例,详细阐述求解过程c.分析极值点对应的函数值和意义2.多元函数的条件极值与最值a.讨论多元函数的条件极值的判定法b.给出一个具体的多元函数,求解其条件极值和最值c.分析条件极值和最值对应的函数值和意义3.利用MATLAB进行多元函数极值与最值的计算a.MATLAB求解多元函数极值与最值的基本语法和函数b.给出一个多元函数的具体问题,在MATLAB中进行求解c.分析结果的准确性和可行性四、曲线积分与曲面积分实验1.曲线积分的计算方法与应用a.介绍曲线积分的定义和计算方法b.给出一个具体的曲线积分问题,详细阐述计算过程c.分析曲线积分结果的几何意义2.曲线积分的应用举例a.讨论曲线积分在实际问题中的应用b.给出一个实际问题,使用曲线积分进行求解c.分析曲线积分结果的实际意义和应用价值3.曲面积分的计算方法与应用a.介绍曲面积分的定义和计算方法b.给出一个具体的曲面积分问题,详细阐述计算过程c.分析曲面积分结果的几何意义五、空间解析几何实验1.空间曲线的参数方程表示与性质a.介绍空间曲线的参数方程表示和性质b.给出一个具体的空间曲线,转化为参数方程表示c.分析参数方程对应的几何意义和性质2.平面与空间直线的位置关系a.讨论平面与空间直线的位置关系的判定方法b.给出一个具体的平面与空间直线的问题,判定其位置关系c.分析位置关系对应的几何意义和应用实例3.空间直线与平面的夹角和距离计算a.介绍空间直线与平面的夹角和距离的计算方法b.给出一个具体的空间直线和平面,计算其夹角和距离c.分析夹角和距离计算结果的几何意义总结:通过本次高等数学数学实验报告(二),我们深入了解了微分方程、级数、多元函数极值与最值、曲线积分、曲面积分以及空间解析几何的相关概念和应用。
数学实验报告 (1)

(1)参数方程:z=2^2^/2^2^sin y x y x ++(-8<=x<=8,-8<=y<=8) (2)程序:[X,Y]=meshgrid(-8::8);r=sqrt(x.^2+y.^2)+eps;Z=sin(r)./r;Mesh(x,y,z)Axis square(3)程序的输出结果:3:球面,椭球面,双叶双曲面,单叶双曲面1球面: (4):参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *R z R y R x 0π<=θ<2* 0<=ϕ<π (5)程序:u=[0:pi/60:2*pi];v=[0:pi/60:pi];[U,V]=meshgrid(u,v);R=3;X=R*sin(v).*cos(u);Y=R*sin(v).*sin(u);Z=R*cos(v);Surf(x,y,z);axis equal;(3)程序输出结果:2椭球面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *c z b y a x 0<=θ<2*π 0<=ϕ<=π (2)程序:ezsurf(‘3*sin(u)*cos(v) ,’3*sin(u)*sin(v)’,’1*cos(u)’,[0,pi,0,2*pi]);(3)程序的输出结果:3单叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕtan sin *sec *cos *sec *z a y a x 0<=θ<2*π -π/2<ϕ<π/2 (2)程序:ezsurf(‘3*sec(u)*cos(v),’3*sec(u)*sin(v)’,’5*tan(u)’,[-pi/2,pi/2,0,2*pi]);axis auto(3)输出程序结果:4双叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕsec *sin *tan *cos *tan *c z b y a x 0<=θ<2*π -π<ϕ<3*π/2,ϕ≠π/2(2)程序:ezsurf(‘3*tan(u)*cos(v)’,’3*tan(u)*sin(v)’,’5*sec(u)’,[-pi/2,3*pi/2,0,2*pi]);axis auto(4) (3)输出程序结果:抛物螺线: (1)参数方程:⎪⎩⎪⎨⎧===2^*sin **cos **t c z t t b y t t a x 0<T<+∞ (2)程序:ezplot3(‘2*t*cos(t)’,’2*t*sin(t)’,’t.^2/3’,[0,50]);(3)输出程序结果:(5)马鞍面: (1)参数方程:z=x^2/9-y^2/4 (-25<=x<=25,-25<=y<=25)(2)程序:[X,Y]=meshgrid(-25:1:25);Z=X.^2/9-Y.^2/4;Surf(X,Y,Z)Title(‘马鞍面’)grid off(3)输出程序结果:(6)黎曼函数:(1)程序:n=100;x=[];y=[];k=1;for q=2:nfor p=1:q-1if gcd(q,p)==1 %利用函数gcd(m,n)可求m和n的最大公约数x(k)=p/q;y(k)=1/q;k=k+1;endendendplot(x,y,’.b’); axis([0,1,0,1])(2)程序输出结果:。
《实验数学》说课稿(通用3篇)

《实验数学》说课稿(通用3篇)《实验数学》说课稿1各位评委老师:大家好!我是本科数学某某号选手,今天我要进行说课的课题是高中数学必修一第一章第三节第一课时《函数单调性与最大(小)值》。
我将从教材分析;教学目标分析;教法、学法;教学过程;教学评价五个方面来陈述我对本节课的设计方案。
恳请在座的专家评委批评指正。
一、教材分析1、教材的地位和作用(1)本节课主要对函数单调性的学习;(2)它是在学习函数概念的基础上进行学习的,同时又为基本初等函数的学习奠定了基础,所以他在教材中起着承前启后的重要作用;(可以看看这一课题的前后章节来写)(3)它是历年高考的热点、难点问题2、教材重、难点重点:函数单调性的定义难点:函数单调性的证明重难点突破:在学生已有知识的基础上,通过认真观察思考,并通过小组合作探究的办法来实现重难点突破。
(这个必须要有)二、教学目标知识目标:(1)函数单调性的定义(2)函数单调性的证明能力目标:培养学生全面分析、抽象和概括的能力,以及了解由简单到复杂,由特殊到一般的化归思想情感目标:培养学生勇于探索的精神和善于合作的意识三、教法学法分析1、教法分析“教必有法而教无定法”,只有方法得当才会有效。
新课程标准之处教师是教学的组织者、引导者、合作者,在教学过程要充分调动学生的积极性、主动性。
本着这一原则,在教学过程中我主要采用以下教学方法:开放式探究法、启发式引导法、小组合作讨论法、反馈式评价法2、学法分析“授人以鱼,不如授人以渔”,最有价值的知识是关于方法的只是。
学生作为教学活动的主题,在学习过程中的参与状态和参与度是影响教学效果最重要的因素。
在学法选择上,我主要采用:自主探究法、观察发现法、合作交流法、归纳总结法。
四、教学过程1、以旧引新,导入新知通过课前小研究让学生自行绘制出一次函数f(x)=x和二次函数f(x)=x^2的图像,并观察函数图象的特点,总结归纳。
通过课上小组讨论归纳,引导学生发现,教师总结:一次函数f(x)=x的图像在定义域是直线上升的,而二次函数f(x)=x^2的图像是一个曲线,在(—∞,0)上是下降的,而在(0,+∞)上是上升的。
数学实验1-3章习题答案
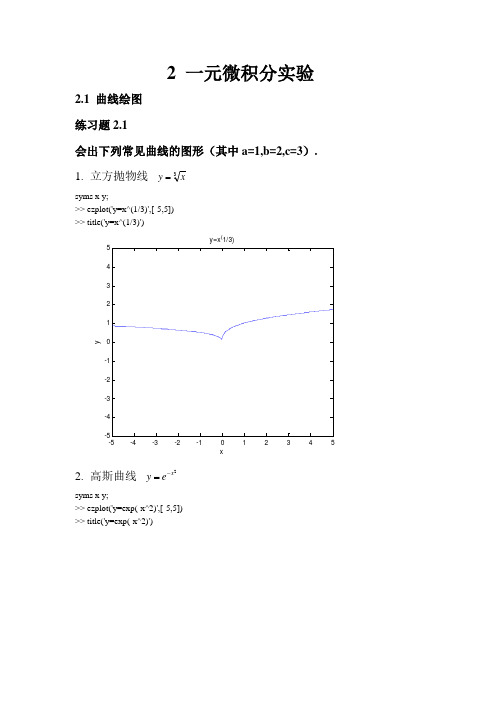
ans =
18.3287
函数的单调区间为:
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间:-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为:
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2:
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值:
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根:
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)
《高等数学实验》课程教学大纲

《高等数学实验》课程教学大纲开课单位(系、教研室、实验室):数学与统计学院高等数学教研室学分:1 总学时:16H课程类别:选修考核方式:考查课程负责人:赵振华课程编号:10801-2基本面向:全校性选修课一、本课程的目的、性质及任务本课程是将高等数学知识、数学软件和计算机应用有机地结合,将高等数学的基本知识直观形象地演示出来的课程。
课程性质:高等数学实验是一门全校性选修课及0402,0405,0408专业的专业选修课程。
课程目的和任务:从高等数学的基本知识出发,借助计算机,让学生能直观理解高等数学的知识,充分调动学生学习的主动性。
培养学生的创新意识,使用计算机并利用数学软件理解高等数学基本知识的能力,最终达到提高学生数学素质和综合能力的目的。
本课程的基本任务是教师主要讲授一些MATLAB的基本知识及其MATLAB软件实现,包括函数图形画法,微分计算,积分计算,级数敛散性判别,矩阵计算,线性方组的解等。
二、本课程的基本要求本课程的教学要求分为三个层次。
凡属较高要求的内容,必须使学生熟练掌握;在教学要求上一般的内容必须使学生掌握;在教学上要求较低的内容要求学生了解(一)MATLAB简介1、了解MATLAB环境,MATLAB的基本使用方法2、熟练掌握MATLAB的基本元素及使用方法、程序语言的编写、函数及M文件(二)基本函数图形的绘制1、熟练掌握常用绘图函数、函数图形的绘制2、熟练掌握函数图形的绘制(三)微积分实验1、熟练掌握用MATLAB表示函数,求极限2、熟练掌握用MATLAB求导数,3、掌握用MATLAB求数值微分4、熟练掌握用MATLAB求一元函数的积分,了解多元函数的积分计算(四)无穷级数实验1、熟练掌握用Matlab判别数项级数的敛散性、2、熟练掌握用Matlab数项级数求和、3、掌握用Matlab求函数项级数的和函数、4、掌握用Matlab求函数()f x的Taylor级数展开式及Fourier级数展开式(五)常微分方程实验1、熟练掌握用Matlab求常微分方程(组)的解析解2、熟练掌握用Matlab求常微分方程(组)初值问题的数值解(六)线性代数实验1、熟练掌握用MATLAB作矩阵的基本运算2、熟练掌握用MATLAB判断向量的相关性3、熟练掌握用MATLAB求线性方程组的解;4、熟练掌握用MATLAB求矩阵的特征值与特征向量5、掌握用MATLAB化二次型标准型(七)综合实验1、熟练掌握通过分析问题来建立数学模型,进而用MATLAB对模型的求解三、本课程与其它课程的关系1、本课程的先修课程:(1)高等数学极限,导数,积分、级数、微分方程等是高等数学实验课程所需要重要知识。
重庆大学数学实验一 matlab的基本应用 参考答案

《数学实验》第一次上机实验1. 设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ,其中E,R,O,S 分别为单位阵、随机阵、零阵和对角阵,试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S 0RS R E A 。
程序及结果:E=eye(3); %创建单位矩阵E% R=rand(3,2); %创建随机矩阵R% O=zeros(2,3); %创建0矩阵% S=diag(1:2); %创建对角矩阵% A=[E,R;O,S]; %创建A 矩阵%B=[E,(R+R*S);zeros(2,3),S^2] %计算等号右边的值%A^2 %计算等号左边的值%运行结果:B =1.00 0 0 1.632.74 0 1.00 0 1.81 1.90 0 0 1.00 0.25 0.29 0 0 0 1.00 0 0 0 0 0 4.00 ans =1.00 0 0 1.632.740 1.00 0 1.81 1.90 0 0 1.00 0.25 0.29 0 0 0 1.00 0 0 0 0 0 4.002.某零售店有9种商品的单件进价(元)、售价(元)及一周的销量如表1.1,问哪种商品的利润最大,哪种商品的利润最小;按收入由小到大,列出所有商品及其收入;求这一周该10种商品的总收入和总利润。
表1.11)程序:a=[7.15 8.25 3.20 10.30 6.68 12.03 16.85 17.51 9.30]; b=[11.10 15.00 6.00 16.25 9.90 18.25 20.80 24.15 15.50]; c=[568 1205 753 580 395 2104 1538 810 694];s=sum((b-a).*c)i=b.*cmax((b-a).*c)min((b-a).*c)[m,n]=sort(b.*c)2)运行结果:s =4.6052e+004i =1.0e+004 *0.6305 1.8075 0.4518 0.9425 0.3911 3.8398 3.1990 1.95621.0757ans =1.3087e+004ans =1.2719e+003m =1.0e+004 *0.3911 0.4518 0.6305 0.9425 1.0757 1.8075 1.9562 3.1990 3.8398n =5 3 1 4 9 2 8 7 63. 近景图将x的取值范围局限于较小的区间内可以画出函数的近景图,用于显示函数的局部特性。
第一章 高中数学实验的总体构想-【触摸数学】GeoGebra高中数学实验探究与应用教程

概述作为学生,大家肯定会常常思考:数学应该怎样学习效率高?怎样学习内化快?作为教师,我们也长期为这个问题所困扰:教学中学生遇到了疑难,教师除了一遍又一遍的讲解,还有什么办法可以帮助他们更快找到答案?对于其中的抽象问题,还有什么途径帮他们更好去掌握?解决以上问题的方法,可谓仁者见仁,智者见智,但有一点是相同的,那就是提高学生的数学素养,构造学生完善的知识体系是当务之急.而构造知识体系最重要的就是要学生真正理解知识、掌握知识,并能灵活应用知识,为达到这一点,就要求我们教学中力求让学生不但知其然更知其所以然.所以面对这个问题我的答案是数学实验:通过数学实验把知识变成看得见摸得着的东西,亲手触摸它,亲身感受它,消除它的神秘感和抽象感,然后驾驭它.我在高中数学这一方“土地”摸爬滚打了26年,仍然对高中数学学习的一个细节记忆犹新:上高中的时候,三角函数中的“和差化积”与“积化和差”这8个公式我总是记不住,即使上了大学,这种情况仍然没有改观.可奇怪的是,经过一轮授课后,这8个公式却被我轻而易举地记下来了.肯定不止我一个人有这样的体验,有些学习成绩好的学生很愿意给其他同学讲解题目,表面看来浪费了自己不少时间,但事实上通过讲解,使自己对知识理解变得更加深刻,记得也更加牢固了.其实都是一个道理:我们亲身经历了这些数学知识的生成过程,亲手触摸过它的门道,清楚它的每一道“沟坎”.因为亲历,所以掌握牢固;因为触摸,所以内化得更快.那么,如何提高数学学习效率?在数学教学中如何让学生体验知识形成过程?如何提高学生数学探究能力和数学建模能力,给他们创造“触摸”数学的机会?我认为,数学实验是切实行之有效的方法.何谓数学实验?目前还没有统一的明确界定,通常指的是“为获得某种数学理论,检验某个数学猜想,解决某类数学问题,实验者运用一定的物质手段,在数学思维活动的积极参与下,在典型的实验环境中或特定的实验条件下所进行的一种数学实践探索活动”.可以预见,数学实验的开展将为学生提供触摸数学的机会,促使学生主动融入数学学习的各个环节,有效地培养学生创新意识和实践能力,这是对传统数学教学手段的有益补充.正是基于这样的认知,笔者才提出基于数学实验的教学创新.尝试通过这本书,为学生的学习提供一种有效的辅助手段,为教师的教学提供一种全新的教学模式,为读者的数学学习提供一个全新的视角,给广大数学爱好者提供一种别样的数学研究体验.第一章高中数学实验的总体构想数学的学习几乎贯穿了学生的整个学习生涯,其重要性不言而喻.随着社会经济的发展和科学技术的进步,数学正在以更快的速度全方位地渗透到社会、科技、生活的方方面面.然而,我们发现,随着学习的深入,越来越多的学生对数学学习产生了厌倦、甚至害怕的心理,基础差的学生就会常常觉得越来越力不从心,从而导致数学成绩“每况愈下”.一方面随着学习内容和知识难度的加深,数学逐渐从形象走向抽象,更主要的原因是学生在课堂上被动地接受知识,缺少对数学知识生成过程的亲身体验,难以构建完整的知识和能力体系.这种情形在高中数学教学中普遍存在,鉴于此种情况,创设高中数学实验室,为学生提供与数学亲密接触的机会就显得十分必要.第1节高中数学实验的目标与任务高中数学实验的总体目标就是服务学生的数学学习,降低数学学习难度,提高数学学习兴趣,激发数学学习热情.具体来说,应着眼于解决三大问题,完成三大任务.1.让学生体验数学知识的生成过程随着学习的深入,高中数学较为抽象的知识随处可见,教师的讲解可能较难让学生对知识有较为透彻的理解.较典型的如在研究二次函数的区间最值时,学生对函数图象的变化所引起的区间最值的改变,通过直观想象是较难掌握的,并且此种题型变化较多:可能对二次函数区间最值产生影响的,除了二次函数图象对称轴的位置,还有区间的位置及图象的开口方向等.因而,在教学中,给学生一个亲身体验探究最值变化过程的机会就显得非常必要.学生通过动手实践,对知识的生成过程将会有更加深入的认识,这将有利于降低学生的学习难度,提高他们的学习兴趣.又如在立体几何学习的初始阶段,学生普遍缺少空间想象力,在三视图的教学过程中,如果能够给学生一些实物模型,让他们动手体验三个视图的生成过程,将加深他们对知识的理解.2.让学生学会探究从教学的总体表现来看,高中学生具有一定的解决问题能力,但提出问题,并对问题开展自主探究的能力较弱.大力提高自主探究能力和水平,不但是科技进步的要求,也是学生个人成长不可或缺的需要.《普通高中数学课程标准(2017年版)》指出:数学探究活动是围绕某个具体的数学问题,开展自主探究、合作研究并最终解决问题的过程.具体表现为:发现和提出有意义的数学问题,猜测合理的数学结论,提出解决问题的思路和方案,通过自主探索、合作研究论证数学结论.数学探究活动是运用数学知识解决数学问题的一类综合实践活动,也是高中阶段数学课程的重要内容.要开展数学探究,除了要有合适的研究课题,重要的一点就是还要有合适的研究平台和操作环境.高中数学实验在这方面将扮演一个不可替代的角色.一些优秀的数学软件(如几何画板、超级画板、GeoGebra等)在进行数学图形变换的时候,都能保持其几何性状不改变(如:用以上软件做了一个直角三角形,则无论如何变换,它都将保持直角三角形这个性状不变),这将十分有利于数学探究活动的开展.3.让学生体验建模数学建模就是从生活、生产、科研中发现问题,根据实际问题建立数学模型;通过对数学模型求解研究,得出研究结论,并根据结论去指导解决实际问题的过程.数学建模研究过程就是开发学生数学应用意识的过程,也是促进理论和实践相结合的有效手段.《普通高中数学课程标准(2017年版)》对高中生的数学建模也提出了明确的要求,要求学生要尝试着去体验数学建模的完整过程.其中如何从现实生活中提炼出数学问题,如何建立数学模型,如何对数学模型开展研究,以上问题是数学建模的重要环节,也是数学实验室必须达成的功能.第2节高中数学实验室的建设要求为使高中数学实验室能够具备以上功能,在建设过程中,就必须对软硬件的要求做好总体规划.规划应遵循够用、好用的基本原则,既要能够保证教学工作的顺利开展,也必须注意避免浪费.1.硬件要求有条件的学校,可以利用专门的场地建设高中数学实验室.在这方面,国内不少公司和厂家都已经有了较为成熟的方案:如广州市皓骏教育科技有限公司提出的动态数学探究实验室建设方案,在软硬件上都给出了详细的规划.按他们的配置,一间可容纳48个学生的数学实验室建设费用,约为37万元.考虑到目前多数中小学不一定具备这样的条件,硬件方面不要做过多的重复建设,可以利用或者改造学校现有的设备和场地.数学模拟实验,可以考虑利用学校现成的电脑室或者云教室,其电脑的硬件配置足够满足数学实验的教学需要.而像前文所说的三视图等动手实验,可以安排在教室或者教研室进行.以上做法虽然因陋就简,但同样能够达到数学实验教学的效果.当然,有条件的学校,还是建议创建一间数学专用实验室.此外,作为传统数学教学不可或缺的数学教具,在数学实验中也有其重要作用.如演示椭圆轨迹生成过程的椭圆板,双曲线、抛物线的演示工具,还有立体几何教学中的几何体模型,以及一些测量角度和长度等工具(如测角仪等在做三角建模时都是必不可少的工具).有些实验(如椭圆轨迹的生成实验、立体几何的三视图实验等),应用计算机进行模拟,虽然可以得到精确的结果,但教学效果不如用传统教具教学来得直观,学生往往也更乐于接受实实在在、能摸得着的东西,所以传统的数学教具也是高中数学实验室的重要组成部分.2.软件要求高中数学实验室对软件的要求不高,主要集中在以下三个方面:(1)机房环境作为数学实验室的机房,要拥有足够一个班教学使用的学生计算机和一台教师计算机,并通过网络互联互通.教师计算机可以对所有的学生计算机进行有效管理,向学生机传递音频、视频信号,同时也必须支持学生机之间的互联互通.上面这些要求,任何一间电脑教室或云教室都是可以实现的.(2)数学软件要开展数学实验,数学软件的选择十分重要.目前主流的有几何画板、超级画板和GeoGebra(以下简称GGB)等.这些软件的功能各具有优势,简要介绍如下:几何画板是由美国Key Curriculum Press公司制作并出版的教育软件,1996年该公司授权人民教育出版社在中国发行该软件的中文版.正如其名“21世纪动态几何”,它能够动态地展现出几何对象的位置关系、运行变化规律,能够满足高中数学教学的基本要求,但其功能仍不完善.要实现某些功能,需要较为繁琐的制作过程.需要特别强调的是该软件受版权保护,如需使用,必须购买正版软件.Z 智能教育平台——超级画板》)是由我国著名数学家、计算机超级画板(全名《Z科学家、科普作家、中国科学院院士张景中教授主持开发,为中国基础教育量身定做的数学教育平台.它是一款知识性和智能型相结合的、多功能的教育工具软件,能很好地满足高中数学教学和实验的各种需要,并且提供了完善的课件库.超级画板自面世以来,以其易学易用的特色和强大功能吸引了许多数学老师、数学教育家和教育技术专家的青睐.需要强调的是,该软件也受版权保护.GGB是奥地利数学家Markus Hohenwarter于2002年创建的动态教学软件,它通过开源的方式不断地更新、完善和推广,从仅支持英、德两种语言到支持包括汉语在内的69种语言,从仅绘制平面图形到绘制3D图形,从只依赖计算机运行到可以在平板电脑和手机等移动端运行,随着免费开源,GGB更新速度变得越来越快,功能也变得越来越强大,而且操作简单.虽有个别应用仍稍有不便(如几何画板和超级画板都可以很方便地制作多页面课件,在课件制作过程中,可以根据需要随意添加删除页面,但GGB在制作多页面课件时,是通过把对象放在不同图层来实现的,因而制作时要设置每个对象所在的图层,并通过代码实现页面的跳转).该软件总体表现优异,是数学实验难得的工作平台.数学软件简要介绍这三款,大家在选用时须考虑三个原则:(1)能满足教学的需要;(2)课件库、资源库的完备性;(3)教师对软件的熟悉程度.各学校应尽可能选择教师比较熟悉软件平台,这有利于减轻教师的教学负担,并能使数学实验在教学中得到较快推广.具体操作时,可选择安装一至两个软件,供教师教学选用.。
数学实验课程全部实验答案

主要涉及的内容有:最基本的矩阵运算(填空),线性方程组(左乘右乘问题)、积分函数、符号变量定义及结果输出形式、多项式回归函数输出结果分析、线性回归函数输出结果分析、多项式的线性运算等相关内容。
实验一:(1)用起泡法对10个数由小到大排序. 即将相邻两个数比较,将小的调到前头. function bubble_sortA=[10 5 64 8 464 35 14 666 57 784]; l=length(A); for i=1:l-1 for j=i+1:l if A(i)>A(j) t=A(i); A(i)=A(j); A(j)=t; end end end B=A实验结果: >> bubble_sort B =5 8 10 14 35 57 64 464 666 784 (2)有一个4*5矩阵,编程求出其最大值及其所处的位置. function findmax(A) a=max(max(A)) [x,y]=find(A==a) 实验结果:>> findmax([54 8 64 999;5496 88 97 6;554 686 5666 655;878 5 87 5454;588 544 5466 3364]) a =5666 x = 3 y = 3 (3)编程求∑=201!n nfunction f=fun3(n) s=1;while n<=20 s=s*n n=n+1; end>> f=fun3(1) f =2.4329e+018(4)有一函数y xy x y x f 2sin ),(2++=,写一程序,输入自变量的值,输出函数值. function f=fun4(x,y) f=x^2+sin(x*y)+2*y end 实验结果: >> f=fun4(2,3) f = 9.7206 f = 9.7206 实验二:1. 绘制如下几种数学曲线(并调制a,b,c,观察图形的变化)(1) 笛卡尔曲线213t atx +=,2213t at y +=(axy y x 333=+) >> syms x y>> a=[1 2 3 4];>> f1=x^3+y^3-3*a(1)*x*y; >> f2=x^3+y^3-3*a(2)*x*y; >> f3=x^3+y^3-3*a(3)*x*y; >> f4=x^3+y^3-3*a(4)*x*y;>> subplot(2,2,1); ezplot(f1) >> subplot(2,2,2);ezplot(f2) >> subplot(2,2,3);ezplot(f3) >> subplot(2,2,4);ezplot(f4)(2) 蔓叶线221t at x +=,231t at y +=(x a x y -=32)>> a=[1 2 3 4];>> f1=y^2-(x^3)/(a(1)-x); >> f2=y^2-(x^3)/(a(2)-x); >> f3=y^2-(x^3)/(a(3)-x); >> f4=y^2-(x^3)/(a(4)-x);>> subplot(2,2,1); ezplot(f1) >> subplot(2,2,2); ezplot(f2) >> subplot(2,2,3);ezplot(f3) >> subplot(2,2,4);ezplot(f4)(3) 星形线t a x 3cos =,t a y 3sin =(323232a y x =+) >> t=0:0.1:2*pi; >> a=[1 2 3 4];>> x1=a(1)*(cos(t).^3); >> y1=a(1)*(sin(t).^3); >> subplot(2,2,1); >> plot(x1,y1)>> x2=a(2)*(cos(t).^3); >> y2=a(2)*(sin(t).^3);>> subplot(2,2,2);plot(x2,y2) >> x3=a(3)*(cos(t).^3); >> y3=a(3)*(sin(t).^3);>> subplot(2,2,3);plot(x3,y3) >> x4=a(4)*(cos(t).^3); >> y4=a(4)*(sin(t).^3);>> subplot(2,2,4);plot(x4,y4)(4) 心形线)cos 1(θ+=a r >> a=[1 2 3 4];>> theta=0:0.1:2*pi;>> r1=a(1)*(1+cos(theta)); >> r2=a(2)*(1+cos(theta));>> r3=a(3)*(1+cos(theta)); >> r4=a(4)*(1+cos(theta));>> subplot(2,2,1);polar(r1,theta) >> subplot(2,2,2);polar(r2,theta) >> subplot(2,2,3);polar(r3,theta) >> subplot(2,2,4);polar(r4,theta)(5) 圆的渐开线)cos (sin ),sin (cos t t t a y t t t a x -=-= >> syms x y >> a=[1 2 3 4];>> x1=a(1).*(cos(t)-t.*sin(t)); >> x2=a(2).*(cos(t)-t.*sin(t)); >> x3=a(3).*(cos(t)-t.*sin(t)); >> x4=a(4).*(cos(t)-t.*sin(t)); >> y1=a(1).*(sin(t)-t.*cos(t)); >> y2=a(2).*(sin(t)-t.*cos(t)); >> y3=a(3).*(sin(t)-t.*cos(t)); >> y4=a(4).*(sin(t)-t.*cos(t)); >> subplot(2,2,1);plot(x1,y1) >> subplot(2,2,2);plot(x2,y2) >> subplot(2,2,3);plot(x3,y3) >> subplot(2,2,4);plot(x4,y4)2.(2)绘制球面4222=++z y x 与柱面1,1,1222222=+=+=+z y z x y x 的图像。
实验1 静电场描绘实验

实验二静电场描绘实验一、实验目的1.了解模拟法描绘静电场的理论依据。
2.学会用模拟法研究静电场,在方格纸上描绘静电场分布的方法。
3.描绘几种静电场的等位线,根据等位线画出电力线。
4.加深对静电场、稳恒电流场的了解。
二、实验设备1.静电场描绘实验模块;2.有机玻璃描绘装置;3.直流电压表、直流稳压源三、实验原理1.模拟法描绘静电场的理论依据带电体在其周围空间所产生的电场,可用电场强度E 和电位U 的空间分布来描述。
为了形象的表示电场的分布情况,常采用等位面和电力线来描述电场。
电力线是按空间各点电场强度的方向顺次连成的曲线,等位面是电场中电位相等的各点所构成的曲面。
电力线和等位面相互正交,有了等位面的图形就可以画出电力线,反之亦然。
我们所说的测量静电场,指的是测绘出静电场中等位面和电力线的分布图形,它是了解电场中一些物理现象或控制带电粒子在电磁场中运动所必须解决的问题,对科研和生产都是十分有用的。
静电场的测量一般采用间接测量的方法,即模拟法。
模拟法是科学研究和工程技术中广泛使用的一种方法。
在自然现象和科学、工程技术问题的研究中,常常会由于研究对象过于庞大、过程变化过快或过慢,环境过于危险等原因而难以直接研究和实地测量,因此需要在实验室里制造一个与研究对象相似的模型,使现象和过程得以重现、延缓或加速,以便进行研究和测量。
模拟法又可分为物理模拟和数学模拟两大类。
如果人为制造的模型与实际研究对象有着相同的物理本质即为物理模拟。
如用“风洞”模拟飞机和火箭在大气中的飞行,用振动台模拟地震对建筑物的影响,用光测弹性法模拟工程构件内的应力分布等。
如果两种不同本质的物理现象或过程遵循相同的数学规律,则可以用其中一种便于研究和测量的现象或过程来模拟另一现象或过程,这就是数学模拟。
用模拟法描绘静电场的方法之一是用电流场代替静电场。
本实验仪采用稳恒电流场模拟描绘静电场。
由电磁学理论可知电解质(或水液)中稳恒电流场与电介质(或真空)中静电场具有相似性。
数学实验——线性代数方程组的数值解

实验5 线性代数方程组的数值解法分1 黄浩 43一、实验目的1.学会用MATLAB软件数值求解线性代数方程组,对迭代法的收敛性和解的稳定性作初步分析;2.通过实例学习用线性代数方程组解决简化的实际问题。
二、For personal use only in study and research; not forcommercial use三、四、实验内容1.《数学实验》第二版(问题1)问题叙述:通过求解线性方程组,理解条件数的意义和方程组性态对解的影响,其中是n阶范德蒙矩阵,即是n阶希尔伯特矩阵,b1,b2分别是的行和。
(1)编程构造(可直接用命令产生)和b1,b2;你能预先知道方程组和的解吗?令n=5,用左除命令求解(用预先知道的解可验证程序)。
(2)令n=5,7,9,…,计算和的条件数。
为观察他们是否病态,做以下试验:b1,b2不变,和的元素,分别加扰动后求解;和不变,b1,b2的分量b1(n),b2(n)分别加扰动后求解。
分析A与b的微小扰动对解的影响。
取10^-10,10^-8,10^-6。
(3)经扰动得到的解记做,计算误差,与用条件数估计的误差相比较。
模型转换及实验过程:(1)小题.由b1,b2为,的行和,可知方程组和的精确解均为n 行全1的列向量。
在n=5的情况下,用matlab编程(程序见四.1),构造,和b1,b2,使用高斯消去法得到的解x1,x2及其相对误差e1,e2(使用excel计算而得)为:由上表可见,当n=5时,所得的解都接近真值,误差在10^-12的量级左右。
(2)小题分别取n=5,7,9,11,13,15,计算和的条件数c1和c2,(程序见四.2),结果如下:由上表可见,二者的条件数都比较大,可能是病态的。
为证实和是否为病态,先保持b不变,对做扰动,得到该情况下的高斯消元解,(程序见四.3),结果如下:(为使结果清晰简洁,在此仅列出n=5,9,13的情况,n=7,11,15略去)=10^-10时:=10^-8时:=10^-6时:由上表可见:a)对于希尔伯特阵,随着阶数的增加,微小扰动对解带来的影响越来越大,到了n=9时,已经有了6倍误差的解,到了n=13时,甚至出现了22倍误差的解元素;而随着的增加,解的偏差似乎也有增加的趋势,但仅凭上述表格无法具体判断(在下一小题中具体叙述)。
义务教育课程标准实验教材五年级数学上册第一章《小数乘小数》

。进行小数乘整数这部分知识的教学,是在学生学习了小数的意义和性质,会进行小数加、减法计算的基础上进行教学的。小数乘的计算在日常的生活中以及进一步学习中都有广泛的应用。小数乘整数是小数乘的重要组成部分,也是进一步学习和探索小数乘小数的基础;学生有了整数乘法的计算方法,积、的变化规律,以及小数乘整数的计算方法等基础,就有利于学生完整地掌握小数乘的计算方法和相关运算规律的理解,提高应用四则计算解决简单实际问题的能力。
板书设计
小数乘小数
2 8.
2 8 8 2 8 8.
7 2 7 2.
1 0.0 8÷100 1 0 0 8.
讨论:为什么最后的1008要除以100?不除以100行吗?依据是什么?
学生学习活动评价设计
通过点积的小数点、小组比赛、反馈练习等形式,让学生进一步掌握小数乘小数的计算方法,尤其是积中的小数点的定位问题。这样既训练了学生的观察能力,比较的能力,又能训练学生主动发现问题,并设法解决相关问题的能力。
预设学生行为
设计意图
一、创设情境,引入新课
二、自主探索,掌握算法
三、进行比较,概括方法
四、巩固练习,深化理解
五、全课总结,拓展延伸
创设情境,引入新课
全课总结,拓展延伸
自主探索,掌握算法
进行比较,概括方法
巩固练习,深化理解
本课注重以学生为主体组织教学,采用合作探究的学习方,一定学生利用现有的知识经验探究小数乘小数的技术方法,通过对比,引导学生归纳小数乘法的计算方法,适当渗透转化的数学思想,培养学生学习能力,可操作性强。
小学生的思维是在有效的数学活动中发生、发展的。新授环节先后组织了两次有效的探究活动。.
两次开放的探究活动,让学生运用原有的知识经验自主地进行估算、口算、笔算,在培养学生的估算能力、计算能力的同时,点亮了教材细节,帮助学生灵活掌握了小数乘小数的算理算法。
数学实验

由上述结论可知所求变换为 2z i z 24 i 或w e . we z 24 3z 2 映射后的内圆半径 r . 3
y 15
1 y
10
0.5
5
x -5 -5
-0.5
5
10
15
20
x -1 -0.5 0.5 1
-10
-15
-1
数学实验
几何变换实验
实验三:比较分式线性映射与 Lagrange 插值
3 2 1 -3 -2 -1 -1 1
-1.5 -1 -0.5
1.5
1 1 w (z ) 2 z
1
0.5
0.5
1
茹科夫斯基变换
数学实验
几何变换实验
机翼周围的空气绕流
数学实验 几何变换实验
极小值原理:设 B 为有界单连通区域, 0 B ,令
H f , f ( z )在B上解析且f (0) f (0) 1 0 .
数学实验
几何变换实验
实验二:如何将偏心圆环变成同心圆环
假设现有两个半径不同的金属圆筒, 要将小的圆筒套在 大圆筒之中,制作成电容器.若它们的中心轴重合,则 容易知道电容器中的电场分布情况,但若中心轴不重 合, 而是平行, 则如何知道这样构造的电容器中的电场 分布?
同心
数学实验
偏心
几何变换实验
求 一 分 式 线 性 变 换 , 把 由 圆 周 C1 : z p r1 及
k 1, k j n k 1, k j
n
( z zk ) ( z j zk )
分式线性映射可以实现圆和圆之间的变换,那么利用 Lagrange 插值公式,得到的插值多项式将通过已知点 的圆映成什么曲线?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
————向量创建与一元函数图形 向量创建与一元函数图形———— 向量创建与一元函数图形
冒号表达式创建向量使用格式 冒号表达式创建向量使用格式 x = x0:step:xn : : x = x0:xn 当步长 step=1 时可省略为 : x0 应大于 xn 当步长 step 为负数时 线性等分函数linspace( )创建[0, 2π]上的等 例1.8 用线性等分函数 创建 分点,绘出正六边形和正十二边形. 分点,绘出正六边形和正十二边形. alpha=linspace(0,2*pi,7) bata=linspace(0,2*pi,13); x1=cos(alpha);y1=sin(alpha); x2=cos(bata);y2=sin(bata); plot(x1,y1,x2,y2)
0 0 1
22/36
——特殊矩阵函数表 特殊矩阵函数表
——
zeros(m,n) eye(m,n) ones(m,n) rand(m,n) randn(m,n) magic(n) hilb(n) invhilb(n) pascal(n) vander(C)
m×n阶零矩阵 × 阶零矩阵 m×n阶单位矩阵 × 阶单位矩阵 m×n阶全 矩阵 阶全1矩阵 × 阶全 m×n阶随机矩阵 × 阶随机矩阵 正态随机数矩阵 n阶魔方矩阵 n阶魔方矩阵 n阶Hilbert矩阵 阶 矩阵 逆Hilbert矩阵 矩阵 n阶Pascal矩阵 阶 矩阵 由向量C生成范德蒙矩阵 由向量 生成范德蒙矩阵
chess
14/36
3.创建向量三种基本方法 创建向量三种基本方法: 创建向量三种基本方法 使用方栝号、使用冒号、使用等分函数。 使用方栝号、使用冒号、使用等分函数。 例1.6 给定 α=150,300,450,600 , 计算 sin α 的值 alpha=[15, 30, 45, 60]*pi/180; sin(alpha) ans = 0.2588 0.5000 0.7071 0.8660 方括号直接输入法是创建向量(和矩阵) 方括号直接输入法是创建向量(和矩阵)的常用 是创建向量 方法,输入时将向量元素用方括号“ ]”括起 方法,输入时将向量元素用方括号“[ ] 括起 元素之间用逗号(或空格)隔开. 来, 元素之间用逗号(或空格)隔开. alpha=(15:15:60)*pi/180;sin(alpha)
1 0.5 0 -0.5 -1
0
2
4
6
8
10
12
14
20/36
用直接方法创建3阶希尔伯特矩阵 例1.17 用直接方法创建 阶希尔伯特矩阵
1 1 / 2 1 / 3 H = 1 / 2 1 / 3 1 / 4 1 / 3 1 / 4 1 / 5
format rat H=[1,1/2,1/3;1/2,1/3,1/4;1/3,1/4,1/5] bar3(H) H= 1 1/2 1/2 1/3 1/3 1/4
10/36
abs(x) sqrt(x) conj(z) round(x) floor(x) rat(x) gcd(x,y) exp(x) log(x) Log10(x)
绝对值 开平方 共轭复数 四舍五入 舍去正小数 分数表示 最大公因数 自然指数 自然对数 10底对数 底对数
angle(z) real(z) imag(z) fix(x) ceil(x) sign(x) rem(x,y) lcm(x,y) pow2(x) log2(x)
A= 1 1/2 1/2 1/3 1/3 1/4 1/3 1/4 1/5
%用函数创建希尔伯特矩阵 %用函数创建希尔伯特矩阵 %创建希尔伯特矩阵的逆阵 创建希尔伯特矩阵的逆阵 %验证 为A的逆 验证B为 的逆 验证
B= 9 -36 30 -36 192 -180 30 -180 180
ans = 1 0 0 1 0 0
2.数学软件 数学软件
——————大规模数值计算 大规模数值计算 数学分析: 数学分析:Mathematics, Maple, SAS, SPSS
3.Matlab简介 简介
——————符号计算 符号计算
4/36
MATLAB (MATrix LABoratory ) 一种解释式语言.易学易用、代码短效率高、 一种解释式语言.易学易用、代码短效率高、 具有强大的数值计算和绘图功能、扩展性强. 具有强大的数值计算和绘图功能、扩展性强. 矩阵的数值运算、数值分析、 矩阵的数值运算、数值分析、数值模拟 数据可视化、绘制 2维/3维 图形 数据可视化、 维 维 可以与FORTRAN、C/C++做数据链接 可以与 、 做数据链接 几百个核心内部函数 信号处理、自动控制、 几十个工具箱(信号处理、自动控制、··· )
16/36
————向量创建与一元函数图形————
命令绘衰减振荡曲线函数: 例1.10 用ezplot()命令绘衰减振荡曲线函数 命令绘衰减振荡曲线函数 y=e -0.5x sin 5x 图形. ezplot('exp(-0.5*x)*sin(5*x)',[0,10,-1,1])
17/36
————向量创建与一元函数图形 向量创建与一元函数图形———— 向量创建与一元函数图形
19/36
例1.13用基本绘图方法绘衰减振荡函数 用基本绘图方法绘衰减振荡函数 y = e– 0.5xsin 5x 的图形并用虚线表示振幅衰减情况。 的图形并用虚线表示振幅衰减情况。 x=0:0.1:4*pi; y= exp(-0.5*x) ; y1=y .*sin(5*x); plot(x,y1,x,y,’--r’,x,-y,’--r’)
A= 8 3 4 1 5 9 6 7 2
12/36
国际象棋发明人向印度国王求赐大麦, 例1.5 国际象棋发明人向印度国王求赐大麦,希望 得到大麦数量由如下规则计算. 得到大麦数量由如下规则计算.在国际象棋棋盘的 64个方格中 第一格放一粒麦粒,第二格放两粒, 个方格中, 64个方格中,第一格放一粒麦粒,第二格放两粒,第 三格放四粒, 三格放四粒,……,以此类推.每格比前一格麦粒数 ,以此类推. 多一倍,直到放满64格为止. 64格为止 多一倍,直到放满64格为止.计算麦粒数表明这些大 麦几乎可以覆盖地球表面. 麦几乎可以覆盖地球表面. 级数:
4/ 15 7/36
工作空间浏览
命令历史窗口
命令窗口
MATLAB桌面 桌面
8/36
编辑窗口、 编辑窗口、
图形窗口
9/36
三角函数与双曲函数 sin asin cos acos tan atan cot acot sec asec csc acsc 正弦函数 反正弦函数 余弦函数 反余弦函数 正切函数 反正切函数 余切函数 反余切函数 正割函数 反正割函数 余割函数 反余割函数 sinh asinh cosh acosh tanh atanh sech asech csch acsch coth acoth 双曲正弦函数 反双曲正弦函数 双曲余弦函数 反双曲余弦函数 双曲正切函数 反双曲正切函数 双曲正割函数 反双曲正割函数 双曲余割函数 反双曲余割函数 双曲余切函数 反双曲余切函数
0.15 0.1 0.05 0 -0.05 -0.1 -0.1 -0.05 0 0.05 0.1 0.15
y= -0.2122 0.1273 -0.0909 0.0707 -0.0579
18/36
————向量创建与一元函数图形————
MATLAB 一元函数绘图方法
ezplot() fplot() plot() 简易绘图方法,优点: 简易绘图方法,优点:快速方便 函数绘图方法,与简易绘图相似. 函数绘图方法,与简易绘图相似.要给定 自变量变化范围 基本绘图方法, 基本绘图方法,利用一元函数自变量的 一系列数据和对应函数值数据绘图。 一系列数据和对应函数值数据绘图。具 有很大灵活性 例如 plot(X,Y), plot(X,Y,’r’), plot(x1,y1,x2,y2) plot(x1,y1,’r’,x2,y2,’b’)
2/36
思考问题,完成实验报告, 思考问题,完成实验报告,提升数学能力 探月卫星速度计算实验
3/36
1.数学建模与数学实验 数学建模与数学实验
实际问题 提取主要忽 数学变量 变量之 数学模型 软件 求解 略次要因素 关系
合理 检验 不合理
数值计算: 数值计算:Matlab, Xmath, Guass, Lindo
5/36
MATLAB常用工具箱
Symbolic Math Optimization Spline Statistics Signal Processing Image Processing 符号运算工具箱 最优化工具箱 样条分析工具箱 统计分析工具箱 信号处理工具箱 图像处理工具箱
14/20 6/36
在解决实际问题时,如果频繁使用同一个数学表达式, 在解决实际问题时,如果频繁使用同一个数学表达式, 则应该定义一个临时函数以方便操作. 则应该定义一个临时函数以方便操作. 定义方法: 定义方法 函数名= inline(‘表达式’) ( 1 并分析函数性质。 并分析函数性质。 例1.11 定义函数 f ( x ) = x sin x fun=inline('x.*sin(1./x)') fplot(fun,[-0.15,0.15]) N=1:5;x=2./(2*N+1)/pi; y=fun(x)
《数学实验》第一章 》
数学实验与MATLAB 数学实验与 向量创建与一元函数图形 矩阵创建与二元函数图形 数据显示与字符串操作
1/36
实验是获取信息的一种活动 实验是获取信息的一种活动 是获取信息 ——观察 猜测 验证 获取信息 观察 数学实验——使用数学软件快速获取有价值数据 使用数学软件快速获取 数学实验 使用数学软件快速获取有价值数据 熟练掌握MATLAB的命令操作方式 的命令操作方式 熟练掌握 掌握MATLAB程序设计方法 程序设计方法 掌握 以MATLAB为操作平台完成实验作业 为操作平台完成实验作业
