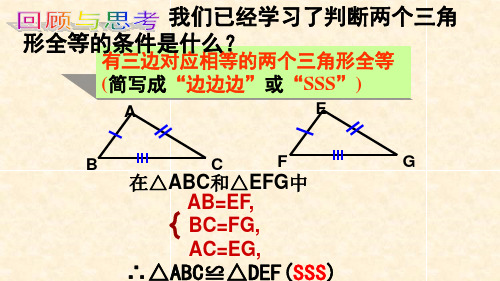
1.5-3边角边,角边角全等
说课教案 三角形全等(二)

说课稿大家好,我说课的内容是八年级上册第十一章第三节,用“角边角”、“角角边”证明两个三角形全等。
一、教材分析本节之前已经学习了两种判定三角形全等的方法,学生对全等三角形的判定有了一定的了解,这为过渡到本节的进一步学习起着铺垫作用。
本节内容是在本章内容中,占据重要的的地位。
它为其它学科和今后的几何学习打下基础。
二、教材目标1、探究并掌握两个三角形全等的条件:“ASA”“AAS”,并能运用它们判别两个三角形是否全等。
2、经历作图、比较、证明等探究过程,提高分析、作图、归纳、表达、逻辑推理等能力。
三、教学重难点重点:理解、掌握三角形全等的条件:“ASA”“AAS”。
难点:探究出“ASA”“AAS”以及它们的运用。
四、学情分析刚进入初二的学生观察、操作、猜想能力较强,但演绎推理、归纳、运用数学意识的思想比较薄弱,思维的广阔性、敏捷性、结密性、灵活性比较欠缺,自主探究和合作学习能力也需要在课堂教学中进一步加强和引导。
五、教学过程1、回顾旧知。
首先通过两个题目回忆前面讨论的用“边边边”、“边角边”证明三角形全等,其中第二题在原有基础上有所提升,且起到承上启下的作用。
题目为已知△ABD≌△ACE,那么△ABE≌△ACD吗?2、引入新课。
探究两角和两角的夹边对应相等,两三角形是否全等,学生经历自己画图、小组合作得出结论。
让学生总结条件中的注意点。
3、题型展现AD平分∠BAC,AD垂直于BC,△ABD≌△ACD吗?此题肯定能很快想到思路,让多个学生叙述过程,老师并要板书过程,目的强调条件顺序为“角边角”。
仍由此图转化条件为:AD平分∠BAC,∠B=∠C,△ABD还全等于△ACD吗?由刚刚讲的“角边角”,学生很容易进入误区,而且坚定的认为这个结论是不成立的,这时老师可以把思路直接说给学生听,让学生自己判断过程的正确性,从而得到全等的第四种判定方法“角角边”,在这里强调“角角边”就是一种判定方法,遇到相应的条件就可以直接用了,无需再转化成“角边角”。
考点05 全等三角形(解析版)

考点五全等三角形知识点整合二、全等三角形1.三角形全等的判定定理:(1)边角边定理:有两边和它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”);(2)角边角定理:有两角和它们的夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA”);(3)边边边定理:有三边对应相等的两个三角形全等(可简写成“边边边”或“SSS”);(4)对于特殊的直角三角形,判定它们全等时,还有HL定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”).2.全等三角形的性质:(1)全等三角形的对应边相等,对应角相等;(2)全等三角形的周长相等,面积相等;(3)全等三角形对应的中线、高线、角平分线、中位线都相等.考向一全等三角形1.从判定两个三角形全等的方法可知,要判定两个三角形全等,需要知道这两个三角形分别有三个元素(其中至少有一个元素是边)对应相等,这样就可以利用题目中的已知边(角)准确地确定要补充的边(角),有目的地完善三角形全等的条件,从而得到判定两个三角形全等的思路:(1)已知两边SASHLSSS ⎧⎪⎨⎪⎩找夹角→找直角→找第三边→(2)已知一边、一角AASSASASAAAS⎧⎪⎧⎪⎨⎪⎨⎪⎪⎪⎩⎩一边为角的对边→找另一角→找夹角的另一边→一边为角的邻边找夹角的另一角→找边的对角→(3)已知两角ASAAAS ⎧⎨⎩找夹边→找其中一角的对边→2.若题中没有全等的三角形,则可根据题中条件合理地添加辅助线,如运用作高法、倍长中线法、截长补短法、分解图形法等来解决运动、拼接、旋转等探究性题目.典例引领1.在学习了全等三角形的判定后,聪明的小惠猜想了一个命题:如果两个三角形有两边和其中一边上的中线分别相等,那么这两个三角形全等.她根据命题的意义画出了图形(如图),并写出了部分已知条件,请你把已知条件补充完整,并写出证明过程.已知:如图,AD 和A D ''分别是ABC 和A B C ''' 的中线,AD A D ''=,AB A B ''=,______.求证:A ABC B C '''≌△△.∴B B '∠=∠,在ABC 和A B C ''' 中,AB A B B B BC B C =⎧⎪∠=∠⎨⎪=''''⎩',∴()SAS ABC A B C ''' ≌,故答案为:BC B C ''=.2.(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图()1,已知:在ABC 中,90BAC ∠=︒,AB AC =,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为点D 、E .证明:DE BD CE =+.(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图()2,将()1中的条件改为:在ABC 中,AB AC =,D 、A 、E 三点都在直线l 上,并且有BDA AEC BAC α∠=∠=∠=,其中α为任意锐角或钝角.请问结论DE BD CE =+是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图()3,过ABC 的边AB 、AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高,延长HA 交EG 于点I ,求证:I 是EG 的中点.【答案】(1)证明见解析;(2)成立,证明见解析;(3)证明见解析.【分析】本题主要考查全等三角形的判定和性质,由条件证明三角形全等得到BD AE =、CE AD =是解题的关键.(1)由条件可证明ADB CEA ≌,可得DA CE =,AE BD =,可得结论;(2)由条件可知180BAD CAE α∠+∠=︒-,且180DBA BAD α∠+∠=︒-,可得DBA CAE ∠=∠,结合条件可证明ADB CEA ≌,同(1)可得出结论;(3)过E 作EM HI ⊥于M ,GN HI ⊥,交HI 的延长线于N .由条件可知EM AH GN ==,可得EM GN =,结合条件可证明EMI GNI ≌,可得出结论I 是EG 的中点.【详解】解:(1)如图1,BD ⊥ 直线l ,CE ⊥直线l ,90BDA CEA ∴∠=∠=︒,90BAC ∠=︒ ,90BAD CAE ∴∠+∠=︒,90BAD ABD ∠+∠=︒ ,CAE ABD ∴∠=∠.在ADB 和CEA 中,BDA AEC DBA EAC AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS ADB CEA ∴ ≌,AE BD ∴=,AD CE =,DE AE AD BD CE ∴=+=+;(2)成立:DE BD CE =+.如图2,α∠=∠= BDA BAC ,180α∴∠+∠=∠+∠=︒-DBA BAD BAD CAE ,DBA CAE ∴∠=∠,在ADB 和CEA 中.BDA AEC DBA EAC AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩.ADB ∴ ≌()AAS ADB CEA ∴ ≌,AE BD ∴=,AD CE =,DE AE AD BD CE ∴=+=+;(3)如图3,过E 作EM HI ⊥于M ,GN HI ⊥,交HI 的延长线于N ,90EMI GNI ∴∠=∠=︒,由(1)和(2)同理可证AEM BAH ≌,AGN CAH ≌,EM AH GN ∴==.EM GN ∴=,在EMI △和GNI △中,EIM GIN EMI GNI EM GN ∠=∠⎧⎪∠=∠⎨⎪=⎩,EMI ∴ ≌()AAS EMI GNI ∴ ≌,EI GI ∴=,I ∴是EG 的中点.3.如图,在ABC 中,AC AB >,D 是BA 延长线上的一点,点E 是CAD ∠的平分线上的一点,EB EC =,过点E 作EF AC ⊥于点F ,EG AD ⊥于点G .(1)求证:EGB EFC≌△△(2)若3AB =,5AC =,求AF 的长.【答案】(1)见解析(2)1【分析】本题主要考查了角平分线的定义、全等三角形的判定与性质等知识,证明AGE AFE ≌是解答本题的关键.(1)先证明AGE AFE ≌,即有EG EF =,结合EB EC =,即可得Rt Rt EGB EFC △≌△;(2)由(1)AGE AFE ≌,Rt Rt EGB EFC △≌△,进而可得BG FC =,根据5AC AC AF FC BG AB AG ==+=+,,,可得25AF FC AF BG AF AB AG AF AB +=+=++=+=,即可得235AF +=,则AF 可求.【详解】(1)证明:∵EG AD ⊥,EF AC ⊥,∴90EGB EFC ∠=︒=∠,∴EGB 和EFC 是直角三角形,∵AE 平分CAD ∠,∴∠=∠EAG EAF ,∵EA EA =,∴()AAS AGE AFE ≌,∴EG EF =,∵EB EC =,∴()Rt Rt HL EGB EFC ≌,(2)∵AGE AFE ≌,Rt Rt EGB EFC △≌△,∴BG FC =,AG AF =,∵5AC AC AF FCBG AB AG ==+=+,,,∴25AF FC AF BG AF AB AG AF AB +=+=++=+=,∵3AB =,∴235AF +=,∴1AF =,即AF 的长为1.4.阅读理解,自主探究:(1)如图1,在ABC 中,90ACB ∠=︒,AC BC =,直线MN 经过点C ,且AD MN ⊥于点D ,BE MN ⊥于点E .求证DE AD BE =+.(2)当直线MN 绕点C 旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时DE 、AD 、BE 之间的数量关系,并说明理由.【答案】(1)见解析(2)(1)中结论不成立,DE AD BE =-,理由见解析.【分析】本题主要考查了全等三角形的判定及性质,直角三角形的两锐角互余,熟练掌握全等三角洲的判定及性质是解题的.()1根据三垂直得出ACD CBE ∠∠=,然后得出ADC 和CEB 全等,从而得出AD CE =,DC BE =,从而得到结论;()2首先证明ADC 和CEB 全等,从而得出AD CE =,DC BE =,得出结论.【详解】(1)解:∵90ACB ∠=︒,∴90ACD BCE ∠∠+=︒,∵AD MN ⊥于D ,BE MN ⊥于E ,∴90ADC CEB ∠∠==︒,90BCE CBE ∠∠+=︒,∴ACD CBE ∠∠=.在ADC 和CEB 中,ADC CEB ACD CBE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ADC CEB ≌,∴AD CE =,DC BE =,∴DE DC CE BE AD =+=+;(2)解:(1)中结论不成立,DE AD BE =-,理由如下:∵90ACB ∠=︒,∴90ACD BCE ∠∠+=︒,∵AD MN ⊥于D ,BE MN ⊥于E ,∴90ADC CEB ∠∠==︒,90BCE CBE ∠∠+=︒,∴ACD CBE ∠∠=.在ADC 和CEB 中,90ADC CBE ACD CBE AC CB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴ADC CEB ≌,∴AD CE =,DC BE =,∴DE CE CD AD BE =-=-.5.如图,AE 与BD 相交于点C ,AC EC =,BC DC =,4cm AB =,点P 从点A 出发,沿A B A →→方向以3cm/s 的速度运动,点Q 从点D 出发,沿D E →方向以1cm/s 的速度运动,P 、Q 两点同时出发,当点P 到达点A 时,P 、Q 两点同时停止运动.设点P 的运动时间为()s t .(1)当403t ≤≤时,线段AP 的长为______,当4833t <≤时,线段AP 的长为______(用含t 的式子表示).(2)请判断AB 与DE 的数量与位置关系,并证明你的结论.(3)连接PQ ,当线段PQ 经过点C 时,求t 的值.在ACP △和ECQ 中,6.如图所示,直线AB 交x 轴正半轴于点(),0A a ,交y 轴正半轴于点()0,B b ,且a 、b 满足50b -=.(1)求A 、B 两点的坐标;(2)如图1所示,D 为OA 的中点,连接BD ,过点O 作OF BD ⊥于点F ,过点A 作AG OA ⊥于点A ,交OF 的延长线于点G ,求点G 的坐标;(3)如图2所示,在(2)的条件下,若AB 交于点E ,连接ED ,求证:BDO EDA ∠=∠.∵AG OA⊥∴904545GAE ∠=︒-︒=︒∴DAE GAE∠=∠又∵AE AE=∴()SAS DAE GAE ≌∴EDA G∠=∠∵()ASA BOD OAG ≌∴BDO G∠=∠∴BDO EDA ∠=∠.7.已知:如图,AB DB =,CB EB =,12∠=∠,求证:A D ∠=∠.【答案】见解析【分析】本题考查了全等三角形的判定与性质,先求出ABC DBE ∠=∠,再利用“SAS ”证明ABC DBE ≌,即可得证,熟练掌握全等三角形的判定与性质是解此题的关键.【详解】证明:12∠=∠ ,12DBC DBC ∴∠+∠=∠+,即ABC DBE ∠=∠,在ABC 和DBE 中,AB DB ABC DBE CB EB =⎧⎪∠=∠⎨⎪=⎩()SAS ABC DBE ∴△≌△,A D ∴∠=∠.变式拓展8.如图,AB ED ∥,AB ED AF DC =,=.求证:EF CB ∥.【答案】证明见解析【分析】本题考查了三角形全等的判定和性质,平行线的判定,根据题意证明()SAS ABC DEF ≌△△,继而得ACB DFE ∠∠=,证明即可.【详解】证明:∵AB ED ∥,∴A D ∠∠=,∵AB ED AF DC =,=,∴AF CD DC CF ++=,即AC DF =,在ABC 和DEF 中,AB DE A D AC DF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABC DEF ≌△△∴ACB DFE ∠∠=,∴EF CB ∥.9.学习与探究:如图1,OP 是MON ∠的平分线,点A 是OP 上任意一点,用圆规分别在OM 、ON 上截取OB OC =,连接AB 、AC ,则AOB AOC ≌△△,判定方法是_________.请你参考这个作全等三角形的方法,解答下列问题:(1)如图2,在ABC 中,ACB ∠是直角,=60B ∠︒,AD 、CE 分别是BAC ∠和BCA ∠的平分线,AD 、CE 相交于点F ,求EFA Ð的度数;(2)在(1)的条件下,请判断FE 与FD 之间的数量关系,并说明理由;(3)如图3,在ABC 中,如果ACB ∠不是直角,而(1)中的其他条件不变,试问在(2)题中所得结论是否仍然成立?若成立,请说明理由;若不成立,也请说明理由.∵AD 是BAC ∠的平分线,∴EAF GAF ∠=∠,在EAF △和GAF 中,∵===AE AG EAF FAG AF AF ⎧⎪∠∠⎨⎪⎩,∴()SAS EAF GAF ≌,∴FE FG =,==60EFA GFA ∠∠︒,∴=1806060=60GFC ∠--︒︒︒︒,又∵==60DFC EFA ∠∠︒,∴DFC GFC ∠=∠,在FDC △和FGC △中∵===DFC GFC FC FC FCG FCD ∠∠⎧⎪⎨⎪∠∠⎩,∴()ASA FDC FGC ≌,∴FD FG =,∴FE FD =.(3)在(2)中的结论FE FD =仍然成立.在AC 上截取AH AE =,连接FH ,如图所示:10.在ABC 中,90ACB ∠=︒,分别过点A 、B 两点作过点C 的直线m 的垂线,垂足分别为点D 、E .(1)如图1,当AC CB =,点A 、B 在直线m 的同侧时,求证:DE AD BE =+;(2)如图2,当AC CB =,点A 、B 在直线m 的异侧时,请问(1)中有关于线段DE 、AD 和BE 三条线段的数量关系的结论还成立吗?若成立,请你给出证明;若不成立,请给出正确结论,并说明理由;(3)如图3,当16cm AC =,30cm CB =,点A 、B 在直线m 的同侧时,一动点M 以每秒2cm 的速度从A 点出发沿A →C →B 路径向终点B 运动,同时另一动点N 以每秒3cm 的速度从B 点出发沿B →C →A 路径向终点A 运动,两点都要到达相应的终点时才能停止运动.在运动过程中,分别过点M 和点N 作MP m ⊥于P ,NQ m ⊥于Q .设运动时间为t 秒,当t 为何值时,MPC 与NQC 全等?【答案】(1)见解析(2)DE AD BE =-,见解析(3)9.2t =或14或16秒【分析】此题是三角形综合题,主要考查了全等三角形的判定和性质,同角的余角相等,判断出ADC CEB ≌是解本题的关键,还用到了分类讨论的思想.(1)根据AD m ⊥于D ,BE m ⊥于E ,得90ADC CEB ∠∠==︒,而90ACB ∠=︒,根据等角的余角相等得ACD CBE ∠∠=,然后根据“AAS ”可判断ADC CEB ≌,则AD CE =,DC BE =,于是DE DC CE BE AD =+=+;(2)同(1)易证ACD CBE ≌,则AD CE =,CD BE =,于是DE CE CD AD BE =-=-;(3)只需根据点M 和点N 的不同位置进行分类讨论即可解决问题.【详解】(1)证明:∵90ACB ∠=︒,∴90ACD BCE ∠∠+=︒,∵AD m ⊥于D ,BE m ⊥于E ,∴90ADC CEB ∠∠==︒,90BCE CBE ∠∠+=︒,∴ACD CBE ∠∠=,在ADC 和CEB 中,ADC CEB ACD CBE AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ADC CEB ≌,∴AD CE =,DC BE =,∴DE DC CE BE AD =+=+;(2)解:结论:DE AD BE =-;理由:∵AD m ⊥,BE m ⊥,∴90ADC CEB ∠∠==︒,∵90ACB ∠=︒,∴90ACD CAD ACD BCE ∠∠∠∠+=+=︒,∴CAD BCE ∠∠=,在ACD 和CBE 中,ADC CEB CAD BCE AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∵MC NC =,∴162303t t -=-,解得:14t =,不合题意;②当810t ≤<时,点M 在BC ∵MC NC =,∴点M 与点N 重合,∴216303t t =﹣﹣,解得:9.2t =;∵MC NC =,∴216330t t -=-,解得:14t =;∵MC NC =,∴21616t -=,解得:16t =;综上所述:当9.2t =或14或1611.在正方形纸片ABCD 中,点M 、N 分别是BC 、AD 上的点,连接MN .(1)问题探究:如图1,作DD MN '⊥,交AB 于点D ¢,求证:MN DD '=;(2)问题解决:如图2,将正方形纸片ABCD 沿过点M 、N 的直线折叠,点D 的对应点D ¢恰好落在AB 上,点C 的对应点为点C ',若12BD '=,4CM =,求线段MN 的长.四边形ABCD 是正方形,∴AD AB =,90DAB ABM ∠=∠=︒, 90∠=︒NHB ,∴四边形ABHN 是矩形,∴AB HN =,DD MN '⊥,∴90DON ∠=︒,∴90OND ODN ∠+∠=︒,90OND MNH ∠+∠=︒,∴ODN MNH ∠=∠,DAD NHM '∠=∠,AD NH =,∴()'ASA ADD HNM ≌,∴MN DD '=;(2)(2)连接MD ',DD ',由折叠的性质得到:C M CM '=,CD C D ='',设正方形的边长为x ,由勾股定理得,2222BD BM D C C M ''''++=,∴()22221244x x +-=+,解得:18x =,∴18AB AD ==,∴18126AD AB BD ''=-=-=,由勾股定理得,2222186360610DD AD AD ''=+=+==,MN 是DD '的垂直平分线,由(1)知,DD MN '=,∴610MN =.12.【问题解决】已知ABC 中,,,,AB AC D A E =三点都在直线1上,且有BDA AEC BAC ∠=∠=∠.如图①,当90BAC ∠=︒时,线段,,DE BD CE 的数量关系为:DE BD CE=+【类比探究】(1)如图②,在(1)的条件下,当0180BAC ︒<∠<︒时,线段,,DE BD CE 的数量关系是'否变化,若不变,请证明:若变化,写出它们的关系式;【拓展应用】(2)如图③,,90AC BC ACB =∠=︒,点C 的坐标为()2,0-,点B 的坐标为()1,2,请求出点A 的坐标.【答案】(1)DE BD CE =+的数量关系不变,理由见解析;(2)(4,3)-【分析】本题考查的是三角形全等的判定和性质、坐标与图形性质,掌握全等三角形的判定定理和性质定理是解题的关键.(1)根据三角形的外角性质得到ABD CAE ∠=∠,证明ABD CAE ≌ ,根据全等三角形的性质解答;(2)过点A 作AM x ⊥轴于点M ,过点B 作BN x ⊥轴于点N ,根据(1)的结论得到ACM BCN ≌△△,根据全等三角形的性质解答即可.【详解】解:(1)DE BD CE =+的数量关系不变,理由如下:BAE ∠ 是ABD 的一个外角,BAE ADB ABD ∴∠=∠+∠,BDA BAC ∠=∠ ,ABD CAE ∴∠=∠,在ABD △和CAE V 中,ABD CAE ADB CEA BA AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)ABD CAE ∴△≌△,AD CE ∴=,BD AE =,DE AD AE BD CE ∴=+=+;(2)过点A 作AM x ⊥轴于点M ,过点B 作BN x ⊥轴于点N ,点C 的坐标为(2,0)-,点B 的坐标为(1,2),2OC ∴=,1ON =,2BN =,3CN ∴=,由(1)可知,ACM BCN ≌△△,3AM CN ∴==,2CM BN ==,4OM OC CM ∴=+=,∴点A 的坐标为(4,3)-.13.【初步探索】(1)如图1,在四边形ABCD 中,AB AD =,90B ADC ∠=∠=︒,120BAD ∠=︒,E 、F 分别是BC 、CD 上的点,且60EAF ∠=︒,探究图中BE 、EF 、FD 之间的数量关系.小芮同学探究此问题的方法是:延长FD 到点G ,使DG BE =,连接AG ,先证明:ABE ADG △≌△,再证明AEF AGF ≌,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD 中,AB AD =,180B D ∠+∠=∠︒,120BAD ∠=︒,E 、F 分别是BC 、CD 上的点,且60EAF ∠=︒,(1)中的结论是否仍然成立,说明理由.【拓展延伸】(3)如图3,在四边形ABCD 中,180ABC ADC ∠+∠=︒,AB AD =,若点E 在CB 的延长线上,点F 在CD 的延长线上,满足EF BE FD =+,请判断EAF ∠与DAB ∠的数量关系.并证明你的结论.【答案】(1)BE FD EF +=;(2)(1)中的结论仍成立,理由见解答过程;(3)11802EAF DAB ∠=︒-∠.理由见解答过程.证明见解析【分析】本题属于四边形综合题,主要考查了全等三角形的判定以及全等三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应角相等进行推导变形.解题时注意:同角的补角相等.(1)根据SAS 可判定ABE ADG △≌△,进而得出BAE DAG ∠=∠,AE AG =,再根据SAS 判定AEF AGF ≌,可得出EF GF DG DF BE DF ==+=+,据此得出结论;(2)延长FD 到点G ,使DG BE =,连接AG ,先根据SAS 判定ABE ADG △≌△,进而得出BAE DAG ∠=∠,AE AG =,再根据SAS 判定AEF AGF ≌,可得出EF GF DG DF BE DF ==+=+;(3)在DC 延长线上取一点G ,使得DG BE =,连接AG ,先根据SAS 判定ADG ABE ≌,再根据SAS 判定AEF AGF ≌,得出FAE FAG ∠=∠,最后根据360FAE FAG GAE ∠+∠+∠=︒,推导得到2360FAE DAB ∠+∠=︒,即可得出结论.【详解】解:(1)BE FD EF +=.理由如下:如图1,延长FD 到点G ,使DG BE =,连接AG ,90ADC ∠=︒ ,18090ADG ADC ∴∠=︒-∠=︒,又90B ∠=︒ ,B ADG ∴∠=∠,在ABE 与ADG △中,AB AD B ADG BE DG =⎧⎪∠=∠⎨⎪=⎩,(SAS)ABE ADG ∴ ≌,BAE DAG ∴∠=∠,AE AG =,120BAD ∠=︒ ,60EAF ∠=︒,60BAE DAF BAD EAF ∴∠+∠=∠-∠=︒,60DAG DAF ∴∠+∠=︒,即60GAF =︒∠,GAF EAF ∴∠=∠;在AEF △与AGF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,180∠+∠=︒,B ADF∴∠=∠,B ADG又AB AD,=≌(SAS)∴ABE ADG∴∠=∠,AE BAE DAG180ABC ADC ∠+∠=︒ ,ADC ABE ∴∠=∠,在ABE 与ADG △中,AB AD B ADG BE DG =⎧⎪∠=∠⎨⎪=⎩,。
1.5.3“角边角(ASA)”2024-2025学年八年级上册数学同步教学设计(浙教版)

在课后持续关注学生的学习进展,及时给予个别辅导和指导,帮助学生克服学习困难,提高学习效果。除了在课堂上关注学生的学习情况外,我还会利用课余时间对学生进行持续关注,及时了解他们在学习过程中遇到的困难和问题。对于有学习困难的学生,我会给予个别辅导和指导,帮助他们克服学习障碍,提高学习效果。同时,我也会鼓励学生利用课余时间进行自主学习和探究,提高他们的学习能力和综合素质。
2. 知识探究
(1) 同学们,请打开教材,我们先来回顾一下全等三角形的定义。全等三角形指的是在形状和大小上都完全相同的两个三角形。那么,如何判断两个三角形是否全等呢?
(2) 接下来,请大家观察教材中的图示,我们发现,如果两个三角形的两个角和它们之间的边分别相等,那么这两个三角形就是全等的。这就是我们今天要学习的角边角(ASA)全等条件。
六、拓展与延伸
1. 同学们,有兴趣的话,可以阅读一下这篇文章《全等三角形的判定方法及其应用》。这篇文章详细介绍了全等三角形的判定方法,包括SSS、SAS、ASA和AAS,以及它们在实际问题中的应用。通过阅读这篇文章,你们可以更深入地了解全等三角形的判定方法,提高你们解决问题的能力。
2. 另外,大家可以尝试解决一些与全等三角形有关的数学竞赛题目。这些题目往往具有一定的挑战性,但只要你们能够灵活运用我们学过的知识,相信你们一定能够解决。这不仅可以提高你们的数学能力,还能培养你们的逻辑思维能力和解决问题的能力。
四、教学资源
1. 软硬件资源:多媒体教学设备、白板、投影仪、计算器、几何模型等。
2. 课程平台:学校教学管理系统、数学学科教学资源库等。
3. 信息化资源:教学课件、视频动画、在线习题库、教育软件等。
4. 教学手段:小组讨论、合作学习、问题引导、案例分析等。
全等三角形判定基础知识讲解

全等三角形判定(基础)【学习目标】1.理解和掌握全等三角形判定方法“边角边”、“角边角”、“角角边”、“边边边”定理.2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定1——“边角边”1. 全等三角形判定1——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”). 要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等. 要点二、全等三角形判定2——“角边角”全等三角形判定2——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).要点诠释:如图,如果∠A =∠'A ,AB =''A B ,∠B =∠'B ,则△ABC ≌△'''A B C . 要点三、全等三角形判定3——“角角边”1.全等三角形判定3——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE ∥BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.要点四、全等三角形判定4——“边边边”全等三角形判定4——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).要点诠释:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C . 要点五、判定方法的选择1.选择哪种判定方法,要根据具体的已知条件而定,见下表:已知条件可选择的判定方法SAS AAS ASA一边一角对应相等两角对应相等ASA AAS两边对应相等SAS SSS2.如何选择三角形证全等(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;(2)可以从已知出发,看已知条件确定证哪两个三角形全等;(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.【典型例题】类型一、全等三角形的判定1——“边角边”1、已知:如图,AB=AD,AC=AE,∠1=∠2.求证:BC=DE.【思路点拨】由条件AB=AD,AC=AE,需要找夹角∠BAC与∠DAE,夹角可由等量代换证得相等.【答案与解析】证明:∵∠1=∠2∴∠1+∠CAD=∠2+∠CAD,即∠BAC=∠DAE在△ABC和△ADE中∴△ABC≌△ADE(SAS)∴BC=DE(全等三角形对应边相等)【总结升华】证明角等的方法之一:利用等式的性质,等量加等量,还是等量.举一反三:【变式】如图,将两个一大、一小的等腰直角三角尺拼接(A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.【答案】AE=CD,并且AE⊥CD证明:延长AE交CD于F,∵△ABC和△DBE是等腰直角三角形∴AB=BC,BD=BE在△ABE和△CBD中∴△ABE≌△CBD(SAS)∴AE=CD,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC=90°∴AE⊥CD类型二、全等三角形的判定2——“角边角”2、已知:如图,E,F在AC上,AD∥CB且AD=CB,∠D=∠B.求证:AE=CF.【答案与解析】证明:∵AD∥CB∴∠A=∠C在△ADF与△CBE中∴△ADF≌△CBE (ASA)∴AF =CE ,AF+EF=CE+EF故得:AE=CF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.举一反三:【变式】如图,AB∥CD,AF∥DE,BE=CF.求证:AB=CD.【答案】证明:∵AB∥CD,∴∠B=∠C.∵AF∥DE,,∴∠AFB=∠DEC.又∵BE=CF,∴BE+EF=CF+EF,即BF=CE.在△ABF和△DCE中,∴△ABF≌△DCE(ASA)∴AB=CD(全等三角形对应边相等).类型三、全等三角形的判定3——“角角边”3、已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明:∵AB⊥AE,AD⊥AC,∴∠CAD=∠BAE=90°∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD在△BAC和△EAD中∴△BAC≌△EAD(AAS)∴AC =AD【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.类型四、全等三角形的判定4——“边边边”4、已知:如图,△RPQ中,RP=RQ,M为PQ的中点.求证:RM平分∠PRQ.【思路点拨】由中点的定义得PM=QM,RM为公共边,则可由SSS定理证明全等.【答案与解析】证明:∵M为PQ的中点(已知),∴PM=QM在△RPM和△RQM中,∴△RPM≌△RQM(SSS).∴∠PRM=∠QRM(全等三角形对应角相等).即RM平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.举一反三:【变式】已知:如图,AD=BC,AC=BD.试证明:∠CAD=∠DBC.【答案】证明:连接DC,在△ACD与△BDC中∴△ACD≌△BDC(SSS)∴∠CAD=∠DBC(全等三角形对应角相等)。
1.5.3全等三角形判定(角边角-角角边)细致

450
A
A 3cm A3cmB A 3cm A3cm
3cm
B
第4页,共19页。
探究与 新知
三角形全等判定公理3
有两个角和这两个角的夹边对应相等的两个三
角形全等,简写成“角边角”或“ASA”
A 几何语言:
在△ABC与△DEF中
∠B=∠E, BC=EF, ∠C=∠F
∴ΔABC≌DEF( ASA )
B
C
例: 如图,O是AB的中点,A= B, AO与C BO全D 等吗?
为什么?
C
两角和夹边对应相等
A
O
B
在 AOC和和BOD中 D
A B (已知)
AO BO (中点的定义) ?
AOC BOD (对顶角相等)
AOC BOD (( ASA))
第12页,共19页。
(1) 图中的两个三角形全等吗? 请说明理由.
五、思考题
如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么? AD与BC呢?
证明:∵ AB∥CD,AD∥BC(已知 )
D
3 1
A
C
2 4
B
∴ ∠1=∠2 ∠3=∠4 (两直线平行,内错角相等)
∴在△ABC与△CDA中 ∠1=∠2 (已证) AC=AC (公共边)
∠3=∠4 (已证)
∴ △ABC≌△CDA(ASA)
(2) AE=AD
(3) BD=CE
证明: 在ABE 和ACD 中, B C (已知) AB AC (已知)
A A (公共角)
D
E
O
B
C
ABE ACD ( ASA)
AE AD (全等三角形对应边相等)
AB AC
初中数学全等三角形公式

初中数学全等三角形公式初中数学全等三角形公式数学是研究数量、结构、变化、空间以及信息等概念的一门学科。
下面是小编为大家收集的初中数学全等三角形公式,欢迎大家分享。
全等三角形的要义:在同一平面内能够完全重合(大小,形状都相等的三角形)的两个三角形称为全等三角形。
全等三角形1全等三角形的对应边、对应角相等2 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等3 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等4 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等5 边边边公理(SSS) 有三边对应相等的两个三角形全等三角形全等的性质:1.全等三角形的对应角相等。
2.全等三角形的对应边相等。
3.全等三角形的对应边上的高对应相等。
4.全等三角形的对应角的角平分线相等。
5.全等三角形的对应边上的中线相等。
6.全等三角形面积相等。
7.全等三角形周长相等。
公式要领总结:斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等。
初中数学全等三角形公式运用大全三角形具有一定的稳定性,所以我们用这个原理来做脚手架及其他支撑物体。
全等三角形公式运用1、性质中三角形全等是条件,结论是对应角、对应边相等。
而全等的判定却刚好相反。
2.利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键。
在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
3,当图中出现两个以上等边三角形时,应首先考虑用SAS找全等三角形。
4.用在实际中,一般我们用全等三角形测相等的距离。
以及相等的角,可以用于工业和军事。
所有学习过的初中数学知识都可以运用到现实的生活中,为我们的生活带来方便。
初中数学正方形定理公式关于正方形定理公式的内容精讲知识,希望同学们很好的掌握下面的内容。
正方形定理公式正方形的特征:①正方形的四边相等;②正方形的四个角都是直角;③正方形的两条对角线相等,且互相垂直平分,每一条对角线平分一组对角;正方形的判定:①有一个角是直角的菱形是正方形;②有一组邻边相等的矩形是正方形。
三角形全等的判定“边角边”判定定理教案

三角形全等的判定-“边角边”判定定理教案一、教学目标:1. 让学生理解并掌握三角形全等的概念。
2. 让学生了解并掌握“边角边”判定定理。
3. 培养学生运用“边角边”判定定理证明三角形全等的能力。
二、教学内容:1. 三角形全等的定义。
2. “边角边”判定定理的内容及其证明。
3. “边角边”判定定理在实际问题中的应用。
三、教学重点:1. 三角形全等的概念。
2. “边角边”判定定理的证明。
四、教学难点:1. 三角形全等的证明。
2. “边角边”判定定理在实际问题中的应用。
五、教学方法:1. 采用讲授法讲解三角形全等的定义和“边角边”判定定理。
2. 利用图形演示法展示三角形全等的证明过程。
3. 运用练习法巩固学生对“边角边”判定定理的理解和应用。
4. 采用小组讨论法培养学生的合作意识和解决问题的能力。
教案一、导入(5分钟)1. 复习三角形全等的概念。
2. 提问:我们已经学习了三角形全等的哪些判定方法?二、新课讲解(15分钟)1. 讲解三角形全等的定义。
2. 引入“边角边”判定定理,讲解其内容及其证明过程。
3. 通过图形演示,让学生直观地理解“边角边”判定定理。
三、实例分析(10分钟)1. 给出实例,让学生运用“边角边”判定定理证明三角形全等。
2. 引导学生分析实例中的关键步骤,巩固对“边角边”判定定理的理解。
四、课堂练习(10分钟)1. 布置练习题,让学生独立完成。
2. 选取部分学生的作业进行点评,讲解错误原因,纠正错误。
五、课堂小结(5分钟)1. 总结本节课所学内容,强调三角形全等的判定方法。
2. 提醒学生在实际问题中运用“边角边”判定定理时,要注意分析题目条件。
六、课后作业(课后自主完成)1. 复习本节课所学内容,整理笔记。
2. 完成课后练习题,巩固对“边角边”判定定理的理解和应用。
六、教学评价:1. 通过课堂讲解、练习和课后作业,评价学生对三角形全等概念和“边角边”判定定理的理解程度。
2. 观察学生在实例分析和练习中的表现,评估其运用“边角边”判定定理解决问题的能力。
1.5三角形全等的判定

1.5三角形全等的判定在我们的数学世界中,三角形全等的判定是一个极其重要的知识点。
它就像是一把神奇的钥匙,能够帮助我们打开解决众多几何问题的大门。
首先,咱们来聊聊什么是三角形全等。
简单说,就是两个三角形的形状和大小完全一样。
那怎么来判定两个三角形是不是全等呢?这就有几种方法啦。
第一种方法是“边边边”(SSS)判定定理。
如果两个三角形的三条边都分别相等,那么这两个三角形就全等。
比如说,有两个三角形,一个三角形的三条边分别是 3 厘米、4 厘米、5 厘米,另一个三角形的三条边也是 3 厘米、4 厘米、5 厘米,那这两个三角形就是全等的。
这就好像是我们做拼图,如果三块拼图的边都能完美地对上,那这三块拼图就是完全一样的。
接下来是“边角边”(SAS)判定定理。
如果两个三角形的两条边及其夹角分别相等,那么这两个三角形全等。
想象一下,一个三角形的两条边分别是 6 厘米和 8 厘米,它们的夹角是 60 度;另一个三角形也有两条边是 6 厘米和 8 厘米,夹角同样是 60 度,那这两个三角形就是一模一样的。
还有“角边角”(ASA)判定定理。
当两个三角形的两个角及其夹边分别相等时,它们全等。
比如一个三角形的两个角分别是 45 度和 90度,夹边是 7 厘米;另一个三角形也有两个角是 45 度和 90 度,夹边也是 7 厘米,那它们肯定全等。
再说说“角角边”(AAS)判定定理。
如果两个三角形的两个角和其中一个角的对边分别相等,那么这两个三角形全等。
打个比方,一个三角形有两个角分别是 30 度和 50 度,30 度角的对边是 5 厘米;另一个三角形也有两个角是 30 度和 50 度,30 度角的对边也是 5 厘米,那这两个三角形就是全等的。
这些判定定理在解决实际问题中非常有用。
比如说,在建筑工地上,工程师要确保两个钢梁组成的三角形结构完全一样,就可以用这些判定定理来进行测量和计算。
在数学考试中,关于三角形全等的判定也是经常出现的考点。
三角形全等的判定方法(5种)例题+练习(全面)

三角形全等的判定方法(5种)例题+练习(全面)本文讲述了全等三角形的判定方法,重点是边角边和角边角。
边角边指两边及其夹角分别相等的两个三角形全等,可以简写成“SAS”。
需要注意的是,必须是两边及其夹角,不能是两边和其中一边的对角。
例如,在图中的△ABC和△ABD中,虽然有一个角和两边相等,但是这两个三角形不全等。
但是在例1中,如果AC=AD,且∠CAB=∠DAB,则可以证明△ACB≌△ADB。
在例2中,如果AD∥BC,且∠ABC=∠DCB,AB=DC,AE=DF,则可以证明BF=CE。
角边角是指两角及其夹边分别相等的两个三角形全等,可以简写成“ASA”。
例如,在例2中,如果AD平分∠BAC,且∠ABD=∠ACD,则可以直接判定△ABD≌△ACD。
在例3中,如果在Rt△ABC中,BC=2cm,CD⊥AB,且EC=BC,EF=5cm,则可以求出AE的长度。
除了边角边和角边角外,还有三种判定全等三角形的条件。
在例5中,如果在△ABC和△DEF中,AB=DE,BC=EF,且有一个角相等,则可以证明△ABC≌△DEF。
在例6中,如果AB∥DE,AB=DE,BF=CE,则可以证明△ABC≌△DEF。
在例7和例8中,分别是通过角平分线和垂线的判定方法来证明两个三角形全等。
总之,掌握全等三角形的判定方法对于解决几何问题非常重要。
1.如图所示,在三角形ABC中,已知AB=DC,∠ABC=∠DCB。
根据角角边相等可知,∠ACB=∠DCB。
又因为AB=DC,所以BC=AC。
因此,根据SSS(边边边)相等可知,△ABC≌△DCB。
同时,∠ACB=∠DCB,AC=BC=DC。
2.如图所示,在三角形ABD和ABF中,已知AD=AE,∠1=∠2,BD=CE。
根据角角边相等可知,∠ABD=∠BCE。
又因为AD=CE,所以BD=BE。
因此,根据SAS(边角边)相等可知,△ABD≌△BCE。
同时,∠ABD=∠BCE,AD=CE=BE。
八年级数学上册 1.5 三角形全等的判定( 教师版P6含解析)

数学八年级上第1章第5节三角形全等的判定(第1课时)【教学目标】 1.了解三角形的稳定性,掌握三角形全等的条件——SSS。
2.会用SSS判定两个三角形全等。
【重难点】重点:判定两个三角形全等的基本事实,三边对应相等两个三角形全等。
难点:“尺规作图”对作图工具作了限制,学生初次遇到。
【教学过程】一、复习旧知:如图1,△ABC≌△DBC,∠A和∠D是对应角,说出另外两组对应角和各组对应边,指出他们的关系,并说明理由。
二、引入新知:使用直尺和圆规根据已知三边画三角形,比较各组所画的三角形,让学生发现这些三角形的共同点三、归纳新知:三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)四、应用新知:例1:如图2,在四边形ABCD中,AB=CD,AD=CB,则∠A=∠C,请说明理由。
AB=CD,(已知)解:在△ABD和△CDB中 AD=CB,(已知)BD=DB,(公共边)∴△ABD≌△CDB。
(SSS)∴∠A=∠C (根据什么?)注意:书写格式必须规范。
例2:已知∠BAC(如图3),用直尺和圆规作∠BAC的平分线AD,并说出该作法正确的理由。
作法1.以点A为圆心,适当长为半径作圆弧,与角两边分别交于点E,F2.分别以E,F为圆心,大于12EF长为半径作圆弧,两弧交于∠BAC内一点D;3.过点A,D作射线AD。
解:通过△AED≌△AED(SSS),证明∠CAD=∠BAD(过程略)五、练习:1. 如图,已知AB=DC,AC=BD,AC、BD相交于点E,过E点作EF∥B C,交CD于F.⑴根据条件,可以直接证明哪两个三角形全等?并加以证明.⑵EF平分∠DEC吗?为什么?解:⑴可证明△ABC≌△DCB.I∵AB=DC,AC=BD,BC=CB,∴△ABC≌△DCB.⑵∵△ABC≌△DCB,∴∠ACB =∠DBC.又∵EF∥B C,∴∠ACB =∠FEC,∴∠DBC =∠DEF,即∠FEC =∠DEF.∴EF平分∠DEC.2.如图,已知AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.证法1:连AD,△ACD和△ABD中,,∴△ACD ≌△ABD (SSS ),∴∠EAD=∠FAD ,即AD 平分∠EAF ,∵DE ⊥AE ,DF ⊥AF ,∴DE=DF .证法2:证△ACD ≌△ABD 后,S △ACD =S △ABD ,AC ·DF/2=BC ·DE/2,∵AC=AB ∴DF=DE【注意】:有时为解题需要,在原图上添一些线,这些线叫做辅助线,辅助线通常画成虚线。
全等三角形的判定-角边角-角角边(最新)知识讲解

(1)AC∥BD,CE=DF, AC=BD
(SAS)
( 2) AC=BD, AC∥BD ∠A=∠B (ASA)
( 3) CE=DF,∠AEC=∠BFD ∠C=∠D (ASA)
( 4)∠ C= ∠D,AC=BD ∠A=∠B A
(ASA)
C
F E
D
B
思考:如果两个三角形有两个角 和其中一个角的对边分别对应相 等,那么这两个三角形是否全等?
用符号语言表达为: AB=DE B C
在△ABC与△DEF中 ∠B=∠E
D
BC=EF
E
F
∴△ABC≌△DEF(SAS)
已知:如图,要得到△ABC≌ △ABD,已经隐含 有条件是__A_B_=__A_B__根据所给的判定方法,在下 列横线上写出还需要的两个条件
(1)_A__C_=_A_D__∠__C_A_B_=__∠_D_A_B (SAS)
如果知道两个三角形的两个角及一条边分别对 应相等,这两个三角形一定全等吗?
这时应该有两种不同的情况: (1)两个角及两角的夹边; (2)两个角及其中一角的对边
图24.2.8
探究1 先任意画出一个△ABC,
再画一个△A'B'C',使A'B'=AB, ∠A'=∠A, ∠B' =∠B 。把画好
的△A'B'C'剪下,放到△ABC上, 它们全等吗?
( 2 ) __B_C_=_B__D__A__C_=_A_D____
(SSS)
C
A
B
D
如图,小明不慎将一块 三角形模具打碎为两 块,他是否可以只带其 中的一块碎片到商店 去,就能配一块与原来 一样的三角形模具吗? 如果可以,带哪块去合 适? 你能说明其中理由吗?
三角形全等的判定“角边角与角角边”(6种题型)-2023年新八年级数学题型(人教版)(解析版)

三角形全等的判定“角边角与角角边”(6种题型)【知识梳理】一、全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).要点诠释:如图,如果∠A =∠'A ,AB =''A B ,∠B =∠'B ,则△ABC ≌△'''A B C .二、全等三角形判定——“角角边” 1.全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.【考点剖析】题型一:用“角边角”直接证明三角形全等例1.如图,∠A =∠B ,AE =BE ,点D 在 AC 边上,∠1=∠2,AE 和BD 相交于点O .求证:△AEC ≌△BED ;【详解】∵AE 和BD 相交于点O ,∴∠AOD=∠BOE .在△AOD 和△BOE 中,∠A=∠B ,∴∠BEO=∠2.又∵∠1=∠2,∴∠1=∠BEO ,∴∠AEC=∠BED .在△AEC 和△BED 中,A B AE BEAEC BED ∠∠⎧⎪⎨⎪∠∠⎩===∴△AEC ≌△BED (ASA ).【变式1】如图,AB =AD ,∠1,DA 平分∠BDE .求证:△ABC ≌△ADE .【解答】证明:∵∠1=∠2,∴∠1+∠DAC =∠2+∠DAC ,∴∠BAC =∠DAE ,∵AB =AD ,∴∠ADB =∠B ,∵DA 平分∠BDE .∴∠ADE =∠ADB ,∴∠ADE =∠B ,在△ABC和△ADE中,{∠ADE=∠B AB=AD∠BAC=∠DAE,∴△ABC≌△ADE(ASA).【变式2】如图,已知∠1=∠2,∠3=∠4,要证BC=CD,证明中判定两个三角形全等的依据是()A.角角角B.角边角C.边角边D.角角边【分析】已知两角对应相等,且有一公共边,利用全等三角形的判定定理进行推理即可.【解答】解:在△ABC与△ADC中,{∠1=∠2 AC=AC∠3=∠4,则△ABC≌△ADC(ASA).∴BC=CD.故选:B.【变式3】(2022•长安区一模)已知:点B、E、C、F在一条直线上,AB∥DE,AC∥DF,BE=CF.求证:△ABC≌△DEF.【解答】证明:∵AB∥DE,∴∠B=∠DEF,∵AC∥DF,∴∠ACB=∠F,∵BE=CF,∴BE+EC=CF+EC,即BC =EF ,在△ABC 和△DEF 中,{∠B =∠DEFBC =EF ∠ACB =∠F,∴△ABC ≌△DEF (ASA ). 题型二:用“角边角”间接证明三角形全等例2.如图,已知AB ∥CD ,AB =CD ,∠A =∠D .求证:AF =DE .【详解】证明:∵AB //CD ,∴∠B =∠C ,在△ABF 和△DCE 中,A D AB CD BC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABF ≌△DCE (ASA ),∴AF =DE .【变式1】已知:如图,E ,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B .求证:AE =CF .【答案与解析】证明:∵AD ∥CB∴∠A =∠C在△ADF 与△CBE 中A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADF ≌△CBE (ASA )∴AF =CE ,AF +EF =CE +EF故得:AE =CF【变式2】如图,AB =AC ,AB ⊥AC ,AD ⊥AE ,且∠ABD =∠ACE .求证:BD =CE .【详解】∵AB ⊥AC ,AD ⊥AE ,∴∠BAE +∠CAE =90°,∠BAE +∠BAD =90°,∴∠CAE =∠BAD .又AB =AC ,∠ABD =∠ACE ,∴△ABD ≌△ACE (ASA ).∴BD =CE .【变式3】如图,要测量河两岸相对两点A 、B 间的距离,在河岸BM 上截取BC =CD ,作ED ⊥BD 交AC 的延长线于点E ,垂足为点D .(DE ≠CD )(1)线段 的长度就是A 、B 两点间的距离(2)请说明(1)成立的理由.【解答】解:(1)线段DE 的长度就是A 、B 两点间的距离;故答案为:DE ;(2)∵AB ⊥BC ,DE ⊥BD∴∠ABC =∠EDC =90°又∵∠ACB =∠DCE ,BC =CD∴△ABC ≌△CDE (ASA )∴AB =DE .【变式4】如图,G 是线段AB 上一点,AC 和DG 相交于点E.请先作出∠ABC 的平分线BF ,交AC 于点F ;然后证明:当AD∥BC,AD =BC ,∠ABC=2∠ADG 时,DE =BF.【答案与解析】证明: ∵AD∥BC,∴∠DAC=∠C∵BF 平分∠ABC∴∠ABC=2∠CBF∵∠ABC=2∠ADG∴∠CBF=∠ADG在△DAE 与△BCF 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF(ASA )∴DE=BF【变式5】已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.【答案】证明:∵MQ 和NR 是△MPN 的高,∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA )∴PM =HN【变式6】如图,已知224m ABC S =△,AD 平分BAC ∠,且AD BD ⊥于点D ,则ADC S =△________2m .【答案】12【详解】解:如图,延长BD 交AC 于点E ,∵AD 平分BAC ∠,AD BD ⊥,∴BAD EAD ∠=∠,90ADB ADE ∠=∠=︒.∵AD AD =,∴()ADB ADE ASA ≌.∴BD DE =.∴ABD AED S S =△△,BCD ECD S S =. ∴12ABD BCD AED ECD ABC S S S S S =++=△△△△△.即12ADC ABC S S =.∵224m ABC S =△,∴212m ADC S =△.故答案为:12.【变式7】(2022秋•苏州期中)如图,△ABC 中,AD 是BC 边上的中线,E ,F 为直线AD 上的点,连接BE ,CF ,且BE ∥CF .(1)求证:△BDE ≌△CDF ;(2)若AE =13,AF =7,试求DE 的长.【解答】(1)证明:∵AD 是BC 边上的中线,∴BD =CD ,∵BE ∥CF ,∴∠DBE =∠DCF ,在△BDE 和△CDF 中,,∴△BDE ≌△CDF (ASA );(2)解:∵AE =13,AF =7,∴EF =AE ﹣AF =13﹣7=6,∵△BDE ≌△CDF ,∴DE =DF ,∵DE +DF =EF =6,∴DE =3.题型三:用“角角边”直接证明三角形全等例3.如图,在四边形ABCD中,E是对角线AC上一点,AD∥BC,∠ADC=∠ACD,∠CED+∠B=180°.求证:△ADE≌△CAB.【解答】证明:∵∠ADC=∠ACD,∴AD=AC,∵AD∥BC,∴∠DAE=∠ACB,∵∠CED+∠B=180°,∠CED+∠AED=180°,∴∠AED=∠B,在△ADE与△CAB中,{∠DAE=∠ACB ∠AED=∠BAD=AC,∴△ADE≌△CAB(AAS).【变式】(202210块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B 分别与木墙的顶端重合.(1)求证:△ADC≌△CEB;(2)求两堵木墙之间的距离.【解答】(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,∴∠BCE=∠DAC在△ADC 和△CEB 中,∴△ADC ≌△CEB (AAS ); (2)解:由题意得:AD =2×3=6(cm ),BE =7×2=14(cm ),∵△ADC ≌△CEB ,∴EC =AD =6cm ,DC =BE =14cm ,∴DE =DC +CE =20(cm ),答:两堵木墙之间的距离为20cm .题型四:用“角角边”间接证明三角形全等例4、已知:如图,AB ⊥AE ,AD ⊥AC ,∠E =∠B ,DE =CB .求证:AD =AC .【答案与解析】证明:∵AB ⊥AE ,AD ⊥AC ,∴∠CAD =∠BAE =90°∴∠CAD +∠DAB =∠BAE +∠DAB ,即∠BAC =∠EAD在△BAC 和△EAD 中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC ≌△EAD (AAS )∴AC =AD【变式】已知:如图,90ACB ∠=︒,AC BC =,CD 是经过点C 的一条直线,过点A 、B 分别作AE CD ⊥、 BF CD ⊥,垂足为E 、F ,求证:CE BF =.【答案与解析】证明:∵ CD AE ⊥,CD BF ⊥∴︒=∠=∠90BFC AEC∴︒=∠+∠90B BCF∵,90︒=∠ACB∴︒=∠+∠90ACF BCF∴B ACF ∠=∠在BCF ∆和CAE ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠BC AC B ACE BFC AEC∴BCF ∆≌CAE ∆(AAS )∴BF CE =【总结升华】要证BF CE =,只需证含有这两个线段的BCF ∆≌CAE ∆.同角的余角相等是找角等的好方法.题型五:“边角边”与“角角边”综合应用例5.如图,120CAB ABD ∠+∠=AD 、BC 分别平分CAB ∠、ABD ∠,AD 与BC 交于点O .(1)求AOB ∠的度数;(2)说明AB AC BD =+的理由.【答案】(1)120°;(2)见解析【详解】解:(1)∵AD ,BC 分别平分∠CAB 和∠ABD ,∠CAB +∠ABD =120°,∴∠OAB +∠OBA =60°,∴∠AOB =180°-60°=120°;(2)在AB 上截取AE =AC ,∵∠CAO=∠EAO,AO=AO,∴△AOC≌△AOE(SAS),∴∠C=∠AEO,∵∠C+∠D=(180°-∠CAB-∠ABC)+(180°-∠ABD-∠BAD)=180°,∴∠AEO+∠D=180°,∵∠AEO+∠BEO=180°,∴∠BEO=∠D,又∠EBO=∠DBO,BO=BO,∴△OBE≌△OBD(AAS),∴BD=BE,又AC=AE,∴AC+BD=AE+BE=A B.【变式】如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)求证:①△ADC≌△CEB;②DE=AD+BE.(2)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE又怎样的关系?并加以证明.【答案】(1)①证明见解析;②证明见解析;(2)DE=AD-BE,证明见解析.【详解】解:(1)①证明:∵AD⊥DE,BE⊥DE,∴∠ADC=∠BEC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,∴∠DAC=∠BCE,在△ADC 和△CEB 中,CDA BEC DAC ECB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△CEB (AAS ).②证明:由(1)知:△ADC ≌△CEB ,∴AD =CE ,CD =BE ,∵DC +CE =DE ,∴AD +BE =DE .(2)成立.证明:∵BE ⊥EC ,AD ⊥CE ,∴∠ADC =∠BEC =90°,∴∠EBC +∠ECB =90°,∵∠ACB =90°,∴∠ECB +∠ACE =90°,∴∠ACD =∠EBC ,在△ADC 和△CEB 中,ACD CBE ADC BEC AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS ),∴AD =CE ,CD =BE ,∴DE =EC -CD =AD -BE .题型六:尺规作图——利用角边角或角角边做三角形例6、已知三角形的两角及其夹边,求作这个三角形已知:∠α,∠β和线段c ,如图4-4-21所示.图4-4-21求作:△ABC ,使∠A =∠α,∠B =∠β,AB =c .作法:(1)作∠DAF =∠α;图4-4-224-4-23(2)在射线AF 上截取线段AB =c ;图4-4-24(3)以B 为顶点,以BA 为一边,在AB 的同侧作∠ABE =∠β,BE 交AD 于点C .△ABC 就是所求作的三角形.[点析] 我们这样作出的三角形是唯一的,依据是两角及其夹边分别相等的两个三角形全等. 例7.已知:角α,β和线段a ,如图4-4-29所示,求作:△ABC ,使∠A =∠α,∠B =∠β,BC =a .图4-4-29[解析] 本题所给条件是两角及其中一角的对边,可利用三角形内角和定理求出∠C ,再利用两角夹边作图. 解: 如图4-4-30所示:(1)作∠γ=180°-∠α-∠β;(2)作线段BC =a ;(3)分别以B ,C 为顶点,以BC 为一边作∠CBM =∠β,∠BCN =∠γ;(4)射线BM ,CN 交于点A .△ABC 就是所求作的三角形.图4-4-30【变式】(2022春·陕西·七年级陕西师大附中校考期中)尺规作图已知:α∠,∠β和线段a ,求作ABC ,使A α∠=∠,2B β∠=∠,AB a =.要求:不写作法,保留作图痕迹,标明字母.【详解】解:如图,△ABC即为所求..【过关检测】一、单选题A.带①去B.带②去C.带③去D.①②③都带去【答案】A【分析】根据全等三角形的判定可进行求解【详解】解:第①块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.故选:A.【点睛】此题主要考查了全等三角形的判定方法的开放性的题,要求学生将所学的知识运用于实际生活中,要认真观察图形,根据已知选择方法.≌过程中,先作2.(2023春·广东佛山·七年级校考期中)如图,在用尺规作图得到DBC ABCDBC ABC ∠=∠,再作DCB ACB ∠=∠,从而得到DBC ABC ≌,其中运用的三角形全等的判定方法是( )A .SASB .ASAC .AASD .SSS【答案】B 【分析】根据题意分析可得DBC ABC ∠=∠,DCB ACB ∠=∠,再加上公共边BC BC =,根据AAS ,即可判断DBC ABC ≌.【详解】解:∵得DBC ABC ∠=∠, BC BC =,DCB ACB ∠=∠,∴DBC ABC≌()ASA , 故选:B .【点睛】本题考查了作一个角等于已知角,全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.3.(2023春·重庆沙坪坝·七年级重庆一中校考期末)如图,OC 平分AOB ∠,点P 是射线OC 上一点,PM OB ⊥于点M ,点N 是射线OA 上的一个动点,连接PN ,若6PM =,则PN 的长度不可能是( )【答案】D 【分析】如图所示,过点P 作PH OA ⊥于H ,证明POH POM △≌△得到6PH PM ==,由垂线段最短可知PN PH ≥,由此即可得到答案.【详解】解:如图所示,过点P 作PH OA ⊥于H ,∵PM OB ⊥,∴90PHO PMO ==︒∠∠,∵OC 平分AOB ∠,∴POH POM ∠=∠,又∵OP OP =,∴()AAS POH POM △≌△,∴6PH PM ==,由垂线段最短可知PN PH ≥,∵(264036=>,∴6,∴四个选项中,只有D 选项符合题意,故选:D .【点睛】本题主要考查了全等三角形的性质与判定,垂线段最短,实数比较大小,正确作出辅助线构造全等三角形是解题的关键. 4.(2023春·陕西咸阳·七年级统考期末)如图,AD BC ∥,ABC ∠的平分线BP 与BAD ∠的平分线AP 相交于点P ,作PE AB ⊥于点E ,若4PE =,则点P 到AD 与BC 的距离之和为( )A .4B .6C .8D .10【答案】C【分析】如图所示,过点P 作FG AD ⊥与F ,延长FP 交BC 于G ,先证明AD FG ⊥,由角平分线的定义得到EBP GBP =∠∠,进而证明EBP GBP △≌△得到4PG PE ==,同理可得4PF PE ==,则8FG PF PG =+=,由此即可得到答案.【详解】解:如图所示,过点P 作FG AD ⊥与F ,延长FP 交BC 于G ,∵AD BC ∥,∴AD FG ⊥,∵PE AB ⊥,∴90PFA PEA PEB PGB ====︒∠∠∠∠,∵BP 平分ABC ∠,∴EBP GBP =∠∠,又∵BP BP =,∴()AAS EBP GBP △≌△,∴4PG PE ==,同理可得4PF PE ==,∴8FG PF PG =+=,∴点P 到AD 与BC 的距离之和为8,故选C .【点睛】本题主要考查了平行线的性质,全等三角形的性质与判定,角平分线的定义,平行线间的距离等等,正确作出辅助线构造全等三角形是解题的关键. 5.(2023春·福建福州·七年级福建省福州第十六中学校考期末)如图,90C ∠=︒,点M 是BC 的中点,DM 平分ADC ∠,且8CB =,则点M 到线段AD 的最小距离为( )A .2B .3C .4D .5【答案】C 【分析】如图所示,过点M 作ME AD ⊥于E ,证明MDE MDC △≌△,得到ME MC =,再根据线段中点的定义得到142ME MC BC ===,根据垂线段最短可知点M 到线段AD 的最小距离为4.【详解】解:如图所示,过点M 作ME AD ⊥于E ,∴90MED C ==︒∠∠,∵DM 平分ADC ∠,∴MDE MDC =∠∠,又∵MD MD =,∴()AAS MDE MDC △≌△,∴ME MC =,∵点M 是BC 的中点,8CB =,∴142ME MC BC ===,∴点M 到线段AD 的最小距离为4,故选:C .【点睛】本题主要考查了全等三角形的性质与判定,角平分线的定义,垂线段最短等等,正确作出辅助线构造全等三角形是解题的关键.6.(2023·全国·八年级假期作业)如图,点E 在ABC 外部,点D 在ABC 的BC 边上,DE 交AC 于F ,若123∠=∠=∠,AE AC =,则( ).A .ABD AFE △≌△B .AFE ADC ≌△△ C .AFE DFC ≌△△D .ABC ADE △≌△ 【答案】D 【分析】首先根据题意得到BAC DAE ∠=∠,E C ∠=∠,然后根据ASA 证明ABC ADE △≌△.【详解】解:∵12∠=∠,∴12DAC DAC ∠+∠=∠+∠,∴BAC DAE ∠=∠,∵23∠∠=,AFE DFC ∠=∠,∴E C ∠=∠,∴在ABC 和ADE V 中,BAC DAE AC AEC E ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴()ASA ABC ADE ≌△△, 故选:D .【点睛】此题主要考查全等三角形的判定,解题的关键是熟知全等三角形的判定定理.7.(2023·浙江·八年级假期作业)小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带( )A .带①去B .带②去C .带③去D .①②③都带去【答案】B 【分析】本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.【详解】解:①、③、④块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去, 只有第②块有完整的两角及夹边,符合ASA ,满足题目要求的条件,是符合题意的.故选:B .【点睛】本题主要考查三角形全等的判定,看这4块玻璃中哪个包含的条件符合某个判定.判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS . 8.(2023春·浙江宁波·七年级校考期末)如图,ABC 的两条高AD 和BF 相交于点E ,8AD BD ==,10AC =,2AE =,则BF 的长为( )A .11.2B .11.5C .12.5D .13【答案】A 【分析】先证明BDE ADC △≌△,可得 6DE DC ==,14BC =,而10AC =,再由等面积法可得答案.【详解】解:∵ABC 的两条高AD 和BF 相交于点E ,∴90ADB ADC BFA ∠=∠=︒=∠,∵AEF BED ∠=∠,∴DBE DAC ∠=∠,∵8AD BD ==,2AE =,∴BDE ADC △≌△,6DE =,∴6DE DC ==,∴14BC =,而10AC =,由等面积法可得:111481022BF ⨯⨯=⨯⨯,解得:11.2BF =;故选A【点睛】本题考查的是三角形的内角和定理的应用,全等三角形的判定与性质,等面积法的应用,证明BDE ADC △≌△是解本题的关键. 9.(2023春·辽宁沈阳·七年级沈阳市第一二六中学校考阶段练习)如图,抗日战争期间,为了炸毁敌人的碉堡,需要测出我军阵地与敌人碉堡的距离.我军战士想到一个办法,他先面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部点B ;然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E 上;最后,他用步测的办法量出自己与E 点的距离,从而推算出我军阵地与敌人碉堡的距离,这里判定ABC DEF ≌△△的理由可以是( )A . SSSB . SASC . ASAD . AAA【答案】C 【分析】根据垂直的定义和全等三角形的判定定理即可得到结论.【详解】解:∵士兵的视线通过帽檐正好落在碉堡的底部点B ,然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E 上,∴A D ∠=∠,∵AC BC ⊥,DF EF ^,∴90ACB DFE ∠=∠=︒,∵AC DF =,∴判定ABC DEF ≌△△的理由是ASA . 故选C .【点睛】本题主要考查了全等三角形的应用,分析题意找到相等的角和边判定三角形的全等是解题的关键.10.(2023春·四川达州·八年级统考期末)如图,已知BP 是ABC ∠的平分线,AP BP ⊥,若212cm BPC S =△,则ABC 的面积( )A .224cmB .230cmC .236cmD .不能确定【答案】A【分析】延长AP 交BC 于点C ,根据题意,易证()ASA ABP DBP ≌,因为APC △和DPC △同高等底,所以面积相等,根据等量代换便可得出2224cm ABC BPC S S ==.【详解】如图所示,延长AP ,交BC 于点D ,,∵AP BP ⊥,∴90APB DPB ∠=∠=︒,∵BP 是ABC ∠的角平分线,∴ABP DBP ∠=∠,在ABP 和DBP 中,ABP DBP BP BP APB DPB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴()ASA ABP DBP ≌,∴AP DP =,∴ABP DBP S S =△△,∵APC △和DPC △同底等高,∴APC DPC S S =△,∴PBC DPB DPC ABP APC S S S S S =+=+△△△△,∴2224ABC BPC S S cm ==,故选:C .【点睛】本题考查了三角形的角平分线和全等三角形的判定,解题的关键是熟练运用三角形的角平分线和全等三角形的判定.二、填空题 11.(2023·浙江·八年级假期作业)如图,D 在AB 上,E 在AC 上,且B C ∠=∠,补充一个条件______后,可用“AAS ”判断ABE ACD ≌.【答案】BE CD =或AE AD =【分析】由于两个三角形已经具备B C ∠=∠,A A ∠=∠,故要找边的条件,只要不是这两对角的夹边即可.【详解】解:∵B C ∠=∠,A A ∠=∠,∴若用“AAS ”判断ABE ACD ≌,可补充的条件是BE CD =或AE AD =;故答案为:BE CD =或AE AD =.【点睛】本题考查了全等三角形的判定,熟知掌握判定三角形全等的条件是解题的关键.七年级期末)如图,在ABC 中, 【答案】ASA【分析】由AD BC ⊥、AD 平分BAC ∠、AD AD =可得出两个三角形对应的两个角及其夹边相等,于是可以利用ASA 判定这两个三角形全等.【详解】∵AD BC ⊥,∴90BDA CDA ︒=∠=∠.∵AD 平分BAC ∠,∴BAD ∠CAD =∠.在ABD △与ACD 中,BDA CDA AD AD BAD CAD ∠=∠⎧⎪=⎨⎪∠=∠⎩ ∴()ASA ABD ACD ≌.故答案为:ASA【点睛】本题考查了三角形全等的判定条件,解题的关键是找到两个三角形对应的边角相等. 13.(2023春·陕西榆林·七年级统考期末)如图,AB CD ⊥,且AB CD =,连接AD ,CE AD ⊥于点E ,BF AD ⊥于点F .若8CE =,5BF =,4EF =,则AD 的长为________.【答案】9【分析】只要证明(AAS)ABF CDE ≌,可得8AF CE ==,5BF DE ==,推出AD AF DF =+即可得出答案.【详解】解:∵AB CD ⊥,CE AD ⊥,BF AD ⊥,∴90AFB CED ∠=∠=︒,90A D ∠+∠=︒,90C D ∠=∠=︒,∴A C ∠=∠,∵AB CD =,∴(AAS)ABF CDE ≌,∴8AF CE ==,5BF DE ==,∵4EF =,∴()8549AD AF DF =+=+−=,故答案为:9.【点睛】本题考查全等三角形的判定与性质,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型. 14.(2023春·山东枣庄·七年级统考期末)如图,A ,B 两个建筑物分别位于河的两岸,为了测量它们之间的距离,可以沿河岸作射线BF ,且使BF AB ⊥,在BF 上截取BC CD =,过D 点作DE BF ⊥,使E C A ,,在一条直线上,测得16DE =米,则A ,B 之间的距离为______米.【答案】16【分析】根据已知条件可得ABC EDC △≌△,从而得到DE AB =,从而得解.【详解】∵BF AB DE BF ⊥⊥,,∴90B EDC ∠=∠=°,∵90B EDC ∠=∠=,BC CD BCA DCE =∠=∠,,∴()ASA ABC EDC ≌△△,∴DE AB =.又∵16DE =米,∴16AB =米,即A B ,之间的距离为16米.【点睛】此题主要考查全等三角形的应用,解题的关键是熟知全等三角形的判定方法.15.(2023·广东茂名·统考一模)如图,点A 、D 、C 、F 在同一直线上,AB DE ∥,AD CF =,添加一个条件,使ABC DEF ≌△△,这个条件可以是______.(只需写一种情况)【答案】BC EF ∥或B E ∠=∠或BCA EFD ∠=∠或AB DE =(答案不唯一)【分析】先证明A EDF ∠=∠及AC DF =,然后利用全等三角形的判定定理分析即可得解.【详解】解∶BC EF ∥或B E ∠=∠或BCA EFD ∠=∠或AB DE =,理由是∶∵AB DE ∥,∴A EDF ∠=∠,∵AD CF =,∴AD CD CF CD +=+即AC DF =,当BC EF ∥时,有BCA EFD ∠=∠,则() ASA ABC DEF ≌, 当BCA EFD ∠=∠时,则() ASA ABC DEF ≌, 当B E ∠=∠时,则() AAS ABC DEF ≌, 当AB DE =时,则() SAS ABC DEF ≌,故答案为∶BC EF ∥或B E ∠=∠或BCA EFD ∠=∠或AB DE =.【点睛】本题考查了对全等三角形的判定定理的应用,掌握全等三角形的判定定理有SAS , ASA , AAS , SSS 是解题的关键. 16.(2023春·上海虹口·七年级上外附中校考期末)如图,有一种简易的测距工具,为了测量地面上的点M 与点O 的距离(两点之间有障碍无法直接测量),在点O 处立竖杆PO ,并将顶端的活动杆PQ 对准点M ,固定活动杆与竖杆的角度后,转动工具至空旷处,标记活动杆的延长线与地面的交点N ,测量点N 与点O 的距离,该距离即为点M 与点O 的距离.此种工具用到了全等三角形的判定,其判定理由是______.【答案】两个角及其夹边对应相等的两个三角形全等【分析】根据全等三角形的判定方法进行分析,即可得到答案.【详解】解:在POM 和PON △中,90OP OPPOM PON ⎪=⎨⎪∠=∠=︒⎩, ()ASA POM PON ∴≌,∴判定理由是两个角及其夹边对应相等的两个三角形全等,故答案为:两个角及其夹边对应相等的两个三角形全等.【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解题关键.【答案】 = 180BCA α∠+∠=︒【分析】①求出90BEC AFC ∠=∠=︒,CBE ACF ∠=∠,根据AAS 证BCE CAF ≌△△,推出BE CF =,CE AF =即可得出结果;②求出CBE ACF ∠=∠,由AAS 证BCE CAF ≌△△,推出BE CF =,CE AF =即可得出结果.【详解】解:①90BCA ∠=︒,90α∠=︒,90BCE CBE ∴∠+∠=︒,90BCE ACF ∠+∠=︒,CBE ACF ∴∠=∠,在BCE 和CAF V 中,BEC CFACB CA ⎪∠=∠⎨⎪=⎩,(AAS)BCE CAF ∴△≌△,BE CF ∴=,CE AF =,||||EF CF CE BE AF ∴=−=−,②α∠与BCA ∠应满足180BCA α∠+∠=︒,在BCE 中,180180CBE BCE BEC α∠+∠=︒−∠=︒−∠,180BCA α∠=︒−∠,BCA CBE BCE ∴∠=∠+∠,ACF BCE BCA ∠+∠=∠,CBE ACF ∴∠=∠,在BCE 和CAF V 中,CBE ACF BEC CFACB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)BCE CAF ∴△≌△, BE CF ∴=,CE AF =,||||EF CF CE BE AF ∴=−=−,故答案为:=,180BCA α∠+∠=︒.【点睛】本题是三角形综合题,主要考查了全等三角形的判定与性质、三角形的面积计算、三角形的外角性质等知识;解题的关键是判断出BCE CAF ≌△△. ABC 的角平分线,过点【答案】4【分析】延长CE 与BA 的延长线相交于点F ,利用ASA 证明ABD △和ACF △全等,进而利用全等三角形的性质解答即可.【详解】解:如图,延长CE 与BA 的延长线相交于点F ,90EBF F ∠+∠=︒,90ACF F ∠+∠=︒,EBF ACF ∴∠=∠,在ABD △和ACF △中,EBF ACF AB ACBAC CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ASA ABD ACF ∴≌, BD CF ∴=,BD Q 是ABC ∠的平分线,EBC EBF ∴∠=∠.在BCE 和BFE △中,BE BECEB FEB ⎪=⎨⎪∠=∠⎩,()ASA BCE BFE ∴≌, CE EF ∴=,2CF CE ∴=,24BD CF CE ∴===.故答案为:4.【点睛】本题主要考查了全等三角形的性质和判定,理解题意、灵活运用全等三角形的判定与性质是解题的关键.三、解答题【答案】(1)见解析(2)5【分析】(1)首先根据垂直判定AB EF ∥,得到ABC F ∠=∠,再利用AAS 证明即可;(2)根据全等三角形的性质可得9AB CF ==,4BC EF ==,再利用线段的和差计算即可.【详解】(1)解:∵CD AB ⊥,EF CE ⊥,∴AB EF ∥,∴ABC F ∠=∠,在ABC 和CFE 中,ACB EAC CE ⎪∠=∠⎨⎪=⎩, ∴()AAS ABC CFE △△≌; (2)∵ABC CFE △△≌, ∴9AB CF ==,4BC EF ==,∴5BF CF BC =−=.【点睛】本题考查了全等三角形的判定和性质,平行线的判定和性质,解题的关键是找准条件,证明三角形全等. 20.(2023春·陕西西安·七年级西安市铁一中学校考期末)如图,A ,C ,D 三点共线,ABC 和CDE 落在AD 的同侧,AB CE ∥,BC DE =,B D ∠=∠.求证:AB CE AD +=.【答案】见解析【分析】证明()AAS ABC CDE ≌,得出AB CD =,BC CE =,即可证明结论.【详解】解:∵AB CE ∥,∴A DCE ∠=∠,∵B D ∠=∠,BC DE =,∴()AAS ABC CDE ≌,∴AB CD =,BC CE =,∴AB CE CD AC AD +=+=.【点睛】本题主要考查了平行线的性质,三角形全等的判定和性质,解题的关键是熟练掌握三角形全等的判定方法证明ABC CDE △≌△.21.(2022秋·八年级课时练习)已知αβ∠∠,和线段a (下图),用直尺和圆规作ABC ,使A B AB a αβ∠=∠∠=∠=,,.【答案】见解析 【分析】先作出线段AB a =,再根据作与已知角相等的角的尺规作图方法作DAB EBA αβ∠=∠∠=∠,即可得到答案.【详解】解:作法如下图.1.作一条线段AB a =.2.分别以A ,B 为顶点,在AB 的同侧作DAB EBA αβ∠=∠∠=∠,,DA 与EB 相交于点C .ABC 就是所求作的三角形.【点睛】本题主要考查了三角形的尺规作图,熟知相关作图方法是解题的关键.22.(2023春·全国·七年级专题练习)如图,已知ABC ,请根据“ASA”作出DEF ,使DEF ABC ≌.【答案】见解析【分析】先作MEN B ∠=∠,再在EM 上截取ED BA =,在EN 上截取EF BC =,从而得到DEF ABC ≌.【详解】解:如图,DEF 为所作.【点睛】本题考查了作图-复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了全等三角形的判定. 23.(2023春·山西太原·七年级校考阶段练习)如图,点B 、F 、C 、E 在同一条直线上,已知FB CE =,AB DE ∥,ACB DFE ∠=∠,试说明:AC DF =.【答案】见解析【分析】利用ASA 定理证明三角形全等,然后利用全等三角形的性质分析求解.【详解】解:∵FB CE =,∴FB FC CE FC +=+,即BC EF =,∵AB DE ∥,∴B E ∠=∠,在ABC 和DEF 中B E BC EF ACB DFE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABC DEF ≌△△, ∴AC DF =.【点睛】此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法:SSS 、SAS 、ASA 、AAS 、HL .三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.24.(2020秋·广东广州·八年级海珠外国语实验中学校考阶段练习)如图,已知:EC AC =,BCE DCA ∠=∠,A E ∠=∠.求证:AB ED =.【答案】见解析【分析】先求出ACB ECD ∠=∠,再利用“角边角”证明ABC 和EDC △全等,然后根据全等三角形对应边相等证明即可.【详解】证明:∵BCE DCA ∠=∠,∴BCE ACE DCA ACE ∠+∠=∠+∠,即ACB ECD ∠=∠.在ABC 和EDC △中,∵ACB ECD AC ECA E ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ASA ABC EDC ≌△△.∴AB ED =.【点睛】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.25.(2023春·福建宁德·七年级校考阶段练习)如图,点B ,F ,C ,E 在直线l 上(F ,C 之间不能直接测量),点A ,D 在l 异侧,测得AB DE =,AB DE ∥,A D ∠=∠.(1)求证:ABC DEF ≌△△; (2)若10BE =,3BF =,求FC 的长度.【答案】(1)见解析(2)4【分析】(1)由AB DE ∥,得ABC DEF ∠=∠,而AB DE =,A D ∠=∠,即可根据全等三角形的判定定理“ASA ”证明ABC DEF ≌△△; (2)根据全等三角形的性质得BC EF =,则3BF CE ==,即可求得FC 的长度.【详解】(1)解:证明:∵AB DE ∥,∴ABC DEF ∠=∠,在ABC 和DEF 中,A D AB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩ ∴()ASA ABC DEF ≌△△; (2)解:由(1)知()ASA ABC DEF ≌△△,∴BC EF =, ∴BF FC CE FC +=+,∴3BF CE ==,∵10BE =,∴10334FC BE BF CE =−−=−−=,∴FC 的长度是4.【点睛】此题重点考查全等三角形的判定与性质、平行线的性质等知识,根据平行线的性质证明ABC DEF ∠=∠是解题的关键. 26.(2023·浙江·八年级假期作业)如图,ABC 中,BD CD =,连接BE ,CF ,且BE CF ∥.(1)求证:BDE CDF ≌;(2)若15AE =,8AF =,试求DE 的长.【答案】(1)证明见解析(2)72【分析】(1)根据平行线的性质可得BED CFD Ð=Ð,根据全等三角形的判定即可证明;(2)根据全等三角形的性质可得DE DF =,即可求得.【详解】(1)证明:∵BE CF ∥,∴BED CFD Ð=Ð,∵BDE CDF ∠=∠,BD CD =,∴()AAS BDE CDF ≌;(2)由(1)结论可得DE DF =,∵1587EF AE AF =−=−=,∴72DE =.【点睛】全等三角形的判定和性质,熟练掌握平行线的性质,全等三角形的判定和性质是解题的关键. 27.(2023春·江西鹰潭·七年级校考阶段练习)将两个三角形纸板ABC 和DBE 按如图所示的方式摆放,连接DC .已知DBA CBE ∠=∠,BDE BAC ∠=∠,AC DE DC ==.(1)试说明ABC DBE ≌△△.(2)若72ACD ∠=︒,求BED ∠的度数.【答案】(1)见解析(2)36BED ∠=︒【分析】(1)利用AAS 证明三角形全等即可;(2)全等三角形的性质,得到BED BCA ∠=∠,证明()SSS DBC ABC ≌,得到1362BCD BCA ACD ∠=∠=∠=︒,即可得解.【详解】(1)解:因为DBA CBE ∠=∠,所以DBA ABE CBE ABE ∠+∠=∠+∠,即DBE ABC ∠=∠.在ABC 和DBE 中,ABC DBE BAC BDEAC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩, 所以()AAS ABC DBE ≌. (2)因为ABC DBE ≌△△, 所以BD BA =,BCA BED ∠=∠.在DBC △和ABC 中,DC AC CB CBBD BA =⎧⎪=⎨⎪=⎩, 所以()SSS DBC ABC ≌, 所以1362BCD BCA ACD ∠=∠=∠=︒,所以36BED BCA ∠=∠=︒.【点睛】本题考查全等三角形的判定和性质.解题的关键是证明三角形全等. 28.(2023春·河南驻马店·七年级统考期末)如图,线段AD 是ABC 的中线,分别过点B 、C 作AD 所在直线的垂线,垂足分别为E 、F .(1)请问BDE 与CDF 全等吗?说明理由;(2)若ACF △的面积为10,CDF 的面积为6,求ABE 的面积.【答案】(1)BDE CDF ≌△△,见解析 (2)22【分析】(1)利用AAS 证明三角形全等即可.(2)根据中线性质,得到,ABD ACD ACF CDF CDF ==+=△△△△△BDE △S S S S S S ,结合ABEABD BDE S S S =+△△△计算即可. 【详解】(1)BDE CDF ≌△△,理由如下: ∵AD 是ABC 的中线,∴BD CD =,∵BE AE ⊥,CF AE ⊥,∴90BED CFD ∠=∠=︒,在BDE 和CDF 中,BED CFD BDE CDFBD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS BDE CDF ≌.(2)∵10ACF S =△,6CDF S =△,BDE CDF ≌,∴10616ACD ACF CDF S S S =+=+=△△△,6BDE CDF S S ==,∵BD CD =∴ABD △和ACD 是等底同高的三角形∴16ABD ACD S S ==△△∴16622ABE ABD BDE S S S =+=+=△△△.【点睛】本题考查了三角形全等的判定和性质,中线的性质,三角形面积的计算,熟练掌握三角形全等的判定和性质,中线的性质是解题的关键. 29.(2019·七年级单元测试)(1)求证:等边三角形内的任意一点到两腰的距离之和等于定长.(提示:添加辅助线证明)(2)如图所示,在三角形ABC 中,点D 是三角形内一点,连接DA 、DB 、DC ,若,=∠=∠AB AC ADB ADC ,求证:AD 平分BAC ∠.【答案】(1)详见解析;(2)详见解析.【分析】(1)已知点P 是等边三角形ABC 内的任意一点,过点P 分别作三边的垂线,分别交三边于点D 、点E 、点F .求证PD PE PF ++为定长,即可完成证明;(2)(面积法)过点A 作AE BD ⊥交BD 延长线于点E ,再过点A 作AF CD ⊥交CD 延长线于点F.因为ADB ADC ∠=∠,所以ADE ADF ∠=∠,因此(AAS)ADF ADE ≅,得到AF AE =.进而AFC AEB ≅,得到ABD ACD ∠=∠,因此BAD CAD ∠=∠,即AD 平分BAC ∠.【详解】(1) 已知:等边如图三角形ABC ,P 为三角形ABC 内任意一点,PD ⊥AB, PF ⊥AC, PE ⊥BC, 求证:PD+PE+PF 为定值.证明:如图:过点A 作AG BC ⊥,垂足为点G ,分别连接AP 、BP 、CP .∵ABC ABP BCP CAP S S S S =++, ∴11112222BC AG BC PE AC PF AB PD =++又∵BC=AB=AC∴AG=PE+PF+PD,即PD PE PF AG ++=定长.∴等边三角形内的任意一点到两腰的距离之和等于定长.(2)过点A 作AE BD ⊥交BD 延长线于点E ,再过点A 作AF CD ⊥交CD 延长线于点F.∵ADB ADC ∠=∠,∴ADE ADF ∠=∠,又∵AD=AD∴(AAS)ADF ADE ≅,∴AF AE =∴AFC AEB ≅,∴ABD ACD ∠=∠,∴BAD CAD ∠=∠,即AD 平分BAC ∠.【点睛】本题考查了等边三角形的性质和全等三角形的性质和判定,其中做出辅助线是解答本题的关键.。
全等三角形的判定-角边角和角角边

在选择时,可以根据已知条件的多少和问题的具体要求来决定使用哪种判定法。例如,如果 已知条件更符合角边角(ASA)判定法的条件,那么选择角边角(ASA)判定法可能更为简 便和直接。
PART 05
全等三角形的应用
两种方法的应用范围
角边角(ASA)判定法
01
适用于已知两个角和它们之间
的边的情况。
02
在几何证明和实际问题中广泛
应用,如建筑设计、地图制作
等。
03
角角边(AAS)判定法
04
适用于已知两个角和一个非夹
角的边的情况。
05
在解决一些特定问题时更为方
便,如测量问题、航海问题等
。
06
两种方法的选择原则
选择原则
角边角判定法的应用
在证明两个三角形全等时,如果已知条件符合角边角判定法 ,可以直接应用该判定法得出结论。
角边角判定法也可以用于解决一些实际问题,例如测量、绘 图等。
角边角判定法的证明
根据三角形的内角和性质,两个三角形的两组对应角相等,则它们的第三组对应角 也相等。
由于夹边相等,根据三角形的边角边全等判定,这两个三角形全等。
因此,角边角判定法得证。
PART 03
角角边判定法
REPORTING
WENKU DESIGN
角角边判定法的定义
两个三角形中,如果两个角分别相等,且这两个角所夹的一边也相等,则这两个 三角形全等。
简称"AAS"或"角角边"判定法。
角角边判定法的应用
在证明两个三角形全等时,如果已知条件符合角角边判定 法,可以直接应用此判定法证明三角形全等。
探索三角形全等的条件

探索三角形全等的条件作者:向进来源:《数学教学通讯(教师阅读)》2012年第07期摘要:笔者设计了一个教学案例,通过引导在学生回顾全等三角形的性质基础之上自然地过渡到探索三角形全等的条件上来. 在探索的过程中,出现了6个要素,这几个要素又应该怎么来选择,从而引起学生认知上的好奇,激发了学生的探究欲望,为学生提供“探索中学习”的时间和空间,突出自主、合作、探究式学习提供了必要的保证.关键词:三角形,全等,SSS教学背景1. 教学内容分析(1)本节教学内容是在学生学习了三角形的有关要素和性质、全等图形的特征的基础上,进一步研究三角形全等的条件.三角形全等的条件是应用全等三角形解决问题的前提,学习全等三角形的特征及后面将要学习的三角形全等的(“ASA”、“AAS”、“SAS”)判别方法作为探索三角形全等的核心内容,其内容在本章乃至整个初中数学中占有非常重要的基础性地位.本节教学共分三个课时,本节课是第一课时,主要内容是探索三角形全等的条件(SSS)和三角形的稳定性.而三角形全等条件的探索不仅能使学生深入理解三角形全等的条件,更能使学生体会分析问题、解决问题的方法.知识不难,难点在于教师通过设计学生活动,帮助学生形成分析问题的方法,并给学生创设新的问题情境,使学生运用方法,形成独立分析问题、解决问题的能力.(2)教材的重点:三角形全等条件的探索过程.教材从设置情境提出问题,到动手操作、交流,直至归纳得出结论,整个过程力图使学生不仅得到两个三角形全等的条件,更重要的是经历知识的形成过程,体会一种分析问题的方法,积累数学活动经验,这将有利于学生更好地理解数学、应用数学.(3)教材难点:三角形全等条件的探索过程中,特别是提出问题后,学生面对开放性问题,要做出全面、正确的分析,并对各种情况进行讨论.而初一学生还不具备独立系统的推理论证几何问题的能力,思维有一定的局限性,考虑问题不够全面,因此对初一学生有一定的难度.2. 学情分析本班学生学习基础不够好,在认知水平、学习能力、学习习惯上都有着很大的差异.在教学之前他们已经初步认识了三角形,了解了图形全等的概念及特征,掌握了全等图形的对应边、对应角的关系,这为探究三角形全等的条件做好了知识上的准备.另外,学生也基本具备了利用已知条件画三角形的能力,具备探索的热情和愿望,为学生主动参与本节课的操作、探究做好了准备.教学设计1. 学习方式对于全等三角形的研究,实际是平面几何中对封闭的两个图形关系研究的第一步.它是两个三角形间最简单、最常见的关系.它不仅是学习后面知识的基础,并且是证明线段相等、角相等以及两线互相垂直、平行的重要依据.因此必须熟练地掌握全等三角形的判定方法,并且能够灵活的应用.为了使学生更好地掌握这一部分内容,笔者遵循启发式教学原则,用设问形式创设问题情景,设计一系列实践活动,引导学生操作、观察、探索、交流、发现、思维,使学生经历从现实世界抽象出几何模型和运用所学内容解决实际问题的过程,真正把学生放到主体位置.2. 学习任务充分利用教科书提供的素材和活动,鼓励学生经历观察、操作、推理、想象等活动,发展学生的空间观念,体会分析问题、解决问题的方法,积累数学活动经验.培养学生有条理的思考、表达和交流的能力,并且在直观操作的基础上,将直观与简单推理相结合,注意学生推理意识的建立和对推理过程的理解,能运用自己的方式有条理的表达推理过程,为证明能力的培养打下基础.3. 学生的认知起点?摇学生通过前面的学习已了解了图形的全等的概念及特征,掌握了全等图形的对应边、对应角的关系,这为探究三角形全等的条件做好了知识上的准备.另外,学生也具备了利用已知条件作三角形的基本作图能力,这使学生能主动参与本节课的操作、探究成为可能.4. 教学目标(1)学生在教师引导下,积极主动地经历探索三角形全等的条件的过程,体会利用操作、归纳获得数学结论的过程.(2)掌握三角形全等的“边边边”、“边角边”、“角边角”、“角角边”的判定方法,了解三角形的稳定性,能用三角形的全等解决一些实际问题.(3)培养学生的空间观念,推理能力,发展有条理地表达能力,积累数学活动经验.5. 教学的重点与难点重点:三角形全等条件的探索过程是本节课的重点.从设置情景提出问题,到动手操作,交流,直至归纳得出结论,整个过程学生不仅得到了两个三角形全等的条件,更重要的是经历了知识的形成过程,体会了一种分析问题的方法,积累了数学活动经验,这将有利于学生更好的理解数学,应用数学.难点:三角形全等条件的探索过程,特别是创设出问题后,学生面对开放性问题,要做出全面、正确得分析,并对各种情况进行讨论,对初一学生有一定的难度.根据初一学生年龄、生理及心理特征,还不具备独立系统地推理论证几何问题的能力,思维受到一定的局限,考虑问题不够全面,因此要充分发挥教师的主导作用,适时点拨、引导,尽可能调动所有学生的积极性、主动性参与到合作探讨中来,使学生在与他人的合作交流中获取新知,并使个性思维得以发展.6. 教学过程7. 教学反思本节课的设计体现了以教师为主导、学生为主体,以知识为载体、以培养学生的思维能力为重点的教学思想.教师以探究任务引导学生自学自悟的方式,提供了学生自主合作探究的舞台,营造了思维驰骋的空间,在经历知识的发现过程中,培养了学生分类、探究、合作、归纳的能力.在课堂教学设计中,让学生在“做”的过程中,借助已有的知识和方法主动探索新知识,扩大认知结构.“乐思方有思泉涌”,在课堂教学中,时时注意营造积极的思维状态,关注学生的思维发展过程,创设民主、宽松、和谐的课堂气氛,让学生畅所欲言,这样学生的创造火花才会不断闪现,个性才得以发展.不足之处是每个环节的教学时间不易把握,基础知识训练相对较少.8.案例点评这节课以引导学生研究、探索、发现为主线,以激发学生参与教学活动、积极思维、创造性地解决问题为目标,有以下几个方面的特色:(1)尊重学生已有的知识和经验.本课教师首先引导学生回顾全等三角形的条件,这就激活了学生原有的知识,为本课的学习作了知识准备,然后学生通过全等三角形的条件探究三角形全等的条件,体现出学生学习新知识是在原有的知识基础上自我建构、自我生成的过程.(2)创造性地使用教材.本课教师在教学中对教材进行了重组,将教材中的引入例作为教材处理,精选随堂练习和课后习题中的密切联系生活实际的问题作为课堂练习,让学生体会数学在生活中的魅力,体现出教师是“用教材”,而不是简单地“教教材”.(3)注重学生在学习过程中的自主体验.教学过程中教师给学生留出了充分的活动时间和想象空间,鼓励每位学生动手、动口、动脑,积极参与到活动和实践中来.教学中将操作实验、自主探索、合作交流、积极思考等学习方式贯穿数学学习的始终,体现了新课程倡导的自主、合作、探究的学习方式.。
“三角形全等的条件”学习要点及注意事项

“三角形全等的条件”学习要点及注意事项 2014.5.9一、三角形全等的条件:1、三边对应相等的两个三角形全等,简写为“边边边”,或SSS ;2、两角及其夹边对应相等的两个三角形全等,简写为“角边角”,或ASA ;3、两角及其中一角的对边对应相等的两个三角形全等,简写为“角角边”,或AAS ;4、两边及其夹角对应相等的两个三角形全等,简写为“边角边”,或SAS ;注意:(1)条件中的边、角一定是三角形中的边、角!(2)条件中只有对应相等的边、对应相等的角;(3)“边边角”不能保证两个三角形全等!!二、过程的书写要求:先交待所要证的两个三角形,其次用单边大括号把三个条件写在一起,得出两个三角形全等,并在后面注明理由;例:如图 ,AB=AC , ∠CDA =∠BEA, △ACD 与△ABE 全等吗?为什么?解: 在△ACD 和△ABE 中,∠CDA =∠BEA (已知)∵ ∠ A = ∠A (公共角) AB= AC (已知)∴ △ACD ≌△ABE (AAS )注意事项:(1)按判定条件的顺序书写,例如上例中,利用的是“AAS ”,书写时先写两个角的条件,再写边的条件;(2)如果所需的条件不是题中直接给出,则先证明,再按上面要求书写;例:如图,O 是AB 的中点,∠A =∠B , △AOC 与△BOD 全等吗?为什么?解: △AOC ≌△BOD 理由:∵ O 是AB 的中点,∴ AO=BO在 △AOC 与△BOD 中,∠A =∠ B (已知) ∵ AO=BO (已证) ∠AOC= ∠BOD (对顶角相等)∴ △AOC ≌△BOD (ASA )说明:(1)条件中一定是相等的边、角,所以要把“中点”的条件转化为相等的边;(2)对顶角相等是能直接得到的结论,不需要先证明;(3)除对顶角相等可以直接写在条件中外,公共边、公共角也能直接作为条件写;A OD C B AE C DB。
初中数学_利用三角形全等测距离教学设计学情分析教材分析课后反思

《利用三角形全等测距离》教学设计执教者指导教师一、课题:利用三角形全等测距离二、解读理念:面向全体学生,着眼于学生的全面发展,帮助学生过积极健康的生活,促进学生个性发展;尊重学生,充分调动学生学习的主动性和积极性;引导学生解决成长过程中的实际问题;鼓励学生实施自主、合作、探究学习,注重培养学生的独立思考能力和实践能力。
三、教材分析:1、地位和作用:这节课是在学生学习了全等三角形的性质及其判定条件之后的一节综合应用课。
利用三角形全等解决实际问题,首先就要把实际问题转化为三角形全等问题。
其目的是培养学生构建数学模型,并用数学知识来解决实际问题。
同时,培养学生说理表达能力,为今后学习几何证明打下良好的基础。
2、教育教学目标:根据新《课标》要求和上述教材分析,结合学生的情况,我制定了以下教学目标:知识目标:能够利用三角形全等解决实际问题。
能力目标:通过自主探究、实验,培养学生的自主探究能力、小组合作能力、语言表达能力,以及灵活运用所学解决实际问题的能力。
情感目标:通过学习使学生明白数学来源于生活,学习数学是为了解决实际问题,培养学生科学的学习态度,同时通过多媒体演示激发学生探究数学问题的兴趣,通过小组合作,培养合作意识。
3. 重点,难点以及确定依据:教学重点:根据新课标的要求以及对教学目标的分析将重点设定为能够利用三角形全等测量距离。
教学难点:针对本节课内容及学生的心理、认知结构将难点设定为灵活利用三角形全等解决实际问题。
四、教学策略本节课涉及的知识点不多,知识的切入点比较低。
教师以多媒体为教学平台,通过精心设计的问题串和活动系列来落实知识点并不断地制造思维兴奋点,让学生脑、嘴、手动起来,充分调动学生的学习积极性,达到事半功倍的教学效果。
在教学中,教师主要采用启发引导的方法,鼓励学生发现问题,利用所学解决问题,在探究阶段,教师应关注学生的思路、方法,鼓励学生小组合作,教师进行适当点拨,以这种形式突出重点,突破难点,同时培养学生的合作意识。
专题1.5 全等三角形的判定【八大题型】(举一反三)(浙教版)(原卷版)

专题1.5 全等三角形的判定【八大题型】【浙教版】【题型1 全等三角形的判定条件】 (1)【题型2 证明两个三角形全等】 (2)【题型3 全等三角形的判定与性质(证两次全等)】 (3)【题型4 全等三角形的判定与性质(证垂直)】 (4)【题型5 全等三角形的判定与性质(多结论)】 (5)【题型6 全等三角形的判定与性质(探究角度之间的关系)】 (6)【题型7 全等三角形的判定与性质(探究线段之间的关系)】 (8)【题型8 全等三角形的应用】 (9)【题型1 全等三角形的判定条件】【例1】(2022春•顺德区期末)如图,∠A=∠D=90°,给出下列条件:①AB=DC,②OB=OC,③∠ABC=∠DCB,④∠ABO=∠DCO,从中添加一个条件后,能证明△ABC≌△DCB的是()A.①②③B.②③④C.①②④D.①③④【变式1-1】(2021秋•庐阳区期末)如图,点B、E在线段CD上,若∠A=∠DEF,则添加下列条件,不一定能使△ABC≌△EFD的是()A.∠C=∠D,AC=DE B.BC=DF,AC=DEC.∠ABC=∠DFE,AC=DE D.AC=DE,AB=EF【变式1-2】(2021秋•源汇区校级期末)如图,已知∠1=∠2,AC=AD,增加下列条件之一:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()A.1个B.2个C.3个D.4个【变式1-3】(2022秋•佳木斯期末)在△ABC和△DEF中,其中∠C=∠F,则下列条件:①AC=DF,∠A=∠D;②AC=DF,BC=EF;③∠A=∠D,∠B=∠E;④AB=DE,∠B=∠E;⑤AC=DF,AB=DE.其中能够判定这两个三角形全等的是()A.①②④B.①②⑤C.②③④D.③④⑤【题型2 证明两个三角形全等】【例2】(2022春•鼓楼区校级期末)如图,点A,E,F,B在同一直线上,CE⊥AB,DF⊥AB,垂足分别为E,F,AE=BF,∠A=∠B.求证:△ADF≌△BCE.【变式2-1】(2021秋•肥西县期末)已知,如图,AB=AE,AB∥DE,∠ECB=65°,∠D=115°,求证:△ABC≌△EAD.【变式2-2】(2021秋•信州区校级期中)如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE ⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:△BDE≌△CDF.【变式2-3】(2022•河源模拟)如图,在四边形ABCD中,AD∥BC,点M为对角线AC上一点,连接BM,若AC=BC,∠AMB=∠BCD,求证:△ADC≌△CMB.【题型3 全等三角形的判定与性质(证两次全等)】【例3】(2022春•徐汇区校级期末)如图,已知AE∥DF,OE=OF,∠B=∠C,求证:AB=CD.【变式3-1】(2021春•横山区期中)如图,AB=BC,∠BAD=∠BCD=90°,点D是EF上一点,AE⊥EF于E,CF⊥EF于F,AE=CF,连接BD,求证:Rt△ADE≌Rt△CDF.【变式3-2】(2021秋•石阡县期末)如图,AB=AC,E、D分别是AB、AC的中点,AF⊥BD,垂足为点F,AG⊥CE,垂足为点G,试判断AF与AG的数量关系,并说明理由.【变式3-3】(2021秋•沂源县期末)如图,AD=AC,AB=AE,∠DAB=∠CAE.(1)△ADE与△ACB全等吗?说明理由;(2)判断线段DF与CF的数量关系,并说明理由.【题型4 全等三角形的判定与性质(证垂直)】【例4】(2022秋•孟津县期末)如图,BM,CN分别是钝角△ABC的高,点Q是射线CN上的点,点P在线段BM上,且BP=AC,CQ=AB,请问AP与AQ有什么样的关系?请说明理由.【变式4-1】(2022春•金牛区校级期中)如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE 上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.(1)求证:∠ABE=∠ACG;(2)试判:AG与AD的关系?并说明理由.【变式4-2】(2021春•亭湖区校级期末)如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB =CF,BE=AC.(1)求证:AE=AF;(2)AE与AF有何位置关系.请说明理由.【变式4-3】(2021春•泰兴市期末)如图,在锐角△ABC中,AD⊥BC于点D,点E在AD上,DE=DC,BD=AD,点F为BC的中点,连接EF并延长至点M,使FM=EF,连接CM.(1)求证:BE=AC;(2)试判断线段AC与线段MC的关系,并证明你的结论.【题型5 全等三角形的判定与性质(多结论)】【例5】(2022春•九龙坡区校级期末)如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,过点A作AF ∥BC且AF=AD,点E是AC上一点且AE=AB,连接EF,DE.连接FD交BE于点G.下列结论中正确的有()个.①∠F AE=∠DAB;②BD=EF;③FD平分∠AFE;④S四边形ABDE=S四边形ADEF;⑤BG=GE.A.2B.3C.4D.5【变式5-1】(2021秋•垦利区期末)如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM ⊥CE于P,交BC于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论:①AP=MP;②BC=9;③∠MAN=30°;④AM=AN.其中正确的有()A.4个B.3个C.2个D.1个【变式5-2】(2021春•锦州期末)如图,在△AOB和△COD中,OA=OB,OC=OD(OA<OC),∠AOB =∠COD=α,直线AC,BD交于点M,连接OM.下列结论:①AC=BD,②∠OAM=∠OBM,③∠AMB=α,④OM平分∠BOC,其中正确结论的个数是()A.4B.3C.2D.1【变式5-3】(2021春•江北区校级期末)如图,已知AB=AC,点D、E分别在AC、AB上且AE=AD,连接EC,BD,EC交BD于点M,连接AM,过点A分别作AF⊥CE,AG⊥BD,垂足分别为F、G,下列结论:①△EBM≌△DCM;②∠EMB=∠F AG;③MA平分∠EMD;④若点E是AB的中点,则BM+AC >EM+BD;⑤如果S△BEM=S△ADM,则E是AB的中点;其中正确结论的个数为()A.2个B.3个C.4个D.5个【题型6 全等三角形的判定与性质(探究角度之间的关系)】【例6】(2022春•杏花岭区校级期中)已知AB=AC,AD=AE,∠BAC=∠DAE.(1)如图1,当点D在BC上时,求证:BD=CE;(2)如图2,当点D、E、C在同一直线上,且∠BAC=α,∠BAE=β时,求∠DBC的度数(用含α和β的式子表示).【变式6-1】(2022•南京模拟)在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE=度;(2)设∠BAC=α,∠DCE=β.①如图2,当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时α与β之间的数量关系(不需证明).【变式6-2】(2022秋•江夏区期末)已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.(1)如图1,若∠DAB=60°,则∠AFG=;(2)如图2,若∠DAB=90°,则∠AFG=;(3)如图3,若∠DAB=α,试探究∠AFG与α的数量关系,并给予证明.【变式6-3】(2021秋•肥西县期末)在△ABC中,AB=AC,D是直线BC上一点,连接AD,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.(1)如图,当点D在BC延长线上移动时,若∠BAC=26°,则∠DCE=.(2)设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.【题型7 全等三角形的判定与性质(探究线段之间的关系)】【例7】(2022春•沙坪坝区校级期中)如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD 交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.(1)当∠A=80°时,求∠EDC的度数;(2)求证:CF=FG+CE.【变式7-1】(2022•黄州区校级模拟)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE;(2)求∠F AE的度数;(3)求证:CD=2BF+DE.【变式7-2】(2021秋•两江新区期末)在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.(1)求证:AB=BD;(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.【变式7-3】(2022春•济南期中)把两个全等的直角三角板的斜边重合,组成一个四边形ACBD以D为顶点作∠MDN,交边AC、BC于M、N.(1)若∠ACD=30°,∠MDN=60°,当∠MDN绕点D旋转时,AM、MN、BN三条线段之间有何种数量关系?证明你的结论;(2)当∠ACD+∠MDN=90°时,AM、MN、BN三条线段之间有何数量关系?证明你的结论;(3)如图③,在(2)的条件下,若将M、N改在CA、BC的延长线上,完成图3,其余条件不变,则AM、MN、BN之间有何数量关系(直接写出结论,不必证明)【题型8 全等三角形的应用】【例8】(2022春•二七区期末)为了测量一池塘的两端A,B之间的距离,同学们想出了如下的两种方案:方案①如图1,先在平地上取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,BC至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长;方案②如图2,过点B作AB的垂线BF,在BF上取C,D两点,使BC=CD,接着过D作BD的垂线DE,在垂线上选一点E,使A、C、E三点在一条直线上,则测出DE的长即是AB的距离.问:(1)方案①是否可行?请说明理由;(2)方案②是否可行?请说明理由;(3)小明说在方案②中,并不一定需要BF⊥AB,DE⊥BF,只需要就可以了,请把小明所说的条件补上.【变式8-1】(2021春•普宁市期末)学校为开展数学实践活动,成立了以小明为首的户外测量小组,测量小组带有测量工具:绳子、拉尺、小红旗、测角器(可测量两个点分别到测量者连线之间的夹角大小).小明小组的任务是测量某池塘不能直接到达的两个端点A、B之间的距离.(1)小明小组提出了测量方案:在池塘南面的空地上(如图),取一个可直接到达A、B的点C,用绳子连接AC和BC,并利用绳子分别延长AC至D、BC至E,使用拉尺丈量CD=CA、CE=CB,确定D、E两个点后,最后用拉尺直接量出线段DE的长,则端点A、B之间的距离就是DE的长.你认为小明小组测量方案正确吗?请说明理由.(2)你还有不同于小明小组的其他测量方法吗?请写出其中一个完整的测量方案(在备用图1中画出简图,但不必说明理由).(3)假设池塘南面(即点D、E附近区域)没有足够空地(或空地有障碍物或不可直达等不可测量情况),而点B的右侧区域有足够空地并可用于测量,请你设计一个可行的测量方案(在备用图2中画出图形),并说明理由.【变式8-2】(2022春•金乡县期中)如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼AB的高度,首先他们在两栋单元楼之间选定一点E,然后小华在自己家阳台C处测得E处的俯角为∠1,小明站在E处测得眼睛F到AB楼端点A的仰角为∠2,发现∠1与∠2互余,已知EF=1米,BE=CD=20米,BD=58米,试求单元楼AB的高.【变式8-3】(2022春•郑州期末)阅读并完成相应的任务.如图,小明站在堤岸凉亭A点处,正对他的B点(AB与堤岸垂直)停有一艘游艇,他想知道凉亭与这艘游艇之间的距离,于是制定了如下方案.课题测凉亭与游艇之间的距离测量工具皮尺等测量方案示意图(不完整)测量步骤①小明沿堤岸走到电线杆C旁(直线AC与堤岸平行);②再往前走相同的距离,到达D点;③他到达D点后向左转90度直行,当自己,电线杆与游艇在一条直线上时停下来,此时小明位于点E处.测量数据AC=20米,CD=20米,DE=8米(1)任务一:根据题意将测量方案示意图补充完整.(2)任务二:①凉亭与游艇之间的距离是米.②请你说明小明方案正确的理由.。
三角形全等的判定---角边角、角角边

《三角形全等的判定(角边角,角角边)》教学设计一、内容和内容解析(一)内容人教版《义务教育课程标准实验教科书·数学》八年级上册“12.2三角形全等的判定”(角边角,角角边).(二)内容解析全等三角形是研究图形的重要工具,只有掌握全等三角形的有关内容,并且能灵活的加以运用,才能学好等腰三角形、四边形和圆等内容,同时为今后研究轴对称、旋转等全等变换打下良好的基础.此外,也由于它在日常生活中有着广泛的应用,研究全等三角形,具有重要的意义.发展学生的合情推理和初步的演绎推理能力是《数学课程标准》的重要要求之一.本章是在七年级下册第五章出现证明和证明格式的基础上,进一步介绍了推理论证的方法.通过定理内容的规范化书写,并在例习题中注重分析思路,让学生学会思考、学会清楚地表达思考的过程,可以进一步培养学生的推理能力.同时,“12.2三角形全等的判定”中几种判定方法,是作为基本事实提出来的,通过画图和实验,让学生确信其正确性,符合学生的认知水平.这样的分析问题、解决问题的方法,对全章乃至以后的学习都是至关重要的.本节课是全等三角形判定的第三课时,主要探究利用“角边角”和“角角边”两种方法判定三角形全等,以及简单应用.探索三角形全等的条件,不仅是“全等三角形”知识体系的重要组成部分,而且在探索过程中所体现的思想方法,为学生主动获取知识、感悟三角形全等的数学本质、积累数学活动经验、体验运用类比的方法研究问题等,提供了很好的素材. 通过本节课的学习,可以加深学生对已学几何图形的认识,并为今后的学习奠定基础.(三)教学重点掌握角边角和角角边两个判定三角形全等的方法及简单应用.二、教学目标和目标解析(一)目标1.掌握角边角、角角边判定两个三角形全等的方法及简单应用.2.学会分析法、综合法解决问题.3.让学生在数学学习的过程中获得解决问题的经验.4.逐步养成良好的个性思维品质.(二)目标解析1.使学生掌握角边角、角角边判定两个三角形全等的方法,会运用这两种方法解决问题.2.通过有关的证明及应用,教给学生一些基本的数学思想方法,使学生逐步学会分别从题设或结论出发,寻找论证思路,学会用综合法证明问题,从而提高学生分析问题、解决问题的能力.3.通过学生探究特殊角度、特殊边长的三角形全等的条件,再由教师利用课件演示数学事实,让学生充分参与到数学学习的过程中来,获得解决问题的经验;通过习题变式,从中体会事物之间的相互联系与区别,从而进一步培养学生的辩证唯物主义观点.4.探究本课的两个判定方法,使学生经历“实践——观察——猜想——验证——归纳——概括”的认知过程,培养学生良好的个性思维品质.三、学生情况分析基于学生的学习基础,在研究几何图形的方法和合情推理方面还存在欠缺.本节课是学生在已经掌握了边边边和边角边判定之后,继续探索三角形全等的条件.他们已经了解了一些探究的思路,也经历过一些探究的过程:动手实践、观察猜想、归纳总结、巩固应用等.因此,本节课的学习,可以引导学生类比前面的研究方法.另外,由于本节课所探究的两种方法,其图形不易辨别,那么,学生如何分析图形之间的内在联系,如何清晰地表达数学思考的过程,也是教师应要特别关注的问题.本课教学难点:是利用角边角、角角边判定两个三角形全等方法的应用及规范化书写.四、教学支持条件分析根据本节课内容的特点,为了更直观、形象的突出重点、突破难点,提高课堂效率,采用以观察发现为主,多媒体演示为辅的教学组织方式,在教学过程中,通过设置一系列例题变式,创设问题情境,启发学生思考,利用画图,结合操作测量,让学生亲身体验知识的产生、发展和形成的过程.五、教学过程设计1.开门见山,引出课题在前面的学习中,我们通过动手画图、观察猜想、总结归纳,对三角形全等的条件进行了探究.主要研究了“三边”对应相等和“两边一角”对应相等的情况,得到了两种判定两个三角形全等的方法.本节课,继续探究“两角一边”对应相等的情况.【设计意图】教师通过引导,帮助学生回忆已学知识,回顾探究的方法,使学生明确本节课要探究的问题,了解探究两个三角形全等的基本思路,弄清知识之间的联系.2.动手操作,实验探究问题1 先在一张纸上画一个△ABC,然后在另一张纸上画△A ,B ,C, ,使A, B, =AB , ∠A = ∠A,∠B = ∠B,△ABC和△A ,B ,C,能够重合吗?(教师引导学生分析画图步骤,用电脑演示画图过程. 同学之间观察对比,通过两个三角形叠放到一起,引导学生观察、猜想)【设计意图】通过学生动手画图,让学生明确已知两角及夹边怎样画出三角形.通过学生展示作品,以及同学之间观察对比,让学生确信结论的正确性.问题2 对于任意的两个三角形,当满足“两角及夹边”对应相等时,这两个三角形就一定能够全等吗?教师用电脑展示,给学生以直观的印象,学生总结得到角边角判定方法,教师给出符号语言的规范格式,强调“对应”的含义.【设计意图】通过观察多媒体动态演示的过程,进一步强化对两个三角形所满足条件的直观感知,使学生在验证猜想的过程中,获得解决问题的经验.3.应用新知,探究归纳问题3 解答下面的问题,你能得到什么结论?如图1,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?你能利用角边角证明你的结论吗?C DA'A B E 图1(教师提出问题,学生思考,找寻方法.师生共同总结角角边的判定方法,给出符号语言的规范格式)【设计意图】通过本题的练习,让学生在尝试运用角边角判定两个三角形全等的过程中,进一步加深对三个条件的理解.同时,训练学生的表达能力,使学生能清晰、有条理地表达自己的思考过程,做到言之有理、落笔有据.4.拓广探索,综合运用练习1 已知:如图,AB=A′ C ,∠A=∠A′,∠B=∠C求证:△ABE≌ △ A′ CD2、如图,已知AB=DE , ∠A =∠D , ,∠B=∠E ,则△ABC ≌△DEF 的理由是:3、如图,已知AB=DE ,∠A=∠D ,,∠C=∠F ,则△ABC ≌△DEF 的理由是:练习1、如图 ,AB=AC,∠B=∠C,那么△ABE 和△ACD 全等吗?为什么?(由学生分析,教师展示解答过程。
1.5全等三角形的判定(2)
以2.5cm,3.5cm为三角形的两边,长
度为2.5cm的边所对的角为40° ,情况
又怎样?动手画一画,你发现了什么?
C
F
A
40°
B
40°
D
E
结论:两边及其一边所对的角相
等,两个三角形不一定全等
课堂小结:
1. 目前有几种方法判定三角形全等?
2. 线段垂直平分线的概念
3. 线段垂直平分线的性质:线段垂直平分线上的点 到线段两端点的距离相等.
几何语言表述如下:
在A BC和ABC 中
AB AB(已知)
B B(已知)
BC
BC (已知)
ABC ABC(SAS)
例3 如图AC与BD相交于点O.已知
OA=OC,OB=OD,说△AOB≌△COD 的理
由.
解;在AOB和COD中 A
B
OA OC (已知) OBAOBODCO(D(已知对)顶角相等D)
将你画出的三角形和其他同学画的三角形进行比 较,它们互相重合吗?
由此,你得到了什么结论?
全等三角形的判定公理2:
两边及其夹角对应相等的两个三角形全等(简写 成“边角边”或“SAS”)
➢注 意 这个角一定要是两条边的夹角
有一个角和夹这个角的两边对应相等的两个
三角形全等(简写成“边角边”或“SAS”)
O C
∴△AOB≌△COD (SAS)
垂直于一条线段,并且平分这条线段 的直线叫做这条线段的垂直平分线,简 称中垂线.
点C是线段AB的垂直平分线上的特殊的
点,还是任意的点?由此你能得到什么结论?
线段垂直平分线
l
上的点到线段两
C
端的距离相等。 A
O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B B
C
3、如图,AD=AE,DC=EB,那么△ABE 和 、如图, ,那么△ △ACD全等吗? 全等 A D E
B B
C
练习2. 如图,已知AB= , 练习 如图,已知 =AE, ∠C=∠D, ∠BAD=∠EAC,则 ∠ , = , BC=ED.请说明理由。 请说明理由。 = 请说明理由
BAC的平分线上的一点 的平分线上的一点, 例1.如图,点P是∠ BAC的平分线上的一点, 1.如图, 如图 PB⊥AB,PC⊥AC。说明PB=PC的理由。 PB=PC的理由 PB⊥AB,PC⊥AC。说明PB=PC的理由。
有两个角和其中一个角的对边对应相等的两个三 有两个角和其中一个角的对边对应相等的两个三 对边 角形全等(简写成“角角边” AAS”) 角形全等(简写成“角角边”或“AAS”)
议一议
能不能把“AAS 、 ASA”简述为 简述为“ 能不能把“AAS”、“ASA 简述为“有两 个角和一条边对应相等的两个三角形全 C 等”?△ADE和△ABC中 在 ADE和 ABC中
A D
B
C
E
F
想一想: 如图,要说明△ABD≌△ACE,还需增加两 个什么条件?
A E B D C
A D E B
A
C
A C P A B
C
D
B
小结
两 个 三 角 形 全 等
SSS SAS 判定条件 ASA AAS
关键: 找符合要求的完整 的边或角相等 特别注意: 边和角分别对应相等,而不 是分别相等。
SSS SAS
ASA AAS
如图: 如图:点C、F在BE上,∠ACB=∠DFE,BC= 、 在 上 = , = EF。请补充条件:______ 。请补充条件:______ 写一个即可), ),使 (写一个即可),使△ABC≌△DEF ≌
(ASA) )
(AAS) )
试一试
1、如图 ,AB=AC,∠B=∠C,那么△ABE 和 、 那么△ ∠ ∠ 那么 为什么? △ACD全等吗?为什么? 全等 A D E E
B B
C
2、如图,AD=AE,∠B=∠C,那么BE和CD相等 、如图, ∠ ∠ , 和 相等 为什么? 么?为什么? A D E E
∠A = ∠A ∠ADE = ∠B AD = BC
E
A
B D
在△ABC和△DEF中 ABC和 DEF中
∠A = ∠E ∠B = ∠D BC = DE
C A D
F E
B
两角和它们的夹边对应相等的两个三角形全等, 两角和它们的夹边对应相等的两个三角形全等,简 写成“角边角” ASA”。 写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等, 两角和其中一角的对边对应相等的两个三角形全等, 简写成“角角边” 简写成“角角边”或“AAS”
1.5 三角形全等的 条件(3)
1 2 3
C
A
B
AB是∠A、∠B的夹边 是 、 的夹边 ∠A是BC的对角; 是 的对角; 的对角 BC是∠A的对边 是 的对边
合作学: 合作学习:
用量角器和刻度尺画△ABC, 用量角器和刻度尺画△ABC, 使BC=4cm,∠B=45 ,∠C=60 . BC=4cm,
有两个角和这两个角的夹边对应相等的两个三角 有两个角和这两个角的夹边对应相等的两个三角 夹边 形全等(简写成“角边角” 形全等(简写成“角边角”或“ASA”) ASA”) A A’ B C B’ C’
o o
△ABC和△A’ B’ C’中,已知AB=AB ABC和 中 已知AB=AB =∠C,请说出△ C C,请说出 ∠B=∠B ,∠C=∠C,请说出△ABC≌△ABC B 的理由. 的理由. A B C B’ A’ C’
C P A B
角平分线上的点到角两边的距离相等
∵AP平分∠CAB, PB⊥AB, ∵AP平分∠CAB, PB⊥AB,PC⊥AC 平分 (角平分线上的点到角两边的距离相等) ∴PB=PC 角平分线上的点到角两边的距离相等) 如图,△ABC中,∠C=900,AD 是∠CAB的平分线,CD=4cm, 则点D到AB的距离为 4cm
