线段树的简单实现
线段树中的操作方法

线段树中的操作方法
线段树是一种二叉树结构,用于高效地处理区间查询问题。
线段树常用于解决范围最值查询、区间修改等问题。
线段树的操作方法主要包括以下几点:
1. 构建线段树:线段树的构建方法一般是采用递归的方式,将待处理区间一分为二,构建左右子树,然后将左右子树的值合并到根节点。
2. 查询区间最值:对于一个区间查询问题,可以从根节点开始递归地向下查询。
如果当前节点表示的区间与待查询区间完全不重叠,则返回一个无效值。
如果当前节点表示的区间完全包含待查询区间,则返回当前节点的值。
如果当前节点表示的区间与待查询区间相交但不完全包含,则将查询问题分为左右两个子问题,然后将子问题的结果进行合并。
3. 区间修改:对于一个区间修改问题,可以从根节点开始递归地向下修改。
如果当前节点表示的区间与待修改区间完全不重叠,则不需要修改。
如果当前节点表示的区间完全包含待修改区间,则直接将当前节点的值修改为新值。
如果当前节点表示的区间与待修改区间相交但不完全包含,则将修改问题分为左右两个子问题,然后将子问题的结果进行合并。
4. 更新节点:在线段树中,如果某个节点的值发生了变化,则需要更新该节点
以及其父节点的值。
可以从叶节点开始递归地向上更新。
线段树的操作方法可以根据具体问题的需求进行扩展和优化。
以上是线段树的基本操作方法,具体实现时需要根据具体问题进行适当的调整和改进。
『zkw线段树及其简单运用』

『zkw 线段树及其简单运⽤』<更新提⽰><第⼀次更新>阅读本⽂前,请确保已经阅读并理解了如下两篇⽂章:<正⽂>引⼊这是⼀种由THU −zkw ⼤佬发明的数据结构,本质上是经典的线段树区间划分思想,采⽤了⾃底向上的⽅式传递区间信息,避免的递归结构,其代码相对经典线段树更简单,常数更⼩,易于实现。
统计的⼒量-源⾃。
基础⾮递归接下来,我们将讲解zkw 线段树的第⼀种实现形式,⽤于单点修改 区间查询,我们以查询区间最⼤值为例来讲解。
建树普通线段树需要建树,zkw 线段树当然也需要建树。
考虑线段树的⼀个性质,其树上的叶节点代表的往往都是形如[x ,x ]的元区间,⽽且除最后⼀层外,线段树是⼀颗满⼆叉树,所以我们要把这颗线段树的数组⼤⼩先申请好了。
⼀棵满⼆叉树有x 个节点时,它有x +12个叶⼦节点,⽽我们需要⾄少n 个叶⼦节点的线段树,即使x +12≥n ,那么我们设x =1,在x +12<n 时不断执⾏x ∗=2,就能得到⾜够⼤⼩的线段树下标base ,由于线段树的叶⼦节点可能分布在两层,所以保险起见,我们还需再将x 扩⼤⼀倍,即在x +1<n 时不断执⾏x ∗=2就可以了。
得到合适的下标位置后,将1−n 下标位置的原数据直接存⼊线段树的叶⼦节点即可。
其实,我们还需将下标再扩⼤两个位置,即需要保证x >n ,才停⽌执⾏x ∗=2。
其原因是这样的:在执⾏区间查询操作时,我们需要将查询区间[l ,r ]更改为(l ,r )(关于原因,我们之后再分析),才便于zkw 线段树的查询,那么在询问[1,n ]时,可能为调⽤到[0,n +1]的原下标,所以还需再扩⼤两个位置。
得到了合适的下标base 并将1−n 的数据存⼊对应位置后,当然我们还要对1到base −1的线段树位置进⾏区间更新,这个普通的更新就可以了。
Code :单点修改直接在叶节点上修改对应的值,然后更新其每⼀个⽗节点即可。
线段树 区间最大值 模板

线段树区间最大值模板一、引言线段树是一种在区间求最大值的算法,常常用于处理一些涉及区间最大值的问题。
下面我们将介绍线段树的基本概念,并给出使用线段树解决区间最大值问题的模板。
二、线段树的基本概念线段树是一种将线段划分为若干个小区间,并使用树状结构来表示这些区间的划分方式。
在每个节点处,我们可以记录该节点覆盖的区间最大值,这样就可以方便地通过遍历树状结构来求出某个区间的最大值。
三、区间最大值问题的模板模板一:问题描述给定一个区间[a,b],请使用线段树来求出该区间的最大值。
模板二:代码实现假设线段树的节点类型为Node,其中Node包含一个整数值val和两个指向子节点的指针left和right。
以下是使用Python实现的线段树代码:```pythonclassNode:def__init__(self,val=None,left=None,right=None):self.val=valself.left=leftself.right=rightdefbuild_segment_tree(arr,start,end):ifstart>end:returnNonemid=(start+end)//2root=Node(arr[mid])root.left=build_segment_tree(arr,start,mid-1)root.right=build_segment_tree(arr,mid+1,end)returnrootdefquery(root,start,end):ifrootisNone:returnNoneifstart<=root.val<=end:returnroot.valreturnmax(query(root.left,start,end),query(root.right,start,end)) ```使用方法:首先构建线段树,然后通过查询节点来获取区间[a,b]的最大值。
BalancedLineup(线段树的简单了解)

BalancedLineup(线段树的简单了解)个⼈⼼得:线段树就是将⼀段序列拆分为⼀个个单独的节点,不过每俩个节点⼜可以联系在⼀起,所以就能很好的结合,⽐如这⼀题,每次插⼊的时候都将这⼀段区间的最⼤最⼩值更新,就能⼤⼤减少时间。
这个线段树建⽴是以数组的,根节点为0,后⾯每次都是⽗节点*2+1/2。
这题简单的教会了我如何创建线段树,以及⼀些简单的线段树操作,还要继续加深。
For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things simple, he will take a contiguous range of cows from the milking lineup to play the game. However, for all the cows to have fun they should not differ too much in height.Farmer John has made a list of Q (1 ≤ Q ≤ 200,000) potential groups of cows and their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to determine the difference in height between the shortest and the tallest cow in the group.InputLine 1: Two space-separated integers, N and Q.Lines 2..N+1: Line i+1 contains a single integer that is the height of cow iLines N+2..N+Q+1: Two integers A and B (1 ≤ A ≤ B ≤ N), representing the range of cows from A to B inclusive.OutputLines 1..Q: Each line contains a single integer that is a response to a reply and indicates the difference in height between the tallest and shortest cow in the range.Sample Input6 31734251 54 62 2Sample Output631 #include <stdio.h>2 #include <string.h>3 #include<iostream>4 #include <algorithm>5 #include <queue>6using namespace std;7const int inf=0xffffff0;8int maxa=-inf;9int mina=inf;10struct tree11 {12int l,r;13int maxt,mint;14int mid()15 {16return (l+r)/2;17 }1819 };20 tree Tree[800000];21void builttree(int root,int x,int y){22 Tree[root].l=x;23 Tree[root].r=y;24 Tree[root].maxt=-inf;25 Tree[root].mint=inf;26if(x!=y){27 builttree(root*2+1,x,(x+y)/2);28 builttree(root*2+2,(x+y)/2+1,y);29 }30 }31void inserttree(int root,int i,int v){32if(Tree[root].l==i&Tree[root].r==i)33 {34 Tree[root].maxt=Tree[root].mint=v;35return;36 }37 Tree[root].maxt=max(Tree[root].maxt,v);38 Tree[root].mint=min(Tree[root].mint,v);39if(i<=Tree[root].mid())40 inserttree(root*2+1,i,v);41else42 inserttree(root*2+2,i,v);4344 }45void checktree(int root,int x,int y){46if(Tree[root].maxt<=maxa&&Tree[root].mint>=mina) 47return;48if(Tree[root].l==x&&Tree[root].r==y)49 {50 maxa=max(maxa,Tree[root].maxt);51 mina=min(mina,Tree[root].mint);52return ;53 }54if(y<=Tree[root].mid())55 checktree(root*2+1,x,y);56else if(x>Tree[root].mid())57 checktree(root*2+2,x,y);58else {59 checktree(root*2+1,x,Tree[root].mid());60 checktree(root*2+2,Tree[root].mid()+1,y);61 }626364 }65int main()66 {67int n,m;68 scanf("%d%d",&n,&m);69 builttree(0,1,n);70for(int i=1;i<=n;i++)71 {72int x;73 scanf("%d",&x);74 inserttree(0,i,x);75 }76for(int i=1;i<=m;i++)77 {78int x,y;79 scanf("%d%d",&x,&y);80 mina=inf,maxa=-inf;81 checktree(0,x,y);82 printf("%d\n",maxa-mina);83 }8485return0;8687 }。
线段树ppt课件

•
else Count := 0; 连接处颜色相同并且
非底色,则总数减1
统计算法
最左边的颜色
• end • else if r – l > 1 then
最右边的颜色
• begin
最左颜色=最右颜色=本身
•
result := Count(p * 2, l,非(底l +色则r)统d计iv数加2,1 lc, tl) +
•
else if a >= m then Insert(p * 2 + 1, m, r, a, b, c)
•
else begin
•
Insert(p * 2, l, m, a, m, c);
•
Insert(p * 2 + 1, m, r, m, b, c);
•
end;
•
end;
• end;
• end;
示例
• 初始情况 0 0 0 0 0
• [1,2]
10000
• [3,5]
10110
• [4,6]
10111
• [5,6]
10111
4个1
缺点
• 此方法的时间复杂度决定于下标范围的平 方。
• 当下标范围很大时([0,10000]),此方法 效率太低。
离散化的做法
• 基本思想:先把所有端点坐标从小到大排 序,将坐标值与其序号一一对应。这样便 可以将原先的坐标值转化为序号后,对其 应用前一种算法,再将最后结果转化回来 得解。
Wall
分析
• 这道题目是一个经典的模型。在这里,我 们略去某些处理的步骤,直接分析重点问 题,可以把题目抽象地描述如下:x轴上有 若干条线段,求线段覆盖的总长度。
线段树 区间最大值 模板

线段树区间最大值模板线段树是一种二叉树的数据结构,它被广泛应用于解决与区间相关的问题。
其中,区间最大值是线段树的一个常见应用。
在本文中,我将详细介绍线段树的概念和实现,并提供一个用于解决区间最大值问题的模板。
1. 线段树的概念线段树是一种将区间划分为多个子区间并以二叉树形式表示的数据结构。
每个节点代表一个区间,并保存该区间的一些属性,例如区间的最大值、最小值、总和等。
通过将区间逐层划分为子区间,线段树可以高效地处理区间操作。
2. 线段树的实现线段树的实现可以使用数组或链表。
在这里,我将使用数组来实现线段树。
2.1 初始化线段树首先,我们需要定义一个数组来表示线段树。
对于给定的区间,我们可以使用递归的方式将其划分为左右子区间,直到区间的长度为1。
然后,我们将每个区间的最大值保存在线段树的相应节点中。
2.2 更新线段树当某个区间的值发生改变时,我们需要更新线段树中相应的节点。
首先,我们找到包含要更新的值的叶子节点,并更新该节点的值。
然后,我们通过递归地向上更新父节点的值,直到根节点。
2.3 查询线段树查询线段树的最大值需要考虑两种情况。
如果查询的区间与当前节点的区间完全重叠,那么我们可以直接返回该节点保存的最大值。
否则,我们需要继续向下递归查询左右子节点,并返回两者中的最大值。
3. 线段树区间最大值的模板下面是一个用于解决区间最大值问题的线段树模板:```#include <iostream>#include <vector>#include <climits>using namespace std;// 定义线段树节点的数据结构struct SegmentTreeNode {int start;int end;int max_value;SegmentTreeNode* left;SegmentTreeNode* right;SegmentTreeNode(int s, int e) : start(s), end(e), max_value(INT_MIN),left(nullptr), right(nullptr) {}};// 构建线段树SegmentTreeNode* buildSegmentTree(vector<int>& nums, int start, int end) { if (start > end) return nullptr;SegmentTreeNode* root = new SegmentTreeNode(start, end);if (start == end) {root->max_value = nums[start];} else {int mid = start + (end - start) / 2;root->left = buildSegmentTree(nums, start, mid);root->right = buildSegmentTree(nums, mid + 1, end);root->max_value = max(root->left->max_value, root->right->max_value); }return root;}// 更新线段树中的值void updateSegmentTree(SegmentTreeNode* root, int index, int value) {if (!root) return;if (root->start == root->end) {root->max_value = value;} else {int mid = root->start + (root->end - root->start) / 2;if (index <= mid) {updateSegmentTree(root->left, index, value);} else {updateSegmentTree(root->right, index, value);}root->max_value = max(root->left->max_value, root->right->max_value);}}// 查询线段树中的最大值int querySegmentTree(SegmentTreeNode* root, int start, int end) {if (!root) return INT_MIN;if (root->start == start && root->end == end) {return root->max_value;} else {int mid = root->start + (root->end - root->start) / 2;if (end <= mid) {return querySegmentTree(root->left, start, end);} else if (start > mid) {return querySegmentTree(root->right, start, end);} else {return max(querySegmentTree(root->left, start, mid), querySegmentTree(root->right, mid + 1, end));}}}int main() {vector<int> nums = {1, 3, 5, 7, 9, 11};int n = nums.size();SegmentTreeNode* root = buildSegmentTree(nums, 0, n - 1);updateSegmentTree(root, 2, 10);int max_value = querySegmentTree(root, 1, 4);cout << "Max value in range [1, 4]: " << max_value << endl;return 0;}```这是一个完整的线段树模板,可以根据具体的问题进行修改和扩展。
线段树详解及例题

线段树详解及例题一、线段树的概念线段树(Segment Tree)是一种用于解决区间查询问题的数据结构,常用于静态区间查询和动态区间查询,也被称为区间树。
二、线段树的构建线段树是一棵二叉树,其每个节点都代表一个区间。
首先,我们将待处理的区间按照二叉树的方式进行划分,生成一棵满二叉树。
这里我们以求一段区间内元素的和为例:(1)首先,将整个区间 $[1,n]$ 分为两个部分,设左边区间为$[1,mid]$,右边区间为 $[mid+1,n]$。
这里的 $mid$ 是 $(1+n)/2$ 的值。
(2)然后,将左区间和右区间再分别划分成两个子区间并进行相加,直到区间大小为 1,构建出一棵完整的线段树。
三、线段树的维护构建好线段树之后,我们需要对其进行维护,以便能够快速地查询给定区间的值。
设线段树中某个节点代表区间 $[l,r]$,那么这个节点的值等于 $[l,r]$ 区间中所有元素的和。
如果需要对线段树进行更新,我们可以利用递归的方式向下更新每个节点的值。
当需要将 $[l,r]$ 区间中的某个元素修改为 $x$ 时,我们可以将其视为将线段树上区间 $[l,r]$ 的值都减去原来元素的值再加上 $x$。
四、线段树的查询线段树的查询包括单点查询和区间查询两种方式:(1)单点查询:即查询线段树中某个节点所代表的区间的值。
(2)区间查询:即查询线段树中 $[l,r]$ 区间内所有元素的和。
五、应用实例下面通过几道例题来说明线段树的应用。
问题一:给定一个序列,更新其中某个元素的值,并求出其区间和。
样例输入:8 1 3 -4 2 8 10 9 62 5 2样例输出:17问题二:对一个序列进行 $m$ 次操作,每次操作为在 $L$ 到 $R$ 的区间内加上 $c$,并输出最终改变后的序列。
样例输入:5 31 3 23 5 32 4 1样例输出:2 5 4 0 2以上就是关于线段树的详细介绍和几个应用示例,希望可以对读者有所帮助。
统计的力量——线段树详细教程

清华大学 张昆玮
24
2019年9月7日
*我们可以直接找到一个数对应的叶子 *不用自顶向下慢慢地找啊找 *“直接加 4 ”多简单!
*…… *直接找到叶子? *无限遐想中……
*
清华大学 张昆玮
25
2019年9月7日
*
清华大学 张昆玮
可以直接找到叶子?
26
2019年9月7日
(0,5)?
1
2
3
4
5
6
*没了? *没了。
*
清华大学 张昆玮
34Βιβλιοθήκη 2019年9月7日*仅使用了两倍原数组的空间 *其中还完整地包括了原数组 *构造容易:
* For i=M-1 downto 1 do T[i]=T[2i]+T[2i+1];
*太好写了!好理解! *自底向上,只访问一次,而且不一定访问到顶层 *实践中非常快,与树状数组接近 *为什么呢?后面再讲。
2019年9月7日
*我之前用这种写法做过不少题…… *大家都说我的代码看不懂 *我说这就是一个树状数组 *写树状数组的人说没有lowbit *我说那就算是线段树吧 *大家不相信非递归的线段树这么短…… *我:……
*
清华大学 张昆玮
43
2019年9月7日
*
清华大学 张昆玮
44
懒惰即美德。
2019年9月7日
13
2019年9月7日
*原因是区间和的性质非常好 *满足区间减法 *区间减法什么的最讨厌了!后面再说! *不过直接前缀和不是万能的! *如果修改元素的话……
清华大学 张昆玮
*
14
2019年9月7日
数据结构 直接存储原数组 直接存储前缀和
线段树的概念与应用

线段树的概念与应用线段树(Segment Tree)是一种用于解决区间查询问题的数据结构。
它可以高效地支持以下两种操作:区间修改和区间查询。
线段树的应用非常广泛,在离线查询、区间统计、区间更新等问题中有着重要的作用。
一、概念线段树是一颗二叉树,其中每个节点代表了一个区间。
根节点表示整个待查询区间,而叶子节点表示的是单个元素。
每个内部节点包含了其子节点所代表区间的并集。
二、构建线段树线段树的构建过程是自底向上的。
将待查询数组划分成一颗满二叉树,并将每个区间的和存储在相应的节点中。
对于叶子节点,直接存储对应元素的值。
而非叶子节点的值可以通过其子节点的值计算得到。
三、线段树的查询对于区间查询操作,可以通过递归方式实现。
从根节点开始,判断查询区间和当前节点所代表的区间是否有交集。
若没有交集,则返回当前节点的默认值。
若查询区间包含当前节点所代表的区间,则返回当前节点存储的值。
否则,将查询区间分割成左右两部分继续递归查询。
四、线段树的更新对于区间更新操作,也可以通过递归方式实现。
与查询操作类似,首先判断查询区间和当前节点所代表的区间的关系。
若没有交集,则无需更新。
若查询区间包含当前节点所代表的区间,则直接更新当前节点的值。
否则,将更新操作分割成左右两部分继续递归更新。
五、应用案例:区间最值查询一个常见的线段树应用是求解某个区间的最值。
以查询区间最小值为例,可以通过线段树来高效地解决。
首先构建线段树,然后进行区间查询时,分为以下几种情况处理:若当前节点所代表的区间完全包含于查询区间,则直接返回该节点的值;若当前节点所代表的区间与查询区间没有交集,则返回默认值;否则,将查询区间分割成左右两部分继续递归查询,最后返回两个子区间查询结果的较小值。
六、总结线段树是一种非常有用的数据结构,能够高效地解决区间查询问题。
通过合理的构建和操作,线段树可以应用于多种场景,如区间最值查询、离线查询等。
熟练掌握线段树的概念和应用方法,对解决问题具有重要意义。
线段树求解区间最长递增子序列问题

线段树求解区间最长递增子序列问题区间最长递增子序列问题是指在给定的序列中找出一个区间,该区间内的子序列是递增的且具有最长长度。
为了解决这个问题,我们可以使用线段树的数据结构。
线段树是一种用于快速解决区间查询问题的树状数据结构。
对于区间最长递增子序列问题,我们可以通过建立线段树来实现。
首先,我们需要将原始序列分割成若干区间,每个区间有一个对应的节点。
每个节点存储这个区间内的最长递增子序列的长度。
然后,我们可以通过递归地建立线段树来实现。
在建立线段树时,我们首先将原始序列分为两半,然后递归地对每个子区间进行相同的分割操作。
当递归到只剩下一个元素时,该节点的最长递增子序列的长度为1。
接下来,我们需要将每个节点的子树的最长递增子序列的长度合并到父节点中。
对于一个父节点的区间来说,其最长递增子序列的长度可以由左子节点的最长递增子序列和右子节点的最长递增子序列合并得到。
具体合并的过程是比较左子节点的最长递增子序列的长度和右子节点的最长递增子序列的长度,取较大值即为父节点的最长递增子序列的长度。
当线段树建立完毕后,我们可以通过查询操作来求解区间最长递增子序列问题。
对于每个查询,我们从根节点开始,比较查询区间和当前节点的区间。
如果查询区间完全包含当前节点的区间,那么返回当前节点的最长递增子序列的长度。
如果查询区间与当前节点的区间有交集,那么递归地查找左子节点和右子节点,然后分别返回两个子节点的最长递增子序列的长度的较大值。
通过线段树,我们可以高效地解决区间最长递增子序列问题。
每次查询的时间复杂度为O(logn),其中n是序列的长度。
然而,建立线段树的时间复杂度较高,为O(nlogn)。
因此,在需要频繁查询但很少修改的情况下,使用线段树是一个高效的选择。
总结起来,线段树是一种用于解决区间查询问题的数据结构。
通过建立线段树,可以高效地求解区间最长递增子序列问题,每次查询的时间复杂度为O(logn)。
浅谈线段树原理及实现

浅谈线段树原理及实现⼤家好,给⼤家介绍完了树状数组(有兴趣的读者可以在我的博客⽂章中阅读),现在来给⼤家介绍另⼀种数据结构——线段树。
它们结构都有共同点,但是线段树更为复杂,功能也更为强⼤,接下来就会⼀步⼀步向你介绍线段树的功能和⽤法。
线段树(Segment Tree)的简介:线段树是⼀种⼆叉搜索树,它将⼀个区间划分成⼀些单元区间,每个单元区间对应线段树中的⼀个叶结点,它基于分之思想,⽤于在线性区间上完成动态统计,它的思想主要是将线性的区间递归划分成长度相同的两段,直到叶⼦节点,每个叶⼦表⽰⼀个数据,向上每⼀层⽗亲节点都涵盖了所有⼉⼦节点,模型图如下:在图上,我们可以看出,它的根节点即为我们需要修改和统计的线段,它将其划分成两段⼦线段,运⽤了⼆分的思想mid=(l+r)/2,我们再来想想看⼀个节点应该包含什么数据,⾸先肯定是它的范围L和R,在就是⼀个数据域date,⾄于这个date存储什么数据,那就根据需要⽽定,例如可以存储这⼀段的最值,也可存储这⼀段的和等等,当然也可以都存储,⽆⾮就是多⼏个变量,基本的节点信息就是这些,然后再考虑⼀下⽤多⼤的数组来存储,根据上图,我们可以发现由于是⼆分的思想,所以不⼀定是理想的满⼆叉树,⼀个节点可能会有空的⼦节点,N个节点的满⼆叉树节点为N+N/2+N/4+...+1=2*N-1,然后再下⾯⼀层节点数为2N,要空余出来,所以存储1~N数组要开4*N,可以⽤⼀下代码表⽰:struct Segment_tree{int l,r;int date;}node[SIZE*4];由此我们可以总结⼀下线段树节点的特点:线段树每个节点代表着⼀个区间。
线段树的根节点表⽰统计范围区间1~n。
线段树每个叶⼦节点代表着⼀个数值。
对于每个除叶⼦节点外的节点[L,R],它的左⼦节点[L,mid],右⼦节点[mid+1,R]。
对于编号为i的节点,左⼦节点编号2*i,右⼦节点编号2*i+1。
区间绝对值线段树

区间绝对值线段树引言:在计算机科学中,线段树是一种常用的数据结构,用于解决一类与区间相关的问题。
而区间绝对值线段树是一种特殊的线段树,它能够高效地处理区间内元素的绝对值操作。
本文将介绍区间绝对值线段树的原理、应用场景以及实现方法。
一、原理:区间绝对值线段树是在传统线段树的基础上进行改进得到的。
它的基本思想是将区间划分为多个子区间,每个子区间维护一个值,该值表示该子区间内所有元素的绝对值之和。
通过构建这样一棵线段树,可以快速地进行区间内元素绝对值的查询和更新操作。
二、应用场景:区间绝对值线段树在很多实际问题中都有广泛的应用。
以下是一些常见的应用场景:1. 区间最值查询:给定一个区间,求出该区间内元素的绝对值的最大值或最小值。
例如,在一个数组中,我们希望快速找到某个区间内元素绝对值的最大值,这时就可以利用区间绝对值线段树来解决。
2. 区间修改操作:给定一个区间和一个增量值,将该区间内的所有元素的绝对值都增加或减少相同的数值。
例如,在一个数列中,我们希望将某个区间内的所有元素的绝对值都加上一个固定值,这时可以利用区间绝对值线段树来实现。
3. 区间绝对值和查询:给定一个区间,求出该区间内所有元素绝对值的和。
例如,在某个数列中,我们希望快速求出某个区间内所有元素绝对值的和,这时可以利用区间绝对值线段树来解决。
三、实现方法:区间绝对值线段树的实现方法如下:1. 构建线段树:首先需要确定线段树的结构,通常使用数组或树的形式表示。
对于每个节点,需要记录该节点表示的区间范围、节点的值以及左右子节点的指针。
2. 初始化线段树:将线段树的所有节点的值初始化为0或其他合适的初始值。
3. 插入和更新操作:对于需要插入或更新的区间,从根节点开始递归地向下更新每个节点的值,直到达到叶子节点。
更新节点的值时,需要考虑区间是否与节点表示的区间有重叠,如果有重叠则更新对应的值。
4. 查询操作:对于需要查询的区间,从根节点开始递归地向下查询每个节点的值,直到达到叶子节点。
线段树(原理简述+C++代码)

线段树(原理简述+C++代码)线段树简述线段树的特点:操作逻辑是树的逻辑(左右⼦节点概念)底层数据存储却是⽤数字实现的。
说⽩了,线段树对应的是⼀棵完全⼆叉树,每个节点在数组中的位置就是该该节点在层序遍历中的序号(从1开始)。
基于数组实现我们能⽅便的访问⼀个节点的左右⼦节点,设当前节点存储序号idx,则左右⼦节点为存储序号分别为idx*2和idx*2+1。
线段树有什么⽤?考虑⼀个场景,我们有⼀个数组ori[1:n],在任意时刻我们希望把某区间ori[a:b]内的数据同时更新(加上某个数),或者是查询区间ori[a:b]内所有数字的和。
要实现这样⼀个功能,如果采⽤原始的实现的话,操作复杂度是O(b−a),在区间较⼤时复杂度不可接受。
1. 优化查询复杂度,如果我们能把b−a拆分成为 2 的幂次的加和,并且存储了这些区间的信息,那么我们可以将这些区间的的加起来即为总和。
优化后复杂度为O(log2(n))。
2. 优化更新复杂度,引⼊⼀个 lazy 优化(需要额外的O(n) 空间),同样能把更新复杂度优化到O(log2(n))。
lazy ⽤⽽实现这两点刚好就可以⽤线段树来实现,线段树的每个节点包含的信息是某区间内的信息。
如下图在整个线段树的实现中,我们只有⼀个数组arr[]⽤来保存节点的值(某区间内数的和)。
原始数组ori[]已经被映射到了arr[]中,不再单独占⽤存储空间。
考虑查询sum(ori[3:7]),拆分可得sum(ori[3:7]) = sum(ori[3:4]) + sum(ori[5:6]) + sum(ori[7,7]),即访问arr[]的5,6,14号节点即可。
显然借助arr[]就可以实现log(N) 复杂度;更新时我们同样可以将区间拆分,同样考虑更新区间ori[3:7],拆分为ori[3:4], ori[5:6], ori[7:7],ori[3:4]对应arr[]的 5 号节点,更新到 5号节点后不在往下更新,映⼊⼀个 lazy 变量来缓存更新信息,待下次查询或者更新到 5 节点的⼦节点时再把该缓存信息更新到⼦节点。
菜鸟都能理解的线段树入门经典
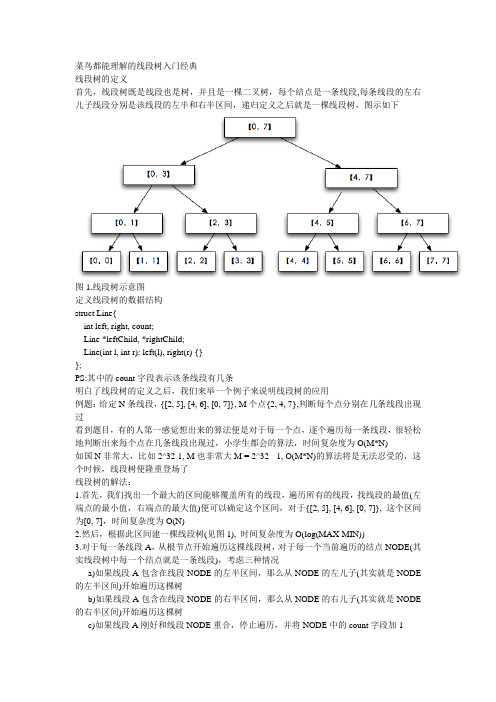
菜鸟都能理解的线段树入门经典线段树的定义首先,线段树既是线段也是树,并且是一棵二叉树,每个结点是一条线段,每条线段的左右儿子线段分别是该线段的左半和右半区间,递归定义之后就是一棵线段树,图示如下图1.线段树示意图定义线段树的数据结构struct Line{int left, right, count;Line *leftChild, *rightChild;Line(int l, int r): left(l), right(r) {}};PS:其中的count字段表示该条线段有几条明白了线段树的定义之后,我们来举一个例子来说明线段树的应用例题:给定N条线段,{[2, 5], [4, 6], [0, 7]}, M个点{2, 4, 7},判断每个点分别在几条线段出现过看到题目,有的人第一感觉想出来的算法便是对于每一个点,逐个遍历每一条线段,很轻松地判断出来每个点在几条线段出现过,小学生都会的算法,时间复杂度为O(M*N)如国N非常大,比如2^32-1, M也非常大M = 2^32 - 1, O(M*N)的算法将是无法忍受的,这个时候,线段树便隆重登场了线段树的解法:1.首先,我们找出一个最大的区间能够覆盖所有的线段,遍历所有的线段,找线段的最值(左端点的最小值,右端点的最大值)便可以确定这个区间,对于{[2, 5], [4, 6], [0, 7]}, 这个区间为[0, 7],时间复杂度为O(N)2.然后,根据此区间建一棵线段树(见图1), 时间复杂度为O(log(MAX-MIN))3.对于每一条线段A,从根节点开始遍历这棵线段树,对于每一个当前遍历的结点NODE(其实线段树中每一个结点就是一条线段),考虑三种情况a)如果线段A包含在线段NODE的左半区间,那么从NODE的左儿子(其实就是NODE 的左半区间)开始遍历这棵树b)如果线段A包含在线段NODE的右半区间,那么从NODE的右儿子(其实就是NODE 的右半区间)开始遍历这棵树c)如果线段A刚好和线段NODE重合,停止遍历,并将NODE中的count字段加1d)除了以上的情况,就将线段A的左半部分在NODE的左儿子处遍历,将A的右半部分在NODE的右儿子处遍历补充说明:对于以上的步骤,所做的工作其实就是不断地分割每一条线段,使得分割后的每一条小线段刚好能够落在线段树上,举个例子,比如要分割[2, 5],首先将[2, 5]和[0, 7]比较,符合情况d, 将A分成[2, 3]与[4, 5]I)对于[2, 3]从[0, 7]的左半区间[0, 3]开始遍历将[2, 3]与[0, 3]比较,满足情况b,那么从[0, 3]的右半区间[2, 3]开始遍历,发现刚好重合,便将结点[2, 3]count字段加1II)对于[4, 5]从[0, 7]的右半区间[4, 7]开始遍历将[4, 5]与[4, 7]比较,满足情况b,从[4, 7]的左半区间[4, 5]开始遍历,发现刚好重合,便将结点[4, 5]count字段加1于是对于[2, 5]分割之后线段树的情况为图2图2.分割[2,5]之后线段树的情况显然,我们看到,上述的遍历操作起始就是将[2, 5]按照线段树中的线段来分割,分割后的[2, 3]与[4, 5]其实是与[2, 5]完全等效的最后,我们将剩下的两条线段按照同样的步骤进行分割之后,线段树的情况如下图3这一步的时间复杂度为O(N*log(MAX-MIN))4.最后,对于每一个值我们就可以开始遍历这一颗线段树,加上对于结点的count字段便是在线段中出现的次数比如对于4,首先遍历[0, 7],次数= 0+1=1;4在右半区间,遍历[4, 7],次数= 1+0=0;4在[4, 7]左半区间, 次数= 1+2=3;4在[4, 5]左半区间,次数= 3+0 = 4,遍历结束,次数= 3说明4在三条线段中出现过,同理可求其他的值,这一步的时间复杂度为O(M*log(MAX-MIN))最后,总的时间复杂度为O(N)+O(log(MAX-MIN))+O(N*log(MAX-MIN))+(M*log(MAX-MIN)) = O((M+N)*log(MAX-MIN))由于log(MAX-MIX)<=64所以最后的时间复杂度为O(M+N)最后,放出源码[cpp] view plaincopy#include <iostream>using namespace std;struct Line{int left, right, count;Line *leftChild, *rightChild;Line(int l, int r): left(l), right(r) {}};//建立一棵空线段树void createTree(Line *root) {int left = root->left;int right = root->right;if (left < right) {int mid = (left + right) / 2;Line *lc = new Line(left, mid);Line *rc = new Line(mid + 1, right);root->leftChild = lc;root->rightChild = rc;createTree(lc);createTree(rc);}}//将线段[l, r]分割void insertLine(Line *root, int l, int r) {cout << l << " " << r << endl;cout << root->left << " " << root->right << endl << endl;if (l == root->left && r == root->right) {root->count += 1;} else if (l <= r) {int rmid = (root->left + root->right) / 2;if (r <= rmid) {insertLine(root->leftChild, l, r);} else if (l >= rmid + 1) {insertLine(root->rightChild, l, r);} else {int mid = (l + r) / 2;insertLine(root->leftChild, l, mid);insertLine(root->rightChild, mid + 1, r);}}}//树的中序遍历(测试用)void inOrder(Line* root) {if (root != NULL) {inOrder(root->leftChild);printf("[%d, %d], %d\n", root->left, root->right, root->count);inOrder(root->rightChild);}}//获取值n在线段上出现的次数int getCount(Line* root, int n) {int c = 0;if (root->left <= n&&n <= root->right)c += root->count;if (root->left == root->right)return c;int mid = (root->left + root->right) / 2;if (n <= mid)c += getCount(root->leftChild, n);elsec += getCount(root->rightChild, n);return c;}int main() {int l[3] = {2, 4, 0};int r[3] = {5, 6, 7};int MIN = l[0];int MAX = r[0];for (int i = 1; i < 3; ++i) {if (MIN > l[i]) MIN = l[i];if (MAX < r[i]) MAX = r[i];}Line *root = new Line(MIN, MAX);createTree(root);for (int i = 0; i < 3; ++i) {insertLine(root, l[i], r[i]);}inOrder(root);int N;while (cin >> N) {cout << getCount(root, N) << endl; }return 0;}。
线段树学习

这几天一直在学线段树,觉得很爽。
线段树顾名思义就是由线段组成的数,准确的说呢是区间。
那么,线段树有什么用呢?线段树的基本操作。
打线段树一定要注意到底是a,b还是l,r。
别弄错了。
L,r是编号而已。
A,b是左右边界。
学习一种数据结构,个人认为需要掌握它的基本操作。
1.建树。
procedure make(l,r:longint);var mid,now:longint;begininc(tot);t[tot].a:=l;t[tot].b:=r;t[tot].min:=maxlongint;now:=tot;mid:=(l+r) shr 1;if mid>l thenbegint[now].l:=tot+1;make(l,mid);t[now].r:=tot+1;make(mid,r);end;end;2.查找最值。
function getmin(i,l,r:longint):longint;var now,mid:longint;beginif (l<=t[i].a) and (t[i].b<=r) then exit(t[i].min);mid:=(t[i].a+t[i].b) shr 1;now:=maxlongint;if l<mid then now:=min(now,getmin(t[i].l,l,r));if r>mid then now:=min(now,getmin(t[i].r,l,r));exit(now);end;3.修改单个点的值。
procedure insert(i,j,x:longint);var mid:longint;beginif t[i].a=t[i].b-1 thenbegint[i].min:=x;exit;end;mid:=(t[i].a+t[i].b) shr 1;if j<=mid then insert(t[i].l,j,x) else insert(t[i].r,j,x); t[i].min:=min(t[t[i].l].min,t[t[i].r].min);end;4.修改一段区间。
线段树详解与实现

线段树详解与实现此篇⽂章⽤于记录《玩转数据结构》课程的学习笔记什么是线段树线段树也被称为区间树,英⽂名为Segment Tree或者Interval tree,是⼀种⾼级的数据结构。
这种数据结构更多出现在竞赛中,在常见的本科数据结构教材⾥没有介绍这种数据结构。
但是,在⾯试中却有可能碰到和线段树相关的问题。
那么为什么会产⽣线段树这种数据结构,线段树到底是为了解决什么样的⼀种问题呢?其实这⾥的线段可以理解为区间,线段树就是为了解决区间问题的。
有⼀个很经典的线段树问题是:区间染⾊。
假设有⼀⾯墙,长度为 n,每次选择⼀段墙进⾏染⾊。
在区间染⾊的过程中,每次选择⼀段区间进⾏染⾊,这时新的颜⾊可能会覆盖之前的颜⾊。
最后的问题是:在经过 m 次染⾊操作后,我们可以在整个区间看见多少种颜⾊?更加普遍的说法是:在经过 m 次染⾊操作后,我们可以在区间[i, j]内看见多少种颜⾊?由于第⼀个问题是第⼆个问题的⼀个特例,我们采⽤第⼆种问题来思考解决⽅法。
从上⾯可以看出,我们对于区间,有 2 种操作,分别是染⾊操作和查询区间的颜⾊,使⽤更加⼀般的说法,染⾊操作就是更新区间,查询区间的颜⾊就是查询区间。
这类问题⾥⾯,更加常见的的是区间查询:⼀个数组存放的不再是颜⾊,⽽是具体的数字,查询某个区间[i, j]的统计值。
这⾥的统计值是指:区间内最⼤值、最⼩值、或者这个区间的数字和。
⽐如:查询 2018 年注册的⽤户中消费最⾼的⽤户查询 2018 年注册的⽤户中消费最低的⽤户注意上⾯两种情况都是动态查询,我们查询的消费数据不只是 2018 的消费数据。
如果我们想查询 2018 年中消费最⾼的⽤户,那么 2018 年的数据已经固定了,我们直接在这⼀年的数据中进⾏统计分析就⾏了。
但是⼀个 2018 年注册的⽤户,在 2019 年、2020 年都可能会有消费。
我们实际上查询的是:2018 年注册的⽤户中,到现在为⽌,消费最⾼的⽤户。
这种情况下,数据是在动态变化的,也就是说:2017 年注册的⽤户中,每个⽤户的消费额是会更新的,这就对应到更新区间的操作。
线段叠加——线段树

线段叠加——线段树2006/11/10 下午07:40我们往往遇到这样的问题,研究的对象是数量庞大的线段,普通的方法往往是O(n^2),的,而用线段树我们可以做到O(nlogn)。
线段树是一棵完全二叉树,它的根节点代表一个区间[a,b],左结点是[a,(a+b) div 2],右结点是[(a+b) div 2,b],且左右结点分别是线段树,注意我们这里说的是线段,[a,b]即表示数轴上a,b两点间的线段,所以左结点和右结点并没有交。
线段数的基本操作有插入、查找、删除,而插入删除的操作都是建立在查找的基础上的:查找线段[a,b]根据当前结点的边界中点把[a,b]分成最多2部分,然后递归查找它的左右结点。
删除[a,b]找到[a,b]后,将其结点的相关数据清除即可,不需要删除结点。
插入[a,b]找到[a,b]后,添加其结点的相关数据。
相关数据依题目的要求不同而不同,这里不一一列举。
因为线段树是一棵完全二叉树,所以可以用数组模拟,父结点s,左孩子s*2,右孩子s*2+1。
线段树的复杂度就是查找的复杂度,不难证明每层最多只访问2个结点,而总层数是log(b-a),所以复杂度是O(2log(b-a))=O(logn)Const Maxn=120000; {最多支持120000条线段,即支持Long_x<=60000}Type TreeNode=Recorda,b,Left,Right:Longint;Cover,bj:shortint; {记录线段是否被覆盖;线段的标记}End;V ar i,j,k,m,n,tot,c,d,Ans:longint;Tree:array[0..Maxn] of TreeNode;Procedure MakeTree(a,b:Longint); {建立线段树的过程}V ar Now:longint;Begininc(tot);Now:=tot;Tree[Now].a:=a;Tree[Now].b:=b;if a+1<b thenbeginTree[Now].Left:=tot+1;MakeTree(a,(a+b) shr 1);Tree[Now].Right:=tot+1;MakeTree((a+b) shr 1,b);end;End;Procedure Init; {读入数据并预处理的过程}Beginassign(input,'sample1.in');reset(input);assign(output,'sample1.out');rewrite(output);readln(n,m);fillchar(Tree,sizeof(Tree),0);tot:=0;MakeTree(1,n);End;Procedure Clean(Num:Longint); {更新标记的过程}BeginTree[Num].Cover:=0;Tree[Num].bj:=0;Tree[Tree[Num].Left].bj:=-1; Tree[Tree[Num].Right].bj:=-1;End;Procedure Insert(Num,c,d:longint); {涂色的过程}V ar Mid:longint;Beginif Tree[Num].bj=-1 then Clean(Num); {若被标记则更新}if Tree[Num].Cover=1 then exit; {若线段已被涂色,退出过程}if (c<=Tree[Num].a)and(d>=Tree[Num].b) thenbeginTree[Num].Cover:=1;exit;end;Mid:=(Tree[Num].a+Tree[Num].b) shr 1;if c<Mid then Insert(Tree[Num].Left,c,d);if d>Mid then Insert(Tree[Num].Right,c,d);End;Procedure Delete(Num,c,d:Longint); {擦除颜色的过程}V ar Mid:Longint;Beginif Tree[Num].bj=-1 then Exit; {若线段被标记,说明该线段已不复存在,无需再进行删除,退出过程}if (c<=Tree[Num].a)and(d>=Tree[Num].b) thenbeginTree[Num].Cover:=0;Tree[Tree[Num].Left].bj:=-1;Tree[Tree[Num].Right].bj:=-1;{把线段已被删除的信息传给左右儿子}exit;end;if Tree[Num].Cover=1 then {若该线段是被涂了色的}beginTree[Num].Cover:=0;Tree[Tree[Num].Left].bj:=-1;Tree[Tree[Num].Right].bj:=-1; {先删除}if Tree[Num].a<c then Insert(Num,Tree[Num].a,c); {再插入}if d<Tree[Num].b then Insert(Num,d,Tree[Num].b);endelse {否则继续对左右儿子调用删除过程}beginMid:=(Tree[Num].a+Tree[Num].b) shr 1;if c<Mid then Delete(Tree[Num].Left,c,d);if d>Mid then Delete(Tree[Num].Right,c,d);end;End;Procedure Calculate(Num:longint);{计算被覆盖的单位线段条数的过程}Beginif Num=0 then exit; {父亲已是叶子结点了(叶子节点的儿子为0),返回}if Tree[Num].bj=-1 then exit; {线段被标记,说明已不存在,返回}if Tree[Num].Cover=1 thenbegininc(Ans,Tree[Num].b-Tree[Num].a);exit;end;Calculate(Tree[Num].Left);Calculate(Tree[Num].Right);End;Procedure Main; {主过程}V ar i,k:longint;Beginfor i:=1 to m dobeginreadln(k,c,d);if k=1 then Insert(1,c,d)else Delete(1,c,d);end;Ans:=0;Calculate(1);Writeln(Ans);Close(output);End;Begin {主程序}Init;Main;End.。
线段树解决区间查询问题的数据结构

线段树解决区间查询问题的数据结构线段树(Segment Tree)是一种常用的数据结构,用于解决区间查询问题。
它可以高效地进行区间操作,如查询某一区间的最大值、最小值、求和等。
本文将介绍线段树的概念和原理,并通过实例演示其应用。
一、线段树的定义与特点线段树是一种二叉树结构,其每个节点表示一个区间。
根节点对应整个数组或区间,而每个叶子节点则表示数组中的一个元素。
线段树的构建和查询操作都是基于区间的。
线段树具有以下特点:1. 根节点对应整个数组或区间,其左子节点和右子节点分别表示左半部分和右半部分的区间;2. 若某个区间仅包含一个元素,则该节点为叶子节点,存储该元素的值;3. 若某个区间包含多个元素,则该节点存储区间内元素的某种统计特征(如最大值、最小值、和等);4. 线段树的构建时间复杂度为O(nlogn),查询时间复杂度为O(logn),其中n为区间长度。
二、线段树的构建线段树的构建是通过递归的方式进行的。
首先将整个数组或区间划分为左右两半,然后分别构建左子树和右子树,最后将左右子树的统计结果更新到父节点中。
具体构建过程如下:1. 若当前节点对应的区间仅包含一个元素,则为叶子节点,将该元素的值存储到该节点中;2. 否则,将当前区间一分为二,分别构建左子树和右子树;3. 左子树对应左半部分的区间,右子树对应右半部分的区间;4. 构建左子树和右子树后,将左子树和右子树的统计结果更新到当前节点中。
三、线段树的查询线段树的查询是通过递归的方式进行的。
根据查询的区间和当前节点的区间关系,可以将查询问题转化为以下几种情况:1. 查询区间与当前节点的区间完全相同,直接返回当前节点存储的统计结果;2. 查询区间与当前节点的区间没有交集,返回一个表示无效值(如负无穷大);3. 查询区间与当前节点的区间部分相交,继续递归查询左子树和右子树,然后将统计结果合并。
具体查询过程如下:1. 若当前节点对应的区间与查询区间完全相同,直接返回当前节点存储的统计结果;2. 若当前节点对应的区间与查询区间没有交集,返回一个表示无效值(如负无穷大);3. 若当前节点对应的区间部分相交,递归查询左子树和右子树;4. 将左右子树查询结果合并,返回合并后的统计值。
线段树(数组实现)

线段树(数组实现)最近看了很多学长发的资料,吸取了别⼈的优点,把query函数更改的更加合理了。
—————————————————————我是分割线———————————————————————————————————————————— 线段树是⼀棵完美⼆叉树,树上的每个节点都维护⼀个区间。
根维护的是整个区间,每个节点维护的是⽗亲的区间⼆等分后的其中⼀个⼦区间。
当有n个元素时,对区间的操作可以在O(logn)的时间内完成。
所以,线段树是擅长处理区间的! 从⽹上找了⼀个图:RMQ(range minimum query)问题: 在给定数列a0,a1...a n,给定s和t,线段树可以求a s...a t的最值,以求最⼩值为例,如下图: 每个节点维护对应区间的最⼩值,例如根节点维护的是下标1到8的最⼩值,左⼦树维护的是1到4,右⼦书维护的是5到6,以此类推。
建树时,⽗节点取左右⼦节点的较⼩者。
我⽐较喜欢⽤数组建树,因为⾮常简单清晰,下⾯是初始化线段树的代码:1#define max 9999999992int k,n,tree[10005];//n这⾥是数列⾥数字的个数3void init(){4 k=1;//k这⾥是树最后⼀层的叶⼦个数5while(k<n)//除第⼀层外,树的每⼀层都有2的n次⽅个节点,所以这⾥求的是k⼤于n的最⼩节点数6 k<<=1;//输⼊的数字个数n可能⼩于最下⾯⼀层的叶⼦数7for(int i=1;i<=2*k-1;i++)//2*k-1是整个树节点的个数,全部设置为max,反正⽗节点取的是较⼩者8 tree[i]=max;9 } n⼩于k时,树最后⼀层的其他值已经是max,所以不影响⽗节点,下⾯是线段树每插⼊⼀个值的更新:1void update(int pos,int val){//pos是树的下标,val是数的值2 pos+=k-1;//这⾥数组下标是从1到n,树的下标也是从1到n,这就是叶⼦节点与数组下标的对应关系,⼤家可以画⼀画3 tree[pos]=val;4while(k>1){5 pos/=2;//⽗节点6 tree[pos]=tree[pos*2]<tree[pos*2+1]?tree[pos*2]:tree[pos*2+1];7 }8 } 下⾯⽐较关键的是给定下标区间查找,我会在注释⾥说明:1//调⽤时query(输⼊a,输⼊b,1,1,k)2int query(int a,int b,int pos,int l,int r){//a和b是想要查找的下标区间,l和r是当前节点维护的下标区间,pos是当前节点下标3if(a<=l&&b>=r)//查找终结的条件就是想查找的区间⼤于节点维护的区间4return tree[pos];5int mid = (l+r)/2;6if(a<=m)7int a = query(a,b,pos*2,l,m);8if(b>m)9int b = query(a,b,pos*2+1,m+1,r);10return a<b?a:b;11 } OK,到这⾥,基本的算法就实现了,注意⼀下树的⼤⼩⼀定要合适。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线段树的简单实现:#i nclude <stdio.h>#i nclude <alloc.h>#define MaxSize 1000typedef char ElemType;typedef struct node{int i,j;int cover;struct node *lchild,*rchild;} ITree;//建立线段树ITree *CreateTree(int a,int b){ITree *r;if(b<a) return NULL;r=(ITree *)malloc(sizeof(ITree));r->i=a;r->j=b;r->cover=0;if(b-a>1){r->lchild=CreateTree(a,(a+b)/2);r->rchild=CreateTree((a+b)/2,b);}else r->lchild=r->rchild=NULL;return r;}//线段树的插入void InsTree(ITree *r,int a,int b){int mid;if(a<=r->i&&r->j<=b) r->cover++;else{mid=(r->i+r->j)/2;if(b<=mid) InsTree(r->lchild,a,b);else if(mid<=a) InsTree(r->rchild,a,b);else{InsTree(r->lchild,a,mid);InsTree(r->rchild,mid,b);}}}//线段树的删除void DelTree(ITree *r,int a,int b){int mid;if(a<=r->i&&r->j<=b) r->cover--;else{mid=(r->i+r->j)/2;if(b<=mid) DelTree(r->lchild,a,b);else if(mid<=a) DelTree(r->rchild,a,b);else{DelTree(r->lchild,a,mid);DelTree(r->rchild,mid,b);}}}//计算线段树的测度int Count(ITree *r){if(r->cover>0) return r->j-r->i;else if(r->j-r->i==1) return 0;else return Count(r->lchild)+Count(r->rchild);}//主函数int main(){ITree *r;int a,b,a1,b1,a2,b2,a3,b3,n,i;printf("请输入线段树的区间端点:");while(scanf("%d%d",&a,&b)!=EOF){r=CreateTree(a,b);printf("请输入插入3条线段的区间端点:");scanf("%d%d%d%d%d%d",&a1,&b1,&a2,&b2,&a3,&b3);InsTree(r,a1,b1);InsTree(r,a2,b2);InsTree(r,a3,b3);printf("插入3条线段后线段树的测度为%d\n",Count(r));printf("请输入删除2条线段的区间端点:");scanf("%d%d%d%d",&a1,&b1,&a2,&b2);DelTree(r,a1,b1);DelTree(r,a2,b2);printf("删除2条线段后线段树的测度为%d\n",Count(r));printf("\n请输入线段树的区间端点:");}return 0; }pku 2528(离散化+线段树)2010-03-16 16:42#include<iostream> #include<algorithm>using namespace std;struct node{int left,right;int count;}tree[160020];int poster[10003][2];int flag[20003];int hash[10000003];//hash函数。
int sum;int cmp(const void *a,const void *b){return *(int *)a-*(int *)b;}void Build(int k,int i,int j)//利用完全二叉树建树。
{tree[k].left=i;tree[k].right=j;tree[k].count=0;if(i!=j){int mid=(i+j)/2;Build(2*k,i,mid);Build(2*k+1,mid+1,j);}return ;}void Insert(int i,int color,int from,int to){if(tree[i].left==from&&tree[i].right==to){tree[i].count=color;return ;}if(tree[i].count==color)return ;if(tree[i].count!=-1&&tree[i].count!=color)//这个if语句很重要,就是他,搞了很长时间。
{tree[2*i].count=tree[i].count;tree[2*i+1].count=tree[i].count;tree[i].count=-1;}int mid=(tree[i].left+tree[i].right)>>1;if(to<=mid){Insert(i*2,color,from,to);}else if(from>mid)Insert(1+2*i,color,from,to);else{Insert(i*2,color,from,mid);Insert(i*2+1,color,mid+1,to);}return ;}void query(int i){if(tree[i].count>=0){if(flag[tree[i].count]==0){sum++;}flag[tree[i].count]++;return ;}query(i*2);query(i*2+1);return ;}int main(){int i,j,k;int t,n;scanf("%d",&t);while(t--){memset(flag,0,sizeof(flag));scanf("%d",&n);j=0;k=1;for(i=1;i<=n;i++){scanf("%d%d",&poster[i][0],&poster[i][1]);flag[j++]=poster[i][0];flag[j++]=poster[i][1];}qsort(flag,j,sizeof(flag[0]),cmp);//离散化处理。
hash[flag[0]]=1;for(i=1;i<j;i++){if(flag[i]!=flag[i-1])k++;hash[flag[i]]=k;}Build(1,1,k);//建立空的线段树memset(flag,0,sizeof(flag));for(i=1;i<=n;i++){Insert(1,i,hash[poster[i][0]],hash[poster[i][1]]);//插入}sum=0;query(1);//计算可以看到总的海报数量printf("%d\n",sum);}return 0;}pku 2777(线段树)2010-03-16 18:49#include<iostream> using namespace std;const int hmax=100005;int flag[100];int sum=0;struct node{int left,right;int color;}board[4*hmax];void Build(int k,int from,int to){board[k].left=from;board[k].right=to;board[k].color=1;if(from!=to){int mid=(from+to)>>1;Build(2*k,from,mid);Build(2*k+1,mid+1,to);}return ;}void update(int i,int from,int to,int color){if(board[i].left==from&&board[i].right==to){board[i].color=color;return ;}if(board[i].color==color)return ;if(board[i].color!=color&&board[i].color){board[2*i].color=board[i].color;board[2*i+1].color=board[i].color;board[i].color=0;}int mid=(board[i].left+board[i].right)>>1;if(to<=mid){update(i*2,from,to,color);}else if(from>mid)update(i*2+1,from,to,color);else{update(i*2,from,mid,color);update(i*2+1,mid+1,to,color);}return ;}void query(int i,int from,int to){if(board[i].color){if(!flag[board[i].color]){sum++;}flag[board[i].color]++;return ;}int mid=(board[i].left+board[i].right)>>1; if(to<=mid){query(i*2,from,to);}else if(from>mid)query(i*2+1,from,to);else{query(i*2,from,mid);query(i*2+1,mid+1,to);}return ;}int main(){int i,a,b,c,k;int L,T,O;char s1[3];while(scanf("%d%d%d",&L,&T,&O)!=EOF) {Build(1,1,L);for(i=0;i<O;i++){scanf("%s",s1);if(s1[0]=='C'){scanf("%d%d%d",&a,&b,&c);if(a>b){k=a;a=b;b=k;}update(1,a,b,c);}else{scanf("%d%d",&a,&b);if(a>b){k=a;a=b;b=k;}sum=0;memset(flag,0,sizeof(flag));query(1,a,b);printf("%d\n",sum);}}}return 0;}pku 2777(线段树)2010-03-16 18:49#include<iostream> using namespace std;const int hmax=100005;int flag[100];int sum=0;struct node{int left,right;int color;}board[4*hmax];void Build(int k,int from,int to){board[k].left=from;board[k].right=to;board[k].color=1;if(from!=to){int mid=(from+to)>>1;Build(2*k,from,mid);Build(2*k+1,mid+1,to);}return ;}void update(int i,int from,int to,int color){if(board[i].left==from&&board[i].right==to){board[i].color=color;return ;}if(board[i].color==color)return ;if(board[i].color!=color&&board[i].color){board[2*i].color=board[i].color;board[2*i+1].color=board[i].color;board[i].color=0;}int mid=(board[i].left+board[i].right)>>1;if(to<=mid){update(i*2,from,to,color);}else if(from>mid)update(i*2+1,from,to,color);else{update(i*2,from,mid,color);update(i*2+1,mid+1,to,color);}return ;}void query(int i,int from,int to){if(board[i].color){if(!flag[board[i].color]){sum++;}flag[board[i].color]++;return ;}int mid=(board[i].left+board[i].right)>>1; if(to<=mid){query(i*2,from,to);}else if(from>mid)query(i*2+1,from,to);else{query(i*2,from,mid);query(i*2+1,mid+1,to);}return ;}int main(){int i,a,b,c,k;int L,T,O;char s1[3];while(scanf("%d%d%d",&L,&T,&O)!=EOF) {Build(1,1,L);for(i=0;i<O;i++){scanf("%s",s1);if(s1[0]=='C'){scanf("%d%d%d",&a,&b,&c);if(a>b){k=a;a=b;b=k;}update(1,a,b,c);}else{scanf("%d%d",&a,&b);if(a>b){k=a;a=b;b=k;}sum=0;memset(flag,0,sizeof(flag));query(1,a,b);printf("%d\n",sum);}}}return 0;}pku 1177(线段树)2010-03-30 11:48强烈推荐先看看国家集训队的论文---陈宏的论文#include<iostream>#include<algorithm>using namespace std;const int hmax=40006;struct seg_tree{int left,right;int count;int cl,cr;int segment;int seg;}node[2*hmax];struct rect{int start,end;int x;int tag;}line[hmax];int hash[hmax],lisan[hmax];;int Y[hmax],n;int cmp(rect a,rect b){return (a.x<b.x)? 1:0;}void Build(int i,int from,int to){node[i].left=from;node[i].right=to;node[i].count=0;node[i].cl=node[i].cr=0;node[i].segment=0;node[i].seg=0;if(to-from>1){int mid=(1+node[i].left+node[i].right)>>1;Build(2*i,from,mid);Build(2*i+1,mid,to);}return;}void update(int i,int from,int to){if(node[i].count>0){node[i].segment=lisan[node[i].right]-lisan[node[i].left];node[i].seg=1;node[i].cl=node[i].cr=1;}else if(node[i].right-node[i].left>1){node[i].segment=(node[2*i].segment+node[2*i+1].segment);node[i].cl=node[2*i].cl;node[i].cr=node[2*i+1].cr;node[i].seg=node[2*i].seg+node[2*i+1].seg;if(node[2*i].cr&&node[2*i+1].cl)node[i].seg--;}else{node[i].segment=0;node[i].cl=node[i].cr=0;node[i].seg=0;}}void Insert(int i,int from,int to,int tag){if(from<=node[i].left&&to>=node[i].right)node[i].count+=tag;else{int mid=(1+node[i].left+node[i].right)>>1;if(from<mid)Insert(2*i,from,to,tag);if(to>mid)Insert(2*i+1,from,to,tag);}update(i,from,to);}int main(){int i,j,k;int x1,x2,y1,y2;while(EOF!=scanf("%d",&n)){for(i=j=0;j<n;j++){scanf("%d%d%d%d",&x1,&y1,&x2,&y2);line[i].start=line[i+1].start=y1;line[i].end=line[i+1].end=y2;line[i].x=x1;line[i+1].x=x2;line[i].tag=1;line[i+1].tag=-1;Y[i]=y1;Y[i+1]=y2;i+=2;}sort(Y,Y+2*n);sort(line,line+2*n,cmp);/*for(i=0;i<2*n;i++)cout<<Y[i]<<endl;cout<<endl;for(i=0;i<2*n;i++)cout<<line[i].x<<" "<<line[i].start<<" "<<line[i].end<<" "<<line[i].tag<<endl;cout<<endl;*/lisan[1]=Y[0];hash[Y[0]+10000]=1;k=1;for(i=1;i<2*n;i++){if(Y[i]==Y[i-1])continue;k++;lisan[k]=Y[i];hash[Y[i]+10000]=k;}Build(1,1,k);int from,to;int pre=0, len=0;int sum=0;line[2*n].x=line[2*n-1].x;for(i=0;i<2*n;i++){from=hash[line[i].start+10000];to=hash[line[i].end+10000];Insert(1,from,to,line[i].tag);len=node[1].segment;sum+=2*node[1].seg*(line[i+1].x-line[i].x);if(len>=pre)sum+=len-pre;elsesum+=pre-len;pre=len;}printf("%d\n",sum);}return 0;}/*-6-4481010141516202225-15 0 10 1-5 8 25 10 -6 4 12 15 22 15 0 10 -110 15 22 -115 -4 14 116 -6 4 -120 8 25 -1 24 -4 14 -1 30 10 20 1 34 0 16 1 36 10 20 -1 40 0 16 -1POJ 2182 Lost Cows 我的第一道线段树题目!DescriptionN (2 <= N <= 8,000) cows have unique brands in the range 1..N. In a spectacular display of poor judgment, they visited the neighborhood 'watering hole' and drank a few too many beers before dinner. When it was time to line up for their evening meal, they did not line up in the required ascending numerical order of their brands.Regrettably, FJ does not have a way to sort them. Furthermore, he's not very good at observing problems. Instead of writing down each cow's brand, he determined a rather silly statistic: For each cow in line, he knows the number of cows that precede that cow in line that do, in fact, have smaller brands than that cow.Given this data, tell FJ the exact ordering of the cows.Input* Line 1: A single integer, N* Lines 2..N: These N-1 lines describe the number of cows that precede a given cow in line and have brands smaller than that cow. Of course, no cows precede the first cow in line, so she is not listed. Line 2 of the input describes the number of preceding cows whose brands are smaller than the cow in slot #2; line 3 describes the number of preceding cows whose brands are smaller than the cow in slot #3; and so on.Output* Lines 1..N: Each of the N lines of output tells the brand of a cow in line. Line #1 of the output tells the brand of the first cow in line; line 2 tells the brand of the second cow; and so on. Sample Input5121Sample Output24531解题思路:对于一个给定序列,从后面往前面看是前面有几个数字是比他小的,0代表前面没有数字比他小,所以肯定是1,把1去掉。
