两个变量的自同态及自同构
线性空间的同构与同态

线性空间的同构与同态线性空间是很多高阶数学领域所需要用到的基本概念,因此在线性代数的学习中,我们不得不对线性空间基本的性质、定义、等价性、基础定理等有一个深刻的理解。
当然,线性空间的同构与同态作为线性变换的代名词,也是我们学习线性空间理论时,需要重点关注的。
一、线性空间同构同构,是数学中一个十分重要的概念。
它指的是两个结构相同、具有相同性质的数学对象。
更准确地说,如果两个集合之间存在一一对应,且它们之间的映射不仅是单射还是满射,那么这两个集合就是同构的。
对于线性空间,它满足向量的加法和数量的乘法这两个运算规则,因此,我们可以要求用以下方式定义两个线性空间的同构:定义:若存在双射映射$f:V\to W$,并满足:1. $\forall u,v\in V$,有$f(u+v)=f(u)+f(v)$。
2. $\forall u\in V$和$c\in F$,有$f(cu)=cf(u)$。
则称线性空间$V$和$W$之间存在同构,称$f$为同构映射。
其中,$F$是一个数域,它是一个固定的标量(标量乘法满足分配律、结合律、单位元和逆元等基本性质)。
同构可以理解为两个向量空间“外形”相同,尽管它们之间的标量乘法、向量加法的具体运算方式可能不同。
关于线性空间同构,我们有如下三个重要结论:(1)同构是一种双射关系,即两个线性空间同构当且仅当它们的维度相等。
(2)两个线性空间同构,则它们必须同构于数域$F$上的$n$维线性空间$F^n$。
(3)两个线性空间同构,当且仅当它们的基底个数相等。
通过上述结论,我们可以发现,实际上同构所关注的是两个线性空间的向量基。
只有当两个线性空间的维度相等、同构映射满足条件时,它们才是同构的。
因此,为了构造同构映射,我们通常需要找到两个向量空间之间的一个映射,满足一一对应、线性、满射的性质,这样才能实现同构。
二、线性空间同态同态是另一个重要的概念。
它们也是线性代数中常用的术语,他们主要与线性空间中的变换相关。
离散数学-同态和同构

离散算法设计
同态和同构可以用于设计高效的离散算法, 如通过同态映射将问题转化为易于处理的数
学形式,从而降低计算复杂度。
05
同态和同构的实例分析
BIG DATA EMPOWERS TO CREATE A NEW
ERA
二次方程的同态和同构分析
要点一
总结词
要点二
详细描述
在二次方程中,同态和同构的概念主要应用于方程的变形 和等价分类。
拓扑同构映射保持了原拓扑空间中的拓扑性质,即如果映射$f: X rightarrow Y$是 拓扑空间$X, Y$之间的同构映射,那么对于任意子集$U subseteq X$,有$f(U)$是 $Y$中的开集当且仅当$U$是$X$中的开集。
保持连通性
拓扑同构映射保持了原拓扑空间中的连通性,即如果映射$f: X rightarrow Y$是拓 扑空间$X, Y$之间的同构映射,那么对于任意子集$A subseteq X, B subseteq Y$, 有$(A subseteq B) Leftrightarrow (f(A) subseteq f(B))$。
逻辑同构的性质
保持逻辑关系
逻辑同构映射保持了原逻辑系统中的逻辑关系,即如果映射$f: L_1 rightarrow L_2$是逻辑系统$L_1, L_2$之间的同构映射,那么对于任意命题$varphi in L_1, psi in L_2$,有$(L_1 models varphi) Leftrightarrow (L_2 models psi)$。
的。
同构的性质
同构是一种更强的相似性关系,它不仅保持了群的基本运算性质,还要求存在一个双射 的映射。这意味着原始群和目标群在某种程度上是完全相同的。
同态与同构

离散结构同态与同构教学目标基本要求(1)掌握同态映射与同构映射的定义(2)掌握同态映射与同构映射的判定方法重点难点(1)同态映射的证明同态映射定义:设V1=<A,∘>和V2=<B,∗>是同类型的代数系统,f:A→B,且∀x, y∈A 有f(x∘y) = f(x)∗f(y), 则称f 是V1到V2的同态映射,简称同态.同态分类:(1) 如果f是单射,则称为单同态(2) 如果f是满射,则称为满同态,这时称V2是V1的同态像,记作V1∼ V2(3) 如果f是双射,则称为同构,也称代数系统V1同构于V2,记作V1 ≅ V2(4) 如果V1 = V2,则称作自同态实例例:设G为非0实数集R*关于普通乘法构成的代数系统,判断下述函数是否为G的自同态?如果不是,说明理由. 如果是,判别它们是否为单同态、满同态、同构.(1) f(x) = |x| +1(2) f(x) = |x|(3) f(x) = 0(4) f(x) = 2解:(1) 不是同态, 因为f(2×2)=f(4)=5, f(2)×f(2)=3×3=9(2) 是同态,不是单同态,也不是满同态,因为f(1)= f(−1), 且 ran f中没有负数.(3) 不是G 的自同态,因为f不是 G 到 G 的函数实例例:(1) 设V1=<Z,+>, V2=<Z n,⊕>.其中Z为整数集,+为普通加法;Z n={0,1,…,n−1},⊕为模n,f (x)=(x)mod n加. 令f: Z→Znf 是V1到V2的满同态.【f满射,f(x1+x2)=(x1+x2)mod n=(x1 mod n )⊕(x2 mod n)=f(x1)⊕f(x2)】(2) 设V1=<R,+>, V2=<R*,· >,其中R和R*分别为实数集与非零实数集,+ 和 · 分别表示普通加法与乘法.令f: R→R*,f (x)= e xf是V1到V2的单同态. 【f单射,f(x1+x2)=e(x1+x2)=e x1· e x2=f(x1) · f(x2)】(3) 设V=<Z,+>,其中Z为整数集,+为普通加法. ∀a∈Z,令f a : Z→Z,f a (x)=ax,f a 是V的自同态. 【f(x1+x2)=a(x1+x2)=ax1+ax2=f(x1)+f(x2)】当a=0时称f为零同态;为自同构;当a=±1时,称fa例. 证明<Z4,+4>与<X, >同构。
S3,S4的自同态和自同构(近世代数)

题目:S3,S4的自同态和自同构学院:数学与统计学院专业:数学与应用数学姓名:学号:指导教师:时间: 2012年6月17日摘要本文讨论了三次对称群S3和四次对称群S4各自所拥有的子群,以及找出S3,S4各自的自同态,自同构,检验各自的子群在自同态和自同构下是否保持不变。
关键词: 对称群,子群,不变子群,自同态,自同构。
一、S4和S4的子群:假如对于代数运算 和 来说,有一个A到A的同态映射存在,我们就说,这个映射是一个同态满射,并说,对于代数运算 和 来说,A与A同态。
假如对于代数运算 和 来说,有一个A到A的同构映射存在,我们就说,对于代数运算 和 来说,A与A同构。
S3={(1),(12),(13),(23),(123),(132)},S4={(1),(12),(34),(13),(24),(14),(23),(123),(132),(134),(143),(124),(142),(234),(243),(1234),(1243),(1324),(1342),(1423),(1432),(12)(34),(13)(24),(14)(23)}.其中,在S3里,(1)、(12) 、(13) 、(23)的逆元就是它们自己本身, (123)与(132)互为逆元。
在S4里,(1) 、(12) 、(34) 、(13) 、(24) 、(14)、(23) 、(12)(34) 、(13)(24) 、(14)(23) 的逆元就是它们自己本身,(123)与(132)互为逆元,(134)与(143)互为逆元, (124)与(142) 互为逆元,(234)与(243) 互为逆元,(1234)与(1432) 互为逆元,(1243)与(1342) 互为逆元,(1324)与(1423) 互为逆元。
S 3的子群有H1={(1)},H2={(1),(12)},H3={(1),(13)},H4={(1),(23)} ,H5={(1),(123),(132)},H 6=S3。
第一章 9同构-自同构

三: 自同构 定义2 : 对于代数运算 和 和来说的一个A 与A间的同构映射叫做一个对于代数运算 来说的A的自同构.
例2: A={1,2,3} 1 2 3 1 3 3 3 2 3 3 3 3 3 3 3 :1 2,2 1,3 3 ,对于 来说A的自同构.
例1:A={1,2,3},B={4,5,6} 4 5 6 1 2 3 1 3 3 3 4 6 6 6 2 3 3 3 5 6 6 6 3 3 3 3 6 6 6 6
:1 4,2 5,3 6
ab 3 6 a b
二: 同构的内涵 A={1,2,3},B={4,5,6} 假定对于代数运算来说A与 A 同构,那 么对于代数运算来说A与A 没有什么本质性 的区别,只有命名上的不同,若一个集合有一 个只于这个集合的代数运算有关的性质,那 么另一个集合有一个完全类似的性质.
a a 对于 A, n A, ( ) n 2 2
例4:(Z,+),(Z, )之间能否建立同构关系?
• 现在我们看两个任意的,对于代数运算 和 来说 是同构的集合 A和 A .我们可以假定,
A {a , b , c ,...}
小结
A {a , b , c ,...} 之下, • 并且在 A与 A 间的同构映射 a a ,b b , c c ,… • 由于同构映射的性质,我们知道,
定理1: 集合A的一个分类决定 A元间的一个 等价关系. 证明: 我们利用给的一个分类来做一个等价 关系,我们规定: a a,当且仅当a,b同在一类的时候. 这样A的元间的一个关系,我们证明它是一个 等价关系 1: a与a同类,所以 a a 2: 若是a,b在同一类,那么b,a也在同一类, 所以 a b b a 3: 若是a,b在同一类,b,c在同一类,那么a,c 在同一类所以 a b,b c a c
8.3同态与同构
如果*(或△)是可交换的(可结合的或等幂 的),则○(或⊙)在f(A)中也是可交换的(可 结合的或幂等的)
如果*对△是可分配的,则○对⊙在f(A)中也 是可分配的。 如果*对△是可吸收的,则○和⊙在f(A)中也 是可吸收的。 如果e是A中关于*运算的单位元,θ 是A中关于 *运算的零元,则f(e)和f(θ )分别是f(A)中关 于○运算的单位元和零元
○ 1 1 1 2 2 ◎ a a a b b
2
2
1
b
b
a
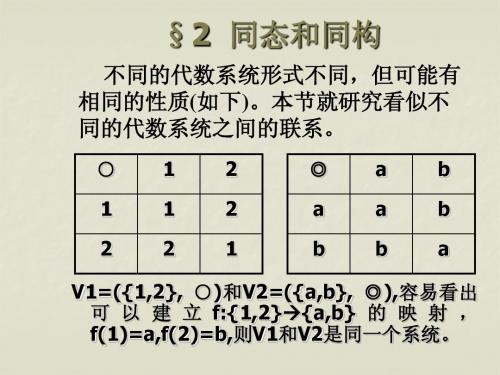
V1=({1,2}, ○ )和V2=({a,b}, ◎ ),容易看出 可 以 建 立 f:{1,2}{a,b} 的 映 射 , f(1)=a,f(2)=b,则V1和V2是同一个系统。
同态: 设 V1=(G,※)和V2=(S,ο)是两个代数系 统,※和ο分别是G和S上的二元运算,设f是从G到 S 上 的 一 个 映 射 , 且 对 a,bG, 有 f(a※b)=f(a)ο ο f(b) f(b),则称 f 为从 V1 到 V2 的一个 f(a※b)=f(a) 同态映射,简称为同态。 同态
④如果 V1=V2=V,h 是从 V 到 V 的同态 ( 同构 ) ) 函数,称f是V的自同态(自同构)。
例1: (Z, +)和(Zn , +n)是两个代数系统,其中+n 是模n加法Zn={ 0,1,2, … , n-1},令映射f : ZZn , f(x)=(x)(mod n),则f是(Z, +),则(Zn , +n) 的满同态。
c
d a b
d
a b c
0
1 2 3
0
1 2 3
1
2 3 0
2
3lt;Z,+>,给定a∈Z,令фa: ZZ, фa(x)=ax,则фa是V到V的自 同态。
(大学)离散数学:第四章代数系统 第二节 代数系统间的同构与同态

• 从定理3可见当< Y,° >是< X, >的满同态象时,如果对< Y,° >的 性质不了解,则可 通 过 满 同 态 函 数 将 < X, >上的性质带到< Y,° >中去。因此在研究一个新代数系统时,首先应考虑它是否与已有的代数 系统同构或同态,若某个新的代数系统与原有的熟知的代数系统有这种 同态关系,则对新的代数系统研究起来就容易多了。
定理1 代数系统间的同构关系R是X上的等价关系, 其中 X={A | A是代数系统}。 由等价关系的定义知要证R是 1)自反的; 2)对称的; 3)传递的。
2.3 代数系统间的同态
定义4 设A1= < X,f1,f2,···,fm> 和A2= < Y,g1,g2, ···,gm> 是两个同类 型的代数系统。若存在函数h:XY,对A1 和A2 中每一对相 应的运算满足同态公式,则称 h 是从 A1到 A2的同态函数,并 称< h(X),g1,g2, ···,gm> 是A1的同态象。
• 从定义4可知,同构实际上是一种特殊的同态。同态的概念和同构的概念 不同,同构是无方向性的,即对两个同构的代数系统来说是相互同构。
但同态是有方向性的,从A1 到 A2 有同态函数存在,从 A2 到A1就未必有 同态函数存在,即同态的概念不可逆。另外当 h 是满同态函数时,A1的 同态象就是 A2 。
定义1 设 A= < X,f1,f2,···,fm > 和 B= < Y,g1,g2,···,g n > 是两个代数 系统, f1,f2,···,fm 是X上的 m 个运算, g1,g2,···,g n是Y上的 n 个运算。若 1) m = n; 2) f i 和相对应的g i的运算的阶相等, i= 1, ···,m;
高等工程数学课件--2.1 代数运算,同态与同构

(1) 若 对 适合左分配律,则 对 适合左分配律;
定理2.1.4 设 A, B, C 是三个非空集合, ,,
分别是A, B, C 上的代数运算。 如果是A到B 的同构映射, 是B到C的同构映射, 则 (1) 是B到A的同构映射;
a b b a e,
则称 b 为 a 的逆元, 记为 b a 1 。 半群G上的代数运算 一般用通常的乘法符号“ . ”表示,并且 通常省略。
定理2.2.1 设G是一个半群,则
(1)如果G有单位元,则单位元是唯一的; (2)如果 a G有逆元a ,则 a 是唯一的,并且 (a 1 ) 1 a ; (3)如果 a, b G 是可逆的,则 ab 也是可逆的,并且
(2) Ker ( )是G的子群; (3) 是一个单映射 Ker ( ) {e}.
定理2.2.11 设 G , G, G是三个群,如果是G到
G的同构映射, 是G到G的同构映射, 则 (1) 是G到G的同构映射; (2) 是G到G的同构映射 。
-1
2.2.4
(2)
A A到C的映射称为A到C的代数运算;
A对代数运算是封闭的。
(3) A A 到A的映射称为A的代数运算或A的二元运算,也称集合
一个代数运算是一个特殊的映射。如果有A 与B到C的一个代数运算记为“ ”, 则由定义,对 任意 A, b B ,经过代数运算 得唯一的 C , c a 即 :(a,b)→c,记为c=a b . 例2.1.1 R
第2章 代数结构与线性空间
2.1 代数运算,同态与同构
2.2 群 2.3 环与域 2.4 线性空间
2.5 模
同态基本定理及两个重要的同构定理

同态基本定理及两个重要的同构定理
定理1(同态基本定理)设是一个群.则
(1) 的任意商群都是的一个满同态像;
(2) 若是的一个满同态像,比如其同态映射是则
证明: (1)是例5的结论;
(2) 由命题4,是的不变子群,令
.
因为是满同态,中的每一个元素都可写成的形式,并且由命题4证明知道,
是一个双射,又
所以是同构映射.
定理1(2)中的同构映射也称为由同态诱导的同构映射.
上面我们讲了群同态上的一个非常重要的定理,同态基本定理。
下面的几个定理是同态基本定理的应用,而这些结论本身也是非常重要的定理。
定理2设是群的两个不变子群,则都是的不变子群,并且
证明:首先,是的不变子群,是的不变子群,是的不变子群,(同学们可以作为一种练习自已证明一下)。
所以与都有意义,
即它们均构成商群. 则且是群到
的一个映射.由于的每一个元素都有形式,故是满射.另外,对
所以是同态映射. 按同态基本定理,因此,只须证明即可. 事实上,
当且仅当
定理3 设是群的两个不变子群,则
证明:令由可得所以是映射,并且
所以是满同态. 又
当且仅当所以由同态基本定理,。
【word】带有限性条件Abel群的自同态环和自同构群

带有限性条件Abel群的自同态环和自同构群数学年刊2011,32A(6):665—678带有限性条件Abel群的自同态环和自同构群冰廖军杨艳刘合国.提要给出了带极大或极小条件的Abel群A的自同构群以及自同态环的相伴Lie环是可解或幂零的充要条件.同时也给出了群A=Q0Q0…0Q的自同构群是可解或幂零的充要条件,以及群A的自同态环的相伴Lie环是可解或幂零的充要条件.关键词自同构群,自同态环,可解,幂零MR(2000)主题分类20K30,20F16,20F18中图法分类O152.2文献标志码A文章编号1000—8314(2011)06—0665—141引言本文采用文f121的术语和符号,一般情况下计算群的自同构群和研究群的自同构群的性质是很困难的,即使对Abel群也是如此.从结合环R出发,自然地可以构造一个Lie环L,方法如下:定义L的加群为_R的加法群(R,+)以及Lie积为[X,Y]=xy—yx,通常记为_R(~,称为的相伴Lie环.Abel群的自同态环EndA是结合环,则可以构造Lie环End(一.因此我们可以研究Abel群的自同态环的相伴Lie 环的可解,幂零性质对群结构的影响.同样地,也可以通过研究Abel群的白同构群AutA的可解,幂零性质来分析群A的结构.本文将对几类带有有限性条件的Abel 群进行讨论,并给出了它们的自同态环的相伴Lie环是可解,幂零以及自同构群是可解,幂零的充要条件.在多数情况下它们具有相似性.其实这也并不偶然,正是由于这些Abel群是由它的自同态环或者自同构群所确定.第2节首先给出了有限AbelP一群的自同构群AutA可解的充要条件,接着利用自同构群的稳定自同构的一个结论(见引理2.3),分别给出了带极大和极小条件的Abel群的自同构群是可解,幂零的充要条件.在定理2.6一定理2.10中,分别给出了有限AbelP一群,带极大条件的Abel群和带极小条件的Abelp-群的自同态环的相伴Lie环是可解,幂零的充要条件.当P≠3时,有限Abelp-群的自同构群AutA可解当且仅当群A的自同态环的相伴Lie环End(一)可解.对于带极大,极小条件的Abel群的自同构群AutA的可解性和群的自同态环的相伴Lie环End(一)的可解性,定理2.2一定理2.3和定理2.8一定理2.9分别相对应,在它们的幂零性的论述中,定理2.4和定理2.10相对应.设A=Q0Q.0…④Q,其中Q={丌pmI?Tti,m∈Z},这里7rk为某pi∈k 些素数的集合.第3节对群A讨论了类似的问题:定理3.1和定理3.2分别给出了A的本文2011年2月25日收到,2011年6月18日收到修改稿.北京大学数学科学学院,北京100871.E—mail:*************.ca0湖北大学数学系,武汉430062.E—mail:******************0通讯作者.湖北大学数学系,武汉430062.E—mail:**************.cn国家自然科学基金(No.10971054)资助的项目.数学年刊32卷A辑自同构群AutA是可解,幂零的充要条件,定理3.4给出了群A的自同态环的相伴Lie环EndA(一)是可解,幂零的充要条件.此时AutA是可解(幂零)的当且仅当EndA㈠是可解(幂零)的.定理3.3表明,A的自同构群AutA可解和B1是一致的.除去P=2的情况,比较定理2.4,定理2.10,定理3.2和定理3.4可以知道,对于我们所讨论的Abel群A,的自同构群AutA和自同态环的相伴Lie环EndA(一)是幂零的当且仅当它们是交换的.而且此时它们都具有相对简单的结构:AutA和EndA【一)是幂零(交换)的,如果A是满足极大条件的Abel群,当且仅当A是循环的;如果是满足极小条件的Abel群,当且仅当A是循环的或者是拟循环群的直和;如果A=Q0Q0…0Q当且仅当每一个Q是全不变的.2带极大或极小条件的Abel群设有限Abelp-群有分解A=(zpn)h0(n.)0…0(nr),其中r,ft是正整数,0<nl<n2<…<n.记群A的自同态环EndA=,群A的自同构群为AutA.下列的事实,见文【3-6】.(a)群A的自同态环=EndA可以表示成r×r矩阵环(岛),其中岛=Hom((nt)”,(n));(b)环有Jaeobson根=(),其中=pCi~;当i≠J时,J=(C)AutA的极大正规子群是△=1+.引理2.1【】除了n=2,IFI=2,3外,GL(F)是不可解的.以下总约定P为素数,z为整数环,Zp为进整数环,n=Z/(pZ)为模P剩余类环或P阶循环群.引理2.2(i)群GL2(Z)以及GL2(Zp)不可解;(ii)当素数P>2时,上的上三角可逆矩阵群()不是幂零的;(iii)当素数P>3时,Aut(m0n)不是幂零的.证记[,Y]=[z,Y,Y,…,],其中Y出现n次.环的满同态:Z一诱导群的满同态GL2(Z)一GL2(),同态像GL2()在P>3时是不可解的,因而GL~(Z)不可解.类似地,GL2(Zp)不可解.GL2(Z2)&,是可解的,而中一5-是平凡的,因此不是幂零的.考虑上的上三角可逆矩阵群(zp),由于[(G0o)]=(.1),当P>2时,取a:2,则[(((.1)组因此()不是幂零的.不妨设m≠佗(否则GL2(n)不可解),Aut(m0n)在Q1(m0n)上的限制同构于(),因此Aut(m0n)不是幂零的.6期廖军杨艳刘合国带有限性条件Abel群的自同态环和自同构群667定理2.1设是有限Abelp-群,且A=(n)”0(n).0…0(n),其中r是正整数,n1<n2<…<礼,ft都是正整数.则(1)当P>3时,AutA可解当且仅当f1:f2=…=0=1;(2)当P=2或3时,Aut可解当且仅当li≤2(1≤i≤r)证(1)当P>3,ll=12=…=f=1时,由文【8]中推论2.9知AutA△(一1),这里△=(AutA)是AutA的极大正规子群,因此是幂零群,则是可解群,(zp一1)是Abel群,即AutA是可解子群△=Op(AutA)被Abel群的扩张,因而是可解的.反之,假设存在某个li>1,则GL2(zpn.)≤AutA,但是GL2(nt)的商群GL2()是不可解的,矛盾.所以?1=f2=…=0=1.(2)当P=2或3时,ct≤2(1≤i≤r),由文[8】中定理1.1和命题2.2知rAutA△×lJGLt(),t=1这里△=(AutA),它是幂零的因而是可解的.由引理 2.1,当2t≤2时,GLl(zp)是可解群,则兀GLt()是可解的.则AutA是可解子群△=Op(AutA)被可解群0=lr兀GLf,()的扩张,因而是可解的.反之,假设存在某个fi>2,则GL3(nt)≤AutA,但是GL3(nt)的商群GL3()是不可解的,矛盾.所以li≤2.事实上,对于有界Abelp-群也有同样的结论,定理2.1的证明也同样适用.另一方面,有限Abel群可以分解为有限Abelp-群的直和,每个分支都是全不变的,则是特征子群,所以有限Abel群的自同构群可以分解为有限Abelp-群自同构群的直积.因此对有限Abel群总可以约化到定理2.1的情形,类似地对有界Abel群也一样.为便于叙述,我们首先给出下面的引理,它是本文计算某些自同构群的基础.引理2.3设是Abel群,B是的特征子群,且A=B0,则AutA=Horn(C,B)(AutB×Aut).证的所有稳定B的自同构构成AutA的一个子群,记为Aut(A)B,即Aut()B={∈AutAIB”=B).由于是A的特征子群,所以AutA=Aut(A)B.由文f9]中定理2.1知Aut(A)8=Der,B)Pair(C,B).由于A是Abel群B与C的直和,即A=B0C,因此平凡地作用在Abel 群B上,则导子就是它们之间的同态,即Der(C,B)=Hom(C,),668数学年刊32卷A辑并且由直接验算Pair(C,B)满足的条件,可知Pair(C,B)=AutB×AutC,因此AutA=Hom(C,B)(AutB×Aut),AutB×AutC在Hom(C,B)上的作用为(,(,))一&.定理2.2设是满足极大条件的Abel群,则AutA可解的充要条件是的挠子群的白同构群是可解的且ro(A)≤1.证若AutA可解,由引理2.2,GL2(Z)不可解,知ro(A)≤1,并且A的挠子群的自同构群是AutA的子群,因此是可解的,必要性已证.下证充分性.注意到的挠子群是A的特征子群,设为,如果TO(A):0,则A是有限群,此时归为定理2.1的情形.不妨设TO(A)=1,则A=T0Z,由引理2.3,可得AutA=Hom(Z,T))日(AutTXAutz),其中Hom(Z,T)T,AutZ=Z2.由假设,有AutT可解,因此AutA可解.类似地,对于满足极小条件的Abel群有下面的定理.定理2.3设4是满足极小条件的Abelp-群,则AutA可解的充要条件是A的既约子群R的自同构群是可解的且的极大可除子群D的秩r(D)≤1.证设A是满足极小条件的Abelp-群,的极大可除子群为D,既约子群为R,则‘A=D0R且D是A的特征子群.由引理2.3,可得AutA=Hom(R,D)>日(AutD×AutR),而Horn(R,D)是Abel群,因此AutA可解的充要条件是AutD,AutR是可解的,引理2.2说明GL2(Zp)不可解,其中z是P一进整数环.因此的极大可除子群D的秩r(D)≤1.若r(D)=1,即D=z..,熟知当P>2时,AutZp..~10zp.当P=2 时,AutZ2..Z20z2,其中z是进整数环.反之,4的既约子群R的自同构群是可解的且的极大可除子群D的秩r(D)≤1时,AutA可解.注意到满足极小条件的Abel群的自同构群是其P一子群自同构群的直积,因此满足极小条件的Abel群的自同构群是可解的充要条件是其所有子群的自同构群都是可解的.于是,结合定理2.1和定理2.3我们可以得到满足极小条件的Abel 群的自同构群是可解的充要条件.由引理2.2和引理2.3可以得到下面的定理.定理2.4(i)有限Abel2’-群A的白同构群AutA幂零的充要条件是rp(A)≤1,当且仅当是循环群;(ii)满足极大条件的Abel群且其挠子群是2一群的自同构群AutA 幂零的充要条件是有限且(A)≤1或A=Z,即为循环群;(iii)满足极小条件的Abel2/_群的自同构群AutA幂零的充要条件是A有限且rv(A)≤l或A=0...6期廖军杨艳刘合国带有限性条件Abel群的自同态环和自同构群669证(i)不妨设是有限AbelP一群,由引理2.2,当P>2时,T2()不是幂零的,因此不含形如m0的子群,即是循环群,rp(A)≤1.反之显然.(ii)假设Z=n0Z,则AutAn(AutnX),计算[(1,(1,1)),(0,(1,))]l其中Oz是z的二阶自同构,注意到它的作用方式把它写成矩阵形式[((呈)]=(.12)这里(一2)≠0是因为是2一群,因此AutA不是幂零的,所以或者有限或者自由循环,当有限时,由(i)知也是循环的.(iii)此时的证明方法同(为了处理P=2的情形,我们需要下面定理,见文『1O].稳定性定理设群G忠实地作用在群上,G稳定的如下长度为2的正规群列1≤W<记Z:=41(W)是的中f1.,它自然地作成一个一模,则G≤Der(v/z),其中Der(Z)是到z的所有导子作成的Abel群.定理2.5(i)设是有限Abel2-群,且A=(Z2n)0(Z2n2).0…0(Z2)L,这里nl<?22<…<几,l是正整数,则AutA幂零的充要条件是l=1.(ii)设是自由Abel群与Abel2-群的直和,则A的自同构群AutA幂零当且仅当A=2r2n0Z2nz0?-?0Z2n0Z,这里礼1<礼2<…<72r.(iii)满足极小条件的Abel2-群A的自同构群AutA幂零当且仅当A=Z2n①Z2nz0…0n0..,这里札1<佗2<-??<竹r.证(i)设是有限Abel2-群,且A=(Z2n)h0(Z2n.)120?-?0(Z2n),这里几1<?22<…<n,ll是正整数.当所有的i,1=1时,群4的自同构群AutA是一个2一群,因此是幂零的.反之假设存在某个ft>1,则GL2(n)≤AutA 且它的一个商群是GL(),由引理2.2是非幂零的,矛盾.(ii)设是自由Abel群与Abel2一群的直和,且自由子群是自由循环群z若Abel2一子群B=Z2n0Z2n①…0Z2(其中?21<礼2<…<礼),它是特征子群,由引理2.3,可得AutA=Hom(Z,B)×(AutB×Autz),其中Horn(Z,B)B,AutB是一个2一群,AutZZ2,则AutA是一个2一群,因此是幂零的.670数学年刊32卷A辑当A=Z2n0Z2n.0…0n0z时,证明其自同构群是幂零的另一个方法是:设C=2”A={2”aIa∈),其中n>n,则C2Z,它是的特征子群,A/Cz2n10Z2n20…0Z2n0zn.考虑G=AutA在0≤C<A上的自然作用.记ca(c)={∈GIc.=c,c∈), Cc(A/C):{∈Gl(a+)=a+C,a+C∈A/C},贝0c/ca(c)≤AutC,C/Ca(A/C)≤Aut(A/C),且c/ca(c)rhCa(A/C)≤c/cc(c)XG/Ca(A/C),又cc(c)nCc(A/C)稳定,0<C<A,故根据稳定性定理知cc(c)nCG(A/C)≤Der(A/C,),A/C是有限的,而C是自由循环群,因此Der(A/C,C):Hom(A/C,C)=0.AutA/C是一个2一群,AutC,则G≤AutC×Aut(A/C)是幂零群.反之若AutA是幂零群,则AutA的子群AutB是幂零的,当且仅当B=Z2n0Z2”0…0…由于GL2(Z)不是幂零的,因此自由子群是自由循环群z,因此A=z2n0Z2n20…0n0Z,其中nl<n2<…<nr.(iii)由(ii)以及引理2.2知条件是必要的,下证充分性.设A=Z2n0Z2n20…0n0..,这里仡1<n2<…<nr,设B:Q2n(A)={0∈Al2ha=0),其中n>n,则Bz2n10z2n20…0n0n,它是A的特征子群.考虑G=AutA在0≤B<A上的自然作用.记Ca(B)=fQ∈G1b.=b,b∈B),Cc(A/B)={∈Gl(a+B)”=a+B,a+B∈A/B},则C/Ca(B)≤AutB,C/CG(A/B)≤Aut(A/B),且C/CG(B)nCc(A/B)≤C/Cc(B)×C/Cc(A/B).又Cc(B)nCc(A/B)稳定,0<B<A,故根据稳定性定理知Cc(B)nCc(A/B)≤Der(A/B,B),A/BZ2o.是可除的,而B有限,因此Der(A/B,B)=Hom(A/B,B)=0.AutA/B(o.)=Z20Z2是Abel群,由(i)知AutB是一个2一群,则C≤AutBXAut(A/B)是幂零群.下面讨论带极大,极小条件的Abel群的自同态环构成的Lie环是可解,幂零的条件,为此需要下面的引理.引理2.4(m)(一)可解,坞()(一)不可解.证直接计算可得[(),()]=(c—brz+-cyd一.6cr一一d).6期廖军杨艳刘合国带有限性条件Abel群的自同态环和自同构群671设L=M2(Z2)(一,则由上面的计算知则则)lm)为了计算,在上式中令d=一a,r=一x,有[),G)]=(2.b…z-cyn名一),{(m).令b=2b1,c:2c1,Y=2yl,=2zl,有),()]一blz…l-cly哪yza-bmlx/,)c∈m)归纳地,知M2(Z2m)(一)可解.记K=M3(Z2)(_.,则K=(e),其中表示(J)位置为1,其它位置全为0的矩由于当i≠J时,,eij1=eij,[eij,eft]=eli—ejj,有K=(eij,eii—eli≠歹).又因n>2,存在k满足k≠i,k≠J,i≠J,则eij=【eik,ekj],eii一jJ=【eij,e所以K=K≠0,因此不可解,即M3(Z2)(一)不可解引理2.5当P>2时,()(一)不可解;相伴Lie环(z)(一)和(zp)(一)不可解.证取L=(el2,e21>,由于(e12,e21】=ell—e22,【611一e22,el2】=2e12,【ell—e22,e21】=一2e21, 则el1一e22,e12,e21∈L,归纳地,对任意的正整数此()(一)不可解.m,有el1一e22,e12,e21∈(,则()≠0,L不可解,因()(一)是(z)(一)和Mn(Zp)(一)在自然同态z一以及zp一下诱导的Lie环同态像,因此(z)(一)和(zp)(一)不可解.定理2.6设P是奇素数,记A=(n)ll④(n.)④…0(),这里扎1<n2<…<n,如是正整数,则End(一)可解的充要条件是如=1672数学年刊32卷A辑证如果End(一)可解,由引理2.5知1=1,否则存在一个子环()(一)不可解,矛盾.另一方面,如果li=1,则A=n10zpn20 0EndA{(aij)laijEHorn(,’))且i<J,Pln巧.记L=End(_.,Cij=∑(aikakj—bikakj),如果cij∈L,则PlCij,i≤J.归纳地, Cij∈(,对任意的i,J,有PI.,且当i<J时,P.l,继续重复上述过程,直到Cij=0,因此可解.也可以用另外一种方法来证明可解:EndA在【21(A)上的限制就是n一诱导的环同态,即对每一位置模P,同态像是上的一个三角矩阵,同态的核是每个位置元素都能被P整除的数,即0Mod(p).由环的同态得到Lie环的一个同态,结合可解Lie环在扩张下封闭的性质得到Lie环L=End(一)是可解的.定理2.7设A=(Z2n)/10(Z2)120…0(Z2),这里n1<Tt2<…<n,f是正整数,则End(一)可解的充要条件是ft≤2证设fi≤2,自然同态z2n.一z2诱导的环同态,End(一)的同态像是一个下对角矩阵,并且对角线上是1阶或2阶可解块,因此同态像可解,同时核满足2Ia同上述定理相同的证明方式,知其可解,得到End(一)可解.反之,由引理2.4,如果End(一)可解,则li≤2.定理2.8设A是满足极大条件的Abel群,则End(一)可解的充要条件是EndA可解且_r0(A)≤1.证设A=0A0Z,0A是A的全不变子群,).(~EndAEndZEndA【H.m(z)J(,z/),又(0EndAp)~0EndA和z(一)都是可解的,按分块矩阵计算知EndA(一)是可解的.反之,End是End(一)的子环显然可解,且()(一)不可解,因此ro()≤1.类似的方法可以得到下面极小条件下的定理.定理2.9设是满足极小条件的Abel群,则End(一)可解的充要条件是EndA可解.End可解当且仅当End磷可解且rank(Dp)≤1,其中Rp和Dp分别是A的既约子群和极大可除子群.的引理2.6(z)(一)不是幂零的,若=n0m,n<m,则EndA(一)不是幂零证注意到对任意的正整数n,[el2,?tc22]=el2≠0由引理2.5和引理2.6,立即可得下面的定理6期廖军杨艳刘合国带有限性条件Abel群的自同态环和自同构群673定理2.10(i)有限Abel群的自同态环的相伴Lie环幂零的充要条件是rp(A)≤1;(ii)满足极大条件的Abel群A的自同态环的相伴Lie环幂零的充要条件是有限且口(A)≤1或A=z;(iii)满足极小条件的Abel群的自同态环的相伴Lie环幂零的充要条件是有限且rp(A)≤1或A=0..;P(iv)满足极大或极小条件的Abel群4的自同态环的相伴Lie环幂零的充要条件是的自同态环的相伴Lie环是Abel的.3完全分解的无挠Abel群下面考虑这样一类Abel群,首先介绍符号和一些简单的结论:记丌为某些素数的集合,设Q={兀.mIm,m∈Z}.对群Q有下列简单事Pl∈7r实:(a)Q的元具有无限丌一高,有限丌一高,即任意的P∈7r,P高为0(3,否则为有限.(b)Q的任意一个自同态可以由1的像完全决定.事实上,m=(m?1)妒=m?1;由(pp)=1,知p?(p)=1,因此(p)妒=p1妒,所以(兀m)妒=兀m?1;pp(c)如果71”17I”2,则Horn(Q,Q.)=0,否贝0Horn(Q,Q.)Q.事实上,如果丌17r2,存在P∈丌1一丌2,Q中的任意元具有无限71”1一高,特别地,1具有无限高,若∈Hom(QQ.),则1∈Q.也具有无限p一高,则1=0,因此Horn(Q丌l1Q)=0.如果71”171-2,任意的∈Hom(Q丌¨Q.),由1的像1完全决定,而1∈Q.,因此Horn(Q,Q.)Q..特别地,EndQ=Horn(Q,Q)Q.(d)AutQQ={l=士11p.,Pi∈7r,仃∈z)z2①ZI.特别地,AutQpQ=r,oZ2④Z.这是因为EndQ=Horn(Q,Q)Q,因此AutQQ.若兀m∈Q,则存在p:.兀他∈Q,使1=兀m兀n=兀m佗,贝0mn=1,m=土1.pppp设A:Q0Q.0…0Q此时称是”完全分解”的,首先我们讨论秩为2即=Q0Q.的情形.A=Q0Q的自同态环和自同构群具有下面的矩阵表达形式:EndA竺{I兰三}I∈Itom(p,Q),{,J=1,2},AutA』【【2()可逆,∈H.m(Q,Q)下面按集合71”1和71”2的包含关系分别讨论群A=Q0Q.的白同构群以及自同构群的可解幂零性.(i)当71”171”2,71”271”1时,记71”1=71”2=7r.End[g>(,AutGL2(674数学年刊32卷A辑由于GL2(Z)≤GL2(Q),而GL2(Z)是不可解群,因此GL2(Q)也不可解.GL2(Q)的中5-为CGL2(Q)=)aEQA),铡).易知O.charA,而A=Q0O由引理2.3,知AutAHom(O,O)>日(AutOXAutO)O.(Q.×Q)是可解的,但不是幂零的,事实上,Aut(!)f.∈AutQ.,c∈AutQ~,bEHom(Q,Q:>.若(!)∈~AutA,则()=)=I1c+)=(舌,6=..取是嵌入同态,则.限制在Q等于c,记为..所以()a01),即(~AutA=()I.).若1)∈(~2AutA,则对任意的)∈AutA,有[(6)j(舌tA又(=(.一)一[(),(吾)]=(n0一一ac一-16.)(0一一X--一1)(a..b)(苦Y) =(.1).由于(01)∈<Aut,其中=一a-1bc+X--1yz+a-ix一(6一y)zc=0,对任意的∈Q.,∈Q,Y∈Q成立.若Y=0,即一a-1bc+a-ix_1bzc=0,则b=0,且2C--lyz—a-1-1yzc=0,则a】=c.因此()=()∈(AutA,AutA=(AutA≤AutA,AutA不是幂零群.6期廖军杨艳刘合国带有限性条件Abel群的自同态环和自同构群675当I71-2J<..时,AutA=Q.(AutQ×AutQ.)是有限生成的可解群,但不是多循环的,由于Q.不是有限生成的.而超可解是多循环的,因此它不是超可解的.(iii)当71”171”2,7r27r1时,E..%OZI#ll~.,此时AutA是Abel群.因此若AutA是超可解或多循环的,则AutA是幂零的且是Abel的.当且仅当7rl丌2,7r27r1.一般地,有下面定理.定理3.1设A=Q0Q.0…0Q其中Q:{nm}mi,m∈Z},这里.1rk为某些素数的集合,则AutA可解当且仅当对任意的i≠J,71”i≠7rj.证当7’=2时,由前面的叙述(i)一(iii)知AutA可解当且仅当71”1≠71”2.先证充分性.假设对某个i≠J,7I”i=,当k≠i,时,设A1={∈AutAl使在Q上的限制为1,即lQ:1Q),则1是AutA的子群,且A1GL2(Q.),而GL2(Q)是不可解的,从而1是不可解的,于是AutA不可解,与已知矛盾.再证必要性.如果对任意的i≠J,亿≠,那么存在一个元,不妨记为丌,满足对任意的i≠r,有丌,否则,必有某两个集合相等,与已知矛盾.这样的丌称为集合{『1≤i≤r)的极大元.显然QcharA,则.r一1,,r一1,AutAHorn(0QQ)>日(Aut0Q×AutQ~r)jt=1i=1,r一1,r一1其中Horn(0QQ)0Horn(QQ)与AutQ都是Abel的,对r进行归,i=1=1 r一1纳,知Aut0Q是可解的,因此AutA是可解的.=1定理3.2设A;Q0Q.0…0Q其中Q:{npmIIYt,,m∈Z},这,pt∈丌’里丌为某些素数的集合,则AutA幂零当且仅当对任意的i≠J,死.证当r=2时,由前面的叙述知道AutA幂零当且仅当丌1/1”2,丌2丌1.先证充分性.如果对某个i≠J,7ri7r{,当k≠i,J时,设A1={∈AutAI使在Q上的限制为1,即lQ=1Q),则A1是AutA的子群,当死:时,A1GL~(Q);当时,AutAQ)日(AutQ×AutQ),而aL2(Q)和Q丌j(AutQ×AutQ丌j)都不是幂零群,因此A1不是幂零的,与AutA幂零矛盾.再证必要性.如果对任意的i≠J,7ri,则Horn(QQ)=0.676?数学年刊32卷A辑因此EndAA,AutA(Q)×(Q)×-??×(Q)日≥(z2.z’z’),=1AutA是Abel的,因而是幂零的.推论3.1设A=Q0Q0…0Q其中Q:{兀pmI?gti,m∈Z},这Pl∈.a-k. 里丌为某些素数的集合.则下列条件等价:fa)AutA是多循环的;(b)AutA是超可解的;fC]CAutA是幂零的;(d)AutA是Abel的.注意到群G称为是B的,如果G有一个正规列G=G1>G2>>Gn=1,即G司G,且Gi/Gi+1≤Q或Gi/Gi+l≤Q/z.定理3.3设A=Q0Q0…0Q其中Q={兀pmImt,仇∈z},这Pi∈7rk0里7r为某些素数的集合,则AutA是B1的当且仅当AutA是可解的. 证充分性显然,因为由定义B是可解的.下证必要性.当r=2时,AutAQ>日(AutQ×AutQ.)或AutA=r-oAutQl×AutQ2.若AutAQ:(AutQ×AutQ.),贝40<Q2<QZ2<Q.(Z20Z2)<Q.(Z20Z20Z)<Q>日(Z20Z20Z)<<Q.(Z20Z20Z/】+l.I)=AutA是AutA=Q.(AutQ×AutQ.)的一个正规列,其商因子分别为QZ2,Z2,Z,-? z,而QZ是Q的子群,是O,/Z的子群,因此AutA是B1的.如果AutA=e-,4AutQ1×AutQ2Zg.0Zl10Z20Zl,则AutA是Abel群,且可以分解为和z的直和,因此也是B1的.所以当r=2时,AutA是可解的则是B1的.当r≥3时,由定理3.1,存在一个极大元丌,使QcharA,则AutAHorn((~QQ)×(Al1t0QAutQ).记s=ml7r,1≤i<r)l,有r一1r一1Horn(Q,Q)Horn(Q,Q)Q,6期廖军杨艳刘合国带有限性条件Abel群的自同态环和自同构群677可以得到,r一1,AutAQ(Aut≥Q×AutQ).因Q,AutQ是B1的,由归纳假设Aut0Q是B1的,易知AutA是B1的. 定理3.4设A=Q0Q.0…0Q其中Q={兀pmlmi,m∈Z},这里丌k为某些素数的集合,则(a)EndA(一)可解的充要条件是7i”i≠对任意的i≠J;(b)EndA(一)幂零的充要条件是71”i对任意的i≠J,此时它是Abel的,其中End(一)是由自同态环EndA的加法群以及Lie积Y]=xy—yx构成的相伴Lie环.证先讨论r:2的情形:(i)当71”1=71”2时,EndA=(Q),由于(z)(一)≤(Q)(一)是不可解的,所以M2(Q)(一)不可解;(ii)当丌丌.,7r2丌时,End(Q~l.Q.)(%g),此时它构造的Lie环是可解的不是幂零的,因为[e12,n~22】:e12;(iii)当7r1丌z,7r271”1时,End(Q.Q.)(%.),此时的Lie环是幂零的,并且是交换的.一般地,如果71”i≠对任意的i≠J,则存在一个极大元丌,即7r,设A=B0Q,那么Q是全不变的,Ena(EBH.m),由于EndB(一)是可解的,因此EndA(一)可解.反之,显然有≠霄j对任意的i≠J.这就证明了第一部分.71”i对任意的i≠J,此时EndA0EndQAi是Abel的,因此是幂零的.反之由r=2情形易得对任意的i≠J,7ri参考文献[1]RobinsonDJS.Acourseinthetheoryofgroups[M].2nded.NewY ork:Spri nger—V erlag,1995.【2]KhukhroEI.p-AutomorphismsoffiniteP—groups[M】.Cambridge:Ca mbridgeUniver—sityPress,1998.[31Avifi6MA,SchultzP.Theuppercentralseriesofap-groupactingonaboun dedAbelianP—Group[EB/OL].arXiv:math.GR/0606605.『41Avifi6MA,SchultzP.TheendomorphismringofaboundedAbelianp-gro up[M]//678数学年刊32卷A辑AbelianGroups,RingsandModules,ContemporaryMathematics.V ol273,P rovidence,RI:AmerMathSoc,2001:75—84.[5】FuchsL.InfiniteAbeliangroupsV olI[M].NewY ork:AcademicPress,1970.[6]HausenJ,SchultzP.Themaximalnormalp-subgroupoftheautomorphism groupofanAbelianp-group[J】_ProcAmerMathSoc,1998,216:2525—2533. [7]AlperinJL,BellRB.Groupsandrepresentations[M】.NewY ork:Springe r—V erlag,1995.[8]Avifi6MA.SplittingtheautomorphismgroupofanAbelianp-group 【EB/OL].arXiv:math.GR/0603747.【9]樊恽,黄平安.分裂扩张的稳定自同构群[J].数学年刊,2001,22A(6):791—796.[10】SegalD.Polycyclicgroups[M】.Cambridge:CambridgeUniversityPress,19 83.EndomorphismRingsandAutomorphismGroupsof AbelianGroupswithFinitenessConditionsLIAOJunYANGY an.LIUHeguo. SchoolofMathematicalSciences,PekingUniversity,Beijing100871,China. E—mail:*************.an2DepartmentofMathematics,HubeiUniversity,Wuhan430062,China. E—mail:unicornyy~163.corn3Correspondingauthor.DepartmentofMathematics,HubeiUniversity,Wlu han430062,China.E—mail:ghliu~.ca AbstractLetAbeanAbeliangroupwithmaximumorminimumcondition.Th eauthors givenecessaryandsufficientconditionsfortheautomorphismgroup(resp.Li eringasso—ciatedwiththeendomorphismring)beingsolvable(resp.nilpotent).Moreove r,necessary andsufficientconditionsfortheautomorphismgroup(resp.Lieringassociate dwiththeendomorphismring)beingsolvable(resp.nilpotent)forA=Q7r10Q20…0Q 7rarealsogiven.KeywordsAutomorphismgroup,Endomorphismring,Solvable,Nilpotent 2000MRSubjectClassification20K30,20F16,20F18。
z2^n的自同构

z2^n的自同构在数学中,自同构指的是一个结构在自身的映射下保持不变的性质。
在本文中,我们将探讨一个特定的数学问题,即什么情况下,一个数字z的2的n次方运算结果能够与z本身保持不变。
本文将通过定义和例子来解释什么是z2^n的自同构。
首先,让我们明确自同构的概念。
自同构是指一个结构在自身的映射下保持不变的性质。
对于数学中的运算符号和操作,自同构意味着应用这些运算符号和操作后结果不会改变。
在我们的问题中,我们关注的是数学中的指数运算符号“^”,当一个数字z的结果仍然等于z时,我们可以说z2^n存在自同构。
现在让我们来探讨一些例子,以便更好地理解z2^n的自同构。
假设我们选取一个整数z为3,并将n设为2,即我们要找到z2^2的自同构。
根据指数运算的定义,z2^2等于3的平方再乘以2,即(3^2)*2=18。
然而,很明显18并不等于3,因此我们可以说z2^2不存在自同构。
接下来,让我们尝试另一个例子。
仍然选取整数z为3,但这次将n设为1,即我们要找到z2^1的自同构。
根据指数运算的定义,z2^1等于3的平方,即3^2=9。
显然,9等于3,因此我们可以说z2^1存在自同构。
现在,我们来思考一个更一般的问题,即z2^n什么情况下存在自同构?为了回答这个问题,让我们先考虑指数运算的性质。
根据指数运算的规律,x^1等于x本身,也就是说,一个数字的一次方运算结果与该数字本身相等。
因此,我们可以推断出当n等于1时,z2^n一定存在自同构。
接下来,让我们考虑指数运算的另一个规律,即任何数字的零次方等于1。
换句话说,x^0等于1,其中x为任何数字。
因此,当n等于0时,z2^n也存在自同构。
除了n等于1和0的情况外,我们还需要考虑其他可能的情况。
根据指数运算的定义,当n大于1时,z2^n等于z自己乘以n个z。
因此,我们可以推断出当z等于1或-1时,z2^n存在自同构。
这是因为1和-1的任何非负整数次方运算结果仍然等于1和-1本身。
整环上二元多项式代数的自同构

整环上二元多项式代数的自同构自同构是一种构造,通常用于对构造字符串或集合的元素,使用一个转换变换,使其自己与自己同构。
在完整环上二元多项式代数中,自同构有下列形式:
- 自反构:一种自同构,在一定角度上,元素被视为自身的一张映射;
- 循环构:一种自同构,在某种程度上,元素被视为应当循环重复的;
- 对称构:一种自同构,在给定的转换变换下,元素与其反置子相象;
- 复制构:一种自同构,在一定角度上,元素被重新定义成其自身的一个复制品。
S3,S4的自同态和自同构(近世代数)

题目:S3,S4的自同态和自同构学院:数学与统计学院专业:数学与应用数学姓名:学号:指导教师:时间: 2012年6月17日摘要本文讨论了三次对称群S3和四次对称群S4各自所拥有的子群,以及找出S3,S4各自的自同态,自同构,检验各自的子群在自同态和自同构下是否保持不变。
关键词: 对称群,子群,不变子群,自同态,自同构。
一、S4和S4的子群:假如对于代数运算 和 来说,有一个A到A的同态映射存在,我们就说,这个映射是一个同态满射,并说,对于代数运算 和 来说,A与A同态。
假如对于代数运算 和 来说,有一个A到A的同构映射存在,我们就说,对于代数运算 和 来说,A与A同构。
S3={(1),(12),(13),(23),(123),(132)},S4={(1),(12),(34),(13),(24),(14),(23),(123),(132),(134),(143),(124),(142),(234),(243),(1234),(1243),(1324),(1342),(1423),(1432),(12)(34),(13)(24),(14)(23)}.其中,在S3里,(1)、(12) 、(13) 、(23)的逆元就是它们自己本身, (123)与(132)互为逆元。
在S4里,(1) 、(12) 、(34) 、(13) 、(24) 、(14)、(23) 、(12)(34) 、(13)(24) 、(14)(23) 的逆元就是它们自己本身,(123)与(132)互为逆元,(134)与(143)互为逆元, (124)与(142) 互为逆元,(234)与(243) 互为逆元,(1234)与(1432) 互为逆元,(1243)与(1342) 互为逆元,(1324)与(1423) 互为逆元。
S 3的子群有H1={(1)},H2={(1),(12)},H3={(1),(13)},H4={(1),(23)} ,H5={(1),(123),(132)},H 6=S3。
同构和自同态

同构和自同态一、引言同构和自同态是数学领域中的重要概念,它们在代数学、图论、拓扑学等多个领域都有广泛的应用。
本文将深入探讨同构和自同态的概念、性质以及其在不同领域中的应用。
二、同构2.1 概念同构是指两个结构之间存在一一对应的关系,这种关系保持了结构的某些性质。
在数学中,同构通常用来描述两个代数结构之间的关系,比如群、环、域等。
2.2 同构的性质同构具有以下性质: 1. 一一对应关系:同构是一种一一对应的关系,每个元素在同构映射下都有唯一的对应元素。
2. 保持运算:同构映射保持运算,即对于两个元素的运算,它们在同构映射下的映射结果也是对应的运算结果。
3. 保持结构:同构映射保持结构的性质,比如群的同构映射会保持群的封闭性、结合律等性质。
2.3 同构的例子下面以群的同构为例,来说明同构的概念和性质。
2.3.1 群的定义群是一种代数结构,它由一个集合和一个二元运算组成,满足封闭性、结合律、单位元和逆元的性质。
2.3.2 同构的定义设有两个群G和H,如果存在一个双射f:G→H,且满足对于任意的a, b∈G,有f(a·b) = f(a)·f(b),则称G和H是同构的,记作G≅H。
2.3.3 同构的性质同构保持群的封闭性、结合律、单位元和逆元的性质。
2.4 同构的应用同构在代数学、图论、拓扑学等多个领域中都有广泛的应用。
2.4.1 代数学中的应用在代数学中,同构可以帮助我们研究不同代数结构之间的关系,比如同构可以用来判断两个环是否相同,或者两个域是否同构等。
2.4.2 图论中的应用在图论中,同构可以用来判断两个图是否同构。
同构图是指具有相同的图结构,即图中的顶点和边可以一一对应。
2.4.3 拓扑学中的应用在拓扑学中,同构可以用来刻画空间的同构性质。
同构的拓扑空间具有相同的拓扑结构,即它们可以通过一个连续的双射相互映射。
三、自同态3.1 概念自同态是指一个结构自身到自身的同态映射。
在数学中,自同态可以用来描述一个结构的对称性质。
同构及同态在代数中的应用论文

同构及同态在代数中的应用摘要:在近世代数的主要内容是研究所谓代数系统,即带有运算的集合,而在近世代数中同态与同构又是其一等重要的概念,在近世代数中有重要的作用。
在不同的代数系统中同态成为同构的条件不同,本文给出了同态成为同构的条件,论述了同构在不同代数系统上的一些应用,从中说明了同态与同构的重要性。
关键词:同态;同构;群;环1 代数系统的同态与同构1.1同态映射及同态的定义一个A 到A 的映射φ,叫做一个对于代数运算 和 来说的,A 到A 的同态映射,假如,在φ之下,不管a 和b 是A 的哪两个元,只要a a →,b b →就有 a b a b →定义1:假如对于代数运算 和 来说,就有一个A 到A 的满射的同态映射存在,我们就说,这个映射是一个同态满射,并说,对于代数运算 和 来说,A 与A 同态。
定义2: 我们说,一个A 与A 间的一一映射φ是一个对于代数运算 与 来说的,A 与A 间的同构映射(简称同构),假如在φ之下,不管a ,b 是A 的哪两个元,只要a a →,b b →就有 a b a b →1.2同态与同构的联系1)从定义上看2)一个无限集可以与它的子集同态或同构,但一个有限集只能与它的子集同态而不能同构关于代数系统的同态有以下定理:定理1 :假定,对于代数运算 和 来说,A 与A 同态。
那么,(1)若 适合结合律, 也适合结合律;(2)若 适合交换律, 也适合交换律。
定理2:假定,⊗,⊕都是集合A 的代数运算,⊗,⊕都是集合A 的代数运算,并且存在一个A 到A 的满射φ,使得A 与A 对于代数运算⊗,⊗来说同态,对于代数运算⊕,⊕来说也同态。
那么,(1)若⊗,⊕适合第一分配律,⊗,⊕也适合第一分配律;(2)若⊗,⊕适合第二分配律,⊗,⊕也适合第二分配律。
2群的同态与同构2.1群的同态与同构定义定义3: 给定群(),G 和群(),G ⨯称集G 到集G 的一个映射φ:G G →是群G 到群G 的一个同态映射(简称同态),如果对任意a ,b ∈G ,有()()()a b a b φφφ=⨯当φ是单(满)射时,称φ为单(满)同态;当φ是一一映射时,称φ为G 与G 间的同构映射(简称同构,记为G G ≅); 当φ是群G 到群G 得一个同态时,令ker φ={x G ∈|()x e φ'=,e '是G 的单位元},称之为φ的核。
离散数学-同态和同构

一、同态与同构
例1(c):证明代数< N, +>和< I+,·>是不同构的。
证明:使用反证法。假设h是从<N, +>到<I+, ·>的一个同构。因为h
是从N到I+的一个满函数, 必有x∈N( x≥2) 和某质数p(p≥3), 使h(x)=p
(h(x1)*′h(x2))*′h(x3)=h(x1*x2)*′h(x3)=h((x1*x2)*x3) =h(x1*(x2*x3))=h(x1)*′h(x2*x3) =h(x1)*′(h(x2)*′h(x3))
所以, *′是可交换(或可结合的)。证毕。
二、同态代数的性质
例2:设S = {a, b, c, d}, S′={0, 1, 2, 3}, 代数A=<S, *>和B=<S′,* >由下表
· f0 f1 f2 f3 f0 f0 f1 f2 f3 f1 f1 f2 f3 f0 f2 f2 f3 f0 f1 f3 f3 f0 f1 f2
+4 0 1 2 3 00123 11230 22301 33012
一、同态与同构
例1(b)证明:<F, ·, f 0>,F={f 0, f 1, f 2, f 3};< N4, +4, 0>,N4={0, 1, 2, 3}
作映射h∶F→N4, h(f i) = i (i=0, 1, 2, 3) (1) h∶F → N4双射; (2) h(f 0) =0; (3)任取f i, f j∈F, i, j∈ N4, 因为h(f i) = i , h(f j) = j ,所以 h(f i·f j) = h(f i+j) = h(f (i+j) mod 4) = (i+j) mod 4 = i +4 j = h(f i) +4h(f j)。
400浅谈代数系统上的同态与同构

400浅谈代数系统上的同态与同构何东东(陕西理工学院数学与计算机科学学院数教专业11级1班,陕西 汉中 723000)指导教师:郑红梅[摘要] 同态与同构是代数学中最重要,最基本的概念之一.本文通过总结同态与同构在各个代数系统上的一些应用,说明它们在代数学中的重要性.[关键词] 半群;群;环;格;同态;同构1 预备知识同态、同构是代数学中的重要概念,它们是研究群、环等代数系统的重要手段.同态是保持代数系统结构的映射,同态是同构的推广.同态与同构是代数学中最重要,最基本的概念之一.本文通过总结同态与同构在各个代数系统上的一些应用,说明它们在代数学中的重要性.下面首先对同态与同构的相关概念进行简单介绍.定义1.1]1[设集合A 到A 各有代数运算 和 ,且ϕ是A 到A 的一个映射.如果ϕ保持运算,即对A 中任意元素a ,b ,在ϕ之下由a a →,b b →总可得b a b a →,亦即b a b a =或)()()(b a b a ϕϕϕ =,则称ϕ为代数系统A 到A 的一个同态映射,若ϕ又是满射,则称ϕ为同态满射.如果A 到A 存在同态满射,则简称A 与A 同态,记为A A ~.定义 1.2]1[设ϕ是A 到A 的一个(关于代数运算 及 )同态满射.如果ϕ又是单射(即ϕ是双射),则称ϕ是A 到A 的一个同构映射.如果A 到A 存在同构映射,就说A 与A 同构,记为A A ≅.否则,即若A 到A 不存在任何同构映射,则称A 与A 不同构.A 到自身的同态映射,称为A 的自同态映射,简称A 的自同态.同样,A 到自身的同构映射,叫做A 的自同构映射,简称A 的自同构.定义1.3]2[设(S ,≤)是序列集,S T ⊆.如果存在S u ∈,使得)(T t u t ∈∀≤,则称u 为T 的一个上界.如果T 的一个上界u 具有如下的性质:对于T 的任一上界u ',都有u u '≤,则称u 为T 的一个最小上界,记为lub T .如果存在S l ∈使得)(T t T l ∈∀≤,则称l 为T 的一个下界.如果T 的一个下界l 具有以下性质:对于T 的任一个下界l ',都有l l ≤',则称l 为T 的一个最大下界,记为glb T .S 的上界和下界(如果存在,显然唯一)分别称为幺元和零元,记为1和0.由偏序的反对称性可知:偏序集中任意指定的两个元素的最小上界和最大下界有唯一性(如果它们存在).设),(≤L 是一个偏序集,如果L 中的任意两个元素都有最小上界和最大下界,则称),(≤L 是一个格.只含有有限多个元素的格称为有限格,否则称为无限格.定义 1.4]2[设R 是幺环,M 是一个交换群,如果映射(称R 在M 上的作用)M M R →⨯,ax x a ),(.满足下列条件:(1);,,,)(M y x R a ay ax y x a ∈∈∀+=+(2);,,,)(M x R b a bx ax x b a ∈∈∀+=+(3);,,),()(M x R b a bx a x ab ∈∈∀=(4),,1M x x x ∈∀=则称M 为环R 上的一个左模,或左R 模.如果将(3)改为;,,),()(R b a M x ax b x ab ∈∈∀=其余条件不变,则称M 为环R 上的一个右模,或右R 模.理论上讲,右模和左模没有本质的区别.如果M 为环R 上的一个右模,令R '为R 的反同构的环,则M 构成R '上的左模,当然,若R 是交换环,则R 上的左模和右模没有区别.定理1.1]3[设代数系统),( A 和)( ,A 同态,则(1)若 适合结合律, 也适合结合律;(2)若适合交换律, 也适合交换律.定理 1.2]3[设⊗,⊕为集合A 的代数运算,⊗,⊕为集合A 的代数运算,且存在A 到A 的满射φ,使得A 与A 对于代数运算⊗,⊗来说同态,对于代数运算⊕,⊕来说也同态,那么(1)若⊗,⊕适合第一分配律,⊗,⊕也适合左分配律;(2)若⊗,⊕适合右分配律,⊗,⊕也适合右分配律. 2 主要内容下面将分别讨论群,环,格,模上同态同构在其中的应用以及比较它们在同态同构中的不同.2.1 群同态与同构定义2.1.1]4[设G 是一个非空集合, 是它的一个代数运算,如果满足以下条件:(1)结合律成立,即对G 中任意元素c b a ,,都有)()(c b a c b a =;(2)G 中有元素e ,叫做G 的左单位元,它对G 中每一个元素a 都有a a e = ;(3)对G 中每一个元素a ,在G 中都有元素1-a ,叫做a 的左逆元,使e a a =- 1;则称G 对代数运算 为一个群.定义 2.1.2]4[设G 和1G 是群,映射1:G G →ϕ称为由G 到1G 的群同态,如果ϕ保持群运算,即∀G b a ∈,,都有)()()(b a ab ϕϕϕ=.如果ϕ为单(满)射,则称ϕ为单(满)同态.定义 2.1.3]4[既单又满的同态称为同构.如果存在由G 到1G 的一个同构,则称G 同构于1G ,也说G 和1G 是同构的,记为1G G ≅.群G 到自身的同态及同构具有重要的意义,称之为群G 的自同态和自同构.)(End G 表示G 的全体自同态构成的集合,)(Aut G 表示G 的全体自同构构成的集合.对于映射的乘法,)(End G 构成一个有幺元的半群,而)(Aut G 构成一个群,称为G 的自同构群.定义2.1.4]4[像通常的映射一样,)(G ϕ称为ϕ的像,记为ϕim .又将1e 的原像称为ϕ的核,记为ϕker ,即})(|{ker 1e a G a =∈=ϕϕ.定理2.1.1]4[设1:G G →ϕ是群同态.则ϕϕim G ≅ker /.证明 记H =ϕker ,定义映射,im /:ϕψ→H G ).(a aH ϕ验证ψ是良定义的,即)(aH ψ与陪集代表a 的选取无关.如果bH aH =,即aH b ∈,则存在H h ∈使得ah b =.故)()()()()()()(aH a h a ah b bH ψϕϕϕϕϕψ=====,即ψ良定义.下面证明ψ是群同构,也就是证明ψ是单射,并且ψ也是满射.)()()()()()()))(((bH aH b a ab abH bH aH ψψϕϕϕψψ====,所以ψ是群同态.又设1)(e aH =ψ(1G 的幺元),即1)(e a =ϕ,故H a ∈,即)/(的幺元H G H aH =,所以ψ是单射.最后设ϕim g ∈,则存在G a ∈使得g a =)(ϕ.于是g a aH ==)()(ϕψ,这说明ψ必是满射.所以ψ同构.定理 2.1.2]3[设G 是一个群,G 是一个代数运算(也称为乘法)的集合.如果G G ~,那么G 也是一个群.证明 因为G G ~,G 是群,其乘法满足结合律,故由定理1.1得,G 的乘法也满足结合律.设e 是群G 的单位元,a 是G 的任一元素,又设ϕ是G 到G 的满同态,且在ϕ之下e e →,a a → 于是a a e =,但是a ea =,故a a e = ,即e 是G 的单位元.又设1-a →1-a,则a a a a 11--→.但是e a a =-1,故e a a =-1,即1-a 是a 的逆元.因此,G 也是一个群. 本定理的意义在于,要验证一个集合G 对所指的代数运算作成群时,可找到一个已知群,并通过同态来实现.定理 2.1.3]4[设ϕ是群G 到群G 的一个同态映射(不一定是满射),则群G 的单位元的像是群G 的单位元,G 的元素a 的逆元的像是a 的像的逆元,即11--=a a 或11)()(--=a a ϕϕ.应该注意,如果集合G 与G 各有一个代数运算,且G G ~,则当G 为群时,G 却不一定是群.例 1 令G ={全体正负奇数},代数运算为数的普通乘法;又}1,1{-=G 关于数的普通乘法作成群,令ϕ:正奇数1→,负奇数-1→.则易知ϕ是G 到G 的一个同态满射,故G G ~.G 是群,但G 却不是群.当然,若G 与G 为各有一个代数运算的代数系统,且G G ≅,则当G 与G 中有一个是群时,另一个必然是群.例2 设G 是一个群,N 是G 的正规子群.令G a aN a f ∈∀=,)(.显然f 是群G 到商群N G 的满同态,这个满同态称为群G 到商群N G 的自然同态.定理2.1.4]4[设是G 到G 的同态映射(不一定是满映射),则1)当G H ≤时,有G H ≤)(ϕ且H ~)(H ϕ;2)当G H ≤时,有ϕG H ≤)(-1ϕ,且在ϕ之下诱导出)(-1H ϕ到H 的一个同态映射. 证明 1)任取a ,b )(H ϕ∈且在ϕ之下令a a →,b b →.其中H b a ∈,.由于G H ≤,故H ab ∈,且b a ab →. 从而)(H b a ϕ∈,即)(H ϕ对G 的乘法封闭,且 )(~H H ϕ.但H 是子群,从而)(H ϕ也是群且是G 的子群.2)当G H ≤时,由于)(-1H ϕ显然非空,任取)(,1H b a -∈ϕ,且在ϕ之下令a a →,b b →则11--→b a ab ,其中,H b a ∈,.而G H ≤,故H b a ∈-1,从而1-b a )(-1H ϕ→,即G H ≤)(-1ϕ且显然ϕ诱导出)(-1H ϕ到H 的一个同态映射.定理2.1.5]3[群G 到群G 的同态映射ϕ是单射的充要条件,群G 的单位元e 的逆象只有e .证明 必要性显然,下证充分性.设ϕ是群G 到群G 的任一同态映射,且在ϕ之下e 的逆象只有e .又设在ϕ之下a a →,b b →,当b a ≠时,必有b a ≠:又若b a =,则由于e b a ab =→--11,故b a e ab ==-,1,矛盾.因此,ϕ是单射. 定理 2.1.6]3[设f 是群G 到G '的一个满同态.若N 是G 的正规子群,则)(N f 是G '的正规子群.证明 设N 是G 的正规子群,可得,)(N f 是G '的子群.对于任意的)(N f n ∈'和任意的G a '∈',去N n ∈和G a ∈,使得n n f '=)(,a a f '=)(. 于是,有 )()())()(()()(111N f ana f a f n f a f a n a ∈=='''---,所以)(N f 是G '的正规子群.性质1]4[任何群G 与自身同构;证明 首先,对于任何群G ,单位变换G I 就是G 到自身的一个同构,因此G G ≅.所以性质成立.性质2]4[若群1G 与群2G 同构,则群2G 与群1G 同构;证明 1G 和2G 是两个群,并且1G 2G ≅,我们有b a b a f f ''=''-))((1,b a b f f a f f b f a f f ''=''=''----))(())(())()((1111,从而)()()(111b f a f b a f ''=''---.因此1-f是群2G 到群1G 的同构,从而12G G ≅,所以性质成立.性质3]4[若群1G 与群2G 同构,群2G 与群3G 同构,则群1G 与群3G 同构;证明 假设1G ,2G 和3G 都是群,并且21G G ≅,32G G ≅,不妨设f 是群1G 到2G 的同构,g 是群2G 到3G 的同构.容易验证,gf 是群1G 到3G 的同构,因此31G G ≅,所以性质成立.定理2.1.7]2[设G 是一个群,N 是G 的正规子群.(1) 若H 是G 的子群,则 N HN N H H )()(≅ .(2) 若H 是G 的正规子群且H N ⊆,则H G N H H G ≅)()(.推论2.1.8]4[设1:G G →ϕ是群同态,则ϕϕim G ≅ker /.定理2.1.9]4[(Cayley 定理)任何一个群都与某个变换群同构.证明 设G 是群.对与每一个G a ∈,定义G 的变换a σ如下: G x ax x a ∈∀=,)(σ.显而易见,a σ是G 的一一变换. 令{}G a G a ∈='σ.下面我们来阐明G '是G 上的一个变换群. 事实上,显然,我们有G I e G '∈=σ.此外对于任意的a σ,G b '∈σ,我们有)())((x abx x ab b a σσσ==,)())((11x I x x aa x G a a ===--σσ, )())((11x I x ax a x G a a ===--σσ,G x ∈∀,从而,G ab b a '∈=σσσ,G a a a a I ==--σσσσ11,所以,G '是G 上的一个变换群.现在考察由下式定义的G 到G '的映射fa a f σ=)(,G a ∈∀.显而易见,f 是满射.对于任意的G b a ∈,我们有b a b f a f σσ=⇒=)()( b a e e b a =⇒=⇒)()(σσ.因此f 是单射,从而,f 是双射.此外,我们有)()()(b f a f ab f b a ab ===σσσ,G b a ∈∀,.所以f 是G 到G '的同构,从而G G '≅.推论2.1.10]4[任何一个有限群都与某个置换群同构.2.2 环同态与同构由于环是有加,乘两种运算的代数系统,因此,定义同态映射时必须同时保持加,乘的同态性.定义2.2.1]5[设R 是一个环,S 是有加法和乘法的两种运算的代数系统,称R 到S 中的一个映射σ是环R 到S 中的一个同态映射,如果 )()()(b a b a σσσ+=+,)()()(b a ab σσσ=.若R 到R '上有一个同态映射,则称R 到R '同态,记为R ~R '.定义 2.2.2]5[如果σ是环R 到R '的一个同态映射,并且σ又是双射时,则称σ为环R 到R '的一个同构映射,当R 与R '之间存在同构映射时,称环R 与R '同构,记为R R ≅,特别的,当R R =时,称σ为环的一个自同构.定理2.2.1]5[设R 是一个环,S 是一个有加法和乘法的运算系统,若σ是R 到S 中的同态映射,则)(R R σ='也是一个环;)0(σ为R '的零元0';)()(a a σσ-=-;若R 有幺元而R '不止有一个元素,则R '有幺元且,σ(1)就是R '的壹1';若R a ∈可逆,则)(a σ在R '中可逆而且)(1-a σ就是1)(-a σ.设σ是R 到R '上的同态映射,R '的零0'的逆映像)0(1'-σ叫σ的核.定理2.2.2]5[(环同态基本定理)设R 和R 是两个环,且R R ~.则1)这个同态的核N ,即零元的全体逆像,是R 的一个理想;2)R N R ≅/证明 设ϕ是环R 到环R 的一个同态满射.1)易知,核N 首先是环R 的一个子加群;其次,设R r N a ∈∈,,则r r a →→,0.于是在ϕ之下有00,00=→=→r ar r ra ,故N ar ra ∈,,即N 是R 的理想.2)令)(:a N a ϕσ→+,则由群同态基本定理知,作为加群,σ是N R /到R 的一个同构映射.又由于N ab N b N a +=++))((,而)()()(b a ab ϕϕϕ=,因此σ是N R /到环R 的一个同构映射,从而R N R ≅/.此定理表明,在同构意义下,每个环能而且只能与商环同态.推论2.2.3]6[设1:R R →ϕ是环同态,则1ker /R R ≅ϕ.定理 2.2.4]6[同态映射σ的核N 是R 的理想,设a '是R '的任意元素,则a '的逆映像})({)(1a a R a a '=∈='-σσ是N 的一个剩余类.证明 因为σ是R 的加法群到R '的加法群上面的一个同态映射,所以σ的核)0(1'=-σN 是R的一个子群,且a '的逆映象)(1a '-σ是模N 的一个剩余类.现在再证N 做成理想.即证:若N a ∈,R x ∈,则N ax ∈,N xa ∈,事实上,0)()()('==x a ax σσσ,故N ax ∈,同样可证N xa ∈.对于R 的任意理想N ,是否有一个环R '而且有R 到R '的一个同态映射σ使N 刚好就是σ的核呢?答案也是肯定的.由群中已证的结果,模N 的所有剩余类按照剩余类的加法作成一个加法群,就是R 对于N 的商群N R ,规定N a a +=)(σ,即N a a +→:σ这样规定的σ便是群R 到群N R 上的一个同态映射,其核为N .规定剩余类的乘法,以使σ成为环R 到系统N R 上的同态映射.设A ,B 是N 的两个剩余类,任取A a ∈,B b ∈,规定包含ab 的剩余类N ab C +=为A 与B 的积,而AB C =,))((N b N a N ab ++=+.若另取A a ∈',B b ∈',则包含a 'b '的剩余类和包含ab 的剩余类是一样的,可见上面的乘法规定由A ,B 完全确定,与b a ,的选择无关.由σ的定义,N a a +=)(σ,N b b +=)(σ,N ab ab +=)(σ.但由上面的剩余类乘法的定义,))((N b N a N ab ++=+,故)()()(b a ab σσσ=.所以,σ是环R 到运算系统N R 上的一个同态映射.因此,N R 是一个环,于是有:定理 2.2.5]7[按照上述剩余类的加法和乘法,R 对于理想N 的所有剩余类的集合N R 是一个环,规定N a a +=)(σ,则σ是R 到N R 上的一个同态映射,其核为N .N R 叫做R 对于N 的剩余环,前面定理所说的加法和乘法的同态性,其实是说剩余环N R 中的加法和乘法运算可由剩余类中的任意元素来确定,剩余类的运算与其中元素的特殊选择无关.剩余环N R 有了这加法和乘法两种运算,就与环R 同态.定理 2.2.6]7[(第一同构定理)设R 是环,是R 的理想,则在自然同态I R R /:→π,I r r + .下,(1)R 的包含I 的子环与I R /的子环一一对应.(2)在此对应下,理想对应理想.(3)若J 是R 的理想且I J ⊇,则)/)(/(/I J I R J R ≅.定理 2.2.7]7[(第二同构定理)设R 是环,I 是R 的理想,S 是R 的子环,则(1)I S ⋂是S 的理想.(2))(/)(I S S I S I ⋂≅+.定理 2.2.8]8[若σ是环R 到R '上的一个同态映射,其核为N ,则R '与N R 同构:R '≅N R .证明 设a '是R '的任意元素,则)(-1a 'σ是N 的一个剩余类A .规定R '的a '和这个N R 的A对应.这样,我们规定了R '到N R 上的一个一对一映射τ,τ:N R R /→',a ' A .下面证明τ是同构,即证明:若R b a '∈'',,则)()()(b a b a '+'='+'τττ,)()()(b a b a ''=''τττ. 事实上,若A a =')(σ,B b =')(τ,即N a A a +=='-)(1τ,N b B b +=='-)(1σ,其中,A a ∈B b ∈,则因b a b a '+'=+)(σ,b a ab ''=)(σ,故 N b a b a ++='+'-)(1σ,N ab b a +=''-)(1σ,B A b a +='+'-)(1σ,AB b a =''-)(1σ.于是)()()(b a B A b a '+'=+=''ττσ,)()()(b a AB b a ''==''τττ.故τ是R '到N R 上的一个同构对应.定理 2.2.9]8[设环R 同态于R ':R R '~于是R 与N 间的子环与R '的子环一一对应,大环对应大环,小环对应小环,理想对应理想.2.3 其他代数系统上的同态与同构定义 2.3.1]9[(模同态与同构)设M 和T 都是R 模,T M →:ϕ是映射.如果ϕ满足下述两个条件:(1)M y x y x y x ∈∀+=+,),()()(ϕϕϕ.(2)M x R a x a ax ∈∈∀=,),()(ϕϕ.则称ϕ为M 到T 的一个R 模同态.如果ϕ又是单(满)射,则称ϕ为R 模的单(满)同态.定义 2.3.2]9[如果,ϕ既单又满,则称ϕ为模同构.此时,也称为M 和T 是同构的,记作T M ≅,由M 到T 的所有R 模同态构成的集合记为),(Ho m T M R ;如果M T =,记),(Hom T M R 为)(End M R ,其元素称为M 的自同态.定义 2.3.3]10[(格同态与同构)设21:L L f →,1,L y x ∈∀有)()()(y f x f y x f ∧=∧,)()()(y f x f y x f ∨=∨则称f 为1L 到2L 的同态.如果f 是双射的,就称f 是1L <,1∨,>∧1到>∧∨<222,,L 的格同构,也称格>≤<11,L 和>≤<22,L 同构. 定理2.3.4]9[(同态基本定理)设T M →:ϕ是模同态.ϕϕim ker /→M ,)(x x ϕ是模同构,其中ϕker +=x x 是x 所代表的陪集.定理2.3.5]9[(第一同构定理)设N 为M 的子模,N M M /:→π是典范同态,则在π下的包含N 的子模与N M /一一对应,对于M 的包含N 的子模H ,有同构 )//()/(/N H N M H M →,)/()(N H x H x ++π .定理2.3.6]9[(第二同构定理)设H 和N 为M 的子模,则有同构)(/)(N H H N N H ⋂→+,)()(N H h N n h ⋂+++ ),(N n H h ∈∈∀.可以想象:环上的模的性质依赖与环的性质.环的性质越丰富,其上的模的结构就越简单.定理2.3.7]10[f 是格1L 到2L 的同态,则1,L b a ∈,)()(b f a f b a ≤⇒≤.证明 b a ≤)()()()()()()(b f a f a f b f a f a f b a f a b a ≤⇒=∧⇒=∧⇒=∧⇒.注意 )()(b f a f ≤不一定推出b a ≤.定理3.2.8]10[f 为双射.f 为格1L 到2L 的同构当且仅当)()(,,1b f a f b a L b a ≤⇔≤∈∀. 证明 必要性:)()(b f a f b a ≤⇒≤显然成立,若)()(b f a f ≤成立,则)()()(a f b f a f =∧,因为f 是同构,有)()(a f b a f =∧,由单射性a b a =∧,所以b a ≤.充分性:只须证明f 是同态映射,即:)()()(b a f b f a f ∧=∧,)()()(b a f b f a f ∨=∨.b a b b a a ∨≤∨≤,)()(),()(a f b f b a f a f ≤∨≤⇒)()()(b a f b f a f ∨≤∨⇒,2)()(L b f a f ∈∨))()()((1b f a f d f L d ∨=∈∃⇒,d b d a d f b f d f a f ≤≤⇒≤≤,)()(),()()()()(b f a f b a f d b a ∨≤∨⇒≤∨⇒)()()(b a f b f a f ∨=∨∴同理)()()(b a f b f a f ∧=∧.3 小结同态只保持两个代数系统的部分性质,而同构却能使两个代数系统的结构完全相同.但同态关系比同构易建立.虽然同态比起同构有其不足,但它的确是比同构应用更广泛也更灵活的一种研究代数系统的有效方法.在我们学习的过程中应该加强它们之间的联系与区别,这对于技术人员,工程人员,高等理工科院校本科生,研究生是必不可少的基础数学知识,有着重要的学习意义以及应用价值.参考文献[1].杨子胥.近世代数[M].北京:高等教育出版社.2011.21-107.[2].赵春来,徐明曜.抽象代数Ⅰ[M].北京:北京大学出版社.2008.143-153.[3].张禾瑞.近世代数基础(修订本)[M].高等教育出版社.1978.31-48.[4] 崔亚琼.浅谈同构在代数中的应用[J].大同职业技术学院学报,2005,1(19):75-76.[5].杨子胥.近世代数(第二版)[M].北京:高等教育出版社.2003.81-105.[6].张禾瑞,郝炳新.近世代数基础[M].高等教育出版社.1988.30-42.[7].刘绍学.近世代数基础[M].北京:高等教育出版社.1999.45-52.[8] 杨树生.代数系统的同态与同构[J].内蒙古民族大学学报,2004,6(19):1-2.[9] J.M.Howie:An Introduction to semigroup theory[M].London:Published for the London Mathematical Society by Academic prees Inc,1975.1-156.[10] 崔亚琼.浅谈同构在代数中的应用[J].大同职业技术学院学报,2005,1(19):75-76.A T entative Discussion on the Homomorphism and Isomorphism of the Algebraic SystemDongdong He(Grade11,Class1, Major in Mathematics Education Speciality, School of Mathematics and ComputerScience, Shaanxi University of Technology, Hanzhong 723000,Shaanxi)Tutor: Hongmei ZhengAbstract : One of the most important and elementary concept in algebra is homomorphism and isomorphism.The application of the homomorphism and isomorphism on several algebraic systems is summarized in this paper,which shows the importance on the algebra.Key words: Semigroup; Group; Ring; Lattic; Homomorphism; Isomorphism。
153代数系统的同态与同构

f(θ)是V2中零元,θ为V1中相应运算零元
f(a-1)是 f(a)的逆元
10
几点说明
1. 满同态条件重要. 如果不是满同态,有关性质只能在同
态像中成立. 例如
V =< A,⋅ >
A
=
a 0
0 b
|
a,
b
∈
R,
f : A → A,
推论 代数系统的同构具有自反、对称、传递的性质. 8
同态像是映到代数系统的子代数
定理1 设 V1 =< A,o1 ,o2 ,..., or > 与V2 =< B,o1', o2',..., or '>
是同类型的代数系统,对于 i=1,2,…,r,oi与oi′是ki 元运算, f:A→B是V1到V2的同态,则 f(A)关于V2中的运算构成代 数系统,且是V2的子代数,称为V1在 f 下的同态像.
oi (a 1 , a 2 ,..., a ki ) ∼ oi (b1 , b2 ,..., bki ) ∼关于oi运算具有置换性质,根据oi的任意性,定理得证. 19
实例
例2 V=<Z4,⊕>, fi : Z4→Z4, fi(x) = (ix) mod 4,i = 0,1,2,3
函数
f0(x)=0, x=0,1,2,3
统的下述性质:
交换、结合、幂等、分配、吸收 单位元、零元、逆元 消去律不一定保持
7
同态的合成仍旧是同态
命题 若 f:V1→V2, g:V2→V3为同态映射,则 g∘f:V1→V3也 为同态映射.
证 根据集合论的定理,g∘f: V1→V3为映射. 任取V1,V2,V3中一组对应的运算 o1,o2,o3, 设为 k 元运算. ∀x1, x2, … , xk∈V1,
9 同构 自同构.docx

§9 同构 自同构定义 设,分别为,A A 的一个代数运算,若有一个A 到A 的一一映射ϕ使得()()(),a b a b ϕϕϕ=则称ϕ是对于运算,来说的A 与A 间的同构映射(简称同构).若存在A 与A 间的同构映射,则称对代数运算,来说,A 与A 同构,记为.A A ≅例1 {}{}1,2,3,4,5,6A A ==则:14,25,36ϕ是一个A 与A 间的同构映射.ϕ为A 与A 间的一个一一映射,()()()()36,6,a b a b ϕϕϕϕ===()()(),,a b a b a b A ϕϕϕ∴=∀∈ϕ∴为A 与A 间的同构映射.定理 若ϕ是对于代数运算,来说A 玉A 间的同构映射,则1ϕ-是对代数运算,来说,A与A 间的同构映射. 证ϕ为A 与A 间的一一映射,1ϕ-∴为A 与A 间的一一映射, ,a b A ∀∈,设()()11,a a b b ϕϕ--==,则()(),.a a b b ϕϕ==()()()a b a b a b ϕϕϕ==,()()()111,a b a b a b ϕϕϕ---∴==1ϕ-∴为A 与A 间的同构映射.推论 设,分别为,A A 的两个代数运算,若A A ≅,则.A A ≅定义 设是集合A 的一个代数运算,若A 的一一变换ϕ满足,()()(),,a b a b a b A ϕϕϕ=∀∈,则称ϕ是对代数运算来说的集合A 的自同构. 例2{}1,2,3A =:12,21,33ϕ是一个对来说的A 的自同构.()()()()()()3,3,,,a b a b a b a b a b Aϕϕϕϕϕϕ==∴=∀∈作业:P23,2 P26,2。
