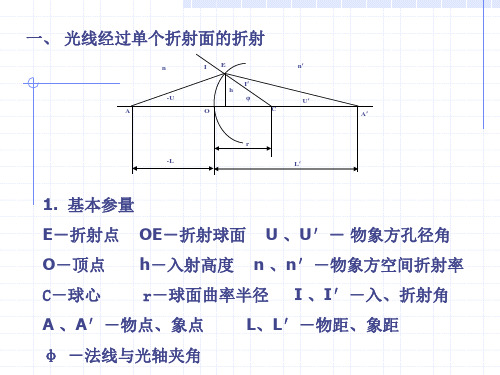
2 球面与共轴球面系统

h lu l u
1 1 1 1 ( ) Q n( ) n r l r l
6、四个常用的推导公式：
2013-8-4
OE of HUST
n n nu nu h r n n n n l l r
11
2013-8-4
OE of HUST
12
逆时针为“－”
夹角的优先级：“光轴－光线－法线”
3、所有参量是含符号的量，但图示标为参量的大小。
2013-8-4 OE of HUST 5
四、 远轴光的计算公式（实际光线光路计算）（点成象） 给定n、 n′、r，已知L、U，求解L′、 U′ 其中U、 U′较大，远轴光线成像（大光路）
n I E n′
2、物象关系的研究方法：光线的光路计算。逐
面计算物象的位置、大小、虚实、正倒等特性。 3、子午面— 包含物面与光轴的截面。 主要讨论子午面内的光线的光路计算。
2013-8-4
OE of HUST
2
二、基本参量(五点、五角、四线)
1、五点：E－折射 点 ，O－顶点， C －球心 ，A 、A′－ 物点、象点；
3）物点位于物方无限远时，入射光线位置由高度h决定。
h sin I r
2013-8-4 OE of HUST 7
五、 近轴光计算公式（小光路光线计算公式）
U、U′、I、I′很小，正弦值可用弧度代替。（基本量均小写）
lr u r n i i n u u i i i l r r u i
第二章 球面与共轴球面系统
§ 2－1 单个折射球面的折射
主要内容：
1、共轴球面系统及研究方法；
2、基本参量； 3、符号法则； 4、远轴光计算公式； 5、近轴光计算公式；
6、四个常用的推导公式。
2013-8-4 OE of HUST 1
一、共轴球面系统及研究方法 1、 共轴球面系统： 光学系统一般由球面和平 面组成，各球面球心在一条直线（光轴）上。
2013-8-4
OE of HUST
13
2013-8-4
OE of HUST
14
2013-8-4
OE of HUST
15
2013-8-4
OE of HUST
16
2013-8-4
OE of HUST
17
2013-8-4
OE of HUST
18
2013-8-4
OE of HUST
19
例：厚透镜：
4、远轴光计算公式:
Lr sin I sin U r n sin I sin I n U U I I （点成象） sin I L r r sin U
2013-8-4
OE of HUST
10
小结：
5、近轴光计算公式：
lr i u r n i i n u u i i i l r r u
2013-8-4 OE of HUST 3
三、 符号法则（线段和角度，便于统一计算）
1、线段：规定光线从左向右传播
a）沿轴线段 L、L′、r、d
以O为原点， 与光线传播方向相同，为“＋” 与光线传播方向相反，为“－” b）折射面的间隔d：一般取“＋” c）垂轴线段 h
在光轴之上，为“＋”
在光轴之下，为“－”
2013-8-4 OE of HUST 4
2、角度：
a）孔径角：光线与光轴夹角U、U′ 以光轴转向光线成的锐角来度量， 顺时针为“＋”
逆时针为“－”
b）光线与法线夹角I、I′ 以光线转向法线成的锐角来度量，顺时针为“＋”
逆时针为“－”
c）光轴与法线的夹角φ
以光轴转向法线成的锐角来度量，顺时针为“＋”
OE of HUST
21
§ 2－4 球面反射镜
令 n′= -n，
n n n n l l r
1 1 2 l l r
n l l n l l n 2 2 n
β <0， l 、 l′同号，物象虚实一致。 β >0， l 、 l′异号，物象虚实相反。 当物沿光轴移动时，像总是以相反 的方向沿轴移动。
1

J uy u y
2013-8-4 OE of HUST 22
说明：
1. 当物处于球心时，有：
l l r
1, 1, 1
2.
l
r l f 2
3. 通过球心的光线被反射镜原路反射回来，球面反 射镜对其曲率中心为等光程面。
c：
n n nu nu h rn n l l r
（常用的物象位置关系）
OE of HUST 9
2013-8-4
小结：
1、共轴球面系统及研究方法(共轴球面系统、子午面、逐面计算)； 2、基本参量(五点、五角、四线)； 3、符号法则:线段(方向)、角度(锐角、优先级)、图示(标量)；
作业题3：一月凸薄透镜的两个球面半径为r1 =-200mm， r2 ＝-150mm，n=1.5，后表面凸面渡银，在前表面前方 400mm处的轴上放一高为10mm的物，求最后所成像的位置、 大小、正倒、虚实。
2013-8-4
OE of HUST
24
2013-8-4 OE of HUST 8
六、 常用推导公式
a： h
lu l u （物象方的截距与孔径角之积不变）
1 1 1 1 ( ) b：阿贝不变量: Q n( ) n r l r l
(物象方的折射率、球面半径和截距之间的关系)
Q随物象空间折射率、共轭点位置变化而变化。
4. 对于平面反射镜，有：
2013-8-4
r 1 1 0 l l l 1 OE of HUST l
23
作业题1：凹面反射镜半径为-400mm，物放在何处成放大两 倍的实像？放在何处成放大两倍的虚像？ 作业题2：有一玻璃半球，折射率为1.5，半径50mm，其中 的平面渡银。一高10mm的小物体放在球面顶点前方 100mm处，求物经过系统成像后的位置、大小、正倒、虚实。
2013-8-4
OE of HUST
20
例：一玻璃棒（n=1.5），长500mm，两端面为半球 面，半径分别为50mm和100mm，一箭头高1mm，垂 直位于左端球面顶点之前200mm处的轴线上，求箭头 经玻璃棒成像后像的位置、大小、正倒、虚实。
r1=50 n=1.5
-r2=100
200
500
2013-8-4
l r
n r l r nl nl r
说明：1）l′＝f (r、 n、n′、 l) 2）l′与u无关，象方光束同心，近轴光以细光束成完善象。
3）成的完善像称为高斯像，由l′决定；通过高斯像点垂直于 光轴的像面称为高斯像面；构成物象关系的一对点称为共轭点。 h 4）物位于无限远， i r
n
I
E
n′
I′ h -U A O φ C U′ A′
r
-L
L′
2、五角：孔径角－光轴转向光线的锐角（U 、U′－ 物、象 方孔径角）；入、折射角－光线转向法线的锐角（I 、 I′）； φ －光轴转向法线的锐角； 3、四线：截距：顶点到光线与光轴交点的距离（L、L′－物 方截距、象方截距）；r－球面曲率半径； h－入射高度； 4、界面：n 、n′－物象方空间折射率；OE－折射球面 。
Lr sin I sin U r n sin I sin I n U U I I sin I rr L sin U
2013-8-4
I′
h -U A O φ C U′ A′
r
-L
L′
OE of HUST
6
说明：
1）L′＝f (U、L、n、n′、r) 2）当L为定值时，L′随U变化而变化，象方光束失去 同心性，成不完善象，形成球差。