2015届安徽省江南十校高三期末大联考理科数学试题(含答案详解)扫描版
安徽省江淮十校2015届高三11月联考数学理试题 Word版含答案

2015届“江淮十校”十一月联考试卷数学(理)试题本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试用时120分钟. 第Ⅰ卷(选择题 共50分)一、选择题:本题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一个选项符合题意. 1.命题“对任意x R∈,总有210x +>”的否定是( )A.“对任意,x R ∉总有210x +>” B. “对任意,x R ∈总有210x +≤”C. “存在,x R ∈总有210x +>” D. “存在,x R ∈总有210x +≤”2.已知全集U R =,集合{|}A x y =,集合{|,}xB y y e x R ==∈,则(C )R A B =A.{|2}x x >B.{|01}x x <≤C.{|12}x x <≤D.{|0}x x <3.函数,1()1,11x f x x x ≤=⎨>⎪-⎩的大致图像是()4.已知函数()f x 的定义域为(32,1)a a -+,且(1)f x +为偶函数,则实数a 的值可以是 ( )A.23 B.2 C.4 D.65.若(,),2παπ∈且cos 2sin()4παα=-,则si n α的值为( )A.12-B.12 C.1 D.1-6.已知函数()cos()(A 0,0,R)f x A x ωϕωϕ=+>>∈,则“()f x 是奇函数”是“2πϕ=”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 7.已知1,3,0,O A O B O A O B ==⋅=点C 在AOB ∠内,且30,A O C ∠=︒设(,),OC mOA nOB m n R =+∈则mn的值为( )A.2B.52 C.3 D.48.定义在R 上的函数()f x 满足:对任意,,R αβ∈总有()[()()]2014f f f αβαβ+-+=,则下列说法正确的是( )A.()1f x +是奇函数B.()1f x -是奇函数C.()2014f x +是奇函数D.()2014f x -是奇函数9.已知定义在(0,)2π上的函数()f x ,'()f x 为其导函数,且()'()tanf x f x x <⋅恒成立,则( )A.()()43ππ>()()63f ππ< C.()()64f ππ> D.(1)2()sin16f f π<⋅10.设函数()ln f x x =的定义域为(,)M +∞,且0M >,且对任意,,(,),a b c M ∈+∞若,,a b c 是直角三角形的三边长,且(),(),()f a f b f c 也能成为三角形的三边长,则M 的最小值为 ( ) A.B.C. D.2第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.函数221()1x f x x -=+的值域时______________. 13.函数2()1f x mx x =-+有两个零点分别属于区间(0,2),(2,3),则m 的范围为_____. 14.已知正方形ABCD 的边长为2,P 是正方形ABCD 的外接圆上的动点,则AB AP ⋅的最大值为 _______________.15.对任意两份非零的平面向量α和β,定义,⋅⋅αβαβ=ββ若平面向量a,b 满足0,≥>a b a与b 的夹角[0,]4πθ∈,且a b 和ba 都在集合{|,n }nm m ∈∈Z Z 中,给出下列命题:①若1,m =则ab =b a =1;②若2m =,则12=ab .③若3m =,则a b 的取值最多为7个; ④若4m =,则ab 的取值无限多个;其中正确命题序号是_____________(把所有正确命题的序号都填上).三、本大题共6小题,满分75分,解答应写出必要的文字说明、证明过程或演算步骤. 16.(本题满分12分)已知函数()sin()(0,0)2f x x πωϕωϕ=+><≤的部分图像如图所示.(1)求()f x 的解析式;(2)求使不等式'()1f x ≥成立的x 的取值集合,其中'()f x 为()f x 的导函数.17.(本小题满分12分)已知函数222,0(),0x x x f x ax bx x ⎧-+≥⎪=⎨+<⎪⎩为奇函数. (1)求a b -的值;(2)若函数()f x 在区间[1,2]m --上单调递增,求实数m 的取值范围.18.(本小题满分12分)已知函数1()sin().62f x x π=-+(1)若11[0,],(),210x f x π∈=求cos x 得值; (2)在ABC ∆中,角,,A B C 的对边分别是,,,a b c且满足2cos 2,b A c ≤求()f B 的取值范围.20.(本小题满分13分)设二次函数2(),f x x ax b =-+集合{|()}A x f x x ==. (1)若{1,2},A =求函数()f x 的解析式;(2)若2()()2F x f x a a =+--且(1)0,f =且()F x 在[0,1]上单调递增,求实数a 的取值范围.21.(本小题满分13分)已知函数21()ln ,()3f x x x g x ax bx==-,其中,a b ∈R .(1)若2()6f x x ax ≥-+-在(0,)+∞上恒成立,求实数a 的取值范围; (2)当23b a =-时,若3(1)()2f x g x +≤对[0,)x ∈+∞恒成立,求a 的最小值.2015届江淮十校11月联考 理科数学参考答案一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填在答题卡的相应位置)题号 1 2 3 4 5 6 7 8 9 10 选项 D A B B A B C C B A二、填空题(本大题共5小题,每小题5分,共25分).11. (-1,1] 12. 2e .13. 21,94⎛⎫ ⎪⎝⎭14. 2+15. ① ③三、解答题(本大题共6小题,共75分.解答应写出文字说明.证明过程或演算步骤,并在答题卡的制定区域内答题.)16. 解:(1)∵T =2×(5π6-π3)=π,∴ω=2ππ2.又点(π3,0)是f(x)=sin(2x +φ)的一个对称中心,∴2×π3+φ=kπ,k ∈Z ,φ=kπ-2π3令k =1,得φ=π3.y =sin(2x +π3)(2),,3x k k k Zπππ⎡⎤∈-∈⎢⎥⎣⎦17.(1)令0x <,0x ->()()22[2]2f x f x x x x x=--=---=+.∴1,2a b ==,∴1a b -=-.(2)()f x =222,02,0{x x x x x x -≥+<()f x 在[-1,1]上递增,∴[12][1,1]m --⊆-,, ∴2121{m m ->--≤,13m ⇒<≤.1181()sin()62f x x π=-+、解:()11()10f x =,∴3sin()65x π-=;又∵[0,]2x π∈,∴[,]663x πππ-∈-,即4cos()65x π-=3cos cos[()]cos()cos sin()sin 66666610x x x x ππππππ∴=-+=---=22bcosA 2c 2sin cos 2sin 2sin cos 2sin()2sin cos 2[sin cos cos sin ]2sin cos cos (0,]6B A c A B A A B AB A A B A B A A B A B B π≤≤⇒≤+⇒≤+-⇒≥⇒≥⇒∈()由-得:∴1sin()(,0]62B π-∈-,即11()sin()()(0,]622f B B f B π=-+⇒∈19.解:(1)设B 类型汽车的价值为x 万元,顾客得到的油费为y 万元, 则A 类型汽车的价值为(10)x -万元,由题意得,11(10)ln(1)ln(1)11010y x m x m m x =-++=+-+,(19x ≤≤),(2)由1,0110m y y x ''=-=+得得101x m =-①当1011,00.2m m -≤<≤即时,0,[1,9]y y '≤在是减函数随B 类型汽车投放金额x 万元的增加,顾客得到的油费逐渐减少。
安徽省“江南十校”2015届高三联考理科综合试卷(扫描版,含答案).pdf

汽车在18—20s内的位移 (1分)
故汽车在前20s的位移 (1分)
23. (16分)解:
是粒子做圆周运动的半径
即
1分
(2),所以电场对带电粒子单次通过的时间为,显然,粒子首次通过电场中是加速运动,粒子应该带负电。
由
2015年江南十校理科综合参考答案
物理学科
选择题:(42分,每空6分,均为单选项,错选、多选、不选不得分)
题号14151617181920答案CDDBCCA21.(1)BE(3分,少选、错选不得分)
(2)①A;②(4分,每空2分)
()等于等于或?;(4分,每空2分)
④等于等于
1分
本题有其它解法,正确的对照评分标准给分。
24. (20分)解析:⑴小球A从顶部运动到底部过程根据功能关系有:
(2分)
在最低点,由牛顿第二定律知:, (2分)
联立可解得: 678 N (1分)
⑵小球第一次转回到顶部碰前状况,设其速度为,根据题意可知,损失部分机械能,重力势能不变,
(2分)
解得 (1分)
小球A在顶部与钢球碰撞,由动量守恒定律、机械能守恒定律得:
(2分)
(2分)
联立解得:,负号表示与碰前入射速度方向相反
同理可得,碰撞n次以后瞬间的速度为,则:
,负号表示与碰前入射速度方向相反,(1分) 小球要能与钢球碰撞则必须能完成完整的圆周运动,所以碰n次后假定再次到达P位置,其速度一定有: (1分) 所以: (1分) 解得:,由于n是自然数,所以,小球A可以与4 个钢球碰撞; ⑶第一个钢球碰后速度: (1分) 第4个钢球碰撞后速度: (1分) 由于两球是分别朝向左右两边做平抛运动的,所以水平距离是: 平抛时间是: (1分) ,,(1分) 得 (1分) 2015年江南十校理科综合参考答案 化学学科 7-13:CDBDB CA 选择题选解: 7. C项中常温常压下2.24L CO2转化为标准状况体积小于2.24L,故转移电子数小于0.2NA; D项,各物质均为分子晶体,汽化均克服分子间作用力。 8.A项中KMnO4会氧化浓HCl,一般用稀硫酸酸化;C项中氧化乙醇。 10.A项中炭粉也为还原剂,会参与反应;C项温度不变,K不变,比值不变;D项依据三段法和K值可求。 13.A项中由Ksp知Fe3+水解程度大;D项中f点处Al(OH)3已部分溶解为AlO2—或[Al(OH)4]—,此时通入足量CO2气体 ,会再一次产生沉淀。 25. (17分)1)三 ⅣA (2分)(2分) 2)< > > (3分) (2分)(2分) 放热 (分) MgI2<MgBr2<MgCl2<MgF2 (2分) MgBr2(s)+2(g)===MgCl2(s)+ Br2(l)ΔH= kJ·mol-1(3分) 26.(17分)C6H6O2 (2分)(2分); ⑵ (酚羟基(分),FeCl3溶液(2分) (3分) (3分) 、(4分) (1) b (2分) (2)Fe3+易转化为Fe(OH) 3沉淀(2分) (3)Fe2(SO4)3 + n H2O=Fe2(OH)n(SO4)3-0.5n + n/2H2SO4(2分) (4)NaClO3NaNO21 mol,NaClO3 1/6 mol,乘以单价,NaClO3更合适 (5) 乙流程,因为该法氧化相同量Fe2+,原料成本较低非洲爪蟾的卵母细胞在低渗溶液不膨胀CHIP28合成的 mRNA注入非洲爪蟾的卵母细胞中,在低渗溶液中,卵母细胞迅速膨胀非洲爪蟾的卵母细胞在低渗溶液不膨胀在低渗溶液 膨胀CHIP28有关。故C错 C. 解析:根据图甲可知,埃博拉病毒没有逆转录过程;通过胞饮侵入人体细胞,所以蛋白质也进入了宿主细胞;通 过复制产生的RNA可以组装子代病毒;应该用灭活病毒的蛋白质作为抗原。故C正确 A. 解析:树干变黑会影响浅色个体的出生率和死亡率,因为许多浅色个体可能在没有交配、产卵前已被天敌捕食 ;树干变黑后,K值可能有变化,因为环境条件改变了;第2年S基因频率是约23%,SS基因型频率是约11.5%;在2-10年间 ,种群数量会下降,主要是自然选择的作用。故A对 C. 解析:胰岛素作用于不同的靶细胞效应不同可能与靶细胞的受体不同有关,如胰岛素作用于胰岛A细胞抑制胰高 血糖素的合成与分泌,作用于肝细胞促进肝糖原合成;体内血糖升高可引起胰岛B细胞和胰岛A细胞分别产生兴奋和抑制 的效应;血糖调节不仅有神经-体液调节,也与免疫调节有关,如自身免疫病;胰高血糖素和肾上腺素作用于肝细胞 ,都可促进肝糖原的水解。故C错 C. 解析: “两个四分体上出现两个黄色、两个绿色荧光点”说明细胞中发生的是非同源染色体相互交换了片段 ,这属于染色体结构变异;变异个体减数分裂时由于“任何一对等位基因的缺失会导致雄配子失去与卵细胞受精的能力
安徽省江南十校联考高三上学期期末数学试卷(理科) Word版含解析
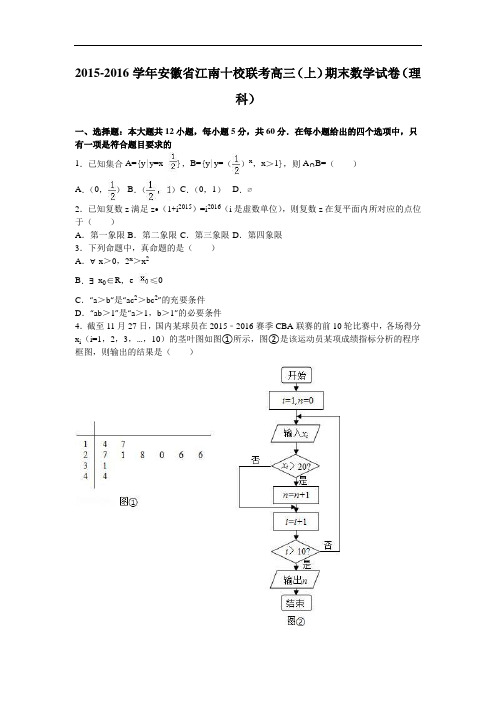
2015-2016学年安徽省江南十校联考高三(上)期末数学试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的1.已知集合A={y|y=x},B={y|y=()x,x>1},则A∩B=()A.(0,)B.()C.(0,1)D.∅2.已知复数z满足z•(1+i2015)=i2016(i是虚数单位),则复数z在复平面内所对应的点位于()A.第一象限 B.第二象限 C.第三象限 D.第四象限3.下列命题中,真命题的是()A.∀x>0,2x>x2B.∃x0∈R,e≤0C.“a>b“是“ac2>bc2”的充要条件D.“ab>1”是“a>1,b>1”的必要条件4.截至11月27日,国内某球员在2015﹣2016赛季CBA联赛的前10轮比赛中,各场得分x i(i=1,2,3,…,10)的茎叶图如图①所示,图②是该运动员某项成绩指标分析的程序框图,则输出的结果是()A.8 B.7 C.6 D.55.将函数y=cos2x的图象向右平移φ个单位得到函数y=cos2x﹣sin2x的图象,则φ的一个可能取值为()A.B.C. D.6.某中学高一、高二各有一个文科和一个理科两个实验班,现将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学,每个班级去一所高校,每所高校至少有一个班级去,则恰好有一个文科班和一个理科班分配到上海交通大学的概率为()A.B.C.D.7.已知实数x,y满足,且目标函数z=y﹣x取得最小值﹣4,则k等于()A.B.C.﹣D.﹣8.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=,且a2=b2+c2﹣bc,则△ABC的面积S的最大值为()A.B.C.D.9.已知△ABC的边BC上一动点D满足=n(n∈N*),=x+y,则数列{(n+1)x}的前n项和为()A. B. C.D.10.若抛物线C1:y=x2的焦点F到双曲线C2:﹣=1(a>0,b>0)的一条渐近线的距离为,抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=﹣1的距离之和的最小时为,则双曲线C2的方程为()A.﹣y2=1 B.x2﹣=1 C.﹣=1 D.﹣=111.一个三棱锥的三视图如图所示,则它的体积为()A .B .1C .D .212.函数f (x )=1+x ﹣+﹣+…+﹣在区间[﹣2,2]上的零点个数为( ) A .1 B .2 C .3 D .4二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置13.已知(+)5的展开式中的常数项为80,则65x 的系数为______.14.已知正数x ,y 满足2x +y=1,则4x 2+y 2+的最小值为______.15.若对于任意实数t ,圆C 1:(x +4)2+y 2=1与圆C 2:(x ﹣t )2+(y ﹣at +2)2=1都没有公共点,则实数a 的取值范围是______.16.已知函数f (x )=sin (ωx +φ)(ω>0,﹣≤φ≤)的图象如图所示,若函数g (x )=3[f (x )]3﹣4f (x )+m 在x 上有4个不同的零点,则实数m 的取值范围是______.三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤,解答写在答题卡的指定区域17.已知在各项均为正数的等比数列{a n }中,a 1=2,且2a 1,a 3,3a 2成等差数列. (Ⅰ)求等比数列{a n }的通项公式;(Ⅱ)若c n =a n •(),n=1,2,3,…,且数列{c n }为单调递减数列,求λ的取值范围.18.从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.(Ⅰ)求这40件样本该项质量指标的平均数;(Ⅱ)从180(含180)以上的样本中随机抽取2件,记质量指标在[185,190]的件数为X ,求X 的分布列及数学期望.19.如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=,PA=PD=CD=CB=1,E总是线段PB上的动点.(Ⅰ)当E点在什么位置时,CE∥平面PAD?证明你的结论.(Ⅱ)对于(Ⅰ)中的点E,求AE与底面ABCD所成角的正弦值;(Ⅲ)求二面角A﹣PD﹣C的正弦值.20.已知椭圆C的左、右焦点F1,F2在x轴上,左顶点为A,离心率e=,过原点O的直线(与x轴不重合)与椭圆C交于P,Q两点,直线PA,QA分别与y轴交于M,N两点,△PF1F2的周长为8+4.(Ⅰ)求椭圆C的标准方程;(Ⅱ)求的值;(Ⅲ)求四边形MF1NF2面积的最小值.21.已知函数f(x)=e﹣ax2(其中e是自然对数的底数).(Ⅰ)判断函数f(x)的奇偶性;(Ⅱ)若f(x)≤0在定义域内恒成立,求实数a的取值范围;(Ⅲ)若a=0,当x>0时,求证:对任意的正整数n都有f()<n!x﹣n.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清楚.选修4-1:几何证明选讲22.已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:(Ⅰ)∠CBT=∠CFT;(Ⅱ)CT2=AE•BF.选修4-4:坐标系与参数方程23.已知曲线C的参数方程为(θ为参数).(Ⅰ)求曲线C的普通方程;(Ⅱ)若倾斜角为45°的直线l经过点P(1,2)且与直线C相交于点A、B,求线段AB的长度.选修4-5:不等式选讲24.设f(x)=|x+3|﹣a|2x﹣1|(Ⅰ)当a=1时,求f(x)>3的解集;(Ⅱ)若f(x)≥0对x∈[﹣1,1]恒成立,求实数a的取值范围.2015-2016学年安徽省江南十校联考高三(上)期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的1.已知集合A={y |y=x },B={y |y=()x ,x >1},则A ∩B=( )A .(0,)B .() C .(0,1) D .∅【考点】指数函数的定义、解析式、定义域和值域;交集及其运算.【分析】利用函数的单调性可得:A=[0,+∞),B=,即可得出A ∩B .【解答】解:A={y |y=x }=[0,+∞),B={y |y=()x ,x >1}=,则A ∩B=,故选:A .2.已知复数z 满足z •(1+i 2015)=i 2016(i 是虚数单位),则复数z 在复平面内所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【考点】复数代数形式的混合运算;复数的代数表示法及其几何意义.【分析】利用复数单位的幂运算,然后利用复数的乘法的运算法则化简求解即可. 【解答】解:复数z 满足z •(1+i 2015)=i 2016,可得z (1﹣i )=1,可得z===.对应点的坐标().故选:A .3.下列命题中,真命题的是( ) A .∀x >0,2x >x 2B .∃x 0∈R ,e≤0C .“a >b “是“ac 2>bc 2”的充要条件D .“ab >1”是“a >1,b >1”的必要条件 【考点】特称命题;全称命题.【分析】根据含有量词的命题的定义进行判断即可.【解答】解:A .若x=3,则23=8,32=9,此时2x >x 2不成立,故A 错误, B .∵∀x ∈R ,e x >0,∴∃x 0∈R ,e≤0不成立,故B 错误,C.当c=0,当a>b时,“ac2>bc2”不成立,即“a>b“是“ac2>bc2”的充要条件错误,故C错误,D.当a>1,b>1时,ab>1成立,即“ab>1”是“a>1,b>1”的必要条件成立,故D正确,故选:D4.截至11月27日,国内某球员在2015﹣2016赛季CBA联赛的前10轮比赛中,各场得分x i(i=1,2,3,…,10)的茎叶图如图①所示,图②是该运动员某项成绩指标分析的程序框图,则输出的结果是()A.8 B.7 C.6 D.5【考点】程序框图.【分析】模拟执行程序框图,得到程序的功能,由茎叶图写出所有的数据,计算得分超过20分(不包括20分)的场数即可得解.【解答】解:模拟执行程序框图,可得其功能是计算得分超过20分(不包括20分)的场数,有茎叶图知,各场得分的数据为:14,17,27,21,28,20,26,26,31,44,∴根据茎叶图可知得分超过20分(不包括20分)的场数有7场.故选:B.5.将函数y=cos2x的图象向右平移φ个单位得到函数y=cos2x﹣sin2x的图象,则φ的一个可能取值为()A.B.C. D.【考点】函数y=Asin(ωx+φ)的图象变换;由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】由和差角的公式化简可得y=2cos2(x﹣),由三角函数图象变换的规则可得.【解答】解:∵y=cos2x﹣sin2x=2cos(2x+)=2cos(2x﹣)=2cos2(x﹣),∴φ的一个可能取值为.故选:D.6.某中学高一、高二各有一个文科和一个理科两个实验班,现将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学,每个班级去一所高校,每所高校至少有一个班级去,则恰好有一个文科班和一个理科班分配到上海交通大学的概率为()A.B.C.D.【考点】古典概型及其概率计算公式.【分析】求出所有的分配方案和符合条件的分配方案,代入概率计算公式计算.【解答】解:将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学,每所高校至少有一个班级去,则共有24﹣2=14种分配方案.恰有一个文科班和一个理科班分配到上海交通大学的方案共有2×2=4种,∴P==.故选:B.7.已知实数x,y满足,且目标函数z=y﹣x取得最小值﹣4,则k等于()A.B.C.﹣D.﹣【考点】简单线性规划.【分析】由约束条件作出可行域,由题意可知,直线y=x+z经过可行域,且在y轴上的截距的最小值为﹣4时,直线kx﹣y+2过点(4,0),由此求得k的值.【解答】解:如图,由题意可知,直线y=x+z经过可行域,且在y轴上的截距的最小值为﹣4.∴直线kx﹣y+2过点(4,0),从而可得k=.故选:D.8.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=,且a2=b2+c2﹣bc,则△ABC的面积S的最大值为()A.B.C.D.【考点】余弦定理.【分析】由已知及余弦定理可得cosA=,解得A=,由余弦定理可得:b2+c2=3+bc,利用基本不等式可求bc≤3,根据三角形面积公式即可得解.【解答】解:∵a2=b2+c2﹣bc,∴由余弦定理可得:cosA==,A为三角形内角,解得A=,∵a=,∴3=b2+c2﹣bc,可得:b2+c2=3+bc,∵b2+c2≥2bc(当且仅当b=c时,等号成立),∴2bc≤3+bc,解得bc≤3,∴S△ABC=bcsinA=bc≤.故选:C.9.已知△ABC的边BC上一动点D满足=n(n∈N*),=x+y,则数列{(n+1)x}的前n项和为()A. B. C.D.【考点】数列的求和;向量的共线定理.【分析】通过=n(n∈N*)可知=+,与=x+y比较可得x=,进而计算可得结论.【解答】解:∵=n(n∈N*),∴=+,又∵=x+y,∴x=,∴数列{(n+1)x}是首项、公差均为1的等差数列,∴则数列{(n+1)x}的前n项和为,故选:C.10.若抛物线C1:y=x2的焦点F到双曲线C2:﹣=1(a>0,b>0)的一条渐近线的距离为,抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=﹣1的距离之和的最小时为,则双曲线C2的方程为()A.﹣y2=1 B.x2﹣=1 C.﹣=1 D.﹣=1【考点】圆锥曲线的综合.【分析】确定抛物线的焦点坐标,双曲线的渐近线方程,利用抛物线C1:y=x2的焦点F到双曲线C2:﹣=1(a>0,b>0)的一条渐近线的距离为,可得=,再利用抛物线的定义,结合抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=﹣1的距离之和的最小时为,可得c2+1=5,从而可求双曲线的几何量,可得结论.【解答】解:抛物线C1:y=x2的焦点F(0,1),双曲线C2:﹣=1(a>0,b>0)的一条渐近线方程为bx﹣ay=0,∵抛物线C1:y=x2的焦点F到双曲线C2:﹣=1(a>0,b>0)的一条渐近线的距离为,∴=,∵直线y=﹣1是抛物线的准线,抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=﹣1的距离之和的最小时为,∴根据抛物线的定义可知,当P,F及双曲线C2的一个焦点三点共线时最小,∴c2+1=5,∴c=2,∵c2=a2+b2,∴b=,a=1,∴双曲线的方程为x2﹣=1.故选:B.11.一个三棱锥的三视图如图所示,则它的体积为()A.B.1 C.D.2【考点】由三视图求面积、体积.【分析】由三视图可知该三棱锥为棱长为2的正方体切割得到的,作出图形,结合图形代入体积公式计算.【解答】解:由三视图可知该三棱锥为棱长为2的正方体切割得到的.即三棱锥A1﹣MCD.∴V=××2×2×2=.故选C.12.函数f(x)=1+x﹣+﹣+…+﹣在区间[﹣2,2]上的零点个数为()A.1 B.2 C.3 D.4【考点】根的存在性及根的个数判断.【分析】求导f′(x)=1﹣x+x2﹣x3+…+x2014﹣x2015,分类讨论以确定f(x)的单调性,从而确定函数的极值的正负,从而利用函数的零点判定定理判断即可.【解答】解:∵f(x)=1+x﹣+﹣+…+﹣,∴f′(x)=1﹣x+x2﹣x3+…+x2014﹣x2015,当x=﹣1时,f′(x)=2016>0,当x≠﹣1时,f′(x)=,故当﹣2<x<﹣1或﹣1<x<1时,f′(x)>0;当1<x<2时,f′(x)<0;故f (x )在[﹣2,1]上单调递增,在(1,2]上单调递减, 又∵f (﹣2)<0,f (1)>0,f (2)<0,∴f (x )在(﹣2,1)和(1,2)内各有一个零点, 故选:B .二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置13.已知(+)5的展开式中的常数项为80,则65x 的系数为 40 .【考点】二项式定理.【分析】在二项展开式的通项公式中,令x 的幂指数等于0,求出r 的值,即可求得常数项,再根据常数项等于80求得实数a 的值,从而求得65x 的系数.【解答】解:∵(+)5的展开式中的通项公式为 T r+1=•a r •,令=0,求得r=3,即常数项为•a 3=80,求得a=2.故展开式中的通项公式为 T r+1=•2r•,令r=2,可得则65x 的系数为40,故答案为:40.14.已知正数x ,y 满足2x +y=1,则4x 2+y 2+的最小值为 .【考点】基本不等式在最值问题中的应用.【分析】由基本不等式可得0<xy ≤,令t=xy ,0<t ≤,由4t ﹣在0<t ≤递增,可得最小值.【解答】解:正数x ,y 满足2x +y=1, 可得2x +y ≥2, 即有0<xy ≤,则4x 2+y 2+=(2x +y )2﹣4xy +=1﹣(4xy ﹣),令t=xy ,0<t ≤,由4t ﹣在0<t ≤递增,可得t=时,4t ﹣取得最大值,且为﹣,则4x2+y2+在xy=时,取得最小值,且为1+=.故答案为:.15.若对于任意实数t,圆C1:(x+4)2+y2=1与圆C2:(x﹣t)2+(y﹣at+2)2=1都没有公共点,则实数a的取值范围是a<﹣或a>0.【考点】圆与圆的位置关系及其判定.【分析】通过两个圆的方程求出两个圆的圆心与半径,利用圆心距与半径和与差的关系即可求解.【解答】解:圆C2:(x﹣t)2+(y﹣at+2)2=1的圆心在直线y=ax﹣2上,∴要使圆C1:(x+4)2+y2=1与圆C2:(x﹣t)2+(y﹣at+2)2=1没有公共点,必须使圆心C1(﹣4,0)到直线y=ax﹣2的距离大于两圆半径之和,即d=>2,∴a<﹣或a>0.故答案为:a<﹣或a>0.16.已知函数f(x)=sin(ωx+φ)(ω>0,﹣≤φ≤)的图象如图所示,若函数g(x)=3[f(x)]3﹣4f(x)+m在x上有4个不同的零点,则实数m的取值范围是[,).【考点】由y=Asin(ωx+φ)的部分图象确定其解析式;函数的零点与方程根的关系.【分析】利用由y=Asin(ωx+φ)的部分图象可求得A,T,从而可得ω,又曲线经过(,0),|φ|<,可得φ的值,从而可求函数f(x)的解析式,将函数进行换元,转化为一元二次函数问题,由导数求出单调区间,结合函数f(x)的图象,即可确定m的取值范围.【解答】解:由图知T=4(﹣)=2π,∴ω=1,∴f(x)=sin(x+φ),∵f()=0,∴+φ=kπ,k∈Z.∴φ=kπ﹣,k∈Z.又|φ|≤,∴φ=,∴函数f(x)的解析式为:f(x)=sin(x+).由f(x)的图象可知,对于f(x)∈[,1)上的每一个值,对应着[﹣,]上的两个x值,又g(x)=3[f(x)]3﹣4f(x)+m=0,⇔m=﹣3[f(x)]3+4f(x)有4个不同的零点,令f(x)=t,则m=﹣3t3+4t.∵m′=﹣9t2+4=﹣9(t+)(t﹣),∴m=﹣3t3+4t在[,]上单调递增,在[,1]上单调递减,而当t=时,m=;当t=时,m=;当t=1时,m=1,结合图象可知,对于m∈[,)上的每一个值,对应着t=f(x)∈[,1)上的两个值,进而对应着[﹣,]上的4个x值.故答案为:[,).三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤,解答写在答题卡的指定区域17.已知在各项均为正数的等比数列{a n}中,a1=2,且2a1,a3,3a2成等差数列.(Ⅰ)求等比数列{a n}的通项公式;(Ⅱ)若c n=a n•(),n=1,2,3,…,且数列{c n}为单调递减数列,求λ的取值范围.【考点】等差数列与等比数列的综合.【分析】(Ⅰ)设等比数列的公比为q(q>0),由等差数列的中项性质和等比数列的通项公式,解方程可得q=2,进而得到所求通项;(Ⅱ)把数列{a n}的通项公式a n代入c n=2n•(﹣λ),由c n+1﹣c n分离λ后,求出﹣的最大值得答案.【解答】解:(Ⅰ)设等比数列的公比为q(q>0),由2a1,a3,3a2成等差数列,可得2a3=2a1+3a2,即为2a1q2=2a1+3a1q,可得2q2﹣3q﹣2=0,解得q=2(﹣舍去),则a n=a1q n﹣1=2n;(Ⅱ)c n=a n•()=2n•(),由数列{c n}为单调递减数列,可得则c n+1﹣c n=2n+1•(﹣λ)﹣2n•()=2n•(﹣﹣λ)<0对一切n∈N*恒成立,即﹣﹣λ<0,即λ>﹣==,当n=1或2时,n+取得最小值,且为3,则﹣的最大值为=,即有λ>.即λ的取值范围是(,+∞).18.从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.(Ⅰ)求这40件样本该项质量指标的平均数;(Ⅱ)从180(含180)以上的样本中随机抽取2件,记质量指标在[185,190]的件数为X,求X的分布列及数学期望.【考点】离散型随机变量的期望与方差.【分析】(Ⅰ)根据频率分布直方图,计算数据的平均值是各小矩形底边中点与对应的频率乘积的和;(Ⅱ)首先分别求质量指标在[180,185]的件数:0.020×5×40=4,质量指标在[185,190]的件数有:0.010×5×40=2,然后求出X=0、1、2时的概率,进而求出X的分布列及数学期望即可.【解答】解:(Ⅰ)由频率分布直方图可知,这40件样本该项质量指标的平均数=162.5×0.05+167.5×0.125+172.5×0.35+177.5×0.325+182.5×0.1+187.5×0.05=174.75cm;(Ⅱ)由频率分布直方图可知,质量指标在[180,185]的件数:0.020×5×40=4,质量指标在[185,190]的件数有:0.010×5×40=2,∴X的可能值为:0,1,2;P(X=0)==,P(X=1)==,P(X=2)==,数学期望E(X)=0×+1×+2×=.19.如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=,PA=PD=CD=CB=1,E总是线段PB上的动点.(Ⅰ)当E点在什么位置时,CE∥平面PAD?证明你的结论.(Ⅱ)对于(Ⅰ)中的点E,求AE与底面ABCD所成角的正弦值;(Ⅲ)求二面角A﹣PD﹣C的正弦值.【考点】用空间向量求平面间的夹角;平面与平面垂直的性质;二面角的平面角及求法.【分析】(Ⅰ)取PA的中点F,连接DF,EF,由已知结合三角形中位线定理可得四边形DFEC是平行四边形,从而得到CE∥DF.再由线面平行的判定得答案;(Ⅱ)由题意证明OA,OG,OP两两互相垂直,故以OA,OG,OP所在直线分别为x,y,z轴建立如图所示空间直角坐标系Oxyz.求出所用点的坐标,求得的坐标,再求出底面ABCD的一个法向量,则AE与底面ABCD所成角的正弦值可求;(Ⅲ)分别求出平面APD与平面PCD的一个法向量,求出两法向量所成角的余弦值,则二面角A﹣PD﹣C的正弦值可求.【解答】解:(Ⅰ)当E为PB的中点时,CE∥平面PAD.证明如下:取PA的中点F,连接DF,EF,则EF∥,.由已知CD,CD=,则EF∥CD,EF=CD.∴四边形DFEC是平行四边形,∴CE∥DF.又CE⊄平面PAD,DF⊂平面PAD,∴CE∥平面PAD;(Ⅱ)取AD中点O,AB的中点G,连接OP,OG,∵PA=PD,∴PO⊥AD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PO⊥平面ABCD.由已知可得AD2+BD2=AB2,∴BD⊥AD,又OG∥BD,∴OG⊥AD,∴OA,OG,OP两两互相垂直,故以OA,OG,OP所在直线分别为x,y,z轴建立如图所示空间直角坐标系Oxyz.A(),P(0,0,),B(),E(),D(),C(,,0).∴,是平面ABCD的一个法向量,设AE与底面ABCD所成角为θ,则sinθ=|cos|==;(Ⅲ)平面APD的一个法向量为,,=(,,﹣).再设平面PCD的一个法向量为,由,得,取z=1,则x=﹣1,y=﹣1,∴.∴二面角A﹣PD﹣C的余弦值的绝对值为=.∴二面角A﹣PD﹣C的正弦值为.20.已知椭圆C的左、右焦点F1,F2在x轴上,左顶点为A,离心率e=,过原点O的直线(与x轴不重合)与椭圆C交于P,Q两点,直线PA,QA分别与y轴交于M,N两点,△PF1F2的周长为8+4.(Ⅰ)求椭圆C的标准方程;(Ⅱ)求的值;(Ⅲ)求四边形MF1NF2面积的最小值.【考点】直线与圆锥曲线的综合问题.【分析】(Ⅰ)根据e=,2a+2c=8+4,求解即可;(Ⅱ)设P(x0,y0),则Q(﹣x0,﹣y0),求出的坐标,然后求的值即可;(Ⅲ)先把四边形MF1NF2面积表示出来,然后求其最小值即可.【解答】解:(Ⅰ)∵e=,2a+2c=8+4,∴a=4,c=2,∴b=2,故椭圆的方程为:(Ⅱ)设P(x0,y0),则Q(﹣x0,﹣y0),且,即,∵A(﹣4,0),∴直线PA的方程为y=,∴M(0,).同理,直线QA的方程为,∴N(0,),又F 1(﹣2,0),∴,,∴=12+(Ⅲ)|MN |=||=||=||=|,∴四边形MF 1NF 2的面积S==,∵|y 0|∈(0,2],∴当y 0=±2时,S 有最小值8.21.已知函数f (x )=e﹣ax 2(其中e 是自然对数的底数).(Ⅰ)判断函数f (x )的奇偶性;(Ⅱ)若f (x )≤0在定义域内恒成立,求实数a 的取值范围;(Ⅲ)若a=0,当x >0时,求证:对任意的正整数n 都有f ()<n!x ﹣n .【考点】函数恒成立问题. 【分析】(Ⅰ)利用定义判断,先判断定义域关于原点对称,再判断f (﹣x )=f (x );(Ⅱ)不等式可整理为a ≥恒成立,只需求出右式的最大值即可,利用构造函数令g(x )=,求出导函数g'(x )=﹣(2x +1),得出函数的单调性,求出最大值;(Ⅲ)若a=0,f (x )=,得出x n <n!e x ,利用数学归纳法证明不等式对一切n ∈N *都成立即可. 【解答】解:(Ⅰ)函数定义域为(﹣∞,0)∪(0,+∞)关于原点对称, ∵f (﹣x )=f (x ),∴函数f (x )为偶函数;(Ⅱ)由偶函数性质可知,只需求当x ∈(﹣∞,0)时, f (x )=﹣ax 2≤0恒成立,∴a ≥恒成立,令g (x )=,g'(x )=﹣(2x +1),当x ∈(﹣∞,)时,g'(x )>0,g (x )递增,当x ∈(,0)时,g'(x )<0,g (x )递减,∴g(x)的最大值为g(﹣)=4e﹣2,∴a≥4e﹣2,(Ⅲ)若a=0,f(x)=e,当x>0时,f(x)=,f()=e﹣x<n!x﹣n.∴x n<n!e x,(i)当n=1时,设g(x)=e x﹣x,(x>0),∵x>0时,g'(x)=e x﹣1>0,∴g(x)是增函数,故g(x)>g(0)=1>0,即e x>x,(x>0)所以,当n=1时,不等式成立(ii)假设n=k(k∈N*)时,不等式成立,即x k<k!•e x当n=k+1时设h(x)=(k+1)!•e x﹣x k+1,(x>0)有h'(x)=(k+1)!•e x﹣(k+1)x k=(k+1)(k!•e x﹣x k)>0故h(x)=(k+1)!•e x﹣x k+1,(x>0)为增函数,所以,h(x)>h(0)=(k+1)!>0,即x k+1<(k+1)!•e x,这说明当n=k+1时不等式也成立,根据(i)(ii)可知不等式对一切n∈N*都成立,故原不等式对一切n∈N*都成立.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清楚.选修4-1:几何证明选讲22.已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:(Ⅰ)∠CBT=∠CFT;(Ⅱ)CT2=AE•BF.【考点】与圆有关的比例线段.【分析】(Ⅰ)证明B,C,T,F四点共圆,可得∠CBT=∠CFT;(Ⅱ)延长EF与ABM交于P,利用△PBF∽△PTC,△PAE∽△PTC,结合切割线定理,即可证明CT2=AE•BF.【解答】证明:(Ⅰ)∵OT⊥EF,BF⊥AB,∠CTF=∠CBF=90°,∴∠CTF+∠CBF=180°,∴B,C,T,F四点共圆,∴∠CBT=∠CFT;(Ⅱ)延长EF与ABM交于P,则△PBF∽△PTC,∴=①,△PAE∽△PTC,∴=②①×②=由切割线定理可得PT2=PA•PB,∴CT2=AE•BF.选修4-4:坐标系与参数方程23.已知曲线C的参数方程为(θ为参数).(Ⅰ)求曲线C的普通方程;(Ⅱ)若倾斜角为45°的直线l经过点P(1,2)且与直线C相交于点A、B,求线段AB的长度.【考点】参数方程化成普通方程.【分析】(I)用x,y表示出cosθ,sinθ,根据正余弦的平方和等于1消参数得到普通方程;(II)写出直线l的参数方程,代入曲线的普通方程得到关于参数t的一元二次方程,根据参数的几何意义解出AB.【解答】解:(1)∵(θ为参数),∴cosθ=,sinθ=,∴.∴曲线C的普通方程为.(II)直线l的参数方程为(t为参数).将l的参数方程代入得7t2+22t+14=0,设A,B两点对应的参数分别为t1,t2,则t1+t2=﹣,t1t2=2.∴t1,t2符号相同.∴|AB|=|t1﹣t2|===.选修4-5:不等式选讲24.设f(x)=|x+3|﹣a|2x﹣1|(Ⅰ)当a=1时,求f(x)>3的解集;(Ⅱ)若f(x)≥0对x∈[﹣1,1]恒成立,求实数a的取值范围.【考点】函数恒成立问题;绝对值不等式的解法.【分析】(Ⅰ)当a=1时,对x分类讨论,去绝对值,分别求出f(x)>3,得解集为(,1);(Ⅱ)若f(x)≥0对x∈[﹣1,1]恒成立,对x分类讨论:当x=时,a∈R;当x≠时,||≥a对[﹣1,)∪(,1]恒成立,只需求出左式的最小值即可.利用分离常数法得出=+∈(﹣∞,﹣)∪(4,+∞),进而求出最小值.【解答】解:(Ⅰ)当a=1时,当x<﹣3时,f(x)=x﹣4,f(x)>3,∴无解当﹣3≤x≤时,f(x)=3x+2,f(x)>3,∴<x,当x>时,f(x)=4﹣x,f(x)>3,∴x<1,∴解集为(,1);(Ⅱ)若f(x)≥0对x∈[﹣1,1]恒成立,∴|x+3|≥a|2x﹣1|恒成立,当x=时,a∈R,当x≠时,∴||≥a对[﹣1,)∪(,1]恒成立,∵=+∈(﹣∞,﹣)∪(4,+∞),∴||的最小值为,∴a≤.2016年9月14日。
安徽省江淮十校2015届高三11月联考数学理试卷(WORD版)

2015届“江淮十校”十一月联考试卷数学(理)试题本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试用时120分钟.第Ⅰ卷(选择题 共50分)一、选择题:本题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一个选项符合题意.1.命题“对任意x R ∈,总有210x +>”的否定是 ( )A.“对任意,x R ∉总有210x +>” B. “对任意,x R ∈总有210x +≤”C. “存在,x R ∈总有210x +>”D. “存在,x R ∈总有210x +≤”2.已知全集U R =,集合{|A x y ==,集合{|,}x B y y e x R ==∈,则(C )R A B =A.{|2}x x > B.{|01}x x <≤ C.{|12}x x <≤ D.{|0}x x <3.函数1()1,11x f x x x ≤=⎨>⎪-⎩的大致图像是 ()4.已知函数()f x 的定义域为(32,1)a a -+,且(1)f x +为偶函数,则实数a 的值可以是 ( )A.23B.2C.4D.65.若(,),2παπ∈且cos 2sin()4παα=-,则sin 2α的值为 ( ) A.12- B.12C.1D.1-6.已知函数()cos()(A 0,0,R)f x A x ωϕωϕ=+>>∈,则“()f x 是奇函数”是“2πϕ=”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 7.已知1,3,0,O A O B O A O B ==⋅=点C 在AOB∠内,且30A O C ∠=︒设(,),OC mOA nOB m n R =+∈则mn的值为 ( )A.2B.52C.3D.48.定义在R 上的函数()f x 满足:对任意,,R αβ∈总有()[()()]2014f f f αβαβ+-+=,则下列说法正确的是 ( ) A.()1f x +是奇函数 B.()1f x -是奇函数 C.()2014f x +是奇函数 D.()2014f x -是奇函数9.已知定义在(0,)2π上的函数()f x ,'()f x 为其导函数,且()'()tan f x f x x <⋅恒成立,则( )()()43ππ> ()()63f ππ< ()()64f ππ> D.(1)2()sin16f f π<⋅10.设函数()ln f x x =的定义域为(,)M +∞,且0M >,且对任意,,(,),a b c M ∈+∞若,,a b c 是直角三角形的三边长,且(),(),()f a f b f c 也能成为三角形的三边长,则M的最小值为 ( )B. C. D.2第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.函数221()1x f x x -=+的值域时______________.13.函数2()1f x mx x =-+有两个零点分别属于区间(0,2),(2,3),则m 的范围为_____.14.已知正方形A B C D 的边长为2,P是正方形A B C D 的外接圆上的动点,则AB AP ⋅的最大值为_______________.15.对任意两份非零的平面向量α和β,定义,⋅⋅αβαβ=ββ若平面向量a,b 满足0,≥>a b a 与b 的夹角[0,]4πθ∈,且ab 和b a 都在集合{|,n }nm m∈∈Z Z 中,给出下列命题: ①若1,m =则a b =ba =1;②若2m =,则12=a b . ③若3m =,则a b 的取值最多为7个; ④若4m =,则ab 的取值无限多个;其中正确命题序号是_____________(把所有正确命题的序号都填上).三、本大题共6小题,满分75分,解答应写出必要的文字说明、证明过程或演算步骤. 16.(本题满分12分)已知函数()sin()(0,0)2f x x πωϕωϕ=+><≤的部分图像如图所示.(1)求()f x 的解析式;(2)求使不等式'()1f x ≥成立的x 的取值集合,其中'()f x 为()f x 的导函数.17.(本小题满分12分) 已知函数222,0(),0x x x f x ax bx x ⎧-+≥⎪=⎨+<⎪⎩为奇函数.(1)求a b -的值; (2)若函数()f x 在区间[1,2]m --上单调递增,求实数m 的取值范围.18.(本小题满分12分)已知函数1()sin().62f x x π=-+(1)若11[0,],(),210x f x π∈=求cos x 得值;(2)在ABC ∆中,角,,A B C 的对边分别是,,,a b c 且满足2cos 2,b A c ≤求()f B 的取值范围.20.(本小题满分13分) 设二次函数2(),f x x ax b =-+集合{|()}A x f x x ==.(1)若{1,2},A =求函数()f x 的解析式;(2)若2()()2F x f x a a =+--且(1)0,f =且()F x 在[0,1]上单调递增,求实数a 的取值范围.21.(本小题满分13分) 已知函数21()ln ,()3f x x xg x ax bx ==-,其中,a b ∈R .(1)若2()6f x x ax ≥-+-在(0,)+∞上恒成立,求实数a 的取值范围;(2)当23b a =-时,若3(1)()2f xg x +≤对[0,)x ∈+∞恒成立,求a 的最小值.2015届江淮十校11月联考理科数学参考答案一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符二、填空题(本大题共5小题,每小题5分,共25分). 11. (-1,1] 12. 2e . 13. 21,94⎛⎫⎪⎝⎭14. 2+ 15. ① ③三、解答题(本大题共6小题,共75分.解答应写出文字说明.证明过程或演算步骤,并在答题卡的制定区域内答题.) 16. 解:(1)∵T =2×(5π6-π3)=π,∴ω=2ππ=2.又点(π3,0)是f (x )=sin(2x +φ)的一个对称中心,∴2×π3+φ=k π,k ∈Z ,φ=k π-2π3令k =1,得φ=π3.y =sin(2x +π3)(2),,3x k k k Z πππ⎡⎤∈-∈⎢⎥⎣⎦17.(1)令0x <,0x ->()()22[2]2f x f x x x x x =--=---=+. ∴1,2a b ==,∴1a b -=-. (2) ()f x =222,02,0{x x x x x x -≥+<()f x 在[-1,1]上递增, ∴[12][1,1]m --⊆-,,∴2121{m m ->--≤,13m ⇒<≤.1181()sin()62f x x π=-+、解:()11()10f x =,∴3sin()65x π-=;又∵[0,]2x π∈,∴[,]663x πππ-∈-,即4cos()65x π-=3cos cos[()]cos()cos sin()sin 6666661010x x x x ππππππ∴=-+=---=-22bcosA 2c 2sin cos 2sin 2sin cos 2sin()2sin cos 2[sin cos cos sin ]2sin cos cos (0,]6B A c A B A A B AB A A B A B A A B A B B π≤≤⇒≤+⇒≤+⇒≥⇒≥⇒∈()由-得: ∴1sin()(,0]62B π-∈-,即11()sin()()(0,]622f B B f B π=-+⇒∈ 19.解:(1)设B 类型汽车的价值为x 万元,顾客得到的油费为y 万元,则A 类型汽车的价值为(10)x -万元,由题意得,11(10)ln(1)ln(1)11010y x m x m m x =-++=+-+,(19x ≤≤), (2)由1,0110m y y x ''=-=+得得101x m =- ①当1011,00.2m m -≤<≤即时,0,[1,9]y y '≤在是减函数 随B 类型汽车投放金额x 万元的增加,顾客得到的油费逐渐减少。
安徽省“江淮十校”2015届高三4月联考数学(理)试题 含解析

一、选择题:(共50分)1.在复平面内,复数21i i+-(i 是虚数单位)对应的点位于( )A.第一象限 B 。
第二象限 C 。
第三象限 D 。
第四象限 【答案】A 【解析】试题分析:2(2)(1)221131(1)(1)1122i i i i i i ii i +++++-===+--++,对应的点13(,)22,在第一象限,选A 。
考点:复数的运算,复数的几何意义。
2.集合A={0,2,a },B={a 2},若A ∪B=A ,则a 的值有 ( ) A 。
1个 B. 2个 C. 3个 D 。
4个 【答案】C考点:集合的概念,集合的运算与子集的概念。
3。
8(3)x y -的展开式中x 6y 2项的系数是 ( )A 。
28 B. 84 C 。
—28 D 。
—84 【答案】B考点:二项式定理。
4。
已知α、β表示两个不同的平面,m 为平面内的一条直线,则“α//β”是“m//β”的 ( )A 。
充分不必要条件B 。
必要不充分条件 C. 充要条件 D. 既不充分也不充要条件【答案】A 【解析】试题分析:由面面平行的性质定理知////m αββ⇒,但当//m β时,α与β也可能相交,故应选A 。
考点:面面平行与线面平行,充分必要条件. 5.圆x 2+y 2=40y +-=截得的弦长为( )A。
B。
C 。
3 D 。
2【答案】D 【解析】试题分析:圆心为(0,0)O ,半径为2r =0y +-=的距离为d ==2l ===.考点:直线和圆相交弦长问题。
.6。
一个几何体的三视图如图所示,则该几何体的体积为 ( )A.43πB.23π C。
23π+D.23π+【答案】B 【解析】试题分析:该几何体是一个组合体,下面是半球,上面是正四棱锥,且正四棱锥的底面是半球大圆的内接正方形,2212223(2)313333V ππ=⨯⨯+⨯=+. 考点:三视图与几何体的体积。
7。
在等差数列{a n }中a 1=—2015,其前n 项和为S n ,若2S 6—3S 4=24,则S 2015= ( )A 。
安徽省江淮名校2015届高三第三次联考数学(理)试题 扫描版含答案

数学(理科)试卷满分:150分 考试时间:120分钟第Ⅰ卷(选择题 满分50分)一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.选A解析:{|2},{|13},{|31}{|1}R R A x x B x x C B x x A C B x x =<=<<=≥≤=≤或,,2.C3.D4.选C解析:22(1,0)3)2,3)O C O A O B λλλλ=-+=-+=,即()C λ-,又120AOC ∠=所以3tan120=1λ= , 5.D6.A 解析:由41a a <得31q >即1q >,由53a a <得21q >即1q >或1q <-7.B解析:211334214322144C C C C A A ∙∙= 8.选D解析:03(1)3(1)ay a y z x x -==∙+--表示阴影部分内的点P 到点(A 连线斜率的3a 倍,由图可知连线斜率恒大于或等于0,故当P 为(0,1)时z 的最大值为18,所以10130(1)8a -=--得38a =, 9.D 解析:作出()y f x =的图像如下所示,则()()F x f x a =-的零点即为函数()y f x =与y a =图像交点的横坐标,由图可知共有五个零点,不妨设为12345,,,,x x x x x 且12345x x x x x <<<<,从图中可看出1x 与2x 关于直线3x =-对称,4x 与5x 关于直线3x =对称,故12452(3)230x x x x +++=⨯-+⨯=,当(1,0)x ∈-时12()log (1)f x x =--+,因此由12log (1)x a --+=解得312a x =-,故1234512a x x x x x ++++=-10.选B . 由()cos sin 0f x x x x '=-=得cos sin 0x x x -=,显然cos 0x ≠所以1tan x x=,易知方程1tan x x =的实根就是()f x 的极值点。
2015届江淮十校8月联考数学(理科)试卷及参考答案(扫描版)

2015届江淮十校8月联考数学(理科)答案第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.1. D2.A3. D4. B5. C6. B7. A8. B9. B 10. C.第II 卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分 11. 4π 12. 516 13. 2 14. 1,2⎛⎫+∞ ⎪⎝⎭15. ②③④⑤三、解答题:本大题共6小题,计75分.解答应写出必要的文字说明,证明过程或演算步骤16. (I )由三角函数定义知, 34cos ,sin .55αα== ………………………(2分),3COB πα∠=+cos()cos cos sin sin 333πππααα∴+=-= ………(5分)所以点B . ………………………(6分) (II )222cos()3BC πα=-+, ………………………(9分)02πα<<Q ,5336πππα∴<+<, 1cos()()32πα∴+∈,2(1,2BC ∴∈+,BC ⎛∴∈ ⎝⎭. …………………(12分) 17.(本小题12分)(Ⅰ)由图象可知第五组为:0.02530030⨯⨯=人,第 五组、第一组、第四组、第二组、第三组的人数以次是一个以30分为首项,总和为300的等差数列,所以第五组、第一组、第四组、第二组、第三组的人数以次是30人,45人,60人,75人,90人.则绘制的频率分布直方图如右图所示.………….6分(Ⅱ)第四组中抽取人数:660490⨯=人,第五组中抽取人数:630290⨯=人,所以两组共6人.设第四组抽取的四人为1234,,,A A A A ,第五组抽取的2人为12,B B ,这六人分成两组有两种情况,情况一:12,B B 在同一小组:123412(,,),(,,)A A A A B B ;124312(,,),(,,)A A A A B B ;134212(,,),(,,)A A A A B B ;234112(,,),(,,)A A A A B B ,共有4种可能结果,情况二:12,B B 不在同一小组:112234(,,),(,,)B A A B A A ;113224(,,),(,,)B A A B A A ;114223(,,),(,,)B A A B A A ;123214(,,),(,,)B A A B A A ;124213(,,),(,,)B A A B A A ;134212(,,),(,,)B A A B A A ,共有6种可能结果,两种情况总共10种可能结果,所以两人被分在一组的概率为42105=. ….12分 另解:两人被分在一组的概率为1433632225C P C C A ==.(此法亦可相应给分) 18.(本小题12分)(Ⅰ)证明:Q 矩形ABCD ⊥面ABE , CB ⊂面ABCD且CB ⊥AB∴CB ⊥面ABE ,从而AE ⊥BC ①………3.分又Q 在半圆ABE 中,AB 为直径,∴90AEB ∠=o即AE ⊥BE ②由①②知:AE ⊥面BCE ,故有:EA EC ⊥, …………………….…6分(Ⅱ) Q AB//CD, ∴ AB//面DCE.又Q 面DCE I 面ABE=EF,∴AB//EF在等腰梯形ABEF 中,EF=1,AF=1,120AFE ∠=o ,………………….…9分∴1sin1202S EF AF =⨯⨯⨯=o ,11133E ADF D AEF AEF AD V V S --∆==⨯⨯==. …………………12分 19.(本小题12分)解:(Ⅰ)由1123(2)n n n a a a n +-=-≥得112()(2)n n n n a a a a n +--=-≥,则1{}n n a a +-是以211a a -=为首项,以12为公比的等比数列 .........4分 (Ⅱ)由(Ⅰ)知:211()2n n n a a ---=,累加可得214()2n n a -=-................8分则123n n a m a m +-<-即为:2114()22134()2n n m m ----<--,显然4m ≥时无解,则易求得123,,11 2.m m m n n n ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩.................................12分 注:若由123n n a m a m +-<-得到()()132n n a m a m +-<-即1n m a ->亦即3142n m -⎛⎫>- ⎪⎝⎭,从而得出结果*4312,,1112m m m m n n n n N ≥===⎧⎧⎧⎧⎨⎨⎨⎨===∈⎩⎩⎩⎩,或可酌情给分.20. (本小题13分)解:(I ) 直线AM 的方程为:(1)(0,1)y m x m =+≠±与圆22:1O x y += 联立得22212(,)11m m M m m-++…………………………………………………….3分 由22212(0,1),(,),(,0)11m m C M N x m m-++三点共线,得出1(,0)1m N m +-…....…6分 (Ⅱ).将直线BC 的直线方程1x y +=与(1)(0,1)y m x m =+≠± 联立得12(,)11m m P m m-++…………………………………………………………...8分 故有22202(1)1111(1)(1)211PN m m m m m n k m m m m m m---+====-+--+-+-………………….11分 即:21m n -=……………………………………………………………….13分21. (本小题14分)解: (Ⅰ)∵,αβ是方程210x mx --=的两个根, ∴,1m αβαβ+==-,∴2222()1()1()m f αααβαβααααβααβα--+-====+-- , ∴()1f αα=……………………………………………………… (4分)(Ⅱ)∵222222(1)2()()()(1)(1)x mx x x f x x x αβ----'=-=-++, 当(,)x αβ∈时,()0f x '>,∴()f x 在(,)αβ上单调递增.(此处用定义证明亦可)…(8分)(Ⅲ)∵()0λαμβμβααλμλμ+--=>++,同理可证:λαμβαβλμ+<<+ ∴由(Ⅱ)可知:()()()f f f λαμβαβλμ+<<+,()()()f f f μαλβαβλμ+<<+, ∴|()()||()()|f f f f λαμβμαλβαβλμλμ++-<-++, ……………………(12分) 由(Ⅰ)可知,1()f αα=,1()f ββ=,1αβ=-, ∴11|()()|||||||f f βααβαβαβαβ--=-==-, ∴|()()|||f f λαμβμαλβαβλμλμ++-<-++.……………………………………(14分)。
2015年安徽省“江南十校”高三联考数学(理科)第21题第(Ⅱ)问另解

2 2 Sn 1 S n 2 2
S n1 1 n 1 (n 1) 2
S 1 2 S2 S12 2 2 2 2 2
2 将上面子累加得, S n 1 2(
S S 2 S3 1 1 1 n ) ( 2 2 2 ) 2 3 n 2 3 n 1 1 1 1 n 1 n n
(3n 3)an 4n 6 (n N * ) . n
3n 1 ,数列 {bn } 的前 n 项和为 S n . an 2 4 (ⅰ)证明: bn 1 bn 2 b2 n ; 5 S S S 2 (ⅱ)证明:当 n 2 时, Sn 2( 2 3 n ) 2 3 n
又
1 1 1 1 1 1 1 1 1 1 2 2 = 2 2 3 n 1 2 2 3 (n 1) n 1 2 2 3
2 1 2( Sn
S S 2 S3 1 n ) (1 ) 2 3 n n S S S S S 1 S 2 即 Sn 2( 2 3 n ) 2( 2 3 n ) 2 3 n n 2 3 n
an 2 3n 1 , an n 3n 1 2 n n
第(Ⅱ)问另解: (Ⅱ)由(Ⅰ)得,
bn
3n 1 1 an 2 n
1 1 1 4 n 1 n 2 2n 5
另解 1 (ⅰ)原不等式即为:
易知 ln x x 1( x 0, x 1) ,所以 ln( x 1) x( x 1, x 0) ,
令x 下同另解 1.
1
★阮飞数学教学资料★
(ⅱ)由此可得, S n 1
1 1 1 2 3 n 1 1 另解 当 n 2 时, Sn Sn 1 ,所以 n 2, Sn Sn1 ,两边平方得: n n S Sn 1 1 2 2 2 2 Sn 2 n 2 Sn 1 ,所以 Sn Sn 1 2 n n n n2
