梁的内力计算
主梁内力计算

主梁的内力计算主梁的内力计算包括恒载内力计算和活载内力计算。
根据上述梁跨结构纵、横截面的布置,计算活载作用下的梁桥荷载横向分布系数,求出各主梁控制截面(取跨中、四分点、变化点截面及支点截面)的恒载和最大活载内力,然后再进行主梁内力组合。
一、恒载内力计算1、恒载集度⑴预制梁自重(第一期恒载)①.跨中截面段主梁自重(四分点截面至跨中截面,长7.25m )(1)0.861625.07.25156.165g KN =⨯⨯=②.马蹄抬高与腹板变宽段梁的自重近似计算(长3.7m ) 主梁端部截面面积为A=1.176m 2()(2) 1.17600.8616 3.725.0/294.239g KN =+⨯⨯=③.支点段梁的自重(长3.55m )(3) 1.1760 3.5525.0=104.37g KN =⨯⨯④.横隔梁的自重 中横隔梁体积为:()30.16 1.590.920.240.72/20.120.12/20.219072m ⨯⨯-⨯-⨯= 端横隔梁体积为:()30.25 1.840.80.20.6/20.353m ⨯⨯-⨯=故半跨内横隔梁重量()(4)20.21907210.3532519.7786g KN =⨯+⨯⨯=⑤.主梁永久作用集度()156.16594.239104.3719.7786/14.9825.00/g KN m KN m I =+++= (2)第二期恒载①翼缘板中间湿接缝集度()50.40.1625.0 1.6/g KN m =⨯⨯=②现浇部分横隔梁一片中横隔梁(现浇部分)体积:30.16 1.590.20.05088m ⨯⨯= 一片端横隔梁(现浇部分)体积:30.250.2 1.840.092m ⨯⨯= 故()()630.0508820.09225.0/29.960.2809/g KN m =⨯+⨯⨯=③桥面铺装层6cm 沥青混凝土铺装:0.0612.52317.25/KN m ⨯⨯=将桥面铺装重量均分给五片主梁,则()717.25/5 3.45/g KN m ==④防撞栏:两侧防撞栏均分给五片主梁,则()87.52/53/g KN m =⨯=⑤主梁二期永久作用集度II 1.60.2809 3.4538.3309/g KN m =+++=2、永久作用效用:下面进行永久作用效用计算(参照图1-4),设c 为计算截面至左侧支座的距离,并令/a c l =。
第六章 主梁内力计算

3 3
步骤: 1 、恒载集度(均布荷载) 2 、恒载内力(材料力学方法)
想一想: 中梁与边梁的恒载计算有何区别?
二、活载内力计算 1 .计算方法 主梁活载内力计算分两步 ① 求横向分布系数 m ② 应用主梁内力影响线,将荷载乘 m 后,在纵向 按最不利位置布载,求得主梁最大活载内力。 活载内力计算一般方法 —— 采用车道荷载
第二节 横隔梁内力计算
横梁的作用与受力特点
作用: 加强结构的横向联系 保证全结构的整体性
受力特点: 受力接近于弹性地基梁 影响面的正负纵向位置基本一致 影响面值从跨中向端部逐渐减小
一、刚性横梁法计算横隔梁内力
1、计算图式
2、横梁内力影响线
3、作用在横梁上的计算荷载 按杠杆原理在两根横梁间分布
结构重力弯矩
3)考虑有效工作宽度后的支点剪力 车轮布置在支承附近
注意:汽车荷载采用车辆荷载计算
2、悬臂板的内力 1)计算模式假定
铰接悬臂板——车轮作用在铰缝上 悬臂板——车轮作用在悬臂端
2)铰接悬臂板
汽车荷载
结构重力
2)悬臂板
汽车荷载
结构重力
第四节 结构挠度与预拱度计算
一、钢筋混凝土梁桥 计算公式——一般简支梁挠度计算公式 刚度取值——0.85EhI0 活载挠度计算时不计冲击系数(静活载) 二、预应力混凝土梁桥 刚度取值——0.85EhIh 必须考虑预应力产生的挠度
按承载能力极限状态设计效应组合 按正常使用极限状态设计效应组合
当按承载能力极限状态设计时:
0 S ud 0 ( Gi S Gik Q1 S Q1k c Qj S Qjk )
i 1 j 1
m
n
2、内力包络图
主梁内力计算

二、 主梁内力计算[1][2][3][4][5]1.恒载集度(1)主梁:10.080.14[0.20 1.5()(2.00.2)]2512.45/2g KN m +=⨯+⨯-⨯= (2)横隔梁 对于边主梁:20.080.1420.20.150.16[(1.3)()525]/21.50.965/222g KN m +-+⎛⎫=-⨯⨯⨯⨯= ⎪⎝⎭对于中主梁:'220.965 1.93/g KN m =⨯=(3)桥面铺装层:30.05 2.1210.08 2.123 6.069/g KN m =⨯⨯+⨯⨯=(4)栏杆和人行道:4 4.52/5 1.8/g KN m =⨯= 作用于边主梁的全部恒载强度:12.450.965 6.069 1.821.284/i g g KN m ==+++=∑作用于中主梁的全部恒载强度:12.03 2.27 6.069 1.822.245/i g g KN m ==+++=∑2.恒载内力的计算边跨弯矩剪力影响线1#及5#梁内力(边跨)跨中弯矩 21121.521.521.2841115.4152424l l M l g KN m =⨯⋅⨯=⨯⨯⨯=⋅ 跨中剪力 20l V =支点剪力 01121.521.284228.2032Q KN =⨯⨯⨯= 1/4跨处弯矩: 131321.521.521.284922.362216216M l l g KN m =⨯⨯⨯=⨯⨯⨯⨯=⋅ 1/4跨处剪力:/4131121.50.7521.28421.50.2521.284114.4022424l Q KN =⨯⨯⨯⨯-⨯⨯⨯⨯=2#、3#及4#梁内力(中间跨) 跨中弯矩 2121.50.521.522.2451285.344244l l M l g KN m =⨯⨯⨯=⨯⨯⨯= 跨中剪力 20l V =支点剪力 01121.522.245239.1342Q KN =⨯⨯⨯= 1/4跨处弯矩: '131321.521.522.245964.008216216M l l g KN m =⨯⨯⨯=⨯⨯⨯⨯=⋅ 1/4跨处剪力:/4131121.50.7520.38521.50.2522.245119.5672424l Q KN =⨯⨯⨯⨯-⨯⨯⨯⨯=3.活载内力1 . 汽车荷载冲击系数主梁横截面图结构跨中处的单位长度量:321.284102169.623/9.81c G m kg m g ⨯===主梁截面形心到T 梁上缘的距离:(11*(200-20)*(11/2)+(150*20)*(150*(1/2)47.40.47411*(200-20)+150*20y cm m ===跨中截面惯性矩:323274*********(20020)11(20020)11(47.4)2015020150(47.4)1221221.14100.11410c I cm m =⨯-⨯+-⨯⨯-+⨯⨯+⨯⨯-=⨯=⨯查表 E 取102.810a p ⨯10223.142.8100.1144.122221.52169.623c c EI f Hz l m π⨯⨯===⨯1.514Hz f Hz ≤≤0.1767ln 0.01570.1767ln 4.120.01570.234f μ=-=⨯-= 所以冲击系数:110.234 1.234μ+=+=2. 汽车荷载作用公路—Ⅰ级均布荷载 10.5/k q KN m =对于集中荷载,当5l ≤时,180/k P KN m =;当50l ≥时,360/k P KN m = 当550l <<时,采用内插法 公路—Ⅱ为公路—Ⅰ级的0.75倍 则0.7510.57.875/k q KN m =⨯= ()21.550.75180360180184.5505k P KN -⎡⎤=⨯+⨯-=⎢⎥-⎣⎦当计算剪力时候 184.5 1.2221.4k PKN =⨯= 计算车道荷载的跨中弯矩、剪力的计算对于双车道,折减系数 1.0ξ= 跨中弯矩影响线如下图3. 跨中弯矩的设计,21121.521.557.782424l l m Ω=⨯⨯=⨯⨯=由于跨中弯矩横向分布系数1#、5#梁最大,所以只需计算1#、5#梁的弯矩,计算如下: 对于1#梁车道均布荷载作用下(1)1,2Mm q cq l kq kμξ=+Ω1.23410.667.87557.78370.584KN m =⨯⨯⨯⨯=⋅ 车道集中荷载作用下1,2(1)kcq lk k P M m P y μξ=+21.51.23410.66184.5807.6704KN m =⨯⨯⨯⨯=⋅ 则,,222370.584807.6701178.254kkl llq P M M M KN m =+=+=⋅跨中人群荷载最大弯矩人群荷载集度313or P KN =⨯=1,20.675357.78117.004l cr or rM m P KN m =Ω=⨯⨯=⋅对于2#和4#梁计算公路—Ⅱ级汽车活载的跨中弯矩:121,22(1)(1)k k Q k cq cq MmP y m q kμξμξ+=++Ω21.51.23410.53184.5 1.23410.537.87557.78946.1744KN m =⨯⨯⨯⨯+⨯⨯⨯⨯=⋅ 计算人群荷载的跨中弯矩:人群荷载集度: 313or P KN =⨯=122,20.4375357.7875.836cr or Q k Mm P KN m =Ω=⨯⨯=⋅对于3#梁计算公路—Ⅱ级汽车活载的跨中弯矩:12,233(1)(1)Q k k k cq cq MmP y mq kμξμξ+=++Ω21.51.23410.4184.5 1.23410.47.87557.78714.0944KN m =⨯⨯⨯⨯+⨯⨯⨯⨯=⋅ 计算人群荷载的跨中弯矩:人群荷载集度: 313or P KN =⨯=132,20.4357.7869.336cr or Q k Mm P KN m =Ω=⨯⨯=⋅4. 跨中剪力的计算 跨中剪力影响线如下图:21121.51 2.687522222l m Ω=⨯=⨯⨯=对于1#和5#梁计算公路—Ⅱ级汽车活载的跨中剪力:1,011(1)(1)1.23410.66221.40.5 1.23410.667.875 2.6875107.395Q k cq k k cq k Q m P y m q KNμξμξ=+++Ω=⨯⨯⨯⨯+⨯⨯⨯⨯=计算人群荷载的跨中剪力:12,20.6753 2.6875 5.442lcr or Q k Qm P KN =Ω=⨯⨯=对于2#和4#梁计算公路—Ⅱ级汽车活载的跨中剪力:1,022(1)(1)1.23410.53221.40.5 1.23410.537.875 2.687586.242Q k cq k k cq k Q m P y m q KNμξμξ=+++Ω=⨯⨯⨯⨯+⨯⨯⨯⨯=计算人群荷载的跨中剪力:22,20.43753 2.6875 3.528l cr or Q k Qm P KN =Ω=⨯⨯=对于3#梁计算公路—Ⅱ级汽车活载的跨中剪力:1,033(1)(1)1.23410.4221.40.5 1.23410.47.875 2.687565.088Q k cq k k cq k Q m P y m q KNμξμξ=+++Ω=⨯⨯⨯⨯+⨯⨯⨯⨯=计算人群荷载的跨中剪力:32,20.43 2.6875 3.225l cr or Q k Qm P KN =Ω=⨯⨯=5. 支点截面剪力的计算 剪力影响线如下图所示:211121.510.7522l m Ω=⨯⨯=⨯=横向分布系数变化区段的长度21.55.35 5.42a m =-= 对于1#和5#梁附加三角形重心影响线坐标 : 1121.5 5.4/21.50.9163y ⎛⎫=⨯-⨯= ⎪⎝⎭0.083y '=()11111,0(1) 5.41.23410.66221.41 1.23410.667.87510.75 1.2341(0.43750.66)7.875(0.9160.083)2244.376(1)(1)2cq k cq oq cq Q k k k k m q KNaQ m P y m m q yμξμξμξ++Ω+=⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯-⨯⨯+==++- 计算人群荷载的支点剪力:()1112,02or or cr or cr Q k aQ m P m m P y =⋅⋅Ω+⋅-⋅⋅()5.40.675310.75 1.3750.6753(0.9160.083)27.4392KN =⨯⨯+⨯-⨯⨯+= 对于2#和4#梁计算公路—Ⅱ级汽车活载的支点剪力(如下图所示):()22221,0(1) 5.41.2341.53221.41 1.23410.537.87510.75 1.2341(0.71250.53)7.875(0.9160.083)2204.951(1)(1)2cq k cq oq cq Q k k k k m q KNaQ m P y m m q yμξμξμξ++Ω+=⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯-⨯⨯+==++- 计算人群荷载的支点剪力: ()2222,02or or cr or cr Q k aQ m P m m P y =⋅⋅Ω+⋅-⋅⋅()5.40.4375310.7500.43753(0.9160.083)10.5652KN =⨯⨯+⨯-⨯⨯+= 对于3#梁计算公路—Ⅰ级汽车活载的支点剪力(如下图所示):()33331,0(1) 5.41.23410.4221.41 1.23410.47.87510.75 1.2341(0.7250.4)7.875(0.9160.083)2159.588(1)(1)2cq k oq oq cq Q k k k k m q KNa Q m P y m m q yμξμξμξ++Ω+=⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯-⨯⨯+==++- 计算人群荷载的支点剪力:()3332,02or or cr or cr Q k aQ m P m m P y =⋅⋅Ω+⋅-⋅⋅()5.40.4310.7500.43(0.9160.083)9.9322KN =⨯⨯+⨯-⨯⨯+= 6. 1/4跨弯矩的计算 1/4跨弯矩的影响线如下图2131321.521.543.336216216l l m ⨯Ω=⨯⨯=⨯⨯=对于1#和5#梁计算公路—Ⅰ级汽车活载的1/4跨弯矩:141,11(1)(1)k k Q k cq cq MmP y mq kμξμξ+=++Ω1.23410.66184.5 4.031 1.3410.667.87543.336883.660KN m =⨯⨯⨯⨯+⨯⨯⨯⨯=⋅计算人群荷载的跨中弯矩:人群荷载集度: 313or P KN =⨯=112,40.675343.33687.756cr or Q k Mm P KN m =Ω=⨯⨯=⋅对于2#和4#梁计算公路—Ⅰ级汽车活载的1/4跨弯矩: 141,22(1)(1)k k Q k cq cq MmP y mq kμξμξ+=++Ω1.23410.53184.5 4.031 1.23410.537.87543.336709.605KN m =⨯⨯⨯⨯+⨯⨯⨯⨯=⋅ 计算人群荷载的跨中弯矩:人群荷载集度: 313or P KN =⨯= 122,40.4375343.33656.879cr or Q k M m P KN m =Ω=⨯⨯=⋅对于3#梁计算公路—Ⅰ级汽车活载的1/4跨弯矩:141,33(1)(1)k k Q k cq cq MmP y mq kμξμξ+=++Ω1.23410.4184.5 4.031 1.23410.47.87543.336535.551KN m =⨯⨯⨯⨯+⨯⨯⨯⨯=⋅计算人群荷载的跨中弯矩:人群荷载集度: 313or P KN =⨯= 122,40.4343.33652.003cr or Q k M m P KN m =Ω=⨯⨯=⋅7. 1/4跨剪力的计算 1/4跨剪力影响线如下图:公路-II级Q1/4影响线人群荷载Q1/4影响线187.5KN10.5.5KN/m3KN/m2131321.50.750.75 6.0472422l m ⨯Ω=⨯⨯=⨯⨯=对于1#和5#梁 计算公路—Ⅰ级汽车活载的1/4跨剪力:1,011(1)(1)1.23410.66221.40.75 1.23410.667.875 6.047174.021Q k cq k k cq k Q m P y m q KNμξμξ=+++Ω=⨯⨯⨯⨯+⨯⨯⨯⨯=计算人群荷载的跨中剪力:12,20.6753 6.04712.245lcr or Q k Q m P KN =Ω=⨯⨯=对于2#和4#梁计算公路—Ⅰ级汽车活载的1/4跨剪力:1,022(1)(1)1.23410.53221.40.75 1.23410.537.875 6.047139.745Q k cq k k cq k Q m P y m q KNμξμξ=+++Ω=⨯⨯⨯⨯+⨯⨯⨯⨯=计算人群荷载的跨中剪力:22,20.43753 6.0477.933l cr or Q k Q m P KN =Ω=⨯⨯=对于3#梁计算公路—Ⅰ级汽车活载的跨中剪力:1,033(1)(1)1.23410.4221.40.75 1.23410.47.875 6.047105.468Q k cq k k cq k Q m P y m q KNμξμξ=+++Ω=⨯⨯⨯⨯+⨯⨯⨯⨯=计算人群荷载的跨中剪力:32,20.43 6.0477.253l cr or Q k Q m P KN =Ω=⨯⨯=8. 荷载组合1112()nno ud o Gi Gik Q q k c Qj QJK i j r s r r s r s r s φ===++∑∑其中 1.2Gir =,1 1.4Q r =, 1.4Qj r =, 1.0o r =,0.8c φ=跨中弯矩组合:梁# 恒载(KN/m )活载(KN/m )组合值(KN/m )汽车人群 1、5 1229.816 1178.254 117.004 3256.379 2、4 1285.344 946.174 75.836 2951.993 31285.344707.15069.6332610.412 跨中剪力组合:梁# 恒载(KN/m )活载(KN/m )组合值(KN/m )汽车人群 1、5 0 107.395 5.442 156.448 2、4 0 86.242 3.528 124.6902 365.0883.22594.7352 支点剪力组合:梁# 恒载(KN/m )活载(KN/m )组合值(KN/m )汽车人群 1、5 228.203 244.376 27.439 646.7017 2、4 239.134 204.951 10.565 585.725 3239.134159.5889.932521.5078 1/4跨弯矩组合:梁# 恒载(KN/m )活载(KN/m )组合值(KN/m )汽车人群 1、5 922.362 883.660 87.756 2442.245 2、4 964.008 709.605 56.879 2213.961 3964.008535.55152.0021964.823 1/4跨剪力组合:梁# 恒载(KN/m )活载(KN/m )组合值(KN/m )汽车人群 1、5 114.402 174.21 12.245 394.8908 2、4 119.567 139.754 7.933 348.021 3119.567105.4687.253299.259。
主梁内力计算

主梁的内力计算主梁的内力计算包括恒载内力计算和活载内力计算。
根据上述梁跨结构纵、横截面的布置,计算活载作用下的梁桥荷载横向分布系数,求出各主梁控制截面(取跨中、四分点、变化点截面及支点截面)的恒载和最大活载内力,然后再进行主梁内力组合。
一、恒载内力计算1、恒载集度⑴预制梁自重(第一期恒载)①.跨中截面段主梁自重(四分点截面至跨中截面,长7.25m )(1)0.861625.07.25156.165g KN =⨯⨯=②.马蹄抬高与腹板变宽段梁的自重近似计算(长3.7m ) 主梁端部截面面积为A=1.176m 2()(2) 1.17600.8616 3.725.0/294.239g KN =+⨯⨯=③.支点段梁的自重(长3.55m )(3) 1.1760 3.5525.0=104.37g KN =⨯⨯④.横隔梁的自重 中横隔梁体积为:()30.16 1.590.920.240.72/20.120.12/20.219072m ⨯⨯-⨯-⨯= 端横隔梁体积为:()30.25 1.840.80.20.6/20.353m ⨯⨯-⨯=故半跨内横隔梁重量()(4)20.21907210.3532519.7786g KN =⨯+⨯⨯=⑤.主梁永久作用集度()156.16594.239104.3719.7786/14.9825.00/g KN m KN m I =+++= (2)第二期恒载①翼缘板中间湿接缝集度()50.40.1625.0 1.6/g KN m =⨯⨯=②现浇部分横隔梁一片中横隔梁(现浇部分)体积:30.16 1.590.20.05088m ⨯⨯= 一片端横隔梁(现浇部分)体积:30.250.2 1.840.092m ⨯⨯= 故()()630.0508820.09225.0/29.960.2809/g KN m =⨯+⨯⨯=③桥面铺装层6cm 沥青混凝土铺装:0.0612.52317.25/KN m ⨯⨯=将桥面铺装重量均分给五片主梁,则()717.25/5 3.45/g KN m ==④防撞栏:两侧防撞栏均分给五片主梁,则()87.52/53/g KN m =⨯=⑤主梁二期永久作用集度II 1.60.2809 3.4538.3309/g KN m =+++=2、永久作用效用:下面进行永久作用效用计算(参照图1-4),设c 为计算截面至左侧支座的距离,并令/a c l =。
单跨静定梁的内力计算

单跨静定梁的内力计算单跨静定梁的内力计算是结构工程中重要的计算内容之一。
静定梁是指在受力状态下,其内力可以通过静力学原理直接计算得出的梁结构。
而单跨静定梁是指只有一个支座的静定梁,是静力学中最简单的结构之一。
在计算单跨静定梁的内力时,首先需要明确梁的受力情况。
在单跨静定梁中,通常会受到集中力、均布载荷或者集中力和均布载荷的组合作用。
根据力的平衡条件和梁的几何特性,可以计算出梁的内力,包括弯矩和剪力。
在计算单跨静定梁的内力时,可以采用梁的截面法。
根据力的平衡条件,可以先计算出支座的水平力和垂直力,然后通过力和力矩的平衡条件计算出梁的内力。
在计算弯矩和剪力时,需要根据梁的几何形状和受力情况,采用力的平衡和力矩平衡的原理进行计算。
在计算单跨静定梁的内力时,需要注意以下几点:1. 确定梁的受力情况:包括集中力、均布载荷的大小和作用位置等。
2. 绘制梁的受力图:根据受力情况,绘制出梁的受力图,明确受力的方向和大小。
3. 采用力的平衡和力矩平衡的原理计算内力:根据力的平衡和力矩平衡的原理,计算出梁的内力,包括弯矩和剪力。
4. 考虑梁的内力图:根据计算出的内力,绘制出梁的内力图,明确各处的内力分布情况。
通过以上步骤,可以准确计算出单跨静定梁的内力,为梁的设计和施工提供重要的参考依据。
在实际工程中,计算出的内力可以用来确定梁的截面尺寸和材料的选择,确保梁的受力性能符合设计要求,保证梁的安全性和稳定性。
同时,计算出的内力也可以用来指导梁的施工和监测,确保梁的受力状态符合设计要求,提高梁的使用性能和寿命。
总的来说,单跨静定梁的内力计算是结构工程中的基础计算内容,通过合理的计算方法和步骤,可以准确计算出梁的内力,为梁的设计和施工提供重要的参考依据,确保梁的受力性能符合设计要求,提高梁的使用性能和寿命。
希望以上内容能够对您的工作和学习有所帮助。
有限元分析梁单元内力计算
1.385 0 3.462 1.385 0 3.462 0 0 0
0 252 0 0 252 0 0 0 0
3.462 0 11.541 3.462 0 5.711 0 0 0
K
103
1.385 0
0 252
3.462 0
253.385 0 0 253.385
3.462 3.462
py3 m3
px3
6.25
5.208
py3 m3
6. 引入约束条件, 构成总体方程
2 px1 p y1
2.5 m1 3
4.25
1.385
0
3.462
103
1.385 0
0 252 0 0 252
3.462 0
11.541 3.462
0
1.385 0
0
0 1.385 3.462 0 1.385 3.462
[
K112
]
[
K
2 23
]
103
0 252
3.462 0
11.542 0
0 252
3.462 0
5.771 0
0 1.385 3.462 0 1.385 3.462
0 3.462 5.771 0 3.462 11.542
3. 单元刚度矩阵的座标变换
求:每根梁的内力。
P2 1kN P1 4kN
2.5m
解:
1.建座标系,对梁单元各节点编号 如图所示。
2.5m
2单元,三节点系统(即自然划分。也可以在集中 力作用处设一节点)。由于每一节点有3个自由度 ,故系统有9个自由度。总刚度矩阵[K]为9×9阶
y 2
5m
②3
梁的内力

MA=0
MC=FA×2=30×2kN·m=60kN·m
CD段:没有均布荷载作用,弯矩图是一条斜直线,需确定MC和MD左 MD左=FA×4-F×2=(30×4-20×2)kN·m=80kN·m
D截面:有逆时针方向的集中力偶M作用,弯矩图向上突变M=40kN·m
MD右=MD左-M=(80-40)kN·m=40kN·m
截面上必有弯矩M,且M=FAC。当左段梁若平衡,横截面 上必有两个内力分量:平行于横截面的竖向内力Fs以及位 于荷载作用面的内力偶M。内力Fs称梁横截面内的剪力, 而内力偶M称为梁横截面内的弯矩。
Fs
C
A
M
FA
x
若以右段梁为研究对象,由作用力与反作用力定律可知,
右段梁横截面上的内力值仍为Fs和M,指向与左段梁横截面
MBF0
F 6 M q 4 2 F A 8 0
解之得:
FA 30kN FB 30kN
(2)画剪力图
从左向右作图,全梁分为A端、AC段、C端、CD段、DB段和B端。
31
FA=30kN AC段:没有均布荷载作用,剪力图为一条水平线:FC左=FA右=30kN C端:有向下的集中力F作用,剪力图向下突变F=20kN
Mx=FA x-qx2/2= 81/32qa2
BC段:没有均布荷载作用,弯矩图是一条斜直线,需确定MB和MC。
MC 0
29
剪力图与弯矩图
30
[例] 如图所示,试画出该梁的剪力图和弯矩图。
F=20kN M=40kN
FA
FB
解:(1)计算支座反力 以整梁为研究对象,由平衡方程得:
MAF0
F B 8 M F 2 q 4 6 0
M144 kNm
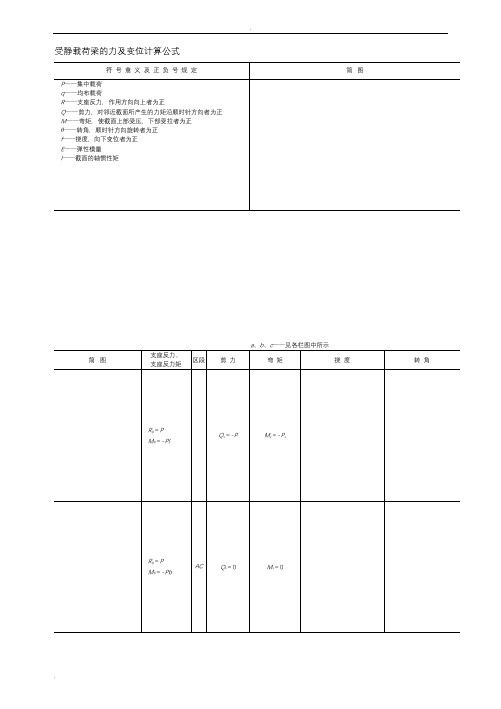
受静载荷梁的内力及变位计算公式

受静载荷梁的内力及变位计算公式1.集中力的作用下的受静载荷梁内力计算公式:(1)弯矩(M)的计算公式:M=F*x其中,M是梁的弯矩,F是集中力,x是集中力作用点到支点的距离。
(2)剪力(V)的计算公式:V=F其中,V是梁的剪力,F是集中力。
2.均布力的作用下的受静载荷梁内力计算公式:(1)弯矩(M)的计算公式:M=w*x^2/2其中,M是梁的弯矩,w是均布力的单位长度的大小,x是梁上的任意一点到支点的距离。
(2)剪力(V)的计算公式:V=w*x其中,V是梁的剪力,w是均布力的单位长度的大小,x是梁上的任意一点到支点的距离。
3.其他外力作用下的受静载荷梁内力计算公式:当存在多个外力作用在梁上时,我们可以将其分解为集中力和均布力的叠加。
然后可以使用前面提到的公式来计算相应的内力。
变位计算公式主要有两种方法,分别是力偏心法和位移法。
4.力偏心法:利用力偏心引起的弯矩和剪力,根据梁的弹性理论和材料的本构关系,可以计算出梁的变位。
其中,弯矩引起的变位可由以下公式计算:δ=M*l^2/(2*E*I)其中,δ是梁的变形,M是梁上弯矩的最大值,l是梁的长度,E是梁的弹性模量,I是梁的截面惯性矩。
剪力引起的变位可由以下公式计算:δ=V*l/(G*A)其中,δ是梁的变形,V是梁上剪力的最大值,l是梁的长度,G是梁的剪切模量,A是梁的截面面积。
5.位移法:利用位移函数法,将梁的各个节点的位移表示为节点位移和激励项的组合,可以通过解线性代数方程组得到梁的节点位移。
其中,节点位移可以用来计算梁的变位。
综上所述,受静载荷梁的内力和变位计算可以通过公式和方法进行求解。
具体的计算公式和方法取决于梁的受力情况和边界条件。
在实际工程中,通常会采用数值分析方法,如有限元法等,来计算受静载荷梁的内力和变位。
受静载荷梁的内力及变位计算公式

受静载荷梁的内力及变位计算公式受静载荷梁的内力及变位计算公式符号意义及正负号规定简图P——集中载荷q——均布载荷R——支座反力,作用方向向上者为正Q——剪力,对邻近截面所产生的力矩沿顺时针方向者为正M——弯矩,使截面上部受压,下部受拉者为正θ——转角,顺时针方向旋转者为正f——挠度,向下变位者为正E——弹性模量I——截面的轴惯性矩a、b、c——见各栏图中所示简图支座反力、支座反力矩区段剪力弯矩挠度转角R B=PM B=-PlQ x=-P M x=-P xR B=PM B=-PbAC Q x=0M x=0CB Q x=-P M x=-P(x-a)R B=nPR B=qlQ x=-qxR B=qcM B=-qcbAC Q x=0M x=0CD Q x=-q(x-d)DB Q x=-qc M x=-qc(x-a)ACCBR B=0M B=M x=-MQ x=0M x=-M?ω值见表梁分段的比值及ω的函数表;a、b、c——见各栏中所示简图支座反力、支座反力矩区段剪力弯矩挠度转角R A=R B=ACCBR A=R B=ACCBM x=Pa(1-ξ)M C=M max=R A=R B=PAC Qx=P M x=PxCD Q x=0M x=M max=PaCDDB若a>c:当n为奇数:当n为偶数:当n为奇数:当n为偶数:当n为奇数:当n为偶数:当n为奇数:当n为偶数:R A=R B=qaAC Q x=q(a-x)CD Q x=0R A=R B=ACCDCDDBR A=R B=qcAC Q x=qc M x=qcxCDDE Q x=0M x=M max=qcb当x=ACACCB若a>b,M x=M(1-ξ)M max=MM0=M2-M1若M1>M2:M max=M1ACM x=MξM C左=MαCBM x=-MζM C右=-Mβ?ω值见表梁分段的比值及ω的函数表;——见各栏图中所示简图支座反力、支座反力矩区段剪力弯矩挠度转角???ACCB当x=:AC Q x=R A M x=R A xCB Q x=R A-P M x=R Ax-P(x-a)Q MCD Qx=R A-P M x=R A x-P(x-a)DB Q x=R A-2P M x=R A x-P(2x-l)M C=M max=R A a当x=:R B=qc-R AM B=R A l-qcbAC Q x=R A M x=R A xCD Qx=R A-q(x-d)DB Qx=R A-qc M x=R A x-qc(x-a)当x=:M max=当x=:当x=:M max=当x=:AC当x=:M max=当x=:M A=M max=MAC?Q x=R ACBM C右=M max=M+M C左?ω值见表梁分段的比值及ω的函数表;a、b、c——见各栏图中所示简图支座反力、支座反力矩区段剪力弯矩挠度转角AC反弯点在及处R A=R B=PAC Qx=P M x=Pl(ξ-ωRα)CD Q x=0AC Q x=R A M x=M A+R A xCB Q x=R A-P M x=M A+R A x-P(x-a)若当n为奇数:当n为偶数:当n为奇数:当n为偶数:当n为奇数:当n为偶数:当n为奇数:当n为偶数:反弯点在x=及x=处R A=R B=qaACCD Qx=0ACCDAC Q x=R A M x=M A+R A xR B=qc=R ACD Q x=R A-q(x-d )DB Q x=R A-qc M x=M A+R Ax-qc(x-a)当x=:M max=当x=:ACACCDACQ x=R AM x=M A+R A xCB Mx=M A+R A x+M?5.带悬臂的梁简图支座反力、支座反力矩区段剪力弯矩挠度转角R A=P(1+λ)AC Q x=-P M x=-PxRM AB QM(1+当R A=R B=PM A=M B=-PmAC Q x=-P M x=-Px当x=m+时:AB Q x=0M x=-PmACABQ x=-qxQ x=R A-qxAC Qx=-qx当x=m+时:ABR A=R B=qmAC Q x=-qx当x=m+时:AB Q x=0M A=-PmAC Q x=-P M x=-Px:ABMx=-Px+R A(x-m)ACABQ x=-qxQ x=R A-qx当m=时:M B=0AC Qx=-qxAB Q x=RA-qxM A=MAC Q x=0M x=MAB M x=-RA(x-m)+M6.双跨、三跨梁OAM O=M B=0DE=AC=FG=两支点中间:x=处:R A=(q1l1+q2l2)-(R O+R B)OAM O=M B=0M O=M C=0OAABM O=M D=0x=处:R B=P1+P2-(R O+R2)M O=M D=0 ?。
《主梁内力计算》PPT课件

2
4
24
4
(81.4)
(595.0)
x=1/2
00:16
Q=0 (0)
M 1 16.0619.52 763.4 8
(793.3)
1 活载内力计算方法
•活载内力计算方法
计算步骤 求横向分布系数m; 应用主梁内力影响线,将荷载乘m后,在纵向按 最不利位置布载,求得主梁最大活载内力。
计算方法
4 主梁内力计算例题
简支梁基频的简化计算公式:
f
EIc 2l 2 mc
mc G g
单根主梁:
A 0.3902m2 , Ic 0.066146m4 ,
G 0.3902 25 9.76N / m
G g 9.76 9.81 0.995103 NS 3 m2
C30混凝土
E 1010 N m2
3.4主梁内力计算
00:16
主梁内力计算
•计算截面的确定
小跨径简支梁:
计算跨中截面的
、支M点m截ax面和跨中截面的剪力;
剪力:支点、跨中按直线变化;
弯矩:支点、跨中按二次抛物线变化
Mx
4Mmax x(l x) l2
大跨径简支梁:
还应计算 截L面、截面变化处等的弯矩和剪力。 4
00:16
1 恒载内力计算
S 867.72
73.1
13.39 74.68
88.07
3.75
00:16
4 主梁内力计算例题
计算车道荷载、人群荷载的支点截面剪力
m变化区荷载重心处的内力影响线坐标为:
y 1(19.5 1 4.9) 19.5 0.916 3
车道荷载支点截面剪力:
S
(1
)
工程力学梁的内力及其求法

取梁分析,受力如图b
? MC ? 0
解得
? MB ? 0
FB
l
?
F
l 2
?
0
F FB ? ? 2
?? ?
3l , ? FC l ? F 2 ? 0
F (a) A
l/2
C l/2
F (b) A
C FC
D
B
l/2
B FB
解得
FC
?
3F 2
(2)计算D截面上的剪力 FSD和弯矩MD
? Fy ? 0 , FC ? F ? FSD ? 0
F
(a) A
CLeabharlann DB得FSD
?
FC
?
F
?
F 2
l/2
l/2
l/2
对截面D的形心O取矩
F (c) A
C
D
F SD MD
? MO ? 0,
?
FC
l 2
?
Fl
?
MD
?
0
FC
MD D
B
F SD
FB
l Fl
得
MD
? ? Fl ? FC
?? 2
4
(上侧纤维受拉)
简便法:
(1) 横截面上的剪力,在数值上等于该截面任意一侧(左侧或右侧)脱离体 上所有外力沿该截面投影的代数和。如果外力对截面有顺时针转动的趋势则为 正,反之为负。
§9-2 梁的内力及其求法
一、梁的剪力和弯矩
(a) A FA
F m
m x
l
(b) A
FS M
FA F
(c)
M
FS
梁在竖向荷载作用下,其横截面上的内力有剪 力和弯矩。
3-1_梁的内力计算与多跨静定梁

2、刚结点上各杆端弯矩及集中力偶应满足结点的力矩平衡。两杆相交刚结 点无 m 作用时,两杆端弯矩等值,同侧受拉。
3、具有定向连结的杆端剪力等于零,如无横向荷载作用,该端弯矩为零。 4.无何载区段 5.均布荷载区段 ↓↓↓↓↓↓
+
-
6.集中力作用处 发生突变
F + -
7.力偶作用处
FQ图
平行轴线
无变化
l-x
B q(l-x)/2 q B C FyC
D
FyD
x 2 6lx l 2 0
对于BD杆:
1 1 2 1 FyD ( ql 0.414215ql 0.17157l q [0.17157l ]2 ) 0.414215ql l 2 2
CD跨最大弯矩为:
M
x 0.17157l , M C M E 0.085787ql 2
20
10 40
M 图(kN· m)
例3-2-3 求 x 的值,使梁正、负弯矩相等。 解:BD跨为基本部分, A E B AB跨为附属部分。
q
C x l D
AB跨跨中弯矩 ME 为: 1 q M E q(l x )2 8 A E BD跨支座C负弯矩 MC 为: 1 1 q(l-x)/2 M C q(l x ) x qx 2 2 2 令 ME = MC 得: 1 1 1 q(l x)2 q(l x) x qx 2 8 2 2
FRA 17kN
17
m=16kNm
F G B
1m 1m FyB 7kN
⑵ 求控制截面的内力值 取AC部分为隔离体,可计算得:
A C FQC
9
+
C D E F G B
MC
工程力学梁的内力及其求法

一、梁的剪力和弯矩
(a) A FA
F m
m x
l
(b) A
FS M
FA F
(c)
M
FS
梁在竖向荷载作用下,其横截面上的内力有剪 力和弯矩。
B
FB
剪力FS:沿截面切线方向的内力。单位为N
或kN
弯矩M:梁的横截面上作用在纵向平面内 的内力偶矩。单位是N·m或kN·m
B
FB
二、剪力、弯矩符号的规定
FS
FS
FS
FS
(a)
(b)
M
M
M
M
(a)
(b)
1.剪力符号规定:截面上的剪力如果有使考虑的脱离体有顺时针转动的趋势 则为正,反之为负。
2.弯矩符号规定:截面上的弯矩如果使考虑的脱离体下侧纵向纤维受拉为正, 反之如果使考虑的脱离体上侧纵向纤维受拉为负。
三、内力计算(截面法、简便法)
截面法:
F
m
(a) A FA
F
(a) A
C
D
B
得
FSD
?
FC
?
F
?
F 2
l/2
l/2
l/2
对截面D的形心O取矩
F (c) A
C
D
F SD MD
? MO ? 0,
?
FC
l 2
?
Fl
?
MD
?
0
FC
MD D
B
F SD
FB
l Fl
得
MD
? ? Fl ? FC
?? 2
4
(上侧纤维受拉)
简便法:
(1) 横截面上的剪力,在数值上等于该截面任意一侧(左侧或右侧)脱离体 上所有外力沿该截面投影的代数和。如果外力对截面有顺时针转动的趋势则为 正,反之为负。
3-1 梁内力计算&静定多跨梁

第3章 静定结构的受力分析
防 灾 科 技 学 院
五、分段叠加法作弯矩图
MA
q
MB
P
q
YA YB M 假定:在外荷载作用下,结构 A
分段叠加法的理论依据:
M
A
B
B
A
q
MB
NB q Y B MB
构件材料均处于线弹性阶段。 NA
MA MB
M 图中:OA段即为线弹性阶段
MAYA
AB段为非线性弹性阶段 M
A G B C D E F q
l/2 MG=ql2/12
ql2/24 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
MG=ql2/8
由于多跨静定梁设置了带伸臂的基本部分,这不仅使 中间支座处产生了负弯矩,它将降低跨中正弯矩;另外减少 了附属部分的跨度。因此多跨静定梁较相应的多个简支梁 弯矩分布均匀,节省材料,但其构造要复杂一些!!
qa qa/2
↓↓↓↓↓↓↓↓↓↓↓
2qa
qa/2
q
qa/2
-3qa/4
9qa/4
第3章 静定结构的受力分析
防 灾 科 技 学 院
qa
q
↓↓↓↓↓↓↓↓↓↓↓
qa
a
a
2qa
qa
- +
a 3qa/4 qa qa/4
2a
a 9qa/4
qa/2
- +
a
a qa/2
qa/2
7qa/4
-
qa qa2
qa/2
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
A
q
G
B
C
D
E
F
(完整版)梁的内力计算
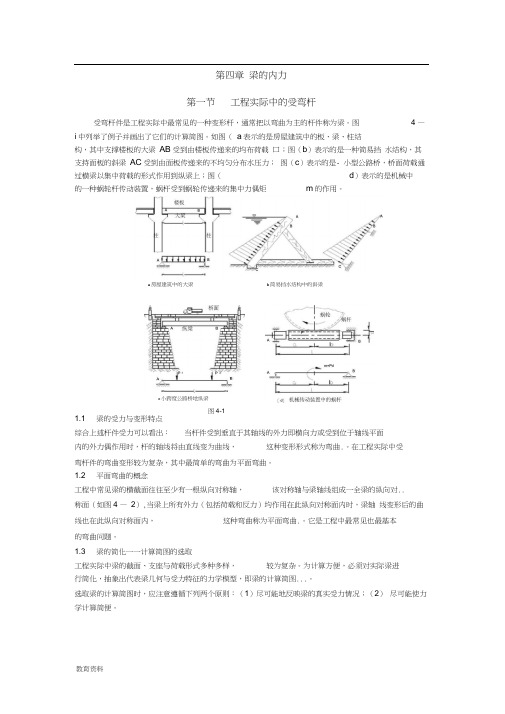
第四章梁的内力第一节工程实际中的受弯杆受弯杆件是工程实际中最常见的一种变形杆,通常把以弯曲为主的杆件称为梁。
图 4 —i中列举了例子并画出了它们的计算简图。
如图(a表示的是房屋建筑中的板、梁、柱结构,其中支撑楼板的大梁AB受到由楼板传递来的均布荷载口;图(b)表示的是一种简易挡水结构,其支持面板的斜梁AC受到由面板传递来的不均匀分布水压力;图(c)表示的是- 小型公路桥,桥面荷载通过横梁以集中荷载的形式作用到纵梁上;图(d)表示的是机械中的一种蜗轮杆传动装置,蜗杆受到蜗轮传递来的集中力偶矩m的作用。
1.1 梁的受力与变形特点综合上述杆件受力可以看出:当杆件受到垂直于其轴线的外力即横向力或受到位于轴线平面内的外力偶作用时,杆的轴线将由直线变为曲线,这种变形形式称为弯曲.。
在工程实际中受弯杆件的弯曲变形较为复杂,其中最简单的弯曲为平面弯曲。
1.2 平面弯曲的概念工程中常见梁的横截面往往至少有一根纵向对称轴,该对称轴与梁轴线组成一全梁的纵向对..称面(如图4 —2),当梁上所有外力(包括荷载和反力)均作用在此纵向对称面内时,梁轴线变形后的曲线也在此纵向对称面内,这种弯曲称为平面弯曲.。
它是工程中最常见也最基本的弯曲问题。
1.3 梁的简化一一计算简图的选取工程实际中梁的截面、支座与荷载形式多种多样,较为复杂。
为计算方便,必须对实际梁进行简化,抽象出代表梁几何与受力特征的力学模型,即梁的计算简图...。
选取梁的计算简图时,应注意遵循下列两个原则:(1)尽可能地反映梁的真实受力情况;(2)尽可能使力学计算简便。
a房屋建筑中的大梁c小跨度公路桥地纵梁图4-1b简易挡水结构中的斜梁图4-2 梁的平面弯曲一般从梁本身、支座及荷载等三方面进行简化:(1) 梁本身简化一一以轴线代替梁,梁的长度称为跨度; (2) 荷载简化一一将荷载简化为集中力、线分布力或力偶等; (3) 支座简化——主要简化为以下三种典型支座:(a ) 活动铰支座(或辊轴支座),其构造图及支座简图如图4— 3 (a )所示。
第3章-1内力计算

4)画轴力图 要求某杆件的轴力,通常是以剪力图为基础, 要求某杆件的轴力,通常是以剪力图为基础, 取出节点把已知的剪力标上, 取出节点把已知的剪力标上,利用两个方程即 可求出轴力。 可求出轴力。
4
+
4 C +
B
FNBC
B 4 - A
-4
FNBA
+4
剪力图
D
∑X =0
FNBC = −4
∑Y = 0
FNBA = −4
件右侧受拉为正。 件右侧受拉为正。
§3-1 梁的内力计算回顾
正 MAB
NAB QAB A端
杆端内力
B端
MBA
正
NBA QBA
弯矩图习惯绘在杆件受拉的一侧, 弯矩图习惯绘在杆件受拉的一侧,不需标正 负号。轴力和剪力图可绘在杆件的任一侧,但需 负号。轴力和剪力图可绘在杆件的任一侧, 标明正负号。 标明正负号。
2)画弯矩图
区段叠加法
3)画剪力图 要求杆件上某点的剪力, 要求杆件上某点的剪力,通常是以弯矩图为 基础,取一隔离体(要求剪力的点为杆端), 基础,取一隔离体(要求剪力的点为杆端), 把作用在杆件上的荷载及已知的弯矩标上, 把作用在杆件上的荷载及已知的弯矩标上,利 用取矩方程或水平或竖向的平衡方程即可求出 所要的剪力。 所要的剪力。 求图示杆件的剪力图。 例:求图示杆件的剪力图。
A 2 8 C 26 E 30 8 G
弯矩图
6、内力计算及内力图 步骤:求反力 步骤: 1)求反力 画弯矩图 画剪力图 画轴力图
(1)上部结构与基础的联系为3个时,对整体利用3个 上部结构与基础的联系为3个时,对整体利用3 平衡方程,就可求得反力。 平衡方程,就可求得反力。 例:
4m 4kN B C 1kN/m A 2m D 2m
2-5-3主梁内力计算

PDF 文件使用 "pdfFactory Pro" 试用版本创建
5.5.1 横隔梁的内力影响线
如图所示,当桥梁在跨中有单位荷载P=1作用时,各 主梁承受的荷载为Ri(i=1,2,…,n)。由力的平衡条 件,可求出横隔梁任意截面r的计算公式。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
a ( m0r − mcr ) 人群荷载: S r = qr m Ω + y ∑ i cr 2
式中:Sq、Sr——分别为汽车和人群荷载作用下的作用效应标 准值(弯矩或剪力); (1+μ)——汽车荷载的冲击系数; ξ——多车道汽车荷载横向折减系数; m0、mc——分别为支点、跨中截面的横向分布系数; Pk、qk——分别为车道荷载的集中荷载、均布荷载的标 准值; qr——人群荷载的标准值; Ω——车道均布荷载、人群荷载对应的内力影响线面 积; mpk——与车道荷载的集中荷载对应的横向分布系数; ypk——与车道荷载的集中荷载对应的影响线竖标,一般 取相应影响线区域的峰值。
a ( m0q − mcq ) Sq = (1 + µ ) ξ PK ( mpk ypk )max + (1 + µ ) ξ qK mcq Ω + yi ∑ 2
n
人群荷载:
a ( m0r − mcr ) Sr = qr mc r Ω + yi ∑ 2
PDF 文件使用 "pdfFactory Pro" 试用版本创建
简支梁内力包络图
0 l /4 l /2 l
弯矩包络图
3l/4
l
Qmax
M max
受静载荷梁的内力及变位计算公式
Qx=RA
Mx=RAx
CB
Qx=RA-P
Mx=RAx-P(x-a)
AC
Qx=RA
Mx=RAx
CD
Qx=RA-P
Mx=RAx-P(x-a)
DB
Qx=RA-2P
Mx=RAx-P(2x-l)
MC=Mmax=RAa
当x=0.422l:
RB=qc-RA
MB=RAl-qcb
AC
Qx=RA
Mx=RAx
CD
Qx=RA-q(x-d)
DB
Qx=RA-qc
Mx=RAx-qc(x-a)
当x=0.447l:
Mmax=0.0298ql2
当x=0.447l:
当x=0.329l:
Mmax=0.0423ql2
当x=0.402l:
AC
当x=0.415l:
Mmax=0.0475ql2
当x=0.430l:
MA=Mmax=M
AC
Qx=RA
CB
MC右=Mmax
=M+MC左
ω值见表梁分段的比值及ω的函数表;
a、b、c——见各栏图中所示
简图
支座反力、
支座反力矩
区段
剪力
弯矩
挠度
转角
AC
反弯点在
及 处
RA=RB=P
AC
Qx=P
Mx=Pl(ξ-ωRα)
CD
Qx=0
AC
Qx=RA
Mx=MA+RAx
CB
Qx=RA-P
Mx=MA+RAx-P(x-a)
若a>b,当 :
当n为奇数:
受静载荷梁的力及变位计算公式
符号意义及正负号规定
静定梁的内力—单跨静定梁的内力计算(建筑力学)

MO 0 : M FA x 0
B FB
F
lx
c
FQ FA
M FA x
与横截面相切的内力,称为剪力FQ , 常用单位为N或kN 。
作用在外力作用平面内(纵向对称平面
B
内)的内力偶,其力偶矩称为弯矩M,
FB 常用单位为
N m或 k N m 。
注:不论是左段还是右段隔离体计算出的内力应该是同 一截面上的内力,在大小、性质上应该是相同的结果。
MB 0
FA 4 4 2 21 0 FA 2kN
(2)计算各截面上的剪力
FQ1 FQ2 FQ3 = 2kN FQ4 2+6=4kN FQ4 2 2=4kN
4kN m 2kN/m
12 3
Aபைடு நூலகம்
B4 C
FA
2m
FB
2m
2m
(2)计算各截面上的弯矩
M1 2 2 4kN m(上部受拉) M2 2 2 4 0
M1
qa
a 2
Fa
0
M1
qa
a 2
Fa
4
2
2 2
5
2
18kN
m
(上部受拉)
应用举例
[例2] 如图所示简支梁,已知:F1=F2=30kN, 求1-1横截面上的剪力和弯矩。
F1 1
A
1
FA 1m 1m
2m
F2 B
2m FB
F1 1 M1
1 FA 1m 1m FQ1
M11
F2
1 FS1 2m
2m FB
(2) 代替 留下一部分(脱离体),并以内力代替弃去部分对保留部分的作用。
(3) 平衡 对脱离体建立静力平衡方程,求解未知力。 注意: 取出的梁段上保留作用于该段上的所有外力(包括荷载和支座反力),在截开的 截面上画出未知的剪力和弯矩时,剪力和弯矩均假设为正向。
第三章第二节 主梁结构内力计算

第二节 主梁结构内力计算
(一)在施工过程中结构不发生体系转换。 如在满堂支架现浇、整孔吊装或在静定 结构中采用悬臂施工方法等场合,主梁 自重作用于桥上时,结构已是最终体系, 因而主梁自重内力,如主梁为等截面, 其自重集度为沿跨长均布,可按均布荷 载乘主梁内力影响线总面积计算;如主 梁为变截面,自重集度沿跨长变化,则 可按下式计算:
第二节 主梁结构内力计算
一、恒载内力计算 主梁恒载内力,包括主装、人行道、栏杆、灯柱等) 引起的主梁后期恒载内力,以下简称为 后期恒载内力。
第二节 主梁结构内力计算
主梁自重是在结构逐步形成的过程中作用于桥上的, 因而它的计算与施工方法有密切关系。特别在大、中 跨预应力混凝土超静定梁桥的施工过程中不断有体系 转换过程,在计算主梁自重内力时必须分阶段进行, 有一定的复杂性。而后期恒载作用于桥上时,主梁结 构已形成最终体系,主梁后期恒载内力的计算就可直 接应用结构内力影响线。随着预应力工艺、悬臂施工 方法等的发展,预应力混凝土梁桥的施工方法得到不 断创新和发展。然而,书中不可能逐一介绍各种施工 方法的主梁自重内力计算。主梁自重内力计算方法可 归纳为两大类:
第二节 主梁结构内力计算
主梁内力包括恒载内力、活载内力和附加内力 (如风力或离心力引起的内力)。对于超静定 梁,还应包括由于预加力、混凝土徐变、收缩 和温度变化等引起的结构次内力。将它们按规 范的规定进行组合,从中挑选最大设计内力, 依此进行配筋设计和应力验算。设计实践表明: 在这几部分内力中,恒、活载内力是主要的, 一般它们占整个设计最大内力的80~90%以上。 本章主要叙述这两部分内力的计算,至于附加 内力和结构次内力的计算方法将在后面章节中 作介绍。
3、逐跨施工 主梁自重内力图,应由各施工阶段时的自重 内力图迭加而成
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 梁的内力第一节 工程实际中的受弯杆受弯杆件是工程实际中最常见的一种变形杆,通常把以弯曲为主的杆件称为梁。
图4-1中列举了例子并画出了它们的计算简图。
如图(a )表示的是房屋建筑中的板、梁、柱结构,其中支撑楼板的大梁AB 受到由楼板传递来的均布荷载q ;图(b )表示的是一种简易挡水结构,其支持面板的斜梁AC 受到由面板传递来的不均匀分布水压力;图(c )表示的是一小型公路桥,桥面荷载通过横梁以集中荷载的形式作用到纵梁上;图(d )表示的是机械中的一种蜗轮杆传动装置,蜗杆受到蜗轮传递来的集中力偶矩m 的作用。
a房屋建筑中的大梁b简易挡水结构中的斜梁c小跨度公路桥地纵梁d机械传动装置中的蜗杆图4-1 工程实际中的受弯杆1.1 梁的受力与变形特点 综合上述杆件受力可以看出:当杆件受到垂直于其轴线的外力即横向力或受到位于轴线平面内的外力偶作用时,杆的轴线将由直线变为曲线,这种变形形式称为弯曲..。
在工程实际中受弯杆件的弯曲变形较为复杂,其中最简单的弯曲为平面弯曲。
1.2 平面弯曲的概念工程中常见梁的横截面往往至少有一根纵向对称轴,该对称轴与梁轴线组成一全梁的纵向对...称面..(如图4-2),当梁上所有外力(包括荷载和反力)均作用在此纵向对称面内时,梁轴线变形后的曲线也在此纵向对称面内,这种弯曲称为平面弯曲....。
它是工程中最常见也最基本的弯曲问题。
1.3 梁的简化——计算简图的选取工程实际中梁的截面、支座与荷载形式多种多样,较为复杂。
为计算方便,必须对实际梁进行简化,抽象出代表梁几何与受力特征的力学模型,即梁的计算简图....。
选取梁的计算简图时,应注意遵循下列两个原则:(1)尽可能地反映梁的真实受力情况;(2)尽可能使力学计算简便。
图4-2 梁的平面弯曲一般从梁本身、支座及荷载等三方面进行简化:(1)梁本身简化——以轴线代替梁,梁的长度称为跨度;(2)荷载简化——将荷载简化为集中力、线分布力或力偶等;(3)支座简化——主要简化为以下三种典型支座:(a)活动铰支座(或辊轴支座),其构造图及支座简图如图4-3(a)所示。
这种支座只限制梁在沿垂直于支承平面方向的位移,其支座反力过铰心且垂直于支承面,用Y A表示。
(b)固定铰支座,其构造与支座简图如图4-3(b)所示。
这种支座限制梁在支承处沿任何方向的线位移,但不限制角位移,其支座反力过铰心两互相垂直分力,用X A、Y A表示。
(c)固定端支座,其构造与支座简图如图4-3(c)所示。
这种支座限制梁端的线位移(移动)及角位移(转动),其反力可用三个分量X A、Y A及m A来表示。
图4-1中所示几种工程实际中梁的计算简图就是采用上述简化方法得出来的。
A枢轴梁辊轴支承垫板A梁Aa活动铰支座Ab固定铰支座AAm Ac固定端支座图4-3 三种典型支座1.4 梁的基本形式根椐梁的支座形式和支承位置不同,简单形式的梁有如下三种形式: (1)简支梁。
梁的支座为一端固定铰,一端活动铰(如图4-4(a )); (2)外伸梁。
简支梁两端或一端伸出支座之外(如图4-4(b ),(c )); (3)悬臂梁。
梁的支座为一端固定,一端自由(如图4-4(d ))。
() 简支梁2() 一端外伸梁() 两端外伸梁() 悬臂梁图4-4 梁的类型这三种梁的共同特点是支座反力仅有三个,可由静力平衡条件全部求得,故也称为静定梁...。
第二节 梁的内力——剪力和弯矩2.1 截面法求梁的内力为进行梁的设计,需求梁的内力,求梁任一截面内力仍采用截面法,以图4-5(a )为例,梁在外力(荷载P 和反力Y A 、Y B )作用下处于平衡状态。
在需求梁的内力x 处用一假想截面m-n 将梁截开分为两段。
取任意一段,如左段为脱离体。
由于梁原来处于平衡状态,取出的任一部分也应保持平衡。
从图4-5(b )可知,左脱离体A 端原作用有一向上的支座反力Y A ,要使它保持平衡,由0Y =∑和0M =∑,在切开的截面m-n 上必然存在两个内力分量:内力Q 和内力偶矩M 。
内力分量Q 位于横截面上,称为剪力..;内力偶矩M 位于纵向(YB图4-5 用截面法求梁的内力对称平面内,称为弯矩..。
对左脱离体列平衡方程:由0Y =∑,有Y A-Q =0则得 由0cM=∑,有0A Y x M ⋅-=则得 A M Y x =⋅注意此处是对截面形心c 取矩,因剪力Q 通过截面形心c 点,故在力矩方程中为零。
同样可取右脱离体,由平衡方程求出梁截面m-n 上的内力Q 和M ,其结果与左脱离体求得的Q 、M 大小相等,方向(或转向)相反,互为作用力与反作用力关系。
为使梁同一截面内力符号一致,必须联系到变形状态规定它们的正负号。
若从梁m-n 处取一微段梁dx ,由于剪力Q 作用会使微段发生下错动的剪切变形。
我们规定:使微段梁发生左端向上而右端向下相对错动的剪力Q 为正(如图4-6(a )),反之为负(如图4-6(b ));使微段梁弯曲为向下凸时的弯矩M 为正,反之为负(如图4-6(c )、(d ))。
根据如上符号规定,图4-5中m-n 截面内力符号均为正。
下面举例说明怎样用截面法求梁任一截面的内力。
例4-1外伸梁如图4-7(a ),已知均布荷载q 和集中力偶2m qa =,求指定1-1、2-2、3-3截面内力。
(c )(d )图4-6 剪力,弯矩的正负号规定之一2(c )Q (d )图4-7 例题4-1图解(1)求支座反力设支座反力Y A 、Y B 如图所示。
由平衡方程0AM =∑ 5202B Y a m qa a ⋅--⋅= 得 74B Y qa =由0Y =∑ 0AB YY qa -+-=得 34A Y q a = 由0BM=∑校核支座反力223220242A a qa Y a m qa qa a qa ⋅--⋅=⋅--=所求反力无误。
(2)求1-1截面内力由1-1截面将梁分为两段,取左段梁为脱离体,并假设截面剪力Q 1和弯矩M 1均为正...,如图4-7(b )所示。
由0Y =∑ 10AYQ --=得 134A Q Y qa =-=- 由10M=∑ 10A Y a M m ⋅+-=得 2221344A q M m Y a qa qa a =-⋅=-= 求得的Q 1结果为负值,说明剪力实际方向与假设相反,且为负剪力;M 1结果为正值,说明弯矩实际转向与假设相同,且为正弯矩。
(3)求2-2截面(B 截面右侧一点)内力由2-2截面将梁分为两段,取右段梁为脱离体,截面上剪力Q 2和弯矩M 2均设为正,如图4-7(c )。
由0Y =∑ 20Qq a -=得 2Q q a = 由20M =∑ 202aM q a --⋅= 得 222qa M =-(4)求3-3截面(D 截面左侧边一点)内力取右端为脱离体,3-3截面无限靠近D 点,线分布力q 的分布长度趋于0,则3-3截面上Q 3=0,M 3=0。
2.2截面法直接由外力求截面内力的法则上例说明了运用截面法求任一截面内力的方法。
因脱离体的平衡条件0Y =∑的含义为:脱离体上所有外力和内力在Y 轴方向投影的代数和为零。
其中只有剪力Q 为未知量,移到方程式右边即得直接由外力求任一截面剪力的法则:(1)某截面的剪力等于该截面一侧所有外力在截面上投影的代数和,即Y Q Y =∑∑左侧外力右侧外力(或) (4-2-1) 代数和中的符号为截面左侧向上的外力(或右侧向下的外力)使截面产生正的剪力,反之产生负剪力,如图4-8(a )所示,截面上的剪力为正。
同样,脱离体平衡条件0cM=∑的含义为:脱离体上所有外力和内力对截面形心取力矩的代数和为零。
其中只有弯矩M 为未知量,移到方程右边即得直接由外力求任一截面弯矩的法则:(b )外Q (+)PM (+)(a )图4-8 剪力,弯矩的正负号规定之二左上右下 剪力为正左顺右逆弯矩为正(2)某截面的弯矩等于该截面一侧所有外力对截面形心力矩的代数和,即M c c M M =∑∑右侧外力左侧外力(或) (4-4-2) 代数和中的符号为截面的左边绕截面顺时针转的力矩或力偶矩(或右边绕截面逆时针转的力矩或力偶矩)使截面产生正的弯矩,反之产生负弯矩。
如图4-8(b )所示,截面上的弯矩为正。
这样,运用上述两法则就不必取脱离体,可用式(4-2-1)和(4-2-2)直接由截面左侧(或右侧)外力计算任一截面剪力和弯矩。
此两法则是由截面法推出的,但比截面法用起来更方便快捷,对于求梁的内力极为有用,必须熟练掌握。
读者可用此方法验证例4-1的结果是否正确。
第三节 剪力图与弯矩图在一般情况下,梁截面上的内力(剪力和弯矩)随截面位置x 的不同而变化,故横截面的剪力和弯矩都可表示为截面位置x 的函数,即(),()Q Q x M M x ==通常把它们分别叫做剪力方程....和弯矩方程....。
在写这些方程时,一般是以梁左端为x 坐标原点,但为计算方便,有时也可将原点取在梁右端或梁上任意点。
由剪力方程和弯矩方程,我们可以了解剪力和弯矩沿全梁各截面上的变化情况,从而找出最大内力截面即危险截面作为将来设计的依据。
为了形象地表示剪力、弯矩沿梁长的变化情况,可根据剪力方程和弯矩方程分别绘制剪力图...和弯矩图...。
根据剪力方程和弯矩方程作剪力图和弯矩图的方法与前面轴力图及扭矩图作法类似,即以梁横截面沿轴线的位置为横坐标x ,以横截面上的剪力或弯矩为纵坐标,按照适当的比例绘出Q =Q (x )或M =M (x )的曲线。
绘制剪力图时,一般规定正号剪力画在x 轴上侧,负号剪力画在x 轴下侧,并注上正负号;绘制弯矩图时则规定正弯矩画在x 轴的下侧,负弯矩画在x 轴的上侧,这也就是把弯矩图画在梁受拉的一侧,以便钢筋混凝土梁根据弯矩图配置钢筋。
弯矩图可以不注正负号。
由剪力图和弯矩图可直观确定梁剪力、弯矩的最大值及其所在截面位置。
例4-2 作图4-9(a )所示简支梁受均布荷载的剪力图和弯矩图。
ql 2ql2=177.5kN图图ql2=276.9kN.m2()()()图4-9 例题4-2图解 (1)求支座反力 由0Y =∑和对称条件知2A B ql Y Y ==(2)列出剪力方程和弯矩方程:以左端A 为原点,并将x 表示在图上。
()()02A qlQ x Y qx qx x l =-=-<< (a ) ()()20222Ax x ql qx M x Y qa x x l =-⋅=-≤≤ (b )注意,由于反力/2A Y ql =的指向是朝上的,它将使梁的任一截面上产生正号的剪力和弯矩,因此在式(a )和式(b )中它们的符号均为正;由于均布荷载q 的指向是朝下的,它将使左段梁的任一截面上产生负号的剪力和弯矩,分布力q 的合力为分布力图的面积qx ,且作用在分布力图的形心2x处,而分布力对截面形心的力矩的大小为其合力乘以合力到截面形心的距离即2x qx ⋅,因此在式(a )中的qx 项和式(b )中的22qx 项都带负号。
