2019年高考数学一轮复习课时分层训练26平面向量的概念及线性运算
高考数学一轮复习学案:5.1 平面向量的概念及线性运算(含答案)

高考数学一轮复习学案:5.1 平面向量的概念及线性运算(含答案)5.1平面向量的概念及线性运算平面向量的概念及线性运算最新考纲考情考向分析1.了解向量的实际背景2.理解平面向量的概念,理解两个向量相等的含义3.理解向量的几何表示4.掌握向量加法.减法的运算,并理解其几何意义5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义6.了解向量线性运算的性质及其几何意义.主要考查平面向量的线性运算加法.减法.数乘向量及其几何意义.共线向量定理常与三角函数.解析几何交汇考查,有时也会有创新的新定义问题;题型以选择题.填空题为主,属于中低档题目偶尔会在解答题中作为工具出现.1向量的有关概念名称定义备注向量既有大小,又有方向的量;向量的大小叫做向量的长度或称模平面向量是自由向量零向量长度为0的向量;其方向是任意的记作0单位向量长度等于1个单位长度的向量非零向量a的单位向量为a|a|平行向量共线向量方向相同或相反的非零向量0与任一向量平行或共线相等向量长度相等且方向相同的向量两向量只有相等或不等,不能比较大小相反向量长度相等且方向相反的向量0的相反向量为02.向量的线性运算向量运算定义法则或几何意义运算律加法求两个向量和的运算3交换律abba;4结合律abcabc减法求a与b的相反向量b的和的运算abab数乘求实数与向量a的积的运算6|a||||a|;7当0时,a与a的方向相同;当0时,a与a的方向相反;当0时,a08aa;9aaa;10abab3.共线向量定理向量aa0与b共线,当且仅当有唯一一个实数,使ba.知识拓展1一般地,首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量,即A1A2A2A3A3A4An1AnA1An,特别地,一个封闭图形,首尾连接而成的向量和为零向量2若P为线段AB的中点,O为平面内任一点,则OP12OAOB3.OAOBOC,为实数,若点A,B,C共线,则1.题组一思考辨析1判断下列结论是否正确请在括号中打“”或“”1向量与有向线段是一样的,因此可以用有向线段来表示向量2|a|与|b|是否相等与a,b的方向无关3若ab,bc,则ac.4若向量AB与向量CD是共线向量,则A,B,C,D四点在一条直线上5当两个非零向量a,b共线时,一定有ba,反之成立6若两个向量共线,则其方向必定相同或相反题组二教材改编2P86例4已知ABCD的对角线AC和BD相交于点O,且OAa,OBb,则DC______,BC________.用a,b表示答案baab 解析如图,DCABOBOAba,BCOCOBOAOBab.3P108B组T5在平行四边形ABCD中,若|ABAD||ABAD|,则四边形ABCD的形状为________答案矩形解析如图,因为ABADAC,ABADDB,所以|AC||DB|.由对角线长相等的平行四边形是矩形可知,四边形ABCD是矩形题组三易错自纠4对于非零向量a,b,“ab0”是“ab”的A充分不必要条件B必要不充分条件C充要条件D既不充分也不必要条件答案A解析若ab0,则ab,所以ab.若ab,则ab0不一定成立,故前者是后者的充分不必要条件5设向量a,b不平行,向量ab 与a2b平行,则实数____________.答案12解析向量a,b不平行,a2b0,又向量ab与a2b平行,则存在唯一的实数,使aba2b 成立,即aba2b,则,12,解得12.6设D,E分别是ABC的边AB,BC上的点,AD12AB,BE23BC.若DE1AB2AC1,2为实数,则12的值为________答案12解析DEDBBE12AB23BC12AB23BAAC16AB23AC,116,223,即1212.题型一题型一平面向量的概念平面向量的概念1给出下列四个命题若|a||b|,则ab;若A,B,C,D是不共线的四点,则ABDC是四边形ABCD为平行四边形的充要条件;若ab,bc,则ac;ab的充要条件是|a||b|且ab.其中正确命题的序号是ABCD答案A解析不正确两个向量的长度相等,但它们的方向不一定相同;正确ABDC,|AB||DC|且ABDC,又A,B,C,D是不共线的四点,四边形ABCD为平行四边形,反之,若四边形ABCD为平行四边形,则ABDC且|AB||DC|,ABDC;正确ab,a,b的长度相等且方向相同,又bc,b,c的长度相等且方向相同,a,c的长度相等且方向相同,故ac;不正确当ab且方向相反时,即使|a||b|,也不能得到ab,故|a||b|且ab不是ab的充要条件,而是必要不充分条件综上所述,正确命题的序号是.故选A.2设a0为单位向量,若a为平面内的某个向量,则a|a|a0;若a与a0平行,则a|a|a0;若a与a0平行且|a|1,则aa0.上述命题中,假命题的个数是A0B1C2D3答案D解析向量是既有大小又有方向的量,a与|a|a0的模相同,但方向不一定相同,故是假命题;若a与a0平行,则a与a0的方向有两种情况一是同向,二是反向,反向时a|a|a0,故也是假命题综上所述,假命题的个数是3.思维升华向量有关概念的关键点1向量定义的关键是方向和长度2非零共线向量的关键是方向相同或相反,长度没有限制3相等向量的关键是方向相同且长度相等4单位向量的关键是长度都是一个单位长度5零向量的关键是长度是0,规定零向量与任何向量共线题型二题型二平面向量的线性运算平面向量的线性运算命题点1向量的线性运算典例1在ABC中,ABc,ACb,若点D满足BD2DC,则AD等于A.23b13cB.53c23bC.23b13cD.13b23c答案A解析BD2DC,ADABBD2DC2ACAD,3AD2ACAB,AD23AC13AB23b13c.2xx青海西宁一模如图,在ABC中,点D在BC 边上,且CD2DB,点E在AD边上,且AD3AE,则用向量AB,AC表示CE为A.29AB89ACB.29AB89ACC.29AB79ACD.29AB79AC答案B解析由平面向量的三角形法则及向量共线的性质可得CEAEAC13ADAC13AB13BCAC13AB13ACABAC29AB89AC.命题点2根据向量线性运算求参数典例1在ABC中,点M,N满足AM2MC,BNNC.若MNxAByAC,则x________,y______.答案1216解析MNMCCN13AC12CB13AC12ABAC12AB16ACxAByAC,x12,y16.2在ABC中,点D在线段BC的延长线上,且BC3CD,点O 在线段CD上与点C,D不重合,若AOxAB1xAC,则x的取值范围是A.0,12B.0,13C.12,0D.13,0答案D解析设COyBC,AOACCOACyBCACyACAByAB1yAC.BC3CD,点O在线段CD上与点C,D不重合,y0,13,AOxAB1xAC,xy,x13,0.思维升华平面向量线性运算问题的常见类型及解题策略1向量加法或减法的几何意义向量加法和减法均适合三角形法则2求已知向量的和一般共起点的向量求和用平行四边形法则;求差用三角形法则;求首尾相连向量的和用三角形法则3求参数问题可以通过研究向量间的关系,通过向量的运算将向量表示出来,进行比较,求参数的值跟踪训练1如图,在正方形ABCD中,点E是DC的中点,点F是BC上的一个靠近点B的三等分点,那么EF等于A.12AB13ADB.14AB12ADC.13AB12DAD.12AB23AD答案D解析在CEF中,有EFECCF.因为点E为DC 的中点,所以EC12DC.因为点F为BC上的一个靠近点B的三等分点,所以CF23CB.所以EF12DC23CB12AB23DA12AB23AD,故选D.2如图,直线EF与平行四边形ABCD的两边AB,AD分别交于E,F两点,且与对角线AC交于点K,其中,AE25AB,AF12AD,AKAC,则的值为______答案29解析AE25AB,AF12AD,AB52AE,AD2AF.由向量加法的平行四边形法则可知,ACABAD,AKACABAD52AE2AF52AE2AF,E,F,K三点共线,5221,29.题型三题型三共线向量定理的应用共线向量定理的应用典例设两个非零向量a与b不共线1若ABab,BC2a8b,CD3ab,求证A,B,D三点共线;2试确定实数k,使kab和akb共线1证明ABab,BC2a8b,CD3ab,BDBCCD2a8b3ab2a8b3a3b5ab5AB,AB,BD共线又它们有公共点B,A,B,D三点共线2解假设kab与akb共线,则存在实数,使kabakb,即kak1b.又a,b是两个不共线的非零向量,kk10.消去,得k210,k1.引申探究若将本例1中“BC2a8b”改为“BCamb”,则m为何值时,A,B,D三点共线解BCCDamb3ab4am3b,即BD4am3b.若A,B,D三点共线,则存在实数,使BDAB.即4am3bab4,m3,解得m7.故当m7时,A,B,D三点共线思维升华1证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系当两向量共线且有公共点时,才能得出三点共线2向量a,b 共线是指存在不全为零的实数1,2,使1a2b0成立,若1a2b0,当且仅当120时成立,则向量a,b不共线跟踪训练1xx资阳模拟已知向量ABa3b,BC5a3b,CD3a3b,则AA,B,C三点共线BA,B,D三点共线CA,C,D三点共线DB,C,D三点共线答案B解析BDBCCD2a6b2a3b2AB,BD,AB共线,又有公共点B,A,B,D三点共线故选B.2已知A,B,C是直线l上不同的三个点,点O不在直线l 上,则使等式x2OAxOBBC0成立的实数x的取值集合为A0BC1D0,1答案C解析BCOCOB,x2OAxOBOCOB0,即OCx2OAx1OB,A,B,C三点共线,x2x11,即x2x0,解得x0或x1.当x0时,x2OAxOBBC0,此时B1,C两点重合,不合题意,舍去故x1.故选C.容易忽视的零向量典例下列叙述错误的是________填序号若非零向量a与b方向相同或相反,则ab与a,b之一的方向相同;|a||b||ab|a与b方向相同;向量b与向量a共线的充要条件是有且只有一个实数,使得ba;ABBA0;若ab,则ab.错解展示中两个向量的和仍是一个向量,所以ABBA0.错误答案现场纠错解析对于,当ab0时,其方向任意,它与a,b的方向都不相同对于,当a,b之一为零向量时结论不成立对于,当a0且b0时,有无数个值;当a0但b0或a0但b0时,不存在对于,由于两个向量之和仍是一个向量,所以ABBA0.对于,当0时,不管a与b的大小与方向如何,都有ab,此时不一定有ab.故均错答案纠错心得在考虑向量共线问题时,要注意考虑零向量.。
2019年高考数学一轮复习 平面向量的概念及线性运算

量 e1,e2 叫做表示这个平面所有向量的一组 基底 . 注意:(1)构成基底的两向量不共线; (2)基底给定,同一向量的分解形式唯一; (3)若 λ1e1+λ2e2=0,则 λ1=λ2=0.
复习目标 课前预习 高频考点 课时小结
课后练习
1.在平行四边形中,如图: (1)若 a,b 为不共线的两个向量,则 a+b,a-b 为以 a,b 为邻边的平行四边形的两条对角线表示的向 量. 1 → (2)AO= (a+b). 2 (3)|a+b|2+|a-b|2=2(|a|2+|b|2). 2.在△ABC 中: → =1(PA → +PB → +PC → )(向量式)⇔G 是△ABC 的重心. (1)PG 3 → +GB → +GC → =0. (2)G 为△ABC 的重心⇔GA → → AB AC (3)λ( + )(λ≠0)所在直线(即∠BAC 的平分线所在直线) → → |AB| |AC| 过△ABC 的内心.
复习目标
课前预习
高频考点
课时小结
课后练习
1.向量的有关概念 (1) 向量的定义 :既有 ________ 又有 ________ 的量叫作向 方向 大小 量.用有向线段表示向量时,有向线段的长度表示向量的 大小(叫作向量的模) ,有向线段的箭头所指的方向表示向量的 ___________________
复习目标 课前预习 高频考点 课时小结
课后练习
3.共线的有关结论: → ,AC → 共线. ①A,B,C 三点共线⇔AB → =xOB → +yOC → (x,y 为实数),若点 A,B,C 共线,则 x ②OA +y=1. 4.一般地,首尾顺次相接的多个向量的和等于从第一个向量 → → 起点指向最后一个向量的终点的向量, 即A→ 1A2+A2A3+A3A4+…+ An -1An=A→ 1An . 特别地,一个封闭图形,首尾连接而成的向量和为 零向量.
高考数学一轮复习专题训练—平面向量的概念及线性运算
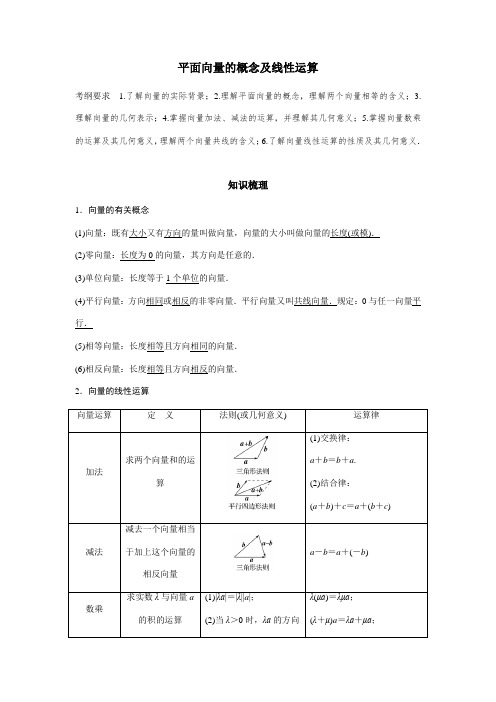
平面向量的概念及线性运算考纲要求 1.了解向量的实际背景;2.理解平面向量的概念,理解两个向量相等的含义;3.理解向量的几何表示;4.掌握向量加法、减法的运算,并理解其几何意义;5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义;6.了解向量线性运算的性质及其几何意义.知识梳理1.向量的有关概念(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或模).(2)零向量:长度为0的向量,其方向是任意的.(3)单位向量:长度等于1个单位的向量.(4)平行向量:方向相同或相反的非零向量.平行向量又叫共线向量.规定:0与任一向量平行.(5)相等向量:长度相等且方向相同的向量.(6)相反向量:长度相等且方向相反的向量.2.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律:a+b=b+a.(2)结合律:(a+b)+c=a+(b+c)减法减去一个向量相当于加上这个向量的相反向量a-b=a+(-b)数乘求实数λ与向量a的积的运算(1)|λa|=|λ||a|;(2)当λ>0时,λa的方向λ(μa)=λμa;(λ+μ)a=λa+μa;与a 的方向相同;当λ<0时,λa 的方向与a 的方向相反;当λ=0时,λa =0λ(a +b )=λa +λb3.共线向量定理向量a (a ≠0)与b 共线的充要条件是存在唯一一个实数λ,使得b =λa .1.一般地,首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量,即A 1A 2→+A 2A 3→+A 3A 4→+…+A n -1A n =A 1A n →,特别地, 一个封闭图形,首尾连接而成的向量和为零向量.2.中点公式的向量形式:若P 为线段AB 的中点,O 为平面内任一点,则OP →=12(OA →+OB →).3.OA →=λOB →+μOC →(λ,μ为实数),若点A ,B ,C 共线,则λ+μ=1.4.解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是考虑向量的方向;二是要特别注意零向量的特殊性,考虑零向量是否也满足条件.诊断自测1.判断下列结论正误(在括号内打“√”或“×”) (1)|a |与|b |是否相等与a ,b 的方向无关.( ) (2)若a ∥b ,b ∥c ,则a ∥c .( )(3)向量AB →与向量CD →是共线向量,则A ,B ,C ,D 四点在一条直线上.( ) (4)当两个非零向量a ,b 共线时,一定有b =λa ,反之成立.( ) 答案 (1)√ (2)× (3)× (4)√解析 (2)若b =0,则a 与c 不一定平行.(3)共线向量所在的直线可以重合,也可以平行,则A ,B ,C ,D 四点不一定在一条直线上.2.给出下列命题:①零向量的长度为零,方向是任意的;②若a ,b 都是单位向量,则a =b ;③向量AB →与BA →相等.则所有正确命题的序号是( ) A .① B .③C .①③D .①②答案 A解析 根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量AB →与BA →互为相反向量,故③错误.3.设M 为△ABC 所在平面内一点,且BC →=3CM →,则( ) A.AM →=-13AB →+43AC →B .AM →=13AB →-43AC →C.AM →=43AB →+13AC →D .AM →=43AB →-13AC →答案 A解析 由BC →=3CM →,得CM →=13BC →,所以AM →=AC →+CM →=AC →+13BC →=AC →+13(BA →+AC →)=-13AB →+43AC →.4.(2021·日照调研)若四边形ABCD 满足AD →=12BC →且|AB →|=|DC →|,则四边形ABCD 的形状是( ) A .等腰梯形 B .矩形 C .正方形 D .菱形答案 A解析 因为AD →=12BC →,所以AD →∥BC →,且|AD →|=12|BC →|,所以四边形ABCD 为以AD 为上底边,BC 为下底边的梯形.又|AB →|=|DC →|,因此四边形ABCD 是等腰梯形.5.(2021·长沙调研)已知点O 为△ABC 的外接圆的圆心,且OA →+OB →+CO →=0,则△ABC 的内角A 等于( ) A .30° B .45° C .60° D .90°答案 A解析 由OA →+OB →+CO →=0,得OA →+OB →=OC →, 又O 为△ABC 的外接圆的圆心,根据加法的几何意义,四边形OACB 为菱形,且∠CAO =60°,因此∠CAB =30°.6.(2020·哈尔滨质检)设a 与b 是两个不共线向量,且向量a +λb 与-(b -2a )共线,则λ=________. 答案 -12解析 由已知2a -b ≠0,依题意知向量a +λb 与2a -b 共线,设a +λb =k (2a -b ),则有(1-2k )a +(k +λ)b =0,因为a ,b 是两个不共线向量,故a 与b 均不为零向量,所以⎩⎪⎨⎪⎧1-2k =0,k +λ=0,解得k =12,λ=-12.考点一 平面向量的概念1.给出下列四个命题: ①若|a |=|b |,则a =b ;②若A ,B ,C ,D 是不共线的四点,则“AB →=DC →”是“四边形ABCD 为平行四边形”的充要条件;③若a =b ,b =c ,则a =c ; ④a =b 的充要条件是|a |=|b |且a ∥b . 其中正确命题的序号是( ) A .②③B .①②C .③④D .②④答案 A解析 ①不正确.两个向量的长度相等,但它们的方向不一定相同.②正确.∵AB →=DC →,∴|AB →|=|DC →|且AB →∥DC →,又A ,B ,C ,D 是不共线的四点,∴四边形ABCD 为平行四边形;反之,若四边形ABCD 为平行四边形,则|AB →|=|DC →|, AB →∥DC →且AB →,DC →方向相同,因此AB →=DC →.③正确.∵a =b ,∴a ,b 的长度相等且方向相同,又b =c ,∴b ,c 的长度相等且方向相同,∴a ,c 的长度相等且方向相同,故a =c .④不正确.当a ∥b 且方向相反时,即使|a |=|b |,也不能得到a =b ,故|a |=|b |且a ∥b 不是a =b 的充要条件,而是必要不充分条件. 综上所述,正确命题的序号是②③.2.设a ,b 都是非零向量,下列四个条件,使a |a |=b|b |成立的充要条件是( )A .a =bB .a =2bC .a ∥b 且|a |=|b |D .a ∥b 且方向相同答案 D 解析a |a |表示a 方向的单位向量,因此a |a |=b|b |的充要条件是a 与b 同向. 3.给出下列说法:①非零向量a 与b 同向是a =b 的必要不充分条件; ②若AB →与BC →共线,则A ,B ,C 三点在同一条直线上; ③a 与b 是非零向量,若a 与b 同向,则a 与-b 反向; ④设λ,μ为实数,若λa =μb ,则a 与b 共线. 其中错误说法的序号是________. 答案 ④解析 根据向量的有关概念可知①②③正确,对于④,当λ=μ=0时,a 与b 不一定共线,故④错误.感悟升华 1.相等的向量不仅模相等,而且方向要相同,所以相等向量一定是平行向量,而平行向量未必是相等向量.2.向量与数量不同,数量可以比较大小,向量则不能,但向量的模是非负数,可以比较大小.向量可以平移,与起点无关,平移后的向量与原向量相等. 3.(1)单位向量的特征是长度都是1个单位.(2)零向量的特征是长度是0,并规定零向量与任何向量平行. 考点二 向量的线性运算角度1 平面向量的加、减运算的几何意义【例1】 已知两个非零向量a ,b 满足|a +b |=|a -b |,则下列结论正确的是( ) A .a ∥b B .a ⊥b C .|a |=|b | D .a +b =a -b答案 B解析 由已知a ,b 不共线,在▱ABCD 中,设AB →=a ,AD →=b ,由|a +b |=|a -b |,知|AC →|= |DB →|,从而▱ABCD 为矩形,即AB ⊥AD ,故a ⊥b .角度2 向量的线性运算【例2】 (2021·成都七中诊断)如图,AB 是圆O 的一条直径,C ,D 为半圆弧的两个三等分点,则AB →=( )A.AC →-AD → B .2AC →-2AD → C.AD →-AC →D .2AD →-2AC → 答案 D解析 连接CD ,∵C ,D 是半圆弧的三等分点, ∴CD ∥AB ,且AB =2CD ,因此AB →=2CD →=2(AD →-AC →)=2AD →-2AC →. 角度3 利用向量的线性运算求参数【例3】 (2021·长春调研)在△ABC 中,延长BC 至点M 使得BC =2CM ,连接AM ,点N 为AM 上一点且AN →=13AM →,若AN →=λAB →+μAC →,则λ+μ=( )A.13 B .12C .-12D .-13答案 A解析 由题意,知AN →=13AM →=13(AB →+BM →)=13AB →+13×32BC →=13AB →+12(AC →-AB →)=-16AB →+12AC →,又AN →=λAB →+μAC →,所以λ=-16,μ=12,则λ+μ=13.感悟升华 1.(1)解决平面向量线性运算问题的关键在于熟练地找出图形中的相等向量,并能熟练运用相反向量将加减法相互转化.(2)在求向量时要尽可能转化到平行四边形或三角形中,运用平行四边形法则、三角形法则及三角形中位线定理、相似三角形对应边成比例等平面几何的性质,把未知向量转化为用已知向量线性表示.2.与向量的线性运算有关的参数问题,一般是构造三角形,利用向量运算的三角形法则进行加法或减法运算,然后通过建立方程(组)即可求得相关参数的值.【训练1】 (1)在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB →=( )A.34AB →-14AC → B .14AB →-34AC →C.34AB →+14AC → D .14AB →+34AC →(2)(2021·济南质检)在正六边形ABCDEF 中,对角线BD ,CF 相交于点P .若AP →=xAB →+yAF →,则x +y =( ) A .2B .52C .3D .72答案 (1)A (2)B解析 (1)∵E 是AD 的中点,∴EA →=-12AD →,∴EB →=EA →+AB →=-12AD →+AB →,又知D 是BC 的中点,∴AD →=12(AB →+AC →),因此EB →=-14(AB →+AC →)+AB →=34AB →-14AC →.(2)如图,记正六边形ABCDEF 的中心为点O ,连接OB ,OD ,易证四边形OBCD 为菱形,且P 恰为其中心,于是FP →=32FO →=32AB →,因此AP →=AF →+FP →=32AB →+AF →,因为AP →=xAB →+yAF →,所以x =32且y =1,故x +y =52.考点三 共线定理及其应用【例4】 (1)设e 1与e 2是两个不共线向量,AB →=3e 1+2e 2,CB →=ke 1+e 2,CD →=3e 1-2ke 2,若A ,B ,D 三点共线,则k 的值为________.(2)(2021·合肥模拟)在平行四边形 ABCD 中,若DE →=EC →,AE 交BD 于F ,则AF →=( ) A.23AB →+13AD → B .23AB →-13AD →C.13AB →-23AD → D .13AB →+23AD →答案 (1)-94(2)D解析 (1)因为A ,B ,D 三点共线,所以必存在一个实数λ,使得AB →=λBD →. 又AB →=3e 1+2e 2,CB →=ke 1+e 2,CD →=3e 1-2ke 2, 所以BD →=CD →-CB →=3e 1-2ke 2-(ke 1+e 2) =(3-k )e 1-(2k +1)e 2,所以3e 1+2e 2=λ(3-k )e 1-λ(2k +1)e 2,又e 1与e 2不共线,所以⎩⎪⎨⎪⎧3=λ3-k ,2=-λ2k +1,解得k =-94.(2)如图所示,∵DE →=EC →, ∴E 为CD 中点, 设AF →=λAE → =λ⎝⎛⎭⎫AB →+BC →+12CD → =λ⎝⎛⎭⎫AB →+AD →-12AB →=λ2AB →+λAD →.又∵点B ,F ,D 共线,∴λ2+λ=1,解得λ=23.故AF →=13AB →+23AD →.感悟升华 1.证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.2.向量a ,b 共线是指存在不全为零的实数λ1,λ2,使λ1a +λ2b =0成立.【训练2】 (1)已知a ,b 是不共线的向量,AB →=λa +b ,AC →=a +μb ,λ,μ∈R ,则A ,B ,C 三点共线的充要条件为( ) A .λ+μ=2 B .λ-μ=1 C .λμ=-1D .λμ=1(2)已知A ,B ,C 是直线l 上不同的三个点,点O 不在直线l 上,则使等式x 2OA →+xOB →+BC →=0成立的实数x 的取值集合为________. 答案 (1)D (2){-1}解析 (1)因为A ,B ,C 三点共线,所以AB →∥AC →,设AB →=mAC →(m ≠0),则λa +b =m (a +μb ),由于a 与b 不共线,所以⎩⎪⎨⎪⎧λ=m ,1=mμ,所以λμ=1.(2)因为BC →=OC →-OB →,所以x 2OA →+xOB →+OC →-OB →=0,即OC →=-x 2OA →-(x -1)OB →,因为A ,B ,C 三点共线, 所以-x 2-(x -1)=1,即x 2+x =0, 解得x =0或x =-1.当x =0时,x 2OA →+xOB →+BC →=0,此时B ,C 两点重合, 不合题意,舍去.故x =-1.A 级 基础巩固一、选择题1.已知下列各式:①AB →+BC →+CA →;②AB →+MB →+BO →+OM →;③OA →+OB →+BO →+CO →;④AB →-AC →+BD →-CD →,其中结果为零向量的是( ) A .① B .② C .①③ D .①④答案 D解析 利用向量运算,易知①,④的结果为零向量. 2.已知AB →=a +5b ,BC →=-3a +6b ,CD →=4a -b ,则( ) A .A ,B ,D 三点共线 B .A ,B ,C 三点共线 C .B ,C ,D 三点共线 D .A ,C ,D 三点共线答案 A解析 由题意得BD →=BC →+CD →=a +5b =AB →,又BD →、AB →有公共点B ,所以A ,B ,D 三点共线.故选A.3.设a 是非零向量,λ是非零实数,下列结论中正确的是( ) A .a 与λa 的方向相反 B .a 与λ2a 的方向相同 C .|-λa |≥|a | D .|-λa |≥|λ|·a答案 B解析 当λ>0时,a 与λa 的方向相同,A 错,a 与λ2a 的方向相同,B 正确;当|λ|<1时, |-λa |<|a |,C 错;|-λa |=|λ||a |,D 错,故选B.4.在△ABC 中,G 为重心,记AB →=a ,AC →=b ,则CG →=( ) A.13a -23b B .13a +23bC.23a -13b D .23a +13b答案 A解析 因为G 为△ABC 的重心, 所以AG →=13(AB →+AC →)=13a +13b ,所以CG →=CA →+AG →=-b +13a +13b =13a -23b .5.(2021·衡水调研)如图所示,在正方形ABCD 中,E 为BC 的中点,F 为AE 的中点,则DF →=( )A .-12AB →+34AD →B.12AB →+23AD →C.13AB →-12AD →D.12AB →-34AD → 答案 D解析 DF →=AF →-AD →, AE →=AB →+BE →.∵E 为BC 的中点,F 为AE 的中点, ∴AF →=12AE →,BE →=12BC →,∴DF →=AF →-AD →=12AE →-AD →=12(AB →+BE →)-AD →=12AB →+14BC →-AD →, 又BC →=AD →,∴DF →=12AB →-34AD →.6. (2021·东北三省三校联考)如图,在平行四边形ABCD 中,E 为BC 的中点,F 为DE 的中点,若AF →=xAB →+34AD →,则x =( )A.34 B .23C .12D .14答案 C解析 连接AE ,因为F 为DE 的中点,所以AF →=12(AD →+AE →),而AE →=AB →+BE →=AB →+12BC →=AB →+12AD →,所以AF →=12(AD →+AE →)=12⎝⎛⎭⎫AD →+AB →+12AD → =12AB →+34AD →, 又AF →=xAB →+34AD →,所以x =12.7.如图所示,设O 是△ABC 内部一点,且OA →+OC →=-2OB →,则△ABC 与△AOC 的面积之比为( )A .4∶1B .2∶1C .3∶2D .4∶3答案 B解析 取AC 的中点D ,连接OD ,则OA →+OC →=2OD →,所以OB →=-OD →,所以O 是AC 边上的中线BD 的中点, 所以S △ABC =2S △OAC ,所以△ABC 与△AOC 面积之比为2∶1.8.在△ABC 中,点D 在线段BC 的延长线上,且BC →=3CD →,点O 在线段CD 上(与点C ,D 不重合),若AO →=xAB →+(1-x )AC →,则x 的取值范围是( ) A.⎝⎛⎭⎫0,12 B .⎝⎛⎭⎫0,13 C.⎝⎛⎭⎫-12,0 D .⎝⎛⎭⎫-13,0 答案 D解析 设CO →=yBC →,因为AO →=AC →+CO →=AC →+yBC → =AC →+y (AC →-AB →)=-yAB →+(1+y )AC →. 因为BC →=3CD →,∴CO →=3yCD →,0<3y <1, 点O 在线段CD 上(与点C ,D 不重合), 所以y ∈⎝⎛⎭⎫0,13,因为AO →=xAB →+(1-x )AC →, 所以x =-y ,所以x ∈⎝⎛⎭⎫-13,0. 二、填空题9.设向量a ,b 不平行,向量λa +b 与a +2b 平行,则实数λ=____________. 答案 12解析 ∵向量a ,b 不平行,∴a +2b ≠0,又向量λa +b 与a +2b 平行,则存在唯一的实数μ,使λa +b =μ(a +2b )成立,即λa +b =μa +2μb ,则得⎩⎪⎨⎪⎧λ=μ,1=2μ,解得λ=μ=12.10.已知S 是△ABC 所在平面外一点,D 是SC 的中点,若BD →=xAB →+yAC →+zAS →,则x +y+z =________. 答案 0解析 依题意得BD →=AD →-AB →=12(AS →+AC →)-AB →=-AB →+12AC →+12AS →,因此x +y +z =-1+12+12=0. 11.若点O 是△ABC 所在平面内的一点,且满足|OB →-OC →|=|OB →+OC →-2OA →|,则△ABC 的形状为________. 答案 直角三角形解析 OB →+OC →-2OA →=(OB →-OA →)+(OC →-OA →)=AB →+AC →,OB →-OC →=CB →=AB →-AC →, ∴|AB →+AC →|=|AB →-AC →|.故A ,B ,C 为矩形的三个顶点,△ABC 为直角三角形.12.在△AOB 中,AC →=15AB →,D 为OB 的中点,若DC →=λOA →+μOB →,则λμ的值为________.答案 -625解析 因为AC →=15AB →,所以AC →=15(OB →-OA →),因为D 为OB 的中点,所以OD →=12OB →,所以DC →=DO →+OC →=-12OB →+(OA →+AC →)=-12OB →+OA →+15(OB →-OA →)=45OA →-310OB →,所以λ=45,μ=-310,则λμ的值为-625.B 级 能力提升13.(多选题)(2021·济南调研)下列命题正确的是( )A .若A ,B ,C ,D 四点在同一条直线上,且AB =CD ,则AB →=CD →B .在△ABC 中,若O 点满足OA →+OB →+OC →=0,则O 点是△ABC 的重心C .若a =(1,1),把a 向右平移2个单位,得到的向量的坐标为(3,1)D .在△ABC 中,若CP →=λ⎝ ⎛⎭⎪⎫CA →|CA →|+CB →|CB →|,则P 点的轨迹经过△ABC 的内心答案 BD 解析 如图,A ,B ,C ,D 四点满足条件,但AB →≠CD →,故A 错误;对于B ,设BC 的中点为D ,当OA →+OB →+OC →=0时,能得到OA →=-(OB →+OC →),所以OA →=-2OD →,所以O 是△ABC 的重心,故B 正确.对于C ,向量由向量的方向和模确定,平移不改变这两个量,故C 错误.对于D ,根据向量加法的几何意义知,以CA →|CA →|,CB→|CB →|为邻边所得到的平行四边形是菱形,点P 在该菱形的对角线上,由菱形的对角线平分一组对角,得P 点在∠ACB 的平分线所在直线上,故D 正确.14.(2021·河南名校联考)在△ABC 中,D ,E 分别为BC ,AC 边上的点,且BD →=2DC →,若BE →=λAB →+34AD →,则λ=( )A .-54B .-43C .-45D .-34答案 A解析 如图,设AE →=xAC →,则BE →=AE →-AB →=xAC →-AB →=x (AD →+DC →)-AB →=x ⎝⎛⎭⎫AD →+12BD →-AB →=xAD →+x 2(AD →-AB →)-AB →=-⎝⎛⎭⎫x 2+1AB →+3x 2AD →. 因为BE →=λAB →+34AD →,所以32x =34,解得x =12.因此λ=-⎝⎛⎭⎫x 2+1=-54. 15.直线l 上有不同的三点A ,B ,C ,O 是直线l 外一点,对于向量OA →=(1-cos α)OB →+ sin αOC →(α是锐角)总成立,则α=________. 答案 45°解析 因为直线l 上有不同的三点A ,B ,C ,所以存在实数λ,使得BA →=λBC →, 所以OA →-OB →=λ(OC →-OB →), 即OA →=(1-λ)OB →+λOC →,所以⎩⎪⎨⎪⎧1-λ=1-cos α,λ=sin α,所以sin α=cos α,因为α是锐角,所以α=45°.16.(2020·兰州诊断)在直角梯形ABCD 中,∠A =90°,∠B =30°,AB =23,BC =2,点E 在线段CD 上,若AE →=AD →+μAB →,则μ的取值范围是________. 答案 ⎣⎡⎦⎤0,12 解析 由已知AD =1,CD =3,所以AB →=2DC →. 因为点E 在线段CD 上, 所以DE →=λDC →(0≤λ≤1).因为AE →=AD →+DE →=AD →+λDC →=AD →+λ2AB →,又AE →=AD →+μAB →,所以μ=λ2.1因为0≤λ≤1,所以0≤μ≤2.。
高考数学第一轮复习-第5章 第1讲 平面向量的概念及线性运算 平面向量的基本定理

高考数学第一轮复习 第五章 平面向量第1讲 平面向量的概念及线性运算 平面向量的基本定理考点一 平面向量的线性运算及几何意义入门测1.思维辨析(1)单位向量只与模有关,与方向无关.( ) (2)零向量的模等于0,没有方向.( ) (3)若两个向量共线,则其方向必定相同.( ) (4)若a ∥b ,b ∥c ,则必有a ∥c .( ) (5)AB →+BA →=0.( )2.如图,在正方形ABCD 中,AC 与BD 交于点O ,AB →+BO →+OC →=( )A .0 B.AD →C.AC →D.BD →3.设a 、b 是两个不共线向量,AB →=2a +p b ,BC →=a +b ,CD →=a -2b ,若A 、B 、D 三点共线,则实数p 的值为________.解题法命题法 对概念的理解、运算和共线定理的应用 典例 (1)下列说法中: ①若|a |=|b |,则a =b ;②若A ,B ,C ,D 是不共线的四点,则AB →=DC →是四边形ABCD 为平行四边形的充要条件;③若a =b ,b =c ,则a =c ;④a =b 的充要条件是|a |=|b |且a ∥b ; ⑤若a ∥b ,b ∥c ,则a ∥c . 其中正确命题的序号是( ) A .②③B .①②C .③④D .④⑤(2)已知O ,A ,B 是平面上的三个点,直线AB 上有一点C ,满足2AC →+CB →=0,则OC →=( )A .2OA →-OB → B .-OA →+2OB → C.23OA →-13OB →D .-13OA →+23OB →(3)已知向量a ,b 不共线,c =k a +b (k ∈R ),d =a -b ,如果 c ∥d ,那么( )A .k =1且c 与d 同向B .k =1且c 与d 反向C .k =-1且c 与d 同向D .k =-1且c 与d 反向对点练1.设D 为△ABC 所在平面内一点,BC →=3CD →,则( ) A.AD →=-13AB →+43AC →B.AD →=13AB →-43AC →C.AD →=43AB →+13AC →D.AD →=43AB →-13AC →2.已知点A ,B ,C 在圆x 2+y 2=1上运动,且AB ⊥BC .若点P 的坐标为(2,0),则|P A →+PB →+PC →|的最大值为( )A .6B .7C .8D .93.对任意向量a ,b ,下列关系式中不恒成立的是( )A .|a ·b |≤|a ||b |B .|a -b |≤||a |-|b ||C .(a +b )2=|a +b |2D .(a +b )·(a -b )=a 2-b 24.记max{x ,y }=⎩⎪⎨⎪⎧ x ,x ≥y ,y ,x <y ,min{x ,y }=⎩⎪⎨⎪⎧y ,x ≥y ,x ,x <y ,设a ,b 为平面向量,则( )A .min{|a +b |,|a -b |}≤min{|a |,|b |}B .min{|a +b |,|a -b |}≥min{|a |,|b |}C .max{|a +b |2,|a -b |2}≤|a |2+|b |2D .max{|a +b |2,|a -b |2}≥|a |2+|b |25.设向量a ,b 不平行,向量λa +b 与a +2b 平行,则实数λ=________.6.已知向量OA →⊥AB →,|OA →|=3,则OA →·OB →=________.7.设0<θ<π2,向量a =(sin2θ,cos θ),b =(cos θ,1),若a ∥b ,则tan θ=________.考点二 平面向量的基本定理及坐标表示入门测1.思维辨析(1)平面向量不论经过怎样的平移变换之后其坐标不变.( ) (2)平面内任何两个不共线的向量均可作为一组基底.( )(3)向量AB →与BC →的夹角为∠ABC .( )(4)在同一组基底下同一向量的表现形式是唯一的.( )2.已知点A (-1,1),点B (2,y ),向量a =(1,2),若AB →∥a ,则实数y 的值为( ) A .5 B .6 C .7D .8 3.在平行四边形ABCD 中,AC 为一条对角线,若AB →=(2,4),AC →=(1,3),则BD →=( )A .(-2,-4)B .(-3,-5)C .(3,5)D .(2,4)解题法命题法 向量共线,垂直的条件和共线向量基本定理的应用典例 (1)在下列向量组中,可以把向量a =(3,2)表示出来的是( ) A .e 1=(0,0),e 2=(1,2) B .e 1=(-1,2),e 2=(5,-2) C .e 1=(3,5),e 2=(6,10) D .e 1=(2,-3),e 2=(-2,3)(2)已知向量a =(1,-2),b =(m,4),且a ∥b ,则2a -b =( ) A .(4,0) B .(0,4) C .(4,-8)D .(-4,8)(3)在梯形ABCD 中,已知AB ∥CD ,AB =2CD ,M ,N 分别为CD ,BC 的中点.若AB →=λAM→+μAN →,则λ+μ=________.【解题法】 平面向量基本定理的应用及其坐标运算技巧 (1)共线问题的解题策略①向量共线的充要条件中,当两向量共线时,通常只有非零向量才能表示与之共线的其他向量,注意待定系数法和方程思想的运用.②证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得到三点共线.③若a 与b 不共线且λa =μb ,则λ=μ=0.④直线的向量式参数方程,A ,P ,B 三点共线⇔OP →=(1-t )·OA →+tOB →(O 为平面内任一点,t∈R ).⑤OA →=λOB →+μOC →(λ,μ为实数),若A ,B ,C 三点共线,则λ+μ=1. (2)用平面向量基本定理解决问题的一般思路①先选择一组基底,并运用平面向量基本定理将条件和结论表示成该基底的线性组合,再进行向量的运算.②在基底未给出的情况下,合理地选取基底会给解题带来方便,另外,要熟练运用线段中点的向量表达式.(3)坐标运算的技巧向量的坐标运算主要是利用加、减、数乘运算法则进行,若已知有向线段两端点的坐标,则应先求出向量的坐标,解题过程中要注意方程思想的运用及正确使用运算法则,以向量为载体,可以解决三角函数、解析几何中的有关问题.对点练1.已知向量a =(1,2),b =(3,1),则b -a =( ) A .(-2,1) B .(2,-1) C .(2,0) D .(4,3) 2.已知向量a =(1,2),b =(2,-3).若向量c 满足(c +a )∥b ,c ⊥(a +b ),则c =( )A.⎝⎛⎭⎫79,73B.⎝⎛⎭⎫-73,-79C.⎝⎛⎭⎫73,79D.⎝⎛⎭⎫-79,-73 3.在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+yAC →,则x =_______;y =_______.4.已知向量a =(2,1),b =(1,-2).若m a +n b =(9,-8)(m ,n ∈R ),则m -n 的值为________. 5.设向量a =(3,3),b =(1,-1).若(a +λb )⊥(a -λb ),则实数λ=________.6.在平面直角坐标系中,O 为原点,A (-1,0),B (0,3),C (3,0),动点D 满足|CD →|=1,则|OA →+OB →+OD →|的最大值是________.7. 如图所示,在△ABC 中,点M 是AB 的中点,且AN →=12NC →,BN 与CM 相交于点E ,设AB→=a ,AC →=b ,用基底a ,b 表示向量AE →=________.微型专题 以向量坐标运算为载体的创新问题创新考向以向量的坐标运算为载体的创新问题是近几年高考命题的一个热点,综合考查向量与函数等知识,考查学生的应变能力与创新能力.创新例题在平面直角坐标系中,若O 为坐标原点,则A ,B ,C 三点在同一直线上的充要条件为存在唯一的实数λ,使得OC →=λOA →+(1-λ)OB →成立,此时称实数λ为“向量OC →关于OA →和OB →的终点共线分解系数”.若已知P 1(3,1),P 2(-1,3),P 1,P 2,P 3三点共线且向量OP 3→与向量a =(1,-1)共线,则“向量OP 3→关于OP 1→和OP 2→的终点共线分解系数”为( )A .-3B .3C .1D .-1已知平行四边形三个顶点的坐标分别为(-1,0),(3,0),(1,-5),求第四个顶点的坐标.课时练 基础组1已知非零向量a ,b ,则“a +b =0”是“a ∥b ”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分又不必要条件2.已知△ABC 的三个顶点A ,B ,C 及其所在平面内一点P 满足P A →+PB →+PC →=AB →,则( )A .P 在△ABC 内B .P 在△ABC 外 C .P 在直线AB 上D .P 是AC 边的一个三等分点3.如图所示,在平行四边形ABCD 中,E 是BC 的中点,F 是AE 的中点,若AB →=a ,AD →=b ,则AF →=( )A.12a +14b B.14a +12b C.12a -14b D.14a -12b 4.设a =(1,2),b =(1,1),c =a +k b .若b ⊥c ,则实数k 的值等于( )A .-32B .-53C.53D.32 5.设向量a =(x,1),b =(4,x ),且a ,b 方向相反,则x 的值是( )A .2B .-2C .±2D .0 6.[2016·武邑中学模拟]已知向量OA →=(k,12),OB →=(4,5),OC →=(-k,10),且A ,B ,C 三点共线,则k 的值是( )A .-23B.43C.12D.137.如图,已知|OA →|=1,|OB →|=3,OA →·OB →=0,点C 在线段AB 上,且∠AOC =30°,设OC →=mOA →+nOB →(m ,n ∈R ),则mn=( )A.13 B .3 C.33D. 38.O 是平面上一定点,A 、B 、C 是平面上不共线的三个点,动点P 满足OP→=OA→+λ⎝ ⎛⎭⎪⎫AB →|AB →|+AC →|AC →|,λ∈[0,+∞),则P 的轨迹一定通过△ABC 的( ) A .外心 B .内心 C .重心D .垂心9.已知D 为三角形ABC 边BC 的中点,点P 满足P A →+BP →+CP →=0,AP →=λPD →,则实数λ的值为________.10. △ABC 的三内角A 、B 、C 所对的边分别为a 、b 、c ,设向量m =(3c -b ,a -b ),n =(3a +3b ,c ),m ∥n ,则cos A =________.11.已知点O (0,0)、A (1,2)、B (4,5)及OP →=OA →+tAB →,试问: (1)t 为何值时,P 在x 轴上?在y 轴上?P 在第三象限?(2)四边形OABP 能否成为平行四边形?若能,求出相应的t 值;若不能,请说明理由. 12.在直角坐标系xOy 中,已知点A (1,1),B (2,3),C (3,2),点P (x ,y )在△ABC 三边围成的区域(含边界)上.(1)若P A →+PB →+PC →=0,求|OP →|;(2)设OP →=mAB →+nAC →(m ,n ∈R ),用x ,y 表示m -n ,并求m -n 的最大值.能力组13设a 是已知的平面向量且a ≠0,关于向量a 的分解,有如下四个命题: ①给定向量b ,总存在向量c ,使a =b +c ;②给定向量b 和c ,总存在实数λ和μ,使a =λb +μc ;③给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使a =λb +μc ; ④给定正数λ和μ,总存在单位向量b 和单位向量c ,使a =λb +μc .上述命题中的向量b ,c 和a 在同一平面内且两两不共线,则真命题的个数是( ) A .1 B .2 C .3D .4 14.已知向量OA →=(1,3),OB →=(3,-1),且AP →=2PB →,则点P 的坐标为( ) A .(2,-4) B.⎝⎛⎭⎫23,-43 C.⎝⎛⎭⎫73,13D .(-2,4)15.在△ABC 中,∠ACB 为钝角,AC =BC =1,CO →=xCA →+yCB →且x +y =1,函数f (m )=|CA→-mCB →|的最小值为32,则|CO →|的最小值为________.16.如图,已知△OCB 中,A 是CB 的中点,D 是将OB →分成2∶1的一个内分点,DC 和OA交于点E ,设OA →=a ,OB →=b .(1)用a 和b 表示向量OC →,DC →; (2)若OE →=λOA →,求实数λ的值.。
2019-2020年高三数学一轮复习讲义 平面向量的概念及线性运算教案 新人教A版

2019-2020年高三数学一轮复习讲义 平面向量的概念及线性运算教案 新人教A 版自主梳理1.向量的有关概念(1)向量的定义:既有__大小____又有__方向____的量叫做向量.平面向量是自由向量 (2)表示方法: 用 有向线段 来表示向量.有向线段的长度表示向量的大小,箭头所指的方向表示向量的方向. 用字母a ,b ,…或用AB →,BC →,…表示. (3)模:向量的__长度____叫向量的模,记作___ |a |__或____. 向量的两要素向量具有大小和方向两个要素.用有向线段表示向量时,与有向线段起点的位置没有关系.同向且等长的有向线段都表示同一向量.或者说长度相等、方向相同的向量是相等的.向量只有相等或不等,而没有谁大谁小之说,即向量不能比较大小.(4)零向量:长度为零的向量叫做零向量,记作0;零向量的方向是__任意的___. (5)单位向量:长度为_1个___单位长度的向量叫做单位向量.与a 平行的单位向量e =__±a|a|___. (6)平行向量:方向__相同___或__相反__的__非零___向量;平行向量又叫___ 共线向量_________,任一组平行向量都可以移到同一直线上.规定:0与任一向量_平行 __. 向量平行与直线平行的区别向量平行包括向量共线和重合的情况,而直线平行不包括共线的情况.因而要利用向量平行证明向量所在直线平行,必须说明这两条直线不重合.(7)相等向量:长度___相等___且方向__相同___的向量.2.向量的加法运算及其几何意义(1)已知非零向量a ,b ,在平面内任取一点A ,作AB →=a ,BC →=b ,则向量AC →叫做a 与b 的 和 ,记作 a +b ,即 a +b =AB →+BC →= AC →,这种求向量和的方法叫做向量加法的 三角形法则 . (2)以同一点O 为起点的两个已知向量a ,b 为邻边作平行四边形OACB ,则以O 为起点的对角线OA →就是a 与b 的和,这种作两个向量和的方法叫做向量加法的 平行四边形法则 .(3)加法运算律a +b =___ b +a _____ (交换律);(a +b )+c =__ a +(b +c )__________(结合律). 3.向量的减法及其几何意义 (1)相反向量与a ____长度相等__、____方向相反__的向量,叫做a 的相反向量,记作__-a ____. (2)向量的减法① 定义a -b =a +__(-b ) __,即减去一个向量相当于加上这个向量的__相反向量____.② 图,AB →=a ,,AD →=b ,则AC →= a +b ,DB →=__ a -b ____.4.向量数乘运算及其几何意义(1)定义:实数λ与向量a 的积是一个向量,记作__λa ____,它的长度与方向规定如下: ①|λa |=___|λ||a | ___;②当λ>0时,λa 与a 的方向__相同____;当λ<0时,λa 与a 的方向__相反______;当λ=0时,λa =____. (2)运算律设λ,μ是两个实数,则① λ(μa )=__(λμ)a ___.(结合律)② (λ+μ)a =__λa +μa ___.(第一分配律) ③λ(a +b )=__λa +λb ____.(第二分配律) (3)两个向量共线定理:向量b 与a (a ≠0)共线的充要条件是存在唯一一个实数λ,使b =λa .5.重要结论PG →=13(PA →+PB →+PC →)⇔G 为△ABC 的___重心__;PA →+PB →+PC →=0⇔P 为△ABC 的___重心___.3.共线向量定理向量a (a ≠0)与b 共线的充要条件是存在唯一一个实数λ,使得___ b =λa _. 自我检测1.设点M 是线段BC 的中点,点A 在直线BC 外,,|,|则|AM →|等于 ( )A .8B .4C .2D .1 1.2.下列四个命题:①对于实数m 和向量a ,b ,恒有m (a -b )=m a -m b ;②对于实数m 和向量a ,b (m ∈R ),若m a =m b ,则a =b ;③若m a =n a (m ,n ∈R ,a ≠0),则m =n ; ④若a =b ,b =c ,则a =c , 其中正确命题的个数为 ( )A .1B .2C .3D .42.C [①根据实数与向量积的运算可判断其正确;②当m =0时,m a =m b =0,但a 与b 不一定相等,故②错误;③正确;④由于向量相等具有传递性,故④正确.] 3.如图,正六边形ABCDEF 中,++=( )A .0 B. C. D .4.设P 是△ABC 所在平面内的一点,+=2,则( )A.=0 B .+=0 C.+=0 D.+=05.在平行ABCD 中,AB →=a ,AD →=b ,AN →=3NC →,M 为BC 的中点,则MN →等于 ( )A .-14a +14bB .-12a +12bC .a +12bD .-34a +34bA [由AN →=3NC →得4AN →=3AC →=3(a +b ),又AM →=a +12b ,所以MN →=34(a +b )-⎝ ⎛⎭⎪⎫a +12b =-14a +14b .] 6.已知△ABC 和点M 满足MA →+MB →+MC →=0.若存在实数m 使得AB →+AC →=m 成立,则m 等于 ( )A .2B .3C .4D .5 B [由题目条件可知,M 为△ABC 的重心,连接AM 并延长交BC 于D , 则AM →=23AD →,①因为AD 为中线,AB →+AC →=2AD →=mAM →,即2AD →=mAM →,② 联立①②可得m =3.]7.在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的中点,若AC →=λAE →+μAF →,其中λ、μ∈R ,则λ+μ=______.解析 设AB →=a ,AD →=b ,那么AE →=a +b ,AF →=a +12b ,又∵AC →=a +b ,AC →=23(AE →+AF →),即λ=μ=23,∴λ+μ=43.例1 ①有向线段就是向量,向量就是有向线段;②向量a 与向量b 平行,则a 与b 的方向相同或相反;③向量AB →与向量CD →共线,则A 、B 、C 、D 四点共线; ④如果a ∥b ,b ∥c ,那么a ∥c .⑤a =b 的充要条件是|a |=|b |且a ∥b .以上命题中正确的个数为 ( )A .1B .2C .3D .0 [①不正确,向量可以用有向线段表示,但向量不是有向线段;②不正确,若a 与b 中有一个为零向量时也互相平行,但零向量的方向是不确定的,故两向量方向不一定相同或相反;③不正确,共线向量所在的直线可以重合,也可以平行; ④不正确,如果b =0时,则a 与c 不一定平行.探究提高 (1)正确理解向量的相关概念及其含义是解题的关键. (2)相等向量具有传递性,非零向量的平行也具有传递性. (3)共线向量即为平行向量,它们均与起点无关.(4)向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象移动混为一谈.(5)非零向量a 与a |a |的关系是:a |a |是a 方向上的单位向量.变式训练1 (1)下列命题中正确的有________(填写所有正确命题的序号). ①|a |=|b |⇒a =b ; ②若a =b ,b =c ,则a =c ;③|a |=0⇒a =0; ④若 a =b ,则|a|=|b|;⑤若λ=0,则λa =0;⑥若A 、B 、C 、D 是不共线的四点,则AB →=DC →⇔四边形ABCD 是平行四边形.⑦若将所有的单位向量都平移到同一个起点,则它们的终点在同一个单位圆上. 变式训练1解析 ①模相同,方向不一定相同,故①不正确;②两向量相等,要满足模相等且方向相同,故向量相等具备传递性,②正确; ③ 只有零向量的模才为0,故③正确;⑥④AB →=DC →,即模相等且方向相同,即平行四边形对边平行且相等.故⑥正确. 故应选②③④⑤⑥⑦.(2)判断下列命题是否正确,不正确的请说明理由. (1)若向量a 与b 同向,且|a |>|b |,则a>b ;(2)若|a |=|b |,则a 与b 的长度相等且方向相同或相反; (3)若|a |=|b |,且a 与b 方向相同,则a =b ;(4)由于零向量的方向不确定,故零向量不与任意向量平行; (5)若向量a 与向量b 平行,则向量a 与b 的方向相同或相反; (6)起点不同,但方向相同且模相等的几个向量是相等向量; (7)任一向量与它的相反向量不相等.解 (1)不正确,因为向量只讨论相等和不等,而不能比较大小.(2)不正确,因为向量模相等与向量的方向无关.(3)正确.(4)不正确,因为规定零向量与任意向量平行.(5)不正确,因为两者中若有零向量,零向量的方向是任意的.(6)正确. 对于一个向量只要不改变其大小与方向,是可以任意平行移动的. (7)不正确,因为零向量可以与它的相反向量相等.二 向量的线性运算例2 在△ABC 中,D 、E 分别为BC 、AC 边 上的中点,G 为BE 上一点,且GB =2GE , 设AB →=a ,AC →=b ,试用a ,b 表示AD →,AG →.解 AD →=12(AB →+AC →)=12a +12b ;AG →=AB →+BG →=AB →+23BE →=AB →+13(BA →+BC →)=23AB →+13(AC →-AB →)=13AB →+13AC →=13a +13b .探究提高 (1)解题的关键在于搞清构成三角形的三个问题间的相互关系,能熟练地找出图形中的相等向量,并能熟练运用相反向量将加减法相互转化.(2)用几个基本向量表示某个向量问题的基本技巧:①观察各向量的位置;②寻找相应的三角形或多边形;③运用法则找关系;④化简结果. 变式训练2 (1)在△ABC 中,E 、F 分别为AC 、AB 的 中点,BE 与CF 相交于G 点,设AB →=a ,AC →=b , 试用a ,b 表示AG →.解 AG →=AB →+BG →=AB →+λBE →= == .又AG →=AC →+CG →=AC →+mCF →=AC →+m 2(CA →+CB →)=(1-m )AC →+m 2AB →=m2a +(1-m )b ,∴⎩⎪⎨⎪⎧1-λ=m21-m =λ2,解得λ=m =23,∴AG →=13a +13b .(2)如图所示,若四边形ABCD 是一个等腰梯形,AB ∥DC ,M 、N 分别是DC 、AB 的中点,已知AB →=a ,AD →=b ,DC →=c ,试用a 、b 、c 表示BC →,MN →,DN →+CN →.变式迁移2 解 BC →=BA →+AD →+DC →题型三 共线向量问题例3 设两个非零向量a 与b 不共线,(1)若AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ),求证:A 、B 、D 三点共线; (2)试确定实数k ,使k a +b 和a +k b 共线.(1)证明 ∵AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ), ∴BD →=BC →+CD →=2a +8b +3(a -b)=2a +8b +3a -3b =5(a +b )=5AB →. ∴AB →、BD →共线,又∵它们有公共点B , ∴A 、B 、D 三点共线.(2)解 ∵k a +b 与a +k b 共线, ∴存在实数λ,使k a +b =λ(a +k b ), 即k a +b =λa +λk b .∴(k -λ)a =(λk -1)b . ∵a 、b 是不共线的两个非零向量,∴k -λ=λk -1=0,∴k 2-1=0.∴k =±1.探究提高 (1)证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.(2)向量a 、b 共线是指存在不全为零的实数λ1,λ2,使λ1a +λ2b =0成立,若λ1a +λ2b =0,当且仅当λ1=λ2=0时成立,则向量a 、b 不共线.变式训练3 (1) 设两个非零向量e 1和e 2不共线.①如果AB →=e 1-e 2,BC →=3e 1+2e 2,CD →=-8e 1-2e 2,求证:A 、C 、D 三点共线;②如果AB →=e 1+e 2,BC →=2e 1-3e 2,CD →=2e 1-k e 2,且A 、C 、D 三点共线,求k 的值.(1)证明∵AB →=e 1-e 2,BC →=3e 1+2e 2,CD →=-8e 1-2e 2, ∴AC →=AB →+BC →=e 1-e 2+3e 1+2e 2=4e 1+e 2=(-8e 1-2e 2) =CD →. ∴AC →与CD →共线.又∵AC →与CD →有公共点C ,∴A 、C 、D 三点共线.(2)AC →=AB →+BC →=(e 1+e 2)+(2e 1-3e 2) =3e 1-2e 2,∵A 、C 、D 三点共线, ∴AC →与CD →共线.从而存在实数λ使得AC →=λCD → 即3e 1-2e 2=λ(2e 1-k e 2).由平面向量的基本定理得⎩⎪⎨⎪⎧3=2λ,-2=-λk .解之,得⎩⎪⎨⎪⎧λ=32,k =43.∴k 的值为43.(2)如图所示,△ABC 中,在AC 上取一点N ,使得AN =13AC ,在AB 上取一点M ,使得AM =13AB ,在BN 的延长线上取点P ,使得NP =12BN ,在CM 的延长 线上取点Q ,使得MQ →=λCM →时,AP →=QA →,试确定λ的值. 解:∵AP →=NP →-NA →=12(BN →-CN →)=12(BN →+NC →)=12BC →, QA →=MA →-MQ →=12BM →+λMC →,又∵AP →=QA →,∴12BM →+λMC →=12BC →,即λMC →=12MC →,∴λ=12.(3)如图所示,平行四边形ABCD 中,AD →=b ,AB →=a ,M 为AB 中点,N 为BD 靠近B 的三等分点,求证:M 、N 、C 三点共线.证明 在△ABD 中BD →=AD →-AB →.因为AB →=a, AD →=b ,所以BD →=b -a .由共线向量定理知:CM →∥CN →,又∵CM →与CN →有公共点C ,∴M 、N 、C 三点共线.(4)设,不共线,点P 在AB 上,求证:=λ+μ且λ+μ=1,λ,μ∈R . 证明:∵P 在AB 上,∴与共线. ∴=t .∴-=t (-). ∴=+t -t =(1-t )+t .设1-t =λ,t =μ,则=λ+μ且λ+μ=1,λ,μ∈R .用方程思想解决平面向量的线性运算问题如图所示,在△ABO 中,OC →=14OA →, OD →=12OB →,AD 与BC相交于点M ,设OA →=a , OB →=b .试用a 和b 表示向量OM →.解 设OM →=m a +n b ,则AM →=OM →-OA →=m a +n b -a =(m -1)a +n b .AD →=OD →-OA →=12OB →-OA →=-a +12b .又∵A 、M 、D 三点共线,∴AM →与AD →共线.∴存在实数t ,使得AM →=tAD →,即(m -1)a +n b =t ⎝ ⎛⎭⎪⎫-a +12b .∴(m -1)a +n b =-t a +12t b .∴⎩⎪⎨⎪⎧m -1=-t n =t 2,消去t 得,m -1=-2n ,即m +2n =1.①又∵CM →=OM →-OC →=m a +n b -14a =⎝ ⎛⎭⎪⎫m -14a +n b ,CB →=OB →-OC →=b -14a =-14a +b .又∵C 、M 、B 三点共线,∴CM →与CB →共线.∴存在实数t 1,使得CM →=t 1CB →,∴⎝ ⎛⎭⎪⎫m -14a +n b =t 1⎝ ⎛⎭⎪⎫-14a +b ,∴⎩⎪⎨⎪⎧m -14=-14t 1n =t 1,消去t 1得,4m +n =1.②由①②得m =17,n =37,∴OM →=17a +37b .变式训练4综合问题如图,OM ∥AB ,点P 在由射线OM 、线段OB 及AB 的延长线围成 的阴影区域内(不含边界)运动,且OP →=xOA →+yOB →,则x 的取值范围是 ________;当x =-12时,y 的取值范围是________.解析:由题意得:OP →=a ·OM →+b ·OB →(a ,b ∈R +,0<b <1)=a ·λAB →+b ·OB → (λ>0)=a λ(OB →-OA →)+b ·OB =-αλ·OA →+(αλ+b )·OB →.由-a λ<0,求得x ∈(-∞,0).又由OP →=xOA →+yOB →,则有0<x +y <1,当x =-12时,有0<-12+y <1,求得:y ∈⎝ ⎛⎭⎪⎫12,32.答案:(-∞,0) ⎝ ⎛⎭⎪⎫12,32变式训练5如图,平面内有三个向量 其中的夹角为1200,的夹角为300, 且||1,|23,OA OB OC ===|||则 的值是_6__.在△ABC 中, O 是△ABC 的重心.∠A,∠B, ∠C 的对边分别为a ,b ,c,若 求证△ABC 是等边三角形.λμ+平面向量的概念及线性运算练习一一、选择题1.若O 、E 、F 是不共线的任意三点,则以下各式中成立的是 ( ) A.EF →=OF →+OE → B.EF →=OF →-OE → C.EF →=-OF →+OE → D. EF →=-OF →-OE →2. 已知O 是△ABC 所在平面内一点,D 为BC 边中点,且2OA →+OB →+OC →=0,那么( ) A .AO →=OD →B.AO →=2OD →C.AO →=3OD →D.2AO →=OD →3.如图,正六边形 ABCDEF 中,++= ( ) A .0 B . C .D .4. 设P 是△ABC 所在平面内的一点,+=2,则( ) A .P 、A 、B 三点共线 B .P 、A 、C 三点共线 C .P 、B 、C 三点共线D .以上均不正确5.已知向量a ,b 不共线,c =k a +b (k ∈R ),d =a -b .如果c ∥d ,那么 ( )A.k =1且c 与d 同向B.k =1且c 与d 反向C.k =-1且c 与d 同向 D .k =-1且c 与d 反向6.在△ABC 中,已知D 是AB 边上一点,AD →=2DB →,CD →=13CA →+λCB →,则λ等于( )A .23 B.13 C .-13 D .-237. 在△ABC 中,M 为边BC 上任意一点,N 为AM 中点, =λ+μ,则λ+μ的值为( ) A .12B.13C.14D .18.在四边形ABCD 中,=,且·=0,则四边形ABCD 是 ( )A .矩形B .菱形C .直角梯形D .等腰梯形9.如图,e1,e 2为互相垂直的单位向量,则 向量a -b 可表示为 ( ) A .3e 2-e 1 B .-2e 1-4e 2 C .e 1-3e 2 D .3e 1-e 210.已知向量p =a |a |+b|b |,其中a 、b 均为非零向量,则|p |的取值范围是 ( )A .[0,2]B .[0,1]C .(0,2]D .[0,2]11.化简:(1)AB →+BC →+CD →=________; (2)AB →-AD →-DC →=________;(3)(AB →-CD →)-(AC →-BD →)=________.12.已知在平面上不共线的四点O 、A 、B 、C ,若OA →-3OB →+2OC →=0,则|AB →||BC →|=__2______.13.下列命题:①平行向量一定相等;②不相等的向量一定不平行;③平行于同一个向量的两个向量是共线向量;④相等向量一定共线.其中不正确命题的序号是_______.14.已知D 为三角形ABC 边BC 的中点,点P 满足PA →+BP →+CP →=0,AP →=λPD →,则实数λ的值为_____-2____.15.已知|a |=3,|b |=5,且a =λb ,则实数λ的值是____ __. 解析:∵a =λb ,∴a 与b 共线,λ=±35.16.已知a ,b 是不共线的向量,若=λ1a +b ,=a +λ2b (λ1,λ2∈R),则A 、B 、C 三点共线的充要条件为_____.解析:A 、B 、C 三点共线⇔∥⇔λ1λ2-1×1=0⇔λ1λ2=1.17.已知|a |=6,|b |=8,且|a +b |=|a -b |,则|a -b |=__10______.18.已知3x +4y =a,2x -3y =b ,其中a ,b 为已知向量,则向量x =________,y =________.答案:317a +417b 217a -317b19.设两个非零向量a 与b 不共线,(1)若=a +b ,=2a +8b ,=3(a -b ),求证:A 、B 、D 三点共线. (2) 试判断A 、C 、D 三点是否共线,并说明理由. (3)试确定实数k ,使ka +b 和a +kb 共线. 解 (1)∵=a +b ,=2a +8b , =3(a -b ), ∴=+=2a +8b +3(a -b ), =2a +8b +3a -3b =5(a +b )=5.∴、共线,又∵它们有公共点B ,∴A 、B 、D 三点共线. (2)解:A 、C 、D 三点不共线. ∵=a +b ,BC =2a +8b , ∴=+=a +b +2a +8b =3a +9b . 而=3a -3b ,假设存在λ∈R ,使得=λ, 即3a +9b =3λa -3λb .则⎩⎪⎨⎪⎧3=3λ,9=-3λ显然满足上述条件的实数λ不存在,故A 、C 、D 三点不共线.(3)∵ka +b 与a +kb 共线,∴存在实数λ,使ka +b =λ(a +kb ),即ka +b =λa +λkb . ∴(k -λ)a =(λk -1)b .∵a 、b 是不共线的两个非零向量,∴k -λ=λk -1=0,∴k 2-1=0,∴k =±1.20.设两个非零向量e 1和e 2不共线.如果=e 1+e 2,=2e 1-3e 2,=2e 1-ke 2,且A 、C 、D 三点共线,求k 的值.=+=(e 1+e 2)+(2e 1-3e 2)=3e 1-2e 2,∵A 、C 、D 三点共线,∴与共线,从而存在实数λ使得=λ,即3e 1-2e 2=λ(2e 1-ke 2),得⎩⎪⎨⎪⎧3=2λ,-2=-λk ,解得λ=32,k =43.平面向量的概念及线性运算练习二1.给出下列命题:①两个具有公共终点的向量,一定是共线向量; ②两个向量不能比较大小,但它们的模能比较大小;③λa =0 (λ为实数),则λ必为零;④λ,μ为实数,若λa =μb ,则a 与b 共线. 其中错误命题的个数为( )A.1B.2 C .3 D.42.平面向量a ,b 共线的充要条件是 ( ) A .a ,b 方向相同 B .a ,b 两向量中至少有一个为0C .存在λ∈R ,使b =λaD .存在不全为零的实数λ1,λ2,使λ1a +λ2b =0解析:a ,b 共线时,a ,b 方向相同或相反,故A 错.a ,b 共线时,a ,b 不一定是零向量,故B 错.当b =λa 时,a ,b 一定共线,若b ≠0,a =0,则b =λa 不成立,故C 错.排除A 、B 、C.3.下列命题是假命题的是 ( ) A .对于两个非零向量a 、b ,若存在一个实数k 满足a =k b ,则a 、b 共线 B .若a =b ,则|a |=|b | C .若a 、b 为两个非零向量,则|a +b |>|a -b | D .若a 、b 为两个方向相同的向量,则|a +b |=|a |+|b |4.设a ,b 是任意的两个向量,λ∈R ,给出下面四个结论: ①若a 与b 共线,则b =λa ;②若b =-λa ,则a 与b 共线; ③若a =λb ,则a 与b 共线;④当b ≠0时,a 与b 共线的充要条件是有且只有一个实数λ=λ1,使得a =λ1b .其中正确的结论有 ( ) A .①② B .①③ C .①③④ D .②③④5.已知点O ,N 在△ABC 所在平面内,且||=||=||,++=0,则点O ,N 依次是△ABC 的( ) A .重心 外心B .重心 内心C .外心 重心D .外心 内心解析:由||=||=||知,O 为△ABC 的外心;++=0,知,N 为△ABC 的重心. 答案:C6.已知△ABC 中,点D 是BC 的中点,过点D 的直线分别交直线AB 、AC 于E 、F 两点,若=λ (λ>0),=μ (μ>0),则1λ+4μ的最小值是( )A .9B.72 C .5 D.92解析:由题意得,+=2=λ+μ⇔=λ2+μ2,又D 、E 、F 在同一条直线上,可得λ2+μ2=1.所以1λ+4μ=(λ2+μ2)(1λ+4μ)=52+2λμ+μ2λ≥52+2=92,当且仅当2λ=μ时取等号.答案:D7.已知△ABC 的三个顶点A 、B 、C 及平面内一点P 满足+ +=,则点P 与△ABC 的关系为( )A .P 在△ABC 内部B .P 在△ABC 外部C .P 在AB 边所在直线上D .P 是AC 边的一个三等分点 解析:∵++=, ∴++=-,∴=-2=2, ∴P 是AC 边的一个三等分点.8.O 是平面上一定点,A 、B 、C 是平面上不共线的三个点,动点P 满足OP →=OA →+λ(AB →+AC →),λ∈(0,+∞),则点P 的轨迹一定通过△ABC 的 ( ) A .外心 B .垂心 C .内心 D .重心9.已知P 是△ABC 所在平面内的一点,若CB →=λPA →+PB →,其中λ∈R ,则点P 一定在( ) A.△ABC 的内部 B .AC 边所在直线上 C. AB 边所在直线上 D.BC 边所在直线上10.O 是平面上一定点,A 、B 、C 是平面上不共线的三个点,动点P 满足:OP →=OA →+λ ⎝ ⎛⎭⎪⎪⎫AB →|AB →|+AC →|AC →|,λ∈[0,+∞),则P 的轨迹一定通过△ABC 的 ( )A.外心B .内心 C.重心D.垂心解:由条件得=λ,因与都是单位向量,故点P 在∠BAC 的平分线上,所以点P 的轨迹通过△ABC 的内心.选B.11.在平行四边形ABCD 中,AC 与BD 交于点O ,E 是线段OD 的中点,AE 的延长线与CD 交于点F .若AC →=a ,BD →=b ,则AF →= ( ) A.14a +12b B.13a +23b C.12a +14b D .23a +13b 解析:∵AF →=AC →+CF →=a +23CD →=a +13(b -a )=23a +13b .故选D.12.设a 、b 是两个不共线向量,AB →=2a +p b ,BC →=a +b ,CD →=a -2b ,若A 、B 、D 三点共线,则实数p 的值为___-1_______.13.已知向量a ,b 是两个非零向量,则在下列四个条件中,能使a 、b 共线的条件是_________(将正确的序号填在横线上).①2a -3b =4e ,且a +2b =-3e ; ②存在相异实数λ、μ,使λ·a +μ·b =0; ③x ·a +y ·b =0(实数x ,y 满足x +y =0);④若四边形ABCD 是梯形,则AB →与CD →共线. 14.已知=a ,OP 2→=b ,P 1P 2→=λPP 2→,则OP →=_________.1λa +λ-1λb=a +λ-1λ(b -a )=1λa +λ-1λb .15.如图,以向量OA →=a ,OB →=b 为边作▱OADB , BM →=13BC →,CN →=13CD →,用a 、b 表示OM →、ON →、MN →.解 ∵BA →=OA →-OB →=a -b , BM →=16BA →=16a -16b ,∴OM →=OB →+BM →=16a +56b .又OD →=a +b ,∴ON →=OC →+13CD →=12OD →+16OD →=23OD →=23(a +b ).∴MN →=ON →-OM →=23a +23b -16a -56b =12a -16b .即OM →=16a +56b ,ON →=23a +23b , MN →=12a -16b .16.若a ,b 是两个不共线的非零向量,a 与b 起点相同,则当t 为何值时,a ,t b ,13(a +b )三向量的终点在同一条直线上?解 设OA →=a ,OB →=t b ,OC →=13(a +b ),∴AC →=OC →-OA →=-23a +13b ,AB →=OB →-OA →=t b -a .要使A 、B 、C 三点共线,只需AC →=λAB →. 即-23a +13b =λt b -λa .∴有⎩⎪⎨⎪⎧ -23=-λ,13=λt ,⇒⎩⎪⎨⎪⎧λ=23,t =12.∴当t =12时,三向量终点在同一直线上.平面向量的概念及线性运算练习三1.若△ABC 满足|CB →|=|AB →+AC →|,则△ABC 的形状必定为 ( )A .等腰直角三角形B .直角三角形C .等腰三角形D .等边三角形2.命题p :a 与b 是方向相同的非零向量,命题q: a 与b 是两平行向量,则命题p 是命题q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 3.在△ABC 所在平面上有一点P ,满足PA →+PB →+PC →=AB →,则△PBC 与△ABC 的面积之比是( ) A.13 B.12 C .23 D.344.设A 1,A 2,A 3,A 4是平面直角坐标系中两两不同的四点,若=λ (λ∈R),=μ (μ∈R),且1λ+1μ=2,则称A 3,A 4调和分割A 1,A 2.已知平面上的点C (c,0),D (d,0)(c ,d ∈R)调和分割点A (0,0),B (1,0),则下面说法正确的是( )A .C 可能是线段AB 的中点 B .D 可能是线段AB 的中点C .C ,D 可能同时在线段AB 上 D .C ,D 不可能同时在线段AB 的延长线上解 依题意,若C ,D 调和分割点A ,B ,则有=λ,=μ,且1λ+1μ=2.若C 是线段AB 的中点,则有=12,此时λ=12.又1μ+1λ=2,∴1μ=0,不可能成立.因此选项A 不正确,同理B 也不正确.若C ,D 同时在线段AB 上,由=λ,=μ知0<λ<1,0<μ<1,此时1λ+1μ>2,与已知1λ+1μ=2矛盾,因此选项C 不正确. 若C ,D 同时在线段AB 的延长线上,则=λ时,λ>1,=μ时,μ>1,此时1λ+1μ<2,与已知1λ+1μ=2矛盾,故C ,D 不可能同时在线段AB 的延长线上.5.设a ,b 是两个不共线的非零向量,若8a +k b 与k a +2b 共线,则实数k =__±4______. 解析:因为8a +kb 与ka +2b 共线,所以存在实数λ,使8a +kb =λ(ka +2b ),即(8-λk )a+(k -2λ)b =0.又a ,b 是两个不共线的非零向量,故⎩⎪⎨⎪⎧8-λk =0,k -2λ=0,解得k =±4.6.如图所示,平面内的两条相交直线OP1和OP 2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若=a +b ,且点P 落在第Ⅲ部分,则实数a ,b 满足a ________0,b ________0(用“>”,“<”或“=”填空).解析:由于点P 落在第Ⅲ部分,且=a +b ,则根据实数与向量的积的定义及平行四边形法则知a >0,b <0. 答案:> <7.设向量a ,b 满足|a |=25,b =(2,1),且a 与b 的方向相反,则a 的坐标为_(-4,-2)_______.解析:设a =(x ,y ),x <0,y <0,则x -2y =0且x 2+y 2=20,解得x =4,y =2(舍去),或者x =-4,y =-2,即a =(-4,-2).8.已知等差数列{a n }的前n 项和为S n ,若=a 1+a 200,且A ,B ,C 三点共线(该直线不过原点O ),则S200=_100_____9.如图,在△ABC 中,AN →=13NC →,P 是BN 上的一点,若AP →=mAB →+211AC →,则实数m 的值为____311_____.10.如图所示,在△ABC 中,点O 是BC 的中点.过点O 的直线分别交 直线AB 、AC 于不同的两点M 、N ,若AB →=mAM →,AC →=nAN →,则m +n 的值为____.解析 方法一 若M 与B 重合,N 与C 重合, 则m +n =2.方法二 ∵2=+=m +n ,=m 2=m 2.∵O 、M 、N 共线,∴m 2+n2=1. ∴m +n =2. 11. 已知直线x +y =a 与圆x 2+y 2=4交于A 、B 两点,且|OA →+OB →|=|OA →-OB →|,其中O 为坐标原点,则实数a 的值为___±2_____.12.如下图,两块斜边长相等的直角三角板拼在一起,若 AD →=xAB →+yAC →,则x =______,y =__________.作DF ⊥AB 交AB 的延长线于F ,设AB =AC =1⇒BC =DE =2,∵∠DEB =60°,∴BD =62. 由∠DBF =45°,得DF =BF =62×22=32,所以BF →=32AB →FD →=32AC →,所以AD →=AB →+BF →+FD →=()AB →+32AC →.14.△ABC 的外接圆的圆心为O ,两条边上的高的交点为H ,OH →=m (OA →+OB →+OC →),则实数m =________.解析:如图所示,连接BO ,并延长交圆O 于点D ,连接CH ,CD ,AD ,则∠BCD =∠BAD =90°,∴CD ⊥BC ,AD ⊥AB .又H 为△ABC的垂心,∴AH ⊥BC ,CH ⊥AB . ∴CD ∥AH ,AD ∥HC .∴四边形AHCD 为平行四边形. ∴AH →=DC →=OC →-OD →.∵O 为BD 的中点,∴OB →=-OD →.∴OH →=OA →+AH →=OA →+OC →-OD →=OA →+OB →+OC →. ∴m =1.故填1.15.设O 是△ABC 内部一点,且OA →+OC →=-2OB →,则△AOB 与△AOC 的面积之比为___12_____.三、解答题16.如图,在△ABC 中,,BN 与CM 交于P 点,且AB →=a ,AC →=b .用a ,b 表示AP →.解析:由题意知:AM →=13AB →=13a ,AN →=14AC →=14b ,BN →=AN →-AB →=14b -a ,CM →=AM →-AC →=13a -b .设PN →=λBN →,PM →=μCM →,则PN →=λ4b -λa ,PM →=μ3a -μb ,∴AP →=AN →-PN →=14b -(λ4b -λa )=λa +1-λ4b ,AP →=AM →-PM →=13a -(μ3a -μb )=1-μ3a +μb 而AP →=AP →,∴λa +1-λ4b =1-μ3a +μb而a ,b 不共线.∴λ=1-μ3且1-λ4=μ.∴λ=311.因此AP →=311a +211b .17已知点G 是△ABO 的重心,M 是AB 边的中点. (1)求GA →+GB →+GO →;(2)若PQ 过△ABO 的重心G ,且OA →=a ,OB →=b ,OP →=m a ,OQ →=n b , 求证:1m +1n=3.(1)解 ∵GA →+GB →=2GM →,又2GM →=-GO →, ∴GA →+GB →+GO →=-GO →+GO →=0. (2)证明 显然OM →=12(a +b ).因为G 是△ABO 的重心,所以OG →=23OM →=13(a +b ).由P 、G 、Q 三点共线,得PG →∥GQ →, 所以,有且只有一个实数λ,使PG →=λGQ →. 而PG →=OG →-OP →=13(a +b )-m a =⎝ ⎛⎭⎪⎫13-m a +13b ,GQ →=OQ →-OG →=n b -13(a +b )=-13a +⎝⎛⎭⎪⎫n -13b ,所以⎝ ⎛⎭⎪⎫13-m a +13b =λ⎣⎢⎡⎦⎥⎤-13a +⎝⎛⎭⎪⎫n -13b .又因为a 、b 不共线,所以⎩⎪⎨⎪⎧13-m =-13λ13=λ⎝ ⎛⎭⎪⎫n -13,消去λ,整理得3mn =m +n ,故1m +1n=3.。
高考数学一轮复习第1讲 平面向量的概念及线性运算

第1讲 平面向量的概念及线性运算1.向量的有关概念 名称定义备注向量 既有01大小又有02方向的量;向量的大小叫做向量的长度(或称模)平面向量是自由向量零向量长度为030的向量记作0,其方向是任意的 单位向量长度等于041个单位的向量与非零向量a 平行的单位向量为±a|a|平行向量方向相同或05相反的非零向量(又叫做共线向量)0与任一向量平行或共线相等向量 长度相等且方向06相同的向量 两向量只有相等或不相等,不能比较大小相反向量长度相等且方向07相反的向量0的相反向量为02.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算交换律:a+b=08b+a;结合律:(a+b)+c=09a+(b+c)续表向量运算定义法则(或几何意义)运算律减法求a与b的相反向量-b的和的运算a-b=a+(-b)数乘求实数λ与向量a的积的运算|λa|=10|λ||a|,当λ>0时,λa与a的方向11相同;当λ<0时,λa与a的方向12相反;当λ=0时,λa=130λ(μa)=(λμ)a;(λ+μ)a=14λa+μa;λ(a+b)=15λa+λb3.共线向量定理向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa.1.一般地,首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量,即A1A2→+A2A3→+A3A4→+…+A n -1A n =A1An →.特别地,一个封闭图形首尾连接而成的向量和为零向量.2.在△ABC 中,AD ,BE ,CF 分别为三角形三边上的中线,它们交于点G (如图所示),易知G 为△ABC 的重心,则有如下结论:(1)GA →+GB →+GC →=0;(2)AG →=13(AB →+AC →);(3)GD →=12(GB →+GC →)=16(AB →+AC →).3.OA →=λOB →+μOC →(λ,μ为实数),若点A ,B ,C 共线(O 不在直线BC 上),则λ+μ=1.1.已知a ,b 是两个非零向量,且|a +b |=|a |+|b |,则下列说法正确的是( ) A .a +b =0 B .a =bC .a 与b 共线反向D .存在正实数λ,使a =λb答案 D解析 因为a ,b 是两个非零向量,且|a +b |=|a |+|b |,则a 与b 共线同向,故D 正确.2.设平行四边形ABCD 的对角线交于点P ,则下列命题中正确的个数是( ) ①AC →=AB →+AD →;②AP →=12(AB →+AD →);③DB→=AB →-AD →;④PD →=PB →.A .1B .2C .3D .4 答案 C解析 由向量加法的平行四边形法则,知①AC →=AB →+AD →,②AP →=12(AB →+AD →)是正确的;由向量减法的三角形法则,知③DB→=AB→-AD→是正确的;因为PD→,PB→的长度相等,方向相反,所以④PD→=PB→是错误的.故选C.3.如图所示,向量OA→=a,OB→=b,OC→=c,A,B,C三点在一条直线上,且AC→=-3CB→,则()A.c=-12a+32bB.c=32a-12bC.c=-a+2b D.c=a+2b 答案 A解析∵AC→=-3CB→,∴AC→=32AB→,∴OC→-OA→=32(OB→-OA→),∴OC→=32OB→-1 2OA→,即c=-12a+32b.故选A.4.已知线段上A,B,C三点满足BC→=2AB→,则这三点在线段上的位置关系是()答案 A解析根据题意得到BC→和AB→是共线同向的,且BC=2AB,故选A.5.(2020·安徽芜湖模拟)已知▱ABCD的对角线AC,BD相交于点O,且OA→=a,OB→=b,则DC→=________,BC→=________(用a,b表示).答案b-a-a-b解析如图,DC→=AB→=OB→-OA→=b-a,BC→=OC→-OB→=-OA→-OB→=-a-b.6.在四边形ABCD中,对角线AC与BD交于点O,若2OA→+OC→=2OD→+OB→,则四边形ABCD的形状为________.答案梯形解析∵2OA→+OC→=2OD→+OB→,∴2(OA→-OD→)=OB→-OC→,即2DA→=CB→,∴DA→∥CB→,且|DA→|=12|CB→|,∴四边形ABCD是梯形.考向一平面向量的概念例1给出下列命题:①若两个向量相等,则它们的起点相同,终点相同;②若a与b共线,b与c共线,则a与c也共线;③若A,B,C,D是不共线的四点,且AB→=DC→,则四边形ABCD为平行四边形;④a=b的充要条件是|a|=|b|且a∥b;⑤已知λ,μ为实数,若λa=μb,则a与b共线.其中真命题的序号是________.答案③解析①错误,两个向量起点相同,终点相同,则两个向量相等;但两个向量相等,不一定有相同的起点和终点.②错误,若b=0,则a与c不一定共线.③正确,因为AB→=DC→,所以|AB→|=|DC→|且AB→∥DC→;又A,B,C,D是不共线的四点,所以四边形ABCD为平行四边形.④错误,当a∥b且方向相反时,即使|a|=|b|,也不能得到a=b,所以|a|=|b|且a∥b不是a=b的充要条件,而是必要不充分条件.⑤错误,当λ=μ=0时,a与b可以为任意向量,满足λa=μb,但a与b不一定共线.平面向量有关概念的四个关注点(1)相等向量具有传递性,非零向量的平行也具有传递性.(2)共线向量即为平行向量,它们均与起点无关.(3)向量可以平移,平移后的向量与原向量是相等向量,解题时,不要把它与函数图象的移动混淆.(4)非零向量a与a|a|的关系:a|a|是与a同方向的单位向量.1.设a0为单位向量,有下列命题:①若a为平面内的某个向量,则a =|a|a0;②若a与a0平行,则a=|a|a0;③若a与a0平行且|a|=1,则a=a0.其中假命题的个数是()A.0 B.1C.2 D.3答案 D解析向量是既有大小又有方向的量,a与|a|a0的模相同,但方向不一定相同,故①是假命题;若a与a0平行,则a与a0的方向有两种情况:一是同向,二是反向,反向时a=-|a|a0,故②③也是假命题.综上所述,假命题的个数是3.故选D.多角度探究突破考向二 平面向量的线性运算角度1 平面向量线性运算的几何意义例2 (1)已知点O ,A ,B 不在同一条直线上,点P 为该平面上一点,且2OP →=2OA→+BA →,则( ) A .点P 在线段AB 上B .点P 在线段AB 的反向延长线上C .点P 在线段AB 的延长线上D .点P 不在直线AB 上 答案 B解析 因为2OP →=2OA →+BA →,所以2AP →=BA →,所以点P 在线段AB 的反向延长线上.(2)(2017·全国卷Ⅱ)设非零向量a ,b 满足|a +b |=|a -b |,则( ) A .a ⊥b B .|a |=|b | C .a ∥b D .|a |>|b |答案 A解析 解法一:(利用向量加法的平行四边形法则)在▱ABCD 中,设AB→=a ,AD →=b ,由|a +b |=|a -b |知|AC→|=|DB →|,从而▱ABCD 为矩形,即AB ⊥AD ,故a ⊥b .故选A.解法二:∵|a +b |=|a -b |,∴|a +b |2=|a -b |2.∴a 2+b 2+2a ·b =a 2+b 2-2a ·b .∴a ·b =0.∴a ⊥b .故选A.角度2 平面向量线性运算例3 (1)(2021·安徽芜湖质量检测)如图所示,下列结论正确的是( ) ①PQ →=32a +32b ;②PT →=-32a -32b ;③PS →=32a -12b ;④PR →=32a +b .A .①②B .③④C .①③D .②④答案 C解析 由a +b =23PQ →,知PQ →=32a +32b ,①正确;由a -b =23PT →,知PT →=32a -32b ,②错误;PS →=PT →+b ,故PS →=32a -12b ,③正确;PR →=PT →+2b =32a +12b ,④错误.故正确的为①③,故选C.(2)(2020·淄博二模)在平行四边形ABCD 中,DE →=3EC →,若AE 交BD 于点M ,则AM→=( ) A.13AB →+23AD → B .37AB →+47AD →C.23AB →+13AD → D .27AB →+57AD →答案 B解析 ∵DE →=3EC →,∴E 为线段DC 上靠近点C 的四等分点.显然△ABM ∽△EDM ,即AMEM =ABED =43,∴AM →=47AE →=47(AD →+DE →)=47⎝ ⎛⎭⎪⎪⎫AD →+34AB →=37AB →+47AD →.故选B.角度3 利用线性运算求参数例4 (1)(2020·石家庄质检)在△ABC 中,O 为△ABC 的重心,若BO →=λAB →+μAC→,则λ-2μ=( ) A .-12B .-1C .43D .-43答案 D解析 设AC 的中点为D ,因为O 为△ABC 的重心,所以BO →=23BD →=23(BA →+AD →)=-23AB →+23×12AC →=-23AB →+13AC →,所以λ=-23,μ=13,所以λ-2μ=-43,故选D.(2) 如图所示,矩形ABCD 的对角线相交于点O ,E 为AO 的中点,若DE →=λAB →+μAD→(λ,μ为实数),则λ2+μ2=( )A.58B .14C .1D .516答案 A解析DE→=12DA→+12DO→=12DA→+14DB→=12DA→+14(DA→+AB→)=14AB→-34AD→,所以λ=14,μ=-34,故λ2+μ2=58.故选A.向量线性运算的解题策略(1)向量加减的常用法则是平行四边形法则和三角形法则,一般共起点的向量求和用平行四边形法则,求差用三角形法则,求首尾相连向量的和用三角形法则.(2)找出图形中的相等向量、共线向量,将所求向量与已知向量转化到同一个平行四边形或三角形中求解.(3)利用向量的线性运算求参数的步骤:先通过向量的线性运算用两个不共线的向量表示有关向量,然后对比向量等式求出参数或建立方程(组)求解.2.已知四边形ABCD是平行四边形,O为平面上任意一点,设OA→=a,OB→=b,OC→=c,OD→=d,则()A.a+b+c+d=0 B.a-b+c-d=0C.a+b-c-d=0 D.a-b-c+d=0答案 B解析如图所示,a-b=BA→,c-d=DC→,∵四边形ABCD是平行四边形,∴AB綊DC,且BA→与DC→反向,即BA→+DC→=0,也就是a-b+c-d=0.3. (2020·湖南师范大学附中模拟)如图所示,在正方形ABCD中,E为AB的中点,F 为CE 的中点,则AF→=( )A.34AB →+14AD →B.14AB →+34AD →C.12AB →+AD → D.34AB →+12AD → 答案 D解析 根据题意得AF →=12(AC →+AE →),又因为AC →=AB →+AD →,AE →=12AB →,所以AF→=12⎝ ⎛⎭⎪⎪⎫AB →+AD →+12AB →=34AB →+12AD →.故选D. 4.(2020·洛阳尖子生第二次联考)在△ABC 中,点D 在线段BC 上,且BD →=2DC→,点O 在线段CD 上(与点C ,D 不重合).若AO →=x AB →+(1-x )AC →,则x 的取值范围是________.答案 ⎝⎛⎭⎪⎪⎫0,13解析 解法一:AO→=x AB →+(1-x )AC →=x (AB →-AC →)+AC →,即AO →-AC →=x (AB →-AC→),所以CO →=x CB →,所以|CO →||CB→|=x .因为BD→=2DC →,所以BC →=3DC →,则0<x <|DC →||BC→|=13,所以x 的取值范围是⎝ ⎛⎭⎪⎪⎫0,13.解法二:设BO →=λBC →,λ∈⎝ ⎛⎭⎪⎪⎫23,1,则AO →=AB →+BO →=AB →+λBC →=(1-λ)AB →+λAC →=x AB →+(1-x )AC →,则x =1-λ∈⎝⎛⎭⎪⎪⎫0,13.考向三 共线向量定理的应用例5 (1)设e 1与e 2是两个不共线向量,AB →=3e 1+2e 2,CB →=k e 1+e 2,CD →=3e 1-2k e 2,若A ,B ,D 三点共线,则k 的值为( )A .-94B .-49C .-38D .不存在答案 A解析 由题意,A ,B ,D 三点共线,故必存在一个实数λ,使得AB→=λBD →.又因为AB →=3e 1+2e 2,CB →=k e 1+e 2,CD →=3e 1-2k e 2,所以BD →=CD →-CB →=3e 1-2k e 2-(k e 1+e 2)=(3-k )e 1-(2k +1)e 2,所以3e 1+2e 2=λ(3-k )e 1-λ(2k +1)e 2,所以错误!解得k =-94.故选A.(2)(2020·滨州二模)已知O ,A ,B ,C 为平面α内的四点,其中A ,B ,C 三点共线,点O 在直线AB 外,且满足OA →=1x OB →+2yOC →.其中x >0,y >0,则x +8y 的最小值为( )A .21B .25C .27D .34答案 B解析 根据题意,A ,B ,C 三点共线,点O 在直线AB 外,OA →=1x OB →+2y OC →.设BA→=λBC →(λ≠0,λ≠1),则OA →=OB →+BA →=OB →+λBC →=OB →+λ(OC →-OB →)=λOC →+(1-λ)OB →,∴⎩⎪⎨⎪⎧1-λ=1x,λ=2y,消去λ得1x +2y =1,∴x +8y =(x +8y )⎝ ⎛⎭⎪⎪⎫1x +2y =1+2x y +8y x +16≥17+22x y ·8y x =25(当且仅当x =5,y =52时等式成立).故选B. (1)三点共线问题可转化为向量共线问题来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.根据A ,B ,C 三点共线求参数问题,只需将问题转化为AC →=λAB →,再利用对应系数相等列出方程组,进而解出系数.(2)三点共线的一个常用结论:A ,B ,C 三点共线⇔存在实数λ,μ对平面内任意一点O (O 不在直线BC 上)满足OA→=λOB →+μOC →(λ+μ=1).5.已知向量a ,b 不共线,且c =λa +b ,d =a +(2λ-1)b ,若c 与d 共线反向,则实数λ的值为( )A .1B .-12C .12D .-2答案 B解析 由于c 与d 共线反向,则存在实数k 使c =k d (k <0),于是λa +b =k [a +(2λ-1)b ],整理得λa +b =k a +(2λk -k )b .由于a ,b 不共线,所以有⎩⎪⎨⎪⎧λ=k ,2λk-k =1,整理得2λ2-λ-1=0,解得λ=1或λ=-12.又因为k <0,所以λ<0,故λ=-12.故选B.6.(2020·江苏高考)在△ABC 中,AB =4,AC =3,∠BAC =90°,D 在边BC 上,延长AD 到P ,使得AP =9,若PA →=m PB →+⎝ ⎛⎭⎪⎪⎫32-m PC →(m 为常数),则CD 的长度是________.答案 0或185解析 ∵A ,D ,P 三点共线,∴可设PA →=λPD →(λ>0).∵PA →=m PB →+⎝ ⎛⎭⎪⎪⎫32-m PC →,∴λPD →=m PB →+⎝ ⎛⎭⎪⎪⎫32-m PC →,即PD →=m λPB →+⎝ ⎛⎭⎪⎪⎫32-m λPC →.若m ≠0且m ≠32,则B ,D ,C三点共线,∴mλ+⎝ ⎛⎭⎪⎪⎫32-m λ=1,即λ=32.∵AP =9,∴PD =6,∴AD =3.∵AB =4,AC=3,∠BAC =90°,∴BC =AB2+AC2=5,∴cos ∠ACB =AC BC=35.设CD =x ,根据余弦定理可得cos ∠ACD =AC2+CD2-AD22AC·CD =x 6=AC BC =35,则x =185,∴CD 的长度为185.当m =0时,PA →=32PC →,C ,D 重合,此时CD 的长度为0,当m =32时,PA →=32PB →,B ,D 重合,此时P A =12,不符合题意,舍去.故CD 的长度为0或185.一、单项选择题1.如图,O 是平行四边形ABCD 的两条对角线的交点,则下列等式正确的是( )A.DA→-DC →=AC → B.DA→+DC →=DO → C.OA→-OB →+AD →=DB → D.AO →+OB →+BC →=AC → 答案 D解析 对于A ,DA→-DC →=CA →,错误;对于B ,DA →+DC →=2DO →,错误;对于C ,OA →-OB →+AD →=BA →+AD →=BD →,错误;对于D ,AO →+OB →+BC →=AB →+BC →=AC →,正确.故选D.2.已知向量i 与j 不共线,且AB →=i +m j ,AD →=n i +j ,若A ,B ,D 三点共线,则实数m ,n 应该满足的条件是( )A .m +n =1B .m +n =-1C .mn =1D .mn =-1答案 C解析 由A ,B ,D 共线可设AB →=λAD →,于是有i +m j =λ(n i +j )=λn i +λj .又i ,j 不共线,因此⎩⎪⎨⎪⎧λn =1,λ=m ,即有mn =1.3.已知O 是△ABC 所在平面内一点,D 为BC 边的中点,且2OA →+OB →+OC →=0,那么( )A.AO →=OD → B .AO →=2OD →C.AO →=DO → D .AO→=2DO → 答案 A解析 由D 是BC 边的中点,可得OB →+OC →=2OD →,故2OA →+2OD →=0,所以AO →=OD→.故选A. 4.(2020·西北师大附中模拟)设a ,b 都是非零向量,下列四个条件中,使a|a|=b|b|成立的充分条件是( )A .a =-bB .a ⊥bC .a =2bD .a ⊥b 且|a|=|b| 答案 C解析 由于a ,b 都是非零向量,若a|a|=b|b|成立,则a 与b 需要满足共线同向.5.(2020·山东威海月考)设P 是△ABC 所在平面内的一点,且CP →=2PA →,则△P AB与△PBC 的面积之比是( )A.13B .12C .23D .34答案 B解析 ∵CP →=2PA →,∴P 为边AC 靠近A 点的三等分点,∴△P AB 与△PBC 的面积比为1∶2.6.设D ,E ,F 分别为△ABC 的三边BC ,CA ,AB 的中点,则EB →+FC →=( )A.AD→ B .12AD →C.BC → D .12BC →答案 A解析 设AB →=a ,AC →=b ,则EB →=-12b +a ,FC →=-12a +b ,从而EB→+FC →=⎝ ⎛⎭⎪⎪⎫-12b +a +⎝ ⎛⎭⎪⎪⎫-12a +b =12(a +b )=AD →.故选A. 7.如图所示,已知AB 是圆O 的直径,点C ,D 是半圆弧的两个三等分点,AB →=a ,AC→=b ,则AD →=( )A .a -12bB .12a -bC .a +12bD .12a +b答案 D解析 连接CD ,由点C ,D 是半圆弧的三等分点,得CD ∥AB ,且CD →=12AB →=12a ,所以AD →=AC →+CD →=b +12a .8.设M 为平行四边形ABCD 对角线的交点,O 为平行四边形ABCD 所在平面内任意一点,则OA→+OB →+OC →+OD →等于( )A.OM → B .2OM → C .3OM → D .4OM→ 答案 D解析 OA →+OB →+OC →+OD →=(OA →+OC →)+(OB →+OD →)=2OM →+2OM →=4OM →.故选D.9.(2020·山东济宁月考)如图,在△ABC 中,点D 在BC 边上,且CD =2DB ,点E 在AD 边上,且AD =3AE ,则用向量AB→,AC →表示CE →为( )A.29AB →+89AC → B .29AB →-89AC →C.29AB →+79AC → D .29AB →-79AC →答案 B解析 由平面向量的三角形法则及向量共线的性质可得CE →=AE →-AC →=13AD →-AC→=13⎝ ⎛⎭⎪⎪⎫AB →+13BC →-AC →=13[AB →+13(AC →-AB →)]-AC →=29AB →-89AC →.10.(2020·河北衡水调研)一直线l 与平行四边形ABCD 中的两边AB ,AD 分别交于点E ,F ,且交其对角线AC 于点M ,若AB →=2AE →,AD →=3AF →,AM →=λAB →-μAC →(λ,μ∈R ),则52μ-λ=( )A .-12B .1C .32D .-3答案 A解析 AM→=λAB →-μAC →=λAB →-μ(AB →+AD →)=(λ-μ)AB →-μAD →=2(λ-μ)AE →-3μAF →,因为E ,M ,F 三点共线,所以2(λ-μ)+(-3μ)=1,即2λ-5μ=1,所以52μ-λ=-12.故选A.二、多项选择题11.设a ,b 是不共线的两个平面向量,已知PQ →=a +sin α·b ,其中α∈(0,2π),QR→=2a -b .若P ,Q ,R 三点共线,则角α的值可以为( )A.π6 B .5π6C .7π6D .11π6答案 CD解析 因为a ,b 是不共线的两个平面向量,所以2a -b ≠0.即QR→≠0,因为P ,Q ,R 三点共线,所以PQ →与QR →共线,所以存在实数λ,使PQ →=λQR →,所以a +sin α·b =2λa -λb ,所以⎩⎪⎨⎪⎧1=2λ,sinα=-λ,解得sin α=-12.又α∈(0,2π),故α可为7π6或11π6.12.(2021·福建福清高三模拟)设点M 是△ABC 所在平面内一点,则下列说法正确的是( )A .若AM →=12AB →+12AC →,则点M 是边BC 的中点B .若AM→=2AB →-AC →,则点M 在边BC 的延长线上C .若AM→=-BM →-CM →,则点M 是△ABC 的重心D .若AM →=x AB →+y AC →,且x +y =12,则△MBC 的面积是△ABC 的面积的12答案 ACD解析 A 中,AM →=12AB →+12AC →⇒12AM →-12AB →=12AC →-12AM →,即BM→=MC →,则点M 是边BC 的中点;B 中,AM→=2AB →-AC →⇒AM →-AB →=AB →-AC →,所以BM →=CB →,则点M 在边CB 的延长线上,所以B 错误;C 中,设BC 中点为D ,则AM→=-BM →-CM →=MB →+MC →=2MD →,由重心性质可知C 正确;D 中,AM →=x AB →+y AC →,且x +y =12⇒2AM →=2x AB →+2y AC →,2x +2y =1.设AD →=2AM →,所以AD →=2x AB →+2y AC →,2x +2y =1,可知B ,C ,D 三点共线,所以△MBC 的面积是△ABC 面积的12.故选ACD.三、填空题13.若AP →=12PB →,AB →=(λ+1)BP →,则λ=________. 答案 -52解析 如图,由AP →=12PB →,可知点P 是线段AB 上靠近点A 的三等分点,则AB →=-32BP →,结合题意可得λ+1=-32,所以λ=-52.14.向量a ,b ,c 在正方形网格中的位置如图所示.若向量λa +b 与c 共线,则实数λ=________.答案 2解析 由题中所给图象可得,2a +b =c ,又c =μ(λa +b ),所以λ=2.15.若点O 是△ABC 所在平面内的一点,且满足|OB→-OC →|=|OB →+OC →-2OA →|,则△ABC 的形状为________.答案 直角三角形解析 因为OB→+OC →-2OA →=OB →-OA →+OC →-OA →=AB →+AC →,OB →-OC →=CB →=AB →-AC →,所以|AB →+AC →|=|AB →-AC →|,即AB →·AC→=0,故AB →⊥AC →,所以△ABC 为直角三角形.16.在直角梯形ABCD 中,∠A =90°,∠B =30°,AB =23,BC =2,点E 在线段CD 上(点E 不与点C ,D 重合),若AE→=AD →+μAB →,则μ的取值范围是________. 答案 0<μ<12解析 由题意可求得AD =1,CD =3,∴AB→=2DC →.∵点E 在线段CD 上(点E 不与点C ,D 重合),∴DE →=λDC →(0<λ<1).∵AE →=AD →+DE →,又AE →=AD →+μAB →=AD →+2μDC →=AD →+2μλDE →,∴2μλ=1,即μ=λ2.∵0<λ<1,∴0<μ<12.。
高三一轮复习资料 第1节 平面向量的概念及线性运算

第五章 平面向量第1节 平面向量的概念及线性运算基础打磨1.已知向量a ,b 不共线,AB ⃗⃗⃗⃗⃗ =a+3b ,BC ⃗⃗⃗⃗⃗ =5a+3b ,CD ⃗⃗⃗⃗⃗ =-3a+3b ,则().A .A ,B ,C 三点共线 B .A ,B ,D 三点共线 C .A ,C ,D 三点共线D .B ,C ,D 三点共线2.(2020届武汉调研)设M 为平行四边形ABCD 对角线的交点,O 为平行四边形ABCD 所在平面内的任意一点,则OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ +OD ⃗⃗⃗⃗⃗⃗ =( ). A .OM⃗⃗⃗⃗⃗⃗ B .2OM⃗⃗⃗⃗⃗⃗ C .3OM⃗⃗⃗⃗⃗⃗ D .4OM⃗⃗⃗⃗⃗⃗ 3.(2020届山西太原模拟)在△ABC 中,AN⃗⃗⃗⃗⃗⃗ =14NC ⃗⃗⃗⃗⃗ ,P 是直线BN 上一点,若AP ⃗⃗⃗⃗⃗ =m AB ⃗⃗⃗⃗⃗ +25AC ⃗⃗⃗⃗⃗ ,则实数m 的值为( ).A .-4B .-1C .1D .44.(2020届湖南省娄底市高三上学期期末)已知平行四边形ABCD 的对角线相交于点O ,E 为平面内一点,且AE⃗⃗⃗⃗⃗ =13EC ⃗⃗⃗⃗⃗ ,若BE ⃗⃗⃗⃗⃗ =x BA ⃗⃗⃗⃗⃗ +y BD ⃗⃗⃗⃗⃗⃗ (x ,y ∈R),则x+y=( ). A.1 B.-12 C.34 D.145.(2020届枣庄模拟)设D 为△ABC 所在平面内一点,AD⃗⃗⃗⃗⃗ =-13AB ⃗⃗⃗⃗⃗ +43AC ⃗⃗⃗⃗⃗ ,若BC ⃗⃗⃗⃗⃗ =λDC ⃗⃗⃗⃗⃗ (λ∈R),则λ=( ).A .2B .3C .-2D .-36.(辽宁省丹东市2020届高三总复习质量测试)在△ABC 中,AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ =2AD ⃗⃗⃗⃗⃗ ,AE ⃗⃗⃗⃗⃗ +DE ⃗⃗⃗⃗⃗ =0,若EB ⃗⃗⃗⃗⃗ =x AB ⃗⃗⃗⃗⃗ +y AC ⃗⃗⃗⃗⃗ ,则( ). A .y=3xB .x=3yC .y=-3xD .x=-3y7.(2020届湖北孝感二模)设D ,E ,F 分别为△ABC 的边BC ,CA ,AB 的中点,则DA⃗⃗⃗⃗⃗ +2EB ⃗⃗⃗⃗⃗ +3FC ⃗⃗⃗⃗⃗ =( ).A .12AD ⃗⃗⃗⃗⃗ B .32AD ⃗⃗⃗⃗⃗ C .12AC ⃗⃗⃗⃗⃗D .32AC ⃗⃗⃗⃗⃗8.(2020届辽宁丹东五校协作体联考)已知P 是△ABC 所在平面上的一点,满足PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =2AB ⃗⃗⃗⃗⃗ ,若S △ABC =6,则△PAB 的面积为( ). A .2 B .3 C .4 D .89.(山东省德州市2020届高三第二次练习)设向量a ,b 不平行,向量a+14λb 与-a+b 平行,则实数λ= .10.(2020届钦州质检)已知e 1,e 2为平面内两个不共线的向量,MN ⃗⃗⃗⃗⃗⃗⃗ =2e 1-3e 2,NP ⃗⃗⃗⃗⃗⃗ =λe 1+6e 2,若M ,N ,P 三点共线,则λ= .能力拔高11.(江西省南昌市2020届高三模拟)在△ABC 中,D 为BC 上一点,E 是AD 的中点,若BD ⃗⃗⃗⃗⃗⃗ =λDC ⃗⃗⃗⃗⃗ ,CE ⃗⃗⃗⃗⃗ =13AB ⃗⃗⃗⃗⃗ +μAC⃗⃗⃗⃗⃗ ,则λ+μ=( ). A .13B .-13C .76D .-7612.如图,已知AB 是圆O 的直径,点C ,D 是半圆弧的两个三等分点,AB ⃗⃗⃗⃗⃗ =a ,AC ⃗⃗⃗⃗⃗ =b ,则AD ⃗⃗⃗⃗⃗ =( ). A .a-12b B .12a-b C .a+12bD .12a+b13.(2020届河北、河南、山西三省联考)如图,在等边△ABC 中,O 为△ABC 的重心,点D 为BC 边上靠近点B 的四等分点,若OD⃗⃗⃗⃗⃗⃗ =x AB ⃗⃗⃗⃗⃗ +y AC ⃗⃗⃗⃗⃗ ,则x+y=( ).A .112B .13C .23D .3414.已知A ,B ,C 是平面上不共线的三点,O 是△ABC 的重心,若点P 满足OP ⃗⃗⃗⃗⃗ =13(2OA ⃗⃗⃗⃗⃗ +12OB ⃗⃗⃗⃗⃗ +12OC ⃗⃗⃗⃗⃗ ),则点P 一定为△ABC 的( ). A .BC 边中线的中点B .BC 边中线的三等分点(非重心) C .重心D .BC 边的中点思维拓展15.(2020届河南郑州阶段测试)如图所示,在△ABO 中,OC ⃗⃗⃗⃗⃗ =14OA ⃗⃗⃗⃗⃗ ,OD ⃗⃗⃗⃗⃗⃗ =12OB ⃗⃗⃗⃗⃗ ,AD 与BC 相交于M ,设OA ⃗⃗⃗⃗⃗ =a ,OB ⃗⃗⃗⃗⃗ =b ,则用a 和b 表示向量OM⃗⃗⃗⃗⃗⃗ = . 16.(山东省烟台市、菏泽市2020届高三高考适应性练习)在△ABC 中,点O 是BC 的三等分点,|OC ⃗⃗⃗⃗⃗ |=2|OB ⃗⃗⃗⃗⃗ |,过点O 的直线分别交AB ,AC 或其延长线于不同的两点E ,F ,且AB ⃗⃗⃗⃗⃗ =m AE ⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ =n AF⃗⃗⃗⃗⃗ ,若1m +t n的最小值为83,则正数t 的值为 .。
2019届高三文数一轮复习第1节 平面向量的概念及线性运算

共线向量,熟练运用向量的加法法则和运算律求解.
︱高中总复习︱一轮·文数
考查角度2:用已知向量表示未知向量
【例 3】 在平行四边形 ABCD 中, AB =e1, AC =e2, NC = .(用 e1 ,e2 表示)
1 1 AC , BM = MC ,则 MN = 4 2
2 1 2 解析:如图所示, MN = CN - CM = CN +2 BM = CN + BC =- e2+ (e2-e1)= 3 4 3
0 与任一向量平行( 或共线) 两个向量只有相等或不相等,不能比较大小 0 的相反向量为 0
︱高中总复习︱一轮·文数
3.向量的线性运算
向量运算 定义 法则(或几何意义) 运算律 交换律: a+b= b+a ; 结合律: (a+b)+c=
加法
求两个向量和的运算
a+(b+c)
减法
求 a 与 b 的相反向量-b 的和的运算叫做 a 与 b 的差 |λ a|= |λ ||a| . 当λ >0 时,λ a 的方向与 a 的方向 相同;当λ <0 时 ,λ a 的方向与 a 的方向 相反;当λ =0 时,λ a= 0
︱高中总复习︱一轮·文数
第四篇
平面向量(必修4)
︱高中总复习︱一轮·文数
六年新课标全国卷试题分析 高考考点、示例分布图 命题特点 1.高考在本篇一般命制1个小题,分值 占5 分. 2.高考在本篇重点考查平面向量的线 性运算、坐标运算、向量的平行与垂 直、求向量的数量积、夹角与模,属 容易题. 3.本篇一般不涉及解答题,在知识的 交汇上往往以函数的定义域、值域、 不等式的解集、曲线的点集为载体进 行考查,难度不大.
2019高考数学一轮复习5.1平面向量的概念及线性运算课件理新人教B

|������|
知识梳理 考点自测
名称 定 义 平行 方向 相同 或 相反 的非零向 向量 量 共线 方向相同或相反 的非零向量又叫做 向量 共线向量
相等 长度 相等 且方向 相同 的向 向量 量
相反 长度 相等 且方向 相反 的向 向量 量
-3-
备注
零向量与任一向量 平行 或共线
例1(1)对于非零向量a,b,“a+b=0”是“a∥b”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
(2)给出下列命题:
①若|a|=|b|,则a=b或a=-b;②若A,B,C,D是不共线的四点,则“������������ = ������������”
是“四边形ABCD为平行四边形”的充要条件;③若两个向量相等,则
D.点D在CB的延长线上
作������������' = ������������,连接 AD',则������������ + ������������ = ������������ + ������������' = ������������' = ������������, 所以 D'和 D 重合,所以点 D 在 CB 的延长线上.故选 D.
关闭
依题意,得������������ = ������������,故������������ + ������������=0,即������������ − ������������ + ������������ − ������������=0,即 ������������ − ������������ + ������������ − ������������=0,则 a-b+c-d=0,故选 A.
高考数学一轮复习配餐作业26平面向量的概念及其线性运算含解析理

配餐作业(二十六) 平面向量的概念及其线性运算(时间:40分钟)一、选择题1.设a 是非零向量,λ是非零实数,下列结论中正确的是( ) A .a 与λa 的方向相反 B .a 与λ2a 的方向相同 C .|-λa |≥|a |D .|-λa |≥|λ|·a解析 对于A ,当λ>0时,a 与λa 的方向相同,当λ<0时,a 与λa 的方向相反,B 正确;对于C ,|-λa |=|-λ||a |,由于|-λ|的大小不确定,故|-λa |与|a |的大小关系不确定;对于D ,|λ|a 是向量,而|-λa |表示长度,两者不能比较大小。
故选B 。
答案 B2.已知向量a ,b ,c 中任意两个都不共线,但a +b 与c 共线,且b +c 与a 共线,则向量a +b +c =( )A .aB .bC .cD .0解析 依题意,设a +b =m c ,b +c =n a ,则有(a +b )-(b +c )=m c -n a ,即a -c =m c -n a 。
又a 与c 不共线,于是有m =-1,n =-1,a +b =-c ,a +b +c =0。
故选D 。
答案 D3.设M 是△ABC 所在平面上的一点,且MB →+32MA →+32MC →=0,D 是AC 的中点,则|MD →||BM →|的值为( )A.13 B.12 C .1D .2解析 ∵D 是AC 的中点,延长MD 至E ,使得DE =MD , ∴四边形MAEC 为平行四边形, ∴MD →=12ME →=12(MA →+MC →)。
∵MB →+32MA →+32MC →=0,∴MB →=-32(MA →+MC →)=-3MD →,∴|MD →||BM →|=|MD →||-3MD →|=13,故选A 。
答案 A4.设D ,E ,F 分别是△ABC 的三边BC ,CA ,AB 上的点,且DC →=2BD →,CE →=2EA →,AF →=2FB →,则AD →+BE →+CF →与BC →( )A .反向平行B .同向平行C .互相垂直D .既不平行也不垂直解析 由题意得AD →=AB →+BD →=AB →+13BC →,BE →=BA →+AE →=BA →+13AC →, CF →=CB →+BF →=CB →+13BA →,因此AD →+BE →+CF →=CB →+13(BC →+AC →+BA →)=CB →+23BC →=-13BC →,故AD →+BE →+CF →与BC →反向平行。
高考数学一轮总复习 第26讲 平面向量的概念及线性运算课件 文 新课标

二 向量的线性运算
【例 2】如图所示,在△ABC 中,D、E 分别是 AB、 AC 边的中点,M、N 分别是 DE、BC 的中点,已知B→C= a,B→D=b,试用 a、b 分别表示D→E、C→E和M→N.
素材2
已知点 O(0,0),A(1,2),B(4,5),P 为一动点,及O→P= O→A+tA→B.
(1)|λa|= 11
;
(2)当λ>0时,λa的方向与a的方向
当λ1<2 0时,λa的方向与a的方向
λ=013时,λa=
.
14
; ;当
运算律:交换律、分配律、结合律.
4.平面向量共线定理
向量b与非零向量a共线的充分必要条件
是15
.
5.平面向量基本定理
如果e1、e2是同一平面内两个16
的
向量,那么对这个平面内任一向量
1.向量的坐标表示主要依据平面向量的 基本定理,平面向量 一 一 对应 实数对(x,y),任 何一个平面向量都有惟一的坐标表示,但
是每一个坐标所表示的向量却不一定惟一.
也就是说,向量的坐标表示和向量不是一
一对应的关系,但和起点为原点的向量是 一一对应的关系.即向量(x,y) 一 一 对应 OA
a,17
.实数λ1,λ2,使a=λ1e1+λ2e2.
6.平面向量的坐标表示
在平面直角坐标系内,分别取与x轴、y
轴正方向相同的两个单位向量i、j作为基底,
对任一向量a,18
x、y,使得
a=xi+yj,则实数对 19 叫做向量a的直角坐标,
记作a=(x,y),其中x、y分别叫做a在x轴、y 轴上的坐标,a=(x,y)叫做向量a的坐标表示.
定零向量的方向是任意的.
2019年高考数学一轮复习课时分层训练26平面向量的概念及线性运算理北师大版最新.doc

课时分层训练(二十六) 平面向量的概念及线性运算A 组 基础达标一、选择题1.给出下列命题:①零向量的长度为零,方向是任意的;②若a ,b 都是单位向量,则a =b ;③向量AB →与BA →相等.则所有正确命题的序号是( )A .①B .③C .①③D .①②A [根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量AB →与BA →互为相反向量,故③错误.]2.(2018·武汉调研)设a 是非零向量,λ是非零实数,则下列结论正确的是( )【导学号:79140147】A .a 与-λa 的方向相反B .|-λa |≥|a |C .a 与λ2a 的方向相同 D .|-λa |≥|λ|aC [A 中,当λ<0时,a 与-λa 方向相同,故A 不正确;B 中,当-1<λ<1时,|-λa |<|a |,故B 不正确;C 中,因为λ2>0,所以a 与λ2a 方向相同,故C 正确;D 中,向量不能比较大小,故D 不正确,故选C.]3.(2017·广东东莞二模)如图411所示,已知AC →=3BC →,OA →=a ,OB →=b ,OC →=c ,则下列等式中成立的是( )图411A .c =32b -12aB .c =2b -aC .c =2a -bD .c =32a -12bA [因为AC →=3BC →,OA →=a ,OB →=b ,所以OC →=OA →+AC →=OA →+32AB →=OA →+32(OB →-OA →)=32OB→-12OA →=32b -12a ,故选A.] 4.(2017·全国卷Ⅱ)设非零向量a ,b 满足|a +b |=|a -b |,则( )A .a ⊥bB .|a |=|b |C .a ∥bD .|a |>|b |A [法一:∵|a +b |=|a -b |,∴|a +b |2=|a -b |2. ∴a 2+b 2+2a·b =a 2+b 2-2a·b . ∴a·b =0.∴a ⊥b . 故选A.法二:在▱ABCD 中,设AB →=a ,AD →=b , 由|a +b |=|a -b |知|AC →|=|DB →|,从而四边形ABCD 为矩形,即AB ⊥AD ,故a ⊥b .故选A.]5.(2017·河南中原名校4月联考)如图412所示,矩形ABCD 的对角线相交于点O ,E 为AO 的中点,若DE →=λAB →+μAD →(λ,μ为实数),则λ2+μ2=( )图412A.58B.14 C .1 D.516A [DE →=12DA →+12DO →=12DA →+14DB →=12DA →+14(DA →+AB →)=14AB →-34AD →,所以λ=14,μ=-34,故λ2+μ2=58,故选A.]二、填空题6.已知O 为四边形ABCD 所在平面内一点,且向量OA →,OB →,OC →,OD →满足等式OA →+OC →=OB →+OD →,则四边形ABCD 的形状为________.平行四边形 [由OA →+OC →=OB →+OD →得OA →-OB →=OD →-OC →, 所以BA →=CD →,所以四边形ABCD 为平行四边形.]7.(2015·全国卷Ⅱ)设向量a ,b 不平行,向量λa +b 与a +2b 平行,则实数λ=________.12[∵λa +b 与a +2b 平行,∴λa +b =t (a +2b ),即λa +b =t a +2t b ,∴⎩⎪⎨⎪⎧λ=t ,1=2t ,解得⎩⎪⎨⎪⎧λ=12,t =12.]8.在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=x AB →+y AC →,则x =________;y =________.【导学号:79140148】12 -16 [∵AM →=2MC →,∴AM →=23AC →. ∵BN →=NC →,∴AN →=12(AB →+AC →),∴MN →=AN →-AM →=12(AB →+AC →)-23AC →=12AB →-16AC →. 又MN →=x AB →+y AC →,∴x =12,y =-16.]三、解答题9.如图413,在△ABC 中,D ,E 分别为BC ,AC 边上的中点,G 为BE 上一点,且GB =2GE ,设AB →=a ,AC →=b ,试用a ,b 表示AD →,AG →.图413[解] AD →=12(AB →+AC →)=12a +12b .AG →=AB →+BG →=AB →+23BE →=AB →+13(BA →+BC →)=23AB →+13(AC →-AB →) =13AB →+13AC → =13a +13b . 10.设e 1,e 2是两个不共线的向量,已知AB →=2e 1-8e 2,CB →=e 1+3e 2,CD →=2e 1-e 2.(1)求证:A ,B ,D 三点共线;(2)若BF →=3e 1-k e 2,且B ,D ,F 三点共线,求k 的值.[解] (1)证明:由已知得BD →=CD →-CB →=(2e 1-e 2)-(e 1+3e 2)=e 1-4e 2, ∵AB →=2e 1-8e 2,∴AB →=2BD →. 又∵AB →与BD →有公共点B , ∴A ,B ,D 三点共线. (2)由(1)可知BD →=e 1-4e 2,∵BF →=3e 1-k e 2,且B ,D ,F 三点共线, ∴BF →=λBD →(λ∈R ), 即3e 1-k e 2=λe 1-4λe 2,即⎩⎪⎨⎪⎧λ=3,-k =-4λ.解得k =12.B 组 能力提升11.(2017·河北衡水中学三调考试)在△ABC 中,AN →=14NC →,若P 是直线BN 上的一点,且满足AP →=m AB →+25AC →,则实数m 的值为( )【导学号:79140149】A .-4B .-1C .1D .4B [根据题意设BP →=n BN →(n ∈R ),则AP →=AB →+BP →=AB →+n BN →=AB →+n (AN →-AB →)=AB →+n ⎝ ⎛⎭⎪⎫15AC →-AB →=(1-n )AB →+n 5AC →,又AP →=m AB →+25AC →,∴⎩⎪⎨⎪⎧1-n =m ,n 5=25,解得⎩⎪⎨⎪⎧n =2,m =-1,故选B.]12.设O 在△ABC 的内部,D 为AB 的中点,且OA →+OB →+2OC →=0,则△ABC 的面积与△AOC 的面积的比值为( )A .3B .4C .5D .6B [如图,∵D 为AB 的中点,则OD →=12(OA →+OB →),又OA →+OB →+2OC →=0,∴OD →=-OC →,∴O 为CD 的中点,又∵D 为AB 中点,∴S △AOC =12S △ADC =14S △ABC ,则S△ABCS△AOC=4.]13.(2017·辽宁大连高三双基测试)如图414,在△ABC 中,AB =2,BC =3,∠ABC =60°,AH ⊥BC 于点H ,M 为AH 的中点.若AM →=λAB →+μBC →,则λ+μ=________.图41423 [因为AB =2,∠ABC =60°,AH ⊥BC ,所以BH =1.因为BC =3,所以BH =13BC . 因为点M 为AH 的中点,所以AM →=12AH →=12(AB →+BH →)=12⎝ ⎛⎭⎪⎫AB →+13BC →=12AB →+16BC →,又AM →=λAB→+μBC →,所以λ=12,μ=16,所以λ+μ=23.]14.已知O ,A ,B 是不共线的三点,且OP →=m OA →+n OB →(m ,n ∈R ).【导学号:79140150】(1)若m +n =1,求证:A ,P ,B 三点共线; (2)若A ,P ,B 三点共线,求证:m +n =1. [证明] (1)若m +n =1, 则OP →=m OA →+(1-m )OB → =OB →+m (OA →-OB →), ∴OP →-OB →=m (OA →-OB →), 即BP →=m BA →,∴BP →与BA →共线. 又∵BP →与BA →有公共点B , ∴A ,P ,B 三点共线. (2)若A ,P ,B 三点共线, 则存在实数λ,使BP →=λBA →, ∴OP →-OB →=λ(OA →-OB →). 又OP →=m OA →+n OB →.故有m OA →+(n -1)OB →=λOA →-λOB →,即(m -λ)OA →+(n +λ-1)OB →=0. ∵O ,A ,B 不共线,∴OA →,OB →不共线,∴⎩⎪⎨⎪⎧m -λ=0,n +λ-1=0,∴m +n =1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时分层训练(二十六) 平面向量的概念及线性运算A 组 基础达标一、选择题1.给出下列命题:①零向量的长度为零,方向是任意的;②若a ,b 都是单位向量,则a =b ;③向量AB →与BA →相等.则所有正确命题的序号是( )A .①B .③C .①③D .①②A [根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量AB →与BA →互为相反向量,故③错误.]2.(2018·武汉调研)设a 是非零向量,λ是非零实数,则下列结论正确的是( )【导学号:79140147】A .a 与-λa 的方向相反B .|-λa |≥|a |C .a 与λ2a 的方向相同D .|-λa |≥|λ|aC [A 中,当λ<0时,a 与-λa 方向相同,故A 不正确;B 中,当-1<λ<1时,|-λa |<|a |,故B 不正确;C 中,因为λ2>0,所以a 与λ2a 方向相同,故C 正确;D 中,向量不能比较大小,故D 不正确,故选C.]3.(2017·广东东莞二模)如图411所示,已知AC →=3BC →,OA →=a ,OB →=b ,OC →=c ,则下列等式中成立的是( )图411A .c =3b -1aB .c =2b -aC .c =2a -bD .c =32a -12bA [因为AC →=3BC →,OA →=a ,OB →=b ,所以OC →=OA →+AC →=OA →+32AB →=OA →+32(OB →-OA →)=32OB →-12OA →=32b -12a ,故选A.] 4.(2017·全国卷Ⅱ)设非零向量a ,b 满足|a +b |=|a -b |,则( )A .a⊥bB .|a |=|b |C .a∥bD .|a |>|b |A [法一:∵|a +b |=|a -b |,∴|a +b |2=|a -b |2. ∴a 2+b 2+2a·b =a 2+b 2-2a·b . ∴a·b =0.∴a⊥b . 故选A.法二:在▱ABCD 中,设AB →=a ,AD →=b , 由|a +b |=|a -b |知|AC →|=|DB →|,从而四边形ABCD 为矩形,即AB ⊥AD ,故a⊥b .故选A.]5.(2017·河南中原名校4月联考)如图412所示,矩形ABCD 的对角线相交于点O ,E 为AO 的中点,若DE →=λAB →+μAD →(λ,μ为实数),则λ2+μ2=( )图412A.58B.14 C .1 D.516A [DE →=12DA →+12DO →=12DA →+14DB →=12DA →+14(DA →+AB →)=14AB →-34AD →,所以λ=14,μ=-34,故λ2+μ2=58,故选A.] 二、填空题6.已知O 为四边形ABCD 所在平面内一点,且向量OA →,OB →,OC →,OD →满足等式OA →+OC→=OB →+OD →,则四边形ABCD 的形状为________.平行四边形 [由OA →+OC →=OB →+OD →得OA →-OB →=OD →-OC →, 所以BA →=CD →,所以四边形ABCD 为平行四边形.]7.(2015·全国卷Ⅱ)设向量a ,b 不平行,向量λa +b 与a +2b 平行,则实数λ=________.12[∵λa +b 与a +2b 平行,∴λa +b =t (a +2b ), 即λa +b =t a +2t b ,∴⎩⎨⎧λ=t ,1=2t ,解得⎩⎪⎨⎪⎧λ=12,t =12.]8.在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+yAC →,则x =________;y =________.【导学号:79140148】12 -16 [∵AM →=2MC →,∴AM →=23AC →. ∵BN →=NC →,∴AN →=12(AB →+AC →),∴MN →=AN →-AM →=12(AB →+AC →)-23AC →=12AB →-16AC →. 又MN →=xAB →+yAC →,∴x =12,y =-16.]三、解答题9.如图413,在△ABC 中,D ,E 分别为BC ,AC 边上的中点,G 为BE 上一点,且GB =2GE ,设AB →=a ,AC →=b ,试用a ,b 表示AD →,AG →.图413[解] AD →=12(AB →+AC →)=12a +12b .AG →=AB →+BG →=AB →+23BE →=AB →+13(BA →+BC →)=23AB →+13(AC →-AB →) =13AB →+13AC → =13a +13b . 10.设e 1,e 2是两个不共线的向量,已知AB →=2e 1-8e 2,CB →=e 1+3e 2,CD →=2e 1-e 2.(1)求证:A ,B ,D 三点共线;(2)若BF →=3e 1-k e 2,且B ,D ,F 三点共线,求k 的值.[解] (1)证明:由已知得BD →=CD →-CB →=(2e 1-e 2)-(e 1+3e 2)=e 1-4e 2, ∵AB →=2e 1-8e 2,∴AB →=2BD →. 又∵AB →与BD →有公共点B , ∴A ,B ,D 三点共线. (2)由(1)可知BD →=e 1-4e 2,∵BF →=3e 1-k e 2,且B ,D ,F 三点共线, ∴BF →=λBD →(λ∈R ), 即3e 1-k e 2=λe 1-4λe 2,即⎩⎨⎧λ=3,-k =-4λ.解得k =12. B 组 能力提升11.(2017·河北衡水中学三调考试)在△ABC 中,AN →=14NC →,若P 是直线BN 上的一点,且满足AP →=mAB →+25AC →,则实数m 的值为( )【导学号:79140149】A .-4B .-1C .1D .4B [根据题意设BP →=nBN →(n ∈R ),则AP →=AB →+BP →=AB →+nBN →=AB →+n (AN →-AB →)=AB →+n ⎝ ⎛⎭⎪⎫15AC →-AB →=(1-n )AB →+n 5AC →,又AP →=mAB →+25AC →,∴⎩⎨⎧1-n =m ,n 5=25,解得⎩⎨⎧n =2,m =-1,故选B.] 12.设O 在△ABC 的内部,D 为AB 的中点,且OA →+OB →+2OC →=0,则△ABC 的面积与△AOC 的面积的比值为( )A .3B .4C .5D .6B [如图,∵D 为AB 的中点,则OD →=12(OA →+OB →),又OA →+OB →+2OC →=0,∴OD →=-OC →,∴O 为CD 的中点,又∵D 为AB 中点,∴S △AOC =12S △ADC =14S △ABC ,则S △ABCS △AOC=4.]13.(2017·辽宁大连高三双基测试)如图414,在△ABC 中,AB =2,BC =3,∠ABC =60°,AH ⊥BC 于点H ,M 为AH 的中点.若AM →=λAB →+μBC →,则λ+μ=________.图41423 [因为AB =2,∠ABC =60°,AH ⊥BC ,所以BH =1.因为BC =3,所以BH =13BC . 因为点M 为AH 的中点,所以AM →=12AH →=12(AB →+BH →)=12⎝ ⎛⎭⎪⎫AB →+13BC →=12AB →+16BC →,又AM→=λAB →+μBC →,所以λ=12,μ=16,所以λ+μ=23.]14.已知O ,A ,B 是不共线的三点,且OP →=mOA →+nOB →(m ,n ∈R ).【导学号:79140150】(1)若m +n =1,求证:A ,P ,B 三点共线; (2)若A ,P ,B 三点共线,求证:m +n =1. [证明] (1)若m +n =1, 则OP →=mOA →+(1-m )OB → =OB →+m (OA →-OB →), ∴OP →-OB →=m (OA →-OB →), 即BP →=mBA →,∴BP →与BA →共线. 又∵BP →与BA →有公共点B , ∴A ,P ,B 三点共线. (2)若A ,P ,B 三点共线, 则存在实数λ,使BP →=λBA →, ∴OP →-OB →=λ(OA →-OB →). 又OP →=mOA →+nOB →.故有mOA →+(n -1)OB →=λOA →-λOB →, 即(m -λ)OA →+(n +λ-1)OB →=0.∵O ,A ,B 不共线,∴OA →,OB →不共线,∴⎩⎨⎧m -λ=0,n +λ-1=0,∴m +n =1.。
