信息论课程知识总结

老师整理的信息论知识点

Chp02知识点：自信息量：1）)(log )(i i x p x I -=2）对数采用的底不同，自信息量的单位不同。

2----比特（bit ）、e----奈特（nat ）、10----哈特（Hart ） 3）物理意义：事件i x 发生以前，表示事件i x 发生的不确定性的大小；事件i x 发生以后，表示事件i x 所含有或所能提供的信息量。

平均自信息量（信息熵）：1）)(log )()]([)(1i qi i i x p x p x I E x H ∑=-==2）对数采用的底不同，平均自信息量的单位不同。

2----比特/符号、e----奈特/符号、10----哈特/符号。

3）物理意义：对信源的整体的不确定性的统计描述。

表示信源输出前，信源的平均不确定性；信源输出后每个消息或符号所提供的平均信息量。

4）信息熵的基本性质：对称性、确定性、非负性、扩展性、连续性、递推性、极值性、上凸性。

互信息：1）)()|(log)|()();(i j i j i i j i x p y x p y x I x I y x I =-=2）含义：已知事件j y 后所消除的关于事件i x 的不确定性，对信息的传递起到了定量表示。

平均互信息：1）定义：2）性质：联合熵和条件熵：各类熵之间的关系：数据处理定理：Chp03知识点：依据不同标准信源的分类：离散单符号信源：1）概率空间表示：2）信息熵：)(log )()]([)(1i qi i i x p x p x I E x H ∑=-==，表示离散单符号信源的平均不确定性。

离散多符号信源：用平均符号熵和极限熵来描述离散多符号信源的平均不确定性。

平均符号熵：)...(1)(21N N X X X H NX H =极限熵（熵率）：)(lim )(X H X H N N ∞>-∞= （1）离散平稳信源（各维联合概率分布均与时间起点无关的信源。

）（2）离散无记忆信源：信源各消息符号彼此互不相关。

信息论总结与复习

状态、状态转移、状态转移图、稳定状态、稳态方程
（3）稳态符号概率：（4）稳态信息熵：
结论：N阶马氏信源稳态信息熵(即极限熵)等于N+1阶条件熵。
第一部分、信息论基础
1.1 信源的信息理论
[例1] 已知二阶马尔可夫信源的条件概率：
p(0|00)=p(1|11)=0.8；p(0|01)=p(1|10)=0.6；
(2)联合熵：
H(XY)= -0.21log0.21 –0.14log0.14 –0.35log0.35 –0.12log0.12 –0.09log0.09–0.09log0.09 =2.3924 bit/符号
第一部分、信息论基础
1.2 信道的信息理论
(3)噪声熵：
由和
H(Y | X)= – 0.21log0.3 –0.14log0.2 –0.35log0.5
（4）无噪有损信道：分组多对一（归并），其传输矩阵应具有多行一列的分块对角化形式。
（5）对称信道：传输矩阵的各行都是一些相同元素的重排，各列也是一些相同元素的重排。
第一部分、信息论基础
1.2 信道的信息理论
3、信道有关的信息熵：
（1）信源熵 (先验熵)：
（2）噪声熵 (散布度)：
（3）联合熵：（4）接收符号熵：
–0.12log0.4 –0.09log0.3–0.09log0.3
==（0.21+0.12，0.14+0.09，0.35+0.09） = （0.33, 0.23, 0.44）
H(Y)= -0.33log0.33 -0.23log0.23 -0.44log0.44
[例3]求对称信道解：C =log4-H(0.2,0.3,0.2,0.3) =2+(0.2log0.2+0.3log0.3)×2 = 0.03 bit/符号；的信道容量。

信息论总结

D
香农编码：
二进制香农码的编码步骤如下： ⑴将信源符号按概率从大到小的顺序排列, p(a1)≥ p(a2)≥…≥ p(an) ⑵确定满足下列不等式的整数Ki , －log2 p(ai)≤ Ki <1－log2 p(ai) ⑶令p(a1)=0,用Pi表示第i个码字的累加概率，
⑷将Pi用二进制表示,并取小数点后Ki位作为符号ai的编码。
m元霍夫曼编码的编码方式类同于二元霍夫曼编码，不同的是每次把m个符号合并成一个新的信源符号，并分别用0,1，……，m-1等码元表示。为了使短码得到充分利用，使平均码长为最短，必须使最后一步缩减信源有m个信源符号。因此对于m 元编码，信源s的符号个数必须满足q=(m-1) θ+m, θ是缩减的次数.
L →∞
5 马尔可夫信源的极限熵：
H ∞ = H m +1 = ∑ p ( si ) H ( X | si ) p( si ) = Wi
i
H ( X | si ) = −∑ p ( x j | si ) log p ( x j | si )
j
6
H∞ (X ) η 冗余度： = H ( X ) ０ ≤ η ≤１ m
游程编码：
若规定二元序列总是从“0”开始,第一个游程是“0”游程,则第二个游程必为“1”游程,第三个又是“0”游程……。对于随机序列,游程长度是随机的其取值可为1,2,3,…，直至无穷。游程长度序列/游程序列：用交替出现的“0”游程和“1” 游程长度表示任意二元序列。游程变换：是一种一一对应的变换,也是可逆变换。例如：二元序列000101110010001… 可变换成如下游程序列 31132131
i i i =1 i =1 L L
Ｌ

(完整版)老师整理的信息论知识点

Chp02知识点：自信息量：1）)(log )(i i x p x I -=2）对数采用的底不同，自信息量的单位不同。

2----比特（bit ）、e----奈特（nat ）、10----哈特（Hart ） 3）物理意义：事件i x 发生以前，表示事件i x 发生的不确定性的大小；事件i x 发生以后，表示事件i x 所含有或所能提供的信息量。

平均自信息量（信息熵）：1）)(log )()]([)(1i qi i i x p x p x I E x H ∑=-==2）对数采用的底不同，平均自信息量的单位不同。

2----比特/符号、e----奈特/符号、10----哈特/符号。

3）物理意义：对信源的整体的不确定性的统计描述。

表示信源输出前，信源的平均不确定性；信源输出后每个消息或符号所提供的平均信息量。

4）信息熵的基本性质：对称性、确定性、非负性、扩展性、连续性、递推性、极值性、上凸性。

互信息：1）)()|(log)|()();(i j i j i i j i x p y x p y x I x I y x I =-=2）含义：已知事件j y 后所消除的关于事件i x 的不确定性，对信息的传递起到了定量表示。

平均互信息：1）定义：2）性质：联合熵和条件熵：各类熵之间的关系：数据处理定理：Chp03知识点：依据不同标准信源的分类：离散单符号信源：1）概率空间表示：2）信息熵：)(log )()]([)(1i qi i i x p x p x I E x H ∑=-==，表示离散单符号信源的平均不确定性。

离散多符号信源：用平均符号熵和极限熵来描述离散多符号信源的平均不确定性。

平均符号熵：)...(1)(21N N X X X H NX H =极限熵（熵率）：)(lim )(X H X H N N ∞>-∞= （1）离散平稳信源（各维联合概率分布均与时间起点无关的信源。

）（2）离散无记忆信源：信源各消息符号彼此互不相关。

信息论重点-(新)

1．消息定义信息的通俗概念:消息就是信息,用文字、符号、数据、语言、音符、图片、图像等能够被人们感觉器官所感知的形式，把客观物质运动和主观思维活动的状态表达出来，就成为消息，消息中包含信息,消息是信息的载体。

信号是表示消息的物理量，包括电信号、光信号等。

信号中携带着消息，信号是消息的载体。

信息的狭义概念（香农信息)：信息是对事物运动状态或存在方式的不确定性的描述。

信息的广义概念信息是认识主体（人、生物、机器)所感受的和表达的事物运动的状态和运动状态变化的方式。

➢ 语法信息(语法信息是指信息存在和运动的状态与方式.） ➢ 语义信息（语义信息是指信宿接收和理解的信息的内容。

） ➢ 语用信息(语用信息是指信息内容对信宿的有用性。

）2．狭义信息论、广义信息论。

狭义信息论：信息论是在信息可以量度的基础上，对如何有效，可靠地传递信息进行研究的科学.它涉及信息量度,信息特性，信息传输速率，信道容量,干扰对信息传输的影响等方面的知识。

广义信息论：信息是物质的普遍属性,所谓物质系统的信息是指它所属的物理系统在同一切其他物质系统全面相互作用（或联系）过程中，以质、能和波动的形式所呈现的结构、状态和历史。

包含通信的全部统计问题的研究，除了香农信息论之外，还包括信号设计,噪声理论，信号的检测与估值等.3。

自信息互信息定义性质及物理意义自信息量： ()log ()i x i I x P x =-是无量纲的，一般根据对数的底来定义单位：当对数底为2时，自信息量的单位为比特;对数底为e 时,其单位为奈特;对数底为10时，其单位为哈特自信息量性质：I （x i ）是随机量；I(x i ）是非负值；I(x i ）是P （x i )的单调递减函数.自信息物理意义： 1。

事件发生前描述该事件发生的不确定性的大小 2.事件发生后表示该事件所含有（提供）的信息量互信息量:互信息量的性质：1) 互信息的对称性2) 互信息可为零3) 互信息可为正值或负值4) 任何两个事件之间的互信息不可能大于其中任一事件的自信息互信息物理意义： 1。

信息论期末总结

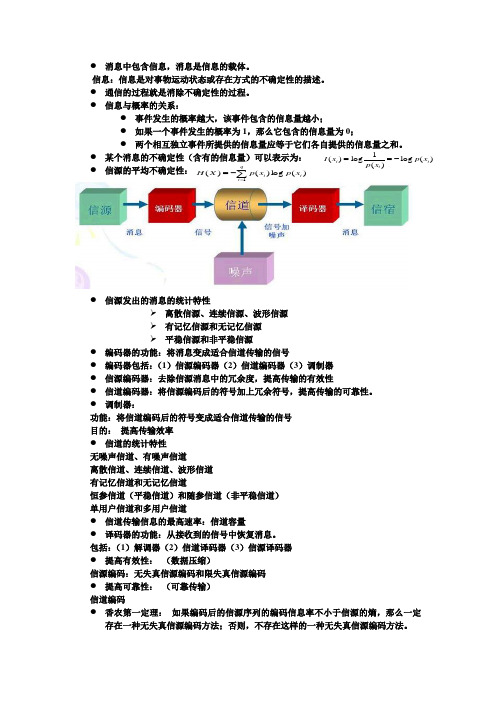
● 消息中包含信息，消息是信息的载体。

信息：信息是对事物运动状态或存在方式的不确定性的描述。

● 通信的过程就是消除不确定性的过程。

● 信息与概率的关系：● 事件发生的概率越大，该事件包含的信息量越小；● 如果一个事件发生的概率为1，那么它包含的信息量为0；●● 某个消息的不确定性（含有的信息量）可以表示为： ● 信源的平均不确定性：● 信源发出的消息的统计特性离散信源、连续信源、波形信源有记忆信源和无记忆信源平稳信源和非平稳信源● 编码器的功能：将消息变成适合信道传输的信号 ● 编码器包括：（1）信源编码器（2）信道编码器（3）调制器 ● 信源编码器：去除信源消息中的冗余度，提高传输的有效性● 信道编码器：将信源编码后的符号加上冗余符号，提高传输的可靠性。

● 调制器：功能：将信道编码后的符号变成适合信道传输的信号目的：提高传输效率 ● 信道的统计特性无噪声信道、有噪声信道离散信道、连续信道、波形信道有记忆信道和无记忆信道恒参信道（平稳信道）和随参信道（非平稳信道）单用户信道和多用户信道● 信道传输信息的最高速率：信道容量● 译码器的功能：从接收到的信号中恢复消息。

包括：（1）解调器（2）信道译码器（3）信源译码器 ● 提高有效性：（数据压缩）信源编码：无失真信源编码和限失真信源编码 ● 提高可靠性：（可靠传输）信道编码● 香农第一定理：如果编码后的信源序列的编码信息率不小于信源的熵，那么一定存在一种无失真信源编码方法；否则，不存在这样的一种无失真信源编码方法。

∑=-=qi i i x p x p X H 1)(log )()(● 香农第二定理：如果信道的信息传输率小于信道容量，那么总可以找到一种编码方式，使得当编码序列足够长时传输差错任意小；否则，不存在使差错任意小的信道编码方式。

● 香农第三定理：对于任意的失真度，只要码字足够长，那么总可以找到一种编码方法，使编码后的编码信息率，而码的平均失真度。

信息论复习笔记

信息论复习笔记(总23页) -本页仅作为预览文档封面，使用时请删除本页-1. 绪论信息论回答了通信的两个最基本问题:（1）数据压缩的极限；（2）信道传输速率的极限；信息、消息和信号消息：信息的載體（能被感知和理解、進行傳遞和獲取）信息：事物運動狀態或存在方式的不確定性的描述（香農）先驗概率：P(a i)自信息：I(a i)=log[P-1(a i)]；（信息接收的不確定性）互信息：I(a i;b i)= log[P-1(a i)]- log[P-1(a i|b i)];（信息接收的多少度量）（若信道無干擾，則互信息等於自信息等於0）優點：明確的數學模型、定量計算；缺點：有適用範圍；信號；通信系统的模型通信系统的基本要求:有效、可靠、保密、认证2. 离散信源及其信息测度﹣离散信源的定义：輸出信息數有限、每次只輸出一個；﹣自信息的定义及物理意义事件發生前：事件發生的不確定性；事件發生后：時間含有的信息量；信息熵的定义及物理意义,信息熵的基本性质定義：自信息的數學期望（ H(X)= -∑[ P(a i)logP(a i) ] ）信源的總體信息測度（1）每個消息所提供的平均信息量；（2）信源輸出前，信源的平均不確定性；性質：（1）對稱性；（2）確定性；（3）非負性；（4）擴展性（可拆開）；（5）可加性；[ H(XY)=H(X)+H(Y) ]（6）強可加性；[ H(XY)=H(X)+H(Y|X) ]（7）遞增性；（8）極值性; [ H(p1,p2,p3…,p q)≤H(q-1,,…, q-1)= logq ]等概率分佈信源的平均不確定性最大，稱為最大離散熵定理；—离散无记忆信源的扩展信源—扩展信源的熵 H(X) = NH(X)—离散平稳信源：联合概率分布与时间起点无关；熵：联合熵 H(X1X2)=∑∑P(a i a j)logP(a i a j)条件熵 H(X2|X1)=-∑∑P(a i a j)logP(a i|a j)关系：H(X1X2)=H(X1)+H(X2|X1)熵率:离散平稳信源的极限熵 = limH(X N|X1X2…X N-1)—马尔可夫信源:某一时刻的输出只与此刻信源所处的状态有关而与以前的状态及以前的输出符号都无关；—马尔可夫信源的熵：H m+1=H(X m+1|X1X2…X m)—信源剩余度熵的相对率η= H极限/H0信源剩余度（输出符号间依赖强度）γ= 1-η=1-H极限/H0 3. 离散信道及其信道容量—H(X;Y)=H(X)-H(X|Y)—离散信道的数学模型—信道矩阵性質（1）P(a i bj)=P(a i)P(b j|a i)=P(b j)P(a i|b j)；（2）[ P(b1) ] [ P(a1) ][ P(b2) ] [ P(a2) ][ P(b3) ] = [ P(a4) ] （r≠s）[ … ] [ … ][ P(b s) ] [ P(a r) ]（3）輸出端收到的任一b j一定是輸入符號a r中的某一個送入信道；─信道疑义度的定义：收到Y後對變量X尚存在的平均不確定性：H(X|Y)=E[H(X|b j)]=∑P(xy)log-1P(X|Y)物理意义:噪聲造成的影響大小；─平均互信息的定义：收到Y後平均每個符號獲得的關於X的信息量（物理意義：反映輸入輸出兩個隨機變量之間的統計約束關係）：I(X;Y)= H(X)-H(X|Y) = ∑P(xy)P(y|x)P-1(y)無噪一一對應信道中：I(X;Y)=H(X)=H(Y)＝0—信道容量的定义：信道每秒鐘平均傳輸的信息量稱為信息傳輸速率，最大信息傳輸率稱為信道容量；—信道容量的计算:无噪信道(求H(X)極值)：C = logr对称信道（信道矩陣的每一行或列是另一行或列的置換）：C = logs-H(p1,p2,…,p s)强对称信道：C = logr-plog(r-1)-H(p)；准对称信道：C = logr-H(p1,p2,…,p s)-∑N k logM k（Nk是第k個子矩陣行元素之和，Mk是第k個子矩陣列元素之和）一般离散信道（對所有可能的輸入概率分佈求平均互信息的最大值）：C =λ＋loge條件：I(x i;Y) = ∑s j=1P(b j|a i)*log[P(b j|a i)/P(b j)]≤ C—数据处理定理如果X、Y、Z组成一个马尔科夫链，则有I(X;Z)≤I(X;Y)I(X;Z)≤I(Y;Z)信息不增性原理一般的数据处理原理I(S;Z)≤I(S;Y)I(S;Z)≤I(X;Z)I(S;Z)≤I(X;Y)—信道剩余度= C-I(X;Y)相对剩余度 = 1-I(X;Y)/C无损信道的相对剩余度 = 1-H(X)/logr4. 波形信源和波形信道連續信源的相對熵: h(X)Δ= ﹣∫R p(x)logp(x)dx 波形信源的差熵：h(x(t))Δ=lim N->★h(X1X2…X N)连续信源的差熵：均匀分布连续信源的差熵:N維均勻分佈：高斯信源的差熵：N維高斯信源的差熵：差熵的性质：（1）可加性；（2）凸性；（3）可負性；（4）變換性（X1->X2,差熵會變化）；（5）極值性：離散信源的信源符號等概率分佈時信源的熵最大;連續信源：﹣當峰值功率受限為p^時（輸出信號的瞬時電壓限制為±(p^)1/2），此時信源輸出的連續隨機變量限制在[a,b]內，信源具有最大熵：h=log(b-a)如果隨機矢量取值受限，則各隨機分量統計獨立并均勻分佈時具有最大熵；﹣當信源輸出信號的平均功率被限定為P，則其信號幅度的概率密度分佈為高斯分佈時，信源有最大熵：h=1/2＊log2πePN維連續平穩信源如果其N維隨機序列的協方差矩陣C被限定，則N維隨機矢量為正太分佈時信源的熵最大。

信息论知识点总结

信息论知识点总结信息论是一门研究信息传递和处理的科学，主要涉及信息量度、信息特性、信息传输速率、信道容量、干扰对信息传输的影响等方面的知识。

以下是信息论的一些重要知识点：1. 信息量度：信息量是对信息的度量，用于衡量信息的多少。

信息的大小与随机事件的概率有关，熵是衡量随机变量分布的混乱程度，即随机分布各事件发生的信息量的期望值。

2. 信道容量：信道容量是描述信道传输信息能力的指标，表示信道在每秒内所能传输的最大信息量。

对于有噪声的信道，需要通过编码技术来达到信道容量。

3. 条件熵：条件熵是在给定某个条件下的熵，用于衡量在已知某个条件的情况下，随机变量的不确定性。

4. 相对熵（KL散度）：相对熵是衡量两个概率分布之间的差异，也称为KL 散度。

如果两个分布相同，相对熵为0。

5. 信息传输速率：信息传输速率是指单位时间内传输的信息量，是评价通信系统性能的重要参数。

6. 干扰对信息传输的影响：在信息传输过程中，各种干扰因素会对信息传输产生影响，如噪声、失真、衰减等。

为了提高信息传输的可靠性和有效性，需要采取抗干扰措施。

7. 信息压缩：信息压缩是减少数据存储空间和提高数据传输效率的一种技术。

常见的压缩算法有Huffman编码、LZ77、LZ78等。

8. 纠错编码：纠错编码是一种用于检测和纠正错误的技术，广泛应用于通信和存储领域。

常见的纠错编码有奇偶校验、CRC等。

9. 加密编码：加密编码是一种保护信息安全的技术，通过对数据进行加密处理，防止未经授权的访问和泄露。

常见的加密编码有AES、RSA等。

以上是信息论的一些重要知识点，希望对您有所帮助。