西北工业大学高等数学期末测试题
西北工业大学《高等数学2B》2019-2020学年第二学期期末试卷

.
∫∫ 5. 设曲面 Σ 是圆锥面=z x2 + y2 ( 0 ≤ z ≤ 2) , 则曲面积分 z dS 的值为 Σ
.
二、选择题(共 15 分,每小题 3 分)
1. 下列级数中收敛的是 (
).
∞
∑ (A) (−1)n n=1
∑ (B) ∞ tan π
n=3 n
∑∞ 4n −1
(C) n=1 n2 + n
2
2
的曲线段.
= 解: P
x= x2 ++ yy2 , Q
y x2
+= − yx2 , 则 ∂∂Py
x= 2( x−22+xyy 2−)2y 2
∂Q , 故曲线积分与路径无关, ∂x
选取= 圆弧 C : x π= cosθ , y π sinθ , θ: π → 0, 则
2
2
∫ ∫ L
(x
+
y)dx x2
六、证明题(本题 5 分)
设常数 a
>
0, 对 ∀ n ∈ N+ ,
un
>
0,
vn
>
0,
且
vn
un un+1
− vn+1
≥
a.
∞
∑ 证明: 级数 un 收敛.
n=1
证明:
vn
un un+1
−
vn+1
≥
a
>
0
即
unvn − un+1vn+1 ≥ a > 0 , un+1
于是
unvn − un+1vn+1 > 0,
2015-2016高等数学(上)期末试题A卷解答与评分标准

2x 3 x 1 x 1
2
x 1 x 1 2! 2 2! 1 2 因为 f x 2 , f x 2 2 3 x 1 x 1 x 1 x 13 1 2 n 所以 f n x 1 n ! n 2 , 3 , n 1 n 1 x 1 x 1 10 因此 f 0 10!
1 x 2 x 1 arctan x x ln 1 x 2 C 2
(4 分) (6 分)
2、
x2
1 x
3 2 2
dx
(1 分) (2 分)
解 设 x tan x x2 tan2 t sin 2 t 2 dx sec tdt dt 3 cost sec3 t 2 2 1 x
共6页 西北工业大学命题专用纸
第3页
四、计算题(每小题 6 分,共 18 分) 1、 2 x 1 arctan x dx 解 原式 x 2 x arctanx
x2 x 1 x2
dx
(3 分)
1 x xx 1 arctanx 1 dx 2 1 x2 1 x
由条件知 lima cos x b a b 0
x 0
(2 分)
所以 lim
x 0
a cos x b a sin x a sin x a lim lim 1 x2 3 2 x 0 x 0 2x 2 x 2 ln 1 x 2 1 x
(7 分)
所以,向量 c 是向量 a 和向量 b 的角平分向量。
(8 分)
2024届陕西省西安市西北工业大学高一数学第二学期期末经典试题含解析

2024届陕西省西安市西北工业大学高一数学第二学期期末经典试题考生须知: 1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的1.ABC ∆中,下列结论:①若A B >,则sin sin A B >,②sin()sin A B C +=,③cos()cos +=A B C ,④若ABC ∆是锐角三角形,则sin cos A B >,其中正确的个数是( ) A .1B .2C .3D .42.如图,正方形ABCD 中,M 是BC 的中点,若AC AM BD λμ=+,则λμ+=( )A .43B .53C .158D .23.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,120ABC ∠=︒,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为( ) A .8B .9C .10D .74.[]x 表示不超过x 的最大整数,设函数2()ln(1)h x x x =++,则函数()[()][()]f x h x h x =+-的值域为( )A .{0}B .{2,0}-C .{1,0,1}-D .{1,0}-5.已知等差数列中,,.若公差为某一自然数,则n 的所有可能取值为( ) A .3,23,69B .4,24,70C .4,23,70D .3,24,706.如图,在正方体1111ABCD A B C D -中,已知M ,N 分别为棱AB ,1AB 的中点,A .90°B .60°C .45°D .30°7.设复数12z i =+(是虚数单位),则在复平面内,复数2z 对应的点的坐标为( ) A .()3,4-B .()5,4C .()3,2-D .()3,48.若直线l 过两点(1,2)A ,(3,6)B ,则l 的斜率为( ) A .12B .12-C .2D .2-9.设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,若2,3sin 5sin b c a A B +==,则角C =( )A .3πB .23π C .34πD .56π10.已知259a =°,sin15cos15b =+°°,2231cos31c =°°,则实数a 、b 、c 的大小关系是()A .a c b <<a c b <<B .a b c <<C .a c b ≥≥D .a b c ≥≥二、填空题:本大题共6小题,每小题5分,共30分。
西北工业大学高数期末试题10-11二学期B卷及答案
共6页第1页班级:学号:姓名:班级:学号:姓名:高等数学2009--2010第二学期期终考试试题答案及评分标准A卷一、1、-8,2、,3、,4、8π,5、,6、。
二、1, 2、,3、,4、,5、3,6、[]2121+-,,缺闭区间扣一分。
三、1、解:设切点…………………2分由已知条件得:,得到.………..4分切平面方程为即……………..6分2、解:……………..3分……………..6分3、解:………………4分………………6分四、1、解:g f fy xx u v∂∂∂=+∂∂∂,g f fx yy u v∂∂∂=-∂∂∂,…………….2分vfvfxvufxyufyx∂∂+∂∂+∂∂∂+∂∂=∂∂2222222222g,vfvfyvufxyufxy∂∂-∂∂+∂∂∂-∂∂=∂∂2222222222g, ………………..5分222222g gx yx y∂∂+=+∂∂………………6分2.解:设dydppyp=''=',y,………………………2分得到舍去)(,0y==+ppdydp,解得ycp1=,100(,)dy f x y dx⎰83π12eπ+1415-{}00000(,,),,2,1P x y z n x y=-224000sind d drππθϕϕ⎰⎰143π0021221x y-==-2230x y z+--=2200002,1, 3.2xx y z y===+=2(2)2(1)(3)0x y z-+---=231131()12y yyydy e dxy y e dy e∂=-=-⎰⎰⎰8232008222336dz d drz dzπθππ==⎰⎰⎰2y1=-由初始条件yy 21,21c 1='=, ………………………4分 22c x y +=, 由初12=c ,其特解为1,12+=+=x y x y 或。
……………………..6分 3.、解:由xQy p ∂∂=∂∂,得x e x f x f x f =-'-'')()()(,………………2分 x x x e y e c e c Y 21,221-=+=*-,由初始条件61,3221-==c c , x x x e e e x f 216132)(2--=- ……….4分(1,1)(0,0)()2()()x f x f x e ydx f x dy ''⎡⎤+++⎣⎦⎰ =⎰-+=-+--101212216134216134e e e dy e e e ). ……………….6分五、解:1151lim lim (1)55n n n n n na n a n ++→∞→∞⋅==+⋅, ∴收敛半径为5R =…………………..2分 当5x =-时, 15n n∞=∑发散; 当5x =时,11(1)5n n n -∞=-⋅∑收敛 ∴收敛区间为(5,5]-…………………………………………………4分 设和函数1111111100110(1)()(1)55 [(1)][(1)()]5551 ln(1), (5,5]5515n n n n nn n n n xx n n n n n n x x S x x x n n t x t x dt dt n x x dt x x t -∞∞+-==∞∞---==-==-⋅⋅'=-=-⋅==+∈-+∑∑∑∑⎰⎰⎰………..…7分 …………………….8分六、解:设旋转曲面S 的方程为 12222=++z y x ,--------------------1分给定的方向 )0,21,21(0-=l方向导数函数)(2c o s c o s c o s y x zf y f x f l f -=∂∂+∂∂+∂∂=∂∂γβα --------2分 设)12()(2222-+++-=z y x y x L λ, ---------------3分令 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=++==∂∂=+-=∂∂=+=∂∂1202022042222z y x z z Ly y L x x Lλλλ ------------------4分解之得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=02242z y x λλ 23±=λ ------------------6分23=λ,得S 上的点为)0,36,66(-,此时3-=∂∂l f 23-=λ,得S 上的点为)0,36,66(-,此时3=∂∂lf所以,所求的S 上的点为)0,36,66(- ------------------7分 七、解:……………………3分000()()(x)lim()(1)()lim lim x x x x x f x x f x f x f x e f x e x x∆→∆∆→∆→+∆-'=∆-∆=+∆∆(x)()(0),(),(0)0,0..xx x f f x f e y ax c e f c y axe ''=+=+=∴== 111100(x)(1)(1)(1)!!x x x x n n n n f axe aexe ae x e aee x x ae ae n n ---+∞∞=====-+--=+∑∑………………………6分………………………7分(2009)(1)2010ae f =n=100(1)(1)=ae (1)!!(1)(1),.!n nn nn x x ae n n n x ae x R n ∞∞=∞=--+-+-=∈∑∑∑。
西安工业大学高数期末考试题及答案试题

高等数学(Ⅱ)期末参考答案一、填空题(每小题3分,共36分) 1.=⎪⎪⎭⎫ ⎝⎛+∞→∞→xy x xy 11lim ==⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫⎝⎛+∞→∞→∞→∞→⋅∞→∞→01lim111lim 11lim e xy xy yxyy x yxy y x y x 1 .2.函数),(y x z z =由方程0sin=+xy e xz 确定,则=-=-=∂∂xzzy xex y xF F yz cos 1xzex x y2cos -.3.设函数222ln zy x u ++=,则它在点)1,1,1(0-M 处的方向导数的最大值为33.4.设函数y xy ax x y x f 22),(22+++=在点)1,1(-处取得极值,则常数=a 5-.5.空间曲线x zx y-==1,222在点)22,1,21(处的切线方程为212211121--=-=-z y x .6.改变积分次序:==⎰⎰-dy y x f dx I x x 22020),(dx y x f dy yy⎰⎰-+--2211111),( .7.设平面曲线L 为下半圆周21x y --=,则=⋅=⋅=+⎰⎰π2221211)(LLds ds y x π .8.设∑为曲面22y x z +=在10≤≤z 的部分,则⎰⎰∑=xdS 0 .9.设,0,10,)(⎩⎨⎧<≤<≤-=-ππx x e x f x 则其以π2为周期的傅里叶级数在π=x 处收敛于)1(21πe + .10.设321,,y y y 是微分方程)()()(x f y x q y x p y =+'+''的三个不同的解,且≠--3221y y y y 常数,则微分方程的通解为 1322211)()(y y y C y y C +-+- .11.函数x x f -=21)(展开为x 的幂级数的形式为)2,2(2101-∈∑∞=+x x nn n .12.微分方程xxe y xy =-'1的通解为 xxe Cx + .二、计算下列各题(每小题6分,共18分) 1.设),(xyex y f z =,)(x y ϕ=,其中ϕ,f 均为一阶可微函数,求dxdz .解:)(221y x y e f xyx y f dxdz xy'+⋅'+-'⋅'=))()(()()(221x x x e f xx x x f xyϕϕϕϕ'+⋅'+-'⋅'=2.求曲面)(21422y x z +-=与平面2=z 所围立体的体积.解:所围立体在xoy 面的投影域4:22≤+y x D ,所围立体的体积d x d y y x d x d y d x d y y x V DDD⎰⎰⎰⎰⎰⎰+-=⎭⎬⎫⎩⎨⎧-+-=)(2122)](214[2222πππθππ448212222202=-=-⨯=⎰⎰r d r r d3.在曲面6632222=++z y x 上第一卦限部分求一点,使该点的切平面与已知平面1=++z y x 平行.解:设曲面在第一卦限的切点的坐标为),,(z y x M ,令=),,(z y x F 6632222-++z y x ,则切平面的法向量)6,4,2(),,(z y x F F F n M z y x ==, 已知平面1=++z y x 的法向量)1,1,1(1=n依题意1//n n,即令t z y x ===161412代入曲面方程中解的2,3,6===z y x ,即切点坐标为)2,3,6(M . 三、计算下列各题(每小题6分,共18分) 1.设Ω是由锥面22yx z +=与半球面221yx z --=围成的空间区域,∑是Ω的整个边界的外侧,求曲面积分⎰⎰∑++zdxdy ydzdx xdydz .解:已知x z y x P =),,(,y z y x Q =),,(,z z y x R =),,(,由高斯公式有dv zR yQ xP zdxdy ydzdx xdydz ⎰⎰⎰⎰⎰Ω∑∂∂+∂∂+∂∂=++)(dr r d d dv ϕϕθππsin 3312204⎰⎰⎰⎰⎰⎰==Ωππ)22(31)221(23-=⨯-⨯⨯=2.写出级数 ++++43227252321的通项,判别该级数的敛散性.若级数收敛时,试求其和.解:该数项级数的通项为nn n u 212-=;级数为正项级数,由于21121221limlim1=-+⋅=∞→+∞→n n u u n nn n , 由比值审敛法知该级数收敛.令)1,1()()(22)12()(211111-∈-=-=-=∑∑∑∞=∞=-∞=x x s x xs xxn x xn x s n nn n nn ,则xx xdt ntdt t s n xn nn x-===∑⎰∑⎰∞=∞=-1)(1111,于是2011)1(1)()(x dt t s dx d x s x -=⎥⎦⎤⎢⎣⎡=⎰, 又xx xx s n n-==∑∞=1)(12,所以)1,1()1(1)1(2)(222-∈-+=---=x x xx xx x x x s ,于是3)1(21)12()21(21221=⎥⎦⎤⎢⎣⎡-+=-==∞=∑x nn x x x n s .3.求微分方程x e y y y 223=+'-''的通解.解:微分方程对应的齐次线性微分方程的特征方程0232=+-r r 的特征根为2,121==r r ,x e x f 2)(=的1=λ为特征方程的单根,则原方程的特解为xAxey =*,代入原方程中得2-=A ,齐次线性微分方程的通解为x x e C e C Y 221+=,所以原方程的通解为=+=*y Y y x x x xe e C e C 2221-+.四、计算下列各题(每小题6分,共18分) 1.求函数22)(4),(y x y x y x f ---=的极值.解:由于x y x f x 24),(-=,y y x f y 24),(--=,令,0),(0),(⎩⎨⎧==y x f y x f y x 得驻点,22⎩⎨⎧-==y x 又 2),(-==y x f A xx ,0),(==y x f B xy ,2),(-==y x f C yy ,及4)()2,2(2-=--AC B ,则点)2,2(-位极大值点,极大值为8)2(2)]2(2[4)2,2(22=-----=-f .2.求幂级数∑∞=-12)1(n nnn x 的收敛半径及收敛域.解:令 1-=x t ,则nn nn nn t n n x ∑∑∞=∞==-11212)1(,由于212)1(2limlim11=+=+∞→+∞→n n n nn n n n a a ,则收敛半径2=R .又当2-=t 时,级数∑∞=-1)1(n nn收敛,当2=t 时,级数∑∞=11n n发散,所以)2,2[-∈t ,即级数的收敛域为)3,1[-.3.设),()sin(yx x xy z ϕ+=,其中),(v u ϕ具有二阶偏导数,求yx z ∂∂∂2.解:),(1),()c o s (21yx x yyx x xy y xz ϕϕ'+'+=∂∂,)(),(1),(1)(),()sin()cos(222222122yx yx x yyx x yyx yx x xy xy xy yx z -⋅''+'--⋅''+-=∂∂∂ϕϕϕ五、(本题5分)求函数2),(22+-=y x y x f 在椭圆域}14|),{(22≤+=yx y x D 上的最大值和最小值.解:由于x y x f x 2),(=,y y x f y 2),(-=,令,0),(0),(⎩⎨⎧==y x f y x f y x 在D 内求得驻点)0,0(. 在D 的边界上,设)14(2),,(2222-+++-=yx y x y x F λλ,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+==+-==+=)3(014),,()2(0212),,()1(022),,(22y x y x F y y y x F x x y x F yx λλλλλλ 当0≠x ,由(1)得1-=λ,代入(2)得0=y ,在代入(3)得⎩⎨⎧=±=01y x ;同理当0≠y 得⎩⎨⎧±==20y x ;由于2)0,0(=f , 3)0,1(=±f , 2)2,0(-=±f ,所以最大值为3,最小值为2-.六、(本题5分)设在上半平面}0|),{(>=y y x D 内,函数),(y x f 具有连续偏导数,且对任意的0>t 都有),(),(2y x f t ty tx f -=,证明对D 内的任意分段光滑的有向简单闭曲线L ,都有0),(),(=-⎰dy y x xf dx y x yf L.解:由格林公式,对D 内的任意分段光滑的有向简单闭曲线L ,⎰⎰⎰----±=-1)],(),(),(),([),(),(D y x Ldxdyy x yf y x f y x xf y x f dyy x xf dx y x yf .dxdy y x yf y x xf y x f y D x )],(),(),(2[1---±=⎰⎰ (*)由于函数),(y x f 具有连续偏导数,且对任意的0>t 都有),(),(2y x f t ty tx f -=,即),(),(2ty tx f y x f t =上式两端对t 求导有),(),(),(221ty tx f y ty tx f x y x tf '+'= 特取1=t 得),(),(),(2y x yf y x xf y x f y x += 由(*)式既有0),(),(=-⎰dy y x xf dx y x yf L。
西北工业大学试题高等数学期末考试题

8.______________________
9. ______________________ 二、选择题(每小题 4 分, 共 40 分) 题号 答案 1 2 3 4
10._______________________
5
6
7
8
9
10
教务处印制
共6页
第 4页
西北工业大学命题专用纸
三、 (10 分) 计算曲面积分
′′ ′′ ′ (D) 2 x 2 f12 + xyf 22 + f 2
1 x2
g′
y x3
g ′′ .
∫∫
D
R 2 x 2 y 2 d x d y, 其中 D 是由圆周 x 2 + y 2 = R y 所围成的闭区域,则
有 I =(
(A) 0;
)
(B)
1 3 ; R (3 π 4) 9
(C)
1.______________________
2.______________________
3.______________________
4.______________________
5.______________________
6.______________________
7.______________________
1
3
2 x 1
e y d y = ____________;
2
8. 设 L 为取顺时针方向的圆周 x 2 + y 2 = 2 在第一象限中的部分,则曲线积分
∫ x d y 2 y d x = ________;
L
共6页 第 1页
全国985重点大学-西北工业大学-高等数学第二学期期终考试试卷答案及评分标准

高等数学2009--2010第二学期期终考试试题答案及评分标准A卷一、1、-8,2、,3、,4、8π,5、,6、。
二、1, 2、,3、,4、,5、3,6、[]2121+-,,缺闭区间扣一分。
三、1、解:设切点…………………2分由已知条件得:,得到.………..4分切平面方程为即……………..6分2、解:……………..3分……………..6分3、解:………………4分………………6分四、1、解:g f fy xx u v∂∂∂=+∂∂∂,g f fx yy u v∂∂∂=-∂∂∂,…………….2分vfvfxvufxyufyx∂∂+∂∂+∂∂∂+∂∂=∂∂2222222222g,vfvfyvufxyufxy∂∂-∂∂+∂∂∂-∂∂=∂∂2222222222g, ………………..5分222222g gx yx y∂∂+=+∂∂………………6分2.解:设dydppyp=''=',y,………………………2分得到舍去)(,0y==+ppdydp,解得ycp1=,由初始条件yy21,21c1='=,………………………4分100(,)dy f x y dx⎰83π12eπ+1415-{}00000(,,),,2,1P x y z n x y=-224000sind d drππθϕϕ⎰⎰143π0021221x y-==-2230x y z+--=2200002,1, 3.2xx y z y===+=2(2)2(1)(3)0x y z-+---=231131()12yyyydy e dxy y e dy e∂=-=-⎰⎰⎰8232008222336dz d drz dzπθππ==⎰⎰⎰2y1=-22c x y +=, 由初12=c , 其特解为1,12+=+=x y x y 或。
……………………..6分3.、解:由xQ y p ∂∂=∂∂,得x e x f x f x f =-'-'')()()(,………………2分 x x x e y e c e c Y 21,221-=+=*-, 由初始条件61,3221-==c c , x x x e e e x f 216132)(2--=- ……….4分 (1,1)(0,0)()2()()x f x f x e ydx f x dy ''⎡⎤+++⎣⎦⎰ =⎰-+=-+--101212216134216134e e e dy e e e ). ……………….6分五、解:1151lim lim (1)55n n n n n na n a n ++→∞→∞⋅==+⋅, ∴收敛半径为5R =…………………..2分 当5x =-时, 15n n ∞=∑发散; 当5x =时,11(1)5n n n -∞=-⋅∑收敛 ∴收敛区间为(5,5]-…………………………………………………4分 设和函数1111111100110(1)()(1)55 [(1)][(1)()]5551 ln(1), (5,5]5515n n n n n n n n n x x n n n n n n x x S x x x n n t x t x dt dt n x x dt x x t -∞∞+-==∞∞---==-==-⋅⋅'=-=-⋅==+∈-+∑∑∑∑⎰⎰⎰………..…7分 …………………….8分六、解:设旋转曲面S 的方程为 12222=++z y x ,--------------------1分给定的方向 )0,21,21(0-=l方向导数函数 )(2c o s c o s c o s y x zf y f x f l f -=∂∂+∂∂+∂∂=∂∂γβα --------2分 设)12()(2222-+++-=z y x y x L λ, ---------------3分令 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=++==∂∂=+-=∂∂=+=∂∂1202022042222z y x z zL y y L x x L λλλ ------------------4分 解之得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=02242z y x λλ 23±=λ ------------------6分 23=λ,得S 上的点为)0,36,66(-,此时3-=∂∂l f 23-=λ,得S 上的点为)0,36,66(-,此时3=∂∂lf 所以,所求的S 上的点为)0,36,66(- ------------------7分 七、解:……………………3分………………………6分………………………7分(2009)(1)2010ae f =000()()(x)lim ()(1)()lim lim x x x x x f x x f x f x f x e f x e x x ∆→∆∆→∆→+∆-'=∆-∆=+∆∆(x)()(0),(),(0)0,0..x x x f f x f e y ax c e f c y axe ''=+=+=∴== 111100(x)(1)(1)(1)!!x x x x n n n n f axe aexe ae x e aee x x ae ae n n ---+∞∞=====-+--=+∑∑n=100(1)(1)=ae (1)!!(1)(1),.!n nn nn x x ae n n n x ae x R n ∞∞=∞=--+-+-=∈∑∑∑。
2020西北工业大学高等数学试题

1复习试题1. 填空题(1)方程32210x x +++=在实数范围内实根的个数为1;(2) 平面曲线ln(1)y x x =+在区间(1,)−+∞是凹的. 解 (1)令32()21,f x x x =+++ 则有2(1)20,(0)10,()320,f f f x x ′−=<=>=++>由零点定理及函数的单调性可知, 方程()0f x =在区间(,+)−∞∞内有唯一实根(1,0),ξ∈− 即原方程实根的个数为1.(2) 函数ln(1)y x x =+的定义域为(1,+).−∞ 22ln(1),.1(1)x xy x y x x +′′′=++=++ 易知当(1,+)x ∈−∞时, 0,y ′′> 因此曲线ln(1)y x x =+在整个定义域(1,+)−∞上是凹的.2. 请在下列题中选择四个结论中正确的一个:(1) 设函数()f x 在[0,1]上满足()0,f x ′′> 且(0)0,f ′= 则(1),(0),f f ′′ (1)(0)f f −或(0)(1)f f −的大小顺序是( B ).(A)(1)(0)(1)(0);f f f f ′′>>− (B)(1)(1)(0)(0);f f f f ′′>−> (C)(1)(0)(1)(0);f f f f ′′−>> (D)(1)(0)(1)(0).f f f f ′′>−>(2) 函数()f x 在点0x x =处取得极大值, 则( D ) .0(A)()0;f x ′= 0(B)()0;f x ′′< 0(C)()0f x ′=且0()0;f x ′′< 0(D)()0f x ′=或不存在.(3) 设函数()f x 具有三阶连续导数, 且()f x 满足等式2()[()],f x f x x ′′′+= 又(0)0,f ′= 则( C ).(A)(0)f 是()f x 的极大值; (B)(0)f 是()f x 的极小值; (C)点(0,(0))f 是曲线()y f x =的拐点;(D)(0)f 不是()f x 的极值, 点(0,(0))f 也不是曲线()y f x =的拐点. 解 (1) 对函数()f x 在[0,1]应用拉氏中值定理, 可得(1)(0)(),(0,1).f f f ξξ′−=∈因为()0,f x ′′> 故()f x ′在[0,1]上单调增加, 所以当[0,1]x ∈时, (1)()(1)(0)(0),f f f f f ξ′′′>=−> 即应选B.2(2) 根据函数取得极值的必要条件可知, 应选D. (3) 已知等式两端关于x 求导一次, 可得()2()() 1.f x f x f x ′′′′′′+=在已知等式及上式中令x=0, 可得(0)0,(0)1,f f ′′′′′== 即00()(0)()(0)limlim 10,0x x f x f f x f x x→→′′′′′′−′′′===>−由极限的保号性知, ()f x ′′在0x =两侧邻近处异号, 所以(0,(0))f 是曲线()y f x =的拐点. 又根据泰勒公式, 有22()()()(0)(0)(0),2!2!f f f x f f x x f x ξξ′′′′′=++=+ 其中ξ介于x 与0之间. 由极值的定义知, (0)f 不是()f x 的极值, 故应选C.3. 设()f x 在[0,1]上连续, 在(0,1)内可导, 且1(0)(1)0,()1,2f f f === 试证至少存在一点(0,1),ξ∈ 使() 1.f ξ′=解 令()(),F x f x x =− 易知()F x 在[0,1]上连续, 在(0,1)内可导, 且(0)(0)00,F f =−= 1111()()0,2222F f =−=> (1)(1)110.F f =−=−<由零点定理知, 在1(,1)2内至少存在一点,η 使得()0.F η= 对()F x 在[0,]η上用一次罗尔中值定理, 可知至少存在一点(0,),ξη∈ 使()()10,F f ξξ′′=−=即() 1.f ξ′=4. 设()f x 在[,]a b 上连续, 在(,)a b 内可导, 证明存在(,),a b ξ∈ 使得11[()()]()().n n n n b f b a f a n f f b aξξξξ−′−=+− 解 令()(),n F x x f x = 依题可知()F x 在[,]a b 上连续, 在(,)a b 内可导, 由拉氏中值定理, 可知至少存在一点(,),a b ξ∈ 使1()()()()(),()n n F b F a F n f f b a ξξξξξ−−′′==+−故命题成立.5. 设0,a b << 函数()f x 在[,]a b 上连续, 在(,)a b 内可导, 试利用柯西中值定理证明: 存在一点(,),a b ξ∈ 使得()()()ln .bf b f a f aξξ′−=解 令()ln ,F x x = 依题可知(),()f x F x 在[,]a b 上连续, 在(,)a b 内可导, 且当(,)x a b ∈时, 1()0,F x x′=> 由柯西中值定理, 可知至少存在一点(,),a b ξ∈ 使3()()()()(),1()()()f b f a f f f F b F a F ξξξξξξ′′−′===′−故命题成立.6. 求下列极限:(1) 11lim();1ln x x x x→−− (2) 11lim ()(0,0);x x x x a b a b →+∞−>> (3) 21lim (sin cos );x x x x→∞+ (4) 1ln(1lim;arccot x x x →+∞+ (5) 11112lim ,nxx x xn x a a a n →∞⎛⎞++⎜⎟⎜⎟⎜⎟⎝⎠其中12,,,0.n a a a > 解 (1) 001111ln 11ln 1lim()lim = lim11ln (1)ln ln x x x x x x x x x x x x x x x→→→−++−−=−−−+ 0011ln ln 11lim=lim =.ln 1ln 112x x x x x x x x x →→+=+−++(2) 1111011220211ln ()ln ()lim()limlim11xx xx x x x x x a a b b a b x x x a b xx →+∞→+∞→+∞−−−−−==−11lim(ln ln )ln .xxx aa ab b b→+∞=−=(3) 21ln(sincos )210lim ln(sincos lim (10x x x x x x x x→∞→∞++=∵ 22221121cos ()sin ()2cos sinlimlim 2,21121(sin cos )()sin cosx x x x x x x x x x x x x →∞→∞−−−−===+−+ 221lim (sincos =e .x x x x→∞∴+4(4) 2020211()11ln(1)11limlim lim 1.1arccot (1)1x x x x x x x x x xx →+∞→+∞→+∞−+++===+−+ (5) 1111111212ln()ln 0lim ln(lim(10xxx x xx n nx x a a a a a a nnx n nx→∞→∞++++−= ∵ 111112221111221(ln ln ln )()lim1()()xxxn n x xxx na a a a a a x n a a a x →∞+++−=++−1212ln ln ln ln(),nn a a a na a a n+++==1111212lim .nxx x xn n x a a a a a a n →∞⎛⎞++⎜⎟∴=⎜⎟⎜⎟⎝⎠7. 在区间(,)−∞+∞内方程1142cos 0x x x +−=有几个实根?解 令1142()cos ,f x x x x =+− 则()f x 在(,)−∞+∞上连续, 且为偶函数, 只需考虑它在[0,)+∞上的零点情况.当0x >时, 314211()sin .42f x x x x −−′=++显然(0)10,f =−<(1)2cos10,f =−> 且当(0,1)x ∈时, ()0,f x ′> 因此函数()f x 在(0,1)内有且仅有一个实根. 当1x ≥时, 11421,x x +> 而cos 1,x ≤ 因此当1x ≥时, ()0,f x > 即()f x 在[1,)+∞上无实根. 综上所述, ()f x 在[0,)+∞上有且仅有一个实根. 因此原方程在(,)−∞+∞上有且仅有两个实根.8. 试讨论方程e (0)x x a a −=>有几个实根. 解 令()e ,x f x x a −=− 则有()e (1).x f x x −′=−5令()0,f x ′= 可得唯一驻点为1,x = 且当(,1)x ∈−∞时, ()0,f x ′> 当(1,)x ∈+∞时, ()0,f x ′< 因此1(1)e f a −=−为函数的极大值.又lim (),lim (),x x f x f x a →−∞→+∞=−∞=−所以1(1)e f a −=−也是函数的最大值(即点1(1,e )a −−为曲线()f x 的最高点), 且曲线有水平渐近线.y a =− 因此当1(1)e 0,f a −=−< 即1e a −>时, 方程e (0)x x a a −=>无实根;当1(1)e 0,f a −=−= 即1e a −=时, 方程e (0)x x a a −=>有且仅有一个实根; 当1(1)e 0,f a −=−> 即10e a −<<时, 方程e (0)x x a a −=>有两个实根.9. 试问a 为何值时, 函数1()sin sin 33f x a x x =+在π3x =处取得极值? 它是极大值还是极小值? 并求此值.解 若函数1()sin sin 33f x a x x =+在π3x =处取得极值, 则应有π3π()(cos cos3)0,3x f a x x =′=+= 因此 2.a = 又()2sin 3sin 3,f x x x ′′=−−π()0,3f ′′=< 故π(3f 是极大值,10. 单调函数的导数是否必为单调函数? 研究下面的例子: ()sin .f x x x =+解 单调函数的导数未必为单调函数, 如函数()sin ,f x x x =+ 由于()1cos 0,f x x ′=+≥ 因此函数()f x 在整个定义域上是单调增加的. 但其导函数()f x ′是周期函数, 显然不是单调函数.11. 问,a b 为何值时, 点(1,3)为曲线32y ax bx =+的拐点? 解 若点(1,3)为曲线32y ax bx =+的拐点, 则应有321111()3,(62)0,x x x x y ax bx y ax b ====⎧=+=⎪⎨′′=+=⎪⎩ 即3,620,a b a b +=⎧⎨+=⎩ 从而可得39,.22a b =−= 12. 求抛物线2,y =ax bx c ++ 使它和sin y x =在点π(,1)2处有共同的切线和相6等的曲率.解 依题, 要使抛物线过点π(,1),2 则应有2π2()1,ax bx c ++= 要使抛物线和曲线sin y x =在点π(,1)2处有共同的切线和相等的曲率, 则应有ππ22332222ππ22(2)cos ,2sin ,[1(2)](1cos )x x x x ax b x a x ax b x ====⎧+=⎪⎪⎪⎪−⎨=⎪⎪+++⎪⎪⎩从而可得方程组2ππ1,42π0,21,a b c a b a ⎧++=⎪⎪⎪+=⎨⎪=⎪⎪⎩ 解得21ππ,,1.228a b c =±==±∓ 此时抛物线的方程为221ππ1228y x x =−++或221ππ1.228y x x =−++−13. 试证明下列不等式:(1) 当1x <时, 1e ;1x x≤− (2) 当1x >时,ln(1).ln 1x xx x+>+ 解 (1) 作辅助函数()e (1)1,x f x x =−− 考察1x <时函数的性态.令()e 0,x f x x ′=−= 可得唯一驻点为0,x = 且当(,0)x ∈−∞时, ()0,f x ′> 当(0,1)x ∈时, ()0,f x ′< 因此(0)0f =为函数在(,1)−∞上的极大值, 也是最大值. 故当1x <时, ()(0)0,f x f <= 即e (1)1,x x −< 因此1e .1x x≤− (2) 作辅助函数()ln ,g x x x = 考察1x >时函数的性态. 易知当1x >时, ()ln 10,g x x ′=+> 所以()g x 在(1,)+∞上是单调增加的, 故当1x >时, (1)(),g x g x +> 即(1)ln(1)ln ,x x x x ++> 从而有 ln(1).ln 1x xx x+>+ 14. 设()f x 在[,)a +∞上二阶可导, 且()0,()0,f a f a ′>< 又当x a >时()0,f x ′′< 证明方程()0f x =在(,)a +∞内必有且仅有一个实根.7解 因为当x a >时, ()0,f x ′′< 所以()f x ′在(,)a +∞上单调减少, 故当x a >时, ()()0,f x f a ′′<< 从而()f x 在(,)a +∞上单调减少.注意到()0,f a > 根据零点 定理, 只需说明存在一点, 使得 该点处的函数值为负即可. 由图 3.11可以看出, 曲线()f x 在点 (,())a f a 处的切线与x 轴交点的 横坐标b 处, 应有()0.f b <下面证明这一结论.曲线在点(,())a f a 处的切线 方程为()()().y f a f a x a ′−=−上式中令0,y = 可得().()f a b a f a =−′显然.b a >将函数()f x 在x a =处展成一阶泰勒公式, 有2()()()()()(),2!f f x f a f a x a x a ξ′′′=+−+− 其中ξ介于x 与a 之间. 在上式中令,x b = 则依题有22()()()()()()()()()()()()2!()2!f f a f f b f a f a b a b a f a f a b a f a ξξ′′′′′′=+−+−=+−+−′2()()0.2!f b a ξ′′=−< 于是我们有()0,()0,f a f b >< 根据零点定理及函数的单调性可知, 方程()0f x =在(,)a +∞内必有且仅有一个实根.15. 设函数()f x 在[,]a b 上连续, 在(,)a b 内可导, 且()()1,f a f b == 试证明存在,(,),a b ξη∈ 使得e [()()] 1.f f ηξηη−′+=解 令()e (),x F x f x = 依题可知()F x 在[,]a b 上连续, 在(,)a b 内可导, 由拉氏中值定理, 可知至少存在一点(,),a b η∈ 使()()(),()F b F a F b a ξ−′=−即 e ()e ()e e ==e [()()].b a b a f b f a f f b a b aηηη−−′+−−再对函数()e x g x =在[,]a b 上应用一次拉氏中值定理, 可知至少存在一点(,),a b ξ∈ 使图3.118e e =e .b a b aξ−−以上两式相除, 便得e [()()] 1.f f ηξηη−′+=。
西工大数学考试卷七年级

一、选择题(每题3分,共30分)1. 下列各数中,是负数的是()A. -3B. 0C. 3D. -52. 下列各数中,是正数的是()A. -2B. 0C. 1D. -13. 下列各数中,是整数的是()A. 2.5B. -3C. 1.2D. 04. 下列各数中,是奇数的是()A. 4B. 3C. 6D. 55. 下列各数中,是偶数的是()A. 3B. 5C. 2D. 76. 下列各数中,是质数的是()A. 10B. 11C. 8D. 97. 下列各数中,是合数的是()A. 7B. 13C. 4D. 28. 下列各数中,是互质数的是()A. 15和16B. 12和18C. 9和10D. 6和249. 下列各数中,是同类二次根式的是()A. √2和√8B. √3和√9C. √5和√25D. √7和√4910. 下列各数中,是立方根的是()A. ∛27B. ∛64C. ∛1D. ∛0二、填空题(每题5分,共25分)11. 一个数的相反数是-5,那么这个数是______。
12. 0的绝对值是______。
13. 2的平方根是______。
14. 下列各数中,绝对值最小的是______。
A. -3B. 3C. -2D. 215. 下列各数中,是同类二次根式的是______。
A. √3和√9B. √2和√4C. √5和√25D. √7和√49三、解答题(每题10分,共30分)16. 计算下列各式的值。
(1)|-5| + 3 - (-2)(2)2.5 × (-4) ÷ 5(3)(-3)² × (-2)³17. 判断下列各数是否为质数,并说明理由。
(1)17(2)14(3)2318. 已知a=5,b=-3,求下列各式的值。
(1)a² + b²(2)|a - b| + 2ab(3)a³ - b³四、应用题(20分)19. 学校组织了一次数学竞赛,共有50名学生参加。
西安工业大学高数09-10第一学期(1)期末考题及答案分析

西安⼯业⼤学⾼数09-10第⼀学期(1)期末考题及答案分析⾼等数学(A )期末考试试题⼀、单项选择题(每⼩题3分,共15分)1.当0→x 时,下列变量极限不存在的是(). (A )x arctan ;(B )xx 1sin;(C )xx +-11ln;(D )x e 1.2.0)(,0)(00<''='x f x f 是函数)(x f y =在0x x =处取得极⼤值的⼀个()(A )充分必要条件;(B )充分条件,⾮必要条件;(C )必要条件,⾮充分条件;(D )既⾮充分条件,⼜⾮必要条件.3.下列等式成⽴的是()(A ))()(x f dx x f d =?;(B )dx x f dx x f d )()(=?;(C ))()(x f dx x f ='? (D )dx x f dx x f ?=')()(. 4.设)(x f 在],[b a 上⾮负,在),(b a 内,0)(,0)(>''>'x f x f 记[])()(21b f a f ab I +-=,dxx f I b a=)(2,)()(3a f a b I -=,则()(A )321I I I <<;(B )132I I I <<;(C )123I I I <<;(D )213I I I <<. 5.关于函数dte t xf t)1()(的极值,正确的是()(A )极⼩值为f -=1)1(;(B )极⼩值为 e f -=2)1(;(C )极⼤值为 e f -=1)1(;(D )极⼤值为 e f -=2)1(. ⼆、填空题(每⼩题3分,共15分) 1.设0→x 时,)cos(1ax -与12 -xe是等价⽆穷⼩,则=a .2.设函数)(x f 可导,)(cos 2x f y =,则=dy .3.设曲线的⽅程是)1ln(2x y +=,则曲线的拐点是 .4.不定积分=+?dx x x 1 .5.设曲线)(x f y =上任⼀点),(y x M 处的切线,恒垂直于此点与原点的连线,则y满⾜的微分⽅程是 .三、完成下列各题(每⼩题6分,共36分) 1. 求极限??--→x e xx 111lim 0. 2. 设 ,212=-=tt ey e x 求 22dx yd . 3.设函数)(x y 是由1)1(022=+-?dt t y x y所确定,求dy .4.设xx sin 是)(x f 的⼀个原函数,求dx x f x ?')(.5设?∞+-∞→=+121lim dx xex xaxx ,求a .6.求⼀阶微分⽅程yedxdy x -=-+1)1(的通解.四、(7分)设())1(1ln )(21>++=?x xx dt tt f x ,求dxx f ?)(.五、(7分)已知)(x f 在点6=x 的邻域内为可导函数,且,0)(lim 6=→x f x ,2009)(lim 6='→x f x 求极限 .)6()(lim3666x dtdu u f t x t x -→六、(8分)在抛物线)30(2≤≤=x x y 上求⼀点P ,过P 点作抛物线的切线,使此切线与抛物线及直线3,0==x y 所围成的图形⾯积最⼩.七、(7分)设 ,0<+≥+=x ex x x f x 求?-2)1(dx x f .⼋、(5分)已知函数)(x f 在),2[∞+上可导,0)(>x f ,且满⾜不等式)(])([x f x xf -≤'.试证在),2[∞+上2)(xA x f ≤,其中A 为与x ⽆关的常数.⾼等数学(A )期末考试试题参考答案及评分标准(2010年1⽉5⽇)⼀、单项选择题(每⼩题3分,共15分) 1.D 2.B 3.B 4.C 5.B ⼆、填空题(每⼩题3分,共15分).12±2. xdx sin )x (cosf 22'- 3 . )ln ,(21±4. C )x ()x (++-+2325132152 5.yx dxdy -=三、完成下列各题(每⼩题6分,共36分).1. 解:)e (x )e (x lim x e lim xxx x x 1111100---=??? ?--→→……………………………………………..1分 21x x +-=→………………………………………………..2分xel i mxx 210-=→………………………………………………….....2分2120-=-=→xx limx ………………………………………………….1分2. 解:ttt eee dxdy 1222==………………………………………………………………………3分tttteeee dxy d 322222121-…………………………………...…………………….3分3. 解:两端同时对x 求导得…………………………………………………………………..1分 0122 2=+-+dxdy )y (dxdy xxy ………………………………………………….3分2212x y xy dxdy -+=……………………………………………………………..….1分即dx xy xydy 2212-+=………………………………………..………………………1分4. 解:由题意知2xxsin x cos x )xx sin ()x (f -='=……………………………………2分则)x (df x dx )x (f x ??=' ………………………………………………………. …….…1分 dx )x (f )x (xf ?-=…………………………………………………………….…… 2分C xx sin x cos C xx sin x………………………….1分5解:因为 aaxx axx ex lim x lim 2222121=+=??+∞→∞→………………………………2分[][]+∞-+∞→+∞-+∞-+∞-+∞--+-=+-=-=?111xxxee)ex (lim dx exexdedx xeeeelim e)e (lim xx xx 2111=+-+-=-+∞→+∞→……………..…………………..3分所以 )(l n a eea122122-= =………………………………...………....1分6.解:由题意得y+11,也即dx x dy eeyy 111+=+……………………….2分两端同时积分得C ln )x ln()e ln(dx x dy eeyyy++=+?+=+?11111………3分所以原微分⽅程的通解为 )x (C ey11+=+ 或 []11-+=)x (C ln y ………….....1分四、(7分)解:对()211xx ln dt t)t (f x ++=?两端同时求导得……………………..1分222x (xx x)x (f +=+=++++ =……...2分C x)x(d xdx xx dx )x (f ++=++= +=∴2222111121 1…………...3分五、(7分)解:2 6603666636)x (du)u (f x lim)x x t x --=-→→…………………………2分)x ()x (xf du )u (f limxx --=?→6666………………………………………………2分660-'---=→)x (f x )x (f )x (f limx …………………………………………2分2009= …………………………………………………………………...…1分六、(8分)在抛物线)x (x y 302≤≤=上求⼀点P ,过P 点作抛物线的切线,使此切线与抛物线及直线30==x ,y 所围成的图形⾯积最⼩.解:设切点P 的坐标为)x ()y ,x (30000≤≤,则切线斜率为002x )x (y =',切线⽅程为 )x x (x y y 0002-=-,即2002x x x y -=,…………………………….1分令0=y ,得切线与x 轴交点的横坐标为20x ,令3=x ,得切线与直线3=x 交点的纵坐标为2006x x -,要使此切线与抛物线及直线30==x ,y 所围成的图形⾯积最⼩,既是切线与直线30==x ,y 所围成的图形⾯积最⼤…………………………………………….2分设该⾯积为S ,则)x x )(x ()x (S 2000062321--=………………..……………….2分[]0000020026641262321641x )x ()x ()x )(x ()x x ()x (S ---=--=')x )(x (002643--=………………………..……………………………..2分令00=')x (S ,得惟⼀驻点20=x ,依题意,该驻点就是使)x (S 0取得最⼤值的点,所以所求的点P 的坐标为),()y ,x (4200=…………………………………………...…….1分七、(7分)解:?---======-11111201dx )x (f dt )t (f dx )x (f x t ……………………..2分[]1001100111111111)x ln(de)ee(dx xdx exxxx+++-=+++=--….3分[][][])e (ln )x ln()eln(x x12111001+=+++-=-………….........………2分⼋、(5分)已知函数)x (f 在),[∞+2上可导,0>)x (f ,且满⾜不等式)x (f ])x (xf [-≤'.试证在),[∞+2上2xA )x (f ≤,其中A 为与x ⽆关的常数.证:由于)x (f 在),[∞+2上可导,0>)x (f ,则x)x (f )x (f )x (f )x (f x )x (f )x (f ])x (xf [2-≤'?-≤'+?-≤'…..2分于是当2>x 时有dt t dt )t (f )t (f x x ?-≤'222……………………………….1分即[][]222222442222x)(f )x (f x(f )x (f x ln )(f )x (f ln t ln )t (f ln x x ≤≤≤?-≤-令)(f A 24=,代⼊即证………………………………………………………………2分。
【经典期末卷】大学高数(下)期末测试题及答案

第 1 页 (共 10 页)班级(学生填写): 姓名: 学号: 命题: 审题: 审批: ----------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ------------------------------------------------------- (答题不能超出密封线)第 2 页(共10 页)第 3 页 (共 10 页)班级(学生填写): 姓名 学号: ----------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ------------------------------------------------------- (答题不能超出密封线)第 4 页 (共 10 页)三. 计算题(一)(每小题6分,共36分)1.计算:22xy De d σ+⎰⎰,其中D 是由圆周224x y +=所围成的闭区域。
2.计算三重积分xdxdydz Ω⎰⎰⎰,其中Ω为三个坐标面及平面21x y z ++=所围成的闭区域。
3.计算xyzdxdydz Ω⎰⎰⎰,其中Ω是由曲面2221x y z ++=,0,0,0x y z ≥≥≥所围成.第 5 页 (共 10 页)班级(学生填写): 姓名 学号: ----------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ------------------------------------------------------- (答题不能超出密封线)4.求2d d Dxx y y⎰⎰,其中D 为1xy =,y x =及2x =所围成的区域。
西北工业大学《高等数学A1》2020–2021学年第一学期期末试卷

2020-2021学年第一学期高等数学期末考试西北工业大学2020年第1学期高等数学期末考试试卷2020-2021学年第1学期考试科目:高等数学AⅠ考试类型:(闭卷)考试考试时间:120分钟学号姓名年级专业题号一二三四总分得分评阅人一、填空题(本大题共5小题,每小题3分,共15分)1.0sin 5lim 2x xx→=。
2.曲线2x xe e y -+=在点(0,1)处的曲率是。
3.设()f x 可导,[]ln ()y f x =,则dy =。
4.不定积分⎰=。
5.反常积分60x e dx +∞-⎰=。
二、单项选择题(本大题共5小题,每小题3分,共15分)1.设函数,则A.B.C.D.2.设曲线如图示,则函数在区间内().得分得分得分A.有一个极大值点和一个极小值点B.没有极大值点,也没有极小值点C.有两个极小值点D.有两个极大值点3.极限().A.B.C.D.4.函数的图形如图示,则().A.是该函数的一个极小值点,且为最小值点B.是该函数的一个极小值点,但不是为最小值点C.是该函数的一个极大值点2020-2021学年第一学期高等数学期末考试D.不是该函数的一个极值点5.若定积分(). A.B.C.D.三、计算题(本大题共7小题,每小题7分,共49分)1.求函数212x x y +=的极值与拐点.解:函数的定义域(-∞,+∞)。
2.设抛物线24x y -=上有两点(1,3)A -,(3,5)B -,在弧A B 上,求一点(,)P x y 使ABP ∆的面积最大.3.已知()x f 的一个原函数为2ln x ,则试求:()⎰'xf x dx .确定2x y e =2(x -2)的单调区间.4.设方程2290y xy -+=确定隐函数()y y x =,求d d y x。
5.求函数321x y x =-的单调区间,极值和拐点。
6.计算定积分1ln ex xdx ⎰。
.7.求不定积分3。
三、计算题(本大题共7小题,每小题7分,共49分)1.计算极限10(1)limxx x e x →+-.2.dx t A dy t A t f y ex t f t f t f )()()(cos 0)()(2)(=⎪⎩⎪⎨⎧==≠'使试求若可微且设.3.设)(x f 在[a ,b ]上连续,且],[)()()(b a x dtt f t x x F xa∈-=⎰,试求出)(x F ''。
高等数学作业册自测题(西工大)参考附标准答案

高等数学作业册自测题(西工大)参考附标准答案高等数学(Ⅱ)期末自测题参考答案(选自西北工业大学2005级高数考题)一、填空题(每小题3分,共36分)1.=???? ??+∞→∞→x y x xy 11lim ==+=+∞→∞→∞→∞→?∞→∞→01lim111lim 11lim e xy xy yxyy x yxy y x y x 1 .2.函数),(y x z z =由方程0sin =+x y e xz 确定,则=-=-=??xz z y xe x y x F F y z cos 1xz ex x y 2cos - . 3.设函数222lnz y x u ++=,则它在点)1,1,1(0-M 处的方向导数的最大值为33. 4.设函数y xy ax x y x f 22),(22+++=在点)1,1(-处取得极值,则常数=a 5-.5.空间曲线x z x y -==1,222在点)22,1,21(处的切线方程为212211121--=-=-z y x .6.改变积分次序:==-dy y x f dx I x x 2202),(dx y x f dy y y ?-+--2211111),( .7.设平面曲线L 为下半圆周21x y --=,则=?= =+??π2221211)(LLds ds y x π . 8.设∑为曲面22y x z +=在10≤≤z 的部分,则??∑=xdS 0 .9.设,0,10,)(?<≤<≤-=-ππx x e x f x 则其以π2为周期的傅里叶级数在π=x 处收敛于)1(21πe + . 10.设321,,y y y 是微分方程)()()(x f y x q y x p y =+'+''的三个不同的解,且≠--3221y y y y 常数,则微分方程的通解为 1322211)()(y y y C y y C +-+- .11.函数x x f -=21)(展开为x 的幂级数的形式为)2,2(2101-∈∑∞=+x xn n n .12.微分方程x xe y xy =-'1的通解为 x xe Cx + . 二、计算下列各题(每小题6分,共18分)1.设),(xye xy f z =,)(x y ?=,其中?,f 均为一阶可微函数,求dxdz . 解:)(221y x y e f x y x y f dx dz xy'+?'+-'?'= ))()(()()(221x x x e f xx x x f xy'+?'+-'?'= 2.求曲面)(21422y x z +-=与平面2=z 所围立体的体积.解:所围立体在xoy 面的投影域4:22≤+y x D ,所围立体的体积dxdy y x dxdy dxdy y x V D DD +-=???-+-=)(2122)](214[2222πππθππ4482122202202=-=-?=??rdr r d3.在曲面6632222=++z y x 上第一卦限部分求一点,使该点的切平面与已知平面1=++z y x 平行.解:设曲面在第一卦限的切点的坐标为),,(z y x M ,令=),,(z y x F 6632222-++z y x ,则切平面的法向量)6,4,2(),,(z y x F F F n M z y x ==,已知平面1=++z y x 的法向量)1,1,1(1=n依题意1//n n,即令t z y x ===161412 代入曲面方程中解的2,3,6===z y x ,即切点坐标为)2,3,6(M . 三、计算下列各题(每小题6分,共18分) 1.设Ω是由锥面22y x z +=与半球面221y x z --=围成的空间区域,∑是Ω的整个边界的外侧,求曲面积分∑++zdxdy ydzdx xdydz .解:已知x z y x P =),,(,y z y x Q =),,(,z z y x R =),,(,由高斯公式有dv zR y Q x P zdxdy ydzdx xdydz Ω∑+??+??=++)(dr r d d dv ??θππsin 33122040==Ωππ)22(31)221(23-=?-= 2.写出级数++++43227252321的通项,判别该级数的敛散性.若级数收敛时,试求其和. 解:该数项级数的通项为nn n u 212-=;级数为正项级数,由于 21121221lim lim1=-+?=∞→+∞→n n u u n nn n ,由比值审敛法知该级数收敛.令)1,1()()(22)12()(211111-∈-=-=-=∑∑∑∞=∞=-∞=x x s x xs x xn x x n x s n n n n nn ,则xxx dt ntdt t s n xn n n x-===∑?∑?∞=∞=-1)(1111,于是2011)1(1)()(x dt t s dx d x s x -= =?,又xxx x s n n -==∑∞=1)(12,所以)1,1()1(1)1(2)(222-∈-+=---=x x x x x x x x x s ,于是3)1(21)12()21(21221=-+=-==∞=∑x n n x x x n s .3.求微分方程xe y y y 223=+'-''的通解.解:微分方程对应的齐次线性微分方程的特征方程0232=+-r r 的特征根为2,121==r r ,x e x f 2)(=的1=λ为特征方程的单根,则原方程的特解为x Axe y =*,代入原方程中得2-=A ,齐次线性微分方程的通解为xxe C e C Y 221+=,所以原方程的通解为=+=*y Y y x x x xe e C e C 2221-+.四、计算下列各题(每小题6分,共18分) 1.求函数22)(4),(y x y x y x f ---=的极值.解:由于x y x f x 24),(-=,y y x f y 24),(--=,令,0),(0),(??==y x f y x f yx 得驻点,22-==y x又 2),(-==y x f A xx ,0),(==y x f B xy ,2),(-==y x f C yy ,及4)()2,2(2-=--AC B ,则点)2,2(-位极大值点,极大值为8)2(2)]2(2[4)2,2(22=-----=-f .2.求幂级数∑∞=-12)1(n nnn x 的收敛半径及收敛域. 解:令 1-=x t ,则 nn nn n n t n n x ∑∑∞=∞==-11212)1(,由于212)1(2lim lim 11=+=+∞→+∞→n n n nn n n n a a ,则收敛半径2=R .又当2-=t 时,级数∑∞=-1)1(n n n 收敛,当2=t 时,级数∑∞=11n n发散,所以)2,2[-∈t ,即级数的收敛域为)3,1[-.3.设),()sin(yxx xy z ?+=,其中),(v u ?具有二阶偏导数,求y x z 2. 解:),(1),()cos(21yxx y y x x xy y x z ??'+'+=??,)(),(1),(1)(),()sin()cos(222222122yxy x x y y x x y y x y x x xy xy xy y x z -?''+'--?''+-=五、(本题5分)求函数2),(22+-=y x y x f 在椭圆域}14|),{(22≤+=y x y x D 上的最大值和最小值.解:由于x y x f x 2),(=,y y x f y 2),(-=,令,0),(0),(==y x f y x f yx 在D 内求得驻点)0,0(.在D 的边界上,设)14(2),,(2222-+++-=y x y x y x F λλ,得=-+==+-==+=)3(014),,()2(0212),,()1(022),,(22y x y x F y y y x F x x y x F yx λλλλλλ 当0≠x ,由(1)得1-=λ,代入(2)得0=y ,在代入(3)得??=±=01y x ;同理当0≠y 得?±==20y x ;由于2)0,0(=f ,3)0,1(=±f , 2)2,0(-=±f ,所以最大值为3,最小值为2-.六、(本题5分)设在上半平面}0|),{(>=y y x D 内,函数),(y x f 具有连续偏导数,且对任意的0>t 都有),(),(2y x f tty tx f -=,证明对D 内的任意分段光滑的有向简单闭曲线L ,都有0),(),(=-?dy y x xf dx y x yf L.解:由格林公式,对D 内的任意分段光滑的有向简单闭曲线L ,----±=-1)],(),(),(),([),(),(D y xLdxdyy x yfy x f y x xf y x f dyy x xf dx y x yf .dxdy y x yf y x xf y x f y D x )],(),(),(2[1---±=?? (*)由于函数),(y x f 具有连续偏导数,且对任意的0>t 都有),(),(2y x f tty tx f -=,则该式两端对t 求导有),(2),(),(321y x f t ty tx f y ty tx f x --='+'特取1=t 得0),(2),(),(=++y x f y x yf y x xf y x由(*)式既有0),(),(=-?dy y x xf dx y x yf L。
陕西省西安市西北工业大学2025届数学高三上期末复习检测试题含解析

陕西省西安市西北工业大学2025届数学高三上期末复习检测试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若向量(1,5),(2,1)a b ==-,则(2)a a b ⋅+=( )A .30B .31C .32D .332.设集合{|0}A x x =>,{}2|log (31)2B x x =-<,则( ).A .50,3AB ⎛⎫= ⎪⎝⎭ B .10,3A B ⎛⎤= ⎥⎝⎦C .1,3A B ⎛⎫⋃=+∞ ⎪⎝⎭ D .(0,)A B =+∞3.已知集合{}2|230A x x x =--<,集合{|10}B x x =-≥,则()A B ⋂=R( ). A .(,1)[3,)-∞+∞ B .(,1][3,)-∞+∞ C .(,1)(3,)-∞+∞D .(1,3) 4.已知抛物线2()20C x py p :=>的焦点为1(0)F ,,若抛物线C 上的点A 关于直线22l y x +:=对称的点B 恰好在射线()113y x ≤=上,则直线AF 被C 截得的弦长为( ) A .919 B .1009 C .1189 D .12795.如图,四边形ABCD 为正方形,延长CD 至E ,使得DE CD =,点P 在线段CD 上运动.设AP x AB y AE =+,则x y +的取值范围是( )A .[]1,2B .[]1,3C .[]2,3D .[]2,46.已知函数()f x 的定义域为()0,∞+,且()()2224m f m f f n n ⎛⎫ ⎪⎝⎭⋅=,当01x <<时,()0f x <.若()42f =,则函数()f x 在[]1,16上的最大值为( )A .4B .6C .3D .87.若平面向量,,a b c ,满足||2,||4,4,||3a b a b c a b ==⋅=-+=,则||c b -的最大值为( ) A .523+ B .523- C .2133+ D .2133-8.做抛掷一枚骰子的试验,当出现1点或2点时,就说这次试验成功,假设骰子是质地均匀的.则在3次这样的试验中成功次数X 的期望为( )A .B .C .1D .2 9.已知函数,其中04?,?04b c ≤≤≤≤,记函数满足条件:(2)12{(2)4f f ≤-≤为事件A ,则事件A 发生的概率为A .14B .58C .38D .12 10.若2332a b a b +=+,则下列关系式正确的个数是( ) ①0b a << ②a b = ③01a b <<< ④1b a <<A .1B .2C .3D .411.若将函数()2sin 16f x x π⎛⎫=+- ⎪⎝⎭的图象上各点横坐标缩短到原来的12(纵坐标不变)得到函数()g x 的图象,则下列说法正确的是( )A .函数()g x 在0 6π⎛⎫ ⎪⎝⎭,上单调递增 B .函数()g x 的周期是2π C .函数()g x 的图象关于点 012π⎛⎫- ⎪⎝⎭,对称 D .函数()g x 在0 6π⎛⎫ ⎪⎝⎭,上最大值是1 12.已知函数1()2x f x e x -=+-的零点为m ,若存在实数n 使230x ax a --+=且||1m n -≤,则实数a 的取值范围是( )A .[2,4]B .72,3⎡⎤⎢⎥⎣⎦C .7,33⎡⎤⎢⎥⎣⎦D .[2,3]二、填空题:本题共4小题,每小题5分,共20分。
西北工业大学高等数学期末测试题

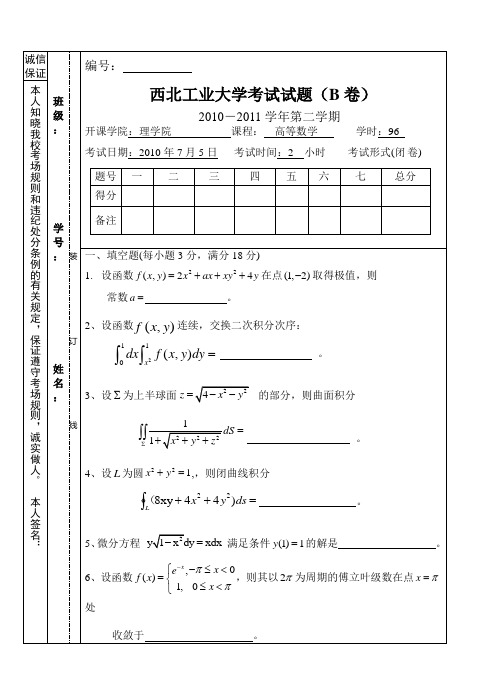
保证
班
级
:
学
号
:
姓
名
:
装
订
线
编号:
西北工业大学考试试题(卷)
2009-2010学年第一学期
开课学院:理学院课程:高等数学学时:96
考试日期:2010年1月20日考试时间:2小时考试形式( )( )卷
本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场规则,诚实做人。 本人签名:
题号
一
二
三
四
注:1.命题纸上一般不留答题位置,试题请用小四、宋体打印且不出框。
2.命题教师和审题教师姓名应在试卷存档时填写。共6页 第1页
西北工业大学命题专用纸
二、计算题(每小题6分,共30分)
1、设 ,求 , .
2、已知 在 处连续,求 值.
3、求不定积分 .
共6页 第2页
西北工业大学命题专用纸
4、求经过点 且垂直于平面 与 的平面方程.
五
六
七
总分
得分
一、填空题(每小题3分,共30分)
1、 ________________.
2、设 的一个原函数是 ,则 ____________________.
3、平面曲线 在区间_________________是向上凹的.
4、函数 的极小值点是___________________.
5、设函数 ,则 _______________________.
6、函数 的反函数是 __________________.
7、已知当 时, 是比 高阶的无穷小量,则 __________.
8、设函数 在 处可导,且 ,则 __________.
9、设 可导, ,则 ___________________.
西北工业大学《高等数学A1》2018-2019学年第一学期期末试卷B卷

西北工业大学试卷(B 卷) 课程高等数学A(1) 一、单项选择题(每小题3分,共30分)2018~2019学年第1 学期1.下列函数中,( )是奇函数. ()A ()tan sec 1f x x x =-+ ()B ()2x xe ef x -+=()C ()()()22f x x x x =-+()D ()cos cos x f x x x e =2.若()f x 在区间(),a b 内,()0,f x '>()0,f x ''< 则在(),a b 内()y f x =( ). ()A 单调增加且曲线是凹的 ()B 单调减少且曲线是凹的()C 单调减少且曲线是凸的()D 单调增加且曲线是凸的3.下列函数在点0x =处连续的是( ).()A ()21sin ,01,0x x f x xx ⎧≠⎪=⎨⎪=⎩ ()B y =()C (),0sin 0,x e x f x x x x⎧≤⎪=⎨<⎪⎩ ()D 1xy e =4.极限()()1201lim sin 1x x x x x -→⎛⎫++= ⎪⎝⎭( ).()A e ()B 1e - ()C 11e -- ()D 11e -+5.当0→x 时,以下结论不正确的是( ).()A ln(1)~x x +()B 1~x e x -()C 1cos ~x 212x ()D 1~x - 6.设()()f x dx F x C =+⎰,则下列结论正确的是( ).()A ()()F x dx f x C '=+⎰ ()B ()()d f x dx f x dx dx⎡⎤=⎣⎦⎰()C ()()d f x dx f x ⎡⎤=⎣⎦⎰()D ()()d f x dx f x dx ⎡⎤=⎣⎦⎰ 7.下列导数正确的是( ),其中,a b 为常数。
()A 222b x ab a d e dxe edx=-⎰()B 222x t x a a d e dt e e dx =-⎰()C 22b t x x d e dt e dx=⎰ ()D 2242x t x a d e dt xe dx=⎰ 8.设函数1sin sin 22y a x x =+在x =3π处取得极值,则=a ( ).()A 0()B 1()C 2()D 39.设)(x f 在],[b a 上连续,则在],[b a ()a b <上至少有一点ξ,使得( ).()A 0)(='ξf()B a b a f b f f --=')()()(ξ()C 0)(=ξf()D ab dx x f abf -=⎰)()(ξ10.连续曲线(),y f x =直线x a =,x b =()a b <及x 轴所围图形的面积为( ).()A 2()baf x dx π⎰()B ()baf x dx ⎰()C ()baf x dx ⎰()D 2()baf x dx π⎰二、计算(每小题6分,共30分)1.求极限20tan sin lim sin ln(1)x x xx x →-⋅+;2.求极限sin ln(1)d x x t t→+23.设221arctan 1x y x -=+,求dy ;4.设()y y x =是由231x t y t t ⎧=-⎨=-⎩确定,求22d ydx . 5.()y y x =满足:()()ln[sin()]()y f x x f x x x x o x ∆=+∆-=+∆∆+∆,求,.y y ''' 三、计算下列积分(每小题6分,共24分) 1.2100(1)d x x x +⎰; 2.0ax x ⎰;3.1ln d eex x ⎰;4.221ln xdx x +∞-⎰. 四、(本题10分)求位于曲线x y e =下方,该曲线过原点的切线的左方以及x 轴上方之间图形的面积.五、(本题6分)证明不等式:1240222d 2xxe e x e ---≤≤-⎰.。
西北工业大学复变历年期末试题

一、填空(每题3分,共30分)1=____________。
(一) 2、1cos sin (0)i θθθπ++≤≤的三角表示形式为____________。
(一) 3、若2222()2()f z x xy y i y axy x =+-++-在复平面内处处解析,实常数a =____________。
(二) 4、)i i =____________。
(二) 5、若)(z f 在2<z 内解析,1:=z c 取正向,则=''⎰dz zz f Ccos )(____________。
(三)6、函数23(1)(3)()cos()2z z f z z ππ--=+的孤立奇点为____________。
(四)7、方程0chz =的根为________。
(二)8、1w z=将z 平面的圆11z -=映射为w 平面的________。
(一)9、将sec z 在i z =处展开成的幂级数的收敛半径为________。
(四)10、5cos 1(,0)z Res z -=____________。
(五)二、证明(每题6分,共12分) 1.设01z <,证明:若1,z =则011z z z z-=-。
(一)2.设函数()f z u iv =+在区域D 内解析,()f z 在D 内恒为常数,试证明()f z 在D 内也为常数。
(二)三、计算题(每题6分,共30分) 1.dz zzC ⎰++11,其中C 由起点1沿曲线it e z =逆时针方向至终点i 。
(三) 2.dz z z ⎰=+222)1(1(三、五) 3.dz z z z ⎰=+4cos 1(五) 4.2220(1)(4)x dx x x +∞++⎰(五) 5.2sin 16x xdx x+∞+⎰ (五)四、(8分)已知解析函数()f z u iv =+的实部为(sin cos )x u e y y x y =-,且(0)0f =,求()f z 。
西安工业大学高数期末考试题附标准答案试题

高等数学(H)期末参考答案、填空题(每小题 3分,共36 分)u = ln ..x 2• y 2• z 2,则它在点 M °(1, -1,1)处地方向导数地最大值为f (x, y) =2x 2 ax xy 22y 在点(1, -1)处取得极值,则常数 a =「5.7.设平面曲线L 为下半圆周y 二 - .1 - x28.设匕为曲面z = . x 2 y 2在0岂z 乞1地部分,贝U I I xdS 二0 .10.设y 1, y 2, y 是微分方程 9 p(x)y ' q(x)y 二f (x)地三个不同地解,且 y —社=常 y 2 -y 3数,则微分方程地通解为C’y , -y 2) • C 2(y 2 - y 3) * % .2 21 2,贝U [ (x + y ) ds = (1 -ds = ? 4 兀=三5.空 线 y 2 二 2x, z 2 = 1「x 在点 (>,J 处地切线方程为1 x --2 1=_y -1 .2 z ―— 2 1 一 2i 22 2x _x 26.改变积分次序:I dx ,f (x, y)dy -1 1 • 1 _y°dy 亠口? f(x,y)dx .L 1 1.lim 1 —X f1 xy-V二 lim i 1 — xy丿劣xy 丿 Jlim 1 丄 阚Ixy 丿Hr 12.函数z二z(x, y)由方程e^ sin 》=0确定,则 —=xcyF yF1 y-cos- x x xz xeco 显X ~2 xz x e3.设函数4.设函数 9.设 f (x) n -xe1,--•::: x ■ 0 ,则其以2兀为周期地傅里叶级数在处收敛于 0 岂 x :二'11.函数f(x) =1 展开为x 地幕级数地形式为 a 」yx n(-2, 2).2—x n^2n41112.微分方程y y = xe x地通解为Cx - xe xx-------二、计算下列各题(每小题6分,共18分)1•设z 二f(y,e xy),y =(x),其中f,「均为一阶可微函数,求 x解:虫=f 「yx 2 yf 2 e xy( y xy)dxx二2f 2 e xy( (x) X : (x))x2.求曲面z =4(x 2y 2)与平面z = 2所围立体地体积. 2解:所围立体在xoy 面地投影域D : x2• y 2_ 4,所围立体地体积V = M[4_;(x 2+y 2)] _2Rxdy = 2JJdxdy —1 2二.22d : r rdr =8 二-4 二-4 ■:解:设曲面在第一卦限地切点地坐标为M (x, y, z),令F (x, y,z) = x 22y 23z 2「66,则切平面地法向量n = (F x , F y , F Z )M 二(2x, 4y, 6z),已知平面x y ^1地法向量n 1 =(1, 1, 1)依题意n//ni ,即 空=41 =央令t1 1 1代入曲面方程中解地 x =6, y =3, z=2,即切点坐标为 M (6, 3, 2). 三、计算下列各题(每小题6分,共18分)1.设门是由锥面.x 2 y 2与半球面z= J -x 2 -y 2围成地空间区域,dz dx(x 2 y 2)dxdyD3.在曲面x 2 2y 23z-66上第一卦限部分求一点,使该点地切平面与 已知平面2x s(x)_ (1 _x)2 _1 xx2(5 (1)),1s(2)二x+ x 2_ I X(2n-1)于 . n 1 2 _(1 - X) 1 x=2边界地外侧,求曲面积分[jxdydz- ydzdx • zdxdy .Q(x, y,z)=y , R(x, y,z) = z ,由高斯公式有cP cQcR ■i I xdydz ydzdx zdxdy 二 ()dv ¥ ¥r rr L\、x _y_z= 3 ! i idv = 3 o dr °4d [;r 2sin : drQ=3 2 二(1 2) [=(2-、2)二 2 3 13 572.写出级数--飞 N •…地通项,判别该级数地敛散性.若级数收敛时,试求其和2 2 2 2limUnl^im 1,n = u n n=2 2n —12由比值审敛法知该级数收敛.令解:已知 P(x, y,z) = x , 解:该数项级数地通项为 U n 二2n -1 2n;级数为正项级数,由于s(x) oOoo八(2n -1) x n= 2x'二 nxn -1oOn=2x®(x)-s 2(x) x (—1,1),x :: Xo3(t)dt 二 I 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7、已知当 时, 是比 高阶的无穷小量,则 __________.
8、设函数 在 处可导,且 ,则 __________.
9、设 可导, ,则 ___________________.
10、曲线 上 对应点处的切线方程是_____________________.
五
六
七
总分
得分
一、填空题(每小题3分,共30分)
1、 ________________.
2、设 的一个原函数是 ,则 ____________________.
3、平面曲线 在区间_________________是向上凹的.
4、函数 的极小值点是___________________.
5、设函数 ,则 _______________________.
5、已知 ,求 .
共6页 第3页
西北工业大学命题专用纸
三、(8分)证明方程 在 内有且仅有一个实根.
四、(8分)设 ,试求常数 、 ,使 处处
可导.
共6页 第4页
西北工业大学命题专用纸
五 、(10分)如图,求图中阴影部分面积的最大值和最小值(其中
).
共6页 第5页
西北工业大学命题专用纸
六、(8分)求由曲线 及 轴所围成的图形绕直线 旋
注:1.命题纸上一般不留答题位置,试题请用小四、宋体打印且不出框。
2.命题教师和审题教师姓名应在试卷存档时填写。共6页 第1页
西北工业大学命题专用纸
二、计算题(每小题6分,共30分)
1、设 ,求 , .
2、已知 在 处连续,求 值.
3、求不定积分 .
共6页 第2页
西北工业大学命题专用纸
4、求经过点 且垂直于平面 与 的平面方程.
诚信
保证
班
级
:
学
号
:
姓
名
:
装
订
线
编号:
西北工业大学考试试题(卷)
2009-2010学年第一学期
开课学院:理学院课程:高等数学学时:96
考试日期:2010年1月20日考试时间:2小时考试形式( )( )卷
本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场规则,诚实做人。 本人签名:题号一二
三
四
转所得的旋转体的体积.
七、(6分) 在 上可导,且 ,试证:存
在 ,使 .
共6页 第6页
