高三立体几何复习讲义:多面体与旋转体
多面体旋转体精编版

多面体和旋转体一. 教学内容:1. 主要内容:多面体和旋转体2. 考点分析:多面体和旋转体每年必考,不仅有直接求多面体和旋转体的面积和体积问题,也有已知面积或体积求几何体中某些元素或元素间的关系问题,近年来即使是考查空间线面位置关系的问题,也常以几何体为依托,该部分内容不仅在选择题、填空题中考,也在解答题中出现。
解答题在高考中一直保持中档题的水平,近几年高考立体几何试题多采用一题多问的形式,降低了起点,分散了难点,既有证明,也有计算,一般要求学生先证后算,证明严谨、清楚,计算准确。
【典型例题】例1. 三棱锥,,,,求这个P ABC PA a AB AC a PAB PBC BAC -===∠=∠=∠=︒260 三棱锥的体积。
分析:由题设∠=∠=︒PAB PAC 60∴∠P ABC O BAC 在平面上的射影必在的平分线上又,,可知是正三角形∠=︒=BAC AB AC BC 60∆A 考查方向:考查三棱锥体积的常用求法。
分析一:作在底面上的射影,求和的面积P O PO ∆AB C分析二:注意到且PA AB PAB =∠=︒1260知PA PB ⊥同理,把作为底,则为高PB PC PBC PA ⊥ 分析三:割法、补法解法一:(用公式法解)如图,作底面三角形顶角A 的平分线AD ,交BC 于D ,过P 点作底面的垂线,垂足为O ,由分析知射影O 必在AD 上,易知△ABC 是正三角形,AB=2a ,∴=S a ABC ∆32PC过作,垂足为,连,则P PE AB E OE OE AB ⊥⊥在中,,Rt PAE PAE PA a ∆∠=︒=60∴===⋅︒=PE a AE a OE AE tg a 3223036,, 在中,Rt POE PO PE OE a ∆=-=2263∴=⋅=-V S PO a P ABC ABC 13233∆解法二:(利用等积转换法解)在△PAB 中PA a AB a PAB ==∠=︒,,260∴=+-⋅⋅︒=PB a a a a a 2222222603()()cos∴⊥⊥=∆P A BPA PB PA PC PB PC P 是直角三角形,,同理可证,又 ∴⊥PA PBC 平面在中,,∆PBC PB PC a BC a ===32∴=S a P B C ∆22∴==⋅=--V V S PA a P ABC A PBC PBC 13233∆解法三:(用分割求积法解) 由解法二知,,是中点,连结PB PC a D BC PD ==3∴⊥⊥=B C PD BC AD PD AD D ,,∴⊥BC PAD 平面∴=+==⋅⋅=----V V V V S BD a P ABC B PAD C PAD B PAD PAD 223233∆解法四:(用补形求积法解)延长AP 到Q ,使PQ=a ,连结QB 、QC ,可得一个棱长为2a 的正四面体∴==⋅=--V V a a P A B C Q A B C 121221222333() 例2. 如图,已知直三棱柱,用一平面去截它,得截面,且,ABC A B C B C AA h -=11122221∆A BB h CC h C S 2223==,,若的面积为,求证:∆AB介于截面与下底面之间的几何体体积。
高二-11-多面体与旋转体

1、多面体定义为:由三角形或平面多边形围成的封闭几何体;如:棱柱、棱锥、棱台等几何体都是多面体.2、多面体可以用它的面的数量进行命名,有几个面的多面体就叫做几面体;例如,三棱锥有一个底面和三个侧面,所以是四面体;长方体(四棱柱)有六个面,是六面体.一般地,一个n 棱锥,有一个底面和n 个侧面,所以是n +1面体;n 棱柱或n 棱台有两个底面和n 个侧面,所以是n +2面体;由此可见,面数最少的多面体是四面体,即三棱锥.3、四面体在立体几何中的作用相当于三角形在平面几何中的作用.4、与平面上的正多边形类比,在空间中可以考虑正多面体.如果一个多面体的所有面都是全等的正三角形或正多边形,每个顶点聚集的棱的条数都相等,这个多面体就叫做正多面体.有正四面体、正六面体、正八面体、正十二面体、正二十面体共5种.【例1】下列说法正确的是( )A .多面体至少有3个面B .有2个面平行,其余各面都是梯形的几何体是棱台C .各侧面都是正方形的四棱柱一定是正方体D .棱柱的侧棱相等,侧面是平行四边形【难度】★第11讲 多面体与旋转体 知识梳理例题分析 模块一:多面体 ~~~~~~~~~~~~~~~~~~~~~~~~~【例2】“阿基米德多面体”是由边数不全相同的正多边形围成的多面体,它体现了数学的对称美.将正方体沿交于一个顶点的三条棱的中点截去一个三棱锥,如此截去八个三棱锥得到一个阿基米德多面体,则该阿基米德多面体的棱有条.【难度】★★【例3】图中的十面体的面是由四个正五边形,四个三角形和两个正方形组成的,则图中上正方形面积是下正方形面积的()倍.A.1B.2C.3D.4【难度】★★【难度】★★【例5】如图所示,在长方体ABCD -A ′B ′C ′D ′中,用截面截下一个棱锥C -A ′DD ′,求棱锥C -A ′DD ′的体积与剩余部分的体积之比.【难度】★★1. 由一个平面封闭图形绕其所在平面上的一条定直线旋转一周所形成的空间封闭几何体称为旋转体;这条直线叫做该旋转体的轴.2. 与旋转体类似地可以定义空间中的旋转面:一条平面曲线(包括直线、折线等)绕其所在平面上的一条直线旋转一周所形成的空间图形称为旋转面.3. 圆柱、圆锥和圆台的概念(1)圆柱、圆锥和圆台的定义将矩形、直角三角形、直角梯形分别绕着它的一边、一直角边、垂直于底边的腰所在的直线旋转一周,形成的几何体分别叫做圆柱、圆锥、圆台.(2)与圆柱、圆锥、圆台有关的概念绕着旋转的这条直线叫做轴;垂直于轴的边旋转而成的圆面叫做底面;不垂直于轴的边旋转而成的曲面叫做侧面;无论旋转到什么位置,这条边都叫做母线.模块二:旋转体 ~~~~~~~~~~~~~~~~~~~~~~~~~ 例题分析知识梳理【例1】已知直角梯形ABCD,现绕着它的较长底CD所在的直线旋转一周,所得的几何体包括()A.一个圆柱、一个圆锥B.一个圆柱、两个圆锥C.一个圆台、一个圆柱D.两个圆柱、一个圆台【难度】★【例2】给出以下四个命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是__________.【难度】★【例3】下列给出的图形中,绕给出的轴旋转一周,能形成圆台的是()A.B.C.D.【难度】★【例4】已知AB是直角梯形ABCD与底边垂直的一腰(如图).分别以AB,BC,CD,DA为轴旋转,试说明所得几何体是由哪些简单几何体构成的?【难度】★★【例5】一个直角梯形的两底长为2和5,高为4,将其绕较长的底旋转一周,求所得旋转体的表面积.【难度】★★【难度】★★【例8】将一个边长为2的正三角形以其一边所在直线为旋转轴旋转一周,所得几何体的表面积为.【难度】★★【例9】已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过点C作l⊥CB,以l为轴将梯形ABCD旋转一周,求旋转体的表面积.【难度】★★【例1】如图,AB 是圆柱OO '的一条母线,BC 过底面圆心O ,D 是圆O 上一点.已知5AB BC ==,3CD =.(1)求二面角A DC B −−的大小;(2)将四面体ABCD 绕母线AB 所在的直线旋转一周,求△ACD 的三边在旋转过程中所围成的几何体的体积.【难度】★★【例2】已知在直角三角形ABC 中,AC BC ⊥,2,tan 22BC ABC =∠=(如图所示)(1)若以AC 为轴,直角三角形ABC 旋转一周,求所得几何体的表面积.(2)一只蚂蚁在问题(1)形成的几何体上从点B 绕着几何体的侧面爬行一周回到点B ,求蚂蚁爬行的最短距离.【难度】★★模块三:旋转体综合问题 ~~~~~~~~~~~~~~~~~~~~~~~~~ 例题分析1. 一个多面体至少有 个面.【难度】★2. 下列说法中,正确的是( )A .底面是正多边形,而且侧棱长与底面边长都相等的多面体是正多面体B .正多面体的面不是三角形,就是正方形C .若长方体的各侧面都是正方形,它就是正多面体D .正三棱锥就是正四面体【难度】★3. 如图,多面体的顶点数是 、棱数是 、面数是 .【难度】★4. 将一个正方体切一刀,可能得到的以下几何体中的种类数为( )①四面体;②四棱锥;③四棱柱;④五棱锥;⑤五棱柱;⑥六棱锥;⑦七面体A .3种B .4种C .5种D .以上均不正确 【难度】★★5. 边长为2的正方形ABCD 绕BC 旋转形成一个圆柱,则该圆柱的表面积为 .【难度】★★师生总结 巩固练习7. 正多面体各个面都是全等的正多边形,其中,面数最少的是正四面体,面数最多的是正二十面体,它们被称为柏拉图多面体.如图,正二十面体是由20个等边三角形所组成的正多面体.已知多面体满足:顶点数-棱数+面数2=,则正二十面体的顶点的个数为( )A .30B .20C .12D .10【难度】★★8. 多面体欧拉定理是指对于简单多面体,其顶点数V 、棱数E 及面数F 间有著名的欧拉公式:2V E F −+=,并且多面体所有面的内角总和为(2)360V −⋅.已知某正多面体所有面的内角总和为3600,且各面都为正三角形,设过每个顶点的棱数为n ,则该正多面体的顶点数V = ,棱数E = .【难度】★★9. 用斜二测画法画一个水平放管的平面图,其直观图如图所示,已知3A B ''=,1B C ''=,3A D ''=,且A D B C ''''∥.(1)求原平面图形ABCD 的面积;(2)将原平面图形ABCD 绕BC 旋转一周,求所形成的几何体的表面积和体积.【难度】★★10. 正多面体也称柏拉图立体,被喻为最有规律的立体结构,其所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形,且每一个顶点所接的面数都一样,各相邻面所成二面角都相等).数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体.已知一个正四面体QPTR 和一个正八面体AEFBHC 的棱长都是a (如图),把它们拼接起来,使它们一个表面重合,得到一个新多面体.(1)求新多面体的体积;(2)求二面角A BF C −−的余弦值.【难度】★★1. 2021年10月,麻省理工大学的数学家团队解决了n 维空间中的等角线问题等角线是组直线,这组直线中任意两条直线所成的角都相等.三维空间中,最大的等角线组有6条直线,它们是连接正二十面体的12个相对顶点形成的6条直线.已知棱长为1的正二十面体,其外接球半径为10254+,则三维空间最大等角线组中,任意两条直线形成的角的大小为 (精确到0.1°)【难度】★★★能力提升【难度】★★★。
第八讲多面体及旋转体(一)

第八讲多面体与旋转体(一)知识要求本章内容包括多面体和旋转体中常见的柱、锥、台、球的概念、性质、直观图、展开图的画法以及有关侧面积、体积的计算等.它是考查空间想象能力和逻辑思维能力及其运算能力的重要载体.高考试题中,立体几何试题的分值一般占20%左右,题量一般是五个,选择题、填空题、解答题的比例是3︰1︰1.立体几何试题大多以多面体和旋转体为载体,融线面关系于几何体中,融推理论证于几何量的计算中,融逻辑思维能力、空间想象能力于运算中.从近年高考立体几何试题中,可以发现以多面体和旋转体为载体设计的题目一般占25分左右,是立体几何试题分值的75%以上.涉及多面体或旋转体中有关元素的位置判定,数量的计算或最值的计算常常是以选择题或填空题的形式出现,涉及柱、锥、台体中的线面关系、面面关系的判定及运用于面积或体积的计算大多以中等难度的解答题的形式出现,而在面积或体积的计算中又侧重于体积.近年高考涉及多面体与旋转体的命题改革有所创新与突破,其主要特点是:①注意考查学生的想象、判断、推理与计算的综合能力素质,融推理与运算于一体;②注意对非常规空间几何图形的数量关系和位置关系的考查;③改变了选择题和填空题形式单一的弊端,拓宽了填空题的考查功能,采用多选、多填及开放性等形式,富有挑战性和探索性,体现高考“稳中有变”的思想.对柱、锥、台,会从复杂的空间图形中找出反映几何体特征的平面图形如:直角三角形、直角梯形,寻找有关的几何元素的位置关系,数量关系,并注意几种特殊四棱柱的联系与区别,重视平行于底面的截面的有关性质,树立“还台为锥”的思想,空间问题平面化的思想如:截面、展开图、平移、旋转、射影,应用整体思想、方程思想的策略.对多面体与旋转体的体积问题,应以公式法为基础并注意利用化归与转化思想,即①转移法(利用祖暅原理,把所求几何体的体积转化为与它等底、等高的几何体的体积),②分割求和法,③补形求差法,④换底等积法,沟通有关元素之间的联系,从而完成计算或证明.对多面体与旋转体的表面积除直接利用公式外,还可采用“化整为零”各个击破的策略,并熟悉直截面,轴截面的特性,通过展开图,将空间面积转化为平面面积来处理.解决折叠问题时,要将折叠前后的两个图形对照考察,弄清所涉及的元素在折叠前后的数量关系或位置关系.要计算柱、锥、台表面上两点的最短距离,可采用侧面展开图或全面展开图,化曲折为直.对简单多面体、旋转体的“切”“接”问题,一般是通过选择能够包含各元素间的关系的一个截面(多为轴截面),转化为平面图形或采用“等积法”来解决.应特别注意截面图形与直观图的联系,并注意两者构成元素的异同.对面积、体积的最值问题,一般转化为函数的最值问题加以解决,比较常用的方法是利用均值不等式.综合应用,关键在于沟通几何、代数、三角知识的联系,达到对知识的进一步理解、深化、升华.典型例题 例1.(2001福建)设长方体的三条棱长分别为a 、b 、c ,若长方体所有棱的长度之和为24,一条对角线长度为5,体积为2,则a 1+b 1+c1等于……………………………………( ) A .114 B .411 C .211 D .112 【分析】根据题意可得三个方程,从而求出a ,b ,c ,但计算量太大.若对a 1+b 1+c1变形可得a 1+b 1+c 1=abc ca bc ab ++,故只需求出ab +bc +ca ,从而利用整体思想求解. 【解】由题设,知⎪⎪⎩⎪⎪⎨⎧==++=++.2524)(4222abc c b a c b a∵ (a +b +c )2=a 2+b 2+c 2+2(ab +bc +ca ),∴ 2)212(=25+2(ab +bc +ca ), ∴ ab +bc +ac =211. 从而a 1+b 1+c 1=abc ca bc ab ++=411, 故选B .【点评】本题考查长方体的对角线公式,体积公式.在解题过程中,常对a 、b 、c 设而不求,利用恒等式,整体思想避开繁琐的计算过程,而直接得出结论.若长方体的对角线与交于同一点的三条棱分别成角α、β、γ,则cos 2 α+cos 2 β+cos 2 γ=1,若长方体的对角线与交于同一点的三个面分别成角α、β、γ,则cos 2 α+cos 2 β+cos 2 γ=2,在解题中的应用也应给予重视.例2.已知正三棱柱ABC—A1B1C1,过一面对角线AB1且与另一面对角线BC1平行的平面交上底面A1B1C1的一边A1C1于点D.①确定D点的位置,并证明你的结论;②证明平面AB1D⊥平面AA1D;③若AB=6,AA1=4,求直线BC1与平面AB1D的距离;④若AB︰A1A=k,问是否存在k,使平面AB1D与平面AB1A1所成角的大小为45°?若存在请求出k,若不存在请说明理由.【分析】①要证线面平行,须证线线平行,故可通过补形进行平移.②要证面面垂直,须证线面垂直.③要求线面距离可通过线面平行转化为点面距离.④对探索性性问题,不妨假设存在,然后求解或推理论证.【解】①将正三棱柱ABC—A1B1C1补成直平行六面体ABCE—A1B1C1E1,从而有AE1∥BC1,∴BC1∥面AB1E1.∴面AB1E1为所求平面,此时面AB1E1与A1C1交于D.又A1B1C1E1为平行四边形,∴D为A1C1中点.(或先猜D为A1C1中点,然后予以证明).②连结AD,由直平行六面体定义知AA1⊥面A1B1C1E1,∴AA1⊥B1D,又A1B1C1E1为菱形,∴B1D⊥A1C1,∴ B 1D ⊥面AA 1D ,又 B 1D ⊂面AB 1D ,∴ 面AB 1D ⊥面AA 1D .③∵ BC 1∥平面AB 1D ,∴ 只要求C 1 到平面AB 1D 的距离.又 A 1D =DC 1 故只要求A 1 到面AB 1D 的距离即可.由②,知面AB 1D ⊥面AA 1D ,所以过A 1 作AM ⊥AD ,则A 1M ⊥平面AB 1D .∴ A 1M 为所求.由A 1D ·AA 1=A 1M ·AD ,得:A 1M =512. (或由D AB C V 11-=D C B A V 11-,D C B S 11∆=293,1ADB S ∆=2153,得C 1 到平面AB 1D 的距离为512). ④过D 作DG ⊥A 1B 1 于G ,则DG ⊥面A 1B 1BA ;过G 作GH ⊥AB 1 于H ,连DH ,则DH ⊥AB 1,∴ ∠DHG 为A 1—AB 1—D 的平面角,若∠DHG =45°,设AA 1=a ,则AB =ka ,DG =43ka . ∵ AA 1︰AB 1=GH ︰GB 1, ∴ GH =1432+k ka . ∵ DG =GH ,∴ k =2.∴ 存在k =2,使平面AB 1D 与平面AB 1A 1 所成角的大小为45°.【点评】本题以正三棱柱为载体,考查了线线、线面、面面的位置关系以及距离、角、体积等问题.补形法、等积法是常用技巧,开放性问题是近年高考热点,应予重视.一般地利用三棱锥等积法寻找底面上的高,常将一个底面的顶点选在多面体的同一表面上.例3.各棱长都等于2的斜三棱柱ABC—A1B1C1中,侧面ABB1A1垂直于底面.①问侧棱与底面所成角为多少时,能使B1C⊥AC1;②在①的条件下求此三棱柱的侧面积.【分析】①取AB中点D,设BC1 B1C=O,则DO∥AC1要证B1C⊥AC1只需证DO ⊥B1C又O为B1C中点,∴只需证B1D=DC=3,在△B1BD中由余弦定理可得:∠B1BD=60°,又面B1BAA1⊥底面,∴∠B1BA为侧棱与底面所成角.故可猜测当侧棱与底面成角为60°时,B1C⊥AC1.②棱柱侧面积有两种解法,一是判断各侧面的形状,各个击破,再求各侧面的面积之和,二是求其直截面周长与侧棱长的乘积.【解】①当侧棱与底面成角为60°时,能使B1C⊥AC1.事实上,作B1D⊥AB于D.∵面ABB1A1⊥底面ABC,∴B1D⊥平面ABC.∴∠B1BD为侧棱与底面所成角.∴∠B1BD=60°.又BD=B1E cos 60°=1,∴D为AB中点.∴CD=3.又B1D=3,∴CD=B1D.又O为B1C中点,∴DO⊥B1C而AC1∥DO.∴AC1⊥B1C(或证B1C⊥面ABC1).② 在侧面ABB 1A 1 中11A ABB S 平行四边形=2·2·si n 60°=4×23=23, 在△B 1CD 中,CD =3=B 1D ,∴ B 1C =6.又 BCC 1B 1 为菱形,∴ BC 1=2 BO =222)26(2-=10, 又 AB ⊥面B 1CD ,∴ AB ⊥DO ,又 DO ∥AC 1,∴ AC 1⊥AB .在Rt △ABC 1中,AC 1=222)10(-=6.∴ 11B BCC S 平行四边形=C C AA S 11平行四边形=2110·6=15. ∴ S 侧=11A ABB S 平行四边形+211B BCC S 平行四边形=2(3+15).【点评】① 条件探索型命题,解题时要善于从所给的题断出发,逆向追索,逐步探寻出应具备的条件,然后予以证明.S 棱柱侧=C 直截面×l ,V 棱柱=S 直截面×l ,其中l 为侧棱长.例4.三棱锥P —ABC 中,侧棱P A ⊥底面ABC ,H 是A 在平面PBC 上的射影.① 若H 是△PBC 的重心,则在此三棱锥的棱所在直线中与AC 垂直的直线有几条?② 若H 是△PBC 的重心,且△ABC 是边长为2的正三角形,求二面角P —BC —A 的大小.【分析】① 充分利用线线垂直与线面垂直的相互关系进行挖掘与探求.② 二面角问题关键是“作”“证”“算”,本题关键要利用重心性质及方程思想进行求解.【解】① P A ⊥平面ABC ,AC ⊂平面ABC ,∴ P A ⊥AC ,AH ⊥平面PBC ,CH ⊥PB .∴ AC ⊥PB .∴ AC ⊥平面ABC .又 AB 平面P AB ,∴ AC ⊥AB .故与AC 垂直的直线有P A 、PB 、AB 三条.② 若H 是重心,连结PH 交BC 于D ,可设PH =2 x ,HD =x ,由AB =2,可知AD =3,于是有(3)2=x ·(2 x +x ),则x =1,∴ PD =3.又 D 是BC 的中点,∴ AD ⊥BC .∴ PD ⊥BC .∴ ∠PDA 是二面角P —BC —A 的平面角.由cos ∠PDA =PD AD =33得∠PDA =arc cos 33即为所求. 【点评】① 结论探索型命题,解题时要充分利用已知条件或图形的特征进行全面、透彻分析,从而推理、发现、获取结论.② 要正确区分三棱锥的顶点在底面上的射影何时是底面三角形的外心、内心、重心、中心.例5.棱锥被平行于底面的平面所截,当截面分别平分棱锥的侧棱,侧面积和体积时,相应的截面面积依次为S 1、S 2、S 3,则…………………………………………………………( ) A .S 1<S 2<S 3 B .S 3<S 2<S 1 C .S 2<S 1<S 3 D .S 1<S 3<S 2【分析】棱锥被平行于底面的平面所截,若顶点到截面的距离与顶点到底面的距离之比为k ,则它们对应棱长的比等于k ,底面积(侧面积、全面积)的比等于k 2,体积比等于k 3.【解】设棱锥的底面积为S ,高为h ,以截面为底面的棱锥的高分别为h 1、h 2、h 3,则21S S =21h h ,S S 2=h h 2,SS 3=h h 3 由题意,得 h h 1=21,21)(h h =21,23)(hh =21∴ 21S S =21,S S 2=21,SS 3=321. ∵ 21<21<321, ∴ S 1<S 2<S 3.故选A .【点评】① 对于台体平行于底面的截面,可补台为锥,再利用有关比例性质便可解决.② 棱台中平行于底面的截面及上、下底面面积分别为S 0、S 1、S 2 截面与上下底面的距离之比为m ︰n 时,则0S =nm S n S m ++12,特别地当m =n 时,为中截面公式. ③ 圆台的上下底面半径分别为r 、R ,作平行于底面的截面分别平分圆台的侧棱、侧面积,体积时,若截面分母线(自上到下)的比为m ︰n ,中截面半径为x ,则可利用性质“mrx -=n x R -”,得到相应的截面半径分别为2r R +,222r R +,3332r R +. 例6.一个正三棱台的上、下底面边长分别为3 cm 和6 cm ,高是23cm .求三棱台的① 侧棱长;② 斜高;③ 侧棱与底面所成的角的正切值;④ 侧面与底面所成的角;⑤ 侧面积.【分析】利用图中的直角三角形与直角梯形进行求解.【解】如图,设O 1,O 分别是上、下底面中心,则O 1O =23cm , 连结A 1O 1 并延长交B 1C 1 于D 1,连结AO 并延长交BC 于D ,过A 1 作A 1F ⊥AD 于F ,作D 1E ⊥AD 于E .① 在Rt △A 1AF 中,A 1F =23cm ,AF =AO -A 1O 1=33(6-3)=3(cm ), 所以AA 1=212F A AF +=221(cm ). ② 在Rt △D 1DE 中, D 1E =23,DE =DO -D 1O =63(6-3)=23(cm ), 所以斜边上的高 D 1D =221DE E D +=22)23()23(+=3(cm ). ③ 因为A 1F ⊥底面ABC ,所以∠A 1AF 为侧棱与底面所成的角,所以tan ∠A 1AF =AF F A 1=323=23. ④ 因为D 1D ⊥BC ,AD ⊥BC ,所以∠D 1DA 为侧面与底面所成二面角的平面角,tan ∠D 1DA =DE E D 1=2323=3 所以∠D 1DA =60°.(或还台为锥,设棱锥的高为h ,利用OA =2 OD ,得tan ∠D 1DE =OD h =OAh 2=2 tan ∠A 1AF =3). ⑤ S 侧=21(3×3+3×6)×3=2273(cm 2) (或利用S 侧=︒-60cos 上下S S =2(S 下-S 上)=243(62-32 )=2273). 【点评】对正棱锥、正棱台的问题可转化为直角三角形问题,使高、斜高、斜高在底面上的射影,侧棱、侧棱在底面上的射影,底面边长之半,边心距,外接圆半径及侧棱和底面所成角,侧面和底面所成的二面角等元素转化为直角三角形的边和角,还台为锥有利于整体上把握本章内容和公式.对正棱锥、正棱台,若侧面与底面所成角为α,则可利用公式:S 正棱锥侧=αcos 底S ,S 正棱台侧=αcos 上下S S -(适合选择、填空). 基础练习一、选择题1.设M ={正四棱柱},N ={长方体},P ={直四棱柱},Q ={正方体}则这四个集合的关系是……………………………………………………………………( ) A .P ⊂N ⊂M ⊂Q B .Q ⊂M ⊂N ⊂PC .P ⊂M ⊂N ⊂QD .Q ⊂N ⊂M ⊂P2.如果三棱锥S —ABC 的底面是不等边三角形,侧面与底面所成二面角都相等,且顶点S 在底面的射影O 在△ABC 内,那么O 是三角形的……………………( ) A .垂心 B .重心 C .外心 D .内心3.台体中一个平行于底面的截面把台体分成上、下两部分,若台体的上底面积,截面面积,下底面积之比为1︰4︰9,那么截面把台成分成上、下两部分的体积比为( ) A .278 B .197 C .135 D .53 4.一个圆锥的轴截面的顶角为120°,过顶点的截面的最大值是4,那么此圆锥的侧面积是………………………………………………………………………………( ) A .23π B .43π C .63π D .83π5.夹在两平行平面间的圆锥、球、圆柱在平面内的射影是等圆,那么它们的体积之比是…………………………………………………………………………………( ) A .1︰2︰3 B .2︰3︰6 C .4︰6︰9 D .1︰2︰46.圆台的侧面积是它的内切球表面积的34倍,则圆台母线和底面所成角的大小是( ) A .30° B .45° C .60° D .75°7.设地球半径为R ,在北纬45°圈上A 、B 两地的经度分别为东经165°和西经105°,则A 、B 两地间的球面距离是…………………………………………………( ) A .R B .42π R C .2πR D .3πR 8.在轴截面是直角三角形的圆锥内,有一个体积最大的内接圆柱,则内接圆柱的体积与圆锥的体积的比值为…………………………………………………………( )A .83B .94C .73D .21 9.将边长为a 的正方形ABCD 沿对角线AC 折起,使得BD =a ,则三棱锥D —ABC的体积为…………………………………………………………………………( )A .b a 3B .123aC .123a 3D .122a 3 10.平行四边形两邻边的长为a 和b ,当它分别绕边a 、b 旋转一周后,所形成的几何体的体积之比为………………………………………………………………( ) A .a b B .b a C .3)(a b D .3)(ba 11.如图三棱台ABC —A 1B 1C 1 中,已知S △ABC =S 1,111C B A S =S 2,高为h ,则四面体ACB 1C 1 的体积为………………………………………………………………( )A .3h 21S S B .31S 1h C .31S 2h D .3h (S 1+S 2+21S S ) 12.有三个球一个球内切于正方体的各个面,一球内切正方体各条棱,另一球过正方体的各顶点,则这三球面积比是…………………………………………………( ) A .1︰2︰3 B .1︰2︰3 C .1︰22︰33 D .1︰4︰9二、填空题13.斜三棱柱ABC —A 1B 1C 1 的一个侧面的面积为S ,这个侧面与它对棱的距离为a ,则这个棱柱的体积是______________.14.若正棱台上下底面及侧面的面积比为4︰9︰10,则侧面与底面所成的角大小为________.15.圆锥母线长为3,底面半径为1 cm ,底面圆周上有一点A ,由A 点出发绕圆锥一周回到A 点的最短路线长等于_________________.16.一个正六棱锥,底面边长为2,高为1,则过两条侧棱所作的截面中,最大的截面积等于______________.17.如图是一个正方体的展开图,在原正方体中有以下命题:① AB 与EF 所在直线平行;② AB 与CD 所在直线异面;③ MN 与BF 所在直线成60°角;④ MN 与CD 所在直线互相垂直.其中正确命题的序号是____________(注:把你认为正确的命题都填上)18.若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值是_____________(只需写出一个可能的值).三、解答题19.正三棱台ABC —A ′B ′C ′上、下底面的边长分别为1 cm 和3 cm ,高是36cm . ① 证明AA ′⊥平面BCC ′B ′;② 求正三棱台ABC —A ′B ′C ′的侧面积.20.把半径为R 的圆面剪去一个扇形,设剩下的扇形圆心角为α,将其作为一个圆锥的侧面围成一个圆锥.问α 为多大时,圆锥的体积最大?最大值为多少?21.如图所示四面体ABCD 中,已知AB =m ,CD =n ,还需要知道哪些条件(条件个数应最少)就可以求出四面体ABCD 的体积,并说明理由.参考答案基础练习一、选择题 1.B 2.D 3.B 4.B 5.A 6.C7.D 8.B 9.D 10.A 11.A 12.A二、填空题13.21aS 14.60° 15.33 16.6 17.②④ 18.611或1214或1211三、解答题19.① 提示:还台为锥;② 6.20.α=326π;V =2763π R 3.21.提示:以BD 、DC 为邻边作□BDCE ,利用三棱锥换底等积法得须两个条件得:AB 与CD 的距离h 及所成角θ.。
第七讲:多面体与旋转体

第七讲 多面体与旋转体多面体与旋转体是高中数学的重要内容之一,是考查各种能力的重要载体,其中异直线所成的角、直线与平面所成的角、二面角(理)以及点到平面的距离、简单图形侧面积与体积的计算是高考考查的重点内容。
本讲从内容上来说,主要集中在多面体与旋转体的概念与性质及其应用、截面面积、侧面积、全面积以及各种角与距离的计算等方面;从思想方法上来说,体会化“曲”为“直”、祖恒原理和图形割补等化归思想。
【高考热点】异面直线所成的角、直线与平面所成的角、二面角,空间线面位置关系的判断,面积与体积的计算。
【范例精讲】 例1.(1)正三棱锥S A B C -的侧棱,,SA SB SC 两两垂直,体积为V ,,,A B C '''分别是,,SA SB SC 上的点,且SC C S SB B S SA A S 41,31,21='='=',则三棱锥S A B C '''-的体积为( )(A )V 91(B )V121(C )V241(D )V721(2)如图,在多面体ABC D EF 中,已知A B C D 是边长为1的正方形,且A D EBC F ∆∆、均为正三角形,//,2EF AB EF =,则该多面体的体积为( ) (A 3(B 3(C )43(D )32解:(1)选C ;(2)选A 。
说明:对于第(1)小题,注意转化三棱锥的顶点灵活使用体积计算公式;对于(2)则需要利用图形的割补思想求解。
例2.在北纬45圈上有,A B 两点,设该纬度圈上,A B两点的劣弧长为4R (R 为地球半径),求,A B 两点间的球面距离。
解:设北纬45圈的半径为r ,则4r R =,设O '为北纬45圈的圆心,A O B α'∠=,则4r R α=,24R R α=,2πα=,所以AB R ==,在AB C ∆中,3A OB π∠=,所以,,A B 两点的球面距离等于3R π。
高三立体几何复习讲义:多面体与旋转体

多面体与旋转体一、棱柱1、 由几个多边形围成的封闭的几何体叫做多面体。
2、 两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱。
棱柱的互相平行的两个面叫做棱柱的底面,其余各面叫做棱柱的侧面,相邻的两个侧面的公共边叫做棱柱的侧棱,两个底面间的距离叫做棱柱的高。
棱柱的基本性质:(1) 棱柱的侧面都是平行四边形。
(2) 棱柱的两个底面及平行于底面的截面都是全等的多边形。
3、 侧棱与底面不垂直的的棱柱叫做斜棱柱。
侧棱与底面垂直的棱柱叫做直棱柱。
底面是正多边形的直棱柱叫做正棱柱。
性质:(1) 直棱柱侧面都是矩形。
(2) 直棱柱侧棱与高相等。
(3) 正棱柱的侧面都是全等的矩形。
4、 底面是平行四边形的棱柱叫做平行六面体。
底面是矩形的直棱柱是长方体。
长方体的对角线平方等于三边长的平方和。
5、 夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任何平面所截得的两个截面的面积都相等,那么这两个几何体的体积相等。
6、 h V S =⋅棱柱底. 二、棱锥1、有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
棱锥的这个多边形的面叫做底面,其余各个三角形的面叫做侧面。
相邻的两个侧面的公共边叫做棱锥的侧棱。
各个侧面的公共顶点叫做棱锥的顶点,顶点到底面的距离叫做棱锥的高。
棱锥的基本性质:如果一个棱锥被平行于底面的一个平面所截,那么: (1) 侧棱和高被这个平面分成比例线段; (2) 截面和底面都是相似多边形;(3) 截面面积与底面面积之比,等于顶点到截面与顶点到底面的距离平方之比。
2、如果一个棱锥的底面是正多边形,且顶点在底面的射影是底面的中心,这个棱锥叫做正棱锥。
正棱锥的性质:(1) 各侧棱相等,各侧面都是全等的等腰三角形。
(2) 正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形。
正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
立体几何考点专题复习(一)多面体、旋转体

⽴体⼏何考点专题复习(⼀)多⾯体、旋转体⽴体⼏何考点专题复习(⼀)——多⾯体、旋转体⼀、多⾯体和旋转体(⼀)直观图(斜⼆测画法)原则:1.x轴、y轴的夹⾓画成45°或135°,⼀般画45°。
z轴竖直向上;2.与坐标轴平⾏的直线依然平⾏;3.与x轴、z轴平⾏的线段长度不变,与y轴平⾏的线段长度变为原来的⼀半。
(切记:除以上3条外没有任何可以确定的量)画图步骤:1.在原图上建⽴坐标系,画出直观图坐标系,定位图形与三坐标轴的交点。
2.画与x轴平⾏的线段。
3.画与y轴平⾏的线段,长度变为原来的⼀半。
4.画与z轴平⾏的线段。
(⼆)⾯积和体积公式:侧⾯积公式与体积公式。
求法:割补法或等体积法都常⽤。
例1.若某⼏何体的三视图单位:如图所⽰.画出该⼏何体的直观图;求此⼏何体的体积和表⾯积.【答案】解:根据三视图画出直观图,如图所⽰;该⼏何体可以看成是⼀个直三棱柱去掉两个等底的⼩三棱锥组成的如图,直三棱柱的体积为,两个⼩三棱锥的体积为,故⼏何体的体积为40.在图中,作于点M,则,,,所以,.于是,,梯形⼜矩形,所以⼏何体的表⾯积为梯形矩形.【解析】本题考查了三视图与⼏何体的直观图的关系,⼏何体的表⾯积以及体积的求法问题.根据三视图得出该⼏何体是底⾯为直⾓梯形的直四棱柱,结合图中数据画出⼏何体的直观图;结合图中数据计算该⼏何体的表⾯积和体积.例2.已知⼀个⼏何体的三视图如图所⽰.求此⼏何体的表⾯积;如果点P,Q在正视图中所处的位置为:P为三⾓形的顶点,Q为四边形的顶点,求在该⼏何体的侧⾯上,从点P到点Q的最短路径的长.【答案】解:由三视图知:此⼏何体是⼀个圆锥加⼀个圆柱,其表⾯积是圆锥的侧⾯积、圆柱的侧⾯积和圆柱的⼀个底⾯积之和底⾯圆半径长a,圆柱⾼为2a,圆锥⾼为a,,圆柱侧,圆柱底,圆锥侧所以表⾯.分别沿点P与点Q所在的母线剪开圆柱的侧⾯,并展开铺平,如图所⽰,则,所以P,Q两点在该⼏何体的侧⾯上的最短路径的长为.【解析】本题考查三视图、组合体表⾯积公式及旋转体上最短距离问题,属于基础题.由三视图可以还原⼏何体是上⾯⼀个圆锥加下⾯⼀个圆柱,即可求得表⾯积;沿点P与点Q所在的母线剪开圆柱的侧⾯,并展开铺平,直线距离最短,由勾股定理即可得到答案.⼆、外接球和内切球(⼀)外接球例1.正四棱锥的底⾯积为3,外接球的表⾯积为,则外接球的球⼼到平⾯ABCD的距离为________.【答案】【解析】【分析】本题考查了正四棱锥以及球的结构特征,球的表⾯积由题意,得到中,,从⽽得到结果.【解答】解:如图,设外接球的球⼼为O,半径为R,正四棱锥的底⾯积为3,,,,外接球的表⾯积为,,,中,,,,,球⼼到平⾯ABCD的距离为.故答案为.(⼆)内切球例1.正三棱锥的⾼为1,底⾯边长为2,正三棱锥内有⼀个球与其四个⾯相切则球的表⾯积为______ .【答案】【解析】解:如图,过点P作平⾯ABC于D,连结并延长AD交BC于E,连结PE,是正三⾓形,是BC边上的⾼和中线,D为的中⼼.,,,设球的半径为r,以球⼼O为顶点,棱锥的四个⾯为底⾯把正三棱锥分割为四个⼩棱锥,则,,球的表⾯积为.故答案为:.设球的半径为r,以球⼼O为顶点,棱锥的四个⾯为底⾯把正三棱锥分割为四个⼩棱锥,求出r,由此能求出球的表⾯积.本题考查棱锥的全⾯积和体积的求法,考查球的表⾯积的求法,解题时要认真审题,注意空间思维能⼒的培养.例2.正四⾯体内切球与外接球的体积的⽐为_________.【答案】1:27【解析】【分析】本题是中档题,考查正四⾯体的内切球与外接球的关系,找出两个球的球⼼重合,半径的关系是解题的关键,考查空间想象能⼒,计算能⼒.【解答】解:设正四⾯体为PABC,两球球⼼重合,设为O.设PO的延长线与底⾯ABC的交点为D,则PD为正四⾯体PABC的⾼,底⾯ABC,且,,OD为正四⾯体PABC内切球的半径设正四⾯体PABC底⾯⾯积为S,将球⼼O与四⾯体的4个顶点PABC全部连接,可以得到4个全等的正三棱锥,球⼼为顶点,以正四⾯体⾯为底⾯.每个正三棱锥体积⽽正四⾯体PABC体积,根据前⾯的分析,,所以,,所以,,所以棱长为a的正四⾯体的内切球和外接球的体积之⽐为1:27.故答案为1:三、多⾯体表⾯最短距离例1.在直三棱柱中,底⾯为直⾓三⾓形,,,,P是上⼀动点,如图所⽰,求的最⼩值.【答案】解:在平⾯内,PC在平⾯内,将其铺平后转化为平⾯上的问题解决铺平平⾯、平⾯,如图所⽰计算,,⼜,故是的直⾓三⾓形.C.在中,由余弦定理,得,故.【解析】本题考查了三棱柱的展开图中最短距离问题以及余弦定理,属于中档题,在平⾯内,PC在平⾯内,将其铺平后转化为平⾯上的问题解决铺平平⾯、平⾯,在中,由余弦定理,得.例2.如图所⽰,正四⾯体ABCD中,E是棱AD的中点,P是棱AC上⼀动点,的最⼩值为,则该正四⾯体的外接球⾯积是______.【答案】【解析】解:将侧⾯和展成平⾯图形,如图所⽰:设正四⾯体的棱长为a,则的最⼩值为,.在棱锥中,设底⾯三⾓形BCD的中⼼为M,外接球的球⼼为O,F为BC的中点,则,,.设外接球的半径,则,在中,由勾股定理可得:,解得:.外接球的表⾯积为:.故答案为:.将侧⾯展开,根据的最⼩值可得正四⾯体的棱长,再计算外接球的半径,得出外接球⾯积.本题考查了棱锥的⼏何特征与外接球的表⾯积计算,棱锥侧⾯距离的最值,属于中档题.。
高中数学中的多面体和旋转体

多面体和旋转体是高中数学中的重要概念,它们在几何学中起着重要的作用。
本篇文章将介绍多面体和旋转体的基本概念、性质以及它们在实际生活中的应用。
一、多面体多面体是指由若干个平面多边形围合而成的三维几何体。
每个面都是一个平面多边形,并且相邻两个面的公共边是相交于一点的。
多面体分为凸多面体和凹多面体,如果一个多面体的任何一个面都在另一个面的外部,则这个多面体是凸多面体;否则,这个多面体是凹多面体。
1. 多面体的性质(1)多面体的顶点数V和面数F之间有如下关系:V = F + E - 3,其中E表示边数。
这个公式称为欧拉公式。
(2)多面体的棱数E和面数F之间有如下关系:E = 3F - E - F,这个公式称为欧拉-斯图姆定理。
(3)多面体的对角线数D和面数F之间有如下关系:D = 2F - 4,这个公式称为拉格朗日定理。
2. 多面体的应用(1)多面体在计算机图形学中有着广泛的应用,例如,计算机生成的三维图形通常都是由许多平面多边形构成的。
(2)多面体在机械制造中也有着重要的应用,例如,制造凸轮、齿轮等零件时需要使用凸多面体或凹多面体的概念。
二、旋转体旋转体是指由一条平面曲线绕着它所在的平面内的一条定直线旋转所生成的立体。
曲线称为旋转体的母线,定直线称为旋转体的轴。
1. 旋转体的性质(1)如果一个旋转体的底面是一个圆,则这个旋转体一定是圆柱或圆锥;如果这个圆的半径等于旋转体的底面半径,则这个旋转体是圆柱;否则,这个旋转体是圆锥。
(2)如果一个旋转体的底面是一个椭圆或其他平面曲线,则这个旋转体一定是圆台或球;如果这个椭圆或其他平面曲线是旋转体的底面半径的倍数,则这个旋转体是圆台;否则,这个旋转体是球。
2. 旋转体的应用(1)旋转体在建筑工程中有着广泛的应用,例如,圆柱形和球形建筑物的外壳是由旋转体的概念构成的。
(2)旋转体在油管和通风管道的设计中也有着重要的应用。
认识多面体和旋转体课件

体积计算
对于多面体,体积可以通过计算各个 面的体积之和得到。对于旋转体,体 积可以通过计算底面圆的体积或整个 旋转体的体积得到。
角度和弧度的计算
角度计算
在多面体中,角度可以通过测量各个 面之间的夹角得到。在旋转体中,角 度可以用来描述旋转体的旋转角度。
弧度计算
在旋转体中,弧度可以用来描述旋转 体的旋转程度,通常用于旋转轴的角 度测量。
旋转体的建模
旋转体的建模可以使用旋转几何公式进行,例如圆柱和圆锥可以使用旋转面的几何公式进行建模。
建模方法的比较和选择
01 02
精度和复杂性
使用CAD软件进行建模可以获得高精度的模型,但需要一定的技能和经 验。而使用数学公式进行建模可以创建相对简单的模型,但对于复杂模 型可能不够精确。
适用范围
CAD软件适用于各种类型的多面体和旋转体建模,而数学公式适用于某 些特定类型的模型,例如正多面体和旋转体。
在科学研究和教学中的应用
多面体和旋转体的科学研究价值
多面体和旋转体的研究涉及到几何学、拓扑学、物理学等多个学科领域,对于推动数学 和科学的发展具有重要意义。
多面体和旋转体的教学价值
在数学和工程学科的教学中,多面体和旋转体是重要的教学素材,有助于培养学生的空 间思维、几何直觉和解决实际问题的能力。
THANKS
该直线称为旋转轴, 平面图形称为旋转面 。
旋转体的分类
根据旋转面的形状,旋转体可以 分为圆柱、圆锥、圆台等类型。
根据旋转轴的方向,旋转体可以 分为正轴和斜轴两类。
根据旋转轴与旋转面的关系,旋 转体可以分为直纹和单叶两类。
旋转体的性质
旋转体的侧面是曲面,其展开 后是平面图形。
旋转体的体积和表面积与旋转 面和旋转轴的形状、大小和位 置有关。
多面体和旋转体

第二章多面体和旋转体一多面体§2.1 棱柱一、素质教育目标(一)知识教学点1、棱柱的概念及性质。
2、平等六面体,长方体的概念及长方体的性质。
3、直棱柱直观图的画法4、棱柱侧面积的计算(二)能力训练点1、在学习棱住概念和性质过程中,努力提高学生的观察、抽象和概括能力。
2、通过直棱柱直观图的画法的教学,进一步提高学生的作图和识图能力。
3、通过直棱柱侧面积公式的教学,进一步增强学生把空间形转化为平面图形的意识,使学生进一步掌握化归的数学思想和方法,以提高学生分析问题、解决问题的能力。
(三)德育渗透点1、棱柱概念的形成,是从特殊到一般、具体到抽象的过程;通过教学使学生初步认识辩证唯物主义认识论的观点。
2、通过四面体、平行六面体、直平行六面体、长方体、正方体之间相互关系的教学,使学生树立普遍联系的唯物主义观点。
3、通过运用侧面积公式计算生产实践中具体零件的面积,使学生懂得数学对工、农业生产的意义,激励学生努力学好数学,将来为祖国的“四化”建设做出更大的贡献。
二、教学重点、难点、疑点及解决办法1、教学重点:理解棱柱的概念,掌握棱柱的性质及直棱柱侧面积公式,能利用性质及侧面积公式解决有关问题。
2、教学难点:直棱柱直观图的画法3、教学疑点:直棱柱的判断,注意引导学生严格按定义三、课时安排本课题建议安排3课时四、教与学过程设计第一课时节棱柱的概念及性质(一)引入将画有图2-1、图2-2、图2-3的小黑板挂出师:今天这一节课我们学习棱柱的概念和性质(给出课题),以上三个图形所表示的模型均为棱柱,下面我们一起来研究它们的共同特点。
(二)棱柱及有关概念的定义师:大家注意到图2-1到图2-3所表示的几何本均由一些面围成,而面与面之间有交线,因此可以从“面”和“线”两个角度去找它们的特点,先观察图2-1。
(1)首先看面:从面和面的关系及面的开头引导学生讨论,得出结论;有两个面互相平行,其余各面为四边形。
(2)再看线:从线与线之间的引导学生得出结论:每相邻两个四边形的公共边都互相平行。
多面体旋转体

多面体和旋转体一. 教学内容:1. 主要内容:多面体和旋转体2. 考点分析:多面体和旋转体每年必考,不仅有直接求多面体和旋转体的面积和体积问题,也有已知面积或体积求几何体中某些元素或元素间的关系问题,近年来即使是考查空间线面位置关系的问题,也常以几何体为依托,该部分内容不仅在选择题、填空题中考,也在解答题中出现。
解答题在高考中一直保持中档题的水平,近几年高考立体几何试题多采用一题多问的形式,降低了起点,分散了难点,既有证明,也有计算,一般要求学生先证后算,证明严谨、清楚,计算准确。
【典型例题】例1. 三棱锥,,,,求这个P ABC PA a AB AC a PAB PBC BAC -===∠=∠=∠=︒260 三棱锥的体积。
分析:由题设∠=∠=︒PAB PAC 60∴∠P ABC O BAC 在平面上的射影必在的平分线上又,,可知是正三角形∠=︒=BAC AB AC BC 60∆A 考查方向:考查三棱锥体积的常用求法。
分析一:作在底面上的射影,求和的面积P O PO ∆AB C分析二:注意到且PA AB PAB =∠=︒1260知PA PB ⊥同理,把作为底,则为高PB PC PBC PA ⊥ 分析三:割法、补法解法一:(用公式法解)如图,作底面三角形顶角A 的平分线AD ,交BC 于D ,过P 点作底面的垂线,垂足为O ,由分析知射影O 必在AD 上,易知△ABC 是正三角形,AB=2a ,∴=S a ABC ∆32PC过作,垂足为,连,则P PE AB E OE OE AB ⊥⊥在中,,Rt PAE PAE PA a ∆∠=︒=60∴===⋅︒=PE a AE a OE AE tg a 3223036,, 在中,Rt POE PO PE OE a ∆=-=2263∴=⋅=-V S PO a P ABC ABC 13233∆解法二:(利用等积转换法解)在△PAB 中PA a AB a PAB ==∠=︒,,260∴=+-⋅⋅︒=PB a a a a a 2222222603()()cos∴⊥⊥=∆P A BPA PB PA PC PB PC P 是直角三角形,,同理可证,又 ∴⊥PA PBC 平面在中,,∆PBC PB PC a BC a ===32∴=S a P B C ∆22∴==⋅=--V V S PA a P ABC A PBC PBC 13233∆解法三:(用分割求积法解) 由解法二知,,是中点,连结PB PC a D BC PD ==3∴⊥⊥=B C PD BC AD PD AD D ,,∴⊥BC PAD 平面∴=+==⋅⋅=----V V V V S BD a P ABC B PAD C PAD B PAD PAD 223233∆解法四:(用补形求积法解)延长AP 到Q ,使PQ=a ,连结QB 、QC ,可得一个棱长为2a 的正四面体∴==⋅=--V V a a P ABC Q ABC 121221222333() 例2. 如图,已知直三棱柱,用一平面去截它,得截面,且,ABC A B C B C AA h -=11122221∆A BB h CC h C S 2223==,,若的面积为,求证:∆AB介于截面与下底面之间的几何体体积。
多面体与旋转体复习
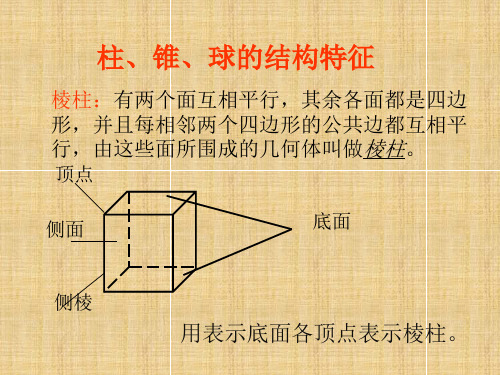
h
最短路程 h2 4 2r 2
例:用两个平行平面去 截半径为 R的球面,两个截面圆 的半径为 15和24,若两截面间的距离为 27, 求球的半径
设球半径为 r
O1 O2 O O 2
A B B
r 2 152 OO1 2 2 2 r 242 OO2 OO 27 OO 2 1
,点 O
(2)球面被不经过球心的平面截得的圆是小圆,被经过球心的平面截得的圆是大圆 (3)球心和截面圆心的连线 垂直 于截面;
2 2 d R r (4)球心到截面的距离 d 与球的半径 R 及截面的半径 r 有下面的关系:
例 : 已 知 圆 柱 的 底 面径 半 为r , 高 为h, 若 一 只 蚂 蚁 从 某 一 条 母 线 的 一 个 端 点 出 发着 沿圆 柱 表 面 爬 行 一 周该 到母 线 的 另 一 个 端 点 , 则 蚂 蚁走 所的 最 短 路 程 为 ?
柱、锥、球的结构特征
棱柱:有两个面互相平行,其余各面都是四边 形,并且每相邻两个四边形的公共边都互相平 行,由这些面所围成的几何体叫做棱柱。
顶点
侧面 底面
侧棱
用表示底面各顶点表示棱柱。
一、棱柱的概念与性质: 1、棱柱的概念:
有两个面 互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行 由这些面所围成的多面体叫做棱柱。 2、棱柱的性质: (1)侧棱都相等,侧面是 平行四边形 ;
顶点
S
轴
侧 面
O
B
底面
四、圆锥的概念与性质: 1、圆锥的概念:以直角三角形 ABC(及其内部)绕其 一条直角边AB所在直线 旋转一周,所形成的几何体叫做圆锥。其中 AB 所在直线叫做圆锥的轴,圆锥用表示它的轴
多面体与旋转体的概念 讲义

多面体与旋转体的概念一、概念整理(一)棱柱与棱锥1、水平放置的平面图形的直观图的“斜二测”画法(1)按右图所示的位置和夹角作三条轴,分别表示铅垂方向,左右方向和前后方向的轴,依次把它们叫做________________________.(2) 规定在z轴和y轴方向上的线段的长度与其表示的真实长度相等,而在x轴方向上,线段的长度是其表示的真实长度的__________。
2、“斜二测”画法的重要性质(1)平行直线的斜二测图__________________;(2)线段及其直线上定比分点的斜二测保持原比例不变。
(三)、旋转体1、旋转体:平面上一条封闭图形所围成的区域绕着它所在平面上的一条定直线旋转而形成的几何体叫做旋转体,定直线叫做______________。
2、圆柱:将_________绕其一条边’OO所在直线旋转一周,所形成的几何体。
(1)圆柱的结构:圆柱的轴:____________;圆柱的母线:____________;圆柱的底面:___________;圆柱的侧面:___________;圆柱的高:____________;(2)圆柱的性质:①底面由与轴垂直的边旋转得到,所以圆柱的底面是圆面且垂直于轴,②轴过两底面圆心且垂直于底面,联接两底面圆心的线段的长等于圆柱的高;③所有母线相互平行,相等且垂直于底面,母线的长等于圆柱的高;④轴截面(经过圆柱的轴的截面)是矩形。
3、圆锥:将_________绕其一条_____边AB所在直线旋转一周,所形成的几何体。
(1)圆锥的结构:圆锥的轴:_____________;圆锥的母线:____________;顶点:_____________;高:_____________;底面:_____________;侧面:_____________;(2)圆锥的性质:a.底面为圆且垂直于轴;b.c.所有母线都经过顶点且相等,各母线与轴的夹角相等。
d.轴截面是等腰三角形。
多面体和旋转体

③棱锥的侧面积与底面积的射影公式: S 侧 = 附:
a l b
S底 cos α
(侧面与底面成的二面角为 α )
c
以知 c ⊥ l , cos α ⋅ a = b , α 为二面角 a − l − b . 则 S1 =
S 1 1 a ⋅ l ①, S 2 = l ⋅ b ②, cos α ⋅ a = b ③ ⇒ ①②③得 S 侧 = 底 . 2 2 cos α
【巩固练习 B】
1.若三棱锥的三条侧棱两两垂直,且侧棱长均为 3 ,则其外接球的表面积是
2.一个六棱柱的底面是正六边形, 其侧棱垂直底面。 已知该六棱柱的顶点都在同一个球面上, 且该六棱柱的高为 3 , 底面周长为 3,那么这个球的体积为 _________ 3.连结球面上两点的线段称为球的弦.半径为 4 的球的两条弦 AB、CD 的长度分别等于 2 7 、 4 3 ,每条弦的两
精锐教育网站: -6精锐教育· 考试研究院
中国领先的个性化教育品牌 端都在球面上运动,则两弦中点之间距离的最大值为 .
4.在体积为 4 3π 的球的表面上有 A、B,C 三点,AB=1,BC= 2 ,A,C 两点的球面距离为 ABC 的距离为_________.
3 π ,则球心到平面 3
O
注:球内切于四面体: V B − ACD = ⋅S 侧 ⋅R ⋅ 3 + S 底 ⋅R =S 底 ⋅h
R
②外接球:球外接于正四面体,可如图建立关系式.
【典型例题】 典型例题】
例 1: (1)在棱柱中( ) A.只有两个面平行 C.所有的面都是平行四边形 B.所有的棱都平行 D.两底面平行,且各侧棱也互相平行
03多面体和旋转体

课题:多面体和旋转体要点点拨:一、 本章主要内容是多面体和旋转体的概念、性质、面积和体积计算公式。
公理5和公理6是求体积的依据。
“等底面积等高的两个锥体的体积相等”是进行等积变换的基础。
二、 多面体和旋转体的概念是本章的基础,要结合图形透彻理解概念。
例如图1中的几何体是棱柱吗?为什么?三、 注注意几个常用结论:1. 圆锥侧面展开图扇形圆心角:︒⋅=360lr θ;2. 台体中截面面积:2S 0下上+=S S ; 3. 射影面积:θcos ⋅=∆∆ABC D BC S S ,即ABCDBCS S ∆∆=θcos (其中DBC ∆是 ABC ∆在平面α上的射影三角形,θ是平面ABC 与平面DBC 所成二面角的平面角。
如图2)。
4. 球面距离的概念及求法:球面上两点的距离就是过这两点的大圆夹在这两点间的劣弧的长。
求半径为r 的球面上两点的距离,关键是求出这两点的球心角。
常见的有以下三种情况:① 两点在同一径线上,即两地的径度相同,此时只需知道两地的纬度数即可。
② 两点在同一纬线上,即两点的纬度相同,此时需知道两点的径度(如图3)。
由两点的径度可求两点的径度差,即角PIQ 的度数,由纬度数可求小圆的半径PI 、QI ,从而可求弦PQ 的长,进而在三角形POQ 中可求地心角POQ 。
③ 两点既不在同一径线上,又不在同一纬线上。
这种情况更复杂一些,我们不作要求。
求球面距离重点是第②种情况。
四、 常用方法:求面积、体积常用的方法有割补法(如求斜棱柱的侧面积、习题十四中5题);换位法(如课本上习题十三中的第6题、总复习题中第8题)求点面距离常用三棱锥的体积来求。
五、思想方法:1、转化与化归:空间问题平面化;台体问题锥体化。
2、运动变化的思想:柱、台、锥本是互不相同的三种几何体,但它们在一定的条件下相互转化,如当棱台的上底面扩大为与下底面全等且对应边平行时,就变为棱柱;当上底面缩为一个点时就变为棱锥。
相应地棱柱、棱台、棱锥的面积、体积公式之间也有相应的关系。
认识多面体与旋转体

作业
1、理解概念; 2、画出生活中的多面体 和旋转体各两个 并找出多面体的面、棱 、顶点以及旋转 体的轴和母线。
2、认识旋转体:
2、认识旋转体:
一条平面曲线绕定直线旋 转一周所围成的几何体叫做 旋转体,定直线叫做旋转体 的轴,这条曲线叫做旋转体 的母线。
轴
母线
课堂小结
面 空 多面体 :由若干个平面多边形围成的几何体 棱 顶点 间 几 何 母线 体 旋转体 :封闭的旋转面围成的几何体
轴
1、认识多面体:
D1 C1 B1
面
由若干个平面多边形围成 A1 的几何体叫做多面体 顶点
围成多面体的每个多边形叫 做这个多面体的面,两个面的公 共边叫做多面体的棱,棱和棱的 对角线 公共点叫做多面体的顶点。 连接不在同一面上的两 个顶点的线段叫做多面体的 A
D
C棱ຫໍສະໝຸດ 对角线。B1、认识多面体:
2、认识旋转体:
101认识空间几何体只考虑物体的形状和大小不考虑其他因素那么由这些物体抽象出来的空间图形就叫空间几何体由若干个平面多边形围成的几何体叫做多面体1认识多面体
认识多面体与旋转体
§ 10.1认识空间几何体
1、认识多面体:
只考虑物体的形状和大小, 不考虑其他因素,那么由 这些物体抽象出来的空间 图形就叫空间几何体
多面体与球知识点
多面体与旋转体知识要点归纳
二、空间几何体的三视图和直观图
1.中心投影:光由一点向外散射形成的投影,叫做中心投影。
中心投影的投影线交于一点。
2.平行投影:在一束平行光线照射下形成的投影,叫做平行投影。
投影线正对着投影面时,叫做正投影,否则叫做斜投影。
平行投影的投影线是平行的。
3.三视图
正视图:光线从几何体的前面向后面正投影,得到的投影图叫做几何体的正视图。
侧视图:光线从几何体的左面向右面正投影,得到的投影图叫做几何体的侧视图。
俯视图:光线从几何体的上面向下面正投影,得到的投影图叫做几何体的俯视图。
画法:长对正、高平齐、宽相等。
4.直观图(斜二测画法)
(1)画坐标轴:把已知图形中互相垂直的x轴和y轴,在直观图中画成
45(或
135)角的x'轴和y'轴,
(2)画底面:已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x'轴和y'轴的线段。
已知图形中平行于x轴的线段,在直观图中保持长度不
变,平行于y轴的线段,长度为原来的一半。
(3)画侧棱:侧棱的长度与原来几何体的侧棱的长度一样。
高中数学几何探究多面体与旋转体的性质

高中数学几何探究多面体与旋转体的性质在高中数学的几何领域中,多面体与旋转体是两个极为重要的概念,它们具有丰富而独特的性质,值得我们深入探究。
多面体,简单来说,就是由若干个平面多边形围成的几何体。
常见的多面体有四面体、六面体(也就是正方体和长方体)、八面体等等。
多面体的性质首先体现在其面、棱和顶点的数量关系上。
以最简单的四面体为例,它有四个面、六条棱和四个顶点。
而对于更复杂的多面体,我们可以通过欧拉公式来描述它们面、棱和顶点之间的关系,即:面数+顶点数棱数= 2。
多面体的表面积计算也是一个重要的方面。
对于规则的多面体,如正方体、长方体,我们可以直接通过其边长计算出各个面的面积,然后相加得到表面积。
而对于不规则的多面体,可能需要将其分割成若干个规则的部分,分别计算面积后再求和。
多面体的体积计算则需要根据其形状和特点选择合适的方法。
例如,正方体和长方体的体积可以通过长、宽、高的乘积来计算;三棱柱的体积是底面积乘以高;三棱锥的体积则是三分之一底面积乘以高。
再来看看旋转体。
旋转体是由平面图形绕着一条直线旋转所形成的几何体。
常见的旋转体有圆柱、圆锥、圆台、球等。
圆柱是由矩形绕着其中一边旋转一周得到的。
它的性质包括两个底面是全等的圆,侧面展开图是一个矩形。
圆柱的表面积由两个底面积和侧面积组成,底面积是圆的面积,侧面积则是矩形的面积,也就是底面圆的周长乘以圆柱的高。
圆柱的体积等于底面积乘以高。
圆锥是由直角三角形绕着其中一条直角边旋转一周得到的。
它只有一个底面,是一个圆,侧面展开图是一个扇形。
圆锥的表面积包括底面积和侧面积,侧面积的计算需要用到扇形的面积公式。
圆锥的体积是三分之一底面积乘以高。
圆台可以看作是一个大圆锥减去一个小圆锥得到的。
它有两个底面,侧面展开图是一个扇环。
圆台的表面积和体积的计算相对复杂一些,需要综合运用圆和圆锥的相关知识。
球是到定点的距离等于定长的点的集合。
球的表面积公式是4πr²,体积公式是三分之四πr³。
高考复习指导讲义第八章多面体和旋转体
高考复习指导讲义第八章多面体和旋转体一、考纲要求1. 理解棱柱、棱锥、棱台、圆柱、圆台、球及其有关概念和性质2. 掌握直棱柱、正棱锥、正棱台和圆柱、圆锥、圆台、球的表面积和体积公式(球缺体积公式不要求记住),并能运用这些公式进行计算•3. 了解多面体和旋转体的概念,能正确画出直棱柱、正棱住、正棱台、圆柱、圆锥、圆台的直观图.4. 对于截面问题,只要求会解决与几种特殊的截面(棱柱、棱锥、棱台的对角面,棱柱的直截面,圆柱、圆锥、圆台的轴截面和平行于底面的截面,球的截面)以及已给出图形或它的全部顶点的其他截面的有关问题.二、知识结构1. 几种常凸多面体间的关系2. 棱柱、棱锥、棱台的基本概念和主要性质名称棱柱直棱柱正棱柱图形1 a1 1i ■1 ;4 ■4 ¥.-1- —A.<■* k /定义有两个面互相平仃,而其余每相邻两个面的交线都互相平行的多面体侧棱垂直于底面的棱柱底面是正多边形的直棱柱侧棱平行且相等平行且相等平行且相等侧面的形状平行四边形矩形全等的矩形对角面的形状平行四边形矩形矩形平行于底面的截面的形状与底面全等的多边形与底面全等的多边形与底面全等的正多边形4.面积和体积公式下表中S表示面积,c'、c分别表示上、下底面周长,h表斜高,h'表示斜高,I表示侧棱长.(7)正四面体内任意一点到四个面的距离之和为定值(等于正直角四面体的性质 有一个三面角的各个面角都是直角的四面体叫做直角四面体四面体有下列性质:如图,在直角四面体 AOCB 中/ AOB=Z BOC M COA=90 , OA=a,OB=b,OC=c >则① 不含直角的底面 ABC 是锐角三角形;② 直角顶点O 在底面上的射影H 是厶ABC 的垂心;1③ 体积 V= abc ;6④ 底面△ ABC =— ,a2b 2b 2c 2c 2a 2 ;2⑤ S △ABC F S X BHC • S ^ABC ; ⑥ S 2 △ BO(=S △ AO +S △AO C=S △ ABC11 1+ +2 、c⑧外切球半径 R= 1 . a 2 b 2 c 2 ;2名称 侧面积(S 侧) 全面积(S 全) 体积(V) 棱 棱柱 直截面周长x lS 侧+2S 底S 底• h=S 直截面• h柱直棱柱 ch S底,h棱锥棱锥 各侧面积之和■— S 底• h3正棱锥 1『 —ch 2S 侧+S 底棱台:各侧面面积之和1—h(S 上底+S 下底棱 台正棱台1 -(c+c ' )h '2S 侧+S 上底+S 下底3+JS 下底S 下底)设正四面体的棱长为 a ,则这个正四面体的(1)全面积S全=3 a 2;⑵体积v=2123a ;(3)对棱中点连线段的长d=a ;2(4)相邻两面所成的一二面角 .6 a ; 4 1a =arccos -3(5)外接球半径R=(6)内切球半径r=.6a.12⑦OH 2b 25.正四面体的性质⑨内切球半径r= S A OB £ 吟七碎a +b + c6.旋转体 圆柱、圆锥、圆台、球的公式 (1)面积和体积公式圆柱圆锥 圆台 球S 侧 2 n rl n rl n (r 1+r 2)lS 全2 n r(l+r)n r(l+r) n (r 计r 2)1+ n2 2(r 1+r 2)24 n RVn r 2h(即 n r 2l)1 2 -n r h 31 — n32 2h(r 1+nr 2+r 2)4 3 —n R 3表中I 、h 分别表示母线、咼,r 表示圆柱、圆锥与球冠的底半径, r i 、「2分别表示圆台上、下底面半径,R 表示半径.(2)圆锥、圆台某些数量关系②圆锥 圆锥轴截面两腰的夹角叫圆锥的顶角如图,圆锥的顶角为3,母线与下底面所成角为 a ,母线为I ,高为h ,底面半径为r , 则pa =COS —=2a +E=90° 二彳2h=ls in a r-r ' =lcos a .③球的截面用一个平面去截一个球,截面是圆面.⑴ 过球心的截面截得的圆叫做球的大圆;不经过球心的截面截得的圆叫做球的小圆 (2) 球心与截面圆圆心的连线垂直于截面(3) 球心和截面距离d,球半径R,截面半径r 有关系:r= . R 2-d 2 .(3)球冠、球带和球缺① 球缺 球面被平面所截得的一部分叫做球冠, 截得的圆(圆周)叫做球冠的底,垂直于截面 的直径被截得的一段叫做相应球冠的高.球冠也可以看作一段圆弧绕经过它的一个端点的直径旋转一周所成的曲面 球冠的面积公式 若球的半径为 R,球冠的高为h ,则S 球冠=2 n Rh其中h 表示球冠的高,R 是球冠所在的球的半径. ② 球带 球面在两个平行截面之间的部分叫做球带 .球带也可以看作一段圆弧绕它所在的半圆的直径旋转一周所成的曲面 球带的面积公式 若球的半径为 R,球带的高为h ,则sin②圆台 别为r '、Pa =sin — 2r I *如图,圆台母线与下底面所成角为a ,母线为I ,高为h , 上、下底面半径分r ,则cosS球带=2 n Rh③球缺用一个平面截球体所得的部分叫做球缺,截面叫做球缺的底面,直径被截得的线段长叫做球缺的高•垂直于截面的球缺的体积公式若球的半径为R,球缺的高h,底面半径为r,则1 2V球缺=n h (3R-h)=3 1 2 2 n h(3r +h ) 6、知识点、能力点提示(一)多面体例1 如图,三棱柱ABC-ABC中,若E、F分别为AB AC的中点,平I 柱分成体积为V i、7的两部分,那么V i : w= ________________ .解:设三棱柱的高为h,上下底的面积为S,体积为V,则V=V+V a= Sh. ••• E、F分别为AB AC的中点,EBG将三棱S A AEF=—S,11 17M= —h(s+—S+ S )= Sh3 4 . ^12V2=Sh-V1 = —Sh,12••• W: Va=7 : 5.例2 一个长方体全面积是20cm2,所有棱长的和是24cm,求长方体的对角线长EG • tg / EFG= =1,/ EFG=45 . GF应选C.例4设正六棱锥的底面边长为 1,侧棱长为,5,那么它的体 积为()设正六棱锥的高为 h ,则h= ( . 5)2 -12 =2.V =1 X 口 X 2-3.34应选C.例5如果三棱锥S- ABC 的底面是不等边三角形,侧面与底面所成的二面角都相等, 且顶点S 在底面的射影 O 在厶ABC 内,那么O 是厶ABC 的()A.垂心B.重心C.外心D .内心解:作 OEL AB OF 丄 BC, OM 丄 CA •••/ SEO 2 SFO 玄 SMO, •••△ SEO^A SFO^^ SMO. • OE=OF=OM.• 0为厶ABC 的内心,应选 D.解:设长方体的长、宽、高、对角线长分别为2(xy+yz+zx)=20 依题意得:: 4(x+y+Z)=24 由② 2得:x 2+y 2+z 2+2xy+2yz+2xz=36 由③-①得x 2+y 2+z 2=16 即 I =16 •/ l=4(cm). 例3如图,正三棱锥 S — ABC 的侧棱和底面 点,那么异面直线 EF 与SA 所成的角等于() A.90 ° B.60 ° 解:取AC 的中点G,连结FG EG •/ FG// SA •••/ GFE 为异面直线EF 与SA 所成的角.1正三棱锥的棱长为 1,则GF=GE 二.2•••顶点到A 、B C 等距,△ ABC 等边 •顶点在底面 ABC 的射影0是厶ABC 的中心, 即"正三棱锥中两相对棱垂直”•••/ FGE=90 . xcm 、ycm zcm> lcm①边长相等,如果E 、F 分别为AB SC 的中C .450D.30从而SA 在底面上的射影丄 Bfc SA 丄 BC,A.6、3B.2、3D.2解:由已知可得正六棱锥的底面积例6 在棱长为1的正方体 ABC —A i BCD 中,M 和N 分别为AB 和BB 的中点,那么直 线AM 和CN 所成角的余弦值是()B.卫10C .35D.-5解:如图,设 P 为AA 的中点,Q 为AiM 的中点,贝U DP// CN PQ 〃 AM •••/ DPQ 是异面直线 AM 和CN 的成角. 在厶DPC 中, DP=. DA 2 AP 2PQ=! AM=! X 5 =丄,2 2 2 4DQ= DA 12 A 1Q 2 = DD 12 D 1A 12 A 1Q 2.33 4由余弦定理得cos / DPQ=兰PQ -DQ2 DP PQ(空)2 •(二)2-I-33)22 442逅西=25.又异面直线所成的角的范围是(0, •••直线AM 和CN 所成角的余弦值是90°).25.应选D.例7 已知三棱锥A — BCD 勺体积是S 和S.设面ABC 和面DBC 所成的二面角是V,棱BC 的长是a ,面ABC 和面DBC 的面积分别是 a ,那么 sin a = ________解:如图,作 AQL 面BCD 于 0,作0E ! BC 于E ,连结 AE.1由 V=—AO ・ S,3得 AO=g2S又 S 1=AE- BC,得 AE= 1 a由三垂线定理知,AE± BC•••/ AEC 是二面角 A — BC- D 的平面角. 即/ AEC a ,例8若正棱锥的底面边长与侧棱长相等,则该棱锥 一定不是() A.三棱锥B.四棱锥C.五棱锥D.六棱锥解:该棱锥一定不是正六棱锥 •否则设正棱锥 S- ABCDE 符合题设,则在△ SAB 和△ CAB 中(C 为顶点S 在底面的射影),•/ SA=SB=AB=CA=CB,• △ SAB^A CAB但厶CAB>^A SAB 在底面的射影,不可能••应选D.例9 如图,AB i C i — ABC 是直三棱柱,/ BCA= 90°,点 D 、F i 分别是 点,若BC=CA=CC 则BD 与AF i 所成的角的余 弦值是()• sin a =sin / AEC=ACAE 3 2S-|S 10C.旦10易知 FE=DB= B^2B 1D 1212 (J 2由/ BCA=90,得 AE=J AC 2 +CE 2AFjAA +AF 1 =十 +(》2 =乎 由余弦定理有cos / EFA=EF 2 FA 2 - AE 2 2 EF FA62.52'5 2p(I 5) rJ 6 <52 ----- -----2 2■ 30 10即BD 和AF 1成角的余弦值是 30 10解:设BC=CA=CC1.取BC中点E,连结EF、DF,贝U EF// BD/ EFA为BD和AF所成的角•应选A.例10 一个三棱锥,如果它的底面是直角三角形,那么它的三个侧面()A.必然都是非直角三角形B.至多只能有一个是直角三角形C.至多只能有二个直角三角形D.可能都是直角三角形解:如图,三棱锥P—ABC中,/ ABC=9C° , PA!面ABC.则PAL AC, PAL AB,△ PAC^D^ PAB都是直角三角形.又/ ACB=90,即ACL BC••• PC丄CB 即/ PCB=90 ,•••△ PCB也是直角三角形.应选D.例11侧棱长为3cm,底面边长为4cm的正四棱锥的体积为______________ cm3.解:由已知有底面对角线长为 4 2 cm.h= .,32 -(2.2)2=1(cm)1 12 16 3V=_ • h • S=—X1X4 = — (cm)3 3 3例12 已知长方体ABCD-A B' C' D'中,棱AA' =5, AB=12,那么直线B' C'和平面A BCD的距离是解:如图•/ B' C'// BC, B' C'二面A C, BC二面AC,• B' C'//面A C.•••点B到平面A BCD的距离即直线 B ' C'到平面A' BCD的距离.作B ' H丄A ' B 于H,又CBL面A ' ABB' , B ' H 二面A ' ABB' , B' H 商A ' B,所以B ' H± CB,从而B ' H丄平面A ' BCD .•/ B ' H- A ' B=B' A' • B' B,° BABB 12^5 60A'B 13 13即直线B ' C'到平面A' BCD的距离是一.13(二)旋转体例13如果圆台的上底面半径为5,下底面半径为R 中截面把圆台分为上、下两个圆台,它们的侧面积的比为 1 : 2,那么R=()A.10B.15C.20D.25解D.例14长方体一个顶点上三条棱的长度分别为面上,这个球的表面积是3, 4, 5,且它的8个顶点都在同一球A.20 .2 7tB.25 2 nC.50 nD.200 n解:设长方体的对角线长为 I ,球半径为R ,由已知及对称性知l=2R,l= . 32 42 52 =5 2,得 R=— . 2 . 2••• S 球=4 n R=50 n 应选C.例15 若母线长为4的圆锥的轴截面的面积为 8,则圆锥的侧面积为 ______ (结果中保1解:设轴截面SAB 贝U SA=SB=4,S SAE =8= SA- SB- sin / SBA 得 sin /ASB=1,2• / ASB=90 , AB=V 2 SA=4/2 , AB — —• - S 侧=n rl= n () - SA=n - 2打2 - 4=8 . 2 n .2例16如果等边圆柱(即底面直径与母线相等的圆柱)的体 积是16 n cm 3,那么它的底半径等于()D.2cm解: 16 n = n r - (2r )=2 n r ,得 r=2(cm ) 应选D.例17圆柱轴截面的周长1为定值,那么圆柱体积的最大值是()应选A.AB 和圆锥的轴的距离为 1,则该圆锥的体积为 ____________解:如图0为底面圆心,OCL AB 于C. 由OA=OE 得C 为AB 中点,A.4 勺 2 cmB.4cmC.2 -牛2 cm1 \ 3A.( )n61 1 ()3 n 4 4解:设r 为底半径,I 为母线.1 - 4r由 4r+2l=1,得 l=2B.( 1)3 n3C.( 1)3nD.V=n r 2l= - n8 1= n8(2r)(2r)(2l) 2r 2r 2l )3等号仅当2r=2l1丁)=81即r=l= 时成立.6(4r 2l7t3 1 3 1 3-()=()n . 36例18设圆锥底面圆周上两点 A 、B 间的距离为2,圆锥顶点到直线AB 的距离为.3 ,由SA=SB C为AB中点得SC± AB于C. • 0C=1,SC=. 3 ,AC=CB=1,so= .SO 2-OC 2 = . ( 3)2 -12 -.2 , 0B= ,0C 2 BC 2 = ,2 .二 V=1 n • OB • SO=1 n ( . 2 ) 2=红 n .3 3 3例19在一个实心圆锥体的零部件, 它的轴截面是边 长为10厘米的等边三角形,现要在它的整个表面镀上一层防腐材料,已知每平方厘米的工料价为0.1元,则需要费用_____ 元(n 取 3.2).解:设圆锥的底半径为 r,由已知有r=5cm,母线长为10cm.2 2S 全=n • 5 + n • 5 • 10=75 n = 240(cm )元•侧面展开圆心角为 240 °,该圆锥的体积是()n解:设圆锥底半径为r , 240° =4 n =N ,得3 I• h= . |2 - r222,2' 5 一(—)=一33• V=[ n r 2h=i n3 3(2)2•邑倍n3 3 81应选C.(三)综合题赏析 例21如图,平面 在直线 MN 上,/ ACM N BCN =45°, A-MN-B 是 60 求:(1)点A 到平面3的距离;(2) 二面角A — BC- M 的大小. 解:⑴作AH L 平面3于H HD£ MN 于 D, A — MN-B 的平面角,所以/ ADH=60 . 在 Rt △ ACD 中,/ ACD=45,/ ADC=90 , a 和3相交于直线MN 点 A 在平面a 上,点B 在平面3上, 的二面角,AC=1. • AD 』AC 』• 1 =)2 2 2在 Rt △ ADH 中,AH=AD sin Z ADH 「• sin60 °2•••工料价为 240X 0.仁24 例20圆锥母线长为I4 n81B.-8 n81 C. — n81D.1081由已知有2 r=3即点A 到平面3的距离是一6 ,4⑵设二面角A — BC- M 为0度,在等腰Rt △ ADC 中,由斜边 AC=1,得DC=ADW?2在 Rt △ ADH 中, DH=AD 2 - AH 2作HE!直线BC 于 E ,则/ AEH •••/ HCB =180° -( / HCD # BCN)=180 ° - / HCD-45,• sin / HCE=sin(45••• HE=HC sin / HCE=34tg / AEH=A H ^-6HE 3即0 =arctg —6 为所求.3例22 如图,ABCD 是边长为, ABCD GC=2. 求点B 到平面EFG 的距离. 解:连 GB GE GF FE 、FB , _1 o-V B —EFG = — dS A GFE3 _ 1 _ 2V B —EF(=Vs -BEF =— X GCS BEF = — S △ BEF 3 34的正方形,E 、F 分别是AB AD 的中点, 设点B 到面EFG 的距离为d.GC 垂直平面... d=GC SB EF =2J S^EF S.E FG在 Rt △ DHC 中, HC= CD 2 DH 2.10 4旦一面角A - BC- M 的平面角.+ /HCD) =几2/HCD+c,2(DH _ DC) = 32HC 4HCS A BEF=- S △AB F=-( -AF- AB)=2,2 2 2在△ EFG 中,GF=GE= GC2 CF? =2 、. 6 ,EF=2 .2 ,故它的周长之半1P=_(EF+FG+GE)=2. 6 +22•••S A EFG= P(P - EF)(P - EF)(P- GE) P(P-EF)(P-EF)(P-GE)=2 . 11••• d=2 2=U2,11 11即点B到平面EFG的距离是2.. 11例23 如图,在直三棱柱ABC-ABC1 中,/ ACB=90,/ BAC=30 , BC=1,AA=J6 ,M 是CG的中点.求证:AB丄AM证明:由题设知BC丄AC, BC丄CC• BC丄侧面AACC.连C1A,贝U C1A是B1A在面AACG上的射影•设AC 1与A 1M交于点D.在Rt △ A1B1G 中,BQ=1, / B1AC=Z BAC=30,得•电=6 = (2)A1C1:,3在Rt△ A1G M中,△^=二3= _2MC1yf66AA 1 A1C1A C二 1 1,又/ AAG=/ACM=90°,•••△AAC s^ ACM,得/ 3=Z 4由AA1 // CC,得/ 仁/2,•/ CDM M CAA= 90°,•AG 丄AM.由三垂线定理,得AB丄AM.例24如图,圆锥的轴截面为等腰Rt△ SAB Q为底面圆周上一点(1) 若QB的中点为C, OH L SC,求证OH丄平面SBQ⑵如果/ AOQ=60 , QB=2 3,求此圆锥的体积;晁⑶如果二面角A—SB— Q的大小为arctg ,求/ AOQ的大小.3q2 解:⑴连0C.•/ SQ=SB OQ=OB,QC=CB•••Q BL SC, QB 丄OC 得 OBL 面 SOC. •/ OH 面 SOC 得 QB1 OH 又 OHL SC, • OHL 面 SQB. ⑵连AQ.T Q 为底面圆周上的一点, AB 为直径,• AQL QB在 Rt △ AQB 中,/ QBA=30 , QB=2〕3cos30•••△ SAB 是等腰直角三角形.1• SO — AB=2,2 1 o8 • V 圆锥=n • OA • SO — n33⑶过Q 作QM L AB 于M.由于面SAB 丄面ABQ 得QM L 面SAB.作MPL SB 于P,连PQ 则由三垂线定理知 QPL SB. • / MPQ 是二面角 A — SB- Q 的平面角. -■.: 6/ MPQ=arctg 为已知,3设圆锥底半径为r, / AOQ a ,在 Rt △ MPB 中 , / PBM=45 , MB=r(1+cos a ),2• MP= r(1+cos a )2Rsin : _ . 6 sin :3----------------- ,即---231 cos :3r(1 cos :)• AB=2.3=4,故/ AOQ=60 2例25 如图,ABC — ABC 是正三棱柱,D 是AC 中点. (1)证明AB //平面DBC ;⑵假设AB L BC ,求以BC 为棱、以DBC 与CBC 为面的二面角a 的度数. 证明:⑴ 由于ABG — ABC 是正三棱柱,故四边形 BBCC 是矩形 连BQ 交BC 于E ,则B&EC,连DE. 在^ ABC 中,AD=DC 得 DE// AB . 又 AB 二面 DBC , DE 二面 DBC , • AB //平面 DBC.⑵作DF L BC 于F ,贝U DF 丄面BBCC ;连EF ,贝U EF 是ED 在面BBCC 上的射影. •/ AB 丄 BG ,又由(1)知,AB // DE • DEI BC ,从而 BC 丄 EF • ••/ DEF 是二面角a 的平面角.1设 AC=1,贝U DC=_.2•/△ ABC 是正三角形.•••在 Rt △ DCF 中,DF=DC sinC=二,41CF=DC■ cosC=—.4取BC 中点G,因BE=EC 故EG! BC. 在 Rt △ BEF 中, EF 2=BF - GF3 1 又 BF=BC-FC — ,GF=.44• EF=3 - - , 得 EF=—34 2 4即二面角a 为45□ 5例 26 如图,梯形 ABCD 中, AD// BC, / ABC —,AB=a,AD=3a, / ADC=arcsin ,PA 丄面2ABCD,PA=^:(1) 二面角P — CD-A 的大小(用反三角函数表示): (2) 点A 到平面PBC 的距离. 解:⑴作AE 丄直线CD 于 E 连PE.••• tg / DEF=D-EF也4^4=1. / DEF=45由PAL面ABCD据三垂线定理知PEI CD. •••/ PEA是二面角P—CD- A的平面角.在 Rt △ AED 中,AD=3a, / ADE=arcsin5••• AE=A D sin / ADE 旦卫5 PA 在 Rt △ PAE,中 tg / PEA=一AE:丄 PEA=arctg -3⑵作AF U PB 于H 由 PAL 面 ABCD 得 PB 丄 BC. 又AB 丄BC,得BC 丄面PAB 得BC 丄AH • AH!面PBC AH 的长为点 A 到面PBC 的距离 在等腰 Rt △ PAB 中,AH=)a.2•••点A 到平面PBC 的距离是a2例27 如图,已知 Rt △ ABC 的两直角边 AC=2 BC=3, P 为 斜边AB 上一点,现沿 C P 将此直三角形析成直二面角 A — PC- B , AB=. 7,求二面角P — AC-B 的大小.解:由已知 A — CP-B 是直二面角,作 BDL CP 于D,贝U BD 丄平面 ACP 作 DEI AC 于E , 则BE L AC / BED 是二面角 P — AG- B 的平面角•作AF 丄DC 于F ,连BF ,则/ AFB 丄.2设/ ACP a ,则/ BCP —- a ,2在Rt △ AFB 中A B'=AF 2+F B'=A F'+D ^+D F'=7■/ AF=2sin a ,CF=2cos a BD=3sin(90 ° - a )-3cos a CD=3sin(90 ° - a )-3cos a DF=CD-CF=3sin a -2cos a2 2 2• (2sin a ) +(3cos a ) +(3sin a -2cos a ) =7JT 解得a =—.4在 Rt △ BED 中即二面角 P — CD- A 的大小为arctg>5323 DE=CD sin a =3sin a =— 2tg Z BED=BD = . 2 .DE/•Z BED=arctg .一 2即二面角P — AC — B 的大小是arctg 2例28设三棱锥S — ABC 的底面为等腰直角三角形,已知该直角三角形的斜边 10, 三棱锥的侧棱 SA=SB=SC=1,求:(1) 顶点S 到底面的距离;(2) 侧棱SB 与底面所有角的大小(用反三角函数表示); (3) 二面角A — SB-C 的大小(用反三角函数表示); 解:如图(1 )作SO L 底面 ABC 由已知 SA=SB=S (知,O 为底面△ ABC 的外心, 又厶ABC 为直角三角形,故 O 为斜边AC 的中点. ••• SO=、SA 2 -AO 2 = ,132 -52 =12. 即顶点S 到底面的距离是12.⑵Z SOB 是 SB 与底面ABC 所成的角.SO 12 Z COB=arcsin=arcsin -SB13⑶作AD 丄SB 于D,连结CD. •/ SB 丄 AD,SB 丄 AC. • SB 丄平面ADC• CD! SB, Z ADC 是二面角 A — SB-C 的平面角• 易得 AB=BC=5 :2AD =DC 31325 • Z ADC=arccos(- )31325即二面角 A — SB — C 的大小是arccos(-).313例29 如图,在平行六面体 ABC —A1B1GD 中,AB=5. AD=4,AA=3,AB 丄 AD, Z AAB=/ AAD=—.3(1) 求证:顶点 A 在底面ABCD 的射影O 在Z BAD 的平分线上; (2) 求这个平行六面体的体积 V.解:(1)连AO,则AO 丄底面,作 OM L AB 于M , ON 丄AD 于N,连AM , AN , A O ,由三垂 线定理得 AM 丄AB, AN 丄AD又Z AAM Z AAN.AC 长为A• Rt △ ANA^ Rt △ A1MA••• AM=AN,得OM=ON.•••点O在/ BAD的平分线上⑵V=302四、能力训练(一)选择题1.长方体一个顶点上的三条棱的长分别是3, 4, 5,且它的八个顶点都球的表面积是A.20 2 nB.25 2 nC.50 nD.200 n 2. 两球体积和是 A.33. 地球表面北纬 距离与地球表面AA.3 : 24. 已知圆锥内有12 n ,且两球大圆周长的和是B.26n ,则这两个球半径的差是C.1() D.0.5 60°圈上有A 、B 两点,它们的经度差为 180°, A 、B 两点沿纬度圈的B 两点最短距离的比是()B.2 : 3C.3 : 4D.4: 3(球冠部分)之比为18: 5,则圆锥母线间最大夹角为 ()55A.2arccosB.2arcs in66C.2arcsin -6D. n1 -arcs in65.球O 的半径R A B 、C 为球面上三点,A 与B 、A 与C 的球面距离为2球面距离为二R ,则球O 在二面角B-OA-C 内的部分的体积是()31 A.-9B. 1 n R 33D.A n R 3276.三棱锥A-BCD 的高AH=3.3 a ,且H 是底面△ BCD 的垂心,若 AB=AC 二面角 A-B C-D为60°,ABC 的重心,贝U HG 的长为()A. ■. 10 a C. ,6a7.底面半径为R 高为H 的圆锥的内接正方体的棱长为H 2R、2RHB.H R-A /'2RHC. ---------------H 2RD.、2RHH • 3R8. 棱锥P-ABCD.90ABCD 且PB=2PA 那么侧面 ABP 与10. 三棱锥一条棱长为x,其余各条棱长都等于1,则体积F (x )最大时,x 的取值是() C.V2(二)填空题11. 已知球面上A 、B C 三点所在的截面与球心距离是球半径的一半, 则球面面积是 ____________ .12. 已知球的两个平行截面的面积分别为 5 n 和8 n,它们位 于球心的同一侧,且相距为1,则这个球的半径是13. 一个正方体的所有顶点都在球面上,若这个球的体积是 V,则这个正方体的体积是14. 把一个木制的棱长为 1的正方体镟成一个尽可能大的球,则镟去部分的体积是15. 把一个大金属球 表面涂漆,需油漆 2.4kg ,若把这个金属球熔化,制成 6 4个半径相等的小金属球(设损耗为零),将这些小金属球表面涂漆,需用油漆 __________ .16. 在长方体 ABCD-ABQD 中,已知 AB=2, AA=AD=1则截面 ABC 和ABQ 所成的二面 角等于 ________ .17. 棱锥的底面是斜边为 C,锐角为30°的直角三角形,各侧棱与底面都成 45°角,则它的体积是 _________ .18. 如果一个球的外切圆锥的高是这个球半径的 3倍,那么圆锥侧面积和球面积的比为19. _____________________________________________正四棱台ABCD-ABQD ,上底AB=1,下底AB 1=2,侧棱AA 与底面成60。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多面体与旋转体一、棱柱1、 由几个多边形围成的封闭的几何体叫做多面体。
2、 两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱。
棱柱的互相平行的两个面叫做棱柱的底面,其余各面叫做棱柱的侧面,相邻的两个侧面的公共边叫做棱柱的侧棱,两个底面间的距离叫做棱柱的高。
棱柱的基本性质:(1) 棱柱的侧面都是平行四边形。
(2) 棱柱的两个底面及平行于底面的截面都是全等的多边形。
3、 侧棱与底面不垂直的的棱柱叫做斜棱柱。
侧棱与底面垂直的棱柱叫做直棱柱。
底面是正多边形的直棱柱叫做正棱柱。
性质:(1) 直棱柱侧面都是矩形。
(2) 直棱柱侧棱与高相等。
(3) 正棱柱的侧面都是全等的矩形。
4、 底面是平行四边形的棱柱叫做平行六面体。
底面是矩形的直棱柱是长方体。
长方体的对角线平方等于三边长的平方和。
5、 夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任何平面所截得的两个截面的面积都相等,那么这两个几何体的体积相等。
6、 h V S =⋅棱柱底. 二、棱锥1、有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
棱锥的这个多边形的面叫做底面,其余各个三角形的面叫做侧面。
相邻的两个侧面的公共边叫做棱锥的侧棱。
各个侧面的公共顶点叫做棱锥的顶点,顶点到底面的距离叫做棱锥的高。
棱锥的基本性质:如果一个棱锥被平行于底面的一个平面所截,那么: (1) 侧棱和高被这个平面分成比例线段;(2) 截面和底面都是相似多边形;(3) 截面面积与底面面积之比,等于顶点到截面与顶点到底面的距离平方之比。
2、如果一个棱锥的底面是正多边形,且顶点在底面的射影是底面的中心,这个棱锥叫做正棱锥。
正棱锥的性质:(1) 各侧棱相等,各侧面都是全等的等腰三角形。
(2) 正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形。
正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
3、各个面都是全等的等边三角形的三棱锥称为正四面体。
正多面体:4、h 3V S =⋅棱柱底三、圆柱、圆锥与球将矩形ABCD (及其内部)绕其一条边AB 所在直线旋转一周,所形成的几何体叫做圆柱,AB 所在直线叫做圆柱的轴,线段AD 和BC 旋转而成的圆面叫做圆柱的底面,线段CD 旋转而成的曲面叫做圆柱的侧面,CD 叫做圆柱侧面的一条母线,圆柱的两个底面间的距离(即AB 得长度)叫做圆柱的高。
2S rh π=侧,222S rh r ππ=+全,2V r h π=将直角三角形ABC (及其内部)绕其一条直角边AB 所在直线旋转一周,所形成的几何体叫做圆锥,AB 所在直线叫做圆锥的轴,点A 叫做圆锥的顶点,直角边BC 旋转而成的圆面叫做圆锥的底面,斜边AC 旋转而成的曲面叫做圆锥的侧面,斜边AC 叫做圆锥侧面的一条母线,圆锥的顶点到底面间的距离(即AB 的长度)叫做圆锥的高。
S rl π=侧,2S rl r ππ=+全,213V r h π=将圆心为O 的半圆(及其内部)绕起直径AB 所在的直线旋转一周,所形成的几何体叫做球,半圆的圆弧所形成的曲面叫做球面,易知,点O 到球面上任意点的距离都相等,把点O 称为球心,把原半圆的半径和直径分别称为球的半径和球的直径。
平面上的两点之间线段最短,该线段的长度就是两点之间的距离,类似地,要定义球面上两点之间的距离,也应该在球面上找到联结两点的最短路径,该路径的长度就是球面上亮点之间的距离。
可以证明,在联结球面上亮点的路径中,通过该两点的大圆劣弧最短,因此该弧的长度就是这两点的球面距离。
24S r π=表,343V r π=一、选择题1、正四棱锥的侧棱长为32,侧棱与底面所成的角为︒60,则该棱锥的体积为( )A .3B .6C .9D .18【解:如图,3sin 602332PO PC =︒==;21cos 60233,226,16.3ACP ABCD AC OC PC S BD OC OC V S PO -=︒=====∴=⋅= 故选B 】2、已知三棱柱111ABC A BC -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( )A .13BCD .23【解:B ,由题意知三棱锥1A ABC -为正四面体,设棱长为a,则1AB =,棱柱的高1AO ===(即点1B 到底面ABC 的距离),故1AB 与底面ABC 所成角的正弦值为113AO AB =】ABCDPO601A 1B 1C ABCOE22V a h⇒==】4、设M、N是球O的半径OP上的两点,且NP MN OM==,分别过N、M、O作垂直于OP的面截球得三个圆,则这三个圆的面积之比为:(A)3:5:6(B)3:6:8(C)5:7:9(D)5:8:9【解:由题知,M、N是OP的三等分点,三个圆的面积之比即为半径的平方之比.在球的轴载面图中易求得:2228()39R RR-=,22225()39R RR-=,故三个圆的半径的平方之比为:22285::99R R R,故本题选D.】5、长方体1111ABCD A B C D-的各顶点都在半径为1的球面上,其中1::AB AD AA=,则两,A B点的球面距离为( )A.4πB.3πC.2πD.23π【解:设12,,AB a AD a AA===,则有()222222128R AC AB AD AA a==++=,R∴=,即有,AO BO==2,,2AB a AOBπ=∴∠=而=1.2R ABπ又因为,故的球面距离为】6、一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是O PM NA1ABCOD1B1C1DOPA CABCD【解:设底面边长为a,231,32AO a a ==∴= 133=224S a a ∴=底,1334P ABC V S PO -∴==底。
故选C 。
】7、两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD 与正这样的方体的某一个平面平行,且各顶点...均在正方体的面上,则几何体体积的可能值有(A )1个 (B )2个 (C )3个 (D )无穷多个【解:由于两个正四棱锥相同,所以所求几何体的中心在正四棱锥底面正方形ABCD 中心,由对称性知正四棱锥的高为正方体棱长的一半,影响几何体体积的只能是正四棱锥底面正方形ABCD 的面积,问题转化为边长为1的正方形的内接正方形有多少种,所以选D.】8、设地球半径为R ,北纬030圈上有,A B 两地,它们的经度相差0120,则这两地间的纬度线的长为( )(A )23R π (B )6Rπ(C )3R(D )3Rπ 【解:cos302r R R =︒=, 2333RAB r ππ∴=两地的纬线长为。
提示:这里要求掌握经度和纬度这两个概念。
】二、填空题9、下面是关于三棱锥的四个命题:①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥. ②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥. ③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.④侧棱与底面所成的角相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥. 其中,真命题的编号是_____________.(写出所有真命题的编号)【解:正确的命题为①④,②的反例:△ABC 为正三角形,侧面中AB=AP=AC ,PB=PC≠AP ,满足侧面都是等腰三角形,但不是正三棱锥。
③的反例:△ABC 为正三角形,三个侧面的高相等,所以满足侧面积都相等,但顶点P 在底面的射影O 落在△ABC 外,是△ABC 的旁心,而不是中心,所以P-ABC 是斜三棱锥。
】10、平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件: 充要条件①两组相对侧面分别平行;一组相对侧面平行且全等; 充要条件② 对角线交于一点;底面是平行四边形; (写出你认为正确的两个充要条件)11、(09上海高考题)已知三个球的半径321,,R R R 满足32132R R R =+,则它们的表面积321,,S S S 满足的等量关系是 .【解:因为32132R R R =+===】12、若一条直线与一个正四棱柱各个面所成的角都为α,则cos α=______【解:不妨认为一个正四棱柱为正方体,与正方体的所有面成角相等时,为与相交于同一顶点的三个相互垂直的平面所成角相等,即为体对角线与该正方体所成角.故cos α==.】 A1A BCD1B 1C 1D APCAPC13、圆柱的侧面展开图是边长为2π和3π的矩形,则圆柱的体积为 。
【解:(1)若底面周长为2π,则圆柱高为3π,圆柱的体积为23π; (2)若底面周长为3π,则圆柱高为2π,圆柱的体积为292π;】14、若圆锥的全面积是底面积的三倍,则它的侧面展开图的圆心角是 。
【解:如图,设底面半径为r ,侧面母线为a ,则底面积为2r π,侧面积为ra π,所以表面积2()S r ra r r a πππ=+=+,又2()3r r a rππ+=,则2a r =,所以侧面展开图的圆心角为222r rarπππ==。
】15、已知半径为2的半球内有一内接正六棱锥P ABCDEF -,则此正六棱锥的侧面积是________.【解:显然正六棱锥P ABCDEF -的底面的外接圆是球的一个大圆,于是可求得底面边长为2,又正六棱锥P ABCDEF -的高依题意可得为2,依此可求得16、(2010春考题)在右图所示的斜截圆柱中,已知圆柱底面的直径为40cm ,母线长最短50cm ,最长80cm ,则斜截圆柱的侧面面积S=______cm 2。
【解:2600π;】17、若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为60°的菱形,则该棱柱的体积为POraPAB【解:如图,依题意可知,1A ABC -为棱长为2的正四面体,过点1A 作AB 的高,与AB 交于D,11A D A A ∴==1123AO A D AO ∴==∴==111112223ABCV SA O AB A D A O ∴===⨯= 】18、有两个相同的直三棱柱,高为a2,底面三角形的三边长分别为)0(5,4,3>a a a a 。
用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,表面积最小的是一个四棱柱,则a 的取值范围是__________。
【解:两个相同的直三棱柱并排放拼成一个三棱柱或四棱柱,有三种情况:四棱柱有一种,就是边长为a 5的边重合在一起,表面积为242a +28,三棱柱有两种,边长为a 4的边重合在一起,表面积为242a +32,边长为a 3的边重合在一起,表面积为242a +36 ,两个相同的直三棱柱竖直放在一起,有一种情况表面积为122a+48。
