线性系统的能控性和能观性
第三章 线性控制系统的能控性和能观性PPT课件

.
1
在现代控制理论中,能控性和能观性是两个重 要的概念,是卡尔曼(Kalman)在1960年首先提出 来的,它是最优控制和最优估计的设计基础。
现代控制理论是建立在用状态空间描述的基 础上的。状态方程描述了输入u(t)引起状态x(t)的 变化过程;输出方程则描述了由状态变化引起的输 出y(t)的变化。
可以看出,系统中某一状态的能控和系统的 状态完全能控在含义上是不同的。
.
7
几点说明:
1) 在线性定常系统中,为简便计,可以假定初始 时刻t0=0,初始状态为x(0),而任意终端状态就指 定为零状态,即 x(tf )0
2) 也可以假定x(t0)=0,而x(tf)为任意终端状态, 换句话说,若存在一个无约束控制作用u(t),在 有限时间[t0, tf]能将x(t)由零状态驱动到任意x(tf)。 在这种情况下,称为状态的能达性。
.
13
b b 1b 2b n T
为简明起见,下面举三个具有上述类型的二阶 系统,对能控性加以剖析。
x 0 1 0 2 x b 0 2 u ; yc1 c2x
(3-3)
x 0 1 1 1 x b 0 2 u; yc1 c2x
(3-4)
x 0 1 1 1 x b 0 1 u; yc1 c2x
具有约旦标准型系统矩阵的单输入系统,状态
方程为
x Λ b xu
(3-1)
或
x J b xu
(3-2)
1
0
2
Λ
3
0
n
12 3 n 即n个根互异
.
12
1 1
1 1
0
0
1
1
m 1
0
能控性与能观性

假使输出矩阵C中有某一列全为零,譬如说第2列中c12, c22, …, cm2均为零,则在 t y(t)中将不包含 e 2 x20这个自由分量,亦即不包含 x2(t)这个状态变量,很明显,这 个x2(t)不可能从y(t)的测量值中推算出来,即x2(t)是不能观的状态。
系统是状态完全能控的
x 2 1 x2 b2u y c1 c2 x
1 1 b1 x x u; 0 0 1
对于式(3-5)的系统
x 1 1 x1 x2 b1u x 2 1 x2
x2不受u(t)的控制,而为不能控的系统。
对式(3-3)的系统,系统矩阵A为对角线型,其标量微分方程形式为
x 1 1 x1
x 2 2 x2 b2u
x 2
x 1
1 1 0 x x u; 0 1 b2
对于式(3-4)的系统
y c1 c2 x
x 1 1 x1 x2
c13 c23 c33
1 2 1t 1t 1t e x10 te x20 t e x30 2! x1 (t ) 1t 1t e x20 te x30 这时,状态方程的解为 x(t ) x2 (t ) x ( t ) 3 1t e x 30
从而
y1 (t ) c11 c12 y (t ) y2 (t ) c21 c22 y3 (t ) c31 c32
第4章(1)线性控制系统的能控性和能观性

第4章(1)线性控制系统的能控性和能观性第四章线性控制系统的能控性和能观性在现代控制理论中,能控性(Controllability)和能观性(Observ- ability)是两个重要的概念,它是卡尔曼(Kalman)在1960年提出的,是最优控制和最优估计的设计基础。
能观(测)性针对的是系统状态空间模型中的状态的可观测性,它反映系统的内部状态x(t)(通常是不可以直接测量的)被系统的输出量y(t)(通常是可以直接测量的)所反映的能⼒。
能控性严格上说有两种,⼀种是系统控制输⼊u(t)对系统内部状态x(t)的控制能⼒,另⼀种是控制输⼊u(t)对系统输出y(t)的控制能⼒。
但是⼀般没有特别指明时,指的都是状态的可控性。
所以,系统的能控性和能观性研究⼀般都是基于系统的状态空间表达式的。
4-1 线性连续定常系统的能控性定义对于单输⼊n 阶线性定常连续系统bu Ax x+= 若存在⼀个分段连续的控制函数u(t),能在有限的时间段 []f t t ,0内把系统从0t 时刻的初始状态()0t x 转移到任意指定的终态()f t x ,那么就称系统在0t 时刻的状态()0t x 是能控的;如果系统每⼀个状态()0t x 都能控,那么就称系统是状态完全可控的。
反之,只要有⼀个状态不可控,我们就称系统不可控。
对于线性定常连续系统,为简便计,可以假设00=t ,()0=f t x ,即00=t 时刻的任意初始状态()0x ,在有限时间段转移到零状态()0=f t x (原点)。
4-2线性连续定常系统的能控性判别4-2-1具有约旦标准型系统的能控性判别 1.单输⼊系统具有约旦标准型系统bu x x+Λ==Λn λλλλ0000000000000321n λλλλ≠≠≠≠ 321即为n 个互异根或bu Jx x+==++n m m J λλλλλλ000000000000000100000000121111m 个重根1λn-m 个互异根n m m λλλ≠≠≠++ 21 例:分析下列系统的能控性(1)u b x x+??=221000λλ[]x c c y 21=解:?=111x xλ 1x 与u ⽆关,即不受u 控制 ?+=u b x x2222λ 2x 为能控状态该系统为状态不完全能控,因⽽为不能控系统。
能控性和能观测性

0 0
0 0
−1 0
0 2
0 1
0 0
0⎥⎥ 0⎥
x
+
⎢⎢0 ⎢0
0 0
04⎥⎥⎥u
⎢
⎥⎢
⎥
⎢ 0 0 0 0 0 2 0 0⎥ ⎢1 2 0⎥
⎢ ⎢
0
0
0
0 0 0 2 0⎥⎥
⎢⎢0 3 3⎥⎥
⎢⎣ 0 0 0 0 0 0 0 5⎥⎦ ⎣⎢3 0 0⎥⎦
解:此为8阶系统,n=8
19
S=
⎡0 0 0 1 0 0 −2 0 0 3 0 0 −4 0 0 5 0 0 −6 0 0 7 0 0 ⎤
再证必要性,即已知系统能控,证明rankS=n。
同样采用反证法假设rankS<n,表明S的各行线性相关,那么一
定存在一个非零的向量α使
α T [B AB L An−1B] = 0,
α T Ai B = 0,i = 1,2,Ln −1
12
α T Ai B = 0, i = 1,2,Ln −1
根据凯莱-哈密尔顿定理 α T Ai B = 0, i = n, n +1,L
α T e−At B = α T [I − At + 1 A2t 2 − 1 A3t3 + L]B
2!
3!
= α T B −α T ABt + 1 α T A2Bt 2 − 1 α T A3Bt 3 + L = 0
2!
3!
∫t1 [α T e−Aτ B][α T e−Aτ B]T dτ = 0
0
∫ ∫ t1 α T e−Aτ BBT e−ATταdτ = α T t1 e−Aτ BBT e−ATτ dτα
第3章_线性控制系统的能控性和能观性

证明 定理3.3-1
y(t1) 0(t1)Im 1(t1)Im n1(t1)Im C
y(t2) 0(t2)Im
1(t2)Im
n1(t2)ImC
A x(0)
y(tf)
0(tf)Im
1(tf)Im
n1(tf)ImCnA 1
上式表明,根据在(0,tf)时间间隔的测量值 y(t1),y(t2),…,y(tf),能将初始状态x(0)唯一地 确定下来的充要条件是能观测性矩阵N满秩。
4)不可控
18
3.1.2 线性定常系统的能控性判别
3.可控性约当型判据
J1
设
x AxBu
J2
xu
Jk
若 A为约当型,则状态完全可控的充要条件是:
每一个约当块的最后一行相应的 阵中所有的行 元素不全为零。(若两个约当块有相同特征值,此
结论不成立。)
精选可编辑ppt
19
3.1.2 线性定常系统的能控性判别
➢本章结构
• 第3章 线性控制系统的能控性和能观性 ✓3.1 能控性 ✓3.2 能观性 ✓3.3 能控性与能观性的对偶关系 ✓3.4 零极点对消与能控性和能观性的关系
精选可编辑ppt
1
引言
状态空间模型建立了输入、状态、输出之间的关系
u
x
y x Ax Bu
y Cx Du
状态方程反映了控制输入对状态的影响;输出方程 反映系统输出对控制输入和状态的依赖
10
3.1 能控性
3.1.2 线性定常系统的能控性判别
证明 定理3.1-1
n1
x(0) AkBk B AB A2B k0
0
An1B1
n1
若系统是能控的,那么对于任意给定的初始状态x(0)都
第3章 能控性和能观性

t 0, t 1
0
W (0, t1 ) 奇异,
与已知条件矛盾
rank W n
说明:1.
在应用格拉姆矩阵判据时计算矩阵指数
函数以及积分的计算量非常大,所以这一判据主要 用在理论分析中。 2. 矩阵W可以利用Matlab函数ctrb(A,B)来计算, 不过其计算在数值上容易导致病态,所以建议使用
1.2 可观性
[例]电路 ((信息)观测的可能性)
如果 u 0,不管电容储存了多少电荷, 由于 y 0 无法知道状态(信息) 图 假定输入恒为0
u
R
R C R
y
R
(信息)观测的可能性
y ce At x0 (未知量
有输入时
At t
(u 0) x0 )
y y ce
0
y ce x0 ce A(t )bu( )d
, T An1B 0
B AB
T
系统不可控。
n1 T A B W 0 rank W n
充分性:证明过程与上相反。
所以输入维数增加 那么特征值 i 不可控。 约当标准形判据 线性定常系统可控的充分必要条件是 系统可控的可能性增加。
T i T i
t 0 A( t )
bu ( )d 可将它看做输出
已知
可观性的直观意义和定义
所谓系统可观是指通过观测系统的外部变量即输 入输出变量就能正确地知道系统的内部状态。 定义 如果基于有限长的输入输出数据:
u(t ), y(t ),
0 t T
能唯一地确定系统的初始状态 x0 ,则称点 x0 可观 测。进一步,如果状态空间中任意的初始状态 x0 都可观测,则称系统可观测。
线性系统能控性能控性与能观性

时变系统
能达性定义及判据 能观性定义及判据
①Gram 判据 ①Gram 矩阵非奇异
离散时间线性
能控性判据 ①Gram 判据②秩判据
rank H GH G n 1 H n
时不变系统
能达性判据 能观性判据 ①Gram 判据②秩判据 ①Gram 判据②秩判据
三、连续时间线性时不变系统的结构分解
* * 于物理构成,问题的提法;取输出反馈控制律 u Fy v ,对任意给定期望极点组 1 , * 2 , n ,确定
一个反馈矩阵 F ,使导出的输出反馈闭环系统
x A BFC x Bv y Cx
的所有特征值实现期望的配置,即有 i A BFC * i , i 1,2, , n 。 输出反馈局限性: (1)对完全能控连续时间线性时不变受控系统,输出反馈一般不能任意配置系 统全部极点。 (2)对完全能控 n 维 SISO-LTIC 受控系统,输出反馈只能使闭环极点配置到根轨迹上。 扩大输出反馈配置功能的一个途径是采用动态输出反馈, 即在采用输出反馈同时附加引入补偿器。 可以证明,通过合理选取补偿器机构和特性,可对带补偿器输出反馈系统的全部极点进行任意配置。 4.2 状态反馈镇定问题 4.2.1 所谓的镇定问题就是,对给定的线性时不变受控系统,确定状态反馈控制律 u Kx v ,使 导出的状态反馈闭环系统 x A BK x Bv 为渐进稳定,即闭环系统特征值均具有负实部。 镇定问题实质上属于极点区域配置问题,对于镇定问题,系统闭环极点的综合目标,并不要求配 置于任意指定期望位置,而只要求配置于复平面的左半开平面上。 4.2.2 可镇定条件
4.1.2 极点配置问题的算法 [极点配置定理] 对 n 维连续时间线性时不变系统,系统可通过状态反馈任意配置全部 n 个极点 即特征值的充分必要条件是 A, B完全能控。 [多输入状态反馈阵算法] 给定 n 维多输入连续时间时不变受控系统 A, B 和一组任意的期望闭
线性系统理论(第四章)线性系统的能控性和能观测性

An1B] T S 0
rankS n 系统状态不能控,与已知矛盾。
同理可证充分性。
例 线性定常连续系统的状态方程如下,判断其能控性。
0 1 0 0 0 1
0 0 1 0 1 0
x
x u0 0 0 1 Nhomakorabea0
1
0 0 5 0 2 0
系统的特征值: 1 2 0 ,3 5 ,4 5
当 1 2 0 时:
② 系统能控:如果状态空间中的所有非零状态都是在 t0 时 刻可控的,则称系统在 t0 时刻是完全可控,简称系统在 时刻 t0 可控。如果系统对任意初始时刻 t0 完全可控, 则称系统一致可控。
③系统不完全能控:如果对给定得初始时刻 t0 Tt ,如果状
态空间中存在一个或一些非零状态在 t0 时刻是不可控的,则 称系统在 t0 时刻是不完全可控的,也称系统是不可控的。
x0TWC (0, t1)x0
t1 0
x0T
eAt
BBT
eAT t
x0
dt
t1 0
BT
eAT t
x0
2
dt
0,
BT eATt x0 0
x(t1) eAt1 x0
t1 eA(t1t) Bu(t) d t 0
0
x0
et1 -At1
0
Bu(t) d t
x0
2
x0T x0
[
et1 -At1
An1B] T S 0
T Ai B 0; i 0,1,2, ,n 1 应用凯-哈定理 An , An1 均可表示为A 的 n-1 阶多项式
T Ai B 0; i 0,1,2,3,
对 t1 0
(1)i T
Ai t i i!
现代控制理论基础_周军_第三章能控性和能观测性

3.1 线性定常系统的能控性线性系统的能控性和能观测性概念是卡尔曼在1960年首先提出来的。
当系统用状态空间描述以后,能控性、能观测性成为线性系统的一个重要结构特性。
这是由于系统需用状态方程和输出方程两个方程来描述输入-输出关系,状态作为被控量,输出量仅是状态的线性组合,于是有“能否找到使任意初态转移到任意终态的控制量”的问题,即能控性问题。
并非所有状态都受输入量的控制,有时只存在使任意初态转移到确定终态而不是任意终态的控制。
还有“能否由测量到的由状态分量线性组合起来的输出量来确定出各状态分量”的问题,即能观测性问题。
并非所有状态分量都可由其线性组合起来的输出测量值来确定。
能控性、能观测性在现代控制系统的分析综合中占有很重要的地位,也是许多最优控制、最优估计问题的解的存在条件,本章主要介绍能控性、能观测性与状态空间结构的关系。
第一节线性定常系统的能控性能控性分为状态能控性、输出能控性(如不特别指明便泛指状态能控性)。
状态能控性问题只与状态方程有关,下面对定常离散系统、定常连续系统分别进行研究(各自又包含单输入与多输入两种情况):一、离散系统的状态可控性引例设单输入离散状态方程为:初始状态为:用递推法可解得状态序列:可看出状态变量只能在+1或-1之间周期变化,不受的控制,不能从初态转移到任意给定的状态,以致影响状态向量也不能在作用下转移成任意给定的状态向量。
系统中只要有一个状态变量不受控制,便称作状态不完全可控,简称不可控。
可控性与系统矩阵及输入矩阵密切相关,是系统的一种固有特性。
下面来进行一般分析。
设单输入离散系统状态方程为:(3-1)式中,为维状态向量;为纯量,且在区间是常数,其幅值不受约束;为维非奇异矩阵,为系统矩阵;为维输入矩阵:表示离散瞬时,为采样周期。
初始状态任意给定,设为;终端状态任意给定,设为,为研究方便,且不失一般性地假定。
单输入离散系统状态可控性定义如下:在有限时间间隔内,存在无约束的阶梯控制信号,,,能使系统从任意初态转移到任意终态,则称系统是状态完全可控的,简称是可控的。
第4章(3) 线性控制系统的能控性和能观性

4-6线性系统的结构分解能控子空间+不能控子空间能观子空间+不能观子空间4-6-1按能控性分解设线性定常系统⎩⎨⎧=+=CxyBuAxx是状态不完全能控的,其能控性判矩阵:[]BAABBM n1-=的秩()nnMrank<=1则存在非奇异变换zRxc=变换为⎩⎨⎧=+=zCyuBzAz其中()1121nnnzzz-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=()()11112212111nnnnnnAAAARRAcc--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-,()11110nnnBBRBc-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-[]()1121nnnCCCRCc-==[]n n c R R R R R 121=前1n 个列矢量为M 中1n 个线性无关的列,另外1n n -个列矢量,在确保c R 非奇异的条件下,完全是任意的。
分解为能控的1n 维子系统:21211111z A u B z A z++= 和不能控的1n n -维子系统:2222z A z =例:设线性定常系统如下,判别其能控性,若不是完全能控的,试将该系统按能控性分解。
u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=011310301100 []x y 210-=解:(1)判别能控性[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==2103111012b A Ab bM因为 ()n M rank =<=32,所以,系统是不完全能控的。
(1) 构造非奇异变换阵c R⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110011001c R (第三列的元素任意选取,确保c R 为非奇异)非奇异变换 z R x c =u z u z bu R z AR R zc c c ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=+=----0011002211100111100110011100110013103011001100110011111[]z z CR y c 211--==分解为二维能控子系统:能控标准Ⅱ型u z z z ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡--=01212110211 和一维不能控子系统:[]221z z-= 4-6-2按能观性分解设线性定常系统 ⎩⎨⎧=+=Cxy Bu Ax x是状态不完全能观的,其能控性判矩阵:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=-1n CA CA C N 的秩 ()n n N rank <=1 则存在非奇异变换 z R x 0=变换为 ⎩⎨⎧=+=z C y uB z A z其中 ()1121n n n z z z -⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=()()11112221110100n n n n n n A A A AR R A --⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==- , ()112110n n n B B B R B -⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-[]()111n n n C CR C c -== , ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=-''12'110'n n R R R R R前1n 个行矢量为N 中个1n 个线性无关的行,另外1n n -个行矢量,在确保1-R 非奇异的条件下,完全是任意的。
第三章线性系统的能控性与能观性2

Hale Waihona Puke .解:Sc [b Ab]
Sc b Ab b1 b2
1b1 b1b2 (2 1 ) 2b2
0
如果rank Sc =2, 则必须要求 b1 0, b2
4. 定理3:设 x Ax Bu , 若A为约当标准形,且每个约当块所 对应的特征值均不相同,则状态完全能控 的充要条件是:
且
ri1 ri 2 rii i
由 Bik (k 1,2,, i ) 的最后一行组 成的矩阵:
bri1 r bri 2 对i 1, 2, , l均为行线性无关 Bi bri i 则系统能控
例:设 x Ax Bu ,已知
第三章 线性系统的能控性和能观性
3.1 能控性的定义 3.2 线性定常系统的能控性判别 3.3 线性定常连续系统的能观性 3.4 离散时间系统的能控性与能观性 3.5 时变系统的能控性与能观性 3.6 能控性与能观性的对偶关系 3.7 状态空间表达式的能控标准型与能观标准型 3.8 线性定常系统结构分解 3.9 传递函数矩阵的实现 3.10传递函数中零极点对消与状态能控性、能观性之间 的关系
定理2:若
x Ax Bu
若A为对角型,且对角线上的元素均不相同, 则状态完全能控的充要条件为: B中没有任意一行的元素全为零.
x1 1 x1 b11u1b12u2 b1 pu p
x2 2 x2 b21u1b22u2 b2 pu p
例:线性系统的状态方程为 x Ax bu 其中: 1 0 b1 A b 0 2 b2
Ci C1i1 C1i2 C1ii
第三章能控性与能观性

(3-11) Ax Bu x 式中,x为n维状态向量,u为r维输入向量, A、B分别 为 n n、 n r 常数阵。 式(3-11)系统状态完全能控的充分必要条件是 能控性判别矩阵
Qc B AB A2 B An1 B
满秩,即
(3-12)
rankQc rankB AB A2 B An1 B n
24
rankQc rankB AB A2 B An1 B n
25
【例3-5】动态系统的状态方程如下,试判断其能 控性。
0 0 x a 0 1 0 a1 0 0 0 u 1 x a2 1
解
2
本章首先介绍能控性与能观测性的概念及定义, 在此基础上,介绍判别系统能控性与能观测性的准 则,及如何通过线性非奇异变换将能控系统和能观 测系统的状态空间表达式化为能控标准型与能观测 标准型。然后介绍能控性与能观测性之间的对偶关 系、能控性及能观测性与传递函数的关系,以及如 何对不能控和不能观测系统进行结构分解。再后, 讨论线性离散系统的能控性与能观测性问题。本章 最后介绍MATLAB在系统能控性与能观测性分析中 的应用。
13
2.系统能观测 对于式(3-10)所示线性时变连续系统,如果指 t f > t0 , 定初始时刻t0 Td ,存在一个有限时刻 t f Td , t [t 0 , t f ] 对于所有 ,系统的输出 y(t)能惟一确定 t 0 时 t0 时 x0 刻的任意非零的初始状态向量 ,则称系统在 刻状态是完全能观测,简称系统能观测。如果系统对 于任意 均是能观测的(即系统的能观测性与初 t0 Td t0 Td 始时刻 的选取无关),则称系统是一致完全能 观测。
线性系统理论第4章 线性系统的能控性和能观测性
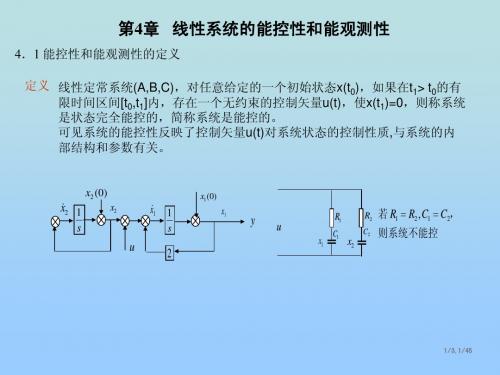
满秩,即rankQ o=n
结论5
n 维连续时间线性时不变系统完全能观测的充分必要条件为:
SI A rank n S C C
或
i I A 为系统特征值 rank n , 1 , 2 ,n C
Wc [0, t1 ] e At BBe A t dt
T
t1
0
为非奇异。
结论3:n 维连续时间线性时变系统 x A(t ) x B(t )u x(t 0 ) x0
设A(t),B(t)对t为n-1阶连续可微,定义
t, t0 J
M 0 (t ) B (t ) d M 0 (t ) dt d M 2 (t ) A(t ) M 1 (t ) M 1 (t ) dt d M n 1 (t ) A(t ) M n 2 (t ) M n 2 (t ) dt M 1 (t ) A(t ) M 0 (t )
6/8,9/45
1 L QC [b, Ab] 0
R3 R4 1 R1 R2 2 L R1 R2 R3 R4 1 R2 R4 LC R1 R2 R3 R4
线性系统理论4能控性和能观性

如果存在某个时刻 t1 t0,使得rankQ O (t1 ) n
t0 为不能观测的。
定义 4.1.6 对于线性时变系统
x A(t)x
, x(t0 ) x0 , t0 , t J
y C(t)x
如果状态空间中所有状态都是时刻 t0(t0 J )
的能观测状态,则称系统在时刻 t0 是完全能
观测的。如果对于任何 t0 [T1,T2] 系统均是在
t0 时刻为能观测的,则称系统在 [T1,T2 ]
在 t0 , t1 上行线性独立,即对任意 n
维非零向量 z 都有
zT (t1 , )B( ) 0, t0 t1
4.2.3 基于系统参数矩阵的判据
定理 4.2.3 假设系统
x A(t)x B(t)u, t J
中的 A(t) 和 B(t) 的每个元分别是 n 2和
n 1 一次连续可微函数,记 B1(t) B(t)
那么它能控的充分必要条件是:
det b Ab An1b 0
4.3.3 PBH判据
定理4.3.2 定常线性系统
x Ax Bu, x(t0 ) x0 , t t0
能控的充分必要条件是,对每个 (A)
都有 rank A In B n 其中, ( A)
表示 A 的特征值集合。
推论 4.3.3 定常线性系统
2
dt
x0T T
(t1 , t0 )Wc1(t1 , t0 )(t1 , t0
)x0
4.2.2 基于状态转移矩阵的判据
定理 4.2.2 假设 A(t) 和 B(t) 都是 t
的连续函数矩阵,则系统
x A(t)x B(t)u, t J
在t0 时刻能控的充分必要条件是存在某
现代控制理论_第3章_能控性和能观测性

T
解 令0,1,2,得状态序列
2 1 x 1 x 0 gu 0 2 0 u 0 1 1
x2 k 1 2 x2 k u k
初始状态为:x1 0 1,x2 0 1 用递推法可解得状态序列:
k 0 k 1 k k 1, x1 k x1 k 1 1
k
x1 1 x1 0 1 x2 1 2 x2 0 u 0 2 u 0 x1 2 x1 1 1
故能控。
例3-3
设 、x 0
g 同例3-1, 1 2 1,试判断能控性。
T
1 1 1 2 S1 rank g g g rank 2 2 2 1 3 解 rank 1 1 1 故不能控。
关于研究单输入离散系统状态可控性的方法可推广到多输入系 统。设系统状态方程为:
rankS1 rank g g 2g n2g n1g n
(3-7)
(3-8)
使用该式判断能控性比较方便,不必进行求逆运算,式(3-5)至 S 式(3-8)均称为能控性判据。 1,S1均称为单输入离散系统能控性 矩阵,由该式显见状态能控性取决于系统矩阵 及输入矩阵g 。 当rank S1 n时,系统不可控,不存在能使任意x 0 转移到x n 0 的控制。
点 击 观 看
第一节
线性定常系统的能控性
能控性分为状态能控性、输出能控性(如不特别指明便泛指状 态能控性)。状态能控性问题只与状态方程有关,下面对定常 离散系统、定常连续系统分别进行研究(各自又包含单输入与 多输入两种情况):
现代控制理论-4-线性系统的能控性和能观测性-第7讲

能控性的定义
能控性是指对于一个线性系统,如果 存在一个控制输入,使得系统状态能 够在有限的时间内从任意初始状态转 移到任意目标状态,则称该系统为能 控的。
能控性的判断依据是系统的能控性矩 阵,如果该矩阵满秩,则系统能控。
能观测性的定义
能观测性是指对于一个线性系统,如果存在一个观测器,能够通过系统的输出测量并估计出系统的所有状态,则称该系统为 能观测的。
传递函数判据
对于线性时不变系统,如果传递 函数的零点和极点个数满足一定 条件,则系统能观测;否则系统 不能观测。
03
能控性和能观测性的应用
在控制系统设计中的应用
系统性能分析
通过分析系统的能控性和能观测性,可以评估系统的稳定 性和动态性能,从而优化系统设计。
控制器设计
在控制器设计中,需要考虑系统的能控性和能观测性,以 确保控制器能够有效地控制系统的状态并观测系统的状态。
初始状态和目标状态
系统初始和目标状态的定义,以及它们对最优控 制策略的影响。
最优控制问题的求解方法
动态规划
将最优控制问题分解为一系列子问题, 通过求解子问题的最优解逐步逼近原问
题的最优解。
极大值原理
通过求解极值条件来找到最优控制输 入,适用于具有特定性能指标的最优
控制问题。
线性二次调节器
通过最小化状态和控制输入的二次范 数来求解最优控制问题,适用于线性 二次最优控制问题。
现代控制理论-4-线性系统 的能控性和能观测性-第7讲
目录
• 线性系统的能控性和能观测性的 定义
• 能控性和能观测性的判定方法 • 能控性和能观测性的应用 • 线性系统的状态反馈和状态观测
器设计
目录
• 线性系统的最优控制问题 • 现代控制理论的发展趋势和前沿
现代控制理论线性控制系统的能控与能观性

判断线性控制系统稳定性的方法有多 种,如劳斯判据、赫尔维茨判据等。
03
能控性与能观性概念
能控性概念
能控性是指对于一个线性控制系统,如果存在一个控 制输入,使得状态变量从任意初始状态能够被驱动到
任意目标状态,则称该系统是能控的。
能控性的判断依据是系统的能控性矩阵,如果该矩阵 非奇异,则系统是能控的,否则系统不能控。
线性控制系统是控制系统的一种重要 类型,其能控性和能观性是评价系统 性能的重要指标。
研究意义
能控性和能观性是现代控制理论中的基本概念,对线性控制系统的分析和设计具有重要意义。
研究线性控制系统的能控性和能观性有助于深入了解系统的动态行为,为优化控制策略和控制系统的 稳定性提供理论支持。
02
线性控制系统基础
04
线性控制系统的能控性分析
能控性的判断方法
矩阵判据
通过判断线性系统的状态矩阵是否满足能控性矩阵的 条件,从而判断系统的能控性。
传递函数判据
根据线性系统的传递函数,通过分析其极点和零点, 判断系统的能控性。
状态方程判据
通过分析线性系统的状态方程,判断其是否具有能控 性。
能控性的改善方法
增加控制输入
能观性分析
能观性分析在智能交通系统中同样重要,它 有助于确定交通系统的状态是否能被其传感 器完全监测。这涉及到对传感器精度、道路 条件以及传感器布局等因素的考虑。
07
结论与展望
研究结论
1
线性控制系统能控性与能观性是现代控制理论中 的重要概念,对于系统的分析和设计具有重要意 义。
2
通过研究线性控制系统的能控性和能观性,可以 深入了解系统的动态特性和行为,为控制系统设 计和优化提供理论支持。
线性系统的能控性和能观性

3.约当规范型矩阵
若A是约当阵,且B阵中与每个约当块最后一行相对应 的行的元素不全为零,则系统可控。反之为零一行所 对应的状态不可控。
例.判断能控性
• 4 1. x 0
0 5
x1 x2
12u
7 0 0 2
•
2. x
0
5
0
x
0
0 0 3 7
1 1 0 4 2
3.
•
x
0
e3t
0
te3t
e3t
t
x(t) e At x(0) e A(t )Bu( )d
0
x1(t)
x2
(t
)
e3t
0
te3t e3t
x1(0)
x2
(0)
t 0
e 3(t
0
)
(t
)e3(t e3(t )
)
10u(
)d
t
x1(t) e3t x1(0) te3t x2 (0) (t )e3(t )u( )d
0
t
x2 (t) e3t x2 (0) e3(t )u( )d
0
t
y(t) x1(t) e3t x1(0) te3t x2 (0) (t )e3(t )u( )d
可见:1.两个状态变量中均有输入的作用,可0 控
2.输出中有两个状态变量的出现,输出可以反映初始状态,可测
例.如图所示,1、2表示蓄水池,u1、u2表示输入流量,R1、 R2液阻,H1、H2液面高度A1、A2截面积,问 (1)仅用一个调节阀,应放在何处? (2)仅用一个液位计,应放在何处?
Z (S ) U (S )
S
2.5 1
S2
1 1.5S
